Curvature effects in charge-regulated lipid bilayers

Abstract

We formulate a theory of electrostatic interactions in lipid bilayer membranes where both monolayer leaflets contain dissociable moieties that are subject to charge regulation. We specifically investigate the coupling between membrane curvature and charge regulation of a lipid bilayer vesicle using both the linear Debye–Hückel (DH) and the non-linear Poisson–Boltzmann (PB) theory. We find that charge regulation of an otherwise symmetric bilayer membrane can induce charge symmetry breaking, non-linear flexoelectricity and anomalous curvature dependence of free energy. The pH effects investigated go beyond the paradigm of electrostatic renormalization of the mechano-elastic properties of membranes.

---

1 Introduction

The effects of electrostatic interactions^1,2 on properties of lipid bilayer membranes are significant, ubiquitous and biologically³ and biomedically⁴ relevant, since naturally occurring as well as technologically relevant lipids usually carry numerous dissociable or polar groups,⁵ and lipid membrane charge density has been identified as a universal parameter that quantifies the transfection efficiency of lamellar cationic lipid–DNA complexes.⁴ The particular relevance of electrostatic interactions in lipidic systems very clearly transpired from the structural principles of the two vaccines approved against COVID-19 in December 2020 and based on the cationic lipid vesicle vector and the anionic mRNA payload developed by Pfizer/BioNTech⁶ and Moderna.⁷ In general, charged lipids capable of modulating their charge depending on the bathing environmental conditions, have been recognized as a key component of ionizable lipid nanoparticles which are currently acknowledged as one of the most advanced non-viral vectors for the efficient delivery of nucleic acids.⁸

While electrostatic interactions in bio-soft matter are universal,⁹ there is a fundamental difference between the standard colloid electrostatics and membrane electrostatics,¹⁰ in the sense that the membrane charge, just as the protein charge,^11–13 depends on the solution environment of the lipid¹⁴ and its changes can engender also changes in the shape of the lipids and concomitant structure of lipid assemblies. One example of this solution environment effect would be changes in protonation/deprotonation equilibria of the dissociable phospholipid moieties depending on the solution pH, that in general affect the charge of lipids' headgroup, and another would be the modification of the strength of electrostatic interactions wrought by the ionic strength of the bathing aqueous solution that affects the ionic screening. In particular, for therapeutic gene delivery¹⁵ ionizable lipids are designed to have positive charges at acidic pH in the production stage to ensure a strong interaction with nucleic acids, after which they should become almost neutral under physiological conditions (pH 7.4) to prevent sequestration in the liver, and should finally turn positive again upon being introduced into a typical acidic environment of the endosomes, promoting the delivery of the genetic cargo, followed finally by release of the genetic cargo at neutral pH enabling the cargo to interact with the cell machinery.⁸

To connect the dissociation equilibria of dissociable surface groups and electrostatic fields, Ninham and Parsegian (NP)¹⁶ introduced the charge regulation (CR) mechanism, that couples the Langmuir isotherm model of the local charge association/dissociation process with the local electrostatic potential,¹ resulting in an electrostatic self-consistent boundary condition. The NP model can be generalized to include other adsorption isotherms, depending on the detailed nature of the dissociation process.¹⁷

The protonation/deprotonation equilibria at the dissociable surface groups in phospholipid membranes involve local pH and local bathing solution ion concentrations, which in general differ from the bulk conditions.¹⁸ This implies that the changes in the bathing solution properties will have a pronounced effect on the effective charge of the membrane, thus modifying pHsensing and pHresponse of lipid membranes.¹⁹ In fact, pH-dependence of the lipid charging state can directly enable an ionizable lipid with a dissociation constant pK_a ∼ 6.5 to be neutral in the blood circulation, thus preserving a bilayer structure, and then revert to its charged protonated form at an endo-lysosomal pH, consequently reverting to an hexagonal phase upon contact with anionic membrane lipids.²⁰

In what follows we will show that even in the case of a chemically symmetric curved membrane, i.e. with the same lipid composition on the inner and outer leaflets, the CR process introduces a charge asymmetry and an out-of-plane membrane polarization vector in a highly non-linear fashion, characterized by a sudden symmetry breaking transition involving in all other respects chemically identical outer and inner leaflet surfaces of the membrane. This phenomenology closely parallels the recently discovered symmetry breaking charge transitions in interactions between pairs²¹ or stacks²² of charged membranes as well as the complex coacervation driven by the charge symmetry broken states in solutions of macroions with dissociable surface moieties.²³

Charged lipids

Different naturally occurring charged lipid species, an important fraction of which is anionic,²⁴ represent a notable part of biological membranes, and consequently their role in the structural, dynamical and mechanical properties of model lipid bilayers as well as their effect on the membrane proteins is of great biological interest.²⁵ The less commonly occurring cationic lipids, on the other hand, have played an important role as the main charged component of the cationic liposome vectors for nucleic acid therapeutics.¹⁵

The charge of phospholipid polar heads originates in deprotonated phosphate groups, protonated amine group, and deprotonated carboxylate group, with the corresponding dissociation constants expected to lie in the region of 0 ≤ pK_a ≤ 2 for the primary phosphate group, in the region 6 ≤ pK_a ≤ 7 for the secondary phosphate group, in the region 3 ≤ pK_a ≤ 5 for the carboxylate groups, and 9 ≤ pK_a ≤ 11 for the primary amine group.²⁶ Since in the subsequent analysis the effect of the electrostatic interactions – including the local polarity, the ionic strength and the distribution of neighboring dissociable groups – will be considered explicitly, we consider only the intrinsic pK_a, noting that even in the absence of CR certain structural and continuum electrostatic effects are sometimes included in the calculation of the dissociation constants when determined by e.g. PROPKA.²⁷

Of the different phospholipids, phosphatidylcholines have very low pK_a and can be considered as undissociated, but in particular phosphatidylserine, phosphatidylinositol, as well as phosphatidylglycerol, phosphatidylethanolamine, cardiolipin and phosphatidic acid all contain at least one dissociable moiety at relevant pH conditions and should be considered as potentially charged.²⁸ Among the cationic lipids DOTAP (1,2-dioleoyl-3-trimethylammonium-propane) remains charged irrespective of pH, while the amine groups of other cationic lipids acquire their charge by protonation only below a certain pH.²⁹ As an extreme case one could mention the custom-synthesized cationic lipid MVLBG2 with a headgroup that bears no less than 16 positive charges at full protonation.⁴ In ionizable lipids the quaternary ammonium head of cationic lipids can be in addition substituted with a titratable molecular moiety with an engineered dissociation constant that would ensure the charge would be mouldable by the environmental pH.⁸ Among the ionizable lipids that respond strongly to pH in the relevant range one can list DODAP (1,2-dioleoyl-3-dimethylammonium propane), DLinDMA, DLin-KC2-DMA and finally DLin-MC3-DMA, all of them used for proper lipid vector formation in cytosolic delivery of therapeutic cargo as reviewed recently in ref. 8.

Protonation and pH effects

Detection and response of the cells to either global pH environment or local pH gradients is crucial for optimal cellular metabolism, growth and proliferation.³⁰ The sensing of pH heterogeneities is important for initiating migration, polarization and deformations of lipid bilayer assemblies¹⁹ and can be driven by protonation changes of phospholipids that can furthermore directly affect the membrane curvature.³¹ In fact pH regulation of phospholipid charges have been implicated in pH-induced migration, pH-induced bilayer local or global deformation, as well as pH-induced vesicle chemical polarization.¹⁹ The fact that the charge state of many phospholipids depends on the solution pH implicates by and large a charge regulation mechanism as indeed first proposed for surfaces containing dissociable groups by Ninham and Parsegian.¹⁶

In addition, the phospholipid protonation state and the membrane charge distribution can modify the interaction energy with a protein on approach to the membrane.³² This effect too is due to perturbed protonation equilibrium at the membrane titratable sites, with phospholipid charge regulation determining the strength and even the sign of the protein-membrane interaction in variable chemical environments.³³ Charge regulation can thus be seen as a biological pH-sensitive switch for protein binding to phospholipid membranes and thus conferring signaling functions to different types of lipids.³⁴

Curvature and lipid dissociation effects

Global and local changes in pH, inducing changes in the charged states of lipids, can affect lipid vesicle shape deformations as well as phase-separated domain formation.¹⁹ Usually these effects are framed within the electrostatic contribution to the mechano-elastic properties of membranes, such as surface tension and bending rigidity, which have been reviewed in detail, see e.g. ref. 24, 35 and 36. Electrostatic coupling of membrane charges leads to a salt concentration dependent increase in the bending rigidity of the charged membrane compared to a charge-free membrane.³⁷ Usually the details of lipid dissociation mechanism are not considered in these works and analyses going beyond the fixed charge assumption, incorporating direct lipid charge dissociation models, are less common but have been nevertheless invoked when modelling the flexoelectric properties of membranes.³⁸ In fact Langmuir adsorption isotherm was used to estimate the change in the surface density of counterions on the inner and outer leaflet surface of the phospholipid membrane induced by the coupling between curvature and electrostatics.³⁹

In what follows we will present a detailed analysis of the charge regulation effects in a system, see Fig. 1, comprised of a single spherical unilamellar lipid vesicle of a fixed phospholipid membrane thickness w ≃ 4 nm, dielectric constant ε_p ≃ 5 and a variable inner radius R, immersed in a simple univalent aqueous electrolyte solution, of dielectric constant ε_w ≃ 80. We will use the full Poisson–Boltzmann (PB) theory to evaluate the electrostatic part of the free energy, as well as the often invoked and easier to implement linearized Debye–Hückel (DH) theory in the second order curvature expansion approximation. This will allow us to ascertain which effects are non-linear in nature as far as electrostatics is concerned. We will show that charge regulation of an otherwise symmetric bilayer membrane induces three important phenomena: charge symmetry breaking, non-linear flexoelectricity and anomalous curvature dependence of free energy and that in general the pH effects go beyond the paradigm of electrostatic renormalization of the mechano-elastic properties of membranes.

Fig. 1 Left: A schematic rendition of a spherical charged vesicle of inner and outer radii R and R + w, respectively, immersed in a salt solution. The inner (outer) surfaces of the bilayer carry ionizable groups and are characterized by a charge density σ₁ (σ₂). The lipid bilayer (indicated in gray) of width w and dielectric constant ε_p ≃ 5 separates the interior of the shell from the outer region, both of which are typically aqueous phases characterized by a dielectric constant ε_w ≃ 80. All the ionic species in both regions are assumed to be in chemical equilibrium defined by the bulk chemical potentials. Both the inner and outer surfaces of the bilayer carry fixed numbers of negatively charged surface groups (denoted in red) as well as neutral sites where (de)protonation reactions (indicated by the arrows) can take place leading to surface charge densities σ₁ and σ₂. Center and right: the color-coded electrostatic potential profile for the symmetric case, corresponding to σ₁ = σ₂ = 0.5 e nm⁻² and for the asymmetric case with σ₁ = −σ₂ = 0.5 e nm⁻² obtained from the charge regulation calculation as explained in the main text. For both cases, R = 20 nm, w = 1 nm, and κ_D = 1.22 nm⁻¹ are used.

The outline of the paper is as follows: In Section 2, we describe the details of the charge regulation model and formalism for this study. Section 3 is devoted for the results of the study. Finally, the discussion of the results of the curvature effects in charge-regulated lipid bilayers is given in Section 4.

2 Model and formalism

2.1 Model

The description of charge regulation is model specific and there is no universal model that would be applicable to any situation encountered in biophysical systems. We base our model on the preponderance of three different types of interactions that can be deemed as important in the context of ionizable lipids: (i) electrostatic interactions, (ii) non-electrostatic adsorption interactions and (iii) adsorption site entropy.

We consider a charged spherical vesicle with a salt solution on the two sides of its bilayer membrane as shown in Fig. 1. The inner and the outer radii of the charged shell are given by R₁ = R and R₂ = R + w, respectively. While the model considers a globally curved vesicle, it nevertheless provides also some insight into the local curvature deformations which are formally much less accessible to detailed calculations. The connection is analogous to the global and local curvature effects in stiff polyelectrolytes such as DNA.⁴⁰

The lipid bilayer is composed of two charge-regulated monolayers with charge densities σ_1,2. These charge densities stem from (de)protonation reactions or dissociation/adsorption of mobile charges taking place at chargeable sites present in each monolayer. We assume that n_1,2 is the number of negative lipid heads per surface area and Θn_1,2 is the number of neutral lipid heads per surface area of the inner and outer monolayers, respectively. The phospholipid bilayers are assumed to be incompressible (see ref. 37 and references therein) so that

where R₀ is the radius of the neutral plane, R_i = R₀ ± w/2, while − and + occur for i = 1 and 2, and n₀ is the dissociable lipid density at the neutral plane. To the lowest order in mean curvature and thickness of the bilayer w, this can be expanded to obtain

Furthermore, η_1,2 are the fractions of the neutral lipid heads where the adsorption/desorption of cations can take place on the inner and outer monolayers, respectively. By definition, η_1,2 ∈ [0,1]. e is the elementary charge (e > 0). Note that here we have modified the model discussed in ref. 21. The connection between lipid density, charge density and adsorbed fraction is as follows:

σ_i = −n_ie + Θn_ieη_i. (1)

In our model, σ_1,2 and η_1,2 are assumed to be uniform over the two constituting monolayers of the membrane, and we specifically consider the case Θ = 2 for simplicity. This assumption reduces eqn (1) to

with −en_1,2 ≤ σ_1,2 ≤ en_1,2, implying that the charge of the membrane can change sign as a consequence of a mixture and different levels of dissociation of anionic and cationic lipid components as well as membrane embedded proteins, in general. Other choices of Θ are of course also possible depending on the exact composition of the bilayer and the pertaining dissociation constants. This does not, however, impact the qualitative features of our results. The Debye screening length (λ_D) varies from about 0.34 nm to 10.75 nm corresponding to the monovalent salt concentration ranging from 1–0.001 M.⁴¹

Charge regulation can be quantified either through the chemical equilibrium of dissociable sites at the bounding surface or through the surface free energy if the interactions between the solution charges and the surface is characterized by short-range ion-specific interactions.¹⁷ The latter seems more appropriate within the context of mean-field electrostatics.

In general, charge regulation is related to any non-trivial, i.e. non-zero, form of the surface free energy describing different models of surface-ion solution interactions.¹⁰ The single site dissociation model can be related to van’t Hoff adsorption isotherm, Langmuir (Henderson–Hasselbalch) adsorption isotherm, Frumkin–Fowler–Guggenheim adsorption isotherm and others.¹⁷ Following the analysis of charged surfactant systems⁴² we base our phospholipid charge regulation model on the Frumkin–Fowler–Guggenheim isotherm⁴³ defined with the phenomenological free energy of adsorption sites at surface density n in the units of thermal energy k_BT = 1/β as

where the integral is over the surface with dissociable groups and ρ is the radius vector on this surface. For a spherical surface of radius R, |ρ| = R. The dimensionless parameters α and χ, both expressed in thermal units in the above definition, are phenomenological and describe the non-electrostatic parts of the adsorption energy and of the surface lateral Flory interaction strength, respectively. A more general, non-local version of the latter would contribute a term,to the free energy, which, however, we will not pursue in what follows, limiting ourselves to the simplified Frumkin–Fowler–Guggenheim isotherm of eqn (3). In polymer solution theory and regular solution theory χ is referred to as the Flory–Huggins interaction parameter while in the context of the Frumkin–Fowler–Guggenheim isotherm it is referred to as the Flory lateral interaction strength.⁴³

The dependence of the adsorption energy α on the bulk concentration of the dissociation product (e.g., p = protons, ions) is model specific,¹⁴ but can be written as a sum of

α = Δg + μ = Δg + k_BT ln a_p (5)

where Δg is the dissociation free energy difference, while the chemical potential μ = k_BT ln a_p of the dissociation product is expressed through the absolute activity, a_p, that contains also the excess part dependent on the contribution of electrostatic interactions, see ref. 44. On the mean-field PB level the chemical potential is given by the ideal gas form, which does not take into account the electrostatic interactions, with the activity proportional to the concentration. Therefore in this case

α = k_BT ln K_a + k_BT ln[c⁺] (6)

with the equilibrium constant K_a, defined standardly as Δg = k_BT ln K_a. For protonation/deprotonation reactions corresponding to AH⁺ ⇌ A + H⁺ and AH ⇌ A⁻ + H⁺ we then have μ = k_BT ln[H⁺] and consequentlywhere now . In what follows we will use α to quantify the non-electrostatic surface interactions with the forms eqn (6) and (7) implied for the general ion dissociation and protonation/deprotonation, respectively.

Furthermore, χ, as in the related lattice regular solutions theories (e.g., the Flory–Huggins theory⁴⁵) describes the short-range interactions between nearest neighbor adsorption sites on the macroion surface.⁴⁶χ ≥0 represents the tendency of protonated/deprotonated lipid headgroups on the macroion surface adsorption sites to phase separate into domains. The microscopic source of this lipid demixing energy could be due to some mismatch of head-group–head-group interactions, such as hydrogen bonding between neutral lipids, water-structuring forces, or nonelectrostatic ion-mediated interactions between lipids across two apposed bilayers for small interlamellar separations, see also ref. 42.

Adding the electrostatic energy, as will be done in the next section, our model will therefore incorporate all three fundamental interactions: electrostatic interactions, non-electrostatic interactions between the lipids and the solution ions as well as non-electrostatic interactions between the adsorbed ions, and the adsorption site entropy.

2.2 Electrostatic free energy

We start with the standard Poisson–Boltzmann free energy, or the Debye–Hückel free energy in the linearized case, that depends on the charges and the curvature. There are various ways to write down the PB free energy¹ and we choose the field description, with the radially varying electrostatic potential ψ (r) as the only relevant variable. The total electrostatic free energy of our model system is thenwhere n_I is the univalent electrolyte concentration in the bulk, R₁ = R and R₂ = R + w, while the equilibrium value of ψ (r) is obtained from the corresponding Euler–Lagrange equation. The volume integral extends over all the regions except the bilayer interior. The electrostatic part of the thermodynamic potential can then be written with the help of the Casimir charging formula (for details see ref. 47) which allows one to write the full thermodynamic potential of the system in the form of a surface integralwhere i = 1,2 corresponds to inner/outer leaflets of the bilayer. In the above equation note the integral of the boundary potential over the surface charge densities, pertinent to the full non-linear PB theory. From here it also clearly follows thatwhich we will invoke in the mean-field form of the charge regulation boundary conditions to be introduced later.

A common approach to electrostatic effects in membranes is via the DH approximation together with small curvature, second order expansion.^24,35,36 In the DH approximation, valid specifically for βeψ(r) ≪ 1, the corresponding expressions for the electrostatic free energy eqn (8) simplifies considerably to

where the inverse square of the Debye screening length λ_D is given by

κ_D² = 2n_Iβe²/(ε_wε₀)

and the volume integral again extends over all the regions except the bilayer interior. Eqn (11) is then further reduced tosince the potentials are linear functions of the charge density and the integrals over surface charge densities in the Casimir formula can be evaluated explicitly. Within the phospholipid core of the bilayer the electrostatic energy is simplywhere the volume integral now extends over the bilayer interior. While the free energies eqn (8) and (11) imply the PB and the DH equation in the regions accessible to electrolyte ions,⁴⁸ respectively, eqn (13) leads to the standard Laplace equation inside the lipid dielectric core.

The explicit DH expression for a charged spherical dielectric shell electrostatic free energy as a function of the radius of curvature was obtained in an analytical form in ref. 49. This was expanded up to the inverse quadratic order in curvature in eqn (23) of ref. 41. This is the analytical formula that we use in the DH part of our calculations. The second order curvature expansion was standardly taken as a point of departure for the electrostatic renormalization of the mechanical properties of membranes, such as surface tension and bending rigidity.^50–54 The methodology of solving the non-linear PB theory is the same as used in our previous publications^21–23,48 and will not be reiterated again.

2.3 Charge regulation free energy

Assuming that the inner and outer membrane surfaces are chemically identical we presume that the surface charge regulation process can be described by the Frumkin–Fowler–Guggenheim adsorption isotherm, including the adsorption energy, the interaction energy between adsorbed species and the site entropy.

The corresponding free energy is then given by eqn (3) so that the charge regulation free energy density of the inner and outer membrane surfaces denoted by i = 1,2 read as

This can be furthermore normalized w.r.t. the inner area 4πR² which is used later. Formally, the first two terms in the free energy are enthalpic in origin, while the other terms are the mixing entropy of charged sites with the surface area fraction η and neutralized sites with the surface area fraction 1 − η. The phenomenological constants of course contain enthalpic as well as entropic contributions from other microscopic order parameters which are not considered explicitly.

As we already stated, the dissociation constants of anionic phospholipids such as PS, PE, or PA lie in the region of 0 ≤ pK_a ≤ 11,^26,28 while for cationic lipids such as DLin-KC2-DMA, DLin-MC3-DMA, DLin-DMA, DODMA, and DODAP the dissociation constants have been estimated to lie in the region of 5 ≤ pK_a ≤ 7.⁵⁵ Assuming the possible pH to be in the interval 1 ≤ pH ≤ 12, the corresponding adsorption energy parameter α would be within the interval −25 ≲ α = (pK_a − pH) ln 10 ≲ +25. The value of the Flory lateral interaction strength χ is less certain and we are aware of only one instance where it was estimated from experimental data for ion induced lamellar-lamellar phase transition in charge regulated surfactant systems, where it can be on the order of a few 10 in dimensionless units of eqn (14).⁴² These high values would be needed to overcome the electrostatic repulsion between similarly-charged lipids in this highly charged system. Without more detailed experimental input it thus seems reasonable to investigate the consequences of our theory for −30 ≤ α ≤ 30 and 0 ≤ χ ≤ 40.

It is important to reiterate at this point that other charge regulation models are of course possible¹⁷ and have been, apart from the protonation/deprotonation example, proposed for various dissociable groups in different contexts.¹⁰ Our reasoning in choosing the particular Frumkin–Fowler–Guggenheim isotherm was guided by its simplicity in the way it takes into account the salient features of the dissociation process on the membrane surface, and the fact that the implied phenomenology has been analyzed before in the context of charged soft matter systems.⁴²

2.4 The total free energy density, equilibrium charge configuration and flexoelectricity

Combining now the electrostatic free energy and the charge regulation free energy, we are led to the explicit form of the total free energy of our model system as

β[scr F, script letter F]_tot (n₁,n₂;η₁,η₂;R₁,R₂) = β[scr F, script letter F]_ES (n₁,n₂;η₁,η₂;R₁,R₂) + β[scr F, script letter F]_CR (n₁;η₁;R₁) + β[scr F, script letter F]_CR (n₂;η₂;R₂). (15)

In order to find the equilibrium state of the system, the total free energy eqn (15) then needs to be minimized with respect to the variables η_1,2. Introducing the dimensionless total free energy aswhere κ_D = λ_D⁻¹ is the inverse Debye screening length and [small script l]_B is the Bjerrum length, it can be derived that [scr F, script letter F] depends only on the dimensionless electrostatic potential u = β eψ, dimensional radial coordinate x = κ_Dr and dimensionless surface densityand thus

[scr F, script letter F] = [scr F, script letter F] (x₁,x₂,ñ₁,ñ₂;η₁,η₂). (18)

Instead of the x_1,2 = κ_DR_1,2 one can just as well introduce h ≡ 1/(κ_DR) and κ_Dw, assuming R₁ = R, R₂ = R + w, which is what we will do when plotting and analyzing the figures. The minimization of [scr F, script letter F] with respect to η₁,η₂, corresponding to thermodynamic equilibrium, then yields the degrees of dissociation on both membrane surfaces as a function of parameters x₁,x₂,ñ₁,ñ₂, i.e. the curvature and the surface density of the dissociable lipids.

As will become clear when we present the numerical results, for some values of these parameters the equilibrium can be characterized as a charge symmetry broken state, corresponding to η₁ ≠ η₂. In that case the two surfaces have different charge or can even become oppositely charged.

The existence of charge symmetry broken states of a curved membrane has important consequences, among which flexoelectricity deserves special attention.^38,56 Flexoelectricity is a general mechano-electric phenomenon in liquid crystal physics but has important consequences specifically in the context of lipid membranes as argued by Petrov and collaborators.^57,58 In the small deformation continuum limit regime, the induced flexoelectric polarization is proportional to the membrane curvature and a simple Langmuir isotherm based charge regulation model was invoked as a possible microscopic origin for the flexoelectric coefficient in the seminal work of Derzhansky and coworkers.³⁹ The magnitude of the out-of-plane flexoelectric surface polarization density p_S is defined as

p_S ∼ |σ₁ − σ₂|w, (19)

being proportional to the difference in the surface charge densities. In the linear theory the surface polarization density, as well as the difference in the two surface charge densities, are proportional to the curvature of the membrane,³⁸ but – as we will see – this is not generally the case for charge regulated membranes which would then present a case of soft non-linear flexoelectricity⁵⁹ or at least flexoelectricity with variable flexoelectric coefficient.

2.5 Charge regulation boundary condition

The thermodynamic equilibrium is now obtained by minimizing the free energy eqn (15). We get two equations that correspond to charge regulation boundary conditions for i = 1,2By taking into account eqn (2) and (10), as well as the form of the charge regulation free energy eqn (14) we then derive the dissociation isotherm aswhich can be solved for η_i = η_i (α, χ, ψ_i). From the above equation, combined with eqn (5) it follows that on the mean-field level electrostatic interactions directly renormalize the dissociation equilibrium constant pK_a ln 10 → pK_a ln 10 − 2β eψ. The above boundary condition corresponds to the Frumkin–Fowler–Guggenheim adsorption isotherm^17,43 which is often invoked as a model in charge regulation problems.^21,22,46,60 In terms of the surface charge density, eqn (2), the adsorption isotherm for protonation (+ charge, basic headgroups) and for deprotonation (− charge, acidic headgroups) can be obtained aswith i = 1,2 still standing for the inner and outer surface of the membrane, while e is positive/negative for basic/acidic headgroups. Obviously the charged/uncharged state of the protonized/deprotonized lipid headgroups corresponds to a different sign of α and χ.

The boundary condition derived above, together with the solution of either full PB equation or the linearized DH version for the electrostatic potential constitute the basic equations of our model the solutions of which we address next.

3 Results

For all the numerical evaluations presented herein, we have used typical system parameters such as the Bjerrum length [small script l]_B = 0.74 nm, the membrane thickness w = 4 nm, the dielectric constant of water ε_w = 80 and that of the lipid as ε_p = 5. For the dimensionless lipid density at the neutral plane, ñ₀, defined in eqn (17), we took a reasonable value which for an aqueous uni-univalent electrolyte solution of 140 mM salt concentration (inverse Debye length κ_D = 1.215 nm⁻¹, or equivalently, screening length λ_D = 0.823 nm), corresponds to n₀ = 1 nm⁻². With fixed ñ₀, because of the scaling relations, eqn (17), changing the screening length implies also changing the lipid density at the neutral plane, n₀.

In making sense of the numerical results we need to take due cognizance of the fact that our continuous electrostatic formulation remains valid only for radii of curvature much larger then the thickness of the membrane, R ≫ w. Because all of the distances are scaled by the Debye length this furthermore implies that once the screening length is chosen, the numerical results are consistent only for h × (κ_Dw) ≪ 1.

The two interaction parameters α and χ can be varied within relevant ranges, −30 ≤ α ≤ 30 and 0 ≤ χ ≤ 40 as argued before. In order to convert the dimensionless paramaters to physical ones, we note from eqn (7) that (pK_a − pH) = α/ln 10 and χ is given in thermal units. In addition, we also present the differences between the full non-linear PB theory and the linearized DH theory expanded to the second order in the curvature of the membrane. This comparison is important since the linearized DH theory expanded to second order in curvature is often used to quantify the electrostatic and curvature effects in membranes.⁶¹ Clearly both calculations exhibit similar qualitative features, but can be quantitatively quite different. We scan the parameter space in order to identify the important phenomena connected with charge regulation, which is our primary focus here, but do not specifically apply our model to any particular lipid membrane system.

From our previous works^21,22 on two CR surfaces interacting across an electrolyte solution we know that depending upon the values of the parameters α and χ the Frumkin–Fowler–Guggenheim adsorption isotherm can lead to a charge symmetry breaking transition, corresponding to unequal equilibrium charge of two surfaces. This happens as a result of a competition among the three major interactions present in the system: the adsorption energy of ions or protons onto the charge-regulated surfaces, interaction of neighboring protonated sites on the surface and the electrostatic interaction between two charge-regulated surfaces. While the last one is at play only for a pair of surfaces, the former two are relevant even for a single CR surface and it can be shown that they lead to equally deep minima of the grand potential for charge densities differing in magnitude as well as in sign for each CR surface in the absence of the other. A pair of interacting surfaces then automatically adopts an asymmetric charge distribution owing to an electrostatic-attraction-mediated reduction of the system energy. The charge asymmetry was found to be highest around the line χ = −2α and the charge symmetry broken region persisted also in the neighborhood of this line in the earlier works.^21,22 The present case, describing a dielectric layer sandwiched between electrolyte layers, differs from the model of ref. 21, pertinent to an electrolyte layer sandwiched between dielectric layers in the sense that the region between the two charged phospholipid leaflets is a dielectric, impermeable to electrolyte ions, while the electrolyte solution fills the rest of the space. The salient features of the charging behavior thus display a rather different behavior.

In fact while in our system we still find a symmetry breaking transition in the charging fractions, η_1,2, the symmetry broken charge region and the symmetric charge regions occupy switched places in the (α, χ) “phase diagram” if compared to the case of ref. 21; the line χ = −2α and its neighborhood thus corresponds to the symmetric charge region, while the rest of the “phase diagram” is symmetry broken. In addition, the extent of the symmetric region also depends on the curvature of the membrane, h, in such a way that the larger the curvature the larger is the extent of the charge symmetry broken region. This trend starts already at very small values of curvature. We now elucidate these statements in all the relevant detail.

We note that the parameters relevant for the plots are the dimensionless dissociation energy α, the dimensionless lateral pair interaction energy of occupied neighboring sites χ, and the dimensionless curvature h, see Table 1 for definitions. As already stated, when converting from dimensionless to physical quantities, once the screening length is chosen, one can only consider numerical results for h × (κ_Dw) ≪ 1.

Table 1 Different variables and their meanings. α and χ are dimensionless energies expressed in the units of the thermal energy and are of non-electrostatic origins

Symbol	Definition
n 1,2	Density of lipid headgroups
η 1,2	Fractions of charged lipids; 0 ≤ η1,2 ≤ 1
e	Elementary charge (e > 0)
σ 1,2	Charge densities of the two monolayers;
R 1,2	Radius of the monolayers; R1,2 = R, R + w
w	Width of the bilayer; w = R2 − R1
α	(De)protonation energy; α = (pKa − pH)ln 10
χ	Lateral pair interaction energy of occupied neighboring sites
ε w,p	Dielectric constants of water or lipid
β	Inverse thermal energy; β = 1/(kBT)
λ D	Debye screening length; λD^2 = εwε0/(2nIβe^2)
κ D	Inverse Debye length; κD = 1/λD
[small script l] B	Bjerrum length; [small script l]B = βe^2/(4πεwε0)
h	Dimensionless curvature; h = 1/(κDR)
n I	Bulk ionic strength
ψ	Mean-field electrostatic potential

---

The two charge fractions η_1,2 as a function of α are displayed for different χ and a fixed membrane curvature h in Fig. 2. Clearly, for χ = 20 even at the small curvature h = 0.02 (corresponding to R = 41.15 nm), both the PB and DH results show a pronounced charge asymmetry, which becomes even more prominent for higher values of h, see Fig. 3 for details. This charge asymmetry corresponds to the charge symmetry breaking in the bilayer. In addition, the charge fractions are not only different but can exhibit a discontinuous transition as a function of α. For χ = 20 only the PB results show this transition for η₂, whereas the DH results do not; for χ = 35 the PB results show a discontinuity for both η₁ and η₂, while the DH results show a discontinuity only for η₂ in the charge state of the lipids. As the curvature is increased the system remains in a charge symmetry broken state between the outer and inner leaflets of the membrane. We therefore conclude that for a spherical vesicle with finite, even if small, curvature the charge regulation standardly leads to a charge symmetry broken state. As a result the values for the charge fractions of the inner and the outer membrane layer differ even if the two leaflets of the lipid membrane are chemically identical. In addition, depending on the values of the charge regulation model parameters and curvature, the dependence of η_1,2 on either α or χ can be continuous or discontinuous.

Fig. 2 The fraction η_1,2 of neutral lipid heads that are charged as function of the dimensionless adsorption/dissociation energy α at two different values of the strength χ of in-plane interaction between charged lipid heads for the dimensionless curvature h = 0.02. Both α and χ are expressed in the units of the thermal energy k_BT. As one can infer from the plots, the discontinuous transition in at least on of the η_1,2 starts to show up at a smaller χ-value within PB theory compared to that within the DH theory. In addition, the results also show symmetry-broken states (η₁ ≠ η₂) for χ = 20 within the PB theory and for both choices of the χ-parameter within the DH theory.

Fig. 3 The variation of the absolute value of the difference of the charge densities at the two surfaces of the bilayer, |σ₁ − σ₂|, expressed in the units of e nm⁻², as function of α and χ for four different choices of the curvature h = 0.1,0.5,1.0,2.0 obtained within the DH theory (left panels) as well as within the PB theory (right panels). The white regions in each plot correspond to symmetric states with σ₁ = σ₂ whereas the colored regions correspond to asymmetric states with σ₁ ≠ σ₂.

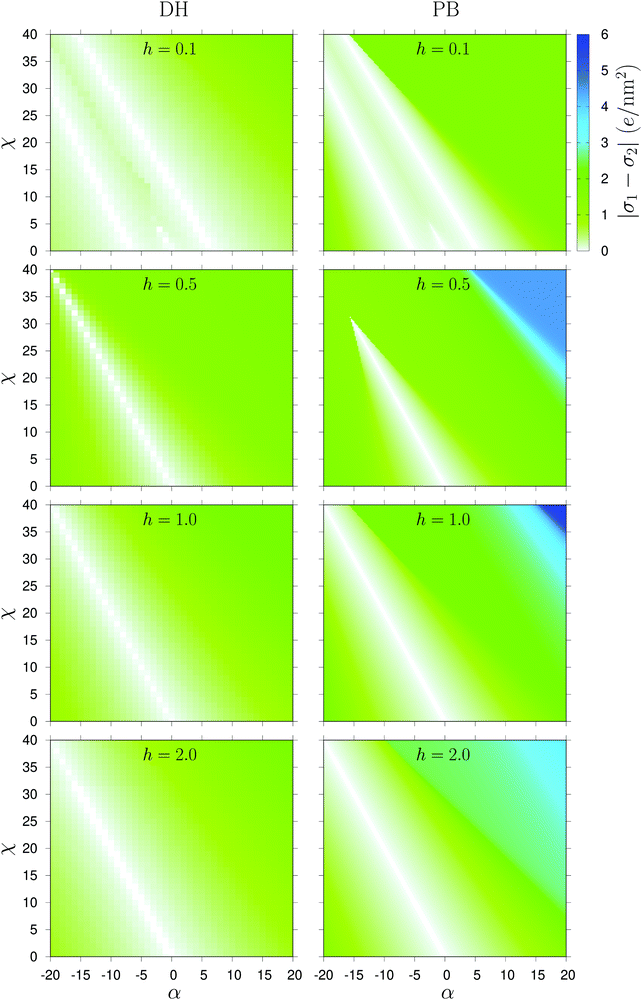
In order to be able to analyze the dependence of the charge densities σ₁,σ₂ of the two membrane leaflets on the charge regulation parameters, we present a phase diagram in Fig. 3 that shows the variation of |σ₁ − σ₂| as a function of α ∈ [−20,20] and χ ∈ [0,40] for h = 0.1,0.5,1.0, and 2.0. The (white) regions, corresponding to charge symmetric states of the two leaflets, are clearly discerned and their location and extent depends on α and χ, as well as on the bilayer curvature h, which obviously has a profound effect on the charge state of the bilayer, i.e. on the value of |σ₁ − σ₂|. We reiterate that in the previous work^21,22 the symmetry broken region was centered on the line χ = −2α, while in the present case it is the symmetric state which is centered on that line, while the rest of the phase diagram corresponds to a symmetry broken state.

In addition, for h = 0.1, we actually see not one but three regions of charge symmetric states, corresponding to σ₁ = σ₂ (indicated by white color in Fig. 3, almost coinciding for both non-linear PB and linear DH calculations. From the phase diagram it is difficult to see what the three symmetric branches correspond to, but we will later show that they correspond to the change in sign of the charge density difference, σ₁ − σ₂. Among the regions with charge symmetry, the one centered on χ = −2α (the middle region) passes through almost the same range of α for both calculations. At h = 0.5, the line χ = −2α fully passes through the range α ∈ [−20,0] in the DH theory, while in the PB theory, the line is terminated at α ≈ −16. Further increasing the dimensionless curvature to 1.0 and beyond, the line is terminated at α = −20 for both theories. The more pronounced asymmetric states in Fig. 3 of the PB case extend over a broader region than for the DH case at h = 0.1 and 0.5. With increasing h up to 1.0 and higher, the phase diagram shows clearly that only the PB case can exhibit the highest asymmetry (represented by dark blue color, while the DH solution remains broadly less asymmetric. Also the PB theory exhibits a wider range of |σ₁ − σ₂| values than the DH solution.

We now turn our attention to the details of the curvature dependence of the charge state of the membrane. At the beginning a caveat is in order: smaller values of the curvature are only accessible in the DH approximation, whereas the solution of the full PB theory take unreasonably long time because the system size has to be increases concurrently with the decrease in curvature. It is for this reason that the curvature dependence in the PB theory is truncated at finite values of curvature.

The curvature dependence of the difference between the inner and outer charge density, σ₁ − σ₂, for negative and positive values of α is fully displayed in Fig. 4 and 5, respectively. Obviously this dependence is fundamentally non-monotonic, including the changes of sign. For negative values of α, see Fig. 4, the difference σ₁ − σ₂ is a non-monotonic function of the curvature exhibiting regions of unbroken charge symmetry, corresponding to σ₁ = σ₂, as well as regions of broken charge symmetry with σ₁≠ σ₂, with the difference between the two surface charge densities varying from positive values to negative values on increasing the curvature. In fact this behavior can be seen clearly also in Fig. 3 where it corresponds to a curvature cut through the three lines of charge symmetry for a fixed (α, χ) combination in the phase diagram. Clearly for a sufficiently negative α, e.g. for (α, χ) combination (−20,5), the difference between the inner and outer charge density, σ₁ − σ₂ ceases to change sign within both the theories, but their non-monotonic behavior is still retained. The two thus represent separate features of the charging state of the curved bilayer. The behavior for the positive values of α, see Fig. 5, differs significantly. For a variety of (α, χ) cuts through the phase diagram we detect here no changes in sign for the difference between the inner and outer charge density, but we do see remarkable non-monotonicity in its dependence on curvature with very clear-cut differences between the PB and DH results. Nevertheless, σ₁ − σ₂ seems to increase for small curvature, reaching a local maximum, then dropping and increasing again but less steeply for larger curvatures. As for the range of curvatures that we display on Fig. 5, one also needs to consider the inherent limitations of the continuum assumptions which form the basis of the present calculations and the curvature should not be extended to arbitrary large values.

Fig. 4 Variations of the differences in the charge densities, σ₁ − σ₂, expressed in the units of e nm⁻², as function of the curvature h for different combinations of the α and the χ parameters with α being always negative (corresponding to a favorable adsorption free energy for the protons onto the vesicle surfaces). Within both the theories (DH theory in the upper panel and PB theory in the lower panel) the results are qualitatively the same, i.e. for α and χ satisfying the relation χ = −2α, the charge density difference σ₁ − σ₂ shows a discontinuous transition from a finite non-zero value to zero as the curvature h is increased. However, for other combinations of the α and χ parameters, the charge density difference σ₁ − σ₂ do not show any such discontinuous transition.

Fig. 5 Variations of the differences in the charge densities, σ₁ − σ₂, expressed in the units of e nm⁻², as function of the curvature h for different combinations of the α and the χ parameters with α being always positive. Within both the theories (DH theory in the upper panel and PB theory in the lower panel), one observes a similar trend, i.e. the charge density difference σ₁ − σ₂ increases initially to reach a maximum, then goes down and increases again following a minimum. Within the range of h considered here, the results obtained within the DH theory shows the occurrence of a second maximum as well.

The curvature dependence of the difference in surface charge density between the inner and outer leaflet, σ₁ − σ₂, implies the existence of a dipolar moment in the direction of the normal of the bilayer, see eqn (19), and therefore also the existence of flexoelectricity, but with a variable magnitude and sign of the flexoelectric coefficient. Clearly, the region of a simple proportionality between the bilayer polarization and curvature is limited and depends crucially on the charge regulation parameters.

For α > 0, Fig. 5, the difference σ₁ − σ₂ does not in general change sign, but remains nevertheless non-monotonic so that the system remains in a broken charge symmetry state for all indicated values of the charge regulation parameters α and χ. The calculations seem to indicate two separate regions of approximately linear flexoelectricity, but with flexoelectric coefficients of different magnitude: one at small curvatures (below h ≃ 0.5 for PB calculations and h ≃ 0.1 for DH calculations) and another one at larger curvatures (above h ≃ 0.75 for PB calculations and h ≃ 0.2 for DH calculations), until finally σ₁ − σ₂ varies only weakly with curvature.

For α ≪ 0, Fig. 4, the situation seems more complicated and also the differences between the PB and DH calculations more evident. There appears a linear flexoelectric regime at very small curvatures that changes sign for larger curvatures (evident for e.g. α, χ = −20, 5 or −10, 10 case for PB and DH calculations, Fig. 4). As χ is increased the linear flexoelectric regime for small curvatures is eventually cut short for large enough curvatures and the system fully restores its charge symmetry with vanishing flexoelectricity (evident for e.g. α, χ = −15, 30 case for PB and DH calculations, Fig. 4). Since the PB calculation cannot probe the regime of very small curvature because of numerical problems we can rely only on the DH results that show a vanishing flexoelectricity also for very small curvatures at not too large α < 0 and χ > 0. The non-linear features of flexoelectricity just described are pertinent to the charge regulation model which takes into account certain salient features of the phospholipid protonation/deprotonation or other charge dissociation reactions at the membrane-electrolyte solution boundary. They do not appear in fixed charge models of membrane electrostatics. Furthermore it is clear that the property of flexoelectricity depends crucially on the membrane dissociation properties as well as the solution conditions, and is thus far from being a universal property of the membrane composition.

We finally examine the hypothesis that the electrostatic effects in membrane can be reduced to a renormalized spontaneous curvature and renormalized bending rigidity, standardly invoked in the context of electrostatic interactions in phospholipid membranes.^35,37,41 In Fig. 6 we plot the curvature dependence of the equilibrium electrostatic surface free energy density as obtained from the linearized DH or fully non-linear PB theory. If indeed the electrostatic effects could be reduced solely to renormalized values of the bending rigidity and spontaneous curvature, then the curvature dependence of the equilibrium electrostatic surface free energy density should show a parabolic dependence centered at the spontaneous curvature. What we observe in Fig. 6 corroborates this expectations but only for positive values of α. In general, and in particular for negative values of α, however, the curvature dependence exhibits a behavior quite different from these expectations. In this case one observes, see Fig. 6, multiple curvature minima and in some cases a vanishing value of the electrostatic free energy as both surfaces become completely neutralized. The paradigm of renormalized spontaneous curvature and renormalized bending rigidity has thus only a limited validity and its range of applicability depends again crucially on the phospholipid dissociation properties and solution conditions. The membrane composition, affecting the two charge regulation parameters, indeed plays a role in the curvature properties but so do the bathing solution conditions that collectively determine the nature and magnitude of electrostatic effects.

Fig. 6 Variations of the electrostatic part of the free energy per unit inner surface area 4π R², expressed in the units of k_BT nm⁻², as function of the curvature h for different α and χ values. For a given (α, χ) parameter combination, the results obtained within the linearized PB or DH theory are plotted using red dashed lines whereas those obtained using the nonlinear PB theory are plotted using solid blue lines. Contrary to the widely used approximation, does not in general show a h²-dependence. While it does mostly vary ∝ h² or for α > 0, the situation is richer for α < 0 involving the presence of multiple minima and even vanishing contribution corresponding to charge-neutral surfaces for sufficiently large curvature values.

4 Discussion

There are of course a plethora of works based on molecular and coarse grained simulations of lipid bilayers and their interactions^62–65 but none of these studies exhaustively explored the contribution of electrostatic interactions to the charge states of dissociable lipid headgroups.⁸ Even in the most accurate parametrization of the lipid molecular force fields that take into account the dissociation state of the lipid headgroup through the partial charges, the charge regulation, i.e. the dependence of the dissociation state on the local bathing solution conditions, is usually not considered.⁶⁶ To include the effects discussed in our paper one would need to implement the charge dissociation reactions explicitly into the simulation scheme along the lines of recent advances in the simulation techniques for reaction ensembles.^44,67 Inclusion of the explicit charge regulation model into the detailed mean-field electrostatic theory applied to a curved phospholipid bilayer membrane allowed us to uncover and analyse several effects that have heretofore remained outside the paradigm of electrostatic renormalization of the membrane mechanical properties.³⁷

The first effect depending on the detailed charge regulation mechanism is the charge symmetry breaking, leading to unequal charges of the inner and outer phospholipid membrane surface even if – and this is important – they be chemically identical, i.e. described by the same free energy parameters. This effect was first observed in the case of membranes interacting across an electrolyte solution,^21,22 however, the charge symmetry breaking for a curved bilayer differs from this case since the two charged surfaces in a membrane interact across a simple dielectric, and charge symmetry breaking is in some sense inverse to the case of interacting membranes. In the most drastic case the charge symmetry broken state can be characterized by one of the monolayers near neutral and only one charged (see the case corresponding to χ = 20 and α ≈ −9 in Fig. 2, for example).

The second important effect is the existence of non-linear flexoelectricity,⁵⁹ with flexoelectricity itself being well known and even explained by a type of charge regulation mechanism for membranes.³⁹ While sophisticated electrostatic models have been formulated for flexoelectricity analysis,⁶⁸ more detailed charge regulation description and full mean-field electrostatic theory indicate that the flexoelectric constitutive relation is in general not linear and in addition its form depends crucially on the charge regulation parameters. Only certain intervals of dissociation parameters would correspond coarsely to a linear flexoelectric constitutive relation, with dipolar moment proportional to the curvature.⁶⁸ In general, however, the proportionality is non-linear or there might actually be no flexoelectricity for sufficiently large curvatures.

The last important modification in our analysis of the charge regulation effects is the dependence of the free energy on the curvature. As stated before, the prevailing paradigm is to see the electrostatic effects as commonly renormalizing the elasto-mechanical properties of the membrane, such as surface tension, curvature and bending rigidity (for a recent description see ref. 37). Our results indicate that this is not the complete story and that the free energy of a charge-regulated phospholipid membrane exhibits a much richer variety of curvature dependence. Only for a limited interval of the phospholipid dissociation parameters does one indeed observe a clear quadratic dependence on curvature that would be consistent with the electrostatic renormalization of the membrane elasto-mechanics.

The bilayer membrane asymmetry need not necessarily involve the obviously asymmetric protein distribution in biological membranes. It can also exhibit differences in lipid composition between the two leaflets⁶⁹ or be a consequence of different solution conditions across the separating membrane.⁷⁰ Based on our calculations we can state that even without any compositional asymmetry, or any solution asymmetry, the phospholipid dissociation coupled to electrostatic interactions and curvature would itself contribute an essential charge asymmetry to the otherwise completely symmetric membrane properties.

Experimentally, the very same model that we used above to describe the charge regulated membrane electrostatics was used to elucidate the liquid–liquid (L_α → L_α′) phase transition observed in osmotic pressure measurements of certain charged amphiphilic membranes.⁴² The phenomenon of charge symmetry breaking, that can induce attractions between chemically identical membranes, was argued to induce an attractive disjoining pressure in plant thylakoid membranes and photosynthetic membranes of a family of cyanobacteria.²² We are thus confident that the charge regulation effects coupled to membrane curvature are real and could be detected in solutions of varying acidity and salt activity. While there is no lack in experiments probing the effects of pH on membrane properties of giant unilamellar vesicle such as a pH change induced vesicle migration and global deformation,⁷¹ vesicle polarization coupled to phase-separated membrane domains⁷² and the effect of localized pH heterogeneities on membrane deformations,⁷³ a systematic quantitative comparison between expected pH-induced effects and observed membrane response is lacking. One of the reasons for this is that the pH-curvature coupling is complicated and non-linear, as we argued and demonstrated above. The phenomenology of this coupling presented in this work should help to elucidate the details of the pH effects and the role played by the dissociation mechanism in phospholipid membranes.

While the measured effective rigidity of lipid membranes seem to corroborate the paradigm of electrostatic renormalization of elasto-mechanical properties of membranes,³⁷ the experimental work of Angelova and collaborators, quantifying the effects of pH changes on lipid membrane deformations, polarization and migration of lipid bilayer assemblies seem to present a more complicated picture.^19,71,72 They demonstrated that a global or a local pH change can induce localized deformations of the membrane as well as the whole vesicle, polarization in membranes with phase separated lipid domains as well as whole vesicle migration. The models of pH effects used in this context are usually not based on explicit free energy contributions of charge dissociation, being the starting point of our work, but rather build upon assumed effective values of the membrane charges, and while the experimental studies do show the existence of different instabilities the detailed quantitative connection with our work is at present difficult to establish. Nevertheless, our elucidation of the coupling between the charging processes in lipid membranes and electrostatic interactions in general provide a solid underpinning for these type of phenomena which are clearly beyond the paradigm of electrostatic renormalization of elasto-mechanical properties of membranes. This specifically applies also to the reverse problem of the local pH deviation from the bulk value in the vicinity of a curved phospholipid vesicle where the interfacial pH has been measured as a function of the curvature-radius of the membrane.⁷⁴ The phenomenology revealed by these experiments is within the purview of our calculations and will be the focus of our future work.

Finally, our methodology and the model used have understandably and unavoidably many limitations. First of all, the limitations inherent in the PB continuum electrostatics, applying also to our theory, are well known and understood.¹ The assumption of incompressibily is relatively standard in membrane physics but of course entails certain well recognized limitations.³⁷ We only consider a quenched membrane state with fixed density and type of lipids, thus disregarding the annealing of the composition either by in plane diffusion or by trans-membrane flip-flops of different lipid species both associated presumably with large(er) time scales.⁷⁵ We do not exactly specify the composition of the membrane, neither its lipid part nor, possibly even more important, the membrane protein counterpart,³³ aiming for salient characteristics of the behavior and disregarding the certainly important consequences of molecular identity.¹⁸ We believe that irrespective of all these acknowledged limitations we uncover some features of membrane electrostatics which can be crucial in assessing and controlling the behavior of charged, decorated lipid vesicles.

Author contributions

All authors were involved in Conceptualization of this project, PK and AM were involved in developing the required Software and performed the calculations, RP was involved in Supervision of the calculations, and all authors were involved in Visualization and Writing of the MS.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

RP and PK acknowledge funding from the Key Project No. 12034019 of the National Natural Science Foundation of China and the 1000-Talents Program of the Chinese Foreign Experts Bureau and the School of Physics, University of Chinese Academy of Sciences.

Notes and references

1. T. Markovich, D. Andelman and R. Podgornik, in Handbook of Lipid Membranes, ed. C. R. Safynia and J. O. Raedler, Taylor & Francis, 2021.
2. G. V. Bossa, K. Bohinc and S. May, in Handbook of Lipid Membranes, ed. C. R. Safynia and J. O. Raedler, Taylor & Francis, 2021.
3. Y. Hong and D. G. Brown, Langmuir, 2008, 24, 5003–5009.
4. K. K. Ewert, P. Scodeller, L. Simón-Gracia, V. M. Steffes, E. A. Wonder, T. Teesalu and C. R. Safinya, Pharmaceutics, 2021, 13, 1365.
5. G. Cevc, Biochim. Biophys. Acta, Rev. Biomembr., 1990, 1031, 311–382.
6. M. J. Mulligan, K. E. Lyke, N. Kitchin, J. Absalon, A. Gurtman, S. Lockhart, K. Neuzil, V. Raabe, R. Bailey, K. A. Swanson, P. Li, K. Koury, W. Kalina, D. Cooper, C. Fontes-Garfias, P.-Y. Shi, Ö. Türeci, K. R. Tompkins, E. E. Walsh, R. Frenck, A. R. Falsey, P. R. Dormitzer, W. C. Gruber, U. Sahin and K. U. Jansen, Nature, 2020, 586, 589–593.
7. L. R. Baden, H. M. E. Sahly, B. Essink, K. Kotloff, S. Frey, R. Novak, D. Diemert, S. A. Spector, N. Rouphael, C. B. Creech, J. McGettigan, S. Khetan, N. Segall, J. Solis, A. Brosz, C. Fierro, H. Schwartz, K. Neuzil, L. Corey, P. Gilbert, H. Janes, D. Follmann, M. Marovich, J. Mascola, L. Polakowski, J. Ledgerwood, B. S. Graham, H. Bennett, R. Pajon, C. Knightly, B. Leav, W. Deng, H. Zhou, S. Han, M. Ivarsson, J. Miller and T. Zaks, N. Engl. J. Med., 2021, 384, 403–416.
8. M. Schlich, R. Palomba, G. Costabile, S. Mizrahy, M. Pannuzzo, D. Peer and P. Decuzzi, Bioeng. Transl. Med., 2021, 6, e10213.
9. Electrostatic Effects in Soft Matter and Biophysics, ed. C. Holm, P. Kekicheff and R. Podgornik, Kluwer, Dordrecht, 1st edn, 2001.
10. M. Borkovec, B. Jönsson and G. J. M. Koper, in Surface and Colloid Science. Surface and Colloid Science, ed. E. Matijević, Springer, 2001.
11. M. Lund and B. Jönsson, Biochemistry, 2005, 44, 5722–5727.
12. F. L. Barroso da Silva and B. Jönsson, Soft Matter, 2009, 5, 2862–2868.
13. F. L. B. da Silva and L. G. Dias, Biophys. Rev., 2017, 9, 699–728.
14. Y. Avni, T. Markovich, R. Podgornik and D. Andelman, Soft Matter, 2018, 14, 6058–6069.
15. R. Podgornik, D. Harries, J. DeRouchey, H. H. Strey and V. A. Parsegian, in Gene and Cell Therapy: Therapeutic Mechanisms and Strategies, ed. N. S. Templeton, CRC Press, 2008, pp. 443–484.
16. B. W. Ninham and V. A. Parsegian, J. Theor. Biol., 1971, 31, 405.
17. R. Podgornik, J. Chem. Phys., 2018, 149, 104701.
18. R. J. Nap, A. L. Božič, I. Szleifer and R. Podgornik, Biophys. J., 2014, 107, 1970–1979.
19. M. I. Angelova, A.-F. Bitbol, M. Seigneuret, G. Staneva, A. Kodama, Y. Sakuma, T. Kawakatsu, M. Imai and N. Puff, Biochim. Biophys. Acta, Biomembr., 2018, 1860, 2042–2063.
20. M. Jayaraman, S. M. Ansell, B. L. Mui, Y. K. Tam, J. Chen, X. Du, D. Butler, L. Eltepu, S. Matsuda, J. K. Narayanannair, K. G. Rajeev, I. M. Hafez, A. Akinc, M. A. Maier, M. A. Tracy, P. R. Cullis, T. D. Madden, M. Manoharan and M. J. Hope, Angew. Chem., Int. Ed., 2012, 51, 8529–8533.
21. A. Majee, M. Bier and R. Podgornik, Soft Matter, 2018, 14, 985–991.
22. A. Majee, M. Bier, R. Blossey and R. Podgornik, Phys. Rev. E, 2019, 100, 050601.
23. A. Majee, M. Bier, R. Blossey and R. Podgornik, Phys. Rev. Res., 2020, 2, 043417.
24. V. V. Galassi and N. Wilke, Membranes, 2021, 11, 478.
25. S. Pöyry and I. Vattulainen, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 2322–2333.
26. D. Marsh, Handbook of Lipid Bilayers, CRC Press, 2nd edn, 2013.
27. M. H. M. Olsson, C. R. Søndergaard, M. Rostkowski and J. H. Jensen, J. Chem. Theory Comput., 2011, 7, 525–537.
28. G. Cevc, in Encyclopedia of Biophysics, ed. G. C. K. Roberts and A. Watts, Springer Berlin Heidelberg, 2018.
29. R. Leventis and J. R. Silvius, Biochim. Biophys. Acta, Biomembr., 1990, 1023, 124–132.
30. J. R. Casey, S. Grinstein and J. Orlowski, Nat. Rev. Mol. Cell Biol., 2010, 11, 50–61.
31. N. Ben-Dov and R. Korenstein, PLoS One, 2012, 7, e35204.
32. M. Lund and B. Jönsson, Q. Rev. Biophys., 2013, 46, 265–281.
33. L. Javidpour, A. Božič, A. Naji and R. Podgornik, Soft Matter, 2021, 17, 4296–4303.
34. E. Tanguy, N. Kassas and N. Vitale, Biomolecules, 2018, 8, 20.
35. D. Andelman, in Handbook of Biological Physics: Structure and Dynamics of Membranes, ed. R. Lipowsky and E. Sackmann, Elsevier, 1995.
36. A. Fogden and B. Ninham, Adv. Colloid Interface Sci., 1999, 83, 85–110.
37. H. A. Faizi, S. L. Frey, J. Steinkühler, R. Dimova and P. M. Vlahovska, Soft Matter, 2019, 15, 6006–6013.
38. A. G. Petrov, The Lyotropic State of Matter: Molecular Physics and Living Matter Physics, CRC Press, New York, 1st edn, 1999.
39. K. Hristova, I. Bivas, A. G. Petrov and A. Derzhanski, Mol. Cryst. Liq. Cryst., 1991, 200, 71–77.
40. M. Le Bret, J. Chem. Phys., 1982, 76, 6243–6255.
41. H. R. Shojaei, A. L. Božič, M. Murugappan and R. Podgornik, Phys. Rev. E, 2016, 93, 052415.
42. D. Harries, R. Podgornik, V. A. Parsegian, E. Mar-Or and D. Andelman, J. Chem. Phys., 2006, 124, 224702.
43. L. Koopal, W. Tan and M. Avena, Adv. Colloid Interface Sci., 2020, 280, 102138.
44. J. Landsgesell, P. Hebbeker, O. Rud, R. Lunkad, P. Košovan and C. Holm, Macromolecules, 2020, 53, 3007–3020.
45. I. Teraoka, Polymer solutions: An Introduction to Physical Properties, John Wiley & Sons, Inc., New York, 2002.
46. Y. Avni, R. Podgornik and D. Andelman, J. Chem. Phys., 2020, 153, 024901.
47. E. J. Verwey and J. T. G. Overbeek, Theory of the stability of Lyophobic Colloids, Elsevier, Amsterdam, 1948.
48. A. Majee, M. Bier and S. Dietrich, J. Chem. Phys., 2016, 145, 064707.
49. A. S. Šiber and R. Podgornik, Phys. Rev. E, 2007, 76, 061906.
50. M. Winterhalter and W. Helfrich, J. Phys. Chem., 1988, 92, 6865–6867.
51. D. J. Mitchell and B. W. Ninham, Langmuir, 1989, 5, 1121–1123.
52. H. Lekkerkerker, Phys. A, 1990, 167, 384–394.
53. B. Duplantier, R. E. Goldstein, V. Romero-Rochn and A. I. Pesci, Phys. Rev. Lett., 1990, 65, 508–511.
54. J. L. Harden, C. Marques, J. F. Joanny and D. Andelman, Langmuir, 1992, 8, 1170–1175.
55. M. J. Carrasco, S. Alishetty, M.-G. Alameh, H. Said, L. Wright, M. Paige, O. Soliman, D. Weissman, T. E. Cleveland, A. Grishaev and M. D. Buschmann, Commun. Biol., 2021, 4, 956.
56. F. Ahmadpoor and P. Sharma, Nanoscale, 2015, 7, 16555–16570.
57. A. G. Petrov, Biochim. Biophys. Acta, Biomembr., 2002, 1561, 1–25.
58. A. G. Petrov, Anal. Chim. Acta, 2006, 568, 70–83.
59. Q. Deng, L. Liu and P. Sharma, J. Mech. Phys. Solids, 2014, 62, 209–227.
60. Y. Avni, D. Andelman and R. Podgornik, Curr. Opin. Electrochem., 2019, 13, 70–77.
61. C. R. Safinya and J. Radler, Handbook of Lipid Membranes: Molecular, Functional, and Materials Aspects, CRC Press, 2021.
62. S. E. Feller, Curr. Opin. Colloid Interface Sci., 2000, 5, 217–223.
63. Z.-J. Wang and M. Deserno, J. Phys. Chem. B, 2010, 114, 11207–11220.
64. D. S. Bruhn, M. A. Lomholt and H. Khandelia, J. Phys. Chem. B, 2016, 120, 4812–4817.
65. S. Y. Joshi and S. A. Deshmukh, Mol. Simul., 2021, 47, 786–803.
66. Y. Yu, A. Krämer, R. M. Venable, B. R. Brooks, J. B. Klauda and R. W. Pastor, J. Chem. Theory Comput., 2021, 17, 1581–1595.
67. T. Curk, J. Yuan and E. Luijten, J. Chem. Phys., 2022, 156, 044122.
68. B. Loubet, P. L. Hansen and M. A. Lomholt, Phys. Rev. E, 2013, 88, 062715.
69. H. I. Ingólfsson, M. N. Melo, F. J. van Eerden, C. Arnarez, C. A. Lopez, T. A. Wassenaar, X. Periole, A. H. de Vries, D. P. Tieleman and S. J. Marrink, J. Am. Chem. Soc., 2014, 136, 14554–14559.
70. M. Karimi, J. Steinkühler, D. Roy, R. Dasgupta, R. Lipowsky and R. Dimova, Nano Lett., 2018, 18, 7816–7821.
71. A. Kodama, Y. Sakuma, M. Imai, Y. Oya, T. Kawakatsu, N. Puff and M. I. Angelova, Soft Matter, 2016, 12, 2877–2886.
72. G. Staneva, N. Puff, M. Seigneuret, H. Conjeaud and M. I. Angelova, Langmuir, 2012, 28, 16327–16337.
73. N. Khalifat, J.-B. Fournier, M. I. Angelova and N. Puff, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2724–2733.
74. Y. Sarkar, R. Majumder, S. Das, A. Ray and P. P. Parui, Langmuir, 2018, 34, 6271–6284.
75. A. Hossein and M. Deserno, Biophys. J., 2020, 118, 624–642.

---

Footnote

† These authors contributed equally to this work and have a shared co-first authorship.

---