Hydrodynamic and geometric effects in the sedimentation of model run-and-tumble microswimmers

Abstract

The sedimentation process in an active suspension is the result of the competition between gravity and the autonomous motion of particles. We carry out simulations of run-and-tumble squirmers that move in a fluid medium, focusing on the dependence of the non-equilibrium steady state on the swimming properties. We find that for large enough activity, the density profiles are no longer simple exponentials; we recover the numerical results through the introduction of a local effective temperature, suggesting that the breakdown of the Perrin-like exponential form is a collective effect due to fluid-mediated dynamic correlations among particles. We show that analogous concepts can also fit the case of active non-motile particles, for which we report the first study of this kind. Moreover, we provide evidence of scenarios where the solvent hydrodynamics induces non-local effects which require the full three-dimensional dynamics to be taken into account in order to understand sedimentation in active suspensions. Finally, analyzing the statistics of the orientations of microswimmers, the emergence of a height-dependent polar order in the system is discussed.

---

1 Introduction

A number of microorganisms (bacteria, algae, etc.…) have the ability to swim in a liquid environment through the generation of autonomous motion at the expense of their metabolism, thus being intrinsically out-of-equilibrium. As such, these systems lead to new challenges such as the understanding of how collective phenomena and self-organization emerge from the relevant features of the propulsion mechanism.^1–4 In this perspective a suspension of active particles is qualitatively different from a suspension of passive ones. Maybe the simplest, yet not trivial, example of this is the case of a constant external forcing on the suspension, such as gravity in the sedimentation process. In fact, when thermal fluctuations are negligible (as in the case of particles above the micron size), while passive particles would inevitably precipitate, active suspensions maintain a finite sedimentation length that grows with the self-propulsion speed. This result was predicted theoretically for dry suspensions (i.e. where the solvent hydrodynamics is neglected) of non-interacting run-and-tumble particles^5,6 and, then, confirmed in numerical simulations with point-like dipoles⁷ and experimentally in suspensions of active colloids.⁸ Suspensions of self-propelled particles under gravity have been also reported to display a complex orientational dynamics, with the development of an associated polar order^9,10 or even, in the case of bottom-heavy particles, to the inversion of the sedimentation profiles.¹¹ In this paper we present a computational study of sedimentation in active suspensions, where hydrodynamics is fully resolved near and far from the particle surface. We provide evidence that hydrodynamic correlations induce important deviations from the phenomenology for dry suspensions in the steady state of both self-propelled swimmers and “shakers”, namely active particles that stir the fluid around them without achieving a directed motion, for which, to the best of our knowledge, this study represents the first of this kind. The sedimentation profiles observed when activity is intense are captured through a simple extension of a drift-diffusion model with height dependent effective temperature. We show that pullers develop a distal region of constant density (a supernatant) whose emergence depends on both the activity/gravity ratio and the confining geometry (i.e. the cell aspect-ratio). We also address the statistics of the microswimmer orientation, finding that, in the regime of small tumbling frequency, the suspension develops a polar order whose characteristics are strongly dependent on the type of swimmer.

2 Numerical method and simulation details

The velocity field of the solvent (of dynamic viscosity η) is evolved by means of a lattice Boltzmann (LB) method¹² with nineteen lattice speeds in three dimensions (D3Q19).¹³ Swimmers are modelled as solid spherical objects of radius R. The correct momentum exchange and mass conservation through the set of boundary links (between grid points in and out the sphere) representing the particles is implemented according to the bounce-back-on-links scheme.^14–16 In order to mimic the surface deformations inducing the microswimmer motion, we adopt a simplified version of the squirmer model,^17,18 whereby only the tangential polar component of the axisymmetric velocity prescribed at the particle surface is non-zero, u_s = u_s(θ)[small straight theta, Greek, circumflex]. Furthermore, just the first two terms in the series expansion of u_s(θ) are retained:^19,20

u_s(θ) = (B₁ + B₂ cos(θ))sin(θ), (1)

where θ = arccos(ê·r̂_s) is the angle formed by the squirmer orientation unit vector, ê, and the position on the surface, r̂_s = x_s/R, relative to the particle centre of mass position (see Fig. 1 for a schematic representation of the model microswimmer just described). It should be pointed out that the prescription (1) cannot cope with unsteady flows, like those occurring when flagellar beating is involved, in short times, but it is effective on scales much longer than a typical flagellar or ciliary cycle.²¹ The parameter B₁ > 0 in eqn (1) is related to the propulsion speed, which is , whereas the second parameter, B₂, determines the strength of the stresslet, [scr S, script letter S] ∝ηR²B₂, generated by the swimmer in the surrounding fluid (and, hence, it is related to the amplitude of the injected vorticity).¹⁹ The ratio , such that β ∈ (−∞, + ∞), quantifies the relative intensity of apolar stresses and polar self-propulsion and classifies swimmers in “pushers”, β < 0 (including bacteria like, e.g., E. coli), “pullers”, β > 0 (such as the algae Chlamydomonas), and “potential” swimmers, β = 0 (i.e. swimmers that simply self-propel without generating vorticity, like the alga V. carteri or certain artificial swimmers).^{17,19,22–24} Every τ time step the particles randomise their orientation ê with uniform probability over the interval [0, π], thus accounting for the characteristic run-and-tumble mechanism, which can be seen as a source of diffusion for particles that, we recall here, are insensitive to thermal fluctuations.^25,26 Different probability distributions of tumbling angles can, in principle, characterise actual microswimmers. For E. coli, for instance, the distribution is peaked around ∼65° and is rather skewed towards smaller values.²⁵ It is known, though, that, when looked at over time scales t ≫ τ, the run-and-tumble motion leads to a diffusive dynamics, irrespective of the specific statistical properties of the tumbling events, but for a dependence of the diffusion coefficient on the mean angle.^25,27–29

Fig. 1 Snapshot of a simulation, seen on the (x, z) plane, in the statistically steady state; L and H indicate the sizes of the box, L × L × H. Inset: Sketch of a squirmer particle of radius R. X is the position of the centre of mass, x_s is the position on the surface, ê is the characteristic orientation unit vector, defining the appropriate swimming direction, and the polar angle reads .

Our model, featuring finite size resolved particles, equipped with the squirming motion, is then able to capture hydrodynamic effects in the sedimentation of active suspensions, both in their far and near field manifestations, although when particles are close to contact or swimming takes place near the walls, the dynamics on short time scales might be not accurately described for flagellated microorganisms.

We simulate suspensions, of volume fraction ϕ = 0.07, in three-dimensional boxes of size L × L × H, with height H ≈ 80R and variable aspect-ratio Γ = L/H (see Fig. 1 for a graphical sketch). The height value is chosen to be large enough to exceed the maximum theoretically expected sedimentation length (over the explored range of parameters and for cases where such theoretical control is available), so as to guarantee that the upper bound will not affect the results. Two solid walls (with no-slip boundary conditions for the fluid velocity) confine the system in the z-direction, while periodic boundary conditions along the x, y directions hold. The number of particles, with radius R = 2.3 (in lattice-spacing units), range between ∼500 and ∼3 × 10⁴). We introduce a reference velocity, v_g = μF_g (where F_g is the gravity force magnitude and μ = 1/(6πηR) is the particle mobility), i.e. the sedimentation velocity of a passive particle, and a reference time, t_c = R/v_p (where v_p = |v_p|), that is basically the time an isolated particle takes to displace its own radius. In terms of v_g and t_c, the following dimensionless parameters can be defined, namely

which, together with β, govern the squirmers’ motion. In order to investigate how the swimming characteristics and the system geometry affect the sedimentation profiles, we performed several runs exploring the parameter space spanned by (χ₁, χ₂, β, Γ). Unless differently specified, we fix [small tau, Greek, macron] ≈ 4.3, corresponding to a run time much longer than the typical time the flow field takes to relax and adapt to the new orientation; the latter, given the low Reynolds number dynamics, can be taken as t_ν ∼ R²/ν, the viscous time of diffusion around the particle (ν being the solvent kinematic viscosity), so that τ/t_ν ≈ 30.

3 Sedimentation profiles

We start each run with the active particles homogeneously distributed in space, with random orientations. To check that a (non-equilibrium) statistically steady state is reached, we follow the time evolution of the average height , where ρ(z, t) is the (unsteady) normalized particle density (i.e. ρ(z, t)dz is the probability of finding a particle centred between z and z + dz at the time t). We consider as the steady state the time interval during which h(t) fluctuates by less than ∼5%. All data shown hereafter are meant to be averaged over such time interval. Our aim is to study the impact that activity, in terms of χ₁ and β, has on the squirmer sedimentation, and to characterize the emerging dynamical regimes, checking whether and how hydrodynamic effects come into play. According to the theory,^5,6 as χ₁ → 1, all particles concentrate at the bottom wall. Instead, when χ₁ ≫ 1 (i.e., in the self-propulsion dominated regime) the steady state sedimentation profile should display an exponential form ρ(z) ∼ e^−z/λ, with a sedimentation length depending on the single particle velocity (and, hence, on χ₁) aswhere [small script l] = v_pτ ≈ 4.3R ≈ 0.06H is the microswimmer's run length. This result has been found to be in agreement with experimental observations⁸ and numerical simulations.⁷ The exponential profile also characterizes equilibrium systems, as in the classical Perrin's experiment for (thermal) colloids;³⁰ the sedimentation length is determined by the particle diffusivity, D, and the gravity force as λ^(eq) = D/(μF_g) and depends, therefore, through the Stokes–Einstein relation D = μk_BT, on the system temperature T, namely λ^(eq) = k_BT/F_g. The formal analogy with the passive (equilibrium) case suggests, then, to introduce an effective temperature as follows:such that the sedimentation length reads λ = k_BT^(1p)_eff/F_g.

In Fig. 2 we plot the time-averaged steady state density profiles of potential swimmers (β = 0) for χ₁ ∈ [1, 20]. This range of values is compatible with those expected for typical bacteria, such as E. coli or B. subtilis whose swimming speeds are v_p ∼ 15–30 μm s⁻¹,^25,31,32 in terrestrial gravity (v_g ∼ 1–2.5 μm s⁻¹), for which it would be χ₁ ∼ 6–30.⁶

Fig. 2 Main panel: Density profiles in microswimmer suspensions for various values of the propulsion/gravity ratio χ₁, at β = 0 and Γ = 0.35. For χ₁ close to one, the particles accumulate at the bottom wall, showing a crystal order (as the regularly spaced peaks in ρ suggest). For large χ₁ the expected exponential profile is recovered. Inset: Dependence of the sedimentation length λ (computed out of exponential fits of the density profiles) (□) on the propulsion/gravity ratio χ₁. The dashed line depicts the theoretical expectation λ/χ₁ = [small script l]/3 ≈ 1.45R, eqn (3), valid for χ₁ ≫ 1.

For values close to one, as expected, microswimmers uniformly fall down under the action of gravity; however, due to the finite size of particles, the sedimentation length remains finite. The particles in the sediment tend to organize themselves in layers with a crystal-like order, noticeable from the peaks in the density profile, close to the bottom wall, displaced from each other by about one diameter (2R), as found also in a previous computational study.¹⁰ At increasing χ₁, swimmers occupy an increasingly larger volume of liquid and, correspondingly, ρ(z) shows, over the whole box length, the predicted exponential profile⁶ with a sedimentation length growing linearly with χ₁ (see inset of Fig. 2).

If we increase |β| (thus intensifying the activity) to large enough values, for a fixed χ₁, the deviation from the exponential profile can be important, as one can see from Fig. 3, where we plot the particle density ρ(z) for three cases with same χ₁ = 10 and β = 0, ±10. For the sake of comparison of the chosen values of β with those expected for actual microswimmers, consider that, e.g., E. coli swims at a speed v_p ∼ 20 μm s⁻¹,²⁵ exerting a force dipole of amplitude f ∼ 0.4 pN and length δ ∼ 2 μm;³¹ therefore, and |B₂| ∼ [scr S, script letter S]/(ηδ²) ∼ f/(ηδ) ≈ 200 μm s⁻¹, where [scr S, script letter S] ∼ fδ is the stresslet, give |β| = |B₂|/B₁≈7.

Fig. 3 Main panel: Density profiles in microswimmer suspensions with χ₁ = 10, β = 0, ±10 and Γ = 0.35 (data are vertically shifted for clarity). The lines represent the predictions coming from the numerical integration of eqn (7) with λ = 15 and α₁ = 1 (see the text for the discussion of the model parameters) for β = 0 (dashed line), β = −10 (solid line) and β= + 10 (dotted line). Inset: Fluid velocity fluctuations as a function of the system height for the case β = − 10.

In the pushers/pullers case (β ≠ 0), dynamic correlations are so intense that recovering a Perrin-like form just with the introduction of a global effective diffusion coefficient as coming from single particle dynamics is no longer possible.⁸ The larger the |β|, the stronger is the departure of the sedimentation profile from being exponential; indeed we found that deviations start to be relevant from |β| ≈ 5.⁷

4 Extended diffusive model

4.1 Local effective temperature

Due to hydrodynamic correlations the dynamics of an active particle in the suspension is affected by the presence of the others through the generation of motion within the liquid, which acts as a bath at an effective temperature (measuring the fluid agitation). We can understand these effects extending a diffusive model proposed to describe sedimentation in active colloidal suspensions,⁸ based on the Smoluchowski equation ∂_tρ = −∇·J, determined by the flux J = −D̃∇ρ + [small mu, Greek, tilde]F_gρ. The ratio of the local diffusion coefficient, D̃, and particle mobility, [small mu, Greek, tilde], by virtue of a generalized Stokes–Einstein relation, represents the effective temperature field. Assuming that in the steady state the density will depend only on z, the zero flux boundary conditions at the walls gives

We propose an effective temperature of the form T_eff =T^(1p)_eff + T^(coll)_eff, consisting of two terms: the single-particle effective temperature, eqn (4), accounting for the self-propulsion, plus a contribution proportional to the fluid velocity fluctuations, T^(coll)_eff, capturing the collective effects due to hydrodynamic interactions. However, since in the steady state microswimmers are distributed inhomogeneously over the volume (with a density increasing from top to bottom), the fluid velocity fluctuations (where ) are also expected to vary with z (as indeed it can be seen in the inset of Fig. 3). This entails a height dependent effective temperature T_eff(z) = T^(1p)_eff + T^(coll)_eff(z), leading, upon insertion in (5), to an equation for the sedimentation density which can be recast in the following form:

where λ = (k_BT^(1p)_eff)/F_g is the sedimentation length discussed in the previous section. We assume, then, T^(coll)_eff(z) ∝σ_δu²(z) to hold, so that we can finally writewith α₁ a free parameter representing the proportionality constant between T^(coll)_eff and σ_δu². Eqn (7) is integrated numerically, with σ_δu² taken from the simulations. Comparing the result with the measured density profiles (see Fig. 3), we find that the proposal of gauging the global effective temperature to a height dependence works well for β = 0 and β < 0. The phenomenology of pullers (β > 10) appears, however, to be more complicated: in fact, while the density profile can be recovered where the concentration is higher, the presence of a region of constant density, denoting the formation of a supernatant floating over the sedimentation layer, eludes the generalized diffusive model.

4.2 The case of shakers

Another striking instance of how crucial the role played by hydrodynamics can be is provided by the regime where |β| → ∞, i.e. B₁ goes to zero while B₂ stays finite. This regime corresponds to active suspensions where particles do not self-propel but generate motion in the fluid and are relevant for microswimmers known as shakers,^1,33 like, e.g., melanocytes.³⁴ Since both their propelling velocity and the effect of thermal fluctuations are negligible, such a suspension would undergo a gravitational collapse, if one could completely neglect the presence of the solvent. However, as shown in Fig. 4, the steady state density profiles develop a sedimentation layer, whose width increases with χ₂ (defined in (2)). The observed width cannot be interpreted simply as a result of the close packing of the particles, which would imply, in fact, a value of around 8R, much smaller than the measured one. We try to recover the sedimentation profiles of shakers following the same ideas of the previous section. We must integrate numerically eqn (5), with a vanishing one-particle contribution to the effective temperature, T^(1p)_eff = 0, since for shakers B₁ = 0 ⇔ v_p = 0, such that T_eff(z) = T^(coll)_eff(z) = α₂(σ_δu²(z)/v_B2²) (here we indicate the phenomenological parameter as α₂ in order to distinguish it from that of self-propellers). The reference speed v_B2 = |B₂|/3 is the magnitude of the velocity field generated by a shaker, averaged over its surface, i.e., where u_s is given by eqn (1). The stationary Smoluchowski equation, then, readsthe results of the numerical integration of eqn (8) for shakers with negative χ₂ with two different values of gravity are reported in Fig. 4, showing, again, good agreement.

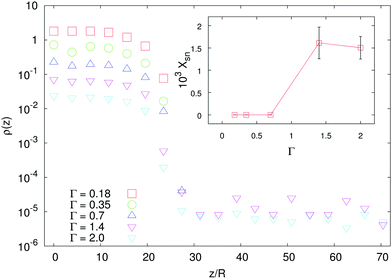
Fig. 4 Main panel: Density profiles of shakers with two different χ₂ < 0 and Γ = 0.35 (here and in the inset data are vertically shifted for clarity). The larger the |χ₂| the longer the density tail (i.e. the wider is the region occupied by particles). The lines are the theoretical predictions coming from the numerical integration of eqn (8), where the function σ_δu²(z) is taken from the simulations, with α₂ = 4.4. Inset: Density profiles of shakers with |χ₂| = 5 (green triangles), |χ₂| = 10 (red squares) and |χ₂| = 20 (blue circles). Data for both pullers (χ₂ > 0, full symbols) and pushers (χ₂ < 0, empty symbols) are reported; notice the formation of the supernatant in the puller case for large enough χ₂.

Analogously to the case of pullers, shakers with χ₂ > 0 develop (for χ₂ large enough) a distal region of constant density in the sedimentation profile (see the inset of Fig. 4). The emergence of such supernatant is due to the sediment which acts as a pump and generates motion in higher layers of fluid. It is, then, a genuinely three-dimensional and non-local effect, two features which make also our formalism based on a height dependent effective temperature fail. To support this picture, we show that, for a fixed value of χ₂, the supernatant disappears when decreasing the aspect-ratio Γ of the cell below unity (see Fig. 5).

Fig. 5 Main panel: Density profiles for shakers with χ₂ = 8.3 for various aspect ratios Γ = L/H (data are vertically shifted for clarity). Inset: Fraction of particles in the supernatant region, computed as (ζ₀ being the minimum height such that ρ(z) = 0, for some Γ and for z > ζ₀), as a function of the aspect ratio of the cell: notice that for Γ < 1, X_sn = 0, i.e. no supernatant develops.

This is, indeed, a manifestation of three-dimensionality: using an analogy with a Rayleigh–Bénard system,³⁵ we argue that the geometry favors (or does not) the development of a large scale flow which can (or cannot) sustain the supernatant. In fact, the difference in the fluid flow pattern generated by a single particle, either a pusher or a puller, is not strong enough to sustain the different macroscopic patterns observed if the swimmers are randomly oriented (as a matter of fact, no supernatant is observed for pushers, or shakers with χ₂ < 0). Hence, a collective organization of the swimmers is required to produce the observed macroscopic flows. We will next address the emergence of orientational order in the sedimentation profiles of microswimmers.

5 Orientational statistics

The emergence and the dynamical relevance of anisotropic ordering in active fluid systems has been widely recognized in the literature.^1,9,36 We study the orientational statistics measuring the joint probability distribution function (PDF) of the particle elevation and vertical component of the squirmer characteristic vector, P(z, ê_z). For squirmers with χ₁ = 10, β = 0 and run time [small tau, Greek, macron] ≈ 4.3 we find a bimodal distribution symmetrically peaked at ê_z = ±1 (with a slight imbalance towards ê_z = −1), for any z, as expected under the assumption of a factorized joint PDF, P(z, ê_z) ∼ ρ(z)Φ(ê_z).²⁶ However, it was shown theoretically, in the context of active Brownian particles, that such factorization could only be possible for the vanishing Péclet number;⁹ otherwise, when Pe ∼ O(1), the suspension develops a polar order which is non-trivially correlated with the height. We recall, here, that for athermal, run-and-tumble particles an effective diffusivity can be defined, proportional to the tumbling rate, [small tau, Greek, macron]⁻¹;²⁶ hence the effective Péclet number grows at Pe ∼ [small tau, Greek, macron]. 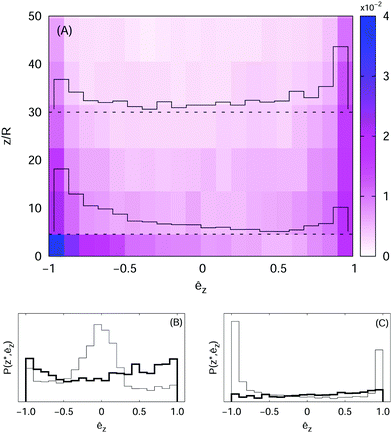We increase, therefore, [small tau, Greek, macron] to probe this regime. We remark, incidentally, that it is also possible to modulate the effective diffusivity by changing the mean tumbling angle; thus in real systems one must expect that the statistics of reorientations also affects the polar order. Indeed, for [small tau, Greek, macron] ≈ 30, we observe from the joint PDF, shown in Fig. 6(A) as a colour map, a larger probability of finding downward oriented particles close to the wall, whereas the opposite trend appears at higher elevations, which means that in the bulk the active particles preferentially swim upwards (i.e. against gravity), in line with the theoretical results.⁹ To highlight this behaviour we also report the orientation PDFs, P(z*, ê_z)/ρ(z*), as histograms at two heights, z* = 2R and z* = 30R.

Fig. 6 Panel (A): Joint probability distribution function, P(z, ê_z), of elevation, z, and vertical component of the orientation unit vector, ê_z, for microswimmers with β = 0; the histograms depicted as continuous lines highlight the orientation PDF, P(z*, ê_z)/ρ(z*), at two different elevations: z* = 2R and z* = 30R (indicated with dashed lines). Panel (B): Orientation PDFs for pushers, β = −10, at z* = 2R (thin line) and z* = 30R (thick line). Panel (C): Same as panel (B) but for pullers, β = +10.

It is worth noting that the chosen value of [small tau, Greek, macron] is comparable, for instance, with that of E. coli, for which, having v_p ≈ 25 μm s⁻¹ and a typical run time of ∼1 s ^25,37 and size R ∼ 1 μm, one gets [small tau, Greek, macron] = v_pτ/R ≈ 25.

For β ≠ 0 we expect this scenario to break down, because the generation of fluid motion acts as an effective source of noise; in fact, we observe that, close to the wall, the PDF is peaked around ê_z ≈ 0 for β < 0, and it is bimodal (with a higher peak at ê_z ≈ −1) for β > 0, while in the bulk it is rather uniform in both cases (panels (B) and (C) of Fig. 6). As anticipated in the previous section, such different orientational ordering between pushers and pullers turns out to have an impact also on the swimmers’ distribution in space, as indicated by the sedimentation profiles.

6 Conclusions

We have presented a computational study of suspensions of run-and-tumble squirmers under gravity. Thanks to the built-in properties of the mesoscopic approach adopted we could take into account both the finite size of particles and the hydrodynamics of the solvent. In the case of potential swimmers, agreement has been found with theoretical predictions regarding (i) the dependence of the density profiles on the activity/gravity ratio and (ii) the emergence of a polar order from the inspection of distributions of particle orientations. We have provided evidence, not reported so far, that, for pushers and pullers with large enough β, the hydrodynamic flows induced by their collective motion determine sedimentation profiles that cannot be understood in terms of a single swimmer response to the gravitational field. This feature appeared particularly distinctive in the emblematic case of shakers, whose sedimentation problem was never studied before. We have, then, proposed a generalised diffusive model, based on the concept of a height dependent collective effective temperature that proved to be able to recover the observed sedimentation profiles. Moreover, we showed that the profiles of pullers and shakers with positive β may develop a tail in the bulk of roughly constant density, signalling the presence of a supernatant, depending on the activity/gravity ratio (the parameter χ₂) but also on the system geometry (the aspect-ratio Γ). The emergence of such a supernatant, no previous observation of which we are aware of, is probably connected to the complex correlation between spatial organization of the microswimmers in the sediment and generated flows in the solvent, which deserves further investigation.

Overall, our findings, along the lines of recent studies,^10,38 emphasize the importance of exploring, theoretically, numerically and experimentally, the full three-dimensional dynamics for the sake of a better understanding of the sedimentation phenomenology in active suspensions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge MICINN and DURSI for financial support under Project No. PGC2018-098373-B-I00, and 2017SGR- 884, respectively. IP acknowledges SNSF for financial support under Project No. 200021-175719. This work was possible thanks to the access to the MareNostrum Supercomputer at Barcelona Supercomputing Center (BSC) and also through the Partnership for Advanced Computing in Europe (PRACE).

Notes and references

1. M. Marchetti, J.-F. Joanny, S. Ramaswamy, T. Liverpool, J. Prost, M. Rao and R. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189.
2. J. Elgeti, R. Winkler and G. Gompper, Rev. Prog. Phys., 2015, 78, 056601.
3. R. Simha and S. Ramaswamy, Phys. Rev. Lett., 2002, 89, 058101.
4. I. Llopis and I. Pagonabarraga, Europhys. Lett., 2006, 75, 999–1005.
5. J. Tailleur and M. Cates, Phys. Rev. Lett., 2008, 100, 21803.
6. J. Tailleur and M. Cates, Europhys. Lett., 2009, 86, 60002.
7. R. Nash, R. Adhikari, J. Tailleur and M. Cates, Phys. Rev. Lett., 2010, 104, 258101.
8. J. Palacci, C. Cottin-Bizonne, C. Ybert and L. Bocquet, Phys. Rev. Lett., 2010, 105, 088304.
9. M. Enculescu and H. Stark, Phys. Rev. Lett., 2011, 107, 058301.
10. J.-T. Kuhr, J. Blaschke, F. Rühle and H. Stark, Soft Matter, 2017, 13, 7548–7555.
11. K. Wolff, A. Hahn and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2013, 36, 43.
12. S. Succi, The lattice Boltzmann equation for complex states of flowing matter, Oxford University Press, 2018.
13. J.-C. Desplat, I. Pagonabarraga and P. Bladon, Comput. Phys. Commun., 2001, 134, 273–290.
14. A. Ladd, J. Fluid Mech., 1994, 271, 285–309.
15. A. Ladd, J. Fluid Mech., 1994, 271, 311–339.
16. N.-Q. Nguyen and A. Ladd, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 046708.
17. M. Lighthill, Comm. Pure Appl. Math., 1952, 5, 109–118.
18. J. Blake, J. Fluid Mech., 1971, 46, 199–208.
19. T. Ishikawa, M. Simmonds and T. Pedley, J. Fluid Mech., 2006, 568, 119–160.
20. R. Matas-Navarro and I. Pagonabarraga, Eur. Phys. J. E: Soft Matter Biol. Phys., 2010, 33, 27–39.
21. L. Zhu, E. Lauga and L. Brandt, J. Fluid Mech., 2013, 726, 285–311.
22. K. Drescher, R. Goldstein, N. Michel, M. Polin and I. Tuval, Phys. Rev. Lett., 2010, 105, 168101.
23. S. Thutupalli, R. Seemann and S. Herminghaus, New J. Phys., 2011, 13, 073021.
24. A. Evans, T. Ishikawa, T. Yamaguchi and E. Lauga, Phys. Fluids, 2011, 23, 111702.
25. H. Berg and D. Brown, Nature, 1972, 239, 500–504.
26. A. Solon, M. Cates and J. Tailleur, Eur. Phys. J. E: Soft Matter Biol. Phys., 2015, 224, 1231–1262.
27. P. Lovely and F. Dahlquist, J. Theor. Biol., 1975, 50, 477–496.
28. J. Saragosti, P. Silberzan and A. Baguin, PLoS One, 2012, 7, e35412.
29. A. Villa-Torrealba, C. Chávez-Raby, P. de Castro and R. Soto, Phys. Rev. E, 2020, 101, 062607.
30. J. Perrin, Ann. Chim. Phys., 1909, 8, 5–114.
31. K. Drescher, J. Dunkel, L. Cisneros, S. Ganguly and R. Goldstein, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 10940–10945.
32. A. Hamby, D. Vig, S. Safonova and C. Wolgemuth, Sci. Adv., 2018, 4, eaau0125.
33. S. Ramachandran, P. S. Kumar and I. Pagonabarraga, Eur. Phys. J. E: Soft Matter Biol. Phys., 2006, 20, 151–158.
34. H. Gruler, U. Dewald and M. Eberhardt, Eur. Phys. J. B, 1999, 11, 187–192.
35. S. Chandrasekhar, Hydrodynamic and hydromagnetic stability, Oxford University Press, 1961.
36. S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345.
37. T. Ishiwaka, G. Sekiya, Y. Imai and T. Yamaguchi, Biophys. J., 2007, 93, 2217–2225.
38. F. Rühle and H. Stark, Eur. Phys. J. E: Soft Matter Biol. Phys., 2020, 43, 26.

---