Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Scale-invariance in miniature coarse-grained red blood cells by fluctuation analysis†
Paul
Appshaw
 *a,
Annela M.
Seddon
b and
Simon
Hanna
a
*a,
Annela M.
Seddon
b and
Simon
Hanna
a
aSchool of Physics, HH Wills Physics Laboratory, University of Bristol, BS8 1TL, UK. E-mail: paul.appshaw@bristol.ac.uk
bBristol Centre for Functional Nanomaterials, HH Wills Physics Laboratory, University of Bristol, BS8 1TL, UK
First published on 7th January 2022
Abstract
To accurately represent the morphological and elastic properties of a human red blood cell, Fu et al. [Fu et al., Lennard-Jones type pair-potential method for coarse-grained lipid bilayer membrane simulations in LAMMPS, 2017, 210, 193–203] recently developed a coarse-grained molecular dynamics model with particular detail in the membrane. However, such a model accrues an extremely high computational cost for whole-cell simulation when assuming an appropriate length scaling – that of the bilayer thickness. To date, the model has only simulated “miniature” cells in order to circumvent this, with the a priori assumption that these miniaturised cells correctly represent their full-sized counterparts. The present work assesses the validity of this approach, by testing the scale invariance of the model through simulating cells of various diameters; first qualitatively in their shape evolution, then quantitatively by measuring their bending rigidity through fluctuation analysis. Cells of diameter of at least 0.5 μm were able to form the characteristic biconcave shape of human red blood cells, though smaller cells instead equilibrated to bowl-shaped stomatocytes. Thermal fluctuation analysis showed the bending rigidity to be constant over all cell sizes tested, and consistent between measurements on the whole-cell and on a planar section of bilayer. This is as expected from the theory on both counts. Therefore, we confirm that the evaluated model is a good representation of a full-size RBC when the model diameter is ≥0.5 μm, in terms of the morphological and mechanical properties investigated.
1 Introduction
The red blood cell (RBC) is the simplest and most well researched blood-borne cell, making it an ideal candidate on which to develop techniques in whole-cell computational modelling.1–3 It is a highly deformable, “rubbery” cell, able to recover its shape after squeezing through very narrow capillaries.4 The RBC is primarily comprised of a 2-component membrane, enclosing a cytoplasm fluid interior. The cell membrane is solely responsible for the elastic response of the cell due to the entirely viscous nature of the cytoplasm,5 with the cytoplasm instead responsible for the volume incompressibility of the cell.6 The membrane is composed of a lipid bilayer and distinct cytoskeleton network bound to its inner surface, connected by transmembrane proteins. As the membrane thickness is much lower than the diameter of the whole cell, it has three-dimensional structure describable by two-dimensional elastic parameters.7 The resistance to bending of the cell is then characterised by the bending rigidity B. The lipid bilayer is essentially a two-dimensional fluid-like structure embedded in three-dimensional space, resistant to bending, but unable to sustain in-plane shear stress due to its highly diffusive nature.8 Conversely, the cytoskeleton resists shear deformation but has negligible bending resistance. Therefore, the bending rigidity of the whole-cell is dominantly produced by the bilayer, and should be measurable solely from a plane of bilayer lipids.8–10Measuring the bending rigidities of mesoscopic vesicles such as the RBC has been of experimental interest for decades, prompting development of many competing techniques.11–15 When observed in vitro, the RBC membrane is seen to flicker, now understood to be its experiencing stochastic thermal fluctuations.16 The first quantitative analysis of this phenomenon was performed by Brochard and Lennon in 1975.11 Using phase-contrast microscopy, they extracted the bending rigidity from the power spectrum of fluctuations, pioneering the methodology of fluctuation analysis (spectroscopy). To improve upon the measurement accuracy, fluctuation analysis has been under continued development ever since, and successfully applied to a wide range of mesoscopic vesicles.17–23 When performed experimentally, a camera captures consecutive snapshots of the cell membrane in the focal plane of the microscope (so-called “contours”), allowing the bending rigidity to be calculated from analysis of their thermal undulations over time. In 1995, Strey et al.24 approximated B = 4 × 10−19 J from the excitations of just four orthogonal points on the RBC membrane. Faucon and Mitov21,25 introduced consideration of the reduced membrane tension to account for conservation of the vesicle surface area and volume. Using their method, Rodríguez-García determined B = 2.7 ± 0.6 × 10−19 J from healthy RBCs, and Gracia et al.14B = 2.25 ± 0.8 × 10−19 J from lipids extracted from the RBC membrane.
Computational RBC models have been developed under many different formalisms. To date, the most popular have been those most computationally efficient, namely continuum methods such as the finite element method (FEM), and the aggressively coarse-grained (CG), dissipative-particle-dynamics (DPD).2,3,26 However, with the ever increasing power of High Performance Computing (HPC) facilities, CG models of higher resolution and complexity have seen increasing popularity; notably the coarse-grained-molecular-dynamics (CGMD) RBC model developed successively by Drouffe et al.,27 Yuan et al.28 and Fu et al.29 In this CGMD formalism, the molecules comprising the bilayer, cytoskeleton and transmembrane proteins are explicitly represented as CG particles that interact through Lennard-Jones-like potentials and Hookean bindings. To give meaningful separation between the two distinct membrane components, the length-scale of the system is defined by the thickness of the cell bilayer (5 nm). The elastic properties are dictated by the broader physics of the complete system and not explicitly specified in the interaction potentials. Conversely, comparative DPD and continuum RBC models require the a priori knowledge of elastic moduli, made explicit within their model functions.30,31 Therefore, the CGMD model is unique in allowing evolution of these properties, crucially enabling the testing of how elastic parameters change under new stimuli.
However, CGMD cell models such as this are very computationally expensive, due to their high resolution requiring a very large number of particles to comprise a full-scale cell. Therefore, they have historically had simulations restricted to only small patches of membrane.8,32 Only recently has a full-scale CGMD RBC been modelled in its entirety31. Despite being an implicit-fluid model with notable care taken to ensure computational efficiency, simulating the full-scale cell (consisting of 3.2 million particles) for 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 time-steps on 20 CPU cores still took on the order of a day. An alternative approach has been to simulate cells in “miniature”, as has been done to date with the whole-cell CGMD model of Fu et al.29,33 To increase computational efficiency, cells are built from a far smaller number of particles. However, as the same high resolution length scaling is maintained, the physical cell size is significantly reduced. To our knowledge, such CGMD models of RBCs have only been validated qualitatively by studying their shape at rest and under flow conditions, with no quantitative verification of this “miniature cell” approach yet conducted.
000 time-steps on 20 CPU cores still took on the order of a day. An alternative approach has been to simulate cells in “miniature”, as has been done to date with the whole-cell CGMD model of Fu et al.29,33 To increase computational efficiency, cells are built from a far smaller number of particles. However, as the same high resolution length scaling is maintained, the physical cell size is significantly reduced. To our knowledge, such CGMD models of RBCs have only been validated qualitatively by studying their shape at rest and under flow conditions, with no quantitative verification of this “miniature cell” approach yet conducted.
1.1 Aims
The present work gives, to the best of our knowledge, the first quantitative assessment of the “miniature cell” approach to the CGMD RBC model of Fu et al.29 We do this by measuring the bending rigidity B through fluctuation analysis, confirming its scale invariability in the whole-cell, and dominance by the lipid bilayer. Firstly, the simulation methodology is outlined, before attempting the evolution of initially spherical cells of various model diameters to a biconcave stable state. The evolved whole-cell systems then have many contours recorded over an order of ms, allowing determination of B from fluctuation analysis. These results are then assessed against mechanical-cell and RBC theory along with past in vitro studies, to discuss the invariance of aspects of the model to the physical cell diameter.2 Materials and methods
2.1 RBC model
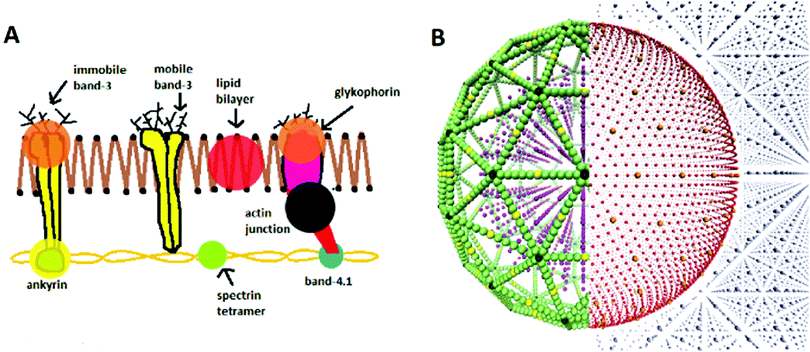
The model used in this work is that of Fu et al.,29 who built upon the lipid membrane model of Yuan et al.28 The model is that for a CGMD, 2-component RBC, with explicit representations of the lipid bilayer, cytoskeleton, and internal and external fluid particles (see Fig. 1A). The lipid bilayer is represented as a one-particle-thick monolayer of CG spherical particles, each representing a large number of constituent lipids. In determining a distance dependant function for lipid-lipid interactions in the bilayer, it is challenging to find a form that produces the correct diffusion of particles. It has been shown that the classical 12-6 Lennard-Jones (LJ) potential only produces two membrane phases, a solid at low temperatures and gas at high temperatures.34 At small separations the inter-particle forces are too strong to permit particle diffusion, and at large separations too weak to keep particles bound together. To provide the intermediate fluid phase necessary to allow such behaviour, a two branch interparticle function can be adopted.28This work adopts the lipid–lipid interaction potential of Yuan et al.,28 hereafter referred to as the Yuan potential. The Yuan potential has been shown to represent well the mechanical properties of a RBC bilayer membrane, including a diffusive fluid phase, due to the separation of attractive and repulsive branches.29 It has an orientational dependence which allows the complex lipid hydrophobicity to be represented, being essential for the self-assembly of the bilayer in an aqueous environment.8,35 The membrane properties of spontaneous curvature c0, bending rigidity B and diffusivity D are conveniently characterised by three Yuan model parameters, θ0, μY and ζ respectively. θ0 signifies the most energetically favourable angular configuration between particles, with μY weighting the energy penalty for deviation away from this. ζ controls the slope of the attractive branch of the potential. The potential also features the LJ-like parameters of length σ, energy well depth ε and cut-off radius rc. See S1 of the ESI† for further detail on the formalism of the potential.
While bilayer–bilayer interactions are managed by the Yuan potential, all other particle–particle interactions operate through classic 12-6 LJ potential functions. Assuming a typical RBC curvature c0 ∼ −0.5 m−1, the membrane curvature is parameterised as sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 = −1.41 × 10−3
θ0 = −1.41 × 10−3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36,37 (see S1 of the ESI† for detail on this calculation). A Hookean harmonic bond-potential is also used to couple the transmembrane proteins of the lipid bilayer to the cytoskeleton. The characteristic biconcave RBC shape can only be attained if the in-plane shear elastic energy is relaxed to zero, achieved in the biological cell by the constant structural remodelling of the spectrin network.8In silico this can be achieved by modifying the equilibrium bond length in the bond-potential so that the bond energy is initially zero, thus the cytoskeleton is initially stress free. The equilibrium bond length is made to be a variable corresponding to the initial bond lengths between each particle pair, rather than a constant as in the standard Hookean potential.29 The cell is then able to relax to a biconcave shape. The model parameterisation used is summarised in Table 1, generally following Fu et al.29 However, the particle masses set by Fu et al. fail to reproduce comparative elastic and diffusive properties in our simulations. Instead, better agreement is found with the mass of all membrane particles
36,37 (see S1 of the ESI† for detail on this calculation). A Hookean harmonic bond-potential is also used to couple the transmembrane proteins of the lipid bilayer to the cytoskeleton. The characteristic biconcave RBC shape can only be attained if the in-plane shear elastic energy is relaxed to zero, achieved in the biological cell by the constant structural remodelling of the spectrin network.8In silico this can be achieved by modifying the equilibrium bond length in the bond-potential so that the bond energy is initially zero, thus the cytoskeleton is initially stress free. The equilibrium bond length is made to be a variable corresponding to the initial bond lengths between each particle pair, rather than a constant as in the standard Hookean potential.29 The cell is then able to relax to a biconcave shape. The model parameterisation used is summarised in Table 1, generally following Fu et al.29 However, the particle masses set by Fu et al. fail to reproduce comparative elastic and diffusive properties in our simulations. Instead, better agreement is found with the mass of all membrane particles  , and all other particles σm.
, and all other particles σm.
| Particle interaction | Pair potential | σ | ε | r cut | ζ | μ Y | sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ0 θ0 |
|---|---|---|---|---|---|---|---|
| Fluid–fluid | LJ | 2.7 | 0.2 | ||||
| Fluid–cytoskeleton | LJ | 1.0 | 0.2 | ||||
| Cytoskeleton–cytoskeleton | LJ | 1.0 | 0.2 | ||||
| Bilayer–bilayer | Yuan | 1.0 | 1.0 | 2.6 | 4 | 3 | −1.41 × 10−3* |
| Bilayer–cytoskeleton | LJ | 1.0 | 0.2 | ||||
| Bilayer–fluid | LJ | 1.0 | 0.2 |
| Particle type | m M | ||||||
|---|---|---|---|---|---|---|---|
| Bilayer, cytoskeleton | 0.5* | ||||||
| fluid | 1.0* |
Simulations are run utilising the LAMMPS molecular dynamics coding package,38 operated as a library within Python. LAMMPS handles the thermodynamic evolution of the system, while particular biophysical calculations are performed in the parent Python code. Nose–Hoover algorithms are used for thermostat and barrostot thermodynamics, as documented by Shinoda et al.39 Initial particle configurations are input from an independent Python code which generates a 3D “supercell” volume containing the configuration of pseudo-particle types as required (see Fig. 1B), alongside particle classifications interpretable by LAMMPS. Simulations are performed in the system of non-dimensionalised LJ units. However, to compare results with past in vitro studies, quantities must then be converted to SI units. In the presented formalism, each variable i has an associated dimensional conversion parameter σi which relates the non-dimensional “model” LJ unit (denoted iM) to “real” SI unit (denoted iR). For example, the conversion of a length r from LJ units to meters is denoted rR[m] = σr[m]rM. All simulations were run on 1–4 nodes of the local supercomputer, with each node having two 14 core 2.4 GHz Intel E5-2680 v4 (Broadwell) CPUs, and 128 GB of RAM. See S2 and S3 of the ESI† for detail on the conversion of each physical unit and benchmark of the model respectively.
2.2 Planar fluctuation analysis
As RBC lipid membranes have a thickness much less than the diameter of the whole cell, they are classically describable as thermally fluctuating 2-dimensional sheets, with elastic energy dependant on their bending rigidity B and tension Σ.12 Furthermore, the lipid bilayer dominates the bending rigidity of the whole cell, as the internal plasma is entirely viscous and the cytoskeleton has negligible rigidity compared to the bilayer. Therefore, the bending rigidity of the whole cell should be representable solely from a planar patch of lipid membrane.7,8,32The bending rigidity of a planar membrane patch can be calculated by planar fluctuation analysis, from its height fluctuation spectrum.12 In the Monge representation, the height spectrum of the square planar membrane is given by h(r) ≡ h(x, y) = zi − 〈h〉, being the offset in height from the average across the entire membrane 〈h〉.40 The height of a cell zi is defined simply by the mean height of all particles within its bounds. Performing a 2D fast Fourier transform (FFT) on h(r) then gives the fluctuation spectra
 | (1) |
 | (2) |
2.3 Whole-cell fluctuation analysis
Once each cell has been equilibrated to its stable state, vesicle fluctuation analysis can be performed to determine the bending rigidity of the whole-cell. Simulations of the stable-state cells record the passive thermal fluctuations within series of contours: two-dimensional slices of membrane as seen from a top down view. As the biconcave regions were prompted to develop through the z axis, contours are taken in the (x, y) plane, thus having radial fluctuations measured in the plane of the disc. To remove stochastic rotation of the vesicle, the net angular momentum of membrane particles is set to zero at the start of each time-step. As fluctuation analysis is non-invasive, the orientation and centre-point of the cells then remain approximately fixed throughout the simulations. For each cell, contours are taken every 1000 steps (20 μs), for 1000 contours in total.As we have direct access to the coordinate data of each CG particle constituting our simulated vesicle, a contour detection algorithm is not necessary. Instead, we determine a contour from the explicit position data of our CG lipids at a given time. Each lipid particle in the vesicle membrane at time t has Cartesian coordinates r(x, y, z, t). Converting to spherical coordinates in the equatorial cross-section (at θ = π/2) gives its radial position  at angle ϕ = tan−1(y/x) around the membrane disc, relative to the midpoint of the vesicle (x0, y0, z0 = 0, t). The midpoint is simply defined as the centre of the maximum and minimum x and y coordinates of all lipids within the membrane, x0 = (xmax − xmin)/2 and y0 = (ymax − ymin)/2 respectively, approximately equivalent to the centre of mass.
at angle ϕ = tan−1(y/x) around the membrane disc, relative to the midpoint of the vesicle (x0, y0, z0 = 0, t). The midpoint is simply defined as the centre of the maximum and minimum x and y coordinates of all lipids within the membrane, x0 = (xmax − xmin)/2 and y0 = (ymax − ymin)/2 respectively, approximately equivalent to the centre of mass.
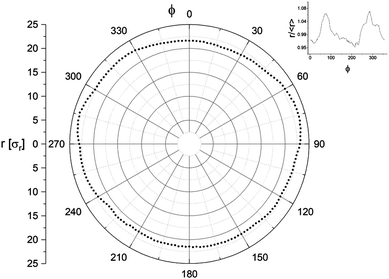
The angular distribution of a contour 0 ≤ ϕ ≤ 2π is segmented into Nϕ segments ϕi, each having radius ρ(ϕi, t) simply defined by the lipid within that segment at the largest radius. The ϕ-average radius of a particular contour is expressed as ρ(t) = 〈ρ(ϕi, t)〉. Fig. 2 shows an example polar plot of a contour. While our simulations are not subject to the resolution limit incurred through optical microscopy, a similar limit is instead imposed by our level of coarse-graining. As we maintain the same level of coarse-graining between all cells (defined by length unit σr = 5 nm) but simulate cells of different diameter, the larger cells comprise more particles and thus have a greater potential “resolution” in their contours. To maintain consistency between cells, we therefore make the number of radial arcs Nϕ depend on DM. As the contour circumference is πDM and the lipid–lipid spacing is ∼σr, there will be approximately πDM CG lipids cosmprising a contour. For the resolution to be sufficient, the number of contour segments must be a minimum of half the number of particles comprising that contour, meaning Nϕ > πDM/(2σr). Rounding the numbers slightly, we thus define Nϕ = 3.6DM.
Once the simulations have completed and all the contours have been recorded, a separate Python code is used for their analysis. The method employed is that developed successively by Faucon et al.,21 Mitov et al.,25 and Melerard et al.42 By decomposing the contour fluctuations into the spherical harmonics basis, their mean square amplitude can be derived to be
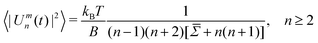 | (3) |
 .21 The mode n = 0 corresponds to variations in the mean vesicle radius, and n = 1 to variation in the centre of mass. Neither of these are relevant for the fluctuation analysis, so only modes n ≥ 2 are considered.
.21 The mode n = 0 corresponds to variations in the mean vesicle radius, and n = 1 to variation in the centre of mass. Neither of these are relevant for the fluctuation analysis, so only modes n ≥ 2 are considered.
To establish a connection between the experimentally observable two-dimensional contour slices and three-dimensional model that leads to eqn (3), the angular auto-correlation function (ACF) is introduced. Use of the angular ACF acts to correct for this dimensional simplification, mitigating almost all associated error in the intermediate modes; the modes that are most useful to experimentalists.21 For a given contour, the angular ACF is given by42
 | (4) |
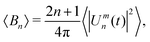 | (5) |
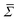 can then be determined from a χ2 fit of 〈Bn〉 against n. See S4 of the ESI† for a more thorough description of the analysis method.
can then be determined from a χ2 fit of 〈Bn〉 against n. See S4 of the ESI† for a more thorough description of the analysis method.
3 Results
3.1 Cell equilibration
To test the miniature-cell methodology, whole-cells are generated at various model diameters DM, with smaller cells comprising proportionally fewer CG particles. Before fluctuation analysis can be performed, the cells must first be evolved to their biconcave stable state. Each cell is initially generated as a spherical configuration of CG particles suspended within a fluid of water-like CG particles. The cell membrane is generated as two concentric spherical shells of bilayer and inner cytoskeleton, enclosing an internal CG fluid representing the cytoplasm. Largely following Fu et al.,29 each particle type is then thermodynamically activated sequentially as follows:• An isothermal–isobaric (NPT) ensemble is applied to the external water over 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. Concurrently, the canonical ensemble (NVT) is applied to the internal fluid, only being under the influence of a thermostat.
000 steps. Concurrently, the canonical ensemble (NVT) is applied to the internal fluid, only being under the influence of a thermostat.
• The spectrin, ankyrin and junctional complexes of the cytoskeleton are then equilibrated with the NPT ensemble over 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps.
000 steps.
• Finally, the lipids and transmembrane proteins in the bilayer are equilibrated using the NVT ensemble over 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps.
000 steps.
Each cell is equilibrated from its initially spherical state with time-step length τ = 0.02σt, pressure PM = 0.05, and temperature ramping from TM = 0.02–0.23.29 Under the default parameterisation of Table 1, the shape evolution was found to introduce significant instabilities, and often result in the cells “popping”. To prevent this, some model parameters are changed specifically for these initial shape evolution simulations: the membrane particles have their mass increased to σm, and the energy well depth in the Yuan potential is increased to ε = 1.5, to temporarily strengthen the lipid bindings.
Membrane folding is then induced by reducing the initial number of internal fluid particles NIF,0 to a final number NIF (see Table 2). Small, equal and opposite forces are also applied to circular areas on each XY face of the cell to promote biconcave indents to manifest perpendicular to the XY-plane. Particles are deleted gradually to a final fraction of internal fluid particles nIF = NIF/NIF,0, differing with cell size. The rate of compression has an effect on both the equilibrium shape and stability of the transition.7,29 All cells have NIF reduced at a constant rate of 3% every 5000 time-steps, determined to be most conducive to achieving a biconcave final state. The concave regions of the cells then develop gradually with the compression. Deviation from this rate results in alternative unwanted vesicle transitions such as to prolate, dumbbell rods, or inward or outward budding.7
Only cells with diameter DM ≥ 100 (DR ≥ 0.5 μm) were able to achieve a biconcave discocyte final state, with smaller cells instead relaxing to bowl-shaped stomatocytes (see Table 2). The degree of biconcavity in a healthy RBC can be characterised by the volume–radius ratio V/R3 = 1.57.37 An optimal particle fraction nIF for each cell is found by slowly deleting internal fluid particles until a target volume-radius ratio is reached. To achieve a consistent volume–radius ratio between cell sizes nIF is found to be inversely proportional to DM. Furthermore, below a critical ratio V/R3 ≲ 1.9 the internal fluid becomes unable to fill the region between the two enclosing membrane edges, closing the gap. This critical ratio does not appear to have a direct relationship with cell-size. However, the effect is more pronounced for the biconcave cells, being suppressed in the bowl-shaped DM < 100 (DR < 0.5 μm) cells. To maintain consistency between cells, nIF is chosen such that cells are compressed to V/R3 = 2.0 ± 0.1, slightly higher than that of a physical RBC. However, cells of diameter DM ≥ 100 still achieved morphologies closely resembling those of a healthy human RBC (see Table 2).
3.2 Planar fluctuation analysis
To measure the bending rigidity of the lipid bilayer specifically, planar fluctuation analysis is performed on a two-dimensional patch of CG lipids. A square patch of isolated lipid membrane of side lengths LM = 120 is generated, suspended within a super-cell volume of dimensions {LX, LY, LZ}M = {122.0, 122.0, 32.4}. Simulations of this system are run over 2 × 106 steps of length τ = 0.001σt, equilibrated using a Berendsen barostat such as to achieve zero surface tension. To approximate the bending rigidity, the height fluctuation spectra of the patch is determined by eqn (1). On length-scales shorter than the thickness of the membrane, protrusion modes dominate the fluctuation spectra and eqn (2) breaks down.40 To avoid this, the membrane is mapped to a discrete 2D grid of size Nq2 such that the unit grid size l = L/Nq is greater than the thickness of the membrane: namely l = 2σr. Fig. 3 shows the resulting spectrum in the small wave-number region, where a fit of eqn (2) determines B2D = 18.3kBT, matching closely the result of B = 18kBT by Fu et al.29A further use of this planar bilayer system is to determine the system time-scale, through measuring the mean-squared-displacement (MSD).8 Comparing the resolved diffusivity against a typical value for an RBC bilayer reveals the approximate simulation time scale of σt = 80 ns, matching closely with the previous value σt = 100 ns of Fu et al.29 See S2.1 of the ESI† for detail on this calculation.
3.3 Whole-cell fluctuation analysis
To calculate the bending rigidity of the stable RBCs, the whole-cell fluctuation analysis is employed on the evolved cells. The coefficients 〈Bn(t)〉 are taken from the mean of 6 repeat simulations of each cell size, with standard error taken in that mean. In the bending dominated regime, the relaxation time of a mode n in a cell of radius R can be approximated as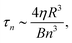 | (6) |
 , causing an overestimation in B. There is also a notable cutoff at n∼ 30, beyond which B exponentially falls, indicating a resolution limit. The surface tension fit poorly, likely due to a combination of high error in the coefficients, and fits being performed at high modal regimes where the surface tension is insignificant. Therefore, we performed the fits fixing an assumed approximation
, causing an overestimation in B. There is also a notable cutoff at n∼ 30, beyond which B exponentially falls, indicating a resolution limit. The surface tension fit poorly, likely due to a combination of high error in the coefficients, and fits being performed at high modal regimes where the surface tension is insignificant. Therefore, we performed the fits fixing an assumed approximation 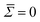 .43 To confirm that these modal ranges produced non-correlated coefficients 〈Bn〉, the time-lag ACF was generated over extended simulations of the DM = 50 (DR = 0.25 μm) and DM = 150 (DR = 0.75 μm) cells. Within these chosen spectral ranges, no notable correlation was seen within the first 1000 contours.
.43 To confirm that these modal ranges produced non-correlated coefficients 〈Bn〉, the time-lag ACF was generated over extended simulations of the DM = 50 (DR = 0.25 μm) and DM = 150 (DR = 0.75 μm) cells. Within these chosen spectral ranges, no notable correlation was seen within the first 1000 contours.
| D M | D R (μm) | n min | n max | B (kBT) | Reduced-χ2 |
|---|---|---|---|---|---|
| 50 | 0.25 | 4 | 24 | 17.0 ± 0.9 | 3.2 |
| 75 | 0.375 | 5 | 28 | 17.3 ± 0.8 | 8.6 |
| 100 | 0.5 | 5 | 29 | 18.9 ± 0.6 | 5.2 |
| 125 | 0.625 | 8 | 29 | 16.3 ± 0.7 | 1.6 |
| 150 | 0.75 | 10 | 29 | 18.0 ± 0.7 | 2.6 |
| 175 | 0.875 | 13 | 29 | 19.5 ± 1.0 | 1.8 |
| 200 | 1.0 | 14 | 29 | 19.6 ± 2.0 | 7.0 |
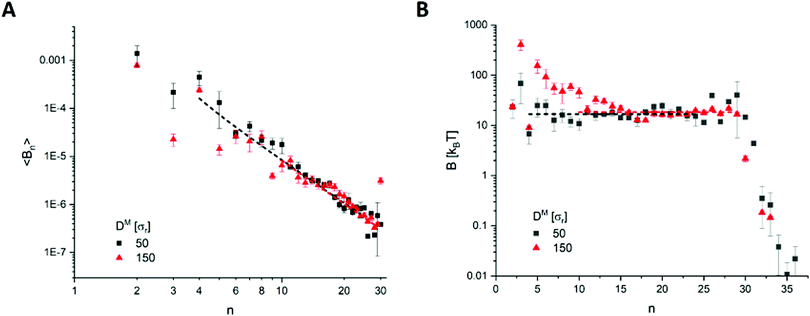 | ||
| Fig. 4 Example results from the DM = 50 (DR = 0.25 μm) and DM = 150 (DR = 0.75 μm) cells, with (A) fitting over the spectrum of coefficients 〈Bn(t)〉, and (B) the bending rigidity B as calculated by eqn (5). | ||
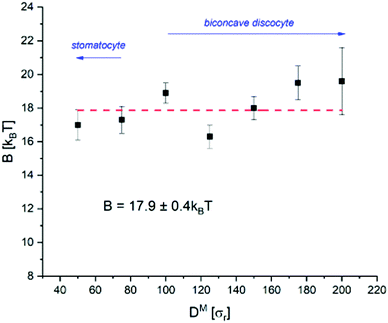
From Fig. 5, there does not appear to be any notable relationship between B and D within the bounds of error, indicating B to indeed be invariant to the physical cell diameter across the sizes tested. While there appears to be a slight increase at DM > 150 (DR > 0.75 μm), we do not believe this to be significant considering the much larger uncertainty in measurement of these largest cells. The mean rigidity across all cells is determined to be B3D = 17.9 ± 0.4kBT. However, there is more scatter about the mean than can be accounted for by the calculated error for multiple cell-sizes. This is most likely due to an under-representation of the error. For example, the complex evolved morphological differences between each cell-size may have introduced measurement error that has not been possible to account for. Given our energy unit σε = 1.76 × 10−20 J, our mean bending rigidity of B3D = 17.9 ± 0.4kBT = 3.15 × 10−19 J matches well with the literature on healthy human RBCs (2–9 × 10−19 J14,16,44). Furthermore, the result from the analysis on the two-dimensional patch of bilayer (B2D = 18.3kBT) also falls within the margin of error of B3D. Therefore, we have shown the model correctly reproduces the theory on both counts: (1) the bending rigidity is invariant to the cell diameter, and (2) the bending rigidity of the whole cell can be represented solely from a planar section of its bilayer.
4 Discussion
The primary goal of this work has been to study the scale invariance of the employed CGMD RBC model, to help justify the use of miniaturised cells in future studies. As hoped, we have observed invariance to cell size in both the cell morphology and in the bending rigidity as calculated through fluctuation analysis. However, the CG nature of the model did introduce limitations on the morphology and contour resolution. Cells of different physical diameter were found to evolve to different total morphology (biconcave discocyte or stomatocyte), and cells of the same size would also develop varied non-axial deformities within these shapes. For example, cells would develop as non-axial discocytes where the cell thickness was non-uniform, or having concave regions of varying depth and shape. Only cells of DM ≥ 100 evolved to the characteristic biconcave discocyte shape of a healthy RBC, with smaller cells relaxing to bowl-shaped stomatocytes (see Table 2). This variation in morphology is most likely due to the number of degrees of freedom available from the number of constituent CG particles. Smaller cells are comprised of fewer particles, thus will have fewer degrees of freedom for their configuration, making them less versatile to shape transitions. Therefore, we consider it reasonable to have found a lower DM limit on the cells able to form the more complex biconcave shape, and a complex relationship between DM and optimal internal fluid fraction nIF.Similarly, the CG nature of the model introduced a resolution limit on the fluctuation spectra. However, by applying the fluctuation analysis to contours of relative decomposition Nϕ = 3.6DM, a measurable range of modes was achieved for all cell sizes tested. Noise in the analysed spectra was notably higher for DM > 150 (DR > 0.75 μm), resulting in larger uncertainties in measurement of B. Considering the longer relaxation times in these larger cells this is not surprising, as they would require significantly longer simulation times to avoid producing poorer statistics. Computational limitations from poor model scaling (see S3 of the ESI†) made this unfeasible, thus also the reliable testing of cells of DM > 200 (DR > 1.0 μm). Considering this, the bending rigidity as measured by whole-cell fluctuation analysis is determined to be invariant to RBC scale based on the measured range of 0.25–1.0 μm diameter.
4.1 Experimental differences
When applying fluctuation analysis, there are some notable differences between the methodology when applied in silico to in vitro. Fundamentally, the bending rigidity of a vesicle is extracted by measuring the spatial undulations of its membrane over time. This is achieved experimentally through light microscopy, where a camera captures consecutive images of a vesicle over a chosen exposure time. As a microscope only allows visualisation in its focal plane, one is experimentally limited to capturing two-dimensional contour slices of the vesicle. The inherently three-dimensional analysis must then be simplified to the two-dimensional contours available, with the error this introduces being relative to the discrepancy of a vesicle from being spherical. As our simulations provide direct access to the fully three-dimensional position data of the constituent particles, this experimental restriction is not forced upon us. However, the purpose of this work is to verify that the utilised model correctly represents certain properties of the physical cell. By approaching this through comparison against past in vitro studies, it is best to emulate those experimental methods as closely as possible. Therefore, we still restrict ourselves to the same two-dimensional contour analysis, to best compare our results against such experimental studies.There are many other benefits to not requiring a camera, notably in the potential resolution of a contour. As cameras have a finite resolution, there is then an upper limit to the fidelity at which a point on the membrane can be determined by optical microscopy. Experimentally, once a digital image of the cell has been captured, the radial profile of the membrane must be extracted by some form of “contour detection algorithm”. This is typically performed by classifying peaks in a grey-level intensity spectrum across the image. A fluctuation of wavelength shorter than the pixel size or resolution will then not be detectable. The early approaches of Faucon et al.21 and Duwe et al.45 achieved accuracies of 100 nm and 250 nm respectively, of the order of the image pixel (being around 100 nm). By using more precisely the sigmoid-shape of the grey-level profile, Pecreaux et al.15 achieved an order of magnitude improvement, with radial measurements of the contour within 10 nm. Our having direct access to the particle positions bypasses these considerations. However, we have instead a comparable resolution-like limit from our level of coarse-graining. Each of our spherical CG lipids is σr = 5 nm in diameter, also with minimum inter-particle separation of σr. This then implies a comparable maximum resolution to that of Pecreaux et al.15 We observed a hard resolution limit at n = 30, lower than implied from our CG resolution. The wavelength of a mode is λ ∼ πDM/n. The 30th mode thus has a wavelength λ ∼ 5σr for the DM = 50 cell and λ ∼ 16σr for the DM = 150 cell. If our resolution limit was σr = 5 nm as expected, we should theoretically be able to measure modes in their 100's. This discrepancy is most likely due to the discrete particle nature of the model.
Cameras introduce a further source of error in their aperture time (shutter speed) τSS: the length of time over which light is collected to take the image. The higher the mode of a fluctuation, the higher its frequency and the shorter its relaxation time. Therefore, τSS introduces a limit to the wave-numbers detectable, with only fluctuations having a longer lifetime being measurable (τn > τSS). From eqn (6), for a typical camera exposure time of τSS = 33 ms measuring fluctuations of an 8 μm diameter RBC of B = 10−19 J in a solvent of η = 10−3 kg m−1 s−1, this corresponds to a lower limit of n ∼ 4.15
While our simulations are not limited by a cameras shutter speed, they are notably more constrained by the total exposure time – the length of time over which contours are taken. The lower the mode, the longer its relaxation time thus the longer time it takes to gain sufficient statistics in its spectrum of configurations. While in vitro experiments are able to collect thousands of contours over minutes (2000 contours over 1 minute,15 3–4000 contours over ∼2 minutes,23 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 contours over 10 minutes42), we are heavily constrained by our model timescale σt. To maintain numerical stability in the simulations, the shortest time-step size possible was τ = 0.02σt = 1.6 ns. To simulate just 5 seconds of the DM = 150 cell would then take up to 40 days to complete (see S3 of the ESI† for a benchmark). From eqn (6), it will take ∼1000 time-steps for the 5th mode in our DM = 150 cell to complete a single relaxation. Therefore, it is not possible for us to gain comparable statistics in the lower modes.
000 contours over 10 minutes42), we are heavily constrained by our model timescale σt. To maintain numerical stability in the simulations, the shortest time-step size possible was τ = 0.02σt = 1.6 ns. To simulate just 5 seconds of the DM = 150 cell would then take up to 40 days to complete (see S3 of the ESI† for a benchmark). From eqn (6), it will take ∼1000 time-steps for the 5th mode in our DM = 150 cell to complete a single relaxation. Therefore, it is not possible for us to gain comparable statistics in the lower modes.
Fundamentally, this combination of considerations of contour resolution, shutter speed and exposure time define the spectral-range of modes best considered in fluctuation analysis. Fluctuations of wavelength shorter than the optical resolution are not detectable, and those rapid relaxation times will be shorter than can be captured within a cameras shutter speed. In practice, this means that light microscopy is unable to reliably measure modes n ≳ 20.46 Conversely, our comparatively high resolution and lack of a shutter speed allows reliable measurement at higher mode numbers (n ≲ 30). However, our very short exposure time heavily limits our ability to gain statistical significance in the lower modes, becoming even more pronounced with increasing cell size. Therefore, we analysed spectral ranges relative to the cell-diameter. Each cell had contours recorded every 1000 time-steps, for a total of 1000 contours. From eqn (6), this then equates to measuring at least 1500 full fluctuations in each assessed mode. However, even on a state of the art HPC, it was infeasible to simulate cells more than just an 1/8th the diameter of a full-scale RBC for a sufficient time to gain statistically meaningful results from this analysis. This highlights the computational challenges faced when attempting whole-cell CGMD simulation, and practical benefit of the miniature-cell approach.
5 Conclusion
The scale invariance of a CGMD model for a single RBC has been tested in silico, first qualitatively through the shape evolution, then quantitatively through fluctuation analysis. By evolving cells of various diameter from their initially spherical configurations, those of DM ≥ 100 (DR ≥ 0.5 μm) were found able to develop the characteristic biconcave discocyte shape of a healthy RBC. The passive thermal fluctuations of all evolved cells were then observed in their equatorial contours, and the bending rigidity calculated through fluctuation analysis using the angular ACF. The theory on RBC mechanics states that: (1) the bending rigidity of cells of micron-order diameter should be invariant to size; and (2) that the bending rigidity of the whole-cell should be equivalent to that of an isolated plane of its lipid bilayer. The model successfully represented the theory on both counts. No notable relationship was found between the rigidity and cell size over the range 50 ≤ DM ≤ 200 (0.25 ≤ DR ≤ 1.0 μm) tested, and the value B2D = 18.3kBT determined from the lipid plane fell within the margin of error of the mean from the whole-cell analysis B3D = 17.9 ± 0.4kBT. However, the very short exposure time computationally feasible at the larger cell sizes resulted in poor statistics for cells DM > 150 (DR > 0.75 μm), with significant increase in the measurement uncertainty. Therefore, we conclude the use of miniature CGMD cells of 100 ≤ DM ≤ 150 best able to reproduce the morphological and elastic responses of an RBC in silico, in the properties tested. This finding supports the use of the miniature cell approach in further studies, with its considerable computational advantages opening up numerous possibilities in simulations of physically larger, more numerous and more complex CGMD cellular systems than have been performed to-date.Author contributions
P. A. carried out all research, simulations, data analysis and writing of the article. S. H. and A. M. S. supervised the research and reviewed drafts of the manuscript, as the primary and secondary PhD supervisors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank S.-P. Fu for their help in initial implementation of the model, and N. J. Brooks for helpful discussion about fluctuation analysis. This work was carried out using the computational facilities of the Advanced Computing Research Centre, University of Bristol – http://www.bris.ac.uk/acrc/. P. A. was funded through an EPSRC studentship EP/R513179/1.Notes and references
- T. Ye, N. Phan-Thien and C. T. Lim, J. Biomech., 2016, 49, 2255–2266 CrossRef PubMed.
- X. Li, P. M. Vlahovska and G. E. Karniadakis, Soft Matter, 2013, 9, 28–37 RSC.
- X. Li, H. Lu and Z. Peng, Handbook of Materials Modeling: Applications: Current and Emerging Materials, 2020, pp. 2593–2609 Search PubMed.
- X. Li, Z. Peng, H. Lei, M. Dao and G. E. Karniadakis, Philos. Trans. R. Soc. A, 2014, 372, 20130389 CrossRef PubMed.
- S. Henon, G. Lenormand, A. Richert and F. Gallet, Biophys. J., 1999, 76, 1145–1151 CrossRef CAS PubMed.
- C. T. Lim, M. Dao, S. Suresh, C. H. Sow and K. T. Chew, Acta Mater., 2004, 52, 1837–1845 CrossRef CAS.
- H. Yuan, C. Huang and S. Zhang, Soft Matter, 2010, 6, 4571–4579 RSC.
- H. Li and G. Lykotrafitis, Biophys. J., 2012, 102, 75–84 CrossRef CAS PubMed.
- N. M. Geekiyanage, M. A. Balanant, E. Sauret, S. Saha, R. Flower, C. T. Lim and Y. Gu, PLoS One, 2019, 14, e0215447 CrossRef CAS PubMed.
- Z. Peng, X. Li, I. V. Pivkin, M. Dao, G. E. Karniadakis and S. Suresh, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 13356–13361 CrossRef CAS PubMed.
- F. Brochard and J. F. Lennon, J. Phys., 1975, 36, 1035–1047 CrossRef.
- M. Mutz and W. Helfrich, J. Phys., 1990, 51, 991–1001 CrossRef CAS.
- E. A. Evans, Biophys. J., 1983, 43, 27–30 CrossRef CAS PubMed.
- R. Garcia, N. Bezlyepkina, R. Knorr, R. Lipowsky and R. Dimova, Soft Matter, 2010, 6, 1472–1482 RSC.
- J. Pécréaux, H.-G. Döbereiner, J. Prost, J.-F. Joanny and P. Bassereau, Eur. Phys. J. E: Soft Matter Biol. Phys., 2004, 13, 277–290 CrossRef PubMed.
- Y.-Z. Yoon, H. Hong, A. Brown, D. C. Kim, D. J. Kang, V. L. Lew and P. Cicuta, Biophys. J., 2009, 97, 1606–1615 CrossRef CAS PubMed.
- M. B. Schneider, J. T. Jenkins and W. W. Webb, J. Phys., 1984, 45, 1457–1472 CrossRef CAS.
- H. Engelhardt, H. P. Duwe and E. Sackmann, J. Phys. Lett., 1985, 46, 395–400 CrossRef CAS.
- I. Bivas, P. Hanusse, P. Bothorel, J. Lalanne and O. Aguerre-Chariol, J. Phys., 1987, 48, 855–867 CrossRef.
- S. T. Milner and S. A. Safran, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 4371–4379 CrossRef CAS PubMed.
- J. Faucon, M. D. Mitov, P. Méléard, I. Bivas and P. Bothorel, J. Phys., 1989, 50, 2389–2414 CrossRef.
- M. I. Angelova, S. Soléau, P. Méléard, F. Faucon and P. Bothorel, Trends in Colloid and Interface Science VI, Darmstadt, 1992, pp. 127–131 Search PubMed.
- J. Henriksen, A. C. Rowat and J. H. Ipsen, Eur. Biophys., 2004, 33, 732–741 CrossRef CAS PubMed.
- H. Strey, M. Peterson and E. Sackmann, Biophys. J., 1995, 69, 478–488 CrossRef CAS PubMed.
- M. D. Mitov, J. F. Faucon, P. Méléard, I. Bivas and P. Bothorel, in Advances in Supramolecular Chemistry Vol. 2, ed. G. W. Gokel, Jai Press, Greenwich, 1992, pp. 93–139 Search PubMed.
- V. Rajagopal, W. R. Holmes and P. V. S. Lee, Wiley Interdiscip. Rev.: Syst. Biol. Med., 2018, 10, e1407 Search PubMed.
- J. Drouffe, A. Maggs and S. Leibler, Science, 1991, 254, 1353–1356 CrossRef CAS PubMed.
- H. Yuan, C. Huang, J. Li, G. Lykotrafitis and S. Zhang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82, 011905 CrossRef PubMed.
- S.-P. Fu, Z. Peng, H. Yuan, R. Kfoury and Y.-N. Young, Comput. Phys. Commun., 2017, 210, 193–203 CrossRef CAS.
- D. A. Fedosov, B. Caswell and G. E. Karniadakis, Biophys. J., 2010, 98, 2215–2225 CrossRef CAS PubMed.
- Y.-H. Tang, L. Lu, H. Li, C. Evangelinos, L. Grinberg, V. Sachdeva and G. E. Karniadakis, Biophys. J., 2017, 112, 2030–2037 CrossRef CAS PubMed.
- H. Li and G. Lykotrafitis, Biophys. J., 2014, 107, 642–653 CrossRef CAS PubMed.
- M. Becton, R. D. Averett and X. Wang, Biomech. Model. Mechanobiol., 2019, 18, 425–433 CrossRef PubMed.
- I. R. Cooke, K. Kremer and M. Deserno, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 72, 011506 CrossRef PubMed.
- H. Noguchi, J. Phys. Soc., 2009, 78, 041007 CrossRef.
- C. Pozrikidis, Math. Med. Biol., 2005, 22, 34–52 CrossRef CAS PubMed.
- D. Hartmann, Biomech. Model. Mechanobiol., 2010, 9, 1–17 CrossRef PubMed.
- A. P. Thompson, S. J. Plimpton and W. Mattson, J. Chem. Phys., 2009, 131, 154107 CrossRef PubMed.
- W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 134103 CrossRef.
- Z.-J. Wang and D. Frenkel, J. Chem. Phys., 2005, 122, 234711 CrossRef PubMed.
- M.-J. Huang, R. Kapral, A. S. Mikhailov and H.-Y. Chen, J. Chem. Phys., 2012, 137, 055101 CrossRef PubMed.
- P. Méléard, T. Pott, H. Bouvrais and J. H. Ipsen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 116 CrossRef PubMed.
- F. Jähnig, Biophys. J., 1996, 71, 1348–1349 CrossRef.
- J. Evans, W. Gratzer, N. Mohandas, K. Parker and J. Sleep, Biophys. J., 2008, 94, 4134–4144 CrossRef CAS PubMed.
- H. P. Duwe, J. Kaes and E. Sackmann, J. Phys., 1990, 51, 945–961 CrossRef CAS.
- Y. Z. Yoon, J. P. Hale, P. G. Petrov and P. Cicuta, J. Phys.: Condens. Matter, 2010, 22, 062101 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01542g |
| This journal is © The Royal Society of Chemistry 2022 |