 Open Access Article
Open Access ArticleThe fuzzy sphere morphology is responsible for the increase in light scattering during the shrinkage of thermoresponsive microgels†
Ekaterina
Ponomareva
 a,
Ben
Tadgell
b,
Marco
Hildebrandt
a,
Marcel
Krüsmann
a,
Sylvain
Prévost
a,
Ben
Tadgell
b,
Marco
Hildebrandt
a,
Marcel
Krüsmann
a,
Sylvain
Prévost
 c,
Paul
Mulvaney
c,
Paul
Mulvaney
 b and
Matthias
Karg
b and
Matthias
Karg
 *a
*a
aInstitut für Physikalische Chemie I: Kolloide und Nanooptik, Heinrich-Heine-Universität Düsseldorf, Universitätsstrase 1, D-40225 Düsseldorf, Germany. E-mail: karg@hhu.de
bARC Centre of Excellence in Exciton Science, The University of Melbourne, School of Chemistry, Parkville, VIC 3010, Australia
cLarge Scale Structures, Institut Laue-Langevin, 71 avenue des Martyrs, CS 20156, 38042, Grenoble Cedex 9, France
First published on 13th December 2021
Abstract
Thermoresponsive microgels undergo a volume phase transition from a swollen state under good solvent conditions to a collapsed state under poor solvent conditions. The most prominent examples of such responsive systems are based on poly-(N-isopropylacrylamide). When cross-linked with N,N′-methylenebisacrylamide, such microgels typically possess a fuzzy-spherelike morphology with a higher cross-linked core and a loosely cross-linked fuzzy shell. Despite the efforts devoted to understanding the internal structure of microgels and their kinetics during collapse/swelling, the origins of the accompanying changes in light scattering intensity have barely been addressed. In this work, we study core–shell microgels that contain small gold nanoparticle cores with microgel shells of different thicknesses and cross-linker densities. All microgels are small enough to fulfill the Rayleigh-Debye-Gans criterion at all stages of swelling. Due to the high X-ray contrast of the gold cores, we can use absolute intensity small-angle X-ray scattering to determine the number density in the dilute dispersions. This allows us to extract polymer volume fractions of the microgels at different stages of swelling from form factor analysis of small-angle neutron scattering data. We match our findings to results from temperature-dependent absorbance measurements. The increase in absorbance during the shrinkage of the microgels is related to the transition from fuzzy spheres to hard sphere-like scattering objects with a rather homogeneous density profile. We provide a first attempt to model experimental spectra using finite difference time domain simulations that take into account the structural changes during the volume phase transition. Our findings significantly contribute to the understanding of the optical properties of thermoresponsive microgels. Further, we provide polymer volume fractions and microgel refractive indices as a function of the swelling state.
1 Introduction
Microgels are soft polymeric objects with dimensions in the colloidal regime and an internal gel-like structure.1 The properties of microgels lie between those of colloids, surfactants and macromolecules.2 Under good solvent conditions, microgels can be swollen by enormous amounts of solvent rendering them soft and deformable.3–8 Responsive, or so-called ‘smart’, microgels are composed of polymers that respond to external stimuli such as temperature, pH, ionic strength and light. This response manifests itself asi a significant reduction in the microgel volume in response to the stimulus, due to the release of solvent from the microgel interior. The most prominent examples are poly-(N-isopropylacrylamide) (PNIPAM) microgels. These gels feature a volume phase transition (VPT) in water with a transition temperature (VPTT) close to human body temperature. This VPT behavior is related to the lower critical solution temperature (LCST) behavior of linear PNIPAM homopolymers with a transition temperature, TLCST, of approximately 32 °C.9 PNIPAM microgels were first introduced by Pelton and Chibante who used free radical polymerization for the microgel preparation.10 Due to faster consumption of the chemical cross-linker N,N′-methylenebisacrylamide (BIS) during the precipitation polymerization of NIPAM, PNIPAM microgels possess an inhomogeneous polymer density.11 The swollen state microgel structure can be considered as core–shell-like with a denser, more highly cross-linked core and a less highly cross-linked outer shell.12,13 Above the VPTT, collapsed microgels can be considered as hard sphere-like with a homogeneous polymer density. This structural transition has been the topic of countless studies. Small-angle neutron scattering is one of the most frequently used methods for the investigation of the microgel form factor. Stieger et al. introduced a radial density profile model that describes the form factor of microgels in the swollen as well as in the collapsed state.14 This fuzzy sphere model assumes an inner microgel core of homogeneous polymer content and an outer fuzzy shell with a continuously decaying polymer content. The model is well accepted and has been applied to many different microgel systems. Due to the fascinating development of superresolution optical microscopy techniques, the inhomogeneous network structure has also been confirmed by real-space imaging.15–17 Nowadays, computational numerical methods are powerful tools for describing microgels and their internal structure.18,19 While atomistic simulations are suitable for small systems, monomer-resolved models allow for simulations at longer times and larger length-scales.The swelling behavior of thermoresponsive microgels is often described by the Flory–Rehner theory.20,21 While the evolution of the hydrodynamic particle size can be precisely measured by dynamic light scattering (DLS), the Flory–Rehner theory also requires the polymer volume fraction at a specified reference state. Several studies use volume fractions of collapsed microgels as the reference state where variations in cross-linking density appear rather negligible.14,22–25 Nevertheless, reference volume fractions used in literature vary significantly and are often estimated from different experiments.12,14,22–28
Surprisingly, little attention has been paid to how the UV-visible spectroscopic properties of PNIPAM microgels depend on their state of swelling and thus polymer volume fraction. A priori, one would expect a decrease in light scattering intensity and thus absorbance when microgels collapse. The Rayleigh–Debye–Gans (RDG) approximation, which holds for particles that have a low refractive index contrast and dimensions smaller than the wavelength of visible light, would predict that the scattering intensity increases with the sixth power of the radius of scattering objects (R6). However, absorbance is in fact observed to increase when microgels collapse in response to external stimuli as, for example, temperature. This is commonly attributed to the increase in microgel refractive index due to the release of water and the resulting increase in polymer volume fraction.29–33 Any increase in refractive index can be monitored optically by using gold nanoparticles as plasmonic probes. Since the localized surface plasmon resonance (LSPR) of gold nanoparticles is sensitive to the effective refractive index environment in the close viscinity of the nanoparticle surface, even small changes can be monitored as predicted theoretically34 and demonstrated in experiments using gold–PNIPAM hybrid microgels.29,35–38 In order to use the LSPR to monitor structural transitions in thermoresponsive microgels one has to keep in mind that the intensity of light scattered by the microgels also changes during the VPT. Since this scattering is wavelength dependent, LSPR positions extracted directly from UV-Vis spectra are often not correct due to the visible background scattering. As the wavelength scaling of the microgel scattering changes during microgel collapse, the LSPR is also affected. This can be accounted for by subtraction of the scattering contribution from measured spectra as described in detail in the ESI,† of the paper by Rauh et al.39 When scattering dominates the spectral response of gold–microgel hybrid particles, either due to small dimensions of the gold particles or very large microgel sizes, the extraction of LSPR positions from experimental spectra becomes highly defective or simply impossible.
In this work, we study the VPT behavior of core–shell (CS) microgels that feature small gold nanoparticle cores and thermoresponsive PNIPAM microgel shells. The general structure of these microgels is depicted in Scheme 1. Importantly the gold cores are too small to significantly influence the swelling behavior of the PNIPAM microgels. Thus, physically our CS microgels can be considered comparable to classical PNIPAM microgels that do not feature inorganic cores. We systematically study the influence of the microgel size and cross-linking density on the polymer volume fraction during different stages of swelling.
The CS microgels are colloidally stable in water below and above the VPTT. We used absolute intensity small-angle X-ray scattering (SAXS) to determine the particle number concentration using the large contrast in X-ray scattering of the otherwise negligible gold cores. Using form factor analysis of SANS data, we determined the polymer density profiles for different states of swelling from which we could derive refractive index profiles. Effective volume averaged refractive indices of the microgels were also determined by refractometry. Given the microgel size and the average refractive index, all studied microgels fulfill the RDG criterion, even in the collapsed state. This is different to other studies in literature where larger microgels were employed and a transition from RDG scattering in the swollen state to Mie scattering in the collapsed state was observed.31 We followed the VPT by simple absorbance measurements using temperature-dependent UV-Vis spectroscopy. The observed increase in absorbance, i.e. sample turbidity, as the microgels collapse could not be described by RDG theory using effective, averaged microgel refractive indices. A core–shell model was used to calculate theoretical scattering cross-sections on the basis of finite difference time domain (FDTD) simulations. With our work, we attempt to link the microgel morphology and structural transitions during the VPT to the visible wavelength absorbance of dilute microgel dispersions. A general light scattering theory that allows one to precisely account for the microgel structure is currently not available.
2 Experimental section
2.1 Chemicals
Gold(III) chloride trihydrate (HAuCl4; Sigma-Aldrich, ≥99.999%), sodium citrate dihydrate (Sigma-Aldrich, ≥99%), sodium dodecyl sulfate (SDS; Sigma-Aldrich, p.a.), butenylamine hydrochloride (BA; Sigma-Aldrich, 97%), N-isopropylacrylamide (NIPAM; TCI, >98.0%), N,N'-methylenebisacrylamide (BIS; Sigma-Aldrich, ≥99%), potassium peroxodisulfate (PPS; Sigma-Aldrich, ≥99%), heavy water (D2O; Deutero GmbH, 99.9%) and 1,4-dioxane (p.a., Fisher Chemicals) were used as received. Water was purified with a MilliQ system (Millipore). The final resistivity of water was 18 MΩ cm. MilliQ-water was used for all syntheses and purifications.2.2 Synthesis
| Sample | NIPAM | BIS | Nominal molar ratio of cross-linkera (mol%) | R h swollen (nm) | R h collapsed (nm) |
|---|---|---|---|---|---|
| m (g) | m (g) | ||||
| a The nominal molar cross-linker ratio values are the ones used in the synthesis and not the ratios in the final microgel polymer network. | |||||
| CS1 | 0.228 | 0.048 | 15.3 | 111 (0.03) | 78 (0.04) |
| CS2 | 0.587 | 0.134 | 16.7 | 164 (0.02) | 118 (0.02) |
| CS3 | 0.946 | 0.194 | 14.8 | 190 (0.03) | 139 (0.01) |
| CS4 | 0.587 | 0.040 | 5.0 | 186 (0.04) | 104 (0.02) |
| CS5 | 0.587 | 0.200 | 24.9 | 157 (0.03) | 124 (0.02) |
2.3 Methods
3 Theory
3.1 LCST and cloud point of PNIPAM
In aqueous dispersion, PNIPAM features a miscibility gap above the LCST at TLCST. When heated to T > TLCST, the PNIPAM chains demix due to a drastically reduced solubility. For PNIPAM and LCST polymers in general, this demixing behavior is typically followed by turbidity measurements yielding the cloud point temperature Tcp. Below Tcp the polymer chains are in a soluble state. At Tcp the phase transition occurs and the polymer solution becomes turbid due to the formation of collapsed aggregates. This clouding of the solution is typically easy to monitor by a steep increase in turbidity. However, it is highly recommended to follow standard protocols for such measurements as reported values of Tcp can strongly differ due to differences in polymer concentration, wavelength, heating rate etc.45 Furthermore, it is important to note that Tcp and the LCST are typically not the same. The LCST corresponds to the temperature at the minimum of the binodal for which the concentration is equal to the lower critical solution concentration (LCSC).45,46 Thus, concentration dependent measurements are required if the LCST is to be determined. Often ignored is also that chain ends, e.g. from a chain transfer agent used in RAFT polymerization, can significantly alter the phase transition of a thermoresponsive polymer and affect Tcp, in particular for those with a low molecular weight. The molecular weight distribution is another factor crucial to the demixing as longer chains tend to precipitate first.46The LCST behavior of PNIPAM in water is responsible for the volume phase transition observed for PNIPAM microgels.
3.2 Light scattering and turbidity of PNIPAM microgels
In this work we study the optical response of dilute aqueous dispersions of thermoresponsive microgels composed of PNIPAM cross-linked with BIS. Thus, the system is significantly different to linear PNIPAM homopolymer chains in solution: (1) the cross-linker introduces chemical heterogenities that are distributed inhomogeneously within the microgels. (2) As a consequence of (1), the number of monomer units between two cross-linking points has a large dispersity and increases towards the outer periphery of the microgels. (3) The outer fuzzy corona of the microgels contains uncross-linked dangling ends. (4) The anionic radical initiator used in the synthesis introduces sulfate groups that are deprotonated at neutral and basic pH. As a consequence the microgels are slightly ionic.Despite these structural and chemical differences, the VPT of PNIPAM microgels is accompanied by similar turbidity changes to those observed for linear PNIPAM homopolymer chains. It is worth distinguishing between the two cases: (1) non-ionic microgels or ionic microgels at sufficiently high ionic strength will aggregate at temperatures close to the phase transition temperature where steric stabilization is lost. Here, attractive forces dominate and the microgels lose their soft repulsive character.47 The formation of aggregates is accompanied by a steep increase in turbidity similar to the behavior of individual polymer chains discussed before. (2) With given high enough electrostatic stabilization, i.e. through charged groups from an ionic radical initiator or chargeable comonomers, repulsive interactions dominate even at temperatures well above the phase transition temperature. In this case, the dispersion remains colloidally stable and shows a continuous increase in turbidity during the VPT from the swollen to the collapsed state.
The second case will be the one relevant to this study. Due to the typical microgel size, aqueous microgel dispersions are turbid even at low concentrations and under good solvent conditions. This turbidity is caused by light scattering due to a refractive index mismatch between microgels and water as dispersing medium. Generally, the light scattering properties of a colloidal dispersion can be described by the RDG theory if the following criteria are fulfilled:48
(1) The refractive index of the scattering objects, np, is close to the refractive index of the dispersing medium, ns:
| |1 − m| ≪ 1 | (1) |
 | (2) |
(2) The phase shift is small:
| kns2R|1 − m| ≪ 1 | (3) |
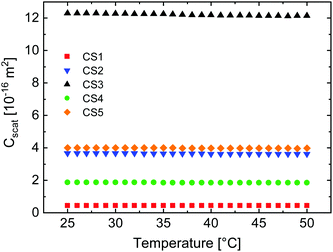
Here, k = 2π/λ is the magnitude of the wave vector ![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) with the wavelength λ and R is the radius of the scattering object. Substitution gives:
with the wavelength λ and R is the radius of the scattering object. Substitution gives:
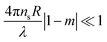 | (4) |
As we will show later, both criteria are well fulfilled for our CS microgels in the swollen state and even in the collapsed state where the refractive index contrast is significantly higher.
The scattering cross-section of an RDG scatterer, CRDGsca is given by:48,49
 | (5) |
Thus, at a given wavelength λ, the intensity of RDG scattering depends only on the particle radius and the refractive index contrast. In contrast to simple homogeneous spheres such as polystyrene or silica particles that possess a homogeneous refractive index, PNIPAM microgels are swollen by solvent with a solvent content that depends on the swelling state, i.e. the dispersion temperature. It is therefore necessary to consider the volume fractions of polymer (ϕ) and water (ϕwater = 1 − ϕ) inside the microgels to estimate the value of np:
| np = ϕ·npolymer + (1 − ϕ)·nwater | (6) |
The volume fraction of polymer is given by:
 | (7) |
Here, Vpolymer is the total volume of polymer – in our case PNIPAM – inside one microgel and Vmicrogel is the volume of the microgel with radius R. For thermoresponsive microgels, Vmicrogel and thus ϕ depend on temperature. Assuming that Vpolymer does not change in the temperature window considered in this work, i.e. 25 to 50 °C, ϕ scales with R as:
| ϕ(T) ∝ R−3(T) | (8) |
As ϕ increases when the microgels shrink, np also increases (see eqn (6)). This will in turn increase the light scattering. On the other hand, one has to keep in mind that the RDG scattering scales with the sixth power of R, leading to a reduction in scattering when the microgel shrinks, i.e. R decreases. We will later on address how each factor influences the scattering behavior of our CS microgels.
3.3 Absorbance measurements and scattering cross-section
The attenuation of incoming light of intensity I0 due to scattering and/or absorption by a sample is given by the Beer–Lambert law:| I(d) = I0exp(−CextNd) | (9) |
Here, I(d) is the intensity after the sample, Cext is the extinction cross-section, N is the number density of the sample and d refers to the pathlength. In the case of a non-absorbing sample that contains objects that only scatter light, the extinction is directly related to the scattering cross-section Cscat, i.e. Cext = Cscat. In a standard absorbance spectroscopy experiment, the measured absorbance A from a turbid, non-absorbing sample is given by:
 | (10) |
For more information regarding the conversion leading to eqn (10) please see the ESI.† Depending on the size of the scattering objects and the refractive index difference between particles with np and dispersing medium with ns, different theories can be applied to calculate and predict Cscat. In general, given a sample of low polydispersity scatterers, absorbance measurements can be applied to determine particle sizes.50 In this work, we will show that simple absorbance measurements are well-suited for following the scattering increase during microgel collapse.
4 Results and discussion
We used seeded precipitation polymerizations to synthesize Au–PNIPAM CS microgels that differ in thickness and cross-linking of the shells. All syntheses were performed with polycrystalline, monodisperse AuNP cores. Three batches of cores were synthesized to yield the quantities needed for all CS systems. The average diameter of the cores from TEM is 15.3 nm for all batches. The standard deviation of the diameter shows small differences between the batches. On average the polydispersity is 10%. For the PNIPAM encapsulations, only the amounts of monomer and cross-linker were varied to yield the different CS particles (see Table 1). We want to highlight that the core volume is negligible with respect to the total microgel volume (≪1%) for all samples. Consequently, we do not expect any significant influence of the cores on the swelling behavior of the PNIPAM shells. Physically the CS particles behave just like standard microgels without cores – apart from the absorption that is related to the LSPR of the AuNPs.39 The role of the cores is twofold in our study: (1) the cores act as seeds for the precipitation of PNIPAM during the polymerization and thus allow for precise control of the microgel size.41 (2) The cores serve as useful markers due to their LSPR properties and large scattering contrast in SAXS.Before looking at the optical properties of the microgels in detail, we will discuss some of their general properties.
4.1 General characterization of CS microgels
The core size and shape as well as the morphology of the overall CS microgels were studied by TEM. Fig. 1(a) shows representative TEM images of all five microgel batches. Due to the large difference in electron density, the cores and PNIPAM shells can be clearly distinguished. All samples have single AuNP cores homogeneously encapsulated in the PNIPAM shells. A detailed analysis of several TEM images for each of the five CS microgels revealed that on average less than 5% of the microgels have no core. In the case of CS4, that is the sample with the lowest cross-linking density, the core positions seem to be mostly off-centre. This is something that we observed before for CS microgels with a cross-linker density of 10 mol%.39 The gold cores are not covalently bound to the PNIPAM network and thus are rather mobile in microgels with larger mesh sizes, i.e. lower cross-linking densities. Therefore, after the synthesis performed above the VPTT, we expect that the cores can change their position in the microgels when the samples are cooled down to room temperature leading to swelling of the PNIPAM network. For this work, the exact position of the cores in the CS particles is not important as long as each microgel contains a single NP core. Image analysis reveals an average core diameter of 15.3 nm. Due to the high vacuum conditions during the TEM investigation and due to the sample preparation (drying), the microgels are imaged in their collapsed state. Therefore, the overall CS diameter appears smaller than the respective hydrodynamic diameter in the swollen state at 25 °C. Nevertheless, the TEM images show clearly the increasing shell size for CS1 to CS2 to CS3.Fig. 1(b) shows photographs of dilute aqueous dispersions of the different microgels recorded at ambient conditions, i.e. with the microgels in their swollen states. The slightly red appearance of the samples is caused by the LSPR of the gold cores leading to absorption of light in the green part of the visible spectrum. UV-Vis absorbance spectra of the AuNP cores from the different batches are shown in Fig. S1 in the ESI.† As expected, because of their similar size and polydispersity, the spectra overlap perfectly. All batches reveal the typical dipolar LSPR at approximately λLSPR = 518 nm. The images of the CS microgels in the top row of Fig. 1(b) show the increase in turbidity with increasing shell thickness from CS1 to CS3 caused by scattering from the microgels. The samples in the bottom row exhibit similar turbidity due to their similar size. At a closer look one can see a slight increase in turbidity from CS4 to CS2 to CS5, i.e. from left to right in the photograph. This increase is related to the increasing cross-linking density in agreement with our earlier findings.37 The differences in shell thickness and cross-linking are nicely revealed by results from DLS measurements. Fig. S2 in the ESI,† shows swelling curves obtained from temperature dependent measurements. All samples show the typical VPT behavior of PNIPAM microgels with continuously decreasing hydrodynamic radii, Rh, from the swollen state until plateaus are reached with nearly constant Rh at temperatures of 40 °C and higher. Aggregation of the microgels is not observed at any of the investigated temperatures. Even in the fully collapsed state where polymer–polymer interactions are favored, colloidal stability is high enough to prevent aggregation. The respective values of Rh in the swollen and collapsed state are summarized in Table 1. For a better comparison of the swelling characteristics of the microgels, we look at the deswelling ratios, α, in Fig. 2. α is defined as the ratio of the hydrodynamic volume at any temperature T, Vh(T), and the respective hydrodynamic volume in the swollen state Vh,swollen:
 | (11) |
For our CS microgels, we consider only the volume of the swellable PNIPAM shell to calculate α:
 | (12) |
Here, Rcore corresponds to the radius of the rigid AuNP cores, that do not change their volume in response to temperature in the relevant temperature window. We used data from the sigmoidal fits to the swelling curves at 25 °C to calculate Vh,swollen (see Table 1).
In Fig. 2(a) the deswelling behavior of the three microgels with different shell thicknesses but similar cross-linker contents are compared. The data of the different samples nearly collapse onto a common master curve with very similar VPTTs and only slight fluctuations – mostly at lower temperatures. Furthermore, very similar values of α of approximately 0.4 are reached at 50 °C. In other words, the shrunken state volume of the PNIPAM shells is only about 40% of the swollen state volume. The overlap of the data for the different CS batches indicates that indeed the degree of cross-linking is very similar for CS1–3.51 In contrast, Fig. 2(b) compares the deswelling behavior of the set of samples with different nominal cross-linker contents. The relative volume change between swollen and collapsed state is largest for CS4, which has the lowest nominal cross-linker content. In that case the values of α are smallest in the shrunken state (approximately 0.2). In contrast CS5 shows minimum values of α of approximately 0.5 at 50 °C. Thus, the DLS data confirm the increase in cross-linking density from CS4 to CS2 to CS5.37,39
4.2 Temperature-dependent optical properties
We now want to address the optical properties of the CS microgels and their dependence of the swelling state of the PNIPAM shells. Therefore, we measured absorbance spectra from dilute aqueous dispersions (0.02 wt%) using classical UV-Vis spectroscopy. Full spectra measured at different temperatures covering the VPT of the PNIPAM shells are shown in the ESI† (Fig. S3). Generally, the spectra reveal two contributions: (1) the LSPR of the AuNP cores. Due to the small size of the cores, scattering is negligible and their interaction with light is dominated by absorption.52 (2) Light scattering from the PNIPAM shells that manifests itself as a continuous increase in absorbance with decreasing wavelength. Further details of the spectra are discussed in the ESI.† Here, we want to focus on the observed increase in absorbance with increasing temperature, i.e. when the shells collapse due to the VPT behavior. Fig. 3(a)–(e) show measured and normalized absorbances at selected wavelengths as a function of temperature for all CS microgels.For a better direct comparison we normalized all data for each sample using the absorbances measured at λ = 300 nm in the fully collapsed state, i.e. at 60 °C. Due to the power law scaling of the wavelength in RDG scattering (∝λ−4, see eqn (5)), the absorbances at a given temperature decrease with increasing wavelength, i.e. from 300 to 400 to 523 nm, for each sample. We will come back to the experimentally observed power law scaling at a later stage in this work. At a given wavelength all samples show a continuous increase in absorbance with increasing temperature in the region of the VPT, i.e. when the microgels collapse. The sigmoidal fits (solid lines) match the data very precisely. Comparing the different samples we find similar relative increases in absorbance for CS1–CS3, i.e. the samples with similar cross-linker densities but different shell thicknesses. In contrast, the relative change in absorbance significantly differs when comparing the samples with different cross-linker densities but similar shell thicknesses. CS5, the most cross-linked microgel, shows the smallest increase in absorbance with temperature. CS4, the sample with the lowest cross-linking, shows the largest increase in absorbance. These findings are in good agreement with the temperature-induced changes in Rh measured by DLS. To prove that we can use the absorbances as a measure for the light scattering properties of the microgels, we performed SLS measurements at λ = 632.8 nm as a function of temperature. Fig. S4 in the ESI,† compares normalized, relative scattering intensities from SLS to the corresponding normalized, relative absorbances measured at λ = 632.5 nm using UV-Vis spectroscopy. For each sample the data from both methods overlap perfectly. This demonstrates that the measured absorbances are indeed related to light scattering and that the relative changes as a function of temperature directly reflect its changes. This is not only the case for λ ≈ 633 nm but also for other wavelengths as the perfect overlap between normalized absorbances at different wavelengths illustrates (see Fig. S5 in the ESI†). VPTTs determined from the sigmoidal fits to the SLS and UV-Vis spectroscopy data are summarized in Table 2.
| Sample | VPTT (UV-Vis) [°C] | VPTT (SLS) [°C] |
|---|---|---|
| CS1 | 33.5 ± 0.3 | 33.6 ± 0.3 |
| CS2 | 33.9 ± 0.2 | 34.1 ± 0.2 |
| CS3 | 33.0 ± 0.2 | 33.3 ± 0.2 |
| CS4 | 32.1 ± 0.2 | 32.8 ± 0.2 |
| CS5 | 34.1 ± 0.3 | 34.4 ± 0.3 |
The listed VPTTs range between 32.1 and 34.4 °C, while for each sample, both techniques reveal the same VPTTs within the experimental error. Samples CS1–3 possess very similar VPTTs. In contrast, the samples with different cross-linker contents show increasing VPTTs with increasing cross-linking, i.e. CS5 has the highest, CS4 the lowest VPTT. This dependence on the cross-linker content is in agreement with results from other studies on classical PNIPAM microgels (without cores).28
Now, we want to derive the correlation between the swelling state of the microgels and the scattering intensity. Since we know the evolution of Rh as a function of temperature for all samples, we can derive the correlation between absorbances at given λ and the respective Rh. To be able to compare all samples, independent of their different swelling capacities, we calculate the difference in radius at each temperature with respect to the collapsed state, ΔRh(T), and normalize by the maximum difference in size between the fully swollen and collapsed state, ΔmaxRh:
 | (13) |
Similarly, we calculate the difference in absorbance at temperature T with respect to the minimum absorbance in the swollen state, ΔA(T), and normalize by the maximum difference in absorbance, ΔmaxA:
 | (14) |
Both quantities reflect the extent to which Rh and A respectively, have changed at a given temperature in relation to the maximum possible changes in Rh, respectively A. For Rh, we can treat  as a measure for the degree of swelling, i.e. if the value is 0, the microgels are fully collapsed, if the value is 1, the microgels are fully swollen. Fig. 3(f) compares the respective results for all samples based on measured absorbances at λ = 300 nm. The normalized change in absorbance scales linearly with the normalized change in Rh and the slope is −1. In other words, the absolute absorbance difference with respect to the swollen state, ΔA(T), is directly proportional to the absolute radius difference with respect to the collapsed state, ΔRh(T). This implies that, for example, a temperature induced swelling by 10% results in a 10% decrease in normalised absorbance. This behavior is found for all five microgels. All data points collapse onto a master curve in Fig. 3(f). We are not aware that such a relationship has been identified previously in literature dealing with PNIPAM microgels. Ultimately the observed relation is very convenient, because it allows the derivation of the microgel size and its temperature-induced changes using simple absorbance measurements. In the following section we want to address the internal structure of the microgels and the resulting volume fraction of polymer.
as a measure for the degree of swelling, i.e. if the value is 0, the microgels are fully collapsed, if the value is 1, the microgels are fully swollen. Fig. 3(f) compares the respective results for all samples based on measured absorbances at λ = 300 nm. The normalized change in absorbance scales linearly with the normalized change in Rh and the slope is −1. In other words, the absolute absorbance difference with respect to the swollen state, ΔA(T), is directly proportional to the absolute radius difference with respect to the collapsed state, ΔRh(T). This implies that, for example, a temperature induced swelling by 10% results in a 10% decrease in normalised absorbance. This behavior is found for all five microgels. All data points collapse onto a master curve in Fig. 3(f). We are not aware that such a relationship has been identified previously in literature dealing with PNIPAM microgels. Ultimately the observed relation is very convenient, because it allows the derivation of the microgel size and its temperature-induced changes using simple absorbance measurements. In the following section we want to address the internal structure of the microgels and the resulting volume fraction of polymer.
4.3 Volume fraction of polymer from absolute intensity small-angle scattering experiments
The measured absorbances, that result dominantly from light scattering of the microgels discussed in the previous section, depend on three sample parameters: (1) the number density N, that is the number of CS microgels per sample volume, i.e. per cm3; (2) the refractive index contrast; and (3) the particle radius R.The precise determination of N, in particular for dilute microgel dispersions as used in our case, is challenging. In principle, N can be derived from the microgel volume fraction ϕmicrogel, that is the volume occupied by the microgels in relation to the total volume of the dispersion, V. If the volume of a single microgel is ν0, the number density can be calculated:
 | (15) |
Probably the most commonly applied method to measure ϕmicrogel in dilute dispersion where ϕmicrogel is equal to the generalized volume fraction ζ, is via measurements of the relative viscosity.3,8,53 To then calculate N requires knowledge of ν0 that is particularly difficult to define for swollen microgels due to their fuzzy sphere morphology and the presence of dangling ends in the outer microgel periphery. Depending on which radius is used for the calculation of the microgel volume (e.g. hydrodynamic radius, Guinier radius, sphere radius from SLS), values of ν0 differ strongly. Here, we choose a completely different approach to determine N and make use of the strong scattering contrast of our small AuNP cores: we use absolute intensity SAXS data and form factor analysis of the strong scattering signal from the AuNP cores to determine the number density of cores. Knowing that each microgel contains exactly one core, the number density of the cores is equal to N. The corresponding SAXS data including Guinier plots and detailed explanation of the calculations to determine N from samples of known weight concentration can be found in the ESI† (Fig. S6 and S7). The determined values of N now also allow us to calculate extinction cross-sections from the measured absorbances (see eqn (9) and (10)). Fig. S8 in the ESI,† shows the respective results for the swollen and collapsed state of the CS microgels. As expected, for a given wavelength, the extinction cross-section increases with increasing microgel shell thickness, i.e. from CS1 to CS3, and for increasing cross-linking density, i.e. from CS4 to CS2 to CS5. This behavior is found for both states of swelling.
With the resulting correlation between N and the weight concentration of our samples, we can now address the refractive index contrast of the microgels. We do this in two different ways: using refractive index measurements and using absolute intensity SANS measurements. Measured refractive indices from the refractometer, ndispersion, obtained from CS microgel dispersions of known weight concentration are listed in Table S3 and shown in Fig. S9 in the ESI.† Since we know the relation between weight concentration and N from analysis of our absolute intensity SAXS data, we can estimate the volume fraction of microgels, ϕmicrogel, using the hydrodynamic volumes Vh in eqn (15). With ϕmicrogel we can then use the Maxwell–Garnett mixing rule54,55 to calculate the effective, volume averaged microgel refractive index, nmicrogel,eff:
 | (16) |
The determined values of nmicrogel,eff along with the resulting effective polymer volume fractions, ϕeff, are listed Table 3. Here, ϕeff was calculated using eqn (6) with nmicrogel,eff as the input parameter for np.
In the swollen state, the determined effective, average refractive indices of the microgels lie between 1.342 and 1.371, with CS4 and CS5 having the lowest and highest refractive indices respectively. These values correspond to an averaged polymer content of 6% (CS4) and 23% (CS5) respectively. The CS1–3 microgels possess very similar polymer contents of 15–18%. As expected these values lie between the determined polymer content of CS4 and CS5, which have lower and higher cross-linker contents respectively. In the collapsed state, the trend is not that clear. At 32%, the CS4 microgels have the lowest effective polymer content, indicating that these lowest cross-linked microgels contain the largest amount of water in their collapsed state. Next, CS2, CS3 and CS5 have similar polymer contents in the range from 38 to 45%. The CS1 microgels with the thinnest PNIPAM shell, but similar cross-linker content to CS2 and CS3, have the highest polymer content of 57% in the collapsed state. These values serve as a first estimate from simple and quick refractive index measurements. However, we want to note that the determined values might be inaccurate despite the high precision of the refractive index values (see Table S3 in the ESI†). Potential sources of error are the precision of N from absolute intensity SAXS, the validity of the Maxwell-Garnett mixing rule for microgel dispersions and the use of the hydrodynamic radius to estimate ϕmicrogel. In the following we will show that only the latter factor, i.e. the use of the hydrodynamic microgel size, is relevant to the reliability of the determined values of nmicrogel,eff and consequently ϕeff. Already minor deviations in radius strongly affect the resulting refractive index of the polymer shell, where a reduction of the radius by a few nanometers leads to significantly increased values of ϕeff. Before we address this in more detail, it is useful to use the values from refractive index measurements to reconfirm that the microgels generally fulfill the RDG criterium (eqn (4)). Table 3 lists the resulting values of  for the swollen and collapsed states. With values ranging between 0.05 and 0.14 the RDG criterium is well fulfilled in the swollen state. In the collapsed state the values are larger, by a factor of approximately 2, but still small enough that it is justified to treat the collapsed microgels formally as RDG scatterers.
for the swollen and collapsed states. With values ranging between 0.05 and 0.14 the RDG criterium is well fulfilled in the swollen state. In the collapsed state the values are larger, by a factor of approximately 2, but still small enough that it is justified to treat the collapsed microgels formally as RDG scatterers.
We will now turn to the SANS measurements of the CS microgels and outline an alternative method to determine the polymer volume fraction. The scattering profiles measured at different states of swelling are shown in Fig. 4.
All scattering profiles can be well described by a combination of a scattering contribution from the incoherent background, an Ornstein-Zernicke contribution to account for dynamic network fluctuations and the fuzzy sphere model to account for the microgel form factor. The latter model was first introduced for microgels by Stieger et al.14 and comprises an inner microgel region with homogeneous density and a radius, Rbox. The thickness of the fuzzy shell is defined by the parameter σ. The total microgel radius, RSANS is given by RSANS = Rbox + 4σ. The fits to the data shown as solid lines in Fig. 4 describe the experimental data very well. Some small deviations in the mid q-range (at approximately 0.1 nm−1) that are particularly visible for CS5 at 25 °C might be related to static internal inhomogeneities. Further details of the fuzzy sphere model and the fitting of our SANS data can be found in the ESI.† We want to highlight that recently more complex models have been derived for the description of the internal microgel morphology and the microgel form factors.19,56 These extended models might also be applicable to our samples and might provide more realistic density profiles. However, due to the limited resolution and the instrumental smearing in our SANS experiments, we want to stay with the well-established fuzzy sphere model and avoid increasing the number of fitting parameters because these will be used in the optical simulations presented later on in this work. We now want to focus on the fit results. For temperatures below (25 °C) and close to the VPTT (35 and 37 °C), the best form factor fits with the fuzzy sphere model yield values of σ > 0 nm. We want to highlight that a simple polydisperse sphere fit does not lead to a good description of the scattering data at these temperatures. Only in the fully collapsed state, at 50 °C, the fuzzy sphere model yields σ = 0 nm and the model becomes equivalent to a polydisperse sphere form factor. In other words, the fully collapsed microgels resemble the scattering behavior of homogeneous, hard spheres in agreement with earlier findings for PNIPAM microgels, including those with ultra low cross-linker density.57–59Fig. 5 summarizes the results from our SANS measurements using CS2 as an example.
At 50 °C, the polymer volume fraction profile ϕ(R) is consistent with a typical hard sphere-like profile with a constant value at R ≤ RSANS. Here RSANS = Rbox and σ = 0 nm. The constant polymer volume fraction of the microgels is approximately 0.41. In other words, the collapsed microgel CS2 still contains almost 60% solvent by volume (here: D2O). With decreasing temperature and consequently increasing swelling, the thickness of the fuzzy shell, σ, increases while Rbox remains almost constant. From 37 down to 25 °C, the polymer volume fraction of the inner homogeneous microgel part (R ≤ Rbox) decreases from approximately 0.3 to approximately 0.18. The swollen CS2 microgel contains over 80% solvent by volume in the inner region of the microgel. The fact that Rbox remains almost constant while ϕ(R ≤ Rbox) continuously decreases with increasing degrees of swelling indicates rearrangement of the chains from the fuzzy corona during swelling/deswelling. The microgels undergo a transition from fuzzy spheres, with a gradually decreasing polymer density in the fuzzy corona, to homogeneous hard sphere-like particles with a simple box profile, as the temperature increases. During this transition the effective polymer volume fraction increases continuously with increasing temperature until the microgels are fully collapsed. Due to limited beamtime, we could not perform measurements at temperatures higher than 50 °C. However, our absorbance data show only negligible changes in absorbance above 50 °C (see Fig. S4 in the ESI†). Therefore, we conclude that the SANS profiles will also not show any significant changes for higher temperatures. As Fig. 6(a)–(e) shows, the SANS analysis yields very similar results for all CS microgels where the same temperature-dependent trend is observed for each system.
All fit parameters from the SANS analysis are listed in Tables S4–S8 (ESI†) and the different radii from DLS and SANS are summarized in Fig. S10 in the ESI.† The tables also list the radii of gyration Rg obtained from model-free Guinier analysis of the low q scattering regions. It is useful to compare the values of Rg with Rh. For homogeneous, hard spheres we expect to find  .60 In the swollen state (25 °C) the ratios Rg/Rh of our CS microgels are in the range of 0.56–0.71 and thus significantly smaller than the hard sphere value. This can be explained by the fuzzy corona and the dangling ends that contribute to Rh but less to Rg.22,61 When temperature is increased and the microgels collapse, the ratios increase to 0.68–0.74. Thus, the transition from fuzzy spheres to hard sphere-like particles is also reflected by Rg/Rh. Comparing the samples with the different cross-linker densities, we see the strongest change in Rg/Rh for CS4 – the microgels with the lowest cross-linker density. CS4 exhibits the smallest Rg/Rh value of 0.56 in the swollen state and a significantly increased value of 0.72 in the collapsed state. This is in agreement with polymer volume fraction profiles shown in Fig. 6(d) where the inner microgel volume contains 90% solvent by volume in the swollen state – significantly more than the other microgels. The CS4 microgels are the softest among the series of microgels studied. In contrast, the other microgels with higher cross-linking density and thus more rigid polymer networks, exhibit smaller changes in Rg/Rh with temperature. Surprisingly, the polymer volume fraction in the fully collapsed state is very similar for all microgels ranging between approximately 37.5% (CS5) and 45% (CS3 and CS4). Only CS1 shows a slightly higher polymer content of approximately 50% in the collapsed state. These are the smallest microgels and potentially possess more inhomogeneities in the polymer network. Thus, the CS1 microgels show a slightly different behavior than CS2 and CS3 with similar cross-linker contents. Generally the calculated polymer volume fractions in the collapsed state are in good agreement with values reported in literature,14,25 where, for example, Lopez and Richtering estimate a value of 0.44, independent of the cross-linking density and molar mass.24 The collapsed state of microgels is often used as the reference state, for example, when the swelling behavior is described by the Flory–Rehner theory.12,23,24 In this case precise knowledge of the polymer volume fraction is crucial. While this value is often estimated rather than precisely measured,12,28 we provide an approach to determine the polymer volume fraction with great confidence. Furthermore, the values from our collapsed state SANS data are in good agreement with the results from refractive index measurements (Table 3) despite the slightly larger variation between samples for the latter dataset. This agreement supports our previous hypothesis that the dominant error in the evaluation of the refractive index measurements is related to the use of Rh in order to estimate the microgel volume fraction. The collapsed state is therefore the ideal reference state (ϕ = ϕ0), because the microgels can be treated as homogeneous hard sphere-like particles with a homogeneous density profile and thus homogeneous refractive index. Similar polymer contents were determined independent of the shell thickness and the cross-linker content. We highly recommend the collapsed state to be used as the reference state in future studies on microgels.
.60 In the swollen state (25 °C) the ratios Rg/Rh of our CS microgels are in the range of 0.56–0.71 and thus significantly smaller than the hard sphere value. This can be explained by the fuzzy corona and the dangling ends that contribute to Rh but less to Rg.22,61 When temperature is increased and the microgels collapse, the ratios increase to 0.68–0.74. Thus, the transition from fuzzy spheres to hard sphere-like particles is also reflected by Rg/Rh. Comparing the samples with the different cross-linker densities, we see the strongest change in Rg/Rh for CS4 – the microgels with the lowest cross-linker density. CS4 exhibits the smallest Rg/Rh value of 0.56 in the swollen state and a significantly increased value of 0.72 in the collapsed state. This is in agreement with polymer volume fraction profiles shown in Fig. 6(d) where the inner microgel volume contains 90% solvent by volume in the swollen state – significantly more than the other microgels. The CS4 microgels are the softest among the series of microgels studied. In contrast, the other microgels with higher cross-linking density and thus more rigid polymer networks, exhibit smaller changes in Rg/Rh with temperature. Surprisingly, the polymer volume fraction in the fully collapsed state is very similar for all microgels ranging between approximately 37.5% (CS5) and 45% (CS3 and CS4). Only CS1 shows a slightly higher polymer content of approximately 50% in the collapsed state. These are the smallest microgels and potentially possess more inhomogeneities in the polymer network. Thus, the CS1 microgels show a slightly different behavior than CS2 and CS3 with similar cross-linker contents. Generally the calculated polymer volume fractions in the collapsed state are in good agreement with values reported in literature,14,25 where, for example, Lopez and Richtering estimate a value of 0.44, independent of the cross-linking density and molar mass.24 The collapsed state of microgels is often used as the reference state, for example, when the swelling behavior is described by the Flory–Rehner theory.12,23,24 In this case precise knowledge of the polymer volume fraction is crucial. While this value is often estimated rather than precisely measured,12,28 we provide an approach to determine the polymer volume fraction with great confidence. Furthermore, the values from our collapsed state SANS data are in good agreement with the results from refractive index measurements (Table 3) despite the slightly larger variation between samples for the latter dataset. This agreement supports our previous hypothesis that the dominant error in the evaluation of the refractive index measurements is related to the use of Rh in order to estimate the microgel volume fraction. The collapsed state is therefore the ideal reference state (ϕ = ϕ0), because the microgels can be treated as homogeneous hard sphere-like particles with a homogeneous density profile and thus homogeneous refractive index. Similar polymer contents were determined independent of the shell thickness and the cross-linker content. We highly recommend the collapsed state to be used as the reference state in future studies on microgels.
 | ||
| Fig. 6 (a)–(e) Radial polymer volume fraction profiles at four different temperatures as obtained from analysis of the SANS data using the fuzzy sphere model. (f) Calculated effective polymer volume fraction as a function of the temperature for all CS microgels. The effective volume fractions were calculated using the fully collapsed state as the reference state and the temperature-dependent hydrodynamic radii according to eqn (17). | ||
4.4 Light scattering properties based on effective, average volume fractions
With the results from collapsed state SANS, we now want to derive the effective, average polymer volume fractions ϕeff for different states of swelling using the hydrodynamic radii from DLS at different temperatures: | (17) |
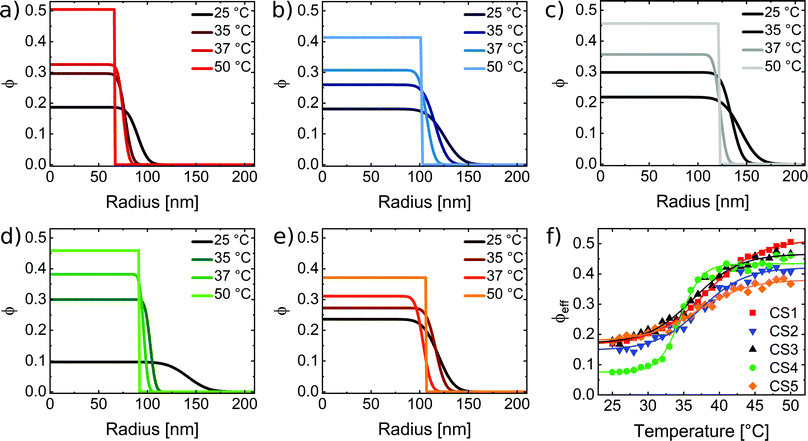
We want to emphasize that this simple estimation does not take into account the transition from hard sphere-like behavior at the reference state (50 °C) to the fuzzy sphere morphology in the swollen state. Therefore, ϕeff rather corresponds to the volume averaged polymer volume fraction with respect to the hydrodynamic microgel volume. Fig. 6(f) compares the temperature evolution of ϕeff for all CS microgels. As expected the capacity for solvent uptake is the largest for the CS4 particles, which have the lowest cross-linking. In the fully swollen state, the CS4 microgels contain on average less than 10% polymer. For the other, higher cross-linked CS microgels, the average polymer content approaches values between 15 and 20% in the swollen state. Again we find good agreement with the values from refractive index measurements (Table 3) that also do not take into account internal density variations. In order to relate the polymer volume fractions to the light scattering properties of the microgels, we have to calculate the refractive index contrast using eqn (6) with the values of ϕeff. Since we performed the absorbance measurements in H2O, we use nH2O = 1.33 as the refractive index of the dispersing medium at λ = 589.3 nm.62 To determine the refractive index of our PNIPAM microgel shells, nPNIPAM, we measured the refractive index of dispersions of the CS3 microgels at λ = 589.3 nm and 25 °C. The microgel dispersions were prepared from freeze-dried microgels and we took into account a residual water content of 5.7%.39 In addition to the dispersion measurements, we measured a polymer film prepared from linear PNIPAM homopolymer. Fig. S9 in the ESI,† shows the measured refractive indices from dispersions of different weight concentrations and the PNIPAM homopolymer film. A linear scaling was observed and extrapolation to 100% polymer yielded nPNIPAM = 1.50. Using this value, we calculated neff(T) according to eqn (6) which we then used to calculate CRDGsca according to eqn (5). Fig. 7 shows the resulting scattering cross-sections as a function of temperature.
 | ||
| Fig. 7 Calculated scattering cross-sections as a function of temperature according to eqn (5). | ||
For all CS microgels CRDGsca remains nearly constant over the whole temperature range. On closer inspection, a slight decrease with increasing temperature is observed – opposite to the experimentally observed trend from absorbance measurements. However, the decrease is only 1–2% and therefore negligible. Obviously the approach of using effective, average microgel volume fractions and measured hydrodynamic radii from DLS for RDG calculations does not describe the experimental results. Nevertheless, this finding is very important as it shows that for an optically homogeneous sphere composed of solvent and non-absorbing material (PNIPAM in our case) changes in size do not lead to noticeable changes in turbidity when the amount of material (PNIPAM) is conserved and only the solvent content is allowed to change. Although it is debatable whether Rh is the correct radius for this estimation, we claim that the main discrepancy arises due to the value used for the effective volume fraction, ϕeff(T), that ignores the fuzzy sphere character of the swollen microgels. This is supported by findings from Small et al. who investigated the scattering properties of core–shell particles with different refractive index contrasts.63 They found that a different refractive index shell strongly influences the scattering intensity. For a shell refractive index close to that of the medium, the scattering is reduced. In order to account for our density profiles in the swollen state, we use FDTD simulations to calculate the scattering cross-sections in the following.
4.5 Light scattering properties based on the fuzzy sphere model
In order to account for the fuzzy sphere character of our swollen CS microgels, we used FDTD simulations to determine the theoretical scattering behavior. Table 4 lists the radii and refractive indices obtained from SANS that were used for the simulations.| Sample | Swollen state | Collapsed state | |||||
|---|---|---|---|---|---|---|---|
| R box [nm] | R t [nm] | R SANS [nm] | n box | n shell | R SANS [nm] | n | |
| CS1 | 74.2 | 33.4 | 107.6 | 1.364 | 1.348 | 66.5 | 1.417 |
| CS2 | 99.2 | 55.6 | 154.8 | 1.363 | 1.347 | 102.0 | 1.401 |
| CS3 | 116.6 | 57.2 | 173.8 | 1.368 | 1.350 | 122.0 | 1.410 |
| CS4 | 110.5 | 66.2 | 176.7 | 1.348 | 1.340 | 91.6 | 1.410 |
| CS5 | 95.3 | 50.4 | 145.7 | 1.372 | 1.352 | 106.2 | 1.391 |
To simulate the scattering in the swollen state we used a simple core–shell model to describe the microgel shell. In this model the core corresponds to the inner microgel region with R = Rbox and a polymer volume fraction, ϕbox, and a shell with thickness Rt that corresponds to the total thickness of the fuzzy shell. Thus, we use RSANS as the total microgel radius. The refractive index of the shell, nshell, corresponds to ϕshell = 0.5ϕbox as defined by the fuzzy sphere model. The collapsed state (50 °C) was simulated with a simple sphere of homogeneous refractive index and radius RSANS. A gold sphere of 12 nm in diameter was included to account for the absorption contribution of the AuNP cores in our CS microgels. The diameter was chosen to be slightly smaller than the experimental diameter from TEM since otherwise the absorption of the cores was strongly overestimated. Since the simulation uses monodisperse, perfectly spherical gold particles and also damping effects are less precisely considered – in particular for small AuNPs, as in our case – smaller gold dimensions are required to match better to the LSPR strength experimentally observed. In the experiment we deal with polydisperse (approximately 10%) and polycrystalline AuNPs that are only nearly spherical in shape. Fig. 8 compares the results from FDTD simulations (dashed lines) to the measured absorbance spectra (solid lines). The experimental and simulated spectra were normalized at the wavelength of 400 nm allowing a direct qualitative comparison.
At a first glance, the agreement between experimentally measured scattering and the numerical simulation is good for both states of swelling. In the collapsed state (c and d), the scattering model, which treats the microgel as a sphere with homogeneous refractive index, matches well to the experimental result and supports the interpretation of the collapsed state as being hard-sphere-like. In the swollen state (a and b) our simple core–shell model with the shell accounting for the fuzzy microgel corona of lower polymer density yields satisfactory results for all samples. To provide a more quantitative comparison of the scattering, we look at the power law scaling (absorbance ∝λ−β) with the wavelength exponent β.64 For RDG scatterers we expect to find β = 4 according to eqn (5). Indeed this is the case for the absorbance measured and simulated for spherical SiO2 particles with Rh = 14 nm in water. Fig. S11 in the ESI,† shows the perfect agreement between experimental data and simulated scattering cross-sections. The data perfectly follows the expected wavelength scaling of λ−4 for RDG scatterers. In the case of our CS microgels, we find significantly smaller values than β = 4. Table 5 compares the values of β determined from experimental and simulated spectra in the swollen and collapsed state.
| Sample | Swollen state | Collapsed state | ||
|---|---|---|---|---|
| β(experiment) | β(FDTD) | β(experiment) | β(FDTD) | |
| CS1 | 2.36 | 1.46 | 2.73 | 2.28 |
| CS2 | 2.88 | 2.00 | 3.03 | 2.23 |
| CS3 | 2.86 | 2.14 | 3.05 | 2.41 |
| CS4 | 2.63 | 1.77 | 2.89 | 2.22 |
| CS5 | 2.93 | 2.11 | 3.05 | 2.24 |
In the swollen state, the simulated values of β range between 1.77 and 2.14 and between 2.36 and 2.93 in experiment. Nevertheless, there is a clear increase in β with increasing cross-linker density. The same trend is observed in the collapsed state where values are higher than in the swollen state and range between 2.22 and 2.41 for the simulations and between 2.73 and 3.05 in experiment. In all cases the values of β are smaller in the simulated spectra than in experiment. Comparing the samples with different shell thicknesses but similar cross-linker density, we find almost the same values of β for both states for CS2 and CS3. Only the CS1 microgels stand out with significantly smaller values. This deviation agrees with our previous discussion that the CS1 particles with the thinnest shell amongst the series might possess more inhomogeneities in the polymer network. Comparing the swollen and collapsed state, we find higher values of β, which indicates that the scattering becomes closer to the RDG prediction for homogeneous spheres. However, both particle size and refractive index influence the wavelength exponent.65 Heller et al. reported that for increasing sizes of scatterers, the wavelength exponent decreases until reaching 0.64 This is the case for particles that do not fulfill the criterium of being “very small” compared to the wavelength. Our observed underestimation of β from FDTD simulations is more pronounced in the swollen state where the microgels are significantly larger despite their refractive index being lower. In the collapsed state wavelength exponents from FDTD are closer to the experimental values indicating that optically our microgels can be considered as more homogeneous sphere-like. However, the scattering is obviously still far from matching the RDG prediction.
While the internal structure of PNIPAM microgels appears well understood and the fuzzy sphere model is well accepted, our data reveal the complexity when it comes to understanding simple absorbance properties: during the temperature induced collapse, PNIPAM microgels show an increase in scattering that cannot be explained by the RDG theory for homogeneous refractive index spheres. Even in the collapsed state, where SANS data clearly reveal the form factor of polydisperse hard spheres with a homogeneous polymer distribution, measured absorbances can neither be described with the RDG model nor by Mie theory calculations (see Fig. S12 in the ESI†). This becomes particularly evident when comparing the power law scaling of the wavelength dependence. While refractive index measurements and form factor analysis yield very reasonable polymer volume fractions from which refractive index profiles can be derived, theoretical scattering cross-sections from FDTD simulation cannot reproduce the experimentally observed power law scaling of the wavelength-dependent absorbances.
Our study clearly shows that the fuzzy sphere structure of swollen microgels is responsible for the observed increase in absorbance during the VPT. In the swollen state, where the thickness of the fuzzy shell is largest and its effective, average refractive index is the lowest, the shell basically does not contribute to the visible wavelength scattering. Using the experimentally determined refractive indices of the inner microgel core (nbox) and of the fuzzy shell (nshell) to calculate the refractive index contrast term in eqn (5), we find a four times lower refractive index contrast of the fuzzy shell. As the fuzzy shell collapses during the VPT, polymer material from the fuzzy shell collapses on the inner microgel core that increases in polymer volume fraction. Consequently, the refractive index contrast of the inner, rather homogeneous core region increases leading to an increase in absorbance. This is supported by our finding of nearly constant radii, Rbox, during the microgel collapse and the increase in polymer volume fraction in the core region as observed from the analysis of our SANS data.
With this work we want to stimulate further research in this direction – in particular in the development of theories that describe the optical scattering cross-sections of thermoresponsive microgels. To the best of our knowledge a model suitable for PNIPAM microgels does not exist so far. This knowledge gap hampers the quantitative analysis of microgels in general where it would be highly beneficial if, for example, number concentrations could be extracted from simple absorbance measurements. Furthermore, we believe that simple, fast and importantly, almost error-free absorbance measurements could be used to investigate the structural transitions of thermoresponsive microgels ingreat detail – given a precise theoretical model is available.
5 Conclusion
In a similar way to linear PNIPAM homopolymer chains, PNIPAM microgels show an increase in turbidity when undergoing a phase transition from good to poor solvent conditions. However, the origin of this turbidity increase is significantly different. We studied this behavior in detail using core–shell microgels with small gold nanoparticle cores and much larger PNIPAM shells of different thickness and cross-linking. Importantly, the measured absorbances in the visible wavelength range were strongly dominated by the light scattering from the PNIPAM shells while the absorption of the cores was almost negligible. Based on the microgel sizes and their effective, average refractive indices all samples studied fulfilled the RDG criterium in swollen and collapsed state. SANS measurements were used to determine the polymer density profiles and particle radii. Density profiles are very similar for similarly cross-linked microgels independent of their size. The cross-linker density largely determines the polymer volume fractions in the swollen state, while differences in the collapsed state are rather small. The relative change in absorbance during the volume phase transition is directly related to the determined changes in microgel size, polymer volume fraction and thus refractive index. Using the collapsed state as a reference state, we could derive the temperature-dependent profiles of the effective polymer volume fraction and refractive index. RDG calculations of the scattering cross-section using the latter data could not reproduce the increase in absorbance during shrinkage of the microgels. The fuzzy sphere character of the swollen microgels that was clearly identified by SANS measurements at temperatures close to and below the volume phase transition temperature was then taken into account in theoretical scattering calculations using FDTD simulations. The simulated spectra were found to match quite reasonably to the experimental absorbances despite significantly smaller power law exponents for the wavelength-dependence. We attribute the increase in absorbance (or turbidity) during the temperature induced microgel collapse to the transition from fuzzy spheres to hard sphere-like scatterers. In the swollen state where a significant fraction of the total microgel is forming the fuzzy shell with a continuously decreasing polymer density towards the surrounding medium, the fuzzy shell does not contribute significantly to the scattering. The scattering is dominated by the inner microgel region with a rather homogeneous polymer distribution and constant refractive index. As the microgels collapse due to an increase in temperature, the thickness of the fuzzy shell decreases, the polymer volume fraction in the inner microgel region rises and therefore the scattering increases until the microgels are fully collapsed. In the fully collapsed state, polymer material from the fuzzy shell has fully collapsed onto the inner homogeneous microgel core and chain rearrangements lead to a rather homogeneous polymer density profile. We therefore attribute the observed increase in microgel turbidity during the volume phase transition to changes related to the fuzzy shell.A theory that precisely describes the light scattering properties of microgels is currently missing. With this work, we want to stimulate further research in this direction and provide a first general basis towards the understanding of simple absorbance spectra from thermoresponsive microgels. Such measurements are simple, quick and allow for great resolution in time resolved studies of microgel swelling and deswelling phenomena. With a better understanding of the optical properties of microgels – ideally matching measured cross-sections to the respective state of swelling and the internal microgel structure – one could follow the volume phase transition with great time resolution while revealing internal structural transitions. A time-resolved deswelling study using temperature jump spectroscopy is currently in progress and will be presented elsewhere.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the Melbourne Advanced Microscopy Facility (Bio 21, The University of Melbourne) for access to electron microscopes and Heyou Zhang from the University of Melbourne for his support with the TEM measurements. The authors thank the Institut Laue-Langevin for allocation of SANS beamtime on D11 via EASY access; data are available on demand (DOI: 10.5291/ILL-DATA.EASY-632). The authors are also grateful for financial support from the German Academic Exchange Service (DAAD) through its Thematic Network Melbourne-Bayreuth Polymer/Colloid Network, sponsored from funds of the Federal Ministry of Education and Research (BMBF). The authors thank the Center for Structural Studies (CSS) that is funded by the Deutsche Forschungsgemeinschaft (DFG Grant numbers 417919780 and INST 208/761-1 FUGG) for access to the SAXS instrument. P. M. thanks the ARC for support through Grant CE170100026. M. K. acknowledges the German Research Foundation (DFG) for funding under grant KA3880/6-1. The authors thank Gary Bryant (RMIT, Melbourne, Australia) for valuable discussions.References
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider, I. I. Potemkin and W. Richtering, Nanogels and Microgels: From Model Colloids to Applications, Recent Developments, and Future Trends, Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed.
- F. A. Plamper and W. Richtering, Functional Microgels and Microgel Systems, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- H. Senff and W. Richtering, Temperature sensitive microgel suspensions: colloidal phase behavior and rheology of soft spheres, J. Chem. Phys., 1999, 111, 1705–1711 CrossRef CAS.
- H. Bachman, A. C. Brown, K. C. Clarke, K. S. Dhada, A. Douglas, C. E. Hansen, E. Herman, J. S. Hyatt, P. Kodlekere, Z. Meng, S. Saxena, M. W. Spears Jr, N. Welsch and L. A. Lyon, Ultrasoft, highly deformable microgels, Soft Matter, 2015, 11, 2018–2028 RSC.
- M. J. Bergman, N. Gnan, M. Obiols-Rabasa, J.-M. Meijer, L. Rovigatti, E. Zaccarelli and P. Schurtenberger, A new look at effective interactions between microgel particles, Nat. Commun., 2018, 9 Search PubMed.
- T. Kureha, H. Minato, D. Suzuki, K. Urayama and M. Shibayama, Concentration dependence of the dynamics of microgel suspensions investigated by dynamic light scattering, Soft Matter, 2019, 15, 5390–5399 RSC.
- S. Bochenek, A. Scotti and W. Richtering, Temperature-sensitive soft microgels at interfaces: air–water versus oil–water, Soft Matter, 2021, 17, 976–988 RSC.
- A. Scotti, Characterization of the volume fraction of soft deformable microgels by means of small-angle neutron scattering with contrast variation, Soft Matter, 2021, 17, 5548–5559 RSC.
- M. Heskins and J. E. Guillet, Solution Properties of Poly(N-isopropylacrylamide), J. Macromol. Sci., Part A: Pure Appl. Chem., 1968, 2, 1441–1455 CrossRef CAS.
- R. H. Pelton and P. Chibante, Preparation of aqueous latices with N-isopropylacrylamide, Colloids Surf., 1986, 20, 247–256 CrossRef CAS.
- X. Wu, R. H. Pelton, A. E. Hamielec, D. R. Woods and W. McPhee, The kinetics of poly(N-isopropylacrylamide) microgel latex formation, Colloid Polym. Sci., 1994, 272, 467–477 CrossRef CAS.
- A. Fernández-Barbero, A. Fernández-Nieves, I. Grillo and E. López-Cabarcos, Structural modifications in the swelling of inhomogeneous microgels by light and neutron scattering, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051803 CrossRef PubMed.
- K. Kratz, T. Hellweg and W. Eimer, Structural changes in PNIPAM microgel particles as seen by SANS, DLS, and EM techniques, Polymer, 2001, 42, 6631–6639 CrossRef CAS.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, Small-angle neutron scattering study of structural changes in temperature sensitive microgel colloids, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- G. M. Conley, S. Nöjd, M. Braibanti, P. Schurtenberger and F. Scheffold, Superresolution microscopy of the volume phase transition of pNIPAM microgels, Colloids Surf., A, 2016, 499, 18–23 CrossRef CAS.
- A. P. H. Gelissen, A. Oppermann, T. Caumanns, P. Hebbeker, S. K. Turnhoff, R. Tiwari, S. Eisold, U. Simon, Y. Lu, J. Mayer, W. Richtering, A. Walther and D. Wöll, 3D Structures of Responsive Nanocompartmentalized Microgels, Nano Lett., 2016, 16, 7295–7301 CrossRef CAS PubMed.
- P. Otto, S. Bergmann, A. Sandmeyer, M. Dirksen, O. Wrede, T. Hellweg and T. Huser, Resolving the internal morphology of core–shell microgels with super-resolution fluorescence microscopy, Nanoscale Adv., 2020, 2, 323–331 RSC.
- L. Rovigatti, N. Gnan, L. Tavagnacco, A. J. Moreno and E. Zaccarelli, Numerical modelling of non-ionic microgels: an overview, Soft Matter, 2019, 15, 1108–1119 RSC.
- A. Ninarello, J. J. Crassous, D. Paloli, F. Camerin, N. Gnan, L. Rovigatti, P. Schurtenberger and E. Zaccarelli, Modeling Microgels with a Controlled Structure across the Volume Phase Transition, Macromolecules, 2019, 52, 7584–7592 CrossRef CAS PubMed.
- P. J. Flory, Principles of polymer chemistry, Cornell University Press, 1953; OCLC: 542497 Search PubMed.
- M. Quesada-Pérez, J. A. Maroto-Centeno, J. Forcada and R. Hidalgo-Alvarez, Gel swelling theories: the classical formalism and recent approaches, Soft Matter, 2011, 7, 10536–10547 RSC.
- I. Varga, T. Gilányi, R. Mészáros, G. Filipcsei and M. Zrínyi, Effect of Cross-Link Density on the Internal Structure of Poly(N-isopropylacrylamide) Microgels, J. Phys. Chem. B, 2001, 105, 9071–9076 CrossRef CAS.
- J. J. Crassous, A. Wittemann, M. Siebenbürger, M. Schrinner, M. Drechsler and M. Ballauff, Direct imaging of temperature-sensitive core-shell latexes by cryogenic transmission electron microscopy, Colloid Polym. Sci., 2008, 286, 805–812 CrossRef CAS.
- C. G. Lopez and W. Richtering, Does Flory–Rehner theory quantitatively describe the swelling of thermoresponsive microgels?, Soft Matter, 2017, 13, 8271–8280 RSC.
- S. Sbeih, P. S. Mohanty, M. R. Morrow and A. Yethiraj, Structural parameters of soft PNIPAM microgel particles as a function of crosslink density, J. Colloid Interface Sci., 2019, 552, 781–793 CrossRef CAS PubMed.
- L. Arleth, X. Xia, R. P. Hjelm, J. Wu and Z. Hu, Volume transition and internal structures of small poly(N-isopropylacrylamide) microgels, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 849–860 CrossRef CAS.
- B. R. Saunders, On the Structure of Poly(N-isopropylacrylamide) Microgel Particles, Langmuir, 2004, 20, 3925–3932 CrossRef CAS PubMed.
- M. Karg, S. Prévost, A. Brandt, D. Wallacher, R. von Klitzing and T. Hellweg, Poly-NIPAM Microgels with Different Cross-Linker Densities. Intelligent Hydrogels, Cham, 2013, 63–76 CAS.
- M. Karg, I. Pastoriza-Santos, J. Pérez-Juste, T. Hellweg and L. Liz-Marzán, Nanorod-Coated PNIPAM Microgels: Thermoresponsive Optical Properties, Small, 2007, 3, 1222–1229 CrossRef CAS PubMed.
- S. Schmidt, H. Motschmann, T. Hellweg and R. von Klitzing, Thermoresponsive surfaces by spin-coating of PNIPAM-co-PAA microgels: a combined AFM and ellipsometry study, Polymer, 2008, 49, 749–756 CrossRef CAS.
- M. Reufer, P. Dıaz-Leyva, I. Lynch and F. Scheffold, Temperature-sensitive poly(NIsopropyl-Acrylamide) microgel particles: a light scattering study, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 28, 165–171 CrossRef CAS PubMed.
- K. Gawlitza, S. T. Turner, F. Polzer, S. Wellert, M. Karg, P. Mulvaney and R. von Klitzing, Interaction of gold nanoparticles with thermoresponsive microgels: influence of the cross-linker density on optical properties, Phys. Chem. Chem. Phys., 2013, 15, 15623 RSC.
- B. Wedel, Y. Hertle, O. Wrede, J. Bookhold and T. Hellweg, Smart Homopolymer Microgels: Influence of the Monomer Structure on the Particle Properties, Polymers, 2016, 8, 162 CrossRef PubMed.
- M. Tagliazucchi, M. G. Blaber, G. C. Schatz, E. A. Weiss and I. Szleifer, Optical Properties of Responsive Hybrid Au@Polymer Nanoparticles, ACS Nano, 2012, 6, 8397–8406 CrossRef CAS PubMed.
- R. Contreras-Cáceres, J. Pacifico, I. Pastoriza-Santos, J. Pérez-Juste, A. Fernández-Barbero and L. M. Liz-Marzán, Au@pNIPAM Thermosensitive Nanostructures: Control over Shell Cross-linking, Overall Dimensions, and Core Growth, Adv. Funct. Mater., 2009, 19, 3070–3076 CrossRef.
- J. Rodríguez-Fernández, M. Fedoruk, C. Hrelescu, A. A. Lutich and J. Feldmann, Triggering the volume phase transition of core–shell Au nanorod–microgel nanocomposites with light, Nanotechnology, 2011, 22, 245708 CrossRef PubMed.
- M. Karg, S. Jaber, T. Hellweg and P. Mulvaney, Surface Plasmon Spectroscopy of Gold-Poly-N-isopropylacrylamide Core–Shell Particles, Langmuir, 2011, 27, 820–827 CrossRef CAS PubMed.
- N. Guarrotxena and I. Quijada-Garrido, Optical and Swelling Stimuli-Response of Functional Hybrid Nanogels: Feasible Route to Achieve Tunable Smart Core@Shell Plasmonic@ Polymer Nanomaterials, Chem. Mater., 2016, 28, 1402–1412 CrossRef CAS.
- A. Rauh, N. Carl, R. Schweins and M. Karg, Role of Absorbing Nanocrystal Cores in Soft Photonic Crystals: A Spectroscopy and SANS Study, Langmuir, 2018, 34, 854–867 CrossRef CAS PubMed.
- J. Turkevich, P. C. Stevenson and J. Hillier, A study of the nucleation and growth processes in the synthesis of colloidal gold, Discuss. Faraday Soc., 1951, 11, 55–75 RSC.
- A. Rauh, T. Honold and M. Karg, Seeded precipitation polymerization for the synthesis of gold-hydrogel core–shell particles: the role of surface functionalization and seed concentration, Colloid Polym. Sci., 2016, 294, 37–47 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, NIH Image to ImageJ: 25 years of image analysis, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- J. Kohlbrecher, SASfit: A Program for Fitting Simple Structural Models to Small Angle Scattering Data, Paul Scherrer Institut, Laboratory for Neutron Scattering, Villigen, Switzerland, 2008 Search PubMed.
- P. B. Johnson and R. W. Christy, Optical Constants of the Noble Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1972, 6, 4370–4379 CrossRef CAS.
- Q. Zhang, C. Weber, U. S. Schubert and R. Hoogenboom, Thermoresponsive polymers with lower critical solution temperature: from fundamental aspects and measuring techniques to recommended turbidimetry conditions, Mater. Horiz., 2017, 4, 109–116 RSC.
- A. Halperin, M. Kröger and F. M. Winnik, Poly(N-isopropylacrylamide) Phase Diagrams: Fifty Years of Research, Angew. Chem., Int. Ed., 2015, 54, 15342–15367 CrossRef CAS PubMed.
- L. K. Månsson, F. Peng, J. J. Crassous and P. Schurtenberger, A microgel-Pickering emulsion route to colloidal molecules with temperature-tunable interaction sites, Soft Matter, 2020, 16, 1908–1921 RSC.
- H. van der Hulst, Light Scattering by Small Particles, Dover Publications, Inc., 1981 Search PubMed.
- M. Kerker, The Scattering of Light and Other Electromagnetic Radiation, Academic Press, New York, 1969 Search PubMed.
- K. Eitel, G. Bryant and H. J. Schöpe, A Hitchhiker's Guide to Particle Sizing Techniques, Langmuir, 2020, 36, 10307–10320 CrossRef CAS PubMed.
- A. Rauh, M. Rey, L. Barbera, M. Zanini, M. Karg and L. Isa, Compression of hard core–soft shell nanoparticles at liquid–liquid interfaces: influence of the shell thickness, Soft Matter, 2017, 13, 158–169 RSC.
- P. K. Jain, K. S. Lee, I. H. El-Sayed and M. A. El-Sayed, Calculated Absorption and Scattering Properties of Gold Nanoparticles of Different Size, Shape, and Composition: Applications in Biological Imaging and Biomedicine, J. Phys. Chem. B, 2006, 110, 7238–7248 CrossRef CAS PubMed.
- M. Stieger, J. S. Pedersen, P. Lindner and W. Richtering, Are Thermoresponsive Microgels Model Systems for Concentrated Colloidal Suspensions? A Rheology and Small-Angle Neutron Scattering Study, Langmuir, 2004, 20, 7283–7292 CrossRef CAS PubMed.
- J. C. M. Garnett and J. X. I. I. Larmor, Colours in metal glasses and in metallic films, Philos. Trans. R. Soc., A, 1904, 203, 385–420 CAS.
- M. Born and E. Wolf, Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, Elsevier, 2013 Search PubMed.
- S. Bergmann, O. Wrede, T. Huser and T. Hellweg, Super-resolution optical microscopy resolves network morphology of smart colloidal microgels, Phys. Chem. Chem. Phys., 2018, 20, 5074–5083 RSC.
- O. Wrede, Y. Reimann, S. Lülsdorf, D. Emmrich, K. Schneider, A. J. Schmid, D. Zauser, Y. Hannappel, A. Beyer, R. Schweins, A. Gölzhäuser, T. Hellweg and T. Sottmann, Volume phase transition kinetics of smart N-n-propylacrylamide microgels studied by time-resolved pressure jump small angle neutron scattering, Sci. Rep., 2018, 8, 13781 CrossRef PubMed.
- V. Y. Rudyak, E. Y. Kozhunova and A. V. Chertovich, Towards the realistic computer model of precipitation polymerization microgels, Sci. Rep., 2019, 9, 13052 CrossRef PubMed.
- A. Scotti, S. Bochenek, M. Brugnoni, M. A. Fernandez-Rodriguez, M. F. Schulte, J. E. Houston, A. P. H. Gelissen, I. I. Potemkin, L. Isa and W. Richtering, Exploring the colloid-to-polymer transition for ultra-low crosslinked microgels from three to two dimensions, Nat. Commun., 2019, 10, 1418 CrossRef CAS PubMed.
- T. Zemb and P. Lindner, Neutron, X-rays and Light. Scattering Methods Applied to Soft Condensed Matter, Elsevier Science, North-Holland Delta Series, 2002 Search PubMed.
- M. Dulle, S. Jaber, S. Rosenfeldt, A. Radulescu, S. Förster, P. Mulvaney and M. Karg, Plasmonic gold–poly(N-isopropylacrylamide) core–shell colloids with homogeneous density profiles: a small angle scattering study, Phys. Chem. Chem. Phys., 2014, 17, 1354–1367 RSC.
- G. M. Hale and M. R. Querry, Optical Constants of Water in the 200 nm to 200 μm Wavelength Region, Appl. Opt., 1973, 12, 555 CrossRef CAS PubMed.
- A. Small, S. Hong and D. Pine, Scattering properties of core–shell particles in plastic matrices, J. Polym. Sci., Part B: Polym. Phys., 2005, 43, 3534–3548 CrossRef CAS.
- W. Heller, H. L. Bhatnagar and M. Nakagaki, Theoretical Investigations on the Light Scattering of Spheres. XIII. The “Wavelength Exponent” of Differential Turbidity Spectra, J. Chem. Phys., 1962, 36, 1163–1170 CrossRef CAS.
- W. Heller, Theoretical Investigations on the Light Scattering of Spheres. XV. The Wavelength Exponents at Small α Values, J. Chem. Phys., 1964, 40, 2700–2705 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01473k |
| This journal is © The Royal Society of Chemistry 2022 |









