Linear shrinkage of hydrogel coatings exposed to flow: interplay between dissolution of water and advective transport

Abstract

We investigate the shrinkage of a surface-grafted water-swollen hydrogel under shear flows of oils by laser scanning confocal microscopy. Interestingly, external shear flows of oil lead to linear dehydration and shrinkage of the hydrogel for all investigated flow conditions irrespective of the chemical nature of the hydrogel. The reason is that the finite solubility of water in oil removes water from the hydrogel continuously by diffusion. The flow advects the water-rich oil, as demonstrated by numerical solutions of the underlying convection-diffusion equation. In line with this hypothesis, shear does not cause gel shrinkage for water-saturated oils or non-solvents. The solubility of water in the oil will tune the dehydration dynamics.

---

1 Introduction

Hydrogels are ubiquitous in our daily lives. Everyday applications range from jelly pudding and diapers to contact lenses and scaffolds in tissue engineering.^1–4 Hydrogels are three-dimensional networks of hydrophilic polymers formed by chemical (covalent) crosslinks or physical (noncovalent) crosslinks such as entanglements that provide physical and structural integrity.^5,6 All hydrogels have in common that they can bind large amounts of water, even as much as 99%.⁷ Most hydrogels are based upon polyelectrolytes, where the macromolecules dissociate ions into the water.^8,9 These ions form a “gas” that wants to expand as much as possible.^10–12 For electrostatic reasons, the oppositely charged polymer network then swells as well. Another class of hydrogels is based upon thermo-responsive macromolecules such as poly-N-isopropylacrylamide (PNIPAm).^13–15 For these hydrogels, the solubility is provided by an interplay between the polar groups and the geometrical match between the local structure of the macromolecule and the short-range structure of water.^16–18 Both mechanisms give rise to a strong water retention capacity, even maintained under mechanical loading conditions, such as squeezing (Fig. 1a).¹⁹

Fig. 1 Experimental approach. (a) The hydrogel beads prove resilient to squeezing and maintain the imbibed water. (b) Preparation of hydrogel coatings covalently attached to a micropillar array via allylamine-functionalization of SU-8 micropillar arrays. The micropillars had a diameter of 30 μm, a height of 10 μm, and a centre-to-centre distance of 60 μm, decorating a 170 μm thick glass coverslip as a substrate. (c) Hydrogel-coated micropillar arrays are contained in a microfluidic flow cell. (d) The hydrogel is swollen with MilliQ water containing fluorescent dye (Atto 488 NHS-Ester, 1 μg g⁻¹). This low concentration ensures that the interfacial tensions remain unmodified. (e) Shrinkage experiment: a flow of silicone oil (yellow) is applied across the hydrogel coating, which leads to shear stresses acting on the hydrogel coating. The evolution of the thickness height of the hydrogel coating above the substrate, h_s(t), is monitored by laser scanning confocal microscopy (LSCM). Can the hydrogel be shrunk with shear flows of oil? And if so, how fast?.

Therefore, there is wide interest in the stability of hydrogels.²⁰ So far, most investigations have focused on the response to changes in bulk thermodynamic parameters (such as temperature or salt concentration).^21–23 Here, we are investigating the interactions of the hydrogel with its surroundings upon subjecting the hydrogel to a steady fluid flow across its surface. The study of the transport of fluids across a hydrogel interface finds vital importance in the fields of water-remediation^24,25 and bio-adhesion in the context of hydrogels used as implants or surgical devices.^26–30 Therefore, the transport and interactions of aqueous fluids across a hydrogel surface/interface are well studied. In contrast, the interactions and transport of non-polar fluids across a hydrogel surface/interface remain unexplored.

We investigate the stability with respect to a non-aqueous liquid that flows past the hydrogel. We find hydrogel shrinkage exclusively caused by the finite solubility of water in the flowing liquid. This even happens when the solubility is low, such as in the case of flowing oil. Here we find that the dehydration rate is correspondingly also very low. This gives rise to a decrease of the hydrogel volume that progresses linearly in time because the flow removes the dissolved water quickly. Interestingly, the dehydration rate seems to be governed only by the properties of the water-oil interface. The polymer component plays no role during the process, spanning roughly an order of magnitude in hydrogel volume. This is even true when comparing a polyelectrolyte gel (poly(acrylic acid), PAA) with a neutral thermoresponsive gel (PNIPAm). The purpose of the present paper is to substantiate this picture by reporting our experimental findings obtained by laser scanning confocal microscopy and the corresponding theoretical analysis based on numerical solutions of the convection-diffusion equation that governs the solute dynamics.

2 Materials and methods

2.1 Materials

SU-8 photoresist was purchased from MicroChem Corp. Trichloro(octadecyl)silane (OTS, >90%), N-isopropylacrylamide (NIPAm, 97%), acrylic acid (AA, 99%), N,N′-methylenebisacrylamide (NMBA, 99%), 2-hydroxy-4′-(2-hydroxyethoxy)-2-methylpropiophenone (Irgacure D-2959) and Allylamine (ALAm, 99,5%) were purchased from Sigma-Aldrich. The fluorescent dye was ATTO 488 NHS-ester (ATTO-TEC GmbH, Germany, diluted in MilliQ water, concentration: 1 μg g⁻¹). As lubricants, silicone oils (PDMS, Sigma-Aldrich, viscosity: 50 cSt and 500 cSt at 25 °C), mineral oil (Paragon Scientific Ltd, viscosity: 100 cSt at 20 °C), Fluorinert^TM FC-70® (Sigma-Aldrich, viscosity: 12 cSt), and olive oil (Bertolli®) were used. All chemicals were used as received. Epoxy resin flow cells (Sticky-Slide VI0.4) were purchased from ibidi GmbH (Germany). The individual channels are 0.5 mm high (including adhesive layer), 17 mm long, and 3.8 mm wide, which amount to a coverable area of 64.6 mm² per channel. Each channel has a volume of 32 μL. Alternatively, flow cells having a height of 0.1 mm, a length of 45 mm, a width of 5 mm, and a volume of 23 μL were used. The flow cells were connected to a peristaltic pump (Reglo-Analog MS4/8, Cole-Parmer GmbH) via polyvinyl chloride (PVC)-tubes (internal diameter = 1.42 mm, Novodirect GmbH Labor und Meßgeräte) and tightly sealing linkers. The fluorescent dye ATTO 488 NHS-ester offers excellent water solubility, strong absorption, high fluorescence quantum yield, and high photostability. The fluorescence is excited most efficiently in the range of 480 and 515 nm. The 488 nm line of an argon laser was used for excitation. The used dye concentrations did not change the interfacial tension of water as verified from interfacial tension measurements.

2.2 Preparation of hydrogel surfaces

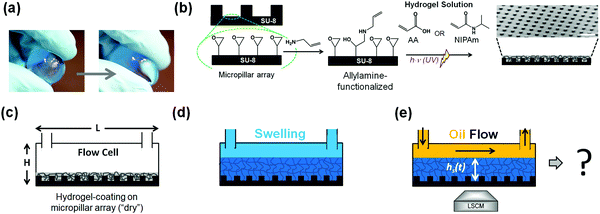
To achieve a homogeneous binding of the hydrogel to a surface, it turned out that a microstructure facilitates the binding. The regular microstructured surface consisted of uniform arrays of cylindrical micropillars fabricated by photolithography using an epoxy-based negative photoresist (i.e., SU-8).^31,32 SU-8 photoresist was spin-coated on oxygen plasma activated glass coverslips (10 min, 300 W) and soft baked (95 °C, 4 min) to evaporate the solvent and densify the deposited film. Illumination with UV-light (mercury lamp, 350 W, 30–35 s) through a photomask induced crosslinking within the exposed portions of the film. Subsequently, a post-exposure baking step (10 min at 65 °C; 2 min at 95 °C; 30 min at 65 °C) was performed to crosslink those areas selectively. The SU-8 micropillars arrays were coated with a hydrogel, Fig. 1a and b. Double functional groups were first introduced onto the SU-8 photoresist-based micropillar array surface via a reaction involving allylamine (ALAm).^33,34 A 5% v/v solution of allylamine in water was prepared and put under stirring for 10 minutes. The thus-prepared solution was poured into a glass box containing the SU-8 micropillar arrays and left for 30 minutes. The amino-groups of ALAm react with the epoxy groups of SU-8 in an SN₂-type reaction, thus exposing the allyl group to the surface. After 30 minutes, the samples were then extensively rinsed with water and left to dry. After the pre-modification, UV-induced radical photopolymerization was used to grow the hydrogel network on SU-8 micropillar arrays. For that purpose, 10% v/v aqueous solutions of NIPAm and AA were prepared by adding a 2% w/w NMBA, with respect to the monomer content, as the crosslinker. Finally, 20 mg of Irgacure D-2959 as initiator was added to the solutions. The micropillar arrays were wetted with 1 mL of hydrogel solution. A glass slide was gently positioned onto the arrays forming a “sandwich structure” by doctor blading to spread the solution drop, avoiding the formation of bubbles. The arrays were placed under a UV lamp at a distance of 7.5 cm (6.0 mW cm⁻²) and irradiated for 20 minutes. After polymerization, the glass slide was removed. The hydrogel formed had more affinity with the micropillars arrays; therefore, only this surface was coated. The thus-obtained hydrogel-functionalized micropillar arrays were washed with water and left to dry. Coating with an acrylic acid-based hydrogel solution establishes PAA-based hydrogel coatings. In contrast, an N-isopropylamide-based hydrogel solution establishes the PNIPAm hydrogels. Scanning Electron Microscopy (SEM) confirms the presence of a homogeneous hydrogel coating (Fig. S1, ESI†).

2.3 Preparation of water-saturated oil

12 mL of MilliQ water was added to 40 mL of 50 cSt silicone oil and stirred at 300 rpm for 72 h. The separation of saturated oil and excess water was performed with a separation funnel. The vessel was sealed during the experiments using paraffin tape.

2.4 Laser scanning confocal microscopy (LSCM)

LSCM allows distinguishing the different fluid phases via fluorescent dyes, which is impossible when using a standard goniometer setup. An inverted laser scanning confocal microscope (LSCM, Leica TCS SP8 SMD) with a 40×/1.11 water immersion objective lens (Olympus) was employed to image the shrinkage, i.e., dehydration of the hydrogel. The horizontal resolution was ≈500 nm, the vertical resolution was ≈1 μm, and the time span in-between successive images was 10–30 min. Confocal image acquisition is a trade-off between image quality and imaging speed. For the data presented in Fig. 2 and 4, the priority was on image quality. Hence, we only performed confocal imaging at one point along the flow channel. Image acquisition parameters like a long pixel dwell time (0.12 ms), a high line average (8), a comparatively small scanning frequency (400 Hz), and a large field of view (291.19 × 291.19 μm × μm, 4096 × 4096 pixel × pixel) ensure optimal image quality, albeit slowing the image acquisition speed. These significant acquisition times render different imaging points along the flow channel (as done for the data presented in Fig. 3) experimentally unfeasible. In Fig. 3, the focus was on the comparison to the simulation results. Hence, the acquisition parameters of the confocal laser scanning microscopy imaging were optimized for faster imaging. The scanned areas in the cross-section images (xz-scans) were 291 × 146 μm² (512 × 256 pixel × pixel). The pixel dwell time was 1.2 μs. We employed a line average of 2. The scanning frequency was 600 Hz. Acquired images of the hydrogel cross-section were evaluated with a custom-written MATLAB® routine. This yields an average height per cross-sectional image.

Fig. 2 Hydrogels encountering a shear flow of oil. (a) Time evolution of side view (xz-scan) laser scanning confocal images (40×/1.1 water immersion objective) demonstrating dehydration of a hydrogel coating consisting of PAA (poly (acrylic acid)) on a micropillar array (consisting of photoresist SU-8). The flow direction of oil is from left to right. The hydrogel coating is swollen with fluorescently labelled MilliQ-water. Dye (Atto-488 NHS-Ester) concentration: 1 μg mL⁻¹. The substrate and the micropillars appear black since they have not been dyed. Silicone oil (viscosity: 50 cSt, density: 0.96 g mL⁻¹, not dyed) is then continuously circulated over the hydrogel-coated micropillar array at a volumetric flow rate Q of 0.48 mL min⁻¹ for 900 min. Pillar dimensions: diameter d = 30 μm, centre-to-centre spacing (“pitch”) p = 60 μm, and pillar height h = 10 μm. All scale bars are 30 μm. (b) The mean height of hydrogels linearly decreases with time while silicone oil (50 cSt) is flowing over the hydrogel (solid blue squares: PAA, flow velocity 50 mm s⁻¹, R² = 0.999, solid blue triangles: PAA, flow velocity 5 mm s⁻¹, R² = 0.999, solid orange circles: PNIPAm, flow velocity 5 mm s⁻¹, R² = 0.998). R² denotes the coefficient of determination. The establishment of the retention thickness takes place sharply (inset). Flow velocities: 5 mm s⁻¹ or 50 mm s⁻¹. (c) The slope of the time evolution of the hydrogel thickness is constant for the investigated parameter range within experimental accuracy (blue: PAA, orange: PNIPAm).

Fig. 3 Dehydration of the hydrogel by diffusion and advection. (a) Sketch of flow channel. Water diffuses into the oil at the shared hydrogel-oil interface. h_S(t) is the height of hydrogel. Dashed white box demarcates position shown in (b) water concentration field in the oil between inlet and outlet, obtained by direct numerical simulation. The dry oil (yellow) enters the flow cell. The water concentration increases in the flow direction. The white lines I–IV correspond to water concentration in the oil of 2, 4, 6, and 8 mM, respectively. (c) h_S(t), evolution on 8 positions along the channel axis (channel height: 100 μm). The hydrogel thickness decreases more slowly in the downstream direction. The dotted lines are linear fits of the measurement data and help to guide the eye. (d) Slope of the time evolution of the hydrogel thickness, along the channel length/oil layer thickness. Solid lines represent results from simulation, while symbols represent the confocal microscopy measurements. The flow cells used for these experiments have a volume of 23 μL, a height of H = 100 μm, a length of L = 45 mm, and a width of W = 5.0 mm. (e) Total water flux, integrated along the entire interface length. For all Pe and Re configurations, the free energy barrier was set to 20.3k_BT.

2.5 Scanning electron microscopy

The micropillar arrays were characterized via scanning electron microscopy (SEM) using a LEO 1530 Gemini scanning electron microscope (Zeiss, Germany). The samples were tilted (45°) to visualize a micropillar array best.

2.6 Model and simulation

Water migrating from the hydrogel into the oil is transported³⁵ as

∂_tc + ∇·(uc − D∇c) = 0. (1)

The concentration of water, c, follows the advective flow of the oil with the hydrodynamic velocity u = u_xe_x + u_ye_y, while it diffuses into the bulk oil with a mobility which we estimate³⁶ as D = 2 × 10⁻⁹ m² s⁻¹. The advective transport term in eqn (1) is an essential part of the dehydration process. Without considering this term, water saturation would occur inside the channel within seconds to minutes, and no dehydration would occur after that. In order to solve eqn (1), we search for u, utilizing the momentum conservation in the (incompressible) bulk oil flow,³⁷ namely

ρ(∂_tu + (u·∇)u) + ∇·(pI + τ) = 0. (2)

Here, ρ and η are the density and the dynamic viscosity of the oil, respectively. Because the dilution of water is minor, we neglect any density changes in the oil phase. p is the hydrostatic pressure, I the identity matrix and τ is the shear tensor, which we consider Newtonian without compression, such that it reads

τ = −η(∇u + (∇u)^T). (3)

We do not consider any transient relaxations, such that the time derivatives in eqn (1) and (2) become zero. We use standard conditions on the domain-boundaries (i.e., no-slip, no-flux cf. Fig. S8 and Table S1, ESI†), except on the shared interface between hydrogel and oil. Here, we utilize a kinematic flux condition, which we discuss in the results and discussion.

We solve eqn (1) and (2), together with the boundary conditions (Fig. S8, Table S1 and eqn (4), ESI†) in the microchannel (microfluidic flow cell) numerically, utilizing the software package COMSOL Multiphysics® 5.5. For discretization, the finite element method is utilized (linear ansatz functions for mass conservation, P2 + P1 elements with consistent stabilization for momentum conservation). The computation domain defined in Fig. S8 (ESI†) was discretized with a structured, Cartesian mesh, holding 15 132 432 degrees of freedom. We added 1.5 mm to the inlet height to let the flow develop into a parabola. Mesh independence was verified by successively increasing the number of degrees of freedom until no variations in the solutions were observed. The equations were solved directly with the MUMPS solver.³⁸

3 Results and discussion

We used a microfluidic flow cell with plastic side and top walls to investigate the hydrogels' flow-induced dehydration. The polymer-coated micropillars (Fig. 1b) formed the base of the cell (Fig. 1c). Next, the flow cell is filled with dyed MilliQ-water (blue) to induce polymer swelling, Fig. 1d. After 30 minutes, a steady-state thickness of the swollen equilibrated hydrogel has been reached, and a flow of neat silicone oil (polydimethylsiloxane, PDMS) was applied, Fig. 1e. Silicone oil offers the advantage of identical chemical characteristics over wide viscosity ranges. We monitored the swollen hydrogels' stability in situ under flow conditions utilizing an inverted laser scanning confocal microscope (LSCM, Fig. S2, ESI†). LSCM allows distinguishing different fluid phases via fluorescent dyes at concentrations sufficiently low that the dyes do not change the system's constituents' interfacial properties.

Within the flow cell (height 500 μm), the flow profile of the oil is approximately parabolic through its depth and uniform through its width. The volumetric flow rates Q established through the flow channel using a peristaltic pump ranged from Q = 0.48 mL min⁻¹ to 4.8 ± 0.2 mL min⁻¹, which resulted in average flow velocities ranging from 5.3 mm s⁻¹ to 53 ± 2 mm s⁻¹. Image acquisition was performed in the middle of the horizontal flow cell with respect to the lateral direction parallel to the flow if not stated otherwise.

The height of the initial swelling (>100 μm for PAA, >50 μm for PNIPAm, Fig. 2a, top, Fig. S3a and S4a, ESI†) is much larger than the pillar height (black, h = 10 μm). The interface between the excess water and the water contained in the hydrogel causes a change in the emission intensity. The difference in light intensity may be attributed to different affinities of the hydrophilic dye to unbound and bound water within the hydrogel or to a shift of the dye's emission signal. The flow of silicone oil (black) leads to progressive shrinkage owed to dehydration of the hydrogel, i.e., water depletion of the coating (Fig. 2a and Fig. S3b–k, ESI†). As dehydration progresses, the remaining portions of the swollen hydrogel conform to the shape of the micropillar array (Fig. 2a, bottom, Fig. S3j–r, ESI†). Eventually, the remaining swollen portions of the hydrogel reach a steady-state retention thickness, which remains unchanged as the oil flow continues (Fig. 2a, bottom, Fig. S3k–r, ESI†).

The quantification of the hydrogel dehydration was performed by extracting the mean height h_s(t) of the hydrogel coating above the substrate (averaged over at least 15 positions). The hydrogel coating thickness, i.e., hydrogel shrinkage, progresses linearly with time (Fig. 2b). Notably, a linear decrease in thickness is found for the polyelectrolyte PAA and the neutral PNIPAm-based hydrogel coatings (Fig. 2b and Fig. S3–S5, ESI†). The shrinkage of the hydrogel coating progresses until the steady-state retention thickness is reached, which happens with a sharp transition (Fig. 2b, inset) and is indicative of residual water content. At first glance, linear dehydration kinetics might be surprising and counterintuitive since hydrogels have been observed to undergo structural changes during dehydration.^39,40

Regardless of the hydrogel coating and the flow characteristics that were considered experimentally (flow velocity and oil viscosity), within experimental accuracy the dehydration kinetics (represented by the slopes of the curve) hardly show any variations (Fig. 2c). We varied the Reynolds number Re = ρvh/η between 0.053 and 0.106. The maximum flow velocity v is set by the pump, the microfluidic flow cell, the channel height h, and the oil density ρ and viscosity η. For the considered Re, our experiments are in the Stokes limit, i.e., the inertia terms in eqn (2) are diminishingly small.

What causes the linear decrease of the thickness with time? One option would be that oil slowly and continuously shears off the water. However, in that case, the shrinkage rate should change with varying oil viscosity or flow velocity. Within the experimental resolution, we did not observe a dependence on velocity or viscosity. We also did not observe a flow-induced dissolution of arrays of discrete oil droplets.⁴¹

To understand hydrogel shrinkage, it is important to keep in mind that silicone oil can take up around 30 mM of water.³⁶ Initially, the entering silicone oil is ‘dry’. The hydrogel contains a large amount of water. Hence, the chemical potential, characterized by an intensive free energy, is unbalanced in the two phases. This imbalance of chemical potential can be regarded as osmotic pressure acting on the water molecules. To equilibrate this imbalance, water migrates via diffusion from one phase (hydrogel) to the other (silicone oil) until the oil is saturated. This is feasible due to the mobility of water in silicone oil, quantified by the diffusivity¹⁸ of approximately D = 2 × 10⁻⁹ m² s⁻¹ for the investigated viscosities. Given the length scale of the channel height h = 100 μm, it can be expected that molecules diffuse in oil from the channel's bottom to its ceiling at a rate of τ_diff.⁻¹ = D/h² ≈ 0.2 s⁻¹. Diffusion of water into oil relaxes the osmotic pressure (balancing the differing chemical potentials). Vice versa, oil enters the hydrogel as well; however, only to such an extremely low degree (<1 ppm) that we neglect it.⁴²

The advective flow of the oil superposes diffusive transport of water molecules. The imposed oil flow of v = 5 mm s⁻¹ creates a situation where the relaxation of the osmotic pressure becomes impossible: dry silicone oil enters the flow channel (l = 53.2 mm) at a rate of τ_diff.⁻¹ = v/l ≈ 0.1 s⁻¹. In fact, the advective transport dominates over the diffusive transport, depicted by the Péclet number (Pe = vl/D = 1.33 × 10⁵ to 5.32 × 10⁶), which relates the two transport mechanisms to each other. Water molecules migrating from the hydrogel into the oil are entrained and quickly removed from the shared interface by the oil flow.

Therefore, the water concentration at the shared interface is unlikely to be in local equilibrium here, i.e., the oil is unsaturated. In this state of imbalance, water molecules in the hydrogel and oil have differing standard enthalpies, which resembles the latent heat of an evaporation process. The differing enthalpy can be considered an energetic barrier at the shared interface, which holds the water molecules within the hydrogel. The free energetic barrier at the shared interface prevents the water molecules from spontaneous migration into the oil flow. We now assume that the escape of a water molecule may be viewed as an activated process, for which Kramers’ theory can be applied.⁴³ According to this theory, the escape rate is

where σ ≈ 1 nm is the thickness of the shared interface, ΔU is the energy barrier height over which water molecules have to diffuse, k_B = 1.380 × 10⁻²³ J K⁻¹ is the Boltzmann constant, and T = 293 K the ambient temperature. We determine the height of the barrier to be in the range of 20.3–21.3k_BT, (see ESI,† S1 Discussion on Free Energy Barrier).

Starting from these assumptions, we conducted a finite element analysis (FEM, model and simulation) of the water distribution in the silicone oil, Fig. 3a and b. The water concentration is low close to the inlet (yellow) and increases along the flow direction. We highlight four lines (I–IV) of constant water concentrations (2, 4, 6, and 8 mM, respectively) to visualize the increasing water concentration along the channel (Fig. 3b). Consequently, dehydration of the hydrogel progresses faster in the upstream direction. This is in line with experimental observations (Fig. 3c and Fig. S6, S7, ESI†). Water enriched oil (approx. 9 mM; however, not saturated) leaves the channel on the right-hand side. Considering the conservation of mass in the hydrogel, we can map the measured vertical hydrogel height to the depleting water flux (Fig. 3d). The grey area in Fig. 3d marks the range of fluxes for the determined barrier heights. The overlaid data (blue squares) from experiments and simulation show excellent agreement, providing further support for these considerations (Fig. 3d). This picture considers the hydrogel's response as instantaneous because of the huge amount of swollen water. This implies neglecting any effects, such as e.g., elastic deformation (Fig. S9, ESI†). We expect that when the hydrogel is nearly fully depleted, these effects cause the sharp transition between the diffusion–advection-dominated regime and the steady-state retention thickness. To obtain insights into the dependency of flow condition and dehydration kinetics, we conducted simulations for Pe from 10² to 10⁸, Fig. 3e. Here, we show dehydration rates integrated along the channel length, shown in Fig. 3a–d. The free energy barrier for these calculations was set to 20.3k_bT. The dehydration rates plateaus in two regimes: for low Pe, i.e., Pe = 10⁵ the dehydration rate is diminishingly small. The oil in the microchannel flows at such low rates, that the entire channel interior saturates and the chemical potential difference between hydrogel and oil flow are close to zero. Water migration from hydrogel to oil phase becomes limited by the very weak oil flow. For Pe ≫ 10⁵, the oil migration levels around 11 mol m⁻¹ s⁻¹. This upper limit of oil migration is limited by the free energy barrier at the hydrogel interface. Only in-between those two plateaus, the dehydration rates depend on the Péclet number (Pe). Note, that taking the low free energy barrier (20.3k_bT) leads to higher dehydration rates. Since we observe no variations of dehydration rates with different flow conditions in the experiments, we expect that the free energy barrier in the experiments is in fact higher, i.e., more favoured towards the 21.3k_bT value.

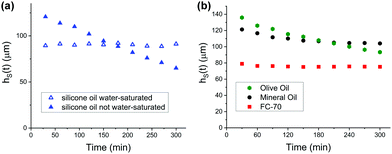
To test the hypothesis that shrinkage is determined by the finite solubility of water in oil, we conducted experiments using water-saturated oil. Indeed, the thickness of the hydrogel remains unaltered beyond sample inhomogeneity (Fig. 4a). In contrast, when conducting the shrinkage experiment with silicone oil, which is not water-saturated, one observes the already familiar linear shrinkage of the hydrogel coating. Therefore, shrinkage (dehydration) can be avoided by subjecting the swollen hydrogel to a shear flow of water-saturated oil. No observable water migration occurs from the water tethered in the hydrogel into the external oil phase.

Fig. 4 Influence of water saturation. (a) Presence (solid triangles) or absence (open triangles) of shrinkage on swollen hydrogel coatings subjected to a shear-flow of neat and water-saturated silicone oil. (b) Olive oil (green hexagons) shows linear shrinkage behaviour analogous to silicone oil. For mineral oil (black circles) and the perfluorinated oil Fluorinert^TM FC-70® (red squares), the oil achieves water saturation early during the shrinkage experiment. Hence, the dehydration comes to a halt, translating into a constant thickness of the hydrogel coating.

To substantiate our findings further, we conducted the same shrinkage experiments with oils that are chemically different from silicone oil. Olive oil (Fig. 4b, green hexagons), a mixture of fatty acids, shows linear shrinkage behaviour analogous to silicone oil. When conducting shrinkage experiments with mineral oil and Fluorinert^TM FC-70® (Perfluorotripentylamine, C₁₅F₃₃N), one observes a nonlinear shrinkage behaviour. The solubility of water in mineral oil (Fig. 4b, black circles) is approximately 0.2 mM, which is two orders of magnitude smaller than the solubility of water in silicone oil (≈30 mM). Hence, water saturation occurs in the early stages of the shrinkage experiment, i.e., after a much shorter time than shrinkage experiments conducted with silicone oil. When conducting shrinkage experiments with Fluorinert^TM FC-70®, the thickness of the hydrogel coating remains constant throughout the shrinkage experiment (Fig. 4b, red squares). The extremely low solubility of water in FC-70®, which lies below 10 μM, explains this observation.

Conclusions

In summary, we have investigated the stability of hydrogels under shear flows of oil. We found experimentally that swollen hydrogels are linearly shrinking irrespective of the investigated flow velocity, oil viscosity, and the hydrogel's chemical nature. A gradient in the chemical potential between the hydrogel and any surrounding phase gives diffusion as a dehydration mechanism. The hydrogel structure can continuously adjust to cope with a wide window of water concentrations without evoking significant thermodynamic changes. The chemical potential gradient vanishes when saturating the oil. In this case, the diffusion-driven dehydration is neutralized. This is confirmed by our control experiment working with water-saturated oils.

Numerical simulations revealed that the interplay between the diffusion of water into the oil phase and the advective transport of the oil is the underlying universal mechanism for the observed shrinkage behaviour. The only condition is that there is a time-scale separation, and the transition of the water into the flowing liquid is sufficiently slow. The finite yet non-vanishing solubility of water in oil proved central to explaining the observed phenomena. Our findings help to improve our understanding of the fundamental physics of hydrogels. The same depletion mechanism (among others) is expected for swollen organogels, which are frequently used as low adhesive surfaces.

Author contributions

Philipp Baumli: Conceptualization, methodology, investigation, visualization, resources, writing – original draft, writing – review & editing, Lukas Hauer: software, formal analysis, validation, data curation, visualization, writing – original draft, writing – review & editing, Emanuela Lorusso: conceptualization, methodology, resources, writing – original draft, Azadeh Sharifi Aghili: resources, investigation, Katharina, I. Hegner: resources, investigation, Maria D’Acunzi: resources, investigation, Jochen S. Gutmann: supervision, writing – review & editing, project administration, Burkhard Dünweg: supervision, writing – review & editing and Doris Vollmer: supervision, writing – review & editing, project administration, funding acquisition.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors acknowledge the funding received from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 722497 (Innovative Training Network) ITN LubISS (P. B., E. L.), the Priority Programme SPP 2171 (D. V., L. H.), the Max Planck – University of Twente Center for Complex Fluid Dynamics (D. V.), and the Max Planck Graduate Center (MPGC) (K. I. H.). The authors thank Hans-Jürgen Butt, Lou Kondic, Detlef Lohse, Abhinav Naga, Harald Pleiner, Walter Richtering, Thomas Vilgis, and William S. Y. Wong for helpful and stimulating discussions. The authors are grateful to Anke Kaltbeitzel and Alexandre Laroche (Airbus) for assisting in confocal microscopy and photography. Open Access funding provided by the Max Planck Society.

Notes and references

1. E. Caló and V. V. Khutoryanskiy, Eur. Polym. J., 2015, 65, 252–267.
2. K. Y. Lee and D. J. Mooney, Chem. Rev., 2001, 101, 1869–1880.
3. Y. Guo, J. Bae, Z. Fang, P. Li, F. Zhao and G. Yu, Chem. Rev., 2020, 120, 7642–7707.
4. N. A. Peppas, J. Z. Hilt, A. Khademhosseini and R. Langer, Adv. Mater., 2006, 18, 1345–1360.
5. T. Tanaka, Sci. Am., 1981, 244(124–136), 138.
6. N. A. Peppas, Y. Huang, M. Torres-Lugo, A. J. H. Ward and J. Zhang, Annu. Rev. Biomed. Eng., 2000, 2, 9–29.
7. P. J. Flory, J. Chem. Phys., 1950, 18, 108–111.
8. C. Yang and Z. Suo, Nat. Rev. Mater., 2018, 3, 125–142.
9. A. Ikegami and N. Imai, J. Polym. Sci., 1962, 56, 133–152.
10. N. Volk, D. Vollmer, M. Schmidt, W. Oppermann and K. Huber, in Polyelectrolytes with Defined Molecular Architecture II, ed. M. Schmidt, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004 DOI:10.1007/b11348, pp. 29–65.
11. M. Schmidt, Polyelectrolytes with Defined Molecular Architecture I, Springer Berlin, Heidelberg, 2004.
12. M. Schmidt, Polyelectrolytes with Defined Molecular Architecture II, Springer Berlin, Heidelberg, 2004.
13. A. Halperin, M. Kröger and F. M. Winnik, Angew. Chem., Int. Ed., 2015, 54, 15342–15367.
14. M. Heskins and J. E. Guillet, J. Macromol. Sci., Part A: Pure Appl. Chem., 1968, 2, 1441–1455.
15. M. A. Haq, Y. Su and D. Wang, Mater. Sci. Eng., C, 2017, 70, 842–855.
16. T. Tanaka, Phys. Rev. Lett., 1978, 40, 820–823.
17. S. Hirotsu, Y. Hirokawa and T. Tanaka, J. Chem. Phys., 1987, 87, 1392–1395.
18. Y. Tamai, H. Tanaka and K. Nakanishi, Macromolecules, 1994, 27, 4498–4508.
19. J. Meid, F. Dierkes, J. Cui, R. Messing, A. J. Crosby, A. Schmidt and W. Richtering, Soft Matter, 2012, 8, 4254–4263.
20. W. Richtering and B. R. Saunders, Soft Matter, 2014, 10, 3695–3702.
21. A. Takahashi, N. Kato and M. Nagasawa, J. Phys. Chem., 1970, 74, 944–946.
22. S. Cai and Z. Suo, J. Mech. Phys. Solids, 2011, 59, 2259–2278.
23. C. Dalgicdir, F. Rodríguez-Ropero and N. F. A. van der Vegt, J. Phys. Chem. B, 2017, 121, 7741–7748.
24. X.-S. Hu, R. Liang and G. Sun, J. Mater. Chem. A, 2018, 6, 17612–17624.
25. A. G. B. Pereira, F. H. A. Rodrigues, A. T. Paulino, A. F. Martins and A. R. Fajardo, J. Cleaner Prod., 2021, 284, 124703.
26. M. P. Lutolf, J. L. Lauer-Fields, H. G. Schmoekel, A. T. Metters, F. E. Weber, G. B. Fields and J. A. Hubbell, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 5413–5418.
27. A. Lauto, D. Mawad and L. J. R. Foster, J. Chem. Technol. Biotechnol., 2008, 83, 464–472.
28. K. D. Kim and N. M. Wright, Spine, 2011, 36.
29. M. Mehdizadeh and J. Yang, Macromol. Biosci., 2013, 13, 271–288.
30. R. Michel, L. Poirier, Q. van Poelvoorde, J. Legagneux, M. Manassero and L. Corté, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 738–743.
31. P. Papadopoulos, L. Mammen, X. Deng, D. Vollmer and H.-J. Butt, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 3254–3258.
32. F. Schellenberger, J. Xie, N. Encinas, A. Hardy, M. Klapper, P. Papadopoulos, H.-J. Butt and D. Vollmer, Soft Matter, 2015, 11, 7617–7626.
33. S. Chatterjee, G. H. Major, B. M. Lunt, M. Kaykhaii and M. R. Linford, Microsc. Microanal., 2016, 22, 964–970.
34. Z. Zhu, P. Chen, K. Liu and C. Escobedo, Micromachines, 2016, 7, 230.
35. R. F. Probstein, Physicochemical Hydrodynamics: An Introduction, Wiley, 2nd edn, 2005.
36. J. A. Barrie and D. Machin, J. Macromol. Sci., Part B: Phys., 1969, 3, 645–672.
37. D. J. Acheson and F. D. J. Acheson, Elementary Fluid Dynamics, Oxford University Press, 1st edn, 1990.
38. P. Amestoy, I. S. Duff, J. Koster and J.-Y. l’Excellent, MUMPS: A Multifrontal Massively Parallel Solver, ERCIM News, ERCIM, 2002, vol. 50, pp. 14–15.
39. G. Kaklamani, D. Cheneler, L. M. Grover, M. J. Adams, S. H. Anastasiadis and J. Bowen, Prog. Biomater., 2017, 6, 157–164.
40. Y. Sekine and T. Ikeda-Fukazawa, J. Chem. Phys., 2009, 130, 034501.
41. L. Bao, V. Spandan, Y. Yang, B. Dyett, R. Verzicco, D. Lohse and X. Zhang, Lab Chip, 2018, 18, 1066–1074.
42. P. Baumli, H. Teisala, H. Bauer, D. Garcia-Gonzalez, V. Damle, F. Geyer, M. D'Acunzi, A. Kaltbeitzel, H.-J. Butt and D. Vollmer, Adv. Sci., 2019, 6, 1900019.
43. H. Risken, The Fokker-Planck Equation: Methods of Solution and Applications, Springer Berlin Heidelberg, Berlin, Heidelberg, 1996 DOI:10.1007/978-3-642-61544-3_4, pp. 63–95.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sm01297e

‡ Contributed equally.

§ Current address: Department of Chemical Engineering, Stanford University, Stanford, CA, USA.

---