Gecko adhesion: a molecular-simulation perspective on the effect of humidity

Abstract

Gecko adhesion is investigated by molecular dynamics simulations. It is known, that the gecko adhesion system shows increased pull-off forces in humid environments. A coarse-grained model of gecko beta keratin, previously developed in our group, is extended and used to elucidate the molecular mechanisms involved in this humidity effect on adhesion. We show that neither the change of the elastic properties of gecko keratin, nor capillary forces, can solely explain the increased pull-off forces of wet gecko keratin. Instead, we establish a molecular picture of gecko adhesion where the interplay between capillary bridges and a mediator effect of water, enhances pull-off forces, consistent with observations in AFM experiments at high humidities. We find that water density is raised locally, in molecular scale asperities of the gecko keratin and that this increase in local water density smoothes the surface-spatula interface. Water, which is absorbed into the keratin, acts as a mediator, and leads during pull-off to the dominant contribution in the van der Waals energy, because the dispersion interactions between water and surface are primarily opposing the pull-off.

---

1 Introduction

Geckos owe their incredible ability to run on walls¹ and even on ceilings due to billions of spatulae at the end of millions of setae on their toes. The spatulae are in molecular close contact with the surface. The mechanisms behind this remarkable adhesive ability have been investigated for decades^2–4 and shown to be, among others, van der Waals interactions. Additionally, gecko adhesion is typically enhanced by increased relative ambient humidity, however, the mechanism behind this humidity effect is still intensively debated.^4–7 The dominant hypothesis is the change in the Young modulus of setae upon swelling.^5,6,8 The potential role of humidity-enhanced capillary forces has also been discussed.^4,9 The special case of a water layer present on all kinds of surfaces^4,6,10 at high humidity has been investigated, and the enhanced adhesion has been explained by either capillary forces or material softening. Mitchell et al.¹¹ recently came to the conclusion, that the two mechanisms are not mutually exclusive, but that capillary forces increase pull-off forces at hydrophilic surfaces and that material softening is responsible for the increased adhesion at hydrophobic surfaces. A molecular perspective on the humidity effect is, to our knowledge, non existent, but of great importance for understanding gecko adhesion and for the design of biologically-inspired synthetic gecko adhesives.

The multi-level hierarchical structure of the gecko adhesion systems begins at the millimeter scale, where millions of setae (around one hundred micrometers long) are situated on lamellae, found on each gecko's toe pad. Fibrillar structures inside the setae containing beta keratin filaments^12,13 split at the end of each seta into hundreds to thousands of spatulae (around one hundred nanometers long).^14,15 This milli- to nanoscale structure gives the gecko the ability to attach its spatulae to a wide range of surface roughnesses.^16,17

As the gecko walks on a substrate the amino acids of the keratin on the spatula surface are in close contact with the surface atoms. We hypothesize that the main driving force of humidity-enhanced adhesion can be explained by van der Waals interactions. To verify the hypothesis we extend a purely Lennard-Jones based coarse-grained model of dry gecko keratin, previously developed in our group,¹³ which was validated against mechanical properties of setae and spatula with the Young modulus and Poisson's ratio, but did not yet encompass adhesion to a surface, by implementing a water and a surface model. The extension of the coarse-grained model allows us to attach the gecko keratin model to a surface and study the effect of water upon pull-off.

To investigate the humidity effect and the role of water on the ability to increase adhesion, this study uses as a first force probe molecular dynamics (FPMD) simulations – to compute pull-off forces of the keratin from a hydrophobic surface with a contact angle of greater than 110°. The primary target of our model is to achieve a balance between realistic, experimental systems and computational efficiency, allowing us to reach the time and length scales necessary to make reasonable comparisons against experimental pull-off forces and pulling velocities. Since our aim is to elucidate molecular mechanisms of the enhanced pull-off force in humid environments on hydrophobic surfaces, we are particularly interested in the experimental conditions of Huber et al.⁴ Their work showed increased pull-off forces of a single spatula with increasing ambient humidity on a hydrophobic octadecyltrichlorosilane self-assembled monolayer (OTS-SAM) surface. Since the water content and hydrophilicity of gecko keratin at given humidities is not known, we use one water content (10 wt%). We also experimentally investigate the upper boundary of water content at very high ambient humidities for gecko keratin-like materials, and show that the water content in our models are within the experimental range of possible water contents.

We use the term hydrophilicity as a way to relate between the experimentally-observed phenomenon which influences the contact angle of water on flat surfaces and our molecular perspective, where the strength of water–keratin energetic interactions and water–water interactions result in a macroscopic experimentally-observable contact angle. Huber et al.⁴ calculated the contact angle of gecko claw keratin and estimated the contact angle for spatula keratin. The gecko claw keratin had a contact angle of around 128°. We show, however, that gecko claw keratin can absorb up to 30% of water content at high humidities. Due to this discrepancy, on one side a super-hydrophobic contact angle and on the other side a major absorption of water, we are skeptical of the contact angle estimated by Huber et al.⁴ for gecko spatula keratin. We expect that there is a correlation between contact angle and water content. The contact angle of water on polyamide surfaces immersed in water shows a decrease in contact angle with exposure time to water¹⁸ and a correlation between water content increase and contact angle decrease is established for increasing hydrophilicity of aliphatic polyamides.¹⁹ Because we do not know the real experimental hydrophilicity of spatula keratin, we create different gecko keratin models with different hydrophilicities. Higher hydrophilicity would result in a smaller contact angle with water, lower hydrophilicity would lead to a larger contact angle. Due to our multiple keratin models-approach, we can study the effect of possible hydrophilicities of adhesive materials on the pull-off force in ambient humidity. This insight into the effect of hydrophilicity of the adhesive material may drive the design of better biologically-inspired synthetic gecko adhesives.

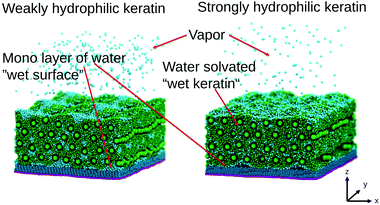
We conduct simulations of bulk keratin, without a surface present, in order to extract mechanical properties. They are validated against experimental results and the effect of water is discussed. We conduct non-equilibrium simulations in which dry or wet keratin is pulled off the surface by an external force, which we call pulling simulations, for short, from here on. We will show an additional effect of water besides the effective reduction of the Young modulus and the capillary forces. In the hypothetical case of a strongly hydrophilic keratin (same applies to synthetic adhesive materials), which may readily absorb water into its interface region between surface and spatula, water acts as a mediator for keratin to surface interactions. Water also smoothes the molecular scale roughness of gecko keratin and allows it to form additional molecular contacts with the underlying surface. This smoothing of the molecular scale roughness due to water may also be a important factor in case of surfaces which are rougher than our OTS-SAM, where water would fill into surface cavities.

There are three main results from this study. First, depending on keratin hydrophilicity, either capillary bridges or a water mediating effect enhances adhesion in scenarios where water is present, which we show by correlating the change in van der Waals interaction with density profiles (Section 3.3.3). Second, we demonstrate that water fills the molecular asperities between the spatula and surface, effectively smoothing the spatula-surface interface. This smoothing is evident in the two-dimensional density profiles and trajectory movies (ESI†), both of which show that water fills into the gaps between keratin and the surface and smoothens the interface (Section 3.3.3). Lastly, because spatula softening cannot explain the enhanced pull-off forces, we challenge the popular hypothesis in gecko adhesion research that water making the keratin soft is solely responsible for the enhanced pull-off forces (Sections 3.1 and 3.3.2). In Section 3.1, we also validate our model against experimental material characteristics.

2 Models and computational details

2.1 Force probe molecular dynamics: pulling simulations

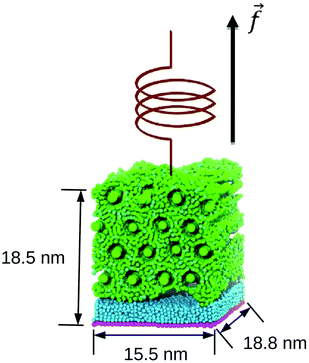
We use FPMD to compute pull-off forces of gecko keratin from a space-fixed surface in presence of different water contents (0 or 10% water content in keratin and/or a water layer between the surface and the keratin or a dry hydrophobic surface). In resemblance to atomic force microscopy (AFM) experiments with gecko setae and spatulae,²⁰ a virtual cantilever is linked to the keratin and the cantilever is moved vertically, away from the surface, until the keratin detaches. To accomplish this setup, the keratin model is placed into contact with a surface, which then strongly adheres to that surface. By moving the virtual cantilever (modelled as a virtual particle) away from its initial position, perpendicular to the surface, a force opposed to the adhesion force is introduced. When the pull-off force exceeds the adhesion force, the gecko keratin adhesive material is lifted from the surface. When in FPMD the adhesion force is larger than the friction forces opposing the pull-off, i.e. internal friction or a water phase in ligand-unbinding experiments, the unbinding process is rapid and is also called rupture event. FPMD is a non-equilibrium molecular dynamics (MD) method which is typically used to gain insight into unfolding pathways²¹ or receptor–ligand unbinding.²²

In our model the virtual particle is linked by a harmonic spring to the center of mass (COM) of the top layer nanofibrils of our gecko keratin model, which reduces the bias on the interface region. We initially position the virtual particle z(t = 0) at the COM of the top layer nanofibrils z = z_COM,EQ := 0 and move it vertically, in z-direction, away from the surface, at different constant pulling velocities. We define z the position of the virtual particle and z_COM the position of the COM of the top layer nanofibrils. The pulling direction of the keratin on the surface is indicated by the arrow in z-direction alongside the typical system size in Fig. 1. Details of the models and computational details follow below.

Fig. 1 Pulling simulation setup. The gecko keratin is shown in green on top of the octadecyltrichlorosilane self-assembled monolayer (cyan) which is linked to the constrained SiO₂ surface (purple). Four layers of nanofibrils are stacked on top of each other, each parallel to the surface. The center of mass of the keratin's top nanofibrils is linked to a virtual particle with an harmonic spring. The virtual particle is moved at constant pulling velocity away from the surface, pulling the keratin off the space-fixed surface.

Moving the virtual particle away from the surface at constant velocity leads to a linear increase in force F_pull = k_pull(vt) with v being the pulling velocity and t the time. Molecular unbinding events lead to an increase of the distance between the keratin and the surface. The force experienced by the keratin is therefore F_pull = k_pull(vt − z(t)), where z(t) denotes the position of the virtual particle in pulling direction.

We use FPMD simulations to investigate the effect of humidity on the pull-off force of gecko keratin. For each set of conditions (pulling velocity, water presence, hydrophilicity), 30 independent runs are performed and averaged.

2.2 Models

2.2.1 Dry gecko keratin model. We extend the biologically inspired coarse-grained two-bead model of gecko setae/spatulae beta keratin developed previously in our group by Endoh et al.¹³ This coarse-grained model for gecko setae/spatulae keratin was targeted at the mechanical characteristics of the Young modulus and Poisson's ratioand is able to reproduce these mechanical properties. It was inspired top-down, by experimental insights, and bottom-up by reparameterizations of the MARTINI force field^23–25 (MARTINI FF). As a reference structure, avian feather beta keratin was used, which is assumed to be close to gecko setae keratin in its nanoscale structure, since the amino acid sequences are very similar between both species.^13,26 The avian feather keratin reference established: (1) the beta-sheet region (Core-box region^12,26) of the peptide folds in similar fashion and forms dimers. (2) The dimers associate to nanofibrils,²⁷ which associate further to a more mesoscale fibrillar structure, also visible in scanning electron microscopy (SEM) cross-sections of gecko setae.¹⁵ (3) The distance between dimers, in the fibril direction and, assuming hexagonal packing, the distance orthogonal to the fibril direction. A more detailed description can be found in the original work.¹³ Endoh et al. mapped the entire sequence of dimer amino acids into a single coarse-grained bead, which was called “Core” bead, or CR bead in short, for its representation of the Core-box region. The keratin amino acid sequence is, however, not only composed of beta-sheet regions forming Core (CR) beads, but surrounded by regions which are predicted to fold in a random-coil like structure, which are known as the head and tail region.^12,28 The average amino acid of the gecko keratin head- and tail sequence, analyzed by Endoh et al., is mapped into a single coarse-grained bead, representing this random-coil region, and are called “Amorphous” (AM) beads. The average¹³ head region is made up of 64 amino acids and the tail region of 23 amino acids, which translates to 87 AM beads in total. The MARTINI FF was used as a start in the parameterization process of this coarse-grained keratin model. The energetic terms overestimate the interactions, and should be viewed as the ideal upper boundary.¹³

The Lennard-Jones parameters of the coarse-grained keratin model are shown in Table 2. The interaction between the CR and the AM beads is ε_CR–AM = 28.6 kJ mol⁻¹ and, given the large size difference between CR and AM beads we shift the potential by a distance r^CR–AM₀. The potential in eqn (1) shifts the position of the singularity to r = r^CR–AM₀.

Like Endoh et al., we use 16 CR beads in the nanofibrillar direction of the simulation box. For the initial configuration a total of 16 nanofibrils are fitted into the initial simulation box of dimensions 15.485 nm, 13.411 nm, and 18.92 nm, with hexagonal packing. We use the same system size as the previous work,¹³ which is in the order of the thickness of a spatula (having a thickness of about 20 nm). More details about the procedure to generate the initial structure can be found in Section S1 (ESI†). A bulk simulation of the dry keratin is used to calculate mechanical properties, in three-dimensional periodic boundary conditions (3D PBC). Dry keratin is placed on top of a hydrophobic surface under 2D PBC, and is used for the pull-off simulations.

2.2.2 Dry gecko setae keratin model on a dry hydrophobic surface. We extend this gecko keratin model with parameters for a hydrophobic surface and for water, and hence, call the old model without water, the dry gecko keratin model. The hydrophobic surface is inspired by work of Huber et al.⁴ (a illustration of the gecko – setae – spatula – molecular level can be found in the work of Sauer et al.²⁹ SEM images of the Spatula attached to a surface in Verenberg et al.³⁰) in which gecko spatulae were pulled-off a octadecyltrichlorosilane self-assembled monolayer (OTS-SAM) covalently bonded to a SiO₂ substrate, as was done by Huber et al. in their experimental study. The SiO₂ substrate is constrained, and does not move, functioning as a space-fixed external potential in the vapor phase surrounding the keratin. We integrate the OTS with the SiO₂ substrate into single coarse-grained molecules made up of two different MARTINI bead types. Five MARTINI C1 type beads are connected in series and the end of this alkane chain is connected to one MARTINI Qa bead. C1 type beads represent the apolar alkane chain and the Qa bead the first layer of the SiO₂ surface, respectively. Huber et al.⁴ measured the height of the monolayer to be 2.4 nm thick; the MARTINI FF maps four heavy atoms to one coarse-grained bead. Our mapping was chosen such, that this thickness is reasonably reproduced by the combined Lennard-Jones radii, leading to the five C1 beads described. The tails of the OTS-SAM are free to move in this model. We freeze, however, the position of the Qa beads after we performed an energy minimization, to obtain a fixed surface. This fixed surface allows the keratin to be pushed against and subsequently pulled-off from. The packing behavior of OTS on a silicon dioxide substrate and the resulting tilt angle of the alkane chain, is well understood.^31–34 Since we include the covalently bonded SiO₂ surface as a bead, it allows straight forward implementation of the equilibrium tilt angle θ^Qa–C1–C1₀. We use a common packing density of 1 molecule per 0.22 nm, which leads to a tilt angle of θ^Qa–C1–C1₀ = 173.0°.³³ The distance between the Qa bead, representing the SiO₂ layer, and the keratin is large enough, that the Lennard-Jones interactions are beyond their cutoff or very rarely sampled during pull-off. A full representation of the SiO₂ layer, including beads which do not carry a C₁₈ alkane, was therefore not used. Table 1 lists the bonded parameters for the OTS-SAM surface molecules.

Table 1 Interaction parameters of one octadecyltrichlorosilane self-assembled monolayer coarse-grained molecule. The equilibrium bond length r₀ and the spring constant k_b are taken from the MARTINI force field. The equilibrium angle θ^Qa–C1–C1₀ is chosen in accordance to Barriga et al.³³ The force constant of the harmonic angle potential k_a is taken from the MARTINI force field

Type	r b (nm)	k b (kJ mol^−1 nm^−1)	Bond angles	θ 0 (deg)	k a (kJ mol^−1)
C1–C1	0.47	1250	C1–C1–C1	180.0	25.0
Qa–C1	0.47	1250	Qa–C1–C1	173.0	25.0

---

Lennard-Jones interaction parameters between the alkane chains (C1 beads) and the keratin are computed by the geometric mixing rule. As mentioned earlier, the interaction parameters in the dry keratin model are overestimated. Additionally, recent studies showed that the MARTINI FF generally overestimates protein aggregation.³⁵ There are many different combination rules to compute nonbonded interaction parameters of the Lennard-Jones potential for unlike interactions. To compute nonbonded interaction parameters between the overestimated interactions from Endoh et al. and the interaction parameters of the MARTINI FF we use scaled geometric mixing. To that effect, we scale the geometric mean of ε_C1–CR and ε_C1–AM by a factor of 0.1. As previously mentioned, we will publish results soon, showing that the pull-off forces of our keratin are comparable with experiment, if the whole spatula is simulated and peel-off is possible. Interactions between the silica Qa beads and the keratin are not computed. Table 2 summarizes the Lennard-Jones interaction parameters of the dry keratin model and the hydrophobic surface.

Table 2 Lennard-Jones interaction parameters of the coarse-grained gecko keratin model and the coarse-grained octadecyltrichlorosilane self-assembled monolayer with itself, and with the dry keratin model. With σ the Lennard-Jones radius, the shift of the Lennard-Jones singularity r₀ and the interaction energy ε

Type	σ (nm)	r 0 (nm)	ε (kJ mol^−1)
AM–AM	0.59	0.0	8.0
CR–AM	0.59	0.8327	28.6
C1–C1	0.47	0.0	3.5
Qa–C1	0.62	0.0	2.0
C1–CR	0.5266	0.8327	1.8917
C1–AM	0.5266	0.0	0.5292
P4–CR	0.5266	0.8327	22.6
BP4–CR	0.5266	0.8327	22.6
P4–AM	0.5266	0.0	6.3
BP4–AM	0.5266	0.0	6.3
P4–C1	0.47	0.0	2.1
BP4–C1	0.47	0.0	2.1

---

Since we equilibrate the bulk keratin with different water contents and varying interactions under NPT conditions, the size of the keratin patch varies slighty in each of the equilibrations, which means there is not one surface fitting all. Instead, we create the surface automatically for each set of water content and interaction parameters. One of the resulting gecko keratin patches pressed against the hydrophobic surface is shown in Fig. 2 with the nanofibrils placed parallel to the surface. Here the surface has the dimensions 15.4156 nm and 18.7958 nm. In contrast to the wet gecko keratin model, no water is included yet. In the systems containing water two 12-6 Lennard-Jones walls, at z = 0 nm and z = 40 nm with interaction parameters of C1, are keeping the water beads from leaving the simulation box. We assume that these walls will not alter our results, since the total energetic interaction of the wall at z = 0 nm with the rest of the system is negligible small (the wall–AM interaction is less then 0.001% of the total Surface–AM interaction energy, or 3.6 × 10⁻⁵% of the total interaction energy of the system). And the wall at z = 40 nm is more than a dozen cutoff lengths away from the keratin throughout our simulations.

Fig. 2 Top: Front view (xz-plane) of the dry gecko keratin. The gecko keratin in green is pushed against the hydrophobic octadecyltrichlorosilane self-assembled monolayer (cyan) during the preloading phase. The fixed SiO₂ beads (purple) do not move throughout the simulation and serve as anchor points in the vacuum. Periodic images are displayed in x and y (grey), in z-direction we do not use periodic images. Bottom: Side view (yz-plane) of the gecko keratin model.

2.2.3 Wet gecko setae keratin model on a hydrophobic surface. The water model employed in our system consists of MARTINI water and antifreeze water (which we will collectively refer to as just water), where we replaced, as is done in the literature,³⁶ 10% of the water beads of type P4 with antifreeze beads of type BP4. This mixture prevents freezing and clustering at 300 K.³⁶ BP4 behaves as P4 with the system, except in its interaction with water itself.³⁶ Each MARTINI water bead maps onto 4 water molecules. In Table 2 the Lennard-Jones parameters for the interaction between water with the keratin and the surface are shown.

Reptilian keratin can take up to 30 wt% (see Section 2.5). We expect a lower water content at typical ambient relative humidity and have, therefore, decided to use 10 wt% throughout this work. Since our water model is a purely Lennard-Jones solvent, we may be able to make generalizations about the influence of solvophobicity of keratin. One of these solvents would be methanol, for example. We will come back to that idea in the conclusion. Fig. 3 shows the bulk wet keratin after water insertion.

Fig. 3 Wet gecko keratin after inserting water under three-dimensional periodic boundary conditions, used later for the calculation of mechanical properties. The keratin in (green) is swollen with water (cyan). Snapshot at 1 bar after 1 μs NPT equilibration.

To generate a system with 10% water content, we use a NPT equilibrated dry gecko keratin system. Then, we step-wise insert water beads as described in Section S2 (ESI†). After the last insertion step we perform an additional NPT equilibration of 50 ns. Fig. 3 shows the wet keratin system after insertion of the water. A bulk simulation of the wet keratin is used to calculate mechanical properties using 3D PBC. A placement of the resulting wet keratin system on top of a hydrophobic surface under 2D slab PBC is used for the pull-off simulations.

In addition to the water inside the wet keratin system, we also place a monolayer of MARTINI water (10% anti-freeze water) between the hydrophobic surface and the keratin, just before the keratin model is pushed against the surface. We call these setups, which represent the case if setae press against hydrophobic surfaces coated in dew drops, wet surface or wet hydrophobic surface. The initial configuration of the monolayer above the hydrophobic surface is at z_waterlayer = maxX(C1;z) + σ_P4 + 0.5 nm, with X(C1;z) the coordinates of the alkane chain beads in z-dimension and σ_P4 the Lennard-Jones radius of the water beads. As an example, one of the wet keratin systems on a wet hydrophobic surface of size 16.3318 nm and 18.4326 nm contain 1071 P4 water beads and 119 BP4 antifreeze beads in the monolayer above the surface, in comparison, the wet keratin contains 4123 water beads.

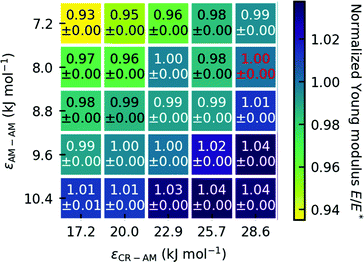
2.3 Parameter variation

To test how robust our choice of interaction parameters is on the properties we want to investigate, we perform parameter variation of the dry gecko keratin model, the wet gecko keratin model as well as their interactions with the hydrophobic surface. The interaction strengths of unlike interactions between the keratin beads and MARTINI water beads are calculated as where as the Lennard-Jones σ were kept. To explore the robustness of our model, we scale the Lennard-Jones potential. In case of the dry keratin this effectively means scaling the well-depth of the Lennard-Jones potential ε of the AM–AM and CR–AM interactions. In case of the wet keratin, the water–amorphous (W–AM) and water–core (W–CR) interactions are scaled (The P4 and BP4 beads of the MARTINI force field, both have the same interactions with keratin and surface). In total, 25 dry keratin systems with different interaction energies ε are equilibrated. We then calculate the mechanical properties, Young modulus and Poisson's ratio, and the pull-off force for all 25 systems. Fig. 4 shows the Young modulus as a function of the parameter variation and Fig. 9 shows five pull-off spectra for five variations of ε_AM–AM at constant ε_CR–AM = 28.6 kJ mol^-1. We concluded, that the trends are robust against parameter variation of the dry keratin and choose the original parameter set for the dry gecko keratin model (ε_AM–AM = 8.0 kJ mol⁻¹ and ε_CR–AM = 28.6 kJ mol⁻¹) for the following parameter variation of the wet gecko keratin model. Here, the W–AM and W–CR interactions are scaled, resulting in an additional 9 wet keratin systems with different hydrophilicities of the keratin. We call the wet keratin model with the smallest scaling factor λ = 0.5, for both W–AM and W–CR interactions, the weakly hydrophilic gecko keratin. The system with λ = 1.0, for W–AM and W–CR, the strongly hydrophilic gecko keratin. Fig. 5 shows the weakly and strongly hydrophilic keratin systems resting above the wet hydrophobic surface.

Fig. 4 Normalized Young modulus E/E*, with the Young modulus E relative to the Young modulus of the original parameters of Endoh et al. E*. The red text highlights the Young modulus of the original model at 12.56 GPa. The Young modulus is robust against variation of ε. We use the standard deviation of the mean as the error.

Fig. 5 Wet gecko keratin systems. The keratin in green is swollen with water (cyan). On the left the weakly hydrophilic keratin shows clustering of water beads and more water in the vapor phase compared to the strongly hydrophilic keratin on the right. The strongly hydrophilic keratin on the right leads to a more uniform distribution of the water beads, especially in the interface region between surface and keratin. In both cases a water vapor above the keratin is visible.

2.4 Computational details

All simulations are carried out using the GROMACS 2018³⁷ software package. The Lennard-Jones cutoff is 2.1 nm. All intermolecular forces are parameterized into our force field, including electrostatics and dispersion interactions, therefore we have no explicit charges present in the system.

The Equilibration procedure for the dry gecko keratin and the wet gecko keratin can be found in the Sections S3 and S4 (ESI†).

2.4.1 Bulk calculations. Production runs to calculate the mechanical bulk properties, Young modulus and Poisson's ratio, are performed under three-dimensional PBC using a time step of 10 fs. A Berendsen thermostat and a semi-isotropic Berendsen barostat³⁸ are used to keep the system at 300 K and 1 bar. The time constant of coupling the temperature is τ_T = 2 ps. The barostat uses a coupling time of τ_p = 5 ps and a compressibility of 4.5 × 10⁻⁵ bar⁻¹ in xy, but a compressibility of 0 bar⁻¹ in z, as was done in the previous work.¹³ Thus, no size fluctuations are allowed in the direction parallel to the nanofibrils. The systems are stretched, i.e. uniformly scaled, in the direction of the nanofibrils, in steps of 1%, ranging from 0% to 5% strain. Simulation times are 100 nm at each strain. After testing for convergence we use the last 70 nm for the computation of the Young modulus and Poisson's ratio. We perform 6 production runs and use the standard deviation of the mean as the error estimate.

2.4.2 Hydrophobic surface equilibration. For the pull-off simulations, we transfer the equilibrated bulk gecko keratin systems into 2D PBC above a hydrophobic surface. The system is only periodic in the coordinates parallel to the surface (x,y). From the bulk keratin NPT equilibrations, we choose a configuration closest to 1 bar pressure, since our pulling simulations are run in NVT conditions. To accomplish that, we choose the latest frame in the trajectory where the squared deviation in the instantaneous pressure is (1 bar − p_inst.)² ≤ 0.03 bar². In our model the keratin fibrils are parallel to the surface (y-direction). The x and y simulation box lengths are used to generate the hydrophobic surface (Section 2.2.2). After inserting the OTS-covered hydrophobic surface into an otherwise empty box of the correct dimensions, it is energy minimized using steepest descent until the maximum force is below 0.1 kJ mol⁻¹ nm⁻¹. For the wet surface systems, we then add a water layer above the hydrophobic surface and perform an energy minimization of the surface and the water together. The keratin systems are inserted, such, that the minimum distance between the surface beads and the keratin beads is 2.0 nm.

2.4.3 Gecko keratin pull-off simulations. The gecko keratin pulling simulations are performed in the NVT ensemble after the hydrophobic surface equilibration (Section 2.4.2). After transferring the dry or wet keratin system above the energy minimized dry or wet hydrophobic surface, the keratin is placed near to the surface. We quickly move the keratin in 7700 simulation steps with a time step of 1 fs and a Berendsen thermostat with a time constant of coupling the temperature of τ_T = 2 ps, closer to the surface. The COM of the top layer of the CR beads z_COM is moved with a harmonic spring, k_push = 3000 kJ mol⁻¹ nm⁻² and a velocity of 10 × 10⁸ μm s⁻¹ (or 10³ nm ns⁻¹), very shortly towards the surface. We then pick a configuration from the resulting trajectory where the minimum distance between any surface bead and any keratin bead is ≈0.3 nm.

We mimic the experimental preloading force for the spatula described by Xu et al.²⁰ over a simulation time of 100 nm. We choose a long equilibration time of 100 nm, but z_COM already converges in around 25 nm. Xu et al.²⁰ used a preload of 10 nm on the spatula that, according to the authors SEM image, had an elliptic area of roughly with 2a the width and 2b the height of the ellipse. This amounts to a pressure of p = 4.24 bar. We translate this experimental preloading to a pushing in the direction towards the surface using a constant force. We want to mention here, that the size of the spatula can be used to calculate the corresponding preloading force, but a comparison of the force needed to pull-off the keratin is not possible. This is because the pull-off force is smaller when an adhesive is peeled off compared to the flat-on-flat pull-off we simulate. This peel-off is not possible to simulate with periodic boundary conditions, which are necessary for our system size. However, we will publish results of a full mesoscale spatula soon, showing that our pull-off forces are comparable to experimental studies if peel-off is taken into account. Instead of simulating the complete peel-off of the spatula, flat-on-flat pull-off simulates just a small section of a spatula, small enough that flat-on-flat pull-off is justified. We calculate the preloading force for all 25 dry keratin and 9 wet keratin systems, given their varying sizes, after equilibration using different interaction parameters and different water contents. As an example, in one of the systems this results in a constant-force preload of F_preload = 73.97 kJ mol⁻¹ nm⁻¹. A Nosé–Hoover thermostat^39,40 is used to keep the systems at 300 K. The time constant of coupling the temperature is τ_T = 2 ps.

Afterwards, we let the system relax to mimic the time when the experimental setup is switched from preloading to pulling. The time this takes in experiments is not mentioned in the literature for gecko spatula pull-off. We give the system 100 nm to relax.

The pull-off runs are simulated with a harmonic spring constant linked to the COM of the top layer nanofibrils which is pulled away from the surface. We varied the harmonic spring constant between 3000 and 7000 kJ mol⁻¹ nm⁻², together with the corresponding pulling velocity to maintain a constant loading rate Ḟ = k_pull·v. We did not see a difference in maximum force, therefore we decide to proceed with a value of k_pull = 5000 kJ mol⁻¹ nm⁻². We discuss the loading rate dependence (changing Ḟ = k_pull·v) below in Fig. 9. Since at this point in our protocol we start from a structure where the keratin is attached to the surface, a jump-in, typically observed in AFM force curves, can not be observed. Every 100 steps we gather the force on the harmonic spring, by which we get a raw force profile over the pulling simulation. Fluctuations in the raw force profile due to the resonance frequency of the harmonic spring and due to thermal fluctuations of the particles linked to this harmonic spring, are artifacts which are smoothed by a Gaussian function (Fig. 6) with a kernel width respective of 0.1 nm, as was done by Sheridan et al.²¹ The pull-off force is the maximum force during the pulling run. It is the force needed to separate the keratin from the surface. This force is obtained by taking the highest value of the smoothed force profiles.

Fig. 6 Force profile of a wet gecko keratin pull-off from a dry hydrophobic octadecyltrichlorosilane self-assembled monolayer with a pulling velocity of v = 3 × 10⁵ μm s⁻¹. The force on the harmonic spring F_pull is plotted against the time t. After smoothing the raw force (transparent blue) with a Gaussian kernel with a width respective of 0.1 nm in the position domain, the resulting smoothed force profile (blue) is used to extract the maximum force during pull-off. The force starts at zero but rises sharply. The Gaussian smoothing leads to non-zero force at t = 0 nm, but this behavior does not influence the smoothed profile afterwards and we only use the maximum force in the smoothed force profile in our investigation.

To test the dependence of the pull-off force on the pulling velocity v (which is proportional to the loading rate), we use different pulling velocities ranging from 3 × 10⁵ μm s⁻¹ to 3 × 10⁷ μm s⁻¹ (or 0.3 to 30 nm ns⁻¹). The pulling velocities used in this work are summarized in Table S1 (ESI†) with their corresponding loading rates Ḟ = k_pull·v. For the range of pulling velocities we perform 30 pull-off runs from the same relaxed structure.

By using kernel density estimation⁴¹ on the maximum pull-off forces extracted from the smoothed force profiles (Fig. 6), the most probable pull-off force is accessible.

To estimate the error in the pull-off forces we perform an additional set of simulations for the weakly hydrophilic wet gecko keratin system. After the wet keratin equilibration (Section 4) we start five pull-off simulations (Section 2.4.3) with different initial velocities. These five blocks repeat the 100 ns preload step and the 100 ns relaxation. For the range of pulling velocities from 3 × 10⁻⁴ μm s⁻¹ to 1 × 10⁻² μm s⁻¹ we perform 30 pull-off runs each. This results in 150 pull-off runs for each pulling velocity or a total of 1050 pull-off runs, used in the estimation of the error. The resulting maximum pull-off forces are accumulated, and, using kernel density estimation we extract the most probable pull-off force for each velocity. From the most probable pull-off forces at each pulling velocity, we calculate the standard deviation between the five blocks. This standard deviation is used as the error estimate in the pull-off forces.

2.5 Experimental assessment of the water content in reptile keratin

Dry shed skin samples (dorsal and ventral scales) of the snake Naja nigricollis and dry pieces of claw tips of the Gekko gecko toes were used in this experiment. Initially, individual samples were weighted at 24 °C and 23% relative humidity using Cubis II Ultra-Micro Balance (Sartorius) with the resolution of 0.1 μg. Then the samples were kept for 48 h at 24 °C and 90% relative humidity and weighted again. Finally, the samples were kept for 48 h at 24 °C and 23% relative humidity and weighted again. The mass loss in % due to the water evaporation was calculated.

3 Results and discussion

3.1 Elastic properties of wet and dry bulk gecko keratin: water-moderated softening of keratin depends on its hydrophilicity

The attachment of spatulae depends on the elastic properties of the keratin in two ways: (1) a flexible spatula is able to follow the surface topography and allows for more contact. (2) The pull-off force, the force needed to separate the spatula from the surface is directly proportional to the Young modulus. To validate the elastic properties of our keratin models, we calculate the Young modulus and Poisson's ratio and validate against experimental results. Fig. 7 shows the stress–strain behavior from 0% to 5% strain ε_zz, of the dry Endoh et al.¹³ model in black, after parameter variation of the dry gecko keratin model in grey and alongside a strongly and weakly hydrophilic gecko keratin in blue and cyan. The parameter variations (grey) (also Fig. 4) show that the dry keratin is robust against variations in the nonbonded interaction parameters, a reason being that most load is taken by the bonds between CR beads, which are largely unaffected by the nonbonded interactions.

Fig. 7 Tensile stress–strain curves for bulk dry gecko keratin (black) at small variations from the original Lennard-Jones interactions energies ε (grey) and wet keratin (10 wt% water). The stress σ_zz is plotted against the strain ε_zz along the fibrillar direction. Strongly hydrophilic keratin (blue) and weakly hydrophilic keratin (cyan) show similar qualitative trend change compared to the dry keratin, as is seen with the trend change in experimental studies on dry versus wet keratin,⁵ as the Young modulus is decreased and the stress–strain curve becomes flatter at strains over 1% to 2%. We use the standard deviation of the mean as the error.

The slope of the first 1% of the stress–strain curve is used to calculate the Young modulus. The calculated Young moduli for all parameter variations of the dry keratin are shown in Fig. 4. The Young modulus of the dry keratin using the original model parameters E* is highlighted in red. The highlighted Young modulus of E* = 12.56 GPa is around 5% less than the result of Endoh et al.¹³ (13.2 GPa). A possible explanation may be the much longer NPT equilibration of 100 nm compared to 7.5 nm and the longer trajectory used for analysis (30 nm versus 7.5 nm). The resulting Young modulus of our models is robust against variation of ε_AM–AM and ε_CR–AM. Decreasing the CR–AM interaction energy from the original ε_CR–AM = 28.6 kJ mol⁻¹ by 40% to ε_CR–AM = 17.2 kJ mol⁻¹ only decreases the elastic modulus to 97% of its original value. Modifying the AM–AM interactions influences the elastic modulus only slightly more.

The hydrophilicity of the gecko keratin, modeled by the interaction between the keratin and the water (ε_W–CR and ε_W–AM) has, however, significantly greater effect on the Young modulus. In experimental stress–strain studies^5,42 the effect of changing the relative ambient humidity (RH) is to flatten the stress–strain curve, leading to a beginning plateau formation above 1% to 2% strain. Increasing RH leads to a greater uptake of water into the keratin, which increases the water content of the material and leads to a reduction of the Young modulus. Qualitatively, in Fig. 7, the flattening of the stress–strain curve is comparable to the behavior of experimentally^5,42 observed deviations due to RH. Since the water content of gecko keratin at these relative ambient humidities is not known, we can take no conclusion of whether the weakly hydrophilic or strongly hydrophilic keratin is closer to experiment, both having a water content of 10%.

We may want to make a very careful observation of the effects of keratin hydrophilicity on the elastic properties, resembling the change in elastic properties due to changing RH. It is however important to keep in mind that changing the hydrophilicity does not entail a change in water content of the keratin and no resulting swelling effects. In experimental work⁴³ the elastic modulus of dry biological materials (e.g. insect exoskeletons) was found to be about five times higher than for the same material affected by ambient humidity. For experimental specimens, typically only the ambient relative humidity (RH) is reported, whereas the corresponding water content appears to be unknown. Also, in the case of avian feathers,⁴² going from 0% RH to 50% RH decreased the Young modulus from 3.66 GPa to 2.58 GPa, which translates to 30%. The change between 50% RH and 100% RH was even more pronounced, with an additional decrease by 43%. This experimentally⁴² found decrease in the elastic modulus with increasing RH in beta keratin materials can be compared with changes we observe (Fig. 8(A)). The Young modulus of our strongly hydrophilic keratin E⁰ (red in Fig. 8), of E⁰ = 6.78 ± 0.31 GPa is 54% of the elastic modulus of the dry keratin, i.e. a decrease of 47%. The weakly hydrophilic keratin, with a Young modulus of 4.75 ± 0.21 GPa is 38% of the dry elastic modulus. Or, as Fig. 8 shows, 70% of the strongly hydrophilic keratin, resulting in a decrease of 30%. This reduction in the elastic modulus from the dry keratin model to the strongly hydrophilic keratin model to the weakly hydrophilic keratin model matches the reduction in Young modulus seen by Taylor et al.⁴² in avian feather keratin. In this careful observation, it would suggest that our strongly hydrophilic gecko keratin model may have the elastic properties of keratin at 50% RH and our weakly hydrophilic keratin model may have the elastic properties at 100% RH. Again, comparison of our computational models to experiments is difficult, since in the literature detailed specifications are often missing.

Fig. 8 (A) Normalized Young modulus E/E⁰ of wet gecko keratin as a function of W–AM and W–CR Lennard-Jones interaction energy ε. The Young modulus E is normalized with the Young modulus of the unscaled Berthelot combination E⁰ for the Lennard-Jones interaction parameter ε between MARTINI force field water and the coarse-grained parameters of the keratin model, representing the strongly hydrophilic keratin. (B) Mean Poisson ratio over 0% to 5% strain of the wet keratin as a function of the Lennard-Jones interaction energies ε. Results from strongly hydrophilic wet gecko keratin (red). We use the standard deviation of the mean as the error and error propagation where two values are compared.

The hydrophilicity of the amorphous phase (W–AM interaction energy) has a stronger effect on the Young modulus than the hydrophilicity of the nanofibrils (W–CR interaction energy). But as a general trend, lowering the hydrophilicity of keratin leads to a decreased Young modulus, independent of whether the amorphous phase or the nanofibrils are less hydrophilic. This general trend can also be seen with Poisson's ratio (Fig. 8(B)). The Eisenberg hydrophobicity scale⁴⁴ of the gecko keratin protein sequences^12,26 shows them on average to be on the more hydrophobic end (〈H〉 > 0.2). Our result indicate that this leads to a more flexible spatula, compared to protein sequences which would be more hydrophilic in nature. One may speculate that there is a evolutionary trend towards a more weakly hydrophilic keratin, making the keratin more flexible in humid environments, which would increase the pull-off force needed to separate the spatula from the surface, as we will see later on. A completely hydrophobic spatula material would, however, not allow the uptake of water and increased RH in humid environments would no longer be beneficial for attachment.

3.2 Assessment of the water content in reptile keratin

We used Gekko gecko (Tokay gecko) as a model system (like most other studies) and, to generalize, these results, we also tested water uptake in a snake. For the snake skin samples the water uptake capacity was 20.16% (SD = 3.97, n = 12), whereas for claw tip of the gecko it was 30.62% (SD = 4.08, n = 4). The obtained results were well repeatable also in several hydration/dehydration cycles. Lower water uptake capacity of the snake skin may be potentially explained by possibly higher lipid content in the skin of this snake species often occupying rather arid regions in comparison to the Tokay geckos living under rather humid ambient conditions.

3.3 Adhesion of gecko keratin to the hydrophobic surface

3.3.1 Pull-off force dependence on the pulling velocity. As the virtual particle is moved vertically away from the surface, the force on the COM of the top layer nanofibrils due to the harmonic potential connecting it to the virtual particle, increases linearly at all pulling velocities until the keratin detaches from the surface. For all fast pulling velocities, periodic oscillations after detachment are observed, which are due to the keratin swinging around the virtual particle, to which it is harmonically bonded (Fig. S1, ESI†). The slow pulling velocities result in a smaller force on the harmonic spring after detachment (the position of the virtual particle is closer to the COM of the top layer nanofibrils during pull-off), and consequently the smaller force in the harmonic spring can be dissipated internally. As expected, the maximum force at the detachment event decreases with decreasing pulling velocities. The computed most probable pull-off forces yield a dynamic force spectrum, the pull-off force F as a function of the pulling velocity v (Fig. 9).

Fig. 9 Dynamic force spectrum for the maximum pull-off force F of dry keratin detachment from a dry hydrophobic surface against pulling velocity v. For five different Lennard-Jones interaction energies ε_AM–AM. Each data point is computed from the most probable pull-off force from a sample of 30 simulations. The standard deviation of the mean of five independently equilibrated force probe molecular dynamics simulations at their corresponding velocities are used as the error estimate. Dashed lines represent the fits to the Bell + friction model.

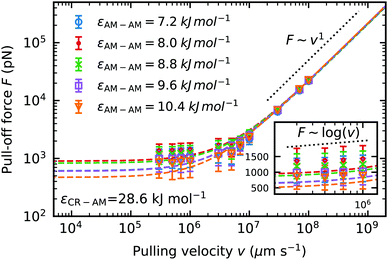
We fit the dynamic force spectrum to the Bell + friction model,^21,45,46 with F the pull-off force, γ the friction coefficient, x_b the distance to the potential barrier and k₀ the dissociation rate at equilibrium loading rates. We compare the pull-off force at a pulling velocity of v = 3 × 10⁵ μm s⁻¹ predicted by the Bell + friction fit, to incorporate the information from the faster pulling velocities. The fit to the Bell + friction model shows for our lowest pulling velocities a deviation from the theoretically predicted scaling of F ∼ log(v) for the limit of very low loading rates (Fig. 9 inset). It should be noted here again, that our low pulling velocities correspond to loading rates in the order of 10¹² pN s⁻¹, which is outside the accessible range of AFM-experiments (the fastest experimental setups²² to date have loading rates reaching 10⁸ pN s⁻¹), hence the limit of low loading rates predicted by theory is not accessible to our molecular dynamics simulations. The theoretically predicted scaling in the limit of high loading rates F ∼ v¹ is clearly visible at pulling velocities v > 10⁸ μm s⁻¹. The largest pull-off force in dry keratin on a dry surface is seen in the model using the original Lennard-Jones interaction energy ε_AM–AM = 8 kJ mol⁻¹ with 932 ± 456 pN. If the original AM–AM interaction is increased or decreased a decrease in pull-off force can be observed. In the most extreme case of ε_AM–AM = 10.4 kJ mol⁻¹ the Young modulus increases by 4% and the pull-off force decreases by ≈50% to 501 ± 45 pN.

3.3.2 Effect of humidity on gecko keratin adhesion: effect of keratin softening not solely responsible for enhanced adhesion. Water content has a reliable effect on the pull-off force of keratin detachment from a hydrophobic surface. If the keratin is swollen with 10% water, the pull-off force is increased, independent on the exact hydrophilicity of the keratin material and independent of the pre-existence of a water layer between the surface and the keratin (“wet surface”) (Fig. 10 and Table S2, ESI†). The increase in the mean pull-off force from the dry keratin on a dry surface F_dd = 932 pN (using ε_AM–AM = 8 kJ mol⁻¹ and ε_CR–AM = 28.6 kJ mol⁻¹) to wet keratin on a dry surface F_wd = 1317 pN is of 41%. Even greater is the effect of a surface water layer on the pull-off force. Here, the mean pull-off force of wet keratin on a wet surface F_ww is nine times larger than F_dd with F_ww = 8440 pN. The pull-off force needed to detach dry weakly hydrophilic keratin from a wet surface F¹_dw clearly shows, that a water layer is a strong modifier of the pull-off force, as dry keratin sticking to a wet surface F¹_dw = 7821 pN is six times stronger than wet keratin to a dry surface (F_wd).

Fig. 10 Mean pull-off forces of four different systems including wet keratin on a dry hydrophobic surface, wet keratin on a wet hydrophobic surface (a layer of water between gecko keratin and the hydrophobic surface during the pushing step, modeling setae flattening water layers on a hydrophobic surface). To establish the pull-off force of dry keratin on a wet surface, pulling simulations with the weakly hydrophilic keratin are used, to compute the pull-off force F¹_dw. Here the error of wet weakly hydrophilic keratin on a wet surface is used. Comparing the mean pull-off forces shows a robust trend of increasing force with increasing amount of water (dry keratin on a dry surface to wet keratin on a wet surface).

Fig. 10 would suggest, that the effect of a water layer and the effect of wet keratin are additive rather than multiplicative/synergetic. The gap-filling capability of the water layer is high, since it is sandwiched between a hydrophobic surface and the keratin, modeling setae flattening water layers on hydrophobic surfaces (Section 2.2.3). Our findings predict that geckos on hydrophobic surfaces in environments with 100% RH, such as on plant leaves in rain forests, can effectively use water layers to enhance their attachment.

For a better comparison between weakly and strongly hydrophilic gecko keratin, the change in pull-off force between a wet keratin on a dry hydrophobic surface F_wd relative to a dry keratin on a dry surface F_dd and a wet keratin on a wet surface F_ww relative to a dry keratin on a wet surface F¹_dw (with superscript 1 for the single, weakly hydrophilic, system), is shown in Fig. 11 and Fig. S2 (ESI†). The effect of wet keratin on the pull-off force on a hydrophobic dry surface (Fig. 11(A)) is best compared to the increase in pull-off force of a single spatula on the octadecyltrichlorosilane self-assembled monolayer of Huber et al.,⁴ with humidity, which ranged from ≈6 nm at 0% RH to ≈9 nm at 60% RH (the size of the spatula was not described in their work, a comparison of absolute pull-off pressures p = F/A may also be misplaced, since experimentally spatulae are pulled off in a way which leads to crack formation, which is absent in our periodic model, essentially a infinite large plate made out of gecko keratin with finite volume. Nonetheless, we included pull-off pressures in Fig. S2 for completeness, ESI†). This increase by 50% is in agreement with our wet keratin model (Fig. 11(A)). Here we see an increase in pull-off force of the strongly hydrophilic wet keratin on a dry surface by ≈50% relative to pull-off force needed to detach the dry keratin. This compares well with our above discussion of the modulus, which suggested that the strongly hydrophilic keratin behaves as if the keratin is at around 50% RH. Weakly hydrophilic wet keratin leads to a pull-off force increase to ≈180%, comparing well with the increased pull-off forces at 100% RH. To repeat, we do not change the water contents and there is no experimental data which would allow us to know how much water content is in gecko keratin at a given RH.

Fig. 11 (A) Pull-off forces of wet keratin attached to a dry surface F_wd relative to the pull-off force of dry keratin on a dry surface F_dd at different Lennard-Jones interaction energies ε for Water–Core (W–CR) and Water–Amorph (W–AM) interactions. (B) Pull-off force of wet keratin on a wet surface F_ww relative to the pull-off force of dry weakly hydrophilic keratin on a wet surface F¹_dw shows the influence of wet keratin on the pull-off force in the context of a wet surface. Wet keratin on both a dry and a wet surface leads to increased pull-off forces compared to dry keratin. (Red) increased pull-off force for the strongly hydrophilic keratin. (Cyan) increases of the weakly hydrophilic keratin.

The effect of swelling the keratin which sits on the top of a surface water layer (going from a dry keratin on a wet surface to a wet keratin on a wet surface) on the pull-off force (Fig. 11(B)) shows a moderate average increase of ≈8% relative to a weakly hydrophilic dry keratin attached to a wet surface. Clearly, the hydrophilicity of the keratin affects the resulting pull-off force, the strongly hydrophilic keratin increases the pull-off force, when wet, by ≈37% (Fig. 11(A)). In contrast, a weakly hydrophilic keratin increases the pull-off force by ≈95% when wet.

The increase in pull-off force can not simply be explained by the change in the elastic modulus (Fig. 8), which would predict the highest pull-off forces for the keratins using the parameter sets ε_CR–W = 22.6 kJ mol⁻¹ and either ε_W–AM = 3.2 kJ mol⁻¹ or ε_W–AM = 4.4 kJ mol⁻¹. Instead the highest pull-off force is observed with the weakly hydrophilic gecko keratin (ε_CR–W = 11.3 kJ mol⁻¹ and ε_W–AM = 3.2 kJ mol⁻¹). Fig. S3 (ESI†) shows minimal to no correlation between increasing Young modulus by hydrophilicity of the wet keratin and increasing pull-off pressures. The minimal trend observable may show increasing pull-off pressures with increasing Young modulus on a dry surface which is contrasted by decreasing pull-off pressures on a wet surface by increasing Young modulus. Additionally, if a water layer is present, the pull-off force of the keratin is not as significantly modified by the hydrophilicity of the keratin, and, therefore not by the change in Young modulus. Which means that the decreased Young modulus at higher humidity can not be solely responsible for the enhanced pull-off forces, putting into question the dominant hypothesis^5,6,17 discussed in the literature.

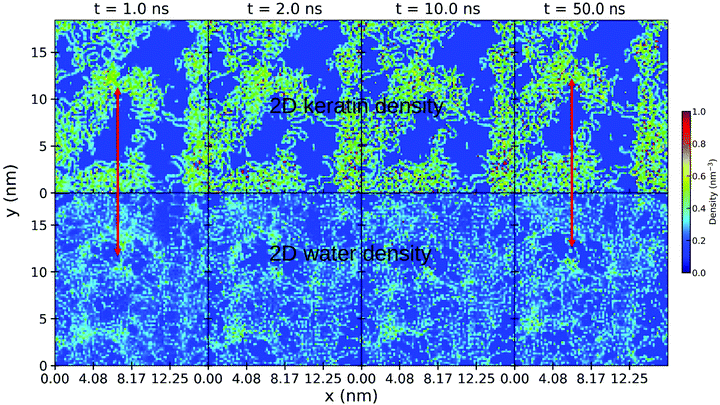
To understand the effect of water on the pull-off force, the location of the water is important. Fig. 12 and 13 show the density maps of keratin and water for the weakly and strongly hydrophilic keratin with a layer of water between the keratin and the surface (in case of the wet surface systems). Comparing the first 1 nm of the preloading step of the weakly hydrophilic keratin, seen on the very left of Fig. 12, to the densities of the last configurations at 50 nm at the very right, it is clearly visible that the water starts to accumulate and is filling the free volume between surface and keratin. This gap-filling and clustering is not as clearly visible in the strongly hydrophilic keratin (Fig. 13). It may be a reasonable assumption that keratin outside computer simulation will encounter a similar free volume between the surface and the material of the spatula. These asperities (roughnesses) between the keratin interface and the surface, may be filled by water, making the keratin interface smooth, which increases the number of attractive interactions between spatula and surface. There is however, to the best of our knowledge, no literature on the nanometer scale roughness of gecko spatulae. There are however images^30,47 on the hundreds of nanometers scale, from which we assume a roughness in the single digits.

Fig. 12 Density profile in the first 0.7 nm layer above the wet surface during preloading of the weakly hydrophilic keratin. The 2D density profile of the gecko keratin is shown at the top and the water density profile is shown at the bottom. Going from left to right, the density plots were calculated at different times during the preload. At t = 0 nm the smallest distance between keratin and the surface is 2.0 nm.

Fig. 13 Density profile in the first 0.7 nm layer above the surface during preloading for the strongly hydrophilic keratin. The 2D density profile of the gecko keratin is shown at the top and the water density profile is shown at the bottom. Going from left to right, the density plots were calculated at different times during the preload. At t = 0 nm the smallest distance between keratin and the surface is 2.0 nm.

3.3.3 Humidity-induced enhancement of keratin-surface adhesion: two molecular mechanisms for two hydration scenarios. To further explore the differences of our models in regard to the strongly (Movies S2 and S2b, ESI†) and weakly (Movie S1, ESI†) hydrophilic keratin, Fig. S4 and S5 (ESI†) show the densities of keratin and water during pull-off from a wet surface. Initially, the water is filling the gaps between the surface and the weakly hydrophilic keratin, but this gap-filling is not seen in case of the strongly hydrophilic keratin (ESI,† Movies S3 and S3b show the weakly hydrophilic gecko keratin pull-off from a dry surface, and ESI,† Movies S4 and S4b show the pull-off of strongly hydrophilic keratin from a dry surface). Thus, in case of the weakly hydrophilic keratin, the higher gap-filling ability may explain the main contribution to the increased pull-off force seen in Fig. 11(A). The formation of water bridges at the contacting asperities lead to a capillary force and subsequently increases the pull-off force.

In contrast, a strongly hydrophilic keratin absorbs the water into the interface region (and probably, on longer time scales, into its volume) which inhibits the formation of capillary bridges (Fig. S5, ESI†). The strongly hydrophilic keratin therefore shows only small capillary bridges, containing a small number of water beads. The water absorbs into the strongly hydrophilic keratin interface and acts as a mediator for keratin–surface interactions. Water beads interact simultaneously with the keratin and with the surface and this molecular bridge acts a proxy for stronger keratin attachment. This mediating effect of water is different from capillary forces in that a volume of water is missing and, therefore, the surface tension of that water volume is not existent. The molecular water bridges enhance attachment by increased dispersion attraction between spatulae and surface. This explains the increased pull-off forces in case of the wet strongly hydrophilic keratin on a dry surface. The keratin interacts with the water and the water, with the surface.

Thus, depending on the hydrophilicity of the keratin, water can form capillary bridges or absorb into the interface and acts as a mediator for enhanced attractive interactions. Table 3 summarizes the resulting water geometries for our wet keratin systems. The capillary bridges seen in Fig. S4 and in ESI,† Movie S1 are of convex shape, because the surface is hydrophobic (the C1 type beads, making up the hydrophobic surface, lead to a contact angle of larger than 110° for the MARTINI water⁴⁸). The capillary force of a convex capillary bridge is much less than that of a capillary bridge of concave shape, which would be present on hydrophilic surfaces.^49,50

Table 3 Geometries of water during pull-off of the wet gecko keratin systems. The weakly hydrophilic keratin (ε_W–AM = 3.2 kJ mol⁻¹ and ε_W–CR = 11.3 kJ mol⁻¹) at the top and the strongly hydrophilic keratin at the bottom (ε_W–AM = 6.3 kJ mol⁻¹ and ε_W–CR = 22.6 kJ mol⁻¹)

ε W–CR (kJ mol^−1)	ε W–AM (kJ mol^−1)	Geometry
11.3	3.2	Capillary bridge
15.8	3.2	Capillary bridge
22.6	3.2	Capillary bridge
11.3	4.4	Capillary bridge
15.8	4.4	—
22.6	4.4	No bridge
11.3	6.3	No bridge
15.8	6.3	No bridge
22.6	6.3	No bridge

---

Since gecko spatula protein sequences¹² are not extremely hydrophilic (Eisenberg et al.⁴⁴ hydrophobicity scale 〈H〉 > 0.2), and since we observe higher gap-filling capability of water at the weakly hydrophilic keratin interface, we assume that capillary forces will play a pronounced role for gecko adhesion on wet surfaces. But we have also shown (Fig. 11(A)) that no such wet surface is necessary for enhanced pull-off forces of wet keratin. Therefore capillary forces can not be solely responsible for the humidity effect, leaving the decreased Young modulus and the mediator effect of water to be significant contributions to the effect of humidity on these surfaces.

To elucidate the underlying molecular mechanism resulting in the attachment differences with different hydrophilic keratins in more detail, the potential energy over the course of 30 pulling runs is decomposed into its different van der Waals contributions. Because fluctuations in the raw force profile (Fig. 6) are due to fluctuations in z_COM, we histogram the van der Waals energetic contributions to their respective positions z_COM,i (binwidth of 0.1 nm). The average and standard deviation of the decomposed energy are calculated for each bin independently. The standard deviation of each bin is used as the error in the energy decomposition plots.

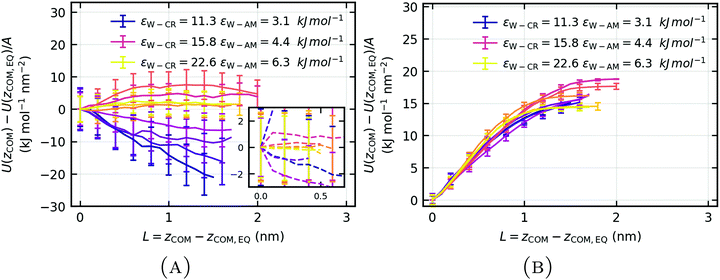
Energy changes as a function of the displacement of wet keratin from the wet and dry surface L = z_COM− z_COM,EQ, are shown in Fig. 14, as ΔU = U(z_COM) − U(z_COM,EQ), normalized with the area A of the systems. The displacement at maximum force (L = 0.40 nm) of the weakly hydrophilic keratin (Fig. 14(A and C)) corresponds roughly to a COM position of z_COM ≈ 18.0 nm. The maximum force (at L = 0.37 nm) during the pull-off of the strongly hydrophilic keratin (Fig. 14(B and D)) corresponds roughly to a COM position of z_COM ≈ 17.9 nm.

Fig. 14 Density profiles of the weakly (A) and strongly (B) hydrophilic gecko keratin on a wet surface during pull-off. Contributions to the van der Waals energy, modeled by the Lennard-Jones interaction energies, of the weakly (C) and strongly (D) hydrophilic keratin. The water–keratin (W–K), water–water (W–W), keratin–surface (K–S) and water–surface (W–S) potential energies are shown as a function of the displacement of the center of mass of the top nanofibril layer from its equilibrium position L = z_COM − z_COM,EQ, normalized with the area A of the systems. Dashed lines represent the energies of the wet keratin on a dry surface (also shown in the insets), solid lines the energies of wet keratin on a wet surface. The decomposed Lennard-Jones energies of 30 force probe molecular dynamics runs are binned according to the instantaneous position z_COM (binwidth of 0.1 nm). The average energy at displacement z_COM and the standard deviation can thus be calculated. Energies are computed at our slowest pulling velocity of 3 × 10⁴ μm s⁻¹. The energies are set to zero at the initial equilibrium configuration, after the relaxation step, when the keratin is attached to the surface. (A and C) represents the weakly hydrophilic keratin (ε_W–AM = 3.2 kJ mol⁻¹ and ε_W–CR = 11.3 kJ mol⁻¹). (B and D) shows the strongly hydrophilic keratin (ε_W–AM = 6.3 kJ mol⁻¹ and ε_W–CR = 22.6 kJ mol⁻¹). We use the standard deviation of the mean as the error.

As the weakly hydrophilic keratin is pulled off from the wet surface, unfavorable water–keratin (W–K, orange), water–surface (W–S, red) and keratin–surface (K–S, purple) oppose the detachment (Fig. 14(C)). However, as the weakly hydrophilic wet keratin detaches from the surface, favorable water–water interactions are created, favoring the detachment process. The pull-off is not dominated by keratin–surface (K–S) van der Waals interactions but by water–keratin (W–K) and water–surface (W–S) interactions. Since the main opposition to detachment is due the loss of favorable water–keratin and water–surface interactions and, additionally, a increase in favorable water–water interactions is observable, the pull-off of weakly hydrophilic keratin from a wet surface is dominated by capillary forces.

In contrast to the opposing capillary forces of the weakly hydrophilic keratin on a wet surface, the pull-off of the strongly hydrophilic keratin from a wet surface seems to be only primarily opposed by the loss of favorable water–surface (W–S, red) interactions (Fig. 14(D)). The water functioned as a mediator for enhanced interactions with the surface. Since the water is absorbed into the interface of the strongly hydrophilic keratin, the pull-off and subsequent loss in water–surface contacts, leads to a increase of favorable interactions between water and keratin (W–K, orange). As the water is removed from the surface during pull-off, it is able to form new, more favorable, water–keratin (W–K) interactions, which aids detachment.

Favorable water–water interactions during pull-off (Fig. 15(A)) of the wet keratin from a wet surface are correlated with the observation of capillary bridges, described in Table 3. When water coalescence into a capillary bridge, water–water energies decrease favorably for pull-off and the change in water–surface energy does not converge directly after the maximum force (Fig. 15(B)). In case of strongly hydrophilic keratin, after the detachment event at L ≈ 0.4 nm, the water–surface interaction energy converges to a plateau at larger separation (Fig. 15(B) yellow). This mechanism is only seen with the more strongly hydrophilic keratin, where the water becomes an extension of the keratin and functions as a mediator for enhanced van der Waals interactions while additionally smoothing its roughnesses. This leads to stronger attachment due to increased opposition against pull-off, by water–surface interactions, when compared to the weakly hydrophilic keratin. Quantitatively this amounts to a difference in water–surface interactions between weakly and strongly hydrophilic keratin, at L = 0.4 nm of U^weakly(L = 0.4 nm) − U^strongly(L = 0.4 nm) = −2.1 kJ mol⁻¹ nm⁻², i.e. the mediator effect in the pull-off of strongly hydrophilic keratin is clearly stronger.

Fig. 15 Water–water Lennard-Jones interaction energies (A) and water–surface energies (B) are shown as a function of the displacement of the center of mass of the top layer nanofibrils from its equilibrium position L = z_COM − z_COM,EQ, normalized with the area A of the systems. Dashed lines represent the energies of the wet keratin on a dry surface (shown in the inset), solid lines represent the energies of wet gecko keratin on a wet surface. The decomposed Lennard-Jones energies of 30 force probe molecular dynamics runs are binned according to the instantaneous position z_COM (binwidth of 0.1 nm). The average energy at displacement z_COM and the standard deviation can thus be calculated. Energies are computed at our slowest pulling velocity of 3 × 10⁴ μm s⁻¹. The energies are set to zero at the initial equilibrium configuration, after the relaxation step, when the keratin is attached to the surface. With increasing hydrophilicity (deep purple to bright yellow) favorable water–water interactions (A) turn unfavorable, as the pull-off no longer shows miniscus bridges. This clear trend which separates weakly and strongly hydrophilic keratin is only seen in case of the pull-off from a wet surface, at a dry surface (inset) this trend is not as clearly observable. The opposing water–surface (B) interactions do not directly converge after pull-off in case of a weakly hydrophilic keratin (deep purple), but show convergence for a strongly hydrophilic keratin (bright yellow). We use the standard deviation of the mean as the error.

Even though the capillary mechanism leads to a strong opposition by water–keratin energy (Fig. 14(C), orange), it is compensated on the hydrophobic surface to a large degree by creation of favorable water–water interactions. Therefore, in the case of weakly hydrophilic keratin, adhesion may not completely make use of this strong water–keratin interaction. This may explain the apparent independence of the hydrophilicity of wet gecko keratin on a wet surface, as seen in Fig. 11(B).

4 Conclusion

We investigated the effect of humidity on the pull-off forces of gecko keratin from surfaces by means of force probe molecular dynamics simulations using a coarse-grained model for keratin, water and a silica surface covered by an alkyl monolayer. To the extend of our knowledge, these are the first non-equilibrium molecular dynamics simulations studying the pull-off of gecko keratin. Since it is not known how much water content is present in gecko keratin at a given humidity, we used an intermediate water content of 10%. What is not known either is the hydrophilicity of gecko keratin. We have, therefore, explored a wide range of different hydrophilicities of our gecko keratin model. Therefore, this work showed robustly the larger pull-off forces needed to detach wet gecko keratin compared to dry gecko keratin. More importantly different molecular mechanisms were detected, how water increases the pull-off forces at high humidities. Our main findings can be summarized as follows: (i) capillary forces dominate the adhesion for weakly hydrophilic gecko keratin on a wet surface; (ii) but capillary forces play no role if gecko keratin is hydrophilic enough, for water to readily absorb from the layer on the surface into the gecko keratin; (iii) water on the surface acts as a mediator for keratin-surface interactions, as it interacts strongly with the gecko keratin, and opposes the pull-off as water–surface interactions are lost; (iv) water smoothes out nanoscale roughnesses in the gecko keratin interface by filling gaps between it and the surface (v) on dry hydrophobic surfaces, capillary forces are far less important; they are completely absent for strongly hydrophilic keratin, and increase moderately in relevance with increasing keratin hydrophobicity; (vi) the mediator effect of water plays a role in the pull-off from dry hydrophobic surfaces, the dominant contributions arise, however, from the reduction in favorable keratin-surface interactions.

Our wet keratin systems showed decreases in the Young moduli with water content comparable to experiment,⁵ especially the qualitative flattening of the stress–strain curve and the starting of a plateau formation above 1% to 2% strain. We have also shown that the dominant hypothesis^5,6,8 of the decreased Young modulus explaining the better adhesion at high humidity, can not be confirmed. The weakly hydrophilic keratin had by a clear margin, not the lowest Young modulus, but showed the highest pull-off forces.

Since our water model is that of the MARTINI force field,^23–25 which is a fairly generic solvent particle without a dipole moment, the mechanisms found here may also be relevant for the influence of solvophobicity of keratin for other solvents, for example, methanol. Previous work⁵¹ found in the chloroform-derived gecko's toe pad extract, NMR peaks at 0.8 ppm (ωCH₃) and 1.1 ppm ((CH₂)_n), classified as non polar lipids. The chloroform extraction reduced the mass of the sample by 8–10 wt%, comparable to our water content. It may be the case, that the effect we observe, may also have some bearing on these lipids. Previous work indeed suggests that, by removing lipids, the maximum shear adhesion of gecko's toe pad shads on hydrophobic surfaces is decreased.⁷

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

T. M. would like to thank Hossein Eslami, Donatas Surblys and Jeffrey M. Young for fruitful discussions. Some simulations for this work were performed on the Lichtenberg-Hochleistungsrechner at Technische Universität Darmstadt.

References

1. Q. Jiang, Z. Wang, J. Zhou, W. Chen and Z. Dai, Analysis of Reaction Force and Locomotor Behavior on Geckos in Time- and Frequency-domain during Climbing on Vertical Substrates, J. Bionic Eng., 2019, 16, 115–129,  DOI:10.1007/s42235-019-0011-x.
2. B. C. Mahendra, Contributions to the bionomics, anatomy, reproduction and development of the Indian house-gecko, Hemidactylus flaviviridis Rüppel, Proc. Indian Acad. Sci., 1941, 13, 288–306.
3. E. Arzt, S. Gorb and R. Spolenak, From micro to nano contacts in biological attachment devices, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 10603–10606,  DOI:10.1073/pnas.1534701100.
4. G. Huber, H. Mantz, R. Spolenak, K. Mecke, K. Jacobs, S. N. Gorb and E. Arzt, Evidence for capillarity contributions to gecko adhesion from single spatula nanomechanical measurements, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 16293–16296,  DOI:10.1073/pnas.0506328102.
5. M. Prowse, M. Wilkinson, J. Puthoff, G. Mayer and K. Autumn, Effects of humidity on the mechanical properties of gecko setae, Acta Biomater., 2010, 7, 733–738,  DOI:10.1016/j.actbio.2010.09.036.
6. J. B. Puthoff, M. S. Prowse, M. Wilkinson and K. Autumn, Changes in materials properties explain the effects of humidity on gecko adhesion, J. Exp. Biol., 2010, 213, 3699–3704,  DOI:10.1242/jeb.047654.
7. A. Y. Stark, S. Subarajan, D. Jain, P. H. Niewiarowski and A. Dhinojwala, Superhydrophobicity of the gecko toe pad: biological optimization versus laboratory maximization, Philos. Trans. Royal Soc., 2016, 374, 20160184,  DOI:10.1098/rsta.2016.0184.41.
8. G. Huber, S. Orso, R. Spolenak, U. G. K. Wegst, S. Enders, S. N. Gorb and E. Arzt, Mechanical properties of a single gecko seta, Mater. Res., 2008, 99, 1113–1118,  DOI:10.3139/146.101750.
9. W. Sun, P. Neuzil, T. S. Kustandi, S. Oh and V. D. Samper, The Nature of the Gecko Lizard Adhesive Force, Biophys. J., 2005, 89, L14–L17,  DOI:10.1529/biophysj.105.065268.
10. Z. Peng, Y. Yang and S. Chen, Coupled effects of the temperature and the relative humidity on gecko adhesion, J. Phys. D: Appl. Phys., 2017, 50, 315402,  DOI:10.1088/1361-6463/aa7a97.
11. C. T. Mitchell, C. B. Dayan, D.-M. Drotlef, M. Sitti and A. Y. Stark, The effect of substrate wettability and modulus on gecko and gecko-inspired synthetic adhesion in variable temperature and humidity, Sci. Rep., 2020, 10, 19748,  DOI:10.1038/s41598-020-76484-6.
12. L. Alibardi, Immunolocalization of specific keratin associated beta-proteins (betakeratins) in the adhesive setae of Gekko gecko, Tissue Cell, 2013, 45, 231–240,  DOI:10.1016/j.tice.2013.01.002.
13. K. S. Endoh, T. Kawakatsu and F. Müller-Plathe, Coarse-Grained Molecular Simulation Model for Gecko Feet Keratin, J. Phys. Chem. B, 2018, 122, 2203–2212,  DOI:10.1021/acs.jpcb.7b10481.
14. R. Ruibal and V. Ernst, The structure of the digital setae of lizards, J. Morphol., 1965, 117, 271–293,  DOI:10.1002/jmor.1051170302.
15. N. W. Rizzo, K. H. Gardner, D. J. Walls, N. M. Keiper-Hrynko, T. S. Ganzke and D. L. Hallahan, Characterization of the structure and composition of gecko adhesive setae, J. R. Soc., Interface, 2006, 3, 441–451,  DOI:10.1098/rsif.2005.0097.42.
16. T. W. Kim and B. Bhushan, Effect of stiffness of multi-level hierarchical attachment system on adhesion enhancement, Ultramicroscopy, 2007, 107, 902–912,  DOI:10.1016/j.ultramic.2006.11.008.
17. G. Huber, S. N. Gorb, N. Hosoda, R. Spolenak and E. Arzt, Influence of surface roughness on gecko adhesion, Acta Biomater., 2007, 3, 607–610,  DOI:10.1016/j.actbio.2007.01.007.
18. C. Canal, R. Molina, E. Bertran and P. Erra, Wettability, ageing and recovery process of plasma-treated polyamide 6, J. Adhes. Sci. Technol., 2004, 18, 1077–1089,  DOI:10.1163/1568561041257487.
19. C. W. Extrand, Water Contact Angles and Hysteresis of Polyamide Surfaces, J. Colloid Interface Sci., 2002, 248, 136–142,  DOI:10.1006/jcis.2001.8172.
20. Q. Xu, Y. Wan, T. S. Hu, T. X. Liu, D. Tao, P. H. Niewiarowski, Y. Tian, Y. Liu, L. Dai, Y. Yang and Z. Xia, Robust self-cleaning and micromanipulation capabilities of gecko spatulae and their bio-mimics, Nat. Commun., 2015, 6, 8949,  DOI:10.1038/ncomms9949.
21. S. Sheridan, F. Gräter and C. Daday, How Fast Is Too Fast in Force-Probe Molecular Dynamics Simulations?, J. Phys. Chem. B, 2019, 123, 3658–3664,  DOI:10.1021/acs.jpcb.9b01251.
22. F. Rico, A. Russek, L. González, H. Grubmüller and S. Scheuring, Heterogeneous and rate-dependent streptavidin–biotin unbinding revealed by high-speed force spectroscopy and atomistic simulations, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 6594–6601,  DOI:10.1073/pnas.1816909116.
23. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, The MARTINI force field: coarse grained model for biomolecular simulations, J. Phys. Chem. B, 2007, 111, 7812–7824,  DOI:10.1021/jp071097f.43.
24. L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S.-J. Marrink, The MARTINI Coarse-Grained Force Field: Extension to Proteins, J. Chem. Theory Comput., 2008, 4, 819–834,  DOI:10.1021/ct700324x.
25. D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, Improved Parameters for the Martini Coarse-Grained Protein Force Field, J. Chem. Theory Comput., 2013, 9, 687–697,  DOI:10.1021/ct300646g.
26. D. L. Hallahan, N. M. Keiper-Hrynko, T. Q. Shang, T. S. Ganzke, M. Toni, L. D. Valle and L. Alibardi, Analysis of gene expression in gecko digital adhesive pads indicates significant production of cysteine- and glycine-rich beta-keratins, J. Exp. Zool. B: Mol. Dev. Evol., 2009, 312B, 58–73,  DOI:10.1002/jez.b.21242.
27. M. Calvaresi, L. Eckhart and L. Alibardi, The molecular organization of the betasheet region in Corneous beta-proteins (beta-keratins) of sauropsids explains its stability and polymerization into filaments, J. Struct. Biol., 2016, 194, 282–291,  DOI:10.1016/j.jsb.2016.03.004.
28. R. D. B. Fraser and D. A. D. Parry, The role of β-sheets in the structure and assembly of keratins, Biophys. Rev., 2009, 1, 27,  DOI:10.1007/s12551-008-0005-0.
29. R. A. Sauer, Multiscale modelling and simulation of the deformation and adhesion of a single gecko seta, Comput. Methods Biomech. Biomed. Eng., 2009, 12, 627–640,  DOI:10.1080/10255840902802917 Publisher: Taylor & Francis eprint.
30. M. Varenberg, N. M. Pugno and S. N. Gorb, Spatulate structures in biological fibrillary adhesion, Soft Matter, 2010, 6, 3269–3272,  10.1039/C003207G.
31. S. R. Wasserman, Y. T. Tao and G. M. Whitesides, Structure and reactivity of alkyl- 44 siloxane monolayers formed by reaction of alkyltrichlorosilanes on silicon substrates, Langmuir, 1989, 5, 1074–1087,  DOI:10.1021/la00088a035.
32. I. M. Tidswell, B. M. Ocko, P. S. Pershan, S. R. Wasserman, G. M. Whitesides and J. D. Axe, X-ray specular reflection studies of silicon coated by organic monolayers (alkylsiloxanes), Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 1111–1128,  DOI:10.1103/PhysRevB.41.1111.
33. J. Barriga, B. Coto and B. Fernandez, Molecular dynamics study of optimal packing structure of OTS self-assembled monolayers on SiO₂ surfaces, Tribol. Int., 2007, 40, 960–966,  DOI:10.1016/j.triboint.2006.02.030.
34. E. E. Flater, W. R. Ashurst and R. W. Carpick, Nanotribology of octadecyltrichlorosilane monolayers and silicon: self-mated versus unmated interfaces and local packing density effects, Langmuir, 2007, 23, 9242–9252,  DOI:10.1021/la063644e.
35. M. Javanainen, H. Martinez-Seara and I. Vattulainen, Excessive aggregation of membrane proteins in the Martini model, PLoS One, 2017, 12,  DOI:10.1371/journal.pone.0187936.
36. P. S. Schmalhorst, F. Deluweit, R. Scherrers, C.-P. Heisenberg and M. Sikora, Overcoming the Limitations of the MARTINI Force Field in Simulations of Polysaccharides, J. Chem. Theory Comput., 2017, 13, 5039–5053,  DOI:10.1021/acs.jctc.7b00374.
37. B. Hess, C. Kutzner, D. van der Spoel and E. Lindahl, GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 435–447,  DOI:10.1021/ct700301q.
38. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690,  DOI:10.1063/1.448118.45.
39. S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519,  DOI:10.1063/1.447334.
40. W. G. Hoover, Canonical dynamics: Equilibrium phase-space distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697,  DOI:10.1103/PhysRevA.31.1695.
41. M. Rosenblatt, Remarks on Some Nonparametric Estimates of a Density Function, Ann. Math. Stat., 1956, 27, 832–837,  DOI:10.1214/aoms/1177728190.
42. A. M. Taylor, R. H. C. Bonser and J. W. Farrent, The influence of hydration on the tensile and compressive properties of avian keratinous tissues, J. Mater. Sci., 2004, 39, 939–942,  DOI:10.1023/B:JMSC.0000012925.92504.08.
43. N. Barbakadze, S. Enders, S. Gorb and E. Arzt, Local mechanical properties of the head articulation cuticle in the beetle Pachnoda marginata (Coleoptera, Scarabaeidae), J. Exp. Biol., 2006, 209, 722–730,  DOI:10.1242/jeb.02065.
44. D. Eisenberg, E. Schwarz, M. Komaromy and R. Wall, Analysis of membrane and surface protein sequences with the hydrophobic moment plot, J. Mol. Biol., 1984, 179, 125–142,  DOI:10.1016/0022-2836(84)90309-7.
45. G. I. Bell, Models for the specific adhesion of cells to cells, Science, 1978, 200, 618–627,  DOI:10.1126/science.347575.
46. H. Grubmüller, Force probe molecular dynamics simulations, Methods Mol. Biol., 2005, 305, 493–515,  DOI:10.1007/978-1-59259-912-7_23.
47. B. N. J. Persson and S. Gorb, The effect of surface roughness on the adhesion of elastic plates with application to biological systems, J. Chem. Phys., 2003, 119, 11437–11444,  DOI:10.1063/1.1621854.
48. A. Ramazani, T. Mandal and R. G. Larson, Modeling the Hydrophobicity of Nanoparticles 46 and Their Interaction with Lipids and Proteins, Langmuir, 2016, 32, 13084–13094,  DOI:10.1021/acs.langmuir.6b01963.
49. M. Dörmann and H.-J. Schmid, Simulation of Capillary Bridges between Particles, Proc. Eng., 2015, 102, 14–23,  DOI:10.1016/j.proeng.2015.01.102.
50. P. A. Kralchevsky and K. Nagayama, Particles at Fluids Interfaces and Membranes, in Studies in Interface Science, ed. P. A. Kralchevsky and K. Nagayama, Elsevier, 2001, vol. 10, pp. 469–502.
51. D. Jain, A. Y. Stark, P. H. Niewiarowski, T. Miyoshi and A. Dhinojwala, NMR spectroscopy reveals the presence and association of lipids and keratin in adhesive gecko setae, Sci. Rep., 2015, 5, 9594,  DOI:10.1038/srep09594.

---

Footnote

† Electronic supplementary information (ESI) available: Section S1: Gecko keratin model creation procedure; Section S2: insertion of water into gecko keratin; Section S3: dry gecko keratin equilibration; Section S4: wet gecko keratin equilibration; Table S1: pulling velocities and loading rates used; Table S2: table of force probe molecular dynamics simulation results; Fig. S1: smoothed force profiles as function of pulling velocity; Fig. S2: pull-off pressures of wet keratin on a dry surface; Fig. S3: pull-off pressures of wet keratin as a function of Young modulus; Fig. S4: density profile of weakly hydrophilic keratin during pull-off; Fig. S5: density profile of weakly hydrophilic keratin during pull-off; Movie S1: pull-off: weakly hydrophilic keratin from wet surface; Movie S2: pull-off: strongly hydrophilic keratin from wet surface; Movie S2b: pull-off: strongly hydrophilic keratin from wet surface (transparent keratin); Movie S3: pull-off: weakly hydrophilic keratin from dry surface; Movie S3b: pull-off: weakly hydrophilic keratin from dry surface (transparent keratin); Movie S4: pull-off: strongly hydrophilic keratin from dry surface; Movie S4b: pull-off: strongly hydrophilic keratin from dry surface (transparent keratin). See DOI: 10.1039/d1sm01232k

---