Open Access Article
Open Access ArticleThe three-center two-positron bond†
Jorge
Charry
 a,
Félix
Moncada
a,
Félix
Moncada
 be,
Matteo
Barborini
be,
Matteo
Barborini
 a,
Laura
Pedraza-González
a,
Laura
Pedraza-González
 c,
Márcio T. do N.
Varella
c,
Márcio T. do N.
Varella
 d,
Alexandre
Tkatchenko
d,
Alexandre
Tkatchenko
 a and
Andrés
Reyes
a and
Andrés
Reyes
 *e
*e
aDepartment of Physics and Materials Science, University of Luxembourg, L-1511 Luxembourg City, Luxembourg
bDepartment of Physics, AlbaNova University Center, Stockholm University, S-106 91 Stockholm, Sweden
cDepartment of Chemistry and Industrial Chemistry, University of Pisa, Via Moruzzi 13, 56124, Pisa, Italy
dInstituto de Física, Universidade de São Paulo, Rua do Matão 1731, São Paulo, São Paulo 05508-090, Brazil
eDepartment of Chemistry, Universidad Nacional de Colombia, Av. Cra 30 #45-03, Bogotá, Colombia. E-mail: areyesv@unal.edu.co
First published on 18th October 2022
Abstract
Computational studies have shown that one or more positrons can stabilize two repelling atomic anions through the formation of two-center positronic bonds. In the present work, we study the energetic stability of a system containing two positrons and three hydride anions, namely 2e+[H33−]. To this aim, we performed a preliminary scan of the potential energy surface of the system with both electrons and positrons in a spin singlet state, with a multi-component MP2 method, that was further refined with variational and diffusion Monte Carlo calculations, and confirmed an equilibrium geometry with D3h symmetry. The local stability of 2e+[H33−] is demonstrated by analyzing the vertical detachment and adiabatic energy dissociation channels. Bonding properties of the positronic compound, such as the equilibrium interatomic distances, force constants, dissociation energies, and bonding densities are compared with those of the purely electronic H3+ and Li3+ systems. Through this analysis, we find compelling similarities between the 2e+[H33−] compound and the trilithium cation. Our results strongly point out the formation of a non-electronic three-center two-positron bond, analogous to the well-known three-center two-electron counterparts, which is fundamentally distinct from the two-center two-positron bond [D. Bressanini, J. Chem. Phys., 2021, 155, 054306], thus extending the concept of positron bonded molecules.
1 Introduction
The techniques to accumulate and manipulate positrons1 and positronium (Ps) atoms2 at very low energies have opened up new research areas in molecular sciences. For instance, a great variety of positronic molecules have been produced and detected.3 In these experiments, positron attachment to vibrationally excited molecules gives rise to positronic compounds. The existence of a different kind of positronic molecules was predicted by Charry et al.4 based on computational simulations. Two otherwise repelling hydride anions can be bound by a positron, and the analysis of the positronic orbital suggested the formation of a positron covalent bond. Subsequent computational studies conducted by Moncada et al.5 pointed out that similar bonds should also exist in positronic dihalides.The positronic dihydride system, denoted as e+[H22−], has attracted considerable attention. Goli and Shahbazian6 addressed the nature of the interaction employing Multi-Component Quantum Theory of Atoms in Molecules (MC-QTAIM). The authors concluded that the accumulation of positron density between the two nuclei would underlie the bonding process, acting as “a positronic glue” that converts the repulsive H22− system into a stable one. The energy stability of positron-bonded dihydrides was further confirmed by quantum Monte Carlo (QMC) calculations performed by Ito et al.,7 Bressanini8 and Charry et al.9 Bressanini also concluded that the bonding is not limited to one positron and in later works10 he showed that two singlet-coupled positrons can form a bond between two hydride anions, thus giving rise to the 2e+[H22−] molecule, or simply (PsH)2. The equilibrium internuclear distance was reduced from 6.4 bohr to 6.0 bohr as the number of positrons was increased from 1 to 2. Unexpectedly, the bond length shortening was accompanied by a reduction in the bond energy (BE), from 23.5 mEh to 10.4 mEh.
These fascinating theoretical results raise questions on how complex positron-bonded compounds can become, or on how far the analogy between electronic and positronic bonds can be stretched. Along these lines, Bressanini11 recently reported the local energy stability of 3e+[H22−], or more simply e+[PsH]2, a stable molecular system containing three positrons, which can be understood as resulting from the reaction (PsH)2 + e+. The present study further explores positronic bonding mechanisms beyond the previously studied two-center to three-center systems. Bressanini has conjectured that a system analogous to H3+ with three protons, six electrons, and two positrons, could be stable.10,11
Based on high-level QMC simulations, we demonstrate that this conjectured system, denoted as 2e+[H33−], is energetically stable. Our results, obtained for the singlet state in the D3h symmetry, point out the existence of a three-center two-positron (3c2p) bond that stabilizes three repelling hydride anions. To gain further insight into the 3c2p bond, we compare it against the analogous three-center two-electron bond 3c2e, which is a well established bonding mechanism found in purely electronic molecules.12–15
The H3+ molecule is probably the best known example of 3c2e bonds,16 in view of its astrochemical relevance.17–19 While the trihydrogen cation could be rated the closest analogue of 2e+[H33−] at first glance, previous studies have consistently shown that the properties of electronic and positronic bonds are closest when the systems have isoelectronic ion cores.4,5 We therefore consider Li3+ as an alternative purely electronic analogue of the di-positronic tri-hydride compound for comparison of the bonding properties. Our results confirm that 2e+[H33−] is stable against dissociation into chemically meaningful products. The presently reported results, which indicate the existence of a new kind of di-positronic stable system, may hopefully expand the landscape of the field.
This paper is organized as follows: in Sec. 2 the methods and numerical procedures are summarized; the properties of the di-positronic system and the purely electronic analogues are presented and discussed in Sec. 3; concluding remarks and perspectives for future work are outlined in Sec. 4.
2 Methods
This study considers electrons and positrons as quantum particles and atomic nuclei as point charges within the Born–Oppenheimer approximation. Exploratory studies of the potential energy surface (PES) of the 2e+[H33−] system were performed at the MP2 level of theory. The MP2 expressions for systems composed of electrons and positrons can be found in ref. 20 and 21. Equilibrium energies and geometries were further refined with the variational Monte Carlo (VMC) and diffusion Monte Carlo (DMC) methods.2.1 Quantum Monte Carlo methods
QMC methods are stochastic techniques employed to integrate the time-independent Schrödinger equation for a given trial wave function, the most common of which are VMC and DMC.22–24 The stochastic integration in VMC is carried out with the Metropolis–Hastings algorithm.25,26 The energy functional is evaluated over a trial wave function which is written as the product of a fermionic part, such as a Slater determinant, and a bosonic component, the Jastrow factor, used to describe explicit correlation between particles. The trial wave function used in this study of electron–positron systems is written as the product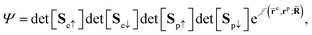 | (1) |
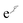 is the Jastrow factor. Several QMC studies have employed similar trial wave functions7,9,27–30 based on products of determinants constructed via atomic basis sets. This particular Jastrow factor was introduced in ref. 9 and it is now generalized for two-positron systems in the present work. The Jastrow factor is built as the sum
is the Jastrow factor. Several QMC studies have employed similar trial wave functions7,9,27–30 based on products of determinants constructed via atomic basis sets. This particular Jastrow factor was introduced in ref. 9 and it is now generalized for two-positron systems in the present work. The Jastrow factor is built as the sum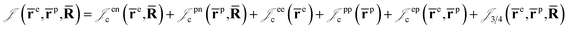 | (2) |
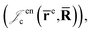 positron–nucleus
positron–nucleus 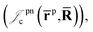 electron–electron
electron–electron 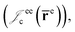 positron–positron
positron–positron 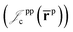 and electron–positron
and electron–positron 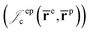 cusps, and a term that describes the dynamical correlation between the fermionic particles in the field of the nuclei
cusps, and a term that describes the dynamical correlation between the fermionic particles in the field of the nuclei 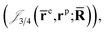 which is an extension of the one defined in ref. 31. The functions used to describe the cusp conditions are of two types. For particle pairs with the same charge we employ slowly decaying functions32 together with a linear combination of Gaussian-type functions (GTFs),
which is an extension of the one defined in ref. 31. The functions used to describe the cusp conditions are of two types. For particle pairs with the same charge we employ slowly decaying functions32 together with a linear combination of Gaussian-type functions (GTFs),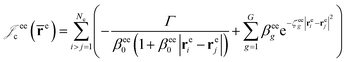 | (3) |
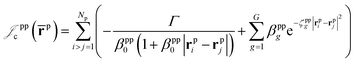 | (4) |
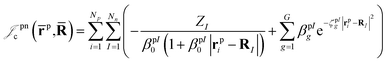 | (5) |
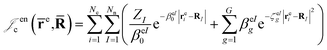 | (6) |
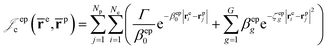 | (7) |
Finally, the dynamical Jastrow factor9,31 is written as a linear combination of products of non-normalized atomic orbitals χq,
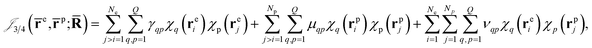 | (8) |
All the parameters of the wave functions are optimized with the stochastic reconfiguration method35,36 using the correlated sampling technique37 to stabilize the convergence if necessary. To better describe the dynamical correlation among the particles, thus improving the binding energy estimates, we also employ the DMC22 method with the fixed-node approximation.38 DMC is a projection method able to converge towards the exact ground state of a system through a time evolution.22 In view of the sign-problem, which appears for fermionic systems, it is necessary to constrain the nodal surface of the wave function (the region where the wave function is zero) by introducing an error in the energy evaluation.22 Yet, it can be shown that FN-DMC, at least in the formalism employed here, is variational with respect to the quality of nodal surfaces, which here are defined by the optimized trial wave functions.
2.2 Computational details
MP2 calculations for the positronic systems were carried out with the LOWDIN software39 using the standard aug-cc-pVTZ basis set40 for electrons with an uncontracted set of (6s4p3d2f) GTFs, denoted as PSX-TZ, for positrons.5 VMC and DMC calculations were performed with the QMeCha9,41 QMC package, published privately on GitHub. The electronic and positronic Slater determinants for the QMC calculations of H systems were constructed from (7s3p2d) primitive GTFs contracted to [4s3p2d], with the initial values of the exponents and contraction coefficients taken from the aug-cc-pVTZ basis set.40,42–44 In the VMC calculations, orbital coefficients, basis set contraction coefficients and GTF exponents were variationally optimized with the stochastic reconfiguration optimization method,31 amounting to 1152 non-zero parameters for 2e+[H33−] in the singlet state, and 837 for 2e+[H33−] in the triplet state. The optimized VMC wave functions were taken as guiding functions in the fixed-node DMC calculations38 performed with 6000 walkers divided into 5000 blocks, each 100 steps long, for a total of 3 × 109 sampled configurations. Calculations were repeated with a time step of 0.005 a.u. to verify the accuracy of the DMC results. Statistical agreement was observed between the results computed with the two time steps. The DMC density plots were obtained by counting the number of particles of each weighted configuration in a three-dimensional grid. The final bonding properties such as energy minimum, equilibrium distances, and forces constants were estimated by fitting our VMC and DMC energy values to a 4th-degree polynomial with respect to one of the internuclear distances.3 Results and discussion
3.1 Energy stability analysis
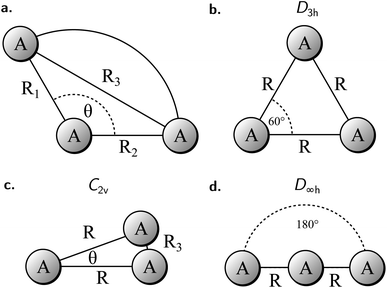
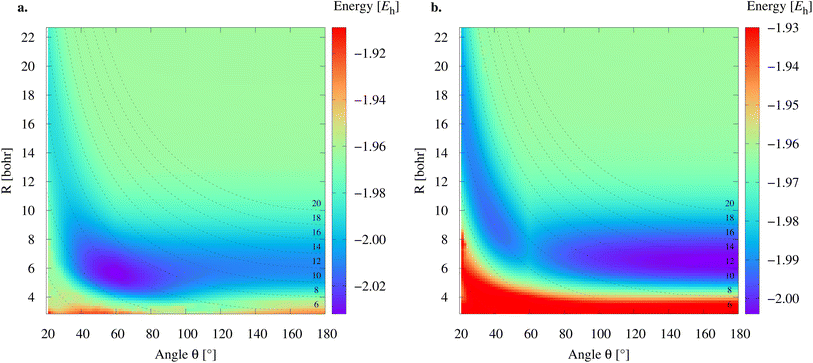
To study the 2e+[H33−] system, we assume the electrons to be in a closed shell singlet state, while for the positrons we investigate both the singlet and triplet states. The initial exploratory studies of the PES are performed at the MP2 level of theory along the coordinates R1 = R2 = R and θ, shown in Fig. 1a, to preserve the symmetry of the charge distribution. The two-dimensional potential energy surfaces obtained for both the singlet and triplet positronic states in that system of coordinates (constrained to C2v symmetry) are shown in Fig. 2, together with the contours for several R3 constant values that are shown as dashed lines. The singlet state displays a single energy minimum with D3h symmetry (see Fig. 1b), corresponding to a triangular configuration with θ = 60° and R ≈ 6 bohr. In contrast, the triplet state has a minimum at a linear conformation with D∞h symmetry (see Fig. 1d) and R ≈ 6 bohr.Further analysis of the PESs in Fig. 2 reveals that both the singlet and triplet states display two regions with low energies (blue color). The first region follows a dissociation path along the R coordinate in the C2v configuration, with the R3 coordinate constrained to 6 bohr. The second region corresponds to the transition between the D3h and D∞h configurations along the angle coordinate, for constant R. The optimal MP2 geometries were further refined with the VMC and DMC methods for both the singlet and triplet states. The minima were located for geometries constrained to D3h and D∞h symmetries. The results shown in Table 1 corroborate the singlet D3h state as the most stable one. Below, we focus the discussion on the lowest-energy 2e+[H33−] singlet state.
| Positronic state | Symmetry | Method | Energy [Eh] | R eq [bohr] |
|---|---|---|---|---|
| Singlet | D 3h | VMC | −2.1489(1) | 6.15(1) |
| DMC | −2.1652(2) | 6.11(1) | ||
| Triplet | D ∞h | VMC | −2.1266(1) | 6.77(2) |
| DMC | −2.1401(4) | 6.62(1) |
We explored the thermodynamic stability of 2e+[H33−] with respect to the dissociation channels given below,
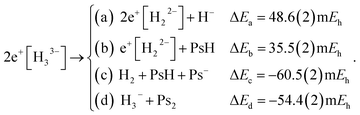 | (9) |
The dissociation energies of channels (9a–9d) were calculated employing the DMC results of Table 1 and the energy data reported in Table S1.† The negative ΔE of channels (9c and 9d) reveal that 2e+[H33−] is thermodynamically unstable with respect to these dissociation products. It is therefore clear that the lowest energy arrangement of a set of three protons, six electrons, and two positrons consists of a sum of dissociated species rather than the bonded D3h structure. Here we must add that the fixed-node errors of the DMC calculations are negligible in the computation of the binding energies, because the nodal surfaces of the purely electronic systems and of the electron–positron ones are described at the same level of theory, leading to a cancellation of errors when computing the energy differences. Moreover, the wave function optimization of the full set of variational parameters in the presence of the correlating Jastrow factor tends to reduce the fixed-node error also in the total energies.
A similar situation was found for positron bonded dihydrides. Previous studies pointed out that (I) e+[H22−],7–9 (II) 2e+[H22−],10 and (III) 3e+[H22−]11 are thermodynamically unstable with respect to dissociation into (I′) H2 + Ps−, (II′) H2 + Ps2 and (III′) H2 + Ps2 + e+, respectively. The local range of stability for the systems I, II and III was explored by comparing the potential energy curves (PECs) for the (I, I′), (II, II′) and (III, III′) pairs. The PEC pairs were found to intersect at internuclear distances considerably shorter than the equilibrium distances of the corresponding positron bonded dihydrides. Those studies further confirmed the kinetic (or local) energy stability of the dihydrides I–III, since their energy barriers, calculated at the crossing points of the potential curves, were found to be sufficiently high to support a few vibrational states.
Along similar lines, we further explore the local stability of 2e+[H33−] around the D3h minimum. We consider the four lowest-energy vertical detachment channels given by
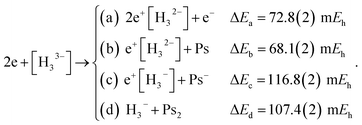 | (10) |
Fig. 3 presents PECs along the R coordinate constraining the system to preserve the D3h symmetry, and along the θ coordinate imposing C2v symmetry with R = 6.1 bohr. Fig. 3a reveals that the energy of 2e+[H33−] along the R coordinate is always lower than those computed for the (10a–10d) channels, and no curve crossings were found. In contrast, Fig. 3b reveals that the PEC of 2e+[H33−] intersects the (10c) potential around 20° and R3 = 2.1 bohr. The stabilization of the (10c) channel as the R3 distance decreases is consistent with the formation of a H2 molecule (R = 1.40 bohr) in the adiabatic channel (9c). Although the (9c) channel energy lies below the 2e+[H33−] energy, the intersections are separated from the D3h minimum by a rather high (≈20 mEh) and broad (θ ≈ 30°) energy barrier across the 2e+[H33−] potential. The PECs in Fig. 3a and b therefore corroborate the local (kinetic) energy stability of the 2e+[H33−] species.
 | ||
| Fig. 3 Potential energy curves for the 2e+[H33−] system and the vertical detachment channels (10a–10d). The energies were computed with the DMC method as functions of the R coordinate in the D3h symmetry (a) and of the θ coordinate in the C2v symmetry (b) fixing R = 6.1 bohr. We employed the lowest energies obtained from variational calculations for Ps− and Ps2,45,46 and the exact value for Ps (−0.25 Eh). | ||
3.2 Comparison with analogous purely electronic systems
As in previous studies of positron bonded dihydrides4 and dihalides,5 we compare the properties of the 2e+[H33−] system with two 3c2e bonded systems, i.e., H3+ and Li3+. Specifically, the equilibrium distances and the force constants for the symmetric stretching (ν1) and bending (ν2) vibrational modes of the D3h ground states, calculated with the DMC method, are shown in Table 2. The equilibrium distance of the positronic molecule (R = 6.11 bohr) is much closer to that of Li3+ (R = 5.64 bohr) that H3+ (R = 1.63 bohr). This result is consistent with our earlier studies, which pointed out that purely electronic molecules with isoelectronic cores are the closest analogues to positron bonded systems. Although larger discrepancies are found for the vibrational frequencies of 2e+[H33−] and Li3+ (roughly a factor of 2), they are still much closer if compared to the frequencies of H3+, having different orders of magnitude. The present calculations for three-center two-particle bonds therefore corroborate the previous findings for diatomic systems.| System | E | R | k ν1 | k ν2 |
|---|---|---|---|---|
| H3+ | −1.346(4) | 1.63(3) | 0.57(5) | 0.16(2) |
| Li3+ | −22.3419(1) | 5.645(7) | 0.0254(3) | 0.0110(4) |
| 2e+[H33−] | −2.1652(2) | 6.11(1) | 0.0114(4) | 0.0047(7) |
The longer equilibrium distances and lower vibrational frequencies also indicate a weaker 3c2p bond compared to the 3c2e analogues. In addition, we contrast the energy stability of 2e+[H33−] with those of the purely electronic Li3+, and H3+. To that aim, we consider the lowest energy chemically meaningful dissociation channels of Li3+, and H3+
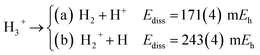 | (11) |
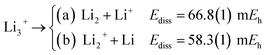 | (12) |
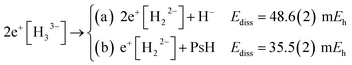 | (13) |
The energies of channels (11) and (12) were calculated employing the DMC energy data reported in Table S1.† We observe that the lowest energy dissociation channel for H3+ (Ediss = 171.84 mEh) involves the formation of a neutral molecule and a proton. Contrastingly, for Li3+ (Ediss = 58.27 mEh) and 2e+[H33−] (Ediss = 35.54 mEh), involves the formation of a neutral atom, and an ionic single particle bonded molecule. It is worth noticing that Ediss of Li3+ and 2e+[H33−] are of the same order and differ considerably from that of H3+ for all dissociation channels considered here.
3.3 Densities
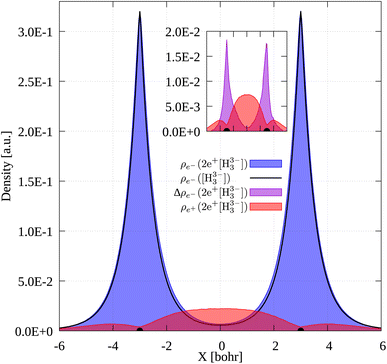
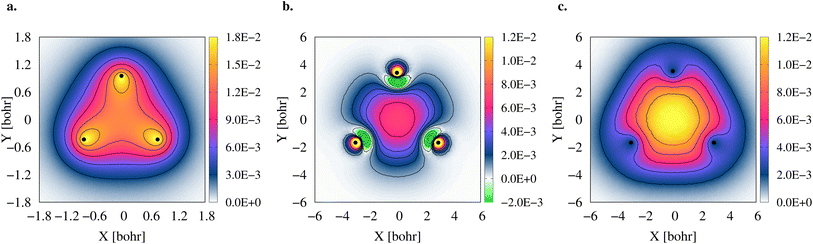
To gain further insight into the 3c2p bond formation, we computed the positron (ρe+) and electron (ρe−) densities of 2e+[H33−]. One-dimensional (1D) cuts of the electron densities obtained for the unbound [H33−] trianion and the bound 2e+[H33−] compound are shown in Fig. 4. The densities are remarkably similar, thus pointing out that the binding mechanism in 2e+[H33−] is not electronic, as previously observed for positronic covalent bonds.4–6 In contrast, the positron density prominently accumulates between the H nuclei, balancing the otherwise repulsive interaction between the anions and producing a slight increase of the electronic density in that region.A comparison between the two-particle bonding densities in three-center systems is carried out in Fig. 5. In H3+ the bonding density presented in Fig. 5a is the total electron density, ρe−. ρe− in H3+ has maxima on top of the nuclei and accumulates around the centroid of the system, where ρe− has a local minimum. For Li3+ the bonding density, Δρe−, displayed in Fig. 5b, was obtained as the ρe− difference between the [Li3+] and [Li3+3] systems, both calculated at the same geometry. Δρe− in Li3+ also displays maxima around the nuclei and accumulates around the centroid, but in this case, has a local maximum at that point. The symmetric accumulation of electronic density in the centroid of the system is a signature of 3c2e bonding. In turn, in 2e+[H33−] the bonding density is the total positron density, ρe+ portrayed in Fig. 5c. ρe+ in 2e+[H33−] is depleted around the nuclei, as expected from the Coulomb interaction, gradually accumulates at the internuclear region and peaks at the centroid, clearly resembling Δρe− of Li3+ in that region. Therefore, this accumulation around the centroid of 2e+[H33−] can be viewed as the formation of a 3c2p bond.
The densities (Fig. 5), vibrational properties (Table 2) and bond energies (eqn (9) and (12)) provide strong evidence that similar three-center two-particle bonding mechanisms are present in Li3+ and in 2e+[H33−].
Now that we have established the local stability of 2e+[H33−], its bonding properties and its similarities with Li3+, it is worth exploring the chemistry of the latter to gain further insight into the chemical implications of the three-center two-positron bond.
Previous studies of the nature of the 3c2e bond in Li3+ based on topological analyses of the electronic density47,48 and an Interference Energy analysis49 have concluded that Li3+ can be considered as the smallest metallic cluster, where the valence electrons in the centroid act as free metallic electrons. Additionally, to explain the relative stability and structure of Li3+, the presence of σ-aromatic or σ-antiaromatic states is still widely discussed.47,49–51 Based on the reported similarities of the bonding densities of 2e+[H33−] and Li3+, we speculate that the positrons in 2e+[H33−] could also be considered as ‘pseudo’-metallic in character and that the positronic delocalization in 2e+[H33−] could provide in the future evidence of a new type of positronic σ-aromaticity or σ-antiaromaticity. Exploring the extension of the metallic bond and aromaticity concepts to positronic molecules would require a more in-depth analysis of the bonding nature. For instance, by employing energy decomposition, quantum interference49 or multicomponent atoms-in-molecules6,52,53 analyses. However, those studies are beyond the scope of the present work.
4 Conclusions
Theoretical studies have evidenced the formation of locally stable systems composed of two repelling atomic anions and one-to-three positrons. The anti-particles are mainly responsible for the conformers' stabilization, thus expanding the definition of chemical bonding beyond the ordinary purely electronic systems.4,6–11 In this work, we have found that two positrons can form a locally stable bound state with three hydride anions in a D3h configuration and singlet spin state. The results suggest the formation of a 3c2p bond, pointing out that the chemical bond concept reaches beyond the positron covalent bonds in two-center molecules, addressed in previous studies. The dissociation products H2 +PsH + Ps− correspond to the lowest-energy configuration of the system comprising two positrons, six electrons and three hydrogen nuclei. Nevertheless, our vertical detachment and adiabatic energy dissociation analysis confirm the local stability of 2e+[H33−] around the D3h equilibrium geometry. A comparative analysis reveals that the positronic molecule is similar to the trilithium cation with isoelectronic atomic cores, although it remarkably differs from the trihydrogen cation. Similarities were found for the equilibrium geometries, force constants for symmetric stretch and bending modes, and also dissociation energies trends. In addition, the electronic (Li3+) and positronic (2e+[H33−]) bonding densities are similar around the internuclear region and equally spread among all three atomic centers, suggesting strong similarities between the 3c2p and 3c2e bonds. The positronic species has longer bond lengths, weaker force constants and lower bond energies than the trilithium cation, which can be viewed as the analogue purely electronic system. This trend does not seem to be general, as it was found for positronic hydrides but not for positronic dihalides.The present results extend the findings of previous studies revealing that two positrons are capable of bonding three otherwise repelling atomic anions. Since positron bonded systems are fundamentally distinct from those formed by positron attachment to stable atoms and molecules, these results will hopefully stimulate further theoretical and experimental researches on novel physical and chemical processes involving those antiparticles.
Data availability
The datasets supporting this article have been uploaded as part of the ESI.†Author contributions
Conceptualization: J. C., F. M., L. P. G., A. R. Formal analysis: J. C., F. M., M. B. Investigation: J. C., F. M., L. P. G., A. R. Funding acquisition: M. T. N. V., A. T., A. R. Methodology: J. C., F. M., M. B., L. P. G., A. T., A. R. Project administration: A. T., A. R. Validation: M. T. N. V., A. T., A. R. Resources: J. C., F. M., M. B., A. T., A. R. Software: J. C., F. M., M. B., A. T., A. R. Supervision: M. T. N. V., A. T., A. R. Visualization: J. C., F. M. Writing – original draft: J. C., F. M., M. B., L. P. G., M. T. N. V., A. T., A. R. Writing – review & editing: J. C., F. M., M. B., L. P. G., M. T. N. V., A. T., A. R.Conflicts of interest
There are no conflicts to declare.Acknowledgements
FM acknowledges financial support from the Colombian Ministry of Sciences (Minciencias) through the “Doctorados Nacionales (757)” program. MTNV acknowledges support from São Paulo Research Foundation, FAPESP (grant no. 2020/16155-7), and National Council for Scientific and Technological Development, CNPq (grant no. 304571/2018-0). JACM acknowledges financial support from the Luxembourg National Research Fund (AFR PhD/19/MS, 13590856). MB acknowledges financial support from the Luxembourg National Research Fund (INTER/DFG/18/12944860). Part of the calculations presented in this paper were carried out using the HPC facilities of the University of Luxembourg54 (see https://hpc.uni.lu).Notes and references
- J. Fajans and C. M. Surko, Phys. Plasmas, 2020, 27, 030601 CrossRef CAS.
- D. B. Cassidy, Eur. Phys. J. D, 2018, 72, 53 CrossRef.
- J. R. Danielson, D. H. E. Dubin, R. G. Greaves and C. M. Surko, Rev. Mod. Phys., 2015, 87, 247–306 CrossRef CAS.
- J. Charry, M. T. d. N. Varella and A. Reyes, Angew. Chem., Int. Ed., 2018, 57, 8859–8864 CrossRef CAS.
- F. Moncada, L. Pedraza-González, J. Charry, M. T. do N. Varella and A. Reyes, Chem. Sci., 2020, 11, 44–52 RSC.
- M. Goli and S. Shahbazian, ChemPhysChem, 2019, 20, 831–837 CrossRef CAS.
- S. Ito, D. Yoshida, Y. Kita and M. Tachikawa, J. Chem. Phys., 2020, 153, 224305 CrossRef CAS PubMed.
- D. Bressanini, J. Chem. Phys., 2021, 154, 054306 CrossRef.
- J. A. Charry Martinez, M. Barborini and A. Tkatchenko, J. Chem. Theory Comput., 2022, 18, 2267–2280 CrossRef CAS PubMed.
- D. Bressanini, J. Chem. Phys., 2021, 155, 054306 CrossRef CAS.
- D. Bressanini, J. Chem. Phys., 2022, 156, 154302 CrossRef CAS.
- R. M. Lobayan, R. C. Bochicchio, A. Torre and L. Lain, J. Chem. Theory Comput., 2011, 7, 979–987 CrossRef CAS.
- J. C. Green, M. L. Green and G. Parkin, Chem. Commun., 2012, 48, 11481–11503 RSC.
- E. S. Smirnova and A. M. Echavarren, Angew. Chem., Int. Ed., 2013, 52, 9023–9026 CrossRef CAS.
- J. J. Duchimaza Heredia, A. D. Sadow and M. S. Gordon, J. Phys. Chem. A, 2018, 122, 9653–9669 CrossRef CAS PubMed.
- O. Chuluunbaatar, S. Obeid, B. Joulakian, A. Gusev, P. Krassovitskiy and L. Sevastianov, Chem. Phys. Lett., 2020, 746, 137304 CrossRef CAS.
- E. Herbst, Philos. Trans. R. Soc. London, Ser. A, 2000, 358, 2523–2534 CrossRef CAS.
- S. Miller, N. Achilleos, G. E. Ballester, T. R. Geballe, R. D. Joseph, R. Prangé, D. Rego, T. Stallard, J. Tennyson, L. M. Trafton and J. Hunter Waite, Philos. Trans. R. Soc. London, Ser. A, 2000, 358, 2485–2502 CrossRef CAS.
- T. Oka, Chem. Rev., 2013, 113, 8738–8761 CrossRef CAS PubMed.
- J. Charry, J. Romero, M. T. d. N. Varella and A. Reyes, Phys. Rev. A, 2014, 89, 052709 CrossRef.
- A. Reyes, F. Moncada and J. Charry, Int. J. Quantum Chem., 2019, 119, e25705 CrossRef.
- W. M. C. Foulkes, L. Mitas, R. J. Needs and G. Rajagopal, Rev. Mod. Phys., 2001, 73, 33–83 CrossRef CAS.
- M. H. Kalos and P. A. Whitlock, in Quantum Monte Carlo, John Wiley & Sons, Ltd, 2008, ch. 8, pp. 159–178 Search PubMed.
- F. Becca and S. Sorella, Quantum Monte Carlo Approaches for Correlated Systems, Cambridge University Press, 2017 Search PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- W. K. Hastings, Biometrika, 1970, 57, 97–109 CrossRef.
- T. Yoshida, G. Miyako, N. Jiang and D. M. Schrader, Phys. Rev. A, 1996, 54, 964–966 CrossRef CAS PubMed.
- Y. Kita, R. Maezono, M. Tachikawa, M. Towler and R. J. Needs, J. Chem. Phys., 2009, 131, 134310 CrossRef.
- Y. Yamada, Y. Kita, M. Tachikawa, M. D. Towler and R. J. Needs, Eur. Phys. J. D, 2014, 68, 63 CrossRef.
- Y. Yamada, Y. Kita and M. Tachikawa, Phys. Rev. A, 2014, 89, 062711 CrossRef.
- M. Casula and S. Sorella, J. Chem. Phys., 2003, 119, 6500–6511 CrossRef CAS.
- S. Fahy, X. W. Wang and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 3503–3522 CrossRef CAS PubMed.
- M. S. Becker, A. A. Broyles and T. Dunn, Phys. Rev., 1968, 175, 224–228 CrossRef CAS.
- C.-J. Huang, C. Filippi and C. J. Umrigar, J. Chem. Phys., 1998, 108, 8838–8847 CrossRef CAS.
- S. Sorella, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 024512 CrossRef.
- S. Sorella, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 241103 CrossRef.
- C. Filippi and C. J. Umrigar, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, R16291–R16294 CrossRef CAS.
- P. J. Reynolds, D. M. Ceperley, B. J. Alder and W. A. Lester, J. Chem. Phys., 1982, 77, 5593–5603 CrossRef CAS.
- R. Flores-Moreno, E. Posada, F. Moncada, J. Romero, J. Charry, M. Díaz-Tinoco, S. A. González, N. F. Aguirre and A. Reyes, Int. J. Quantum Chem., 2014, 114, 50–56 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- M. Barborini, Quantum Mecha (QMeCha) Package α.0.3.0 (Private Repository July, 2021), https://github.com/QMeCha Search PubMed.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, J. Chem. Phys., 1999, 110, 7667–7676 CrossRef CAS.
- V. I. Korobov, Phys. Rev. A, 2000, 61, 064503 CrossRef.
- S. Bubin and L. Adamowicz, Phys. Rev. A, 2006, 74, 052502 CrossRef.
- R. W. Havenith, F. De Proft, P. W. Fowler and P. Geerlings, Chem. Phys. Lett., 2005, 407, 391–396 CrossRef CAS.
- C. Foroutan-Nejad and P. Rashidi-Ranjbar, Comput. Theor. Chem., 2009, 901, 243–248 CAS.
- D. W. O. de Sousa and M. A. C. Nascimento, Phys. Chem. Chem. Phys., 2022, 24, 15958–15972 RSC.
- A. N. Alexandrova and A. I. Boldyrev, J. Phys. Chem. A, 2003, 107, 554–560 CrossRef CAS.
- X. He, C. Guo, M. Li, S. Zhong, X. Wan, C. Rong, P. K. Chattaraj and D. Zhao, J. Mol. Model., 2022, 28, 122 CrossRef CAS.
- M. Goli and S. Shahbazian, Int. J. Quantum Chem., 2011, 111, 1982–1998 CrossRef CAS.
- M. Gharabaghi and S. Shahbazian, J. Chem. Phys., 2017, 146, 154106 CrossRef PubMed.
- S. Varrette, P. Bouvry, H. Cartiaux and F. Georgatos, Proc. of the 2014 Intl. Conf. on High Performance Computing & Simulation (HPCS 2014), Bologna, Italy, 2014, pp. 959–967 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Total energies of the one, two and three atomic species employed in the dissociation energies calculations. Quantum Monte Carlo energies computed at each point of the potential energy curves. See DOI: https://doi.org/10.1039/d2sc04630j |
| This journal is © The Royal Society of Chemistry 2022 |