Open Access Article
Open Access ArticleUnraveling hydridic-to-protonic dihydrogen bond predominance in monohydrated dodecaborate clusters†
Yanrong
Jiang‡
a,
Qinqin
Yuan‡
be,
Wenjin
Cao
 b,
Zhubin
Hu
a,
Yan
Yang
b,
Zhubin
Hu
a,
Yan
Yang
 a,
Cheng
Zhong
d,
Tao
Yang
a,
Haitao
Sun
a,
Cheng
Zhong
d,
Tao
Yang
a,
Haitao
Sun
 *ac,
Xue-Bin
Wang
*ac,
Xue-Bin
Wang
 *b and
Zhenrong
Sun
*ac
*b and
Zhenrong
Sun
*ac
aState Key Laboratory of Precision Spectroscopy, School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China. E-mail: htsun@phy.ecnu.edu.cn; zrsun@phy.ecnu.edu.cn
bPhysical Sciences Division, Pacific Northwest National Laboratory, 902 Battelle Boulevard, P. O. Box 999, MS K8-88, Richland, Washington 99352, USA. E-mail: xuebin.wang@pnnl.gov
cCollaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan, Shanxi 030006, China
dCollege of Chemistry & Molecular Sciences, Wuhan University, Wuhan, Hubei 430072, China
eDepartment of Chemistry, Anhui University, Hefei, Anhui 230601, China
First published on 12th August 2022
Abstract
Hydridic-to-protonic dihydrogen bonds (DHBs) are involved in comprehensive structural and energetic evolution, and significantly affect reactivity and selectivity in solution and solid states. Grand challenges exist in understanding DHBs’ bonding nature and strength, and how to harness DHBs. Herein we launched a combined photoelectron spectroscopy and multiscale theoretical investigation using monohydrated closo-dodecaborate clusters B12X122−·H2O (X = H, F, I) to address such challenges. For the first time, a consistent and unambiguous picture is unraveled demonstrating that B–H⋯H–O DHBs are superior to the conventional B–X⋯H–O HBs, being 1.15 and 4.61 kcal mol−1 stronger than those with X = F and I, respectively. Energy decomposition analyses reveal that induction and dispersion terms make pronounced contributions resulting in a stronger B–H⋯H–O DHB. These findings call out more attention to the prominent roles of DHBs in water environments and pave the way for efficient and eco-friendly catalytic dihydrogen production based on optimized hydridic-to-protonic interactions.
Introduction
The hydrogen bond (HB), first discussed in 1912, represents one of the most important research topics in modern chemistry.1–4 In a typical HB, a protonic hydrogen (HB donor) of an X–Hδ+ bond (X is a highly electronegative atom, e.g., N, O, halogen) interacts with an adjacent lone pair of an electronegative atom (HB acceptor) in the X–Hδ+⋯Aδ− form.5 The HB acceptor Aδ− could be a H atom when it is bonded to an electropositive atom such as boron or transition metal Y, and this can result in a specific HB pattern, X–Hδ+⋯Hδ−–Y, known as hydridic-to-protonic interactions.6 This interaction was first recognized as a real intermolecular N–H⋯H–B attraction in borane–ammonia complexes in 1968,7 and the term “dihydrogen bond” (DHB) was coined in 1995 to describe such chemical bonding patterns,8,9 eighty-three years after the original HB concept was formulated. So far, the DHB has attracted considerable attention due to its involvement in comprehensive structural and energetic evolution, as well as its major impact on reactivity and selectivity in both the solution and solid state.6,10–16 For example, the DHB has manifested its crucial roles in broad and diverse fields such as molecular recognition,17 hydrogen storage materials,18 catalytic dehydrogenation,19,20 synthetic chemistry,21 supramolecular self-assembly,12,22 and drug design.13,23Despite the aforementioned importance and previous experiments (i.e. solution NMR spectroscopy,24–26 neutron diffraction/inelastic neutron scattering technique,27,28 and IR vibrational spectroscopy29–32) and theoretical calculations,6,11,33,34 the nature and strength of DHBs have not been well understood. Particularly, only in rare cases35 has the strength of DHBs been well defined and comparisons made to conventional HBs, but the generality of these observations remains unclear.6 This deficiency of understanding is largely due to the lack of proper models31,32 and precise spectroscopic measurements, in which well-defined DHBs exist without interferences from other conventional HBs and bulk environments. Until now, a direct quantitative measurement of the strength of DHBs and their comparison to typical HBs has not been reported, leading to two important open questions: (1) how strong is a DHB compared to conventional strong HBs? and (2) what is the chemical bonding nature and dynamics in DHB formation?
To address these questions, in this work, a series of size-selected monohydrated closo-dodecaborate clusters B12X122−·H2O (X = H, F, I) were generated and characterized in the gas phase. B12X122− clusters are the most well-known boron-based molecules with icosahedral (Ih) symmetry and exceptionally high electronic and structural stability that are tunable with different ligands X.36–38 In addition, B12X122− molecules also have important medical applications, including boron-based neutron capture therapy of cancer.39 The nucleophilic H atoms in B12H122− allow the formation of sole B–H⋯H–O DHBs in monohydrates, making B12H122−·H2O an ideal model, in which DHBs can be precisely spectroscopically characterized. This model can then be compared to conventional HBs ranging from strong B–F⋯H–O in B12F122−·H2O to weak B–I⋯H–O in B12I122−·H2O. Note that the electronegative fluorine as a HB acceptor always represents a strong HB system, with the bifluoride ion [F–H–F]− as an outstanding example whose HB strength exists at an intersection between a classical electrostatic interaction and a covalent chemical bond.40,41 We combined size-selective cryogenic negative ion photoelectron (NIPE) spectroscopy42,43 and high-level quantum-chemical calculations to directly investigate these solvated anion clusters. The results unraveled herein consistently imply that the B–H⋯H–O DHB is surprisingly strong, even prevailing over the traditionally strong B–F⋯H–O HB. Dynamic simulations further confirm the superior strength and thermodynamic stability of DHBs in B12H122−·H2O.
Results and discussion
NIPE spectra of B12X122−·nH2O (X = H, F, I; n = 0, 1)
Fig. 1 shows the 20 K NIPE spectra of B12X122−·nH2O (X = H, F, I; n = 0, 1). The spectral shapes of hydrated B12X122−·H2O show similar patterns to those of each corresponding isolated B12X122−, with their electron binding energies (EBEs) blue shifted. The B12H122− with the smallest vertical detachment energy (VDE) among the three B12X122− anions exhibits the largest VDE shift with a ΔVDE of 0.31 eV when one H2O molecule is attached, in comparison to the 0.26 and 0.11 eV for X = F and I, respectively (Fig. 1 and Table 1). The measured NIPE spectra provide crucial information for determining the structures of these clusters when combining with theoretical calculations. More importantly, ΔVDE—the VDE difference between a hydrated anion cluster and the corresponding isolated anion, can be regarded as a direct measurement of intrinsic water binding energy (wBE) in anionic hydrated systems.38,44 Therefore, these obtained ΔVDE values unequivocally indicate that the DHB-driven wBE in B12H122−·H2O is superior to those based on traditional HBs in B12X122−·H2O.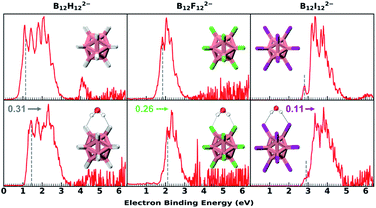 | ||
| Fig. 1 The 20 K NIPE spectra of B12X122−·nH2O (X = H, F, I; n = 0, 1) measured with 193 nm photons. The dashed gray lines denote the spectral vertical detachment energy (VDE) positions. Due to the existence of the repulsive Coulomb barrier (RCB) in photodetaching dianions, spectral bands at higher binding energy are suppressed (see Fig. S1† for comparing 193 and 157 nm spectra). The noisy spikes in the spectrum of the hydrated F beyond 4 eV are due to the imperfect background subtraction originating from weak signals and scaled down by a factor of 0.2 to enhance the presentation clarity. VDE blue shifts upon hydration are noted with the color-coded numbers and arrows. The insets show the lowest-lying structures. Boron, hydrogen, oxygen, fluorine, and iodine atoms are, respectively, coloured in pink, grey, red, green, and magenta. | ||
| VDE (Exp.) | VDE (Cal.) | ΔVDEa (Exp.) | wBE (SAPT) | wBEb (direct ΔE) | |
|---|---|---|---|---|---|
| a Experimentally determined as VDE difference between B12X122−·H2O and isolated B12X122−, which equals the water binding energy (wBE) difference in hydrated dianionic and anionic clusters, i.e., [E(B12X122−·H2O) − E(B12X122−)] − [E(B12X12˙−·H2O) − E(B12X12˙−)]. b Direct ΔE = E(B12H122−·H2O) − E(H2O) − E(B12H122−) at the DLPNO-CCSD(T)/aug-cc-pVTZ(-pp) level with the zero-point energy and entropy corrections. | |||||
| B12H122− | 1.15 | 1.36 | — | — | |
| B12H122−·H2O | 1.46 | 1.70 | 7.15 (0.31) | 14.31 | 12.26 |
| B12F122− | 1.85 | 2.07 | — | — | |
| B12F122−·H2O | 2.11 | 2.34 | 6.00 (0.26) | 13.16 | 11.45 |
| B12I122− | 2.80 | 2.86 | — | — | |
| B12I122−·H2O | 2.91 | 3.05 | 2.54 (0.11) | 8.74 | 9.76 |
B–H⋯H–O DHB versus B–X⋯H–O HB (X = F and I)
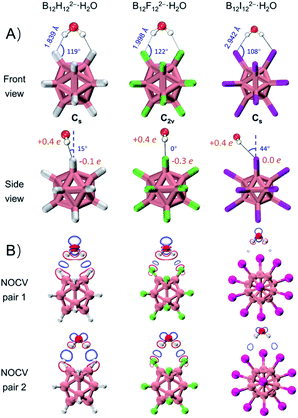
DLPNO-CCSD(T)/aug-cc-pVTZ(-pp) calculations45 predict that these monohydrates share very similar geometric structures with a H2O molecule attaching simultaneously to two adjacent B–X bonds (Fig. 2A) and their calculated VDEs are in good agreement with the experimental results (Tables 1 and S1†). The major geometric difference lies in the dihedral angle between B–X–X–B and H–X–X–H planes, which is 15° for B12H122−·H2O (Cs), 0° for B12F122−·H2O (C2v), and 44° for B12I122−·H2O (Cs). It is worth noting that unlike the X = H or F clusters, B12I122−·H2O tends to have hydrogens of water pointing to the middle valley of two B–I bonds. This is possibly due to the large atomic radius of iodine and its relatively “positive” charge distribution (Fig. 2A and Table S2†). As such, all three B12X122−·H2O clusters feature optimal structures with the formation of two identical B–X⋯H–O bonds, making them an ideal model enabling direct comparison of B–H⋯H–O DHBs with classical B–F(I)⋯H–O HBs in a similar chemical environment.As shown in Table 1, ΔVDEs for B12X122−·H2O, with X = H, F and I, are measured to be 7.15 (0.31), 6.00 (0.26), and 2.54 (0.11) kcal mol−1 (eV), respectively. The results suggest an advantageous binding strength of B12H122−·H2O that is 1.15 and 4.61 kcal mol−1 stronger than those of B12X122−·H2O, X = F and I. The superiority of binding strength of the former over the latter two is in accordance with the trend in their calculated X–H bond lengths/B–X–H angles (1.839 Å/119°, 1.998 Å/122°, and 2.942 Å/108° in B12X122−·H2O, X = H, F, and I, respectively). To compare with the experimental ΔVDEs, theoretical wBEs were calculated using both the symmetry-adapted perturbation theory (SAPT) at the SAPT2+/aug-cc-pVDZ(-pp) level and the direct energy difference (direct ΔE) method at the DLPNO-CCSD(T)/aug-cc-pVTZ(-pp) level with the zero-point energy (ZPE) and entropy corrections. The calculated wBEs are larger than the corresponding ΔVDE values (Table 1) due to the existence of appreciable interactions between the singly charged post-detached B12X12˙− species and water molecule.38,44 However, the differences in the SAPT-calculated wBEs for the three monohydrates indicate that the intermolecular interaction strength in B12H122−·H2O is 1.14 and 5.57 kcal mol−1 larger than that in B12F122−·H2O and B12I122−·H2O, respectively, in excellent agreement with the corresponding measured values of 1.15 and 4.61 kcal mol−1 (vide supra). The wBEs calculated using the direct ΔE-method suggested that the DHB strength in B12H122−·H2O is 0.82 and 2.50 kcal mol−1 larger than that in B12F122−·H2O and B12I122−·H2O, respectively, consistent with the SAPT results. And the contributions of ZPE and entropy corrections to the total wBEs are within 3% for all the clusters, suggesting their negligible effects (Table S3†). The stronger B–H⋯H–O interaction is also evidenced via the extended transition state-natural orbitals for chemical valence (ETS-NOCV)46 analysis (Fig. 2B). The orbital interaction between B12X122− and H2O leads to various degrees of charge transfer (occupied orbitals of B12X122− mixed with unoccupied orbitals of H2O) and electron polarization (occupied orbitals of B12X122− mixed with its own empty orbitals). Based on the first two dominant NOCV pairs, there exists a region of increased electron density marked in blue, and such a density change is more significant in B12H122−·H2O than in B12X122−·H2O (X = F, I). This analysis therefore suggests that the B–H⋯H–O bond is more covalent-like binding and contributes more to the total interaction energy than the other two conventional HBs. To further compare DHBs vs. traditional HBs, quantum theory of atoms-in-molecules (QTAIM) descriptors47 and core–valence bifurcation (CVB)48 indices were calculated based on high-quality wave functions at the bond critical point (BCP) of the intermolecular interaction of interest as listed in Table S4.† Interestingly, the QTAIM descriptors well-defined for traditional HBs show different predictive abilities for the studied DHB. Only the |V(r)|/G(r) descriptor within the QTAIM and the ELF(C–V) index can confirm the binding strength advantage of DHBs, suggesting the robustness and versatility of the two indexes. The |V(r)|/G(r) denotes the ratio of absolute potential energy density |V(r)| to Lagrangian kinetic energy density G(r) at the BCP, and the ELF(C–V) index represents the electron localization function (ELF) bifurcation value between the ELF core domain and valence domain. Notably, most of the QTAIM descriptors based on electron density fail to describe the strength advantage of DHBs herein, highlighting the urgency of collecting more spectroscopic DHB data to benchmark the theoretical descriptors that can be universally operative.
Energy decomposition analysis
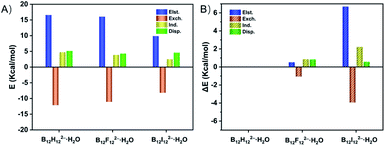
To quantitatively reveal the bonding nature of the B–H⋯H–O DHB, the wBEs are decomposed into four physically meaningful components (Fig. 3 and Table S5A†). It is shown that the larger wBE of B12H122−·H2O arises from its greater electrostatic, induction and dispersion terms than those of B12F122−·H2O and B12I122−·H2O. Specifically, the electrostatic, and induction plus dispersion terms contribute 0.521, and 1.691 kcal mol−1 to the total wBE difference between B12H122−·H2O and B12F122−·H2O (Table S5B†), respectively, suggesting the key role of induction and dispersion terms. The larger contribution of induction plus dispersion terms in B12H122−·H2O can be attributed to its bigger polarizability, i.e., isolated B12H122− (168 a.u.) versus B12F122− (141 a.u.). In contrast, the induction plus dispersion terms only contribute 2.806 kcal mol−1 to the ΔwBE between B12H122−·H2O and B12I122−·H2O, significantly smaller than the 6.701 kcal mol−1 of the electrostatic term, suggesting the essential advantage of the B–H⋯H–O DHB over B–I⋯H–O HB is driven by the well-established electrostatic interaction.Ab initio molecular dynamics simulation
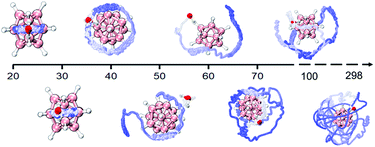
In addition, the DHB predominance is also seen from the analyses of bonding dynamics and molecular vibrations. An extensive ab initio molecular dynamics (AIMD) simulation on B12H122−·H2O (Fig. S2A,† left panel) shows an orderly oscillating pattern of the B–H⋯H–O DHB length with a 263 fs period, in which the lengths of two B–H⋯H–O DHBs are found to increase or decrease simultaneously. However, for the strong B–F⋯H–O HBs in B12F122−·H2O, a clear periodicity in the bond length change is not observed (Fig. S2A,† right panel). The two HBs are anti-correlated, i.e., an increase in one bond length accompanies a decrease in the other one. For a water molecule bound onto a borate cage, there are six vibrational modes to describe the bond length, angle, torsional and wagging motions (Fig. S3†). Based on the simulated vibrational spectra (Fig. S2B and Table S6†), the single water stretching vibrations (symmetric ν74 and asymmetric ν75, around 3700 cm−1) shift to lower frequencies with enhanced intensities upon forming HBs. Such red-shifts of −97 cm−1 for ν75 and −50 cm−1 for ν74 are predicted in B12H122−·H2O, which are more significant than those in B12F122−·H2O (−38 cm−1 and −12 cm−1) and B12I122−·H2O (−22 cm−1 and −8 cm−1). But the bending vibration mode of water around 1600 cm−1 seems to be insensitive to the complexation with B12X122−. Interestingly, in the low frequency region, two new mixed modes labelled ν4 (233 cm−1) and ν5 (253 cm−1) are also predicted in B12H122−·H2O, showing unusual vibrations involving combinations of planar swing and nonplanar torsion (Fig. S4†). The corresponding modes, however, do not exist in B12F122−·H2O or B12I122−·H2O, indicating that these modes are possibly related to the nuclear quantum effect49,50 involving two coupled light H atoms in B12H122−·H2O.In order to further reveal the water binding stability in B12H122−·H2O, temperature-dependent dynamics simulations are conducted (Fig. 4). At 20 K, the water molecule moves back and forth within a limited range restricted by two DHBs. As the temperature increases to 40 K, the water molecule seems to move freely on the spherical surface of B12H122−. As the temperature further increases, the water molecule possesses more freedom. Interestingly, even at temperatures up to 298.15 K, the water molecule can still make irregular movements around the B12H122− cage without completely detaching, in accord with the remaining strong DHB strength.
Conclusions
In summary, a series of hydrated closo-dodecaborate dianions B12X122−·H2O (X = H, F, I) have been investigated by combining experimental NIPE spectroscopy (NIPES) and multiscale theoretical simulation. A consistent conclusion can be drawn that the B–H⋯H–O DHB shows its strength superiority over conventional B–F(I)⋯H–O HBs. The differences of water binding energy determined by NIPES measurements agree well with the theoretical predictions. The strength advantage of B–H⋯H–O DHBs over strong B–F⋯H–O HBs mainly arises from the greater contribution of dispersion and induction terms, although the electrostatic interaction still plays a dominant role when compared with relatively weak B–I⋯H–O HBs. This work, for the first time, quantifies the strength of DHBs, and unequivocally proves the superiority of DHBs over the traditional strong HBs. It is conceivable that DHBs in hydrated metal-hydrides may become even stronger due to more prominent negative charges located on hydrogen ligands, a fact that certainly deserves to be explored more in the future for catalytic reactions and dihydrogen production. Perspectives on implications derived from the superiority of DHBs and how the predominance of DHBs governs the water cluster growth are warranted to better explore aqueous borate chemistry, as anion solvation often plays a key role in understanding the related chemical reactivity and solvation dynamics.51 Therefore, these outstanding molecular properties of DHBs, unravelled in this work, can promote more applications in catalysis, chemical transformations, and selectivity, and have potential to promise new synthetic routes towards rational assembly of novel extended covalent materials and structural coding of water clusters based on the unique dihydrogen interaction.Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.Author contributions
H. S., Z. R. S., and X. B. W. designed the research; Y. J., Q. Y., W. C., Z. H., Y. Y., C. Z., T. Y. and H. S. conducted the research; Y. J., H. S., Z. R. S. and X. B. W. analyzed the data; Y. J., H. S., Z. R. S., and X. B. W. wrote the paper. All the authors contributed to the discussions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work was supported by the National Natural Science Foundation of China (No. 11727810, 12034008 and 51873160), the Shanghai Rising-Star Program (No. 21QA1402600) and the Program of Introducing Talents of Discipline to Universities 111 Project (B12024). The NIPES work was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences, and Biosciences, and performed using EMSL, a national scientific user facility sponsored by DOE's Office of Biological and Environmental Research and located at Pacific Northwest National Laboratory, which is operated by Battelle Memorial Institute for the DOE. We acknowledge the ECNU Multifunctional Platform for Innovation (001) and HPC Research Computing Team for providing computational and storage resources and the support of the NYU-ECNU Center for Computational Chemistry at NYU Shanghai.References
- K. Liu, J. D. Cruzan and R. J. Saykally, Science, 1996, 271, 929–933 CrossRef CAS.
- N. Yang, C. H. Duong and P. J. Kelleher, et al. , Nat. Chem., 2020, 12, 159–164 CrossRef CAS PubMed.
- N. Yang, H. Duong Chinh and J. Kelleher Patrick, et al. , Science, 2019, 364, 275–278 CrossRef CAS PubMed.
- A. Shokri, J. Schmidt and X.-B. Wang, et al. , J. Am. Chem. Soc., 2012, 134, 2094–2099 CrossRef CAS PubMed.
- L. Pauling, The Nature of the Chemical Bond, Cornell University Press, Ithaca, 1960 Search PubMed.
- R. Custelcean and J. E. Jackson, Chem. Rev., 2001, 101, 1963–1980 CrossRef CAS PubMed.
- M. P. Brown and R. W. Heseltine, Chem. Commun., 1968, 1551–1552 RSC.
- T. Richardson, S. de Gala and R. H. Crabtree, et al. , J. Am. Chem. Soc., 1995, 117, 12875–12876 CrossRef CAS.
- R. H. Crabtree, Science, 1998, 282, 2000–2001 CrossRef CAS.
- J. Echeverría, G. Aullón and D. Danovich, et al. , Nat. Chem., 2011, 3, 323–330 CrossRef PubMed.
- R. H. Crabtree, Chem. Rev., 2016, 116, 8750–8769 CrossRef CAS PubMed.
- J. G. Planas, C. Viñas and F. Teixidor, et al. , J. Am. Chem. Soc., 2005, 127, 15976–15982 CrossRef CAS PubMed.
- J. Fanfrlík, M. Lepšík and D. Horinek, et al. , ChemPhysChem, 2006, 7, 1100–1105 CrossRef PubMed.
- X. Chen, J.-C. Zhao and S. G. Shore, Acc. Chem. Res., 2013, 46, 2666–2675 CrossRef CAS PubMed.
- K. Verma and K. S. Viswanathan, Phys. Chem. Chem. Phys., 2017, 19, 19067–19074 RSC.
- Y. Xiao, J. T. Mague and R. A. Pascal Jr, Angew. Chem., Int. Ed., 2018, 57, 2244–2247 CrossRef CAS PubMed.
- P.-F. Cui, Y.-J. Lin and Z.-H. Li, et al. , J. Am. Chem. Soc., 2020, 142, 8532–8538 CrossRef CAS PubMed.
- T. K. A. Hoang and D. M. Antonelli, Adv. Mater., 2009, 21, 1787–1800 CrossRef CAS.
- M. Pang, J.-Y. Chen and S. Zhang, et al. , Nat. Commun., 2020, 11, 1249–1257 CrossRef CAS PubMed.
- A. Rossin, A. Rossi and M. Peruzzini, et al. , ChemPlusChem, 2014, 79, 1316–1325 CrossRef CAS.
- Q. Zhao, R. D. Dewhurst and H. Braunschweig, et al. , Angew. Chem., Int. Ed., 2019, 58, 3268–3278 CrossRef CAS PubMed.
- K. I. Assaf, M. S. Ural and F. Pan, et al. , Angew. Chem., Int. Ed., 2015, 54, 6852–6856 CrossRef CAS PubMed.
- M. Kožíšek, P. Cígler and M. Lepšík, et al. , J. Med. Chem., 2008, 51, 4839–4843 CrossRef PubMed.
- F. A. Jalon, A. Otero and B. R. Manzano, et al. , J. Am. Chem. Soc., 1995, 117, 10123–10124 CrossRef CAS.
- P. A. Maltby, M. Schlaf and M. Steinbeck, et al. , J. Am. Chem. Soc., 1996, 118, 5396–5407 CrossRef CAS.
- R. H. Morris, Coord. Chem. Rev., 2008, 252, 2381–2394 CrossRef CAS.
- R. Bau and M. H. Drabnis, Inorg. Chim. Acta, 1997, 259, 27–50 CrossRef CAS.
- C. Gunanathan, S. C. Capelli and U. Englert, et al. , Eur. J. Inorg. Chem., 2013, 2013, 5075–5080 CrossRef CAS.
- C. Prestipino, L. Regli and J. G. Vitillo, et al. , Chem. Mater., 2006, 18, 1337–1346 CrossRef CAS.
- V. Dryza, B. L. J. Poad and E. J. Bieske, Phys. Chem. Chem. Phys., 2012, 14, 14954–14965 RSC.
- G. Naresh Patwari, T. Ebata and N. Mikami, J. Chem. Phys., 2000, 113, 9885–9888 CrossRef CAS.
- G. N. Patwari, A. Fujii and N. Mikami, J. Chem. Phys., 2006, 124, 241103–241106 CrossRef PubMed.
- F. Maseras, A. Lledós and E. Clot, et al. , Chem. Rev., 2000, 100, 601–636 CrossRef CAS PubMed.
- T. Kar and S. Scheiner, J. Chem. Phys., 2003, 119, 1473–1482 CrossRef CAS.
- R. H. Crabtree, P. E. M. Siegbahn and O. Eisenstein, et al. , Acc. Chem. Res., 1996, 29, 348–354 CrossRef CAS PubMed.
- J. Warneke, G.-L. Hou and E. Aprà, et al. , J. Am. Chem. Soc., 2017, 139, 14749–14756 CrossRef CAS PubMed.
- R. T. Boeré, J. Derendorf and C. Jenne, et al. , Chem.–Eur. J., 2014, 20, 4447–4459 CrossRef PubMed.
- Y. Jiang, Q. Yuan and W. Cao, et al. , Phys. Chem. Chem. Phys., 2021, 23, 13447–13457 RSC.
- A. H. Soloway, W. Tjarks and B. A. Barnum, et al. , Chem. Rev., 1998, 98, 1515–1562 CrossRef CAS PubMed.
- B. Dereka, Q. Yu and H. C. Lewis Nicholas, et al. , Science, 2021, 371, 160–164 CrossRef CAS PubMed.
- R. H. Crabtree, Hydrogen Bonding & Dihydrogen Bonding, John Wiley & Sons, New York, 2005 Search PubMed.
- X.-B. Wang and L.-S. Wang, Rev. Sci. Instrum., 2008, 79, 073108–073115 CrossRef PubMed.
- X.-B. Wang, J. Phys. Chem. A, 2017, 121, 1389–1401 CrossRef CAS PubMed.
- Z. Li, Y. Jiang and Q. Yuan, et al. , Phys. Chem. Chem. Phys., 2020, 22, 7193–7200 RSC.
- L. M. J. Huntington, A. Hansen and F. Neese, et al. , J. Chem. Phys., 2012, 136, 064101–064117 CrossRef PubMed.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed.
- S. Emamian, T. Lu and H. Kruse, et al. , J. Comput. Chem., 2019, 40, 2868–2881 CrossRef CAS PubMed.
- F. Fuster and B. Silvi, Theor. Chem. Acc., 2000, 104, 13–21 Search PubMed.
- M. Ceriotti, J. Cuny and M. Parrinello, et al. , Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 15591–15596 CrossRef CAS PubMed.
- X.-Z. Li, B. Walker and A. Michaelides, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6369–6373 CrossRef CAS.
- A. Lietard, G. Mensa-Bonsu and J. R. R. Verlet, Nat. Chem., 2021, 13, 737–742 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Experimental and computational details, and additional experimental data. See https://doi.org/10.1039/d2sc03986a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |