Entropy directs the self-assembly of supramolecular palladium coordination macrocycles and cages

Abstract

The self-assembly of palladium-based cages is frequently rationalized via the cumulative enthalpy (ΔH) of bonds between coordination nodes (M, i.e., Pd) and ligand (L) components. This focus on enthalpic rationale limits the complete understanding of the Gibbs free energy (ΔG) for self-assembly, as entropic (ΔS) contributions are overlooked. Here, we present a study of the M₂^linL₃ intermediate species (M = dinitrato(N,N,N′,N′-tetramethylethylenediamine)palladium(II), ^linL = 4,4′-bipyridine), formed during the synthesis of triangle-shaped (M₃^linL₃) and square-shaped (M₄^linL₄) coordination macrocycles. Thermochemical analyses by variable temperature (VT) ¹H-NMR revealed that the M₂^linL₃ intermediate exhibited an unfavorable (relative) ΔS compared to M₃^linL₃ (triangle, ΔTΔS = +5.22 kcal mol⁻¹) or M₄^linL₄ (square, ΔTΔS = +2.37 kcal mol⁻¹) macrocycles. Further analysis of these constructs with molecular dynamics (MD) identified that the self-assembly process is driven by ΔG losses facilitated by increases in solvation entropy (ΔS_solv, i.e., depletion of solvent accessible surface area) that drives the self-assembly from “open” intermediates toward “closed” macrocyclic products. Expansion of our computational approach to the analysis of self-assembly in Pd_n^benL_2n cages (^benL = 4,4'-(5-ethoxy-1,3-phenylene)dipyridine), demonstrated that ΔS_solv contributions drive the self-assembly of both thermodynamic cage products (i.e., Pd₁₂^benL₂₄) and kinetically-trapped intermediates (i.e., Pd₈^cL₁₆).

---

Introduction

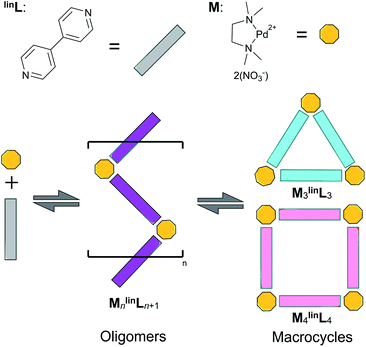
Self-assembled macrocycles,^1–7 cages,^8–13 and oligomers^14–16 featuring palladium-coordination nodes are a mainstay of supramolecular chemistry due to their unique mechanical,^14–18 optoelectronic,^19–28 and catalytic^29–42 applications. The square-planar coordination geometry of the coordination node permits the synthesis of well-defined constructs invoking simple geometric design principles.^43–48 These constructs are formed by the spontaneous self-assembly of palladium-based coordination nodes with ditopic ligands, affording highly-ordered assemblies bearing the minimum Gibbs free energy (ΔG).^43–50 The synthesis of these assemblies from their many constituent components is rationalized by the cumulative enthalpic (ΔH) contributions as a result of the formation of dative bonds between ditopic ligands and Pd-based coordination nodes.^49,50 However, studies of gas-phase reactivity reveal these ΔH contributions decrease with sequential coordination of additional ligands, favoring the formation of coordinatively unsaturated oligomers.⁵¹ In addition, currently only entropic contributions (ΔS) based on statistical arguments are taken into account, implying that assemblies based on a large number of components are entropically largely unfavorable despite many synthetic examples. Whereas similar enthalpic arguments rationalize the difference in energy between various assemblies, it remains unclear why well-defined structures are favored over oligomers as these coordination bonds in principle can be formed with limited constraints. The current rationale for deducing self-assembly thermodynamics is therefore incomplete, which motivates our current study.

The self-assembly of equimolar amounts of dinitrato(N,N,N′,N′-tetramethylethylenediamine)palladium(II) (M) and 4,4′-bipyridine (^linL) affords a mixture of triangular and square macrocycles in equilibrium (Scheme 1).^1,2

Scheme 1 Self-assembly of dinitrato(N,N,N′,N′-tetramethylethylenediamine) palladium(II) (M, yellow) and 4′4-bipyridine (^linL, grey) affording a mixture of triangular (M₃^linL₃, blue) and square (M₄^linL₄, pink) macrocycles alongside oligomer intermediates (M_n^linL_n+1, purple).

Previous reports have leveraged this experimentally accessible equilibrium to measure the relative ΔS and ΔH of triangular and square complexes.⁵ These studies found that ΔS favors the assembly featuring fewer components (i.e., triangles) while ΔH favors the geometric matching between the square-planar metal center and the ligand geometry (i.e., squares).^1,5 The synthesis of (and conversion between) macrocyclic assemblies proceeds via coordinatively unsaturated oligomeric intermediates (Scheme 1, purple).

Interestingly, similar stable oligomer intermediates have been found in the synthesis of polygonal organometallic macrocyclic assemblies.^1–5 The equilibrium between these stable oligomeric intermediates and macrocyclic products may be leveraged to quantify ΔH and ΔS contributions to self-assembly using the literature described NMR-based approach.⁵ Realization of the origin and effect of these thermodynamic contributions enables rational improvement of the self-assembly of highly-ordered constructs used broadly in supramolecular chemistry, including coordination cages, metal–organic frameworks, and dynamic-covalent based constructs.^52,59–62

In this report, we demonstrate that the self-assembly of an equimolar mixture of M and ^linL in deuterated dimethyl sulfoxide (DMSO) affords a mixture of triangular (M₃^linL₃) and square (M₄^linL₄), and oligomeric (M_n^linL_n+1) assemblies as depicted in Scheme 1.^1,6 We employed variable temperature ¹H-NMR (VT-NMR) to determine the ΔH and ΔS of both oligomeric and macrocyclic assemblies, providing unprecedented thermodynamic insights into the self-assembly process. Importantly, this thermodynamic data-enabled validation of a molecular dynamics (MD)⁵² based approach to distinguish respective ΔS contributions arising from the assembly structure (ΔS_struct, eqn S1†)⁵³ and its solvation (ΔS_solv, eqn S2†).⁵⁴ These individual entropic contributions, alongside calculation of ΔH (eqn S3†), ultimately provide an accurate ΔG for self-assembly. We applied our MD-based approach to the study of coordination cages based on 4,4'-(5-ethoxy-1,3-phenylene)dipyridine as a bent ditopic ligand (^benL) and free palladium(II) ions (Pd²⁺), which have been reported in the literature (Scheme 2).^8–13 Thermodynamic estimates derived from MD simulations reveal a ΔS_solv-driven, self-assembly process for macrocycles and cages reminiscent of biopolymer folding.⁵¹ The generalization of our MD-based approach may distinguish between kinetically accessible thermodynamic products (i.e., Pd₁₂^benL₂₄) and undesirable kinetically-trapped intermediate assemblies (e.g. Pd₈^benL₁₆).⁵⁵

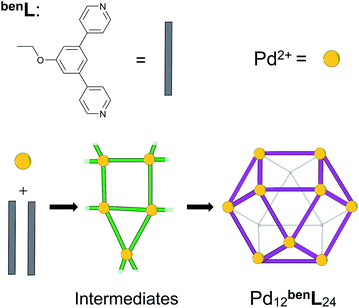Scheme 2 The self-assembly of Pd₁₂^benL₂₄ cages (^benL = 4,4′-(5-ethoxy-1,3-phenylene)dipyridine) via poorly defined reticular intermediates (green).

These computational and experimental studies demonstrate that ΔS drives the self-assembly of supramolecular constructs featuring palladium coordination nodes. As this ΔS contribution arises from solvation, these findings broadly reflect the thermodynamic drive of self-assembly to form compact supramolecular structures. Furthermore, we demonstrate the utility of MD-based approaches to quantify the thermodynamics of large supramolecular systems, providing a methodology that enables in silico studies of self-assembly processes.

Results

Synthesis and characterization of assemblies based on M and linL

Previously, we reported that the absence of trace halide impurities during the self-assembly of coordination cages resulted in slower formation kinetics, giving rise to the observation of intermediates.⁴⁹ Thus, we developed an alternative preparation for M, using a limiting quantity of palladium dichloride to minimize trace chloride (Scheme S1†). With this prepared metal precursor, the self-assembly of stoichiometric quantities of M and ^linL (M : ^linL = 1.0 : 1.0, [M] = 17.1 mM) affords a mixture of macrocyclic (M₃^linL₃ and M₄^linL₄) and oligomeric products evidenced by characteristic ¹H–NMR peaks shown in Fig. 1.

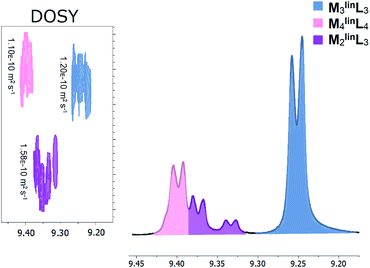Fig. 1 Macrocyclic and oligomeric products observed from the self-assembly of M (17.1 mM) and ^linL (17.1 mM) in DMSO characterized by unique α-pyridyl peaks in ¹H-NMR (Fig. S1†), with inset DOSY (Fig. S2†) diffusograms. Three distinct assemblies were observed and highlighted for clarity: M₃^linL₃ (slate blue), M₄^linL₄ (pink), and M₂^linL₃ (purple). Numerical data is provided below in Table 1.

Peaks corresponding to M₃^linL₃ (δ = 9.24 ppm) and M₄^linL₄ (δ = 9.40 ppm) were consistent with the reported values of these macrocyclic species.³ Two additional peaks (δ = 9.32–9.37 ppm) present, with chemical shifts consistent with reported oligomers,^1,2 and a single diffusion constant (D = 1.56 × 10⁻¹⁰ m² s⁻¹, Fig. 1 inset). These features indicate the presence of a single coordination assembly with a size larger than free ^linL (D = 1.86 × 10⁻¹⁰ m² s⁻¹) but smaller than M₃^linL₃ (D = 1.20 × 10⁻¹⁰ m² s⁻¹). We also observed a near 2 : 1 ratio of α-pyridyl peak areas (Table 1), assuming the overlap of α-pyridyl protons adjacent to coordination, we assigned these peaks to an oligomer species with the composition M₂^linL₃.

Table 1 ¹H-NMR characterization of assemblies based on M and ^linL^a

Assembly	δ α-pyridyl (ppm)	δ β-pyridyl (ppm)	% Area (α-pyridyl)	Diffusion, D (× 10^−10 m^2 s^−1)
a ^1H-NMR Conditions: DMSO, 300 K, 300 MHz. b Outer ligands, i.e., ^linL-M-^linL-M-^linL. c Internal ligand, i.e., ^linL-M-^linL-M-^linL. d Reference values were obtained separately for free ^linL (Fig. S3).
M 3 ^linL 3	9.24	8.28	63.9	1.20
M 4 ^linL 4	9.40	8.21	21.2	1.10
M 2 ^linL 3	9.37	8.24	9.9	1.58
M 2 ^linL 3	9.32	8.19	5.0	1.58
^linL	8.75	7.86	—	1.86

---

While previous studies rationalized that the self-assembly process is driven to maximize the number of coordination bonds formed, affording coordinatively saturated species that minimize the ΔH of the system.¹ However, analysis by Weilandt et al. on mononuclear Pd complexes demonstrated that the formation of successive coordination bonds result in diminishing ΔH contributions to the ΔG of complex formation, which was partially compensated by ΔS.⁵⁶ Our observation of a significant presence of oligomeric (coordinatively unsaturated) assemblies (14.9%, Table 1), we infer that ΔS may play a similarly significant role in macrocycle assembly.

Thermochemical analysis of macrocycle–oligomer equilibria

Following the literature, we employed VT-NMR to quantify the relative abundance of assemblies (M₂^linL₃, M₃^linL₃, and M₄^linL₄) by monitoring the intensity of their unique α-pyridyl peaks (Table 1) over a wide range of temperatures (297.5–350.0 K, see Fig. S12–S16†).⁵ To determine the relative ΔG of M₂^linL₃, M₃^linL₃, and M₄^linL₄ we modeled the system as three orthogonal equilibria between each product and a common pool of reactants (Scheme S2†). These relative ΔG values (Table S1†) were plotted as a function of temperature (Fig. 2), and directly fit with an expanded van ‘t Hoff equation to compute ΔS and ΔH (Scheme S2†).⁵⁸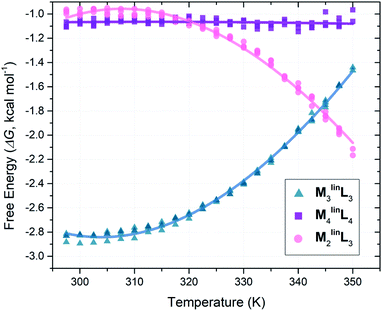

Fig. 2 Plot of ΔG versus temperature plot from VT-NMR measurements (¹H = 300 MHz, DMSO, T_r = 30 s) from quadruplicate temperature sweeps. Free energy values (ΔG) were computed from peak areas (Table 1) with a simplified reaction model (Scheme S2†).

Consistent with literature observations, these experimentally established ΔS and ΔH values confirm that M₃^linL₃ and M₄^linL₄ are the respective ΔS- and ΔH-favored macrocyclic products.⁵ Interestingly, M₂^linL₃ features a lower ΔH than the ΔH-favored M₄^linL₄ (Table 2, ΔΔH = −2.27 kcal mol⁻¹) and an elevated −TΔS compared to the ΔS-favored M₃^linL₃ (Table 2, ΔTΔS = +5.22 kcal mol⁻¹). These results are contrary to established geometric and component-number based rationale for ΔH- and ΔS-favored products.^1,4,5

Table 2 Experimental thermodynamic differences between M₂^linL_3,M₃^linL_3, and M₄^linL₄ coordination assemblies

Assembly	Relative thermodynamic parameters (kcal mol^−1)^a
	ΔH°	−TΔS°	ΔG°
a Values determined for T = 298.15 K by direct fitting a modified van ‘t Hoff model (Scheme S2) to VT-NMR derived ΔG values (Fig. 2).^58
M 3 ^linL 3	0.00 ± 0.20	−2.80 ± 0.19	−2.80 ± 0.02
M 4 ^linL 4	−1.11 ± 0.29	+0.05 ± 0.28	−1.06 ± 0.03
M 2 ^linL 3	−3.38 ± 0.34	+2.42 ± 0.32	−0.96 ± 0.31

---

We surmise that the ΔH of M₂^linL₃ derives from the conformational freedom of the structure, allowing the adoption of an unstrained configuration (∠N–Pd–N = 90°) following the geometric rationale established for M₄^linL₄. However, M₄^linL₄ exhibits an internal strain relative to M₂^linL₃ manifesting as the ΔH-difference between the two complexes (ΔΔH = −2.27 kcal mol⁻¹). As both assemblies are presumed to adopt a conformation where ∠N–Pd–N = 90°, the apparent ΔΔH is not accounted for when a simple geometric rationale is invoked.¹ Moreover, ΔS-differences between the 6-component M₃^linL₃ and 5-component M_2L3 contrast the typical rationale, which correlates the integration of fewer components to a favorable ΔS. These findings highlight how the current rationale for determining ΔS and ΔH contributions is insufficient to account for oligomeric assemblies, necessitating further computational investigation into the origins of internal strain found in M₄^linL₄ and the unexpected ΔS penalties associated with M₂^linL₃ formation.

MD analysis of experimental assemblies

Weilandt et al. suggested that two discrete ΔS factors that exert significant influence on metal–organic complex formation. The first is ΔS_struct, which decreases as more molecules (i.e., components) are required to form a complex.⁵ The other is ΔS_solv, which decreases as more solvent molecules are required to solvate a complex.⁵⁶ Using a previously described methodology,⁵² we developed parameters to simulate assemblies comprised of M and ^linL with accurate ΔH contributions (Fig. S4†). Using these parameters, and GBSA model solvation,⁵⁴ 50 ns trajectories (Fig. S5–S7†) were propagated by MD for M₂^linL₃, M₃^linL₃, and M₄^linL₄ assemblies (Fig. 3). These trajectories were then used to compute the ΔS_struct,⁵³ ΔS_solv,⁵⁴ and ΔH contributions to ΔG (Table 3).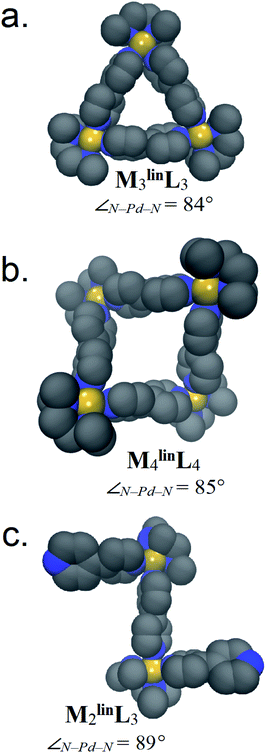

Fig. 3 Representative structures of (a) M₃^linL₃, (b) M₄^linL₄, and (c) M₂^linL₃ are rendered with van der Waals representations of the non-hydrogen atoms. Relative thermodynamic contributions to ΔG are listed below in Table 3. Adjacent to each model is the average ∠N–Pd–N observed during MD.

Table 3 Thermodynamic values of assemblies based on M and ^linL computed from MD trajectories

Assembly	Relative thermodynamic parameters (kcal mol^−1)
	ΔH°	−TΔSstruct°	−TΔSsolv°	ΔG°
M 3 ^linL 3	+0.16	+4.15	−12.24	−7.93
M 4 ^linL 4	−0.32	+6.15	−12.16	−6.33
M 2 ^linL 3	−2.52	+1.30	−4.95	−6.17

---

The thermodynamic contributions to ΔH and ΔS computed from these simulations (Table 3) differ those obtained by VT-NMR (Table 2) in their absolute value. However, the differences (i.e., ΔΔG, ΔΔH, or ΔTΔS) between assemblies measured by simulation and experiment are very similar (see below). The differences in absolute value reflect the different reference states in experimental and computational measurements (Fig. S20†). The reproduction of the relative differences in these physical quantities validates our in silico methodology for the thermodynamic values of these and similar assemblies.

The ΔH difference between M₂^linL₃ and M₄^linL₄ measured by VT-NMR (ΔΔH_exp = +2.28 kcal mol⁻¹, Table 2), is similar to our MD-derived results (ΔΔH_MD = +2.20 kcal mol⁻¹, Table 2). As ΔH generally originates from molecular geometry, we infer that the M₄^linL₄ adopts a geometrically unfavorable (i.e., strained) configuration compared to M₂^linL₃. Visualization of MD trajectory data for M₂^linL₃ assemblies reveals that this oligomer prefers a zig-zag conformation with a near-ideal square-planar coordination geometry at the Pd center (∠N–Pd–N = 89°, Fig. 3c). In contrast, visualization of M₄^linL₄ reveals a folded-square structure that features a hyperbolic geometry (i.e., ∠N–Pd–N = 86°, Fig. 3b) giving rise to an internal strain that is enthalpically unfavorable (i.e., elevates ΔH). Additional simulations of M₄^linL₄ (performed in vacuo) reinforce that these distortions are a consequence of the solvation incurred to minimize the solvent-accessible surface area (Fig. S8†).

The TΔS difference between M₄^linL₄ and M₂^linL₃ measured by VT-NMR (ΔTΔS_exp = +2.36 kcal mol⁻¹, Table 2), is similar to our MD-derived results (ΔTΔS_MD = +2.37 kcal mol⁻¹, Table 2), while other comparisons values have acceptable deviation (Fig. S20†). The calculated −TΔS_struct values from our MD-approach decrease with the number of components (i.e., M₂^linL₃ < M₃^linL₃ < M₄^linL₄), in line with reported trends.^1,5 While, the computed difference of ΔS_struct for M₃^linL₃ and M₄^linL₄ are similar to experimental values (Table 2), differences between both macrocycles vs.M₂^linL₃ deviate significantly (Table 3). The inclusion of −TΔS_solv improves the accounting for ΔS differences between M₂^linL₃, M₃^linL₃, and M₄^linL₄ assemblies (Table 3). This leads us to infer that experimental −TΔS penalties associated with M₂^linL₃ formation originate from these ΔS_solv contributions, in agreement with thermodynamic studies of mono-nuclear Pd complexes.⁵⁶

These thermodynamic parameters demonstrate that ΔS-specifically ΔS_solv-drives the conversion of oligomeric intermediates (i.e., M₂^linL₃) to their macrocyclic product assemblies (i.e., M₃^linL₃ and M₄^linL₄). Moreover, the effect of ΔS_solv may overcome ΔH contributions, resulting in strained and distorted molecular geometries. While chemists have previously exploited ΔH to direct the formation of desired constructs, these findings reveal that ΔS ultimately drives the synthetic process of multi-component self-assembly.

MD modeling of arbitrary M_nLn and M_nLn+1 assemblies

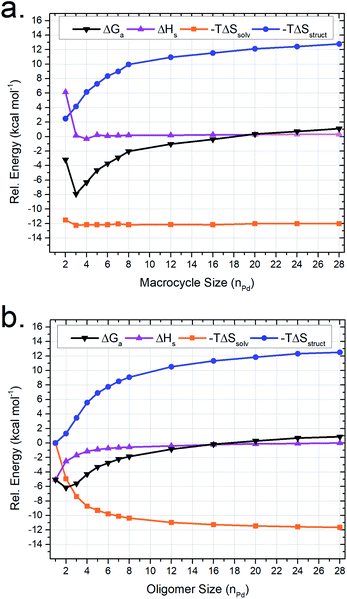
Oligomers similar to (and including) M₂^linL₃ are theorized to form as intermediates in the self-assembly process of larger supramolecular structures (Scheme 1). Therefore, we utilized our MD-based approach to compare a range of oligomeric intermediates (M_n^linL_n+1; n = 1–28) and the potential macrocyclic products (M_n^linL_n; n = 2–28) to elucidate the role of individual thermodynamic parameters (ΔS_solv, ΔS_struct, and ΔH) on ΔG for the self-assembly of macrocycles (Fig. 4).

Fig. 4 MD-calculated thermodynamic parameters for (a) M_n^linL_n macrocyclic and (b) M_n^linL_n+1 oligomeric assemblies. Energy values are plotted on a common scale where −TΔS_solv and −TΔS_struct contributions are plotted relative to M₁^linL₂ while ΔH is plotted relative to M₂₈^linL₂₉. The sum of −TΔS_solv, −TΔS_struct and ΔH values is plotted as ΔG.

The resulting simulations reveal that both macrocyclic (Fig. 4a) and oligomeric (Fig. 4b) assemblies exhibit increasingly unfavorable ΔG with increasing assembly size driven by ΔS_struct contributions. The limited range of assemblies observed by NMR measurements (i.e., M₂^linL₃, M₃^linL₃, and M₄^linL₄) is rationalized by the elevated ΔG experienced for other possible structures. This outcome is consistent with ESI-HRMS analysis (Fig. S9†) that provides qualitative evidence for the existence of larger assemblies in low abundance (i.e., low signal-to-noise).

The value of −TΔS_struct increases with size (Fig. 4, blue trace) for the self-assembly of both oligomeric and macrocyclic products, consistent with the decreased degrees-of-freedom experienced upon aggregation.⁵⁷ Intriguingly, we find a non-linear correlation between the size and ΔH of oligomeric assemblies that is absent for macrocyclic congeners. Visualization of MD trajectory data reveals that larger oligomer assemblies adopt a compact conformation (Fig. S10†), resulting in increased strain (i.e., ΔH penalty) on the palladium–pyridyl bonds compared to the zig-zag conformation found in smaller assemblies such as M₂^linL₃ (Fig. 3c). We infer that these compact suprastructures are necessary to realize a more compact assembly, akin to the folded structure observed for M₄^linL₄ macrocycles (Fig. 3b). This trade-off between −TΔS_solv and ΔH originates from solvation and distinguishes oligomeric assemblies from macrocyclic ones. As −TΔS_solv favors the formation of compact suprastructures, it is reasonable to deduce that the self-assembly of product macrocycles, in general, is driven by ΔS_solv contributions.

MD modeling of reticular cage self-assembly

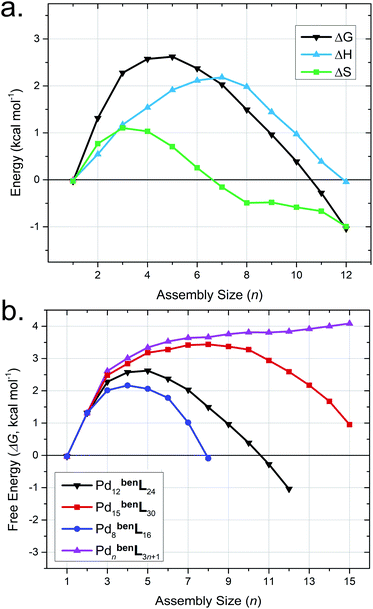
Mixtures of bent ditopic ligands (^benL = 4,4'-(5-ethoxy-1,3-phenylene)dipyridine) and free palladium(II) coordination nodes (Pd) self-assemble to afford cuboctahedral cages (Pd₁₂^benL₂₄) via oligomeric-assembly intermediates. We employed our MD-based approach to gain insight into the self-assembly process,⁵² as incomplete or partial cages (i.e., intermediate assemblies) are currently inaccessible by experimental methods (e.g., CSI-HRMS, ¹H-NMR).⁵¹ We developed models for intermediates of self-assembly (Pd_n^benL_m, where 2n ≤ m ≤ 3n + 1) from contiguous sections extracted from Pd₁₂^benL₂₄, Pd₈^benL₁₆, and Pd₁₅^benL₃₀ cages, as well as a polymeric state (Pd_n^benL_m, where m = 3n +1) geometries. Then we elucidated the self-assembly pathway for these partially-formed constructs from their respective ΔS, ΔH, and ΔG values from MD-simulation (Fig. 5).

Fig. 5 MD-calculated thermodynamic parameters for the Pd_n^benL_m reticular intermediates (2n ≤ m ≤ 3n) for the self-assembly of Pd₁₂^benL₂₄ cages (a), alongside a comparison of the ΔG for Pd_n^benL_m reticular intermediates (2n ≤ m ≤ 3n + 1) for the self-assembly of Pd₁₂^benL₂₄, Pd₁₅^benL₃₀, Pd₈^benL₁₆ cages and Pd_n^benL_3n+1 polymers (b). Computed thermodynamic parameters values are presented relative to the Pd₁^benL₄ complexes.

Our simulations reveal the Pd₁₂^benL₂₄ exhibits a lower ΔH (i.e., minimal geometric strain) compared to congeneric assemblies (Table 4). This observation is consistent with the literature and originates from the decreased metal–ligand bond strain experienced by this particular assembly-configuration.^8–13,49,52 Models of partially-formed assemblies (e.g., Pd₅^benL₁₄) bear an elevated ΔH (Fig. 5a, blue trace) as a result of strain originating from deflation or collapse during MD simulations (Fig. S11†). Parallel observations have been made in M₄^linL₄ macrocycles (Table 2), inferring increases in strain can act to offset penalties from solvation entropy (i.e., ΔS_solv), which leads to an overall elevation in ΔH for the system. The sum of entropic contributions (i.e., ΔS_struct + ΔS_solv = ΔS, Fig. 5a, green trace) suggests that the formation of early intermediates (n <7) is hindered while the self-assembly of spherical cages (n = 12) is encouraged. These results demonstrate that while ΔH directs the polyhedral geometry of the final assembly,^52,55 ΔS drives the structure of self-assembly to be spherical.

Table 4 MD-trajectory derived thermodynamic parameters of Pd_n^benL_2n cages and Pd_n^benL_3n+1 polymers

Assembly	Thermodynamic parameters (kcal mol^−1)^a
	ΔH°	−TΔSstruct°	−TΔSsolv°	ΔG°
a Thermodynamic values are relative to those computed for Pd1^benL4 assemblies. b Linear polymer assembly with the composition Pdn^benL3n+1.
Pd8^benL16	+1.20	+6.58	−7.88	−0.10
Pd12^benL24	−0.04	+6.90	−7.90	−1.04
Pd15^benL30	+1.70	+7.02	−7.77	+0.95
Pd15^benL46^b	+1.60	+5.89	−3.41	+4.08

---

The comparison of the free energy (ΔG) pathways for the self-assembly of different topologies (Fig. 5b) enables us to distinguish between the thermodynamic product (i.e., Pd₁₂^benL₂₄), kinetic traps (e.g., Pd₈^benL₁₆),⁵⁵ and unrealized topologies (e.g., Pd₁₅^benL₃₀, red trace). The maximum ΔG of intermediate assemblies of the Pd₁₅^benL₃₀ pathway (ΔG_max = +3.44 kcal mol⁻¹) is greater than that of the Pd₁₂^benL₂₄ cage (ΔG_max = +2.62 kcal mol⁻¹), rationalizing the possibility that intermediates may spontaneously reconfigure towards the latter structure as it is thermodynamically favored. In contrast, the Pd₈^benL₁₆ pathway features the lowest maximum energy (ΔG_max = +2.17 kcal mol⁻¹) of analyzed pathways demonstrating that kinetic traps are readily identified by our MD-based approach.

Conclusion

The thermochemical analysis of the self-assembly processes in palladium-based coordination macrocycles revealed unexpected ΔS-contributions that drive the formation of higher-order macrocycle assemblies (M₃^linL₃ and M₄^linL₄) from oligomer intermediates (M₂^linL₃). Using an MD-based approach, we found that the driving force for self-assembly originates from the solvation entropy (i.e., ΔS_solv) of oligomeric intermediates that effects surface-area minimization of the construct. Thermodynamic trends were established by MD analysis of larger assemblies, revealing that both ΔS_solv and ΔS_struct direct the formation of assemblies that exhibit similar ΔH. Data from MD models of formation pathways for palladium-based coordination cages reveal that ΔS_solv is responsible for driving the self-assembly process. Further application of our MD approach enables rationalization of the formation Pd₁₂^benL₂₄ cage products over kinetically trapped congeners (i.e., Pd₈^benL₁₆) directly from the computed thermodynamic quantities (ΔS_solv, ΔS_struct, and ΔH) of the intermediate assemblies. Overall, these complementary experimental and computational investigations expose ΔS as the driver for the formation of these desirable highly ordered structures that have broad applications across supramolecular chemistry.

Author contributions

DAP conceived, designed and performed the experiments. EOB contributed ligand materials, performed HR-MS analyses and provided experimental expertise for self-assembly experiments. JNHR and SM supervised the work. DAP, SM, and JNHR wrote the manuscript with all authors providing significant contributions to the analysis and interpretation of the work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank our colleagues Dr Bo Zhang, Catriona James, Dr Andreas Ehlers, and Dr Daan Geerke for their assistance and advice. We thank the European Research Council (ERC Adv. Grant 339786-5354 NAT_CAT) and the sustainable chemistry research program from the University of Amsterdam for financial support.

Notes and references

1. M. Fujita, J. Yazaki and J. Ogura, J. Am. Chem. Soc., 1990, 112(14), 5645–5647,  DOI:10.1021/ja00170a042.
2. M. Ferrer, A. Pedrosa, L. Rodríguez, O. Rossell and M. Vilaseca, Inorg. Chem., 2010, 49(20), 9438–9449,  DOI:10.1021/ic101150p.
3. K. Uehara, K. Kasai and N. Mizuno, Inorg. Chem., 2010, 49(4), 2008–2015,  DOI:10.1021/ic100011a.
4. P. J. Stang, D. H. Cao, S. Saito and A. M. Arif, J. Am. Chem. Soc., 1995, 117(23), 6273–6283,  DOI:10.1021/ja00128a015.
5. T. Weilandt, R. W. Troff, H. Saxell, K. Rissanen and C. A. Schalley, Inorg. Chem., 2008, 47(17), 7588–7598,  DOI:10.1021/ic800334k.
6. M. Fujita, O. Sasaki, T. Mitsuhashi, T. Fujita, J. Yazaki, K. Yamaguchi and K. Ogura, Chem. Commun., 1996, 13, 1535,  10.1039/cc9960001535.
7. M. Fujita, M. Tominaga, A. Hori and B. Therrien, Acc. Chem. Res., 2005, 38(4), 369–378,  DOI:10.1021/ar040153h.
8. K. Harris, D. Fujita and M. Fujita, Chem. Commun., 2013, 49(60), 6703,  10.1039/c3cc43191f.
9. S. R. Seidel and P. J. Stang, Acc. Chem. Res., 2002, 35(11), 972–983,  DOI:10.1021/ar010142d.
10. E. Raee, Y. Yang and T. Liu, Giant, 2021, 5, 100050,  DOI:10.1016/j.giant.2021.100050.
11. R. A. S. Vasdev, D. Preston and J. D. Crowley, Chem.–Asian J., 2017, 12(19), 2513–2523,  DOI:10.1002/asia.201700948.
12. T. K. Ronson, S. Zarra, S. P. Black and J. R. Nitschke, Chem. Commun., 2013, 49(25), 2476,  10.1039/c2cc36363a.
13. S. J. Dalgarno, N. P. Power and J. L. Atwood, Coord. Chem. Rev., 2008, 252(8–9), 825–841,  DOI:10.1016/j.ccr.2007.10.010.
14. E. C. Constable, K. Harris, C. E. Housecroft and M. Neuburger, Dalton Trans., 2011, 40(7), 1524,  10.1039/c0dt01216e.
15. D. Xu and S. L. Craig, Macromolecules, 2011, 44(18), 7478–7488,  DOI:10.1021/ma201386t.
16. D. Xu and S. L. Craig, J. Phys. Chem. Lett., 2010, 1(11), 1683–1686,  DOI:10.1021/jz1004818.
17. A. V. Zhukhovitskiy, M. Zhong, E. G. Keeler, V. K. Michaelis, J. E. P. Sun, M. J. A. Hore, D. J. Pochan, R. G. Griffin, A. P. Willard and J. A. Johnson, Nat. Chem., 2015, 8(1), 33–41,  DOI:10.1038/nchem.2390.
18. S. Krishnaswamy, S. Prusty, D. Chartrand, G. S. Hanan and D. K. Chand, Cryst. Growth Des., 2018, 18(4), 2016–2030,  DOI:10.1021/acs.cgd.7b01425.
19. P. J. Stang and D. H. Cao, J. Am. Chem. Soc., 1994, 116(11), 4981–4982,  DOI:10.1021/ja00090a051.
20. Q. Zhang, D. Tang, J. Zhang, R. Ni, L. Xu, T. He, X. Lin, X. Li, H. Qiu, S. Yin and P. J. Stang, J. Am. Chem. Soc., 2019, 141(44), 17909–17917,  DOI:10.1021/jacs.9b09671.
21. J.-H. Tang, Y. Li, Q. Wu, Z. Wang, S. Hou, K. Tang, Y. Sun, H. Wang, H. Wang, C. Lu, X. Wang, X. Li, D. Wang, J. Yao, C. J. Lambert, N. Tao, Y.-W. Zhong and P. J. Stang, Nat. Commun., 2019, 10(1), 4599,  DOI:10.1038/s41467-019-12534-6.
22. K. Acharyya, S. Bhattacharyya, H. Sepehrpour, S. Chakraborty, S. Lu, B. Shi, X. Li, P. S. Muckherjee and P. J. Stang, J. Am. Chem. Soc., 2019, 141(37), 14565–14569,  DOI:10.1021/jacs.9b08403.
23. H. Zhu, Q. Li, B. Shi, H. Xing, Y. Sun, S. Lu, L. Shangguan, X. Li, F. Huang and P. J. Stang, J. Am. Chem. Soc., 2020, 142(41), 17340–17345,  DOI:10.1021/jacs.0c09598.
24. W. Tuo, Y. Sun, S. Lu, X. Li, Y. Sun and P. J. Stang, J. Am. Chem. Soc., 2020, 142(40), 16930–16934,  DOI:10.1021/jacs.0c08697.
25. Z. Yang, Y. Wang, X. Liu, R. T. Vanderlinden, R. Ni, X. Li and P. J. Stang, J. Am. Chem. Soc., 2020, 142(32), 13689–13964,  DOI:10.1021/jacs.0c06666.
26. Y.-Q. He, W. Fudickar, J.-H. Tang, H. Wang, X. Li, J. Han, Z. Wang, M. Liu, Y.-W. Zhong, T. Linker and P. J. Stang, J. Am. Chem. Soc., 2020, 142(5), 2601–2608,  DOI:10.1021/jacs.9b12693.
27. C. Chen, Y. Sun, Y. Zhao, R. T. van der Linden, W. Tuo, F. Zhang, S. Zhang, H. Sepehrpour, C. Yan, J. Wang, D. Li and P. J. Stang, Proc. Natl. Acad. Sci. U. S. A., 2021, 118,  DOI:10.1073/pnas.2102602118.
28. R. Zaffaroni, E. O. Bobylev, R. Plessius, J. I. van der Vlugt and J. N. H. Reek, J. Am. Chem. Soc., 2020, 142(19), 8837–8847,  DOI:10.1021/jacs.0c01869.
29. Y. Ueda, H. Ito, D. Fujita and M. Fujita, J. Am. Chem. Soc., 2017, 139(17), 6090–6093,  DOI:10.1021/jacs.7b02745.
30. B. Chen, J. J. Holstein, S. Horiuchi, W. G. Hiller and G. H. Clever, J. Am. Chem. Soc., 2019, 141, 8907–8913,  DOI:10.1021/jacs.9b02207.
31. R. Zaffaroni, N. Orth, I. Ivanović-Burmazović and J. N. H. Reek, Angew. Chem., Int. Ed., 2020, 59(42), 18485–18489,  DOI:10.1002/anie.202008298.
32. S. Gonell, X. Caumes, N. Orth, I. Ivanović-Burmazović and J. N. H. Reek, Chem. Sci., 2019, 10, 1316–1321,  10.1039/c8sc03767a.
33. F. Yu, D. Poole, S. Mathew, N. Yan, J. Hessels, N. Orth, I. Ivanović-Burmazović and J. N. H. Reek, Angew. Chem., Int. Ed., 2018, 57(35), 11247–11251,  DOI:10.1002/anie.201805244.
34. R. Gramage-Doria, J. Hessels, S. H. A. M. Leenders, O. Tröppner, M. Dürr, I. Ivanović-Burmazović and J. N. H. Reek, Angew. Chem., Int. Ed., 2014, 53(49), 13380–13384,  DOI:10.1002/anie.201406415.
35. Q.-Q. Wang, S. Gonell, S. H. A. M. Leenders, M. Dürr, I. Ivanović-Burmazović and J. N. H. Reek, Nat. Chem., 2016, 8(3), 225–230,  DOI:10.1038/nchem.2425.
36. L. J. Jongkind, X. Caumes, A. P. T. Hartendorp and J. N. H. Reek, Acc. Chem. Res., 2018, 51(9), 2115–2128,  DOI:10.1021/acs.accounts.8b00345.
37. M. Yoshizawa, J. K. Klosterman and M. Fujita, Angew. Chem., Int. Ed., 2009, 48(19), 3418–3438,  DOI:10.1002/anie.200805340.
38. H. Takezawa, K. Shitozawa and M. Fujita, Nat. Chem., 2020, 12, 574–578,  DOI:10.1038/s41557-020-0455-y.
39. M. Yoshizawa, Science, 2006, 312(5771), 251–254,  DOI:10.1126/science.1124985.
40. W. Wang, Y.-X. Wang and H.-B. Yang, Chem. Soc. Rev., 2016, 45(9), 2656–2693,  10.1039/c5cs00301f.
41. S. Hasegawa, S. L. Meichsner, J. J. Holstein, A. Baksi, M. Kasanmascheff and G. H. Clever, J. Am. Chem. Soc., 2021, 143(26), 9718–9723,  DOI:10.1021/jacs.1c02860.
42. S. Bivaud, S. Goeb, V. Croué, M. Allain, F. Pop and M. Sallé, Beilstein J. Org. Chem., 2015, 11, 966–971,  DOI:10.3762/bjoc.11.108.
43. T. R. Cook, Y.-R. Zheng and P. J. Stang, Chem. Rev., 2012, 113(1), 734–777,  DOI:10.1021/cr3002824.
44. R. Chakrabarty, P. S. Mukherjee and P. J. Stang, Chem. Rev., 2011, 111(11), 6810–6918,  DOI:10.1021/cr200077m.
45. D. Fujita, Y. Ueda, S. Sato, H. Yokoyama, N. Mizuno, T. Kumasaka and M. Fujita, Chem, 2016, 1(1), 91–101,  DOI:10.1016/j.chempr.2016.06.007.
46. C. Liu, E. O. Bobylev, Y. Fu, D. A. Poole, K. Robeyns, C. Fustin, Y. Garcia, J. N. H. Reek and M. L. Singleton, Chem. - Eur. J., 2020, 26(52), 11960–11965,  DOI:10.1002/chem.202001399.
47. M. Fujita, Chem. Soc. Rev., 1998, 27(6), 417,  10.1039/a827417z.
48. A. Tarzia, J. E. M. Lewis and K. E. Jelfs, Angew. Chem., Int. Ed., 2021, 60(38), 20879–20887,  DOI:10.1002/anie.202106721.
49. E. O. Bobylev, D. A. Poole III, B. de Bruin and J. N. H. Reek, Chem. Sci., 2021, 12(22), 7696–7705,  10.1039/d1sc01295a.
50. S. Pullen, J. Tessarolo and G. H. Clever, Chem. Sci., 2021, 12(21), 7269–7293,  10.1039/d1sc01226f.
51. S. Hiraoka, Bull. Chem. Soc. Jpn., 2018, 91(6), 957–978,  DOI:10.1246/bcsj.20180008.
52. D. A. Poole III., E. O. Bobylev, S. Mathew and J. N. H. Reek, Chem. Sci., 2020, 11, 12350–12357,  10.1039/D0SC03992F.
53. R. M. Levy, M. Karplus, J. Kushick and D. Perahia, Macromolecules, 1984, 17(7), 1370–1374,  DOI:10.1021/ma00137a013.
54. R. B. Hermann, J. Phys. Chem., 1972, 76(19), 2754–2759,  DOI:10.1021/j100663a023.
55. D. Fujita, H. Yokoyama, Y. Ueda, S. Sato and M. Fujita, Angew. Chem., Int. Ed., 2014, 54(1), 155–158,  DOI:10.1002/anie.201409216.
56. T. Weilandt, N. L. Löw, G. Schnakenburg, J. Daniels, M. Nieger, C. A. Schalley and A. Lützen, Chem. - Eur. J., 2012, 18(52), 16665–16676,  DOI:10.1002/chem.201202771.
57. D. A. McQuarrie, Statistical Thermodynamics, 1st edn, Harper and Row, 1973.
58. C. G. Maier and K. K. Kelly, J. Am. Chem. Soc., 1932, 54(8), 3243–3246,  DOI:10.1021/ja01347a029.
59. P. Skowronek, B. Warżajtis, U. Rychlewska and J. Gawrońskia, Chem. Commun., 2013, 49, 2524–2526,  10.1039/C3CC39098E.
60. A. J. Greenlee, C. I. Wendell, M. M. Cencer, S. D. Laffoon and J. S. Moore, Trends Chem., 2020, 2(12), 1043–1051,  DOI:10.1016/j.trechm.2020.09.005.
61. A. Bennett, A. F. Cheetham and F.-X. Coudert, Nat. Chem., 2017, 9, 11–16,  DOI:10.1038/nchem.2691.
62. S. Jansze and K. Severin, J. Am. Chem. Soc., 2019, 141(2), 815–819,  DOI:10.1021/jacs.8b12738.

---

Footnote

† Electronic supplementary information (ESI) available: NMR Spectra, calculation details, molecular dynamics parameterization. See https://doi.org/10.1039/d2sc03154j

---