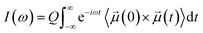Quantum mechanical effects in acid–base chemistry

Abstract

Acid–base chemistry has immense importance for explaining and predicting the chemical products formed by an acid and a base when mixed together. However, the traditional chemistry theories used to describe acid–base reactions do not take into account the effect arising from the quantum mechanical nature of the acidic hydrogen shuttling potential and its dependence on the acid base distance. Here, infrared and NMR spectroscopies, in combination with first principles simulations, are performed to demonstrate that quantum mechanical effects, including electronic and nuclear quantum effects, play an essential role in defining the acid–base chemistry when 1-methylimidazole and acetic acid are mixed together. In particular, it is observed that the acid and the base interact to form a complex containing a strong hydrogen bond, in which the acidic hydrogen atom is neither close to the acid nor to the base, but delocalized between them. In addition, the delocalization of the acidic hydrogen atom in the complex leads to characteristic IR and NMR signatures. The presence of a hydrogen delocalized state in this simple system challenges the conventional knowledge of acid–base chemistry and opens up new avenues for designing materials in which specific properties produced by the hydrogen delocalized state can be harvested.

---

Introduction

The Brønsted–Lowry theory, proposed in 1923, establishes that an acid and a base react by exchanging a proton to form their conjugated base and acid.^1,2 This theory has been widely used in science to predict and explain the chemistry when mixing an acid and a base. The acid–base reaction is typically represented by the following chemical equation,

HA + B ⇄ A⁻ + HB⁺ (1)

where HA and B are the acid and base, respectively, and A⁻ and HB⁺ their conjugated forms. The double arrow in eqn (1) denotes the presence of chemical equilibrium between the species, which is strictly defined by the thermodynamics of the reaction.^3,4 Hence, according to the Brønsted–Lowry acid–base theory, a solution containing an acid and a base can only exist as a mixture of the four components, where the ratio between the reactants and products is defined by the equilibrium constant. It is possible to argue that the Brønsted–Lowry theory should only be used in the context of aqueous solutions and the difference in the acidity constants of HA and HB⁺, defined as ΔpK_a = pK_a(HB⁺) − pK_a(HA), directly represents the equilibrium or equivalently the propensity of the reaction to shift in either direction. Instead, for binary mixtures of non-aqueous solvents the reaction should be expressed in terms of the autoprotolysis of the components,

A⁻ + HB⁺ ⇄ HA + B (2)

where HA and B are the conjugate acid and base of the ionic species, respectively. In this case, the equilibrium constant is expressed as K_S = [HA][B] (see ref. 5) because the K_S values can be directly determined from potentiometric studies without requiring the pK_as of the components in the different solvents.⁶ As the ΔpK_a in aqueous solutions, the pK_S (or equivalently K_S) describes the propensity of the binary mixture to being ionized. Hence, a system with a large positive (negative) value of pK_S will have very low (high) concentration of the neutral species.

The pK_S formalism has been used to predict the ionic conductivity of many molecular liquids and solutions, but it fails to explain cases such as the mixture of acetic acid and 1-methylimidazole.⁷ In aqueous solutions, acetic acid is a weak acid with a pK_a of 4.75,⁸ and 1-methylimidazole is a weak base with a pK_b of 6.99,⁸ and their mixture reacts spontaneously. However, without the aqueous environment, an equimolar binary mixture of acetic acid and 1-methylimidazole does not present appreciable amounts of either imidazolium or acetate ions,⁷ in agreement with its negative pK_S.⁶ The lack of ionic species in these mixtures indicates the absence of proton transfer, or equivalent, the ionization of the neutral species (left direction in eqn (2)). However, the acetic acid and 1-methyl imidazole mixtures have high ionic conductivities comparable to strong acids, and they have been referred to as pseudo-protic ionic liquids because of the lack of ionization.^7,9 Note that this behaviour is not limited to the selected acid–base pair and has been observed in other binary mixtures.¹⁰

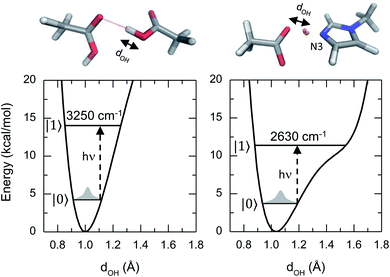
This article reports a previously uncharacterized chemical species formed between acetic acid and 1-methylimidazole that can serve as a molecular framework for explaining the fascinating physico-chemical behaviour of similar acid–base mixtures. Here the hydroxyl group of the acetic acid directly interacts with the unsubstituted nitrogen atom of the imidazole ring, forming an acid–base hydrogen bonded complex (top right panel of Fig. 1). Notably, the hydrogen bond in this acid–base pair has a significantly reduced distance between the O and N atoms, and leads to a different potential energy surface in which the acidic hydrogen atom participating of the hydrogen bond is more delocalized (Fig. 1). This quantum mechanical phenomenon is similar to the effect of reducing the length for a quantum particle confined in a 1D square potential (i.e., particle in the box).

Fig. 1 Geometries and potential energy surfaces along the O–H stretch coordinate of an acetic acid dimer (left) and an acid–base complex (right) from ab initio computations in gas phase. In the top panels, silver, red, blue and white represent C, O, N and H atoms, respectively. The dotted line shows a conventional hydrogen bond, and the orange spheres represent the ring polymer beads of the delocalized proton. In the bottom panels, |0> and |1> represent the ground and first vibrational excited states of the system, respectively.

Hydrogen atom delocalization has often been observed in short and strong hydrogen bonds in the active site of enzymes,^11–14 excess proton and conformationally rigid molecules in solutions,^15–19 but the hydrogen bond complex observed in this work is highly intriguing because the donor and acceptor are two different molecules in solutions where the dynamical structural fluctuations of the two molecules play a major role in determining the geometries and energetics of the complex. It also reveals that electronic and nuclear quantum effects help delocalize the proton conferring an additional stabilization energy to the acid–base complex.

Finally, the formation of a molecular species, rather than ionic species, with a delocalized hydrogen atom in a mixture of simple acids and bases challenges the traditional and current knowledge of acid–base chemistry, since in those theories the acidic hydrogen can only be localized either close to the acid or the base, but not shared in between the two participating moieties. In other words, the Brønsted–Lowry theory does not contemplate the possibility of a molecular species in which the hydrogen is shared between an acid and a base.

Results and discussion

The lack of a chemical reaction between acetic acid and 1-methylimidazole is readily seen in the IR spectra of the acid–base mixtures (Fig. 2a). Across the entire range of molecular ratios spanning X_HA of 0.1 to 0.67, the band corresponding to the asymmetric stretch of acetate, usually located at ∼1560 cm⁻¹,²⁰ is not observed (Fig. S1†). Instead, the addition of acetic acid to 1-methylimidazole leads to the appearance of at least one very broad band between 2200 cm⁻¹ and 3500 cm⁻¹ (blue and red zones in Fig. 2a). This broad band is very visible in the IR spectrum at low molar fractions of the acid (X_HA < 0.1) or the base (X_HA > 0.9, Fig. S2†), but is absent in the pure acid or base. The intensity of the new IR peak presents a significant temperature dependence (Fig. S3†), strongly suggesting that the broad band correspond to the complex and that the complex is directly related to acetic acid. This is because at higher temperature the amount of acid–base complex and its IR signature are reduced while the acetic acid and its corresponding band(s) are increased in agreement with the temperature dependence of a hydrogen bonded system.²¹ In line with the previous results and their interpretation, the new IR band (blue region in Fig. 1a) also shows linear dependence with the acid concentration (Fig. S2†). In addition, a substitution of the acidic hydrogen in acetic acid with deuterium results in a broad band at 1900 cm⁻¹ from the 2300 cm⁻¹ of the pure deuterated acid (Fig. S4†), showcasing the isotopic dependence of the transition frequency of the complex band, or equivalently, the large participation of the O–H stretch in this vibrational mode. Overall, the dependence of the IR features with temperature, acid concentration and the isotopic nature of acidic hydrogen is consistent with broad peak containing the vibrational signature of a one-to-one acid–base complex formed between the acetic acid and 1-methylimidazole (Fig. 1). It is possible to argue that this broad band is a mixed vibrational state involving the out of plane C–O–H bend and O–H stretch,^22–24 and does not come purely from the hydrogen bonded acid–base complex. However, the deuterated sample has broad band at much lower frequency, which suggest that this mode contains a large portion of the O–H stretch and the band is a characteristic IR feature of the complex.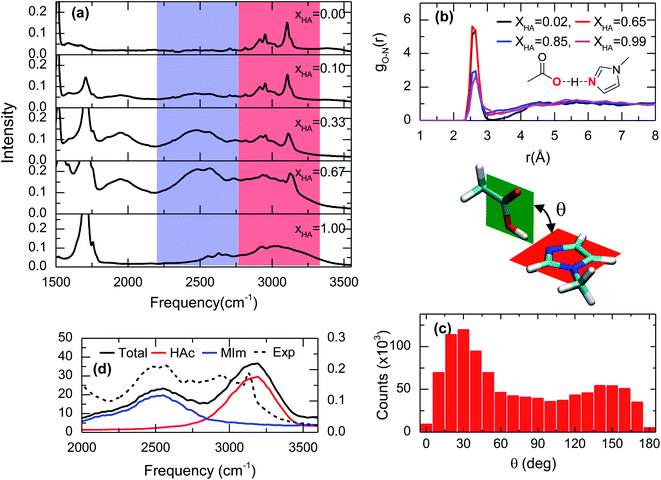

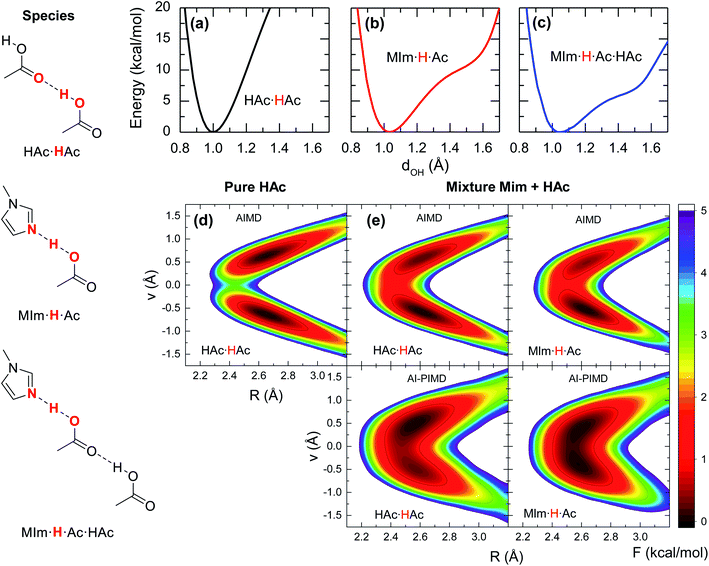
Fig. 2 Spectroscopic and theoretical features of the complex formed from acetic acid and 1-methylimidazole. (a) ATR-FTIR spectra of the mixture of acetic acid and 1-methylimidazole for different molar ratios of acetic acid (X_HA). Spectra with a more expanded axis can be found in the Fig. S1.† (b) Radial distribution functions between the oxygen atom of the hydroxyl group in acetic acid and the unsubstituted nitrogen atom of the imidazole ring (red highlighted atoms of the cartoon) from AIMD simulations at different concentrations. (c) Distribution of the rotation angles between the acid and the base from AIMD simulations. (d) IR spectrum in the 2000–3500 cm⁻¹ region derived from AIMD simulations (X_HA = 0.67), the contributions of the different components: acetic acid (HAc) and 1-methylimidazole (MIm), and the experimental for comparison.

This acid–base complex is not only an intriguing chemical species with specific IR signatures, but also is thermodynamically more stable at room temperature than the acid, the base, and their conjugated pairs as demonstrated by the lack of chemical reactions. It is important to note that ionic species are not directly detected in these mixtures via IR spectroscopy, which is in good agreement with previous studies^7,25 and supports the hypothesis of no traditional acid–base reaction even when the mixture of has an excess enthalpy of ∼−7 kJ mol⁻¹.^6,7,25

The hypothesis that the experimental IR features originates from the formation of an acid–base complex is further validated by ab initio molecular dynamics (AIMD) simulations. These simulations reveal the presence of many different hydrogen bonded structures in the acid–base mixtures. However, in all the investigated concentrations, 1-methylimidazole always forms a one-to-one hydrogen bonded complex with acetic acid (Fig. 1). The AIMD simulations also confirm that the complex is formed by the direct interaction of the hydroxyl group of the acid with the unsubstituted nitrogen of the imidazole ring via a hydrogen bond (Fig. 2b). Notably, it is observed that the acid–base pair forms a hydrogen bond with a distance shorter than 2.7 Å, irrespective of the molar fraction of the acid (Fig. 2b), showcasing that the acid–base complex has a short hydrogen bond at all concentrations. While this hydrogen bond keeps the participating molecules at short distances, the complex appears to have a large number of possible conformations stemming from the almost free thermal rotation of the acid and the base around the hydrogen bond (Fig. 2c). In addition, the hydrogen bonded complexes are not isolated, but generally participating in extended hydrogen bond networks with up to three other acid or base molecules.²⁶

The assignment of the IR bands to the formation of the acid–base complex is confirmed by the IR spectrum computed from the AIMD simulations of the mixture with X_HA = 0.67. In good agreement with the experimental results (Fig. 2a, d and S5†), the theoretical IR spectrum presents at least one band in the 2200–3500 cm⁻¹ region. The decomposition of the simulated IR spectrum shows that the spectral components below 2750 cm⁻¹ originate from 1-methylimidazole and the high frequency component at 3100 cm⁻¹ arises from acetic acid (Fig. 2d). This assignment validates our hypothesis that the formation of the 1-methylimidazole–acetic acid complex gives rise to some of the IR bands seen experimentally in the 2200–3500 cm⁻¹ region of the IR spectra. It is important to note that IR spectrum in the AIMD does not contain mixed states, which strengthens the hypothesis that the IR signatures in the 2200–3500 cm⁻¹ region arise from the complex. Moreover, it is likely that the O–H stretch mode is vibrationally coupled to other modes.^22–24 As previously mentioned, it is likely that the mode has a large contribution of the O–H stretch which explains not only the lack of a pronounced band at ∼2000 cm⁻¹ in the simulated spectrum, but also why the AIMD simulation appropriately captures the IR absorption peak and line shape even without considering the mixing of the vibrational modes. Overall, the strong resemblance between the simulated and the experimental IR spectra (Fig. 2a, d and S5†) strongly indicates that AIMD simulations properly capture the molecular structures of the complexes because the vibrational modes are very sensitive to their local molecular environment.²⁷ Thus far, the experimental and theoretical data evidence the formation of short hydrogen bonds as a result of the formation of the complex between acetic acid and 1-methylimidazole, which are observed through their spectral signatures in the IR region.

Recently, the link between short hydrogen bonds and the appearance of broad vibrational bands at lower frequencies (1000–2000 cm⁻¹) than the hydroxyl stretch (∼3500 cm⁻¹) was demonstrated for the excess proton in solutions.^28–32 For example, a study on the acid aqueous solutions revealed that molecular species, such as the Zundel cation, present broad IR peaks in the same spectral regions arising from vibrational modes directly linked to the shuttling of the excess proton.^33,34 Hence, the broad bands in the IR spectra (Fig. 2a) are attributed to the acidic hydrogen shuttling modes of the complex upon the formation of a short hydrogen bond between acetic acid and 1-methylimidazole. This relation is further confirmed from ab initio frequency calculations of the vibrational modes for representative configurations deduced from the AIMD simulations.

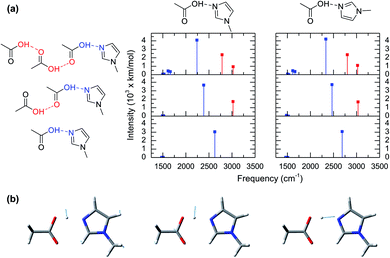
The computed vibrational modes of 6 representative configurations of clusters in gas phase (Fig. 3a) show that all of the complexes exhibit strong vibrational absorptions in the 2200–3000 cm⁻¹ region, in agreement with the experimental and simulated IR spectra from AIMD (Fig. 2a and c). Moreover, all these vibrational modes involve atomic motions directly related to the shuttling of the acidic hydrogen atom in the acetic acid molecule (Fig. 3b). The vibrational mode computations of clusters also reveal the presence of two distinct groups. The first group corresponds to the hydrogen shuttling modes of the acidic hydroxyl group directly interacting with 1-methylimidazole and has transition frequencies below 2750 cm⁻¹ (blue lines in Fig. 3a). In contrast, the second group has transition frequencies between 2750 cm⁻¹ and 3100 cm⁻¹ (red lines in Fig. 3a) and is associated with hydrogen shuttling modes that involve exclusively acetic acid molecules further along the chains of the hydrogen bond network (Fig. 3a). Remarkably, the vibrational modes with displacements of the hydrogen atom parallel to the hydrogen bond (Fig. 3b) have very large transition dipoles (greater than 3000 km mol⁻¹), while the shuttling modes with perpendicular displacements of the hydrogen atom have more typical transition dipoles (∼500 km mol⁻¹).²⁷ The uncharacteristically large transition dipole of the hydrogen shuttling mode explains its mixing with other modes and overtones.^22–24

Fig. 3 Vibrational mode analyses of representative acid–base complexes from ab initio calculations in gas phase. (a) Structures of the complexes composed of acetic acid hydrogen bonded to 1-methylimidazole (left) and their IR vibrational modes. Left and right panels correspond to two different angular conformations of the complex as depicted on the top. Note that the IR absorption peaks are from harmonic frequency calculations, and they are only intended to illustrate the absorption in the broad 2200–3000 cm⁻¹ region. (b) Atomic displacement for the proton shuttling mode of the complex. The left, center and right modes have an associated frequency of ca. 1600 cm⁻¹, 1700 cm⁻¹ and 2200 cm⁻¹, respectively.

Normal mode computations of clusters in gas phase also reveal that the broadness of the hydrogen shuttling bands (Fig. 2a) might arise from the dependence of the vibrational transition frequencies on the geometry of the complex. More specifically, the hydrogen shuttling frequency is strongly dependent on the angle between the planes of the hydrogen bond donor and acceptor (Fig. 2) due to a concomitant shortening of the complex hydrogen bond (Fig. S6†). As a result, the large number of angular conformations adopted by the acid–base pair causes the hydrogen shuttling mode to span in a ∼250 cm⁻¹ region (Fig. S7†). Hence, the exceedingly large transition dipoles and frequency of the hydrogen shuttling modes in the acid–base complex make these shuttling modes easily observed via IR spectroscopy, and the strong dependence of their transition frequencies with the geometrical arrangement of the complex along with its thermally allowed distribution of angles are likely to contribute to the broad bandwidth of these shuttling modes.

Previous studies on the excess proton in aqueous solutions demonstrated that the broad vibrational bands in the IR spectra were directly associated with the changes in the potential energy surface of the proton shuttling coordinate.^31,35 The same effect is observed here for the potential energy surfaces of the hydrogen shuttling coordinate in isolated cluster of both the acid dimer and the acid–base complex (Fig. 4a and b). In the case of the acetic acid dimer, the potential energy surface has a single minimum with a curvature of 439 kcal (Å⁻² mol⁻¹). In contrast, when acetic acid forms a hydrogen bond with 1-methylimidazole, the potential energy surface shows a second minimum with a low barrier of ∼5 kcal mol⁻¹ for transferring the proton between the donor and acceptor atoms, and the curvature in its global minimum reduces to 270 kcal (Å⁻² mol⁻¹). While the associated frequency for the hydrogen shuttling changes from ∼3320 cm⁻¹ in the acid dimer to ∼2600 cm⁻¹ in the acid–base complex, or from ∼2410 cm⁻¹ to ∼1890 cm⁻¹ upon deuteration, and evidences the variations in the curvature of the potential energy surfaces, the shape of the potential surfaces explains why the acid–base complex results in a short hydrogen bond. Unlike the case of the acetic acid dimer (Fig. 4a), the acid–base pair (Fig. 4b) presents a hydrogen transfer barrier (∼5 kcal mol⁻¹) comparable to the zero-point energy of the O–H stretch mode (∼4 kcal mol⁻¹), which allows the delocalization of the hydrogen atom in the potential well. Moreover, the hydrogen delocalization is heightened by hydrogen bonding to an additional acetic acid, as seen in the decrease of the proton transfer barrier by ∼4 kcal mol⁻¹ in potential energy surface for such complex (Fig. 4c) indicating that electronic effects also play a role in the delocalization process.

Fig. 4 Energy profiles for shuttling the acidic hydrogen in the different hydrogen bonded complexes. (a)–(c) Show the potential energy surfaces for stretching the O–H bond in the three hydrogen bonded pairs from ab initio computations in vacuum. (d) and (e) Display the free energy surfaces for the different pairs calculated from the AIMD and AI-PIMD simulations of the pure acid and the solution with X_HA of 0.67, respectively. The free energy surfaces are calculated along the proton sharing coordinate ν and the hydrogen bond length R, and are shifted so that their minimal values are 0.

The special characteristics of hydrogen bond in the acid–base pair are also evaluated from the free energy surfaces of proton shuttling from the AIMD simulations. In the absence of a hydrogen bonded 1-methylimidazole, the shuttling of the acidic hydrogen in an acid dimer (HAc·HAc, Fig. 4d) has two local minima with a barrier of ∼4 kcal mol⁻¹, indicating that the proton is positioned close to one of the two acid molecules forming a normal hydrogen bond. In contrast, the free energy landscape for the shuttling of the acidic hydrogen is drastically altered when 1-methylimidazole is part of the hydrogen bond network. In this case, the barrier for proton shuttling (MIm·H·Ac of Fig. 4e) is four times lower (∼1 kcal mol⁻¹) than in the pure acid. Consequently, the acidic hydrogen in the acid–base complex has a much larger probability of being delocalized within the hydrogen bond than in those of the acid–acid pairs.

Given the quantum mechanical nature of the hydrogen atom (i.e., nuclear quantum effects) and the extent of the delocalization deduced from the AIMD free energy surfaces, the hydrogen atom delocalization is investigated via ab initio path integral molecular dynamics (AI-PIMD) simulations, which include both electronic and nuclear quantum effects.^36–38 The resulting AI-PIMD free energy surfaces show that the hydrogen shuttling potential in the acid–base complex is almost barrier-less (Fig. 4e). Although a similar decrease in the barrier is observed for the other hydrogen bond pairs, the hydrogen shuttling between two acetic acid molecules still maintains its double well shape even in the presence of 1-methylimidazole (mixture). These results demonstrate that nuclear quantum effects of the acidic hydrogen atom play a significant role in the energetics of the acid–base complex. In particular, the quantum nuclear effects lower the hydrogen shuttling barrier, and consequently, favour the delocalization of the hydrogen atom within the hydrogen bond.

The energetic stabilization of chemical species via nuclear quantum effects is not new and has been proposed to play a major role in the formation of the Watson–Crick base pair.³⁹ The presence of significant non-classical effects in the acid–base complex arises from the quantum kinetic energy penalty as a result from localizing a quantum particle, such as the hydrogen atom.¹² Hence, a decrease of the energy barrier in the hydrogen shuttling potential not only results in a reduction of the energy penalty in the system, but also leads to a substantial expansion of the region where the hydrogen atom can be positioned; i.e., delocalization.

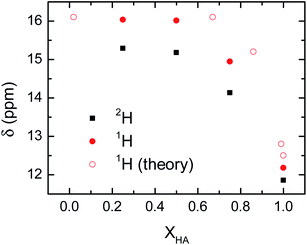
The delocalization of the acid hydrogen in the acetic acid and 1-methylimizadole mixtures is also deduced from the ¹H NMR spectra of the different solutions because one of the most distinctive features of delocalized hydrogen atoms in short hydrogen bonds is their far downfield ¹H NMR chemical shifts.¹² Typically, the ¹H chemical shift for the hydroxyl group of an acid is around 12 ppm.⁴⁰ However, when an acidic hydrogen atom is delocalized within a strong hydrogen bond, the ¹H nucleus is further deshielded resulting in a ¹H chemical shifts well above 14 ppm and sometimes close to 20 ppm.^41,42 This extreme behaviour in the chemical shift of the delocalized hydrogen is also found in the acetic acid and 1-methylimidazole samples, where the addition of 1-methylimidazole shifts the chemical shift of the acid proton from 12 ppm in the pure acid to 15–16 ppm in the mixture (Fig. 5). It is important to note that the observed chemical shift is an average of the chemical shift of the possible species, in this case delocalized and non-delocalized acidic hydrogen atom, due to the ultrafast times scale of the chemical exchange of the process as compared to the NMR time resolution.⁴³ The observed chemical shifts for the hydroxyl proton are in good agreement with the formation of species where the hydrogen atom is delocalized, or equivalently, largely deshielded.

Fig. 5 Experimental and computational ¹H NMR chemical shifts of the hydrogen bonded proton as a function of the concentration of the acid in the mixtures of acetic acid and 1-methylimidazole. The experimental ²H chemical shifts of the acetic acid-1d and 1-methylimidazole are also included for comparison.

Mixtures containing deuterated acetic acid also display a large ²H chemical shifts of the deuterium atom, though they are slightly lower than the corresponding ¹H samples (Fig. 5). The large chemical shift of the ²H nucleus confirms the delocalization of the acidic deuterium atom, where their lower chemical shift as compared to ¹H evidences the quantum mechanical effect driven exclusively by a change in the zero-point fluctuations rather than changes in the interaction potential between the deuterium atom and the carboxylate group.⁴⁴ Computations of the NMR chemical shift for the acidic hydrogen atom in very dilute (X_HA = 0.02) and concentrated (X_HA = 0.67) solutions confirm the large downfield shift in the ¹H NMR region of the acid hydrogen seen in the experimental data (Fig. 5). Hence, the NMR data further validates our hypothesis that the hydrogen delocalization occurs in the mixture of acetic acid and 1-methylimidazole because of the presence of a strong hydrogen bond in the acid–base complex.

Conclusions

This work showcases an intriguing and previously uncharacterized chemical species in acid and base mixtures that stems from the direct and strong hydrogen bond interaction between acetic acid and 1-methylimidazole, which is not predicted by traditional theories of acid–base chemistry. Unlike conventional hydrogen bonded complexes, this acid–base pair forms a short hydrogen bond where the acidic hydrogen atom is delocalized or shared between the donor and acceptor groups. This species with a delocalized acidic hydrogen has distinctive features in the IR and ¹H NMR spectra. In particular, it has a broad vibrational absorption band in the 2250–3000 cm⁻¹ region and an exceedingly large downfield chemical shifts of one of the ¹H nuclei in the complex. The spectroscopic signatures of the complex are assigned, via simulations of the system, to the shuttling vibrational mode and the ¹H nuclei of the acidic hydrogen, respectively. More importantly, the IR and NMR features evidence substantial changes in the potential energy surface (i.e., curvature and lengthening of the O–H bond) associated with the formation of a strong hydrogen bond in the acid–base complex, where the hydrogen atom is delocalized. In addition, it is also established from the theory that both nuclear and electronic quantum mechanical effects play a significant role in defining the structure and energetic of acetic acid and 1-methylimidazole hydrogen bonded complex. Overall, our studies on the mixtures of acetic acid and 1-methylimidazole highlight the importance of quantum mechanical electronic and nuclear effects in defining acid–base chemistry of this pair. However, it is likely that many other acid and base pairs have this interesting behavior. To this end, this study showcases the experimental tools needed (i.e., IR and NMR spectroscopies) and their corresponding signatures for determining the occurrence of proton delocalization in such systems.

Materials and methods

Sample preparation

1-Methylimidazole (99% pure, Alfa Aesar) was dried over a molecular sieve 4 A for 2 days, and acetic acid (glacial, VWR) and acetic acid-d4 (99.5% D, Acros organic) were dried by desiccant-anhydrous Drierite 10–20 mesh without indicator for more than a week. Mixtures were prepared by mixing the acid and the base at different molar ratios. The drying process and sample preparation process were all performed in a nitrogen-filled glovebox to minimize water contamination. The final mixtures were checked by the Karl Fisher titration to ensure a water content less than ∼100 ppm.

Linear infrared spectroscopy

Attenuated total reflection (ATR) FTIR were performed on a Bruker Tensor 27 spectrometer with a resolution of 1 cm⁻¹ and equipped a room temperature DTGS detector, mid-IR source (4000 to 400 cm⁻¹), a KBr beamsplitter and a Pike Miracle single-bounce attenuated total reflectance (ATR) accessory with a ZnSe single crystal. All ATR data were collected as an average over 16 scans at a resolution of 4 cm⁻¹.

NMR spectroscopy

The ¹H and ²H NMR spectra were collected on a 9.4 T (400.13 MHz ¹H and 61.42 MHz ²H resonance frequency) Bruker AVANCE III HD Nanobay spectrometer with Ascend magnet. All the spectra were collected with 16 scans and a 1 s relaxation delay.

Gas phase ab initio computations

This type of calculations involved geometry optimizations, harmonic vibrational frequency calculations and potential energy surface calculations of clusters at the PBE level,⁴⁵ with the D2 dispersion correction⁴⁶ and the 6-311++G(d,p) basis set using the Gaussian 16 software.⁴⁷ Initial configurations of the clusters were built by Avogadro with the classical force field MMFF94.⁴⁸ These calculations were used as zeroth-order pictures to describe how the molecular structures of the complex influence the potential energy surfaces and frequencies of the O–H stretch of the hydrogen bonded acetic acids, and thus, were performed without anharmonic corrections.

Ab initio molecular dynamics simulations

These first principles simulations were used to sample the liquid configurations and to compute the free energy potentials of the hydrogen shuttling mode. AIMD simulations were performed for the liquid mixtures of acetic acid and 1-methylimidazole using between 62 to 72 molecules to represent the different five concentrations (see ESI†) using the CP2K package.⁴⁹ AI-PIMD simulations were performed for the solution with X_HA of 0.67 using CP2K⁴⁹ for the electronic structure evaluations and the i-PI software⁵⁰ for propagating the nuclear motion. The electronic structure was described using the PBE density functional⁴⁵ and the D2 dispersion correction⁴⁶ in accordance with a previous work on the same system, which correctly capture some properties of the system,²⁶ and with this work, where features of the IR and NMR spectra computed from the AIMD present a good agreement with the experimental observations. The Goedecker–Teter–Hutter pseudopotentials⁵¹ were used for the core electrons, and the TZV2P-GTH plane-wave basis set⁵² with a cut-off of 400 Ry was used to describe the valence charge density. Periodic boundary conditions were applied for all the systems. The simulations were performed with a time step of 0.5 fs in the canonical ensemble at 321 K. In the AIMD simulations, the Nose–Hoover thermostat^53,54 was used to control the temperature. In the AI-PIMD simulations, each atom was represented by 6 ring polymer beads using the path integral generalized Langevin equation method.⁵⁵ The AIMD simulations were performed for a total of 300 ps for the mixtures with X_HA of 0.02, 0.67 and 0.86. The simulation lengths were 140 ps and 150 ps for the systems with X_HA of 0.99 and 1.00, respectively. The AI-PIMD simulations were performed for 50 ps. Note that the PBE density functional was used in the quantum chemistry calculations and first principles simulations for their relatively low computational costs, although GGA functionals could overdelocalize the electrons and protons in hydrogen bonded systems.⁵⁶ However, calculations of the potential energy surfaces using the BLYP density functional^57,58 and the D2 dispersion correction⁴⁶ showed that the two density functionals closely match each other (ESI†).

First principle free energy landscapes

The free energy surfaces for transferring the proton in a hydrogen bond were computed for both AIMD and AI-PIMD simulations used different R and ν axis. For a hydrogen bond between two acetic acids, R was defined as the O–O distance and ν as the difference between the two O–H distances, ν = d_O1H − d_O2H, while for a hydrogen bond between acetic acid and 1-methylimidazole, R was the O–N distance and ν = d_OH − d_NH. Here, a pair was considered hydrogen bonded if R ≤ 3.5 Å and the O–H–O or O–H–N angle is equal to or above 135°. The free energies were computed as F = −k_BT ln P(ν, R), where k_B is the Boltzmann constant, T is the simulation temperature, and P(ν, R) is the probability of observing a hydrogen bond with the hydrogen atom at ν and the O–O or O–N distance at R.

IR simulation

The simulated IR spectrum was computed from the AIMD simulations of the acid–base mixture with X_HA of 0.67 using the TRAVIS software.⁵⁹ From Fermi's golden rule, the IR spectrum of a system can be obtained from the Fourier transform of the molecular dipole time correlation function:
where [small mu, Greek, vector](t) is the molecular dipole moment at time t, and Q is a quantum correction factor to account for the lack of nuclear quantum effects in the dipole moments.⁶⁰ The molecular dipole moments were obtained using the maximally localized Wannier function scheme.⁶¹ The Wannier centers were computed every 2.5 fs from the AIMD trajectories using the CP2K software.⁴⁹ This scheme allowed us to decompose the overall IR spectrum into the contributions from the acetic acid and 1-methylimidazole molecules. The IR calculations can be further improved using the simulation trajectories that include both electronic and nuclear quantum effects,⁶² but they were beyond the scope of this study.

NMR simulations

The average ¹H NMR chemical shifts were computed from the AIMD simulations and a universal relation found between the average ¹H NMR chemical shift and the proton position in short hydrogen bonds.¹⁹ This relation establishes that chemical shift is given by δ_H = 20.5–16.1<ν>², where <ν> is the average hydrogen position in the hydrogen bond as previously described. Hence, the ν values of all the hydrogen bonds between −1.0 Å and 1.0 Å, corresponding to shared hydrogen atoms in short hydrogen bonds, were used to obtain <ν> at each concentration of the acid–base mixture.

More details of the computational methods and analyses are provided in the ESI.†

Data availability

The data supporting the findings of this article are available from the corresponding authors upon reasonable request.

Author contributions

D. G. K. and L. W. designed research; X. Z., S. Z., and F. M. L. performed research; X. Z. and S. Z. analysed data; and D. G. K. and L. W. wrote the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. G. K. acknowledges financial support from the LSU Chemistry Department. D. G. K. also acknowledges the High Performance Computing Center at Louisiana State University and the Louisiana Optical Network Initiative (LONI) for computer time. L. W. acknowledges the support from the National Science Foundation through Award No. CHE-1904800. L. W. also thanks the Office of Advanced Research Computing at Rutgers University for providing access to the Amarel server.

References

1. J. N. Brönsted, Recl. Trav. Chim. Pays-Bas, 1923, 42, 718–728.
2. T. M. Lowry, Journal of the Society of Chemical Industry, 1923, 42, 43–47.
3. I. N. Levine, Physical Chemistry, McGraw-Hill, Boston, 6th edn, 2009.
4. D. A. McQuarrie and J. D. Simon, Molecular Thermodynamics, University Science Books, Sausalito, Calif., 1999.
5. K. s. Izutsu, Electrochemistry in Nonaqueous Solutions, Wiley-VCH, Weinheim, 2nd, rev. and enlarged edn, 2009.
6. R. Kanzaki, H. Doi, X. D. Song, S. Hara, S. Ishiguro and Y. Umebayashi, J. Phys. Chem. B, 2012, 116, 14146–14152.
7. H. Doi, X. D. Song, B. Minofar, R. Kanzaki, T. Takamuku and Y. Umebayashi, Chem.–Eur. J., 2013, 19, 11522–11526.
8. D. R. Lide and W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC PressBoca Raton, FL, 2010.
9. R. G. Treble, K. E. Johnson and E. Tosh, Can. J. Chem., 2006, 84, 915–924.
10. N. P. Aravindakshan, K. E. Gemmell, K. E. Johnson and A. L. L. East, J. Chem. Phys., 2018, 149, 094505.
11. W. Cleland and M. M. Kreevoy, Science, 1994, 264, 1887–1890.
12. L. Wang, S. D. Fried, S. G. Boxer and T. E. Markland, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 18454–18459.
13. Y. Wu and S. G. Boxer, Biophys. J., 2016, 110, 546a–547a.
14. S. Dai, L. M. Funk, F. R. von Pappenheim, V. Sautner, M. Paulikat, B. Schroder, J. Uranga, R. A. Mata and K. Tittmann, Nature, 2019, 573, 609–613.
15. D. Marx, M. E. Tuckerman, J. Hutter and M. Parrinello, Nature, 1999, 397, 601–604.
16. M. E. Tuckerman, D. Marx and M. Parrinello, Nature, 2002, 417, 925–929.
17. M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Chem. Rev., 2016, 116, 7529–7550.
18. Z. R. Long, A. O. Atsango, J. A. Napoli, T. E. Markland and M. E. Tuckerman, J. Phys. Chem. Lett., 2020, 11, 6156–6163.
19. S. M. Zhou and L. Wang, Phys. Chem. Chem. Phys., 2020, 22, 4884–4895.
20. L. H. Jones and E. Mclaren, J. Chem. Phys., 1954, 22, 1796–1800.
21. A. C. Guerin, K. Riley, K. Rupnik and D. G. Kuroda, J. Chem. Educ., 2016, 93(6), 1124–1129.
22. A. M. Stingel and P. B. Petersen, J. Phys. Chem. B, 2016, 120, 10768–10779.
23. B. L. Van Hoozen and P. B. Petersen, J. Chem. Phys., 2017, 147, 224304.
24. B. L. Van Hoozen and P. B. Petersen, J. Chem. Phys., 2018, 148, 134309.
25. R. W. Berg, J. N. C. Lopes, R. Ferreira, L. P. N. Rebelo, K. R. Seddon and A. A. Tomaszowska, J. Phys. Chem. A, 2010, 114, 10834–10841.
26. J. Ingenmey, S. Gehrke and B. Kirchner, ChemSusChem, 2018, 11, 1900–1910.
27. B. Blasiak, C. H. Londergan, L. J. Webb and M. Cho, Acc. Chem. Res., 2017, 50, 968–976.
28. J. A. Fournier, W. B. Carpenter, N. H. C. Lewis and A. Tokmakoff, Nat. Chem., 2018, 10, 932–937.
29. H. J. Bakker and H. K. Nienhuys, Science, 2002, 297, 587–590.
30. F. Dahms, B. P. Fingerhut, E. T. J. Nibbering, E. Pines and T. Elsaesser, Science, 2017, 357, 491–494.
31. A. Kundu, F. Dahms, B. P. Fingerhut, E. T. J. Nibbering, E. Pines and T. Elsaesser, J. Phys. Chem. Lett., 2019, 10, 2287–2294.
32. M. Thamer, L. De Marco, K. Ramasesha, A. Mandal and A. Tokmakoff, Science, 2015, 350, 78–82.
33. C. A. Daly, L. M. Streacker, Y. C. Sun, S. R. Pattenaude, A. A. Hassanali, P. B. Petersen, S. A. Corcelli and D. Ben-Arnotz, J. Phys. Chem. Lett., 2017, 8, 5246–5252.
34. R. Biswas, W. Carpenter, J. A. Fournier, G. A. Voth and A. Tokmakoff, J. Chem. Phys., 2017, 146, 154507.
35. B. Dereka, Q. Yu, N. H. C. Lewis, W. B. Carpenter, J. M. Bowman and A. Tokmakoff, Science, 2021, 371, 160–164.
36. D. Marx and M. Parrinello, J. Chem. Phys., 1996, 104, 4077–4082.
37. a. B. J. Berne and D. Thirumalai, Annu. Rev. Phys. Chem., 1986, 37, 401–424.
38. T. E. Markland and M. Ceriotti, Nat. Rev. Chem., 2018, 2, 0109.
39. A. Perez, M. E. Tuckerman, H. P. Hjalmarson and O. A. von Lilienfeld, J. Am. Chem. Soc., 2010, 132, 11510–11515.
40. R. M. Silverstein, G. C. Bassler and T. C. Morrill, Spectrometric Identification of Organic Compounds, Wiley, New York, 4th edn, 1981.
41. P. B. White and M. Hong, J. Phys. Chem. B, 2015, 119, 11581–11589.
42. P. A. Frey, S. A. Whitt and J. B. Tobin, Science, 1994, 264, 1927–1930.
43. R. F. Yuan, J. A. Napoli, C. Yan, O. Marsalek, T. E. Markland and M. D. Fayer, ACS Cent. Sci., 2019, 5, 1269–1277.
44. D. J. O'Leary, D. D. Hickstein, B. K. V. Hansen and P. E. Hansen, J. Org. Chem., 2010, 75, 1331–1342.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
47. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford, CT, 2016.
48. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
49. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
50. V. Kapil, M. Rossi, O. Marsalek, R. Petraglia, Y. Litman, T. Spura, B. Q. Cheng, A. Cuzzocrea, R. H. Meissner, D. M. Wilkins, B. A. Helfrecht, P. Juda, S. P. Bienvenue, W. Fang, J. Kessler, I. Poltavsky, S. Vandenbrande, J. Wieme, C. Corminboeuf, T. D. Kuhne, D. E. Manolopoulos, T. E. Markland, J. O. Richardson, A. Tkatchenko, G. A. Tribello, V. Van Speybroeck and M. Ceriotti, Comput. Phys. Commun., 2019, 236, 214–223.
51. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
52. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
53. S. Nose, J. Chem. Phys., 1984, 81, 511–519.
54. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
55. M. Ceriotti and D. E. Manolopoulos, Phys. Rev. Lett., 2012, 109, 100604.
56. A. J. Cohen, P. Mori-Sanchez and W. T. Yang, Chem. Rev., 2012, 112, 289–320.
57. A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100.
58. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
59. M. Brehm, M. Thomas, S. Gehrke and B. Kirchner, J. Chem. Phys., 2020, 152, 164105.
60. P. L. Silvestrelli, M. Bernasconi and M. Parrinello, Chem. Phys. Lett., 1997, 277, 478–482.
61. M. Thomas, M. Brehm, R. Fligg, P. Vohringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622.
62. V. Kapil, D. M. Wilkins, J. G. Lan and M. Ceriotti, J. Chem. Phys., 2020, 152, 124104.

---

Footnote

† Electronic supplementary information (ESI) available: Additional details in computational methods, experimental IR spectra of the mixtures at different concentrations, temperature and with deuterated samples. Computed frequency for the hydrogen shuttling more as function of the hydrogen bond angle and length. See https://doi.org/10.1039/d2sc01784a

---