Open Access Article
Open Access ArticleUnravelling free volume in branched-cation ionic liquids based on silicon†
Eduards
Bakis
 *a,
Kateryna
Goloviznina
*a,
Kateryna
Goloviznina
 b,
Inês C. M.
Vaz
b,
Inês C. M.
Vaz
 b,
Diana
Sloboda
a,
Daniels
Hazens
a,
Valda
Valkovska
a,
Igors
Klimenkovs
b,
Diana
Sloboda
a,
Daniels
Hazens
a,
Valda
Valkovska
a,
Igors
Klimenkovs
 a,
Agilio
Padua
a,
Agilio
Padua
 b and
Margarida
Costa Gomes
b and
Margarida
Costa Gomes
 *b
*b
aFaculty of Chemistry, University of Latvia, Jelgavas 1, Riga, LV-1004, Latvia. E-mail: eduards.bakis@lu.lv
bLaboratoire de Chimie, ENS de Lyon and CNRS, 46 Allée D’Italie, Lyon 69364, France. E-mail: margarida.costa-gomes@ens-lyon.fr
First published on 5th July 2022
Abstract
The branching of ionic liquid cation sidechains utilizing silicon as the backbone was explored and it was found that this structural feature leads to fluids with remarkably low density and viscosity. The relatively low liquid densities suggest a large free volume in these liquids. Argon solubility was measured using a precise saturation method to probe the relative free volumes. Argon molar solubilities were slightly higher in ionic liquids with alkylsilane and siloxane groups within the cation, compared to carbon-based branched groups. The anion size, however, showed by far the dominant effect on argon solubility. Thermodynamic solvation parameters were derived from the solubility data and the argon solvation environment was modelled utilizing the polarizable CL&Pol force field. Semiquantitative analysis was in agreement with trends established from the experimental data. The results of this investigation demonstrate design principles for targeted ionic liquids when optimisation for the free volume is required, and demonstrate the utility of argon as a simple, noninteracting probe. As more ionic liquids find their way into industrial processes of scale, these findings are important for their utilisation in the capture of any gaseous solute, gas separation, or in processes involving the transformation of gases or small molecules.
Introduction
Since ionic liquids (ILs) are composed solely of cations and anions, the structure of their liquid phases must convey local electroneutrality. Surprisingly enough, this short-range ordering does not lead to crystallisation close to room temperature, providing a range of interesting benefits for the properties of these fluid materials. In addition to their negligible volatility, a unique combination of polarities arises from the co-existence of charge dispersion and segregation linked with the presence of low-charge density molecular residues in one or both ions. A broad range of solutes can be solubilized in ILs as a result. Moreover, after chemical transformation is carried out in an IL, solutes may be separated directly or easily extracted out. Unlike the IL itself, low-molecular-weight molecular solutes can leave the ionic medium under mild pressure changes. This is particularly feasible for solutes with low cohesive energies, such as gases.Compared to molecular liquids, coulombic forces are dominant in ILs, contributing to the maximization of ion packing and increasing molecular friction. As a result, ILs are dense and viscous fluids making the existence of transient voids rare and energetically costly. This leads to ILs with lower free volumes than molecular liquids,1 with a limited capacity to dissolve non-interacting gases.
Several strategies have been successfully adopted to increase the free volume in ILs as many applications would benefit from the use of non-volatile solvents with high gas absorption capacities at ambient temperatures and pressures. For example, by fluorinating the alkyl side-chains in imidazolium-based ILs,39–41 higher solubilities of carbon dioxide but also of nitrogen or oxygen have been achieved in different ILs. Mixing ILs can result in an increase of the molar volume of the mixture when compared to those of the pure components, as quantified by a positive excess molar volume.10,11 This can be a sign of a larger free volume in the mixture that could be occupied by gaseous solutes, thus further enhancing the solubility of non-interacting gas solutes. However, this property has not been explored as mixing of ILs is often close to ideal12 with the molar volume gain rarely exceeding a few cm3 mol−1.13
Recently, the properties of porous materials2 or porous molecular solids,3,4 and of ionic liquids have been gathered by dispersing metal organic frameworks (MOFs) in ILs.7 The gas absorption capacities of both components are combined7 to generate a liquid state with high gas capacity, allowing for chemical transformations5,6 at mild pressures and temperatures.8 These discoveries point towards the importance of having solvents with a high free volume that would lead to high solvation capacities (especially of small-size gas solutes), even when solute–solvent interactions are not favourable.
ILs featuring cationic organosilicon groups have been reported to have reduced viscosities relative to homologous cations with alkyl substituents.32 Their transport properties and microscopic structure have been studied experimentally and using ab initio calculations and molecular dynamics. The microscopic structure of silicon-containing ILs has shown small but significant differences37 from their alkyl substituted counterparts, providing evidence for weaker cation–anion interactions and higher flexibility of the bulkier Si-containing chains. These structural characteristics inhibit ion packing,32 explain the high fluidity of silicon-containing ILs,38 and are compatible with the faster diffusivity of small solutes in these solvents.35 These findings point towards the inclusion of silicon substitution in the cation side-chain as a promising route to prepare ILs with increased free volumes.42
The thermodynamics of gas absorption (physisorption) is characterized by the Gibbs free energy:
| ΔsolG = ΔsolH − TΔsolS | (1) |
Entropic contributions, on the other hand, can be attributed to structural aspects, such as the organization of the solvent molecules around the solutes. It is then clear that another factor that can impact the absorption of small molecular solutes is their size. When the relative size of IL natural occurring voids and solute molecules is comparable, the perturbation of the IL structure for solute accommodation is lower. This leads to a favourable entropic contribution to the absorption of gas that originates from the IL structure itself.
In this study, we aimed to explore design principles for ILs with increased free volume that would contribute to an enhancement in the gas absorption, mainly controlled entropically. The advantage of using such ILs as reaction media is evident when the reactants involved are gases, as it allows milder reaction conditions.
We used a rational molecular design and developed synthetic routes to novel ILs based on silicon. To probe the free volume in ILs experimentally, we measured the solubility of argon at low pressures and calculated the thermodynamic properties of solvation. Direct experimental probes of free volume in ILs have been limited so far41 and inconsistences in how free volume is defined and measured have been observed in the literature. The use of probe molecules that are spherical and non-interacting like argon appear to be a good choice, used frequently to probe porosity in liquids.7
In addition to the experimental study, we decided to use molecular modelling utilizing the recently developed polarisable CL&Pol14–16 force field to validate the gas absorption results and understand the IL cavity structure. Explicit polarization terms realistically account for induction effects in charged systems, enabling a correct description of their structure and dynamics. Among the different families of polarisable force fields for ionic liquids, CL&Pol14,16 stands out due to its indisputable advantages: transferability and easy-extendibility inherited from its predecessor, the fixed-charge CL&P17,18 force field. We adapted the CL&Pol to new alkylsilane and siloxane side groups of the imidazolium family following the procedure available in the literature.
Materials and methods
Synthetic procedures
Syntheses were started from commercially available materials using dried solvents, and are described in detail in the ESI.† All imidazolium salts used as precursors to target ionic liquids, except for 1-octyl-3-methylimidazolium bromide, were purified by recrystallization. Anion metathesis was performed under biphasic conditions (DCM-water extraction). Completeness of anion exchange was tested using the AgNO3 test or nuclear magnetic resonance (NMR) spectroscopy where possible. The ILs were dried for 24 h by stirring at 0.1 mbar and 323 K. The structure and purity of the products were assessed by NMR spectroscopy and high-resolution mass spectrometry.Synthetic routes
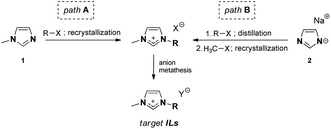
Two different synthetic pathways were utilized towards ILs, as shown in Table 1, both of which involve the preparation of the intermediate salt, followed by anion exchange (Fig. 1).| No | [NTf2]− | [B(CN)4]− | [N(CN)2]− | [OTf]− | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ,η | Ar | MD | ρ,η | Ar | MD | ρ,η | Ar | MD | ρ,η | Ar | MD | |||
| a ρ,η – density and viscosity studied as a function of temperature at 293–353 K. Ar – solubility of argon measured as a function of temperature at 300–345 K. MD – solvation environment modelled via molecular dynamics at 353 K. | ||||||||||||||
| 1 | [C8C1im]+ |
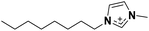
|
✓ | ✓ | ✓ | |||||||||
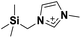
| 2 | [(Np)C1im]+ |
|
✓ | ✓ | ✓ | |||||||||
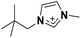
| 3 | [(Me4C5)C1im]+ |
|
✓ | ✓ | ✓ | |||||||||
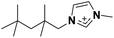
| 4 | [(SiC)C1im]+ |
|
✓ | ✓ | ✓ | |||||||||
| 5 | [(SiCSiC)C1im]+ |
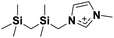
|
✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||
| 6 | [(SiCSiCSiC)C1im]+ |
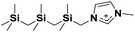
|
✓ | |||||||||||
| 7 | [(SiOSiC)C1im]+ |
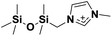
|
✓ | ✓ | ✓ | ✓ | ✓ | |||||||
The exact pathway chosen for each of the cations is listed in Table S10†. Synthetic approaches for the introduction of cation side chains and anion metathesis are described in the ESI.† The final ILs were dried under high vacuum prior to use, and the water content was controlled by Karl-Fischer coulometry.
Density and molar volume
Densities were measured under atmospheric pressure in the temperature range of 293.15–353.15 K using a U-shaped vibrating-tube densimeter (model DMA 5000M; Anton Paar). The calibration of the equipment was verified with air and triple distilled water before and after each measurement. The estimated uncertainties of this equipment are 0.00001 g cm−3 and 0.01 K for density and temperature, respectively. Molecular weights for molar volume calculation were those recommended by IUPAC with precision to the nearest 0.0001 Da.Viscosity
Viscosity measurements were conducted under atmospheric pressure in the temperature range of 293.15–353.15 K using a falling ball-based Anton Paar Lovis 2000 M/ME microviscosimeter. The temperature was controlled to within 0.005 K and measured with an accuracy better than 0.02 K. A 1.8 mm diameter capillary tube, previously calibrated as a function of temperature and angle of measurement with reference oils, was used for the measurements. The overall uncertainty of the viscosity was estimated to be 2%. The water content of the IL samples after density and viscosity measurements was not greater than 130 ppm (Coulometric Karl Fischer C20 titrator from Mettler Toledo).Gas solubility measurements
Gas solubility measurements were performed using an isochoric saturation method, a technique that has been described in previous publications.19,20 In this experimental methodology, a glass cell, of which the volume is precisely known, is first filled with a certain amount of argon. The amount of argon is precisely determined by a pVT measurement, as described by the following equation: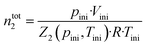 | (2) |
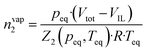 | (3) |
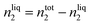 | (4) |
Using this methodology, two considerations are made in this publication: (i) the vapour pressure of the studied ionic liquids is negligible and thus the equilibrium pressure reflects the pressure of the studied gas; (ii) the volume of the ionic liquid does not change upon absorption of argon.
The solubility of argon in the different ionic liquids studied is expressed as the mole fraction of the solute, x:
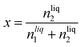 | (5) |
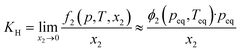 | (6) |
The change in the Gibbs energy, ΔsolG∞, when the argon is transferred from the pure gas state under standard pressure (po = 0.1 MPa) to its infinitely diluted state in the ionic liquid, can be calculated as follows:
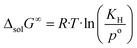 | (7) |
The change in enthalpy and entropy can be determined by calculating the derivative of the Gibbs energy with respect to the temperature:
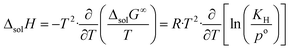 | (8) |
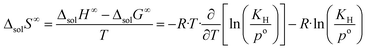 | (9) |
Theoretical methods
Molecular dynamics (MD) simulations were performed in the LAMMPS22 software using the polarisable CL&Pol force field.14,16 Explicit polarisation effects were represented by Drude induced dipoles. The Lennard-Jones potential, inherited from the non-polarisable CL&P force field, was modified in order to avoid double counting of the induction effect.14Periodic cubic boxes containing 100–300 ion pairs of ionic liquid with several atoms of argon added (when required) were equilibrated for 2 ns at 353 K and 1 bar and followed by 10–20 ns production runs. Density calculations and local structure analysis were performed on equilibrium trajectories, while viscosity was evaluated from non-equilibrium MD runs using the periodic perturbation method.15,23 The free energy perturbation method was used to determine the residual chemical potential (μres) of argon in the ILs, from which solubility was evaluated according to
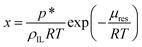 | (10) |
Further details of the force field development procedure, system setup, and simulation conditions are given in the ESI.†
Results and discussion
Ionic liquid design
The chemical properties of ILs are often explained by the nature of their constituent ions, whereas physical properties depend on the liquid structure to which the particular ion combination leads. We explored the free volume in ILs by increasing the volume of the cation, thus aiming to reduce the packing efficiency. Three approaches were considered: (1) branching in the cation side chain, (2) size expansion of the side chain via bond elongation, and (3) flexibilization of the side chain via Si–O–Si linkages. The increase in the side-chain length is a widely exploited cation modification, while efforts on expanding the branching have, so far, been limited. A series of three anions was studied alongside other to evaluate anion effects. Undoubtedly, these ion modifications, amongst all, have an impact on the properties of the liquid other than the free volume. Therefore, the structure–property relationships were evaluated by studying the IL density and viscosity.The choice for cation functionalization with silicon atoms stems from the inherently longer silicon-to-carbon bonds compared to carbon–carbon bonds. The relative bond lengths of some silanes and their carbon counterparts are provided in Fig. 2. As can be seen from the comparison with crystal structure data (Table S11†), the bonds in these moieties generally preserve their length even when part of more complex structures. Inspired by these data and the well-known flexibility and fluidity of siloxanes,24,25 we incorporated these structural fragments within IL cation structures for free volume study. A summary of the ILs prepared and studied in this work, as well as cation abbreviations, is provided in Table 1.
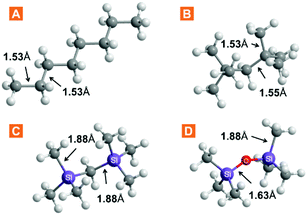 | ||
| Fig. 2 Selected bond lengths in linear and branched molecules incorporated in the IL cation structure. Data obtained via molecular mechanics simulation in Chem3D Pro. | ||
Synthesis of the ILs
Although the well-known IL synthetic pathway A is shorter (Fig. 1), the bottleneck in 1-methylimidazole 1 alkylation is often the low reactivity of the sterically large alkylating agents R-X. This leads to long reaction times and paves the way for possible side reactions and discolouration; elevated reaction temperatures are needed. Pathway B, on the contrary, is longer, but allows for purification of the intermediate alkyl imidazoles via distillation, after which methylation toward imidazolium salts can be performed. Here, the choice of a suitable methylating agent (e.g., methyl tosylate) was the key to ensure that the product was crystalline and, therefore, enabled its purification via recrystallization.An important observation must be made about the anion metathesis procedure for [N(CN)2]− ILs, which could be performed in a conventional manner using the alkali metal dicyanamide salt, in contrast to the conventionally used silver dicyanamide.26 The target [N(CN)2]− IL could be successfully extracted with dichloromethane, and therefore silver halide precipitation avoided. We associate this with the relatively hydrophobic nature of the ion pairs used in this work. However, dicyanamide ILs remained among the most hydrophilic materials studied in this work.
Density and molar volume
Density values at 298 K are presented in Table 2. Across series of various anions, it is immediately clear that the [NTf2]−-based ILs exhibit the highest density. The most unusual feature is the low density of ILs comprising anions that bear cyano-groups, [N(CN)2]− and [B(CN)4]−, which is close to 1 g cm−3.| No | Cation | Anion | ρ/g cm−3 | V m/g cm−3 | η/mPa s |
|---|---|---|---|---|---|
| a calculated average from the literature values30,31 | |||||
| 1 | [C8C1im]+ | [NTf2]− | 1.307![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 718 718 |
359.9 | 93.129 |
| 2 | [(Np)C1im]+ | [NTf2]− | 1.411![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 099 099 |
307.1 | 183.3 |
| 3 | [(Me4C5)C1im]+ | [NTf2]− | 1.311![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 641 641 |
369.5 | 967.4 |
| 4 | [C9C1im]+ | [NTf2]− | 1.2985a | 377.0 | 107.2a |
| 5 | [C8C1im]+ | [B(CN)4]− | 0.975127 | ||
| 6 | [(SiC)C1im]+ | [NTf2]− | 1.376![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 204 204 |
323.3 | 85.6 |
| 7 | [(SiCSiC)C1im]+ | [NTf2]− | 1.299![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 700 700 |
401.4 | 141.2 |
| 8 | [(SiCSiC)C1im]+ | [B(CN)4]− | 0.972![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814 814 |
312.8 | 110.8 |
| 9 | [(SiCSiC)C1im]+ | [N(CN)2]− | 1.004406 | 303.5 | 138.5 |
| 10 | [(SiCSiC)C1im]+ | [OTf]− | 1.159![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 373 373 |
333.6 | 483.2 |
| 11 | [(SiCSiCSiC)C1im]+ | [NTf2]− | 1.214![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 950 |
483.8 | 225.9 |
| 12 | [(SiOSiC)C1im]+ | [NTf2]− | 1.294![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 319 319 |
400.3 | 73.8 |
| 13 | [(SiOSiC)C1im]+ | [B(CN)4]− | 0.984![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
360.1 | 47.4 |
| 14 | [(SiOSiC)C1im]+ | [N(CN)2]− | 1.023890 | 299.4 | 57.2 |
When comparing densities across the series of the same cation, [(SiCSiC)C1im]+ (Table 2), the density first reduces in the order of decrease in anion mass, while the tetracyanoborate stands out from this trend and yields an IL less dense than dicyanamide does, which is the lightest of the anions:
| [NTf2]− > [OTf]− > [N(CN)2]− > [B(CN)4]− |
In fact, [(SiCSiC)C1im][B(CN)4] was found to be the least dense IL among the prepared in this study (Table 2, entry 8). A similar order of anion-dependent densities was observed for the three [(SiOSiC)C1im]+-cation-based ILs (Table 2, entries 12–14) with [(SiOSiC)C1im][B(CN)4] reaching 0.98 g cm−3. Low densities of [B(CN)4]− ILs have been noted previously,27,28 and can be explained with the ion size comparable to common IL anions, but at the same time with a lower mass.28 Common [NTf2]−, for example, is 2.5 times heavier than [B(CN)4]−. Although [N(CN)2]− is even lighter, it is not as voluminous and offers a better packing of the liquid that results in higher densities.
The densities of the three isoelectronic and isostructural [NTf2]− ILs (Table 2, entries 3, 7, and 12) are very similar. The lightest of the cations, [(Me4C5)C1im]+, leads to the most dense liquid amongst the three ILs.
It is not possible to evaluate the properties of the branched [(SiCSiC)C1im]+ in light of its isomeric straight-chain analogue due the highly reactive nature of Si–H bonds. However, among its carbon counterparts, [C9C1im][NTf2] appears to be less dense than its isomer [(Me4C5) C1im][NTf2] (Table 2, entries 3 and 4), suggesting that branching within the carbon-based cation clearly leads to better packing within the liquid than its linear isomer does.
Although incorporation of silicon atoms increases the ion weight, it slightly reduces density – by 1.5% when comparing [(Np)C1im][NTf2] and [(SiC)C1im][NTf2] (entries 2 and 6), and by 1.0% for [(Me4C5)C1im][NTf2] and [(SiCSiC)C1im][NTf2] (entries 3 and 7). This is in agreement with the cation size expansion expected from the longer Si–C bonds formed by silicon.37 In fact, we are the first to accurately report the densities of these two simplest branched ILs, [(Np)C1im][NTf2] and [(SiC)C1im][NTf2], since they were first characterized in 2005.32 Generally, we found the two ILs to be less dense than previously reported, which could be associated with a more sophisticated measurement technique used here. The relative order of the two densities remains as previously reported.
When the silane side-chain is elongated by one more unit of – Si(CH3)2 – and reaches 3 silicon atoms, the [NTf2]− IL density is further reduced (Table 2, entries 6, 7 and 11):
| [(SiC)C1im]+ > [(SiCSiC)C1im]+ > [(SiCSiCSiC)C1im]+ |
This can be explained by the decrease in the relative contribution to the mass of the heavy [NTf2]− anion when the cation size is increased using light atoms.
The molar volumes of all of the studied ILs were found to linearly increase with temperature within the studied temperature range (Fig. S26†). The linear fit parameters obtained for these relationships are provided in Table S4†.
Viscosity
For ILs, a balance between the strength of anion–cation interactions, dispersion, and ion mobility determines one of their most important properties, viscosity. The viscosities of all the prepared samples (Table 2) were measured as a function of temperature and fitted to the Vogel–Fülcher–Tamman–Hesse equation (Fig. 3).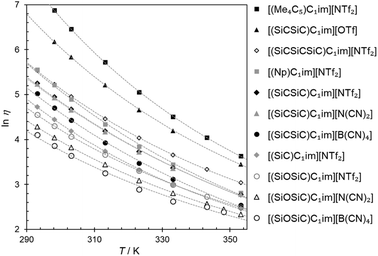 | ||
| Fig. 3 Natural logarithm of viscosity (ln η) for the synthesized ILs as a function of temperature (T). The cation structures and abbreviations are listed in Table 1. The fitting parameters are provided in Table S5†. | ||
Across the ILs studied here, we observed viscosity trends that are consistent for both the [(SiCSiC)C1im]+ and [(SiOSiC)C1im]+ families. The viscosities for ILs of these cations decrease in the following order:
| [NTf2]− > [N(CN)2]−> [B(CN)4]− |
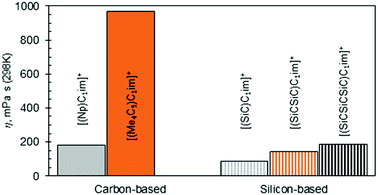
The observation of [(SiC)C1im][NTf2] being less viscous than its carbon counterpart (Table 2, entries 6 and 2) is in good agreement with previous experimental data,32 while the exact viscosity values could be reproduced to within 15%. According to our measurements, at 298 K [(SiC)C1im][NTf2] is 2.1 times less viscous than its carbon counterpart [(Np)C1im][NTf2].
The increase in atom count per ion is expected to give rise to viscosity due to increased dispersion forces and friction, and this effect is reflected in the viscosities of the two higher homologues, [(SiCSiC)C1im][NTf2] and [(Me4C5)C1im][NTf2] (Table 2, entries 7 and 3, and Fig. 4). When the viscosity values are compared, there is a 6.9-fold difference between them. The most remarkable observation here is how little the viscosity increased for the silicon family [(SiCSiC)C1im][NTf2] compared to its isoelectronic carbon counterpart [(Me4C5)C1im][NTf2]. In other words, substitution of the two quaternary carbon atoms by silicon leads to a remarkable reduction in viscosity. When the branched silicon sidechain is extended further, the viscosity remains well below 300 mPa s close to room temperature, as in [(SiCSiCSiC)C1im][NTf2] (Table 2, entry 11). It is hard to imagine that the reduced ion association in Si-based ILs alone32 would be to blame for this stark difference, as the anion is primarily located near the charged ring, remote from the branched sidechain. As noted before,33 torsional rotations of the N–C–Si–C and C–N–C–Si dihedrals in [(SiC)C1im]+ are of significantly lower energy barrier than the carbon counterpart. While this rotational freedom should most certainly be inaccessible in [(Me4C5)C1im]+, in [(SiCSiC)C1im]+ such can exist in multiple locations – near the ring and within the sidechain itself, owing to the additional silicon centre. As a result, intermolecular interactions weaken and can compensate for the increased dispersion.
To a much greater extent, as explained before,25 the rotational freedom is accessible within the siloxane-functionalized cation [(SiOSiC)C1im]+, thus accounting for the lower viscosity of the associated ILs.25 Taking the available viscosity data for ILs of this cation (Table S6†), we have concluded [(SiOSiC)C1im][B(CN)4] (47 mPa s, Table 2, entry 13) to be the second most fluid IL of this cation reported, following [(SiOSiC)C1im][Al(hfip)4] (34 mPa s).34
In conclusion, branching in the cation alkyl side chain leads to an increase in viscosity, but this can be severely reduced by introducing silicon or a Si–O–Si linkage in the cation side-chains.
Argon solubility
The low IL densities suggest a looser ion packing within the liquid state, which could lead to a higher free volume within the liquid. Based on experimental molar volumes and constituent ion van der Waals volumes, Endo et al.35 estimated the free volume fraction in ILs with and without silicon functionalization. Their estimates suggested that the free volume fractions in silicon-based ILs are “generally somewhat larger” than in conventional ones. To this end, we used argon as a weekly interacting probe for the free volume to study the family of silicon-functionalized and branched ionic liquids. Solubilities of this gas were determined at pressures near atmospheric and as a function of temperature. The solubility values at 313 K will be discussed in more detail.In all 9 systems studied, the argon mole fraction solubilities were generally low, in the order of 10−3, corresponding to 1–2 argon atoms per 1000 IL ion pairs. The calculated Henry's law constants KH are summarized in Table S7† and span from 350 bar to around 1300 bar. This should first be rationalized by the weak interactions that noble gases can undergo with the environment. Secondly, as discussed in the Introduction, less volume remains available in a purely ionic environment to accommodate solutes, even as small as argon. Nevertheless, statistically significant differences in argon solubilities for different ILs could be seen.
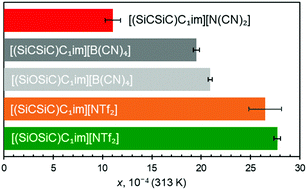
First to note is the impact of different IL anions (Fig. 5) within ILs sharing the same cation. For [(SiCSiC)C1im]+ ILs, an increase in the size of the anion leads to an increase in argon solubility. Although the size difference of [B(CN)4]− and [N(CN)2]− is obvious, as both anions are relatively rigid, the contribution of [NTf2]− might also be related to its conformational flexibility, with the argon solubility being the highest in this IL.
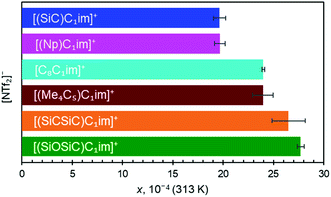
Along the three anions, various cation structures were studied (Fig. 6). The two smallest branched isoelectronic cations, [(SiC)C1im]+ and its carbon counterpart [(Np)C1im]+, did not show measurable differences in argon solubility when paired in liquids with the large [NTf2]− anion, thus demonstrating the relatively small impact a single substitution of C to Si has in this case. It is difficult to speculate, but measurable differences might be expected in such isoelectronic ILs with anions smaller than [NTf2]−.
The effect of C to Si substitutions on argon solubility becomes more apparent in the homologous breached cation with two silicon atoms [(SiCSiC)C1im][NTf2] (Fig. 6), and its respective carbon counterpart [(Me4C5)C1im][NTf2] (Fig. 6). A slightly higher argon mole fraction at equilibrium is measured for [(SiCSiC)C1im][NTf2], even considering experimental uncertainties. It appears that the dominant anion effect on the argon solubility is outweighed only when a higher number of Si atoms are incorporated into the structure of the cation.
The effect of anion size is also consistently apparent when siloxane versions of [B(CN)4]− and [NTf2]− ILs are examined (Fig. 5). The results clearly suggested that argon solubility is higher in [(SiOSiC)C1im][NTf2] than in [(SiOSiC)C1im][B(CN)4]. At the same time, when comparing the cations with Si–O–Si vs. Si–CH2–Si linkages, it appears that the ILs with the flexible siloxane side group exhibit higher argon solubility than their more rigid carbon counterparts (Fig. 5). While clear for the two [B(CN)4]− ILs, the larger argon solubility error bar for [(SiCSiC)C1im][NTf2] does not allow us to fully validate this assumption. Enhancement of argon solubility in the IL with the Si–O–Si linker is likely rooted in the conformational richness of the siloxane group,25 which occupies a larger and less defined space in the liquid.
[C8C1im]+, a linear sidechain-cation relatively similar to [(Me4C5)C1im]+, was examined to assess the effects of branching within alkyl groups. Although both cations have different total carbon atom count within the cation side-chain (8 vs. 9, respectively), the measured argon solubilities allowed a conclusion to be reached that [(Me4C5)C1im][NTf2] can dissolve an amount of argon rather similar to [C8C1im][NTf2]. Given the higher molar volume of C9 than the IL of C8 (Table 2, entries 4 and 5), it is reasonable to expect that the argon solubility in the [C9C1im][NTf2] IL is even higher than in its branched counterpart. This is in good agreement with the proposed closer ion packing in [(Me4C5)C1im][NTf2], suggested by its increased density.
It might be intuitive to propose that the solubility of argon is simply proportional to the molar volume of the IL (Table 2). Although this trend somewhat holds true, there are clear exceptions in our dataset where the molar volume of the three ILs differs by as much as 7%, while the respective argon solubilities are virtually identical (Fig. S24†), and vice versa.
In summary, we observed that the extended cation size and branching can lead to an increase in argon solubility only if the branched structure is based on a silicon backbone and bears more than one silicon atom. The anion plays the predominant role in determining the argon solubility and the free volume within the liquid. Larger and conformationally flexible anions, as well as flexible cations, lead to higher free volumes as can be seen from the studied IL set.
Thermodynamics of the solvation of argon
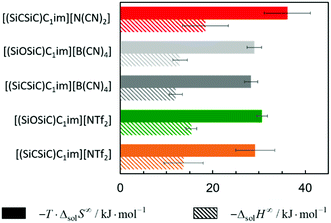
The solubility of argon in the studied ionic liquids is directly related to the Gibbs free energy of solvation, as described by eqn (1). To gain molecular insight into the solubility phenomena, the solvation process can be imagined as the transference of a solute molecule from its gas phase to a cavity in the solvent, followed by relaxation around the solute and the creation of solute–solvent interactions. In this hypothetical model, the nature and size of the solute, and the typically high cohesive energies of the ionic liquids are considered, it can be assumed that the main driving forces of the solvation of argon in these solvents are the free volume of the solvent and the solute–solvent interactions. In a simplistic view, we can relate the free volume of the solvent to the molar entropy of solvation at infinite dilution and the solute–solvent interactions to the molar enthalpy of solvation. This simplification is useful to rationalize the solubility of argon in the different ionic liquids studied and has been proved to be valid for the absorption of other interacting gases in ILs.43In Fig. 7 and 8, the enthalpy and entropy of argon solvation in the different ILs at 313 K are represented. As depicted, the solvation of argon in all ILs is dominated by entropic contributions. The enthalpy of argon solvation is exothermic in all the ILs studied and varies between −12 kJ mol−1 and −20 kJ mol−1 at 313 K. The entropy of solvation is also negative and varies between −90 J mol−1 K−1 and −115 J mol−1 K−1 also at 313 K, depending on the IL. Furthermore, for several of the ILs studied, the thermodynamics of the solvation of argon do not exhibit statistically meaningful difference. This is the result of two main reasons. Firstly, the similarity of the solvents studied and the low solubility of the argon in these solvents, which leads to higher experimental uncertainties. Secondly, the enthalpy and entropy of solvation are not determined directly, but instead derived from the solubility measurements, which increases the associated uncertainty. Some subtle effects are nevertheless noticeable and provide valuable insights.
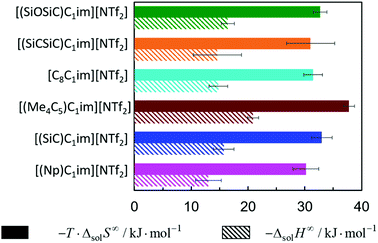 | ||
| Fig. 7 Standard molar enthalpy and entropy of argon solvation in [cation][NTf2] ILs at infinite dilution at 313 K. | ||
From the analysis of Fig. 7, it is noticeable that the entropy of argon solvation in [(SiC)C1im][NTf2] is slightly more negative than in [(Np)C1im][NTf2]. On the contrary, the entropy of argon solvation in the [(SiCSiC)C1im][NTf2] IL is notoriously less negative than in the [(Me4C5)C1im][NTf2] IL. This is in accordance with a significant increase in the free volume of the IL upon the double C to Si substitution, as opposed to the relatively small impact in the case of a single C to Si substitution.
Moreover, the entropy of argon solvation in the [(Me4C5)C1im][NTf2] IL is more negative than in [C8C1im][NTf2]. This observation can be attributed to the difference in the total carbon atom count within the cation side-chain (8 vs. 9, respectively) and knowing that the free volume increases along with the increase in the size of the alkyl chain.36 The more negative entropy of argon solvation in [(Me4C5)C1im][NTf2] thus supports the existence of a closer ion packing of the branched IL.
With respect to the anion effect, the entropy of solvation is more negative in [(SiCSiC)C1im][N(CN)2], which is in accordance with its lower free volume. No statistically significant differences can be found between the entropy of argon solvation in [(SiCSiC)C1im] [B(CN)4] and in [(SiCSiC)C1im][NTf2]. However, the entropy of argon solvation in [(SiOSiC)C1im][NTf2] seems to be more negative than in [(SiOSiC)C1im][B(CN)4]. Again, if we assume that the free volume is reflected in the entropy of solvation, the following trend in the increasing free volume can be considered:
| [N(CN)2]− <[NTf2]− < [B(CN)4]−. |
| [N(CN)2]− < [B(CN)4]− < [NTf2]−; |
It has also been noted that the solubility of argon is higher in ILs containing the [(SiOSiC)C1im]+ cation instead of [(SiCSiC)C1im]+. However, no statistically significant differences can be observed in the enthalpies and entropies of solvation of argon in these ILs.
Argon solubility evaluated with MD
We evaluated the residual chemical potential and the solubility of Ar in [(SiC)C1im][NTf2] and [(SiCSiC)C1im][NTf2] with the CL&Pol polarizable force field to aim for gas solubility prediction in ILs. The computed data were compared to the experimental data reported for a partial pressure of 1 bar and the temperature extrapolated to 353 K, as shown in Table 3. Absolute deviations in residual chemical potential were found to be relatively small, up to 3.5 kJ mol−1. The calculated chemical potential depended mainly on the van der Waals energy required to grow a Lennard-Jones (LJ) sphere in the bulk IL, with the induced dipole contribution being very small (Fig. S2†).| System | μ res/kJ mol−1 | x/10−4 | |
|---|---|---|---|
| [(SiC)C1im][NTf2] | Exp | 8.33 | 6.7 |
| Sim | 5.15 | 18.0 | |
| [(SiCSiC)C1im][NTf2] | Exp | 7.74 | 10.2 |
| Sim | 4.27 | 33.3 | |
The solubility of argon was predicted as expected at a semi-quantitative level, with the values overestimated by about three times, but a general trend of higher argon solubility in [(SiCSiC)C1im][NTf2] than [(SiC)C1im][NTf2] was confirmed. We considered that further calculations involving other ILs would not provide much relevant information because of the simplicity of solute–solvent interactions, the high computational costs, and the availability of experimental data for these systems. Therefore, in this work, Free Energy Perturbation (FEP) calculations were used essentially for validation of the force field.
Local structure analysis
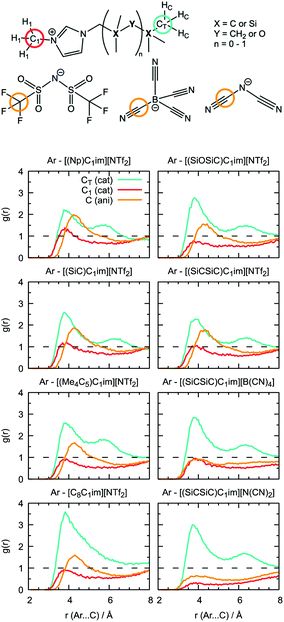
Undoubtedly, MD simulations can provide useful information on the structure of the solutions of argon in the different ILs, allowing us to establish a connection with the gas solubility. We analyzed the local environment of the solute in two sets of ILs: [(Np)C1im]+, [(SiC)C1im]+, [(Me4C5)C1im]+, [C8C1im]+, [(SiCSiC)C1im]+ and [(SiOSiC)C1im]+ with [NTf2]− to study the influence of the side-chain functionalization, and [(SiCSiC)C1im]+ with [NTf2]−, [N(CN)2]− and [B(CN)4]− to reveal the effect of the anions. The radial distribution functions around argon in the above-mentioned systems are included in Fig. 9.In the cation series, we do not observe significant differences upon incorporation of a silicon atom. The terminal methyl groups of the side-chain of the cations compete with the trifluoromethyl groups of the [NTf2]− anion for the solute. The intensities of the CH3 and CF3 radial distribution function (RDF) peaks in [(Np)C1im][NTf2] are comparable. Replacement of a carbon atom by a silicon atom ([(SiC)C1im][NTf2] and [(SiCSiC)C1im][NTf2]) or the presence of a longer side-chain in [(Me4C5)C1im][NTf2] affect the ratio between these two peaks, increasing the probability of finding argon near the side-chain of a cation. This effect is most pronounced when the flexible siloxane group is introduced, with the ratio g(CH3)/g(CF3) reaching almost 2 in [(SiOSiC)C1im][NTf2].
The effect of branching the side-chain can be assessed by comparing [C8C1im][NTf2] with [(Me4C5)C1im][NTf2]. No difference is observed in the intensity of the CF3 peak but a considerable change is identified for CH3, probably due to a more probable argon–IL interaction in [C8C1im][NTf2] when compared to [(Me4C5)C1im][NTf2]. The difference also reflects a dilution effect due to the different number of terminal methyl groups present in the ILs, which are considered in the normalization of the RDF. The contribution of the N-methyl group of the cation is less marked, especially for cations with a longer side-chain ([(Me4C5)C1im][NTf2] and [(SiCSiC)C1im][NTf2]) or containing a siloxane group ([(SiOSiC)C1im][NTf2]).
Replacement of the anion leads to more prominent structural changes. In [(SiCSiC)C1im][NTf2], the probabilities of finding the CH3 and CF3 groups near argon are 2.3 and 1.7, respectively. In [(SiCSiC)C1im][B(CN)4] and [(SiCSiC)C1im][N(CN)2] the intensities of the CH3 peak reach 2.9, while cyano-groups of the anions almost cannot be found around argon (g(CN) ≤ 1). Furthermore, the contribution of the CH3–N group is drastically reduced in [(SiCSiC)C1im][N(CN)2], driven by an interaction of the positively charged CH3-im+-CH2 moiety with the anion (Fig. S4†) instead of the nonpolar argon. These notable changes in the argon environment can be related to different polarity and flexibility of the anions, with a preferential presence of [NTf2]− over [B(CN)4]− or [N(CN)2]−.
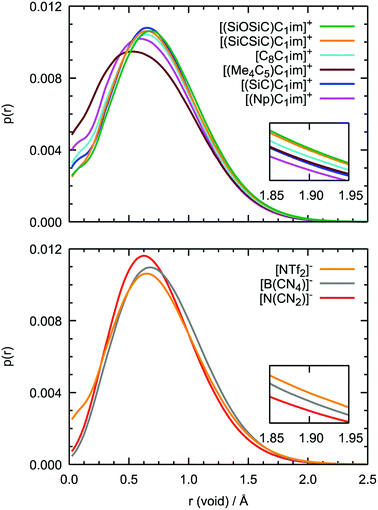
Although the anions have the determining effect on solute–solvent interactions, another relevant contribution to gas solubility is due to free volume, which we aimed to increase in this study through side-chain functionalization. Free volume can be investigated by analyzing the relative occurrence of spontaneous cavities as a function of their size. As shown in Fig. 10, cavities with a radius of 0.5–0.7 Å dominate in all ionic liquids. The contribution of voids with r = 1.9 Å, which is the size capable of embedding argon atoms, is relatively small (in the range of (1–3) × 10−4, with the standard deviation not exceeding 5 × 10−6). The probability of finding cavities with a radius of 1.9 Å decreases with increasing ion rigidity and a shortening of the non-polar side-chain along the cation series [(SiOSiC)C1im]+ > [(SiCSiC)C1im]+ > [C8C1im]+ > [(Me4C5)C1im]+, [(SiC)C1im]+ > [(Np)C1im]+. The same tendency is observed in the anion series, [NTf2]− > [B(CN)4]− > [N(CN)2]−, complemented by the effects of charge delocalization and strengthening of the interaction with the imidazolium core.
Interestingly enough, the trends in the free volume probabilities in the cation and anion series are in accordance with the experimental solubilities of argon, as shown in Fig. 5 and 6. The inconsistencies observed in the cation series can be explained by an overlap of the confidence intervals in the experimental data. Thus, from MD simulations, we can clearly identify the IL with the highest solubility of argon among the studied samples, [(SiOSiC)C1im][NTf2], and free volume analysis thus seems to be a reliable method to choose a good solvent for a small nonpolar gas. Thus, from MD simulations, we can identify the ILs with the highest solubility of argon among the studied samples, [(SiOSiC)C1im][NTf2] and [(SiCSiC)C1im][NTf2], and free volume analysis thus seems to be a reliable method by which to choose a good solvent for a small nonpolar gas.
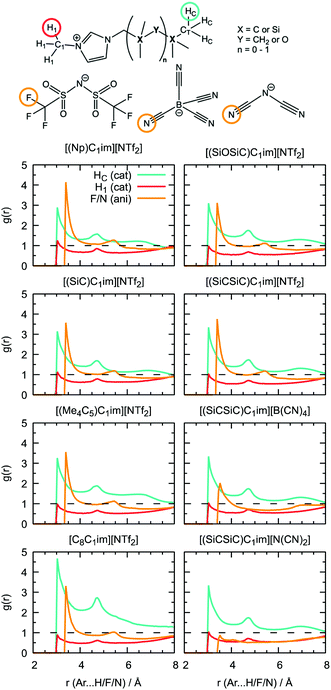
Additional information can be obtained from comparing the local structure around the cavities with the microenvironment of argon in these ILs, through RDF analysis. Voids with a radius of 1.9 Å, were chosen on the basis of the Lennard-Jones diameter of the argon atoms (Fig. 11). Cavitie-s are found to be hydrophobic due to their exposure to long alkyl, alkylsilane, and alkylsiloxane side-chains of the cations and to the anion trifluoromethyl groups (Fig. 12). In [(Np)C1im][NTf2], the probability of finding the NTf2− CF3 groups is much higher than that of the terminal CH3 groups of the cation. The difference between the intensities of these two peaks diminishes with the incorporation of silicon atoms ([(SiC)C1im][NTf2] and [(SiCSiC)C1im][NTf2]), with increasing length of the side-chain ([(Me4C5)C1im][NTf2]), and completely vanishes when a siloxane group is added in [(SiOSiC)C1im][NTf2]. The noticeable increase in the intensity of the CH3 peak intensity, observed in an IL with a linear side-chain, [C8C1im][NTf2], when compared to its branched analogue, [(Me4C5)C1im][NTf2], is due to a dilution effect, as explained above. In all the ILs, the contribution of the CH3–N group in the cavity environment is small, with the intensity of the first peak being always close to 1.
 | ||
| Fig. 11 Snapshot of a [(Np)C1im][NTf2] simulation box with cavities (represented by blue spheres) of a radius of 1.9 Å sufficient to embed argon atoms. | ||
More pronounced changes in the local structure around the voids can be observed when the anion is replaced. While [NTf2]− presents its hydrophobic CF3 group next to the voids, competing with a cation, [B(CN)4]− and, especially, [N(CN)2]− move from the cavities to the charged domains in the IL. This effect is driven by a preferential interaction of the cyano-groups with the imidazolium head group of the cation, forming weak N···H–C hydrogen bonds.
From comparison of the RDFs, we see that the solvation environment of argon is very similar to that of cavities, with the differences being observed only in the ratio of peak intensities, namely among the anion series. The trifluoromethyl groups of [NTf2]− are present in spontaneous cavities more than the terminal methyl groups of the cations. This is opposite to the contribution of these groups to the local structure around argon. The cyano-groups of [B(CN)4]−can still be found in cavity environments, whereas in argon solutions their probability is comparable to that of CH3–N groups. In a [N(CN)2]-based IL, the anion is not present, neither surrounding the argon nor around the cavities. Around cavities, the intensity of peaks due to cations is almost independent of the nature of the counterions, but this independence is not verified in argon solutions.
We confirm through simulations that argon enters nonpolar voids of a suitable size in the ILs, without significantly affecting the internal structure of the solvent. As the interaction between argon and the ILs is mainly dispersive, this gas is indeed a good probe for the free volume analysis of ILs.
Conclusions
We have devised preparative routes to novel ionic liquids that bear heavily branched cation side-chains. We have demonstrated that alkyl silane and siloxane units contribute best to the free volume in the liquid, both increasing the molar volumes and the conformational flexibility of the ion pair.The presented MD methodology of free volume investigation based on the comparison of cavity environment with the local structure of a simple monoatomic gas capable of entering the voids in ILs provides us with complete and reliable information on the free volume nature, which is promising for studying more complex solutes. It allows the identification of the IL with the highest argon solubility without the need for computationally expensive free energy calculations. Successfully extended to new silane and siloxane groups, the CL&Pol polarisable force field also allows us to evaluate gas solubilities on a semi-quantitative level and can be used for prediction of the solubility trends of other systems.
Data availability
The force field parameters are available free of charge on our GitHub repository (https://github.com/paduagroup). For synthetic and measurement data, refer to the ESI.†Author contributions
E. Bakis – conceptualization, funding acquisition, development of synthetic methodology, density, viscosity, and gas solubility measurements, writing – original draft, supervision. K. Goloviznina – force field development, MD simulations, writing – original draft; I. C. M. Vaz – density, viscosity, and gas solubility measurements, thermodynamics data treatment, writing – original draft; D. Sloboda, D. Hazens – synthesis of ILs; V. Valkovska – high resolution mass spectra acquisition; I. Klimenkovs – synthesis of ILs; A. Padua – conceptualization, funding acquisition, writing – review & editing, supervision; M. Costa Gomes – conceptualization, funding acquisition, writing – review & editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
EB acknowledges post-doctoral grant No 1.1.1.2/VIAA/3/19/549 for funding. KG and IV thank IDEX-LYON for financial support (Programme Investissements d’Avenir ANR-16-IDEX-0005). MD simulations were performed on the computer clusters of the GENCI-IDRIS (Grant 2020-A0090800609) and the Pôle Scientifique de Modélisation Numérique (PSMN) at ENS de Lyon. KG acknowledges F. Philippi (Imperial College London) for the force field parameters for the [B(CN)4]− anion. The authors acknowledge Prof. T. Welton (Imperial College London) and Prof. A. Zicmanis (University of Latvia) for helpful discussions.Notes and references
- (a) M. S. Shannon, J. M. Tedstone, S. P. O. Danielsen, M. S. Hindman, A. C. Irvin and J. E. Bara, Ind. Eng. Chem. Res., 2012, 51, 5565–5576 CrossRef CAS; (b) K. Shimizu, M. Tariq, M. F. Costa Gomes, L. P. N. Rebelo and J. N. C. Lopes, J. Phys. Chem. B., 2010, 114, 5831–5834 CrossRef CAS PubMed; (c) A. B. Pereiro, J. M. M. Araújo, S. Martinho, F. Alves, S. Nunes, A. Matias, C. M. M. Duarte, L. P. N. Rebelo and I. M. Marrucho, ACS Sustainable Chem. Eng., 2013, 1, 427–439 CrossRef CAS.
- R. Banerjee, H. Furukawa, D. Britt, C. Knobler, M. O'Keeffe and O. M. Yaghi, J. Am. Chem. Soc., 2009, 131, 3875–3877 CrossRef CAS PubMed.
- G. Durá, V. L. Budarin, J. A. Castro-Osma, P. S. Shuttleworth, S. C. Z. Quek, J. H. Clark and M. North, Angew. Chem., 2016, 128, 9319–9323 CrossRef.
- H. Zhao, X. Luo, H. Zhang, N. Sun, W. Wei and Y. Sun, Greenhouse Gases: Sci. Technol., 2018, 8, 11–36 CrossRef CAS.
- C. Wang, B. An and W. Lin, ACS Catal., 2019, 9, 130–146 CrossRef CAS.
- W.-G. Cui, G.-Y. Zhang, T.-L. Hu and X.-H. Bu, Coord. Chem. Rev., 2019, 387, 79–120 CrossRef CAS.
- (a) N. Giri, M. Del Pópolo, G. Melaugh, R. L. Greenaway, K. Rätzke, T. Koschine, L. Pison, M. F. Costa Gomes, A. I. Cooper and S. L. James, Nature, 2015, 527, 216–221 CrossRef CAS PubMed; (b) J. Avila, C. Červinka, P. Dugas, A. A. H. Pádua and M. Costa Gomes, Adv. Mater. Interfaces, 2021, 8, 2001982 CrossRef CAS.
- Y. Zhou, J. Avila, N. Berthet, S. Legrand, C. C. Santini, M. Costa Gomes and V. Dufaud, Chem. Commun., 2021, 57, 7922–7925 RSC.
- L. Moura, C. C. Santini and M. F. Costa Gomes, Oil Gas Sci. Technol., 2016, 71, 23 CrossRef.
- N. J. Brooks, F. Castiglione, C. M. Doherty, A. Dolan, A. J. Hill, P. A. Hunt, R. P. Matthews, M. Mauri, A. Mele, R. Simonutti, I. J. Villar-Garcia, C. C. Weber and T. Welton, Chem. Sci., 2017, 8, 6359–6374 RSC.
- C. C. Weber, N. J. Brooks, F. Castiglione, M. Mauri, R. Simonutti, A. Mele and T. Welton, Phys. Chem. Chem. Phys., 2019, 21, 5999–6010 RSC.
- H. Niedermeyer, J. P. Hallett, I. J. Villar-Garcia, P. A. Hunt and T. Welton, Chem. Soc. Rev., 2012, 41, 7780–7802 RSC.
- E. Bakis, A. van den Bruinhorst, L. Pison, I. Palazzo, T. Chang, M. Kjellberg, C. C. Weber, M. Costa Gomes and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 4624–4635 RSC.
- K. Goloviznina, J. N. Canongia Lopes, M. Costa Gomes and A. A. H. Pádua, J. Chem. Theory Comput., 2019, 15, 5858–5871 CrossRef CAS PubMed.
- K. Goloviznina, Z. Gong, M. F. Costa Gomes and A. A. H. Pádua, J. Chem. Theory Comput., 2021, 17, 1606–1617 CrossRef CAS PubMed.
- K. Goloviznina, Z. Gong and A. A. H. Padua, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1572 CAS.
- J. N. Canongia Lopes, J. Deschamps and A. A. H. Pádua, J. Phys. Chem. B, 2004, 108, 2038–2047 CrossRef.
- J. N. Canongia Lopes and A. Pádua, Theor. Chem. Acc., 2012, 131, 1129 Search PubMed.
- J. Jacquemin, M. F. Costa Gomes, P. Husson and V. Majer, J. Chem. Thermodyn., 2006, 38, 490–502 CrossRef CAS.
- S. Doblinger, D. S. Silvester and M. Costa Gomes, Fluid Phase Equilib., 2021, 549, 113211 CrossRef CAS.
- J. D. Dymond, K. N. Marsh and R. C. Wilhoit, Virial Coefficients of Pure Gases, Springer-Verlag Berlin Heidelberg, 2002 Search PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- B. Hess, J. Chem. Phys., 2002, 116, 209 CrossRef CAS.
- F. Weinhold and R. West, Organometallics, 2011, 30, 5815–5824 CrossRef CAS.
- H. Niedermeyer, M. A. Ab Rani, P. D. Lickiss, J. P. Hallett, T. Welton, A. J. P. White and P. A. Hunt, Phys. Chem. Chem. Phys., 2010, 12, 2018 RSC.
- D. R. MacFarlane, S. A. Forsyth, J. Golding and G. B. Deacon, Green Chem., 2002, 4, 444–448 RSC.
- T. M. Koller, S. R. Schmid, S. J. Sachnov, M. H. Rausch, P. Wasserscheid and A. P. Fröba, Int. J. Thermophys., 2014, 35, 195–217 CrossRef CAS.
- F. Philippi, D. Rauber, B. Kuttich, T. Kraus, C. W. M. Kay, R. Hempelmann, P. A. Hunt and T. Welton, Phys. Chem. Chem. Phys., 2020, 22, 23038–23056 RSC.
- M. Tariq, P. J. Carvalho, J. A. P. Coutinho, I. M. Marrucho, J. N. C. Lopes and L. P. N. Rebelo, Fluid Phase Equilib., 2011, 301, 22–32 CrossRef CAS.
- M. A. A. Rocha, C. M. S. S. Neves, M. G. Freire, O. Russina, A. Triolo, J. A. P. Coutinho and L. M. N. B. F. Santos, J. Phys. Chem. B, 2013, 117, 10889–10897 CrossRef CAS PubMed.
- M. Tariq, A. P. Serro, J. L. Mata, B. Saramago, J. M. S. S. Esperança, J. N. Canongia Lopes and L. P. N. Rebelo, Fluid Phase Equilib., 2010, 294, 131–138 CrossRef CAS.
- H. Shirota and E. W. Castner, J. Phys. Chem. B, 2005, 109, 21576–21585 CrossRef CAS PubMed.
- F. Philippi and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 6993–7021 RSC.
- S. Bulut, M. A. Ab Rani, T. Welton, P. D. Lickiss and I. Krossing, ChemPhysChem, 2012, 13, 1802–1805 CrossRef CAS PubMed.
- T. Endo, S. Nemugaki, Y. Matsushita, Y. Sakai, H. Ozaki, Y. Hiejima, Y. Kimura and K. Takahashi, Chem. Phys., 2016, 472, 128–134 CrossRef CAS.
- T. Song, M. J. Lubben and J. F. Brennecke, Fluid Phase Equilib., 2020, 504, 112334 CrossRef CAS.
- B. Wu, Y. Yamashita, T. Endo, K. Takahashi and E. W. Castner, J. Chem. Phys., 2016, 145, 244506 CrossRef PubMed.
- H. Shirota, J. Wishart and E. W. Castner, J. Phys. Chem. B, 2007, 111, 4819–4829 CrossRef CAS PubMed.
- D. Almantariotis, T. Gefflaut, J. Y. Coxam, A. A. H. Padua and M. F. Costa Gomes, J. Phys. Chem. B, 2010, 114, 3608–3617 CrossRef CAS PubMed.
- C. S. M. Kang, X. Zhang and D. R. MacFarlane, J. Phys. Chem. C, 2019, 123, 21376–21385 CrossRef CAS.
- M. B. Wenny, N. Molinari, A. H. Slavney, S. Thapa, B. Lee, B. Kozinsky and J. A. Mason, J. Phys. Chem. B, 2022, 126, 1268–21274 CrossRef CAS PubMed.
- B. Wu, H. Shirota, S. Lall-Ramnarine and E. W. Castner, J. Chem. Phys., 2016, 145, 114501 CrossRef.
- L. Moura, C. C. Santini and M. F. Costa Gomes, Oil Gas Sci. Technol., 2016, 71, 23–34 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc01696f |
| This journal is © The Royal Society of Chemistry 2022 |