 Open Access Article
Open Access ArticleA machine learning protocol for revealing ion transport mechanisms from dynamic NMR shifts in paramagnetic battery materials†
Min
Lin
 a,
Jingfang
Xiong
a,
Mintao
Su
a,
Feng
Wang
a,
Xiangsi
Liu
a,
Jingfang
Xiong
a,
Mintao
Su
a,
Feng
Wang
a,
Xiangsi
Liu
 a,
Yifan
Hou
a,
Riqiang
Fu
a,
Yifan
Hou
a,
Riqiang
Fu
 d,
Yong
Yang
d,
Yong
Yang
 *ab and
Jun
Cheng
*ab and
Jun
Cheng
 *ac
*ac
aCollaborative Innovation Center of Chemistry for Energy Materials, State Key Laboratory for Physical Chemistry of Solid Surface, College of Chemistry and Chemical Engineering, Xiamen University, Xiamen 361005, China. E-mail: yyang@xmu.edu.cn
bCollege of Energy, Xiamen University, Xiamen 361005, China
cInnovation Laboratory for Sciences and Technologies of Energy Materials of Fujian Province (IKKEM), Xiamen 361005, China. E-mail: chengjun@xmu.edu.cn
dNational High Magnetic Field Laboratory, 1800 E. Paul Dirac Drive, Tallahassee, FL 32310, USA
First published on 13th June 2022
Abstract
Solid-state nuclear magnetic resonance (ssNMR) provides local environments and dynamic fingerprints of alkali ions in paramagnetic battery materials. Linking the local ionic environments and NMR signals requires expensive first-principles computational tools that have been developed for over a decade. Nevertheless, the assignment of the dynamic NMR spectra of high-rate battery materials is still challenging because the local structures and dynamic information of alkali ions are highly correlated and difficult to acquire. Herein, we develop a novel machine learning (ML) protocol that could not only quickly sample atomic configurations but also predict chemical shifts efficiently, which enables us to calculate dynamic NMR shifts with the accuracy of density functional theory (DFT). Using structurally well-defined P2-type Na2/3(Mg1/3Mn2/3)O2 as an example, we validate the ML protocol and show the significance of dynamic effects on chemical shifts. Moreover, with the protocol, it is demonstrated that the two experimental 23Na shifts (1406 and 1493 ppm) of P2-type Na2/3(Ni1/3Mn2/3)O2 originate from two stacking sequences of transition metal (TM) layers for the first time, which correspond to space groups P63/mcm and P6322, respectively. This ML protocol could help to correlate dynamic ssNMR spectra with the local structures and fast transport of alkali ions and is expected to be applicable to a wide range of fast dynamic systems.
Introduction
The wide application of electric vehicles constantly calls for higher power densities of rechargeable batteries, which require faster alkali-ion diffusion in cathode materials with the structural framework of transition-metal oxides (TMOs).1,2 Hence, understanding the relationship between the atomic structures of cathode materials and alkali-ion diffusions is vitally important.In contrast to diffraction techniques3,4 that are sensitive to long-range and ordered structural features, solid-state nuclear magnetic resonance (ssNMR)5,6 spectroscopy is a unique tool to detect the time-dependent local structures of battery materials. For TMO-based cathode materials, the interpretation of NMR spectra proves very challenging, as the unpaired electrons of TM ions have complicated interactions with the nucleus for which NMR is being observed, resulting in the so-called paramagnetic shifts.7 To this end, the density functional theory (DFT) methodology for calculating paramagnetic shifts has been continuously developed for over a decade.8–12 Nevertheless, the applications of such state-of-the-art computational methods are restricted to slow alkali-ion dynamic systems, e.g., polyanion-type materials8–17 or fully lithiated layered materials,9,18 in which the measured shift corresponds to the local minimum of the potential energy surface (PES) and is characterized by DFT optimized structures (i.e., 0 K). However, for high-rate cathode materials, the fast alkali-ion hopping between distinct chemical sites typically results in fast chemically exchanged NMR spectra at room temperature (RT), named dynamic NMR spectra,19 which represent the weighted average of the chemical shifts of all of the alkali-ion environments involved in chemical exchange.20 Since the dynamic NMR spectra result from the correlated effect between the local environments of the alkali ion and its dynamics, it is extremely difficult to accurately extract the structural information from the dynamic NMR spectra directly through DFT calculations. To the best of our knowledge, there is not yet a rigorous and applicable first-principles methodology for calculating the dynamic NMR shifts of paramagnetic battery materials.
Dynamic NMR spectra have been extensively observed in cathode materials of sodium-ion batteries (SIBs). The 23Na spectra of P-type (Delmas et al.'s notation21) SIB cathode materials are usually dynamic NMR spectra at RT,22–30 due to the large layer spacing that enables fast Na+ diffusion. Even though P2-type Na2/3(Ni1/3Mn2/3)O2 has been intensively studied,31 controversy still exists regarding the 23Na NMR spectra of the as-synthesized materials. Wu et al.24 observed two 23Na shifts in the paramagnetic region, with the dominating one assigned to the P2 phase and the weaker signal with a lower shift to the sodium-poor phase. In contrast, Clément et al.22 assigned the lower shift (1422 ppm) to stacking faults of the O2 phase (Delmas et al.'s notation21). In principle, lowering the temperature could be an option to slow down the exchange dynamics in order to resolve the local environments of the Na+ and its dynamic behind the NMR spectra. For instance, Mukhamedshin et al.29 observed the 23Na shifts of distinct sites of P2-type Na0.67CoO2 in a static NMR experiment below 150 K, which required significant effort in material synthesis to provide aligned single-phase powder samples. However, such a low temperature is not typically available in high-resolution magic-angle-spinning (MAS) ssNMR measurements, where a fast spinning is acquired to obtain high-resolution NMR spectra of powdered paramagnetic battery samples.
Very recently, utilizing highly efficient machine learning potential molecular dynamic (MLPMD)32 simulations that enable sufficient sampling of alkali-ion hopping events, we tentatively calculated the dynamic 23Na NMR shift of P2-type Na2/3(Mg1/3Mn2/3)O2 for the first time.20 Nevertheless, the DFT calculation of the 23Na shift is still based on certain optimized (i.e., 0 K) Na+ patterns due to the high computational cost of chemical shifts. This infantile method neglects the thermal fluctuation effect on the chemical shifts, which limits its wide application. Therefore, developing a solid and widely applicable computational method for dynamic NMR spectra is urgent and important.
In this work, we developed a novel machine learning (ML) protocol for calculating dynamic NMR shifts. Fig. 1 shows a schematic illustration of the protocol that involves two ML models, an MLP model for accelerating configuration sampling, and a Neural Network (NN) model for fast chemical shift prediction, named the NN-NMR model. Specifically, we adopted the well-developed Deep Potential Generator (DP-GEN) scheme33,34 for generating the MLP, which explores new configurations with a concurrent learning approach, and the so-called deep potential (DP)32,35 model is trained iteratively until it reaches the DFT level accuracy. After sufficient sampling of the alkali-ion hopping related to dynamic NMR spectra with long-time DPMD simulations, the chemical shift datasets are generated with sparse configurations of DPMD simulation trajectories and the DFT method. Then, using the smooth overlap of atomic positions (SOAP)36,37 descriptors of local structures and chemical shifts as the input layer and output layer of the NN, respectively (Fig. 2a), the NN-NMR model is trained and tested with the DFT dataset of chemical shifts. Finally, the chemical shifts of dense configurations in DPMD simulation trajectories are predicted using the NN-NMR model.
 | ||
| Fig. 1 Schematic illustration of the machine learning (ML) protocol for calculating the dynamic NMR chemical shifts. | ||
We calculated the dynamic 23Na NMR shift of P2-type Na2/3(Mg1/3Mn2/3)O2 (hereafter denoted as P2-NMMO),38–41 and compared the results with previous computational and experimental results20 for validating the ML protocol. The well-trained NN-NMR model shows highly computational efficiency and accuracy for predicting chemical shifts. Besides, combining with experiments and the dynamic 23Na shifts of P2-type Na2/3(Ni1/3Mn2/3)O2 (hereafter denoted as P2-NNMO) calculated with the protocol, we demonstrated that the lower 23Na shift being debated can be attributed to the averaged 23Na shift of P63/mcm NNMO (Fig. S1a and b†),42 thus clarifying its structural assignment.
Methods
The computational formalism of chemical shifts
The isotropic 23Na shift of a paramagnetic system is composed of four parts, Fermi-contact shift (δFC), pseudo-contact shift (δPC), orbital shift (δorb) and second-order quadrupole shift (δQIS).7,43 Meanwhile, previous studies of the 23Na shift of P2-NMMO and P2-NNMO showed that δFC dominates the total shift.20,22 It is worth noting that δQIS is inversely proportional to the square of the magnetic field strength, and herein 9.4 T suppresses the δQIS of P2-NMMO and P2-NNMO on the order of tens of ppm.20 Therefore, we only calculated δFC with DFT methods (i.e., δDFT = δFC), given by:8,16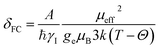 | (1) |
 | (2) |
Density functional theory calculations
All DFT calculations were performed by using VASP44,45 version 5.4.4. with the Projector Augmented Wave (PAW) method.48 For generating the datasets of DP and NN-NMR models, the convergence criterion of self-consistent field (SCF) iterations, K-point, Na pseudopotential, and cut-off energy of the plane-wave basis set is 10−5 eV, 2 × 2 × 2, Na_pv, and 400 eV, respectively (Fig. S3†). The total energies and atomic forces were calculated with the Perdew–Burke–Ernzerhof (PBE)49 functional. To better describe the electronic structures of TM ions that have significant effects on δFC, the hyperfine coupling constant was calculated with the Strongly Constrained and Appropriately Normed50 (SCAN) functional. 2 × 2 × 1 supercell models with 88 atoms were utilized for both NMMO and NNMO, and the cell parameters were fixed as experimental results.20To reasonably compare the total energies of all types of NMMO supercell models (Fig. 4c), the cell parameters and atomic positions were fully relaxed with a higher cut-off energy of 520 eV that provides more accurate stress tensors. The P2 phase supercell adopted the well-known large-zigzag (LZZ, Fig. S1d†)51,52 Na+ pattern. The O2 supercell adopted a honeycomb (Fig. S1e†) Na+ pattern that has the lowest coulomb energy among enumerated structures implemented in the Supercell53 program.
Deep potential training and deep potential molecular dynamics simulations
Since the 200 nanoseconds (ns) DPMD simulation trajectories of P2-NMMO with DFT level accuracy were accomplished in our previous study,20 we directly utilized these trajectories to generate their 23Na δDFT dataset. The DP model of P2-NNMO was also trained in DP-GEN software33 with the same protocol as that of P2-NMMO described in detail in ref. 20 and 33. After six iterations of training, exploration and labeling, 1386 configurations were included in the dataset. The DPMD simulations of supercell models of P63/mcm and P6322 NNMO were carried out by using the LAMMPS54 package with an NVT ensemble at 300 K for 200 ns. All DPMD simulations started with the LZZ Na+ patterns and the time step was 1 femtosecond (fs).The NN-NMR model for predicting chemical shifts
For each trajectory, 500 configurations with a time interval of 400 picoseconds (ps) were extracted and labeled, and thus the DFT datasets of P2-NMMO or P2-NNMO contain 1000 configurations and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 23Na shifts. The SOAP36 vectors of Na+ local environments were generated with the QUIP package and quippy55 interface. The cutoff of the Na+ local region (rcut), the standard deviation of the Gaussian (σ), the number of radial basis functions (nmax), and the maximum degree of spherical harmonics (lmax) are 5.5 Å, 0.5 Å, 9, and 9, respectively. The initialization and training of the NN-NMR model were implemented in Tensorflow56 with the Keras57 Application Program Interface (API). The hidden layer of the NN-NMR model has three sequential layers with 512 nodes per layer (Fig. 2a). Dropouts with a rate of 0.1 and an L2 regularization with λ = 1 × 10−2 were applied to every layer of the NN-NMR model. The learning rate starts with 10−3 and decays inversely during every echo with a decay rate of 5. The total no. of echo is 2000. We performed a 5-fold cross-validation with a training/testing set fraction of 0.8
000 23Na shifts. The SOAP36 vectors of Na+ local environments were generated with the QUIP package and quippy55 interface. The cutoff of the Na+ local region (rcut), the standard deviation of the Gaussian (σ), the number of radial basis functions (nmax), and the maximum degree of spherical harmonics (lmax) are 5.5 Å, 0.5 Å, 9, and 9, respectively. The initialization and training of the NN-NMR model were implemented in Tensorflow56 with the Keras57 Application Program Interface (API). The hidden layer of the NN-NMR model has three sequential layers with 512 nodes per layer (Fig. 2a). Dropouts with a rate of 0.1 and an L2 regularization with λ = 1 × 10−2 were applied to every layer of the NN-NMR model. The learning rate starts with 10−3 and decays inversely during every echo with a decay rate of 5. The total no. of echo is 2000. We performed a 5-fold cross-validation with a training/testing set fraction of 0.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 for all NN-NMR models. An early stop scheme was applied for preventing overfitting. Our encoded training and testing processes of the NN-NMR model are also available at https://github.com/chenggroup/nmr.
0.2 for all NN-NMR models. An early stop scheme was applied for preventing overfitting. Our encoded training and testing processes of the NN-NMR model are also available at https://github.com/chenggroup/nmr.
Results and discussion
Validation of the ML protocol with P2-type Na2/3(Mg1/3Mn2/3)O2
Given that our previous work20 demonstrated that the two 23Na peaks of P2-NMMO, located at 1522 and 1665 ppm, are in-layer dynamic averaged 23Na shifts in space groups P63/mcm and P6322, which correspond to two stacking sequences of transition metal layers, Mg2+ ions stack linearly (Fig. S1b†) and staggered (Fig. S1c†) along the z-axis with a Mg2+/Mn4+ honeycomb superstructure (Fig. S1a†), respectively. In this section, we take P2-NMMO as an example for validating our ML protocol and the NN-NMR model, computational procedures and parameters were presented in the Introduction and Methods sections. Fig. 2b shows that the root-mean-square errors (RMSEs) between the 23Na shift of the testing set calculated with the DFT method (δDFT) and with the NN-NMR model (δNN) decrease with the number (No.) of dataset structures. When No. is 1000, the mean value of 5-fold cross-validation RMSEs is 125 ppm with an R square factor (R2) of 0.96. Given that the 23Na shift of P2-NMMO approximately ranges from 0 to 3000 ppm, an RMSE of 125 ppm indicates that the NN-NMR model of P2-NMMO is highly accurate (Fig. 2c). Besides, the NN-NMR model is also highly efficient; the 23Na δNN of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations taken from 200 ns DPMD trajectories was predicted on an NVIDIA GeForce RTX2080 Ti GPU within 40 minutes, which would take around one year using the DFT method on a single node composed of 28 parallel Intel Xeon E5-2680 v4 CPU cores. The prediction speed of the NN-NMR model is limited by a constant I/O overhead, and the prediction time of a configuration linearly scales with the No. of atoms.
000 configurations taken from 200 ns DPMD trajectories was predicted on an NVIDIA GeForce RTX2080 Ti GPU within 40 minutes, which would take around one year using the DFT method on a single node composed of 28 parallel Intel Xeon E5-2680 v4 CPU cores. The prediction speed of the NN-NMR model is limited by a constant I/O overhead, and the prediction time of a configuration linearly scales with the No. of atoms.
For 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations in each DPMD trajectory of P63/mcm and P6322 NMMO, Fig. 3a shows the histograms of 23Na δNN separately. δNN is mainly distributed between 0 and 3000 ppm, and the histograms are composed of several broad Gaussian peaks, suggesting that the dynamic effect on the 23Na shift is significant. Benefiting from the sufficient configurations of the DP model and 23Na shift sampling of the NN-NMR model, the statistic errors of xy-plane averaged 23Na δNN decrease to sub-ppm (Fig. S10a†). The averaged 23Na δNN of P63/mcm and P6322 is 1638 and 1763 ppm, respectively, which could conclude the same assignment as our previous work.20
000 configurations in each DPMD trajectory of P63/mcm and P6322 NMMO, Fig. 3a shows the histograms of 23Na δNN separately. δNN is mainly distributed between 0 and 3000 ppm, and the histograms are composed of several broad Gaussian peaks, suggesting that the dynamic effect on the 23Na shift is significant. Benefiting from the sufficient configurations of the DP model and 23Na shift sampling of the NN-NMR model, the statistic errors of xy-plane averaged 23Na δNN decrease to sub-ppm (Fig. S10a†). The averaged 23Na δNN of P63/mcm and P6322 is 1638 and 1763 ppm, respectively, which could conclude the same assignment as our previous work.20
To assign the Gaussian peaks of 23Na δNN histograms and understand the difference between the averaged 23Na shift of P63/mcm and P6322, we further analyzed the spatial distributions of the 23Na shift. Given that the Na+ diffusion paths of P2-NMMO are two-dimensional (2D, xy-plane) channels, the grid averaged 23Na δNN on the xy-plane could represent the spatial distributions of the 23Na shift (Fig. 3b and c), and the standard deviations (STDs) of 23Na δNN within the grids are also shown in Fig. S8a and b.† Then, the site-centered circles with a radius of 0.8 Å were utilized for defining the boundaries for all Na sites, and they include most Na+ without double counting, as verified by the finding that the sum of δNN histograms of Na sites approximates to the δNN histogram of the space group (Fig. 3a). By this means, the Na+ occupation fractions and the centered δNN of distinct Na sites can be quantified. In P63/mcm, the centered 23Na δNN of Naedge, NaMn–Mn, and NaMg–Mg sites is 2085, 960, and 1602 ppm with the occupation fractions of 0.586, 0.411, and 0.003, respectively. In P6322, the Naedge (2113 ppm) and NaMn–Mn (965 ppm) shifts, and their Gaussian distributions well agree with those of P63/mcm. Moreover, the NaMn–Mg site shifts (1373 ppm) approximate to the middle point (1284 ppm) of NaMn–Mn and NaMg–Mg site shifts in P63/mcm, which is consistent with the additive character of δFC.9 Therefore, the lower occupation fraction of the lowest shift site (NaMn–Mn) and the higher occupation fraction of the highest shift site (NaMn–Mn) mainly contribute to the higher averaged 23Na shift of P6322.
In our previous method,20 the 23Na shifts of Na sites were calculated with the DFT optimized (i.e., 0 K) LLZ Na+ pattern (Table 1, δLZZ), and the averaged shift of the space group is the occupation weighted shift of distinct Na sites, which neglected the dynamic effect on the 23Na shifts. To clarify the significance of the dynamic effect, we calculated the δLZZ with the DFT method and compared it to the centered 23Na δNN of Na sites. Except for the δLZZ of the Naedge site (2102–2160 ppm) that approximates to its centered 23Na δNN, the δLZZ of NaMn–Mn, NaMg–Mg, and NaMn–Mg sites is 503, 1494, and 1052 ppm, which are considerably lower than their centered 23Na δNN, 960, 1602, and 1373 ppm, respectively. As a result, the averaged shifts of P63/mcm and P6322 calculated with the LZZ pattern are 1452 and 1640 ppm, which are lower than those (1638 and 1763 ppm) calculated with the ML protocol, respectively. Given that experimental shifts20 are 1552 ppm (P63/mcm) and 1665 ppm (P6322), the overestimated shifts of the ML protocol probably are attributed to the errors of the SCAN functional. Comparing with the experimental shift difference (143 ppm) of the two space groups, the ML protocol (125 ppm) gives a better agreement than that calculated with the LZZ pattern (188 ppm). Besides, the ML protocol could calculate the dynamically averaged NMR shift without defining alkali-ion sites, which enables its wide application. For instance, the super-ionic conductors (SICs) that typically have three-dimensional (3D) alkali-ion transport channels and flexible structural frameworks,58 or even electrolytes, in which the alkali-ion sites are not always well defined. It should be noted that most SICs and electrolytes are diamagnetic, and the computational method of their chemical shifts is different from that of paramagnetic electrodes.59 Moreover, the time-averaged 23Na δNN simulated with different periods of time indicates how the shifts of distinct sites merge into the dynamic NMR shift (Fig. S11†).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations, and δexp is the experimental 23Na shift reported in ref. 20
000 configurations, and δexp is the experimental 23Na shift reported in ref. 20
| Space group | Sites | Occupation fractions | δ LZZ/ppm | δ NN/ppm | δ exp (ref. 20)/ppm | ||
|---|---|---|---|---|---|---|---|
| P63/mcm | NaMn–Mn | 0.411 | 503 | 1452 | 960 | 1638 | 1522 |
| NaMg–Mg | 0.003 | 1494 | 1602 | ||||
| Naedge | 0.586 | 2102–2133 | 2085 | ||||
| P6322 | NaMn–Mn | 0.242 | 1640 | 965 | 1763 | 1665 | |
| NaMn–Mg | 0.102 | 1052 | 1373 | ||||
| Naedge | 0.656 | 2139–2160 | 2113 | ||||
Revealing the fine structures of P2-type Na2/3(Ni1/3Mn2/3)O2
Since our ML protocol was successfully validated in P2-NMMO, herein, we extended its application to rationally assign the debated dynamic 23Na NMR shift of as-synthesized P2-NNMO.22,24 Firstly, we synthesized P2-type NNMO with the procedure described in ref. 60. As shown in Fig. 4a, the PXRD diffraction signal can be indexed to the space group P63/mmc, a hexagonal phase with cell parameters a = b = 2.88915 Å and c = 11.14482 Å, which is consistent with ref. 24, 28, 31, 61 and 62. Fig. 4b shows the MAS NMR 23Na spectra at RT, two isotropic shifts located at 1493 (peak 1) and 1406 (peak 2) ppm that well agree with Clément et al.'s22 results (1510 and 1422 ppm).To evaluate the thermodynamic stabilities of debated structures22,24 and other possible structures, we performed DFT calculations of the total energy of related supercell models (see the Methods section). Fig. 4c shows the relative total energies (RTEs) of supercell models by taking the total energy of the P6322 NNMO supercell as a reference. First of all, one Ni2+/Mn4+ disordering results in a RTE of 0.40 eV per supercell, agreeing with the Ni2+/Mn4+ honeycomb superstructure that was evidenced by neutron diffraction (ND).63 Second, the O2 phase is thermodynamically very unstable with a RTE of 2.74 eV per supercell. Besides, the simulated PXRD patterns of a randomly mixed P6322–P63/mc (P2–O2) structure show that a 10–20% mixing O2 phase could lead to remarkable broadening of (004), (104), and (106) peaks (Fig. S12†), which was not observed in the recorded PXRD pattern (Fig. 4a). Therefore, the O2 phase is unlikely to exist in as-synthesized P2-NNMO and was excluded from further investigations. Finally, P63/mcm has a very close RTE (0.04 eV per supercell) with P6322, indicating the possibility of a mixture of P63/mcm and P6322. Note that both P63/mcm and P6322 are secondary phases of P63/mmc with a prerequisite of a Ni2+/Mn4+ honeycomb superstructure, and the superstructure-related XRD peaks should reflect the stacking sequences of TM layers.20 However, the Ni2+/Mn4+ superstructure is invisible for X-rays because Ni2+ and Mn4+ have similar atomic numbers, and the PXRD patterns of mixed P63/mcm–P6322 keep constant among all ranges of fraction ratios (Fig. S12†). Therefore, extending the NMR methodology to identify these indistinguishable structures is very useful as an example of a good compensation for PXRD.
To provide the NMR evidence of P63/mcm–P6322 mixed stacking in P2-NNMO, we applied our novel ML protocol for calculating the dynamic 23Na NMR shift of P63/mcm and P6322. Fig. S2† shows that the RMSE of energies and forces between the well-trained DP model and DFT method is 2.80 × 10−4 ± 6.24 × 10−8 eV per atom and 1.24 × 10−2 ± 2.87 × 10−4 eV Å−1, respectively, suggesting that the DP model reaches the DFT level accuracy. For the accuracy of the NN-NMR model, the RMSE and R2 coefficient of the 23Na shift calculated between with the NN-NMR model and with the DFT method are 83 ppm and 0.97, respectively (Fig. S5†). With the help of the highly accurate and efficient DP and NN-NMR model, the 23Na shifts of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 configurations in 200 ns DPMD simulations were predicted for each space group, and the averaged shift of P6322 and P63/mcm is 1721 and 1636 ppm with negligible statistical errors, respectively (Fig. S10b†). Consequently, peak 1 (1493 ppm) and peak 2 (1406 ppm) in Fig. 4b were assigned to the averaged 23Na shift of P6322 and P63/mcm, respectively. Thus, we concluded that P2-NMMO is composed of a mixed stacking of P6322 and P63/mcm with a fraction of 0.82 and 0.18, respectively.
000 configurations in 200 ns DPMD simulations were predicted for each space group, and the averaged shift of P6322 and P63/mcm is 1721 and 1636 ppm with negligible statistical errors, respectively (Fig. S10b†). Consequently, peak 1 (1493 ppm) and peak 2 (1406 ppm) in Fig. 4b were assigned to the averaged 23Na shift of P6322 and P63/mcm, respectively. Thus, we concluded that P2-NMMO is composed of a mixed stacking of P6322 and P63/mcm with a fraction of 0.82 and 0.18, respectively.
To understand the averaged shift differences of P6322 and P63/mcm NNMO, we adopted the same analysis approach as that of P2-NMMO. The Gaussian peaks in 23Na δNN histograms (Fig. 5a) were assigned according to the xy-plane 23Na δNN maps (Fig. 5b and c). The averaged 23Na δNN of Naedge, NaMn–Mn, and NaNi–Ni sites is 1899, 1225, and 831 ppm with an occupation fraction of 0.651, 0.289 and 0.060 in P63/mcm, respectively. The averaged 23Na δNN of Naedge, NaMn–Mn, and NaMn–Ni sites is 2031, 1275, and 1015 ppm with an occupation fraction of 0.665, 0.128, and 0.207 in P6322, respectively. It is apparent that the higher Naedge shift of P6322 (2031 ppm) than that of P63/mcm (1899 ppm) is the main reason for the higher averaged shift of P6322 P2-NNMO.
The effect of different P2-type stacking sequences (P63/mcm and P6322) on Na+ mobilities
After the stacking sequences of TM layers in P2-type NMMO and NNMO were clearly revealed by combining the NMR experiment and our ML protocol, a remaining question is how these stacking sequences affect Na+ mobilities. Thanks to sufficient sampling of Na+ hopping during 200 ns DPMD simulations, the diffusion coefficients of Na+ (DNa) could be estimated from the root-mean-square-displacement (RMSD) of Na+ with a minor STD64 (Fig. S9a and b†). Interestingly, the DNa of P63/mcm NMMO (1.0 × 10−7 cm2 s−1) is lower than that of P6322 NMMO (4.4 × 10−7 cm2 s−1) by over four times,20 while the DNa of P6322 NNMO (1.0 × 10−6 cm2 s−1) is similar to that of P63/mcm NNMO (9.6 × 10−7 cm2 s−1). To understand the difference between NMMO and NNMO, we proposed a significant blockage effect of Mg2+ on Na+ diffusion. Fig. S7† shows the xy-plane Na+ distribution maps of P2-type NMMO and NNMO obtained from DPMD trajectories, showing honeycomb Na+ diffusion channels. In P63/mcm NMMO, low Na+ occupation of NaMg–Mg sites indicates a blockage effect of Mg2+ on Na+ diffusion, and the blockage effect is mitigated in P6322 NMMO since Mg2+ is staggered along the z-axis (Fig. S1c†), resulting in a higher DNa. In contrast, Ni2+ has no such blockage effect on the Na+ diffusion of P2-NNMO as the occupations of NaNi–Ni and NaMn–Mn sites are similar in P63/mcm NNMO. Therefore, the staggered arrangement of Ni2+ in P6322 NNMO cannot significantly improve the DNa. Given that both Mg2+ and Ni2+ are divalent and Mg–O and Ni–O bonds also have similar lengths of about 2.1 Å, we suggest that the different nature of Mg–O (more ionic) and Ni–O (more covalent) bonds may be responsible for the discrepancy, and a full understanding would merit future investigations.Conclusions
To fast predict the NMR chemical shift of paramagnetic battery materials within DFT accuracy, we presented a machine learning (ML) model, named NN-NMR model that is based on local structure descriptors and a Neural Network (NN). For validation, the NN-NMR model predicted the 23Na shift of P2-type Na2/3(Mg1/3Mn2/3)O2 with high accuracy compared to the DFT values. The NN-NMR model enables us to calculate the chemical shifts of a supercell model with 88 atoms within tens of milliseconds on a GPU, reducing the computational time by several orders of magnitude compared to that of the DFT method on CPUs. Also, its computational cost scales linearly with the No. of atoms, and thus the model can be readily applied to very large systems.We further developed a novel machine learning (ML) protocol to calculate the dynamic NMR shift with DFT accuracy, which combines the machine learning potential (MLP) model and NN-NMR model for accelerating the configurational sampling and chemical shift prediction, respectively. Thanks to sufficient sampling of both configurations and chemical shifts during 200 nanoseconds (ns) MLPMD simulations, the dynamic 23Na shifts of P2-Na2/3(Mg1/3Mn2/3)O2 and P2-Na2/3(Ni1/3Mn2/3)O2 calculated with the ML protocol have negligible statistical errors and agree with our 23Na MAS NMR experimental results. Consequently, two experimental 23Na shifts of P2-Na2/3(Ni1/3Mn2/3)O2 were assigned to the dynamic averaged 23Na NMR signal in two stacking sequences of transition metal (TM) layers, i.e., space group P6322 (1493 ppm) and P63/mcm (1406 ppm), and their fractions were quantified to be 0.82 and 0.18 for the first time, respectively. Besides, comparing the diffusion channels and coefficients of Na+ in P2-Na2/3(Mg1/3Mn2/3)O2 and P2-Na2/3(Ni1/3Mn2/3)O2 obtained from MLPMD simulations, we found that Mg2+ has a blockage effect on Na+ diffusion while Ni2+ has not.
To decouple the effects between local environments and dynamic information behind dynamic NMR spectra, the ML protocol presented here can be easily extended to other fast dynamic systems, such as solutions, diamagnetic solid-state electrolytes (SSEs), etc., and to other nuclei, which will stimulate future work.
Data availability
The python workflow and raw datasets for training and testing the NN-NMR model of P2-type Na2/3(Mg1/3Mn2/3)O2 are available at https://github.com/chenggroup/nmr upon request.Author contributions
M. L. and J. C. designed research. J. C. and Y. Y. supervised the project. M. L., J. X., F. W. and Y. H. developed and encoded the ML protocol. M. L. conducted the NMR shift calculations, DFT calculations, NMR and XRD experiments and data analysis. M. S. and X. L. assisted in materials synthesis. M. L. wrote the initial manuscript. J. C., R. F. and Y. Y. reviewed/edited the manuscript. All authors discussed the results and commented on the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by the National Key Research and Development Program of China (Grant No. 2021YFB2401800), National Natural Science Foundation of China (Grant No. 21991151, 21991150, 21935009, 21761132030, 21861132015, 22021001, 92161113, and 91945301), and Xiamen Science and Technology Plan Project (No. 3502Z20203027). Dr Riqiang Fu acknowledges the support from the National High Magnetic Field Laboratory, which is supported by NSF Cooperative Agreement DMR-1644779 and the State of Florida.References
- A. Van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed.
- A. Grenier, P. J. Reeves, H. Liu, I. D. Seymour, K. Märker, K. M. Wiaderek, P. J. Chupas, C. P. Grey and K. W. Chapman, J. Am. Chem. Soc., 2020, 142, 7001–7011 CrossRef CAS PubMed.
- Z. Gong and Y. Yang, J. Energy Chem., 2018, 27, 1566–1583 CrossRef.
- Z. Gong, W. Zhang, D. Lv, X. Hao, W. Wen, Z. Jiang and Y. Yang, J. Electrochem., 2013, 19, 512–522 CAS.
- O. Pecher, J. Carretero-González, K. J. Griffith and C. P. Grey, Chem. Mater., 2017, 29, 213–242 CrossRef CAS.
- G. Zhong, Z. Liu, D. Wang, Q. Li, R. Fu and Y. Yang, J. Electrochem., 2016, 22, 231–243 CAS.
- A. J. Pell, G. Pintacuda and C. P. Grey, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271 CrossRef CAS PubMed.
- J. Kim, D. S. Middlemiss, N. A. Chernova, B. Y. X. Zhu, C. Masquelier and C. P. Grey, J. Am. Chem. Soc., 2010, 132, 16825–16840 CrossRef CAS PubMed.
- D. S. Middlemiss, A. J. Ilott, R. J. Clément, F. C. Strobridge and C. P. Grey, Chem. Mater., 2013, 25, 1723–1734 CrossRef CAS.
- R. Pigliapochi, A. J. Pell, I. D. Seymour, C. P. Grey, D. Ceresoli and M. Kaupp, Phys. Rev. B, 2017, 95, 054412 CrossRef.
- A. Mondal and M. Kaupp, J. Phys. Chem. Lett., 2018, 9, 1480–1484 CrossRef CAS PubMed.
- A. Mondal, M. W. Gaultois, A. J. Pell, M. Iannuzzi, C. P. Grey, J. Hutter and M. Kaupp, J. Chem. Theory Comput., 2018, 14, 377–394 CrossRef CAS PubMed.
- A. Mondal and M. Kaupp, Solid State Nucl. Magn. Reson., 2019, 101, 89–100 CrossRef CAS PubMed.
- D. L. Smiley, D. Carlier and G. R. Goward, Solid State Nucl. Magn. Reson., 2019, 103, 1–8 CrossRef CAS PubMed.
- R. J. Clément, A. J. Pell, D. S. Middlemiss, F. C. Strobridge, J. K. Miller, M. S. Whittingham, L. Emsley, C. P. Grey and G. Pintacuda, J. Am. Chem. Soc., 2012, 134, 17178–17185 CrossRef PubMed.
- Y. Zhang, A. Castets, D. Carlier, M. Ménétrier and F. Boucher, J. Phys. Chem. C, 2012, 116, 17393–17402 CrossRef CAS.
- G. Mali, C. Sirisopanaporn, C. Masquelier, D. Hanzel and R. Dominko, Chem. Mater., 2011, 23, 2735–2744 CrossRef CAS.
- C. Delmas, D. Carlier, G. Ceder, M. Ménétrier and C. P. Grey, Phys. Rev. B, 2003, 67, 1–14 Search PubMed.
- A. D. Bain, Prog. Nucl. Magn. Reson. Spectrosc., 2003, 43, 63–103 CrossRef CAS.
- M. Lin, X. Liu, Y. Xiang, F. Wang, Y. Liu, R. Fu, J. Cheng and Y. Yang, Angew. Chem., Int. Ed., 2021, 60, 12547–12553 CrossRef CAS PubMed.
- C. Delmas, J.-J. Braconnier and P. Hagenmuller, Mater. Res. Bull., 1982, 17, 117–123 CrossRef CAS.
- R. J. Clément, J. Xu, D. S. Middlemiss, J. Alvarado, C. Ma, Y. S. Meng and C. P. Grey, J. Mater. Chem. A, 2017, 5, 4129–4143 RSC.
- M. Kalapsazova, S. Ivanova, R. Kukeva, S. Simova, S. Wegner, E. Zhecheva and R. Stoyanova, Phys. Chem. Chem. Phys., 2017, 19, 27065–27073 RSC.
- X. Wu, G.-L. Xu, G. Zhong, Z. Gong, M. J. McDonald, S. Zheng, R. Fu, Z. Chen, K. Amine and Y. Yang, ACS Appl. Mater. Interfaces, 2016, 8, 22227–22237 CrossRef CAS PubMed.
- G. Singh, N. Tapia-Ruiz, J. M. Lopez del Amo, U. Maitra, J. W. Somerville, A. R. Armstrong, J. Martinez de Ilarduya, T. Rojo and P. G. Bruce, Chem. Mater., 2016, 28, 5087–5094 CrossRef.
- G. Singh, J. M. López del Amo, M. Galceran, S. Pérez-Villar and T. Rojo, J. Mater. Chem. A, 2015, 3, 6954–6961 RSC.
- E. Gonzalo, M. H. Han, J. M. López del Amo, B. Acebedo, M. Casas-Cabanas and T. Rojo, J. Mater. Chem. A, 2014, 2, 18523–18530 RSC.
- J. Cabana, N. A. Chernova, J. Xiao, M. Roppolo, K. A. Aldi, M. S. Whittingham and C. P. Grey, Inorg. Chem., 2013, 52, 8540–8550 CrossRef CAS PubMed.
- I. R. Mukhamedshin, H. Alloul, G. Collin and N. Blanchard, Phys. Rev. Lett., 2004, 93, 167601 CrossRef CAS PubMed.
- O. H. Han, J. K. Jung, M.-Y. Yi, J. H. Kwak and Y. J. Shin, Solid State Commun, 2000, 117, 65–68 CrossRef CAS.
- J. Zhang, W. Wang, W. Wang, S. Wang and B. Li, ACS Appl. Mater. Interfaces, 2019, 11, 22051–22066 CrossRef CAS PubMed.
- L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed.
- Y. Zhang, H. Wang, W. Chen, J. Zeng, L. Zhang, H. Wang and W. E, Comput. Phys. Commun., 2020, 253, 107206 CrossRef CAS.
- J. Huang, L. Zhang, H. Wang, J. Zhao, J. Cheng and W. E, J. Chem. Phys., 2021, 154, 094703 CrossRef CAS PubMed.
- L. Zhang, J. Han, H. Wang, W. A. Saidi, R. Car and W. E, Adv. Neural Inform. Process. Syst., 2018, 2018, 4436–4446 Search PubMed.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B, 2013, 87, 184115 CrossRef.
- F. M. Paruzzo, A. Hofstetter, F. Musil, S. De, M. Ceriotti and L. Emsley, Nat. Commun., 2018, 9, 4501 CrossRef PubMed.
- J. Vergnet, M. Saubanère, M.-L. Doublet and J.-M. Tarascon, Joule, 2020, 4, 420–434 CrossRef CAS.
- M. Ben Yahia, J. Vergnet, M. Saubanère and M.-L. Doublet, Nat. Mater., 2019, 18, 496–502 CrossRef CAS PubMed.
- K. Dai, J. Wu, Z. Zhuo, Q. Li, S. Sallis, J. Mao, G. Ai, C. Sun, Z. Li, W. E. Gent, W. C. Chueh, Y. Chuang, R. Zeng, Z. Shen, F. Pan, S. Yan, L. F. J. Piper, Z. Hussain, G. Liu and W. Yang, Joule, 2019, 3, 518–541 CrossRef CAS.
- U. Maitra, R. A. House, J. W. Somerville, N. Tapia-Ruiz, J. G. Lozano, N. Guerrini, R. Hao, K. Luo, L. Jin, M. A. Pérez-Osorio, F. Massel, D. M. Pickup, S. Ramos, X. Lu, D. E. McNally, A. V. Chadwick, F. Giustino, T. Schmitt, L. C. Duda, M. R. Roberts and P. G. Bruce, Nat. Chem., 2018, 10, 288–295 CrossRef CAS PubMed.
- C. Delmas, Adv. Energy Mater., 2018, 8, 1–9 Search PubMed.
- V. G. Malkin, M. Kaupp and M. Bühl, Calculation of NMR and EPR Parameters, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2004 Search PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B, 2000, 62, 6158–6179 CrossRef.
- R. Declerck, E. Pauwels, V. Van Speybroeck and M. Waroquier, Phys. Rev. B, 2006, 74, 245103 CrossRef.
- F. Han, Problems in Solid State Physics with Solutions, 2012, vol. 50, pp. 391–396 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. Sun, A. Ruzsinszky and J. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- Y. S. Meng, Y. Hinuma and G. Ceder, J. Chem. Phys., 2008, 128, 104708 CrossRef PubMed.
- D. H. Lee, J. Xu and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 3304 RSC.
- K. Okhotnikov, T. Charpentier and S. Cadars, J. Cheminform., 2016, 8, 17 CrossRef PubMed.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. R. Kermode, J. Phys. Condens. Matter, 2020, 32, 305901 CrossRef CAS PubMed.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, et al., TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, 2015, https://www.tensorflow.org/ Search PubMed.
- F. Chollet, Keras, 2015, https://keras.io Search PubMed.
- L. Kahle, A. Musaelian, N. Marzari and B. Kozinsky, Phys. Rev. Mater., 2019, 3, 055404 CrossRef CAS.
- C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azaïs, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779 CrossRef CAS PubMed.
- W. Zuo, J. Qiu, C. Hong, X. Liu, J. Li, G. F. Ortiz, Q. Li, S. Zheng, G. R. Zheng and Y. Yang, ACS Appl. Energy Mater., 2019, 2, 4914–4924 CrossRef CAS.
- Z. Lu and J. R. Dahn, J. Electrochem. Soc., 2001, 148, A1225 CrossRef CAS.
- J. Cabana, N. A. Chernova, J. Xiao, M. Roppolo, K. A. Aldi, M. S. Whittingham and C. P. Grey, Inorg. Chem., 2013, 52, 8540–8550 CrossRef CAS PubMed.
- N. Tapia-Ruiz, W. M. Dose, N. Sharma, H. Chen, J. Heath, J. W. Somerville, U. Maitra, M. S. Islam and P. G. Bruce, Energy Environ. Sci., 2018, 11, 1470–1479 RSC.
- X. He, Y. Zhu, A. Epstein and Y. Mo, npj Comput. Mater., 2018, 4, 18 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2sc01306a. |
| This journal is © The Royal Society of Chemistry 2022 |




