Open Access Article
Open Access ArticleAmplification of weak chiral inductions for excellent control over the helical orientation of discrete topologically chiral (M3L2)n polyhedra†
Yuya
Domoto
 *a,
Kidai
Yamamoto
a,
Shumpei
Horie
a,
Zhengsu
Yu
a and
Makoto
Fujita
*ab
*a,
Kidai
Yamamoto
a,
Shumpei
Horie
a,
Zhengsu
Yu
a and
Makoto
Fujita
*ab
aDepartment of Applied Chemistry, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8656, Japan. E-mail: domoto@appchem.t.u-tokyo.ac.jp; mfujita@appchem.t.u-tokyo.ac.jp
bDivision of Advanced Molecular Science, Institute for Molecular Science, National Institutes of Natural Sciences, 5-1 Higashiyama, Myodaiji-cho, Okazaki-shi, Aichi 444-8787, Japan
First published on 22nd March 2022
Abstract
Superb control over the helical chirality of discrete (M3L2)n polyhedra (n = 2,4,8, M = CuI or AgI) created from the self-assembly of propeller-shaped ligands (L) equipped with chiral side chains is demonstrated here. Almost perfect chiral induction (>99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) of the helical orientation of the framework was achieved for the largest (M3L2)8 cube with 48 small chiral side chains (diameter: ∼5 nm), while no or moderate chiral induction was observed for smaller polyhedra (n = 2, 4). Thus, amplification of the weak chiral inductions of each ligand unit is an efficient way to control the chirality of large discrete nanostructures with high structural complexity.
1) of the helical orientation of the framework was achieved for the largest (M3L2)8 cube with 48 small chiral side chains (diameter: ∼5 nm), while no or moderate chiral induction was observed for smaller polyhedra (n = 2, 4). Thus, amplification of the weak chiral inductions of each ligand unit is an efficient way to control the chirality of large discrete nanostructures with high structural complexity.
Introduction
Amplification of chiral induction has previously been observed in double asymmetric synthesis,1 where high enantioselectivity or diastereoselectivity arises from two or more chiral sources (e.g., a chiral substrate and a chiral reagent). With increasing multiplication number (m), the selectivity should be exponentially enhanced because the small free energy differences (ΔEm) that arise from each chiral source accumulate. This process roughly follows the Gibbs free energy equation, ΔG = ΣΔEm = −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, where K is the reaction selectivity or the equilibrium constant of the two states. Exceptional amplification effects have often been observed in polymeric systems, particularly in the formation of helices in long-chain polymers, where the helical sense of the polymer main chain can be perfectly controlled, even when the chiral induction at every monomer unit is small.2–4 In discrete molecular systems, however, there are only a limited number of examples where large amplification effects have been observed,5,6 given that the incorporation of a large number of chiral sources into discrete molecular structures is usually not straightforward. In particular, chirality control over huge and complex discrete nanoarchitectures is believed to open up new concepts in the fields of material science including artificial reaction systems, sensors, and biochemical applications in higher degree of multicomponent manners.7
K, where K is the reaction selectivity or the equilibrium constant of the two states. Exceptional amplification effects have often been observed in polymeric systems, particularly in the formation of helices in long-chain polymers, where the helical sense of the polymer main chain can be perfectly controlled, even when the chiral induction at every monomer unit is small.2–4 In discrete molecular systems, however, there are only a limited number of examples where large amplification effects have been observed,5,6 given that the incorporation of a large number of chiral sources into discrete molecular structures is usually not straightforward. In particular, chirality control over huge and complex discrete nanoarchitectures is believed to open up new concepts in the fields of material science including artificial reaction systems, sensors, and biochemical applications in higher degree of multicomponent manners.7
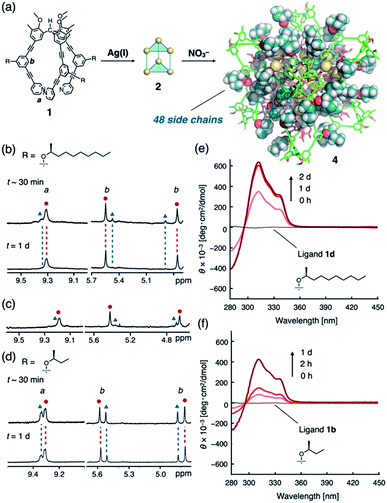
We have recently reported a number of (M3L2)n polyhedra (2a–4a; n = 2, 4, 8; M = CuI or AgI; Fig. 1)8 constructed from ligand 1a through conventional metal–pyridyl coordination9 and secondary metal–acetylene π-coordination.10 The propeller-shaped tripodal ligand 1a can exist in two enantiomeric conformations (Fig. 1a) and, once coordinated to M, oligomerizes to form polyhedral frameworks with diameters of up to ca. 5 nm (Fig. 1b). Crystallographic and spectroscopic studies have shown that the helical sense of all the 1a ligands in the polyhedral frameworks are identical, although the polyhedra exist as racemates. We observed that the (M3L2)n polyhedra have many identical ligand arms directed to outer environments, and thus, substantial chiral induction in the polyhedral frameworks retaining cavity structures could be expected by simply introducing a chiral element to the ligand arm. In addition, note that a series of the (M3L2)n polyhedra contain highly entangled structures based on trifurcate motifs,11–13 exceeding the well classified topologies of conventional knots and links.14 As these structures are inherently topologically chiral,15 it is expected to be interesting to demonstrate their precise regulation for invoking future applications of the newly exploited three-dimensional molecular entanglements.
 | ||
| Fig. 1 (a) Chemical structure of propeller-shaped ligand 1 and its P- and M-forms. Unless otherwise noted, the (S)-2-alkoxy isomers of 1b–e were used in the main study. (b) Schematic representation of the self-assembly of the (M3L2)n coordination polyhedra 2–4 (n = 2, 4, 8) with chiral side chains. Each assembly is formed by the oligomerization of n units of M3L2, a hypothetical intermediate stabilized by metal–acetylene π-coordination. Illustrations in the second column from the left were generated by combining 2-butoxy side chains (molecular-mechanics (MM) models) with polyhedral frameworks based on the reported crystal structures.8a,c Cartoon illustrations in the third column exhibit the entangled structures11 of the (M3L2)n polyhedra, while metal–acetylene π-coordination is omitted for clarity.8c | ||
Therefore, in this study, we designed and synthesized ligands 1b–e (Fig. 1a), which are derivatives of 1a equipped with a chiral substituent on every arm. We found that, while chiral induction from the side chains is negligible or very small for polyhedra 2 (n = 2) and 3 (n = 4), perfect control over the helicity can be achieved in cubic octamer 4 (n = 8) via the remarkable amplification effect of, in total, 48 chiral substituents on the ligand arms. This result demonstrates that the chirality of discrete nanostructures assembled from numerous components can be easily controlled by the amplification effect of weakly chiral elements present on every component.
Results and discussion
Propeller-shaped tripodal ligands 1b–e, which bear chiral (S)-alkoxy side chains on each arm, were designed and prepared according to literature procedures (for details, see the ESI†).8a,16 Firstly, dimeric (M3L2)2 cages 2 were synthesized by mixing [Cu(MeCN)4]BF4 (1.5 equiv., 3.75 mM) with ligand 1b in CD3NO2. The 1H NMR spectra showed two sets of proton signals attributable to dimer 2b (Fig. 2b and S1†), suggesting the formation of two diastereomeric cages with the ligands in either the M- or P-configuration. However, the diastereomeric ratio was ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in both cases even though a chiral substituent is present on each of the 12 side chains. A lack of chiral induction in the (M3L2)2 cage frameworks was also confirmed by the circular dichroism (CD) spectra, which showed no chiral amplification in comparison with the CD spectra of the ligand solutions (Fig. S2†). This absence of chiral induction is presumably due to insufficient steric interactions between the chiral side chains and the cage framework of 2b. In fact, the single-crystal X-ray structure of the cage framework of 2b (Fig. 2d) revealed almost no steric crowding between the side chains and the cage framework. We thus examined ligand 1e with a sterically more crowded (S)-1-phenyl-2-propanoxy group as the chiral substituent (for details, see the ESI†). When cage 2e was assembled from ligand 1e, a small amount of diastereoselectivity was observed (62
1 in both cases even though a chiral substituent is present on each of the 12 side chains. A lack of chiral induction in the (M3L2)2 cage frameworks was also confirmed by the circular dichroism (CD) spectra, which showed no chiral amplification in comparison with the CD spectra of the ligand solutions (Fig. S2†). This absence of chiral induction is presumably due to insufficient steric interactions between the chiral side chains and the cage framework of 2b. In fact, the single-crystal X-ray structure of the cage framework of 2b (Fig. 2d) revealed almost no steric crowding between the side chains and the cage framework. We thus examined ligand 1e with a sterically more crowded (S)-1-phenyl-2-propanoxy group as the chiral substituent (for details, see the ESI†). When cage 2e was assembled from ligand 1e, a small amount of diastereoselectivity was observed (62![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38 by 1H NMR analysis; Fig. S3†), which can be interpreted in terms of increased steric crowding of the bulky groups on the cage (MM model based on partially refined X-ray data; cf. Fig. S4†).
38 by 1H NMR analysis; Fig. S3†), which can be interpreted in terms of increased steric crowding of the bulky groups on the cage (MM model based on partially refined X-ray data; cf. Fig. S4†).
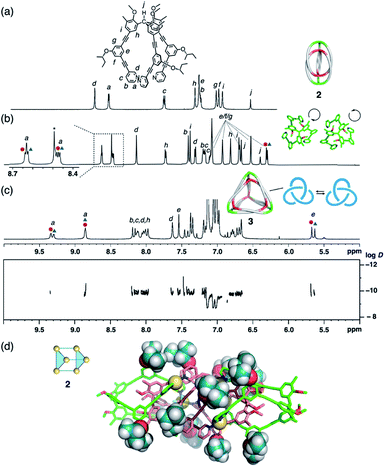 | ||
| Fig. 2 Self-assembly of complex 2b and tetrahedron 3b. Partial 1H NMR spectra of (a) ligand 1b (500 MHz, 300 K, CDCl3), (b) complex 2b (700 MHz, 300 K, CD3NO2), and (c) tetrahedron 3b (500 MHz, 300 K, toluene-d8). Red circles and blue triangles indicate two diastereomeric complexes, respectively. A 1H DOSY spectrum is shown in addition (for details, see Fig. S5†). (d) X-ray crystal structure of 2b; 2-butoxy chains are shown as space-filling models. | ||
The small chiral induction effect observed for cage 2e encouraged us to examine higher-order oligomeric cages, in which a larger number of chiral side chains are present. The self-assembly of tetrahedral (M3L2)43 was thus examined with ligands 1b. After complexation with CuBF4 (1.5 equiv., 3.75 mM; 50 °C for 30 min) in toluene-d8, the formation of 3b was confirmed by 1H and 13C NMR (Fig. 2c and S27–S28†), in addition to 1H diffusion ordered spectroscopy (DOSY) showing a hydrodynamic diameter of ∼4.7 nm (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = −9.8 at 300 K) comparable to that was determined for 3a by X-ray analysis (4.5 nm).8a Here, however, only small diastereomeric ratio (52
D = −9.8 at 300 K) comparable to that was determined for 3a by X-ray analysis (4.5 nm).8a Here, however, only small diastereomeric ratio (52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 48) was observed by 1H NMR (Fig. 2c), which is consistent with the moderately enhanced absorption observed in the CD spectra (Fig. S6†).17
48) was observed by 1H NMR (Fig. 2c), which is consistent with the moderately enhanced absorption observed in the CD spectra (Fig. S6†).17
The helical orientation of ligand 1 forces the generation of a chiral trefoil knot topology14 on every face of the tetrahedral cage 3 (Fig. 2c, right). In this situation, the two enantiomeric forms cannot be interconverted unless the trefoil knot topology is dissociated. Thus, the P- and M-helical orientations of the ligand do not interconvert, except under very slow equilibration via bond dissociation. Therefore, as shown by variable-temperature (VT) 1H NMR experiments (Fig. S7†), the diastereomeric ratio of 3 is not affected by a change in temperature between 273 and 323 K.18
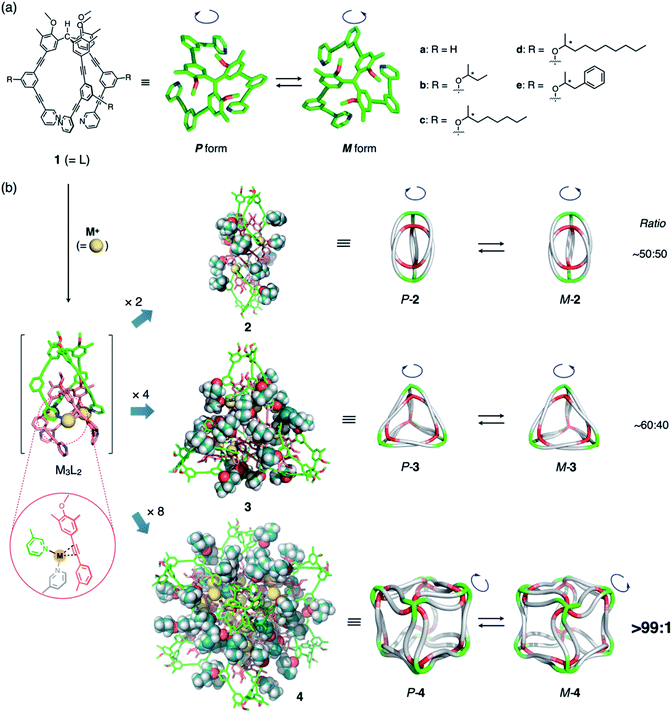
We expected to see a further enhancement in the chiral induction in the (M3L2)n assembly of cube-structured 4 (n = 8). As previously reported,8c cube 4 can only be constructed via the anion-templated conversion of pre-synthesized dimeric cages of 2. Thus, cage 2d was prepared by mixing ligand 1d (with an (S)-2-decanoxy side chain, 2.5 mM) and AgPF6 (1.9 equiv.) in CDCl3/CD3OD (97/3, v/v) at 50 °C for 30 min. Finally, the solution was treated with tetramethylammonium nitrate (TMANO3, 1.0 equiv. in CD3OD at room temperature over 21 h; CDCl3/CD3OD ratio after the template addition was 94/6, v/v) (Fig. 3a).19
To our surprise, we observed the exclusive formation of only one diastereomer of cube 4d (>99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) via1H NMR spectroscopy (Fig. 3b and S11a†). Time-dependent NMR measurements revealed that the selectivity is thermodynamically controlled. Immediately following the addition of TMANO3 (∼30 min), we observed a relatively low selectivity (82
1) via1H NMR spectroscopy (Fig. 3b and S11a†). Time-dependent NMR measurements revealed that the selectivity is thermodynamically controlled. Immediately following the addition of TMANO3 (∼30 min), we observed a relatively low selectivity (82![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 18) that increased to >99
18) that increased to >99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 after stirring the solution for 21 h. This kinetic-to-thermodynamic conversion process was also monitored using CD spectroscopy (Fig. 3e). As precursor 2 is a ∼1
1 after stirring the solution for 21 h. This kinetic-to-thermodynamic conversion process was also monitored using CD spectroscopy (Fig. 3e). As precursor 2 is a ∼1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of diastereomers, the relatively rapid interconversion of 2 to 4 by addition of nitrate initially results in the formation of a kinetic mixture of diastereomers of 4d, which is then converted into the thermodynamic product. Cage 4 was characterized by comparing the 1H and 13C NMR spectra of 4 (Fig. S12†)20 with those of the previously reported 4a.8c1H DOSY measurements indicated the formation of a single species with a diffusion coefficient of D = 1.6 × 10−10 m2 s−1 (log
1 mixture of diastereomers, the relatively rapid interconversion of 2 to 4 by addition of nitrate initially results in the formation of a kinetic mixture of diastereomers of 4d, which is then converted into the thermodynamic product. Cage 4 was characterized by comparing the 1H and 13C NMR spectra of 4 (Fig. S12†)20 with those of the previously reported 4a.8c1H DOSY measurements indicated the formation of a single species with a diffusion coefficient of D = 1.6 × 10−10 m2 s−1 (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D = −9.8 at 287 K; Fig. S13†).
D = −9.8 at 287 K; Fig. S13†).
The use of high polarity solvents (CDCl3/CD3OD (94/6, v/v)) is particularly important to achieve high selectivity. In fact, when the same experiment was conducted in a slightly less polar solvent (CDCl3/CD3OD (97/3, v/v)), the selectivity decreased significantly (max.: 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15; Fig. 3c and S11b†). Presumably, the steric contact of long hydrophobic alkyl chains with the framework of cube 4d becomes more efficient in polar solvents, thus enhancing the chiral induction, as observed in helical polymers.4
15; Fig. 3c and S11b†). Presumably, the steric contact of long hydrophobic alkyl chains with the framework of cube 4d becomes more efficient in polar solvents, thus enhancing the chiral induction, as observed in helical polymers.4
To clarify the secondary steric effects, ligands 1c and 1b with shorter (S)-2-alkoxy side chains were used in the self-assembly of cube 4. In CDCl3/CD3OD (97/3, v/v), a ligand with a 2-octoxy chain (1c) offered comparable selectivity (84![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16; Fig. S15–S16†) to that of 1d (85
16; Fig. S15–S16†) to that of 1d (85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15). In the case of 1b, i.e., a ligand with a much shorter 2-butoxy chain, much lower selectivity (70
15). In the case of 1b, i.e., a ligand with a much shorter 2-butoxy chain, much lower selectivity (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30) was observed even after 18 h of treatment with tetrabutylammonium nitrate (TBANO3) (Fig. 3d and f).
30) was observed even after 18 h of treatment with tetrabutylammonium nitrate (TBANO3) (Fig. 3d and f).
The P and M equilibrium constant (K) can be described by the Gibbs free energy equation, K = exp(−ΔG/RT), where ΔG may roughly be described as m·Eh (Eh: energy difference per chiral unit).4a,b Even though Eh is very small, the accumulation of 48 chiral units (m = 48) in 4d is enough to induce a relatively large ΔG that accounts for the perfect chiral induction. In other words, the diastereomeric ratio of 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for cube 4 (n = 8, m = 48) can be ascribed to an energy difference of only −0.23 kJ mol−1 per chiral group. Whilst the absolute value is small, the accumulation of 48 chiral groups on the surface of the polyhedron can generate a large ΔG that perfectly controls the chirality of the huge polyhedral framework.
1 for cube 4 (n = 8, m = 48) can be ascribed to an energy difference of only −0.23 kJ mol−1 per chiral group. Whilst the absolute value is small, the accumulation of 48 chiral groups on the surface of the polyhedron can generate a large ΔG that perfectly controls the chirality of the huge polyhedral framework.
Conclusions
In conclusion, we have successfully controlled the helicity of discrete (M3L2)n polyhedra by adding small chiral side chains to their highly entangled higher-order frameworks. The results shown here are inspiring as they allow the precise structural regulation of large, complex nanoarchitectures, that are usually difficult to synthesize via the self-assembly of numerous components. This strategy can be expected to stimulate new approaches toward advanced functional nanomaterials15 based on discrete molecular designs.‡Data availability
All the data are shown in the ESI.†Author contributions
Y. D. and M. F. conceived and designed the study. Y. D. and M. F. co-wrote the paper. Y. D., K. Y., S. H., and Z. Y. performed the chemical experiments and analysed the data. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by JSPS KAKENHI grants 19H05461 (to M. F.) and 19K05416 (to Y. D.). Y. D. also acknowledges financial support from the Izumi Science and Technology Foundation, Konica Minolta, Inc., and the Society of Synthetic Organic Chemistry (Japan). The authors thank Dr Tadateru Nishikawa (JEOL RESONANCE Inc.) for assistance with the NMR measurements. Synchrotron X-ray crystallography was performed using the BL26B1 beamline at SPring-8 under proposal numbers 2020A0168 and 2021B1246. We thank the Instrument Center at the Institute for Molecular Sciences (Okazaki, Japan) for providing access to CD spectrometers. This work was partly supported by the Nanotechnology Platform Program ‘Molecule and Material Synthesis’ (JPMXP09S21MS0008) of the Japanese Ministry of Education, Culture, Sports, Science and Technology (MEXT).Notes and references
- S. Masamune, W. Choy, J. S. Petersen and L. R. Sita, Angew. Chem., Int. Ed., 1985, 24, 1–30 CrossRef.
- Y. Okamoto, H. Mohri, T. Nakano and K. Hatada, J. Am. Chem. Soc., 1989, 111, 5952–5954 CrossRef CAS.
- (a) M. M. Green, C. Andreola, B. Muñoz and M. P. Reidy, J. Am. Chem. Soc., 1988, 110, 4063–4065 CrossRef CAS; (b) M. M. Green, N. C. Peterson, T. Sato, A. Teramoto, R. Cook and S. Lifson, Science, 1995, 268, 1860–1866 CrossRef CAS PubMed; (c) H. Nakako, R. Nomura and T. Masuda, Macromolecules, 2001, 34, 1496–1502 CrossRef CAS.
- (a) T. Yamada, Y. Nagata and M. Suginome, Chem. Commun., 2010, 46, 4914–4916 RSC; (b) Y. Nagata, T. Yamada, T. Adachi, Y. Akai, T. Yamamoto and M. Suginome, J. Am. Chem. Soc., 2013, 135, 10104–10113 CrossRef CAS PubMed; (c) Y. Nagata, T. Nishikawa, M. Suginome, S. Sato, M. Sugiyama, L. Porcar, A. Martel, R. Inoue and N. Sato, J. Am. Chem. Soc., 2018, 140, 2722–2726 CrossRef CAS PubMed.
- (a) N. Ousaka, J. K. Clegg and J. R. Nitschke, Angew. Chem., Int. Ed., 2012, 51, 1464–1468 CrossRef CAS PubMed; (b) F. Huang, L. Ma, Y. Che, H. Jiang, X. Chen and Y. Wang, J. Org. Chem., 2018, 83, 733–739 CrossRef CAS PubMed; (c) J. Zhang, D. Luo, C. Ma, L. Huang and Q. Gan, Nat. Commun., 2021, 12, 2659 CrossRef CAS PubMed.
- (a) K. S. Jeong, Y. S. Kim, Y. J. Kim, E. Lee, J. H. Yoon, W. H. Park, Y. W. Park, S.-J. Jeon, Z. H. Kim, J. Kim and N. Jeong, Angew. Chem., Int. Ed., 2006, 45, 8134–8138 CrossRef CAS PubMed; (b) C. Gütz, R. Hovorka, C. Klein, Q.-Q. Jiang, C. Bannwarth, M. Engeser, C. Schmuck, W. Assenmacher, W. Mader, F. Topić, K. Rissanen, S. Grimme and A. Lützen, Angew. Chem., Int. Ed., 2014, 53, 1693–1698 CrossRef PubMed; (c) K.-R. Wang, D.-S. Guo, B.-P. Jiang and Y. Liu, Chem. Commun., 2012, 48, 3644–3646 RSC; (d) M. Gaeta, G. Sortino, R. Randazzo, I. Pisagatti, A. Notti, M. E. Fragalà, M. F. Parisi, A. D'Urso and R. Purrello, Chem.–Eur. J., 2020, 26, 3515–3518 CrossRef CAS PubMed.
- (a) L.-J. Chen, H.-B. Yang and M. Shionoya, Chem. Soc. Rev., 2017, 46, 2555–2576 RSC; (b) M. Pan, K. Wu, J.-H. Zhang and C.-Y. Su, Coord. Chem. Rev., 2019, 378, 333–349 CrossRef CAS.
- (a) Y. Domoto, M. Abe, T. Kikuchi and M. Fujita, Angew. Chem., Int. Ed., 2020, 59, 3450–3454 CrossRef CAS PubMed; (b) Y. Domoto, M. Abe, K. Yamamoto, T. Kikuchi and M. Fujita, Chem. Sci., 2020, 11, 10457–10460 RSC; (c) Y. Domoto, M. Abe and M. Fujita, J. Am. Chem. Soc., 2021, 143, 8578–8582 CrossRef CAS PubMed.
- (a) M. M. Conn and J. Rebek, Chem. Rev., 1997, 97, 1647–1668 CrossRef CAS PubMed; (b) D. L. Caulder and K. N. Raymond, Acc. Chem. Res., 1999, 32, 975–982 CrossRef CAS; (c) R. W. Saalfrank, H. Maid and A. Schuerer, Angew. Chem., Int. Ed., 2008, 47, 8794–8824 CrossRef CAS PubMed; (d) M. M. Smulders, I. A. Riddell, C. Brown and J. R. Nitschke, Chem. Soc. Rev., 2013, 42, 1728–1754 RSC; (e) T. R. Cook and J. P. Stang, Chem. Rev., 2015, 115, 7001–7045 CrossRef CAS PubMed; (f) H. Hou, K. Zhou, F. Jiang, Q. Chen and M. Hong, Isr. J. Chem., 2019, 59, 140–150 CrossRef CAS; (g) M. Han, D. M. Engelhard and G. H. Clever, Chem. Soc. Rev., 2014, 43, 1848–1860 RSC.
- (a) H. Lang, A. Jakob and B. Milde, Organometallics, 2012, 31, 7661–7693 CrossRef CAS; (b) H. Schmidbaur and A. Schier, Organometallics, 2010, 29, 2–23 CrossRef CAS.
- (a) M. O'Keeffe and M. M. J. Treacy, Acta Cryst. A, 2020, 76, 611–621 CrossRef PubMed; (b) T. Castle, M. E. Evans and S. T. Hyde, New J. Chem., 2008, 32, 1484–1492 RSC; (c) S. T. Hyde and M. E. Evans, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2110345118 CrossRef CAS PubMed.
- T. Sawada and M. Fujita, Bull. Chem. Soc. Jpn., 2021, 94, 2342–2350 CrossRef CAS.
- X. Zhao, H. Wang, B. Li, W. Zhang, X. Li, W. Zhao, C. Janiak, A. W. Heard, X.-J. Yang and B. Wu, Angew. Chem., Int. Ed., 2022, 61, e202115042 CAS.
- (a) E. E. Fenlon, Eur. J. Org. Chem., 2008, 5023–5035 CrossRef CAS; (b) K. E. Horner, M. A. Miller, J. W. Steed and P. M. Sutcliffe, Chem. Soc. Rev., 2016, 45, 6432–6448 RSC; (c) S. D. P. Fielden, D. A. Leigh and S. L. Woltering, Angew. Chem., Int. Ed., 2017, 56, 11166–11194 CrossRef CAS PubMed; (d) W.-X. Gao, H.-J. Feng, B.-B. Guo, Y. Lu and G.-X. Jin, Chem. Rev., 2020, 120, 6288–6325 CrossRef CAS PubMed.
- (a) N. Pairault and J. Niemeyer, Synlett, 2018, 29, 689–698 CrossRef CAS; (b) A. H. G. David and J. F. Stoddart, Isr. J. Chem., 2021, 61, 608–621 CrossRef CAS; (c) J. R. J. Maynard and S. M. Goldup, Chem, 2020, 6, 1914–1932 CrossRef CAS; (d) Y. Sang and M. Liu, Chem. Sci., 2022, 13, 633–656 RSC.
- J. Kobayashi, Y. Domoto and T. Kawashima, Chem. Commun., 2009, 6186–6188 RSC.
- Even the use of the ligand with longer side chain (1d) did not show the improvement of the diastereoselectivity (60
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) in the case of assembly 3.
40) in the case of assembly 3. - Significant solvent effects on diastereoselectivity were observed also for the self-assembly of the tetrahedral cages 3 (Fig. S8–S10†).
- The sources and equivalents of the silver (AgPF6 or AgSbF6, 1.5–2.0 equiv.) and nitrate ions (TMANO3 or TBANO3, 0.5–1.5 equiv.) were adjusted to achieve complete convergence of the self-assembly process, which depends on the ligand used.
- Treatment of the solution with a chiral-shift reagent anion (Δ-tris(tetrachlorobenzenediolate)phosphate(V) (Δ-TRISPHAT), 0–0.35 equiv., ref. 21) induced significant shifts of every 1H NMR signal at 287 K (Fig. S14†), indirectly supporting the assignment as a pair of diastereomers.
- (a) J. J. Jodry and J. Lacour, Chem.–Eur. J., 2000, 6, 4297–4304 CrossRef CAS PubMed; (b) S. Hiraoka, K. Harano, T. Tanaka, M. Shiro and M. Shionoya, Angew. Chem., Int. Ed., 2003, 42, 5182–5185 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis details, spectroscopic characterization, and X-ray crystallography data. CCDC 2108704. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d2sc00111j |
| ‡ Crystallographic data for 2b: M = 20583.18, monoclinic, space group P21/n, a = 18.838(4) Å, b = 32.458(6) Å, c = 64.439(13) Å, α = γ = 90°, β = 94.55(3)°, V = 39277(14) Å3, Z = 1, Dc = 0.870 g cm−3, T = 100(2) K, 1.784 < θ < 47.56°, 20892 unique reflections out of 69369 with I > 2σ(I), GoF = 1.290, final R factors R1 = 0.1440 (I > 2σ(I)), wR2 = 0.3746, CCDC deposition number 2108704. |
| This journal is © The Royal Society of Chemistry 2022 |