Open Access Article
Open Access ArticleGrowth kinetics determine the polydispersity and size of PbS and PbSe nanocrystals†
Michael P.
Campos‡
a,
Jonathan
De Roo‡
 ab,
Matthew W.
Greenberg‡
a,
Brandon M.
McMurtry‡
ab,
Matthew W.
Greenberg‡
a,
Brandon M.
McMurtry‡
 a,
Mark P.
Hendricks
ai,
Ellie
Bennett
a,
Mark P.
Hendricks
ai,
Ellie
Bennett
 a,
Natalie
Saenz
a,
Matthew Y.
Sfeir
a,
Natalie
Saenz
a,
Matthew Y.
Sfeir
 cde,
Benjamin
Abécassis
cde,
Benjamin
Abécassis
 fg,
Sanjit K.
Ghose
h and
Jonathan S.
Owen
fg,
Sanjit K.
Ghose
h and
Jonathan S.
Owen
 *a
*a
aDepartment of Chemistry, Columbia University, New York, New York 10027, USA. E-mail: jso2115@columbia.edu
bDepartment of Chemistry, University of Basel, Basel 4058, Switzerland
cCenter for Functional Nanomaterials, Brookhaven National Laboratory, Upton, New York 11973, USA
dPhotonics Initiative, Advanced Science Research Center, City University of New York, New York, New York 10031, USA
eDepartment of Physics, Graduate Center, City University of New York, New York, New York 10016, USA
fENSL, CNRS, Laboratoire de Chimie UMR 5182, 46 allée d’Italie, 69364 Lyon, France
gUniversité Paris-Saclay, CNRS, Laboratoire de Physique des Solides, 91405 Orsay, France
hNational Synchrotron Light Source II, Brookhaven National Laboratory, Brookhaven, New York, USA
iDepartment of Chemistry, Whitman College, Walla Walla, Washington 99362, USA
First published on 17th March 2022
Abstract
A library of thio- and selenourea derivatives is used to adjust the kinetics of PbE (E = S, Se) nanocrystal formation across a 1000-fold range (kr = 10−1 to 10−4 s−1), at several temperatures (80–120 °C), under a standard set of conditions (Pb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) E = 1.2
E = 1.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, [Pb(oleate)2] = 10.8 mM, [chalcogenourea] = 9.0 mM). An induction delay (tind) is observed prior to the onset of nanocrystal absorption during which PbE solute is observed using in situ X-ray total scattering. Density functional theory models fit to the X-ray pair distribution function (PDF) support a Pb2(μ2-S)2(Pb(O2CR)2)2 structure. Absorption spectra of aliquots reveal a continuous increase in the number of nanocrystals over more than half of the total reaction time at low temperatures. A strong correlation between the width of the nucleation phase and reaction temperature is observed that does not correlate with the polydispersity. These findings are antithetical to the critical concentration dependence of nucleation that underpins the La Mer hypothesis and demonstrates that the duration of the nucleation period has a minor influence on the size distribution. The results can be explained by growth kinetics that are size dependent, more rapid at high temperature, and self limiting at low temperatures.
1, [Pb(oleate)2] = 10.8 mM, [chalcogenourea] = 9.0 mM). An induction delay (tind) is observed prior to the onset of nanocrystal absorption during which PbE solute is observed using in situ X-ray total scattering. Density functional theory models fit to the X-ray pair distribution function (PDF) support a Pb2(μ2-S)2(Pb(O2CR)2)2 structure. Absorption spectra of aliquots reveal a continuous increase in the number of nanocrystals over more than half of the total reaction time at low temperatures. A strong correlation between the width of the nucleation phase and reaction temperature is observed that does not correlate with the polydispersity. These findings are antithetical to the critical concentration dependence of nucleation that underpins the La Mer hypothesis and demonstrates that the duration of the nucleation period has a minor influence on the size distribution. The results can be explained by growth kinetics that are size dependent, more rapid at high temperature, and self limiting at low temperatures.
Introduction
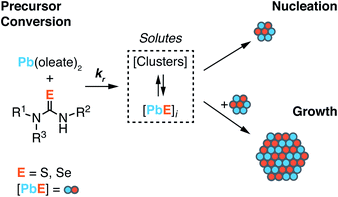
Across a wide range of materials, colloidal nanocrystals can be synthesized with surprising monodispersity.1,2 In many of these syntheses, the kinetics of nanocrystal formation are limited by the irreversible conversion of synthesis precursors to units of the growing crystal. Under such conditions, the temporal evolution of the precipitation can be controlled by the precursor reactivity. In the case of noble metal nanocrystals, for example, the conversion of metal salt precursors is thought to be autocatalytic and occurs at the nanoparticle surface.3–5 On the other hand, metal chalcogenide,6–12 and in some cases, gold13,14 nanocrystals are believed to form by assembly of soluble molecular intermediates produced by the conversion of precursors in homogeneous solution. While nucleation and growth are inherently autocatalytic, as described by Finke and Watzky,15 if the formation of solutes by the precursor reaction is substantially slower than crystal growth, the precipitation kinetics will be governed by the precursor conversion reaction, and the size of the final nanocrystal will be controlled by the precursor reactivity.16A variety of nanocrystal precursors have been designed to adjust the rate at which InP,17–21 CdTe,22 CdSe,12,23 CdS,2,24,25 PbSe,26–29 PbS,30 Cu2−xS,30 FexSy,31 CuInSe2,32 CuInS2,33 and ZnS34 solute is produced. Among these, chalcogenourea derivatives finely adjust the formation of metal chalcogenides over more than a million-fold range of reactivity (Scheme 1).2 The wide range of fine control over the solute supply provides several advantages that simplify synthesis. For example, the precursor reactivity can be appropriately chosen to match the desired crystallization temperature; the nucleation onset can be delayed until the synthesis mixture has achieved a homogeneous composition following the injection, improving the reproducibility and facilitating mechanistic studies;35 the final nanocrystal size can be controlled without modifying other aspects of the synthesis such as the surfactant composition, the precursor concentrations, or quenching the precursor reaction to limit the yield.8,12 These advantages have made it possible to demonstrate a well behaved relationship between the solute supply rate and the final nanocrystal concentration in several materials.2,8,12,17,30,34,36
Nucleation mass balance models developed by Sugimoto describe the connection between solute supply kinetics and the extent of nucleation.9,37,38 These models illustrate how the rate of solute supply during nucleation and the rate of solute consumption by growth dictate the number of crystals that are nucleated ([NC]final). A competition between the growth and the nucleation manifolds for the available solutes governs the extent of nucleation and the final size. In other words, slow growth kinetics can lead to greater numbers of smaller nanocrystals, provided that the role of aggregation and ripening are also considered.
In the present study we investigate the influence of temperature on the final nanocrystal size using nucleation mass balance models as a guide. We leverage the range of reactivity provided by N,N′-di and N,N,N′-trisubstituted chalcogenoureas to independently adjust the solute supply kinetics at several temperatures and infer the temperature dependence of the growth rate from the final nanocrystal size. The absence of nanocrystal ripening and the very narrow size distributions that are characteristic of our model system allow precise determination of the number of nanocrystals formed during nucleation.26,30,39 In addition, we identify conditions where the kinetics of nucleation can be directly observed, as well as conditions where the solutes that accumulate prior to nucleation can be probed with X-ray scattering.
Experimental
General methods
The model nanocrystal synthesis using lead oleate, thio-, and selenoureas is described elsewhere.30,36Synthesis of PbS and PbSe nanocrystals
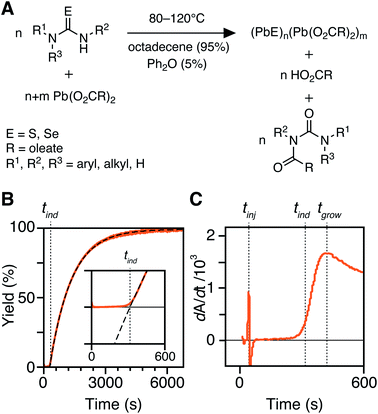
In situ kinetics are obtained as previously described.30 Briefly, in a nitrogen-filled glovebox, three vessels are prepared: (A) lead oleate (166.3 mg, 0.216 mmol, 1.2 equiv.) and hexadecane (19.0 mL) in a 25 mL three-neck round-bottom flask, sealed with three rubber septa. (B) The desired thio- or selenourea (0.216 mmol, 1.2 equiv.) and diphenyl ether (1.288 g, 1.2 mL) are added to a 4 mL scintillation vial, sealed with a rubber septum. (C) Tetrachloroethylene (3.895 g, 2.4 mL) is added to a 1 cm × 1 cm quartz cuvette, sealed with a septum cap. The vessels A and B are then attached to a Schlenk line via argon inlet needles and the in situ optical dip probe is installed under positive argon flow. Both vessels are equilibrated in oil baths set to the desired temperature (>15 minutes). After baseline correction, the recording of the absorbance at 400 nm is started, collecting one data point every 600 ms. The thio- or selenourea solution (1 mL, 0.180 mmol, 1.0 equiv) is injected into the lead oleate solution to initiate the reaction. This results in 20 mL of total solution with a lead oleate concentration of 10.8 mM and a thio- or selenourea concentration of 9.0 mM. The reaction is run for 7–9 half lives (t1/2), at which time the absorbance reaches a plateau. At this time, a 100 μL aliquot is removed and added to the cuvette containing 2.4 mL of tetrachloroethylene to measure the full UV-vis-NIR absorption spectrum.Determination of [PbS] and kr from in situ absorbance
The kinetics of PbS and PbSe nanocrystal formation are measured from the absorbance at λ = 400 nm according to our previous report (Fig. 1).30 At this wavelength the absorbance is independent of NC size and proportional to the number of PbS or PbSe units in nanocrystals (see Discussion Section).40 However, the correlation between the molar concentration of crystalline material and the absorptivity at 400 nm may depend on the size below diameters of 2 nm (∼80 PbE units), which prevents a detailed interpretation of the absorption onset. Regardless, the majority of syntheses studied here produce nanocrystals of much larger size and the absorbance following the onset is a reliable measure of the PbS or PbSe units in crystalline material.41–43An example dip probe trace is displayed in Fig. 1B and C. Two maxima can be observed in the derivative, the first corresponding to the injection time, tinj, and the second corresponding to the time after which the absorbance trace displays single-exponential behavior, tgrow. The data following tgrow were fit to a single exponential function:
| A = Afinal(1 − e−kr(t−tind)) | (1) |
We postulate that the precursor conversion reaction starts at the moment of injection. Using eqn (1), we calculate the concentration of PbE formed during the induction delay, by assuming that kr is equal to the precursor conversion rate constant. The fraction of precursor conversion during the induction delay (find) is calculated according to eqn (2):
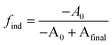 | (2) |
| [PbE]ind = [PbE]final × find | (3) |
The [PbE]ind measured in this way is an underestimate of the solute concentration at tind because the kr under estimates the precursor conversion reactivity. However, the difference is small, as demonstrated in a study to be published elsewhere.44
Measurement of nucleation kinetics, nucleation fraction, and yield using UV-Vis-NIR absorption of aliquots
Quantitative aliquots (0.2 mL) are taken to monitor the nucleation process. Aliquots are injected into a pre-weighed vial in air and immediately cooled to −78 °C to prevent further precursor conversion. Immediate freezing of aliquots causes a feature to appear in the absorption spectrum (λ ∼475 nm) that is assigned to PbS solutes (see below).45 Each aliquot is weighed and diluted with a known amount of tetrachloroethylene (3 mL) prior to recording a UV-Vis-NIR absorption spectrum. A background spectrum was recorded from a known mass of hexadecane and diphenyl ether diluted in tetrachloroethane. The background spectrum was subtracted from the UV-Vis-NIR spectra of aliquots by accounting for the concentration of the hexadecane and diphenyl ether in the aliquot solution. In this way the vibrational overtones of the solvent can be reduced.46The intensity and wavelength of the lowest energy excitonic transition provides a direct measure of the nanocrystal concentration that is unaffected by the absorbance of solutes. Using a size-dependent extinction coefficient the absorbance intensity at the lowest energy excitonic feature is converted to the [NC] at each time point according to a previously described method.47 By using the lowest energy excitonic absorption intensity rather than the absorbance at λ = 400 nm we avoid measuring the absorbance of solutes, which can be misinterpreted as nanocrystal absorbance.45,48,49 On the other hand, upon complete precursor conversion the [NC] reaches a plateau and the solute concentration is assumed to be insignificant. At this point, the [NC]final is determined using the absorbance at λ = 400 nm.40,48 (see ESI†).
Measurements of [NC] taken from the lowest energy excitonic absorbance intensity do not consider the influence of the polydispersity or surface chemistry on the breadth and intensity of the excitonic transition. Mechanisms that induce broadening of this transition (e.g. Ostwald Ripening) will systematically influence the [NC]. However, the broadening caused by the polydispersity of our samples is less than 25% of the total width at reaction temperatures from 90–120 °C (Fig. S28 and S29†), which helps to mitigate this effect. Nonetheless, at high temperatures, a decrease in the observed [NC] can be observed in one case (Fig. S25†).
By measuring the nanocrystal concentration during the synthesis, we can directly determine the rate at which crystallites are produced, a process we define as nucleation. Although our measurement does not capture crystallites much smaller than the ensemble average, this is a minor consideration given the narrow polydispersities that are observed at all time points. While, in principle, ripening and agglomeration can influence the nanocrystal concentration and obscure the nucleation kinetics, these pathways are insignificant at the end of the reaction, as was described in our recent reports.26,30 Moreover, it is consistent with the observation that the concentration of nanocrystals becomes stable after an initial period (Fig. S25†).
Plots of [NC] versus time were fitted to a single exponential to extract an observed nucleation rate constant k[NC] where [NC] is the concentration of nanocrystals at time t, and [NC]final is the final concentration of nanocrystals (eqn (4)). Example fittings are provided in the ESI.† While the true functional form of the nucleation process is unlikely to be first order, the k[NC] provides a convenient method for comparing the relative rates of nucleation and the precursor reaction as the temperature is varied.
| [NC] = [NC]final(1−e−k[NC](t−tind)) | (4) |
The nucleation kinetics were compared to the kinetics of the yield development in aliquots by measuring the [PbS]i using a size independent extinction coefficient (λ = 400 nm). The yield at each time point can also be measured directly from the intensity of the excitonic transition, however, we chose to use the absorbance at λ = 400 nm to capture the absorbance of small clusters, thus providing a better approximation of the precursor conversion kinetics. To account for variations in the amount of aliquoted material in the cuvette, the measured [PbS]i in the cuvette was corrected using the mass of reaction solution and the tetrachloroethylene solvent. The kinetics of PbS formation were determined by fitting the temporal evolution of [PbS]i to the following equation where [PbS]final is the final concentration of [PbS]i (eqn (5)).
| [PbS]i = [PbS]final(1−e−kr(t−tind)) | (5) |
The extracted rate constants (k[NC] and kr) are used to calculate half-lives of the nucleation and precursor conversion reactions (t1/2,[NC] = ln(2)/k[NC] and t1/2,rxn = ln(2)/kr). The ratio of t1/2,[NC] and t1/2,rxn, a so called nucleation fraction, allows the relative duration of the nucleation and growth processes to be compared (see ESI† for details).17
In situ total scattering measurements/pair distribution function analysis
Experiments are carried out using beamline 28-ID-2 at the National Synchrotron Light Source II (NSLS-II) at Brookhaven National Laboratory. X-ray scattering data are collected at room temperature, in rapid acquisition mode, using a 2D PerkinElmer amorphous silicon detector (2048 × 2048 pixels and 200 × 200 μm pixel size) with a sample to detector distance of 202.444 mm. The incident wavelength of the X-rays is λ = 0.1877 Å (66.05 keV). Calibration of the experimental setup is performed using a nickel standard sample.In situ X-ray scattering experiments are performed using a custom designed reactor consisting of a remotely controlled injector, a three neck flask equipped with a temperature probe, a magnetic stirrer, an argon inlet, and submerged in an oil bath. A Hei-FLOW Precision 01 peristaltic pump, and Viton tubing (Cole-Parmer, 1/16′′ID × 1/8′′OD) connects a stainless steel syringe needle to a custom Kapton X-ray flow cell. Precursor injection and triggering of the peristaltic pump are both controlled remotely, allowing diffraction patterns to be collected with the shortest time delay possible following mixing of precursors.
The reaction is initiated by a remotely triggered injection of 7 mL of a 190 mM diglyme solution of an N,N′-disubstituted thiourea or N,N–N′-trisubstituted selenourea (1.33 mmol) into 143 mL of a 11.3 mM solution of lead oleate (1.62 mmol) at 80 °C or 110 °C under argon with stirring. The thiourea and selenourea used for the PbS and PbSe reactions at 80 °C are N-3,5-bis-trifluoromethylphenyl-N′-dodecylthiourea and N-cyclohexyl-2-methylpyrrolidine-1-carboselenoamide, respectively. At 110, °C N-p-methoxyphenyl-N′-dodecylthiourea and N-butylpyrrolidine-1-carboselenoamide were chosen for their relatively slow reactivity (kS = 1.69 × 10−3 s−1, kSe = 2.21 × 10−3 s−1) and similar precursor conversion kinetics. The resulting solution is 10.8 mM (1.2 equiv.) in lead and 8.90 mM (1.0 equiv.) in chalcogen immediately following injection. Following the precursor injection, the peristaltic pump is run at maximum speed for ten seconds to ensure the reaction mixture has reached the X-ray beam and passed through the remainder of the Viton tubing into a waste container that is also under Ar. Following this 10 second period, the flow rate is immediately and automatically set to a slower setting which was experimentally measured to be 4.0 mL min−1 under reaction conditions. After reducing the pumping speed, the acquisition of 30 second X-ray scattering patterns is initiated. Based on the pump rates and reaction volume contained in the Viton tubing, the “in flask” reaction time for each spectrum is estimated as described in the ESI.† An X-ray scattering pattern of the lead(II) oleate precursor solution was acquired over 15 minutes at the reaction temperature by circulating the precursor through the flow cell.
Raw 2D data are corrected for geometrical effects and polarization, then azimuthally integrated to produce 1D scattering intensities versus the magnitude of the momentum transfer Q (where Q = 4π sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ for elastic scattering) using the program Fit2D.50 The program xPDFsuite with PDFgetX3 is used to perform the background subtraction, further corrections, and normalization to obtain the reduced total scattering structure function F(Q), and Fourier transformation to obtain the pair distribution function (PDF), G.51,52 The Qmin is determined by the beamstop.
θ/λ for elastic scattering) using the program Fit2D.50 The program xPDFsuite with PDFgetX3 is used to perform the background subtraction, further corrections, and normalization to obtain the reduced total scattering structure function F(Q), and Fourier transformation to obtain the pair distribution function (PDF), G.51,52 The Qmin is determined by the beamstop.
PDFs are processed with a low Qmax (Qmax = 10.0 Å−1) to reduce statistical noise in order to evaluate low amplitude signals during early reaction time points. Once nanocrystals have formed following nucleation this can be extended out further to 15.0–20.0 Å−1 with only minor effects on the data quality in G(r) (Fig. S12†). Virtual crystal modeling of PbS and PbSe nanoparticle growth is performed using PDFGui, and is described in further detail in the ESI†.53
Results
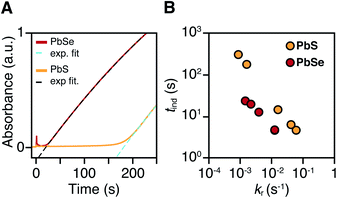
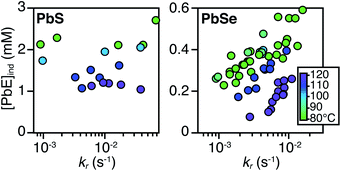
PbS and PbSe nanocrystals were synthesized using thiourea and selenourea reagents with conversion reactivities between 10−1 to 10−4 s−1 at 80–140 °C. Under the conditions studied herein, the induction delay (tind) prior to the appearance of species that absorb λ = 400 nm photons ranges from less than a second to several minutes depending on the material and the precursor reactivity (Fig. 2). At 80 °C the tind prior to the appearance of PbSe absorption is an order of magnitude shorter than the appearance of PbS under nearly identical solute generating conditions (krSe = 1.6 × 10−3 s−1vs. krS = 1.7 × 10−3 s−1) (Fig. 2A). PbSe reactions display shorter tind than PbS reactions over a wide range of conversion reactivity (Fig. 2B). While tind of a few seconds is typical for PbSe, an induction delay exceeding a minute is not uncommon for PbS. In particular, syntheses of PbSe at high temperature (120 °C) have little delay prior to the absorption onset. At this temperature, the delay times are likely influenced by the kinetics of mixing and are insensitive to the precursor reactivity (Fig. S4†). The correlation between the tind and kr over a wide range demonstrates systematic and reproducible reaction conditions over a wide range of conditions in both material systems.The concentration of solute at tind was estimated across two orders of magnitude in the reaction rate and a 30 or 40 °C range of temperature (Fig. 3). PbS reactions reach an order of magnitude higher solute concentrations prior to the development of absorbance at λ = 400 nm ([PbS]ind = 1.0–2.9 mM, [PbSe]ind = 0.15–0.58 mM). These are relatively high concentrations in the case of PbS, and clearly indicate that solutes do not absorb visible light until a larger size is achieved.
As much as 11–32% of the total added sulfur and 1–7% of the total added selenium accumulates as solutes prior to contributing to the absorbance at λ = 400 nm. Moreover, these concentrations are 10–100x greater than the concentration of nanocrystals formed by nucleation (see below). Thus, the solutes produced during the induction time undergo assembly into nuclei and nanocrystals, consistent with a homogeneous nucleation and growth mechanism.
The [PbE]ind depends on both the temperature and the kr. Interestingly, the [PbE]ind observed in PbSe syntheses more than doubles over an order of magnitude increase in kr. The increase suggests that the kinetics of [PbSe]i generation are similar to the kinetics of the precipitation. The growth of PbS, on the other hand, displays a relatively consistent [PbE]ind. These results suggest that larger nanostructures form at a lower [PbE]ind in the case of PbSe. However, differences in the absorptivity of small PbS vs. PbSe clusters could also explain these results.
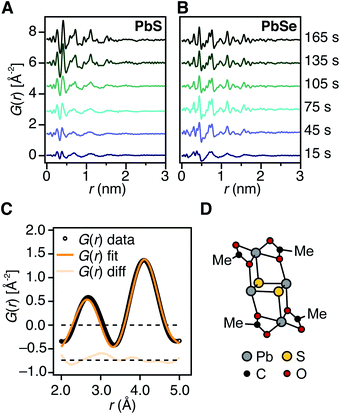
X-ray pair distribution function analysis of early reaction times
To determine the structure of solutes and crystals present during the induction delay, nucleation, and growth stages, in situ synchrotron X-ray total scattering and pair distribution function (PDF) analysis experiments were performed. X-ray PDF has previously been used to study the evolution of metal oxide solutes and nanocrystals (e.g., WO3, SnO2) during hydrothermal synthesis,54–56 and the structures formed during the early stages during metal organic framework synthesis.57At the standard 9 mM concentration used in this study, 30 seconds of acquisition time was required to achieve sufficient signal to perform PDF analysis. This time resolution allowed PDFs to be obtained prior to tind when a relatively slowly reacting thiourea (N-3,5-bis-trifluoromethylphenyl-N′-dodecylthiourea, kr = 1.7 × 10−3 s−1, tind = 182 s) is used (Fig. 4A). These measurements revealed correlations with r < 1 nm that evolve to structures with longer range correlations during the absorption onset. Similar measurements on a PbSe nanocrystal synthesis with comparable kinetics (N-cyclohexyl-2-methylpyrrolidine-1-carboselenoamide, kr = 2.2 × 10−3 s−1, tind = ∼20 s) showed a much more rapid development of long range atomic pair correlations (Fig. 4B). The shorter induction periods prior to optical absorption from PbSe correlates with more rapid appearance of long-range Pb–Se atomic order. This can also clearly be seen in reciprocal space with the appearance of prominent [111], [200], [220], [311], [222] reflections of a rock salt lattice appearing more rapidly in the case of PbSe versus PbS (Fig. S10 and S11†). These observations support the conclusion that the onset of optical absorption at λ = 400 nm is characteristic of mature nanostructures with longer range atomic pair correlations. The colorless solutions prior to this time contain relatively high concentrations of molecular solutes formed by precursor conversion.
The PDF patterns were fit using a periodic PbS or PbSe rock salt model and a spherical envelope dampening function, to estimate the crystallite size at each time point (Fig. 4C and S14–S15†).58 A residual fit function (Rw) was calculated for each pattern, the magnitude of which is indicative of the fit quality. At early times, the Rw is greatest and slowly decreases to its terminal value several minutes following nucleation (Fig. S13†). Thus the rock salt model does not adequately capture the structure of solutes at early times (Fig. S16†).
PDF patterns prior to tind, show nearest (e.g. Pb–S), second nearest (e.g. Pb–Pb and S–S), and third nearest neighbor correlations that are distinct from lead oleate in solution or the solid state and consistent with the formation of molecular PbS solutes (Fig. S17–S21†). Following tind, the PDF data is accurately captured by the spherical nanocrystal model. Several hypothetical discrete PbS solute structures were computed using density functional theory, and their PDFs compared to the experimental data. Among these, a Pb2S2 diamond bound by lead carboxylate (e.g., Pb2(μ2-S)2(Pb(O2CR)2)2) accurately recovers the ratio of the first and second nearest neighbor correlations (Fig. 4C and D). Moreover the PDF pattern evolves with time, temperature, and concentration in a manner that is consistent with a variety of solute structures being present. Assigning the atomic structure of these early solute species and their individual concentrations requires more detailed analysis. However, the correlations present during the induction delay are inconsistent with ordered structures larger in size than Pb2(μ2-S)2(Pb(O2CR)2)2. Thus, we conclude that the solutes accumulating prior to the induction delay are molecular and then slowly assemble into nanocrystals.
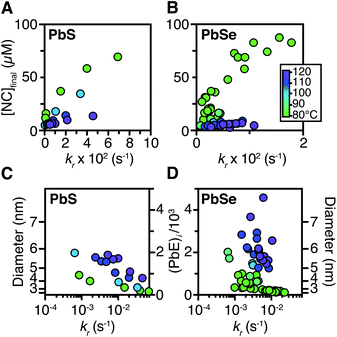
Size control
The influence of the precursor reactivity and temperature on the [NC]final is shown below in Fig. 5. Both low temperatures and more reactive thio- and selenoureas afford a higher [NC]final and a smaller final diameter.30,36 The results are consistent with nucleation mass balance models described by Sugimoto and others,9,37,38 where the growth kinetics increase with increasing temperature. Similarly, under otherwise identical conditions, PbSe nanocrystals reach larger sizes than PbS, which can be attributed to faster growth kinetics.Interestingly, the final size of both PbSe and PbS nanocrystals becomes more sensitive to the precursor reactivity at high temperature, while at the lowest temperature the size remains within 3–4 nm over more than an order of magnitude spread in precursor reactivity. The small range of sizes produced at low temperatures suggests that growth is slow and nucleation continues over long periods. To probe this hypothesis, the nucleation kinetics were monitored with optical spectroscopy.
Nucleation time and polydispersity
To measure the nucleation kinetics, the optical spectrum of timed aliquots is analyzed to extract the [NC] throughout the synthesis. Fig. 6 illustrates a typical spectral evolution and plots the evolving [NC] and [PbE]i. In addition to the steady red shift of the lowest energy excitonic feature, a second feature is visible at high energies (λmax = 475–510 nm) that persists over the first half of the reaction (Fig. S5†).45 Interestingly, this higher energy feature is absent if aliquots are not immediately quenched in an acetone-dry ice bath. We hypothesize that molecular PbS solutes present at the reaction temperature assemble into clusters with an absorbance feature at 475 nm upon rapid cooling.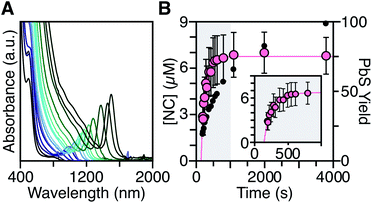 | ||
| Fig. 6 (A) Evolution of the UV-Vis-NIR absorbance spectrum for a reaction of Pb(oleate)2 with N-4-methoxyphenyl-N′-dodecylthiourea at 90 °C. (B) Temporal evolution of [NC] (pink) and PbS yield (black). The shaded portion of the plot is replotted in the inset and shows the extended nucleation period. See the ESI† for a discussion of the uncertainty shown. | ||
To avoid complications from the high energy feature, the temporal evolution of the [NC] extracted from the energy and intensity of the lowest energy excitonic feature was measured across a range of precursor reactivities and reaction temperatures. A slow steady increase in the number of nanocrystals is observed, especially at low temperatures (Fig. 6B and S25†). We have observed similarly prolonged nucleation under identical conditions using in situ X-ray scattering measurements that will be reported elsewhere.44 The increasing nanocrystal concentrations observed here provide a direct measure of the nucleation kinetics because the final nanocrystals do not significantly ripen or agglomerate under these conditions.26,30 Hence, the steadily increasing [NC] shows that crystal nucleation continues throughout a significant fraction of the total reaction time rather than occurring in a burst.
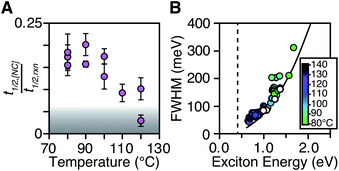
The length of the nucleation period is estimated by fitting the [NC] versus time using eqn (5). Half-lives of the nucleation and precursor conversion reactions (t1/2,[NC] = ln(2)/k[NC] and t1/2,rxn = ln(2)/kr) are extracted and compared to understand the duration of the nucleation period (see ESI† for details).17Fig. 7A plots the nucleation fraction at several temperatures and demonstrates that the nucleation period occurs in a smaller fraction of the reaction time as the temperature is increased. At temperatures > 120 °C the nucleation occurs more rapidly than could be measured, while at the lowest temperatures, nucleation persists for > 50% of the synthesis. The long nucleation times starkly contrast with the so called “burst” of nucleation typically ascribed to monodisperse ensembles of nanocrystals.
The full width at half maximum (FWHM) of the lowest energy excitonic absorbance feature of the final PbS nanocrystals is shown in Fig. 7B. A hole burning transient absorption method previously employed to study PbSe nanocrystals was used to estimate the intrinsic FWHM of several sizes and is shown for comparison.26 These measurements demonstrate that the spectral linewidth of the nanocrystals prepared here are dominated by the intrinsic breadth of a single size rather than the polydispersity. Moreover, the intrinsic linewidth narrows as the size increases, as has been demonstrated in several recent studies (Fig. S29†).20,26,59–61
The polydispersity accounts for ∼20% of the linewidth at all sizes and is not influenced by the temperature despite the significantly shorter nucleation times at high temperature (Fig. 7B and S28–S30†). Similarly, we find no systematic correlation between precursor and the polydispersity (Fig. S31†), further indication that the precursor reactivity is orthogonal to crystal growth. We conclude that the width of the nucleation phase does not correlate with the polydispersity over a wide range of nucleation times. Hence, the narrow polydispersity must be the result of other mechanisms.
PbSe nanocrystals on the other hand showed systematic changes in polydispersity with temperature (Fig. S28†). The narrowest polydispersities are obtained at 100–120 °C, while lower or higher temperatures both broaden the FWHM. The nonmonotonic change suggests multiple competing factors control the polydispersity in that case. Factors such as the precursor solubility at low temperature or the mixing limited kinetics at high temperature may be important. Regardless, these results do not support the conclusion that the polydispersity is related to the width of the nucleation phase.
Discussion
While it is commonly assumed that colloidal quantum dots are formed from homogeneous solute intermediates (e.g. monomers), the identity and concentration of such species is rarely studied. Several pieces of evidence support the formation of solutes in this study. X-Ray PDF patterns acquired in situ at early reaction times display molecular length scale correlations rather than extended crystalline order. These signals increase in intensity prior to tind and then steadily evolve to a pattern with 1–2 nm pair correlations as the solution develops absorption at 400 nm. Likewise, the transient intermediate observed in the absorption spectra of rapidly quenched aliquots also supports the accumulation of solutes that increase and then decrease in concentration over the course of the reaction (Fig. 6A). However, the species in the ex situ and in situ measurements are likely distinct given that the PDF measurements are performed prior to the onset of absorption at λ = 400 nm (albeit at the reaction temperature) while the transient intermediate visible in the spectra of aliquots absorbs strongly at that wavelength. Thus, multiple solute structures are present during nanocrystal growth.Although the [PbE]ind is an indirect measure of the solute concentration, its sensitivity to the temperature and kr (Fig. 3) is consistent with the solute generation and consumption mechanism depicted in Scheme 1. Several observations support this conclusion: (1) more rapid precursor conversion kinetics lead to higher [PbE]ind, behavior more clearly visible in syntheses of PbSe (Fig. 3B). This is consistent with a growth rate that is orthogonal to the precursor reactivity. (2) Large PbSe nanostructures form more rapidly than PbS under otherwise identical conditions (Fig. 4). More rapid PbSe growth kinetics is consistent with the lower [PbSe]ind and the larger final sizes (Fig. 3). (3) The temperature dependence of [PbE]ind can be attributed to a changing growth rate; slower growth kinetics at low temperatures leads to higher [PbE]ind. These pieces of evidence support a homogeneous nucleation and growth mechanism that proceeds via the accumulation of solutes generated by precursor conversion.
While a homogeneous nucleation and growth mechanism is consistent with our results, the slow and persistent nucleation kinetics observed here are inconsistent with La Mer's hypothesis that a “burst of nucleation” explains the narrow size distributions typical of these colloids (Fig. 7B). The lack of correlation between the nucleation fractions and the spectral linewidths demonstrates that the length of the nucleation period does not meaningfully influence the polydispersity under these conditions. We therefore conclude that the polydispersity is primarily determined by size distribution focusing mechanisms where small crystals consume solutes more rapidly than large crystals.
Recent studies of InP,17 CdSe,62,63 Au,64 Ag,65 Ir,4,66 and Pd,65 have also documented long nucleation periods and narrow polydispersities. However, the mechanism observed here is distinct from the autocatalytic surface catalyzed conversion mechanism proposed for metal nanocrystals.4,66 The build-up of persistent solute species and the orthogonality of the precursor conversion and growth kinetics support a distinctly different formation pathway. Nonetheless, it appears that both mechanisms require a size dependent surface reactivity to obtain narrow polydispersities.
Size dependent growth kinetics can also be used to understand the temperature dependence shown in Fig. 5, particularly for PbSe. At the lowest reaction temperatures the ensemble is slow to grow beyond 4 nm in diameter regardless of the solute supply kinetics. A similar observation was recently reported in a study of InP.17 This behavior suggests self-limiting growth where mature nanocrystals reject solutes that go on to nucleate new crystals. At low temperature relatively small sizes reject solutes and nucleation continues over long periods. At higher temperatures, a broader range of sizes consume solutes, shortening the nucleation process and causing an increased sensitivity of the [NC] to the conversion reactivity. Thus, the influence of temperature on the size can also be understood using a model where growth kinetics are size dependent.
Size dependent growth kinetics are a natural consequence of diffusion limited growth kinetics.63,66,67 However, the self-limited growth and continuous nucleation at low temperature strongly suggests that diffusion limitations are unlikely to explain the size dependence observed here. A similar conclusion is reached in a related study on PbS to be published elsewhere.44 More detailed understanding of the factors controlling the growth rate would, therefore, enable the rational optimization of size distributions.
Nucleation mass balance models relate the solute supply kinetics and the number of nanocrystals. Mathematical solutions to those models developed by Sugimoto make the simplifying assumption that nucleation occurs in a narrow range of time and solute concentration. As a result, the rate of crystal growth can be treated as a constant during the nucleation period, and a relatively simple proportionality between the solute supply and consumption and the number of stable nuclei results. While such models are qualitatively consistent with our results (Fig. 5A and B), several other observations made in this study are inconsistent with Sugimoto's underpinning assumptions. The variability of the [PbE]ind with the precursor reactivity, the slow and steady increase in the [NC] over a large proportion of the synthesis, and the size dependent growth kinetics all deviate from Sugimoto's picture. Moving beyond this model requires a more detailed understanding of the solute concentration dependence of the nucleation rate as well as the size dependence of the growth rate.
The size dependent growth kinetics and long nucleation periods are also antithetical to classical thermodynamic pictures where nucleation is characterized by a critical radius and critical solute concentration. These pictures only consider the thermodynamic driving force for solute attachment. However, the size dependent growth kinetics are perhaps easier to understand using a mechanism that is defined by a kinetic picture with a barrier to solute attachment. The connection between such mechanisms and the size and polydispersity requires a substantial revision of current thinking about colloidal crystal formation.
Conclusions
We have investigated the influence of reaction temperature on the growth kinetics of PbS and PbSe across more than an order of magnitude in the rate of solute supply. Consistent differences between the induction delay times, final particle size, nucleation duration, and the extent of nucleation could be observed from the reproducible reaction conditions. PbSe nanocrystals nucleate at lower monomer concentrations and with shorter induction delay times than PbS. Together with the relative sizes obtained under otherwise identical conditions, we demonstrate a higher reactivity of PbSe toward growth as compared to PbS. The long nucleation times observed here do not correlate with the polydispersity, indicating that the narrow polydispersities obtained here result from size dependent growth kinetics. The long nucleation times also suggest that classical thermodynamic pictures do not adequately explain colloidal PbS or PbSe nucleation and growth. Moreover, the factors controlling the nanocrystal size distribution result from nanocrystal surface chemistry and its influence on the solute attachment kinetics, rather than the nucleation.Data availability
Extensive experimental data can be found in the ESI† and is referred to throughout the manuscript!Author contributions
J. S. O. organized the research. B. M. M., J. D. R., M. W. G., and J. S. O. wrote the manuscript. M. P. C., J. D. R., M. P. H., B. M. M. collected and analyzed PbS and PbSe dip probe data. B. A., M. W. G., J. D. R., S. K. G. and J. S. O. conceived and designed the in situ PbS and PbSe PDF experiments. M. W. G., E. B., N. S., S. K. G., B. A., and J. D. R. helped with collection of the in situ PbS and PbSe PDF data. M. W. G. fit PDF patterns and calculated DFT structures of the PbS solute molecules. B. M. M. and M. W. G collected and analyzed UV-Vis-NIR measurement of aliquots taken throughout various PbS reactions and measured the duration of nucleation. M. Y. S. measured the linewidths of PbS and PbSe samples using transient absorption spectroscopy.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Science Foundation under NSF-CHE-2004008. M. W. G. acknowledges support from Brookhaven National Laboratory, National Synchrotron Light Source II Director's Student & Postdoc support program. X-ray scattering data was collected using beamline 28-ID-2 of the National Synchrotron Light Source II, a U.S. DOE Office of Science User Facility operated for the DOE Office of Science by Brookhaven National Laboratory under Contract No. DE- SC0012704. J. D. R acknowledges the Belgian American Education Foundation (B. A. E. F.), Fulbright, Ghent University, and the COMPASS project (H2020-MSCA-RISE-2015-691185) for financial support. B. A. thanks Vincent Klein and the “ELINSTRU” team of the Laboratoire de Physique des Solides for the conception and building of the remotely controlled injector. This research used resources of the Center for Functional Nanomaterials (CFN), which is a U.S. Department of Energy Office of Science User Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704. The authors acknowledge James P. Shanahan for helpful discussion.Notes and references
- J. Park, J. Joo, S. G. Kwon, Y. Jang and T. Hyeon, Synthesis of monodisperse spherical nanocrystals, Angew. Chem., Int. Ed., 2007, 46(25), 4630–4660 CrossRef CAS PubMed.
- L. S. Hamachi, I. Jen-La Plante, A. C. Coryell, J. De Roo and J. S. Owen, Kinetic Control over CdS Nanocrystal Nucleation Using a Library of Thiocarbonates, Thiocarbamates, and Thioureas, Chem. Mater., 2017, 29(20), 8711–8719 CrossRef CAS.
- J. Byun, K. H. Kim, B. K. Kim, J. W. Chang, S. K. Cho and J. J. Kim, Gravimetric analysis of the autocatalytic growth of copper microparticles in aqueous solution, RSC Adv., 2019, 9(65), 37895–37900 RSC.
- M. A. Watzky and R. G. Finke, Transition metal nanocluster formation kinetic and mechanistic studies. A new mechanism when hydrogen is the reductant: Slow, continuous nucleation and fast autocatalytic surface growth, J. Am. Chem. Soc., 1997, 119(43), 10382–10400 CrossRef CAS.
- J. A. Widegren, J. D. Aiken, S. Ozkar and R. G. Finke, Additional investigations of a new kinetic method to follow transition-metal nanocluster formation, including the discovery of heterolytic hydrogen activation in nanocluster nucleation reactions, Chem. Mater., 2001, 13(2), 312–324 CrossRef CAS.
- R. Garcia-Rodriguez, M. P. Hendricks, B. M. Cossairt, H. T. Liu and J. S. Owen, Conversion Reactions of Cadmium Chalcogenide Nanocrystal Precursors, Chem. Mater., 2013, 25(8), 1233–1249 CrossRef CAS.
- F. Wang, V. N. Richards, S. P. Shields and W. E. Buhro, Kinetics and Mechanisms of Aggregative Nanocrystal Growth, Chem. Mater., 2014, 26, 5–21 CrossRef CAS.
- S. Abe, R. K. Capek, B. De Geyter and Z. Hens, Tuning the postfocused size of colloidal nanocrystals by the reaction rate: from theory to application, ACS Nano, 2012, 6(1), 42–53 CrossRef CAS PubMed.
- T. Sugimoto, Preparation of Monodispersed Colloidal Particles, Adv. Colloid Interface, 1987, 28(1), 65–108 CrossRef CAS.
- C. B. Murray, C. R. Kagan and M. G. Bawendi, Synthesis and characterization of monodisperse nanocrystals and close-packed nanocrystal assemblies, Annu. Rev. Mater. Sci., 2000, 30, 545–610 CrossRef CAS.
- Y. Yin and A. P. Alivisatos, Colloidal nanocrystal synthesis and the organic–inorganic interface, Nature, 2005, 437(7059), 664–670 CrossRef CAS PubMed.
- J. S. Owen, E. M. Chan, H. T. Liu and A. P. Alivisatos, Precursor Conversion Kinetics and the Nucleation of Cadmium Selenide Nanocrystals, J. Am. Chem. Soc., 2010, 132(51), 18206–18213 CrossRef CAS PubMed.
- B. Abecassis, F. Testard, Q. Y. Kong, B. Francois and O. Spalla, Influence of Monomer Feeding on a Fast Cold Nanoparticles Synthesis: Time-Resolved XANES and SAXS Experiments, Langmuir, 2010, 26(17), 13847–13854 CrossRef CAS PubMed.
- B. Abecassis, F. Testard, O. Spalla and P. Barboux, Probing in situ the nucleation and growth of gold nanoparticles by small-angle x-ray scattering, Nano Lett., 2007, 7(6), 1723–1727 CrossRef CAS PubMed.
- M. A. Watzky and R. G. Finke, Transition Metal Nanocluster Formation Kinetic and Mechanistic Studies. A New Mechanism When Hydrogen Is the Reductant: Slow, Continuous Nucleation and Fast Autocatalytic Surface Growth, J. Am. Chem. Soc., 1997, 119(43), 10382–10400 CrossRef CAS.
- H. T. Liu, J. S. Owen and A. P. Alivisatos, Mechanistic study of precursor evolution in colloidal group II–VI semiconductor nanocrystal synthesis, J. Am. Chem. Soc., 2007, 129(2), 305–312 CrossRef CAS PubMed.
- B. M. McMurtry, K. Qian, J. K. Teglasi, A. K. Swarnakar, J. De Roo and J. S. Owen, Continuous Nucleation and Size Dependent Growth Kinetics of Indium Phosphide Nanocrystals, Chem. Mater., 2020, 32(10), 4358–4368 CrossRef CAS.
- D. C. Gary, B. A. Glassy and B. M. Cossairt, Investigation of indium phosphide quantum dot nucleation and growth utilizing triarylsilylphosphine precursors, Chem. Mater., 2014, 26(4), 1734–1744 CrossRef CAS.
- D. C. Gary, M. W. Terban, S. J. L. Billinge and B. M. Cossairt, Two-Step Nucleation and Growth of InP Quantum Dots via Magic-Sized Cluster Intermediates, Chem. Mater., 2015, 27(4), 1432–1441 CrossRef CAS.
- J. Cui, A. P. Beyler, I. Coropceanu, L. Cleary, T. R. Avila, Y. Chen, J. M. Cordero, S. L. Heathcote, D. K. Harris, O. Chen, J. S. Cao and M. G. Bawendi, Evolution of the Single-Nanocrystal Photoluminescence Linewidth with Size and Shell: Implications for Exciton-Phonon Coupling and the Optimization of Spectral Linewidths, Nano Lett., 2016, 16(1), 289–296 CrossRef CAS PubMed.
- D. Franke, D. K. Harris, L. Xie, K. F. Jensen and M. G. Bawendi, The Unexpected Influence of Precursor Conversion Rate in the Synthesis of III-V Quantum Dots, Angew. Chem., Int. Ed., 2015, 54(48), 14299–14303 CrossRef CAS PubMed.
- H. Sun, F. Wang and W. E. Buhro, Tellurium Precursor for Nanocrystal Synthesis: Tris(dimethylamino)phosphine Telluride, ACS Nano, 2018, 12(12), 12393–12400 CrossRef CAS PubMed.
- K. De Nolf, R. K. Capek, S. Abe, M. Sluydts, Y. Jang, J. C. Martins, S. Cottenier, E. Lifshitz and Z. Hens, Controlling the size of hot injection made nanocrystals by manipulating the diffusion coefficient of the solute, J. Am. Chem. Soc., 2015, 137(7), 2495–2505 CrossRef CAS PubMed.
- J. Park, A. Jayaraman, X. D. Wang, J. Zhao and H. S. Han, Nanocrystal Precursor Incorporating Separated Reaction Mechanisms for Nucleation and Growth to Unleash the Potential of Heat-up Synthesis, ACS Nano, 2020, 14(9), 11579–11593 CrossRef CAS PubMed.
- J. Park, A. Jayaraman, A. W. Schrader, G. W. Hwang and H.-S. Han, Controllable modulation of precursor reactivity using chemical additives for systematic synthesis of high-quality quantum dots, Nat. Commun., 2020, 11(1), 5748 CrossRef CAS PubMed.
- M. P. Campos, M. P. Hendricks, A. N. Beecher, W. Walravens, R. A. Swain, G. T. Cleveland, Z. Hens, M. Y. Sfeir and J. S. Owen, A Library of Selenourea Precursors to PbSe Nanocrystals with Size Distributions near the Homogeneous Limit, J. Am. Chem. Soc., 2017, 139(6), 2296–2305 CrossRef CAS PubMed.
- A. Preske, S. W. O'Neill, B. D. Swartz, J. Liu, O. V. Prezhdo and T. D. Krauss, Size-Programmed Synthesis of PbSe Quantum Dots via Secondary Phosphine Chalcogenides, Chem. Mater., 2019, 31(20), 8301–8307 CrossRef CAS.
- W.-k. Koh, A. C. Bartnik, F. W. Wise and C. B. Murray, Synthesis of monodisperse PbSe nanorods: a case for oriented attachment, J. Am. Chem. Soc., 2010, 132(11), 3909–3913 CrossRef CAS PubMed.
- W.-k. Koh, Y. Yoon and C. B. Murray, Investigating the phosphine chemistry of Se precursors for the synthesis of PbSe nanorods, Chem. Mater., 2011, 23(7), 1825–1829 CrossRef CAS.
- M. P. Hendricks, M. P. Campos, G. T. Cleveland, I. Jen-La Plante and J. S. Owen, A tunable library of substituted thiourea precursors to metal sulfide nanocrystals, Science, 2015, 348(6240), 1226–1230 CrossRef CAS PubMed.
- J. M. Rhodes, C. A. Jones, L. B. Thal and J. E. Macdonald, Phase-Controlled Colloidal Syntheses of Iron Sulfide Nanocrystals via Sulfur Precursor Reactivity and Direct Pyrite Precipitation, Chem. Mater., 2017, 29(19), 8521–8530 CrossRef CAS.
- B. A. Tappan, G. Barim, J. C. Kwok and R. L. Brutchey, Utilizing Diselenide Precursors toward Rationally Controlled Synthesis of Metastable CuInSe2 Nanocrystals, Chem. Mater., 2018, 30(16), 5704–5713 CrossRef CAS.
- A. C. Berends, W. Van Der Stam, J. P. Hofmann, E. Bladt, J. D. Meeldijk, S. Bals and C. de Mello Donega, Interplay between surface chemistry, precursor reactivity, and temperature determines outcome of ZnS shelling reactions on CuInS2 nanocrystals, Chem. Mater., 2018, 30(7), 2400–2413 CrossRef CAS PubMed.
- E. Bennett, M. W. Greenberg, A. J. Jordan, L. S. Hamachi, S. Banerjee, S. J. L. Billinge and J. S. Owen, Size Dependent Optical Properties and Structure of ZnS Nanocrystals Prepared from a Library of Thioureas, Chem. Mater., 2022, 34(2), 706–717 CrossRef CAS.
- M. P. Campos https://www.youtube.com/watch?v=N7Ppv8bj4zc .
- M. P. Campos, M. P. Hendricks, A. N. Beecher, W. Wslravens, R. A. Swain, G. T. Cleyeland, Z. Hens, M. Y. Sfeir and J. S. Owen, A Library of Selenourea Precursors to PbSe Nanocrystals with Size Distributions near the Homogeneous Limit, J. Am. Chem. Soc., 2017, 139(6), 2296–2305 CrossRef CAS PubMed.
- T. Sugimoto, F. Shiba, T. Sekiguchi and H. Itoh, Spontaneous nucleation of monodisperse silver halide particles from homogeneous gelatin solution I: silver chloride, Colloids Surf., A, 2000, 164(2–3), 183–203 CrossRef CAS.
- D. B. K. Chu, J. S. Owen and B. Peters, Nucleation and Growth Kinetics from LaMer Burst Data, J. Phys. Chem. A, 2017, 121(40), 7511–7517 CrossRef CAS PubMed.
- A. W. Jansons, L. K. Plummer and J. E. Hutchison, Living Nanocrystals, Chem. Mater., 2017, 29(13), 5415–5425 CrossRef CAS.
- I. Moreels, K. Lambert, D. De Muynck, F. Vanhaecke, D. Poelman, J. C. Martins, G. Allan and Z. Hens, Composition and size-dependent extinction coefficient of colloidal PbSe quantum dots, Chem. Mater., 2007, 19(25), 6101–6106 CrossRef CAS.
- R. S. Kane, R. E. Cohen and R. Silbey, Theoretical study of the electronic structure of PbS nanoclusters, J. Phys. Chem., 1996, 100(19), 7928–7932 CrossRef CAS.
- H. X. Zeng, Z. A. Schelly, K. Ueno-Noto and D. S. Marynick, Density functional study of the structures of lead sulfide clusters (PbS)(n) (n=1–9), J. Phys. Chem. A, 2005, 109(8), 1616–1620 CrossRef CAS PubMed.
- S. Wu, H. Zeng and Z. A. Schelly, Preparation of Ultrasmall, Uncapped PbS Quantum Dots via Electroporation of Vesicles, Langmuir, 2005, 21(2), 686–691 CrossRef CAS PubMed.
- B. Abécassis; M. W. Greenberg; V. Bal; B. M. McMurtry; M. P. Campos; L. Guillemeney; B. Mahler; S. Prevost; L. Sharpnack; M. P. Hendricks; D. DeRosha; E. Bennett; N. Saenz; B. Peters and J. S. Owen, Persistent Nucleation and Size Dependent Attachment Kinetics Produce Monodisperse PbS Nanocrystals. In Revision Search PubMed.
- V. S. Gurin, K. N. Kasparov and E. A. Tyavlovskaya, Formation and XPS characterization of small lead sulfide clusters, Colloids Surf., A, 1998, 139(1), 1–5 CrossRef CAS.
- J. Workman Jr. and L. Weyer, Practical Guide to Interpretive Near-Infrared Spectroscopy. 1st edn; CRC Press, 2007 Search PubMed.
- L. Cademartiri, E. Montanari, G. Calestani, A. Migliori, A. Guagliardi and G. A. Ozin, Size-dependent extinction coefficients of PbS quantum dots, J. Am. Chem. Soc., 2006, 128(31), 10337–10346 CrossRef CAS PubMed.
- I. Moreels, K. Lambert, D. Smeets, D. De Muynck, T. Nollet, J. C. Martins, F. Vanhaecke, A. Vantomme, C. Delerue, G. Allan and Z. Hens, Size-Dependent Optical Properties of Colloidal PbS Quantum Dots, ACS Nano, 2009, 3(10), 3023–3030 CrossRef CAS PubMed.
- We note that solutes may continue depositing on nanocrystals after the aliquot is removed from solution and thus the yield of PbS and the radius may not reflect the conditions at the moment the aliquot was extracted. Despite these complications, the kinetics extracted using the in situ absorption and aliquoting methods are similar..
- A. P. Hammersley, Fit2d v12. 012 reference manual v6.0, Internal Report, 2004, ESRF98HA01T Search PubMed.
- P. Juhas, T. Davis, C. L. Farrow and S. J. L. Billinge, PDFgetX3: a rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions, J. Appl. Crystallogr., 2013, 46, 560–566 CrossRef CAS.
- X. Yang; P. Juhas; C. L. Farrow and S. J. Billinge, xPDFsuite: an end-to-end software solution for high throughput pair distribution function transformation, visualization and analysis. arXiv preprint arXiv:1402.3163, 2014.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Bozin, J. Bloch, T. Proffen and S. J. L. Billinge, PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals, J. Phys.: Condens. Matter, 2007, 19(33), 335129 CrossRef PubMed.
- E. D. Bojesen and B. B. Iversen, The chemistry of nucleation, Crystengcomm, 2016, 18(43), 8332–8353 RSC.
- K. M. O. Jensen, M. Christensen, P. Juhas, C. Tyrsted, E. D. Bojesen, N. Lock, S. J. L. Billinge and B. B. Iversen, Revealing the Mechanisms behind SnO2 Nanoparticle Formation and Growth during Hydrothermal Synthesis: An In Situ Total Scattering Study, J. Am. Chem. Soc., 2012, 134(15), 6785–6792 CrossRef CAS PubMed.
- D. Saha, K. M. O. Jensen, C. Tyrsted, E. D. Bojesen, A. H. Mamakhel, A. C. Dippel, M. Christensen and B. B. Iversen, In Situ Total X-Ray Scattering Study of WO3 Nanoparticle Formation under Hydrothermal Conditions, Angew. Chem., Int. Ed., 2014, 53(14), 3667–3670 CrossRef CAS PubMed.
- M. W. Terban, D. Banerjee, S. Ghose, B. Medasani, A. Shukla, B. A. Legg, Y. Zhou, Z. Zhu, M. L. Sushko, J. J. De Yoreo, J. Liu, P. K. Thallapally and S. J. L. Billinge, Early stage structural development of prototypical zeolitic imidazolate framework (ZIF) in solution, Nanoscale, 2018, 10(9), 4291–4300 RSC.
- K. Kodama, S. Iikubo, T. Taguchi and S. Shamoto, Finite size effects of nanoparticles on the atomic pair distribution functions, Acta Crystallogr. A, 2006, 62, 444–453 CrossRef PubMed.
- P. B. Green, P. Narayanan, Z. Q. Li, P. Sohn, C. J. Imperiale and M. W. B. Wilson, Controlling Cluster Intermediates Enables the Synthesis of Small PbS Nanocrystals with Narrow Ensemble Line Widths, Chem. Mater., 2020, 32(9), 4083–4094 CrossRef CAS.
- O. Voznyy, L. Levina, J. Z. Fan, M. Askerka, A. Jain, M. J. Choi, O. Ouellette, P. Todorovic, L. K. Sagar and E. H. Sargent, Machine Learning Accelerates Discovery of Optimal Colloidal Quantum Dot Synthesis, Acs Nano, 2019, 13(10), 11122–11128 CrossRef CAS PubMed.
- J. Ryu, S. D. Park, D. Baranov, I. Rreza, J. S. Owen and D. M. Jonas, Relations between absorption, emission, and excited state chemical potentials from nanocrystal 2D spectra, Sci. Adv., 2021, 7(22), eabf4741 CrossRef CAS PubMed.
- B. Abecassis, C. Bouet, C. Garnero, D. Constantin, N. Lequeux, S. Ithurria, B. Dubertret, B. R. Pauw and D. Pontoni, Real-Time in Situ Probing of High-Temperature Quantum Dots Solution Synthesis, Nano Lett., 2015, 15(4), 2620–2626 CrossRef CAS PubMed.
- P. T. Prins, F. Montanarella, K. Dumbgen, Y. Justo, J. C. van der Bok, S. O. M. Hinterding, J. J. Geuchies, J. Maes, K. De Nolf, S. Deelen, H. Meijer, T. Zinn, A. V. Petukhov, F. T. Rabouw, C. De Mello Donega, D. Vanmaekelbergh and Z. Hens, Extended Nucleation and Superfocusing in Colloidal Semiconductor Nanocrystal Synthesis, Nano Lett., 2021, 21(6), 2487–2496 CrossRef CAS PubMed.
- J. Turkevich, P. C. Stevenson and J. Hillier, A Study of the Nucleation and Growth Processes in the Synthesis of Colloidal Gold, Discuss. Faraday Soc., 1951, 11, 55–75 RSC.
- S. Mozaffari, W. H. Li, C. Thompson, S. Ivanov, S. Seifert, B. Lee, L. Kovarik and A. M. Karim, Colloidal nanoparticle size control: experimental and kinetic modeling investigation of the ligand metal binding role in controlling the nucleation and growth kinetics, Nanoscale, 2017, 9(36), 13772–13785 RSC.
- D. R. Handwerk, P. D. Shipman, C. B. Whitehead, S. Ozkar and R. G. Finke, Mechanism-Enabled Population Balance Modeling of Particle Formation en Route to Particle Average Size and Size Distribution Understanding and Control, J. Am. Chem. Soc., 2019, 141(40), 15827–15839 CrossRef CAS PubMed.
- X. G. Peng, J. Wickham and A. P. Alivisatos, Kinetics of II–VI and III–V colloidal semiconductor nanocrystal growth: “Focusing” of size distributions, J. Am. Chem. Soc., 1998, 120(21), 5343–5344 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc06098h |
| ‡ M. P. C., J. D. R., M. W. G., and B. M. M. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |