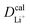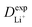Open Access Article
Open Access ArticleUnexpected role of electronic coupling between host redox centers in transport kinetics of lithium ions in olivine phosphate materials
Yu
Gao
ac,
Jun
Huang†
*b,
Yuwen
Liu
a and
Shengli
Chen
 *a
*a
aHubei Key Laboratory of Electrochemical Power Sources, College of Chemistry and Molecular Science, Wuhan University, Wuhan 430072, China. E-mail: slchen@whu.edu.cn
bCollege of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China. E-mail: jhuangelectrochm@qq.com
cSchool of Chemistry and Materials Engineering, Fuyang Normal University, Fuyang, Anhui 236041, China
First published on 1st December 2021
Abstract
The discrepancy between the trend in the diffusion coefficient of a lithium ion (DLi+) and that in the activation energy of ion hopping signals hidden factors determining ion transport kinetics in layered olivine phosphate materials (LiMPO4). Combining density functional theory (DFT) calculations and the Landau–Zener electron transfer theory, we unravel this hidden factor to be the electronic coupling between redox centers of the host materials. The ion transport process in LiMPO4 is newly described as an ion-coupled electron transfer (ET) reaction, where the electronic coupling effect on DLi+ is considered by incorporating the electronic transmission coefficient into the rate constant of the transfer reaction. The new model and DFT calculation results rationalize experimental values of DLi+ for various LiMPO4 (M = Fe, Mn, Co, Ni) materials, which cannot be understood solely by the calculated activation barrier of ion hopping. Interestingly, the electronic coupling between host redox centers is found to play an essential role. Particularly, the sluggish ion mobility in LiFePO4 is due to a very weak electronic coupling. The obtained insights imply that one can improve the rate performance of intercalation materials for metal-ion batteries through modifying the electronic coupling between redox centers of host materials.
1. Introduction
Ion transport in intercalation compounds is an elementary process underpinning rechargeable metal-ion batteries that drive the paradigm shift of storing sustainable and clean energy. LiFePO4, a layered olivine phosphate material composed of earth-abundant and non-toxic elements, exhibits numerous merits such as low cost, high structural stability, and competitive electrochemical performance, and therefore constituting one of the mainstream cathode materials in rechargeable lithium-ion batteries.1–4 Key challenges faced by LiFePO4 include low electronic conductivity (10−10–10−15 S cm−1) and ionic mobility, hindering the realization of high-power devices.5–8 A practical consequence of this is that the charging time of electrical vehicles powered by LixMPO4 is much longer compared to the fuel filling time of conventional fossil-fuelled cars.9–12Therefore, the mechanism and kinetics of ion transport in LiFePO4 has attracted research interest for decades from both computational and experimental sides in the past few years. In experimental studies, the diffusion coefficient of lithium ions, DLi+, in pure LiFePO4 is found to vary between 10−13 and 10−15 cm2 s−1,13–17 while theoretical calculations have arrived at numbers that are several orders of magnitude higher.18–25 Such discrepancy is rooted in the belief that the lithium ion transport through diffusion in the lattice frame of intercalation solids has led to the use of the activation barrier of ion hopping (Ea) to estimate DLi+ according to the following Arrhenius type of kinetic equation:18
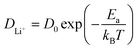 | (1) |
Indeed, there are evidences showing that transport of electrons and Li+ ions is closely coupled in LiFePO4. The electron-coupled Li+ transport26,27 (or equivalently, Li+-coupled electron transfer) mechanism explains why the carbon coating technique,28–30 aimed initially at improving the electronic conductivity, fortuitously increases the ionic diffusivity in LiFePO4. The first experimental clue of the electron-coupled Li+ transport mechanism was reported by Ellis et al.27 They found in Mossbauer measurements that the isomer shift corresponding to the average Fe2+/Fe3+ environment is closely correlated with the Li+ disorder in the lattice, and that Li+ transport is correlated with the vibrational modes of the phosphate lattice. First-principles calculations by Maxisch et al. revealed that the activation energy of Li+-coupled ET is much lower than that of the decoupled transfer process.31 In addition, nonadiabatic molecular dynamics simulations by Tao et al. have also revealed that the Li+ diffusion can be significantly enhanced upon the formation of a small polaron.26
Although widespread experimental and computational efforts underscore the ion-coupled ET nature of Li+ diffusion in LiFePO4, there lacks a quantitative description of Li+ transport kinetics in this coupled charge transfer mechanism. Herein, we propose a kinetic model for ion transport in intercalation solids by describing it as an ion-coupled ET reaction. The electronic effect is incorporated into the model formula by using the Landau–Zener ET theory, which allows the ion transport kinetics to be directly correlated with the electronic coupling between the host redox centers. In the meantime, first-principles calculations based on the density functional theory (DFT) are performed to determine the key parameters in the model formula. The comparison between the model results and experimental data clearly demonstrates the determining role of electronic coupling in the ion dynamics of LiMPO4, and thus providing guidance for rational design of ion-intercalation electrode materials.
2. Results and discussion
2.1 Microkinetic model
LiMPO4 has an olivine structure with O forming a distorted hexagonal close-packed (hcp) framework which accommodates Li and M at the octahedral interstices and P at the tetrahedral interstices respectively (Fig. 1 for LiFePO4). During charging (discharging) processes, Li ions are removed (added) topotactically, maintaining the topology of the MPO4 framework. There are three possible hopping paths for Li ions, corresponding to the motion along the b direction in the hexagonal a–b planes of the oxygen hcp host, that between the b channels in the neighboring hexagonal planes along the c axis, and that between the neighboring b channels in the a–b plane.18 DFT-based nudged elastic band calculations have shown that Li hopping along the b direction has the lowest energetic barrier,18 which was later confirmed in experiments.32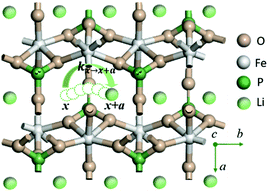 | ||
| Fig. 1 Illustration of Li+ transport via a curved trajectory between adjacent sites along the b direction of LiMPO4. | ||
Considering that lithium ion transport in LiMPO4 is mainly along the b-direction,3–8,18 we can model it as a one-dimensional (1-D) ion hopping process. We adopt the recent idea that the ion hopping in concentrated media corresponds to an ion-vacancy coupled transfer reaction, that is, Ix − Vx ↔ Ix±a − Vx±a.33,34 This underlying idea is that the appearance of an ion at position x is accompanied by the loss of a vacancy there. The rate of this ion-vacancy coupled transfer reaction can be formulated according to the law of mass action, that is33,34
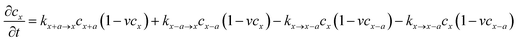 | (2) |
In the spirit of transition state theory and the Brønsted–Evans–Polanyi (BEP) relationship, the rate constants kx→y can be expressed as,
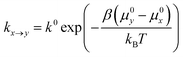 | (3) |
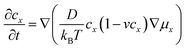 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT),32 where τ0 refers to the average time interval of the ion hopping events. The factor 2 in the denominator of the right-hand side is the consequence of activation entropy when considering that the transition state occupies two vacancies.33,34 It can also be understood that a transition state has the equal probability of 1/2 to go forward and backward. Thus, D can be formulated as,
exp(−Ea/kBT),32 where τ0 refers to the average time interval of the ion hopping events. The factor 2 in the denominator of the right-hand side is the consequence of activation entropy when considering that the transition state occupies two vacancies.33,34 It can also be understood that a transition state has the equal probability of 1/2 to go forward and backward. Thus, D can be formulated as,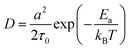 | (5) |
In the case when the activation barrier is negligibly small, e.g., the free diffusion, one has D = a2/2τ0, which is exactly the result of Einstein's diffusion theory for Brownian motion.
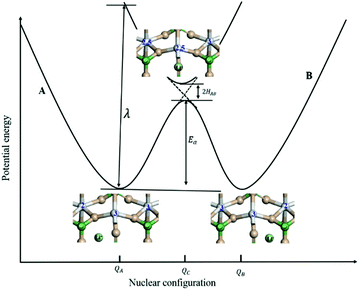
For the electron-coupled ion hopping process, the value of τ0 should be co-determined by electronic and nuclear factors. As a first approximation, we use τ0 = (vnκel)−1, where vn is the effective frequency of nuclear motion and κel the electronic transmission coefficient. Considering that the ion hopping event is mainly a result of the vibration of the M–O bond, we assign the typical frequency (1013 s−1) of the normal vibration of the M–O bond to vn.35 To estimate κel, we use the Landau–Zener formula,36–38 that is, 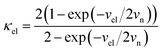 , where
, where 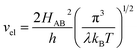 is the electron hopping frequency at the transition state, λ is the configurational reorganization energy of electron transfer (Fig. 2), and HAB is the electronic coupling matrix element which represents the electronic coupling strength between the redox centers,39 which are the neighboring transition metal centers in LiMPO4 (Fig. 2). Thus, we have the following formula for the ion diffusion coefficient:
is the electron hopping frequency at the transition state, λ is the configurational reorganization energy of electron transfer (Fig. 2), and HAB is the electronic coupling matrix element which represents the electronic coupling strength between the redox centers,39 which are the neighboring transition metal centers in LiMPO4 (Fig. 2). Thus, we have the following formula for the ion diffusion coefficient:
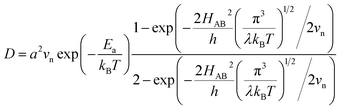 | (6) |
Depending on the magnitude of HAB, an ET process can be adiabatic or nonadiabatic. The adiabatic ET system has a large HAB, which means vel ≫ vn, and therefore κel ≈ 1. In this case, τ0 is mainly determined by the nuclei factor and the ion diffusion coefficient reads D = (1/2)a2vn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT), which corresponds to a thermally activated diffusion process with an Arrhenius type of kinetics as described in eqn (1) and is negligibly effected by the electronic effect. For a nonadiabatic ET with small H2AB and κel, the ion diffusion coefficient reads D = (1/2)a2vel
exp(−Ea/kBT), which corresponds to a thermally activated diffusion process with an Arrhenius type of kinetics as described in eqn (1) and is negligibly effected by the electronic effect. For a nonadiabatic ET with small H2AB and κel, the ion diffusion coefficient reads D = (1/2)a2vel![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Ea/kBT), and can be reformulated as,
exp(−Ea/kBT), and can be reformulated as,
 | (7) |
Due to the fact that the adjacent redox centers in LiMPO4 are separated by relatively large distance, the electronic interactions should be weak, making the ET process mostly nonadiabatic. Therefore, the key parameters determining the Li+ diffusion coefficient include HAB, λ, and Ea.
2.2 DFT-based parameterization
We employed the DFT calculations to determine these model parameters for Li+ transport in LiMPO4 (M = Fe, Mn, Co, Ni). Specifically, minimum energy pathways (MEPs) and saddle points of Li+ hopping were obtained with the climbing-image nudged elastic band (CINEB) method40 in the PWscf (Plane-Wave Self-Consistent Field) module in Quantum ESPRESSO with the ultrasoft pseudopotentials for nuclei and core electrons (see details in the Methods section).41 Usually, 5–7 images are interpolated in CINEB computations to determine the transition states and activation barriers of ion migration in solid crystals. Considering the relatively simple 1-D hopping of Li ions and small change of the solid structure in the hopping process of Li ions in LiMPO4, five images are adequate to identify the transition states.18,20 Therefore, we interpolated five images between the starting and end points in the ion transport process to simulate the intermediate states, with the positions of the starting point and the end point fixed. This can significantly reduce the computation cost without losing the accuracy. The transition states obtained agree with those reported in the literature.18,20The values of HAB were determined by using a large-scale parallel multiconfigurational self-consistent field (MCSCF) implemented in the NWChem computational chemistry code,42 and the bases are set as 6-31g** for P, O and Li, and LANL2DZ ECP for Fe, respectively. In HAB calculations, the reactant and the product had the same configurations as those of the transition state obtained in the CINEB method, but the charges were assigned differently to distinguish the reactant, transition state and product of an ET process (Fig. 2).
A 1a × 2b × 1c (S.G. Pnma) supercell was used in all calculations. The cell contains 8 Li+ sites in total, with 7 sites filled with Li+, thus having a composition of Li0.875MPO4, which is in consistence with the model in previous studies so that the calculated activation barriers are comparable with the reported values.
The configuration reorganization energies (λ) were calculated using the procedure shown in Fig. 3. First, structural optimization was performed to obtain the stable configurations of LiMPO4 (Fig. 3(a)) and MPO4 (Fig. 3(d)), which have energies of E1 and E2 respectively. Then, the LiMPO4 structure was obtained by filling Li atoms in the stable configuration of MPO4 without altering the host structure (Fig. 3(c)), giving a total energy of E3; and the structure of MPO4 was obtained by simply removing all Li atoms from the stable configuration of MPO4 while leaving other constituents unaltered (Fig. 3(b)), which gives an energy of E4. Thus, λ1 = (E3 − E1) is assigned to the reorganization energy of a LiMPO4 site in an ET process, and λ2 = (E4 − E2) to that of a MPO4 site. The total configuration reorganization energy for the ET process between a pair of LiMPO4 and MPO4 sites is the sum of λ1 and λ2, namely, λ = λ1 + λ2.
 | ||
| Fig. 3 Schematic diagram for computation of the configuration reorganization energies of the reaction in LiMPO4. | ||
Fig. 4 shows the energy profiles of MEPs of Li+ hopping between two adjacent sites along the b axis in Li0.875MPO4 (M = Fe, Mn, Ni, and Co) calculated using the CINEB method, with the inset numbers indicating the corresponding Ea values. These values (0.40 eV for LiFePO4, 0.51 eV for LiMnPO4, 0.64 eV for LiCoPO4, and 0.36 eV for LiNiPO4) are close to that obtained from the DFT+U calculations by Dathar et al. (0.47 eV for LiFePO4),20 but differ from those obtained from the Born model of solids (0.55 eV for LiFePO4, 0.62 eV for LiMnPO4, 0.49 eV for LiCoPO4, and 0.44 eV for LiNiPO4)23 and those obtained from the DFT calculations without Hubbard correction for strongly correlated d electrons (0.27 eV for LiFePO4, 0.25 eV for LiMnPO4, 0.36 eV for LiCoPO4, and 0.13 eV for LiNiPO4).18
 | ||
| Fig. 4 DFT-calculated energy profiles of Li+ hopping along the MEP between adjacent Li sites in Li0.875MPO4. | ||
2.3 Electronic coupling
Given the DFT-calculated parameters of a2, HAB, λ, and Ea, we estimated the diffusion coefficients of Li+ using eqn (6). The DFT-calculated parameters and the corresponding theoretical diffusion coefficients are listed in Table 1, where the experimental diffusion coefficients
are listed in Table 1, where the experimental diffusion coefficients 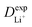 taken from the literature are also given for comparison. It is revealing to note that LiFePO4 and LiNiPO4 show a difference of three orders in experimentally-measured diffusion coefficients, although they have very close Ea values. Besides, compared with LiMnPO4, LiCoPO4 has a higher experimental diffusion coefficient in spite of a larger Ea. Such anomalies indicate that the activation energy inadequately predicts the ion transport kinetics in olivine phosphate materials as described in eqn (1).
taken from the literature are also given for comparison. It is revealing to note that LiFePO4 and LiNiPO4 show a difference of three orders in experimentally-measured diffusion coefficients, although they have very close Ea values. Besides, compared with LiMnPO4, LiCoPO4 has a higher experimental diffusion coefficient in spite of a larger Ea. Such anomalies indicate that the activation energy inadequately predicts the ion transport kinetics in olivine phosphate materials as described in eqn (1).
| M | a (Å) | E a (eV) | λ/4 (eV) | H AB (eV) | v el (s−1) | (cm2 s−1) | (cm2 s−1) |
|---|---|---|---|---|---|---|---|
| Fe | 3.634 | 0.398 | 0.390 | 1.39 × 10−3 | 2.59 × 1010 | 4.43 × 10−13 | 10−15–10−13 (ref. 21–25) |
| Mn | 3.684 | 0.506 | 0.815 | 0.24 × 10−3 | 5.35 × 108 | 2.08 × 10−15 | 10−15–10−14 (ref. 8 and 43–45) |
| Co | 3.572 | 0.639 | 0.179 | 4.91 × 10−3 | 4.78 × 1011 | 6.06 × 10−15 | 10−15–10−12 (ref. 46 and 47) |
| Ni | 3.439 | 0.356 | 0.197 | 3.25 × 10−2 | 1.99 × 1013 | 1.24 × 10−9 | 10−11–10−9 (ref. 48 and 49) |
The inconsistency between diffusion coefficients and hopping activation barriers can be understood when the electronic coupling factors are considered. One can see that the HAB is much higher for LiNiPO4 compared with LiFePO4, and higher for LiCoPO4 compared with LiMnPO4. The 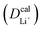 values estimated by considering the electronic factor through the Landau–Zener ET theory reasonably agree with the experimental data. This further confirms the electron-coupled ion transfer mechanism of Li+ transport in these materials and the essential role of the electronic coupling between transition metal centers.
values estimated by considering the electronic factor through the Landau–Zener ET theory reasonably agree with the experimental data. This further confirms the electron-coupled ion transfer mechanism of Li+ transport in these materials and the essential role of the electronic coupling between transition metal centers.
It is also worthwhile mentioning that the potential energy profiles shown in Fig. 4 are in general not parabolic, as assumed in the standard ET theory by Marcus.50 We note that the parabolic potential energy curves are expected only for outer-sphere ET processes involving no molecular structural change other than harmonic relaxation. Nevertheless, the ET process here is accompanied by the nuclear motion of Li atoms, which changes the electronic environment during the course as well. Consequently, the deviation of the real energy profiles from the parabolic curves is unsurprising. As a direct consequence, Ea and λ does not satisfy the relationship of Ea = λ/4 as predicted by the classical Marcus theory (Table 1). More specifically, the deviation is much more pronounced for LiNiPO4 and LiCoPO4 than that for other compounds considered here, suggesting a unusual charge transfer behavior for LiNiPO4 and LiCoPO4.
It is now clear that, owing to the ion-coupled ET nature, neither the thermal diffusion nor the classical ET theory is insufficient for a quantitative description of ion transport kinetics in olivine phosphate materials of LiMPO4. A comprehensive model for the ion-coupled ET process in condensed matters should include the detailed electronic ion–host interactions and their effects on the structural relaxation of the host metal–ligand systems, which are beyond the scope of this work. What we show here is that modelling the ion transport in terms of the hoping reaction kinetics provides a route to access this coupled transfer mechanism. Despite the great approximation, the electron coupling effect can be included in the ion transport kinetics by simply incorporating the electronic transmission coefficient given by Landau–Zener theory into the pre-exponential frequency factor of the rate constant of the hopping reaction. This allows the apparent diffusion coefficient of Li+ in LiMPO4 to be reasonably estimated using the parameters obtained from first-principles computations.
3. Conclusions
We have developed a new theoretical model for Li+ transport in olivine phosphate materials of LiMPO4, which is described as an ion-coupled electron transfer process. In particular, the effect of electronic coupling between host redox centers on the ion transport kinetics is emphasized and can be described using the Landau–Zener theory. In this model, the diffusion coefficient is co-determined by the electronic coupling matrix element between the neighboring transition metal centers, the configuration reorganization energy of electron transfer, and the activation energy of ion hopping. The values of these parameters can be obtained from DFT calculations. The model can rationalize the anomalous trend of diffusion coefficients of Li+ in LiMPO4 (M = Fe, Mn, Co, Ni), which cannot be understood solely by the activation barrier of ion hopping. It is revealed that the electron coupling plays a vital role. The electron-transfer perspective of ion transport in LiMPO4 opens new pathways to design high-performance ion intercalation materials for metal-ion batteries.4. Computations details
Spin-polarized DFT calculations were performed using Quantum Espresso with the ultrasoft pseudopotentials for nuclei and core electrons.41 Generalized gradient approximation (GGA) in the parameterization of the Perdew–Burke–Ernzerhof (PBE) functional was used to describe the exchange–correlation and Hubbard-type correction U was taken into account due to the strongly correlated nature of the Fe 3d electrons.51 As recommended in a previous study, the effective U values for LiMPO4 are set to 4.3 eV, 4.5 eV, 5.7 eV, and 5.1 eV for M = Fe, Mn, Co, and Ni, respectively.52 A kinetic energy cutoff of 30 Ry and a charge-density cutoff of 300 Ry were used in all calculations. Geometry optimization was performed by using BFGS minimization until all the forces acting on each atom were below 10−3 Ry per Bohr and the total energy was converged to within 10−6 Ry. The Brillouin-zones were sampled with a 12 × 5 × 6 k-point mesh for a 1a × 2b × 1c (S.G. Pnma) supercell containing 8 Li sites.Data availability
The data that support the findings of this study are available on request from the corresponding author.Author contributions
SC conceived the project. YG, JH and SC derived the model equations. YG performed the DFT calculations. YL discussed the derivation and results. YG, JH, and SC wrote the paper. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (21673163, 21802170).Notes and references
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4301 CrossRef CAS PubMed.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- J. B. Goodenough, Acc. Chem. Res., 2013, 46, 1053–1061 CrossRef CAS PubMed.
- B. C. Melot and J.-M. Tarascon, Acc. Chem. Res., 2013, 46, 1226–1238 CrossRef CAS PubMed.
- A. Padhi, K. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194 CrossRef CAS.
- A. Yamada, S. C. Chung and K. Hinokuma, J. Electrochem. Soc., 2001, 148, A224–A229 CrossRef CAS.
- S. Y. Chung, J. T. Blocking and Y. M. Chiang, Nat. Mater., 2002, 1, 123–128 CrossRef CAS PubMed.
- C. Delacourt, L. Laffont, R. Bouchet, C. Wurm, J. B. Leriche, J. M. Morcrette and C. Masquelier, J. Electrochem. Soc., 2005, 152, A913–A921 CrossRef CAS.
- R. Chandrasekaran, J. Power Sources, 2014, 271, 622–632 CrossRef CAS.
- B. Kang and G. Ceder, Nature, 2009, 458, 190–193 CrossRef CAS PubMed.
- H. B. Shu, M. F. Chen and F. e. a. Wen, Electrochim. Acta, 2015, 152, 368–377 CrossRef CAS.
- K. Kirshenbaum, D. C. Bock and C. e. a. Lee, Science, 2015, 347, 149–154 CrossRef CAS PubMed.
- S. Franger, F. Le Cras, C. Bourbon and H. Rouault, Electrochem. Solid-State Lett., 2002, 5, A231–A233 CrossRef CAS.
- P. P. Prosini, M. Lisi, D. Zane and M. Pasquali, Solid State Ionics, 2002, 148, 45–51 CrossRef CAS.
- R. Amin, P. Balaya and J. Maier, Electrochem. Solid-State Lett., 2007, 10, A13–A16 CrossRef CAS.
- R. Amin, J. Maier, P. Balaya, D. P. Chen and C. T. Lin, Solid State Ionics, 2008, 179, 1683–1687 CrossRef CAS.
- H. Liu, C. Li, H. P. Zhang, L. J. Fu, Y. P. Wu and H. Q. Wu, J. Power Sources, 2006, 159, 717–720 CrossRef CAS.
- D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, A30–A32 CrossRef CAS.
- C. Kuss, G. Liang and S. B. Schougaard, J. Mater. Chem., 2012, 22, 24889–24893 RSC.
- G. K. P. Dathar, D. Sheppard, K. J. Stevenson and G. Henkelman, Chem. Mater., 2011, 23, 4032–4037 CrossRef CAS.
- R. Kutteh and M. Avdeev, J. Phys. Chem. C, 2014, 118, 11203–11214 CrossRef CAS.
- M. S. Islam, D. J. Driscoll, C. A. J. Fisher and P. R. Slater, Chem. Mater., 2005, 17, 5085–5092 CrossRef CAS.
- C. A. J. Fisher, V. M. H. Prieto and M. S. Islam, Chem. Mater., 2008, 20, 5907–5915 CrossRef CAS.
- K. Hoang and M. Johannes, Chem. Mater., 2011, 23, 3003–3013 CrossRef CAS.
- S. E. Boulfelfel, G. Seifert and S. Leoni, J. Mater. Chem., 2011, 21, 16365–16372 RSC.
- G. H. Tao, J. Phys. Chem. C, 2016, 120, 6938–6952 CrossRef CAS.
- B. Ellis, L. K. Perry and D. H. e. a. Ryan, J. Am. Chem. Soc., 2006, 128, 11416–11422 CrossRef CAS PubMed.
- H. Huang, S. C. Yin and L. F. Nazar, Electrochem. Solid-State Lett., 2001, 10, A170–A172 CrossRef.
- P. S. Herle, B. Ellis, N. Coombs and L. F. Nazar, Nat. Mater., 2004, 3, 147–152 CrossRef CAS PubMed.
- N. D. Trinh, G. Liang and M. e. a. Gauthier, J. Power Sources, 2012, 200, 92–97 CrossRef CAS.
- T. Maxisch, F. Zhou and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 104301 CrossRef.
- S. Nishimura, G. Kobayashi, K. Ohoyama, R. Kanno, M. Yashima and A. Yamada, Nat. Mater., 2008, 7, 707–711 CrossRef CAS PubMed.
- Y. Gao, J. Huang, Y. W. Liu, J. W. Yan, B. W. Mao and S. L. Chen, Sci. China: Chem., 2019, 62, 515–520 CrossRef CAS.
- Z. Zhang, Y. Gao, S. Chen and J. Huang, J. Electrochem. Soc., 2019, 167, 013519 CrossRef.
- N. Sutin, Acc. Chem. Res., 1982, 15, 275–282 CrossRef CAS.
- B. S. Brunschwig, J. Logan, M. D. Newton and N. Sutin, J. Am. Chem. Soc., 1980, 102, 5798–5809 CrossRef CAS.
- M. D. Newton and N. Sutin, Annu. Rev. Phys. Chem., 1984, 35, 437–480 CrossRef CAS.
- J. Frank and E. G. Dymond, Trans. Faraday Soc., 1926, 21, 536 RSC.
- E. U. Condon, Phys. Rev., 1928, 32, 858 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Mills and H. Jónsson, Phys. Rev. Lett., 1994, 72, 1124 CrossRef CAS PubMed.
- A. Farazdel, M. Dupuis, E. Clementi and A. Aviram, J. Am. Chem. Soc., 1990, 112, 4206–4214 CrossRef CAS.
- F. Wen, H. L. Shu and Y. Y. Zhang, Electrochim. Acta, 2016, 214, 85–93 CrossRef CAS.
- L. F. Zhang, Q. Qu, L. Zhang and H. H. Zheng, J. Mater. Chem. A, 2014, 2, 711–719 RSC.
- N. H. Kwon, T. Drezen, I. Exnar, I. Teerlinck, M. Isono and M. Graetzel, Electrochem. Solid-State Lett., 2006, 9, A277–A280 CrossRef CAS.
- J. Xie, N. Imanishi, T. Zhang, A. Hirano, Y. Takeda and O. Yamamoto, J. Power Sources, 2009, 192, 689–692 CrossRef CAS.
- S. Brutti, J. Manzi, D. Meggiolaro, F. M. Vitucci, A. Paolone and O. Palumbo, J. Mater. Chem. A, 2017, 5, 14020–14030 RSC.
- S. Jun, N. Hiroshi and H. Masashi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054111 CrossRef.
- Y. Zhang, Y. Pan, J. Liu, G. Wang and D. X. Cao, Chem. Res. Chin. Univ., 2015, 31, 117–122 CrossRef.
- R. A. Marcus and N. Sutin, Biochim. Biophys. Acta, 1985, 265–322 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L Shang, Y. Wang, X. D. Mei and Z. K. Liu, J. Mater. Chem., 2012, 22, 1142–1149 RSC.
Footnote |
| † Present address: Institute of Theoretical Chemistry, Ulm University, 89069 Ulm, Germany. |
| This journal is © The Royal Society of Chemistry 2022 |