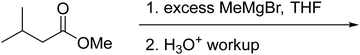Characterization of student problem solving and development of a general workflow for predicting organic reactivity

Abstract

A central practice in the discipline of organic chemistry is the ability to solve certain fundamental problems, including predicting reactivity, proposing mechanisms, and designing syntheses. These problems are encountered frequently by both students and practitioners, who need to utilize vast amounts of content knowledge in specific ways to generate reasonable solutions. To gain insight into how one of these major problem types can be solved, we have investigated student approaches to complex predict-the-product problems through the detailed analysis of think-aloud interviews. This work led to the creation of a general workflow model that describes the reasoning pathways of students with varying levels of expertise when attempting to predict organic reactivity. The problems used in this study were designed to be non-trivial and potentially ambiguous to elicit “true” problem solving and discourage a purely memorization-based approach, even from more experienced organic chemists. Rich descriptions of undergraduate and graduate student interviews are provided, and student thought processes are characterized in terms of common problem-solving actions. These actions were developed into the workflow model using an iterative method that combined results from our analysis with the experiences of instructors and feedback from both undergraduate focus groups and graduate students. The workflow serves as both a potential instructional tool and a model for student thinking. This model is general enough to be applied to both successful and unsuccessful solution pathways by both novice undergraduates and more expert-like graduate students. Characteristics of more successful and more experienced problem solvers are investigated, and concrete strategies that can be recommended to students are discussed. The results of this study complement existing work on other fundamental problem types in organic chemistry and suggest a variety of teaching interventions to develop students into more successful organic problem solvers.

---

Introduction

As instructors of organic chemistry, we aspire to help each of our students develop a foundational understanding of the subject. Learning organic chemistry is more than just memorizing a long list of facts, much to the surprise of many undergraduates (Graulich, 2015; Cooper and Stowe, 2018). On a deeper level, the facts of organic chemistry are organized around a highly interconnected set of concepts that students need to internalize. In general, there has been a growing emphasis on organizing chemistry instruction around interconnected fundamental concepts that span across the discipline (Raker et al., 2013; Cooper et al., 2019; McGill et al., 2019). To develop an integrated understanding of chemistry, students need to develop their practice of chemical thinking to connect concepts and carry out complex decision making and problem solving in the context of chemical systems (Talanquer and Pollard, 2010; Sevian and Talanquer, 2014). Indeed, it can be argued that the primary purpose of internalizing chemical concepts is to be able to use the concepts in the context of solving authentic chemical problems (Bodner and Herron, 2002). Authentic problem solving requires different skills and types of abstract thinking depending on the type of problem and subdiscipline of chemistry (Sevian and Talanquer, 2014; Weinrich and Sevian, 2017).

In organic chemistry, authentic questions that practicing chemists must routinely answer form the basis for assessment of student knowledge, relying heavily on just a few common types of problems:

– Synthesis: How do I make that?

– Predict-the-product: What will happen when I mix these?

– Spectroscopy: What did happen when I mixed those?

– Mechanism: How did it happen?

– Rationalize observation: Why did it happen?

Of these problem types, three are given special priority on organic exams, particularly in the second half of the series: predict-the-product, mechanism, and synthesis. An analysis of two years of second-semester organic chemistry exams at this institution showed that these three question types (and their combination into “roadmap” problems) accounted for 74% of the possible points, with an additional 16% accounted for by “rationalize this observation” questions. Similar results have been found elsewhere; for example, the three priority problems listed above accounted for 75% of second semester exam questions at a large public institution in the Southwestern United States from 2010–2014 (Austin et al., 2015). Note that this does not include the laboratory portion of the course, which has its own set of fundamental questions. Because there are so few of these central problems, an important learning outcome for organic chemistry students is to develop general strategies for approaching each one (Cartrette and Bodner, 2010; Flynn, 2014; Flynn and Featherstone, 2017; Weinrich and Sevian, 2017; Webber and Flynn, 2018). Focusing on how the same problems manifest with different types of reactivity throughout the year provides a common thread through the curriculum that is not always made explicit by instructors.

An important goal for organic chemistry instructors is to help students learn problem-solving skills while explicitly conveying how the concepts being taught are connected through these authentic problems (Sevian and Talanquer, 2014; Graulich, 2015). This task is made easier by having a detailed understanding of the various ways in which students approach these problems. Our work serves to develop more specific descriptions of student thought processes while solving predict-the-product problems to help identify where difficulties might arise. Such an analysis suggests types of scaffolding that would be most appropriate for students who are first learning to answer this major question type in organic chemistry. We describe in-depth studies of how more successful students are approaching problems, which reveal strategies that can be conveyed to other students as well. Additionally, investigations of graduate student reasoning provide an expert-like “target” that novices can be encouraged to move towards.

Problem solving in organic chemistry

Problem solving is central to the field of organic chemistry, and as a result, a substantial amount of the research on organic chemistry education has focused on this topic (Graulich, 2015). Unlike the problems most commonly encountered in general chemistry, organic chemistry problems are non-mathematical, which requires a different set of fundamental skills (Cartrette and Bodner, 2010). In particular, the focus on mechanistic reasoning requires a shift from product-oriented thinking to a more process-oriented mindset (Graulich, 2015).

Researchers have taken two main approaches to investigating how students reason about the central questions in organic chemistry. One method is to take advantage of the large pool of data produced when students turn in exams and problem sets as part of their coursework. Some researchers have used this data to identify strategies that more successful students are more likely to use, such as atom mapping and clearly identifying bonds to be formed during synthesis questions (Bode and Flynn, 2016; Flynn and Featherstone, 2017). However, only a small fraction of student thinking is captured by these written artifacts. An approach that provides a more detailed description of student thought processes is to use think-aloud interviews (Bowen, 1994), in which students are instructed to vocalize their thoughts as they have them while attempting to solve problems. Think-aloud interviews are well-established research methods for studying problem solving in a variety of disciplines (Ericsson and Simon, 1980, 1993; Fonteyn et al., 1993; Charters, 2003), and they are well-suited for the type of detailed analysis we wished to perform.

Several types of organic chemistry questions have been investigated with think-aloud protocols, including synthesis (Flynn, 2014), spectroscopy (Cartrette and Bodner, 2010), and acid–base (Petterson et al., 2020), but the most extensively researched are problems in which the student is instructed to provide a reasonable mechanism for a given organic transformation (Bhattacharyya and Bodner, 2005; Ferguson and Bodner, 2008; Kraft et al., 2010; Bhattacharyya, 2014; Weinrich and Sevian, 2017; Caspari et al., 2018). Complete answers to these questions involve using the electron-pushing formalism, or “arrow-pushing,” to show the flow of electrons throughout the reaction. Students at both the undergraduate and graduate levels commonly take a difference reduction approach to solving mechanism problems in which the final product is given, meaning that a primary goal for these solvers is to successively reduce the difference between starting and ending points. In a study involving graduate students, solvers focused almost exclusively on steps that “get me [closer] to the product” (Bhattacharyya and Bodner, 2005). Students at various levels tend to start problems of this type by mapping atoms between the starting material and the product, even when this was not an explicit strategy introduced during their coursework (Ferguson and Bodner, 2008; Bhattacharyya, 2014).

This focus on “getting to the product” appears to be very robust, leading to some surprising results. DeCocq and Bhattacharyya conducted interviews in which students were asked to propose the product of a single mechanistic step, and later in the interview they were given an identical step but in the context of an overall transformation (DeCocq and Bhattacharyya, 2019). Even after correctly predicting the product of that step earlier, most students changed their answers to something less correct when shown the full transformation for certain problems. The common characteristic of these problems was that the incorrect step led to an intermediate that more closely resembled the ultimate product. An important conclusion from these investigations is that students’ reasoning depends dramatically on what initial information they are given, suggesting that traditional mechanism questions may not fully capture student abilities to engage in more open-ended mechanistic reasoning.

Student approaches to predict-the-product (PtP) problems provide an opportunity to more fully investigate open-ended mechanistic reasoning. Although students are not specifically asked to provide a mechanism along with their solutions, mechanistic reasoning can be a central tool for generating and justifying predictions. Because students often do not draw mechanisms for PtP questions, or will draw one only after making a prediction, some researchers have argued that the electron-pushing formalism is an exercise in symbol manipulation for the students in their research study and that these arrows hold no physical meaning for the students (Bhattacharyya and Bodner, 2005; Grove et al., 2012). In some studies, student use of the electron-pushing formalism when solving PtP problems was sparse, and for the simplest problems, it did not appear to be significantly helpful unless the problem involved an intramolecular step (Grove et al., 2012; Grove et al., 2012). Of the existing publications investigating student reasoning on open-ended PtP questions, many focus on either straightforward transformations with mostly monofunctional starting materials (Grove et al., 2012; Grove et al., 2012) or a limited subset of reaction types (Cruz-Ramírez de Arellano and Towns, 2014; Finkenstaedt-Quinn et al., 2020), although this is not exclusively the case (Webber and Flynn, 2018). Overall, less is known about student thinking when approaching PtP problems that involve more complex molecules and potentially longer reactive pathways. It seems probable that students may engage in more explicit mechanistic reasoning when approaching scenarios that cannot be matched exactly to the canonical reactions they have learned. The work reported here examines student thinking on complex or potentially ambiguous PtP questions that cover a range of different reaction types.

While the major problem types in organic chemistry have been studied through a variety of theoretical lenses, few studies attempt to model the overall flow of student reasoning. One exception is Bhattacharyya's meta-analysis that proposes a model for how students work through mechanism problems (Bhattacharyya, 2014). One potential way to solve a mechanism problem would be to begin with the starting material and reason mechanistically in the forward direction until reaching the desired product. However, this is not how mechanism problems are solved according to this model. Instead, students map the reactant onto the product and look for key differences to identify what type of reaction is occurring. Bhattacharyya proposes a dual path model depending on whether the reaction is a single-step canonical reaction or a multi-step functional group transformation. On both of these paths, electron-pushing arrows are not filled in until after the intermediates or other key reaction elements are already drawn.

As mentioned above, evidence already exists that mechanistic reasoning looks different depending on whether the ultimate product is known (DeCocq and Bhattacharyya, 2019), so a model of how students work through open-ended predict-the-product problems may be quite different than a model for mechanism questions. Developing such a model is the primary focus of this work. In particular, we focus on relatively complex problems that are difficult to answer through a purely memorization-based approach.

Theoretical frameworks

Researchers have been developing general models of human problem solving for decades. One of the earliest was Polya's four-stage model, which involves defining or understanding the problem, making a plan, implementing the plan, and reflecting on the implementation (Polya, 1945). Many other more specific models followed, but most of them included the presence of these same basic stages. An early example in chemistry is the explicit method of problem solving (EMPS) model proposed by Bunce et al., which focuses on mathematical problems in general chemistry (Bunce et al., 1991). The basic steps are identifying what information is given and what is asked for (i.e., defining the problem), recalling relevant rules and equations, making a schematic plan, implementing the plan mathematically, and reviewing the overall solving process.

One example of a qualitatively different model for how people engage in problem solving is the anarchistic model proposed by Bodner, based on earlier work by G.H. Wheatley (Wheatley, 1984; Bodner, 2003). This model includes additional steps that are not explicitly taken in more linear models of problem solving, such as “draw a picture,” “try something,” “try something else,” “read the problem again,” and “when appropriate, strike your forehead”. The purpose of this tongue-in-cheek model is not to suggest that problem solvers should follow the steps as written. Rather, it reflects the fact that false starts and trial-and-error experimentation are common characteristics of the problem-solving process. Under some circumstances, a model with very distinct stages might seem most appropriate, but most of us also recognize in the anarchistic model an accurate description of some of our own problem solving.

The type of model that most accurately describes a given instance of problem solving is closely related to the concept of routine exercises and novel problems (Bodner, 2003). Any given chemistry question can potentially be either an exercise or a problem, depending on who is solving it. The difference between an exercise and a problem lies not in how difficult the question is, but rather in how familiar the solver is with the material and question type. For example, a practicing analytical chemist would be able to solve a titration question by recalling algorithms for getting to a solution, whereas a freshman taking general chemistry for the first time would likely take a longer, more circuitous approach to solving the same problem. The question is an exercise for the experienced chemist but a problem for the student. Using this framework, it has been proposed that linear models with distinct stages are accurate descriptions of how chemists solve exercises, including worked examples in textbooks and lectures. However, for a true problem, a more anarchistic model would be more appropriate (Bodner, 2003). In this work, it is assumed that some students will recognize “what is happening” in a given predict-the-product question and treat it as an exercise. In other cases, students will try a variety of approaches on their way towards determining a solution to a genuine problem. Our analysis attempts to characterize both types of problem-solving, which can each be useful in different situations.

Research questions

The goal of this work is to characterize the problem-solving approaches students use when presented with relatively complex predict-the-product questions. This type of problem was chosen due to its centrality in organic chemistry courses and the opportunity it gives students to engage in open-ended mechanistic reasoning. Characterizing the different actions that students take when problem solving is useful for both instructors and students. As instructors, knowing the specific components of problem solving used by students would allow us to identify student resources as well as areas of difficulty and tailor interventions that build on these resources. From the student's point of view, understanding the components of problem solving would aid in the metacognitive regulation of the student's own thought processes, which is a key attribute of effective problem solving (Schoenfeld, 1987).

To achieve this goal, we interviewed undergraduate students who had completed their first year of organic chemistry using a think-aloud protocol in which they were asked to solve non-trivial predict-the-product problems. Major problem-solving actions were identified, and a model was developed to capture student reasoning processes. This model was then developed into a workflow for how to predict organic reactivity.

Ultimately, we would like our students to move over time to a more successful, expert-like thought process when problem solving. Note that this does not mean that our goal is for our students to be able to approach all problems as exercises. Instead, we would like our students to gain skills that help them work through increasingly complex, real problems. Student problem-solving actions were quantified and compared to identify differences between the approaches of students who were able to reach a reasonable solution and those who were not. Additionally, “key features” were identified that appeared more often in successful solution pathways. Graduate students specializing in organic chemistry were then interviewed to gain insight into more expert-like approaches.

With this data, we seek to answer the following research questions:

1. What are the common characteristics of problem solving in the context of non-trivial predict-the-product problems, and does the workflow model accurately reflect student problem solving?

2. What differentiates successful from unsuccessful problem solvers?

3. What differences are there between the approaches of sophomore undergraduates and more experienced organic chemistry graduate students?

Methods

Problem design

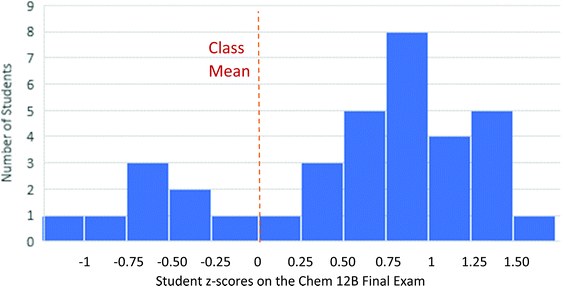
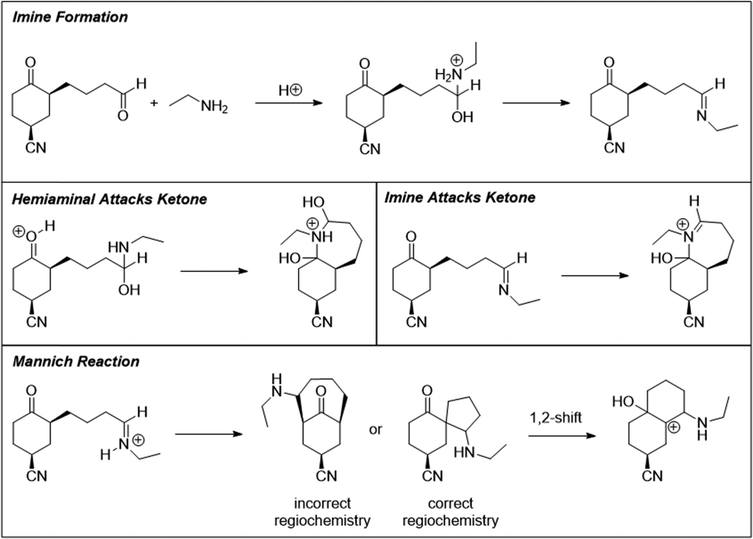
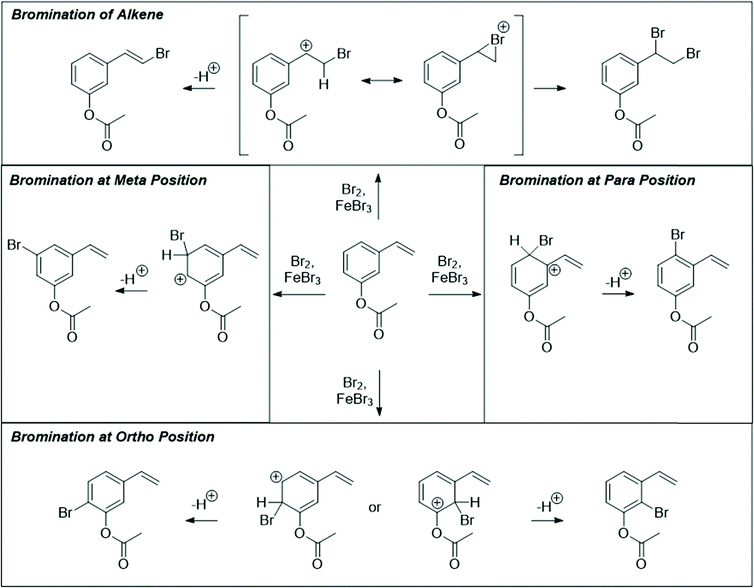
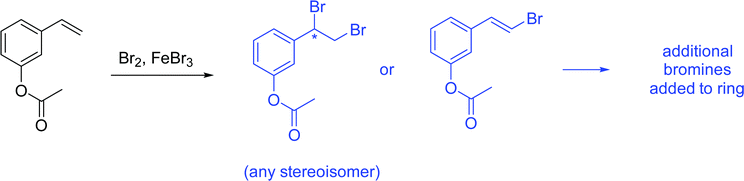
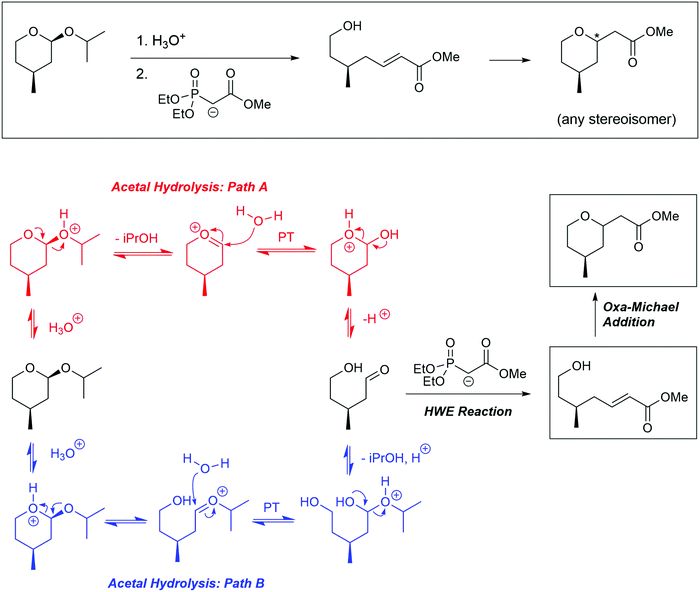
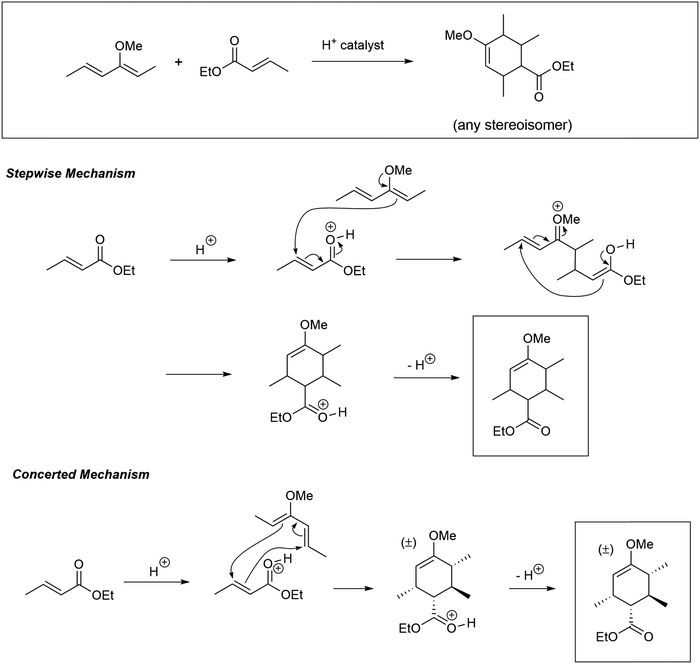
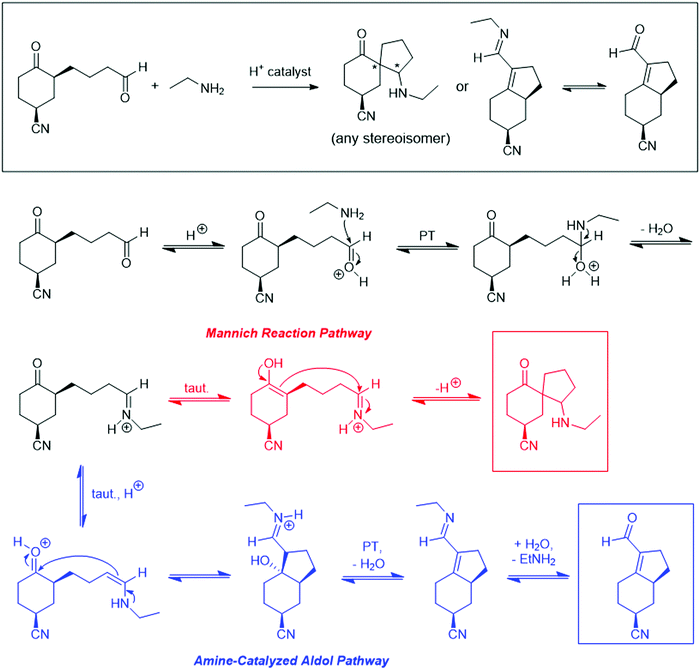
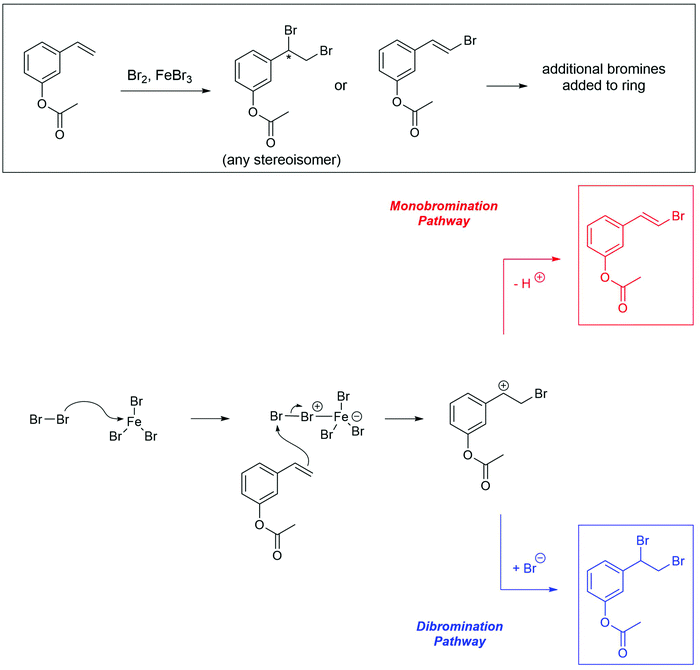
The problems used in this study are shown in Fig. 1. The first question involves the hydrolysis of a cyclic acetal, followed by reaction of the aldehyde intermediate with a Horner-Wadsworth-Emmons (HWE) reagent. The resulting product can then potentially undergo an intramolecular oxa-Michael addition, reforming a six-membered ring. The second question is an acid-catalyzed cycloaddition, which could plausibly proceed through either a concerted or stepwise mechanism. The substrates in the third problem are set up to undergo a Mannich reaction, though an amine-catalyzed intramolecular aldol reaction would also be a reasonable response. In the final problem, the conditions mimic those used in electrophilic aromatic substitution reactions, but bromination is likely to occur first on the more reactive alkene substituent. To ensure that all students would have time to work on each problem during the hour-long interview, the number of problems was capped at four.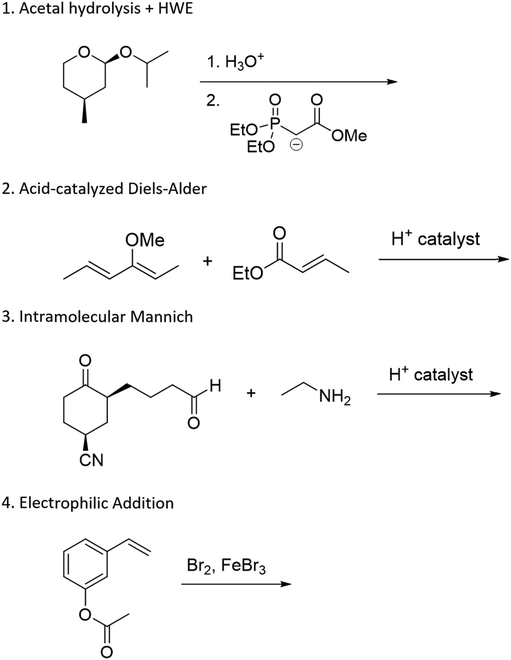

Fig. 1 Problems used in think-aloud interviews. Answers that were considered to be correct for the purposes of this study can be found in the Results section (Fig. 4, 6, 8 and 10).

A primary goal when designing these problems was to make the questions function as problems for most students rather than exercises. We were interested in probing how students think when pushed beyond questions that could be solved by a purely memorization-based approach. To achieve this goal, various aspects of the problems were designed to be potentially ambiguous, and elements were included that might make the reactions seem unfamiliar to the participants. However, specialized reagents were mostly avoided so that students would be able to reason through some reactivity even if they forgot what a given reagent typically does. The problems were reviewed for appropriateness by advanced undergraduate students and an organic faculty member. Pilot testing of think-aloud interviews confirmed that students were interpreting the problems as expected and were able to generate reasonable ideas about each question. All of these problems have the potential to be difficult, but students will rarely have no ideas on how to start working through them.

Multiple types of ambiguity were included in the design of these questions. One source of ambiguity is that there is more than one reasonable answer or solution pathway for each problem. Mechanistic drawings that show the reasonable solution pathways for each of these problems are provided in Appendix F. It was hypothesized that as students gain experience, they are more likely to discuss multiple competing pathways, weighing their relative likelihoods against each other. If there is a clear, unambiguous answer to all problems, this type of reasoning would not be observed. An additional source of ambiguity is that no conditions (solvents, temperature, equivalents) are listed, which is typical of how these types of problems are presented to students in their coursework. It is unclear whether students at different levels of experience make assumptions about conditions, explicitly ask for clarification, or ignore them entirely. In particular, the number of equivalents of the HWE reagent in Problem 1, the amine in Problem 3, and the bromine in Problem 4 may have an effect on the outcome of the reaction. Finally, the problems use relatively complex, generally polyfunctional molecules, in which not every functional group plays a major role in the reaction. Ambiguity about which portions of a molecule are reactive in a given context is often something that students do not gain much experience with until undertaking advanced coursework or research projects.

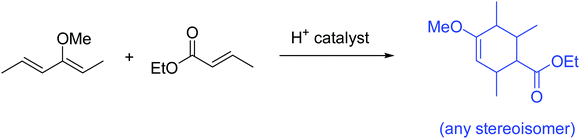
Unfamiliar elements are also a key part of the question design. For example, a cyclic acetal in which one of the alcohols does not leave the molecule upon hydrolysis can lead to confusion when compared to a more prototypical substrate, like the ethylene glycol acetal of acetone. The Diels–Alder question included two features to make the question seem less familiar to students. The first is that the diene is drawn in the s-trans conformation, which can be quite disruptive to the recognition of a possible cycloaddition. Another key feature is the catalyst; Brønsted acids are not the most common catalysts for Diels–Alder reactions, though it was conjectured that some students would propose a stepwise ring formation even if they did not notice the potential concerted reaction. The alkene bromination question makes use of unexpected conditions that are more generally seen when carrying out an electrophilic aromatic substitution reaction.

Previous work on predict-the-product problems has often focused on much simpler transformations in which the most efficient method for answering may be a simple recall of how the given reagent changes the given functional group on the monofunctional starting material. Responses to these problems led these researchers to conclude that students do not value mechanisms as a way to reason about chemical reactivity (Bhattacharyya and Bodner, 2005; Grove et al., 2012), but it seemed plausible that students would make more use of mechanisms when there are more possibilities to take into account. The problems used in this study provide an opportunity to investigate this hypothesis.

Participants and context

All work was conducted at the University of California, Berkeley, a large, research-intensive institution in the Western United States. Procedures used in this research were approved by the University of California, Berkeley Committee for Protection of Human Subjects, Protocol #2015-08-7858.

Participants for research questions 1–2. The first two research questions were addressed using data from 35 undergraduate student participants recruited from Chem 12B in Spring 2018 and Spring 2019, the second-semester organic chemistry course for students majoring in chemistry, chemical biology, or chemical engineering. A recruiting announcement was made to the entire Chem 12B course near the end of each semester in which interviews were conducted. Additionally, regular attendees of the ChemScholars discussion section were sent recruitment emails. ChemScholars is an optional discussion section run by advanced undergraduates that supports the Chem 12B course. The lead researcher attended most ChemScholars discussion sections to provide support for the undergraduate leaders. A majority of the students interviewed (77%) were regular attendees of the ChemScholars discussion section. A range of student “abilities” are represented, as measured by their grade on the Chem 12B final exam (see Fig. 2). It should be noted that this population is not a random sample of all students in Chem 12B. The average interviewee scored 0.6 standard deviations above the mean on the final exam, and only 23% of the interviewees scored below the mean.

Fig. 2 Grade distribution of undergraduate interview participants on the Chem 12B final exam. All scores are converted to z-scores (standard deviations above the mean) to combine data across semesters.

Participants for research question 3. To compare the undergraduate interviews with more advanced chemistry students, nine graduate students were recruited by email from a variety of synthetic organic, organometallic, and chemical biology research groups on campus, using a convenience sampling method. Students ranged from the 2nd through 5th year of their program, and all but one had been a teaching assistant for an organic course in the academic year prior to the interviews.

Think-aloud interviews

Each student volunteer participated in a think-aloud interview (see Appendix A for complete interview protocol). After receiving general instructions, students were first given a warm-up question to practice thinking aloud, and they were given feedback if necessary. They were then asked to solve the four predict-the-product problems in Fig. 1 while attempting to vocalize their thought processes. All questions were presented on separate sheets, one at a time. Each one had the instructions “Predict the major organic product(s) of the following reaction(s). Please indicate stereochemistry where appropriate.” Students were allowed to work uninterrupted until indicating that they had reached a final answer, after which they were asked a few follow-up questions, some of which prompted them to consider other possible outcomes. Answers to follow-up questions were used sparingly in our analysis; most of the focus was on student thoughts prior to any questions. Interviews were audio recorded, and video recordings were taken of student writing. Interviews were transcribed and annotated with what the student was writing while they were talking.

Coding and model development

Characterizing student thinking. The interview transcripts from the Spring 2018 interviews were initially coded to identify the primary problem-solving actions that students took. Through a constant comparative method, a coding scheme was developed to classify the most common student actions. Saturation was achieved with a set of 15 codes, which were then collapsed based on similarity between certain codes into a final set of 12.

Transcripts for all think-aloud interviews were then fully coded with the primary set of 12 codes using MaxQDA software. Only the students’ spontaneous thought processes (i.e., prior to any significant prompting by the interviewer) were coded in this way. Transcripts were coded independently by three researchers, and coding was periodically compared. Any discrepancies were resolved by discussion among researchers. After 40% of the data was coded in this manner, coding for the remaining interviews was completed by a single researcher (MRH).

Proposed workflow. The primary codes were arranged into a flowchart, subsequently referred to as a “workflow,” which serves both as a model for student thought processes during complex PtP problems and as a potential instructional guide for how to approach such problems. The exact form of the workflow was developed over time through discussions among the research team. The pathways outlined on the first complete draft of the workflow (see Appendix B) were informed partially by holistic impressions of the Spring 2018 interviews and partially by the authors’ previous experience as instructors and tutors.

Feedback and workflow revisions. The first draft of the workflow was introduced to advanced undergraduate students who agreed to participate in focus groups. Two focus groups, each containing six students, met to discuss the format of the workflow and its potential usefulness as an educational resource for sophomore undergraduates during their first year of organic chemistry. To accompany the workflow, a one-page document was generated that briefly explained each step and provided prompting questions. Additionally, a set of seven example PtP problems typical of first-semester organic chemistry were provided so that students could better assess the usefulness of the workflow.

A set of revisions was made to the workflow based on feedback from the focus groups. The resulting draft was shown to five graduate students in organic research groups after they participated in think-aloud interviews. Feedback from these students was incorporated into the final draft of the workflow. Additionally, the explanatory document was replaced by longer sets of questions for students to ask themselves at each step of the process (see Appendix C).

Quantitative analysis

After all interviews were coded, subsets of the data were averaged to create profiles enumerating what percentage of the transcripts (by character count) corresponded to each code for various groups of students (e.g., all Spring 2018 interviews, all successfully solved problems, etc.). To determine similarities and differences between different sets of students, the average transcript percentages corresponding to each code were compared using t-tests. The average interview length, as measured by character count, was also a point of comparison between groups. Because multiple tests are run for each group of students (one per code), the conservative Bonferroni correction is used to reduce the rate of false positives. All statistical tests were conducted using Stata software. Further trends in the data were identified using holistic coding. Evidence for the resulting claims was then gathered by quantifying the presence or absence of various features in each interview.

Results and discussion

This study seeks to characterize the ways in which various students approach complex predict-the-product problems, using think-aloud data from 35 undergraduate students and 9 graduate students. We begin with summaries of “what students did” on each problem, which involve rich descriptions of problem-solving approaches and provide a context for the subsequent analysis. This section focuses primarily on undergraduate solution pathways but also highlights informative comparisons to graduate student approaches. We then describe how the coding system and workflow model were developed. After presenting evidence for the validity of our model, comparisons are made between different groups of students to identify how more successful and more expert-like participants approached the problems used in this study.

General description of student problem solving

Problem 1. Several common pathways taken by students on the first problem are shown in Fig. 3. Student thought processes on the first problem initially focused on the reactivity of the HWE reagent, which was often discussed before addressing the first step. Most students (66%) specifically stated that they needed to form a carbonyl group in the first part of the problem in order for the HWE reagent to react properly. Whether students mentioned needing to form a carbonyl group or not, the majority (69%) figured out that they could protonate and then eliminate one of the two acetal oxygens to form one of two possible oxocarbenium ions. Recognizing the electrophilicity of these unstable oxocarbenium intermediates, eight students (23%) used water as a nucleophile to form one of two hemiacetals, which most then converted to an aldehyde product that could react with the HWE reagent in step 2. Other students (31%) instead directly reacted the oxocarbenium intermediates with the nucleophilic HWE reagent. This approach generally caused confusion when it did not produce the expected betaine, but two of the students who used this approach did ultimately form the correct product.

Fig. 3 Common approaches taken by students on Problem 1.

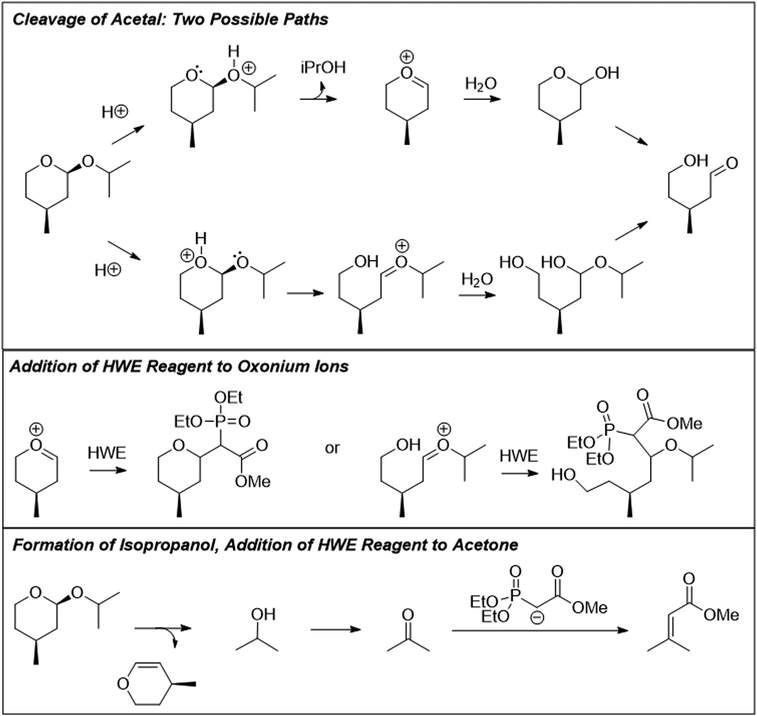
Another common occurrence was for students to recognize the similarity of the starting material to a THP-protected alcohol (37%). Because of this, students often cleaved the acetal into a methyl-DHP group and isopropanol, neither of which provided an appropriate substrate for the HWE reaction. Seven students (20%) resolved this cognitive dissonance by proposing that isopropanol could become oxidized to acetone. Because students knew something about the structure of the intermediate that must be formed (a carbonyl group), they proposed chemically unreasonable transformations to get there as directly as possible. This observation is similar to what DeCocq & Bhattacharyya (2019) found in their studies on how additional information affects mechanistic reasoning.

Student answers were considered “correct” if they proposed either of the product molecules indicated in Fig. 4. Four students (11%) gave perfectly correct answers, and an additional 5 students (15%) gave nearly correct answers with only minor errors, such as inverting the methyl stereocenter when drawing it in a different orientation. Of the 9 students who were correct or nearly so, 8 drew the unsaturated ester, while only 1 recognized the formation of the oxacycle. Recognizing that water was present and might participate in the reaction seemed to be key for reaching a reasonable solution; 63% of students who drew water as a nucleophile proposed a correct answer, compared to 15% of students who did not. Most (74%) students drew a mechanism, but use of the electron-pushing formalism was not associated with greater success on this problem. Students were considered to have drawn a mechanism if they drew out at least one complete step (starting material, electron-pushing arrows, and product).

Fig. 4 Accepted solutions to Problem 1.

Graduate students had a higher success rate on this problem (56%), and they did not follow some of the common pathways taken by the undergraduates. For example, none of the graduate students saw the starting material as a THP-protected alcohol, nor did they attempt to oxidize the resulting isopropanol to acetone so it could be used as a substrate for the HWE reaction. It seems likely that having additional practical laboratory experience contributed to this difference. One would never use a complex chiral starting material as a source of isopropanol in a research context, but more novice students are likely to have seen the “synthesis” of commercially available bulk chemicals on their problem sets and exams.

Problem 2. Student approaches to this problem varied widely depending on whether they recognized a potential Diels–Alder reaction, but recognizing this reaction was not necessary to form the correct cyclic product (see Fig. 5 for common student approaches and Fig. 6 for accepted solutions). About half (54%) of the students did not identify the substrates as a well-matched diene and dienophile pair, largely due to the s-trans conformation of the diene. The 19 students who did not approach the problem as a Diels–Alder reaction generally began by finding nucleophiles and electrophiles to react. Of these students, 8 (23% of total) saw the methoxy lone pairs and the protonated carbonyl group and attempted to do a transesterification, encountering problems once they reached an acylated oxonium.

Fig. 5 Common approaches taken by students on Problem 2.

Fig. 6 Accepted solutions to Problem 2.

The possibility of a Michael addition was recognized by 7 others (20% of total), and while some balked at the fact that the resulting structure still had a positively charged oxygen, 3 students (9% of total) correctly identified the second Michael addition and completed the stepwise cycloaddition to form the six-membered ring.

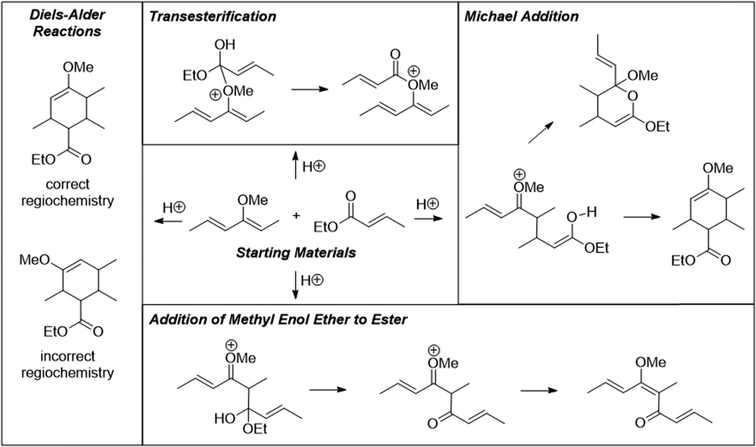
Overall, 16 students (46%) suggested a Diels–Alder reaction, and of the 19 who did not, 13 recognized the possibility immediately upon being shown the diene in the s-cis conformation and asked, “would your thinking have differed if the starting material was drawn this way?” Interestingly, of the 16 who recognized the Diels–Alder possibility, 6 said that it could not be a cycloaddition, remarking that, “I was going to say Diels–Alder but there's no heat,” or, “I'm thinking of a Diels–Alder but that needs heat, so maybe it's a no.” This was an unexpected outcome; we did not anticipate how important the presence of a written Δ was for students to consider the possibility of a thermally allowed pericyclic reaction. In their coursework, students had briefly seen a Lewis acid-catalyzed Diels–Alder reaction in which heat was not explicitly indicated, though never a Brønsted acid-catalyzed one. After recognizing the potential Diels–Alder reaction, students considered the regiochemistry of the cycloaddition by determining which positions on the diene and dienophile were electron-rich or electron-poor. Some students also drew resonance structures to justify their choices. The success rate on this problem was 26%, with an additional 14% recognizing the possible Diels–Alder reaction but drawing an incorrect regiochemical outcome. Most (77%) of the students drew at least one mechanistic step, though generally not after they recognized the possibility of a Diels–Alder reaction.

Four of the graduate students (44%) carried out the Diels–Alder reaction without any prompting. The approaches of the graduate students differed from those of the undergraduates. None combined the substrates with incorrect regiochemistry or used the methoxy lone pairs as a nucleophile. The graduate students were more likely than the undergraduate students (56%) to draw a Michael addition between the enol ether and the unsaturated ester. Three of these students (33%) completed the double Michael addition, reaching the correct cyclic product in a stepwise fashion. Overall five (56%) of the graduate students were successful on this problem.

Problem 3. Students explored a variety of pathways for this problem (see Fig. 7 for common approaches), but most started by condensing the amine and the aldehyde. Students typically began by considering the nucleophilicity and electrophilicity of the different functional groups seen in the starting materials. Essentially all (97%) students decided that the aldehyde was the most reactive electrophile and at some point added the amine to the protonated aldehyde. After this step, 29 students (85%) continued on to form an iminium or imine, while the other 5 students (15%) reacted the nitrogen of the resulting hemiaminal with the ketone to form a seven-membered ring. A few (18%) students left the imine as their final product, but most assumed that there must be additional possible reactivity.

Fig. 7 Common approaches taken by students on Problem 3.

At this point, students proposed multiple different mechanistic paths. Some (18%) attempted cyclization by adding the imine nitrogen to the ketone. Others (47%) recognized the possibility for one or both possible enol tautomers of the ketone. Some students then considered the question of regioselectivity, weighing the relative stability of the two possible enol tautomers as well as the favorability of generating a five-membered or seven-membered ring as a result of the Mannich reaction. In total, 14 students (41%) completed the Mannich transformation to generate a 6-5 spirocycle (Fig. 8), and 9 students (26%) mentioned the Mannich reaction by name. However, half of these students were unhappy with this structure, because “it just looks kinda funky,” and 5 students rejected this answer because they believed that the reaction was not yet complete. Unexpectedly, 4 students (12%) remembered that one place they had seen spirocycles was as an intermediate in the Bischler-Napieralski reaction, which undergoes a 1,2-shift to form a 6-6 fused ring system, and they carried out an analogous shift. Overall, 9 students (26%) successfully drew the Mannich 6-5 spirocycle and stopped at that point. An amine-catalyzed aldol condensation between the two carbonyl groups was also considered acceptable, but no students gave this as their final answer.

Fig. 8 Accepted solutions to Problem 3.

Most graduate students (67%) successfully drew the Mannich spirocycle, and the rest simply stopped at the intermediate imine. Interestingly, only one graduate student mentioned the Mannich reaction by name, even after being asked, “Were you thinking about any named reactions?” Considering the emphasis placed on knowing named reactions in many synthetic organic research groups, this came as a surprise to our research team. Indeed, upon being unable to come up with an answer to this follow-up question, one student noted, “[my advisor] would kill me.”

Problem 4. Students mostly focused on brominating the aromatic ring in this problem, and a few students also attempted to react the bromine with the alkene substituent (see Fig. 9 for common student approaches and Fig. 10 for accepted solutions). As expected, all students recognized the conditions for an electrophilic aromatic substitution reaction. As a result, much of the discussion revolved around using directing group effects to determine which position on the ring would be brominated. Most students (>80%) explicitly referred to both the vinyl and ester substituents as electron-donating, activating, or ortho/para directing. Many of these students were able to provide a clear rationale for categorizing the ester as electron-donating based on fundamental principles of resonance and charge stability. Students often (37%) determined the directing group effect of the vinyl group by categorizing it as a generic alkyl group. Some students also considered steric effects when determining which positions would be brominated, which showed their ability to weigh the effect of different factors when predicting reactivity. All but 6 students (82%) brominated the ring at one or more of the ortho/para positions, and 3 of the remaining students (9%) brominated at the meta position.

Fig. 9 Common approaches taken by students on Problem 4.

Fig. 10 Accepted solutions to Problem 4.

Seven students (21%) also mentioned the possibility of the alkene reacting with the bromine without prompting. Three drew the product of this addition, and 2 (6%) settled on this as their final product. All students were eventually led with prompting to the idea that bromine could react with the alkene. However, students were still more likely to say that the aromatic ring would react first. Some gave chemically based reasons, such as identifying the ester as an “activating group,” which the alkene did not have. However, a more common reason for discounting the alkene addition was “that's [first semester] material!” Another reason given for this decision was that the alkene addition reaction is “too simple” to be correct. This type of non-chemical reasoning has also been found to be prevalent among students in other organic courses at UC Berkeley (Brando, 2019).

Graduate students were much more likely (89%) to propose a direct reaction between the alkene and bromine. However, they too were reluctant to propose a straightforward alkene bromination as their final answer, with only 3 students (33%) stating that this would be the preferred product. Like the undergraduate students, many graduate students saw the aromatic substitution as the “intended” outcome of this reaction, leading them to believe that reaction at the alkene would be an unwanted byproduct, but not the major outcome.

Use of mechanisms. Other studies have suggested that students do not value mechanisms as a method for reasoning through PtP problems (Bhattacharyya and Bodner, 2005; Grove et al., 2012), but the electron-pushing formalism was widely used during problem solving in this study. On Problems 1, 2, and 3, students drew a mechanism 74%, 77%, and 94% of the time, respectively. Only on Problem 4, in which the mechanism is generally assumed to be a straightforward electrophilic aromatic substitution, did students largely forgo the use of mechanisms (only 2 students (6%) drew them). These results suggest that students do value mechanisms as a problem-solving tool, but they may only use them when the problem is sufficiently long or complex.

Interestingly, graduate students were somewhat less likely to utilize the electron-pushing formalism. Mechanisms were drawn by graduate students 56%, 56%, 44%, and 22% of the time on Problems 1–4, respectively. One interpretation of this result is that graduate students have “chunked” collections of steps into transformations like “acetal hydrolysis” or “imine formation” in ways that undergraduate students have not. As a result, the threshold for the use of mechanisms as a reasoning tool appears to be higher.

What are the common characteristics of problem solving in the context of non-trivial predict-the-product problems, and does the workflow model accurately reflect student problem solving?

Characteristics of student problem solving. General problem-solving actions exhibited by multiple students were identified by exploratory coding of a random subset of the Spring 2018 think-aloud transcripts. Unlike the actions described in the previous section that are specific to a single problem, this analysis focused on more abstract themes, such as deciding between competing pathways or checking work, that might be applicable to a broad range of questions. All student discussions pertaining to chemistry were coded to avoid only identifying expected actions.

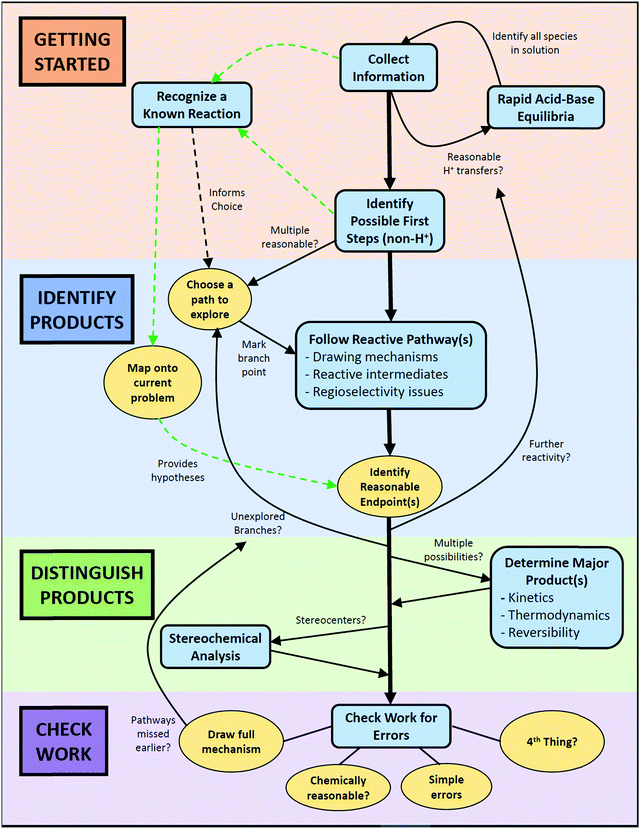
Students frequently started a problem with an initial planning stage. For example, students often started by naming functional groups and reagents, identifying nucleophiles and electrophiles, and noting any unusual structural features. In essence, they were collecting information about the problem (code: CollInfo, see Table 1), specifically outlining the starting conditions for their solving process. After the initial planning stage, students often took one of two pathways depending on whether they recognized the conditions for a specific reaction they had learned.

Table 1 Codes for student problem-solving actions during PtP problems

Code	Abbreviation	Description
Collect information	CollInfo	Student gathers information that might help them solve the problem, both what is on the page and relevant prior knowledge.
Acid–base equilibria	AcidBase	Student talks about proton transfer steps or equilibria between different protonation states.
Identify first steps (non-H^+)	IdentFirst	This code is used to identify the first elementary step proposed after any initial proton transfers.
Follow reactive pathway	FRP	Student starts with a reactive intermediate and goes through one or more steps in an attempt to reach a stable intermediate/product.
Recognize similarity to known reaction	RecogRxn	Student mentions the name or a description of a reaction or transformation.
Map onto current problem	MapTotal	Student maps what they know about a known reaction onto the current problem they are solving.
Identify reasonable endpoints	IdentEnd	Student carries out a last step to reach a final answer and indicates that they are finished.
Propose alternate reactivity	PropAlt	After discussing one possible path/reaction, student backs up and considers a different path/reaction. (Used before student reaches something they consider to be a final answer.)
Decide between pathways/products	Decide	Student has two (or more) identifiable paths or molecules to choose between and makes a decision, sometimes with rationale.
Stereochemical analysis	Stereo	Student talks about determining stereochemical outcomes.
Assess progress	AssessProg	Student pauses to comment on how correct or certain they are.
Check work	CheckTotal	– After reaching something they seem to consider to be a final answer, student looks back to see whether alternate chemical pathways or further reactivity are possible.
		– Student checks for mistakes at any point during the interview

---

In the first pathway, recognition of the similarity of the problem to a known reaction (code: RecogRxn) was followed by the mapping of general knowledge about a reaction onto the current problem (code: MapProb). This mapping process allowed students to identify endpoints that they considered reasonable (code: IdentEnd). Reaching a possible solution in this way can occur either by directly jumping to a product by analogy with the known reaction or by working through the mechanism for the identified reaction using the given substrate. Occasionally, students would draw chemical structures that very strongly suggested that they had a specific reaction in mind, but they did not identify it out loud. In these cases, the implied mapping code was used (code: ImpMap).

In the second pathway, when a student could not identify any known reaction, they took a more step-by-step approach to solving the problem. After considering which potential proton transfers might take place (code: AcidBase), students taking this path used the electron-pushing formalism to identify the first elementary steps that might occur (code: IdentFirst). This process generally resulted in a reactive intermediate from which students could propose a reaction sequence typical of that sort of structure (code: FRP). Determining the resulting stereochemistry (code: Stereo) sometimes occurred in the middle of the solving process and sometimes at the end.

For some students, this was the end of their problem-solving process, but others took this opportunity to check their work by looking for errors (code: CheckError), further reactivity of the proposed product (code: CheckMore), or alternate reactivity of the given substrates (code: CheckAlt). Students who proposed alternate reactivity (code: PropAlt) would then need to decide between the major pathways or products to reach a final solution (code: Decide). Finally, throughout the solving process, students would stop to assess their progress (code: AssessProg).

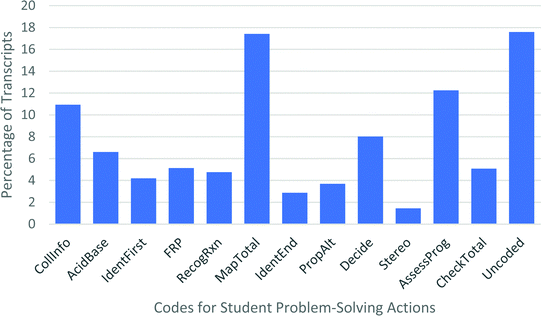
In total, initial coding resulted in a set of 15 codes that were used to characterize student problem solving throughout the study. Due to the similarity between “Map onto current problem” and “Implied mapping,” these were combined into a single code for further analysis (code: MapTotal). Similarly, the three types of checking work were collapsed into a single “CheckTotal” code. These 12 final codes and their descriptions are summarized in Table 1, and examples of student responses corresponding to each code can be found in Appendix E.

Quantifying student problem-solving actions. Once the coding system was developed, all interview transcripts from Spring 2018 and 2019 were fully coded to obtain a quantitative overview of what students were most commonly thinking about as they worked through the problems. With 82% of the transcripts (by character count) identifiable as one of these 12 codes, the large majority of student thinking seems to be captured with this coding system. The percentage of the transcripts coded with each action is shown in Fig. 11. The most common way students spent their time was mapping knowledge about a known reaction onto the given substrates. They also spent a significant amount of time assessing their own progress through the problem. Conversely, this group of students often neglected to consider stereochemistry in their think-aloud discussion, with only about 1% of the total discussion devoted to stereochemistry.

Fig. 11 Frequencies of problem-solving actions by percentage of interview transcripts.

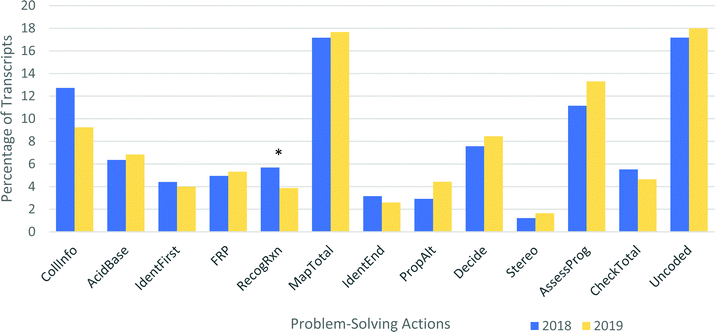
Overall, about 18% of the transcripts were left “uncoded.” What was going on during those periods of time? The largest portion was made up of quotations like “[inaudible muttering], and this [???] looks like this, so…”, in which the student is mumbling to themselves or making statements with unclear referents, so they cannot be unambiguously coded. Other common uncoded segments include comments or questions to the interviewer (e.g., “am I allowed to use notes?”, or “is this supposed to be a really hard problem or should I be worried?”). Most of the uncoded segments do not include clear discussions around chemistry. However, one relatively common occurrence that is not part of the current coding system was for a student to state what they would do if the situation were different (e.g., if water were present, if heat were specifically indicated, if an alcohol were a carbonyl group instead).

This analysis pools student data from 2018 and 2019 and assumes that there are no systematic differences between these years. Both years of Chem 12B students had very similar instructional experiences, and from a holistic perspective, no systematic differences were noted between the interviews in 2018 and 2019. As a result, very similar problem-solving profiles were expected between the two years. This is indeed the case; the percentages in Fig. 12 are nearly indistinguishable from year to year, and only one difference (RecogRxn, p = 0.047, Cohen's d = 0.35) meets the p < 0.05 cutoff for significance. Because multiple comparisons are being made, it is appropriate to apply the Bonferroni correction and adjust the threshold for significance to 0.05/12 = 0.004. By this criterion, none of the differences in coded problem-solving actions are significant. However, there is one significant difference between years: the 2019 cohort spoke about 40% more than students in 2018 (p = 0.002, Cohen's d = 0.54). The reason for this difference is not clear, but one possibility is that the interviewer was more experienced the second year and may have allowed students to speak more before interjecting with follow-up questions.

Fig. 12 Comparison of problem-solving actions by two cohorts of interviewees (*p < 0.05).

Development of the workflow. The set of 12 codes in Table 1 was arranged into a first draft of the workflow (see Appendix B). As described in the Methods section, the form of the workflow was developed through holistic impressions of the think-aloud interviews and discussions among the research team, most of whom have extensive experience as organic instructors. This draft was intended to be a model for student thinking, but we also wanted it to serve as a guide for how to approach predict-the-product questions. A problem-solving workflow for general chemistry questions was developed by Yuriev et al. and shown to be valued by students, and it was postulated that our workflow would be similarly helpful to organic chemistry students (Yuriev et al., 2017). The workflow model is not fully self-explanatory, so an additional one-page document was written to clarify the intended meaning of each component. Many of the explanations took the form of prompting questions that a student might ask themselves at each step of the process.

The first draft of the workflow, the one-page explanatory sheet, and example problems were presented to two focus groups of advanced undergraduates. Feedback on this first draft was largely positive, and several students expressed a desire to have a copy for themselves. The inclusion of different pathways depending on whether a known reaction is recognized was highlighted as particularly important. Students felt that the workflow matched their own thought processes, especially after trying example problems. Student comments included, “it's pretty close to my thinking,” “it's a good match for how we think about it,” and “this is literally what I do.”

The additional one-page document that briefly explains each workflow bubble was considered to be an essential and useful accompaniment to the workflow itself. The prompting questions were considered especially useful, which is consistent with what has been reported in the literature (Ge and Land, 2003; Yuriev et al., 2017). In response to the suggestion that we “focus on being more question-based,” the explanatory sheet was expanded to a two-page document composed entirely of prompting questions that students could ask themselves at each step (see Appendix C).

Most focus group participants felt that the workflow and accompanying materials would be a useful resource for organic students if introduced at the appropriate time. However, some expressed concerns that the full workflow would be overwhelming, especially if given out too early. One student remarked that, “It's kind of scary when you first see it though. It might be a progression situation.” By “progression situation,” they were referring to the idea of first introducing a simplified version before giving out the complete workflow. Other participants agreed, and this was the approach taken when the workflow was eventually introduced to students.

A second draft of the workflow was constructed based on focus group comments and shown to five graduate students with expertise in organic chemistry after they participated in think-aloud interviews. Again, feedback was positive, and students indicated that it captured their own solving process with remarks like, “This is, with a little bit more thoroughness, more or less what I do when I solve a problem.” An additional “Determine most likely pathway(s)” bubble was included based on these interviews, but few other changes were made at this point.

Final workflow. The final workflow included two different forms. The first was a complete version intended to capture the full range of student solving (Fig. 13). It is roughly divided into four phases of problem solving, but with the option to loop back to previous phases as necessary. There are two primary routes that students can take through the diagram. One possibility is to move down the central column, taking a step-by-step approach through the mechanistic possibilities and diverging to other actions as appropriate for the specific problem. The other primary route is to recognize a specific type of reaction and use the “fast lane” to more rapidly generate a plausible solution based on analogy to known reactivity. As a final step, checking one's work can lead the student to revisit previous phases and repeat part or all of the solution-generating process.

Fig. 13 Finalized workflow for solving relatively complex organic predict-the-product problems.

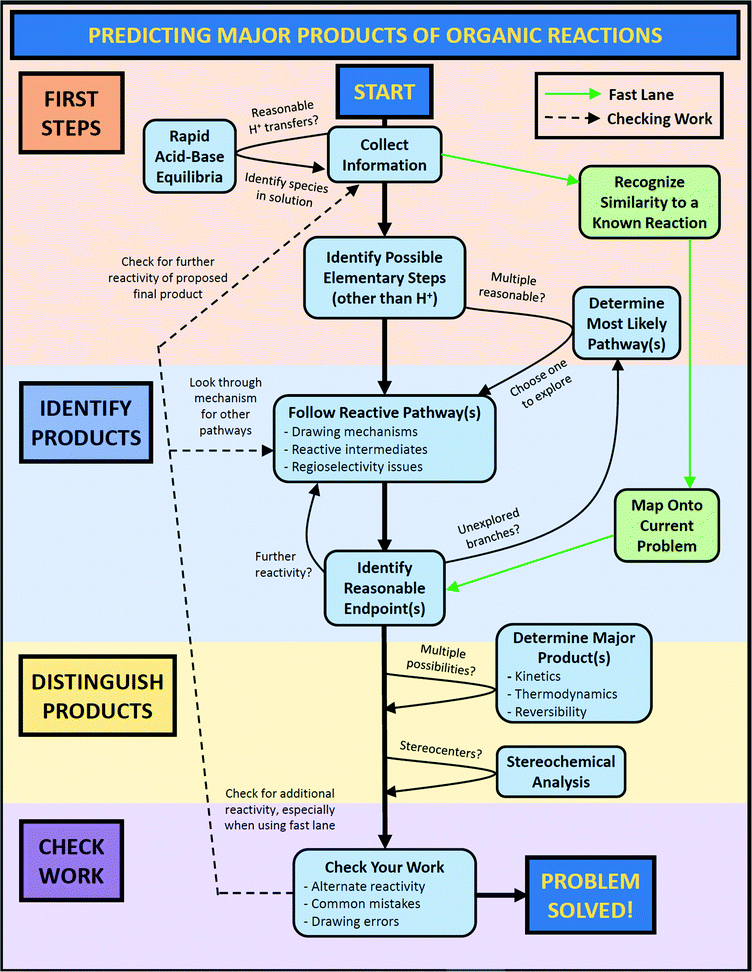
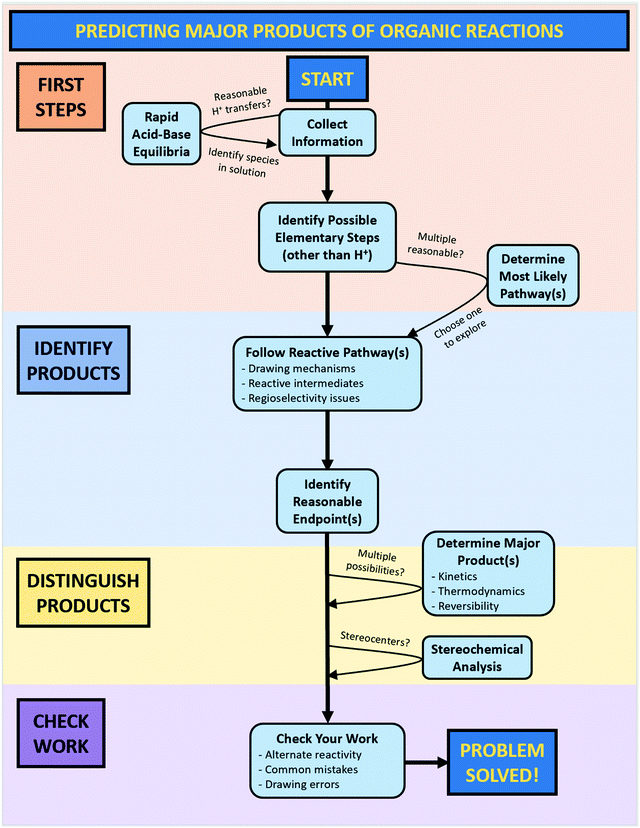
It is important to recognize that even the complete version of the workflow is presented in a somewhat idealized form in that it does not explicitly show every pathway an individual might take while solving a problem. For example, a student might identify a reasonable endpoint and immediately consider the problem to be solved without checking their work, yet there is no arrow that directly connects these two bubbles. When deciding which connections to include in the workflow, we chose to emphasize routes that were commonly taken by students and those that included all four phases of problem-solving. To minimize visual complexity and avoid confusion, we did not include arrows that skipped key steps on the fast lane or central column, or arrows that intersected with other arrows or cut across workflow bubbles.

The other version of the workflow was a simplified form intended for use as a student resource along with the prompting questions (see Appendices C and D). This version emphasized step-by-step mechanistic reasoning and de-emphasized the “shortcut” of predicting products based on the recognition of a known reaction. At the point when this workflow would be introduced, mechanisms are generally short and best considered one step at a time; it is not until later that multi-step mechanisms need to be “chunked” to efficiently determine the outcome(s) of a given reaction.

Model comparisons. Although both the workflow model and the model developed by Bhattacharyya of how students approach mechanism problems are attempting to characterize mechanistic reasoning, they are ultimately quite different due to the information given as part of the problem (Bhattacharyya, 2014). The model developed by Bhattacharyya involves mapping the reactant onto the product and identifying key differences to determine whether the reaction is a single-step canonical reaction or a multi-step functional group transformation. Different paths are taken depending on which type of reaction is identified, and electron-pushing arrows are not added until after intermediates or other reaction features are drawn. However, students cannot “map the reactant onto the product” in a predict-the-product question. Conversely, there is no need to identify an endpoint, distinguish between products, or do stereochemical analysis as part of a mechanism problem. Both models do feature “mapping knowledge onto the current problem” steps, but other than that, similarities are surprisingly low.

One feature that appears similar between the two models is that they both have two pathways through the diagram. However, although they both feature diverging paths, the reason for divergence is different. In the model developed by Bhattacharyya, the path chosen (single- or multi-step transformation) is based on features of the reaction that are recognized when comparing the starting material and product. In our model, the path chosen depends on whether the student recognizes a known reaction at all. Both of Bhattacharyya's pathways would fit best within the workflow “fast lane,” in which a reaction is recognized and knowledge about that reaction is mapped onto the given substrate. The model developed by Bhattacharyya does not attempt to characterize student reasoning when cues in the problem are not sufficient for them to recall the appropriate reaction. Because this model was based on the work of graduate students, it is possible that nearly everyone was able to recall a reaction, so there was not enough data to support a model for those who did not recall any reaction.

Assessing the workflow model – two paths. Roughly speaking, there are two primary paths through the workflow: investigating a mechanism step-by-step (the central column) and recognizing a known reaction followed by applying relevant knowledge (the “fast lane”). The interview transcripts do not cleanly divide into one or the other, as many students (46%) incorporate elements of both paths in their approach. However, the interview transcripts can be divided into two groups based on students’ initial approaches to solving the problem. In one group, students identified a first elementary step other than simple proton transfers (IdentFirst code) before identifying any known reaction. In the other group, students identified a known reaction and did not identify a first elementary step as a separate action. Problem-solving action profiles for these two types of interviews are contrasted in Fig. 14.

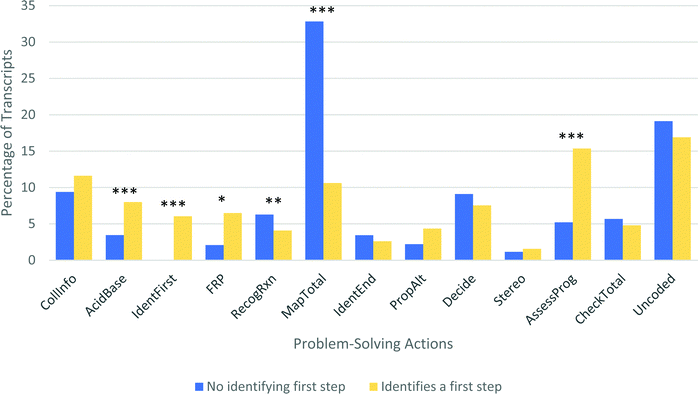Fig. 14 Problem-solving action profiles for students who did or did not identify a first step prior to recognizing a known reaction (* p < 0.05; ** p < 0.01; *** p < 0.004).

There is a clear set of differences between these two types of solution processes. Students with an IdentFirst code in their transcript were significantly more likely to spend their time discussing acid–base chemistry (p < 0.005, Cohen's d = 0.56) or following reactive pathways (p < 0.05, Cohen's d = 0.41). In contrast, students without an IdentFirst code spent significantly more time discussing known reactions (p < 0.01, Cohen's d = 0.47) and mapping their knowledge onto the given problem (p < 0.0001, Cohen's d = 1.05). Additionally, students in these two groups did not score differently on the items that appear on the workflow after the two paths merge (Identify Reasonable Endpoint and beyond). The fact that specific items cluster together with other items on the same pathway, but there are no differences in student actions after the two paths merge at the Identify Reasonable Endpoint node, is evidence in favor of considering the workflow to be an accurate model of student work.

There is a second large difference between these two groups; students who took the Identify First Steps path spent nearly three times as long assessing their progress (p < 0.0005, Cohen's d = 0.68). A common observation made during the interviews was that once students recognized a known reaction, regardless of whether it was the most appropriate reaction, they tended to be overconfident in moving quickly towards an answer. The dramatic difference in assessing progress between these two pathways is consistent with this observation.

It is notable that there was no difference in success rate between students who identified a first step (19%) and those who did not (22%). This is somewhat surprising, because students who recognize a reaction might be expected to perform better than students who do not. However, in these interviews, students often recognized a reaction that was not the most relevant one. In particular, most students recognized the potential for electrophilic aromatic substitution on Problem 4, but that was not the most likely mechanism. Similarly, many students focused on treating the substrate in Problem 1 as a THP-like alcohol protecting group, leading them astray when identifying the important product of the acetal hydrolysis. It is probable that with more straightforward questions, the success rate would be higher for students who recognize a known reaction.

Assessing the workflow model – individual pathways. The analysis above showed that the workflow model and associated coding system captures student thinking on average, but further investigation was needed to determine whether the pathways shown on the workflow represent how individual students approach each problem. To visualize student problem-solving pathways, the progression of codes was drawn directly onto the workflow. For example, one student's approach to Problem 4 is represented in Fig. 15a. After collecting information, this student quickly recognized a specific reaction and mapped what they knew about that reaction onto the given substrate, reaching what at first glance were multiple reasonable answers. The student then decided which of those answers was most likely. However, upon checking their work, they came up with another, even more reasonable solution and decided upon that as their final answer. This student went through the phases of the workflow in a relatively orderly fashion, with just one loop back up after checking their work. Compare this to the reasoning path of the student in Fig. 15b, who was attempting the same problem but went through many different loops before reaching a final solution.

Fig. 15 Student reasoning pathways for Problem 4 mapped onto the workflow. Red lines indicate the order in which students engaged in each step of the process. Part (a) represents a relatively direct path through the workflow, whereas part (b) depicts a more circuitous approach.

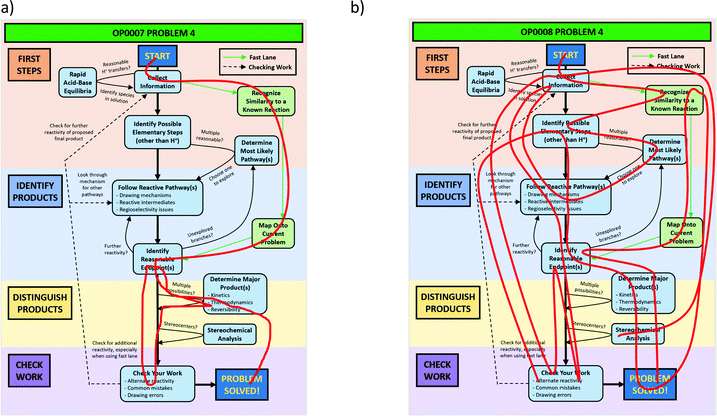
The two different pathways depicted in Fig. 15 are reminiscent of the idea that different types of models may need to be used depending on whether the solver is treating the question as a problem or an exercise (Bodner, 2003). The student in Fig. 15a seemed to have a general idea about how to work through the problem, and they worked through the various phases of problem solving in a relatively linear way. It is likely that they treated the question as an exercise, and as a result, a model with distinct phases matches their solving process. In contrast, the student in Fig. 15b seemed to be treating the question as a genuine problem, taking a more anarchistic approach. Student solution pathways varied quite a bit in complexity, and there was not a clear division between exercises and problems. These examples were chosen to represent common paths at different ends of the continuum.

Overall, the data suggest that student reasoning is well captured by the workflow model. Even though approaches varied widely, they can generally be described by following the various pathways outlined by the workflow. The components of the workflow describe the majority of student actions while problem solving, accounting for 82% of the interview transcripts. Additionally, the clustering of certain problem-solving actions provides support for the dual path model proposed.

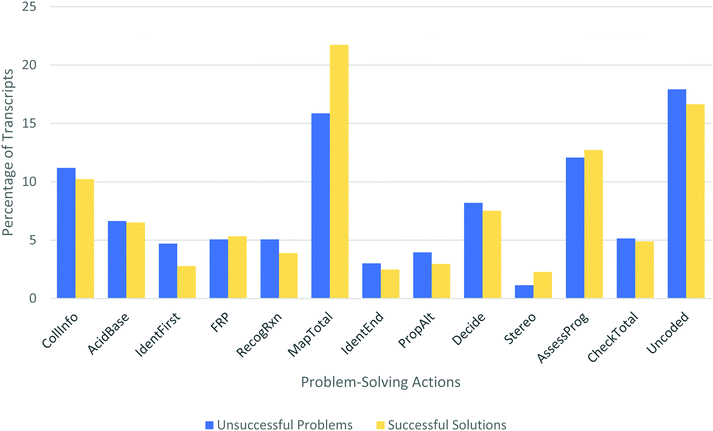
What differentiates successful from unsuccessful problem solvers?

Success on interview questions. Due to the overall difficulty of the problems, the undergraduate students struggled to propose reasonable answers. Out of the 138 problems solved by the 35 undergraduate participants, only 19 resulted in fully correct solutions, with another 10 nearly correct answers (i.e., inverted stereochemistry, extra or missing carbons, etc.). Including all 29, the success rate was 21%.

To identify differences in how successful and unsuccessful solutions were generated, the problem-solving action profiles for these two groups were compared (Fig. 16). Interestingly, no statistically significant differences were found. Of the data we quantified, there was only one significant difference between the more and less successful students: The successful students talked about 35% more than the unsuccessful ones, as measured by character count. While students who eventually proposed correct answers were distributing their work in the same ways, they were simply doing more talking. If student discourse is an accurate representation of their thought process, as is generally assumed during think-aloud interviews, the more successful students were thinking more about the problem than the ones who did not reach a reasonable solution.

Fig. 16 Problem-solving action profiles for more and less successful solvers.

Success on exam questions. In addition to comparing students who were more or less successful on interview questions, we also wanted to look at differences between students who performed better or worse on exams. However, no significant differences were observed between students with higher or lower exam scores. The analysis is similar when comparing the full set of student exams or comparing the students who earned the highest 10 and lowest 10 exam scores. The lack of association between problem-solving actions and success on either interview questions or exams was unexpected. We had hypothesized that certain behaviors like assessing progress or checking work might be more common among successful students, but this was not found to be true. It should be noted that we did not necessarily expect similar performance on interview and exam questions, due to the fact that the interview questions are more complex and ambiguous than the predict-the-product questions generally encountered on exams. In fact, the number of problems correctly answered during the interview was not significantly associated with receiving a higher or lower score on the Chem 12B final exam, which was held within a week of the interview.

Investigating other differences between successful and unsuccessful students. What is it that successful students are doing differently? The problem-solving action profiles above do not differentiate between successful and unsuccessful problem solvers. However, as mentioned earlier, students who spoke more tended to be more successful on interview questions. One possible conclusion from this data is that simple persistence, thinking through a problem a little more, is a key to being successful. Of course, this may not always be feasible, as is often the case on timed exams. Indeed, there was not a significant correlation between speaking more during the interview and final exam score. There are certainly other possible interpretations. For example, it may be that putting one's thoughts into words is beneficial to the solving process, so students who spoke more were more likely to succeed.

Another notable trend involves naming functional groups. Students who explicitly identified the starting material in Problem 1 as an acetal were more likely to be successful (55% vs. 13%). Similarly, all 6 students (100%) who specifically identified a “diene” in Problem 2 noticed the Diels–Alder, compared to 34% of students who didn’t. Additionally, naming the alkene in Problem 4 was associated with recognizing the possibility for reactivity on that side chain. All students referred to the vinyl group, but only 6 students (18%) actually named it an alkene, while most just pointed and called it “that.” Of these 6 students, 5 noticed the potential reactivity at the alkene (83%), whereas only 2 of the remaining 28 (7%) said anything about reaction at the alkene before being prompted to consider it. A possible hypothesis is that the act of naming these functional groups activates relevant knowledge more effectively than just looking at the structure. Alternatively, it is also possible that this naming of functional groups occurs as a result of recognizing the relevance of these explicit features to the problem at hand.

This trend also appeared in the graduate student data. Graduate students were successful 75% of the time when naming the acetal, compared to 40% of the time when they did not. Similarly, both students who named the diene were successful (100%), compared to a 43% success rate for the remaining students. All but one student named the alkene in Problem 4, and that student was the only one not to propose reactivity between the alkene and bromine. Interestingly, the undergraduate students only used the term “alkene,” while graduate students were divided among alkene, styrene, olefin, and vinyl group, reflecting the more extensive vocabulary utilized by more advanced students. Overall, the results from both the undergraduate and graduate interviews suggest that it may be good practice for students to explicitly name the given functional groups as they are starting a problem.

Other keys to success can be identified, but they vary by problem. Seeing the water “hidden” in the H₃O⁺ was helpful for Problem 1; students who drew H₂O on their page were much more likely to be successful (63% vs. 15%). Recognizing the possibility of enolization was necessary for getting to the most likely answers for Problem 3. Being open to further reactivity (Problem 3) or alternate reactivity (Problem 4) also made a difference in some cases. Individual take-away lessons can be drawn from these trends (e.g., always consider whether your solvent might be involved in the reaction, ketones can be “secret nucleophiles,” check whether your proposed product can keep reacting). In addition to learning general strategies, student success may partially depend on having a broad repertoire of these more specific themes and concepts at their disposal. Based on these results, it may be useful for students to create a list of the take-away lessons from problems they have encountered.

What differences are there between the approaches of sophomore undergraduates and more experienced organic chemistry graduate students?

Graduate and undergraduate students took largely similar approaches to the problems used in this study. For many actions, especially those that occur early in the problem-solving process (collecting information, identifying first steps, recognizing known reaction, etc.), there is no real difference between these two groups (Fig. 17). This suggests that, like the undergraduate students, graduate students use both the step-by-step and known reaction pathways, and in about the same ratios. Note that this might not be the case for simpler problems, for which graduate students would be more likely to have the exact transformation shown committed to memory. Also notable is that undergraduate and graduate interviews were nearly the same length on average (by character count).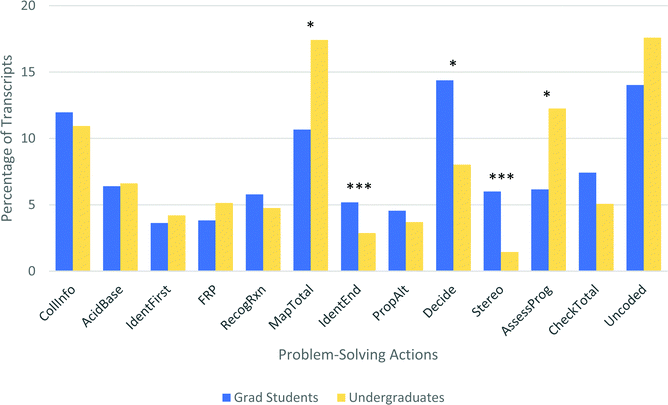

Fig. 17 Problem-solving action profiles for undergraduates and graduate students (* p < 0.05; ** p < 0.01; *** p < 0.004).

However, there are some differences in the relative amount of time spent on various problem-solving actions (Fig. 17). All of these differences fit the p < 0.05 criteria, though if we use the stricter Bonferroni corrected p < 0.004 criteria, only identifying reasonable endpoints (IdentEnd) and stereochemistry (Stereo) can be pointed to confidently as real differences. However, it may be informative to examine all of these differences, because the small sample size of nine graduate students can make it difficult for smaller effects to reach the level of statistical significance.

Graduate students spent nearly twice as much time as undergraduates identifying reasonable solutions (p < 0.005; Cohen's d = 0.61) and deciding between them (p < 0.05; Cohen's d = 0.48). This is consistent with the fact that graduate students were more likely to identify more than one possible solution to the problem. This could be because graduate students recognize more possible paths, but it could also point to the different ways that graduate students think about predicting reactivity. In a course, there is generally one and only one correct answer to a predict-the-product problem. As a result, undergraduates are used to stopping as soon as they find a reasonable answer and moving quickly to the next question, because they often have a time limit for completing the problems. However, in the research lab, such questions are generally approached more deliberately by seeking all reasonable answers and narrowing down which is/are most likely.

Graduate students also spent substantially more time in these interviews discussing stereochemistry (Stereo, p < 0.005; Cohen's d = 0.61). Even though the directions for every problem asked students to indicate stereochemistry, undergraduates often left newly formed stereocenters undefined unless prompted by the interviewer. As a reminder, only the unprompted responses are included in the coding. Anecdotally, stereochemistry seems to be given a lower priority in the Chem 12B curriculum, allowing students to focus more on learning the transformations and less on exactly which stereoisomers are formed. This relative emphasis might be an alternative explanation to a more sweeping generalization like “graduate students consider stereochemistry more important.”

Undergraduates spent more of their time assessing their progress (AssessProg, p < 0.05; Cohen's d = 0.39) and mapping their knowledge about a known reaction onto the current problem (MapTotal, p < 0.05; Cohen's d = 0.35). Undergraduates were not more likely to recognize a known reaction, but they did spend more time figuring out how to apply their knowledge. This is particularly evident on the Diels–Alder question, in which undergraduates slowly worked through a long algorithm to determine the correct regio- and stereochemistry. The difference in assessing progress is unexpected. One hypothesis is that the graduate students were more confident and felt less need to stop and assess along the way. For example, general statements like “this looks so wrong” were extremely common among undergraduates but not among graduate students.

To transition students to a more expert-like approach when solving these problems, a key area for intervention might be increasing the time students spend developing alternate solutions and then deciding between those solutions. To accomplish this, problem sets could include more complex questions with multiple reasonable answers, and students could be instructed to generate two possible answers and rationalize why one is more likely. Alternately, to focus even more closely on the decision-making process, students could be shown a reaction and asked to explain which of several different given solutions is most likely.

Limitations

Self-selection bias among research participants is a common limitation for this type of study. Students who struggled with their organic coursework are understandably less likely to volunteer their time to be observed while solving extra chemistry problems. As a result, over 75% of the sample was above average, as measured by their final exam score, and few students who scored very poorly participated in this study.

Another limitation is that many of the research participants were at some point directly taught by a member of the research team in the ChemScholars discussion section. This may have influenced students’ approaches to problem solving in a particular direction, possibly making it more similar to the resulting workflow. However, the workflow was equally suitable for modeling solutions by non-ChemScholars undergraduates and graduate students, as measured by the percentage of transcripts that could be classified as one of our codes.

Some outcomes from this study should be generalized with caution. Raw numbers on how much time is spent on each action vary widely across problems, so it should not be assumed that similar values would be reproduced using a different set of questions. In addition, the statistical results should be interpreted with caution since this is a relatively small dataset and the results should be interpreted from a primarily qualitative standpoint. Additionally, the workflow is proposed to be a valid model for solving relatively complex predict-the-product problems, but student approaches may differ on a more straightforward set of questions. Indeed, preliminary work with students at the end of their first semester of organic chemistry suggests that a more collapsed model may be more appropriate in some cases.

Conclusions and implications

Through an iterative process, we have developed a workflow for predicting organic reactivity. Think-aloud interviews with students showed that it is an appropriate model for how more novice undergraduates and more expert-like graduate students solve complex predict-the-product problems. Both linear and more anarchistic problem-solving approaches (Bodner, 2003) can be described using the workflow model. The workflow deconstructs a complex problem into individual practices that assist students with systematically making connections between their knowledge of organic reactivity and the problem. Importantly, each of these practices can be improved through teaching. Various potentially useful interventions can be imagined when problems are viewed from this perspective. For example, encouraging students to name all the functional groups before starting a problem would be a useful way of training the “collecting information” skill. If students are struggling to “follow reactive pathways,” a lesson on reactive intermediates might be helpful. Teaching these skills also includes a simple reframing of skills and approaches that are already part of organic courses. For example, teaching students to reason with reaction coordinate diagrams is one way of developing the “determine major product(s)” skill (Popova and Bretz, 2018).

Some researchers have found it useful to differentiate whether student reasoning appears to be based on cases, rules, or models (Kraft et al., 2010; Christian and Talanquer, 2012). When using case-based reasoning, solvers try to find an example in their memories that seems to match the current problem. This approach to problem solving has some similarity to the “fast lane” path through the workflow, although students who chose this track also engaged in other problem-solving approaches. Other paths through the workflow are likely to elicit both rule-based and model-based reasoning. It is important to note that experts make use of all three types of reasoning processes to solve problems.

We observed that students who spoke more were more likely to be successful, and it may be that putting thoughts into words can be a helpful strategy, as suggested by the observation that students who named the functional groups were more successful on the problems used in this study. Studies explicitly comparing student problem solving with and without thinking aloud have not been conducted in organic chemistry. Work in other disciplines suggests that the act of vocalizing one's thoughts may itself affect the problem-solving process (Schooler et al., 1993; Schooler, 2002). If thinking aloud is inherently beneficial for organic chemistry problems, this would be a concrete suggestion that we can give to our students that they can easily implement and are unlikely to be doing already. It may be beneficial to encourage students to include explicit elaborations and explanations in their thinking aloud to further help them in the problem-solving process (Graulich et al., 2019).

While there were some commonalities, the key moments that led to successful solutions were largely idiosyncratic to the individual problem. However, implicit concepts can be abstracted from each of these problems, and these concepts are likely to appear again eventually in future problems. When faced with complex problems in organic chemistry, using a higher level of abstraction and considering implicit properties has been associated with more successful problem solving (Weinrich and Sevian, 2017; Graulich et al., 2019). Having students identify and record “take-away lessons” for each problem as a study technique is a strategy that we have used in our own teaching. Requiring that students engage in this type of analysis helps to reinforce the idea that “course content” is introduced not only through lectures or textbook readings, but also through the assigned problems, which are carefully selected to assess specific learning goals valued by the instructor.

On average, the approaches taken by graduate students were not qualitatively different from those taken by the undergraduates, and there was more variation within each of these groups than between them. Studies that compare expert and novice problem-solving approaches using card sort tasks have often found that novices focus more on surface features, while expert approaches rely on underlying scientific principles (Chi and VanLehn, 2012; Krieter et al., 2016). In card sort tasks specifically involving organic chemistry reactions, some undergraduate students sorted by superficial structural similarities, while graduate students and faculty sorted by types of reactions and mechanisms (Galloway et al., 2018). However, in a subsequent study on organic reaction sorting (Galloway et al., 2019), a great deal of variation was found within a group of students at the same level of experience, which is similar to our results. One difference that we observed between graduate and undergraduate students is that the graduate students spent more time identifying solutions and deciding between them. If we consider this to be expert-like behavior that we would like to guide our students towards, it would benefit us to give students more opportunities to work on complex, open-ended problems that may have more than one reasonable solution.

The workflow model developed here provides a deeper perspective on how both novices and experts approach complex predict-the-product questions, and the conclusions made about student problem-solving actions provide guidance for how to best support our students to be successful solvers. Predicting reactivity is a fundamental chemical practice in organic chemistry, but it is often taught gradually over the course of a year, focusing on whatever functional group or reaction type is the subject of the current unit. There are several new approaches to organic curricula that are designed to help students learn foundational concepts and practices of organic chemistry to be able to more thoughtfully solve problems (Flynn and Ogilvie, 2015; Cooper et al., 2019; McGill et al., 2019; Lipton, 2020). For example, Flynn and coworkers have developed a curriculum that is organized by mechanism type rather than by functional group. This curriculum focuses on teaching the electron pushing formalism before learning particular reactions in order to support students to effectively use this important skill while solving unfamiliar problems (Flynn and Ogilvie, 2015). The curriculum “Organic Chemistry, Life, the Universe and Everything” (OCLUE) focuses on four interconnected foundational concepts and encourages problem solving approaches that support students to develop conceptual knowledge, skills, and practices that enable them to successfully approach unfamiliar problems (Cooper et al., 2019). The evidence from the implementation of these curricula is that these explicit approaches to teaching problem solving help students to solve unfamiliar complex problems successfully (Webber and Flynn, 2018; Houchlei et al., 2021).

We believe that due to the central nature of the predict-the-product problem type, it should be addressed as a distinct topic during the first year of organic chemistry coursework. Once students have gained familiarity with a few different types of organic reactions, they would benefit from being explicitly shown how to apply that knowledge to predict-the-product problems in which the type of reaction is not already known. The workflow model we developed represents one potential scaffold for teaching this practice. The use of a simplified version of the workflow (Appendix D) was demonstrated to students in a large lecture class, and preliminary indications are that it can be a helpful resource if instructors are thoughtful and explicit about when, why, and how it should be used. Additional research will be required to determine how the workflow can best be used to support student learning. Methods for approaching the fundamental question of organic synthesis are well established (Corey and Cheng, 1995), and the work of Bhattacharyya and others provides a starting point for modeling and teaching mechanism problems (Bhattacharyya, 2014; Weinrich and Sevian, 2017). We believe that our work adds to this body of knowledge by elucidating the approaches used to successfully predict organic reactivity.

Conflicts of interest

There are no conflicts to declare.

Appendix A – complete interview protocol

Questions about the course

– Thanks so much for coming, I really appreciate your help.

– For the first part of the interview, I just have a couple background questions and then some general questions about your experiences in 12A and B.

1. Courses

– Did you do the standard 4A/B, 12A/B sequence?

– What other chemistry courses have you taken so far?

2. What is your year in school and intended major?

– Do you have an intended subfield or area of interest?

– Do you know what you’re thinking of doing after?

– Are you looking to join any labs, or have you already? Which ones?

– Have you done any chemistry research prior to joining a lab here?

3. What was your study routine like for organic, both in terms of ongoing learning and exam prep?

– What activities did you spend the most time on?

– What activities were most helpful?

– Were there things you did at first but stopped doing because you did not find them helpful?

– Are there changes you would make if you did it again?

– Did this vary between the two semesters?

4. What were your biggest struggles in organic chemistry?

– Did the biggest issues change over the course of the year?

5. When you see a problem on an exam (let's say predict the products) and you draw a blank at first, what do you do next?

6. What advice would you give to students who are starting 12A in the fall?

Questions about section

Next I have a few questions that pertain to the discussion section(s) you attended. (Only Q8 asked for students not attending ChemScholars)

7. What aspects of section did you find to be most and least useful? Please feel free to be as honest as possible; I am very interested in learning how to improve this section for future.

– What changes would you make?

8. Did you attend any other sections regularly? If so, what was your experience there, and how did it differ from this section.

– What did you find particularly helpful or unhelpful about the other section(s)?

Thinkaloud portion

Part of what I’m trying to study is the detailed thought processes that go on in students’ minds while they are working on solving typical organic chemistry problems. What I’m going to have you do is work through a few predict-the-products organic problems, and I want you to vocalize your thoughts as you have them, to the best of your ability. After you’ve finished working on the problem, let me know. If you are unsure of the answer, treat it like an exam and give your best guess.

Also, I want to say up front that you shouldn’t take these problems as an indicator of how prepared you are for the final, even though they involve similar material. I can explain more about why afterwards.

We’ll have a warm-up question to practice thinking aloud. Do you have any questions for me?

Training problem

[Give paper with training problem:]

Predict the major organic product(s) of the following reactions. Please indicate stereochemistry where appropriate.

I want you to practice thinking aloud on this problem. I may prod you if you stop talking for too long. Also, I should point out that you’re not explaining it to me or anybody else. We’re trying to get at the best approximation of the thoughts you’d have if you were sitting alone, working on this problem without any cameras or stress or time constraints.

Great! For the remaining questions, I will allow you to finish working, and then I will have a number of follow-up questions. Some of those may involve asking you about a “hypothetical student answer” that you have not mentioned; these are asked to everyone and they do not indicate that your initial answer (or the hypothetical answer) is correct or incorrect.

Problems. All questions will have the same instructions. [Each question presented sequentially on separate pieces of paper].

Appendix B – first draft of workflow

Appendix C – prompting questions to accompany workflow

First steps

Collecting information. – What is the potential function (acid, nucleophile, etc.) of each functional group or reagent?

– Is the reaction under acidic, basic, or neutral conditions?

– Which are the most acidic protons in the reaction?

– Is one significantly (∼5 pK_a units) more acidic than the others, or are there multiple comparable protons?

– Where are the strongest bases in the reaction?

– Are there multiple basic atoms of comparable strength?

– Where are the strongest nucleophiles in the reaction?

– Are there any good electrophiles?

– Are there any good leaving groups?

– What types of atoms are they bonded to (e.g., secondary carbon)?

– Is there a solvent shown?

– Is the solvent likely to be involved in the reaction?

– Is there a workup step shown?

– What other conditions are shown?

– How many equivalents of each reagent are used?

– Is a temperature or any other information given? What does that information tell you?

– Are there any particularly unstable features? (e.g., extremely strong acid, base, nucleophile, or electrophile, strained rings, O–O bonds, etc.)

Acid–base equilibria. – Where are the most acidic protons and most basic atoms in the reaction?

– Consider the strongest acid and the strongest base

– Is a proton transfer likely based on pK_avalues?

– Will that proton transfer be reversible or irreversible?

– Are there other comparably acidic protons to consider (especially in reversible situations or if there is excess base)?

– Are there other comparably basic atoms to consider (especially in reversible situations or if there is excess acid)?

Identifying possible first steps. – Where are the strongest nucleophiles and electrophiles in the reaction?

– Consider the strongest nucleophile and the best electrophile

– Is the nucleophile strong enough to attack the electrophile?

– If not, are there any good leaving groups? If so, could it leave spontaneously under the given conditions?

– Are there other competing nucleophiles or electrophiles of comparable strength to consider (especially in a reversible situation)?

– Which of the ∼10 elementary steps you’ve learned could possibly happen at this point?

– Which of these are reversible under the given conditions?

Identifying possible products

Determining major pathways. – Of the possible first steps, are some much more likely than others?

– Are there any steps that would be fast and irreversible?

– Are there multiple possible regioisomers?

– Are any of them minor enough where that path doesn’t need to be followed?

Following reactive pathways. – If there are familiar reactive intermediates (e.g., carbocation, oxyanion, enolate), what steps do they usually undergo to become less reactive?

– Are there multiple possible regioisomers?

– Are any of them minor enough to ignore?

Identifying reasonable endpoint(s). – Are there still strong acids, bases, nucleophiles, or electrophiles present?

– If multiple equivalents are indicated, did more than one get used?

– If a reagent is indicated as catalytic, did you regenerate it in your mechanism?

– Is the substrate neutral, or would it be neutral after aqueous workup?

– Could the proposed product react further under the reaction conditions?

Distinguishing between possible products

Determining major products (if there are multiple possible ones). – What is the fastest reactive pathway? (kinetic considerations)

– What is the most stable attainable product? (thermodynamic considerations)

– Are any steps effectively irreversible under the given conditions?

– Are we generally under kinetic (irreversible) or thermodynamic (reversible) conditions?

– What effects do various conditions (e.g., solvent, temperature) have on the product ratios?

Stereochemical analysis (if there are multiple possible stereoisomers). – What stereochemistry is present in the starting molecules?

– Which steps in the mechanism involve creating or destroying stereocenters (or alkenes with stereochemistry)?

– For each new stereocenter formed, is one isomer heavily favored, slightly favored, or exactly as likely as the other?

Check your work

– Look back through a complete mechanism for the proposed reaction

– Are there alternate branches that might be competitive?

– Can my proposed final product react further under the reaction conditions?

– Did I make any common mistakes?

– Do I have 5 bonds to carbon or nitrogen?

– Am I missing any formal charges?

– Did I make any drawing errors?

– Did I accidentally add or lose any carbon atoms?

– Do I need to add in stereochemistry?

Appendix D – simplified workflow for instruction

Appendix E – example excerpts for each code

Code	Abbreviation	Example
Collect information	CollInfo	“This group looks like a protecting group, which is like… and this is also an acetal, … and I know that these can be used to protect alcohols”
Acid–base equilibria	AcidBase	“Normally if it's just a carbonyl I would think this would protonate here, make it a reactive center”
Identify first steps (non-H^+)	IdentFirst	“Um, I am going to have the amine come in to the aldehyde because that's more reactive”
Follow reactive pathway	FRP	“We have this… this would be attacked by the negative charge on the carbonyl”
Recognize similarity to known reaction	RecogRxn	“I was thinking that the HWE reaction, because of this step”
Map onto current problem	MapTotal	“So that's going to create a double bond there to this guy, this will add to carbonyls”
Identify reasonable endpoints	IdentEnd	“Then our final product would be a 1 2 3 4 5 6-membered ring”
Propose alternate reactivity	PropAlt	“Or what also could possibly happen is if that leaves, then I could form this positive charge, which would be resonance stabilized”
Decide between pathways/products	Decide	“So I'm looking between these two, and it looks like, this one looks more reasonable because this looks like some alcohol that's a good leaving group”
Stereochemical analysis	Stereo	“I want to say that this one is going to be opposite of that one, just because that would make the most sense stereochemically, but I don't think it matters which one goes up and which one goes down”
Assess progress	AssessProg	“Okay, but the problem here is like, there's still a positive charge on the oxygen”
Check work	CheckTotal	“I'm trying to think if this could attack here, that's a weird thing, oh I guess I can try, wait no, then that would form into a 4-membered ring so that probably shouldn't happen”

Appendix F – mechanisms for Problems 1–4

Fig. 18 Reasonable possible mechanistic pathways for Problem 1.

Fig. 19 Reasonable possible mechanistic pathways for Problem 2.

Fig. 20 Reasonable possible mechanistic pathways for Problem 3.

Fig. 21 Reasonable possible mechanistic pathways for Problem 4.

Acknowledgements

M. R. H. would like to thank the UC Regents for a graduate research fellowship. K. A. B. would like to thank the NSF for a graduate research fellowship (NSF-GRFP 2018241803). Z. M. F. would like to thank the UC Berkeley College of Chemistry for additional research funding. The research team would like to thank Richmond Sarpong for reviewing the chemistry problems used in this study. We also appreciate the contributions of Michael Curtis, Ryan Khalaf, Tahoe Fiala, Franco Faucher, and Maura Daly. Finally, we would like to thank the undergraduate and graduate student participants of this study for their willingness to share their valuable time.

References

1. Austin A. C., Ben-Daat H., Zhu M., Atkinson R., Barrows N., and Gould I. R., (2015), Measuring student performance in general organic chemistry, Chem. Educ. Res. Pract., 16(1), 168–178.
2. Bhattacharyya G., (2014), Trials and tribulations: Student approaches and difficulties with proposing mechanisms using the electron-pushing formalism, Chem. Educ. Res. Pract., 15(4), 594–609.
3. Bhattacharyya G. and Bodner G. M., (2005), “It gets me to the product”: How students propose organic mechanisms, J. Chem. Educ., 82(9), 1402–1407.
4. Bode N. E. and Flynn A. B., (2016), Strategies of successful synthesis solutions: Mapping, mechanisms, and more, J. Chem. Educ., 93, 593–604.
5. Bodner G. M., (2003), Problem solving: The difference between what we do and what we tell students to do, Univ. Chem. Educ., 7(2), 37–45.
6. Bodner G. M. and Herron J. D., (2002), Problem Solving in Chemistry, in Chemical Education: Research-based Practice, Kluwer Academic Publishers.
7. Bowen C. W., (1994), Think-aloud methods in chemistry education: Understanding student thinking, J. Chem. Educ., 71(3), 184–190.
8. Brando B., (2019), Study behaviors, problem-solving, and exam design in organic chemistry.
9. Bunce D. M., Gabel D. L., and Samuel J. V., (1991), Enhancing chemistry problem-solving achievement using problem categorization, J. Res. Sci. Teach., 28(6), 505–521.
10. Cartrette D. P. and Bodner G. M., (2010), Non-mathematical problem solving in organic chemistry, J. Res. Sci. Teach., 47(6), 643–660.
11. Caspari I., Weinrich M. L., Sevian H., and Graulich N., (2018), This mechanistic step is ‘“productive”’: Organic chemistry students’ backward-oriented reasoning, Chem. Educ. Res. Pract., 19(1), 42–59.
12. Charters E., (2003), The use of think-aloud methods in qualitative research: An introduction to think-aloud methods, Brock Educ. J., 12(2), 68–82.
13. Chi M. T. H. and VanLehn K. A., (2012), Seeing deep structure from the interactions of surface features, Educ. Psychol., 47(3), 177–188.
14. Christian K. and Talanquer V., (2012), Modes of reasoning in self-initiated study groups in chemistry, Chem. Educ. Res. Pract., 13(3), 286–295.
15. Cooper M. M. and Stowe R. L., (2018), Chemistry Education Research—From Personal Empiricism to Evidence, Theory, and Informed Practice, Chem. Rev., 118(12), 6053–6087.
16. Cooper M. M., Stowe R. L., Crandell O. M., and Klymkowsky M. W., (2019), Organic Chemistry, Life, the Universe and Everything (OCLUE): A Transformed Organic Chemistry Curriculum, J. Chem. Educ., 96(9), 1858–1872.
17. Corey E. J. and Cheng X.-M., (1995), The Logic of Chemical Synthesis, John Wiley & Sons.
18. Cruz-Ramírez de Arellano D. and Towns M. H., (2014), Students’ understanding of alkyl halide reactions in undergraduate organic chemistry, Chem. Educ. Res. Pract., 15(4), 501–515.
19. DeCocq V. and Bhattacharyya G., (2019), TMI (Too much information)! Effects of given information on organic chemistry students’ approaches to solving mechanism tasks, Chem. Educ. Res. Pract., 20(1), 213–228.
20. Ericsson K. A. and Simon H. A., (1980), Verbal reports as data, Psychol. Rev., 87(3), 215–251.
21. Ericsson K. A. and Simon H. A., (1993), Introduction and Summary (Ch. 1), in Protocol analysis: Verbal reports as data, MIT Press, pp. 1–62.
22. Ferguson R. and Bodner G. M., (2008), Making sense of the arrow-pushing formalism among chemistry majors enrolled in organic chemistry, Chem. Educ. Res. Pract., 9(2), 102–113.
23. Finkenstaedt-Quinn S. A., Watts F. M., Petterson M. N., Archer S. R., Snyder-White E. P., and Shultz G. V., (2020), Exploring student thinking about addition reactions, J. Chem. Educ., 97(7), 1852–1862.
24. Flynn A. B., (2014), How do students work through organic synthesis learning activities? Chem. Educ. Res. Pract., 15(4), 747–762.
25. Flynn A. B. and Featherstone R. B., (2017), Language of mechanisms: Exam analysis reveals students’ strengths, strategies, and errors when using the electron-pushing formalism (curved arrows) in new reactions, Chem. Educ. Res. Pract., 18, 64–77.
26. Flynn A. B. and Ogilvie W. W., (2015), Mechanisms before reactions: A mechanistic approach to the organic chemistry curriculum based on patterns of electron flow, J. Chem. Educ., 92, 803–810.
27. Fonteyn M. E., Kuipers B., and Grobe S. J., (1993), A description of think aloud method and protocol analysis, Qual. Health Res., 3(4), 430–441.
28. Galloway K. R., Leung M. W., and Flynn A. B., (2018), A Comparison of How Undergraduates, Graduate Students, and Professors Organize Organic Chemistry Reactions, J. Chem. Educ., 95(3), 355–365.
29. Galloway K. R., Leung M. W., and Flynn A. B., (2019), Patterns of reactions: A card sort task to investigate students’ organization of organic chemistry reactions, Chem. Educ. Res. Pract., 20(1), 30–52.
30. Ge X. and Land S. M., (2003), Scaffolding students’ problem-solving processes in an ill-structured task using question prompts and peer interactions, Educ. Technol. Res. Dev., 51(1), 21–38.
31. Graulich N., (2015), The tip of the iceberg in organic chemistry classes: How do students deal with the invisible? Chem. Educ. Res. Pract., 16, 9–21.
32. Graulich N., Hedtrich S., and Harzenetter R., (2019), Explicit versus implicit similarity – exploring relational conceptual understanding in organic chemistry, Chem. Educ. Res. Pract., 20(4), 924–936.
33. Grove N. P., Cooper M. M., and Cox E. L., (2012), Does mechanistic thinking improve student success in organic chemistry? J. Chem. Educ., 89(7), 850–853.
34. Grove N. P., Cooper M. M., and Rush K. M., (2012), Decorating with arrows: Toward the development of representational competence in organic chemistry, J. Chem. Educ., 89, 844–849.
35. Houchlei S. K., Bloch R. R., and Cooper M. M., (2021), Mechanisms, Models, and Explanations: Analyzing the Mechanistic Paths Students Take to Reach a Product for Familiar and Unfamiliar Organic Reactions, J. Chem. Educ., 98(9), 2751–2764.
36. Kraft A., Strickland A. M., and Bhattacharyya G., (2010), Reasonable reasoning: Multi-variate problem-solving in organic chemistry, Chem. Educ. Res. Pract., 11(4), 281–292.
37. Krieter F. E., Julius R. W., Tanner K. D., Bush S. D., and Scott G. E., (2016), Thinking like a chemist: Development of a chemistry card-sorting task to probe conceptual expertise, J. Chem. Educ., 93(5), 811–820.
38. Lipton M. A., (2020), Reorganization of the Organic Chemistry Curriculum to Improve Student Outcomes, J. Chem. Educ., 97(4), 960–964.
39. McGill T. L., Williams L. C., Mulford D. R., Blakey S. B., Harris R. J., Kindt J. T., et al., (2019), Chemistry Unbound: Designing a New Four-Year Undergraduate Curriculum, J. Chem. Educ., 96(1), 35–46.
40. Petterson M. N., Watts F. M., Snyder-White E. P., Archer S. R., Shultz G. V., and Finkenstaedt-Quinn S. A., (2020), Eliciting student thinking about acid–base reactions via app and paper–pencil based problem solving, Chem. Educ. Res. Pract., 21(3), 878–892.
41. Popova, M. and Bretz, S. L. (2018), Organic chemistry students' challenges with coherence formation between reactions and reaction coordinate diagrams. Chem. Educ. Res. Pract., 19 (3), 732–745.
42. Polya G., (1945), How to solve it: A new aspect of mathematical method, Princeton University Press.
43. Raker J., Holme T., and Murphy K., (2013), The ACS Exams Institute undergraduate chemistry anchoring concepts content map II: Organic chemistry, J. Chem. Educ., 90, 1443–1445.
44. Schoenfeld A., (1987), What's all the fuss about metacognition? Cognitive Science and Mathematics Education, Lawrence Erlbaum Associates, Inc., pp. 189–215.
45. Schooler J. W., (2002), Verbalization produces a transfer inappropriate processing shift, Appl. Cogn. Psychol., 16, 989–997.
46. Schooler J. W., Ohlsson S., and Brooks K., (1993), Thoughts beyond words: When language overshadows insight, J. Exp. Psychol. Gen., 122(2), 166–183.
47. Sevian H. and Talanquer V., (2014), Rethinking chemistry: a learning progression on chemical thinking, Chem Educ Res Pract., 15(1), 10–23.
48. Talanquer V. and Pollard J., (2010), Let's teach how we think instead of what we know, Chem Educ Res Pract., 11(2), 74–83.
49. Webber D. M. and Flynn A. B., (2018), How are students solving familiar and unfamiliar organic chemistry mechanism questions in a new curriculum? J. Chem. Educ., 95(9), 1451–1467.
50. Weinrich M. L. and Sevian H., (2017), Capturing students’ abstraction while solving organic reaction mechanism problems across a semester, Chem. Educ. Res. Pract., 18(1), 169–190.
51. Wheatley G. H., (1984), Problem solving in school mathematics. MEPS Technical Report 84.01, West Lafayette, IN: School Mathematics and Science Center, Purdue University.
52. Yuriev E., Naidu S., Schembri L. S., and Short J. L., (2017), Scaffolding the development of problem-solving skills in chemistry: guiding novice students out of dead ends and false starts, Chem. Educ. Res. Pract., 18(3), 486–504.

---