Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
CFD modeling of a membrane reactor concept for integrated CO2 capture and conversion
Hong
Huang
 *a,
Remzi Can
Samsun
a,
Ralf
Peters
*a,
Remzi Can
Samsun
a,
Ralf
Peters
 a and
Detlef
Stolten
bcd
a and
Detlef
Stolten
bcd
aElectrochemical Process Engineering (IEK-14), Forschungszentrum Jülich GmbH, 52425, Jülich, Germany. E-mail: h.huang@fz-juelich.de; Fax: +49 2461 61 6695; Tel: +49 2461 61 85193
bTechno-Economic Systems Analysis (IEK-3), Forschungszentrum Jülich GmbH, 52425, Jülich, Germany
cJARA-ENERGY, 52056 Aachen, Germany
dChair for Fuel Cells, RWTH Aachen University, 52072, Aachen, Germany
First published on 5th September 2022
Abstract
Capturing CO2 and converting it into valuable products represents a future direction of carbon emissions reduction. The emergence of CO2-permeable membranes has opened up a broad range of new opportunities for efficient CO2 capture and conversion. In this context, this study develops a membrane reactor concept using a ceramic–carbonate dual-phase membrane for integrated CO2 capture and conversion. The membrane reactor has two concentric tubes, with the inner tube being for the flue gas to provide a CO2 source and the outer for the CO2 conversion. The catalyst is coated on the membrane surface instead of being packed in the reactor bed so that the permeated CO2 can be immediately converted, and the CO2 permeation flux can be significantly promoted in this manner. The performance of the developed membrane reactor concept is evaluated based on CFD simulations. The membrane reactor can achieve high CO2 capture rates of over 90% and conversions of up to 95% for the reaction of the reverse water gas shift. The CO productivity is limited by the membrane permeation flux and large reactor volume, and can be increased by compact designs that increase the ratio of the membrane area to the reactor volume, which are simple but effective approaches to increasing CO productivity, but maintain high CO2 capture rates and conversions. The developed membrane reactor concept can be readily applied to any other reaction for integrated CO2 capture and conversion.
1. Introduction
Carbon dioxide capture and utilization (CCU) is regarded as an effective way to reduce CO2 emissions and produce value-added products. Conventionally, CCU processes have adopted a two-step approach, in which CO2 is captured in the first step and then converted in the second. This approach, however, may not be energy-efficient and cost-effective, as the CO2 capture and conversion processes are not coupled. Integrating CO2 capture and conversion into a single step offers an appealing solution that can potentially reduce the energy and cost expenses of CO2 capture and conversion. The idea of integrated CO2 capture and conversion can be achieved by designing multi-functional materials and integrated processes. At the materials level, calcium-based dual-functional materials are suitable candidates. CO2 is captured by reacting with CaO to generate CaCO3, after which the CaCO3 is reduced by H2 or CH4 to produce syngas or other chemicals and fuels. Kim et al.,1 for instance, proposed a process for integrated CO2 capture and conversion, wherein CO2 is captured using CaO and the generated CaCO3 reacts with CH4 to produce syngas. The same idea was also investigated by Hu et al.2 and Tian et al.3 for the dry reforming of methane. Similarly, Duyar et al.4 designed a process using a CaO/γ-Al2O3 sorbent and a Ru-based catalyst, but one difference is that the reducing agent was altered to H2 for CH4 production. Sun et al.5 developed a Ce-modified sorbent and coupled it with reverse water gas shift for the production of CO. At the process level, Jens et al.6 developed an integrated CO2 capture and utilization process. In this process, CO2 is captured by low-temperature methanol, and the CO2-containing methanol solution is then directly subjected to methyl formate synthesis without desorbing CO2. Machida et al.7 developed a novel process for solvent-based CO2 capture, in which the thermal regeneration of solvents is replaced with H2 stripping to reduce the energy consumption, and the mixture of CO2 and H2 can be used for downstream chemical syntheses.With the emergence of CO2-permeable membranes, membrane reactors offer another option for simultaneous CO2 capture and conversion. Anderson et al.8 first realized this idea by developing a ceramic–carbonate dual-phase membrane and used it for the dry reforming of methane. CO2 was separated from the mixture of CO2 and N2 and transported to the other side of the membrane where the reaction took place. At 850 °C, the CO2 permeation flux was 0.17 mL min−1 cm−2 with CO2 and CH4 conversions of 88.5% and 8.1%, respectively. Fabián-Anguiano9 also developed a membrane reactor concept for the oxy-dry reforming of methane by using an oxygen-permeable membrane and a ceramic–carbonate dual-phase membrane. In addition to methane, any other species that react with CO2 can be considered. Chen et al.10 experimentally investigated a ceramic–carbonate dual-phase membrane for CO2 capture and conversion into syngas through the reaction of reverse water gas shift. The CO2 permeation flux was improved by more than an order of magnitude compared to the membrane developed by Anderson et al.,8 up to 4.25 mL min−1 cm−2. At the system level, Fang et al.11 performed a life-cycle analysis of combined CO2 capture and conversion in a membrane reactor. The membrane reactor utilizes a high-temperature mixed electronic and carbonate-ion conductor membrane for CO2 capture and a solid oxide electrolysis cell (SOEC) for CO2/H2O co-electrolysis. The energy consumption for the CO2 capture of the membrane system is only 0.321 MJ kg−1-CO2, which is less than half that of the state-of-the-art MEA (monoethanolamine)-based scrubbing processes, and a system efficiency of 82% was achieved, suggesting that it has advantages for simultaneous CO2 capture and conversion. Studies on CO2 capture and conversion by means of computational fluid dynamics (CFD) simulation are quite limited. Bian et al.12 developed a 2D membrane reactor model for coupling of cyclohexane dehydrogenation and CO2 methanation by using a hydrogen permeable membrane. The coupled rector model could boost methane yield but did not show positive effects on the cyclohexane conversion. Liu et al.13 developed and simulated a water-permeable membrane reactor for the CO2 methanation reaction. Key aspects including operating conditions and species distribution were investigated. Salehi et al.14 presented a novel membrane reactor concept for CO2 hydrogenation to methanol. CO2 is supplied and distributed via a tubular alumina membrane. The CFD simulation results showed that the selectivity of methanol production was improved by 6%.
These early exploratory studies proved the feasibility of using membrane reactors for the simultaneously capture and conversion of CO2 at the same time. Against this backdrop, this study continues to investigate this promising membrane reactor concept. CO2 capture is achieved by using a ceramic–carbonate dual-phase membrane and the conversion of CO2 is based on the reaction of reverse water gas shift. Through detailed CFD modeling and simulations, the effects of operating conditions on conversion and productivity will be investigated and the suitable operating window identified; the importance of geometry characteristics will also be highlighted. This study could make contributions to future designs of this type of membrane reactor for integrated CO2 capture and conversion.
2. The membrane reactor concept
The geometry of the membrane reactor consists of two tubes with the membrane between them, as shown in Fig. 1. The outer tube has a radius of 25 mm, whereas that of the inner is 7 mm; and the length of the reactor is 400 mm.15 H2 is fed into the outer tube where the reaction takes place. In addition, H2 itself acts as the sweep gas, and so no external N2 sweep is needed. The flue gas in the inner tube flows in parallel with H2 to supply the CO2via the membrane. Another important feature of the membrane reactor is the coupling mode of the membrane and catalyst. The design of the catalyst coating on the membrane surface carries two differences compared to packed-bed membrane reactors: one is the reaction mechanism and the other the mass transport one. The permeated CO2 does not need to diffuse through the catalyst channels to the active sites, and therefore the internal mass transport limitations are eliminated. The reaction mechanism is changed from a volumetric to surface reaction so that CO2 can immediately react with H2 after arriving.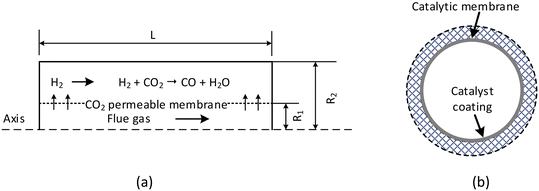 | ||
| Fig. 1 Membrane reactor concept for integrated CO2 capture and conversion: (a) dimensions and configurations of the reactor, R1 = 7 mm, R2 = 25 mm, and L = 400 mm (dimensions taken from ref. 15); and (b) cross-sectional view of the coupling mode of the membrane and catalyst. | ||
3. CFD modeling
This section introduces the fundamentals of CFD modeling, the membrane permeation process and reaction kinetics, as well as implementation using the ANSYS Fluent program.3.1 Mass balance equations
The mass balance of a chemical reactor generally takes a differential form:16 | (1) |
![[v with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0076_20d1.gif) the velocity. The first term on the left-hand side represents the accumulation or loss of mass in the system; the second term is the mass flux by fluid flow. Sm stands for external source terms, such as adsorption or membrane permeation. The above equation is applicable for incompressible and compressible flows. For 2D axisymmetric geometries, the continuity equation is adapted to the following coordinate form:16
the velocity. The first term on the left-hand side represents the accumulation or loss of mass in the system; the second term is the mass flux by fluid flow. Sm stands for external source terms, such as adsorption or membrane permeation. The above equation is applicable for incompressible and compressible flows. For 2D axisymmetric geometries, the continuity equation is adapted to the following coordinate form:16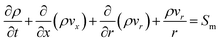 | (2) |
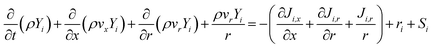 | (3) |
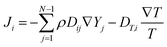 | (4) |
3.2 Membrane permeation modeling
The first step of membrane modeling is the abstraction of the permeation processes, and the second step the modeling of those processes by means of CFD. As indicated by the mass balance in eqn (2) and (3), membrane permeation can be seen as a source term, where the feed side is a positive source and the flue gas side a negative one. For CFD simulations in ANSYS Fluent, as no model is readily available for simulating membrane permeation processes, it is necessary to develop customized models with user-defined functions (UDFs). As the ANSYS Fluent solver is based on the finite volume method, membrane permeation fluxes are converted from area-to volume-specific:17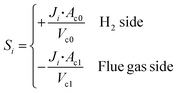 | (5) |
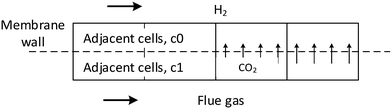
In the above equation, Ac0, Ac1, Vc0, and Vc1 are the areas and volumes of the neighboring cells of the membrane wall, which can be indexed by the built-in functions of F_C0 and F_C1, as shown below (Fig. 2):
The membrane employed here is a YSZ (yttria doped zirconia) ceramic–carbonate dual-phase membrane and its permeation flux is calculated as follows:18
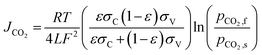 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C, ε the membrane porosity, 0.34, σC and σC are the conductivities of CO32− and O2−, 3.5, and 0.106 S cm−1 at 900 °C, respectively. The permeation flux of CO2 is proportional to the temperature, but it is a logarithmic function of pressure, indicating that it does not significantly influence the CO2 flux.
485 C, ε the membrane porosity, 0.34, σC and σC are the conductivities of CO32− and O2−, 3.5, and 0.106 S cm−1 at 900 °C, respectively. The permeation flux of CO2 is proportional to the temperature, but it is a logarithmic function of pressure, indicating that it does not significantly influence the CO2 flux.
3.3 Reaction kinetics
The reaction of reverse water gas shift adopts a Ni-based catalyst, and its long-term stability is proven at high temperatures of up to 900 °C. The intrinsic kinetics of the catalyst was determined by Wolf et al.,19 as shown in eqn (7) and (8). The equilibrium constant in eqn (9) is taken from the work of Benguerba et al.20 The reaction order with respect to H2 is 0.3, suggesting that it is less influential on the reaction rate than CO2: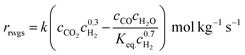 | (7) |
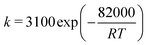 | (8) |
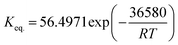 | (9) |
It should be noted that the above reaction rate is based on the catalyst weight, in order to implement it in the simulations, it should be converted into the rate based on the surface area of the membrane:
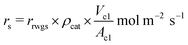 | (10) |
3.4 Model set-up
The simulation set-up details are introduced and explained in this section. To facilitate simulations, the following major assumptions are made:(1) The operation of the membrane reactor is isothermal;
(2) The selectivity of the membrane to CO2 is infinite whereas its selectivities to other gases are zero;
(3) Side reactions of methanation are ignored due to high temperature.
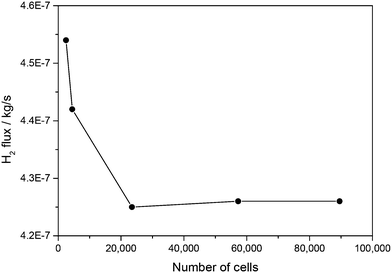
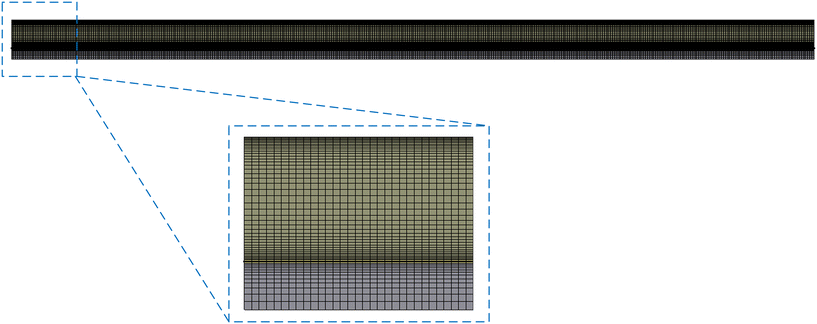
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 469 cell elements are determined as a trade-off between computation effort and solution accuracy. The meshing is achieved by cutting parallel edges into equal numbers of divisions. In order to account for the large gradients of heat and mass transfer within the boundary layers, inflation layers are also added, so the meshes close to the boundaries are denser than those in the inner regions, as shown in Fig. 4.
469 cell elements are determined as a trade-off between computation effort and solution accuracy. The meshing is achieved by cutting parallel edges into equal numbers of divisions. In order to account for the large gradients of heat and mass transfer within the boundary layers, inflation layers are also added, so the meshes close to the boundaries are denser than those in the inner regions, as shown in Fig. 4.
The boundary conditions for the membrane reactor model are detailed in Table 1. The operating pressure does not change the reaction equilibrium of the reverse water gas shift, but higher pressures are beneficial to the productivity and permeation flux of CO2, so the operating pressure was elevated to 30 bar. The outer tube is fed with pure H2 to react with permeated CO2 and the inner tube with a flue gas sourced from a cement plant. The inlet velocities were determined according to the CO2 capture rate and conversion by sensitivity analysis. To reduce thermal stress within the membrane, the inlet temperatures of H2 and flue gas were both 500 °C. The outlet boundary conditions were kept at the default level. The maximum operating temperature of the YSZ dual-phase membrane reactor can be up to 900 °C, which is both favorable for the membrane permeation and reaction, and so the effects of operating temperature were analyzed by setting two temperatures of 800 °C and 900 °C. The reactions were then hooked to the membrane surface to simulate the surface reactions.
| Boundary | Location | Type and value |
|---|---|---|
| Inlets | Feed gas | Velocity inlet: by case study |
| Temperature: 500 °C | ||
| Pure H2 | ||
| Flue gas | Velocity inlet: by case study | |
| Temperature: 500 °C | ||
| Molar fraction: CO2: 0.178, H2O: 0.182, N2: 0.565, O2: 0.075 (ref. 21) | ||
| Outlets | Feed gas | Gauge pressure: 0 bar |
| Backflow turbulent intensity: 5% | ||
| Flue gas | ||
| Backflow turbulent viscosity ratio: 10% | ||
| Walls | Membrane | Heat coupled, reaction enabled |
| Reactor wall | Temperature: 800, 900 °C |
4. Results and discussion
Based on the established membrane reactor concept and the numerical set-ups outlined above, a number of cases were simulated and the performance evaluated.4.1 Conversion and productivity
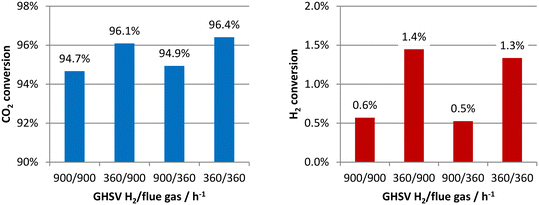
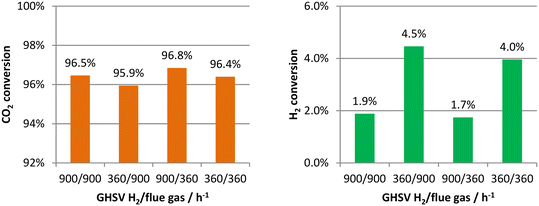
Four cases with different combinations of H2 and flue gas velocities were simulated using the boundary conditions in Table 1. The analyzed range of the gas hourly space velocity (GHSV) was from 360 to 900 h−1, which was determined based on the capture rates of CO2. Later, it will be shown, at the lowest space velocity of 360 h−1, that the CO2 capture rates can be higher than 90%, and so further reducing the space velocity is not necessary. The CO2 and H2 conversions at 900 °C were first analyzed and are presented in Fig. 5. In the left-hand figure, the CO2 conversions are very high in all of the simulated cases. This is not only because of the high reaction temperature. The equilibrium conversion of CO2 at 900 °C with a stoichiometric feed is only 52.9% and the excess amount of H2 also leads to its high conversions. In other words, the high CO2 conversions are partially at the expense of the H2 conversions, as indicated by the low H2 conversions in the right-hand figure. The problem of low H2 conversions can be solved by recycling the unreacted H2. In the left figure, it is also found that the CO2 conversions are mainly affected by the H2 flow rates rather than the flue gas flow rates. Although more H2 input can shift the chemical equilibrium and increase the CO2 conversions, in this membrane reactor concept, H2, in fact, also acts as the sweep gas in addition to as a reactant, and so more CO2 is taken away from the reactor without being reacted at higher H2 flow rates, leading to the lower CO2 conversions.The CO2 conversions at 800 °C are close to those at 900 °C but are still very high, as shown in Fig. 6. Although the converted CO2 at the lower temperature was decreased, the amount of permeated CO2 was as well. The two opposing factors do not significantly reduce the CO2 conversions. The H2 conversions are even lower. A higher temperature is both beneficial to the reaction conversion and CO2 permeation, and so the following analyses only concern the results at 900 °C.
The calculation results of the CO space–time yield (STY) are provided in Table 2. Overall, the CO STY of all cases is not high and does not change significantly at different GHSVs of H2 and flue gas. The first two cases with higher flue gas velocities had slightly higher CO STY. As the CO2 conversions of all the cases approach completion, the CO STY is subject to the amount of permeated CO2. At low flue gas flow rates, the CO2 permeation fluxes are lower due to the lowered CO2 concentration in the flue gas, which will be more specifically analyzed below by ways of CO2 distribution contours. As the reaction temperature and pressure are already high, to change the operating conditions to enhance the CO STY is no longer an efficient way in this circumstance. In the following sections, the CO STY will be improved by modifying the geometric structure of the reactor.
| H2/flue gas/h−1 | CO STY/mol m−3 s−1 | CO2 capture rate |
|---|---|---|
| 900/900 | 0.665 | 39.7% |
| 360/900 | 0.674 | 39.7% |
| 900/360 | 0.608 | 90.6% |
| 360/360 | 0.615 | 90.1% |
As one of the purposes of this membrane reactor concept is to capture CO2 from industrial sources for in situ conversion, another important aspect is the percentage of CO2 captured by membrane permeation. As is also shown in Table 2, the captured CO2 is inversely proportional to the GHSV of the flue gas. At the high flue gas GHSVs, nearly 40% CO2 is captured via membrane permeation. When the GHSV is reduced to 360 h−1, the CO2 capture rate is raised to more than 90%, suggesting that this membrane reactor concept has the potential for efficient CO2 capture. The CO2 flux, according to the flux equation in eqn (6), is a logarithmic function of the CO2 partial pressure ratio between both sides of the membrane, and so the CO2 fluxes are not sensitive to the partial pressure of CO2. This permeation characteristic enables the possibility of high CO2 capture rates from sources even with very low CO2 concentrations using this kind of membrane reactor concept.
4.2 CO2 permeation and reaction rate
The distribution of the CO2 molar fraction is shown in Fig. 7. Here, only the cases with different flow rates of flue gas are presented because the H2 flow rate has little influence on the CO2 distribution. From both contours, the area with a low CO2 molar fraction at 360 h−1 is larger than that at 900 h−1, as indicated by the blue colors, and most of the CO2 is removed. There are no clear boundary layers observed in either contour, as the radius of the flue gas channel is only 7 mm, which is small enough to avoid an obvious concentration polarization in the radial direction. | ||
| Fig. 7 Contours of CO2 molar fractions of the flue gas: (a) H2/flue gas = 900/900; (b) H2/flue gas = 900/360. | ||
The CO2 fluxes along the membrane surface are shown in Fig. 8(a). Again, only the fluxes at flue gas GHSVs of 900 and 360 h−1 are presented in the figure. The CO2 fluxes both increase along the membrane surface in the front end section of the reactor, and the two lines overlap. After a critical point, the trends of the two lines progress differently. The blue line at 900 h−1 continues to slightly increase and remains stable for some distance, and then gradually decreases in the rear end of the reactor. However, the yellow line at 360 h−1 decreases drastically after reaching a maximum point. An overlapping regime and a divergent one are differentiated. In the overlapping regime, the CO2 fluxes are controlled by the inlet temperature. The inlet temperature of the flue gas is lower than the reactor wall temperature and must be heated by the wall, and so the CO2 fluxes increase first. This regime corresponds to the areas in red in the above contours. As ever more CO2 is permeated, the limiting factor becomes the CO2 concentration in the divergent regime. When the flow rate of flue gas is low, the CO2 supply is less and its concentration drops very rapidly. The divergent region corresponds to the areas in blue in the above contours. The corresponding surface reaction rates shown in Fig. 8(b) follow identical trends to those of the CO2 fluxes. On the one hand, the reaction rates, according to the kinetics in eqn (7), are more sensitive to the CO2 concentration as the reaction order with respect to CO2 is higher compared to H2. On the other hand, the excess amount of H2 renders its concentration on the membrane surface at a high and stable level and its influence on the reactions rates much less significant. Thus, the reaction rates are overwhelmingly dominated by the CO2 fluxes. Taking the CO2 and H2 conversions, as well as the reaction kinetics together, it can also be found that the limiting factor to the CO STY is the CO2 permeation flux, and the conversions and productivity will both be improved if the CO2 flux is increased.
 | ||
| Fig. 8 (a) CO2 fluxes along the membrane surface at different GHSVs of the flue gas; and (b) corresponding surface reaction rates along the membrane surface. | ||
The average CO2 fluxes of the four cases are presented in Table 3. The CO2 fluxes with higher flue gas velocities are higher but do not change with the H2 space velocity. The calculated CO2 fluxes are much higher than the value of 0.0153 mol m−2 s−1 at the same temperature measured by Dong et al.22 This is not only because of the higher operating pressure. More importantly, the presence of the reaction quickly consumes the permeated CO2 and reduces the partial pressure of CO2, and thus facilities the transport of CO2 across the membrane, which suggests the advantage of coupling of CO2 capture and conversion using membrane reactors.
| GHSV H2/flue gas/h−1 | 900/900 | 360/900 | 900/360 | 360/360 |
|---|---|---|---|---|
| CO2 flux mol m−2 s−1 | 0.0289 | 0.0289 | 0.0264 | 0.0262 |
4.3 Effects of geometry characteristics
It was previously mentioned that changing the operating conditions is not an efficient way to increase the CO STY. In this section, the enhanced CO productivity will be realized by increasing the ratio of the membrane area to the reactor volume (A/V). Neglecting the thickness of the membrane, the A/V is mathematically expressed as A/V = 2r1/(r22 – r12), where r1 and r2 are the radius of the reactor geometry. The A/V has an important feature in that it only contains the radius and is irrelevant to the reactor's length. It can be changed by adjusting r1, r2 or both. Here, changing the A/V is realized by reducing the dimension of r2 in Fig. 1 from 25 to 15 mm, so that the membrane area is not changed but the reactor volume is reduced, and the resulting A/V is increased from 24.3 to 79.5.The resulting CO2 and H2 conversions are shown in Fig. 9. Comparing the CO2 conversions with those in Fig. 4, no large difference is observed because the amount of permeated CO2 is virtually unchanged. However, one difference is that the CO2 conversions are lower at the lower H2 flow rates, which is a result of two competing factors: although higher H2 space velocities will take more CO2 away from the reactor without being reacted, higher H2 flow rates shift the reaction equilibrium and therefore increase the CO2 conversions. The H2 conversions are much increased, as the H2 input is less.
 | ||
| Fig. 9 CO2 and H2 conversions of the CO2 permeable membrane reactor at 900 °C and 30 bar with A/V = 79.5. | ||
The CO STY and CO2 capture rates are presented in Table 4. Compared to the original geometry shown in Table 2, the CO STY with the increased A/V is more than tripled as a result of the increased A/V. The reduced reactor volume also makes its design of the reactor more compact and its space more effectively utilized. The CO2 capture rates in the table are slightly lower than those with the original geometry, as H2 itself is also the sweep gas and the CO2 permeation resistance is stronger at a low H2 sweep velocity.
| H2/flue gas/h−1 | CO STY/mol m−3 s−1 | CO2 capture rate |
|---|---|---|
| 900/900 | 2.20 | 39.4% |
| 360/900 | 2.03 | 36.5% |
| 900/360 | 2.01 | 89.8% |
| 360/360 | 1.87 | 84.0% |
The surface-averaged CO2 permeation fluxes are calculated and provided in Table 5, The values in the table are slightly decreased compared to those with the original A/V ratio in Table 3, as the H2 input is less and the permeation resistance of CO2 is increased. In summary, changing the A/V can increase the CO STY, whereas the CO2 capture rates and conversions can be maintained for this membrane reactor concept.
| GHSV H2/flue gas/h−1 | 900/900 | 360/900 | 900/360 | 360/360 |
|---|---|---|---|---|
| CO2 flux mol m−2 s−1 | 0.0287 | 0.0266 | 0.0261 | 0.0244 |
5. Conclusions
The development of CO2-permeable membranes has enabled the possibility of integrating CO2 capture and conversion into a single device. This study developed a novel membrane reactor concept in which a ceramic–carbonate dual-phase membrane was used with a catalyst coating on its surface. The membrane reactor featured a tubular design, wherein the inner tube was for the passage of the flue gas to provide a CO2 source and the outer tube was for the conversion of the permeated CO2 by the reverse water gas shift reaction. The membrane reactor's performance was evaluated based on CFD simulations and the major conclusions are summarized below:(1) High CO2 conversions of over 95% were achieved, which is a result of the high reaction temperature and large flow rate of H2. The low H2 conversions were simply due to the excess amount of H2 provided and can be increased by recycling the unreacted H2.
(2) The low space–time yield of the CO of the membrane reactor with the original geometry was caused by the limited CO2 permeation flux and large reactor volume.
(3) The CO2 capture rates can be up to 90%, which suggests the capability of efficient CO2 capture from sources with low CO2 concentrations of this membrane reactor concept.
(4) The CO space–time yield can be improved in compact designs by increasing the ratio of the membrane surface area to the reactor volume. This method is efficient and generally applicable, as it can raise the CO productivity and will not reduce CO2 conversions and capture rates.
The advantage of integrating CO2 capture and conversion using membrane reactors was clearly demonstrated in this study. Although the reverse water gas shift reaction was used as an example for the conversion of CO2 in this study, the applications of this developed membrane reactor concept should not be limited to this reaction and any other reaction for integrated CO2 capture and conversion can be considered.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Guangzhou Elite Project (JY201801) for the scholarship supporting the PhD project of Hong Huang.References
- S. M. Kim, P. M. Abdala, M. Broda, D. Hosseini, C. Copéret and C. Müller, ACS Catal., 2018, 8, 2815–2823 CrossRef CAS.
- J. Hu, P. Hongmanorom, V. V. Galvita, Z. Li and S. Kawi, Appl. Catal., B, 2021, 284, 119734 CrossRef CAS.
- S. Tian, F. Yan, Z. Zhang and J. Jiang, Sci. Adv., 2019, 5, eaav5077 CrossRef CAS PubMed.
- M. S. Duyar, M. A. A. Treviño and R. J. Farrauto, Appl. Catal., B, 2015, 168, 370–376 CrossRef.
- H. Sun, J. Wang, J. Zhao, B. Shen, J. Shi, J. Huang and C. Wu, Appl. Catal., B, 2019, 244, 63–75 CrossRef CAS.
- C. M. Jens, L. Müller, K. Leonhard and A. Bardow, ACS Sustainable Chem. Eng., 2019, 7, 12270–12280 CAS.
- H. Machida, T. Esaki, T. Yamaguchi and K. Norinaga, ACS Sustainable Chem. Eng., 2020, 8, 8732–8740 CrossRef CAS.
- M. Anderson and Y. S. Lin, AIChE J., 2013, 59, 2207–2218 CrossRef CAS.
- J. A. Fabián-Anguiano, C. G. Mendoza-Serrato, C. Gómez-Yáñez, B. Zeifert, X. Ma and J. Ortiz-Landeros, Chem. Eng. Sci., 2019, 210, 115250 CrossRef.
- T. Chen, Z. Wang, L. Liu, S. Pati, M. H. Wai and S. Kawi, Chem. Eng. J., 2020, 379, 122182 CrossRef CAS.
- J. Fang, X. Jin and K. Huang, J. Membr. Sci., 2018, 549, 142–150 CrossRef CAS.
- Z. Bian, H. Xia, W. Zhong, B. Jiang, Y. Yu, Z. Wang and K. Yu, Energy Convers. Manage., 2021, 235, 113989 CrossRef CAS.
- Z. Liu, Z. Bian, Z. Wang and B. Jiang, React. Chem. Eng., 2022, 7, 450–459 RSC.
- M.-S. Salehi, M. Askarishahi, F. Gallucci and H. R. Godini, Chem. Eng. Process., 2021, 160, 108264 CrossRef CAS.
- S. A. M. Said, D. S. A. Simakov, E. M. A. Mokheimer, M. A. Habib, S. Ahmed, M. Waseeuddin and Y. Román-Leshkov, Int. J. Hydrogen Energy, 2015, 40, 3158–3169 CrossRef CAS.
- A. Inc, ANSYS Fluent Theory Guide, 2016 Search PubMed.
- H. Huang, R. C. Samsun, R. Peters and D. Stolten, Chem. Eng. Sci., 2022, 252, 117284 CrossRef CAS.
- J. L. Wade, C. Lee, A. C. West and K. S. Lackner, J. Membr. Sci., 2011, 369, 20–29 CrossRef CAS.
- A. Wolf, A. Jess and C. Kern, Chem. Eng. Technol., 2016, 39, 1040–1048 CrossRef CAS.
- Y. Benguerba, L. Dehimi, M. Virginie, C. Dumas and B. Ernst, React. Kinet., Mech. Catal., 2015, 115, 483–497 CrossRef CAS.
- W. Schakel, C. R. Hung, L.-A. Tokheim, A. H. Strømman, E. Worrell and A. Ramírez, Appl. Energy, 2018, 210, 75–87 CrossRef CAS.
- X. Dong, H.-C. Wu and Y. S. Lin, J. Membr. Sci., 2018, 564, 73–81 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |