Open Access Article
Open Access ArticleTheoretical investigation of C1–C4 hydrocarbons adsorption and separation in a porous metallocavitand†
Biswajit Mohanty a and
Gopal Avashthi
a and
Gopal Avashthi *b
*b
aDepartment of Chemistry, Central University of Haryana (CUH), Mahendergarh 123031, Haryana, India
bSchool of Sciences, P P Savani University, NH-8, GETCO, Near Biltech, Kosamba, 394125, Surat, Gujarat, India. E-mail: gopalavashthi@gmail.com
First published on 29th November 2022
Abstract
The purification of light hydrocarbons is one of the most important chemical processes globally which consumes substantial energy. Porous materials are likely to improve the efficiency of the separation process by acting as regenerable solid adsorbents. To investigate such translational systems, the underlying mechanism of adsorption in the porous materials must be taken into account. Herein we report the adsorption and selective separation of C1–C4 hydrocarbons in the coinage metal-based macrocyclic metallocavitand Pillarplex, which exhibits excellent performance in the adsorption of CH4 at the ambient conditions with a binding energy of −17.9 kcal mol−1. In addition, the endohedral adsorption of C2–C4 hydrocarbon is impressive. The CH4, C2H4, C3H4, and 1,3-butadiene have potential uptake of 2.57, 4.26, 3.60, and 2.95 mmol g−1, respectively at ambient conditions are highest from their respective isomers. Selective separation of C1–C4 hydrocarbons is studied using ideal adsorption solution theory demonstrating its potential for one-step purification of C1–C3 hydrocarbons.
Introduction
The paramount interest in fossil fuels continues in the petrochemical and automobile industry despite their adverse effect on the environment.1,2 Using clean energy technology rather than fossil fuels and capturing greenhouse gases are the translational method to mitigate global warming.3 Natural gas (NG), mainly composed of CH4 can swap the demand for fossil fuels due to its abundance, high energy density, low CO2 emission, and higher figure of merit for on-board applications.4,5 The other varying components of NG are C2H6, C3H8, and C4H10 are used as the basic feedstock in the petrochemical industry, thus it is essential to separate these hydrocarbons (HCs) from CH4 for absolute utilization.2 Conventional methods of adsorption using activated carbons, zeolites, and separation by cryogenic distillation are energy-intensive processes and require harsh working conditions such as high pressure and/or low temperature.6 Therefore, a high throughput cost-effective storage media is required for optimal adsorption and separation of these HCs.Molecular recognition supramolecular chemistry sets a new paradigm to study the adsorption and selective separation of guest molecules via the host–guest mechanism. The cucurbit[n]uril (n = 5,6,7,8,10) and pillar[n]arene (n = 5,6) are versatile macrocyclic molecules and ideal hosts in the supramolecular domain.7,8 Nau et al. studied the C1–C6 HCs within cucurbit[6]urils (CB[6]) for gas sensing and reveals that CB[6] is ideal for isobutene and cyclopentane adsorption.9 Coskun et al. studied the propane/methane separation using pillar[5]arene based conjugated microporous polymer via host–guest chemistry and observed the facile separation of propane from the natural gas mixture.10 Soft porous crystals of [2+3] imide based organic cage (NKPOC-1) and their HC adsorption phenomenon were investigated by Zhang et al. reveal the α-phase of NKOPC-1 selectively adsorbs propyne over propylene and propane at 298 K/1 bar condition.11
However, such organic hosts are restricted in large-scale employment due to their troublesome synthetic separation, purification, and post-synthetic modifications.12 Other than organic hosts, metal–organic frameworks (MOFs) are profound against guest binding using the supramolecular binding approach. The higher storage density of acetylene over ethylene has been studied by Schröder et al. using functionalized MOF by supramolecular binding and separation approach.13 Selective separation of C2–C4 HCs in the Zn2 (sdc)2(bpe) (sdc = 4,4′-stilbenedicarboxylate, bpe = 1,2-bis(4-pyridyl)ethane) MOF has been studied by Li et al., claimed that C2 HC has higher selectivity over C3 and C4.14 Although MOFs are an attractive candidate for HCs capture and separation, their stability remains questionable. The limited stability against reactive species such as water is a major concern as they can debase the MOF during the in-service events.15 The akin chemical properties, polarizability, and kinetic diameters of HCs (CH4, C2H6, C3H8, C2H2 have kinetic diameters of 3.8, 4.4, 4.9, 3.3, 4.2 Å respectively) coerce the complications for HC separations.15,16 As all the light HCs are adsorbent dependent, it is imperative to develop suitable adsorbents for effective HCs separation. Early reports on metal coordinated cavitands, macrocycles, and cages are the flawless supramolecular host with exceptional guest binding effect.17,18 The coinage metal-based organometallic host has potential in the post-synthetic modification, simple synthetic pathway, tunable cavity, tailor-made pore surface, and high stability against air and water.19 Pöthig and Altmann synthesized a well-defined tubular metallocavitand with Au(I) metal center; Pillarplex (PPX) analogous to pillar[5]arenes readily accommodate linear guests with high selectivity.20
To address this challenge, we have investigated the adsorption of small HCs potentially with low carbon content (C1–C4) within the cavity of the PPX. Density functional theory (DFT) is employed to determine the electronic structure and stability of the system. The natural bond orbital (NBO) charge transfer method is used to explore the electronic transfer within the host–guest system. The nature of the interaction between HCs and PPX is analyzed using a non-covalent index (NCI). The individual components of binding energy are computed using the energy decomposition analysis (EDA). The maximum uptake of HCs is studied using the Grand canonical Monte Carlo (GCMC) simulation at various temperatures from 77–340 K and the pressure range from 0.1–10 bar. The isosteric heat of adsorption is computed to determine the thermodynamic stability of the complex. Further, the selectivity of HCs from their counterpart mixtures is studied using ideal adsorption solution theory (IAST) for selective separation using PPX as a separator channel.
Results and discussion
Geometries and energetic
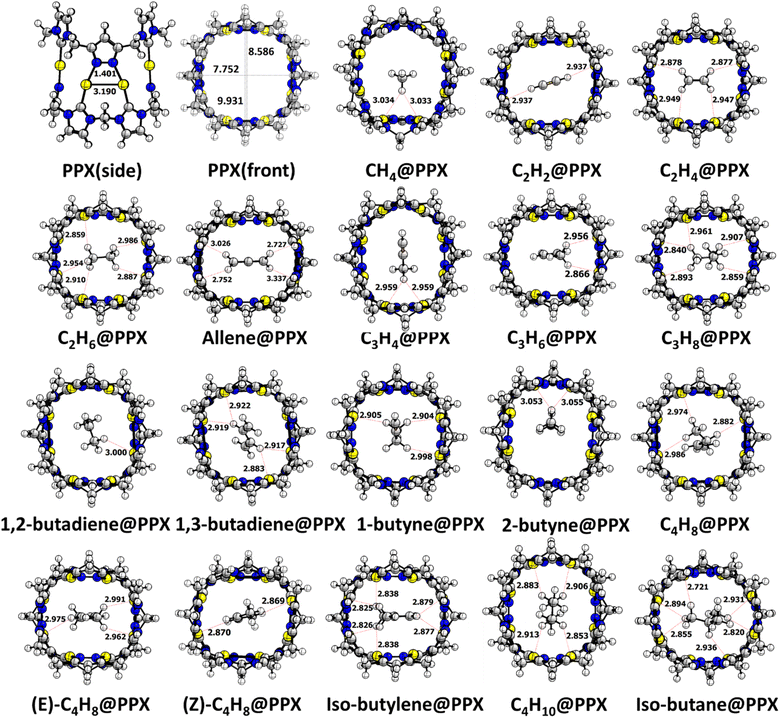
The coherent bond properties of optimized PPX with the experimental report authenticates the befitting of the theoretical approach. The height and width of the PPX are 11.585 Å (expt. 11.700 Å) and 7.658 Å respectively measured between the distance of Au–Au positioned opposite to each other as shown in Fig. S1.† The Au–Au distance is 3.190 Å is congruent to the reported value (expt. 3.005 Å). The existing distance evidence the aurophilic interaction where the Au(I) atoms are packed at a distance that is 0.130 Å shorter than their van der Waals radii (Au: 1.66 Å).The depth of the cavity is 3.785 Å longer than the analogous pillar[5]arene (7.800 Å).20 The structural resemblance with pillar[5]arene rationale PPX as a potential host and required further investigations.
The low carbon content HCs starting from CH4 to C4H8 (C1–C4) and their isomers are studied extensively using PPX to understand the adsorption behavior. The stable HC@PPX complex is discerned by swapping the position and orientation of HCs within the PPX using the B97D2/LanL2DZ level of theory. The potential stable structure is shown in Fig. 1. Since the reports on the gold phosphine complexes were established as the potential catalyst, much attention has been gained in recent times to its structural conformations.21,22 It was found that the excellency of properties arises owing to Au⋯H–C distances which are remarkably short and even shorter than their van der Waals radii (2.86 Å) as well as hydrogen bonds.23
An investigation has been carried out comprising the Au⋯H–C interactions. In CH4@PPX, The CH4 resides closer to the Au atom with a distance of 3.033 Å. C2H2 was placed horizontally symmetrical fashion within the cavity with an Au⋯H–C distance of 2.937 Å. C2H4 and C2H6 molecules are in the horizontally inclined position with multiple Au⋯H–C interactions and a noticeable bond length of less than 3 Å is observed. In C3 HCs, Au⋯H–C interactions are impressive while in allene@PPX and C3H8@PPX some Au⋯H–C distances are found lesser than their van der Waals radii. C4 HCs are well buried inside the cavity of PPX and the majority of Au⋯H–C interactions are in the region of 2.721 to 3.054 Å which pronounce a weak hydrogen bond type interaction. In isobutylene and isobutane, the Au⋯H–C interactive distances are much lower compared to its isomers. The presence of such interactions influences the polarization effect by altering the bond length of HCs within the cavity. Trivial changes in bond lengths are observed for all the encapsulated HCs and details are given in Table S1.† Upon entrapment of HCs, the structural deformation is observed in the PPX, where the Au–Au distance of HC@PPX gets reduced to some extent. Conversely, the Au–Au bond length in allene@PPX (0.019 Å) and isobutane@PPX (0.055 Å) is higher than that of PPX as shown in Table S2.† The unusual Au–Au bond length in allene and isobutane is due to its stronger Au⋯H–C interaction and the distance is 2.727 and 2.721 Å, respectively which is lower than their van der Waal radii. Nonetheless, the N⋯H–C interactions can't be ignored which plays a crucial role in the HCs uptake via hydrogen bonding. Desiraju et al. established the N⋯H–C interaction as a hydrogen bond a weak one, largely electrostatic with a distance between 2.0–3.0 Å and it depends upon the C–H acidity and the –N basicity.24 In HC@PPX the more acidic π-character containing HCs such as allene (2.427 Å), C3H4 (2.616 Å), 1,2-butadiene (2.591 Å), C4H8 (2.547 Å), C4H10 (2.621 Å) and isobutane (2.348 Å) are shows hydrogen bonding while others are in electrostatic regime with N⋯H–C distances ca. 3.0 Å. The Au⋯H–C and N⋯H–C distances are shown in Fig. 2.
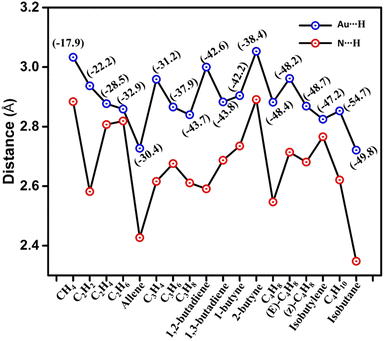 | ||
| Fig. 2 The Au⋯H and N⋯H bond distances in the HC@PPX complex, The net binding energy values are in parenthesis inset in the figure. | ||
Notable interactions exist in the HC@PPX complex, it is obvious to prevail a structural distortion in both PPX and HCs. The deformation energy (DE) is calculated to determine the deformation of PPX upon complexation. The deformation energy (DE) is the energy difference between the total energy of the optimized guest and host molecule and energy after the conformation deformation occurred during the encapsulation process. DE of host and guest is calculated as follows,
| DE (host) = E(host)optsp − E(host)opt |
| DE (guest) = E(guest)optsp − E(guest)opt |
The DE of PPX is higher than the HCs given in Table 1. The DE of PPX in allene@PPX (3.7 kcal mol−1) is the highest and C4H8@PPX (0.4 kcal mol−1) is the least among the studied system. The DE of PPX, in C2H2@PPX, is 1.1 kcal mol−1 and 0.2 kcal mol−1 higher than that of C2H4@PPX and C2H6@PPX and the ease of π electron transfer from HC to the metal center is C2H2 > C2H4 > C2H6. The PPX in C3H8@PPX exhibits DE of 1.6 kcal mol−1 is 1.2, 1.7, and 2.1 kcal mol−1 lower than that of C3H6, C3H4, and allene, respectively due to the unavailability of π electrons. Owing to the presence of orthogonal cumulative π bonds in allene, its complex procures higher deformation. The unsaturated C3H6 and C3H4 amplify the significant π-electron transfer to PPX resulting in higher deformation of PPX in the complex. In C4 isomers the DE of 1,2-butadiene is 0.6 kcal mol−1 higher than 1,3-butadiene and 2-butyne is 2.0 kcal mol−1 higher than 1-butyne. The Z-isomer of C4H8@PPX experiences 0.1 kcal mol−1 higher DE than the E-isomer. The DE of isobutylene@PPX and isobutane@PPX is 3.0 and 1.2 kcal mol−1 higher than C4H8@PPX and C4H10@PPX isomers, respectively. DE unveils the structural distortion of PPX is simulated by the unsaturated HC species. The DE of HCs in the HC@PPX complex is lesser than 1.0 kcal mol−1. Isobutane undergoes maximum distortion with DE of 0.8 kcal mol−1 followed by C4H8 (0.594 kcal mol−1) and C2H2 is least given in Table S3.† As the maximum deformation occurs in guest C4H8, in its complex PPX deforms least. The higher distortion of isobutane is reflected by its bulkier size and larger van der Waals sphere whereas the C2H2 has the least due to its horizontal orientation within the cavity of PPX.
| Gas | ΔE | BSSE | ΔE + ZPE | DE | ΔG298 | ΔH298 |
|---|---|---|---|---|---|---|
| a All the energy units are in kcal mol−1. | ||||||
| CH4 | −17.9 | −18.0 | −17.2 | 1.0 | −8.4 | −16.8 |
| C2H2 | −22.2 | −19.1 | −19.6 | 1.1 | −13.3 | −19.8 |
| C2H4 | −28.5 | −23.5 | −26.9 | 0.9 | −15.6 | −26.8 |
| C2H6 | −32.9 | −27.4 | −31.4 | 0.9 | −19.6 | −31.3 |
| Allene | −30.4 | −26.3 | −28.1 | 3.7 | −14.9 | −28.3 |
| C3H4 | −31.2 | −27.6 | −29.5 | 3.3 | −17.1 | −29.4 |
| C3H6 | −37.9 | −34.1 | −36.1 | 2.8 | −23.9 | −36.0 |
| C3H8 | −43.7 | −38.9 | −41.8 | 1.6 | −28.6 | −41.8 |
| 1,2-Butadiene | −42.6 | −38.2 | −40.9 | 1.6 | −28.1 | −40.7 |
| 1,3-Butadiene | −43.8 | −40.8 | −41.6 | 1.0 | −28.9 | −41.5 |
| 1-Butyne | −42.2 | −36.7 | −40.6 | 0.9 | −27.8 | −40.4 |
| 2-Butyne | −38.4 | −34.0 | −36.8 | 2.9 | −23.8 | −36.7 |
| C4H8 | −48.4 | −42.9 | −46.1 | 0.4 | −32.5 | −46.1 |
| (E)-C4H8 | −48.2 | −42.9 | −45.9 | 3.1 | −32.6 | −46.0 |
| (Z)-C4H8 | −48.7 | −40.3 | −46.6 | 3.2 | −33.4 | −46.5 |
| Isobutylene | −47.2 | −41.8 | −44.3 | 3.4 | −29.7 | −44.6 |
| C4H10 | −54.7 | −48.6 | −52.6 | 1.5 | −38.9 | −52.6 |
| Isobutane | −49.8 | −46.9 | −46.6 | 2.7 | −30.2 | −45.7 |
The binding energy (ΔE), BSSE, and ZPE corrected ΔE (ΔE + ZPE) are computed to determine the interaction strength between HC and PPX as given in Table 1. The ΔE is the energy difference between the HC@PPX and the sum of individual energy components of HC and PPX as expressed in eqn (1).
| ΔE = EHC@PPX − [EHC + EPPX] | (1) |
The ΔE value portrays the interaction of HCs within PPX as fairly high owing to its soft interaction exerted between the Au(I) and HCs unravelled by the Pearson HSAB principle. The CH4 molecule strongly binds to PPX with a ΔE value of −17.9 kcal mol−1. The CH4 uptake capacity of PPX is exceptionally higher than many of the reported systems such as MOF-5 (−4.51 kcal mol−1),25 NI-MOF-74 (−7.78 kcal mol−1),26 Cu24(m-BDC)24(−8.27 kcal mol−1),27 TpPa1 COF (−5.39 kcal mol−1),28 Graphdiyne (−5.18 kcal mol−1)29 etc. The ultrahigh binding energy of CH4 in PPX is due to the strong interaction between the 6s levels of Au(I) and 2a1 orbital of CH4 and the charge transfer through level hybridization from CH4 to Au(I) and not via Au(I) unoccupied orbitals.30
An upraised ΔE value of C2 HCs observed with a lowering in the percentage of s character unveils the stability of C2H6 over C2H2 and C2H4 with ΔE of −32.9 kcal mol−1 is 10.7 and 4.4 kcal mol−1 higher than C2H2 and C2H4 respectively. The higher binding energy of the C2H6 is due to the mixing of the occupied π−(CH3) orbitals with the Au(I) orbitals resulting in an electron charge donation from C2H6 to Au(I) and a partial de-occupation of the π−(CH3).31 The partial de-occupation is reflected in the lowest unoccupied molecular orbital (LUMO) that is formed by the interaction of the occupied π−(CH3) of ethane and unoccupied s-orbitals of Au(I). The C2H4 stabilizes the π mode adsorption and strengthens the Au–C bond by readily balancing between donation and back-donation of electrons which strongly influence the molecular adsorption.32 The C2H2 is oriented in such a fashion that it experiences interaction with the Au(I) px orbital parallel to it via dative interaction by the Dewar–Chatt–Duncanson scheme resulting donation of filled πy orbitals of the ligands into the vacant s orbitals of the metal atoms and the back donation.33 In a confined PPX region, the overlap of orbitals experiences repulsions, hence a steady decline in energy is observed. The binding energy of C2 HCs in PPX is higher than reported benchmark study such as PCN-245 (C2H4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H6: −5.5 kcal mol−1
C2H6: −5.5 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −6.5 kcal mol−1),34 HKUST-1 (C2H4: −5.5 kcal mol−1),35 IRMOF-8 (C2H4
−6.5 kcal mol−1),34 HKUST-1 (C2H4: −5.5 kcal mol−1),35 IRMOF-8 (C2H4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H6: −8.4 kcal mol−1
C2H6: −8.4 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −8.4 kcal mol−1),36 CuBTC(C2H4: −7.1 kcal mol−1),37 Ni(BODC)(TED) (C2H4
−8.4 kcal mol−1),36 CuBTC(C2H4: −7.1 kcal mol−1),37 Ni(BODC)(TED) (C2H4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H6: −6.7 kcal mol−1
C2H6: −6.7 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −7.9 kcal mol−1),38 RPM3-Zn (C2H6: −12.4 kcal mol−1),39 Fe-MOF-74(C2H2
−7.9 kcal mol−1),38 RPM3-Zn (C2H6: −12.4 kcal mol−1),39 Fe-MOF-74(C2H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H4
C2H4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H6: −12.3 kcal mol−1
C2H6: −12.3 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −12.3 kcal mol−1
−12.3 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −8.8 kcal mol−1),40 MUF-15 (C2H4
−8.8 kcal mol−1),40 MUF-15 (C2H4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H6: −8.4 kcal mol−1
C2H6: −8.4 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −8.8 kcal mol−1),41 Fe-MOF-74(C2H2
−8.8 kcal mol−1),41 Fe-MOF-74(C2H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H4
C2H4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C2H6: −6.3 kcal mol−1
C2H6: −6.3 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −5.6 kcal mol−1
−5.6 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −6.1 kcal mol−1),42 etc.
−6.1 kcal mol−1),42 etc.
The ΔE value of C3 HCs is also remarkable where C3H8 possesses maximum binding energy of −43.7 kcal mol−1 which is 13.3, 12.5 and 5.8 kcal mol−1 higher than of allene, C3H4, and C3H6, respectively. The absence of π-electron density in C3H8 portrays higher ΔE value while the existence of orthogonal π-electron density in allene reduce the binding strength to −30.4 kcal mol−1. The ΔE difference in allene/C3H4 (0.8 kcal mol−1), allene/C3H6 (7.5 kcal mol−1), C3H4/C3H6 (6.7 kcal mol−1) is substantial enough for facile separation of individual C3 HCs from their respective mixtures. The obtain ΔE is substantially higher than that of CuBTC (C3H8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H6: −10.8 kcal mol−1
C3H6: −10.8 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −11.1 kcal mol−1),43 Fe-MOF-74 (C3H8
−11.1 kcal mol−1),43 Fe-MOF-74 (C3H8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H6: −9.9 kcal mol−1
C3H6: −9.9 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −14.3 kcal mol−1),40 pyr@Cu-BTC (C3H8
−14.3 kcal mol−1),40 pyr@Cu-BTC (C3H8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H6: −8.7 kcal mol−1
C3H6: −8.7 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −11.6 kcal mol−1),44 UiO-66 (C3H8: 9.9 kcal mol−1),45 Cu-DTO (C3H8
−11.6 kcal mol−1),44 UiO-66 (C3H8: 9.9 kcal mol−1),45 Cu-DTO (C3H8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H6: −14.0 kcal mol−1
C3H6: −14.0 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −33.5 kcal mol−1),46 tpt-Mg-MOF-74 (C3H8: 8.15 kcal mol−1),47 WOFOUR-1-Ni (C3H8
−33.5 kcal mol−1),46 tpt-Mg-MOF-74 (C3H8: 8.15 kcal mol−1),47 WOFOUR-1-Ni (C3H8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C3H6: −11.9 kcal mol−1
C3H6: −11.9 kcal mol−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) −11.3 kcal mol−1)48 etc.
−11.3 kcal mol−1)48 etc.
Furthermore, C4 HCs and their ten isomers are investigated as their contributions to the natural gas mixtures cannot be ignored. C4H10 interacts strongly with an effective binding energy of −54.7 kcal mol−1 whereas the binding strength of 2-butyne is least (−38.4 kcal mol−1). The notable energy difference of 6.3 kcal mol−1 between C4H10 and C4H8 is ideal for the mainstream separation of their mixture. 1,3-butadiene (−43.8 kcal mol−1) exhibits higher binding strength than 1,2 butadiene (−42.6 kcal mol−1) and the binding energy of 1-butyne is −42.2 kcal mol−1 is 3.8 kcal mol−1 higher than 2-butyne. The energy difference between E-C4H8/Z-C4H8 and isobutane/Isobutylene is noteworthy. In general, the binding energy values of HC@PPX are higher than the ever-studied system. Hence, PPX can be a good material for selective adsorption and separation of light HCs. To reduce the errors associated with total binding energy, BSSE and ZPE corrected binding (ΔE + ZPE) energy values are taken into account and no such perceived changes are noticed.
To explore the stability of PPX + HC → HC@PPX inclusion complex, Gibbs free energy (ΔG) has been computed for HC@PPX. The ΔG value for all the studied complexes is found to be negative, proclaiming HC@PPX is exergonic. The higher ΔH reveals the stability of the system is enthalpy driven. The calculated ΔG and ΔH values are given in Table 1. The ΔG values of C1–C4 HCs spaned from −8.4 to −38.9 kcal mol−1 while the ΔH values are in the range of −16.8 to −52.6 kcal mol−1. The entropy change (ΔS) has a negligible effect on the complexation given in Table S3.† Both the ΔG and ΔH values are the least for CH4@PPX while the maximum for C4H10@PPX. Noteworthy ΔG values in C2 and C3 suggest PPX as a material of interest for C2/C3 HCs separation. A trivial ΔG value is observed in C4 HCs, Thus the separation of C4 HC needs an external potential.
To understand the effect of the inter-ligand and cooperativity within the cavity, for example, we have considered some of the π-bonded molecules. It is noticed that the PPX host accommodates only two HC within the cavity while the third one residing the open face of the PPX. Within the cavity C2H2, C2H4, allene, C3H4, 1-butyne, and 2-butyne experience π⋯π interaction at a distance of 3.189, 3.340, 3.364, 3.280, 3.506 and 3.405 Å respectively. The large size of C3H6, and other C4 HC dimers exerted by CH⋯π interactions. The CH⋯π distance in C3H6 is 2.781 Å whereas in 1,2-butadiene, 1,3-butadiene, 2-butyne, C4H8, (E)-C4H8, (Z)-C4H8 and isobutylene, the distance is 3.022, 2.799, 2.526, 2.743, 2.517, 2.743 and 2.513 Å respectively. The π interaction impetus the enhanced adsorption of HCs within the confined cavity.
The cooperative effect is an interesting factor in host–guest supramolecular interaction; therefore, we have computed the cooperative adsorption binding energy (CABE) and adsorption binding energy (ABE). The CABE is calculated by taking out the HC from the PPX host cavity, and single point calculations were carried out with the same orientations as obtained from the PPX cavity and the ABE is evaluated by relaxing the structure obtained from the HC@PPX complex. The ABE of HC@PPX is higher than the CABE value which suggests a cooperative interaction exists in the host–guest system. The CABE, ABE, and C–C bond distance of relax and constrained dimer is shown in Fig. S2.† The relax dimer bond distance is higher than the constrained dimer which claims the cooperative interaction engendered within PPX. C3H4, 1-butyne, 2-butyne, and (E)-C4H8 exhibit higher cooperativity interaction with an energy value of 5.1, 6.5, 6.0, and 8.4 kcal mol−1. Thus, it is well observed that the HCs adsorption within the PPX is asserted by the cooperative effect.
Natural gas sweetening is another stumbling block to the industrial separation of natural gas and acidic gas such as CO2, and H2S. Hence we have studied CO2 and H2S adsorption by PPX using B97D2/LanL2DZ level of theory. The ΔE of CO2 and H2S is −17.6 and −21.9 kcal mol−1 respectively while CH4, C2H6, C3H8 and C4H10 is −17.9, −32.9, −43.7 and −54.7 kcal mo, respectively. The ΔE of an alkane is higher than acidic gas, thus alkane is the superior adsorbate over CO2 and CS2. The ΔG298 value for CO2, H2S is −9.0 and −10.0 kcal mol−1 whereas CH4, C2H6, C3H8 and C4H10 are −8.4, −19.6, −28.6 and −38.9 kcal mol−1, respectively. Hence it will be difficult to separate CH4 in presence of an excessive amount of CO2 and CS2 as the complexation is exergonic and the complexation will be CO2@PPX and CS2@PPX instead of CH4@PPX.
| CH4@PPX + CO2 → CO2@PPX + CH4 ΔG = −0.6 kcal mol−1 |
| CH4@PPX + CS2 → CS2@PPX + CH4 ΔG = −1.6 kcal mol−1 |
The C2–C4 hydrocarbon separation can be easily separated in the presence of CO2 and CS2 as the substitution reaction undergoes endergonic.
| C2H6@PPX + CO2/CS2 → C2H6@PPX + CO2/CS2, ΔG = 10.6/9.6 kcal mol−1 |
| C3H8@PPX + CO2/CS2 → C3H8@PPX + CO2/CS2, ΔG = 19.6/18.6 kcal mol−1 |
| C4H10@PPX + CO2/CS2 → C4H10@PPX + CO2/CS2, ΔG = 29.9/28.8 kcal mol−1 |
The enthalpy contribution in CO2, CS2, CH4, C2H6, C3H8 and C4H10 is −16.3, −21.3, −19.8, −28.3, −40.7, and −52.6 kcal mol−1, respectively imparts the reaction is enthalpy driven and is ideal to use PPX for the separation of HCs except for CH4 in presence of acidic gases.
Electronic charge transfer
Natural bond orbital (NBO) analysis has been performed to articulate the charge transfer between the host–guest system. An apparent charge transfer is discerned from guest HCs to PPX and the ease of charge transfer increases with the HCs size. The significant charge transfer is observed in C4 HCs, C3H6, and C3H8 of ca. 0.10–0.13 e− while for other complexes is ca. 0.10 e−. CH4 (0.05 e−) and C2H2 (0.04 e−) experience very lower e− transfer due to their smaller size. Further illustration proclaims a metal to ligand (HCs) e− transfer (MLCT) exhibits during the complexation process. The MLCT is in the range of 0.01–0.03 e− and it's obvious the back donation of π-electron from the bonding molecular d-orbital of metal to the empty antibonding π* orbital of ligands. The charge transfer values are given in Table S3.† In the complexation, the predominant charge transfer obtains from HCs to PPX.Energy decomposition analysis
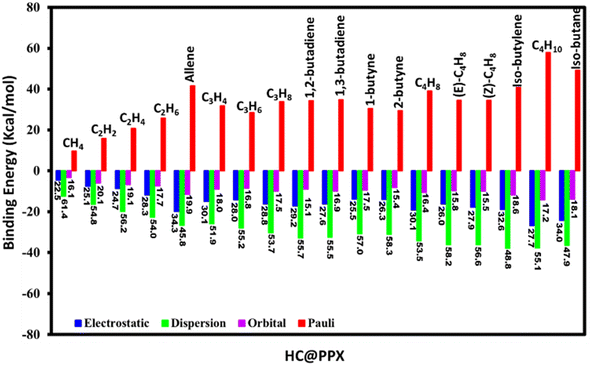
Energy decomposition analysis (EDA) has been accomplished by considering PPX and HC as interacting fragments are provided in Fig. 3 and their corresponding energy and percentage of contribution are given in Table S4.† The dispersion (ΔEdisp) term is the major contributor of ca. 45.8–61.4% to the total interaction. Regardless, the electrostatic (ΔEelct) of ca. 22.5–34.1% and orbital (ΔEorb) of ca. 15.1–20.1% contribute significantly to the total binding energy of the stabilized complex. As expected, the higher ΔEdisp of CH4@PPX is owing to its zero-field dipole and quadrupole moment, instigating the induced dipole interaction between CH4 and the charged portal of PPX. Similarly, C2 HCs exhibit zero field-dipole but unveil positive quadrupole moment and higher polarizability than the former one engenders induced dipole interaction. All C3 HCs experienced a permanent dipole moment except allene, claiming strong dipole–dipole interaction between the HCs and PPX, hence exhibiting notable ΔEelct interaction compared to other HCs. The presence of acidic hydrogen in allene possibly forms the hydrogen bonding interaction with the –N–centered pyrazole portal of PPX. Therefore, the contribution of ΔEelct (34.3%) is the highest among the studied HCs, which reflects the higher ΔEorb (19.9%) and lower ΔEdisp (45.8%) term. In C4 HCs, 1,2-butadiene, 1-butyne, C4H8, (Z)-C4H8, isobutylene, and isobutane interact with the PPX by dipole–dipole interaction due to permanent dipole moment, hence their ΔEelct term ca. 27.8–34.0% from their isomers (ca. 26.0–27.6%). Isobutane and isobutylene experienced weak hydrogen bonding resulting ΔEelct, of 34.0 and 32.6% and the ΔEdisp term is 47.9 and 48.8% respectively is the lowest among the studied system. 2-Butyne, (E)-C4H8 interaction with PPX is purely dispersive like ca. 58%. All-inclusive analysis reveals the combined effect of ΔEdisp and ΔEelct are major factors for HC@PPX stabilization. Although the orbital interaction is trivial but can't be neglected and the contribution of ΔEorb is ca. 15.1–20.1% and stronger interactions are perceived in the complexes containing the acidic hydrogen ligands.Noncovalent interaction
NCI index deciphered the noncovalent interaction in the HC@PPX system as shown in Fig. 4. The presence of green surfaces between HCs and PPX highlights the van der Waals type in nature. The increasing size of the green surface enhances van der Waals interaction and increasing HC size strengthens the van der Waal's contact. The spattered red plot in the imidazole/pyrazole ring center depicts the strain produced by the ring current. The blue color surfaces claim the hydrogen bonding interaction in the stabilized system, according to the presently used color coding scheme. A significant H-bonding is visualized in the allene, isobutylene and isobutane entrapped complex. Furthermore, the plots of reduced density gradient s versus sign (λ2)ρ elucidate better insight into the specific types of interaction present in the complex. Extremely low density, low gradient, and moderately low density and low gradient troughs with a negative sign (λ2)ρ values indicate the presence of attractive dispersion and hydrogen bonding interactions, respectively. Contrary, a low gradient trough appearing in the positive region of sign (λ2)ρ conveys the repulsive interactions produced by ring strain. The superimposed plots are shown in Fig. S3,† where PPX moieties are designated by blue color and complexes, are portrayed in red color. In every system, an additional narrow spike is observed at slightly negative sign (λ2)ρ values around −0.005 a.u. implies the interaction is dispersive.GCMC analysis
The gravimetric uptake of C1–C4 HCs at 77–340 K/0.1–10 bar has been investigated using the PPX host. At 273, 298, and 340 K and 1 bar, CH4 adsorption has been 3.51, 2.37, and 1.33 mmol g−1 and at 10 bar the adsorption values are 5.41, 4.81, and 3.69 mmol g−1, respectively. The CH4 follows type-1 adsorption isotherm and increasing temperature reduces CH4 uptake whereas high pressure induces higher CH4 adsorption. At 77 K the adsorption of CH4 is 5.60 mmol g−1 at 1 bar and 7.31 mmol g−1 at 10 bar pressure.The adsorption isotherm plot of 298 K is shown in Fig. 5(a) while the 77, 273, and 340 K are shown in Fig. S4(a), S5(a), and S6(a),† respectively. The adsorption is higher at 77 K due to the lowering of intermolecular repulsion between the CH4 molecule. 340 K results decrease in CH4 uptake, this can be attributed to high temperature favors the CH4 in the free gaseous state rather than adsorbed state, and also in high temperature the pore volume of the substrate decreases rendering lower adsorption.
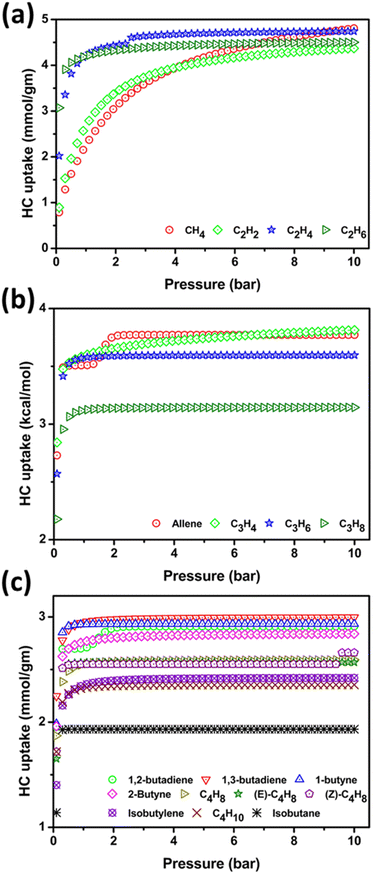 | ||
| Fig. 5 (a) Represents the adsorption isotherm of C1/C2 HCs (b) represents the adsorption isotherm of C3 HCs and (C) depicts C4 HCs at 298 K temperature and pressure 0.1–10 bar. | ||
The uptake of C2H6 (3.0–4.1 mmol g−1) is high compared to its isomers in the low-pressure region (298 K/0.1–1 bar). At high pressure, the C2H4 adsorption is prominent followed by C2H6 and C2H2. The gravimetric uptake of C2H2, C2H4, and C2H6 are 2.80, 4.26, and 4.22 mmol g−1 respectively at ambient conditions while at 10 bar the uptake increases to 4.37, 4.74, and 4.50 mmol g−1 respectively. At 77 K/1 bar the uptake varies C2H2 > C2H4 > C2H6 whereas at 273 K the adsorption strength is C2H4 > C2H6 > C2H2 up to 4 bar and thereafter C2H4 > C2H2 > C2H6. The 340 K is contrary to 273 K i.e. C2H6 > C2H4 > C2H2. This reveals at low-temperature the uptake of unsaturated HC is more effective whereas at high temperatures the C2H6 adsorption is significant. The adsorption isotherms plot of C2 HC at ambient condition is shown in Fig. 5(a) while Fig. S4(a), S5(a), and S6(a),† represents the isotherm plot of 77, 273, and 340 K respectively.
A type-IV adsorption isotherm has been observed for allene shows significant uptake of 3.76 mmol g−1 at 298 K/2 bar whereas other C3 isomers exhibit type-I at 298 K. At ambient conditions, the uptake of allene, C3H4, C3H6, and C3H8 is 3.51, 3.60, 3.57 and 3.12 mmol g−1, respectively are shown in Fig. 5(b), increasing pressure up to 1.5 bar results higher allene uptake followed by C3H4, C3H6, and C3H8. The gravimetric capacity of C3H8 is lower than other C3 isomers due to a larger kinetic diameter of 4.9 Å. At 77 K [Fig. S4(b)†], the adsorption isotherm of C3H4 is moderately higher than allene with increasing pressure and C3H6 adsorption is notably higher than C3H8. At STP [Fig. S5(b)†] the allene uptake is very high and high pressure portrays the C3H4 and allene have an equal propensity for adsorption. Thus, 273 K and 0.1–4 bar could be the ideal setup for selective adsorption of C3 HCs. The adsorption of allene (3.29 mmol g−1), C3H4 (3.20 mmol g−1), and C3H6 (3.33 mmol g−1) swing trivially at 340 K [Fig. S6(b)†], and the uptake of C3H8 (2.90 mmol g−1) is lowest. Increasing pressure reduces the C3H6 adsorption while inducing allene uptake. Unusual behavior is observed in C3H4 uptake capacity at a high-pressure and overall range of temperature which coincides with the allene adsorption isotherm. This can be explained by the activation of π-bond of allene and alkyne by Au(I) attributed to relativistic effects. Though Au(I) is coordinated with the electron-rich NHC groups which propel the π-activation more significantly with C3H4 rather than allene in high-pressure regions.
C4 HC uptake by PPX is in the ideal range, the highest adsorption is observed for 1,3-butadiene and isobutane is least at ambient condition and 1,2-butadiene follows type-IV adsorption while others are of type-I shown in Fig. 5(c). A preference analysis of C4H10, isobutane, 1,3-butadiene and isobutylene over other C4 HCs is investigated owing to its presence in the natural gas mixture. At ambient setup, the uptake capacity of C4H10, isobutane, 1,3-butadiene, and isobutylene are 2.32, 1.93, 2.95, and 2.36 mmol g−1, respectively. The remaining HC adsorption is in the ideal range. Except for 1,3-butadiene (3.08 mmol g−1), other HCs do not have notable uptake in cryogenic condition/1 bar as shown in Fig. S4(c).† An unrelieved uptake of HC has been observed at ambient and STP conditions [Fig. S5(c)†]. At 340 K/1 bar, the adsorption of 1,2-butadiene is high and with increasing pressure, the isobutylene shows steep growth in the adsorption as shown in Fig. S6(c).† The other C4 HC uptake strength is monotonous due to their equal kinetic diameter. Thus, the simulation study reveals that PPX might be a good candidate for the capture of C1–C4 HC under ambient conditions. Further, we have performed the density distribution of the center of mass of HC molecules in GCMC simulation as shown in Fig. S7.† The results from GCMC simulation at ambient condition indicate that the guest HC molecules lies at the center and also adhere to the outer open site of PPX due to the presence of the –N atom in the imidazolylidene motif. C1 and C2 HC show higher density coverage than C3 and C4 due to smaller size and lower kinetic diameter. The thermodynamic view of HC adsorption using PPX at 298 K has been determined using the isosteric heat of adsorption (Qst) and is shown in Fig. 6.
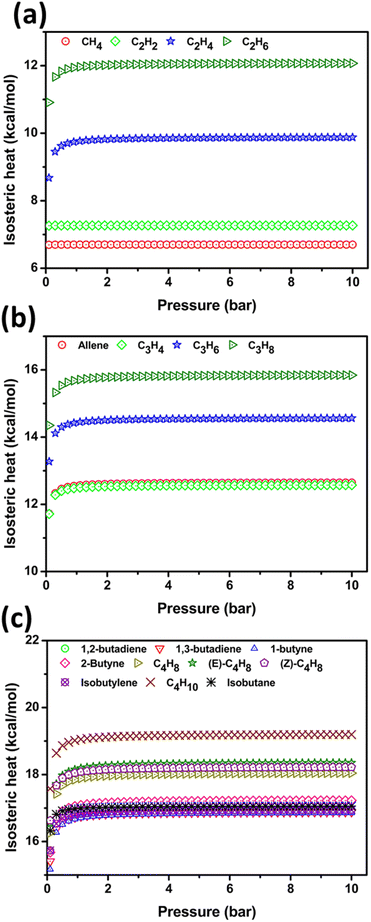 | ||
| Fig. 6 (a) Represents the isosteric heat of adsorption (Qst) of C1/C2 HCs (b) depicts Qst of C3 HCs and (c) portrays Qst of C4 HCs at 298 K temperature. | ||
In C1/C2 HC, the Qst of CH4 and C2H2 are constant over the entire pressure range (0.1–10 bar) whereas C2H4 and C2H6 increase slowly from 0.1–1 bar and afterward remain constant. The increasing Qst value depicts the adsorbate interaction with the PPX and lateral interaction between the adsorbate molecules which is corroborated by the DFT and cooperative binding study. The constant Qst portrays the adsorption that occurs in the energetically homogenous adsorbent which is due to the effect of capillary condensation in the mesoporous material. The onset of capillary condensation results in constant Qst induced by confinement within the pore network. Akin to C2H4 and C2H6, C3 and C4 HCs exhibit the increase in Qst value from 0.1–1 bar enunciates the adsorbate–adsorbent interaction and constant from 1–10 bar attributed by capillary condensation.
Ideal adsorption solution theory
The potential separation of C1–C4 HCs has been investigated using ideal adsorption solution theory (IAST) for equimolar components. At the ambient setup, the selectivity of C2H6 is higher than its counterpart C2 isomers as shown in Fig. 7(a). However, at 273 K the C2H4 separation is more facile shown in Fig. S8(a).† C2H2 selective separation is very much pronounced irrespective of temperature and pressure. The selectivity difference between allene and C3H4 is minor at 298 K and is notable at STP under high pressure shown in Fig. S8(b).† At ambient conditions the selectivity between C3H6 and C3H8 is distinguishable. However, in 273 K all C3 HCs can be easily separable by applying moderate to high pressure and the selectivity is allene > C3H4 > C3H6 > C3H8. The selectivity of C3H6 is preferred over other C3 HCs at a higher temperature of 340 K [Fig. S9(b)†]. Lower temperature and high pressure will be facile for allene separation whereas high temperature leads C3H6 with effective selectivity from its isomers. The selectivity of C4 hydrocarbon is quite lower than C1–C3 HCs. At ambient conditions, the separation of 2-butyne from its isomers is a bottleneck whereas at STP [Fig. S8(c)†] the separation is favorable. 2–10 bar/298 K and 0.1–2 bar/273 is the ideal range for the 2-butyne/1-butyne selective separation. The selectivity of isobutane is least in all conditions. The order of selectivity at 298 K/2–10 bar is 2-butyne > 1-butyne > 1,3-butadiene > 1,2-butadiene > (Z)-C4H8 > (E)-C4H8 ≈ C4H8 > C4H10 ≈ isobutylene > isobutane. The adsorption selectivity is mainly attributed to pore shape, guest size, temperature, and internal surface functionality of pores in the PPX. 298 K, 273 K, and 340 K are ideal temperature conditions for the selective separation of C2, C3, HCs. For C4 HCs more external pressure is required.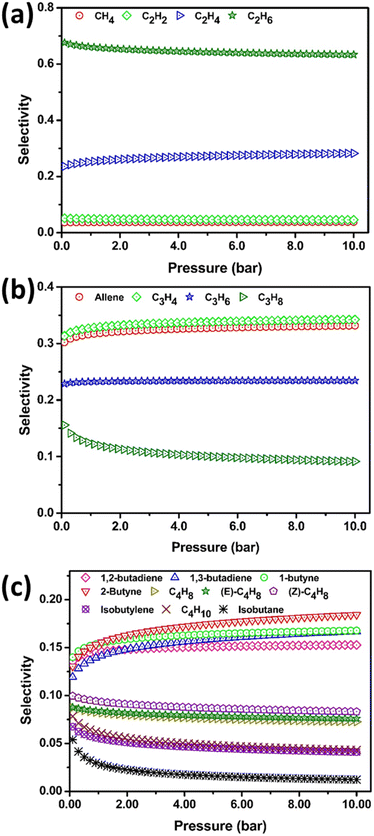 | ||
| Fig. 7 Ideal adsorption solution theory adopted selectivity of HCs by PPX (a) selectivity of C1/C2 HC (b) C3 HCs (C) C4 HCs at 298 K and 0.1–10 bar. | ||
Comparison with benchmark report
Our results are compared with the existing benchmark reports (last three years) on the MOF-based hydrocarbon adsorption under ambient conditions and the comparison is listed in Table S5.† The CH4 adsorption in PPX is remarkable with 2.37 mmol g−1 and only NOTT-101 (5.93 mmol g−1)/-101-IPA (5.98 mmol g−1)49 achieved higher than these limits. The C2H2 adsorption in PPX is 2.80 mmol g−1, although the adsorption is not very good but performs better than UPC-98,50 UMCM-151,51 PFC-5,52 FIR-125,53 NUM-9a,54 JLU-Liu45,55 Zr-OBBA,55 PFC-1/-2,56 NUM-7,57 Cu–F-pymo,58 MOF 1/MOF 2,59 UPC-99,60 NbU-1.61 C2H4 adsorption was also impressive with 4.26 mmol g−1 and only MFM-300(In)62 (4.9 mmol g−1), and Dps-VCo-BDC (7.41 mmol g−1)/tpt-VCo-BDC(6.29 mmol g−1)63 MOF is higher than PPX limit. Similarly, the adsorption of C2H6 in PPX is quite higher with 4.22 mmol g−1 which is better than many of the notable MOFs and only Mg-MOF74(6.1 mmol g−1)47 and its functionalized MOF tpt-Mg-MOF-74 (5.4 mmol g−1), MFM-300(In) (5.1 mmol g−1),62 Gly@HKUST-1s (6.47 mmol g−1),64 Dps-VCo-BDC (8.03 mmol g−1)/tpt-VCo-BDC (6.69 mmol g−1),63 and NPU-1 (4.50 mmol g−1)/NPU-2(4.44 mmol g−1)65 are higher than the PPX. One should also notice the binding energy and selectivity, the binding energy is higher than many of the reported systems, and the selectivity of C2 HCs distinct and have the potential to separate each component.The adsorption of C3 HCs is steady as compared to the other reported results. The C3H4 adsorption is less studied and only MFM-300(In)62 adsorption capacity is 6.30 mmol g−1 which is higher than PPX. The C3H6 adsorption in PPX is 3.57 mmol g−1 is higher than PCN-207-FA (2.17 mmol g−1),66 UMCM-151(3.07 mmol g−1),51 MOF-801(3.50 mmol g−1).67 The C3H8 adsorption in PPX is 3.12 mmol g−1, moreover, the reported MOFs show promising C3H8 adsorption compared to the PPX. Although the uptake of C3 HCs in PPX is quite low but the selectivity is well noticeable. The C4 HC uptake is more propitious and it is observed that the uptake capacity of (E)-C4H8, (Z)-C4H8, 1,3-butadiene, C4H8, isobutylene, C4H10, and isobutene using PPX is higher than the M-Gallate (M = Ni/Mg/Co),68 ZU-36-CO,69 TMOF-1/ZU-619,70 M2(dobdc)/M2(m-dobdc) (M = Mn/Fe/Co/Ni)71 MOFs shown in Table S6.† Only FJI-H19 (ref. 72) and NKM-101a73 show better uptake than PPX.
Computational details
The metallocavitand PPX is a well-defined tubular cavity made up of octanuclear N-heterocyclic carbene complex of Au(I) have been explored in this study. The crystal structure obtained from ref. 20 is further investigated to understand the electronic effect and adsorption properties. The geometry of PPX and HCs entrapped PPX (HC@PPX) has been optimized at B97D2/LanL2DZ level of theory.74,75 The subsequent harmonic vibrational analysis reveals the existence of real frequency in the structure belonging to minima on the potential energy surface (PES). We have computed zero-point energy corrected binding energy (ΔE + ZPE) and basis set superposition error (BSSE) at the same level of theory. The standard counterpoise method proposed by Boys and Bernardi has been adopted for the BSSE correction.76 The natural bond orbital (NBO) analysis has been performed at the B3LYP-D3/Def2-TZVP level of theory to determine the electronic charge transfer within the host–guest complex.74,77 All the calculations are computed using the Gaussian 09 program package.78The energy decomposition analysis (EDA) has been carried out using dispersion corrected hybrid functional B3LYP-D3 with triple-zeta two polarization function TZ2P implemented in the ADF (2017) program.79–82 Zeroth order relativistic approximation (ZORA) method has been incorporated for computation as gold exhibits a large relativistic effect.83 In EDA, the fragment-based computations are invoked to treat PPX as one fragment and the guest molecules are other fragments. The total energy is decomposed into four major energy components viz. electrostatic (Eelct), dispersion (Edisp), orbital (Eorb), and the Pauli term (Epau). The former three energy terms are attractive while the latter one is repulsive. The Eelct term represents the classical electrostatic interaction that exists between the two charged species namely host and guest after complexation. Edisp term arises due to the electronic fluctuation between two adjacent molecules attributed to temporary dipoles in the complex. Eorb is the orbital interactions initiated by the overlapping of occupied and unoccupied atomic orbitals of the host–guest system. The Epau is the Paulis repulsive term exerted by the overlapping of an identical quantum number between the two interacting fragments.
The real-space visualization of interaction has been studied using the NCI index which identifies noncovalent interactions solely based on electron density and its derivatives.84 NCI index is based on the 2D plot of reduced density gradient (RDG), s as a function of electron density ρ(r):
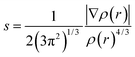 | (2) |
The plot where RDG value approaches zero is identified as the noncovalent region.84 Analysis of electron density determines the binding strength of interacting molecules. However, both attractive and repulsive interactions have a positive correlation with electron density in the corresponding region.85 A real space function sign (λ2) multiplied by electron density ρ(r) is indeed to define the attractive and repulsive term where the curvature λ2 is the second eigenvalue of the Hessian density matrix.86 A negative and positive value of λ2 is identified as strong attractive and repulsive interactions respectively while for van der Waals interaction the value of λ2 approaches to zero.86,87 Multiwfn program has been used to compute the NCI index whereas Chemcraft for the gradient isosurface visualization, where the color codes decide the value of sign (λ2)ρ(r).88,89 Blue and green color represents the attractive hydrogen bonding and van der Waals interaction whereas red color depicts the repulsive strain ensure by steric crowding.
Grand canonical Monte Carlo (GCMC) simulation has been carried out to determine the maximum HCs uptake capacity of PPX at an adsorption temperature of 77, 273, 298, and 340 K and pressure from 0.1 to 10 bar. For each simulation 1 × 105 GCMC cycles were used for equilibration and 1 × 105 cycles were used to assess the ensemble average properties. The simulations were performed using the sorption module of Material Studio.90,91 The universal force field (UFF) parameter has been used to describe the interatomic interaction with a cut-off distance of 12.5 Å has been used for all Lennard–Jones interactions.92 Long-range electrostatic interactions were computed using the Ewald summation method.93 The simulation has been carried out in a 1 × 1 × 2 supercell with imposed periodic boundary conditions in all directions.
The adsorbate uptake capacity using PPX crystal obtained from the GCMC simulation is further utilized for the computation of selective separations. Langmuir adsorption isotherm model has been used to examine the selectivity of individual gas components over multi-component using ideal adsorption solution theory (IAST).94
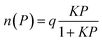 | (3) |
Conclusions
In summary, Au(I) coordinated microporous metallocavitand host, PPX has been investigated for potential HCs adsorption and separation. C1–C4 light HCs have been taken into consideration owing to their availability in the natural gas mixture. DFT study unveils facile adsorption of HCs at ambient conditions with extraordinary binding strength. All the complexes are stable at ambient conditions and the complexation is enthalpy driven. CH4, C2H6, C3H8, and C4H10 are the leading adsorbents with unprecedented binding energy from their respective isomers. The energy difference between the C2H2/C2H4, C2H2/C2H6, allene/C3H6, C3H4/C3H6, C4H8/C4H10 is strong enough for selective separation from their isomers. EDA discerns the nature of interactions that are dominated by dispersion (45.8–61.4%) followed by electrostatic (22.5–34.3%) and orbital (15.1–20.1%) terms which are further corroborated by the NCI index. GCMC simulation predicts the gravimetric uptake of CH4, C2H4, C2H6, C3H4, C3H6, and 1,3-butadiene is very high at 298 K and pressure range up to 10 bar. The magnitude of Qst reveals the high affinity of HCs to the pore volume of the adsorbents and the existence of adsorbate–adsorbate interaction unveils the binding cooperativity. The results of GCMC and Qst corroborated with the DFT and cooperative effect study. The IAST claims that 298 K, 273 K, and 340 K are ideal temperature conditions for the selective separation of C2H6, allene, and 1-butyne from their respective isomers. This work provides an elegant example of N-heterocyclic carbene (NHC) based Au(I) metallocavitand for the HCs separation and effectively more sophisticated porous material can be designed based on these concepts.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author thanks the C-DAC, Pune for the computational facility. The author also thanks to the CUH and SPU for the research infrastructure.References
- Z. Bao, G. Chang, H. Xing, R. Krishna, Q. Ren and B. Chen, Energy Environ. Sci., 2016, 9, 3612–3641 RSC.
- L. Li, X. Wang, J. Liang, Y. Huang, H. Li, Z. Lin and R. Cao, ACS Appl. Mater. Interfaces, 2016, 8, 9777–9781 CrossRef CAS PubMed.
- M. Sharifzadeh, G. Triulzi and C. L. Magee, Energy Environ. Sci., 2019, 12, 2789–2805 RSC.
- A. M. Plonka, X. Chen, H. Wang, R. Krishna, X. Dong, D. Banerjee, W. R. Woerner, Y. Han, J. Li and J. B. Parise, Chem. Mater., 2016, 28, 1636–1646 CrossRef CAS.
- D. Saha, H. A. Grappe, A. Chakraborty and G. Orkoulas, Chem. Rev., 2016, 116, 11436–11499 CrossRef CAS PubMed.
- X. Liu, W. Fan, M. Zhang, G. Li, H. Liu, D. Sun, L. Zhao, H. Zhu and W. Guo, Mater. Chem. Front., 2018, 2, 1146–1154 RSC.
- S. J. Barrow, S. Kasera, M. J. Rowland, J. Del Barrio and O. A. Scherman, Chem. Rev., 2015, 115, 12320–12406 CrossRef CAS.
- T. Ogoshi, T. Yamagishi and Y. Nakamoto, Chem. Rev., 2016, 116, 7937–8002 CrossRef CAS.
- M. Florea and W. M. Nau, Angew. Chem., Int. Ed., 2011, 123, 9510–9514 CrossRef.
- S. N. Talapaneni, D. Kim, G. Barin, O. Buyukcakir, S. H. Je and A. Coskun, Chem. Mater., 2016, 28, 4460–4466 CrossRef CAS.
- Z. Wang, N. Sikdar, S.-Q. Wang, X. Li, M. Yu, X.-H. Bu, Z. Chang, X. Zou, Y. Chen, P. Cheng, K. Yu, M. J. Zaworotko and Z. Zhang, J. Am. Chem. Soc., 2019, 141, 9408–9414 CrossRef PubMed.
- D. G. Liz, A. M. Manfredi, M. Medeiros, R. Montecinos, B. Gómez-González, L. Garcia-Rio and F. Nome, Chem. Commun., 2016, 52, 3167–3170 RSC.
- S. Yang, A. J. Ramirez-Cuesta, R. Newby, V. Garcia-Sakai, P. Manuel, S. K. Callear, S. I. Campbell, C. C. Tang and M. Schröder, Nat. Chem., 2015, 7, 121–129 CrossRef CAS PubMed.
- H. Wang, X.-L. Wang and J. Li, ChemPlusChem, 2016, 81, 872–876 CrossRef CAS PubMed.
- Y. Ming, J. Purewal, J. Yang, C. Xu, R. Soltis, J. Warner, M. Veenstra, M. Gaab, U. Müller and D. J. Siegel, Langmuir, 2015, 31, 4988–4995 CrossRef CAS PubMed.
- X. Liu, C. Hao, J. Li, Y. Wang, Y. Hou, X. Li, L. Zhao, H. Zhu and W. Guo, Inorg. Chem. Front., 2018, 5, 2898–2905 RSC.
- D. Preston, K. F. White, J. E. Lewis, R. A. Vasdev, B. F. Abrahams and J. D. Crowley, Chem.–Eur. J., 2017, 23, 10559–10567 CrossRef CAS PubMed.
- J. Janczak, D. Prochowicz, J. Lewiński, D. Fairen-Jimenez, T. Bereta and J. Lisowski, Chem.–Eur. J., 2016, 22, 598–609 CrossRef CAS.
- J. C. Lin, R. T. Huang, C. S. Lee, A. Bhattacharyya, W. S. Hwang and I. J. Lin, Chem. Rev., 2009, 109, 3561–3598 CrossRef CAS.
- P. J. Altmann and A. Pöthig, J. Am. Chem. Soc., 2016, 138, 13171–13174 CrossRef CAS.
- M. K. Pandey, H. S. Kunchur, D. Mondal, L. Radhakrishna, B. S. Kote and M. S. Balakrishna, Inorg. Chem., 2020, 59, 3642–3658 CrossRef CAS PubMed.
- Md. A. Bakar, M. Sugiuchi, M. Iwasaki, Y. Shichibu and K. Konishi, Nat. Commun., 2017, 8, 576 CrossRef PubMed.
- H. Darmandeh, J. Löffler, N. V. Tzouras, B. Dereli, T. Scherpf, K.-S. Feichtner, S. Vanden Broeck, K. Van Hecke, M. Saab, C. S. J. Cazin, L. Cavallo, S. P. Nolan and V. H. Gessner, Angew. Chem., Int. Ed., 2021, 60, 21014–21024 CrossRef CAS PubMed.
- G. R. Desiraju and T. Steiner, The weak hydrogen bond: in structural chemistry and biology, International Union of Crystal, 2001, vol. 9 Search PubMed.
- E. Tsivion and M. Head-Gordon, J. Phys. Chem. C, 2017, 121, 12091–12100 CrossRef CAS.
- C.-H. Yeh, A. H. Khan, T. Miyazaki and J.-C. Jiang, Phys. Chem. Chem. Phys., 2021, 23, 12270–12279 RSC.
- M. L. McKee, J. Phys. Chem. A, 2019, 123, 6251–6258 CrossRef CAS PubMed.
- A. Sharma, R. Babarao, N. V. Medhekar and A. Malani, Ind. Eng. Chem. Res., 2018, 57, 4767–4778 CrossRef CAS.
- W. Xu, Y. Chen, M. Song, X. Liu, Y. Zhao, M. Zhang and C. Zhang, J. Phys. Chem. C, 2020, 124, 8110–8118 CrossRef CAS.
- D. J. Mowbray, A. Migani, G. Walther, D. M. Cardamone and A. Rubio, J. Phys. Chem. Lett., 2013, 4, 3006–3012 CrossRef CAS.
- S. M. Lang, T. M. Bernhardt, J. M. Bakker, B. Yoon and U. Landman, Int. J. Mass Spectrom., 2019, 435, 241–250 CrossRef CAS.
- A. Lyalin and T. Taketsugu, J. Phys. Chem. C, 2010, 114, 2484–2493 CrossRef CAS.
- P. H. Kasai, J. Am. Chem. Soc., 1983, 105, 6704–6710 CrossRef CAS.
- D. Lv, R. Shi, Y. Chen, Y. Wu, H. Wu, H. Xi, Q. Xia and Z. Li, ACS Appl. Mater. Interfaces, 2018, 10, 8366–8373 CrossRef CAS PubMed.
- C. Campbell, C. A. Ferreiro-Rangel, M. Fischer, J. R. B. Gomes and M. Jorge, J. Phys. Chem. C, 2017, 121, 441–458 CrossRef CAS.
- J. Pires, M. L. Pinto and V. K. Saini, ACS Appl. Mater. Interfaces, 2014, 6, 12093–12099 CrossRef CAS PubMed.
- A. R. Kulkarni and D. S. Sholl, J. Phys. Chem. C, 2016, 120, 23044–23054 CrossRef CAS.
- J. Zhang, Z. Liu, H. Liu, F. Xu, Z. Li and X. Wang, ACS Omega, 2022, 7, 7648–7654 CrossRef CAS PubMed.
- N. Nijem, H. Wu, P. Canepa, A. Marti, K. J. Balkus, T. Thonhauser, J. Li and Y. J. Chabal, J. Am. Chem. Soc., 2012, 134, 15201–15204 CrossRef CAS PubMed.
- P. Verma, X. Xu and D. G. Truhlar, J. Phys. Chem. C, 2013, 117, 12648–12660 CrossRef CAS.
- O. T. Qazvini, R. Babarao, Z.-L. Shi, Y.-B. Zhang and S. G. Telfer, J. Am. Chem. Soc., 2019, 141, 5014–5020 CrossRef CAS PubMed.
- X.-W. Gu, J.-X. Wang, E. Wu, H. Wu, W. Zhou, G. Qian, B. Chen and B. Li, J. Am. Chem. Soc., 2022, 144, 2614–2623 CrossRef CAS PubMed.
- M. Rubeš, A. D. Wiersum, P. L. Llewellyn, L. Grajciar, O. Bludský and P. Nachtigall, J. Phys. Chem. C, 2013, 117, 11159–11167 CrossRef.
- Y. Sun, Z. Ke, Y. Tang, S. Wang, Y. Wu, Q. Xia and Z. Li, Ind. Eng. Chem. Res., 2020, 59, 6202–6209 CrossRef CAS.
- Y. Xiao, Y. Chu, S. Li, Y. Su, J. Tang, J. Xu and F. Deng, J. Phys. Chem. C, 2020, 124, 3738–3746 CrossRef CAS.
- K. C. Kim, C. Y. Lee, D. Fairen-Jimenez, S. T. Nguyen, J. T. Hupp and R. Q. Snurr, J. Phys. Chem. C, 2014, 118, 9086–9092 CrossRef CAS.
- B. L. Suh, T. Hyun, D.-Y. Koh and J. Kim, Chem. Mater., 2021, 33, 7686–7692 CrossRef CAS.
- L. Yang, X. Cui, Q. Ding, Q. Wang, A. Jin, L. Ge and H. Xing, ACS Appl. Mater. Interfaces, 2020, 12, 2525–2530 CrossRef CAS PubMed.
- J.-R. Chen, Y.-Q. Luo, S. He, H.-L. Zhou and X.-C. Huang, Inorg. Chem., 2022, 61, 10417–10424 CrossRef CAS PubMed.
- X. Wang, X. Wang, X. Zhang, W. Fan, Q. Li, W. Jiang, F. Dai and D. Sun, Cryst. Growth Des., 2020, 20, 5670–5675 CrossRef CAS.
- Y. Wang, X. Wang, X. Wang, X. Zhang, W. Fan, D. Liu, L. Zhang, F. Dai and D. Sun, Cryst. Growth Des., 2018, 19, 832–838 CrossRef.
- Q. Yin, J. Lü, H.-F. Li, T.-F. Liu and R. Cao, Cryst. Growth Des., 2019, 19, 4157–4161 CrossRef CAS.
- Y. Sun, M.-Y. Gao, Y. Sun, D.-F. Lu, F. Wang and J. Zhang, Inorg. Chem., 2021, 60, 13955–13959 CrossRef CAS PubMed.
- S.-Q. Yang, F.-Z. Sun, P. Liu, L. Li, R. Krishna, Y.-H. Zhang, Q. Li, L. Zhou and T.-L. Hu, ACS Appl. Mater. Interfaces, 2020, 13, 962–969 CrossRef PubMed.
- J. Gu, X. Sun, L. Kan, J. Qiao, G. Li and Y. Liu, ACS Appl. Mater. Interfaces, 2021, 13, 41680–41687 CrossRef CAS PubMed.
- Q. Yin, Y.-L. Li, L. Li, J. Lü, T.-F. Liu and R. Cao, ACS Appl. Mater. Interfaces, 2019, 11, 17823–17827 CrossRef CAS PubMed.
- F.-Z. Sun, S.-Q. Yang, R. Krishna, Y.-H. Zhang, Y.-P. Xia and T.-L. Hu, ACS Appl. Mater. Interfaces, 2020, 12, 6105–6111 CrossRef CAS PubMed.
- Y. Shi, Y. Xie, H. Cui, Y. Ye, H. Wu, W. Zhou, H. Arman, R.-B. Lin and B. Chen, Adv. Mater., 2021, 33, 2105880 CrossRef CAS PubMed.
- M. Feng, P. Zhou, J. Wang, X. Wang, D. Wang and C. Li, Inorg. Chem., 2022, 61, 11057–11065 CrossRef CAS PubMed.
- X. Wang, X. Zhang, K. Zhang, X. Wang, Y. Wang, W. Fan and F. Dai, Inorg. Chem. Front., 2019, 6, 1152–1157 RSC.
- J. Li, L. Jiang, S. Chen, A. Kirchon, B. Li, Y. Li and H.-C. Zhou, J. Am. Chem. Soc., 2019, 141, 3807–3811 CrossRef CAS PubMed.
- L. Guo, M. Savage, J. H. Carter, X. Han, I. Da Silva, P. Manuel, S. Rudić, C. C. Tang, S. Yang and M. Schröder, Chem. Mater., 2022, 34, 5698–5705 CrossRef CAS PubMed.
- Y. Wang, X. Jia, H. Yang, Y. Wang, X. Chen, A. N. Hong, J. Li, X. Bu and P. Feng, Angew. Chem., Int. Ed., 2020, 132, 19189–19192 CrossRef.
- W. Dong, L. Yang and Y. Huang, Talanta, 2017, 167, 359–366 CrossRef CAS PubMed.
- B. Zhu, J.-W. Cao, S. Mukherjee, T. Pham, T. Zhang, T. Wang, X. Jiang, K. A. Forrest, M. J. Zaworotko and K.-J. Chen, J. Am. Chem. Soc., 2021, 143, 1485–1492 CrossRef CAS PubMed.
- H. He, B. Guo, Y. Liu, L. Zhang and W. Huang, Cryst. Growth Des., 2020, 20, 4882–4885 CrossRef CAS.
- P. Iacomi, F. Formalik, J. Marreiros, J. Shang, J. Rogacka, A. Mohmeyer, P. Behrens, R. Ameloot, B. Kuchta and P. L. Llewellyn, Chem. Mater., 2019, 31, 8413–8423 CrossRef CAS.
- J. Chen, J. Wang, L. Guo, L. Li, Q. Yang, Z. Zhang, Y. Yang, Z. Bao and Q. Ren, ACS Appl. Mater. Interfaces, 2020, 12, 9609–9616 CrossRef CAS PubMed.
- Z. Zhang, B. Tan, P. Wang, X. Cui and H. Xing, AIChE J., 2020, 66, e16236 CAS.
- J. Cui, Z. Zhang, J. Hu, L. Yang, Y. Li, L. Chen, X. Cui and H. Xing, Chem. Eng. J., 2021, 425, 130580 CrossRef CAS.
- B. R. Barnett, S. T. Parker, M. V. Paley, M. I. Gonzalez, N. Biggins, J. Oktawiec and J. R. Long, J. Am. Chem. Soc., 2019, 141, 18325–18333 CrossRef CAS PubMed.
- F. Hu, P. Huang, Z. Di, M. Wu, F. Jiang and M. Hong, Chem. Commun., 2019, 55, 10257–10260 RSC.
- Y. Qiao, X. Chang, J. Zheng, M. Yi, Z. Chang, M.-H. Yu and X.-H. Bu, Inorg. Chem., 2021, 60, 2749–2755 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- F. Weinhold, J. Comput. Chem., 2012, 33, 2363–2379 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman, and D. J. Fox, Gaussian 09, Revision E.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- K. Morokuma, Acc. Chem. Res., 1977, 10, 294–300 CrossRef CAS.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1–10 CrossRef CAS.
- M. von Hopffgarten and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 43–62 CAS.
- E. J. Baerends, T. Ziegler, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo and D. P. Chong, ADF 2022.1, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands Search PubMed.
- J. H. Van Lenthe, S. Faas and J. G. Snijders, Chem. Phys. Lett., 2000, 328, 107–112 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- R. F. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS.
- R. F. Bader, J. Phys. Chem. A, 1998, 102, 7314–7323 CrossRef CAS.
- R. F. Bader and H. Essén, Chem. Phys., 1984, 80, 1943–1960 CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- G. A. Zhurko and D. A. Zhurko, Chemcraft (version 1.7, build 382), 2014 Search PubMed.
- R. L. Akkermans, N. A. Spenley and S. H. Robertson, Mol. Simul., 2013, 39, 1153–1164 CrossRef CAS.
- Accelrys, Materials Studio, San Diego, CA 92121 USA, 2016 Search PubMed.
- A. K. Rappé, C. J. Casewit, K. S. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- H. D. Herce, A. E. Garcia and T. Darden, Chem. Phys., 2007, 126, 124106 Search PubMed.
- A. L. Myers and J. M. Prausnitz, AIChE J., 1965, 11, 121–127 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Includes physical parameters of pristine and encapsulated HCs, DE of HCs, charge transfer properties, Au–Au bond distances, change in entropy, energy decomposition values and their percentage contribution, cooperative effect bond distances, NCI-RDG plot, GCMC adsorption isotherm plot, selectivity graph, and Cartesian coordinates, etc. See DOI: https://doi.org/10.1039/d2ra07183e |
| This journal is © The Royal Society of Chemistry 2022 |