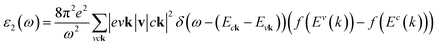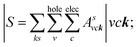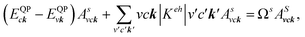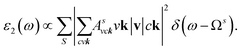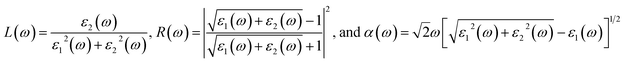Open Access Article
Open Access ArticleFirst-principles simulation insights of electronic and optical properties: Li6PS5Cl system
Nguyen Thi Han a,
Wei Bang-Li
a,
Wei Bang-Li a,
Kuang-I. Lin
a,
Kuang-I. Lin b,
Vo Khuong Dien
b,
Vo Khuong Dien *a and
Ming-Fa Lin
*a and
Ming-Fa Lin *ac
*ac
aDepartment of Physics, National Cheng Kung University, 701 Tainan, Taiwan. E-mail: vokhuongdien@gmail.com
bCore Facility Center, National Cheng Kung University, Tainan 701, Taiwan
cHierarchical Green-Energy Material (Hi-GEM) Research Center, National Cheng Kung University, Taiwan. E-mail: mflin@mail.ncku.edu.tw
First published on 14th November 2022
Abstract
We perform the electronic and optical properties of the Li6PS5Cl compound using first-principles calculation. The featured physical and chemical pictures and orbital hybridizations in all Li–S and P–S chemical bonds are clearly exhibited, such as the optimized geometry, the quasi-particle energy spectra, the band-decomposed charge densities, and the van Hove singularities in the density of states. Furthermore, the calculated results of the presence and absence of electron–hole interactions in optical responses are achieved successfully through the dielectric function, the energy loss functions, the absorption coefficients, and the reflectance spectra. The Li6PS5Cl compound can be useful for extensive applications in all-solid-state batteries and optoelectronic. Our theoretical investigation of Li6PS5Cl material will encourage further studies to fully comprehend the diverse phenomena for other emerging materials.
1. Introduction
The emergence of exceedingly conducive sulfide-based solid-state electrolytes (SSEs) has reignited interest in all-solid-state batteries.1–3 Since these materials have conductivities at room temperature equivalent to that of liquid electrolytes,4,5 they are excellent candidates for all-solid-state batteries.6,7 Among the sulfides, the Li6PS5Cl compound is a promising candidate for diversified applications in all-solid-state batteries8–10 and optoelectronic.11Up till now, the sulfide SSEs has sketched many attentions of researchers because of their high Li-ion conductivities, easy processability, and compatible interface with sulfur-based cathodes.12 For example, Zhang et al. have synthesized a Li6PS5Cl by heating a mixture of Li2S, P2S5, and LiCl to 600 °C at 0.3 °C min−1, and the ionic conductivity of Li6PS5Cl was 1.8 × 10−3 S cm−1 at RT.13 Most recently, the Li6PS5Cl with a very high ionic conductivity of 4.96 × 10−3 S cm−1 at 26.2 °C by sintering the mixed precursors at 550 °C for 10 h are reported by Yu et al.14
Experimentally, the Li6PS5Cl compound has been successfully synthesized and examined by variety measurements. For example, the X-ray diffraction (XRD),15–17 scanning electronic microscopy (SEM),16,18,19 and tunneling electronic microscope (TEM)14,20 measurements can examine the optimized geometric structures and surface monologies on this system. Besides, the angle-resolved photoemission spectroscopy (ARPES)21 and scanning tunneling spectroscopy (STS)22 measurements can verify the energy spectrum depending on frequencies at the occupied states, and the van Hove singularities in the density of states, respectively. However, such measurements are not reported yet in this compound. Furthermore, the delicate measurements on optical properties of the Li6PS5Cl system, such as photoluminescence, absorption, and transmission measurements are absent up till now.
In terms of theory, it is known that the first-principles calculations could give many expected results on electronic and optical properties of emerging materials23–27 and agree well experimental measurements. However, we detected that investigation of first-principles calculations on this compound is still rather limited. For example, only Zhuo Wang et al.,28 have shown the gap energy of 3.4 eV in the density of states of Li6PS5Cl compound by using the HSE method. Meanwhile, a lot of outstanding properties of Li6PS5Cl are not discovered yet by using first-principles calculations. Especially, consideration to probe chemical bonding behaviors in orbital hybridizations, which will be responsible to featured properties, has not still researched yet. It motivated us to perform this topic.
In this article, the optimized geometric structure, quasi-band structure, atom-dominated band structure at various energy ranges, the band-decomposed charge density, charge density distributions, and the van Hove singularities in the density of states (DOS) are disclosed in detail by using the first-principles calculation based on Vienna Ab initio Simulation Package (VASP). Furthermore, examination of optical responses is clearly exposed, such as the plasmon mode in terms of imaginary part and real part of dielectric functions, the energy loss functions, absorption coefficients, and reflectance spectra. More importantly, close associations between electronic and optical properties are revealed in this study. Consequently, our calculated results can provide to experimentalists for testing. The theoretical framework29–32 can be useful for studying the other properties of the emerging materials.31,32
2. Calculation methods
We used the density functional theory (DFT) method33 via the Vienna Ab initio Simulation Package (VASP)34 to investigate the electronic and optical properties of Li6PS5Cl compounds. The Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation35 was used for the exchange-correlation functional. The projector augmented wave (PAW) method36 was utilized for characterization of the ion and valence electron interactions. The cutoff energy for the expansion of the plane wave basis was set to 500 eV. The Brillouin zone was integrated with a special k-point mesh of 30 × 30 × 30 in the Γ-centered sampling technique for the structural optimization.37 The convergence condition of the ground-state is 10−7 eV between two consecutive simulation steps, and all atoms could fully relax during the geometric optimization until the Hellmann–Feynman force acting on each atom was smaller than 0.01 eV. The Heyd–Scuseria–Ernzerhof (HSE06)38 method is added for comparisons.In this letter, the electronic properties of Li6PS5Cl compound have exhibited by using the GW method (G stands for the Green' function and W represents the screened Coulomb potential), in which, the quasi-particle energies were obtained within the GW approximation for the self-energy,39 the response function's cutoff energy was equal to 200 eV, and 7 × 7 × 7-centered k-points sampling was used to represent reciprocal space. The quasi-particle band structure was plotted by using the WANNIER 90 code.40,41 Based on the electronic wave functions, the single-particle excitations were indicated by using Fermi's golden rule.42
In addition to the single particle excitations, the presence of exciton states may have a significant impact on the optical properties. The wave functions related to these bound states of electrons and holes could be expressed by using the following equation:
where: EQPck and EQPvk, respectively, are the quasi-particle energies of the valence and the conduction states as obtained with the GW method. Keh is the kernel describing the correlated electron–hole pairs, and Ωs is the energy of the excited states. The imaginary part of the dielectric function ε2(ω) is calculated from the excitonic states as:
In this part, the Tamm-Dancoff approximation (TDA)44 was calculated, moreover, energy cutoff and k-point sampling are set resemblances as in the GW calculations. Lorentzian with 100 meV broadening was used to replace the delta function. Since we are dealing with low frequency part of the absorption spectra, 7 lowest conduction bands (CBs) and 15 highest valence bands (VBs) in the Bethe–Salpeter kernel are sufficient to describe the excitonic effects. The fully chemical and physical pictures, the physics of the selective optical absorption and the effect of the strong exciton are the main study focus of the current study. Other optical properties, such as the energy loss functions,45 absorption coefficient,46 and reflectivity47 can be obtained from the dielectric function by the following equations:
All parameters in this article are carefully checked for the convergence of the calculations, such as the k-grid and cut-off frequency as seen in Fig. 1.
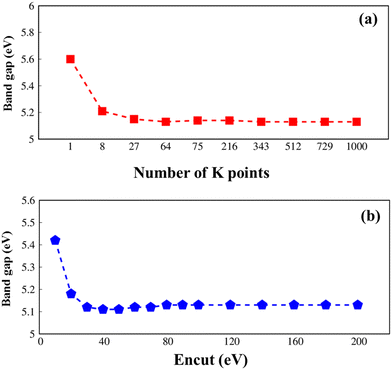 | ||
| Fig. 1 .Convergence of the GW electronic band gap of Li6PS5Cl with considerations to (a) k-grid from 1 × 1 × 1 to 10 × 10 × 10 and (b) cutoff frequency from 10 to 200, respectively. | ||
3. Structural and electronic properties
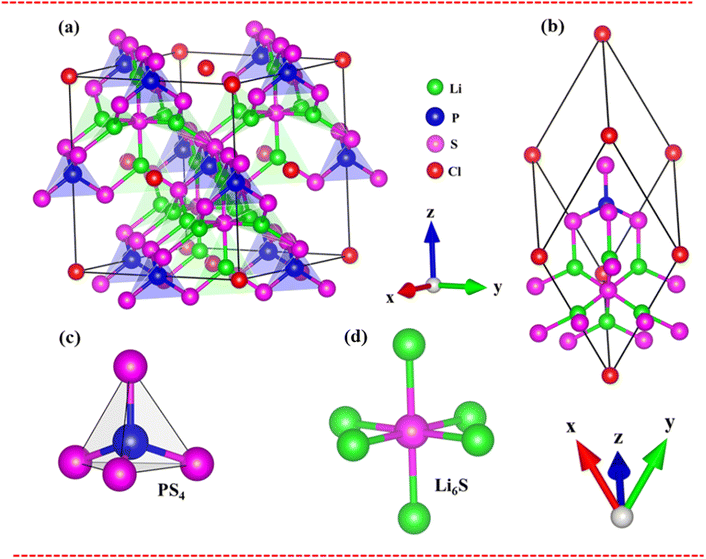
The Li6PS5Cl compound belongs to the face-centered cubic (![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) 43m space group) at room temperature. The conventional and primitive cell of Li6PS5Cl compound is clearly indicated in Fig. 2(a) and (b). Its structure provides octahedral [Li6S], tetrahedral [PS4] units and chlorine ions (Fig. 2(c) and (d). The S ions are occupied in the center of octahedral [Li6S] units or at corners of tetrahedral [PS4] ones. The chemical environments around these two types of S atom are quite different. Besides, halogen Cl is located at interstitial space between tetrahedral [PS4]. The lattice constant for structural relaxation is equal to 10.13 Å of conventional as seen in Table 1. These results are suitable with high-precision X-ray measurements. There exist 13 atoms in a primitive unit cell, including 6-Li, 1-P, 5-S and 1-Cl atoms, in which all the Li–S chemical bond have two different type lengths of 2.32 Å and 2.41 Å, as well as the P–S chemical bonds have identical lengths of 2.06 Å and Li–Cl bonds (very weak) as evidenced in Table 1. Such chemical bonds are highly position-dependent and are responsible for the anisotropic quasi-particle phenomena.
43m space group) at room temperature. The conventional and primitive cell of Li6PS5Cl compound is clearly indicated in Fig. 2(a) and (b). Its structure provides octahedral [Li6S], tetrahedral [PS4] units and chlorine ions (Fig. 2(c) and (d). The S ions are occupied in the center of octahedral [Li6S] units or at corners of tetrahedral [PS4] ones. The chemical environments around these two types of S atom are quite different. Besides, halogen Cl is located at interstitial space between tetrahedral [PS4]. The lattice constant for structural relaxation is equal to 10.13 Å of conventional as seen in Table 1. These results are suitable with high-precision X-ray measurements. There exist 13 atoms in a primitive unit cell, including 6-Li, 1-P, 5-S and 1-Cl atoms, in which all the Li–S chemical bond have two different type lengths of 2.32 Å and 2.41 Å, as well as the P–S chemical bonds have identical lengths of 2.06 Å and Li–Cl bonds (very weak) as evidenced in Table 1. Such chemical bonds are highly position-dependent and are responsible for the anisotropic quasi-particle phenomena.
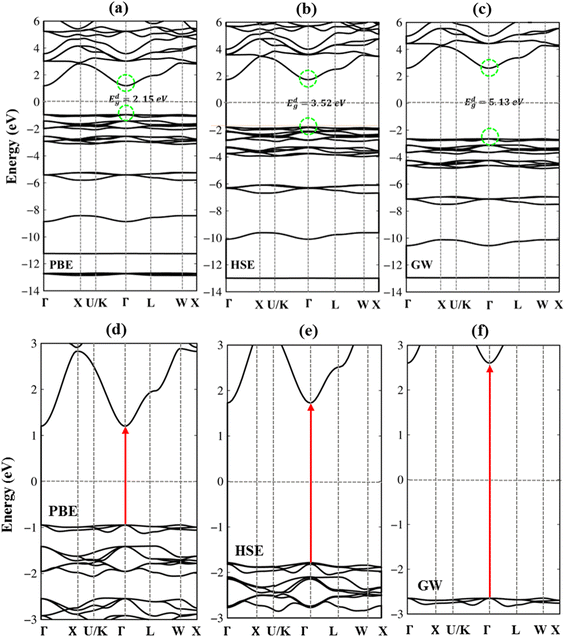
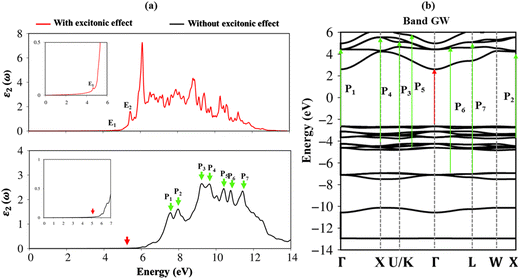
Very interestingly, the three-dimensional (3D) ternary Li6PS5Cl compound exposes unique band structures. In this work, we consider band structure in energy range from −14 eV to 6 eV (Fig. 3(a)–(c)) and from −3 eV to 3 eV (Fig. 3(d)–(f)). The wave-vector-dependent energy spectrum and wave function, the featured quasi-particle properties of this system are indicated along the high-symmetry points. The occupied hole and unoccupied electron spectra are high asymmetry each other spectra about the Fermi level (EF = 0), which directly reflect the very complicated orbital hybridizations in all Li–Cl, Li–S and P–S chemical bonds. The parabolic, linear, and partial flat energy dispersions, a lot of band-edge states, many sub-bands with crossings/non-crossing phenomena are clearly exposed. Most importantly, the conduction-band minimum and the valence-band maximum of relaxed Li6PS5Cl locate at the same Γ point, showing a direct nature (green circles and red arrows). The theoretical prediction for band gap of Li6PS5Cl compound is equal to 2.15 eV (Fig. 3a) under PBE approximations. Using HSE and GW corrections, respectively, provide direct gap values of 3.52 eV (Fig. 3b) and 5.13 eV (Fig. 3c). The former is good agreement with the previous theoretical work,28 while the latter in accordance with the electronic gap measured in STS and requite for the description of excitonic states. Obviously, the large band gap/low dielectric screening, leading to the excitonic effects are very strong and the coupled electron–hole states locate well below the quasi-particle band gap.
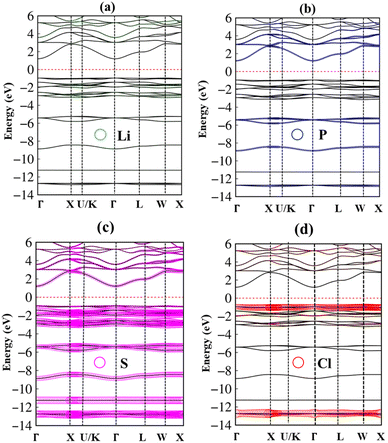
In addition to the basic features of the band structure, the electronic wave functions for occupied hole and unoccupied electron states can reflect useful information on the chemical bonds. Each band state can be considered as a linear superposition of different orbitals. Therefore, it can be decomposed into distinct atomic contributions. The dominance of different atom can be helpful to understand the important roles of the chemical bonds in the electronic properties. The green, blue, pink, and red circles are corresponding to the Li, P, S and Cl atom contributions, respectively (Fig. 4(a)–(d)). In general, the effective occupied and unoccupied states, which are closely related to the orbital hybridizations of the s–sp3, s–sp3 and sp3–sp3 chemical bonds, corresponding to Li–S, Li–Cl and P–S bonds (discussed later) lie in the energy range of the −14 eV < Ec,v < 6.0 eV. Almost all elements have significant contributions to the whole band structure. However, it might be difficult to observe the Lithium-contributions (small green circle) because of the single 2s-orbital. The opposite is true for the P, S and Cl atoms with their contributions which are represented by very large circles in the electronic energy spectrum. Specifically, the sulfur (S) atoms dominate all valence and conduction states since they associate with all the chemical bonds as Li–S and P–S bonds.
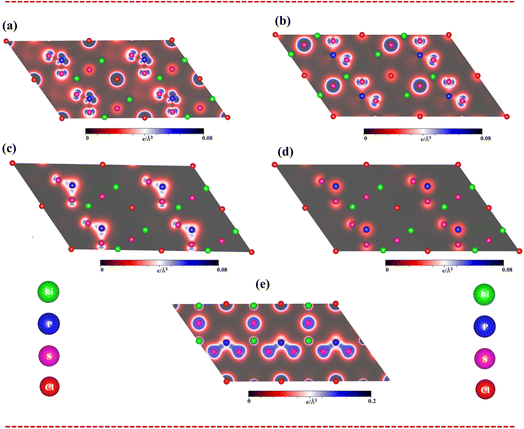
To fully understand bonding characters, the band decomposed charge densities for the Li6PS5Cl compound, which include four active energy domains: (i) the unoccupied states of 2 eV < Ec,v < 6 eV, (ii) the occupied states of −4 eV < Ec,v < −2 eV, (iii) valence states of −6 eV < Ec,v < −4 eV, and (iv) −8 eV < Ec,v < −6 eV, are displayed in Fig. 5(a)–(d). Indeed, the charge density of unoccupied states (Fig. 5a) is dominated by the P-3p and S-3p states. On the other hand, the charge density of occupied states (−4 eV to −2 eV) (Fig. 5b) is governed by the P-3s and S-3p states. The charge density of occupied states (−6 eV to −4 eV) (Fig. 5c) is dominated by the P-3p and S-3p states. Finally, the energy domain of (−8 eV to −6 eV) (Fig. 5d) is governed by the P-3p and S-3p states.
As clearly sketched in Fig. 5(e), the charge density distributions are very useful comprehending to type of all Li–S and P–S chemical bonds. Indeed, there is a noteworthy bonding feature: there is a weak orbital hybridization between Li atoms and S atoms, forming ionic bonds, while the orbital hybridization between P atoms and S atoms is very strong, forming covalent bonds.
Apparently, band-decomposed charge densities and density charge distributions will assist well with band structure and density of states to comprehend the orbital hybridizations in all chemical bonds.
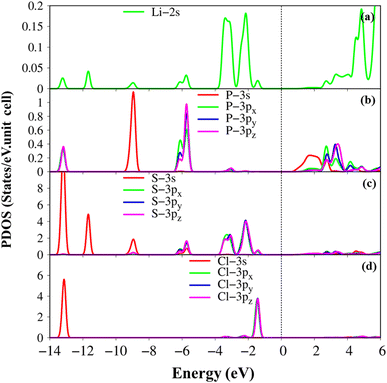
The atom- and projected density of states of the Li6PS5Cl compound is presented in Fig. 6 and 7. The Li-, P-, S- and Cl-orbitals make significant contributions to density of states within a whole energy spectrum (the green, blue, pink, and red curves in Fig. 6, respectively). However, the contributions of P, S and Cl atoms (blue, pink, and red curves) are stronger than Li atom (green curves) because formers provide more active orbitals than with that of the latter. The van Hove singularities of the Li-2s orbital (green curves) and P-/S-/Cl-3s, 3px, 3py, 3pz orbitals (red, green, blue, and pink curves) are merged with each other for both occupied and unoccupied states, forming s–sp3, s–sp3 and sp3–sp3 orbital hybridizations, corresponding to Li–S, Li–Cl and P–S chemical bonds. Besides, the outer 2s-orbital of Li atom is half occupied and has a unique cooperation with the active ones of other atoms. As a result, the Li-related van Hove singularities are available in supporting the orbital hybridizations of each Li–S and Li–Cl bonds. Moreover, the valence state part clearly indicate the strong [3px, 3py, 3pz]–[3px, 3py, 3pz]-orbital hybridizations in P–S chemical bonds, but the weak 2s-[3px, 3py, 3pz] orbital mixings in Li–S and Li–Cl chemical bonds, leading to be comparable with band-decomposed charge densities, and charge density distributions in Fig. 5(b)–(e). Specially, density of states is vanishing in a specific energy range of −1.075 eV ≤ E ≤ 1.075 eV across the Fermi level, indicates a middle gap semiconductor of Eig = 2.15 eV (DFT method). These quasi-particle behaviors are expected to determine the concise physical and chemical pictures of the other properties, such as the threshold transition frequency and prominent absorption structures closely related to the specific orbital hybridizations (consider later).
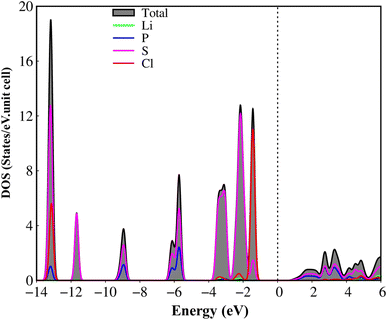 | ||
| Fig. 6 .Van hove singularities in the density of states (DOS) of the Li6PS5Cl compound, coming from Li, P, S and Cl atoms (green, blue, pink, and red curves, respectively) using PBE method. | ||
4. Excitonic effects on optical properties
To fully understand the optical properties of the Li6PS5Cl compound, the imaginary part of dielectric functions in the absence and presence of electron–hole interactions are calculated and shown in Fig. 8a. Clearly, the threshold frequency or optical gap in the absence of electron–hole interaction is equal to the fundamental direct gap of 5.13 eV (red arrow). Of course, to obey the conservation laws, the optical transition process considered in this case cannot induce any crystal momentum transfer. In addition to the optical gap, a lot of prominent peaks are denoted as the green arrows, namely P1–P8, while their corresponding excitations are yielded by using vertical green arrows, respectively in Fig. 8b. The relationship between optical excitations and orbital characters are exposed and designated in Table 2.| Energy (eV) | Label | Vertical excitation in band structure | Orbital hybridizations in P–S bonds |
|---|---|---|---|
| 4.50 | E1 | ||
| 5.13 | E2 | Threshold frequency | 3s, 3px, 3py, 3pz – 3s, 3px, 3py, 3pz |
| 7.40 | P1 | Γ | 3s – 3s, 3px, 3py, 3pz |
| 8.00 | P2 | X | 3s – 3s, 3px, 3py, 3pz |
| 9.20 | P3 | U/K | 3s, 3px, 3py, 3pz – 3s, 3px, 3py, 3pz |
| 9.60 | P4 | X | 3s, 3px, 3py, 3pz – 3s, 3px, 3py, 3pz |
| 10.30 | P5 | Between | 3s – 3s, 3px, 3py, 3pz |
| U/K and Γ | |||
| 11.00 | P6 | Between | 3s – 3s, 3px, 3py, 3pz |
| Γ and L | |||
| 11.40 | P7 | L | 3s – 3s, 3px, 3py, 3pz |
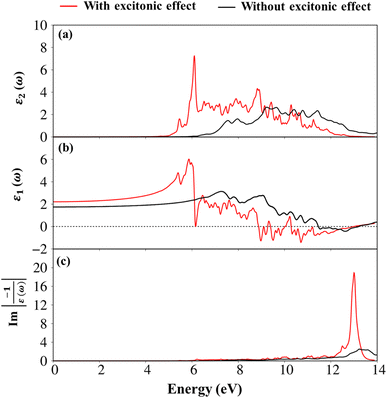
To evaluate the excitonic effects, the electron–hole interactions (called excitonic effects) in imaginary part of dielectric function of Li6PS5Cl compound are also showed in Fig. 8a by seeing red curves. Obviously, after taking into the Coulomb interaction, the enhancement of the electron–hole wave function overlap can create the excitation strength. Therefore, the optical gap value is equal to 4.50 eV (first exciton peak), leading to moving red shift of 0.63 eV (energy binding). The great redshift indicates very strong excitonic effects, and therefore, the stable coupled quasi-particle may survive at the room temperature. Furthermore, the presence of exciton peaks (E1, E2) below the band gap are designed from electron and hole pair interactions at the extreme band edge states, creating to strong excitonic effects. The origin of this scene comes from the large energy band gap/low charge screening combined with rather flat energy sub-bands/large effective mass at the Γ(0,0,0) point, as clearly observed in Fig. 3(d)–(f).
Apparently, the real part ε1(ω),48 and the imaginary part ε2(ω) of the dielectric function ε(ω) are connected each other by the Kramers–Kronig relationship.49 The real part of the dielectric functions is weakly dependent on the energy in the inactive region, such as dielectric constant at zero point ε1(0) are about 2.4 eV (1.7 eV), respectively for presence (absence) of the excitonic effect. Also, ε1(ω) can provide information about the frequencies less, corresponding vanishing range of absorption coefficients α(ω) and low energy reflectance spectrum R(ω).
Interestingly, the simultaneous existence of the zero points of the real part with very weak single-particle transitions exhibit and corresponding to the weak damping of the Plasmon mode of 12.3 eV (13.5 eV) for presence (absence) of excitonic effects, respectively. It is known that the energy loss function (ELF) are especially the collective excitations and then useful for comprehending the screened excitation spectra. The plasmon resonances are about ωp = 12.3 eV (13.5 eV) with (without) excitonic effect which is confirmed by each spectral peak in ELF. This value is rather fitting with the zero points in the real part ε1(ω) and the imaginary part ε2(ω) of the dielectric function in Fig. 9. Very interestingly, the P- (3s, 3px, 3py, 3pz) and S- (3s, 3px, 3py, 3pz) orbitals in P–S chemical bonds are contributed to almost prominent peaks as verified in Fig. 7 and 8.
To consider the other optical properties, we sketch the absorption coefficient (α(ω)) and the reflectance spectra (R(ω)) of Li6PS5Cl compound as showed in Fig. 10(a) and (b). Apparently, the absorption coefficient α(ω) is vanishing while the reflectivity R(ω) is weakly dependent in region from 0 to 4.5 eV (5.13eV) because of lacking to the electronic excitation contributions. Beyond the thresh-hold frequency, α(ω) and R(ω) dramatically change to the excitation model. The different inter-band transitions lead to a rapid increase in the absorption coefficient. The photon energy propagates through the medium and is easily absorbed by the electronic excitations, as observed in Fig. 10(b) by the inverse values of the absorption coefficient of 80 Å (100 Å) for the presence (absence) excitonic effect, respectively. The prominence peak corresponding to the Plasmon mode (ωp) is seen and coincides with the significant decline in R(ω). At the resonance frequency ωp, the reflectance spectra are indicated to vary by 60% (28%) for the presence (absence) under the black (red) curves, respectively.
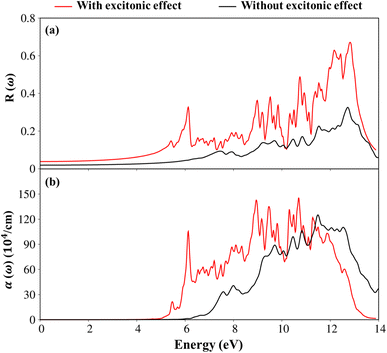 | ||
| Fig. 10 .(a) The reflectance spectra and (b) absorption coefficient with and without excitonic effects of Li6PS5Cl compound, respectively. | ||
5. Conclusions
Summarily, we have attempted to study 3D Li6PS5Cl compound by using first-principles calculations. This system is clearly exposed the featured electronic and optical properties. The crystal symmetry, atom-dominated electronic energy spectrum, band-decomposed charge densities, charge density distribution, and van Hove singularities in density of states are unified under a theoretical framework of quasi-particle viewpoint. This primitive cell compound has 13 atoms (6-Li atoms, 1-P atom, 5-S atoms, and 1-Cl atom), where the position-dependent chemical bonds lead to the highly unusual environment. The cubic crystal symmetry with the significant s–sp3, s–sp3 and sp3–sp3 chemical bonds, corresponding to Li–S, Li–Cl and P–S bonds are responsible for the featured electronic properties: the multi-fold state degeneracies at the high-symmetry points, an direct band gap of Eg = 2.15 eV, 3.52 eV and 5.13 eV for using PBE, HSE and GW methods, respectively, at the Γ point, the high asymmetry of hole and electron bands about the Fermi level, the Li-, P-, S- and Cl- co-dominance within the whole energy range, the non-monotonous and anisotropic wave-vector dependences with the complicated dispersion relations, a lot of band-edge states, the frequent sub-band crossings.In addition to electronic properties, the main features of optical absorption spectra with the presence and absence of excitonic effects are very suitable for establishing the close relations between the specific orbital hybridizations and the vertical transition channels. Plasmon mode value is 12.3 eV (13.5 eV), corresponding to Landau damping (zero points) of the real and imaginary part of the dielectric functions. Such characteristics are attributed to the active orbital hybridizations. Our quasi-particle framework50 is available for discovering the other interesting properties of the emerging materials.
Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This work was financially supported by the Hierarchical Green-Energy Materials (Hi-GEM) Research Center, from The Featured Areas Research Center Program within the framework of the Higher Education Sprout Project by the Ministry of Education (MOE) and the Ministry of Science and Technology (MOST 111-2112-M-006-020) in Taiwan.References
- F. Marchini, S. Saha, D. Alves Dalla Corte and J. M. Tarascon, Li-Rich Layered Sulfide as Cathode Active Materials in All-Solid-State Li–Metal Batteries, ACS Appl. Mater. Interfaces, 2020, 12(13), 15145–15154 CrossRef CAS PubMed.
- M. Li, et al., In Situ Formed Li–Ag Alloy Interface Enables Li10GeP2S12-Based All-Solid-State Lithium Batteries, ACS Appl. Mater. Interfaces, 2021, 13(42), 50076–50082 CrossRef CAS PubMed.
- D. Liu, W. Zhu, Z. Feng, A. Guerfi, A. Vijh and K. Zaghib, Recent progress in sulfide-based solid electrolytes for Li-ion batteries, Mater. Sci. Eng., B, 2016, 213, 169–176 CrossRef CAS.
- M. S. Syali, D. Kumar, K. Mishra and D. Kanchan, Recent advances in electrolytes for room-temperature sodium-sulfur batteries: a review, Energy Storage Materials, 2020, 31, 352–372 CrossRef.
- Y. Yan, et al., A lithium amide-borohydride solid-state electrolyte with lithium-ion conductivities comparable to liquid electrolytes, Adv. Energy Mater., 2017, 7(19), 1700294 CrossRef.
- Y. Kato, et al., High-power all-solid-state batteries using sulfide superionic conductors, Nat. Energy, 2016, 1(4), 1–7 Search PubMed.
- B.-N. Yun, et al., Facile Method for the Formation of Intimate Interfaces in Sulfide-Based All-Solid-State Batteries, ACS Appl. Mater. Interfaces, 2022, 14(7), 9242–9248 CrossRef PubMed.
- C. Yu, F. Zhao, J. Luo, L. Zhang and X. Sun, Recent development of lithium argyrodite solid-state electrolytes for solid-state batteries: synthesis, structure, stability and dynamics, Nano Energy, 2021, 83, 105858 CrossRef CAS.
- S. Wang, et al., High-conductivity argyrodite Li6PS5Cl solid electrolytes prepared via optimized sintering processes for all-solid-state lithium–sulfur batteries, ACS Appl. Mater. Interfaces, 2018, 10(49), 42279–42285 CrossRef CAS PubMed.
- R. Xu, et al., Recent Developments of All-Solid-State Lithium Secondary Batteries with Sulfide Inorganic Electrolytes, Chem.–Eur. J., 2018, 24(23), 6007–6018 CrossRef CAS PubMed.
- O. Ostroverkhova, Organic optoelectronic materials: mechanisms and applications, Chem. Rev., 2016, 116(22), 13279–13412 CrossRef CAS PubMed.
- M. Tatsumisago, M. Nagao and A. Hayashi, Recent development of sulfide solid electrolytes and interfacial modification for all-solid-state rechargeable lithium batteries, J. Asian Ceram. Soc., 2013, 1(1), 17–25 CrossRef.
- Z. Zhang, et al., Synthesis and characterization of argyrodite solid electrolytes for all-solid-state Li-ion batteries, J. Alloys Compd., 2018, 747, 227–235 CrossRef CAS.
- C. Yu, et al., Facile synthesis toward the optimal structure-conductivity characteristics of the argyrodite Li6PS5Cl solid-state electrolyte, ACS Appl. Mater. Interfaces, 2018, 10(39), 33296–33306 CrossRef CAS PubMed.
- N. C. Rosero-Navarro, A. Miura and K. Tadanaga, Preparation of lithium ion conductive Li6PS5Cl solid electrolyte from solution for the fabrication of composite cathode of all-solid-state lithium battery, J. Sol-Gel Sci. Technol., 2019, 89(1), 303–309 CrossRef CAS.
- S. Yubuchi, S. Teragawa, K. Aso, K. Tadanaga, A. Hayashi and M. Tatsumisago, Preparation of high lithium-ion conducting Li6PS5Cl solid electrolyte from ethanol solution for all-solid-state lithium batteries, J. Power Sources, 2015, 293, 941–945 CrossRef CAS.
- C. Yu, L. van Eijck, S. Ganapathy and M. Wagemaker, Synthesis, structure and electrochemical performance of the argyrodite Li6PS5Cl solid electrolyte for Li-ion solid state batteries, Electrochim. Acta, 2016, 215, 93–99 CrossRef CAS.
- J. Zhang, et al., Unraveling the intra and intercycle interfacial evolution of Li6PS5Cl-based all-solid-state lithium batteries, Adv. Energy Mater., 2020, 10(4), 1903311 CrossRef CAS.
- J. Auvergniot, A. Cassel, D. Foix, V. Viallet, V. Seznec and R. Dedryvère, Redox activity of argyrodite Li6PS5Cl electrolyte in all-solid-state Li-ion battery: an XPS study, Solid State Ionics, 2017, 300, 78–85 CrossRef CAS.
- G. Liu, W. Weng, Z. Zhang, L. Wu, J. Yang and X. Yao, Densified Li6PS5Cl nanorods with high ionic conductivity and improved critical current density for all-solid-state lithium batteries, Nano Lett., 2020, 20(9), 6660–6665 CrossRef CAS PubMed.
- B. Lv, T. Qian and H. Ding, Angle-resolved photoemission spectroscopy and its application to topological materials, Nat. Rev. Phys., 2019, 1(10), 609–626 CrossRef.
- K. Hipps, Scanning tunneling spectroscopy (STS), in Handbook of applied solid state spectroscopy, Springer, 2006, pp. 305–350 Search PubMed.
- N. T. Han, V. K. Dien and M.-F. Lin, Excitonic effects in the optical spectra of Li2SiO3 compound, Sci. Rep., 2021, 11(1), 1–10 CrossRef PubMed.
- N. T. Han, et al., Comprehensive understanding of electronic and optical properties of Li2SiO3 compound, in First-Principles Calculations for Cathode, Electrolyte and Anode Battery Materials, IOP Publishing, 2021 Search PubMed.
- N. T. Han, V. K. Dien, N. T. T. Tran, D. K. Nguyen, W.-P. Su and M.-F. Lin, First-principles studies of electronic properties in lithium metasilicate (Li2SiO3), RSC Adv., 2020, 10(41), 24721–24729 RSC.
- N. T. Han, V. K. Dien and M.-F. Lin, Electronic and Optical Properties of CsGeX3 (X = Cl, Br, and I) Compounds, ACS Omega, 2022, 7(29), 25210 CrossRef PubMed.
- V. K. Dien, N. T. Han, W.-P. Su and M.-F. Lin, Spin-dependent optical excitations in LiFeO2, ACS Omega, 2021, 6(39), 25664–25671 CrossRef CAS PubMed.
- Z. Wang and G. Shao, Theoretical design of solid electrolytes with superb ionic conductivity: alloying effect on Li+ transportation in cubic Li6PA5X chalcogenides, J. Mater. Chem. A, 2017, 5(41), 21846–21857 RSC.
- H. Shu, Strain effects on stability, electronic and optical properties of two-dimensional C4X2 (X = F, Cl, Br), J. Mater. Chem. C, 2021, 9(13), 4505–4513 RSC.
- H. Shu, Highly-anisotropic carrier transport and optical properties of two-dimensional titanium trisulfide, J. Mater. Sci., 2022, 57(5), 3486–3496 CrossRef CAS.
- H. Shu, Adjustable electro-optical properties of novel graphene-like SiC2 via strain engineering, Appl. Surf. Sci., 2021, 559, 149956 CrossRef CAS.
- H. Shu, Novel Janus diamane C4 FCl: a stable and moderate bandgap semiconductor with a huge excitonic effect, Phys. Chem. Chem. Phys., 2021, 23(34), 18951–18957 RSC.
- P. Hohenberg and W. Kohn, Density functional theory (DFT), Phys. Rev., 1964, 136, B864 CrossRef.
- J. Hafner, Ab initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29(13), 2044–2078 CrossRef CAS PubMed.
- H. Peng and J. P. Perdew, Rehabilitation of the Perdew-Burke-Ernzerhof generalized gradient approximation for layered materials, Phys. Rev. B, 2017, 95(8), 081105 CrossRef.
- M. Shishkin and G. Kresse, Implementation and performance of the frequency-dependent G W method within the PAW framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(3), 035101 CrossRef.
- J. McClain, Q. Sun, G. K.-L. Chan and T. C. Berkelbach, Gaussian-based coupled-cluster theory for the ground-state and band structure of solids, J. Chem. Theory Comput., 2017, 13(3), 1209–1218 CrossRef CAS PubMed.
- T. M. Henderson, J. Paier and G. E. Scuseria, Accurate treatment of solids with the HSE screened hybrid, Phys. Status Solidi B, 2011, 248(4), 767–774 CrossRef CAS.
- A. Schindlmayr, T. J. Pollehn and R. W. Godby, Spectra and total energies from self-consistent many-body perturbation theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58(19), 12684 CrossRef CAS.
- A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, wannier90: A tool for obtaining maximally-localised Wannier functions, Comput. Phys. Commun., 2008, 178(9), 685–699 CrossRef CAS.
- G. Pizzi, et al., Wannier90 as a community code: new features and applications, J. Phys.: Condens. Matter, 2020, 32(16), 165902 CrossRef CAS PubMed.
- A. Crépieux and P. Bruno, Theory of the anomalous Hall effect from the Kubo formula and the Dirac equation, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64(1), 014416 CrossRef.
- R. Cutkosky, Solutions of a Bethe-Salpeter equation, Phys. Rev., 1954, 96(4), 1135 CrossRef CAS.
- S. Hirata and M. Head-Gordon, Time-dependent density functional theory within the Tamm–Dancoff approximation, Chem. Phys. Lett., 1999, 314(3–4), 291–299 CrossRef CAS.
- T. Nagatomi, R. Shimizu and R. Ritchie, Energy loss functions for electron energy loss spectroscopy, Surf. Sci., 1999, 419(2–3), 158–173 CrossRef CAS.
- S.-I. Thomasson, On the absorption coefficient, Acta Acust. Acust., 1980, 44(4), 265–273 Search PubMed.
- S. Mallick and L. N. Frazer, Practical aspects of reflectivity modeling, Geophysics, 1987, 52(10), 1355–1364 CrossRef.
- G. F. Bertsch, J.-I. Iwata, A. Rubio and K. Yabana, Real-space, real-time method for the dielectric function, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62(12), 7998 CrossRef CAS.
- D. C. Hutchings, M. Sheik-Bahae, D. J. Hagan and E. W. Van Stryland, Kramers-Krönig relations in nonlinear optics, Opt. Quantum Electron., 1992, 24(1), 1–30 CrossRef CAS.
- H. Shu and X. Liu, Tuning electronic and optical properties of graphene/h-BN heterobilayer via surface modification, Appl. Surf. Sci., 2022, 605, 154591 CrossRef CAS.
- C. Yu, et al., Unravelling li-ion transport from picoseconds to seconds: bulk versus interfaces in an argyrodite li6ps5cl–li2s all-solid-state li-ion battery, J. Am. Chem. Soc., 2016, 138(35), 11192–11201 CrossRef CAS PubMed.
- R. P. Rao and S. Adams, Studies of lithium argyrodite solid electrolytes for all-solid-state batteries, Phys. Status Solidi A, 2011, 208(8), 1804–1807 CrossRef CAS.
- K. Hikima, N. H. H. Phuc, H. Tsukasaki, S. Mori, H. Muto and A. Matsuda, High ionic conductivity of multivalent cation doped Li6PS5Cl solid electrolytes synthesized by mechanical milling, RSC Adv., 2020, 10(38), 22304–22310 RSC.
| This journal is © The Royal Society of Chemistry 2022 |