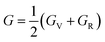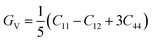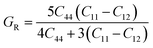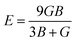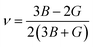DOI:
10.1039/D2RA05602J
(Paper)
RSC Adv., 2022,
12, 32338-32349
Examining computationally the structural, elastic, optical, and electronic properties of CaQCl3 (Q = Li and K) chloroperovskites using DFT framework
Received
7th September 2022
, Accepted 3rd November 2022
First published on 11th November 2022
Abstract
This study presents the investigations of structural, elastic, optical, and electronic properties of CaQCl3 (Q = Li and K) chloroperovskites for the first time using the DFT framework. The WIEN2K and IRelast packages are used in which the exchange–correlation potential of the modified Becke–Johnson potential (TB-mBJ) is used for obtaining better results. The optimized crystal structural parameters comprising the lattice constant, optimum volume, ground state energy, bulk modulus, and the pressure derivative of bulk modulus are computed by fitting the primitive unit cell energy versus primitive unit cell volume using the Birch–Murnaghan equation of state. The elastic properties which consist of cubic elastic constants, Poisson's ratio, elastic moduli, anisotropy factor, and the Pugh ratio are computed using the very precise IRelast package incorporated inside WIEN2K. The electronic properties are analyzed from the computation of electronic bands structure and density of states (DOS), and it is concluded that an indirect band gap of 4.6 eV exists for CaLiCl3 and a direct band gap of 3.3 eV for CaKCl3 which confirms that CaLiCl3 is an insulator while CaKCl3 is a wide band gap semiconductor. The analysis of DOS shows that the greater contribution to the conduction band (CB) occurs because of the “Ca” element whereas in the valence band the major contribution is from the “Cl” element. The spectral curves of various parameters of optical properties from 0 eV up to 42 eV incident photon energies are observed and it is found that the CaQCl3 (Q = Li and K) chloroperovskites are optically active having a high absorption coefficient, optical conductivity, optical reflectivity, and energy loss function from 25 eV to 35 eV incident photon energies. The applications of these materials can be deemed to alter or control electromagnetic radiation in the ultraviolet (UV) spectral regions. In summary, the results for selected CaQCl3 (Q = Li and K) chloroperovskites depict that these are important compounds and can be used as scintillators, and energy storage devices, and in many modern electronic gadgets.
1. Introduction
Discovering the physical properties of materials for practical use has consistently remained a major area of research. Even in a scientifically equipped society, materials scientists are always searching for the best and most effective materials. Perovskites have drawn a lot of interest because of their important applications in optical devices,1–3 energy storage,4 and semiconducting industries.5–9 Researchers in materials science have studied the perovskite materials using DFT10–13 and a wide variety of substances are found in the perovskites family, ranging from insulators to superconductors and from diamagnetic to colossal magnetoresistive (CMR) substances. Perovskite materials are also preferred as lens materials since they do not exhibit the birefringence that makes lens design challenging.14 The common chloroperovskite structure is ABCl3, where “A” and “B” represents alkali metals and alkaline earth metals respectively, whereas “Cl” is the chlorine element. Chloroperovskites possess striking properties, specifically lead-containing chloroperovskites, and have possible use in the optical and electronic industries. The chloroperovskites usually hold a very large band gap due to which its applications can be deemed in many modern energy storage devices. The nature of wide-band-gap energy is suitable for it to absorb or emit ultraviolet (UV) light in applications of optoelectronic devices. Energy storage is a crucial component of a large number and variety of electronic devices, particularly for mobile devices and electric or hybrid vehicles. According to the literature, chloroperovskites are more stable than other halides perovskites.15–17 Due to their special characteristics of tunable laser,18 electron–phonon interactions,19,20 crystal fields,21 ferroelectricity,22 phase transition behaviors,23 antiferromagnetism,24 semiconductivity,25 and as a scintillating material,26 the perovskite compounds have a comprehensive range of applications. The high intensity, high directivity, and high energy27 scintillating materials and scintillators are widely employed in a variety of applications,28,29 including healthcare (medical imaging),30 calorimetry in high energy physics, territorial security,31 industrial screening,32 and astronomy.33 Scintillators are substances that may convert ionizing “X” or photons into light that is visible or almost visible (near ultraviolet). The light emitted will be transformed into an electrical signal that can then be examined depending on the applications.34,35 As a result of high band gaps, high absorption coefficients, and economical manufacturing, chloroperovskite has recently been regarded as a scintillating material.36–38 After extensive research on chloroperovskites, we conclude that the existence of the “Ca” element in the ternary CaQCl3 (Q = Li and K) choloroperovskites shows a significant role in structural, elastic, and optoelectronic properties. Nowadays the DFT is proven to be the most precise and accurate tool for the computation of different various physical properties of a material.39–41 This research intends to provide the first insight into some of the fundamental physical properties of ternary CaQCl3 (Q = Li and K) chloroperovskites for the first time using the DFT framework for the possible applications in energy-storing devices, scintillating materials, and many modern technological devices.
2. Computational methodology
The presented research is done using the WIEN2K42 simulation code to carry out the plane-wave and self-consistent (PWSCF) approach, which is based on DFT (density functional theory).43 For the crystal structural optimization, the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE)44 is employed to compute the fundamental structural properties and elastic properties. The IRelast package45 is used for the computations of different parameters of elastic properties. The exchange–correlation potential of the modified Becke–Johnson potential (TB-mBJ)46 is used for obtaining better results for electronic properties (i.e. band gap and DOS) and optical properties. The number of 2000 K-points is used to sample the first Brillouin zone in reciprocal space. To attain a reasonable degree of convergence, this study takes into account some FP-LAPW basis functions up to RMT × Kmax (where RMT is the minimum radius of the muffin-tin spheres equal to 8 and Kmax specifies the magnitude of the biggest k-vector in the plane wave expansions). The RMT values are chosen for each atom in such a way that there is no overlap and the muffin-tin radii “RMT” for constituent atomic spheres are 2.5, 1.78, and 1.92 atomic units (a. u.) for “Ca”, “Q” where (Q = Li and K), and “Cl”, respectively. The self-consistent field (SCF) computations are observed to have met at 0.001 mRy total energy. The optical properties are computed from the basic complex dielectric function of the form ε(w) = ε1(w) + iε2(w).47 The xcrysden,48 Gnuplot,49 origin50 and xmgrace51 are mainly used in research for graphing purpose. The aforementioned computational is employed for the first insight into some of the physical properties including structural, elastic, optical, and electronic properties of ternary CaQCl3 (Q = Li and K) choloroperovskites.
3. Results and discussion
This portion describes and presents in detail the results obtained for ternary CaQCl3 (Q = Li and K) choloroperovskites using the research methodology presented above. Each physical property is discussed here one by one.
3.1 The structural properties
To access other physical properties (such as electrical, optical, and elastic), the investigation of structural properties for these materials is a crucial stage in the ab initio simulation analysis. In this section, we used the GGA-PBE approximation to examine the structural characteristics of CaQCl3 (Q = Li and K) chloroperovskites belonging to the space group-221 (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The primitive crystalline unit cell of both the CaQCl3 (Q = Li and K) chloroperovskites are depicted in Fig. 1. Both the crystalline unit cell has five (5) atoms, where Ca at Wyckoff positions of (0, 0, 0), Q = Li and K lies at (0.5 0.5 0.5), and Cl positioned at (0, 0.5 0.5). The tolerance factor “τ” is computed for the selected chloroperovskites and found to be 0.94 for CaKCl3 and 0.98 for CaLiCl3, which confirms the cubic structure of the compounds. The fundamental structural parameters including the unit cell optimum volume, unit cell optimum energy, optimized lattice constant, pressure derivative of bulk modulus, and bulk modulus, are determined by fitting the primitive unit cell energy as a function of primitive unit cell volume using the Birch–Murnaghan equation of state,52 as described as:
m). The primitive crystalline unit cell of both the CaQCl3 (Q = Li and K) chloroperovskites are depicted in Fig. 1. Both the crystalline unit cell has five (5) atoms, where Ca at Wyckoff positions of (0, 0, 0), Q = Li and K lies at (0.5 0.5 0.5), and Cl positioned at (0, 0.5 0.5). The tolerance factor “τ” is computed for the selected chloroperovskites and found to be 0.94 for CaKCl3 and 0.98 for CaLiCl3, which confirms the cubic structure of the compounds. The fundamental structural parameters including the unit cell optimum volume, unit cell optimum energy, optimized lattice constant, pressure derivative of bulk modulus, and bulk modulus, are determined by fitting the primitive unit cell energy as a function of primitive unit cell volume using the Birch–Murnaghan equation of state,52 as described as:| |
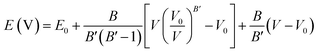 | (1) |
where in the equation above E0, B, B′, V, and V0 are respectively, the optimum value of total energy, the bulk modulus, the pressure derivative of bulk modulus, the total unit cell volume, and the optimized unit cell volume.
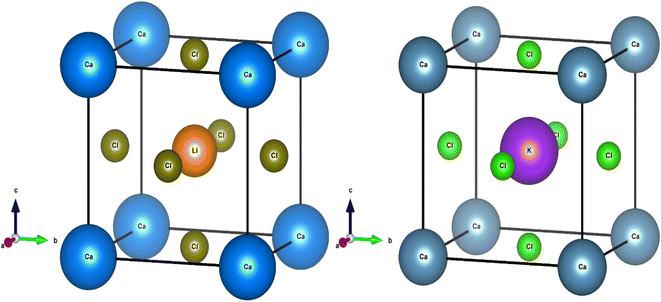 |
| | Fig. 1 The investigated crystal structures of CaQCl3 (Q = Li and K) chloroperovskites. | |
The structural optimization curves computed using the GGA approximation are depicted in Fig. 2, and the optimized values that are obtained from the Birch–Murnaghan fit curves are provided in Table 1.
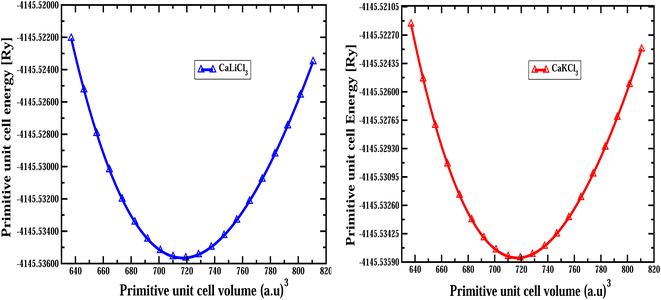 |
| | Fig. 2 The computed optimization of primitive unit cell volume versus primitive unit cell energy for CaQCl3 (Q = Li and K) chloroperovskites in the cubic phase. | |
Table 1 The predicted optimized structural parameters include the lattice constant a0 (Å), bulk modulus B (GPa), pressure derivative of bulk modulus B', optimum volume V0 (a.u)3, ground state energy E0 (Ry), the formation energies ΔHf (eV) and the tolerance factor “τ” for ternary CaQCl3 (Q = Li and K) chloroperovskites
| Optimized structural parameters |
CaKCl3 |
CaLiCl3 |
| a0 (lattice constant) in Å |
5.3795 |
4.6380 |
| B (bulk modulus) in GPa |
79.43 |
72.66 |
| Pressure derivative of bulk modulus B′ (GPa) |
5.76 |
7.21 |
| Optimum volume V0 (a.u)3 |
720.76 |
719.32 |
| Ground state energy E0 (Ry) |
−4145.53 |
−4145.49 |
| ΔHf (eV) |
−8.46 |
−7.93 |
| τ |
0.94 |
0.98 |
The formation energies in the cubic phase of the ternary CaQCl3 (Q = Li and K) chloroperovskites are calculated using the expression below, which proved the chemical stability of the complex compounds.
| | |
ΔHf = Etotal(CaQCl3) − ECa − EQ − 3ECl
| (2) |
where in the above
eqn (2), Δ
Hf is the formation energy,
Etotal(CaQCl
3) is the total optimum energy of CaQCl
3 (Q = Li and K),
ECa is the ground state energy of the “Ca” atom,
EQ shows the ground energy of Q = Li and K atoms and
ECl shows the ground energy of chlorine atom. The values of the formation energies that are computed are listed in
Table 1, and it is revealed that all the results are negative, indicating that ternary CaQCl
3 (Q = Li and K) chloroperovskites compounds may be synthesized experimentally.
3.1.1 Phonon dispersion curves. The phonon dispersion curves along the high symmetries points are computed for CaQCl3 (Q = Li and K) chloroperovskites compounds for the sake of stability purposes. It is seen from the dispersion curves of the Fig. 3 that there exist negative peak dispersion curves below zero frequency limit, indicating that both the materials are unstable.
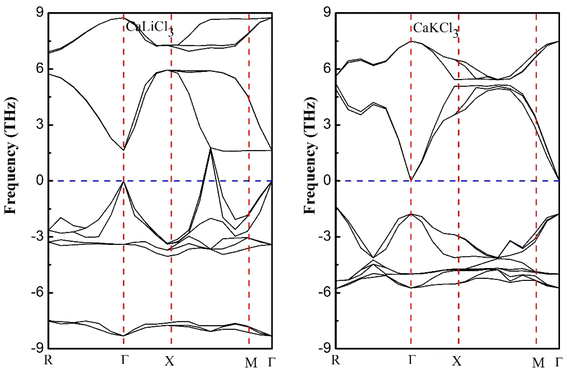 |
| | Fig. 3 Phonon dispersion curves at high symmetries points for ternary CaQCl3 (Q = Li and K) chloroperovskites compounds. | |
3.2 The electronic properties
A first-class study of the electronic band structure and DOS is interested in the electronic properties of a solid to ascertain the nature of chloroperovskite materials, including whether they are metals, semiconductors, or insulators, as well as the kinds of bonds that are formed between the various elements of these materials and their gap energies. After optimizing a material's structure utilizing a 2000 number of k-points in the first Brillouin zone, the band structure of the material can be ascertained using DFT calculations. According to the locations of high symmetry points that is “M–Γ” and “Γ–Γ” shown in Fig. 4, the band structures of both the examined ternary CaQCl3 (Q = Li and K) chloroperovskites compounds are predicted through the TB-mBJ approximation in the Brillouin zone between −6 eV and +6 eV. The band structure for CaLiCl3 shows that the valence band's maximum (VBM) lies at “M” symmetry points, whereas the conduction band's minimal (CBM) is situated at the “Γ” symmetry points. We can infer from this analysis that the band structure has an indirect nature from “M–Γ” with a band gap “Eg” of 4.6 eV for CaLiCl3 and thus act as an insulator. The band structure analysis for CaKCl3 depicts a direct nature from “M–M” with a band gap “Eg” of 3.3 eV and displays the nature of a wide band gap semiconductor. Based on the predicted electronic band gap the application for these materials can be deemed in many energy storage devices and semiconducting industries.
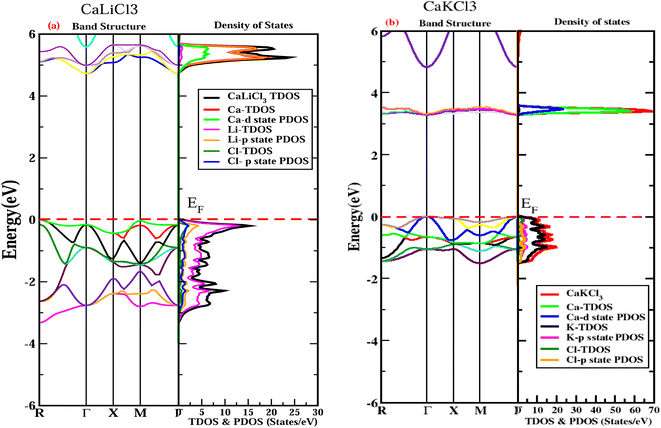 |
| | Fig. 4 The examined fitted electronic band structures and DOS for CaQCl3 (Q = Li and K) chloroperovskites at high symmetries points in the first Brillion zone using TB-mBJ approximation. | |
The deep insight into the electronic properties of materials requires the analysis of DOS which includes TDOS and PDOS (total density of states and partial density of states) as displayed in the Fig. 3 within the energy range of −6 eV to 6 eV for CaQCl3 (Q = Li and K) chloroperovskites. The horizontal red dotted line in both graphs at 0 eV shows the Fermi energy level (EF). The portion of the graph that lies above the Fermi level is known as the conduction band (CB) whereas the portion below depicts the valence band (VB). The DOS describes deeply the contributions of different elemental electronic states to the “VB” and “CB”. The dominant participation in the states of “VB” adjacent to the Fermi level is due to the “Li” elemental part, as shown by the magenta and by Li-p state for CaLiCl3 and “K” and K-p state for CaKCl3 in Fig. 4. The greater contribution in the states of the “CB” occurs from the “Ca” and Ca-d state elements for both the CaQCl3 (Q = Li and K) chloroperovskites compounds. The larger band gap that exists in CaLiCl3 material is because of the Ca-d and Li-p states and in CaKCl3 is due to the Ca-d and K-p states. The electronic band gap depicted in DOS is fully consistent with the gap in the band structures for CaQCl3 (Q = Li and K) chloroperovskites.
3.3 The optical properties
This section of results and discussion describe in very detail the different parameters associated with the optical properties of CaQCl3 (Q = Li and K) chloroperovskites. As it is determined that the compounds CaLiCl3 possess an insulating nature with an indirect band gap and CaKCl3 with a direct wide band gap based on the electronic properties and using the band structure; as a result, these compounds are very suitable for optical applications. The following formulas are used to compute the reflectivity, refractive index, extinction coefficient, and absorption coefficient for several optical properties.53| | |
ε(w) = ε1(w) + iε2(w)
| (3) |
| |
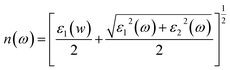 | (4) |
| |
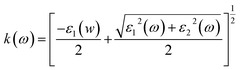 | (5) |
| |
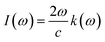 | (6) |
| |
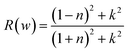 | (7) |
| |
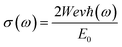 | (8) |
All the fundamental optical properties are computed from the dielectric function in incident photon energies from 0 eV to 42 eV employing the TB-mBJ approach with an optimized lattice constant.
3.3.1 The dielectric function (ε1(w), ε2(w)). The dielectric function is crucial for calculating optical properties since it defines the material's optical reaction at all photon energies. Optical dielectric constants are critical to modeling the electronic and optical properties of materials. The dielectric constant mainly improved the charge density of the materials. The real part represents the ability of the material to store the electric energy and is related to the polarization while the imaginary part is responsible for the damping of the wave and dissipation of energy. It is very clear in Fig. 5 of the real part of the dielectric function that the spectra for both materials are consistent with each other in terms of the pattern. The curves of “ε1(w)” varies from 0 eV incident photon energy up to 42 eV, which shows that at the low range of photon energy the curve rises to a maximum positive peak of 5.3 for CaLiCl3 and 3.7 for CaKCl3. Both the CaQCl3 (Q = Li and K) chloroperovskites achieve negative maximum values which shows polarization in these energy regions. The real static “ε1(0)” dielectric function value for CaLiCl3 is 3 and that for CaKCl3 is 2.5. The analysis of the optical transition from the valence band to the conduction band requires the description and understanding of the imaginary part “ε2(w)” of the dielectric function. The spectra of “ε2(w)” for both the interesting materials are shown on the right side of Fig. 5. The maximum peaks that occur for both materials are 5.8 for CaLiCl3 and 5.6 for CaKCl3 in the photon energy range from 0 eV up to 42 eV. The maximum peaks of “ε2(w)” spectra lie at a high energy photon range, which confirms that both ternary CaQCl3 (Q = Li and K) chloroperovskites compounds possess a very good absorption of light in the ultraviolet range.
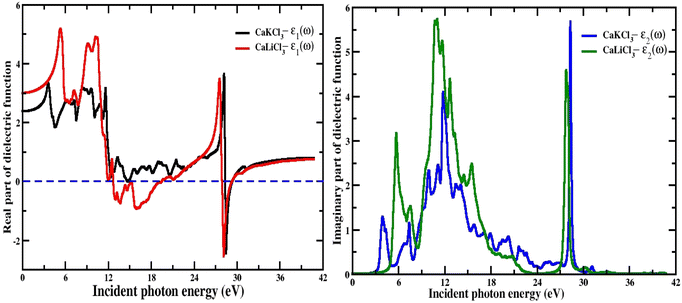 |
| | Fig. 5 The computed real and imaginary parts of dielectric function for CaQCl3 (Q = Li and K) chloroperovskites. | |
3.3.2 The optical conductivity. The connection between the strength of the generated electric field's amplitude and the material's induced current density at a specified frequency is determined by the optical conductivity of a material. The computed optical conductivity spectral curves for both the ternary CaQCl3 (Q = Li and K) chloroperovskites compounds are presented in the Fig. 6 within the incident photon energy ranges from 0 eV up to 42 eV. It is very clear in the Fig. 6 that the optical conductivity starts at the incident photon energy levels which is consistent with the electronic band gap energy. The maximum optical conductivity for CaLiCl3 reaches 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 Ohm−1 cm−1 at 28 eV photon energy while that for CaKCl3 is 17
200 Ohm−1 cm−1 at 28 eV photon energy while that for CaKCl3 is 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 Ohm−1 cm−1 at 26 eV incident photon energy. Both ternary CaQCl3 (Q = Li and K) chloroperovskites compounds possess high optical conductivity at the high energy level, which gives a clue that these materials can be used in the ultraviolet range in optical devices.
250 Ohm−1 cm−1 at 26 eV incident photon energy. Both ternary CaQCl3 (Q = Li and K) chloroperovskites compounds possess high optical conductivity at the high energy level, which gives a clue that these materials can be used in the ultraviolet range in optical devices.
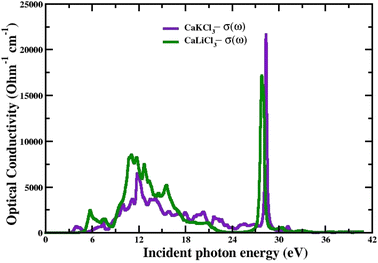 |
| | Fig. 6 The computed optical conductivity for CaQCl3 (Q = Li and K) chloroperovskites. | |
3.3.3 The absorption Co-efficient. It is determined using eqn (6) and is identified as the amount of light intensity absorbed in a unit length of the material.54 Fig. 7, which depicts the absorption coefficient spectrum generated from the TB-mBJ approximation, describes the behavior of the I(w) (absorption coefficient) and how it behaves similarly to the dielectric constant ε(w). We observe that there is no light absorption below the threshold energy, which is very expected given that below the bands, we are unable to induce electronic band transitions from the valence to the conduction band.55 The critical values of I(w) for both the CaQCl3 (Q = Li and K) chloroperovskites are higher than the values of the band gap measured from the band structure. The maximum absorption peak that occurs is 527 cm−1 for CaKCl3 and 521 cm−1 for CaLiCl3 at incident photon energies of 28 eV and 26 eV respectively which are more useful at ultraviolet ranges.
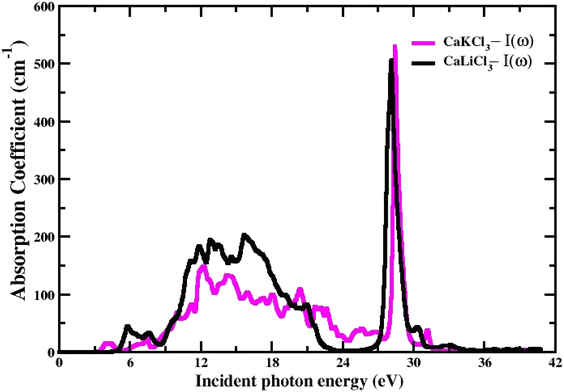 |
| | Fig. 7 The computed absorption coefficient for CaQCl3 (Q = Li and K) chloroperovskites. | |
3.3.4 The extinction co-efficient. The spectrum of extinction coefficient K(ω), investigated for the selected CaQCl3 (Q = Li and K) chloroperovskites materials are presented in Fig. 8 within the incident photon energy from 0 eV up to 42 eV. The high values of K(ω) in the shorter wavelength range indicate that these films are opaque in this range since the extinction coefficient K(ω), is a measure of the amount of light lost owing to scattering and absorption per unit volume. The curve's oscillatory form results from an interference effect that manifests at longer wavelengths. It is very clear from Fig. 8 that both the materials are opaque in the lower range of incident photon energies and the interference effect is observed at the longer wavelengths regions.
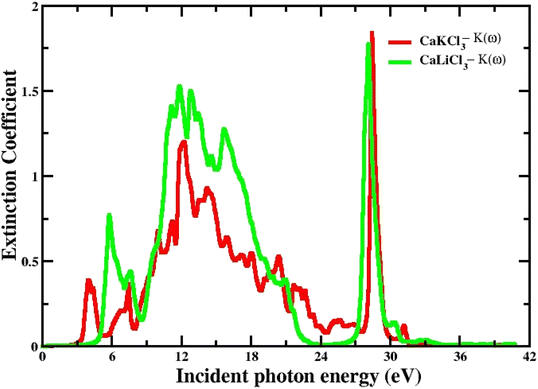 |
| | Fig. 8 The computed extinction co-efficient for CaQCl3 (Q = Li and K) chloroperovskites. | |
3.3.5 The refractive index. The refractive index n(ω), which is determined by eqn (4) and is directly related to the real dielectric function, describes the speed of light propagation at the density of the material and is related directly to the real part of the dielectric function “ε1(w)”. Fig. 9 shows the computed curves of “ε1(w)” in the incident photon energy of 0 eV to 42 eV for ternary CaQCl3 (Q = Li and K) chloroperovskites. The static refractive index n(0) for both compounds is 1.75 for CaLiCl3 and 1.58 for CaKCl3. As can be seen from the Fig. 9 that the refractive index goes on increasing and decreasing patterns while increasing the incident photon energy. The maximum peak of n(ω) occurs for CaLiCl3 is 2.48 and that for CaKCl3 is 2.25.
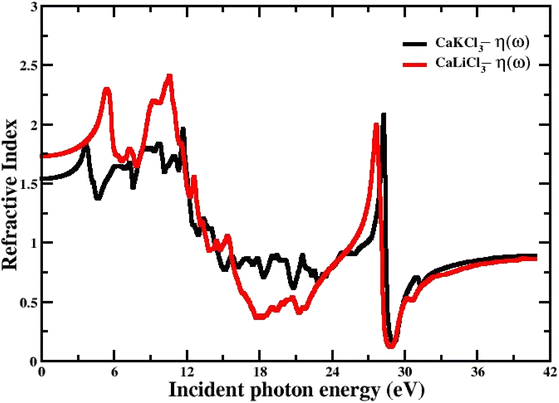 |
| | Fig. 9 The computed refractive index for CaQCl3 (Q = Li and K) chloroperovskites. | |
3.3.6 The optical reflectivity. The power reflected at a material's surface is defined as reflectivity. Fig. 10 shows the R(w) given by eqn (7) and the obtained spectral curves of R(w) for the CaQCl3 (Q = Li and K) chloroperovskites. The static values of R(0) for CaQCl3 (Q = Li and K) are 0.05 for CaKCl3 and 0.08 for CaLiCl3 respectively. The optical reflectivity is very small in the photon energies ranging from 0 eV to 5 eV and further increasing the photon energy the R(w) spectra increases for both the compounds reaches to maximum values of 0.74 for CaLiCl3 and 0.63 for CaKCl3 at the high photon ultraviolet energy ranges.
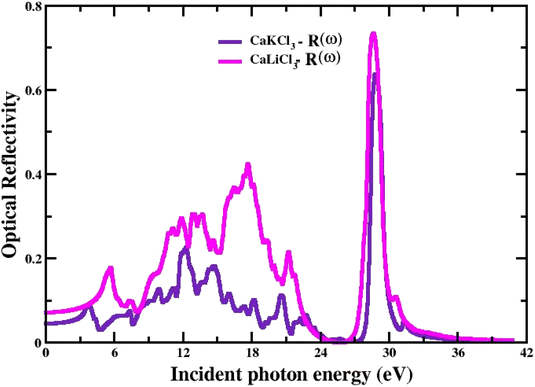 |
| | Fig. 10 The computed optical reflectivity for CaQCl3 (Q = Li and K) chloroperovskites. | |
3.3.7 The energy loss function. The spectrum of energy loss function L(w) that characterize inelastic scattering computed for the ternary CaQCl3 (Q = Li and K) chloroperovskites materials from 0 eV to 42 eV incident photon energy is depicted in Fig. 11. The higher peaks at the high incident photon energy in the L(w) spectra determine the Plasmon energy of these perovskite compounds. The energy loss function reveals the reaction of a solid to an external electromagnetic perturbation.
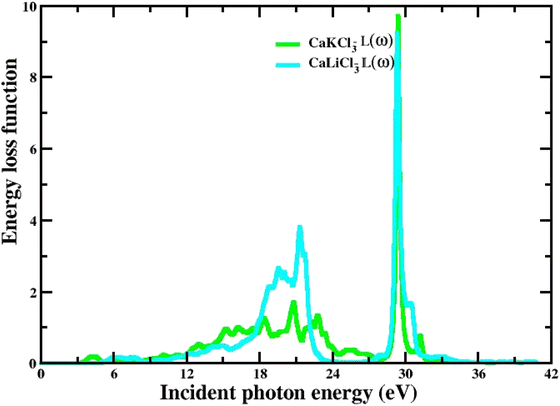 |
| | Fig. 11 The computed energy loss function for CaQCl3 (Q = Li and K) chloroperovskites. | |
3.4 The elastic properties
Research on elastic characteristics is crucial as it provides evidence about the mechanical stability and type of bonding nature of solids materials. The elastic constants for a cubic crystal can be determined using the IRelast package45 and are merely reduced to the three constants C11, C12, and C44. These constants can be utilized to relate the mechanical reaction to the material's ductility or fragility during an elastic domain deformation. In this research, we used the GGA approach to examine the elastic constants for the ternary CaQCl3 (Q = Li and K) chloroperovskites compounds under typical conditions of the simple cubic structure. Using the IRelast package the investigated elastic constants, and other mechanical parameters are summarised in Table 2. The findings unmistakably demonstrate that both of the chloroperovskite materials under investigation exhibit higher compression resistance due to their substantial values of C11 (64.84 GPa) in comparison to C12 (45.76 GPa) and C44 (32.56 GPa) for CaLiCl3 and for CaKCl3 the values are C11 (87.74 GPa) compared to C12 (56.26 GPa) and C44 (38.86 GPa). The investigated elastic constants are positive and the Born–Huang mechanical stability criteria56 C11 > 0, C12 > 0, C44 > 0, C11 + 2C12 > 0, C11 − C12 > 0, and B > 0 predict that both the selected compounds are stable mechanically. We determined two crucial parameters, such as the bulk modulus “B” and the shear modulus “G”, to examine the behavior of a material that either is ductile/brittle. Both “B” and “G” in general are calculated using Voigt and Reuss's estimations.57 The following formulas provide the compressibility modulus and shear modulus Voigt and Reuss approximations, Young's modulus, Passion's ratio, and anisotropy factor:| |
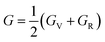 | (9) |
| |
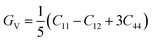 | (10) |
| |
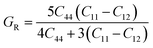 | (11) |
| |
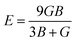 | (12) |
| |
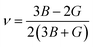 | (13) |
| | |
A = 2C44/(C11 − C12)
| (14) |
where, G, GV, GR, E, ν, and A are the shear modulus, Voigt shear modulus, Reuss shear modulus, Young's modulus, Passion's ratio, and the anisotropy factor respectively.
Table 2 The investigated elastic parameters, including the elastic constant(C11, C12, C44 in GPa), the bulk modulus “B”, shear modulus “G”, Young's modulus “E” and the Cauchy pressure in GPa, the Passion's ratio“ν”, the anisotropy factor “A”, the Pugh ratio “B/G” for ternary CaQCl3 (Q = Li and K) chloroperovskites compounds
| Elastic parameters |
CaLiCl3 |
CaKCl3 |
| C11 |
64.84 |
87.74 |
| C12 |
45.76 |
56.26 |
| C44 |
32.56 |
38.86 |
| B |
78.34 |
81.96 |
| G |
27.52 |
32.45 |
| E |
53.33 |
48.71 |
| ν |
1.23 |
1.78 |
| A |
2.33 |
1.94 |
| Cauchy pressure (C12 − C44) |
13.20 |
17.40 |
| B/G |
2.84 |
2.52 |
The rigidity of a material can be determined from the investigated values of “B” (bulk modulus), “G” (shear modulus), and “E” (Young's modulus). The computed values of B, E, and G are tabulated in Table 2 and the values predict that both the ternary chloroperovskites CaQCl3 (Q = Li and K) compounds are rigid and possess hardness to scratch. To evaluate the fragility and ductility of a material, the Passion's ratio“ν”, is an important parameter. The values of “ν” investigated for both materials are 1.23 for CaLiCl3 and 1.78 for CaKCl3, which suggests that the selected materials are ductile. Another crucial parameter is the Pugh ratio, which determines the brittle or ductile nature of a material. The threshold value for “B/G” (Pugh ratio) is 1.75.58 A material will display a brittle nature if the value of the Pugh ratio is less than 1.75, whereas the greater value shows a ductile nature. As in this work, for both materials, the values of “B/G” is 2.84 for CaLiCl3 and 2.52 for CaKCl3. These computed values for selected chloroperovskites predict that the compounds are ductile. The predicted value of anisotropy factor “A” determine whether the material is isotropic or anisotropic, and its critical value is “1" for isotropic whereas a value below or above “1” indicate anisotropy. The values computed for these chloroperovskites are 2.33 for CaLiCl3 and 1.94 for CaKCl3 and show that both compounds are anisotropic. The Cauchy pressure is also another parameter that determines the ductility of a material. The greater positive value of Cauchy pressure indicates ductility. The computed values of Cauchy pressure are 13.20 GPa for CaLiCl3 and 17.40 GPa for CaKCl3, as can be seen in Table 2.
4. Conclusion
In the current research, the structural, electronic, elastic, and optical properties of ternary chloroperovskites CaQCl3 (Q = Li and K) compounds in the cubic phase are investigated using DFT utilizing the GGA and TB-mBJ approximation within the WIEN2K simulation package. To our best knowledge, there is no available research for these selected perovskites and the key results found through the computational approach are:
• The ternary chloroperovskites CaQCl3 (Q = Li and K) compounds are in the cubic phase and the obtained negative values of formation energy for both compounds indicate that the material is structurally stable and can be experimentally synthesized.
• The analysis of electronic properties (band structure and DOS) shows an indirect nature from “M–Γ” with a band gap “Eg” of 4.6 eV for CaLiCl3 and thus acts as an insulator, whereas, the band structure analysis for CaKCl3 depicts a direct nature from “M–M” with a band gap “Eg” of 3.3 eV and display the nature of wide band gap semiconductor.
• Elastic properties computed through the IRelast package depict that the compounds of interest are classified as mechanically stable, ductile, anisotropic, and hard to scratch.
• The various parameters in optical properties within incident photon energy range from 0 eV to 42 eV are investigated and the results show that the CaQCl3 (Q = Li and K) compounds are optically active in UV-region and can be a good candidate for scintillating materials.
Based on the very precise investigations for the CaQCl3 (Q = Li and K), it can be deemed that both materials are applicable in much modern electronic equipment, energy storage devices, semiconducting industries, and as a scintillating material.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This research was funded by the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R29), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
References
- A. Thatribud, Electronic and optical properties of TiO2 by first-principle calculation (DFT-GW and BSE), Mater. Res. Express, 2019, 6(9), 95021 CrossRef CAS.
- P. Mishra, D. Singh, Y. Sonvane and R. Ahuja, Excitonic effects in the optoelectronic properties of graphene-like BC monolayer, Opt. Mater., 2020, 110, 110476 CrossRef CAS.
- E. Oyeniyi, Electronic and optical properties of Mg3XN (X= P, As, Sb, Bi) antiperovskites: The GW/BSE approach, Solid State Commun., 2022, 355, 114927 CrossRef CAS.
- L. Zhang, J. Miao, J. Li and Q. Li, Halide perovskite materials for energy storage applications, Adv. Funct. Mater., 2020, 30(40), 2003653 CrossRef CAS.
- M. Husain, et al., Structural, electronic, elastic, and magnetic properties of NaQF3 (Q = Ag, Pb, Rh, and Ru) flouroperovskites A first-principle outcomes, Int. J. Energy Res., 2022, 46(3), 2446–2453 CrossRef CAS.
- A. Habib, et al., Insight into the Exemplary Physical Properties of Zn-Based Fluoroperovskite Compounds XZnF3 (X = Al, Cs, Ga, In) Employing Accurate GGA Approach: A First-Principles Study, Materials, 2022, 15(7), 2669 CrossRef CAS PubMed.
- M. Arif, et al., Density functional theory based study of the physical properties of cesium based cubic halide perovskites CsHgX3 (X = F and Cl), Int. J. Energy Res., 2022, 46(3), 2467–2476 CrossRef CAS.
- J. Saddique, et al., Modeling structural, elastic, electronic and optical properties of ternary cubic barium based fluoroperovskites MBaF3 (M = Ga and In) compounds based on DFT, Mater. Sci. Semicond. Process., 2022, 139, 106345 CrossRef CAS.
- S. A. Shah, et al., Insight into the exemplary structural, elastic, electronic and optical nature of GaBeCl3 and InBeCl3: a DFT study, RSC Adv., 2022, 12(13), 8172–8177 RSC.
- S. Riaz, et al., Physical characteristics of NaTaO3 under pressure for electronic devices, Mater. Sci. Semicond. Process., 2021, 133, 105976 CrossRef CAS.
- M. Yaseen, et al., Pressure-induced electronic, optical and thermoelectric properties of cubic SrZrO3: DFT investigation, Phys. B, 2021, 612, 412626 CrossRef CAS.
- M. Yaseen, et al., Strong electron emission from antiferroelectric PLZT (2/95/5) films, Appl. Phys. Lett., 2014, 104(22), 222913 CrossRef.
- D. Li, Z. Ji, C. Luo and H. Wang, Studies of electronic structures and optical properties for cubic SnZrO3 and SnHfO3 under pressure, Ferroelectrics, 2021, 585(1), 230–239 CrossRef CAS.
- N. Erum and M. A. Iqbal, Physical properties of fluorine-based perovskites for vacuum-ultraviolet-transparent lens materials, Chin. J. Phys., 2017, 55(3), 893–903 CrossRef CAS.
- S. R. Kumavat, Y. Sonvane, D. Singh and S. K. Gupta, Two-dimensional CH3NH3PbI3 with high efficiency and superior carrier mobility: A theoretical study, J. Phys. Chem. C, 2019, 123(9), 5231–5239 CrossRef CAS.
- S. Kansara, Y. Sonvane, Pn. Gajjar and S. K. Gupta, 2D BeP2 monolayer: investigation of electronic and optical properties by driven modulated strain, RSC Adv., 2020, 10(45), 26804–26812 RSC.
- S. Kansara, D. Singh, S. K. Gupta and Y. Sonvane, Density functional Studies of structural, electronic and vibrational properties of palladium oxide, Solid State Commun., 2016, 245, 36–41 CrossRef CAS.
- H. Manaa, Y. Guyot and R. Moncorge, Spectroscopic and tunable laser properties of Co2+-doped single crystals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(6), 3633 CrossRef CAS PubMed.
- M. C. M. de Lucas, F. Rodriguez and M. Moreno, Excitation and emission thermal shifts in ABF3: Mn2+ perovskites: coupling with impurity vibrational modes, J. Phys.: Condens. Matter, 1995, 7(38), 7535 CrossRef.
- C. N. Avram, M. G. Brik, I. Tanaka and N. M. Avram, Electron–phonon interaction in the V2+: CsCaF3 laser crystal: geometry of the [VF6]4− complex in the 4T2g excited state, Phys. B, 2005, 355(1–4), 164–171 CrossRef CAS.
- J. M. Garcia-Lastra, J. Y. Buzare, M. T. Barriuso, J. A. Aramburu and M. Moreno, 3 d impurities in normal and inverted perovskites: Differences are not explained by ligand field theory, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(15), 155101 CrossRef.
- S. Shahrokhi, et al., Emergence of ferroelectricity in halide perovskites, Small Methods, 2020, 4(8), 2000149 CrossRef CAS.
- F. Lahoz, B. Villacampa and R. Alcala, The tetragonal to orthorhombic structural phase transition in RbCaF3 single crystals: Influence on the local environment of different nickel probes, J. Phys. Chem. Solids, 1997, 58(6), 881–892 CrossRef CAS.
- B. Ghebouli, M. A. Ghebouli and M. Fatmi, Structural, elastic, electronic, optical and thermal properties of cubic perovskite CsCdF3 under pressure effect, Eur. Phys. J.: Appl. Phys., 2011, 53(3), 30101–30108 CrossRef.
- R. R. Daniels, G. Margaritondo, R. A. Heaton and C. C. Lin, Experimental study of the electronic structure of KMgF3, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27(6), 3878 CrossRef CAS.
- O. D. I. Moseley, T. A. S. Doherty, R. Parmee, M. Anaya and S. D. Stranks, Halide perovskites scintillators: Unique promise and current limitations, J. Mater. Chem. C, 2021, 9(35), 11588–11604 RSC.
- N. Kawano, et al., Effect of organic moieties on the scintillation properties of organic–inorganic layered perovskite-type compounds, Jpn. J. Appl. Phys., 2016, 55(11), 110309 CrossRef.
- S. R. Kumavat, G. Sachdeva, Y. Sonvane and S. K. Gupta, Structural and compositional properties of 2D CH3NH3PbI3 hybrid halide perovskite: a DFT study, RSC Adv., 2022, 12(40), 25924–25931 RSC.
- L. Maduro, S. E. van Heijst and S. Conesa-Boj, First-Principles Calculation of Optoelectronic Properties in 2D Materials: The Polytypic WS2 Case, ACS Phys. Chem. Au, 2022, 2(3), 191–198 CrossRef CAS PubMed.
- P. Lecoq, Development of new scintillators for medical applications, Nucl. Instrum. Methods Phys. Res., Sect. A, 2016, 809, 130–139 CrossRef CAS.
- J. Glodo, Y. Wang and R. Shawgo, New developments in scintillators for security applications, Phys. Procedia, 2017, 90, 285–290 CrossRef CAS.
- S. K. Mathanker, P. R. Weckler and N. Wang, Terahertz (THz) applications in food and agriculture: A review, Trans. ASABE, 2013, 56(3), 1213–1226 Search PubMed.
- M. Güdel and Y. Nazé, X-ray spectroscopy of stars, Astron. Astrophys. Rev., 2009, 17(3), 309–408 CrossRef.
- A. C. Ulpe and T. Bredow, GW-BSE Calculations of Electronic Band Gap and Optical Spectrum of ZnFe2O4: Effect of Cation Distribution and Spin Configuration, ChemPhysChem, 2020, 21(6), 546–551 CrossRef CAS PubMed.
- S. R. Kumavat, Y. Sonvane and S. K. Gupta, Structural, optical, transport, and solar cell properties of 2D halide perovskite MAZX3 (Z = Pb, Sn, and X = Cl, Br, I), J. Appl. Phys., 2020, 128(11), 114304 CrossRef CAS.
- M. N. Murshed, M. E. El Sayed, S. Naji and A. Samir, Electronic and optical properties and upper light yield estimation of new scintillating material TlMgCl3: Ab initio study, Results Phys., 2021, 29, 104695 CrossRef.
- S. Khan, S. U. Zaman, R. Ahmad, N. Mehmood, M. Arif and H. J. Kim, Ab initio investigations of structural, elastic, electronic and optical properties of the fluoroperovskite TIXF3 (X = Ca, Cd, Hg, and Mg) compounds, Mater. Res. Express, 2020, 6(12), 125923 CrossRef.
- Q. V Phan, H. J. Kim, G. Rooh and S. H. Kim, Tl2ZrCl6 crystal: Efficient scintillator for X-and γ-ray spectroscopies, J. Alloys Compd., 2018, 766, 326–330 CrossRef.
- M. Yaseen, et al., Phase transition and thermoelectric properties of cubic KNbO3 under pressure: DFT approach, J. Mater. Res. Technol., 2021, 11, 2106–2113 CrossRef CAS.
- F. Shakoor, et al., Physical characteristics of barium based cubic perovskites, Chem. Phys. Lett., 2021, 779, 138835 CrossRef CAS.
- S. Mubashir, et al., Pressure induced electronic, optical and thermoelectric properties of cubic BaZrO3: A first principle calculations, Optik, 2021, 239, 166694 CrossRef CAS.
- P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka, and J. Luitz, “wien2k,” An Augment. Pl. wave+ local orbitals Progr. Calc. Cryst. Prop., vol. 60, 2001 Search PubMed.
- L. J. Sham and W. Kohn, One-particle properties of an inhomogeneous interacting electron gas, Phys. Rev., 1966, 145(2), 561 CrossRef CAS.
- J. Tao, J. P. Perdew, H. Tang and C. Shahi, Origin of the size-dependence of the equilibrium van der Waals binding between nanostructures, J. Chem. Phys., 2018, 148(7), 74110 CrossRef PubMed.
- M. Jamal, M. Bilal, I. Ahmad and S. Jalali-Asadabadi, IRelast package, J. Alloys Compd., 2018, 735, 569–579 CrossRef CAS.
- D. Koller, F. Tran and P. Blaha, Merits and limits of the modified Becke–Johnson exchange potential, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(19), 195134 CrossRef.
- E. Sakalauskas, et al., Dielectric function and optical properties of Al-rich AlInN alloys pseudomorphically grown on GaN, J. Phys. D: Appl. Phys., 2010, 43(36), 365102 CrossRef.
- A. Kokalj, XCrySDen—a new program for displaying crystalline structures and electron densities, J. Mol. Graphics Modell., 1999, 17(3–4), 176–179 CrossRef CAS PubMed.
- A. Vaught, Graphing with Gnuplot and Xmgr: two graphing packages available under linux, Linux J., 1996, 1996(28es), 7 Search PubMed.
- P. M. Edwards, Origin 7.0: scientific graphing and data analysis software, J. Chem. Inf. Comput. Sci., 2002, 42(5), 1270–1271 CrossRef CAS.
- H. Wainer, Visual Revelations: Elegance, Grace, Impact, and Graphical Displays, Chance, 1991, 4(4), 45–47 CrossRef.
- F. D. Murnaghan, The compressibility of media under extreme pressures, Proc. Natl. Acad. Sci. U. S. A., 1944, 30(9), 244 CrossRef CAS PubMed.
- S. Bouhmaidi, A. Marjaoui, A. Talbi, M. Zanouni, K. Nouneh and L. Setti, A DFT study of electronic, optical and thermoelectric properties of Ge-halide perovskites CsGeX3 (X= F, Cl and Br), Comput. Condens. Matter, 2022, e00663 CrossRef.
- Q. Mahmood, et al., Study of new lead-free double perovskites halides Tl2TiX6 (X = Cl, Br, I) for solar cells and renewable energy devices, J. Solid State Chem., 2022, 308, 122887 CrossRef CAS.
- M. A. Khan, H. A. Alburaih, N. A. Noor and A. Dahshan, Comprehensive investigation of Opto-electronic and transport properties of Cs2ScAgX6 (X = Cl, Br, I) for solar cells and thermoelectric applications, Sol. Energy, 2021, 225, 122–128 CrossRef.
- M. Born, On the stability of crystal lattices. I, Math. Proc. Cambridge Philos. Soc., 1940, 36(2), 160–172 CrossRef CAS.
- R. Hill, The elastic behaviour of a crystalline aggregate, Proc. Phys. Soc., London, Sect. A, 1952, 65(5), 349 CrossRef.
- S. F. Pugh, XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals, London, Edinburgh Dublin Philos. Mag. J. Sci., 1954, 45(367), 823–843 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2022 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Hind Albalawib,
Safa Ezzinecj,
Mongi Amamic,
Tahir Zamand,
Altaf Ur Rehmane,
Mohammad Sohaila,
Rajwali Khana,
Abid Ali Khanf,
Tahirg and
Aurangzeb Khanhi
*a,
Hind Albalawib,
Safa Ezzinecj,
Mongi Amamic,
Tahir Zamand,
Altaf Ur Rehmane,
Mohammad Sohaila,
Rajwali Khana,
Abid Ali Khanf,
Tahirg and
Aurangzeb Khanhi
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). The primitive crystalline unit cell of both the CaQCl3 (Q = Li and K) chloroperovskites are depicted in Fig. 1. Both the crystalline unit cell has five (5) atoms, where Ca at Wyckoff positions of (0, 0, 0), Q = Li and K lies at (0.5 0.5 0.5), and Cl positioned at (0, 0.5 0.5). The tolerance factor “τ” is computed for the selected chloroperovskites and found to be 0.94 for CaKCl3 and 0.98 for CaLiCl3, which confirms the cubic structure of the compounds. The fundamental structural parameters including the unit cell optimum volume, unit cell optimum energy, optimized lattice constant, pressure derivative of bulk modulus, and bulk modulus, are determined by fitting the primitive unit cell energy as a function of primitive unit cell volume using the Birch–Murnaghan equation of state,52 as described as:
m). The primitive crystalline unit cell of both the CaQCl3 (Q = Li and K) chloroperovskites are depicted in Fig. 1. Both the crystalline unit cell has five (5) atoms, where Ca at Wyckoff positions of (0, 0, 0), Q = Li and K lies at (0.5 0.5 0.5), and Cl positioned at (0, 0.5 0.5). The tolerance factor “τ” is computed for the selected chloroperovskites and found to be 0.94 for CaKCl3 and 0.98 for CaLiCl3, which confirms the cubic structure of the compounds. The fundamental structural parameters including the unit cell optimum volume, unit cell optimum energy, optimized lattice constant, pressure derivative of bulk modulus, and bulk modulus, are determined by fitting the primitive unit cell energy as a function of primitive unit cell volume using the Birch–Murnaghan equation of state,52 as described as: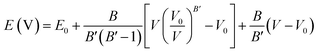


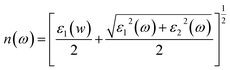
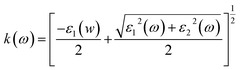
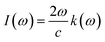
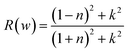
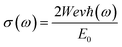
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200 Ohm−1 cm−1 at 28 eV photon energy while that for CaKCl3 is 17
200 Ohm−1 cm−1 at 28 eV photon energy while that for CaKCl3 is 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 Ohm−1 cm−1 at 26 eV incident photon energy. Both ternary CaQCl3 (Q = Li and K) chloroperovskites compounds possess high optical conductivity at the high energy level, which gives a clue that these materials can be used in the ultraviolet range in optical devices.
250 Ohm−1 cm−1 at 26 eV incident photon energy. Both ternary CaQCl3 (Q = Li and K) chloroperovskites compounds possess high optical conductivity at the high energy level, which gives a clue that these materials can be used in the ultraviolet range in optical devices.