Open Access Article
Open Access ArticleEnhancing magnetic coupling through protonation of benzylideneaniline-bridged diradicals and comparison with stilbene- and azobenzene-based diradicals†
Fengying Zhang *a,
Yiwei Fengb,
Xinyu Song
*a,
Yiwei Fengb,
Xinyu Song b and
Yuxiang Bu
b and
Yuxiang Bu b
b
aDepartment of Materials Science and Engineering, Jinzhong University, Jinzhong, 030619, People's Republic of China. E-mail: 978755183@qq.com
bSchool of Chemistry and Chemical Engineering, Shandong University, Jinan, 250100, People's Republic of China
First published on 2nd November 2022
Abstract
Taking nitroxide radicals as spin sources, we explore the intramolecular magnetic coupling interactions of the trans- and cis-forms of benzylideneaniline (BA)-bridged diradicals, in which the central –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit can undergo single protonation to convert to its protonated counterpart or vice versa. The calculated results for these two pairs of diradicals (protonated versus unprotonated trans and cis forms) verify that the signs of their magnetic coupling constants J do not change, but the magnitudes significantly increase after protonation. In the structure, the better conjugation of the protonated trans diradical and two reduced CCNC and CCCN torsion angles of the protonated cis one make for a more efficient spin transport, promoting the spin polarization, thus leading to larger spin couplings. In terms of mechanism, the proton-induced magnetic enhancement should be attributed to strong participation of the coupler BA through its lowest unoccupied molecular orbital (LUMO) with a lower energy level after protonation, and the small HOMO–LUMO (HOMO: highest occupied molecular orbital) gap of the coupler BA through protonation is crucial in explaining such remarkable spin-coupling enhancement. Furthermore, different linking modes of the radical groups to the couplers are also considered to confirm our conclusions. In addition, we also make a comparison of the magnetic coupling strengths among their isoelectronic analogues of BA-, AB- and stilbene-bridged nitroxide diradicals before or after protonation, and find a linear correlation among them. It should be noted that the magnetic behaviors of all these diradicals obey the spin alternation rule and singly occupied molecular orbital (SOMO) effect. This work provides helpful information for the rational design of promising magnetic molecular switches.
N– unit can undergo single protonation to convert to its protonated counterpart or vice versa. The calculated results for these two pairs of diradicals (protonated versus unprotonated trans and cis forms) verify that the signs of their magnetic coupling constants J do not change, but the magnitudes significantly increase after protonation. In the structure, the better conjugation of the protonated trans diradical and two reduced CCNC and CCCN torsion angles of the protonated cis one make for a more efficient spin transport, promoting the spin polarization, thus leading to larger spin couplings. In terms of mechanism, the proton-induced magnetic enhancement should be attributed to strong participation of the coupler BA through its lowest unoccupied molecular orbital (LUMO) with a lower energy level after protonation, and the small HOMO–LUMO (HOMO: highest occupied molecular orbital) gap of the coupler BA through protonation is crucial in explaining such remarkable spin-coupling enhancement. Furthermore, different linking modes of the radical groups to the couplers are also considered to confirm our conclusions. In addition, we also make a comparison of the magnetic coupling strengths among their isoelectronic analogues of BA-, AB- and stilbene-bridged nitroxide diradicals before or after protonation, and find a linear correlation among them. It should be noted that the magnetic behaviors of all these diradicals obey the spin alternation rule and singly occupied molecular orbital (SOMO) effect. This work provides helpful information for the rational design of promising magnetic molecular switches.
1. Introduction
Schiff bases and their metal complexes have attracted intensive attention from experimentalists as well as theoreticians because of possible applications in the fields of medicine, catalysis, analytical chemistry and photochromism.1–11 Aromatic Schiff bases are among the most investigated compounds due to their stability associated with optical and electrical properties.8–19 Benzylideneaniline (BA), an aromatic Schiff base, is of major importance in chemistry and biochemistry, belonging to the family of compounds containing the –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– double bond.8–16 As a kind of significant organic optoelectronic compound, BA and its derivatives have generated considerable interest for their potential optoelectronic properties. For example, it is reported that BA and its derivatives can exhibit favorable nonlinear optical behaviors.8 In addition, BA and its derivatives can undergo a reversible trans/cis isomerization between the stable trans configuration and metastable cis configuration upon photoexcitation.11–15 Based on this photochromic property, Luo et al. investigated systematically the substitution and solvent effects on the cis → trans thermal isomerization kinetics of BA in light of theoretical calculations and NMR spectroscopy experiments.14 Besides, Kawatsuki and coworkers synthesized two types of polymethacrylates with BA-derivative side groups and explored their axis-selective photoreaction and photoinduced orientation depended on the photochromic behavior and the connecting direction of the BA-derivative side groups.15 More interestingly, BA is structurally similar and isoelectronic with photochromic molecules of stilbene (the CH
N– double bond.8–16 As a kind of significant organic optoelectronic compound, BA and its derivatives have generated considerable interest for their potential optoelectronic properties. For example, it is reported that BA and its derivatives can exhibit favorable nonlinear optical behaviors.8 In addition, BA and its derivatives can undergo a reversible trans/cis isomerization between the stable trans configuration and metastable cis configuration upon photoexcitation.11–15 Based on this photochromic property, Luo et al. investigated systematically the substitution and solvent effects on the cis → trans thermal isomerization kinetics of BA in light of theoretical calculations and NMR spectroscopy experiments.14 Besides, Kawatsuki and coworkers synthesized two types of polymethacrylates with BA-derivative side groups and explored their axis-selective photoreaction and photoinduced orientation depended on the photochromic behavior and the connecting direction of the BA-derivative side groups.15 More interestingly, BA is structurally similar and isoelectronic with photochromic molecules of stilbene (the CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH bond) and azobenzene (the N
CH bond) and azobenzene (the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond, AB).12 It has been established that both stilbene and AB are excellent couplers between two magnetic centers and especially the magnetic character of stilbene- or AB-bridged diradicals can change upon irradiation with appropriate wavelengths of light.20–26 However, whether the BA-bridged diradicals could exhibit such photo-switching behaviors has not been reported heretofore. In view of this, we select BA as the target coupler to design novel diradicals and explore their magnetic characters.
N bond, AB).12 It has been established that both stilbene and AB are excellent couplers between two magnetic centers and especially the magnetic character of stilbene- or AB-bridged diradicals can change upon irradiation with appropriate wavelengths of light.20–26 However, whether the BA-bridged diradicals could exhibit such photo-switching behaviors has not been reported heretofore. In view of this, we select BA as the target coupler to design novel diradicals and explore their magnetic characters.
In addition to the photoinduced property, protonation is an efficient strategy to modify BA and its derivatives. The mono-protonated (protonation at the imine nitrogen) trans-BA has been investigated experimentally and theoretically, suggesting that protonation would restore its conjugation through removal of the lone pair of electrons on the imine nitrogen.27,28 According to the literature,29–34 the increased conjugation of trans-BA after protonation can create advantageous condition for spin transmission of the trans-BA-bridged diradical. That is to say, protonation may enhance the magnetic coupling of the trans-BA-bridged diradical. In fact, it has been demonstrated that the proton-induced magnetic regulation (including magnetic switching, enhancement or weakening, etc.) in the organic systems is easy to accomplish and likely to find promising applications in magnetic data storage.26,35–39 Sandberg et al. observed the generation of ground state triplet (T) diradicals by means of the proton-induced intramolecular electron transfer from the donor unit to the cross-conjugated acceptor for the species with a closed-shell (CS) ground state.36 Moreover, Yamashita and coworkers synthesized a solvatochromic phenol-linked imidazole derivative and revealed that this molecule has switchable spin states between CS singlet and broken-symmetry (BS) open-shell singlet state via proton tautomerism.38 In particular, we noticed that the magnetic enhancement occurs for several couples of the AB-bridged diradicals after protonation at the azo unit.26
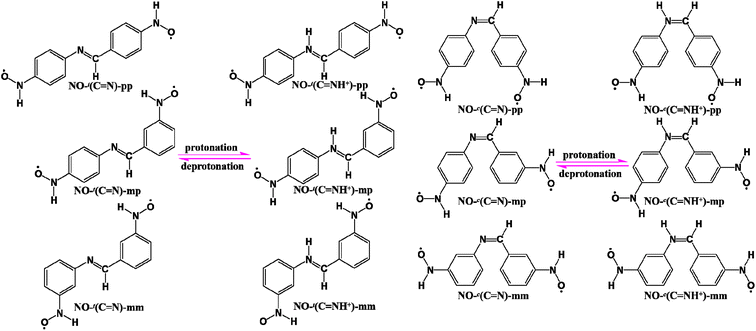
Inspired by these, herein we theoretically design the trans-/cis-BA-based diradicals in which two nitroxide radicals are linked to the para positions (the pp series) of the two phenylene units with respect to the –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit, and the imine nitrogen could undergo single protonation to convert to its protonated counterpart (–CH
N– unit, and the imine nitrogen could undergo single protonation to convert to its protonated counterpart (–CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+–). As evidenced at the B3LYP level of theory, the calculated results suggest that the antiferromagnetic (AFM) couplings of two unprotonated pp-type diradicals are relatively large regardless of the trans or cis configurations, attributed to the good mediating ability of the highest occupied molecular orbital (HOMO) of the coupler BA. Moreover, the dominating finding is that protonation can considerably enhance the AFM couplings of two pp-type diradicals. That is, the signs of their magnetic exchange coupling constants J do not change, but the magnitudes significantly increase after protonation no matter for the trans or cis forms. On the one hand, the changes in geometric structures of diradicals are responsible for such noticeable magnetic enhancement induced by protonation. The better conjugation of the protonated trans diradical and two reduced CCNC and CCCN torsion angles of the protonated cis one make for a more efficient spin transport, promoting the spin polarization and then leading to larger magnetic couplings. On the other hand, the proton-induced magnetic enhancement should be attributed to strong participation of the coupler BA through its lowest unoccupied molecular orbital (LUMO) with a lower energy level after protonation. Furthermore, the small HOMO–LUMO gap of the coupler BA through protonation is significant to assist in the explanation of such remarkable spin-coupling enhancement. In addition, different connection modes of two radical groups to the coupler are also considered to further verify the conclusion of protonation-enhanced magnetic coupling. Interestingly, it is observed that changing the connection modes of two radical groups can not only adjust the magnitude of J but also modifies the sign of J from AFM to ferromagnetism (FM), suggesting a possibility of the connecting-mode-independent magnetic switching. Besides, we also make a comparison of the magnetic coupling strengths among the isoelectronic analogues of BA-, AB- and stilbene-bridged nitroxide diradicals before or after protonation, and find a linear correlation among them. Finally, it is worth mentioning that the magnetic behaviors (including FM and AFM) of all these diradicals can be predicted by means of the spin alternation rule40,41 and singly occupied molecular orbital (SOMO) effect.42 This work may broaden the landscape for the rational design of the BA-bridged modulators or switches and further it is shown that protonation is an effective method to enhance magnetic coupling.
NH+–). As evidenced at the B3LYP level of theory, the calculated results suggest that the antiferromagnetic (AFM) couplings of two unprotonated pp-type diradicals are relatively large regardless of the trans or cis configurations, attributed to the good mediating ability of the highest occupied molecular orbital (HOMO) of the coupler BA. Moreover, the dominating finding is that protonation can considerably enhance the AFM couplings of two pp-type diradicals. That is, the signs of their magnetic exchange coupling constants J do not change, but the magnitudes significantly increase after protonation no matter for the trans or cis forms. On the one hand, the changes in geometric structures of diradicals are responsible for such noticeable magnetic enhancement induced by protonation. The better conjugation of the protonated trans diradical and two reduced CCNC and CCCN torsion angles of the protonated cis one make for a more efficient spin transport, promoting the spin polarization and then leading to larger magnetic couplings. On the other hand, the proton-induced magnetic enhancement should be attributed to strong participation of the coupler BA through its lowest unoccupied molecular orbital (LUMO) with a lower energy level after protonation. Furthermore, the small HOMO–LUMO gap of the coupler BA through protonation is significant to assist in the explanation of such remarkable spin-coupling enhancement. In addition, different connection modes of two radical groups to the coupler are also considered to further verify the conclusion of protonation-enhanced magnetic coupling. Interestingly, it is observed that changing the connection modes of two radical groups can not only adjust the magnitude of J but also modifies the sign of J from AFM to ferromagnetism (FM), suggesting a possibility of the connecting-mode-independent magnetic switching. Besides, we also make a comparison of the magnetic coupling strengths among the isoelectronic analogues of BA-, AB- and stilbene-bridged nitroxide diradicals before or after protonation, and find a linear correlation among them. Finally, it is worth mentioning that the magnetic behaviors (including FM and AFM) of all these diradicals can be predicted by means of the spin alternation rule40,41 and singly occupied molecular orbital (SOMO) effect.42 This work may broaden the landscape for the rational design of the BA-bridged modulators or switches and further it is shown that protonation is an effective method to enhance magnetic coupling.
We explain the terms of spin transport, spin polarization and spin alternation rule mentioned above as follows. For a diradical system, spin transport refers to the distribution of unpaired electrons in the spin center along with the π-conjugated coupling unit and spin polarization results from different interactions between unpaired electrons in partially occupied orbitals and paired electrons. The spin alternation rule states that the adjacent atomic center in a π-conjugated diradical prefers opposite spins, in other words, alternating α and β spins.
2. Design scheme and computational details
In general, both the coupler and radical groups are essential for a diradical. In this context, we choose the relatively stable nitroxide (NO) radical as magnetic centers and attach them to the trans and cis forms of BA at the para positions, respectively, denoted as NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp (t: the trans form) and NO-c(C
N)-pp (t: the trans form) and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp (c: the cis form), as depicted in Scheme 1. After protonation, NO-t(C
N)-pp (c: the cis form), as depicted in Scheme 1. After protonation, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp and NO-c(C
N)-pp and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp convert to NO-t(C
N)-pp convert to NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp and NO-c(C
NH+)-pp and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp, respectively. In addition, to further confirm the protonation effect on the magnetic couplings and meanwhile examine the influence on magnetic characters due to different linking modes, two NO radical groups are linked to the couplers BA/BAH+ in the trans and cis forms at the meta/para (mp) or meta/meta (mm) sites, denoted as NO-t(C
NH+)-pp, respectively. In addition, to further confirm the protonation effect on the magnetic couplings and meanwhile examine the influence on magnetic characters due to different linking modes, two NO radical groups are linked to the couplers BA/BAH+ in the trans and cis forms at the meta/para (mp) or meta/meta (mm) sites, denoted as NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp/NO-t(C
N)-mp/NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mp, NO-c(C
NH+)-mp, NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp/NO-c(C
N)-mp/NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mp, NO-t(C
NH+)-mp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm/NO-t(C
N)-mm/NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mm and NO-c(C
NH+)-mm and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm/NO-c(C
N)-mm/NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mm, respectively, as illustrated in Scheme 1. As isoelectronic analogues of the BA/BAH+-bridged NO diradicals, the AB/ABH+- and stilbene-based NO diradicals of three series in the trans and cis forms are also listed in Scheme S1,† denoted as NO-t(N
NH+)-mm, respectively, as illustrated in Scheme 1. As isoelectronic analogues of the BA/BAH+-bridged NO diradicals, the AB/ABH+- and stilbene-based NO diradicals of three series in the trans and cis forms are also listed in Scheme S1,† denoted as NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp/NO-t(N
N)-pp/NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp, NO-c(N
NH+)-pp, NO-c(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp/NO-c(N
N)-pp/NO-c(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp, NO-t(N
NH+)-pp, NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp/NO-t(N
N)-mp/NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mp, NO-c(N
NH+)-mp, NO-c(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp/NO-c(N
N)-mp/NO-c(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mp, NO-t(N
NH+)-mp, NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm/NO-t(N
N)-mm/NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mm, NO-c(N
NH+)-mm, NO-c(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm/NO-c(N
N)-mm/NO-c(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mm, NO-t(C
NH+)-mm, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-pp, NO-c(C
C)-pp, NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-pp, NO-t(C
C)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-mp, NO-c(C
C)-mp, NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-mp, NO-t(C
C)-mp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-mm and NO-c(C
C)-mm and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-mm, respectively. It should be pointed out that the stilbene-bridged NO diradicals have no protonated counterparts and the following relevant data related to the trans/cis-AB/ABH+-bridged NO diradicals are all from ref. 26.
C)-mm, respectively. It should be pointed out that the stilbene-bridged NO diradicals have no protonated counterparts and the following relevant data related to the trans/cis-AB/ABH+-bridged NO diradicals are all from ref. 26.
The Heisenberg spin Hamitonian can be utilized to express the magnetic exchange interaction between two magnetic centers 1 and 2: Ĥ = −2J Ŝ1 × Ŝ2, where Ŝ1 and Ŝ2 are the respective spin angular momentum operators, with J being the magnetic exchange coupling constant. The positive and negative sign of J is a representative of FM and AFM interactions, respectively. It has been demonstrated that the electronic states of the singlet and triplet would be the eigenstates of the Heisenberg Hamitonian, and their corresponding energy eigenvalues are E(S = 0; S) = 3J/2 and E(S = 1; T) = −J/2. Therefore, for a diradical system, J can be written as: E(S = 1) − E(S = 0) = −2J. That is to say, the J value of a diradical can be evaluated by simply determining the exact singlet and triplet energy values. The unrestricted Hartree–Fock (UHF) methodology based on a single determinantal wave function can be adopted to reasonably describe the triplet geometry, but it is not capable of describing the singlet of a diradical due to the introduction of spin contamination, yielding an unreliable J accordingly.43,44 The multiconfigurational approach and self-consistent field calculations are suitable to estimate J, but these methods are resource intensive and not practical for large molecules.45,46 In this study, we employ the broken-symmetry formalism proposed by Noodleman47,48 in a density functional theory (DFT) framework to evaluate J, which is an alternative approach to properly describe the singlet of a diradical with a lower computational cost. Based on this, the expression of J was developed and pointed out by Yamaguchi and co-workers49,50 with the use of spin-projected methods, given as: J = (EBS − ET)/(〈S2〉T − 〈S2〉BS), where EBS, ET, 〈S2〉BS and 〈S2〉T refer to the energies and average spin square values of the BS and T states, respectively. This formula is considered as the most applicable and popular one for estimating J for the diradical systems.
In principle, the DFT-based methods tend to overestimate J, but the B3LYP functional has been widely accepted to evaluate J of several organic diradical systems.31,51,52 Thus the molecular geometric optimizations and frequency analyses as well as energy calculations of the CS, BS and T states of all these studied diradicals were performed at the (U)B3LYP/6-311++G(d,p) level. To confirm the rationality of some calculated results, the single-point calculations are done using CASSCF(4,6) level with the 6-311++G(d,p) basis set based on the above optimized structures. Besides, a more modern M06-2X function with the 6-311++G(d,p) basis set was adopted to further verify the accuracy of some computational results. Here, we select an adequately large 6-311++G(d,p) basis set with more polarization and diffuse functions to obtain more reliable J of the studied diradicals. All of these DFT calculations were carried out by using the suit of Gaussian 09 program.53
3. Results and discussion
3.1 Magnetic coupling characteristics
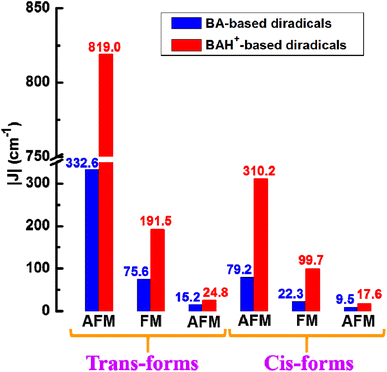
Depending on different connection ways among the coupler (BA or BAH+) and two NO radical groups, we discuss the magnetic coupling characteristics of three kinds of diradicals categorized as the pp, mp and mm series. The calculated absolute J (|J|) in the trans and cis forms are shown in Fig. 1, which are in an order pp > mp > mm for the unprotonated or protonated diradicals. More detailed data including their energies of the CS, BS and T states, 〈S2〉 values associated with J values at the (U)B3LYP/6-311++G(d,p) level are gathered in Table S1.† Regardless of the unprotonated or protonated diradicals, it is observed that the pp- and mm-type ones are all in favor of an AFM interaction, while the mp-type ones are in support of a FM coupling. The above analyses reveal that change of the connecting modes of the radical group can affect not only the magnetic magnitudes but also the magnetic behaviors of the studied diradicals. Besides, it is very interesting to note that the signs of J do not change before and after protonation, but the magnitudes of the protonated diradicals noticeably increase in comparison with those of the unprotonated ones especially for the pp series (Fig. 1). Specifically, through protonation the J value of NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp increases from −332.6 to −819.0 cm−1 (NO-t(C
N)-pp increases from −332.6 to −819.0 cm−1 (NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp). For NO-c(C
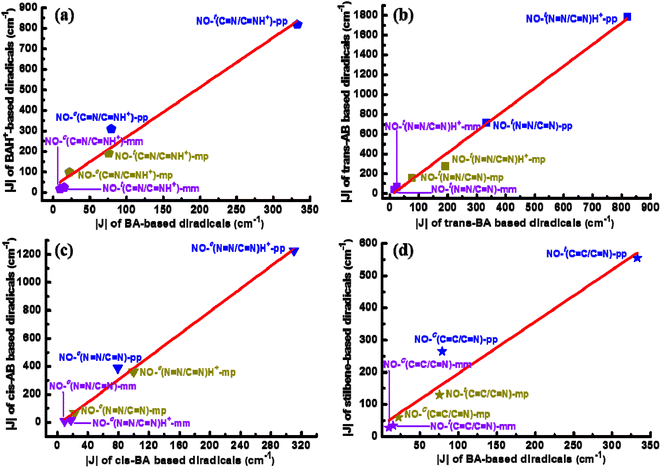
NH+)-pp). For NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, the magnitude of magnetic enhancement induced by protonation is also obvious, being about 231 cm−1. In particular, there is a linear correlation between |J| of three types of the BA-bridged diradicals before and after protonation as shown in Fig. 2a. It is observed that the magnitudes of |J| for the protonated diradicals are about 2.43 times larger than that with the unprotonated ones. In Table S2,† the J values estimated at the UM06-2X/6-311++G(d,p) level are also presented for the purpose of comparison, including diradicals NO-t(C
N)-pp, the magnitude of magnetic enhancement induced by protonation is also obvious, being about 231 cm−1. In particular, there is a linear correlation between |J| of three types of the BA-bridged diradicals before and after protonation as shown in Fig. 2a. It is observed that the magnitudes of |J| for the protonated diradicals are about 2.43 times larger than that with the unprotonated ones. In Table S2,† the J values estimated at the UM06-2X/6-311++G(d,p) level are also presented for the purpose of comparison, including diradicals NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-t(C
N)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp, NO-t(C
NH+)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp, NO-t(C
N)-mp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp, NO-t(C
N)-mp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm and NO-t(C
N)-mm and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm. The results show that the calculated J are relatively accurate by employing B3LYP and M06-2X functions, and after protonation the magnetic enhancement occurs in these three couples of diradical molecules. The B3LYP functional tend to overestimate J, compared with the M06-2X function. The single-point calculations of NO-t(C
N)-mm. The results show that the calculated J are relatively accurate by employing B3LYP and M06-2X functions, and after protonation the magnetic enhancement occurs in these three couples of diradical molecules. The B3LYP functional tend to overestimate J, compared with the M06-2X function. The single-point calculations of NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-t(C
N)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp, NO-t(C
NH+)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp, NO-t(C
N)-mp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp, NO-t(C
N)-mp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm and NO-t(C
N)-mm and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm are also done using CASSCF(4,6) level with the 6-311++G(d,p) basis set. In Table S3,† their related singlet–triplet energy differences are obtained, corresponding to −208.2, −554.2, 50.6, 121.9, −8.6 and −14.6 cm−1, respectively, demonstrating the feasibility by adopting (U)B3LYP/6-311++G(d,p) level again. Furthermore, to fully reflect the protonation-induced magnetic increase and compare the spin-coupling-mediating ability of the coupler BA and its isoelectronic analogues AB and stilbene, Fig. 2 also displays the linear correlations among the computational |J| for the BA-, AB- and stilbene-bridged NO diradicals of the pp, mp and mm series. It can been seen that single protonation of –CH
N)-mm are also done using CASSCF(4,6) level with the 6-311++G(d,p) basis set. In Table S3,† their related singlet–triplet energy differences are obtained, corresponding to −208.2, −554.2, 50.6, 121.9, −8.6 and −14.6 cm−1, respectively, demonstrating the feasibility by adopting (U)B3LYP/6-311++G(d,p) level again. Furthermore, to fully reflect the protonation-induced magnetic increase and compare the spin-coupling-mediating ability of the coupler BA and its isoelectronic analogues AB and stilbene, Fig. 2 also displays the linear correlations among the computational |J| for the BA-, AB- and stilbene-bridged NO diradicals of the pp, mp and mm series. It can been seen that single protonation of –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– or –N
N– or –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit can promote the magnetic couplings of the BA- or AB-bridged diradicals indeed. Moreover, we notice that for the trans diradicals the magnitude of the magnetic coupling strength of the AB-bridged ones is 2.19 times that of the BA-bridged ones before or after protonation (Fig. 2b), while the multiple increases to 4.06 for the cis forms (Fig. 2c). A comparison among the magnitudes of |J| for the BA-bridged verse stilbene-bridged diradicals in the trans and cis forms indicates that the slope is about 1.61 (Fig. 2d). These observations imply that the coupler BA possesses a relatively weaker spin-coupling-mediating ability compared with AB and stilbene. Whereas, we notice that the degree of planarity of the BA-bridged diradicals can highly enhance upon protonation especially for the trans forms, thus facilitating the spin couplings, in contrast to the AB-bridged ones. The structural properties discussed below are responsible to all these observed phenomena including the proton-induced magnetic enhancement and the magnetic differences of diradicals with different connecting modes of the radical groups or different coupling units. It should be noted that the pp-type diradicals are mainly used as examples in the following discussion.
N– unit can promote the magnetic couplings of the BA- or AB-bridged diradicals indeed. Moreover, we notice that for the trans diradicals the magnitude of the magnetic coupling strength of the AB-bridged ones is 2.19 times that of the BA-bridged ones before or after protonation (Fig. 2b), while the multiple increases to 4.06 for the cis forms (Fig. 2c). A comparison among the magnitudes of |J| for the BA-bridged verse stilbene-bridged diradicals in the trans and cis forms indicates that the slope is about 1.61 (Fig. 2d). These observations imply that the coupler BA possesses a relatively weaker spin-coupling-mediating ability compared with AB and stilbene. Whereas, we notice that the degree of planarity of the BA-bridged diradicals can highly enhance upon protonation especially for the trans forms, thus facilitating the spin couplings, in contrast to the AB-bridged ones. The structural properties discussed below are responsible to all these observed phenomena including the proton-induced magnetic enhancement and the magnetic differences of diradicals with different connecting modes of the radical groups or different coupling units. It should be noted that the pp-type diradicals are mainly used as examples in the following discussion.
It is worth mentioning that a representative trans-AB-bridged diradical has been successfully synthesized experimentally, in which two nitronyl nitroxide radicals as the spin centers are attached to the meta/para sites of trans-AB.22 Magnetic susceptibility measurements revealed that the two radical centers coupled in a ferromagnetic way, which is consistent with the sign of J of the mp series of trans-AB or trans-BA-bridged diradicals studied in this paper. Besides, Iwamura et al.20 explored the magnetic coupling between two sterically protected phenoxyl radicals through the cis- and trans-stilbene chromophores by means of their EPR fine structures and concluded that m,m′-isomers of the trans and cis forms exhibit antiferromagnetic couplings. The singlet–triplet energy gaps (ΔES–T = 2J) were estimated to be 0 > ΔES–T > −35 cal mol−1 (1 cal = 4.184 J) for both geometrical isomers. The reported magnitudes and signs of J are in harmony with the mm series of cis- and trans-stilbene-bridged diradicals studied in this paper. The above results demonstrate the rationality of the calculations using B3LYP function.
3.2 Molecular structures
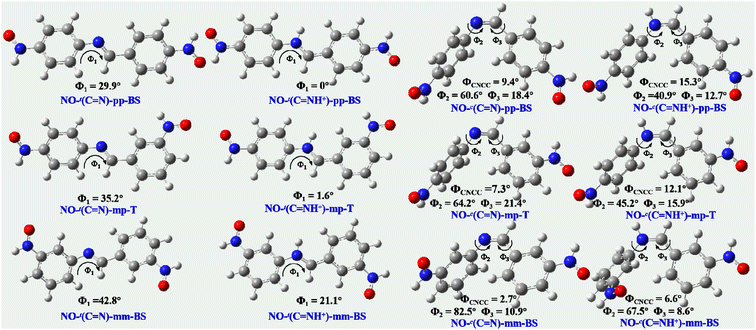
As known, the magnetic coupling strengths are directly relevant to the structural properties of diradicals and their |J| drastically decrease with the increase in the dihedral angle.29–34 The geometric optimizations in Fig. 3 suggest that the coupler BA and two NO radical groups of the unprotonated trans- or cis-diradicals are nonplanar within three series. For the trans diradicals NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-t(C
N)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp and NO-t(C
N)-mp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm, the structural distortions can be attributed to the repulsion between two hydrogen atoms from the bridge –HC
N)-mm, the structural distortions can be attributed to the repulsion between two hydrogen atoms from the bridge –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit and phenylene ring. While the cis diradicals NO-c(C
N– unit and phenylene ring. While the cis diradicals NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-c(C
N)-pp, NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp and NO-c(C
N)-mp and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm adopt the bent conformations with the radicalized phenylene (HON-phenylene) twisted out of the plane of the –HC
N)-mm adopt the bent conformations with the radicalized phenylene (HON-phenylene) twisted out of the plane of the –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit. After protonation, the C–N bond length of the bridge –HC
N– unit. After protonation, the C–N bond length of the bridge –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit for the trans diradicals is stretched and then the repulsion between two hydrogen atoms from the bridge –HC
N– unit for the trans diradicals is stretched and then the repulsion between two hydrogen atoms from the bridge –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit and phenylene ring is largely weakened. As a result, the CCNC torsional angle (ϕ1) between the HON-phenylene radical moiety and bridge –HC
N– unit and phenylene ring is largely weakened. As a result, the CCNC torsional angle (ϕ1) between the HON-phenylene radical moiety and bridge –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit within the protonated trans diradicals decreases for NO-t(C
N– unit within the protonated trans diradicals decreases for NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mm or even reduces to near zero or zero for NO-t(C
NH+)-mm or even reduces to near zero or zero for NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mp and NO-t(C
NH+)-mp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp (see Fig. 3), providing a beneficial condition for spin transport and then facilitating the magnetic interactions. As demonstrated, the torsional angle ϕ1 of NO-t(N
NH+)-pp (see Fig. 3), providing a beneficial condition for spin transport and then facilitating the magnetic interactions. As demonstrated, the torsional angle ϕ1 of NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp decreases from 29.9° to 0° through protonation, leading to a larger |J| value. With regard to the cis diradicals, after protonation the CNCC dihedral angle between two radicalized phenylene and bridge –HC
N)-pp decreases from 29.9° to 0° through protonation, leading to a larger |J| value. With regard to the cis diradicals, after protonation the CNCC dihedral angle between two radicalized phenylene and bridge –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit (ϕCNCC) increases, but the CCNC and CCCN torsional angles (ϕ2 and ϕ3) decrease (Fig. 3), facilitating the spin polarization and enhancing the spin coupling accordingly. As evidenced, after protonation the dihedral angle ϕCNCC of NO-c(C
N– unit (ϕCNCC) increases, but the CCNC and CCCN torsional angles (ϕ2 and ϕ3) decrease (Fig. 3), facilitating the spin polarization and enhancing the spin coupling accordingly. As evidenced, after protonation the dihedral angle ϕCNCC of NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp increases from 9.4° to 15.3°, whereas the torsional angles ϕ2 and ϕ3 decrease from 60.6° to 40.9° and 18.4° to 12.7°, respectively. Consequently, the better conjugation of NO-c(C
N)-pp increases from 9.4° to 15.3°, whereas the torsional angles ϕ2 and ϕ3 decrease from 60.6° to 40.9° and 18.4° to 12.7°, respectively. Consequently, the better conjugation of NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp gives rise to a larger |J| value compared with that of NO-c(C
NH+)-pp gives rise to a larger |J| value compared with that of NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp. Besides, no matter for the unprotonated or protonated diradicals, we observe that the magnetic couplings of the pp, mp and mm-type ones significantly decrease in order with the increasing of the torsional angle ϕ1 in the trans forms or ϕ2 and ϕ3 in the cis forms. As proved, the torsional angle ϕ1 of NO-t(C
N)-pp. Besides, no matter for the unprotonated or protonated diradicals, we observe that the magnetic couplings of the pp, mp and mm-type ones significantly decrease in order with the increasing of the torsional angle ϕ1 in the trans forms or ϕ2 and ϕ3 in the cis forms. As proved, the torsional angle ϕ1 of NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-t(C
N)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp and NO-t(C
N)-mp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm is 29.9°, 35.2° and 42.8° in order, and the corresponding |J| are 332.6, 75.6 and 15.2 cm−1, respectively.
N)-mm is 29.9°, 35.2° and 42.8° in order, and the corresponding |J| are 332.6, 75.6 and 15.2 cm−1, respectively.
As for isoelectronic analogues of BA/BAH+, AB/ABH+ and stilbene-bridged NO diradicals in the trans or cis forms in three series, the order of their magnetic magnitudes is NO–(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) > NO–(C
N) > NO–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C) > NO–(C
C) > NO–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N) or NO–(N
N) or NO–(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+) > NO–(C
NH+) > NO–(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+). Their magnetic differences in the trans forms are mainly due to different bond lengths of the connecting bond linking the coupler and radical group and the shorter connecting bonds of the AB/ABH+-bridged diradicals provide a more facile means of magnetic interaction, while the longer ones create a disadvantage condition for magnetic coupling.51 As evidenced, the connecting bonds of NO-t(N
NH+). Their magnetic differences in the trans forms are mainly due to different bond lengths of the connecting bond linking the coupler and radical group and the shorter connecting bonds of the AB/ABH+-bridged diradicals provide a more facile means of magnetic interaction, while the longer ones create a disadvantage condition for magnetic coupling.51 As evidenced, the connecting bonds of NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-t(C
N)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-pp and NO-t(C
C)-pp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp are 1.382, 1.385 and 1.389 Å in order (see Fig. S1†), and their corresponding |J| are 716.4, 555.4 and 332.6 cm−1, respectively, presenting a negative correlation. Of course, the nonplanar structure of NO-t(C
N)-pp are 1.382, 1.385 and 1.389 Å in order (see Fig. S1†), and their corresponding |J| are 716.4, 555.4 and 332.6 cm−1, respectively, presenting a negative correlation. Of course, the nonplanar structure of NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp is also an important factor for its small |J|. Similarly, the connecting bonds of NO-t((N
N)-pp is also an important factor for its small |J|. Similarly, the connecting bonds of NO-t((N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+))-pp and NO–t(C
NH+))-pp and NO–t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp are 1.370 and 1.381 Å, and the corresponding |J| are 1787.1 and 819.0 cm−1, respectively. For the cis forms, their magnetic differences could be attributed to the conjugation degree and the better conjugation of the AB/ABH+ or stilbene-bridged diradicals generate stronger spin coupling, whereas the worse conjugation of the BA/BAH+-bridged ones produce weaker spin interactions. For example, the torsional angles of NO-c(N
NH+)-pp are 1.370 and 1.381 Å, and the corresponding |J| are 1787.1 and 819.0 cm−1, respectively. For the cis forms, their magnetic differences could be attributed to the conjugation degree and the better conjugation of the AB/ABH+ or stilbene-bridged diradicals generate stronger spin coupling, whereas the worse conjugation of the BA/BAH+-bridged ones produce weaker spin interactions. For example, the torsional angles of NO-c(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp (ϕ4), NO-c(C
N)-pp (ϕ4), NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-pp (ϕ6) and NO-c(C
C)-pp (ϕ6) and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp (ϕ2) are 39.8°, 29.3° and 60.6° in order, and their corresponding |J| are 388.1, 264.9 and 79.2 cm−1, respectively. Analogously, the torsional angles of NO-c(N
N)-pp (ϕ2) are 39.8°, 29.3° and 60.6° in order, and their corresponding |J| are 388.1, 264.9 and 79.2 cm−1, respectively. Analogously, the torsional angles of NO-c(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp (ϕ4) and NO-c(C
NH+)-pp (ϕ4) and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp (ϕ2) are 2.2° and 40.9°, and the corresponding |J| are 1227.9 and 310.2 cm−1, respectively. The detailed data of structural properties for all these studied diradicals are shown in Fig. S1.†
NH+)-pp (ϕ2) are 2.2° and 40.9°, and the corresponding |J| are 1227.9 and 310.2 cm−1, respectively. The detailed data of structural properties for all these studied diradicals are shown in Fig. S1.†
3.3 Spin polarization
Except for the molecular structure, spin polarization is exceedingly instrumental in elucidating the magnetic magnitudes of π-conjugated diradicals.26,51 The magnetic enhancements induced by protonation can be quantitatively interpreted with the help of spin polarization from the NO radical group to the coupler BAH+ on the basis of the Mulliken atomic spin density distributions. Furthermore, the differences in |J| for these BA/BAH+-based diradicals in three series are also attributed to different atomic spin density distributions due to different linking sites of the NO groups. As presented in Fig. 4, it is evident that the average spin density delocalization into the coupler trans- or cis-BA for the protonated diradicals is larger than that of the corresponding unprotonated ones for the pp, mp and mm series. Specifically, 17.4%, 13.7% and 12.3% of spin densities are delocalized to the trans-BA coupler for the unprotonated diradicals NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-t(C
N)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp and NO-t(C
N)-mp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm, while spin polarization is prominently increased to 26.8%, 17.4% and 12.8% in the case of the protonated ones NO-t(C
N)-mm, while spin polarization is prominently increased to 26.8%, 17.4% and 12.8% in the case of the protonated ones NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp, NO-t(C
NH+)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mp and NO-t(C
NH+)-mp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-mm. As a result, the larger spin polarization of these protonated diradicals strengthens the spin coupling interaction between two NO groups. Analogously, after protonation spin polarization towards the cis-BA coupler is enhanced from 15.4% to 23.2%, 13.5% to 16.0% and 12.6% to 13.2%, with respect to NO-c(C
NH+)-mm. As a result, the larger spin polarization of these protonated diradicals strengthens the spin coupling interaction between two NO groups. Analogously, after protonation spin polarization towards the cis-BA coupler is enhanced from 15.4% to 23.2%, 13.5% to 16.0% and 12.6% to 13.2%, with respect to NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-c(C
N)-pp, NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mp and NO-c(C
N)-mp and NO-c(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-mm, further manifesting that protonation can promote the spin polarization effect. On the whole, we can draw the following two conclusions: (1) the protonated diradicals exhibit stronger spin polarization featuring the larger |J|; (2) regardless of the unprotonated or protonated diradicals, it is evident that spin polarization is in an order pp > mp > mm in the trans and cis forms, accordant with their corresponding |J|.
N)-mm, further manifesting that protonation can promote the spin polarization effect. On the whole, we can draw the following two conclusions: (1) the protonated diradicals exhibit stronger spin polarization featuring the larger |J|; (2) regardless of the unprotonated or protonated diradicals, it is evident that spin polarization is in an order pp > mp > mm in the trans and cis forms, accordant with their corresponding |J|.
 | ||
| Fig. 4 Average percentages of atom spin density distributions delocalized into the coupler BA for the unprotonated and protonated NO diradicals. | ||
Similarly, different magnetic magnitudes with respect to isoelectronic analogues of the BA/BAH+, AB/ABH+ and stilbene-bridged NO diradials in the trans or cis forms within three series can also be accounted for by means of the spin polarization effect. For example, the atomic spin density distributions in the NO radical groups are 82.6%, 80.7% and 78.6% for the trans diradicals of NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, NO-t(C
N)-pp, NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-pp and NO-t(C
C)-pp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp (see Fig. S2†), corresponding to 716.4, 555.4 and 332.6 cm−1 in order, which suggests that the largest spin polarization of NO-t(N
N)-pp (see Fig. S2†), corresponding to 716.4, 555.4 and 332.6 cm−1 in order, which suggests that the largest spin polarization of NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp can strongly promote the spin coupling between two NO groups, and the relatively larger spin polarization of NO-t(C
N)-pp can strongly promote the spin coupling between two NO groups, and the relatively larger spin polarization of NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)-pp generates a moderate magnetic interaction, while the smallest spin polarization of NO-t(C
C)-pp generates a moderate magnetic interaction, while the smallest spin polarization of NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp leads to the weakest coupling interaction. With regard to NO-t(N
N)-pp leads to the weakest coupling interaction. With regard to NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp and NO-t(C
NH+)-pp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp, 42.4% spin density is delocalized over the trans-ABH+ coupler and 26.8% spin density is delocalized over the trans-BAH+ coupler, and consequently the larger spin polarization of NO-t(N
NH+)-pp, 42.4% spin density is delocalized over the trans-ABH+ coupler and 26.8% spin density is delocalized over the trans-BAH+ coupler, and consequently the larger spin polarization of NO-t(N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp considerably facilitates magnetic coupling compared with that of NO-t(C
NH+)-pp considerably facilitates magnetic coupling compared with that of NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp. The Mulliken atomic spin density distributions of all the studied diradicals are depicted in Fig. S2.†
NH+)-pp. The Mulliken atomic spin density distributions of all the studied diradicals are depicted in Fig. S2.†
3.4 Mechanism of magnetic interaction
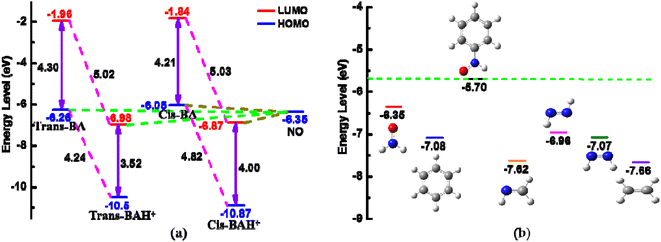
As mentioned above, the magnitude of J of the BA-based diradicals depends greatly on the coplanarity between the radical groups and bridging unit and the more extensive π-conjugation is beneficial to spin polarization for the protonated diradicals, thus promoting the spin coupling interactions. While it has been established that the good conjugation of a diradical arises from an effective molecular orbital overlap between the coupler and radical group.26,54 Thereby it is essential to analyze the orbital properties and orbital energy level of the coupler BA and NO radical group to further clarify the protonation-induced magnetic enhancement. Interestingly, we notice that there is a good orbital matching of two SOMOs of the NO groups with the HOMO of the coupler trans-BA or cis-BA for the unprotonated diradicals, or with the LUMO of the coupler trans-BAH+ or cis-BAH+ for the protonated ones, as depicted in Fig. 5 and S3.† That is, the coupler HOMO plays a large mediating role in controlling the magnetic couplings for the unprotonated diradicals, while the coupler LUMO is more critical in determining the enhanced magnetic interactions for the protonated ones.To quantitatively explain the proton-induced magnetic enhancement and confirm the different magnetic coupling mechanisms of the unprotonated and protonated diradicals, we further examine the orbital energy levels of the coupler and radical group. As shown in Fig. 6a, both the energies of HOMO and LUMO of the coupler trans-BA or cis-BA decrease after protonation. That is to say, introduction of a proton into the couplers trans-BA or cis-BA can decrease not only their HOMO energy levels, but also their LUMO energy levels to a large extent. Specifically, upon protonation the energies of HOMO and LUMO reduce by 4.24 and 5.02 eV for the trans-BA, and by 4.82 and 5.03 eV for the cis-BA, respectively. It has been suggested that if the orbital energies of the SOMO (HOMO) of the radical groups and HOMO of the coupler are very close, they can combine together to form a stable diradical with considerable spin–spin coupling, or vice versa.54 Interestingly, we observe that the energy difference of HOMO between the trans-/cis-BA coupler and NO radical group is very close, demonstrating that the coupler HOMO is critical to adjust the spin coupling of two spin sources for the unprotonated diradicals. While the energy difference of LUMO of the trans-/cis-BAH+ coupler and HOMO of the NO radical group is much smaller, consistent well with the aforementioned opinion that the coupler LUMO plays a decisive role for the magnetic interactions for the protonated diradicals. Furthermore, we have found that small HOMO–LUMO energy gap of the protonated coupler trans-BAH+ (3.52 eV) or cis-BAH+ (4.00 eV) can effectively promote the magnetic coupling of diradical in contrast to that of trans-BA (5.02 eV) or cis-BA (5.03 eV).55,56 The schematic representation of the exchange coupling interactions between two spin centers through the coupler HOMO (the unprotonated diradicals) or LUMO (the unprotonated diradicals) together with its HOMO–LUMO energy gap is collected in Fig. S4.†
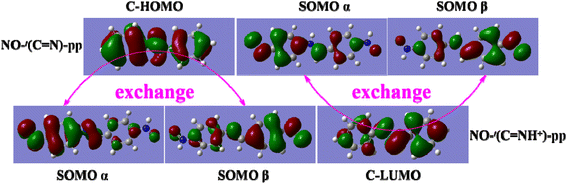 | ||
Fig. 5 Exchange couplings between two SOMOs of diradicals NO-(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp and NO-t(C N)-pp and NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH+)-pp though their corresponding couplers (C) HOMO or LUMO. NH+)-pp though their corresponding couplers (C) HOMO or LUMO. | ||
To further explain different magnetic magnitudes of isoelectronic analogues of the BA, AB and stilbene-based NO diradicals, we also analyze the energy difference between the radical groups and bridging unit among them. The reason is that small energy difference of HOMO between the radical groups and bridging unit is favorable to the formation of a stable diradical, leading to a strong spin coupling. The HOMO energy levels of the model molecular segments including the HON-phenylene radical moiety and NO radical group as well as bridging units –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N–, –HC
N–, –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– and –N
CH– and –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– are illustrated in Fig. 6b. The calculated results reveal that larger HOMO energy differences between HON-phenylene and –HC
N– are illustrated in Fig. 6b. The calculated results reveal that larger HOMO energy differences between HON-phenylene and –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– or –HC
N– or –HC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– give rise to smaller magnetic interactions for the BA or stilbene-bridged diradicals compared with that of the AB-coupled ones. This observation suggests that the orbital energy difference between the radical groups and bridging unit is substantive in governing the degree of spin coupling interaction. Besides, an effective orbital matching of two SOMOs of the NO groups with the HOMO of the coupler AB and stilbene or LUMO of the coupler ABH+ (Fig. S3†) is crucial in determining the magnetic strength as described above. It is worth pointing out that the magnetic behaviors of all the studied diradicals obey the SOMO effect (Fig. S5†) and spin alternation rule (Fig. S6†).
CH– give rise to smaller magnetic interactions for the BA or stilbene-bridged diradicals compared with that of the AB-coupled ones. This observation suggests that the orbital energy difference between the radical groups and bridging unit is substantive in governing the degree of spin coupling interaction. Besides, an effective orbital matching of two SOMOs of the NO groups with the HOMO of the coupler AB and stilbene or LUMO of the coupler ABH+ (Fig. S3†) is crucial in determining the magnetic strength as described above. It is worth pointing out that the magnetic behaviors of all the studied diradicals obey the SOMO effect (Fig. S5†) and spin alternation rule (Fig. S6†).
4. Conclusions
In summary, we theoretically design several couples of the BA-bridged nitroxide diradicals in the trans or cis forms, whose magnetic coupling constants J have significant increases after protonation of the central –CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N– unit of the coupler BA. It is found that although the signs of their J do not change, but the magnitudes remarkably increase after protonation from −332.6 to −819.0 cm−1 for NO-t(C
N– unit of the coupler BA. It is found that although the signs of their J do not change, but the magnitudes remarkably increase after protonation from −332.6 to −819.0 cm−1 for NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp and −79.2 to −310.2 cm−1 for NO-t(C
N)-pp and −79.2 to −310.2 cm−1 for NO-t(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)-pp, respectively. Structurally, the better conjugation of the protonated trans diradical and two reduced CCNC and CCCN torsion angles (ϕ2 and ϕ3) of the protonated cis one create a more favorable condition for spin transmission, promoting the spin polarization and then leading to larger spin couplings. More importantly, the proton-induced magnetic enhancement should be attributed to strong participation of the coupler BA through its LUMO with a lower energy level after protonation, improving spin polarization from the NO radical groups to the coupler BA and facilitating the spin coupling accordingly. Moreover, small HOMO–LUMO gap of the coupler BA through protonation is crucial in explaining such remarkable spin-coupling enhancement. In addition, different linking positions of two NO radical groups to the coupler BA are also considered to further confirm the conclusion of the protonation-enhanced magnetic couplings and we observe that their absolute J (|J|) are in an order pp > mp > mm for the unprotonated or protonated diradicals regardless of the trans or cis forms. Furthermore, we also make a comparison of the magnetic coupling strengths among the isoelectronic analogues of BA-, AB- and stilbene-bridged nitroxide diradicals before or after protonation, and find a linear correlation among them. The spin-coupling-mediating abilities of the isoelectronic analogues are in an order AB > stilbene > BA. Besides, the magnetic behaviors of all these studied diradicals can be qualitatively predicted by means of the spin alternation rule and SOMO effect. This work would open a new prospective for the rational design of the magnetic molecular switches (Fig. 6).
N)-pp, respectively. Structurally, the better conjugation of the protonated trans diradical and two reduced CCNC and CCCN torsion angles (ϕ2 and ϕ3) of the protonated cis one create a more favorable condition for spin transmission, promoting the spin polarization and then leading to larger spin couplings. More importantly, the proton-induced magnetic enhancement should be attributed to strong participation of the coupler BA through its LUMO with a lower energy level after protonation, improving spin polarization from the NO radical groups to the coupler BA and facilitating the spin coupling accordingly. Moreover, small HOMO–LUMO gap of the coupler BA through protonation is crucial in explaining such remarkable spin-coupling enhancement. In addition, different linking positions of two NO radical groups to the coupler BA are also considered to further confirm the conclusion of the protonation-enhanced magnetic couplings and we observe that their absolute J (|J|) are in an order pp > mp > mm for the unprotonated or protonated diradicals regardless of the trans or cis forms. Furthermore, we also make a comparison of the magnetic coupling strengths among the isoelectronic analogues of BA-, AB- and stilbene-bridged nitroxide diradicals before or after protonation, and find a linear correlation among them. The spin-coupling-mediating abilities of the isoelectronic analogues are in an order AB > stilbene > BA. Besides, the magnetic behaviors of all these studied diradicals can be qualitatively predicted by means of the spin alternation rule and SOMO effect. This work would open a new prospective for the rational design of the magnetic molecular switches (Fig. 6).
Author contributions
Fengying Zhang: writing original draft, software, validation, supervision, funding acquisition. Yiwei Feng: data curation. Xinyu Song: conceptualization, software. Yuxiang Bu: conceptualization, software.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are thankful for financial support from the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (No. 2019L0889), the National Youth Natural Fund (62105131), the Scientific and Technology Key Research and Development Project of Jinzhong City (Y201027) and the Shanxi Province Collaborative Innovation Center for Light Materials Modification and Application (No. PY201817).References
- T. Katsuki, Chem. Soc. Rev., 2004, 33, 437–444 RSC
.
- Y. Hu, N. Goodeal, Y. Chen, A. M. Ganose, R. G. Palgrave, H. Bronstein and M. O. Blunt, Chem. Commun., 2016, 52, 9941–9944 RSC
.
- A. Naghipour and A. Fakhri, Catal. Commun., 2016, 73, 39–45 CrossRef CAS
.
- J. Chai, Y. B. Wu, B. S. Yang and B. Liu, J. Mater. Chem. C, 2018, 6, 4057–4064 RSC
.
- X. W. Xu, S. Q. Ma, J. H. Wu, J. T. Yang, B. B. Wang, S. Wang, Q. Li, J. Feng, S. S. You and J. Zhu, J. Mater. Chem. A, 2019, 7, 15420–15431 RSC
.
- M. Maji, S. Acharya, I. Bhattacharya, A. Gupta and A. Mukherjee, Inorg. Chem., 2021, 60, 4744–4754 CrossRef CAS PubMed
.
- X. Zhang, J. Z. Wu, Z. L. Qin, L. J. Qian, L. C. Liu, W. C. Zhang and R. J. Yang, ACS Appl. Polym. Mater., 2022, 4, 2604–2613 CrossRef CAS
.
- C. A. van Walree, O. Franssen, A. W. Marsman, M. C. Flipseb and L. W. Jenneskens, J. Chem. Soc., Perkin Trans. 2, 1997, 799–807 RSC
.
- H. Neuvonen, K. Neuvonen and F. Fölöp, J. Org. Chem., 2006, 71, 3141–3148 CrossRef CAS PubMed
.
- P. Bao and Z. H. Yu, J. Comput. Chem., 2006, 27, 809–824 CrossRef CAS PubMed
.
- L. Óvári, Y. Luo, F. Leyssner, R. Haag, M. Wolf and P. Tegeder, J. Chem. Phys., 2010, 133, 044707 CrossRef PubMed
.
- A. V. Gaenko, A. Devarajan, L. Gagliardi, R. Lindh and G. Orlandi, Theor. Chem. Acc., 2007, 118, 271–279 Search PubMed
.
- R. Mitrić, U. Werner and V. B. Koutecký, J. Chem. Phys., 2008, 129, 164118 CrossRef PubMed
.
- Y. Luo, M. Utecht, J. Dokić, S. Korchak, H. M. Vieth, R. Haag and P. Saalfrank, ChemPhysChem, 2011, 12, 2311–2321 CrossRef CAS PubMed
.
- N. Kawatsuki, H. Matsushita, T. Washio, J. Kozuki, M. Kondo, T. Sasaki and H. Ono, Macromolecules, 2014, 47, 324–332 CrossRef CAS
.
- L. Y. Wang, C. T. Cao and C. Z. Cao, J. Phys. Org. Chem., 2016, 29, 299–304 CrossRef CAS
.
- J. M. O. Sánchez, R. Gelabert, M. Moreno and J. M. Lluch, J. Chem. Phys., 2008, 129, 214308 CrossRef PubMed
.
- P. P. Zhao, P. Lu, Z. Y. Zhao, S. W. Chen, X. Y. Li, C. Deng and Y. Z. Wang, Chem. Eng. J., 2022, 437, 135461 CrossRef CAS
.
- L. Zhai, Y. Jiang, Y. Shi, M. Lv, Y. L. Pu, H. L. Cheng, J. Y. Zhu and K. W. Yang, Bioorg. Chem., 2022, 126, 105910 CrossRef CAS PubMed
.
- T. Mitsumori, N. Koga and H. Iwamura, J. Phys. Org. Chem., 1994, 7, 43–49 CrossRef CAS
.
- A. K. Pal, S. Hansda, S. N. Datta and F. Illas, J. Phys. Chem. A, 2013, 117, 1773–1783 CrossRef CAS PubMed
.
- K. Hamachi, K. Matsuda, T. Itoh and H. Iwamura, Bull. Chem. Soc. Jpn., 1998, 71, 2937–2943 CrossRef CAS
.
- S. I. Nakatsuji, M. Fujino, S. Hasegawa, H. Akutsu, J. I. Yamada and V. S. Gurman, J. Org. Chem., 2007, 72, 2021–2029 CrossRef CAS PubMed
.
- S. Shil and A. Misra, J. Phys. Chem. A, 2010, 114, 2022–2027 CrossRef CAS PubMed
.
- S. N. Datta, A. K. Pal, S. Hansda and I. A. Latif, J. Phys. Chem. A, 2012, 116, 3304–3311 CrossRef CAS PubMed
.
- F. Y. Zhang, X. Y. Song and Y. X. Bu, J. Phys. Chem. C, 2017, 121, 17160–17168 CrossRef CAS
.
- H. Y. Xu, K. Sohlberg and Y. Wei, J. Mol. Struct., 2003, 634, 311–314 CrossRef CAS
.
- H. Bednarski, M. Domański, J. Weszka and K. Sohlberg, J. Mol. Struct., 2009, 908, 122–124 CrossRef CAS
.
- M. E. Ali and S. N. Datta, J. Phys. Chem. A, 2006, 110, 2776–2784 CrossRef CAS PubMed
.
- I. Latif, A. Panda and S. N. Datta, J. Phys. Chem. A, 2009, 113, 1595–1600 CrossRef CAS PubMed
.
- M. E. Ali, V. Staemmler, F. Illas and P. M. Oppeneer, J. Chem. Theory Comput., 2013, 9, 5216–5220 CrossRef CAS PubMed
.
- F. Y. Zhang, X. Y. Song and Y. X. Bu, J. Phys. Chem. C, 2015, 119, 27930–27937 CrossRef CAS
.
- A. Bajaj and M. E. Ali, J. Phys. Chem. C, 2019, 123, 15186–15194 CrossRef CAS
.
- Q. Wang, Z. L. Zhang, H. C. Huang, X. Y. Song and Y. X. Bu, Phys. Chem. Chem. Phys., 2022, 24, 3834–3843 RSC
.
- S. Nishida, Y. Morita, K. Fukui, K. Sato, D. Shiomi, T. Takui and K. Nakasuji, Angew. Chem., 2005, 117, 7443–7446 CrossRef
.
- M. O. Sandberg, O. Nagao, Z. Wu, M. M. Matsushita and T. Sugawara, Chem. Commun., 2008, 3738–3740 RSC
.
- M. Ishida, S. Karasawa, H. Uno, F. Tani and Y. Naruta, Angew. Chem., Int. Ed., 2010, 49, 5906–5909 CrossRef CAS PubMed
.
- H. Yamashita and J. Abe, J. Phys. Chem. A, 2014, 118, 1430–1438 CrossRef CAS PubMed
.
- Q. Wang, X. Y. Song, P. Li and Y. X. Bu, J. Phys. Chem. C, 2019, 123, 10764–10776 CrossRef CAS
.
- C. Trindle and S. N. Datta, Int. J. Quantum Chem., 1996, 57, 781–799 CrossRef CAS
.
- C. Trindle, S. N. Datta and B. Mallik, J. Am. Chem. Soc., 1997, 119, 12947–12951 CrossRef CAS
.
- W. T. Borden and E. R. Davidson, J. Am. Chem. Soc., 1977, 99, 4587–4594 CrossRef CAS
.
- D. Feller, E. R. Davidson and W. T. Borden, Isr. J. Chem., 1983, 23, 105–108 CrossRef CAS
.
- S. Kato, K. Morokuma, D. Feller, E. R. Davidson and W. T. Borden, J. Am. Chem. Soc., 1983, 105, 1791–1795 CrossRef CAS
.
- G. Chung and D. Lee, Chem. Phys. Lett., 2001, 350, 339–344 CrossRef CAS
.
- V. Polo, A. Alberola, J. Andres, J. Anthony and M. Pilkington, Phys. Chem. Chem. Phys., 2008, 10, 857–864 RSC
.
- L. Noodleman, J. Chem. Phys., 1981, 74, 5737–5743 CrossRef CAS
.
- L. Noodleman and E. J. Baerends, J. Am. Chem. Soc., 1984, 106, 2316–2327 CrossRef CAS
.
- K. Yamaguchi, Y. Takahara, T. Fueno and K. Nasu, Jpn. J. Appl. Phys., 1987, 26, L1362–L1364 CrossRef CAS
.
- K. Yamaguchi, F. Jensen, A. Dorigo and K. N. Houk, Chem. Phys. Lett., 1988, 149, 537–542 CrossRef CAS
.
- D. Cho, K. C. Ko and J. Y. Lee, J. Phys. Chem. A, 2014, 118, 5112–5121 CrossRef CAS PubMed
.
- D. Cho, K. C. Ko and J. Y. Lee, Int. J. Quantum Chem., 2016, 116, 578–597 CrossRef CAS
.
- M. J. Frisch, et al., Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, CT, 2009 Search PubMed
.
- Y. W. Feng, F. Y. Zhang, X. Y. Song and Y. X. Bu, Phys. Chem. Chem. Phys., 2017, 19, 5932–5943 RSC
.
- S. Shil, M. Roy and A. Misra, RSC Adv., 2015, 5, 105574–105582 RSC
.
- F. Y. Zhang, Q. Luo, X. F. Song, X. Y. Song and Y. X. Bu, Int. J. Quantum Chem., 2018, 118, e25693 CrossRef
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ra05115j |
| This journal is © The Royal Society of Chemistry 2022 |