Open Access Article
Open Access ArticleEfficient fluorescent recognition of ATP/GTP by a water-soluble bisquinolinium pyridine-2,6-dicarboxamide compound. Crystal structures, spectroscopic studies and interaction mode with DNA†
Alejandro O. Viviano-Posadas a,
Ulises Romero-Mendozaa,
Iván J. Bazany-Rodríguez
a,
Ulises Romero-Mendozaa,
Iván J. Bazany-Rodríguez a,
Rocío V. Velázquez-Castillo
a,
Rocío V. Velázquez-Castillo a,
Diego Martínez-Otero
a,
Diego Martínez-Otero b,
Joanatan M. Bautista-Renedob,
Nelly González-Rivas
b,
Joanatan M. Bautista-Renedob,
Nelly González-Rivas b,
Rodrigo Galindo-Murillo
b,
Rodrigo Galindo-Murillo c,
María K. Salomón-Flores
c,
María K. Salomón-Flores a and
Alejandro Dorazco-González
a and
Alejandro Dorazco-González *a
*a
aInstitute of Chemistry, National Autonomous University of Mexico, Circuito Exterior, Ciudad Universitaria, México, D.F., 04510, Mexico. E-mail: adg@unam.mx; Tel: +52-55-56224514
bCentro Conjunto de Investigación en Química Sustentable UAEM-UNAM, km 14.5 Carrera Toluca-Atlacomulco, Campus UAEMex “El Rosedal” San Cayetano-Toluca, Toluca de Lerdo 50200, Estado de México, Mexico
cDepartment of Medicinal Chemistry, College of Pharmacy, University of Utah, 2000 East 30 South Skaggs 306, Salt Lake City 84112, Utah, USA
First published on 29th September 2022
Abstract
The new dicationic pyridine-2,6-dicarboxamide-based compound 1 bearing two N-alkylquinolinium units was synthesized, structurally determined by single-crystal X-ray diffraction, and studied in-depth as a fluorescent receptor for nucleotides and inorganic phosphorylated anions in pure water. The addition of nucleotides to 1 at pH = 7.0 quenches its blue emission with a selective affinity towards adenosine 5′-triphosphate (ATP) and guanosine 5′-tripohosphate (GTP) over other nucleotides such CTP, UTP, ADP, AMP, dicarboxylates and inorganic anions. On the basis of the spectroscopic tools (1H, 31P NMR, UV-vis, fluorescence), MS measurements and DFT calculations, receptor 1 binds ATP with high affinity (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 5.04) through the simultaneous formation of strong hydrogen bonds and π–π interactions between the adenosine fragment and quinolinium ring with binding energy calculated in 8.7 kcal mol−1. High affinity for ATP/GTP is attributed to the high acidity of amides and preorganized rigid structure of 1. Receptor 1 is an order of magnitude more selective for ATP than GTP. An efficient photoinduced electron transfer quenching mechanism with simultaneous receptor–ATP complexation in both the excited and ground states is proposed. Additionally, multiple spectroscopic studies and molecular dynamics simulations showed that 1 can intercalate into DNA base pairs.
K = 5.04) through the simultaneous formation of strong hydrogen bonds and π–π interactions between the adenosine fragment and quinolinium ring with binding energy calculated in 8.7 kcal mol−1. High affinity for ATP/GTP is attributed to the high acidity of amides and preorganized rigid structure of 1. Receptor 1 is an order of magnitude more selective for ATP than GTP. An efficient photoinduced electron transfer quenching mechanism with simultaneous receptor–ATP complexation in both the excited and ground states is proposed. Additionally, multiple spectroscopic studies and molecular dynamics simulations showed that 1 can intercalate into DNA base pairs.
Introduction
Selective recognition of nucleoside polyphosphates (NPPs) by luminescent molecular receptors remains an active and important area in supramolecular chemistry and analytical sciences1–7 due to their key biochemical functions in genetic information and cellular energy transduction.8 Among the NNPs, adenosine triphosphate (ATP) is the most abundant nucleotide in cells and is the primary chemical energy source in living systems.9 On the other hand, guanosine triphosphate (GTP) regulates a wide variety of cellular processes ranging from protein synthesis, the citric acid cycle and RNA synthesis.10 A variety of human illnesses such as kidney diseases, Alzheimer's, hypoglycemia and cancer are associated with deviations in ATP or GTP levels.11–13 While the need for efficient and selective optical receptors for purine nucleotides (ATP/GTP) is evident, so far, few molecular receptors able to operate efficiently in neutral aqueous media at sub-micromolar concentrations have been described.Fluorescent recognition of ATP/GTP has been dominated by organic artificial receptors containing arrays of hydrogen bond donors of NH/CH type or polycationic moieties as binding sites for the polyphosphate fragments.14–24 Typically, these receptors show binding constants between 102 and 104 M−1.25,26 Consequently, they are suitable to recognize ATP/GTP in the millimolar concentration range, but not significantly below. These receptors also frequently require an organic cosolvent to operate, which seriously limits their intended applications.14,27–31
Optical recognition of ATP or GTP by molecular hosts in water can be achieved with fluorescent imidazolium salts,14,18,27 cyclophanes,19,29 quinoline-based Zn-complexes,3,32 lanthanide complexes4 and bis- 2,6-formylphenol derivatives.16 These luminescent receptors undergo changes in their photophysical properties due to the binding of the polyphosphate motif with the hydrogen bond donors or by coordination to the metal center.33 However, in many cases they are not particularly selective towards purine nucleotides because their chemical structures only contain binding sites for the polyphosphate moieties.7,34 Thus, interference from other nucleotides (CTP, UTP, TTP, ADP, AMP, GDP),16,30,33,35 adenine dinucleotide (NADH)36 and pyrophosphate (PPi)34 can be a problem.
In principle, it should be possible to overcome these limitations by developing a fluorescent molecular receptor with specific, high-affinity, and cooperative binding points for ATP or GTP that includes hydrophilic fragments in its chemical structure. However, the creation of a potent, and selective receptor for GTP/ATP able to operate in a neutral aqueous phase is an ongoing challenge.7 Recent reports in the context of oxyanion recognition have displayed that pyridine-2,6-dicarboxamide-based pincer receptors are able to bind phosphorylated anions through hydrogen bonds.37 Previously, we reported a series of dicationic N-methylated bisquinolinium pyridine-2,6-dicarboxamide receptors with a moderate affinity towards PPi and ATP ranging between 300 and 5400 M−1 in water where the anion-binding is driven mainly by the acidification of the amide NH groups.38
On the hand, quinoline-based dyes as quaternary salts have found many applications in fluorescent molecular recognition of inorganic anions39,40 and as pH-probes.41 They have also been used as efficient DNA intercalators42,43 and G-quadruplex ligands44,45 where the supramolecular complex formed is stabilized by π-stacking interactions between π-electron-rich rings from guanine or adenine and the cationic aromatic π-electron-deficient ring from quinolinium.46
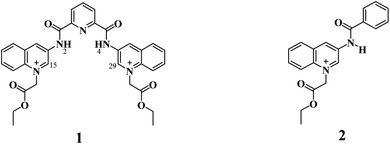
Taking this into account, we surmised that a sensitive optical recognition of ATP/GTP in water is possible with a combination of two binding sites based on a water-soluble pyridine-2,6-dicarboxamide cationic receptor with a high affinity for polyphosphate fragments and fluorescent quinolinium units as a cooperative binding site for purine rings via π–π interactions. The results obtained for a new nucleotide receptor 1 based on bisquinolinium pyridine-dicarboxamide including synthesis, crystal structure, acid–base properties, spectroscopic recognition studies and theoretical DFT calculations are summarized below. For comparison purposes, a related N-alkyl quinolinium benzamide derivative 2 lacking a polyphosphate binding site was also studied.
Results and discussion
Synthesis and crystal structures
Compounds 1 and 2 (Scheme 1) were successfully synthesized by the two-step procedure described in Scheme S1†.47 The synthesis of 1 was initiated by reacting 2,6-pyridinedicarbonyl dichloride with 3-aminoquinoline in dry toluene, and subsequent prolonged treatment with ethyl bromoacetate in dry DMF.The bromide salts of 1 and 2 were isolated in good yield as pale-yellow crystalline powders and pure according to 1H, 13C, DEPT, HSQC NMR spectroscopy (Fig. S1–S18†), and elemental analysis (C, N, H).
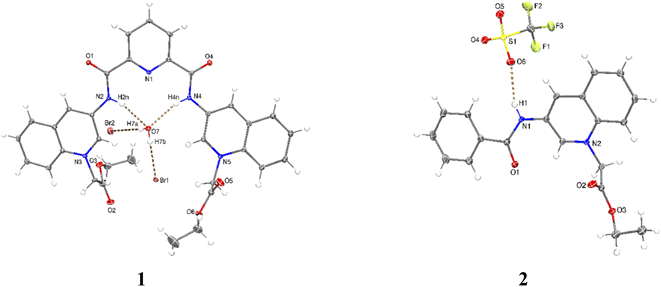
X-ray crystal structures were obtained for bromide salt of 1 and triflate salt of 2 by slow evaporation of methanolic solutions (see Table S1 in the ESI† for crystallographic data). Parameters for selected hydrogen bonding interactions within the crystal packing are collected in Tables S2–S3.†
Perspective views of molecular structures of 1 and 2 are shown in Fig. 1. Crystallographic analysis for 1 shows that it possesses a rather high degree of planarity: the dihedral angles between N-alkylated quinolinium rings and the central pyridine ring are φ = 11.63 and 22.78°. The two carboxamide groups are turned inside the cleft toward each other and are coplanar with the central pyridine ring, this syn–syn conformation has been commonly observed for crystal structures of pyridine-2,6-dicarboxamide derivatives for both macrocyclic50–53 and acyclic species30,34,38,39,47–51 as result of intramolecular hydrogen bonds between the central pyridine and the NH carboxamide groups.
Since the high planarity between the quinolinium rings and the carboxamide groups, the ortho-CH bonds from quinolinium rings show an optimal orientation towards the intracavity, therefore, 1 is a preorganized receptor with a well-defined cavity for recognition of anions. The distances NH⋯HN and ortho-(15)CH⋯HC(29) of 1 are 3.132 and 4.384 Å, respectively. The size of the cavity formed by NH and ortho-CH hydrogen bond donors is favorable for hosting halide ions2 and phosphorylated anions, which induce a peak selectivity over other anions, as has been demonstrated in previous works.52,53
The carbon–nitrogen bond distance Csp2–Nsp2 = 1.364(5) Å of the carboxamide groups in 1 is significantly longer than that found for neutral related derivatives in the range of 1.323–1.350 Å.50
This difference can be induced by the positive charges of lateral quinolinium moieties. The crystal of 1 is strongly hydrated with the consequence that the receptor cavity is occupied by a water molecule where the NH bonds of both carboxamide groups are oriented towards the oxygen atom from the water forming two N–H⋯O hydrogen bonds (Table S2†). It can be expected that a similar binding mode for tetrahedral anions such as phosphorylated-derivatives might occur also via charged-assisted N–H⋯−O–P interactions.48,51,52
Crystal of 2 shows coplanarity between quinolinium and benzyl ring with a dihedral angle of φ = 9.58°, similar structural properties have been reported previously for a benzamide derivative.54 The positive charge of 2 is stabilized by a triflate via N–H⋯O interactions (Table S3†).
Optical and acid–base properties
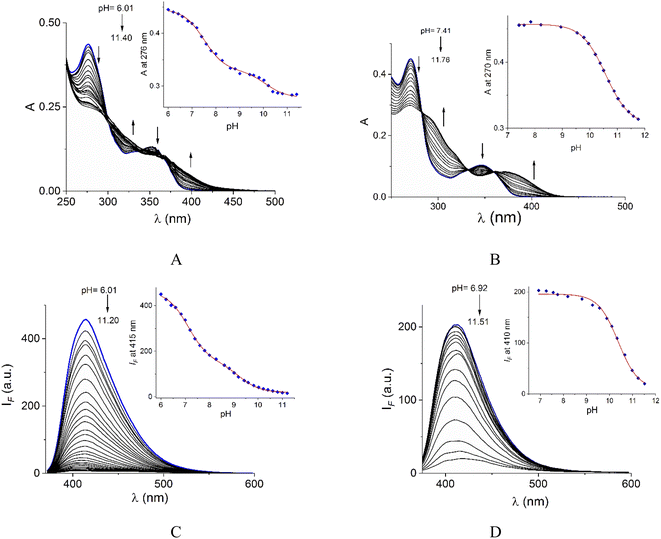
Acid–base properties of bromide salts of 1 and 2 were studied by UV-vis and fluorimetric pH-titrations. Absorption and emission maxima in water at pH = 7.0 are collected in Table 1 and the family of spectra at different pH values are compiled in Fig. 2. In N-alkylquinolinium salts, the long-wavelength absorption band near 350 nm is typically attributed to n → π* electronic transitions55 and the blue/green fluorescence is originated by intramolecular charge transfers (ICT) in the excited state.56λabs (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ε) (pH = 7.0) ε) (pH = 7.0) |
UV-vis | Emission | Fluorimetric titration | |||
|---|---|---|---|---|---|---|
| pKa1 | pKa2 | (λexc = 350 nm) | pK` | pKa2 | ||
| 1 | 276(4.43), 350(3.90) | 7.70 ± 0.02 | 10.10 ± 0.09 | 415 | 7.12 ± 0.03 | 9.23 ± 0.05 |
| 2 | 270(4.16), 346(3.73) | 10.57 ± 0.02 | — | 410 | 10.37 ± 0.04 | — |
Buffered aqueous solutions (10 mM MOPS, pH = 7.0) of bromide salts of 1–2 were stable for several days and followed very well to the Lambert–Beer law up to 50.0 μM, thus these conditions were used for further studies.
On increasing pH, the absorbance at shorter wavelengths (∼275 nm) decreases while at longer wavelengths it increases (∼350 nm) and the blue emission is strongly quenched for both salts. For 2, spectrophotometric titration experiment (Fig. 2B) shows three clear isosbestic points at 282, 330 and 360 nm indicating the chemical equilibrium between the protonated/deprotonated species of the amide group.
In the case of 1, two processes are observed (Fig. 2A), the first one given in the pH range 6.0–8.61 by a sharp decrease in absorbance at the maximum 276 nm with three isosbestic points at 302, 335, and 369 nm. The second process at pH > 8.8 with an increase in absorbance at longer wavelengths. The pKa values calculated are shown in Table 1.
In general, the acid-base dissociation constants are significantly lower than those typical for common amides due to the combination of the strong electron-accepting properties of the central pyridyl ring and the positive charge on quinolinium rings. The absence of the electron-accepting effect by the pyridyl ring in 2 is reflected in a higher pKa value closer to ordinary amides. Species with deprotonated carboxamide groups in 1 and 2 are practically not fluorescent by an intramolecular photoinduced electron transfer (PET) caused by deprotonation in the excited state, forming a non-emitting conjugated base.38
The pKa values of 1 calculated by fluorescence spectroscopy are slightly lower than those calculated by UV-vis suggesting a contribution of the excited state deprotonation (Table 1).
Taking into account the fluorescence emission, the high acidity of the amide groups, the preorganization of the NH/CH donors, and the dicationic nature of water at pH = 7.0 of 1, we explored this compound as a receptor for a series of phosphorylated anions by experimental and theoretical studies.
NPPs recognition studies
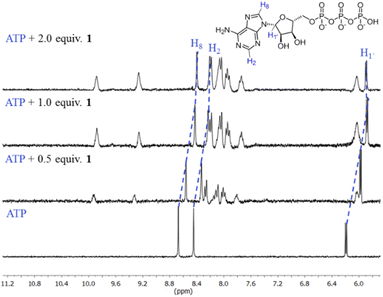
The first evidence for the high affinity of ATP/GTP for 1 was obtained by 31P and 1H NMR measurements. The phosphate binding modes of sodium salts of ATP/GTP with 1 were investigated by 31P NMR spectroscopy in neutral D2O solutions (Fig. 3). The free ATP has signals at −10.77 (γ-P), −11.21 (α-P), and −22.93 (β-P) and the addition of 1.0 equiv. of 1 induces a considerable broadening of terminal γ-P signal with evident downfield shift (Δδ = 1.67 ppm) which can be assigned to the formation of N–H⋯O–P-γ hydrogen bonds. The nature of this shift can be ascribed to a “partial protonation” of the γ-P phosphate as would be expected by the interaction with the NH carboxamide groups. In the case of GTP, the shift of γ-P signal was significantly lower than that observed for ATP. Similar NMR spectroscopic changes, in particular, the downfield shift of 31P-signals have been observed with organic polyammonium-based receptors and they are assigned to the formation of strong hydrogen bonds.57 To gain further information regarding the interaction of adenosine fragment to quinolinium rings, 1H NMR experiments were performed. Fig. 4 shows the aromatic region of 1H NMR spectra of free ATP and with increasing amounts of 1. Clearly, protons of adenine H2, H8 and proton of ribose fragment H1 undergo significant upfield shifts by 0.31–0.58 ppm indicating interactions between adenosine moiety and 1.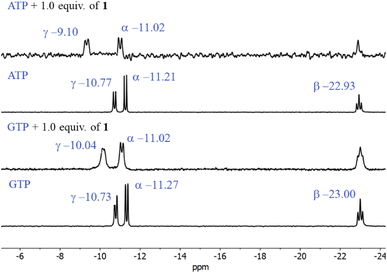 | ||
| Fig. 3 Partial 31P NMR spectra (121.5 MHz, 25 °C) of sodium salts of ATP and GTP (3.0 mM) in the presence of 1.0 equiv. of 1 in D2O at pD = 7.0 (10 mM MOPS). | ||
Such 1H NMR spectral changes have been observed in supramolecular-complexes of ATP with receptors derivatives of acridine-appended polyammonium as a result of π-stacking interactions.22 Reports in the context of ATP-binding proteins have shown that aromatic amino acids drive the binding with the adenosine ring inducing selectivity over the rest of the NPPs.58
There are several examples of receptors for ATP recognition containing aromatic groups linked to polyammonium groups operating through electrostatic and π-stacking interactions with the adenosine ring typically at acid pH.7,22 A new property of receptor 1 is that it provides two simultaneous two-point recognition capable of operating in neutral pure water as observed in NMR experiments.
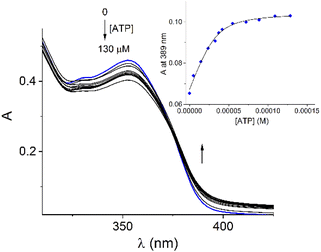
Addition of ATP and GTP to buffered aqueous solutions of 1 at pH = 7.0 induced small, but clearly observed changes in UV-vis spectra. As an example, Fig. 5 displays the family of UV-vis spectra obtained when a neutral aqueous solution of 1 is titrated with ATP. The inset shows the increase of absorbance at 389 nm on the progressive addition of ATP. This profile remained practically unchanged when the 1/ATP ratio reached 1.0 equiv. The variation in the absorbance (ΔA ∼ 0.05) at 389 nm with increasing ATP concentration fits perfectly to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric model with a binding constant of log
1 stoichiometric model with a binding constant of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K = 4.94 ± 0.11. An isosbestic point at 374 nm is observed, which suggests that only two species are in equilibrium (free 1 and its complexed form with ATP). The mass spectrum of 1 in the presence of 1.0 equiv. of ATP by a positive scan of ESI showed practically one species at 652.06 m/z, which was isotopically resolved, and it can be assigned to the dicationic complex 1
K = 4.94 ± 0.11. An isosbestic point at 374 nm is observed, which suggests that only two species are in equilibrium (free 1 and its complexed form with ATP). The mass spectrum of 1 in the presence of 1.0 equiv. of ATP by a positive scan of ESI showed practically one species at 652.06 m/z, which was isotopically resolved, and it can be assigned to the dicationic complex 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, {12+ + ATP2− + Br− + 3Na+ + 2H2O}2+ (676.6 m/z). The experimental signals, separated by 0.5, match well the theoretical isotopic distribution for a complex 1
1, {12+ + ATP2− + Br− + 3Na+ + 2H2O}2+ (676.6 m/z). The experimental signals, separated by 0.5, match well the theoretical isotopic distribution for a complex 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ATP
1, ATP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as is shown in Fig. S20.† These experiments unambiguously confirm the binding of ATP with 1 in neutral water.
1 as is shown in Fig. S20.† These experiments unambiguously confirm the binding of ATP with 1 in neutral water.
In contrast to UV-vis measurements, fluorescence experiments provided strong and reproducible changes of 1 by additions of NPPS. Thus, the interaction of receptors 1–2 with several NPPs and PPi were studied by fluorimetric titration experiments under the same conditions. Next, the addition of ATP and GTP to an aqueous solution of 1 induced a strong quenching as is shown in Fig. 6A and S19.†
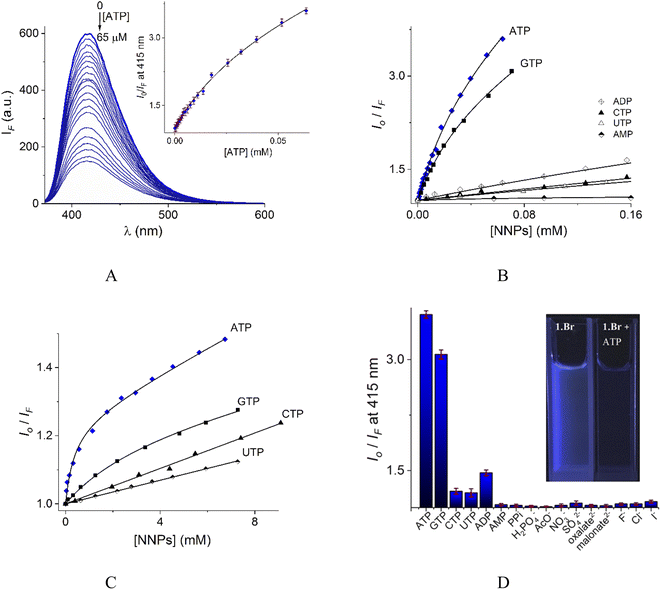 | ||
| Fig. 6 (A) Changes of emission spectra (λex = 350 nm) of buffered aqueous solutions at pH = 7.0 (10 mM MOPS) of 1 (12 μM) upon addition of increasing amounts of ATP at 25 °C. The inset shows the S–V plot at 415 nm. The solid line was obtained by fitting to eqn (1). S–V plots for fluorimetric titration experiments of 1 (B) and 2 (C) (λex = 350 nm, emission at 415 and 410 nm for 1 and 2 respectively) with a series of NNPs at pH = 7.0. (D) The fluorescence quenching at 415 nm of aqueous solution of 1 upon additions of different anions as sodium salts (0.50 mM), average of triplicate experiments. | ||
The Stern–Volmer (S–V) plot at 415 nm (λex = 350 nm) with increasing ATP concentration up to 65 μM shows a clear downward curved profile. This curve shape is typically observed by a combination of static and dynamic quenching. This profile can be very-well fitted to the theoretical eqn (1) proposed by Fabbrizzi59 which takes into account simultaneous static and dynamic quenching when the ground state complexation does not quench the emission completely and the receptor–guest complex still possesses a residual fluorescence intensity (factor ρ).
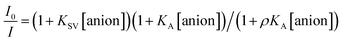 | (1) |
The estimated binding constant (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(ATP) = 5.01 ± 0.03) for static quenching is consistent with that obtained by UV-vis, indicating that complexation is mainly formed in the ground state. High affinities of 1 towards ATP/GTP (log
K(ATP) = 5.01 ± 0.03) for static quenching is consistent with that obtained by UV-vis, indicating that complexation is mainly formed in the ground state. High affinities of 1 towards ATP/GTP (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(ATP) = 5.01 ± 0.03 and log
K(ATP) = 5.01 ± 0.03 and log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K(GTP) = 4.70 ± 0.05) can be attributed to the cooperative two-point recognition which was supported by NMR experiments.47
K(GTP) = 4.70 ± 0.05) can be attributed to the cooperative two-point recognition which was supported by NMR experiments.47
S–V plots for ATP, GTP, CTP, UTP, ADP and AMP are shown in Fig. 6B. In general, titrations for all NPPs show non-linear profiles similar to ATP and GTP with downward curves but with a small quenching effect at saturation.
The calculated parameters corresponding to binding constant with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry (KA), dynamic quenching constant (KSV) and residual factor ρ using eqn (1) for NPPs and PPi are listed in Table 2.
1 stoichiometry (KA), dynamic quenching constant (KSV) and residual factor ρ using eqn (1) for NPPs and PPi are listed in Table 2.
| 1 | 2 | |||||||
|---|---|---|---|---|---|---|---|---|
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KA KA |
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KSV KSV |
ρ | Io/Ia | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KA KA |
log KSV | ρ | Io/I | |
| a Io/I indicates the relative quenching parameter of the fluorescence intensity at 415 and 410 nm of 1 (10 μM) and 2 (10 μM) respectively in the presence of 0.1 mM of the corresponding NPPs.b These data were fitted to classic Stern–Volmer eqn (2).c not calculated. | ||||||||
| ATP | 5.01 ± 0.03 | 3.57 ± 0.02 | 0.24 | 3.61 | 3.13 ± 0.09 | 1.41 ± 0.02 | 0.78 | 1.08 |
| GTP | 4.70 ± 0.05 | 3.32 ± 0.03 | 0.30 | 3.07 | 2.54 ± 0.10 | 1.38 ± 0.05 | 0.85 | 1.05 |
| CTP | 3.46 ± 0.08 | 2.70 ± 0.06 | 0.40 | 1.22 | — | 1.39 ± 0.08b | — | 1.04 |
| UTP | 3.35 ± 0.09 | 2.59 ± 0.10 | 0.50 | 1.20 | — | 1.23 ± 0.10b | — | 1.03 |
| ADP | 3.77 ± 0.09 | 2.79 ± 0.10 | 0.33 | 1.47 | — | c | — | — |
| AMP | 3.16 ± 0.11 | 1.30 ± 0.04 | 0.70 | 1.04 | — | c | — | — |
| PPi | 2.57 ± 0.07 | 1.25 ± 0.07 | 0.74 | 1.03 | — | c | — | — |
Eqn (1) is approximate because it considers similar quenching with a single KSV value for both free and complexed forms of the fluorophore as well as similar rates of photoexcitation of free and its complexed form. A more exact equation was described by Boens,60 however, it includes many adjustable parameters, which cannot be reliably determined from the fitting of plots as those shown in Fig. 6. Another limitation of eqn (1) is that if the static quenching is very strong, the estimated KSV values may have large errors including values of dynamic quenching rate constants (Kq) that can exceed 100% of the upper diffusion limit for dynamic quenching in water which is physically impossible.
Fig. 6D illustrates anion selectivity of 1 at a single wavelength in terms of the fluorescence quenching (Io/IF) induced by additions of different nucleotides, oxyanions and halides ([X−]total = 0.50 mM). In general, inorganic anions, dicarboxylates, pyrimidine nucleosides, ADP and AMP gave a very low response. The addition of GTP resulted in a considerable quenching in emission intensity, but it was still lower than that observed for ATP. This quenching effect by ATP/GTP addition is not unexpected because it is well-known that fluorescent aromatic rings with electron deficiency as quinolinium rings have a strong luminous quenching ability when they are bound to anions through a photoinduced electron transfer (PET) process. Fitting of the S–V plots (Fig. 6C) of 2 with ATP and GTP, gives small binding constants (Table 2) with values of ∼2 orders of magnitude lower than those estimated for 1. CTP and UTP showed no association with 2 and their profiles can be fitted to the classic linear Stern–Volmer equation indicating only dynamic quenching. The binding constant of 1 towards ATP is better than most previously reported water-soluble receptors bearing dicarboxamide groups as binding sites.35,62–66
DFT studies
To gain further insight into the recognition mode of 1 towards ATP/GTP density functional theory calculations were carried out. Final structures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes between ATP/GTP and 1 are presented in Fig. 7.
1 complexes between ATP/GTP and 1 are presented in Fig. 7.
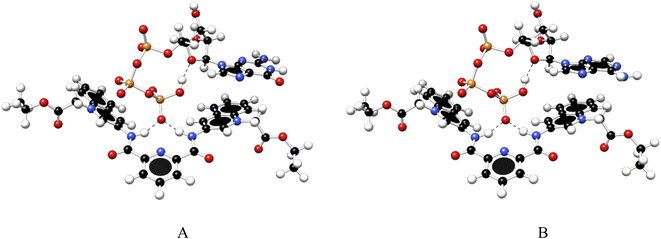 | ||
Fig. 7 Optimized structures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of ATP (A) and GTP (B) with 1, obtained at the PBEh-3c method. 1 complex of ATP (A) and GTP (B) with 1, obtained at the PBEh-3c method. | ||
These structures show the presence of strong hydrogen bond interactions between terminal phosphate groups of the nucleotides and NH carboxamide groups of 1, while the nucleotide aromatic ring interacts with a quinolinium group of 1 across π–π interactions. These calculations are consistent with those observed by NMR experiments.
Interaction energy estimated for all nucleotide bases, presented in Table S4†, shows the affinity order ATP ∼ GTP > CTP > UTP, where ATP is the nucleotide with the highest affinity (Eint = −40.30 kcal mol−1), and UTP (Eint = −22.50 kcal mol−1) is the nucleotide with the lowest affinity for 1. The difference in affinities can be explained in terms of the π–π surface interaction between purine rings and 1, represented by NCI plot, Fig. 8. Clearly, the complexes with the largest interaction surface show the best interaction energies. On the basis of experimental studies and DFT calculations, the chemical equilibrium of the ATP recognition by 1 is shown in Scheme 2.
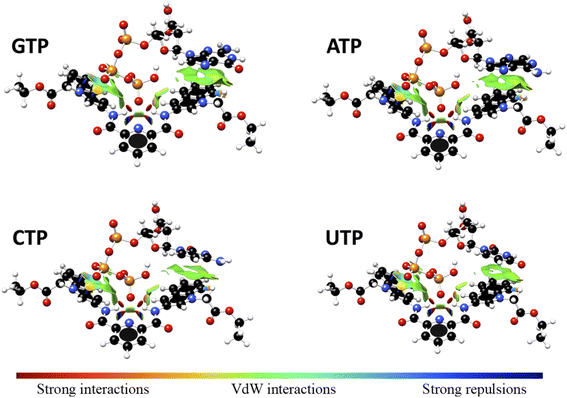 | ||
Fig. 8 Non-Covalent-Interactions-Index of GTP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ATP 1, ATP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, CTP 1, CTP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and UTP 1 and UTP![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 supramolecular complexes, obtained at the PBEh-3c method. 1 supramolecular complexes, obtained at the PBEh-3c method. | ||
Exploring interaction mode of 1 with DNA
The binding of 1 to DNA was also explored by spectroscopic titrations and molecular docking simulations. The binding mode can be preliminarily inferred by UV-vis measurements when comparing the effect of DNA on the absorption spectrum of 1 with the effect of a well-known standard DNA intercalator such as ethidium bromide (EB).67UV-vis spectra of 1 upon increasing amounts of DNA in aqueous solutions at pH = 7.0 are shown in Fig. S21A.† The absorption peak of 1 at 350 nm decreases by the addition of DNA with a considerable bathochromic effect ∼14 nm, additionally, one isosbestic point at 369 nm was observed. Typically, these red-shift and hypochromic effects are spectral changes when small molecules intercalate with DNA.68 For example, EB is a potent intercalating agent for DNA and the supramolecular complex formed is stabilized by π–π stacking interactions. The effect of DNA on the absorption spectrum of EB under the same conditions of 1 is shown in Fig. S21B.† The addition of DNA to aqueous solutions of 1 and EB induced similar absorption changes suggesting intercalation of 1 with DNA. It is well documented that the structural changes of quinolinium derivatives induced by intercalation with DNA reduce the π–π* transition energies resulting in a hypochromic effect.45,68
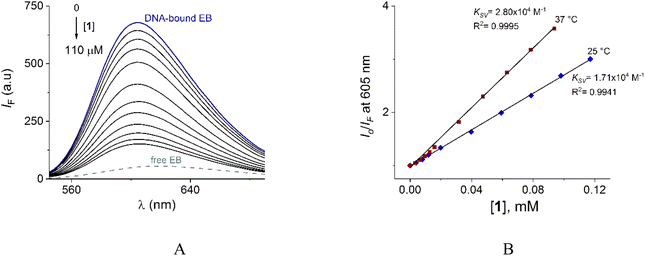
To verify the interaction of 1 with DNA, steady-state competitive titration experiments were conducted using EB as a fluorescent indicator/intercalator. In the presence of DNA, EB emits at 605 nm due to its efficient intercalation between the adjacent DNA base pairs. In contrast, free EB has a very weak emission as is shown in Fig. 9A.
This displacement assay is based on the quenching of emission resulting from the displacement of EB by an intercalator molecule, where the quenching effect is due to the reduction of the number of binding sites on the DNA that are available to the EB.68–70
The family of spectra of DNA-bound EB in the absence and the presence of increasing amounts of 1 at 25° is given in Fig. 9A. There is a significant reduction in the emission intensity about of 77% at saturation of 1. These results indicate that the DNA-bound EB is partially replaced by 1 and the molecules of 1 intercalate into DNA, which is consistent with the above results obtained by UV-vis.
The nature of this quenching effect can be quantitatively analyzed by the linear Stern–Volmer eqn (2).69
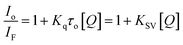 | (2) |
The quenching process is classified into two types: dynamic and static quenching. Dynamic quenching is a collisional quenching and an increase in quenching rate constant values (Kq; KSV = Kqτo) with the increase in temperature is distinctive for this process due to increasing the temperature results in a higher diffusion coefficient. The upper Kq limit value for a dynamic quenching is 2.0 × 1010 L mol−1 s−1.68,69
Next, the nature of the quenching of system DNA–EB by 1 was inferred by comparison of the behavior of the S–V plots at different temperatures (Fig. 9B). Kq values for the studied system were 1.70 × 1012 and 2.80 × 1012 Lmol−1 s−1 at 25 and 37 °C (Table 3). The increase of Kq and KSV values at higher temperatures supports the dynamic quenching processes between system EB and 1. However, the values of Kq are larger than the upper value for dynamic quenching which indicates a contribution of static quenching.68,70,71 Thus, the quenching mechanism of system DNA–EB with 1 can be interpreted as a combined quenching process.
Considering hypothetically that the static binding quenching between DNA and 1 takes place with similar and independent binding sites, the binding constant (KA) and the number of binding sites (n) can be determined by Scatchard eqn (3).68
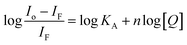 | (3) |
KA and n values were obtained from the intercept and slope of the linear plot of log(Io − IF)/IF versus log [Q] (Fig. S22†) respectively and shown in Table 3. At 25 °C, KA value indicated that 1 is tightly bound to DNA in the micromolar concentration range. The number of binding sites was obtained to be 1.06, indicating 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry between 1 and DNA.
1 stoichiometry between 1 and DNA.
On the other hand, it is known that the secondary structure of DNA can be modified by the intercalation of small molecules, and this structural change can be detected by circular dichroism. If the CD-spectrum strongly changes by the addition of a small molecule, confirms an intercalative binding process.71 Otherwise, when the spectrum remains unchanged, indicates groove binding or simple electrostatic interactions.72 Compound 1 was added to DNA neutral aqueous solution and the CD spectra were recorded. As shown in Fig. S22,† the negative and positive peaks at 242 nm and 282 nm of DNA increase their intensities by adding 1 with a slight shift of the maxima at higher wavelengths. These observed results are consistent with an intercalative binding of 1 with DNA.
Molecular dynamics simulation
Finally, to study the modes of interaction of 1 with a segment of double-stranded DNA, we used the 28-mer palindromic sequenced (CATGCATGCATGCATGCATGCATGCATG). The reduce any bias with regards of the interaction of the molecules with the DNA, three copies of 1 where manually placed near the center of the DNA using a distance of 10 Å from the helical center (Fig. 10).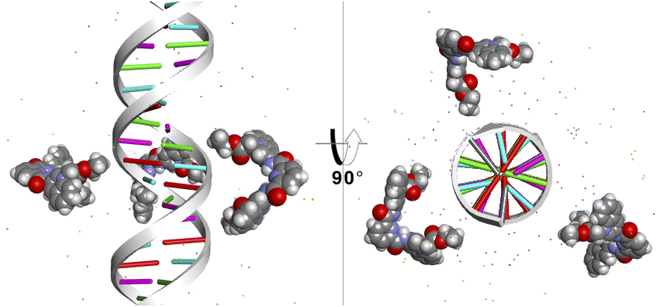 | ||
| Fig. 10 Starting position of the MD simulations. Three molecules of 1 were places at 10 Å from the helical center of the 26-mer. | ||
To detect the interactions of each ligand from the MD simulations, a 3D-histogram was constructed using the entire 36 μs of sampling time calculated. The 3D-histogram grid (depicted in Fig. 11) shows the most populated position of each of the three independent molecules present in the simulations. It is clear that two of the molecules of 1 form a stacking interaction with the terminal base pairs of the DNA for the entire MD simulation. When the molecules are not forming interactions with the bases at the ends of the DNA, they explore different conformations which, suggesting by the 3D histogram, the main mode of interaction is minor groove binding within one of the CATG regions. In Fig. 11, panel A we can observe a representative mode of interaction in the 5′ terminal base-pairs with 1 forming an intercalation type of binding mainly formed between the aromatic rings of the A/T base-pairs and the aromatic rings of 1. In the same figure, panel B we can observe the minor groove type of interaction that is formed between the aromatic rings of 1 and the back-bone of the DNA.
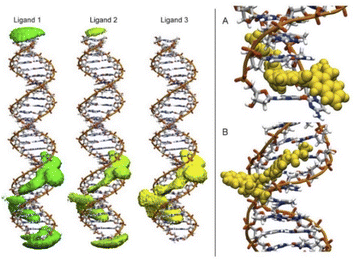 | ||
| Fig. 11 Most populated position of each of the three independent molecules of ligand 1 present in the simulations (left). Representative modes of interaction of 1 with DNA (right). | ||
Conclusions
The dicationic derivative N,N-bis(N-alkylquinolinium)pyridine-2,6-dicarboxamide 1 can be used as a fluorescent receptor for purine nucleotides in neutral aqueous solution in the micromolar concentration range with good selectivity over other nucleoside polyphosphates and phosphorylated inorganic anions.At pH = 7.0, the addition of nucleoside polyphosphates quenches the blue-emission of 1 with the highest efficiency for ATP, which displays highly selective recognition (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KA = 5.01). The quenching process could be explained by a static ATP-complexation PET mechanism possibly in both the excited and the ground state.
KA = 5.01). The quenching process could be explained by a static ATP-complexation PET mechanism possibly in both the excited and the ground state.
The crystal structure of 1, NMR spectroscopic experiments and DFT calculations showed that ATP is bound to 1 through two cooperative binding points involving: (1) strong hydrogen bonds of the type N–H⋯O–P(γ), driven by the high acidity of the amide groups and preorganization of the receptor 1, and (2) stacking interactions between π-electron-rich ring from adenine and the aromatic π-electron-deficient ring from quinolinium.
Furthermore, multiple spectroscopic studies and molecular dynamics simulations showed that 1 can intercalate into DNA base pairs with a binding constant of log ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A(DNA–1) = 4.98.
A(DNA–1) = 4.98.
Overall, these results further highlight the utility of pyridine-2,6-dicarboxamide-based preorganized pincer receptors bearing fluorescent units for supramolecular analytical applications.
Experimental section
General considerations
Chemicals, solvents and instrumentations are listed in ESI†.Chemical synthesis
Compound 1 and 2 were prepared according to a modified procedure reported previously.47 The detail procedure is described in ESI†.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1675.32m (N–H), 1545.42m (N–H), 1371.41m (–CH3), 1203.64m (C–O). Anal. Calcd. For C33H31Br2N5O6: C, 52.61; H, 4.15; N, 9.30. Found: C, 52.53; H, 4.27; N, 9.14.
O), 1675.32m (N–H), 1545.42m (N–H), 1371.41m (–CH3), 1203.64m (C–O). Anal. Calcd. For C33H31Br2N5O6: C, 52.61; H, 4.15; N, 9.30. Found: C, 52.53; H, 4.27; N, 9.14.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), 1673.64m (N–H), 1570.51m (N–H), 1374.45m (–CH3), 1289.56m (C–N), 1208.84m (C–O). Anal. Calcd. For C20H19BrN2O3
O), 1673.64m (N–H), 1570.51m (N–H), 1374.45m (–CH3), 1289.56m (C–N), 1208.84m (C–O). Anal. Calcd. For C20H19BrN2O3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C, 57.84; H, 4.61; N, 6.75. Found: C, 57.53; H, 4.77; N, 6.54.
C, 57.84; H, 4.61; N, 6.75. Found: C, 57.53; H, 4.77; N, 6.54.Crystallographic investigations
The crystallographic data, refinement details and hydrogen bonds parameters for 1 and 2 are summarized in Tables S1–S3.† Data for all compounds were collected on a Bruker APEX II CCD diffractometer at 100 K; using MoKα radiation (k = 0.71073 Å) from an Incoatec ImuS source and a Helios optic monochromator.73 Suitable crystals were coated with hydrocarbon oil, picked up with a nylon loop, and mounted in the cold nitrogen stream of the diffractometer. The structures were solved using intrinsic phasing (SHELXT) and refined by full-matrix least-squares on F2 using the ShelXle GUI.74,75 The hydrogen atoms of the C–H bonds were placed in idealized positions whereas the hydrogen atoms from the O–H moieties and hydrogens for water were localized from the difference electron density map and fixed to standard distances using DFIX instructions, and their position was refined with Uiso tied to the parent atom with distance restraints. CCDC 2118468–2118469 contain the ESI† crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via http://www.ccdc.cam.ac.uk/datarequest/cif.Fluorimetric titration experiments
Titration experiments were performed by adding aliquots of stock solutions of NPPs to a buffered aqueous solution containing MOPS (10 mM, pH = 7.0) of 1 (15 μM). In all these experiments the ionic strength was adjusted to 0.05 M with NaCl. After addition of NPPs, the solution was equilibrated for 1 min. at r. t. before recording the emission spectrum (λex = 350 nm) using a 10 mm quartz cuvette. The experimental data were fitted to corresponding eqn (1) using non-linear least-squares regression with Microcal Origin 8.1 for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 model. The selectivity experiments were performed by adding aliquots of stock solutions of the respective sodium salts of NPPs ([NPPs]final = 0.5 mM) to buffered aqueous solutions containing MOPS at pH = 7.0 of 1 (15 μM) and the emission intensities at 415 nm were recorded. All spectrophotometric experiments were performed in triplicate, and the mean values are reported.
1 model. The selectivity experiments were performed by adding aliquots of stock solutions of the respective sodium salts of NPPs ([NPPs]final = 0.5 mM) to buffered aqueous solutions containing MOPS at pH = 7.0 of 1 (15 μM) and the emission intensities at 415 nm were recorded. All spectrophotometric experiments were performed in triplicate, and the mean values are reported.
Spectrophotometric, 1H and 31P NMR titration experiments
The absorption spectra were recorded after additions of aliquots of ATP stock solution to a buffered (10 mM, MOPS at pH = 7.0 and ionic strength of 0.05 M NaCl) aqueous solutions of 1 (40 μM) in a quartz cuvette placed in a compartment Cary 100 Agilent spectrophotometer thermostated at 25 ± 0.1 °C with a recirculating water bath. 1H NMR titration experiments were performed on a 400 MHz spectrometer at 25 °C in D2O, adding aliquots with more concentrated stock solutions of sodium salts of ATP or GTP in D2O adding aliquots of them to solutions of 1 (2.0 mM) directly to NMR tubes. For 31P NMR experiments, the spectra were recorded at 121.5 MHz using H3PO4 as external standard.Computational details
The geometry optimizations of corresponding 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes between nucleoside triphosphates and 1 were carried out with the Grimme's three-fold corrected (3c) composite method PBEh-3c. This methodology shows excellent performance for non-covalent interaction energies in small and large complexes.76 All structures were confirmed as a minimum of energy according to a no-imaginary frequencies criteria. Interaction energy, Eint, was corrected due to solvent effect using the implicit solvation model CPCM,77 with water as solvent and calculated using the classical reaction model: Eint = Ecomplex − (Eligand + EB3QR), were Ecomplex refer to the energy of 1
1 complexes between nucleoside triphosphates and 1 were carried out with the Grimme's three-fold corrected (3c) composite method PBEh-3c. This methodology shows excellent performance for non-covalent interaction energies in small and large complexes.76 All structures were confirmed as a minimum of energy according to a no-imaginary frequencies criteria. Interaction energy, Eint, was corrected due to solvent effect using the implicit solvation model CPCM,77 with water as solvent and calculated using the classical reaction model: Eint = Ecomplex − (Eligand + EB3QR), were Ecomplex refer to the energy of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex and Eligand and EB3QR refer to energy of ligand and receptor respectively. Non-Covalent-Interactions-Index, NCI, was used for inter-molecular interactions analysis. All calculations were carried out with orca 4.2.0,78 while Multiwfn 3.8 (ref. 79) was used for NCI analysis.80
1 complex and Eligand and EB3QR refer to energy of ligand and receptor respectively. Non-Covalent-Interactions-Index, NCI, was used for inter-molecular interactions analysis. All calculations were carried out with orca 4.2.0,78 while Multiwfn 3.8 (ref. 79) was used for NCI analysis.80
Competitive displacement assays by fluorescence spectroscopy
A stock solution of salmon sperm DNA was prepared by dissolving 5.0 mg in 10 ml of buffered aqueous solution (5.0 mM Tris–HCl and 50.0 mM NaCl) at pH 7.0. A ratio of UV absorbance A280 of 1.86 indicated that DNA was sufficiently free from protein. The DNA concentration was calculated by UV spectrophotometry, using the molar absorption coefficient 6600 M−1 cm−1 at 260 nm.72 The stock solution was diluted accordingly to obtain a 1.0 mM working solution. 1 was dissolved in pure DMSO at stock concentrations of 5.0 mM. To get insight the interaction between 1 and DNA, an ethidium bromide competitive assay was performed. The experiments were carried out in neutral buffered aqueous solutions (5.0 mM Tris–HCl and 50.0 mM NaCl) using a 1.0 cm cuvette containing fixed final concentration of DNA–EB at 250 μM and 50 μM, respectively. This solution was titrated with a concentrated solution of 1. After the addition of the aliquots, the sample was mixed and allowed to equilibrate for 3 min and the fluorescence spectra were recorded at 25 or 37 °C (λex = 520 nm).All fluorescence intensities were corrected by the equation; Icor = Iobse(Aex+Aem)/2, where Icor and Iobs are the corrected and observed intensities, Aex and Aem are the absorbances of 1 at excitation and emission wavelengths.
Molecular dynamics simulation
The AMBER Molecular Dynamics engine (MD) was used to study the interaction of 1 with the double stranded DNA with the sequence: d (CATGCATGCATGCATGCATCATGCATG) built with the DS Visualizer. The structure was solvated with the Optimum Point Charge (OPC)81 water model and NaCl ions were added at a 200 mM concentration to neutralize the charge using the Joung–Cheatham model82 in a truncated octahedron unit cell. Compound 1 was described by the General Amber Force Field83 with the charges calculated using the RESP methodology. Three compounds where manually incorporated to the DNA model and the entire system was minimized using the protocol described by Roe.84 Double stranded DNA was described by the OL15(ref. 85) optimized force field and three independent replicas where run using the GPU PMEMD code.86 Analysis was performed using CPPTRAJ87 as available in AmberTools.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Chem. Eréndira García Rios, Chem María P. Orta Pérez, Chem. M. Angeles Peña González, M. Sc. Lucero M. Ríos Ruiz, M. Sc. L. Carmen Márquez Alonso, M. Sc. Elizabeth Huerta Salazar, Dra. Adriana Romo Pérez and Dra. Beatriz Quiroz García for technical assistance. We thank PAPIIT-UNAM-216220 and CONACYT PRONACES-160671 for financial support. A. O. V.-P., R. V. V.-C. and M. K., S.-F. is grateful to CONACyT for scholarship 868013, 688503 and 848759 respectively and U. R.-M. is grateful to PAPIIT for scholarship 120121. We thank the LANCAD and the Laboratory of Supercomputer at the UAM-Iztapalapa for access to its computer facilities.References
- S. E. Bodman and S. J. Butler, Chem. Sci., 2021, 12, 2716–2734 RSC.
- D. A. McNaughton, M. Fares, G. Picci, P. A. Gale and C. Caltagirone, Coord. Chem. Rev., 2021, 427, 213573 CrossRef CAS.
- M. Pushina, S. Farshbaf, W. Mochida, M. Kanakubo, R. Nishiyabu, Y. Kubo and P. Anzenbacher, Chem.–A Eur. J., 2021, 27, 11344–11351 CrossRef CAS.
- S. H. Hewitt, G. Macey, R. Mailhot, M. R. J. Elsegood, F. Duarte, A. M. Kenwright and S. J. Butler, Chem. Sci., 2020, 11, 3619–3628 RSC.
- R. V. Velázquez-Castillo, M. K. Salomón-Flores, A. O. Viviano-Posadas, I. J. Bazany-Rodríguez, C. Bustos-Brito, J. M. Bautista-Renedo, N. González-Rivas, L. D. Rosales-Vázquez and A. Dorazco-González, Dyes Pigm., 2021, 196, 109827 CrossRef.
- S. Mishra, S. M. Hossain and A. K. Singh, Spectrochim. Acta, Part A, 2020, 240, 118600 CrossRef CAS PubMed.
- A. M. Agafontsev, A. Ravi, T. A. Shumilova, A. S. Oshchepkov and E. A. Kataev, Chem.–A Eur. J., 2019, 25, 2684–2694 CrossRef CAS.
- R. L. P. Adams, J. T. Knowler and D. P. Leader, The Biochemistry of the Nucleic Acids, Springer Netherlands, Dordrecht, 1986 Search PubMed.
- Y. Zhou, Z. Xu and J. Yoon, Chem. Soc. Rev., 2011, 40, 2222 RSC.
- S. Shoji, S. E. Walker and K. Fredrick, ACS Chem. Biol., 2009, 4, 93–107 CrossRef CAS PubMed.
- P. Bhargava and R. G. Schnellmann, Nat. Rev. Nephrol., 2017, 13, 629–646 CrossRef CAS PubMed.
- G. Burnstock, Trends Pharmacol. Sci., 2006, 27, 166–176 CrossRef CAS PubMed.
- J. Downward, Nat. Rev. Cancer, 2003, 3, 11–22 CrossRef CAS PubMed.
- H. Tao, L. He, G. Cheng and Q.-Y. Cao, Dyes Pigm., 2019, 166, 233–238 CrossRef CAS.
- S. Dey, T. Sarkar, A. Majumdar, T. Pathak and K. Ghosh, ChemistrySelect, 2017, 2, 2034–2038 CrossRef CAS.
- A. K. Gupta, A. Dhir and C. P. Pradeep, Eur. J. Org. Chem., 2015, 2015, 122–129 CrossRef CAS.
- L. S. Mittal, P. Sharma, N. Kaur and P. Singh, Anal. Methods, 2019, 11, 5320–5327 RSC.
- N. Wu, J. Lan, L. Yan and J. You, Chem. Commun., 2014, 50, 4438–4441 RSC.
- N. Ahmed, B. Shirinfar, I. S. Youn, M. Yousuf and K. S. Kim, Org. Biomol. Chem., 2013, 11, 6407–6413 RSC.
- N. Ahmed, B. Shirinfar, I. S. Youn, A. Bist, V. Suresh and K. S. Kim, Chem. Commun., 2012, 48, 2662–2664 RSC.
- S. K. Kim, B.-S. Moon, J. H. Park, Y. Il Seo, H. S. Koh, Y. J. Yoon, K. D. Lee and J. Yoon, Tetrahedron Lett., 2005, 46, 6617–6620 CrossRef CAS.
- H. N. Kim, J. H. Moon, S. K. Kim, J. Y. Kwon, Y. J. Jang, J. Y. Lee and J. Yoon, J. Org. Chem., 2011, 76, 3805–3811 CrossRef CAS.
- W. Lang, G. Cheng, R. Peng and Q.-Y. Cao, Dyes Pigm., 2021, 189, 109245 CrossRef CAS.
- N. H. Kim, B. W. Kim, H. Moon, H. Yoo, R. H. Kang, J. K. Hur, Y. Oh, B. M. Kim and D. Kim, Anal. Chim. Acta, 2021, 1152, 338269 CrossRef CAS PubMed.
- H. Y. Kuchelmeister and C. Schmuck, Chem.–A Eur. J., 2011, 17, 5311–5318 CrossRef CAS PubMed.
- S. C. Karunakaran, A. K. Paul and D. Ramaiah, RSC Adv., 2014, 4, 30644–30647 RSC.
- S. Farshbaf and P. Anzenbacher, Chem. Commun., 2019, 55, 1770–1773 RSC.
- X. Zhang, J. Liu, J. Wang, L. Han, S. Ma, M. Zhao and G. Xi, J. Photochem. Photobiol., B, 2021, 223, 112279 CrossRef CAS PubMed.
- A. M. Agafontsev, T. A. Shumilova, A. S. Oshchepkov, F. Hampel and E. A. Kataev, Chem.–A Eur. J., 2020, 26, 9991–9997 CrossRef CAS.
- R. M. Duke, T. McCabe, W. Schmitt and T. Gunnlaugsson, J. Org. Chem., 2012, 77, 3115–3126 CrossRef CAS PubMed.
- S. Kubik, Chem. Soc. Rev., 2010, 39, 3648 RSC.
- I. J. Bazany-Rodríguez, M. K. Salomón-Flores, J. M. Bautista-Renedo, N. González-Rivas and A. Dorazco-González, Inorg. Chem., 2020, 59, 7739–7751 CrossRef PubMed.
- A. E. Hargrove, S. Nieto, T. Zhang, J. L. Sessler and E. V. Anslyn, Chem. Rev., 2011, 111, 6603–6782 CrossRef CAS PubMed.
- H. Chen, Z. Zhou, Z. Li, X. He and J. Shen, Spectrochim. Acta, Part A, 2021, 257, 119792 CrossRef CAS PubMed.
- D. Maity, M. Li, M. Ehlers and C. Schmuck, Chem. Commun., 2017, 53, 208–211 RSC.
- P. Sun, H. Zhang, Y. Sun and J. Liu, Spectrochim. Acta, Part A, 2021, 245, 118919 CrossRef CAS PubMed.
- J. Lohrman, S. Pramanik, S. Kaur, H. Telikepalli, V. W. Day and K. Bowman-James, Org. Biomol. Chem., 2021, 19, 8516–8520 RSC.
- A. Dorazco-González, M. F. Alamo, C. Godoy-Alcántar, H. Höpfl and A. K. Yatsimirsky, RSC Adv., 2014, 4, 455–466 RSC.
- C. D. Geddes, K. Apperson, J. Karolin and D. J. Birch, Anal. Biochem., 2001, 293, 60–66 CrossRef CAS PubMed.
- A. Dorazco-González, H. Höpfl, F. Medrano and A. K. Yatsimirsky, J. Org. Chem., 2010, 75, 2259–2273 CrossRef.
- R. Badugu, Dyes Pigm., 2004, 61, 227–234 CrossRef CAS PubMed.
- X. Xie, O. Reznichenko, L. Chaput, P. Martin, M.-P. Teulade-Fichou and A. Granzhan, Chem.–Eur. J., 2018, 24, 12638–12651 CrossRef CAS.
- C. Miron and A. Petitjean, Synlett, 2018, 29, 1362–1366 CrossRef CAS.
- B.-X. Zheng, W. Long, Y.-H. Zhang, X.-H. Huang, C.-C. Chen, D.-X. Zhong, M.-T. She, Z.-X. Chen, D.-P. Cai, Y.-J. Lu and W.-L. Wong, Sens. Actuators, B, 2020, 314, 128075 CrossRef CAS.
- V. Dhamodharan, S. Harikrishna, C. Jagadeeswaran, K. Halder and P. I. Pradeepkumar, J. Org. Chem., 2012, 77, 229–242 CrossRef CAS PubMed.
- M. D. Gray, P. S. Deore, A. J. Chung, A. J. Van Riesen, R. A. Manderville, P. S. Prabhakar and S. D. Wetmore, Bioconjugate Chem., 2020, 31, 2596–2606 CrossRef CAS.
- I. J. Bazany-Rodríguez, D. Martínez-Otero, J. Barroso-Flores, A. K. Yatsimirsky and A. Dorazco-González, Sens. Actuators, B, 2015, 221, 1348–1355 CrossRef.
- T. Ema, K. Okuda, S. Watanabe, T. Yamasaki, T. Minami, N. A. Esipenko and P. Anzenbacher, Org. Lett., 2014, 16, 1302–1305 CrossRef CAS PubMed.
- S.-O. Kang, T. S. Johnson, V. W. Day and K. Bowman-James, Supramol. Chem., 2018, 30, 305–314 CrossRef CAS.
- H. Goyal, S. Pachisia and R. Gupta, Cryst. Growth Des., 2020, 20, 6117–6128 CrossRef CAS.
- P. Kumar, V. Kumar, S. Pandey and R. Gupta, Dalton Trans., 2018, 47, 9536–9545 RSC.
- P. Kumar, V. Kumar and R. Gupta, Dalton Trans., 2020, 49, 9544–9555 RSC.
- P. Molina, F. Zapata and A. Caballero, Chem. Rev., 2017, 117, 9907–9972 CrossRef CAS PubMed.
- M. Nicolas-Gomez, I. J. Bazany-Rodríguez, E. Plata-Vargas, S. Hernández-Ortega and A. Dorazco-González, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2016, 72, 747–750 CrossRef CAS.
- W. F. Jager, T. S. Hammink, O. van den Berg and F. C. Grozema, J. Org. Chem., 2010, 75, 2169–2178 CrossRef CAS PubMed.
- K. Tanabe, Y. Suzui, M. Hasegawa and T. Kato, J. Am. Chem. Soc., 2012, 134, 5652–5661 CrossRef CAS.
- Y. Fuentes-Martínez, C. Godoy-Alcántar, F. Medrano, A. Dikiy and A. K. Yatsimirsky, Supramol. Chem., 2010, 22, 212–220 CrossRef.
- J. A. Roberts and R. J. Evans, J. Biol. Chem., 2004, 279, 9043–9055 CrossRef CAS PubMed.
- V. Amendola, L. Fabbrizzi and E. Monzani, Chem.–Eur. J., 2004, 10, 76–82 CrossRef CAS PubMed.
- E. Novikov and N. Boens, J. Phys. Chem. A, 2007, 111, 6054–6061 CrossRef CAS.
- K. Ghosh and I. Saha, New J. Chem., 2011, 35, 1397–1402 RSC.
- K. Ghosh and I. Saha, Org. Biomol. Chem., 2012, 10, 9383–9392 RSC.
- S. Dey, T. Sarkar, A. Majumdar, T. Pathak and K. Ghosh, ChemistrySelect, 2017, 2, 2034–2038 CrossRef CAS.
- O. Sunnapu, N. G. Kotla, B. Maddiboyina, S. Marepally, J. Shanmugapriya, K. Sekar, S. Singaravadivel and G. Sivaraman, ChemistrySelect, 2017, 2, 7654–7658 CrossRef CAS.
- K.-Y. Tan, C.-Y. Li, Y.-F. Li, J. Fei, B. Yang, Y.-J. Fu and F. Li, Anal. Chem., 2017, 89, 1749–1756 CrossRef CAS PubMed.
- K. Ghosh, D. Tarafdar, A. Samadder and A. R. Khuda-Bukhsh, RSC Adv., 2015, 5, 35175–35180 RSC.
- M. Sirajuddin, S. Ali and A. Badshah, J. Photochem. Photobiol., B, 2013, 124, 1–19 CrossRef CAS PubMed.
- Y. Sun, S. Bi, D. Song, C. Qiao, D. Mu and H. Zhang, Sens. Actuators, B, 2008, 129, 799–810 CrossRef CAS PubMed.
- E. Oguzcan, Z. Koksal, T. Taskin-Tok, A. Uzgoren-Baran and N. Akbay, Spectrochim. Acta, Part A, 2022, 270, 120787 CrossRef CAS PubMed.
- Principles of Fluorescence Spectroscopy, ed., J. R. Lakowicz, Springer US, Boston, MA, 2006 Search PubMed.
- S. Ozkan, T. Taskin-Tok, A. Uzgoren-Baran and N. Akbay, J. Fluoresc., 2019, 29, 101–110 CrossRef CAS PubMed.
- J. Valdes-García, A. O. Viviano-Posadas, J. Rivera-Chávez, T. Ramírez-Apan, S. Martínez-Vargas, E. Aguirre-Hernández, J. M. German-Acacio, D. Morales-Morales and A. Dorazco-González, J. Mol. Struct., 2022, 1249, 131582 CrossRef.
- APEX 2 Softw. Suite, Bruker AXS Inc., Madison, Wisconsin, USA, 2004 Search PubMed.
- C. B. Hübschle, G. M. Sheldrick and B. Dittrich, ShelXle: A Qt graphical user interface for SHELXL, J. Appl. Crystallogr., 2011, 44, 1281–1284 CrossRef PubMed.
- G. M. Sheldrick, SHELXT - Integrated space-group and crystal-structure determination, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 1–8 Search PubMed.
- S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107 CrossRef PubMed.
- Y. Takano and K. N. Houk, J. Chem. Theory Comput., 2005, 1, 70–77 CrossRef PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef.
- Y. Xiong, P. S. Shabane and A. V. Onufriev, ACS Omega, 2020, 5, 25087–25094 CrossRef CAS PubMed.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020–9041 CrossRef CAS.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef CAS PubMed.
- D. R. Roe and B. R. Brooks, J. Chem. Phys., 2020, 153, 054123 CrossRef CAS PubMed.
- R. Galindo-Murillo, J. C. Robertson, M. Zgarbová, J. Šponer, M. Otyepka, P. Jurečka and T. E. Cheatham, J. Chem. Theory Comput., 2016, 12, 4114–4127 CrossRef CAS PubMed.
- A. W. Götz, M. J. Williamson, D. Xu, D. Poole, S. Le Grand and R. C. Walker, J. Chem. Theory Comput., 2012, 8, 1542–1555 CrossRef PubMed.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Crystallographic data, 1H, 13C, HMSQ, DEPT, MS measurements, atoms in molecules analysis and spectroscopic recognition studies. CCDC 2118468–2118469. For ESI and crystallographic data in CIF or other electronic format see https://doi.org/10.1039/d2ra05040d |
| This journal is © The Royal Society of Chemistry 2022 |