Molecular dynamics simulation study of adsorption of anionic–nonionic surfactants at oil/water interfaces

Abstract

Four anionic–nonionic surfactants with the same headgroups and different units of oxygen ethyl (EO) and oxygen propyl (PO) were adopted to investigate the influence on oil/water interfacial tensions in this article. Molecular dynamics (MD) simulations were conducted to study the interfacial property of the four surfactants. Four parameters were proposed to reveal the effecting mechanism of molecular structure on interfacial tension, which included the interfacial thickness, order parameter of the hydrophobic chain, radial distribution function, and the solvent accessible surface area. In addition, the electrostatic potential of the four surfactants was calculated. The research results indicated that the interface facial mask formed by the surfactants, which contained three EO or three PO units was more stable, and it was easier for the surfactants of six EO or six PO units to form a microemulsion at higher concentrations. The adsorption mechanism of the anionic–nonionic surfactant systems at the oil/water interfaces was supplemented at a molecular level, which provided fundamental guidance for an in-depth understanding of the optimal selection of the surfactants in enhancing oil recovery.

---

1 Introduction

The amphiphilic property of the surfactants, which plays an important role in industrial applications, especially in enhancing oil recovery.^1–3 Anionic surfactants such as petroleum sulfonate and alkylbenzene sulfonate are the most widely applied in oil displacement.^4–6 However, under the complex geological conditions of high salinity and high temperature, anionic surfactants are very easy to precipitate cations in the formation to reduce the oil displacement efficiency. To enable the better application of oil exploitation, it is necessary to research a new type of surfactant for the complex geological environment.^7,8

Compared with anionic surfactants, anionic–nonionic surfactants could effectively solve the above problems caused by high salt and high temperature by designing non-ionic and anionic groups in one molecular structure at the same time. As surfactants for oil repelling, anionic–nonionic surfactants show greater advantages than anionic surfactants, which have led many scientists to use anionic–nonionic surfactants in the petroleum industry. Varadaraj⁹ studied the surface properties of Guerbet polyoxyethylene sodium sulfate, and the results showed that after adding EO groups between the lipophilic groups and hydrophilic groups, its surface/interfacial activity was enhanced. The experiments showed that the foaming and foam stability were also improved, and the degradation performance was better. Witthayapanyanon¹⁰ found that the introduction of additional PO and EO groups in the extended surfactant yielded lower IFT and lower optimum salinity, both of which were desirable in most formulations. Levitt¹¹ researched the behavior of the phase, which showed that after compounding C₁₆–C₁₇–(PO)₃–SO₄Na with C₁₅–C₁₈ IOS (internal olefin sulfonate) and C₂₀–C₂₄ AOS (α-olefin sulfonate), the solubilization parameters of West Texas crude oil were all larger (the corresponding interfacial tension is smaller than 0.003 m N m⁻¹). Asl¹² synthesized two amino acid surfactants to improve oil recovery from oil-wet carbonate reservoirs by altering the wettability of carbonate rocks. The above experimental studies show that appropriate surfactants can be used to improve oil recovery due to their desirable effects on the EOR mechanisms.

However, only these experimental results were not sufficient to understand the microscopic mechanism of surfactant flooding. In this case, MD simulations provided new insights into the molecular behavior at the oil/water interface.^13–17 Lian¹⁸ investigated the micellization behavior and interfacial adsorption process, the typical anionic surfactant 1-dodecanesulfonic sodium (DAS), and nonionic surfactants octylphenol polyoxyethylene ether-n (OP-n, n = 1, 5, and 10) were introduced via MD simulations in his paper. The results reflect that OP₅ molecules exhibit a greater interfacial adsorption tendency than DAS molecules. In addition, the tangled polyethylene oxide chains at the mixed micelle surface decrease the SASA of the sulfonate group and weaken its hydrophilicity. He¹⁹ used the all-atomic MD method to research the molecular array behaviors and dynamic properties of the extended surfactant–alkyl polypropylene ether sulfonate at the oil/water interface. Detailed simulation results, including interfacial thickness, stretch degree, and tilt angle, all indicated that the long PO chain curled near-evenly in a row of 4 PO units at the interface on low concentration and then stretched out to achieve tight alignment at a high concentration. Based on the simulation results, the helical shape of the long PO chain mechanism was proposed at the oil/water interface. Shang²⁰ investigated the effects of the polyethylene oxide chains in a polymer on the micellization behaviors of the anionic surfactant via MD simulations. Gang²¹ studied the interfacial activity for reducing interfacial tension and salt tolerance of NPEOnC (n = 2, 4, and 7) and the effect of the number of the ethoxy unit was quantified, which resulted in a higher salt tolerance of NPEOnC with more ethoxy units. Tummala²² conducted MD simulations for sodium dodecyl sulfate (SDS) and hexaethylene glycol monododecyl ether (C₁₂E₆) adsorbed on silica substrates with varying degrees of hydroxylation; the results shed light on the effects of hydroxylation on the surfactant aggregate morphology. Apart from that, many MD simulation investigations also focused on the interfacial behaviors in various surfactant systems.

Although some of the microscopic aspects of surfactants through the above studies could be inferred, to the best of our knowledge, comparative studies on the oil repelling performance of different surfactants from a molecular perspective are rare, and the microscopic mechanisms of adsorption processes and microemulsion formation need to be further investigated. In this paper, four anionic–nonionic surfactants were selected, and the MD simulation method was used to conduct a systematic study to explain the microscopic mechanism of anionic–nonionic suitable for oil repelling at the molecular level. The paper is organized as follows. In Section 2, the molecular models and simulation methods were provided. The process of adsorption of anionic–nonionic surfactants at the oil/water interface and the formation of the microemulsion were revealed through the interfacial morphology, interfacial tension, order parameter of the hydrophobic chain, and the interaction between the surfactant head group and water; all the above are discussed in Section 3. In Section 4, the findings and conclusions of this study are summarized, summarizing the effects of different structures of anionic–nonionic surfactants on oil repelling efficiency, which had a reference value for the molecular design of surfactants for oil repelling.

2 Methodology

2.1 Simulated molecular structure

The geometry optimization of the anionic–nonionic surfactants molecule was carried out by Gaussian 16 (ref. 23) under the B3LYP function and 6-311++g(d,p) basis set, and the charge distribution was determined by the Restrained ElectroStatic Potential (RESP) method via Multiwfn,^24,25 which was proposed by Kollman.²⁶ The molecular structures of the four surfactants are shown in Fig. 1. EO₃, EO₆, PO₃, and PO₆ were used to represent their corresponding structures for convenience in the paper.

Fig. 1 olecular structure of four surfactants.

2.2 Force field and MD parameters

In the framework of the present study, the gromacs54A7 force field²⁷ was employed to describe the forces exerted among the species in the oil and water mixed solution, which includes bonded and nonbonded interactions. The bonded interactions consist of bond, angle, improper dihedral angle, and torsional dihedral angle terms.

V^bonded (r;s) = V^bond (r;s) + V^angle (r;s) + V^improper (r;s) + V^tosrional (r;s) (1)

On the other hand, non-bonded interactions include van der Waals and electrostatic interactions.

V^nbon(r;s) = V^LJ(r;s) + V^CRF(r;s) (6)

The non-bonded van der Waals interactions were calculated as a sum over all the interacting nonbonded atom pairs using a Lennard–Jones 12/6 interaction function with C₁₂ and C₆ parameters.

Specifically, for the molecular interactions of surfactants, water, and oil, all-atom method was employed to describe the molecules at an atomic scale using the potential energy parameter set GROMOS54A7; the corresponding force field parameters in the database were corrected through the Automated Topology Builder (ATB),^28–30 while the parameters for the water/water interactions were represented by the well-known SPC/E model³¹ with a fixed O–H bond length and H–O–H angle. All bond lengths were constrained using the LINCS algorithm for the surfactants, water, and oil molecules. Moreover, the Particle Mesh Ewald (PME)³² method was used to describe the long-range electrostatic interaction. Finally, Lennard–Jones van der Waals cutoff radius was set to 1.0 nm.

2.3 Molecular models and simulation procedure

The system design in this study was similar to that in our previous work.³³ The simulation box was composed of a water film sandwiched by two oil layers with four anionic–nonionic surfactants separately dispersed at the interfaces. The periodic boundary condition was applied in three dimensions. There were 400 decane molecules in the oil layer and 4000 SPC water models in the water layer in the initial model. The surfactants were stacked at the oil/water interface in the form of orthoclinic crystals using the local script and packmol software,^34,35 and the thickness of the water layer ensured the complementary influence of the surfactants on both the sides; the initial structure is shown in Fig. 2. A total of four systems were simulated, and the number of surfactant molecules in each system was gradually increased to observe the effect of surfactant concentration changes in the system. The molecular composition of system I is shown in Table 1. To observe the effect of surfactant concentration changes in the system, each system was composed of 14 simulated experiments with a constant number of oil and water molecules from 18 to 180. The four systems were added with surfactants corresponding to EO₃, PO₃, EO₆, and PO₆ four structures. Corresponding amounts of sodium ions were added to each system to balance the charge of the system. System I as a typical representative is shown in Fig. 1; the other three systems were similar and would not be repeated. All systems were initially placed in a 5 × 5 × 18 nm box. The oil phase was represented by decane molecules, which were not shown clearly. All simulations were carried out by the GROMACS package^36–38 (edition 5.1.2). During MD simulations, Nosé-Hoover³⁹ and Parrinello–Rahman^40–42 methods were used to control the temperature and the pressure of the systems, respectively. For each simulation system, the steepest descent method and the conjugate gradient method were used successively to minimize the energy. If the biggest force was less than 100 kJ mol⁻¹ nm⁻¹, the energy convergences would be minimized. Then, 1 ns simulation with NVT ensemble was performed to gradually increase the temperature to 318 K, in which only the surfactant molecules were fixed. The aim was to naturally distribute the oil and water around the surfactants. The initial velocity at the corresponding simulated temperature was generated via the Maxwell velocity distribution method. The temperature coupling used a V-rescale thermal bath with a relaxation time of 0.1 ps, then delimited the position, 1 ns NPT equilibrium simulation processed under the 1 atm, in which the system density meeting the reasonable requirements was carried out. V-rescale thermal bath and Berendsen pressure bath were selected for temperature and pressure coupling, respectively, and the relaxation times were 0.1 ps and 0.5 ps, respectively. Finally, a long time 16 ns simulation was performed at an interval of 1 ps, and the data in the last 10 ns of the stable trajectory were collected for the analysis. For temperature and pressure coupling, a Nosé-Hoover thermal bath and a Parrinello–Rahman pressure bath were selected with relaxation times of 0.5 ps and 4 ps. When using NPT, the semi-isotropic pressure coupling type was selected with a pressure value of 1 bar and the box size was fixed in the x and y directions to maintain a constant interface width. The system configuration could be observed by the visualization program visual molecular dynamics.⁴³

Fig. 2 Original configuration of surfactant system simulation (sulfur, oxygen, and carbon belonging to the surfactant molecules were shown in yellow, red, and green by vdw drawing method in VMD, respectively; na(neutralizing anionic surfactants) and water molecules are shown in blue and red by bond drawing method in vmd).

Table 1 System I settings in each simulation run

System I	Water	Decane	Na^+	EO3 surfactant	Equilibrium concentration (mol L^−1)
I-1	4000	400	18	18	0.11
I-2	4000	400	24	24	0.14
I-3	4000	400	32	32	0.19
I-4	4000	400	40	40	0.24
I-5	4000	400	50	50	0.29
I-6	4000	400	60	60	0.35
I-7	4000	400	72	72	0.41
I-8	4000	400	84	84	0.46
I-9	4000	400	98	98	0.52
I-10	4000	400	112	112	0.59
I-11	4000	400	128	128	0.65
I-12	4000	400	144	144	0.72
I-13	4000	400	162	162	0.79
I-14	4000	400	180	180	0.86

---

3 Results and discussion

3.1 Interface morphology

Fig. 3a–d represent the final equilibrium state at the maximum concentration of the four surfactants. The two systems a and b formed a stable and good interface morphology after equilibrium. Due to the amphiphilic nature of the surfactant, its hydrophobic group was inserted into the oil phase, and the hydrophilic group faced the water phase. Compared with the initial state, it could be clearly seen that the interface monolayer film was bent toward the water phase side, and many surfactant molecules had been separated from their original plane. For the two systems c and d, the initial double-layer membrane structure had been completely changed. The reasons may be that when the concentration of the surfactants increases, the surfactants exceeded far from the saturation adsorption in the high concentration state, and the aggregation morphology of surfactants in oil and water changes from bilayer to microemulsion. Second, due to the increase in the EO and PO units, the bigger the area of the hydrophilic head groups, the greater the hydrophobic effect, which resulted in the interfacial tension of the oil film being significantly lower than that of the water film, and the formation of the film to the side of high interfacial tension occurred, then bent to form a W/O microemulsion. Taking the EO₆ surfactants as an example, the formation process of the microemulsion was formed spontaneously with the increase in the surfactant concentration, as shown in Fig. 4. In the beginning, the number of surfactant molecules was small, and the molecules were scattered on the interface. With the number of molecules increasing, the arrangement at the interface became denser and denser. When the number reached about 50, it was close to saturated adsorption. The film bent to one side along with the increase in the number of molecules. When the number of molecules reached 98, the convergence became more obvious, and when the number of molecules reached 162, a stable microemulsion structure was formed.

Fig. 3 Simulation configurations of four surfactant equilibrium states ((a–d) correspond to the simulated equilibrium state when the number of EO₃ PO₃ EO₆ and PO₆ surfactant molecules was 180, sulfur, oxygen, and carbon belonging to the surfactant molecules were shown in yellow, red, and green. For clarity, water molecules were not represented in the graph).

Fig. 4 Schematic diagram of the equilibrium state of different amounts of EO₆ surfactants ((a–d) correspond to the simulated equilibrium state when the number of 18, 50, 98, 162. for clarity, water molecules were not represented in the graph).

3.2 Interfacial tension and thickness

Fig. 5 was the Z-axis mass density distribution curve of each component of four surfactants when the molecular number is 18. The surfactant molecules were classified into two distinct functional groups (head and tail) to investigate detailed molecular distributions. It could be seen from the figure that the simulated oil phase density was about 680 kg m⁻³ and the water density was 980 kg m⁻³, which was close to the actual density at 318 K, and then could preliminarily judge the rationality of the simulation system. The peak difference in the coordinate Z-axis between the oil and water groups reflected the structural feature of the surfactant monolayers at the interface. The water phase was in the middle and the oil phase was on both the sides. The distribution areas of the water phase and oil phase overlap to a certain extent to form an obvious interface. The double-layer film formed by the surfactants was distributed at the oil/water interface, and the head group was in the interface layer near the waterside; in contrast, the tail group was close to the oil phase. The interface thickness could be calculated by the “90–90” standard,⁴⁴ i.e., the distance from 90% of the pure oil phase to 90% of the pure water phase. The results are shown in Fig. 6, which represent the change in the interfacial thickness of each system with the number of surfactant molecules (since the two systems EO₆ and PO₆ formed microemulsions, namely, emulsification, so no comparison was made). The interfacial thickness of the system increases regularly and gradually with the increase in the number of surfactants. At first, due to the small number of surfactant molecules, it was far from reaching the saturated adsorption state, the molecular arrangement was relatively loose, and the interface thickness increased rapidly. When it was close to saturated adsorption with the molecule number increasing, the arrangement of molecules became compact, and the increase in interface thickness was slow. Due to the larger space occupied by PO₃ than the EO₃ structure, in the case of the same number of surfactant molecules, the interface thickness of the PO₃ system was about 0.75 nm larger than that of the EO₃ system.

Fig. 5 Mass density distribution of each component in four surfactants system.

Fig. 6 Interfacial tension and interfacial thickness of four surfactants system.

Because the work of adhesion of crude oil on the rock was proportional to the oil/water interfacial tension,⁴⁵ the reduced interfacial tension would result in decreasing work of adhesion. Thus, the crude oil could easily desorb from the rock surface, thus enhancing oil recovery.

A remarkable aspect of the simulation results was that surfactants lead to different interfacial pressures at oil/water interfaces.^46,47 The value of the interfacial tension was the most important index for evaluating the performance for oil displacement. Therefore, the related formula one to four different systems of the calculation,⁴⁸ such as

where the L_z is the height of the box on the Z-axis, and P_xx, P_yy, and P_zz is the pressure in the x, y, and z directions; the results are shown in Fig. 6. It could be seen from the figure that the interfacial tension of the four surfactants decreased significantly with the surfactant number increasing, and there was an optimal number of surfactants that could minimize the interfacial tension above 0 mN m⁻¹. According to the theory, the state at this time should be saturated adsorption, i.e., the interfacial tension of the surfactant at the critical micelle concentration. The experimental data displayed that when the number of surfactant molecules exceeded the saturation adsorption, the interfacial tension was still further reduced, forming a negative value. The main reason for the negative value was that when the amount of the surfactant went beyond the saturation adsorption, the molecules were irregularly arranged at the interface, the interface changed from a relatively flat state to a wavy undulating state, and the system entered a metastable state. Under the interaction of surfactants, oil, and water molecules, the interfacial area gradually increased. Schulman and Prince^49,50 believed that the presence of the adsorption film could reduce the oil/water interfacial tension to ultralow, and even instantly reach negative interfacial tension to form microemulsions. In their research, the co-surfactant could improve the interface flexibility, make it easy to bend to form a microemulsion mixed film, and at the same time, could reduce the oil/water interfacial tension and increase the surface pressure of the mixed adsorption film. When the surface pressures on both sides of the mixed film were not equal, the membrane would be bent by shearing force, forming a W/O or O/W type microemulsion toward the side of the membrane with high pressure. Combining with Fig. 3, the data showed that in the system studied in this paper, the two surfactant systems of EO₆ and PO₆ finally formed a W/O type microemulsion, while the other two systems still maintained the form of a bilayer film. The principal reason for the phenomenon was that the size of the head group changed with the increase in the number of EO and PO, and then modulated the spontaneous curvature of the aggregates, thus changing the aggregate morphology.

Surfactants with long molecular chains and easy to bend in the research systems could spontaneously form microemulsions because this type of surfactant bilayer film was more flexible and more bendable to form microemulsions under the forces in the system; moreover, the tension value that both the bilayer film and the microemulsion may have negative interfacial tension from the interface value. To form a relatively stable microemulsion system, the interfacial tension needed a small positive value. It could also be inferred that when the number of EO or PO groups was small, the bilayer film formed was more stable. When the number of groups increased, it was easier to form a microemulsion structure. The above results verified the mechanism of the microemulsion formed by the bilayer film theory from the molecular level. EO₆ and PO₆ rapidly decrease the interfacial tension at lower concentrations, and the efficiency of reducing interfacial tension was higher. At the same time, it was found that the interfacial thickness was inversely proportional to the interfacial tension when the interfacial film existed, and the interfacial thickness increased gradually with the decrease in the interfacial tension.

3.3 Molecular orientations at the interface

The interaction between surfactants, oil, and water, especially the state of the tail chain, played an important role in aggregation. It was necessary to study the orientation of the C₁–C₁₂ hydrophobic chain. Therefore, the order parameter (S_z)⁵¹ of the C₁–C₁₂ hydrophobic chain was calculated. S_z concerning the Z-direction was calculated by eqn (9).

θ_z is the angle between C_n−1 and C_n+1 and the Z-axis. Angular brackets are the time average S_z = 1, which means that the connecting line between C_n−1 and C_n+1 was always parallel to the Z-axis during the simulation process; S_Z = −1/2 means continuous and always perpendicular to the Z-axis. The results are shown in Fig. 7. When the order parameter was positive, that was, roughly parallel to the Z-axis, as the number of carbon atoms increased, the closer it was to the end, the lower the degree of order, which indicated that the carbon atoms at the end had greater flexibility and wiggle room. Analyzing the data of EO₃, when the surfactant concentration was low, the curve was almost horizontal, and the molecules could swing freely on the interface. The order of the hydrophobic chains became higher and higher with the number of surfactant molecules increasing, especially when the number of molecules was 162 and 180; the two curves were very approachable, and the order value at the beginning exceeded 0.7. It showed that the molecules were very tight in this state, and the Z-axis was closer to the vertical direction. The data of EO₆ and PO₆ is relatively complex. When the number was small, the same trend occurred as that for the above two surfactants. When the number of surfactants exceeded 40, its value became negative, indicating that the surfactant's tail chain underwent a significant change in the direction, the transition was from the perpendicular to the Z-axis to parallel to the Z-axis. At this stage of change, on account of the interaction between the head group and water being relatively weak, and the aggregation effect of the tail chain being strong, the order degree of the tail chain at the end was higher than that at the beginning. The change of force led to a significant change in the molecular orientation of the surfactant. The system was in a metastable state. When the number of surfactants kept growing to 128, the degree of the order changed again and increased in an increasing direction. When the number of surfactants reached 180, the degree of order reached a positive value again, forming a more stable microemulsion state. Therefore, the molecular orientation of the surfactant tail was consistent with the change in the interfacial tension could be concluded, which explained the stability of the bilayer film and the microscopic mechanism of the conversion to the microemulsion.

Fig. 7 Order parameters of the hydrophobic chain in four surfactants systems with different molecular numbers.

3.4 Surface electrostatic potential of the surfactant molecule

The electrostatic potential (ESP)²⁵ distribution on the surface of the molecules was the key to the electrostatic interaction between molecules. The ESP distribution could effectively analyze the properties of the surfactant molecules and their interaction with other molecules. The EO₃ surfactant results of the calculation of the molecular potential distribution are shown in Fig. 8. Owing to the surfactants with a negative charged body as a whole and the abundant polar groups on the surface of the surfactant molecule, the ESP is distributed in a range from −0.21 eV to 0 eV. Surfactants easily absorbed polar molecules such as water molecules through electrostatic interactions. The area of |ESP| > 10 kcal mol⁻¹ was 98.51% according to the area proportion of different electrostatic potential regions. These regions were considered polar regions, mainly concentrated near sulfur and oxygen atoms, and the next is the EO unit. The molecular head group was mainly negatively charged, which all formed hydrogen bonds with water, and the long carbon-hydrogen bonds would point to the oil phase.

Fig. 8 Surface electrostatic potential distribution of EO₃ units of surfactants.

To further explain the surface properties of the surfactant molecules, the molecular polarity index (MPI)⁵² was calculated according to eqn (10).

where A was the area of the vdw surface, S denoted that integration was performed over the molecular surface, and V(r) stood for ESP. The results of MPI are shown in Table 2. EO₃ > PO₃ > PO₆ > EO₆; the surfactant molecules had stronger polarity and were more easily to bind to the hydrate surface. EO₃ combined more easily with water, while EO₆ was relatively weaker.

Table 2 MPI calculation and area distribution of different electrostatic potentials of four surfactants

Surfactants	MPI kcal mol^−1	|ESP| > 10 kcal mol^−1		|ESP| ≤ 10 kcal mol^−1
		Å^2	%	Å^2	%
EO3	43.70806	503.25	98.51	7.61	1.49
EO6	35.08773	496.01	73.26	181.08	26.74
PO3	41.51257	534.23	94.13	33.29	5.87
PO6	39.13735	647.61	84.19	121.64	15.81

---

3.5 Radial distribution function (RDF)

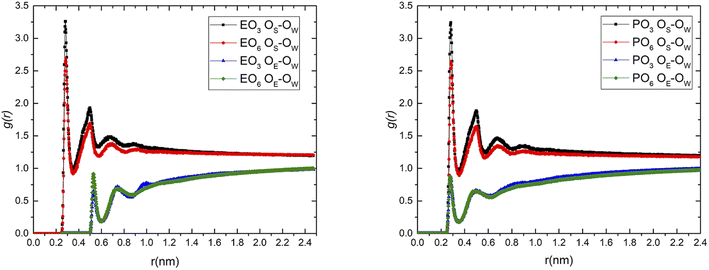
The interaction between the hydrophilic headgroup and water is a crucial parameter determining the decrease in the interfacial tension on the basis of the above analyses. To further verify the ESP calculation results, the binding states of the surfactant polar head, EO, PO units, and the nearby water molecules were obtained by radial distribution function (RDF),^53,54 respectively. RDF was an important method to analyze the interaction between particles. It represented the probability of one particle or group appearing within a specified radius of another particle or group, which provided local structural information at the molecular level.

The RDF of four surfactant head groups (OS), oxyethyl or oxypropyl (OE), and oxygen in water (OW) were extracted respectively, as shown in Fig. 9 (take the system containing 18 EO₃ surfactant molecules as an example), where the RDF of OS and OW function had a similar profile with a first sharp peak (0.28 nm) and a second peak (0.50 nm). Generally, the number of water molecules within the first hydration shell was an effective parameter to evaluate the intensity of interaction between the polar group and water. The more the water molecules within the first hydration shell, the stronger the interaction between the polar group and water. It was easy to know that EO₃ > EO₆ and PO₃ > PO₆; the conclusions were consistent with the ESP calculated above. The first peak of the water molecules of the four surfactants was about 0.28 nm away from the surfactant head group, which was close to the distance of the hydrogen bonds. It was speculated that hydrogen bonds formed chemical hydration layers. The second peak of water molecules was much lower than the first peak, which may be the physical hydration layer of adsorption because of the long-range force. Because of hydrogen bonds, the second hydration layer may also form a hydrogen bond grid with water, thereby forming the third hydration layer. From the RDF of the EO₃ and EO₆ surfactants and water, it could be seen that the EO and PO units form similar hydration conductance with water, and it was worth noting that the effect of interaction with water was significantly smaller than that with the head group of the surfactants, then formed the position of the hydration layer. It was found that water was more easily distributed in the second and third hydration layers formed by the head group of the surfactants and water.

Fig. 9 The RDF of hydrophilic groups or EO (PO) of four surfactants and oxygen in the water.

Hydrogen bonding can quantitatively describe the interaction between the surfactants and water. The average number of hydrogen bonds between the surfactant head group, oxyethyl or oxypropyl and water in the radial distribution function was calculated using a truncation radius of 0.35 nm and an angle of 30° between the acceptor–donor-hydrogen atoms as the basis for hydrogen bonding; the results are shown in Table 3. It can be seen from the table that the number of hydrogen bonds formed between the head group and water was relatively large in the EO₃ and PO₃ systems, while the number of hydrogen bonds formed between the oxyethyl or oxypropyl group and water was relatively large in the EO₆ and PO₆ systems, which verifies the law of the RDF curve.

Table 3 Number of hydrogen bonds between the groups and water molecules

Surfactant groups	The average number of hydrogen bonds (number)	Surfactant groups	The average number of hydrogen bonds (number)
EO3 OS–OW	105.1	EO6 OS–OW	100.82
EO3 OE–OW	21.50	EO6 OE–OW	37.20
PO3 OS–OW	105.47	PO6 OS–OW	87.35
PO3 OE–OW	29.32	PO6 OE–OW	46.49

---

3.6 Solvent accessible surface area (SASA)

All the above discussions focused on the structural properties of the surfactants at the oil/water interfaces. On the other hand, the main mechanism of the surfactant in the EOR process formed a microemulsion structure. The occupied area of the surfactant molecules on the interface would affect the strength of hydrophilic and hydrophobic interactions and determine the number of surfactant molecules contained in the interface. The SASA was calculated by the Gromacs program, which described the average area occupied by the adsorbed molecules on the interface, including the part whose space volume affects the water or oil phase, and the activity when the system was in equilibrium. The smaller the SASA value of the surfactant molecule, the stronger the adsorption ability of the surfactant molecules on the interface and the larger the saturated adsorption capacity (the default probe molecular radius of Gromacs was 1.4 Å). As shown in Fig. 10, taking EO₃ as an example, SASA appeared at a trough in a changing trend with increasing number of surfactants. The reason for this phenomenon may be that the initial surfactant concentration was very low, the surfactants were loosely arranged at the oil/water phase interfaces, and the interaction between the surfactant molecules and between the surfactant and water was relatively small. With the increase in the number of surfactants, the above interaction was strengthened, and the surfactant SASA gradually increased. When the number of surfactants reached about 98, saturated adsorption was achieved, and the surfactants were closely arranged vertically. Currently, the contact area with the solution was the smallest. The number of surfactants continued to increase until it was in a supersaturated state due to the interaction between the surfactant molecules and the interaction of surfactant head groups and water, tail groups, and oil, the surfactant aggregation effect occurred, and the system entered the metastable state, the contact area between the surfactant and the water gradually increased. With the further increase in the surfactant number, the self-charge of the surfactants and the molecular distance of the surfactants were further reduced, increasing the repulsive force between the surfactant head groups, which hindered the aggregation of the surfactants. The magnitude of the effect depended on the charge carried by the surfactant molecules. The electrostatic interaction of the surfactant molecules had been calculated before, and EO₃ had the strongest electrostatic interaction. When the number of surfactants was small, the intermolecular attraction and the interaction between molecules and water was stronger, and the process of reducing the interfacial tension was relatively slow. When the amount of surfactants was large, its repulsive force played a major role, which hindered the aggregation effect and made the surfactant of the bilayer film less prone to deformation. This also explained why EO₆ and PO₆ changed from bilayer to microemulsion when the amount of surfactant increased to a certain extent, while EO₃ and PO₃ could still maintain the oil/water bilayer structure at the same concentration. In the same way, the effectiveness of the four surfactants in reducing the interfacial tension was different. EO₆ and PO₆ achieved the lowest interfacial tension at lower concentrations, while EO₃ and PO₃ required more surfactants to achieve saturated adsorption, which was consistent with the law of interfacial tension calculated above.

Fig. 10 Sasa of surfactants containing EO₃ units at different amounts.

4 Conclusion

MD simulations were carried out to study the aggregation morphology, interface structure, and stability of the bilayer film formed by sulfonate surfactants with EO (PO) units of 3 and 6, and the following conclusions were drawn.

(1) Four surfactants could significantly reduce the oil/water interfacial tension; from the changes in interfacial tension, EO₆ and PO₆ were more effective in reducing the interfacial tension.

(2) The order parameter of the hydrophobic tail chain of the surfactant well described the state of the surfactant at the oil/water interface, which effectively explained the change in the surfactant from the bilayer film to the microemulsion; the simulation showed that without the addition of additives in EO₆ and PO₆, it was easier to form a microemulsion.

(3) The ESP on the surface of the surfactants and the RDF of the head groups oxyethyl or oxypropyl (OE) and oxygen in water explained the hydration of the surfactants from a microscopic point of view. The interfacial film formed by EO₃ and PO₃ was more stable due to the relatively strong electrostatic interaction.

(4) The molecular occupied area characterized the structural changes of the surfactants with concentration, and its regularity was consistent with the parameters of interfacial tension, hydration, and hydrophobic tail chain order, which was a powerful parameter to explain the state of surfactants from a microscopic perspective.

Among the four simulated surfactant systems, EO₆ and PO₆ had better application prospects in enhancing oil recovery than the other two surfactants. Although our simulations were still far from real field experiments, our results provide general guidance for understanding surfactant flooding at the molecular scale. The present study provided visual insights into the microemulsion formation behaviors and the subsequent interfacial adsorption process in anionic–nonionic surfactant systems, which could further expand our understanding of the oil displacement mechanism in anionic–nonionic surfactant systems.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the Natural Science Foundation of Heilongjiang Province (LH2019B028), Doctoral Research Start-up Fund of Heilongjiang Institute of Technology (2020BJ07), Heilongjiang Province Key Research and Development Program Guidance Projects (GZ20210140).

References

1. M.-F. Nazar, S. S. Shah and M. A. Khosa, Microemulsions in Enhanced Oil Recovery: A Review, Pet. Sci. Technol., 2011, 29(13), 1353–1365.
2. M.-S. Kamal, I.-A. Hussein and A.-S. Sultan, Review on Surfactant Flooding: Phase Behavior, Retention, IFT, and Field Applications, Energy Fuels, 2017, 31(8), 7701–7720.
3. L.-Y. Gong, G.-Z. Liao, H.-H. Luan, Q.-S. Chen, X.-B. Nie, D. Liu and Y.-J. Feng, Oil solubilization in sodium dodecyl benzenesulfonate micelles: New insights into surfactant enhanced oil recovery, J. Colloid Interface Sci., 2020, 569, 219–228.
4. A.-Al. Adasani and B.-J. Bai, Analysis of EOR projects and updated screening criteria, J. Pet. Sci. Eng., 2011, 79, 10–24.
5. M.-S. Kamal, I.-A. Hussein and A.-S. Sultan, Review on surfactant flooding: phase behavior, retention, IFT, and field applications, Energy Fuels, 2017, 31(8), 7701–7720.
6. C. Negin, S. Ali and Q. Xie, Most common surfactants employed in chemical enhanced oil recovery, Pet. Sci. Technol., 2017, 3(2), 197–211.
7. S. Chowdhury, S. Shrivastava, A. Kakati and J.-S. Sangwai, Comprehensive Review on the Role of Surfactants in the Chemical Enhanced Oil Recovery Process, Ind. Eng. Chem. Res., 2022, 61(1), 21–64.
8. F. Abdolreza, M.-A. Varfolomeev, I.-A. Ilin, R.-N. Sagirov and S.-A. Sitnov, Synthesis and evaluation of physicochemical properties of new carboxylic acid surfactant based on glucose for enhanced oil recovery, Int. Mul. Sci. Geo., 2018, 14, 851.
9. R. Varadaraj, J. Bock, P. Geissler, S. Zushma, N. Brons and T. Colletti, Influence of ethoxylate distribution on interfacial properties of linear and branched ethoxylate surfactants, J. Colloid Interface Sci., 1991, 147(2), 396–402.
10. A. Witthayapanyanon, E.-J. Acosta, J.-H. Harwell and D.-A. Sabatii, Formulation of ultralow interfacial tension systems using extended surfactants, J. Surfactants Deterg., 2006, 9(4), 331–339.
11. D.-B. Levitt, A.-C. Jackson, C. Heinson, L. Britton, T. Malik and V. Dwarakanath, Identification and evaluation of high-performance EOR surfactants, SPE Reservoir Eval. Eng., 2009, 12(2), 243–253.
12. H.-F. Asl, G. Zargar, A.-K. Manshad, M.-A. Takassi, J.-A. Ali and A. Keshavarz, Experimental investigation into L-Arg and L-Cys eco-friendly surfactants in enhanced oil recovery by considering IFT reduction and wettability alteration, Pet. Sci., 2020, 17(1), 105–117.
13. Z. Gamba, J. Hautman, J.-C. Shelley and M.-L. Klein, Molecular dynamics investigation of a newton black film, Langmuir, 1992, 8(12), 3155–3160.
14. M. Baaden, M. Burgard and G. Wipff, TBP at the water-oil interface: TBP at the water-oil interface: the effect of TBP concentration and water acidity investigated by molecular dynamics simulations, J. Phys. Chem. B, 2001, 105(45), 11131–11141.
15. M. Baaden, F. Berny and G. Wipff, The chloroform/TBP/aqueous nitric acid interfacial system: A molecular dynamics investigation, J. Mol. Liq., 2001, 90(1–3), l–9.
16. H. Yan, P. Cui, C.-B. Liu and S.-L. Yuan, Molecular dynamics simulation of pyrene solubilized in a sodium dodecyl sulfate micelle, Langmuir, 2012, 28(11), 4931–4938.
17. H. Zhao, H.-Y. Sun, N. Qi and Y. Li, Understanding of the foam capability of sugar-based nonionic surfactant from molecular level, Colloids Surf., A, 2018, 551, 165–173.
18. P. Lian, H. Jia, H. Yan, J. Yuan, H.-T. Tang, Z. Li, F.-N. Fan, X.-W. Qin, K. Lv and D. Liu, Effects of Micellization Behavior on the Interfacial Adsorption in Binary Anionic/Nonionic Surfactant Systems: A Molecular Simulation Study, Langmuir, 2021, 37(40), 11835–11843.
19. H.-J. He, H.-Y. Xiao, X.-L. Cao, F.-Q. Yuan, X.-D. Jiang, L. Zhang, L. Zhang and S. Zhao, A helical shape of polyoxypropylene chain for extended surfactant molecule at the water/oil interface: Theoretical and experimental study, Fuel, 2022, 312, 122835.
20. B.-Z. Shang, Z. Wang and R.-G. Larson, Molecular dynamics simulation of interactions between a sodium dodecyl sulfate micelle and a poly (ethylene oxide) polymer, J. Phys. Chem. B, 2008, 112(10), 2888–2900.
21. H.-Z. Gang, X. He, X. He, X. Bao, J. Liu, S. Yang, Y. Li and B.-Z. Mu, Interfacial properties and salt tolerance of carboxylated nonylphenol ethoxylate surfactants, Colloids Surf., A, 2021, 616, 126222.
22. N.-R. Tummala, L. Shi and A. Striolo, Molecular dynamics simulations of surfactants at the silica-water interface: anionic vs. nonionic headgroups, J. Colloid Interface Sci., 2011, 362, 135–143.
23. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, B. 01 Gaussian 16, Revision, Gaussian, Inc., Wallingford CT, 2016.
24. T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592.
25. T. Lu and F. Chen, Quantitative analysis of molecular surface based on improved Marching Tetrahedra algorithm, J. Mol. Graphics Modell., 2012, 38, 314–323.
26. C.-I. Bayly, P. Cieplak, W. Cornell and P.-A. Kollman, A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: the RESP model, J. Phys. Chem., 1993, 97(40), 10269–10280.
27. N. Schmid, A.-P. Eichenberger, A. Choutko, S. Riniker, M. Wing, A.-E. Mark and W.-F. Gunsteren, Definition and testing of the GROMOS force-field versions 54A7 and 54B7, Eur. Biophys. J., 2011, 40(7), 843–856.
28. A.-K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P.-C. Nair, C. Oostenbrink and A.-E. Mark, An Automated force field Topology Builder (ATB) and repository: version 1.0, J. Comput. Chem., 2011, 7(12), 4026–4037.
29. S. Canzar, M. El-Kebir, R. Pool, K. Elbassioni, A.-K. Malde, A.-E. Mark, D.-P. Geerke, L. Stougie and G.-W. Klau, Charge Group Partitioning in Biomolecular Simulation, J. Comput. Biol., 2013, 20, 188–198.
30. K.-B. Koziara, M. Stroet, A.-K. Malde and A.-E. Mark, Testing and validation of the Automated Topology Builder (ATB) version 2.0: prediction of hydration free enthalpies, J. Comput.-Aided Mol. Des., 2014, 28(3), 221–233.
31. H.-J. C. Berendsen, J.-P. M. Postma, W.-F. V. Gunsteren and J. Hermans, Interaction Models for Water in Relation to Protein Hydration, Springer Netherlands, Dordrecht, 1981.
32. U. Essmann, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103(19), 8577–8593.
33. P. Shi, H. Zhang, L. Lin, C.-H. Song, Q.-G. Chen and Z.-S. Li, Molecular dynamics simulation of four typical surfactants at oil/water interface, J. Dispersion Sci. Technol., 2018, 39(9), 1258–1265.
34. J. M. Martínez and L. Martínez, Packing optimization for automated generation of complex system's initial configurations for molecular dynamics and docking, J. Comput. Chem., 2003, 24(7), 819–825.
35. L. Martínez, R. Andrade, E.-G. Birgin and J. M. Martínez, PACKMOL: a package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30(13), 2157–2164.
36. D.-V. D. Spoel, E. Lindahl, B. Hess, G. Groenhof, A.-E. Mark and H.-J. C. Berendsen, GROMACS: fast, flexible, and free, J. Comput. Chem., 2005, 26(16), 1701–1718.
37. B. Hess, C. Kutzner, D.-V. D. Spoel and E. Lindahl, GROMACS 4: algorithms for highly efficient, load-balanced, and scalable molecular simulation, J. Chem. Theory Comput., 2008, 4(3), 435–447.
38. M.-J. Abraham, T. Murtola, R. Schulz, S. Páll, J.-C. Smith, B. Hess, E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, vol. 1-2, pp. 19-25.
39. S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81(1), 511–519.
40. M. Parrinello and A. Rahman, Polymorphic transitions in single crystals: A new molecular dynamics method, J. Appl. Phys., 1981, 52(12), 7182–7190.
41. M. Parrinello and A. Rahman, Strain fluctuations and elastic constants, J. Chem. Phys., 1982, 76(5), 2662–2666.
42. M. Patra and M. Karttunen, Systematic comparison of force fields for microscopic simulations of NaCl in aqueous solutions: diffusion, free energy of hydration, and structural properties, J. Comput. Chem., 2004, 25(5), 678–689.
43. W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38.
44. S.-S. Jang, S.-T. Lin, P.-K. Maiti, M. Blanco, W.-A. Goddard, P. Shuler and Y. Tang, Molecular Dynamics Study of a SurfactantMediated Decane-Water Interface: Effect of Molecular Architecture of Alkyl Benzene Sulfonate, J. Phys. Chem. B, 2004, 108(32), 12130–12140.
45. J.-M. Rosen and J.-T. Kunjappu, Surfactants and Interfacial Phenomena, John Wiley & Sons, Inc., Hoboken, New Jersey, 2012.
46. J. Saien, F. Moghaddamnia and H. Bamdadi, Interfacial tension of methylbenzene-water in the presence of hydrophilic and hydrophobic alumina nanoparticles at different temperatures, J. Chem. Eng. Data, 2013, 58(2), 436–440.
47. X. Li, D.-A. Ross, J. P.-M. Trusler, G.-C. Martin and E. Boek, Molecular dynamics simulations of CO₂ and brine interfacial tension at high temperatures and pressures, J. Phys. Chem. B, 2013, 117(18), 5647–5652.
48. A.-R. Van Buuren, S.-J. Marrink and H.-J. C. Berendsen, A molecular dynamics study of the decane/water interface, J. Phys. Chem., 1993, 97(36), 9206–9212.
49. J.-H. Schulman, W. Stoeckenius and L.-M. Prince, Mechanism of formation and structure of micro emulsions by electron microscopy, J. Phys. Chem., 1959, 63(10), 1677–1680.
50. L. M. Prince, Microemulsions theory and practice, Elsevier, 2012.
51. P.-L. Chau and A.-J. Hardwick, A new order parameter for tetrahedral configurations, Mol. Phys., 1998, 93(3), 511–518.
52. Z. Liu, T. Lu and Q. Chen, Intermolecular Interaction Characteristics of the All-carboatomic Ring, Cyclo[18]Carbon: Focusing on Molecular Adsorption and Stacking, Carbon, 2021, 171, 514–523.
53. L. Koubi, M. Tarek, M.-L. Klein and D. Scharf, Distribution of Halothane in a Dipalmitoylphosphatidylcholine Bilayer from Molecular Dynamics Calculations, Biophys. J., 2000, 78(2), 800–881.
54. C.-F. Lopez, S.-O. Nielsen, M.-L. Klein and P.-B. Moore, Hydrogen bonding structure and dynamics of water at the dimyristoylphosphatidylcholine lipid bilayer surface from a molecular dynamics simulation, J. Phys. Chem. B, 2004, 108(21), 6603–6610.

---

Footnote

† Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra04772a

---