Open Access Article
Open Access ArticleA study of the photochemical behaviour and relaxation mechanisms of anti–syn isomerisation around quinazolinone –N–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) bonds†
bonds†
Michal Hricovíni a,
James R. Asher
a,
James R. Asher bc and
Miloš Hricovíni
bc and
Miloš Hricovíni *a
*a
aInstitute of Chemistry, Slovak Academy of Sciences, Dúbravská cesta 9, 845 38 Bratislava, Slovak Republic. E-mail: milos.hricovini@savba.sk; Fax: +421-2-5941-0222; Tel: +421-2-5941-0323
bInstitute of Inorganic Chemistry, Slovak Academy of Sciences, Dúbravská cesta 9, 845 36 Bratislava, Slovak Republic
cFaculty of Natural Sciences, Department of Inorganic Chemistry, Comenius University, Mlynská Dolina, CH2, 84215, Bratislava, Slovak Republic
First published on 30th September 2022
Abstract
High-resolution NMR experiments revealed that differently substituted quinazolinone-based Schiff bases undergo anti to syn isomerisation on exposure to ultraviolet light in DMSO solution. The degree anti to syn conversion varied significantly upon substitution (between 5% and 100%) and also showed two noteworthy features: that relaxation back to the anti-form goes far faster (by at least 3 orders of magnitude) when the C6 rings B and C have ortho-OH substituents, and that relaxation can also be significantly sped up by addition of acid. Two possible mechanisms explaining the differences in relaxation process have been proposed: (I) the interaction of the azomethine hydrogen with the carbonyl oxygen results in slower reversion to the anti-form and/or (II) suppression of conjugation of the N3 lone pair with the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH double bond by protonation and/or internal H-bonding. Both of these mechanisms have been analysed theoretically.
CH double bond by protonation and/or internal H-bonding. Both of these mechanisms have been analysed theoretically.
1 Introduction
The changes in molecular structures induced by ultraviolet (UV) or visible light play a major role in various biological processes.1–4 Many biomolecules undergo transformation from the energetically most favourable conformation to a higher energy state, often accompanied by bond rotation.5,6 The isomerisation processes depend upon the structures of the photochemically sensitive compounds, but typically involve conjugated systems.7,8 The excitation and the relaxation processes vary upon molecular arrangement in these systems.9,10 The re-isomerisation process can proceed very rapidly, especially in molecules that possess a double bond between the bulky substituents,11,12 although some other systems relax significantly more slowly and require several orders of magnitude more time to reach their initial state.13,14There are numerous nitrogen-containing heterocyclic compounds among those systems that exhibit interesting photochemical behaviour.15,16 Among them, Schiff bases with highly conjugated systems with aromatic substituents bonded to an aliphatic backbone are associated with photochemically-induced biological processes.17 Their properties of chemical and biological significance18–20 can be attributed to the presence of the double bond (N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C or N
C or N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N), often acting as a linkage between aromatic systems.21,22 Schiff bases have applications in many fields,23 e.g. pharmacology,24,25 medicine,26 catalysis,27 dyes28,29 and photoswitching materials.30,31 The biological activity of these molecules can be enhanced by coordination with various metal ions,32–35 due to their excellent chelating properties.36,37 Special attention has been focused on quinazoline-based compounds,38–40 which belong to the class of nitrogen-containing heterocyclic compounds. The photochemical process in quinazolinones proceeds at the –N–N
N), often acting as a linkage between aromatic systems.21,22 Schiff bases have applications in many fields,23 e.g. pharmacology,24,25 medicine,26 catalysis,27 dyes28,29 and photoswitching materials.30,31 The biological activity of these molecules can be enhanced by coordination with various metal ions,32–35 due to their excellent chelating properties.36,37 Special attention has been focused on quinazoline-based compounds,38–40 which belong to the class of nitrogen-containing heterocyclic compounds. The photochemical process in quinazolinones proceeds at the –N–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H) array (in contrast to the N
C(H) array (in contrast to the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond analysed in azobenzene41,42 and its derivatives43,44), which is part of a large π-system including a lone electron pair in the sp2-hybridised orbital of the nitrogen atom of the azomethine group. As shown previously,45,46 photoisomerisation specifically proceeds around the N–N linkage in the –N–N
N bond analysed in azobenzene41,42 and its derivatives43,44), which is part of a large π-system including a lone electron pair in the sp2-hybridised orbital of the nitrogen atom of the azomethine group. As shown previously,45,46 photoisomerisation specifically proceeds around the N–N linkage in the –N–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H) atom array in quinazolinones.
C(H) atom array in quinazolinones.
The present study is a continuation and extension of our research into photoisomerisation in a set of new derivatives with different types of substituents on the aromatic rings. High-resolution NMR spectroscopy, combined with a theoretical study using the DFT methodology, showed that the photoisomerisation process is associated with bond order changes. The bond order change allowed rotation around the –N–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) bond, resulting in the anti- to syn-isomerisation process, i.e. from the more to the less energetically favourable form. Our analysis of a set of differently-substituted compounds enabled us to examine various possible photoisomerisation mechanisms, as well as interesting and significant variations in relaxation time afterwards. A proper understanding of both the photochemical process and the mechanisms of return to thermal equilibrium is crucial for the design and synthesis of compounds with the desired photochemical properties.
bond, resulting in the anti- to syn-isomerisation process, i.e. from the more to the less energetically favourable form. Our analysis of a set of differently-substituted compounds enabled us to examine various possible photoisomerisation mechanisms, as well as interesting and significant variations in relaxation time afterwards. A proper understanding of both the photochemical process and the mechanisms of return to thermal equilibrium is crucial for the design and synthesis of compounds with the desired photochemical properties.
2 Experimental section
2.1. Instruments
The stock solutions of compounds 1–7 (c = 1 mM)40 in DMSO (SeccoSolv, Merck, Germany) were freshly prepared directly before the measurements. High-resolution NMR spectra were recorded in a 5 mm cryoprobe on a Bruker Avance III HD spectrometer at 14 T. One-dimensional 600 MHz 1H and 150 MHz 13C NMR spectra, together with two-dimensional COSY, NOESY, HSQC, and HMBC, enabled determination of the 1H and 13C chemical shifts (referenced to internal TMS) and 1H–1H intramolecular NOEs. Variable-temperature measurements (from 20 °C up to 65 °C) were performed in order to monitor the variations in the chemical shifts of the labile protons. Samples were then exposed to high-powered (500 μW cm−2 at a distance of 5 cm) UV irradiation (365 nm) using a UV/vis lamp (Krüss Optronics, Germany) equipped with vis filters which effectively filter the visible light from the tubes. The possible irradiation times were 5, 10, 15, 30, 45, 60, 75, 90 and 120 minutes, depending on when the compound reached maximum conversion. In some cases (compounds 1 and 6), additional acid–base experiments were performed using 1 mM solutions of CH3COOH and NaOH, in which 3 μl of acid or base were added to the samples prior to UV/vis irradiation. 1D and 2D NMR spectra were then measured at 14 T under the same experimental conditions as before exposure to UV light.2.2. Computational details
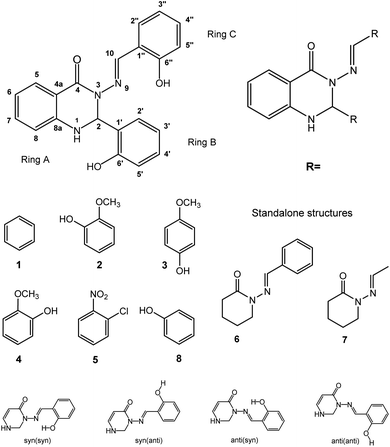
Calculations were performed on the studied compounds 1–7 (shown in Fig. 1) using Gaussian 16 software47 employing the ωB97X-D48 functional and the 6-311++G(2d,2p) basis set. The universal continuum solvation model SMD49 was applied to compute the solvation (DMSO) free energies. The functional ωB97X-D was employed in all types of calculations as it was previously found suitable for calculating similar organic systems.45,46 The convergence criteria were set to tight, using an ultrafine integration grid, for the main calculations of the syn/anti structures and energies (Tables 5 and 6); loose or default convergence criteria, and default integration grid, were used for data in other tables. Use of the default grid introduces small errors to the calculated energies; see ESI, Section S2.2,† for discussion. Theoretical values of NMR spin–spin coupling constants were obtained by the DFT method, employing the ωB97X-D functional and def2-TZVPPD50 basis set. It will be important to discuss the conformers of the molecules, so we choose the following nomenclature. Conformational orientation around the N–N bond will be labelled syn- or anti- according to whether the N–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and N
O and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH moieties are on the same or opposite sides of the N–N bond. Where ortho-OH is present on rings B and C, conformational orientation around the C–C bond in the N
CH moieties are on the same or opposite sides of the N–N bond. Where ortho-OH is present on rings B and C, conformational orientation around the C–C bond in the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–Ar linkage (orientation of ring C) will be labelled (syn) or (anti) according to whether the OH group and N
CH–Ar linkage (orientation of ring C) will be labelled (syn) or (anti) according to whether the OH group and N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond are on the same or opposite sides of the C–C bond. In the former case, an O–H⋯N hydrogen bond is possible. We note that previous work of ours on compound 8 concluded that the (syn) form is probably present,46 on the basis of comparison of theoretical and experimental NMR data; however, we cannot state this with complete certainty and will therefore consider both possibilities, (syn) and (anti), in our analysis.
C double bond are on the same or opposite sides of the C–C bond. In the former case, an O–H⋯N hydrogen bond is possible. We note that previous work of ours on compound 8 concluded that the (syn) form is probably present,46 on the basis of comparison of theoretical and experimental NMR data; however, we cannot state this with complete certainty and will therefore consider both possibilities, (syn) and (anti), in our analysis.
3 Results and discussion
3.1. NMR spectroscopy
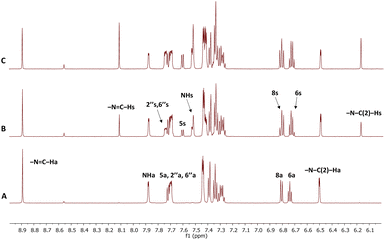
High-resolution NMR experiments have been performed in order to investigate the photoisomerisation behaviour of 1–7. The 600 MHz 1H NMR spectrum of synthetically prepared compound 1 (Fig. 2A) showed that only the anti-isomer of 1 was present in DMSO solution. UV irradiation (365 nm, RT) led to formation of a new set of signals in NMR spectrum (Fig. 2B). The formation of the new resonances started immediately after UV irradiation and increased steadily with the irradiation time up to a maximum of 100% after 75 minutes (Fig. 2C). The analysis of the 1D spectrum, as well as 2D HSQC, HMBC and NOESY, confirmed that the new resonances originated from the syn-isomer, indicating that photoisomerization had taken place. The structures of the two isomers were differentiated by means of intramolecular NOEs and proton–carbon coupling constants and supported by DFT calculations (see later discussion).The magnitudes of one-bond (1JC–H) proton–carbon coupling constants in the azomethine group (–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H) for compounds 1, 4, 6 and 8 are listed in Table 1. The 1JC–H values in 8 were not measured for the syn-isomer form due to fast re-isomerisation; the same is true for 2 and 3. The experimental 1JC–H values for the syn-forms were ∼7–10 Hz larger than those for the anti-forms in the measured derivatives and are comparable to those seen previously.45
C–H) for compounds 1, 4, 6 and 8 are listed in Table 1. The 1JC–H values in 8 were not measured for the syn-isomer form due to fast re-isomerisation; the same is true for 2 and 3. The experimental 1JC–H values for the syn-forms were ∼7–10 Hz larger than those for the anti-forms in the measured derivatives and are comparable to those seen previously.45
These trends were confirmed by DFT calculations, which predicted larger 1JC–H values for the syn-forms in all cases. The somewhat smaller magnitudes (up to 13%) of the theoretical values, compared to experimental ones, are possibly due to small errors in the proton–carbon bond lengths and the electron densities in the azomethine group in the optimised structures. The complete scans of 1JC–H magnitudes on N–N bond rotation, presented for 1, 4 and 6 and 8, are given in ESI, Section S2.1.†
The anti- to syn-degree of conversion (α) and the rate of the re-isomerisation process for investigated compounds 1–7 in DMSO, together with the previously studied derivative 8,46 are listed in Table 2. The experimental data showed that there are marked differences in the photochemical properties among compounds. For example, noticeably different behaviour was seen in compound 1 with respect to all others. This unsubstituted derivative had an α value of about 100%, compared to 25% for 8.
Compound 4 had an α value of up to 22%, with similar values (15–20%) shown by compounds 5 and 6. Compounds 2 and 3 showed rather little (5–6%) anti- to syn-isomerisation whereas the photochemical process in compound 7 either was too fast to monitor by NMR or the degree of conversion was negligible (less than 1%). Thus, these data showed that anti- to syn-isomerisation differed dramatically depending on the position of the substituents on the aromatic rings B and C (Table 2) as well as the presence/absence of the ring A. The absence of the rings A and B considerably hampered anti- to syn-isomerisation (1 vs. 6). The compounds with substituents on rings B and C can be divided into two groups – those with hydroxy groups in the ortho-position (2, 3 and 8), and those without (compound 4 having the hydroxyl group in para-position, compounds 1 and 5 having no OH group). The additional substituent in 2 and 3 (–OCH3), compared to 8, lowered the α value from 25% to about 5%.
Not only the α values but also the speed of the re-isomerisation process (from syn- to anti-forms) to thermodynamic equilibrium depended upon the structure as well. The most noticeable difference was detected between 1 and 8. In 1, thermodynamic equilibrium was not reached even after 18 months (25% presence of the syn-isomer) whereas in 8 it took only about 15 min. Thus, 1 exhibited more than four orders of magnitude slower relaxation compared to 8, though they differ from one another only in the presence of OH groups (at the rings B and C) in the ortho-position. It should be noted that no other changes (apart from anti- to syn-isomerisation and return to the anti-form) have been observed in the NMR spectra in 1 during irradiation or the relaxation process that might indicate decomposition or other processes.
The presence of a hydroxy group in the ortho-position (2, 3, 8) caused significantly shorter relaxation times (on the order of minutes) than seen for the other derivatives (ten weeks or more) where the OH group was in the para-position (4) or not present (1, 5, 6). We examined this phenomenon in more detail by measuring the temperature dependence (20–65 °C) of the azomethine protons' (–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H) chemical shifts in the anti- and syn-forms in selected compounds (Table 3). In the anti-forms, these values varied by ∼2.0–3.0 ppb K−1 between 20 °C and 65 °C; the variations of the mobile protons (OH or NH) were ∼4–7 ppb K−1 for comparison (data not shown). However, the shifts varied considerably less (∼0.7 ppb K−1), or not at all (0 ppb K−1), for the syn-forms for compounds 1, 4, 5 and 6, i.e. compounds that are either not substituted at the benzene rings (1 and 6) or whose substituents are not in the ortho-positions (4 and 5).
C–H) chemical shifts in the anti- and syn-forms in selected compounds (Table 3). In the anti-forms, these values varied by ∼2.0–3.0 ppb K−1 between 20 °C and 65 °C; the variations of the mobile protons (OH or NH) were ∼4–7 ppb K−1 for comparison (data not shown). However, the shifts varied considerably less (∼0.7 ppb K−1), or not at all (0 ppb K−1), for the syn-forms for compounds 1, 4, 5 and 6, i.e. compounds that are either not substituted at the benzene rings (1 and 6) or whose substituents are not in the ortho-positions (4 and 5).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(H) of selected compounds
C(H) of selected compounds
| 20 °C | 25 °C | 35 °C | 45 °C | 55 °C | 65 °C | ppb K−1 | |||
|---|---|---|---|---|---|---|---|---|---|
| a Ref. 46. | |||||||||
| 1 | Anti- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.843 | 8.861 | 8.893 | 8.921 | 8.947 | 8.969 | 2.80 |
| Syn- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.493 | 8.498 | 8.506 | 8.513 | 8.520 | 8.526 | 0.73 | |
| 3 | Anti- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.481 | 8.496 | 8.519 | 8.541 | 8.563 | 8.583 | 2.27 |
| 4 | Anti- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.664 | 8.681 | 8.710 | 8.736 | 8.76 | 8.780 | 2.58 |
| Syn- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.256 | 8.256 | 8.256 | 8.255 | 8.256 | 8.257 | 0 | |
| 5 | Anti- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.986 | 9.005 | 9.040 | 9.071 | 9.098 | 9.123 | 3.04 |
| Syn- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.295 | 8.297 | 8.297 | 8.296 | 8.297 | 8.295 | 0 | |
| 6 | Anti- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.174 | 8.188 | 8.205 | 8.224 | 8.245 | 8.265 | 2.02 |
| Syn- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.270 | 8.267 | 8.260 | 8.252 | 8.245 | 8.237 | −0.73 | |
| 8a | Anti- | –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH– CH– |
8.441 | 8.454 | 8.477 | 8.499 | 8.522 | 8.542 | 2.24 |
The very small shift changes in the syn-forms indicated that weak intramolecular hydrogen bonds between azomethine protons and the carbonyl oxygens were formed and stabilised the syn-forms. However, compounds that have hydroxyl groups in the ortho-position (2, 3 and 8) reverted to thermodynamic equilibrium so fast that the temperature dependence of the proton chemical shifts in the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H group could not be determined in the syn-form. The data could indicate that in the latter case the –N
C–H group could not be determined in the syn-form. The data could indicate that in the latter case the –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH⋯O
CH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bonds were either not formed or significantly weakened.
C hydrogen bonds were either not formed or significantly weakened.
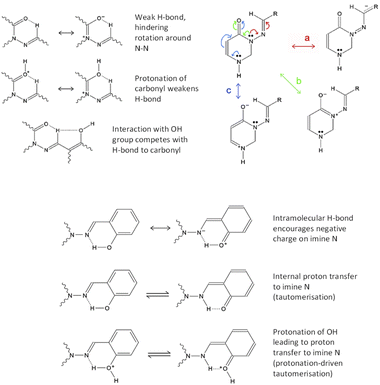
We have several hypotheses explaining the faster relaxation, which are illustrated in Fig. 3. These can be broken down into two types of mechanism, with variations involving protonation or deprotonation of the molecule. (I) The interaction of the azomethine hydrogen with the carbonyl oxygen is expected to slow down reversion to the anti-form (as this weak H-bond is specific to the syn-form); this effect will be weaker if C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O is protonated. If the azomethine hydrogen also interacts with the o-OH group from ring C, this could make it easier to revert to anti (an effect that should be stronger if o-OH is deprotonated). This theory requires the syn(anti)-form to be present, otherwise the o-OH group will be on the wrong side of ring C. This is shown in Fig. 3, upper left. (II) Suppression of conjugation of the N3 lone pair with the N
O is protonated. If the azomethine hydrogen also interacts with the o-OH group from ring C, this could make it easier to revert to anti (an effect that should be stronger if o-OH is deprotonated). This theory requires the syn(anti)-form to be present, otherwise the o-OH group will be on the wrong side of ring C. This is shown in Fig. 3, upper left. (II) Suppression of conjugation of the N3 lone pair with the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH double bond (pathway “a” in Fig. 3, upper right). This conjugation causes resonance structures with N
CH double bond (pathway “a” in Fig. 3, upper right). This conjugation causes resonance structures with N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N double-bond character, and it can be suppressed by decreasing the N
N double-bond character, and it can be suppressed by decreasing the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH double-bond character – either by encouraging the accumulation of negative charge on N9 (the imide nitrogen) by way of an internal H-bond from o-OH, or by protonating N9, which would be faster and easier if done (or mediated) by an adjacent o-OH (i.e. tautomerisation). These both require the syn(syn)-form to be present, so that the o-OH group can interact with N9. This is depicted in Fig. 3, bottom. As discussed later, protonation of N9 (including by tautomerisation) actually leads to a local minimum at D(CNNC) values of 100° or more, leading to a possible two-step mechanism for syn–anti conversion; see theoretical section for more details.
CH double-bond character – either by encouraging the accumulation of negative charge on N9 (the imide nitrogen) by way of an internal H-bond from o-OH, or by protonating N9, which would be faster and easier if done (or mediated) by an adjacent o-OH (i.e. tautomerisation). These both require the syn(syn)-form to be present, so that the o-OH group can interact with N9. This is depicted in Fig. 3, bottom. As discussed later, protonation of N9 (including by tautomerisation) actually leads to a local minimum at D(CNNC) values of 100° or more, leading to a possible two-step mechanism for syn–anti conversion; see theoretical section for more details.
We note also that protonation of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O encourages delocalisation pathway “b” (conjugation of N3 lone pair with C
O encourages delocalisation pathway “b” (conjugation of N3 lone pair with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond), thus discouraging pathway “a”. As mentioned already, protonation of N9 also discourages pathway “a”. Protonation of N1 may weakly discourage pathway “a” by suppressing pathway “c” (which competes with “b”, which competes with “a”). Deprotonation of o-OH or p-OH would result in negative charge delocalising to N9 (as well as to positions 1′′, 3′′ and 5′′ on ring C). Thus, acid/base behaviour affords multiple ways to speed up reversion to the anti-conformer; the question is which mechanisms would be affected by the presence of o-OH specifically.
O bond), thus discouraging pathway “a”. As mentioned already, protonation of N9 also discourages pathway “a”. Protonation of N1 may weakly discourage pathway “a” by suppressing pathway “c” (which competes with “b”, which competes with “a”). Deprotonation of o-OH or p-OH would result in negative charge delocalising to N9 (as well as to positions 1′′, 3′′ and 5′′ on ring C). Thus, acid/base behaviour affords multiple ways to speed up reversion to the anti-conformer; the question is which mechanisms would be affected by the presence of o-OH specifically.
In connection with these questions, we performed NMR experiments for 1 and 6 at acidic pH values. In fact, syn to anti re-isomerisation accelerated by more than two orders of magnitude in compound 1 under acidic conditions: a 52% decrease was reached in one week in acidic conditions, whereas it took 35 weeks under regular conditions. A similarly considerable shortening was also observed for 6 as well (from 14 weeks to 9 hours).
Thus, addition of H+ ions to the system clearly changes the intramolecular interactions in a way that encourages syn- to anti re-isomerisation. In our first hypothesis, this occurs because of protonation of carbonyl oxygen, leading to changes in the π-system (Fig. 3), which results in a weaker –N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH⋯O
CH⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond due to positive charge at the oxygen (Fig. 3, upper right). As that H-bond hinders reversion to anti (being only present in the syn-form), weakening it should decrease the energy barrier to reversion, i.e. speed up syn–anti conversion. Furthermore, protonation of CO should affect the resonance structure balance in the π-system as described earlier, by encouraging the N3 lone pair to delocalise towards oxygen instead of towards ring C (pathway “b” instead of “a” in Fig. 3, upper right), thus decreasing the N–N double-bond character and making rotation around the N–N bond easier. We also note that the interaction of the azomethine proton with o-OH would be enhanced by deprotonation of OH.
C hydrogen bond due to positive charge at the oxygen (Fig. 3, upper right). As that H-bond hinders reversion to anti (being only present in the syn-form), weakening it should decrease the energy barrier to reversion, i.e. speed up syn–anti conversion. Furthermore, protonation of CO should affect the resonance structure balance in the π-system as described earlier, by encouraging the N3 lone pair to delocalise towards oxygen instead of towards ring C (pathway “b” instead of “a” in Fig. 3, upper right), thus decreasing the N–N double-bond character and making rotation around the N–N bond easier. We also note that the interaction of the azomethine proton with o-OH would be enhanced by deprotonation of OH.
The second mechanism, that of decrease in N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH double-bond character (leading to less conjugation of N
CH double-bond character (leading to less conjugation of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH with the N3 lone pair and thus less N–N double-bond character), is also promoted under acidic environment in several ways. Protonation of N9 by internal proton transfer (tautomerisation) may happen in neutral solution, but would be expected to be encouraged by an acidic environment, with the Ar–OH group mediating protonation (see Fig. 3, bottom; calculations find that this is a concerted process, with the H-bonding proton moving to N as the external proton attaches to O). Additionally, if H-bonding to N9 encourages a lower energy barrier for rotation around N–N, this effect might combine with the effect of protonation of CO (as described in the previous paragraph; as mentioned earlier, it's also possible that protonation of N1 might have a similar, though weaker, effect).
CH with the N3 lone pair and thus less N–N double-bond character), is also promoted under acidic environment in several ways. Protonation of N9 by internal proton transfer (tautomerisation) may happen in neutral solution, but would be expected to be encouraged by an acidic environment, with the Ar–OH group mediating protonation (see Fig. 3, bottom; calculations find that this is a concerted process, with the H-bonding proton moving to N as the external proton attaches to O). Additionally, if H-bonding to N9 encourages a lower energy barrier for rotation around N–N, this effect might combine with the effect of protonation of CO (as described in the previous paragraph; as mentioned earlier, it's also possible that protonation of N1 might have a similar, though weaker, effect).
Thus, we have two mechanisms, or classes of mechanism, by which we can explain the faster (by several orders of magnitude) relaxation to thermodynamic equilibrium of compounds 2, 3 and 8, which have o-OH, than compounds having the OH groups in para-positions (compound 4), or without any OH groups (1, 5 and 6).
We note that simplification of molecule 1 to 6, and further truncation to 7, leads to a significant speedup in syn–anti reversion (assuming that 7 reverts so fast that the syn-form is undetectable by NMR) in a manner which may be related to electronic structure effects, but can also be explained entirely in terms of solvent friction. The larger a group, the more difficult it is to rotate without solvent getting in the way. Reversion to anti-form requires either the C4N2 heterocycle or the N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–Ph group (or both together) to rotate about 60° around the N–N bond to reach the energy barrier. For 1, the C4N2 heterocycle has rings A and B attached, hindering its movement, so reversion more or less only occurs by rotation of N
CH–Ph group (or both together) to rotate about 60° around the N–N bond to reach the energy barrier. For 1, the C4N2 heterocycle has rings A and B attached, hindering its movement, so reversion more or less only occurs by rotation of N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–Ph.
CH–Ph.
For 6, rings A and B are absent, so the C4N2 heterocycle can move more freely. For 7, N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–Ph is simplified to N
CH–Ph is simplified to N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–Me, and can move almost without solvent friction.
CH–Me, and can move almost without solvent friction.
We have also carried out experiments in three other solvents (acetone, chloroform and methanol) to get more information on the effect of solvents upon photoisomerisation (Table 4). The α values were found to be considerably lower than in DMSO – about ten times smaller in methanol and CDCl3 (∼2%), with a less drastic decrease in acetone (9%). The smaller degree of conversion in these three solvents was likely caused by the shift of the absorption maximum. The return to thermodynamic equilibrium was also affected by the solvents, suggesting that either the small amounts of water molecules present in various solvents could affect this process, or that dielectric effects are important, implying that charged species or charge-separated resonance structures are involved (note that relaxation gets slower as the dielectric constant goes down).
| Compound 8 | ||||
|---|---|---|---|---|
| DMSO | Methanol | Acetone | CDCl3 | |
| α/% | 25% | ∼2% | 9% | ∼2% |
| tmax/min | 10 | 30 | 15 | 45 |
| trelax | 15 min | 45 min | 50 min | 120 min |
3.2. DFT calculations
The structures of all molecules showed only minor deviations from planarity between rings A and C, while ring B is oriented approximately perpendicularly to this plane. However, deviations from planarity are more pronounced for the syn-isomers (50–70 degrees) than for the anti-isomers (about 15 degrees).
Selected geometric parameters of 1–4, 6 and 7 are listed in Table 6. The bond lengths in the aromatic rings of both the anti- and syn-forms were in the range 1.36–1.41 Å and corresponded to those in structurally-related molecules.51,52
| 1 | 2 | 3 | 4 | 6 | 7 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anti- | Syn- | Anti- | Syn- | Anti- | Syn- | Anti- | Syn- | Anti- | Syn- | Anti- | Syn- | ||
| Bond length | N3–N9 | 1.364 | 1.383 | 1.359 | 1.385 | 1.360 | 1.387 | 1.367 | 1.391 | 1.364 | 1.396 | 1.376 | 1.407 |
| C10–N9 | 1.274 | 1.274 | 1.278 | 1.279 | 1.278 | 1.280 | 1.275 | 1.275 | 1.274 | 1.272 | 1.271 | 1.270 | |
| C10–C1′′ | 1.469 | 1.467 | 1.457 | 1.454 | 1.457 | 1.453 | 1.465 | 1.461 | 1.471 | 1.468 | 1.489 | 1.484 | |
| C1′′–C6′′ | 1.397 | 1.397 | 1.408 | 1.408 | 1.403 | 1.403 | 1.402 | 1.403 | 1.397 | 1.397 | — | — | |
| C4–N3 | 1.388 | 1.382 | 1.387 | 1.385 | 1.386 | 1.385 | 1.386 | 1.381 | 1.383 | 1.371 | 1.377 | 1.366 | |
| C2–N3 | 1.460 | 1.460 | 1.457 | 1.459 | 1.458 | 1.459 | 1.460 | 1.460 | 1.465 | 1.467 | 1.463 | 1.465 | |
| Bond angle | N3–N9–C10 | 120.4 | 117.7 | 122.4 | 118.2 | 122.4 | 117.7 | 120.4 | 116.9 | 120.3 | 116.2 | 120.0 | 115.3 |
| N9–C10–C1′′ | 120.5 | 120.6 | 119.5 | 120.3 | 119.4 | 120.3 | 120.7 | 120.9 | 120.3 | 121.3 | 119.8 | 120.8 | |
| C4–N3–C2 | 121.9 | 120.3 | 122.8 | 120.6 | 122.5 | 120.6 | 122.1 | 120.5 | 124.9 | 124.0 | 125.0 | 124.4 | |
| C8a–N1–C2 | 116.8 | 115.9 | 117.1 | 116.1 | 117.0 | 116.2 | 117.0 | 116.1 | — | — | — | — | |
| N1–C2–N3 | 108.6 | 107.5 | 108.4 | 107.4 | 108.4 | 107.3 | 108.6 | 107.5 | — | — | — | — | |
| C4–N3–N9 | 115.7 | 122.3 | 115.0 | 120.7 | 114.9 | 120.4 | 115.6 | 121.4 | 114.9 | 120.1 | 115.0 | 119.3 | |
| C1′–C2–N3 | 113.0 | 113.5 | 112.4 | 113.3 | 112.5 | 113.4 | 112.9 | 113.7 | — | — | — | — | |
| Torsion angle | C4–N3–N9–C10 | −165.0 | 50.2 | −167.8 | 56.2 | −167.7 | 57.6 | −165.7 | 54.7 | 171.3 | −58.3 | 170.5 | −65.1 |
| C2–N3–N9–C10 | 5.2 | −157.6 | 0.7 | −153.4 | 0.5 | −152.3 | 3.5 | −154.3 | −3.7 | 146.2 | −4.9 | 139.4 | |
| N3–N9–C10–C1′′ | −179.1 | −179.6 | 179.9 | −178.0 | 179.8 | −177.3 | −179.5 | −178.4 | 179.7 | 178.6 | 179.5 | 178.5 | |
| N9–C10–C1′′–C6′′ | 2.2 | 5.6 | −1.9 | 2.1 | −2.5 | 2.5 | −0.4 | 4.1 | −1.9 | −4.8 | — | — | |
| N3–C2–C1′–C2′ | 168.7 | 170.7 | 167.8 | 171.2 | 170.1 | 172.0 | 165.3 | 168.0 | — | — | — | — | |
| N1–C2–N3–C4 | −38.4 | −47.5 | −37.8 | −48.4 | −38.3 | −48.5 | −37.8 | −47.9 | — | — | — | — | |
However, there were clear trends in the bond lengths depending on the position and type of substituents on the rings B and C. The N3–N9 bond has partial double-bond character, as it partakes in a delocalised system stretching from ring A to ring C. The effect of the delocalisation along the C4–N3–N9–C10 array is clearly visible from the calculated bond length values.
The elongation of the N3–N9 bond is seen particularly in the case of the syn-isomer, where the length varies from 1.38 Å to 1.41 Å (Table 6, row 1). This bond length varies in the anti-isomer as well, but less markedly (Table 6, row 1).
Virtually no differences were observed in the C10–C1′′ bond lengths, which are comparable to single bonds in similar systems.53 The C4–N3 bond is shortest for 7 (syn) and longest for 1 (anti), the latter indicating the contraction of this bond with addition of substituents (Table 6, row 5). Incorporation of the ring C into the structure of 7 (forming derivative 6) caused elongation of the bond (1.383 (6) vs. 1.377 (7) Å, both for anti). A significant effect is also seen after addition of the aromatic ring C to the carbon atom C10; there is a clear zigzag double-bond formation in the C4–N3–N9–C10 linkage, where the N3–N9 bond is shortened and the N9–C10 bond is elongated (Table 6, rows 3 and 4, respectively). On the other hand, the differences between 6 and 1 are minimal; the presence of ring B has a negligible effect on the C4–N3–N9–C10 moiety (Fig. 4). Due to the absence of heterocyclic or aromatic rings in the structure 7, different structural changes were seen in this derivative, namely a significant elongation of the N3–N9 bond (the longest out of all the systems) as the result of the shortening of both the N9–C10 (the shortest out of all compounds) and the C4–N3 bonds. The dihedral angle N9–C10–C1′′–C6′′ is almost in plane (within 5 degrees). Rotation around the N–N bond leads to formation of two conformers for this systems as well (anti and syn), in agreement with NMR experiments and in accordance with our evidence.45,46
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–C linkage. These will be termed set a, and the compounds 1a, 2a, 3a, etc. are compounds 1, 2, 3, etc. thus simplified. It should be noted that introduction of ortho-OH on rings A and C leads to numerous possibilities for intramolecular H-bonding that may be relevant, and intermolecular H-bonding can also have a significant effect (most notably on tautomerisation); of the checking of variant conformers and model systems there is no end, and a significant amount of work must be relegated to ESI† or omitted entirely.
CH–C linkage. These will be termed set a, and the compounds 1a, 2a, 3a, etc. are compounds 1, 2, 3, etc. thus simplified. It should be noted that introduction of ortho-OH on rings A and C leads to numerous possibilities for intramolecular H-bonding that may be relevant, and intermolecular H-bonding can also have a significant effect (most notably on tautomerisation); of the checking of variant conformers and model systems there is no end, and a significant amount of work must be relegated to ESI† or omitted entirely.Firstly, as a preliminary consideration, let us examine the protonation energies of two models (C4H2ON)–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–R, in syn-conformation (Fig. 5), with R = Me (system 7) or CH
CH–R, in syn-conformation (Fig. 5), with R = Me (system 7) or CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–OH (in syn(syn)-form). This data is given in Table 7, together with data for system 8a, which is shown (together with its protonated form) in Fig. 6.
CH–OH (in syn(syn)-form). This data is given in Table 7, together with data for system 8a, which is shown (together with its protonated form) in Fig. 6.
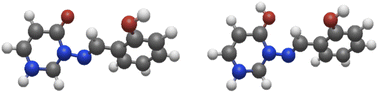 | ||
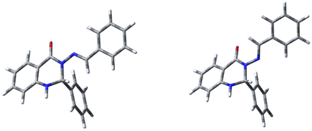
Fig. 5 Left: model system 8a; right: model system 8a-H+ (protonated at C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). The syn(anti) conformation is shown in both cases. O). The syn(anti) conformation is shown in both cases. | ||
| Protonated atom | R = Me (7) | R = CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–OH CH–OH |
8a |
|---|---|---|---|
| Ocarbonyl | −433.8 | −433.3 | −439.2 |
| N1 | −419.2 | −418.2 | |
| N3 | −423.0 | −420.5 | |
| N9 | −436.5 | −438.3 | −444.2 |
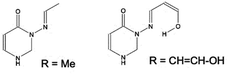 | ||
Fig. 6 Two models (C4H2ON)–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–R, in syn conformation, with R = Me (system 7) or CH CH–R, in syn conformation, with R = Me (system 7) or CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–OH (in syn(syn)-form). CH–OH (in syn(syn)-form). | ||
We find (Table 7) that protonation is easiest for carbonyl oxygen and N9, the imide oxygen, in both cases; and that the presence of an OH group makes it easier to protonate N9, although not by much.
Note that protonation at N9 also allows the molecule to form an extra H-bond, with the protonated centre as the H-bond donor. The system 8a is defined as described earlier, and differs from 7 in replacing Me with ortho-methoxyphenyl. Note that reducing 8a to the R = CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–OH system decreases protonation energy by 5.9 mH in each case, i.e. there is some roughly-constant error introduced by decreasing the size of the molecule.
CH–OH system decreases protonation energy by 5.9 mH in each case, i.e. there is some roughly-constant error introduced by decreasing the size of the molecule.
Next, we shall consider model set a, which lack rings A and B, but still have the heterocycle, ring C, and the N–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH–C linkage. While the truncation of the π-system may have some effect on the behaviour of the molecules, it is expected that the trends will be roughly accurate. Of most interest is the energy barrier for syn–anti isomerisation. This is taken as the difference between the energy of the syn-conformer and the energy maximum at a dihedral bond angle of D(CNNC) = ∼120° (the exact value varies with system). (See our previous paper46 for qualifications: this energy barrier is expected to be a slight underestimate.) This is listed for both model set a and carbonyl-protonated model set a in Table 8. These results were calculated with default integration grid; values for model set a calculated with ultrafine integration grid are listed in ESI, Section S2.2.† We note here that, while the use of a cruder grid leads (usually) to ∼15–20% overestimation of energy barriers, the major trends are not affected; we will mention it when this error has any bearing on our discussion. The use of default grid quality sometimes leads to noise on the order of <0.1 mH in the variation of energy with D(CNNC), causing apparent peak splitting; this is also discussed in ESI S2.2.†
CH–C linkage. While the truncation of the π-system may have some effect on the behaviour of the molecules, it is expected that the trends will be roughly accurate. Of most interest is the energy barrier for syn–anti isomerisation. This is taken as the difference between the energy of the syn-conformer and the energy maximum at a dihedral bond angle of D(CNNC) = ∼120° (the exact value varies with system). (See our previous paper46 for qualifications: this energy barrier is expected to be a slight underestimate.) This is listed for both model set a and carbonyl-protonated model set a in Table 8. These results were calculated with default integration grid; values for model set a calculated with ultrafine integration grid are listed in ESI, Section S2.2.† We note here that, while the use of a cruder grid leads (usually) to ∼15–20% overestimation of energy barriers, the major trends are not affected; we will mention it when this error has any bearing on our discussion. The use of default grid quality sometimes leads to noise on the order of <0.1 mH in the variation of energy with D(CNNC), causing apparent peak splitting; this is also discussed in ESI S2.2.†
| No o-OH | Eb, full | Eb, models a | Eb, models aH+ |
|---|---|---|---|
| 1 | 4.29 | 1.03 | |
| 4 | 2.55 | 3.52 | 0.85 |
| 5 | 4.32 | 6.22 | 1.32 |
| With o-OH | |||
| 2 | 3.47(4.07) | 0.79(0.82) | |
| 3 | 2.49 | 3.90(4.08) | 0.63(0.82) |
| 8 | 2.55 | 3.17(3.96) | 0.19(0.88) |
System 6 is similar to 1a, and the experimental difference in relaxation times may indicate that energy barriers from model set a are underestimated (and may have other, less systematic errors); but an alternative explanation is that the 1 > 6 > 7 trend in relaxation times arises from solvent friction due to molecular size, as mentioned earlier. We lean towards the latter explanation, as comparison with available calculations on the full systems indicates that truncation increases the energy barriers. To assess how well our chosen method treats the energy barrier, Eb energies for 8a were also calculated at the CISD/cc-pVDZ level for comparison (as CISD single-point calculations using DFT-derived geometries [default grid]). The results deviate from DFT (default grid) by less than 0.1 mH for 8a, and are slightly larger than for DFT (default grid) for 8a-H+: 0.52 vs. 0.19 mH for syn(syn), 1.12 vs. 0.88 mH for syn(anti).
With this mentioned, we move on to examining our hypotheses as to mechanism. The results in Table 8 clearly do not support our first hypothesis, regarding carbonyl–azomethine proton interactions. For neutral systems, systems with o-OH in the syn(anti) form (2a, 3a, 8a) all have a higher energy barrier than system 4a – despite the latter having a relaxation time over 3 orders of magnitude higher (see Table 2). Nor does protonation of carbonyl help here, as the syn(anti) protonated forms continue to show overlap between the range of energy barriers for compounds with o-OH (which relax quickly) and the range of compounds without (which relax orders of magnitude more slowly). However, the protonated systems do have significantly lower energy barriers than the neutral systems, for both syn(syn) and syn(anti), which fits with our finding that acidifying the solution speeds up syn–anti relaxation. Calculations on the deprotonated systems find that the anti-form is destabilised, presumably due to so much negative charge delocalising to N9 that repulsion with carbonyl oxygen becomes an issue; deprotonation is thus unlikely to be relevant to syn–anti relaxation.
This is not to say that the effects mentioned in hypothesis (I) do not occur, however; comparing systems 1a and 8a (syn(anti)-form) shows that the effects of o-OH on the weak N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–H⋯O
C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C interaction are real (Table 9). Adding the o-OH group (going from 1a to 8a) decreases the energy barrier by about 10%, and increases both the OCO⋯H distance and the D(CNNC) dihedral angle. However, this 10% energy barrier decrease is outweighed by the variation within the groups of compounds that have (2, 3, 8) or do not have (1, 4, 5) ortho-OH substituents.
C interaction are real (Table 9). Adding the o-OH group (going from 1a to 8a) decreases the energy barrier by about 10%, and increases both the OCO⋯H distance and the D(CNNC) dihedral angle. However, this 10% energy barrier decrease is outweighed by the variation within the groups of compounds that have (2, 3, 8) or do not have (1, 4, 5) ortho-OH substituents.
| System | R(H⋯OCO) | R(H⋯OHO) | D(CNNC) | Eb |
|---|---|---|---|---|
| 1a | 2.20 | — | 35.4 | 4.3 |
| 1a-H+ | 2.70 | — | 69.4 | 1.0 |
| 8a | 2.42 | 2.39 | 54.8 | 4.0 |
| 8a-H+ | 2.71 | 2.37 | 69.4 | 0.9 |
Furthermore, protonation decreases the effect of o-OH: R(H⋯OCO) and D(CNNC) differ between 1a and 8a, but are virtually the same for 1a-H+ and 8a-H+. We note that, as aromatic OH is weakly acidic, there should be a small amount of H+ floating around (in the form of DMSO–H+, or possibly H3O+ from trace water), which makes protonation plausible. This includes systems 2 and 4 where the adjacent OH and OMe groups might be expected to form an internal H-bond, making the OH group less acidic. The same considerations apply to the smaller molecule 2-methoxyphenol, which might also be expected to be less acidic than phenol due to an internal H-bond, but experimentally the two compounds have extremely similar acidities.54
Hypothesis (II), or certain forms of it, are somewhat better-supported by our calculations. The syn(syn) forms, both protonated and unprotonated, show no clear separation between systems with and without o-OH. When using the default grid there is a small gap (<0.1 mH) between the energy barriers of systems with and without o-OH in protonated forms; when using an ultrafine grid (see ESI, Section S2.2 and Table S1†) there is instead a small gap for the unprotonated forms. In any case, the difference is too small on its own to explain an orders-of-magnitude rate difference.
A more promising explanation is that protonation of imide nitrogen (N9) leads to a somewhat different energy profile in which the energy minimum is >90°. This can happen for any system; but in the case of systems with o-OH, it can happen via direct intramolecular proton transfer of the H-bonding proton, i.e. tautomerisation. (Tautomerisation of systems with OH elsewhere is also possible but expected to be slower, as the proton must take an indirect route.) This is plausible as tautomerisation has been observed experimentally for certain other types of Schiff bases.55,56 Thus in Fig. 7, which depicts the energy curves for molecule 8a, we see that the keto-amine tautomer – formed by proton transfer from o-OH to N9 – actually has a minimum at around D(CNNC) = 100°. This provides a potential syn to anti pathway in which, firstly, the tautomer is formed; secondly, the molecule rotates partway around the N–N bond; thirdly, it shifts back to the original tautomer (enol-imine), and is now at the top of the energy barrier; and fourthly, it moves down the potential energy curve to either the syn- or the anti-form.
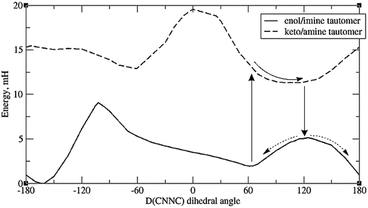 | ||
| Fig. 7 Energy profiles of the two tautomers of 8a, showing a possible pathway for syn–anti isomerisation. Default integration grid was used. | ||
However, it should be mentioned that the energy difference between tautomers (Et) is quite large. For 8a the difference is 9.4 mH (24.6 kJ mol−1), and for the full molecule 8, the difference is 10 mH, or 26 kJ mol−1 – significantly higher than the energy barrier for simple rotation around the CNNC linkage. (Also, the energy gap between the syn-form and the tautomer with the same D(CNNC) value is about 1.5 to 2 mH higher than the difference between syn-form and the optimised keto-amine minima.) Calculations indicate that this energy difference decreases with H-bonding to the OH group – see ESI, Section S2.3.† Such H-bonds are expected to happen from phenolic OH groups on other molecules, as well as traces of water accumulating in the solvent (especially DMSO) over time, so H-bond-assisted tautomerisation seems plausible. Calculations show that H-bonding from phenolic OH (represented by C2H3OH) reduces tautomerisation energy more than H-bonding from water. For the full molecule 8, the tautomerisation energy drops to less than 1 mH when 2 water molecules are attached; preliminary calculations indicate that attaching one water molecule and one C2H3OH to 8a puts the tautomerisation energy below 0, i.e. makes the keto-form more stable. These calculations, however, suffer from the problem that there may be multiple local minima for the {molecule + solvent} system, with different tautomerisation energies. Also, tautomerisation is highly susceptible to dielectric effects: for 8a, the calculated Et is 11.3 mH for DMSO, and 17.7 mH for vacuum (no SCRF). This effect of keto-tautomers of Schiff bases being stabilised in a more polar environment is known from experiment.56 This provides an explanation of why syn–anti relaxation is faster in more polar solvents (Table 4), though it is unclear why relaxation should be slower in MeOH than DMSO – the latter being more polar, but the former contributing more H-bonds.
It should be noted that, while other tautomeric Schiff bases show visible signs of equilibrium in the NMR spectra, our proposed mechanism involves the keto-tautomer arising as a short-lived intermediate when the syn-enol form experiences a particular H-bonding environment. It is presumed to be present in trace amounts and not expected to be visible in the NMR spectrum. (If it were present in detectable amounts we would expect syn–anti relaxation to proceed so fast that the syn-conformer would be undetectable.)
Tautomerisation plus protonation can also be considered: as depicted in Fig. 3, protonation of an o-OH group leads to proton transfer to the imine nitrogen in one concerted step (test calculations failed to find a stable minimum for o-OH2+), resulting in a very similar energy profile to the keto/amine tautomer discussed above. Protonation of N9 is in fact energetically favoured over protonation of carbonyl oxygen for model set a by 3–7 mH (see ESI, Section S2.6 and Table S4†). However, the N9 lone-pair is far less sterically accessible than other sites, with the ring-C ortho-H (or other substituent) and the whole of ring B hindering access to the in-plane position the proton needs to adopt. If, however, N9 is protonated indirectly by protonating o-OH as described above, this problem is sidestepped. This is shown in Fig. 8.
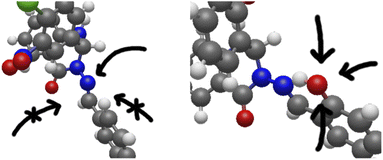 | ||
| Fig. 8 The full systems 5 (left) and 8 (right), shown to illustrate the steric inaccessibility of the N9 lone-pair and the comparative accessibility of the o-OH. | ||
It must be noted that protonation is a higher-energy process than simple rotation, in that (assuming the proton source to be phenolic OH from other Schiff base molecules in solution) the energy required to deprotonate Ar–OH is at least 30 mH larger than the energy gained by protonating either the carbonyl group or N9, which exceeds by far the energy required for simple rotation around N–N, or for tautomerisation of the neutral species. However, protonation would be catalytic here, and it is possible that trace amounts of H+ are present which lead to a significant speedup in reversion to the anti-conformer. If this be the case, however, it may be asked why system 4 (a weakly-acidic system) does not relax faster than 5: while N9-protonation may not happen, some CO-protonation would be expected.
It may also be relevant that proton transfer and tautomerisation are not obstructed by solvent friction, unlike simple rotation around N–N, so solvent friction would not affect the rate-determining step – although it would make it less likely for the keto-amine tautomer to shift from a D(CNNC) dihedral of about 60° to about 100° without relaxing back to the syn form of the enol-imide tautomer first.
4 Conclusions
In summary, the presented work has found a tendency of variously-substituted Schiff bases to undergo anti- to syn-isomerisation on exposure to ultraviolet light. The anti- to syn-conversion varied from non-detectable amounts to about 100%, depending upon substitution. The data also showed two additional noteworthy features: that relaxation back to anti-form goes far faster (by at least 3 orders of magnitude) when the C6 rings B and C have ortho-OH substituents, and that relaxation can also be significantly sped up by addition of acid. Thus, the introduction of other substituents (in addition to the OH group), or the analysis of the unsubstituted form, has significantly extended our knowledge and understanding of the photoisomerisation processes of quinazolinone derivatives.We have proposed and analysed two possible mechanisms, or classes of mechanisms, to explain the differences in relaxation process. Mechanism (I) is interaction of o-OH with the azomethine proton. Our calculations do not support the idea that this significantly affects relaxation rates, as the effect on energy barriers is minimal.
Mechanism (II) is that protonation/internal H-bonding affect the resonance structures in such a way as to change the energy profile of the system on rotation round the N–N bond. Calculations performed on truncated model systems have found that protonation of the molecule lowers the energy barrier to rotation around N–N (explaining the faster relaxation in acidic solution), and identified two possible, and closely-related, explanations involving proton transfer for the o-OH group's effects:
(A) Protonation of N9 (via protonation of o-OH) leads to an energy minimum at significantly higher D(CNNC), and deprotonation leaves the system at the top of the syn–anti energy barrier. Protonation of N9 is sterically hindered, but an o-OH group allows a sterically-accessible mechanism for this to take place. This requires a specific isomer, labelled syn(syn), in which the o-OH is near to N9 rather than to the azomethine proton, and we consider it plausible due to the weakly acidic nature of the systems, which results in very small concentrations of H+ (which, acting as a catalyst, is not required in large amounts).
(B) Tautomerisation, in the absence of (external) protonation, should become possible with certain H-bonding situations, with the mechanism being similar to protonation of N9. While the keto-amine form is a lot higher in energy, it can be stabilised by intermolecular hydrogen bonds: calculations suggest that 2 H-bonds reduce the energy difference between tautomers significantly. This also requires the syn(syn) isomer.
We envisage that additional systems with and without o-OH could confirm the trend that this paper has examined, provide experimental evidence against (or possibly for) mechanism (I), and distinguish between the possibilities (A) and (B) above. A system with o-NH2 would have internal H-bonding to N9, so H-bond-assisted tautomerisation would be possible; protonation of NH2 (by trace water) would only occur in extremely small amounts, and the molecule would not itself be acidic, thus suppressing the protonation mechanism (A); and mechanism (I) would not apply (in-plane H-bonds to aromatic NH2 being impossible). A system with o-Cl or o-F would have mechanism (I) active, but no internal H-bonding to N9 and no production of free H+; delocalisation of negative charge to N9 would occur to a small degree. Additional experiments could be devised to distinguish between mechanisms. Calculation-wise, additional post-HF calculations could be done on small models – this is time-consuming and demanding, but would allow us to judge how well DFT is dealing with the various effects involved.
Author contributions
Michal Hricovíni: formal analysis, investigation, writing – original draft, visualisation. James Asher: formal analysis, writing – original draft, review & editing, visualisation. Miloš Hricovíni: conceptualisation, funding acquisition, investigation, writing – original draft, review & editing. All authors co-wrote the paper and extensively discussed interpretation of the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Slovak Grant Agency VEGA, grants no. 2/0135/21 and 2/0071/22, and the Slovak Research and Development Agency, grant APVV-19-0516. Part of the Gaussian calculations were performed at the Computing Centre of the SAS using the supercomputing infrastructure acquired in projects ITMS 26230120002 and 26210120002, both supported by the Research & Development Operational Program funded by the ERDF.References
- C. Dugave and L. Demange, Chem. Rev., 2003, 103, 2475–2532 CrossRef CAS PubMed.
- R. Croce and H. Van Amerongen, Nat. Chem. Biol., 2014, 10, 492–501 CrossRef CAS PubMed.
- B. Demoulin, S. F. Altavilla, I. Rivalta and M. Garavelli, J. Phys. Chem. Lett., 2017, 8, 4407–4412 CrossRef CAS PubMed.
- T. Kumpulainen, B. Lang, A. Rosspeintner and E. Vauthey, Chem. Rev., 2017, 117, 10826–10939 CrossRef CAS PubMed.
- I. Schapiro, M. N. Ryazantsev, L. M. Frutos, N. Ferré, R. Lindh and M. Olivucci, J. Am. Chem. Soc., 2011, 133, 3354–3364 CrossRef CAS.
- S. Gozem, H. L. Luk, I. Schapiro and M. Olivucci, Chem. Rev., 2017, 117, 13502–13565 CrossRef CAS PubMed.
- G. M. Wyman, Chem. Rev., 1955, 55, 625–657 CrossRef CAS.
- A. J. Pepino, M. A. B. Paci, W. J. Peláez and G. A. Argüello, Phys. Chem. Chem. Phys., 2015, 17, 12927–12934 RSC.
- L. Vuković, C. F. Burmeister, P. Král and G. Groenhof, J. Phys. Chem. Lett., 2013, 4, 1005–1011 CrossRef PubMed.
- Y. T. Wang, X. Y. Liu, G. Cui, W. H. Fang and W. Thiel, Angew. Chem., Int. Ed., 2016, 55, 14009–14013 CrossRef CAS PubMed.
- A. A. Beharry and G. A. Woolley, Chem. Soc. Rev., 2011, 40, 4422–4437 RSC.
- D. P. Aalberts and H. F. Stabenau, Phys. A, 2010, 389, 2981–2986 CrossRef CAS.
- C. E. Weston, R. D. Richardson, P. R. Haycock, A. J. P. White and M. J. Fuchter, J. Am. Chem. Soc., 2014, 136, 11878–11881 CrossRef CAS PubMed.
- B. Shao, H. Qian, Q. Li and I. Aprahamian, J. Am. Chem. Soc., 2020, 141, 8364–8371 CrossRef.
- S. T. Reid, Adv. Heterocycl. Chem., 1982, 30, 239–317 CrossRef CAS.
- A. Watwiangkham, T. Roongcharoen and N. Kungwan, J. Photochem. Photobiol., A, 2020, 389, 112267 CrossRef CAS.
- J. J. Szymczak, M. Barbatti and H. Lischka, J. Phys. Chem. A, 2009, 113, 11907–11918 CrossRef CAS PubMed.
- K. S. Munawar, S. M. Haroon, S. A. Hussain and H. Raza, J. Basic Appl. Sci., 2018, 14, 217–229 CrossRef CAS.
- J. Ceramella, D. Iacopetta, A. Catalano, F. Cirillo, R. Lappano and M. S. Sinicropi, Antibiotics, 2022, 11, 191–214 CrossRef CAS.
- D. Dutta, N. K. Bhattacharyya and J. Biswas, Indian J. Chem.–B Org. Med. Chem., 2021, 60B, 1478–1489 CAS.
- P. Altoè, F. Bernardi, I. Conti, M. Garavelli, F. Negri and G. Orlandi, Theor. Chem. Acc., 2007, 117, 1041–1059 Search PubMed.
- S. Achelle, J. Rodríguez-López and F. Robin-Le Guen, J. Org. Chem., 2014, 79, 7564–7571 CrossRef CAS.
- E. Raczuk, B. Dmochowska, J. Samaszko-Fiertek and J. Madaj, Molecules, 2022, 27, 787 CrossRef CAS PubMed.
- K. P. Rakesh, H. K. Kumara, H. M. Manukumar and D. C. Gowda, Bioorg. Chem., 2019, 87, 252–264 CrossRef CAS PubMed.
- J. Mravljak, L. Slavec, M. Hrast and M. Sova, Molecules, 2021, 26, 6585 CrossRef CAS PubMed.
- T. Khan, S. Zehra, A. Alvi, U. Fatima and A. J. Lawrence, Orient. J. Chem., 2021, 37, 1051–1061 CAS.
- W. Al Zoubi and Y. G. Ko, Appl. Organomet. Chem., 2017, 31, 1–12 Search PubMed.
- K. M. Abuamer, A. A. Maihub, M. M. El-Ajaily, A. M. Etorki, M. M. Abou-Krisha and M. A. Almagani, Int. J. Org. Chem., 2014, 4, 7–15 CrossRef.
- S. M. Borisov, R. Pommer, J. Svec, S. Peters, V. Novakova and I. Klimant, J. Mater. Chem. C, 2018, 6, 8999–9009 RSC.
- S. Helmy, F. A. Leibfarth, S. Oh, J. E. Poelma, C. J. Hawker, J. R. de Alaniz and J. Read, J. Am. Chem. Soc., 2014, 136, 8169–8172 CrossRef CAS PubMed.
- S. Tanaka, H. Sato, Y. Ishida, Y. Deng, T. Haraguchi, T. Akitsu, M. Sugiyama, M. Hara and D. Moon, J. Korean Chem. Soc., 2018, 62, 328–332 CAS.
- M. N. Uddin, S. S. Ahmed and S. M. R. Alam, J. Coord. Chem., 2020, 73, 3109–3149 CrossRef CAS.
- T. L. Yusuf, S. D. Oladipo, S. Zamisa, H. M. Kumalo, I. A. Lawal, M. M. Lawal and N. Mabuba, ACS Omega, 2021, 6, 13704–13718 CrossRef CAS PubMed.
- A. Singh and P. Barman, Top. Curr. Chem., 2021, 379, 29 CrossRef CAS PubMed.
- A. A. Zawia, H. M. A. Hasan, A. M. Najar, A. A. A. Abdusalam and T. Aeyad, J. Pharm. Appl. Chem., 2022, 9, 1–9 Search PubMed.
- A. M. Abu-Dief and I. M. A. Mohamed, Beni-Suef Univ. J. Basic Appl. Sci., 2015, 4, 119–133 Search PubMed.
- A. M. S. Hossain, J. M. Méndez-Arriaga, C. Xia, J. Xie and S. Gómez-Ruiz, Polyhedron, 2022, 217, 115692 CrossRef CAS.
- I. G. Ovchinnikova, G. A. Kim, E. G. Matochkina, M. I. Kodess, N. V. Barykin, O. S. Eltsov, E. V. Nosova, G. L. Rusinov and V. N. Charushin, Russ. Chem. Bull., 2014, 63, 2467–2477 CrossRef CAS.
- I. Khan, S. Zaib, S. Batool, N. Abbas, Z. Ashraf, J. Iqbal and A. Saeed, Bioorg. Med. Chem., 2016, 24, 2361–2381 CrossRef CAS PubMed.
- Z. Hricovíniová, M. Hricovíni and K. Kozics, Chem. Pap., 2018, 72, 1041–1053 CrossRef.
- T. Schultz, J. Quenneville, B. Levine, A. Toniolo, T. J. Martínez, S. Lochbrunner, M. Schmitt, J. P. Shaffer, M. Z. Zgierski and A. Stolow, J. Am. Chem. Soc., 2003, 125, 8098–8099 CrossRef CAS PubMed.
- H. M. D. Bandara and S. C. Burdette, Chem. Soc. Rev., 2012, 41, 1809–1825 RSC.
- J. Garcia-Amorós, A. Sánchez-Ferrer, W. A. Massad, S. Nonell and D. Velasco, Phys. Chem. Chem. Phys., 2010, 12, 13238 RSC.
- A. Georgiev, A. Kostadinov, D. Ivanov, D. Dimov, S. Stoyanov, L. Nedelchev, D. Nazarova and D. Yancheva, Spectrochim. Acta, Part A, 2018, 192, 263–274 CrossRef CAS PubMed.
- M. Hricovíni and M. Hricovíni, Tetrahedron, 2017, 73, 252–261 CrossRef.
- M. Hricovíni, J. Asher and M. Hricovíni, RSC Adv., 2020, 10, 5540–5550 RSC.
- M. J. Frisch, G. W. Trucks, H. Bernhard Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, Ö. Farkas, J. V. Foresman and D. J. Fox, Gaussian 16, Rev. B.01, Wallingford, CT, 2016 Search PubMed.
- Y. S. Lin, G. De Li, S. P. Mao and J. Da Chai, J. Chem. Theory Comput., 2013, 9, 263–272 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef PubMed.
- T. T. Quang, K. P. P. Nguyen and P. E. Hansen, Magn. Reson. Chem., 2005, 43, 302–308 CrossRef PubMed.
- V. Ferraresi-Curotto, G. A. Echeverría, O. E. Piro, R. Pis-Diez and A. C. González-Baró, Spectrochim. Acta, Part A, 2015, 137, 692–700 CrossRef CAS PubMed.
- P. Suna, P. Hota and P. K. Misra, Indian J. Chem., 2016, 55A, 1192–1201 CAS.
- M. Fujio, R. T. Mclver and R. W. Taft, J. Am. Chem. Soc., 1981, 103, 4017–4029 CrossRef CAS.
- V. I. Minkin, A. V. Tsukanov, A. D. Dubonosov and V. A. Bren, J. Mol. Struct., 2011, 998, 179–191 CrossRef CAS.
- D. Yordanov, V. Deneva, A. Georgiev, A. Crochet, K. M. Fromm and L. Antonov, Spectrochim. Acta, Part A, 2020, 237, 118416 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra04529j |
| This journal is © The Royal Society of Chemistry 2022 |