Exchange bias and magnetic memory effect in hole doped Nd_0.78Sr_0.22CoO₃ nanoparticles

Abstract

Nd_0.78Sr_0.22CoO₃ nanoparticles having 89 nm average particle size are synthesized by standard sol–gel techniques. Structural and morphological characterization is performed by X-ray diffraction and FESEM images. DC magnetization studies in the range 1.6 K to 300 K reveal the disordered magnetic phase below 36 K. Existence of this disordered magnetic phase is substantiated by the magnetic memory effect. A significant upturn in the ZFC magnetization below 4.5 K, which is a signature of a dominant ferromagnetic (FM) component, is observed. This FM component may be attributed to the uncompensated (UC) spins at the surface of Nd_0.78Sr_0.22CoO₃ nanoparticles. The presence of the interface of these two magnetic components with significantly different anisotropy results in the exchange bias effect.

---

1. Introduction

The exchange bias effect (EB) is of great importance to promote potential applications in permanent magnet and high-density magnetic storage devices.^1,2 Therefore, the phenomenon of exchange bias has been visited and revisited several times^3–10 over the years, beginning with Meiklejohn and Bean (1956). The exchange bias effect appears due to the pinning mechanism at the interface between two magnetic components with significantly different anisotropy. The typical manifestation of the EB effect is the displacement of the magnetic hysteresis loop and the enhancement of coercivity due to the magnetic field cooling effect. Numerous reports on the EB phenomenon^3–11 are published for artificial interfaces in layered systems and magnetic nanoparticles having distinguishable surface anisotropy from that of the core.^12–14 On the other hand, a handful systems having spontaneous magnetic phase separation within a single crystallographic phase exhibiting the EB phenomenon have also been reported. Mixed-valent manganites and cobaltites with perovskite structure are the most prevailing examples of this kind where ferromagnetic droplets are spontaneously embedded in an antiferromagnetic back ground or spin glass/cluster glass like matrix or ferrimagnetic background creating spontaneous FM/AFM¹⁵ or FM/SG (or CG)^16,17 or FM/FI¹⁸ interface.

An interesting phase diagram has been proposed by Stauffer et al.¹⁹ for the hole doped cobaltite Nd_1−xSr_xCoO₃ for different degree of hole doping. In the low doping regime (0 < x < 0.18) the SG or CG state has been proposed as ground state. With further increase in hole doping ferrimagnetic (FI) and ferromagnetic (FM) ordering is observed in different temperature region for 0.20 ≤ x ≤ 0.60.

In the present work we have restricted the doping of hole near the boundary of these two regimes and synthesized the hole doped Nd_0.78Sr_0.22CoO₃ nanoparticles whose features are expected to be noticeably different from its bulk counterpart.^11,20 Nanoparticles exhibit the exotic features because of its surface anisotropy, large surface to volume ratio and particle size distribution.¹² The EB effect is found to be present in the perovskite Nd_0.78Sr_0.22CoO₃ nanoparticles which may arise because of the presence of two magnetic phases. The ZFC magnetization indicates ferromagnetic (FM) transition followed by a disordered magnetic phase with lowering of temperature even though ferrimagnetic ground state is expected²⁰ in the corresponding bulk counterpart. Magnetic memory effect found in this system corroborates the possible signature of disordered magnetic phase. Moreover, the large surface area of the nanoparticles promotes the uncompensated (UC) spin at the surface of nanoparticles which introduces different anisotropy in the system around 4.5 K. Coexistence of different magnetic anisotropy contributes to the exchange bias effect. The temperature (T) and cooling field (H_cool) dependence of exchange bias field (H_EB) are in tune with the thermal variation of magnetization.

2. Experimental details

2.1 Synthesis

Nd_1-xSr_xCoO₃ with x = 0.22 is prepared by standard sol–gel technique.^16,18 The Nd₂O₃, SrO and Co powder taken in stoichiometric ratio, are dissolved in hydrated nitric acid for preparing metal nitrate solution. Citric acid is then added in proper amount and the solution is stirred rigorously for two days in order to get homogeneous mixture. Proper amount of citric acid is estimated by considering that only two of the metal ions take part in chemical bonding with one molecule of citric acid. This metal citrate precursor is dried and annealed at 873 K for 6 h. The final heat treatment of the sample is done in the form of pellet in two steps at 1073 and 1273 K for 12 h followed by slow cooling at a rate of 0.7 K min⁻¹.

2.2 Characterization: structural, morphological and magnetization

Crystal structure is studied at room temperature using a powder X-ray diffractometer (XRD) (Bruker D8 Advance) with the Cu K_α radiation. Rietveld refinements were performed by using MAUD software. The full width at half maximum (FWHM) of the most intense peak obtained from Rietveld refinements was used to calculate the average particle size. The morphology of the nanoparticles is studied by field emission scanning electron microscopy (FE-SEM) images using the microscope, FEI, INSPECT F50. The particle size distribution in FESEM has been done by using Image-J software. The dc magnetization (M) is measured using a commercial vibrating sample magnetometer, 7T mini VSM, Cryogenics Ltd to study the magnetic properties of the sample. Magnetization (M) measurements as a function of temperature were carried out under the zero field cooled (ZFC) and field cooled (FC) mode. Furthermore, the slow relaxation dynamics and memory effects in the thermal variation of magnetization measured in ZFC protocol have been investigated. Temperature dependence of the FC magnetization were measured with an applied magnetic field of 100 Oe, while that of the ZFC magnetization were measured with an applied field of 100 and 200 Oe. The magnetic hysteresis (M–H) loops measured between ±70 kOe at different temperature in the range 2 K–100 K under different cooling field in the range 2–50 kOe.

3. Results and discussions

3.1 Crystal structure and morphology: XRD and FESEM studies

The X-ray diffraction pattern of Nd_0.78Sr_0.22CoO₃ using CuK_α radiation is shown in Fig. 1. All the peaks in the diffraction pattern could be indexed by the orthorhombic structure as reported earlier.^19,21 Thus, the XRD data confirm the absence of any detectable impurity phase and thereby the crystallographically single phase structure at room temperature is obtained. Rietveld refinement technique²² is used to analyze the XRD data by using orthorhombic structure with Pnma space group and the lattice parameters are estimated as 5.36 (a), 7.58 (b) and 5.37 (c) Å which are consistent with that of earlier report.²¹ The Rietveld refinement fitted graph of Nd_0.78Sr_0.22CoO₃ and the difference from the experimental data are shown in Fig. 1. The particle size (D) and microstrain (ε) of Nd_0.78Sr_0.22CoO₃ nanoparticles are estimated by using Williamson and Hall's²³ modified Scherrer's formula given by

β cos θ = 0.89λ/D + 2ε sin θ (1)

Fig. 1 X-ray diffraction pattern of Nd_0.78Sr_0.22CoO₃ nanoparticles fitted with Rietveld analysis. Inset shows Williamson–Hall plot.

Taking under consideration of the prominent XRD peaks having uniquely defined FWHM a linear fit of β cos θ versus sin θ plot is shown in the inset of Fig. 1. The average particle size and the microstrain (ε) of Nd_0.78Sr_0.22CoO₃ nanoparticles are estimated to be 89 nm and 3.26 × 10⁻³, respectively. Morphology and size of Nd_0.78Sr_0.22CoO₃ nanoparticles are investigated from FESEM image as shown in Fig. 2. Size of Nd_0.78Sr_0.22CoO₃ nanoparticles follows a Gaussian distribution (inset of Fig. 2) with maximum number of particles in the range around 92 nm which is consistent with the XRD results.

Fig. 2 FESEM images of Nd_0.78Sr_0.22CoO₃ nanoparticles. Inset indicates the size distribution of Nd_0.78Sr_0.22CoO₃ nanoparticles following Gaussian distribution shown by continuous fitted line.

3.2 Magnetic properties

3.2.1 Temperature dependence of dc magnetization. The magnetic properties of the Nd_0.78Sr_0.22CoO₃ nanoparticles are probed by dc magnetization studies. The temperature variation of magnetization (M) under the zero field cooled (ZFC) and field cooled (FC) protocol is shown in Fig. 3. In order to measure ZFC magnetization, the sample is cooled down to 1.6 K in absence of magnetic field and the magnetization is measured in heating cycle at 100 Oe magnetic field. For the measurement in FC mode, the sample is cooled under the same field and magnetization is measured during heating from 1.6 K to 300 K. The FC magnetization deviates from ZFC magnetization around 155 K, as depicted in the figure by an arrow.

Fig. 3 Thermal variation of the magnetization of Nd_0.78Sr_0.22CoO₃ nanoparticles measured in FC and ZFC mode at 100 Oe. Inset highlights the low temperature regime of ZFC magnetization measured at 100 Oe and 200 Oe as discussed in the text.

The thermal variation ZFC magnetization depicts a peak around ∼37 K (T_g) followed by an upturn around 4.5 K as evident in Fig. 3 inset. To reveal the origin of the ZFC peak, the temperature dependence of the ZFC magnetization is measured at different applied magnetic fields (H = 100 Oe and 200 Oe) as shown in Fig. 3 inset. The peak at T_g is found to shift slightly toward the low temperature for higher magnetic field. Such a dependence of ZFC peak position on the magnetic field may designate the presence of a metastable state. It may be a signature of a disordered magnetic phase¹³ although the reported experimental data including the neutron and ⁵⁹Co NMR clearly indicate the FI phases at low temperature in Nd_1−xSr_xCoO₃ for x ≥ 0.20.²¹ In the present case, the disordered phase may arise because of the nanostructure of the system. The magnetic memory effect observed in this system measured in ZFC mode may be attributed to the disordered magnetic phase as discussed later in Section 3.2.2.

A significant upturn in the ZFC magnetization below 4.5 K is illustrated in Fig. 3 inset with decrease in temperature down to 1.6 K. This feature becomes more prominent with the increase of measuring magnetic field. This sharp increase of ZFC magnetization indicates the signature of a dominant ferromagnetic (FM) component in the low temperature region. This FM component may be attributed to the uncompensated (UC) spins at the surface of Nd_0.78Sr_0.22CoO₃ nanoparticles as discussed in the recent reviews.²⁴ Appearance of UC-spins typically may bring in a new anisotropy which is different from the core anisotropy. Coexistence of different magnetic anisotropies leads to the exchange bias (EB) effect due to field cooling which is discussed later in the Section 3.2.3.

3.2.2 Magnetic memory effect: characterization of disordered magnetic phase. The slow relaxation dynamics and memory effects in the thermal variation of magnetization measured in ZFC protocol are the ascertaining signatures of the disordered magnetic system. Memory effects observed in the relaxation dynamics are summarized in Fig. 4. It illustrates the isothermal magnetic relaxation at 30 K recorded in 100 Oe for t₁ = 6000 s after zero field cooling from 250 K which is well above the disorder transition (T_g) temperature. After lapse of t₁, the magnetic field is switched off, the temperature decreases down to 25 K and relaxation is measured again in zero field for t₂ = 6000 s. Finally, the temperature is restored to 30 K in zero field and the relaxation is further recorded in 100 Oe for t₃ = 6000 s. To explain the result, the magnetization measured during the aging period t₁ and t₃ is plotted sequentially in the inset of Fig. 5, leaving out the data for time evolution during t₂. Inset of Fig. 4 clearly indicates that the magnetization measured during the time period t₃ appears as a perfect continuation to the curve measured during t₁. This clearly shows that state of the system before temporary cooling is recovered when temperature returns as if the system retains its memory of the previous state. This can be approximated by the stretched exponential function,^25,26

M(t) = M₀ + M_g[1 − exp(−(t/t₀))^β]

where, M₀ and M_g are involved with ferromagnetic and glassy components, respectively. t₀ is the time constant and the dispersion parameter β represents the distribution of relaxation dynamics. For single energy barrier the value of β is 1 whereas β value lies in the range 0 < β < 1 for the system with distribution of energy barriers. Here, the best fit gives M₀ = 0.19609 emu g⁻¹ and β = 0.553, as shown in inset of Fig. 4. The non-zero value of M₀ indicates the presence of ferromagnetic component^25,26 attached in the relaxation dynamics and value of β points the distribution of anisotropy barriers, as generally found in disordered magnetic systems.

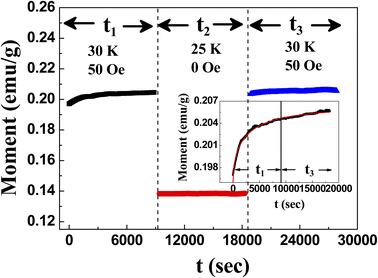Fig. 4 Magnetic relaxation at 30 K in 100 Oe for t₁ and t₃ after cooling down from 250 K in ZFC mode with an intermediate measurement time t₂ in zero field at 25 K.

Fig. 5 Magnetic hysteresis loops measured at 2 K, 8 K, 10 K, 50 K, 75 K and 100 K after cooling the sample from 300 K under H_cool = 50 kOe. Inset highlights the shift of central part of M–H loop measured at 2 K under the cooling field H_cool = 2 kOe and 50 kOe.

3.2.3 Exchange bias effect. To investigate the exchange bias (EB) effect sample is cooled down to 2 K from 300 K under different cooling field (H_cool) ranging from 2 50 kOe. Magnetic hysteresis (M–H) loops measured between ±7 T at different temperature in the range 2 K–100 K, under H_cool = 50 kOe are shown in Fig. 5. The shift of the magnetic hysteresis loop measured at 2 K under H_cool = 2 kOe and 50 kOe as highlighted in the inset of Fig. 5, is a typical manifestation of an exchange bias effect. The shift along the field-axis defined as the exchange bias field (H_EB) and the coercive field (Hc) have been estimated as H_EB = (H⁺_C + H⁻_C)/2 and H_C = (H⁺_C − H⁻_C)/2 respectively, where H⁺_C (H⁻_C) represents the positive (negative) coercive field. The remanence asymmetry defined as EB magnetization (M_EB)¹⁸ is also calculated as M_EB = (M_E⁺ + M_E⁻)/2, where M_E⁺ (M_E⁻) represents positive (negative) remanent magnetization. M_EB/M_S estimated at 2 K for H_cool = 50 kOe is ∼ 0.5 × 10⁻², where M_S is the saturation of magnetization. This value is comparable to that of Nd_0.80Sr_0.2CoO₃.¹⁸ Thermal variation of H_EB, M_EB/M_S and H_C measured under H_cool = 50 kOe are shown in Fig. 6. With the lowering of temperature H_EB increases sharply exhibiting highest value at 2 K as uncompensated (UC) FM phase is observed below 4.5 K. Temperature dependence of the asymmetry parameters are typical for the exchange biased systems viz., Nd_1−xSr_xCoO₃, where EB effect vanishes above FI or spin freezing transition temperature.^18,19 In the present system, the rigid UC spins apply a coupling force on the disordered spins at the interface and a layer of pinned or frozen FM spins are created at the interface when the system is cooled in non-zero field. The pinned or frozen FM spins give rise to the unidirectional shift of the hysteresis loops and reveal the EB effect. Thermal variation of M_EB/M_S is similar to that of H_EB as expected.

Fig. 6 Thermal variation of (a) exchange bias field (H_EB) (b) relative vertical shift (M_EB/M_S) and (c) coercivity (H_C) of Nd_0.78Sr_0.22CoO₃ nanoparticles measured under cooling field H_cool = 50 kOe. M_EB and M_S are the exchange bias magnetization and saturation magnetization.

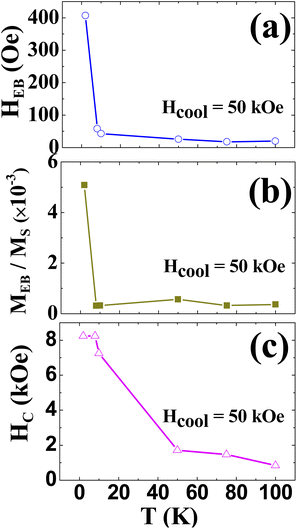
The H_cool dependence of H_EB and M_EB/M_S are shown in the Fig. 7. The value of H_EB increases sharply with H_cool up to 10 kOe and then linearly increases till 50 kOe. H_cool dependence of H_C, as seen in the inset of Fig. 7a is almost similar to that of H_EB, where the sharp increase of H_C is associated with the increase of H_EB. Moreover, the inset of Fig. 7b depicts the linear dependence of M_EB/M_S with H_EB as reported in bulk Nd_0.80Sr_0.2CoO₃.¹⁸ The coexistence of two different magnetic phase viz. FM/FI interface was responsible for exhibiting the exchange bias effect in the bulk Nd_0.80Sr_0.2CoO₃ system,¹⁸ while the cause of exhibiting the same effect in Nd_0.78Sr_0.22CoO₃ nanoparticles is entirely different. Detail dc magnetization studies along with memory effect suggest the existence of UC spins at the surface of the nanoparticles below 4.5 K and magnetic disordered phase below 36 K. The interface of these two magnetic phases with different anisotropy illustrates the exchange bias effect at low temperature in the nanoparticle of Nd_0.78Sr_0.22CoO₃. This exchange bias effect may be tuned by controlling the size and shape of the nanoparticles as UC spin are residing at the surface of the nanoparticles.

Fig. 7 Cooling field (H_cool) dependence of (a) exchange bias field (H_EB) and (b) relative vertical shift (M_EB/M_S) of Nd_0.78Sr_0.22CoO₃ nanoparticles measured at 2 K. Solid lines represent the guide line to eye. The H_cool dependence of coercivity (H_C) and the plot of M_EB/M_S versus H_EB are shown in the inset of (a) and (b), respectively. The solid straight line in the inset of the (b) shows the linear fit.

4. Summary and conclusions

Hole doped Nd_0.80Sr_0.2CoO₃ nanoparticles are synthesized by sol–gel citrate precursor technique. Structural and morphological characterizations performed by X-ray diffraction and FESEM images reveal the average size of the nanoparticles of ∼89 nm. The thermal variation ZFC magnetization reveals a disordered magnetic phase below ∼36 K. This phase is corroborated by magnetic memory as observed at 30 K. This disordered phase may arise because of the nanostructure of the system. Further lowering of temperature down to 1.6 K illustrates a significant upturn in the ZFC magnetization below 4.5 K. This sharp enhancement of ZFC magnetization indicates the signature of a dominant ferromagnetic (FM) component which may be attributed to the uncompensated (UC) spins at the surface of Nd_0.78Sr_0.22CoO₃ nanoparticles. Occurrence of the UC-spins typically may bring in a new anisotropy which is different from the core anisotropy. Coexistence of the different magnetic anisotropies leads to the exchange bias effect. The exchange bias effect (H_EB) sharply increases at low temperature as expected.

Conflicts of interest

There is no conflict of interest to declare.

Acknowledgements

The authors would like to thank DST, Government of India, for developing instrumental facilities like X-ray powder diffractometer (Bruker D8) and FE-SEM (FEI, INSPECT F50) and Cryogenics 7 T mini VSM facility under FIST programme at Jadavpur University. Ruma Ray would like to thank DHESTBT, Government of West Bengal (Project no. 426 (Sanc.)/ST/P/S&T/16G-16/2018) and JU-RUSA 2.0 Major Research Support (Project no. R-11/468/19) for providing the financial support.

References

1. F. S. Luborsky, Electro-Technology, 1962, 107.
2. M. Ohkoshi, K. Tamari, M. Harada, S. Honda and T. Kusuda, Microstructure and Exchange Anisotropy of Co-CoO Sputtered Films with Perpendicular Magnetization, IEEE Trans. J. Magn. Jpn., 1985, 1, 37–38.
3. W. H. Meiklejohn and C. P. Bean, New Magnetic Anisotropy, Phys. Rev., 1956, 102, 1413–1414.
4. R. L. Stamps, Mechanisms for Exchange Bias, J. Phys. D: Appl. Phys., 2000, 33, R247–R268.
5. M. Kiwi, Exchange Bias Theory, J. Magn. Magn. Mater., 2001, 234, 584–595.
6. J. Nogués, J. Sort, V. Langlais, V. Skumryev, S. Suriñach, J. S. Muñoz and M. D. Baró, Exchange Bias in Nanostsructures, Phys. Rep., 2005, 422, 65–117.
7. J. Nogués, J. Sort, V. Langlais, V. Skumryev, S. Suriñach, J. S. Muñoz and M. D. Baró, Exchange Bias in Ferromagnetic Nanoparticles Embedded in an Antiferromagnetic Matrix, Int. J. Nanotechnol., 2005, 2, 23–42.
8. J. Nogués and I. K. Schuller, Exchange Bias, J. Magn. Magn. Mater., 1999, 192, 203–232.
9. S. Giri, M. Patra and S. Majumdar, Exchange Bias Effect in Alloys and Compounds, J. Phys.: Condens. Matter, 2011, 23, 073201.
10. X.-x. Wang, S. Gao, Y. Xu, Q. Li, J. Zhang, Y.-z. Long, Ke-qing Ruan and X.-guang Li, Giant spontaneous exchange bias obtained by tuning magnetic compensation in Samarium ferrite single crystal, Phys. Chem. Chem. Phys., 2018, 20, 3687–3693.
11. A. Punnoose, H. Magnone, M. S. Seehra and J. Bonevich, Bulk to Nanoscale Magnetism and Exchange Bias in CuO Nanoparticles, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 174420.
12. T. N. Shendruk, R. D. Desautels, B. W. Southern and J. V. Lierop, The Effect of Surface Spin Disorder on the Magnetism of γ-Fe₂O₃ Nanoparticle Dispersions, Nanotechnol, 2007, 18, 455704.
13. S. Sarkar, A. Mondal, N. Giri and R. Ray, Spin Glass like Transition and the Exchange Bias Effect in Co3O4 Nanoparticles Anchored onto Graphene Sheets, Phys. Chem. Chem. Phys., 2019, 21, 260–267.
14. S. Das, N. Giri, S. Sarkar, A. Mondal, S. Majumdar, S. Giri and R. Ray, Uncompensated Grain Boundary Spin Driven Exchange Bias Effect in Granular NiO Film, Solid State Commun., 2019, 298, 113642.
15. T. Qian, G. Li, T. Zhang, T. F. Zhou, X. Q. Xiang, X. W. Kang and X. G. Li, Exchange Bias Tuned by Cooling Field in Phase Separated Y_0.2Ca _0.8Mn O₃, Appl. Phys. Lett., 2007, 90, 012503–012513.
16. K. De, R. Ray, R. N. Panda, S. Giri, H. Nakamura and T. Kohara, The Effect of Fe Substitution on Magnetic and Transport Properties of LaMnO₃, J. Magn. Magn. Mater., 2005, 288, 339–346.
17. X. J. Liu, Z. Q. Li, A. Yu, M. L. Liu, W. R. Li, B. L. Li, P. Wu, H. L. Bai and E. Y. Jiang, Magnetic, Electrical Transport and Electron Spin Resonance Studies of Fe-doped Manganite LaMn_0.7Fe_0.3O_3+δ, J. Magn. Magn. Mater., 2007, 313, 354–360.
18. M. Patra, M. Thakur, S. Majumdar and S. Giri, The Exchange Bias Effect in Phase Separated Nd_1−xSr_xCoO₃ at the Spontaneous Ferromagnetic/Ferrimagnetic Interface, J. Phys.: Condens. Matter, 2009, 21, 236004.
19. D. D. Stauffer and C. Leighton, Magnetic Phase Behavior of the Ferrimagnetic Doped Cobaltite Nd_1−xSr_xCoO₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 214414–214417.
20. N. A. Frey, S. Peng, K. Cheng and S. Sun, Magnetic Nanoparticles: Synthesis, Functionalization, and Applications in Bioimaging and Magnetic Energy Storage, Chem. Soc. Rev., 2009, 38, 2532–2542.
21. A. Ghoshray, B. Bandyopadhyay, K. Ghoshray, V. Morchshakov, K. Bärner, I. O. Troyanchuk, H. Nakamura, T. Kohara, G. Y. Liu and G. H. Rao, Phase separation in Nd_1-xSr_xCoO₃ using ⁵⁹Co NMR, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 064424.
22. R. A. Young, Introduction to the Rietveld method, in The Rietveld Method, ed. R. A. Young, Oxford University Press, New York, 1993, pp. 1–38.
23. P. Dutta, M. S. Seehra, S. Thota and J. Kumar, A comparative study of the magnetic properties of bulk and nanocrystalline Co₃O₄, J. Phys.: Condens. Matter, 2008, 20, 015218.
24. R. H. Kodama and A. E. Berkowitz, in Surface Effects in Magnetic Nanoparticles, ed. D. Fiorani, Springer US, Boston, MA, 2005, pp. 189–216.
25. M. Ulrich, J. Garcίa-Otero, J. Rivas and A. Bunde, Slow relaxation in ferromagnetic nanoparticles: Indication of spin-glass behavior, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 024416.
26. S. Biswas, Sk. Sabyasachi, A. Bhaumik and R. Ray, Magnetic Memory Effects in Fe/γ -Fe₂O₃ Nanostructures, IEEE Trans. Magn., 2014, 50(3), 2301107.

---