Individual cascade annealing in BCC tungsten: effects of size and spatial distributions of defects

Abstract

To investigate effects of size and spatial distributions of defects from primary damage to annealing of an individual cascade, molecular dynamics (MD) and object kinetic Monte Carlo (OKMC) are applied for simulating cascade generation and annealing. MD cascade simulations of tungsten are carried out with two typical embedded atom method potentials for cascade energies in the range from 0.1 to 100 keV at 300 K. The simulation results show that even though the number of survival defects varies slightly, these two potentials produce very different interstitial cluster (IC) size distribution and defect spatial distribution with cascade energies larger than 30 keV. Furthermore, OKMC is used to model individual cascade annealing. It demonstrates that larger-sized ICs and closely distributed SIAs in the cascade region will induce a much higher recombination fraction for individual cascade annealing. Therefore, special attention should be paid to the size and spatial distributions of defects for primary damage in the multi-scale simulation framework.

---

1. Introduction

The irradiation of metals under MeV neutrons produces a large population of vacancies and self-interstitial atoms (SIAs)¹ that can form clusters, such as dislocation loops^2,3 and voids. These clusters could further lead to hardening, swelling or embrittlement in materials.⁴ This is critical for materials designed for an environment where the bombardment of high-energy particles is frequent and unavoidable, such as tungsten (W) plasma-facing components under fusion relevant conditions. Understanding the defect production and its relation to material failure is critical for constructing a safe and long-operating reactor.

Many experiments were carried out on W microstructure changes induced by neutron irradiation.^4–6 The transmission electron microscope (TEM) was commonly used to observe interstitial dislocation loops, voids or tungsten–rhenium (Re) precipitates in neutron-irradiated W materials.^4–6 Complementary with experimental investigations, a multi-scale modeling approach has been proposed to study the radiation damage evolution of materials. For instance, primary damage can be simulated via the molecular dynamics (MD) method or binary-collision approximation. Coarse-grained methods, such as the kinetic Monte Carlo (KMC) or mean-field rate theory⁷ can be used to model the subsequent evolution of primary damage. Due to the characteristic time scale of ps and the space scale of nm, MD has been commonly used to investigate the collision cascades of metals like W.^8–12 Several discoveries were made including a transition energy that separates different regimes of energy associated with different defect survival mechanisms, as well as asymmetric defect clustering behavior, i.e., strong differences in SIA versus vacancy clustering.⁸ Nandipati et al. modeled individual cascade annealing process using the object kinetic Monte Carlo (OKMC) method^13,14 and investigated the effects of annealing temperature on annealing efficiency. In the scope of such multi-scaling, two challenging issues exist on the radiation damage effects of W induced by neutron irradiation. First, the reliability of MD simulation greatly depends on the accuracy of the interatomic potential.¹⁵ Due to the absence of reference cases or experimental observations, no “definitely reliable” potential has emerged yet even though many interatomic potentials are available for W until now.¹⁶ Therefore, how much the primary damage is affected by interatomic potentials should be considered. Second, it is also needed to consider the sensitivity of long-term evolution of damage to the specific features of the primary damage distribution from MD simulations. Björkas et al. reported that the accumulation rate of visible interstitial clusters (ICs) under TEM in iron predicted by OKMC depends significantly on the used cascade damage database.¹⁷ On the one hand, due to the small migration barrier of ICs and power-law decaying of the diffusion pre-factor with size¹⁸ for W, variation in the size distribution of ICs with MD potentials has a greater effect on SIA diffusion rate. On the other hand, within our best knowledge, up to now, there is very few annealing simulations for W focused on the effects of defect distribution. Therefore, it is worth studying the effects of defect distribution from primary damage to annealing process of individual cascades.

Based on the above two issues, MD and OKMC are applied for simulating cascade and annealing processes. First, MD simulations are carried out to study the influence of two W interatomic potentials on the defects production, especially focused on the size and spatial distributions of defect clusters. Next, OKMC method is applied to simulate the individual cascade annealing process based on the primary damage database obtained from these two interatomic potentials. We point out that it should be paid special attention to the size and spatial distributions of defects for primary radiation damage in the multi-scale simulation framework.

2. Methods

2.1. Details of MD simulations

Displacement cascades are simulated with the MD code package, LAMMPS,¹⁹ using two typical embedded atom method (EAM) potentials. The first is the Derlet–Nguyen-Manh–Dudarev W potential (DD07)²⁰ modified by Björkas et al. on the repulsive part with ZBL potential²¹ at short-range and the electron density function¹⁸ (denoted DB). The second is derived from the Ackland–Thetford W potential (AT87)²² and modified by Juslin and Wirth²³ to harden the potential at short distances for radiation damage simulations and improve the potential at distances of relevance to self-interstitial configurations (denoted AJ). Although machine learning potential has higher accuracy than EAM potentials, for example, it can describe configurations of divacancies, surfaces and grain boundaries of bcc tungsten very well. Compared to the tersoff, bond order or machine learning potentials, EAM potential is a better compromise between accuracy and speed. Detailed formalism and application of EAM potentials can be found elsewhere.²⁴ Therefore, EAM potentials, DB and AJ, are commonly used to simulate primary radiation damage.^8,9 Furthermore, these two potentials produce different relative stability between 1/2 〈111〉 and 〈100〉 interstitial dislocation loops. Therefore, we can consider the effect of stability on the formation mechanism of interstitial dislocation loops in our future research. Periodic boundary conditions are applied in three Cartesian directions. We have detected carefully to choose a big enough box size to avoid both the influence of boundaries on the cascade and saving computation time. The list of cascade energies, simulation cell sizes and the number of simulation runs is presented in Table 1.

Table 1 List of cascade energies (E_MD), simulation cells (cubes with side length L) and the number of simulations (N_r)

EMD (keV)	L (×a0)	Nr (300 K)
0.10	30	50
0.15	30	50
0.20	30	50
0.30	30	50
0.50	30	50
0.75	30	50
1.00	40	50
1.50	40	50
2.00	40	50
3.00	40	50
5.00	40	50
7.50	40	50
10.0	60	50
15.0	60	50
20.0	60	50
30.0	60	50
50.0	80	20
80.0	120	20
100.0	120	20

---

The entire simulation includes two stages. In stage A, the simulation system is relaxed at the desired ambient pressure and temperature for 10 ps with a MD time step of 1 fs. The system is relaxed within the NPT ensemble (constant number of atoms, pressure and temperature) and the Nosé–Hoover thermostat is applied to all atoms in the system. In stage B, the NVE ensemble (constant number of atoms, volume and total energy) is applied for 50 ps. The temperature damping parameter is chosen as a typical value of 1.0. At the beginning of this stage, a kinetic energy ranging from 0.1 to 100 keV is given to a primary knock-on atom (PKA)²⁵ near the center of the simulation box. The velocity direction of PKA is distributed uniformly and chosen randomly. During this stage, only the atoms within a shell of about 0.6 nm from the outer margin of the simulation box along three axes are thermostat. The time step varies from 1 × 10⁻⁶ to 2 × 10⁻³ ps depending on atomic velocities and forces magnitude. The Wigner–Seitz cells method is used for the identification of point defects. Two defects are considered to belong to the same cluster if their separation is less than a cutoff distance.²⁶ The most stable configuration for a di-interstitial is two parallel 〈111〉 dumbbells separated at the third nearest neighbor (3-nn).⁸ Di-vacancy is attractive for the first nearest neighbor (1-nn) and the second nearest neighbor (2-nn) and becomes repulsive or negligible at larger distances for these two potentials. Thus, the cutoff is selected as 2-nn for vacancy clusters (VCs) and 3-nn for ICs, respectively.

2.2. Details of OKMC simulations

The OKMC algorithm for radiation damage has been expressed in detail elsewhere.^7,27 Briefly, the OKMC method is based on the residence time algorithm²⁸ and follows the evolution of a set of objects given their rates to perform different actions. In our case, the objects are defects (vacancies and SIAs with different sizes) and the actions are defect migration or dissociation/association of a defect from/to defect clusters. The probabilities of migration or dissociation follow the Arrhenius law, i.e., R = R₀ exp(−E_a/k_bT), where E_a is either the migration energy of a defect or the dissociation energy of a defect from a cluster. The dissociation energy is the sum of the binding energy of the defect to the cluster and the migration energy of the defect. R₀ is the jump frequency. Considering all defects have the same probability of disassociating from a cluster, the jump frequency for dissociation is multiplied by the number of defects in the cluster.

Binding energies, migration parameters and capture radius for SIAs, ICs, vacancies and VCs are taken from the OKMC model built by Becquart et al.²⁹ The migration energy of SIAs is 0.013 eV.²⁰ The activation barrier for changing the direction of one-dimensional (1D) SIA motion from one 〈111〉 direction to another is 0.38 eV.²⁹ In the present model all ICs are assumed to be 〈111〉 loops, and the merging of two ICs immediately results in the formation of a larger 〈111〉 loop. Assume that all ICs are mobile with the migration energy of 0.013 eV along one of four 〈111〉 axes.²⁹ The migration rates of ICs vary with cluster size (n) according to ν₀n^−α (ν₀ = 6 × 10¹² s⁻¹, α = 0.5). Rotation between these two of 〈111〉 directions is not thermally activated at 300 K, and correspondingly, all ICs diffuse in 1D, which was assigned randomly to the SIAs and ICs at the initial of a simulation. For a vacancy, the activation barrier for diffusion is taken as 1.66 eV. Vacancy or VCs migrate in three-dimensional (3D), and their diffusion rates decrease with cluster size (n) according to ν₀q¹⁻ⁿ (ν₀ = 6 × 10¹² s⁻¹, q = 1000). The capture radius of SIA and vacancy are 3-nn and 2-nn, respectively. If the capture radius of two defects overlap, defects are allowed to coalesce or recombine depending on their types. The cascade debris obtained from MD in the form of point defects or defect clusters, was used to study the individual cascade annealing process with the open-source code MMonCa.²⁷ The OKMC simulation cell was 162 nm × 162 nm × 162 nm, which is sufficient to simulate the annealing process of individual cascade. Absorbing boundary conditions were adopted in all three directions, i.e., when a defect diffuses out of the box it is removed from the simulation. Twenty OKMC annealing simulations for each MD cascade were performed with different random seeds. All calculations were carried out at 300 K for up to 100 ns.

3. Results and discussion

3.1. Defect production as well as size and spatial distributions of defects

Fig. 1 shows defect production obtained from DB and AJ potentials. Note that the production of DB potential is in good accordance with those of AJ potential in a large range of cascade energies except for 100 keV. This result is unexpected since DB potential has a lower mean displacement threshold energy (85 eV) than that of AJ potential (128 eV) as listed in Table 2. However, this observation is consistent with the study of Fikar et al.¹² in which DD07 and AT87 potentials produce the similar production of survival Frenkel pairs even though these two potentials have different displacement threshold energies. The defect production by the MD simulations is significantly smaller than that predicted with the NRT model.³⁰ We also applied ARC-dpa model³¹ proposed by Nordlund et al. We can see that the ARC-dpa model describes the number of survival Frenkel pairs very well compared with our MD simulations at a wide range of cascade energies (E_MD > E_d).

Fig. 1 Comparison of number of survival Frenkel pairs obtained from DB and AJ potentials at 300 K. NRT-dpa (the dashed black line) is the result of NRT model,³⁰ i.e., N = 0.8E_MD/(2E_d), with E_d = 128 eV. ARC-dpa (the solid blue line) is the result of athermal recombination corrected dpa model,³¹ i.e., N = 0.8E_MD/(2E_d)[(1.0 − c)/(2E_d/0.8)^bE_MD^b + c], with E_d = 128 eV, b = −0.56 and c = 0.31.

Table 2 List of the lattice parameter of W at 300 K (a₀), the migration energy of SIA (Eⁱ_m), the migration energy of vacancy (E^v_m), the mean threshold displacement energy (E_d) and the melting temperature of W (T_m) for DB and AJ potentials

Potential	a0 (nm)	E^im (eV)	E^vm (eV)	Ed (eV)	Tm (K)
DB	0.3175	0.013 (ref. 20)	2.05 (ref. 12)	85 (ref. 11)	3775 ± 50 (ref. 11)
AJ	0.3167	0.027 (ref. 32)	1.45 (ref. 12)	128 (ref. 23)	4100 ± 50 (ref. 23)

---

Fig. 2(a) shows the fraction of clustered SIAs after the primary damage stage for DB and AJ potentials. Note that the fractions of ICs for DB potential are much higher than those for AJ potential when the cascade energies larger than 1 keV. Three ICs formation mechanisms exist: (a) the mechanism of the excess atoms from the high-density region of one shock front deposited into the low-density region associated with the other shock wave,³³ (b) the mechanism of shock wave punching,³⁴ and (c) the thermal diffusion as well as association mechanism related to the migration energy of SIAs (Eⁱ_m). Subcascades are not found with concerned cascade energies during cascade development, hence the mechanism of shock wave punching induces the formation of larger ICs. ICs typically form at thermal spike phase, which occurs within the first 0.5 ps of the cascade development. During this phase, the cascade energy is transferred from atom to atom via replacement collision sequences, which is much faster than that phonon-mediated dissipation allows, hence supersonic shock waves form. Displaced atoms are pushed outwards to the periphery region of cascade, then ICs such as dislocation loops are formed through interstitials agglomeration around a seed of small ICs. This process is very sensitive to the interconnected part of the potentials.^15,35 Furthermore, subsequent capture reactions of SIAs via thermal diffusion increase the size of these large clusters, as indicated by the trend of clustering data as a function of temperature^8,9 and SIA migration energy (Eⁱ_m) as listed in Table 2. The process of shock wave punching, which is applied at all temperatures, differs from the thermal diffusion clustering process. Our position analysis for SIAs and vacancies shown in Fig. 4 exhibits that SIAs are much far away from vacancies for AJ potential compared to the results of DB potential. However, as listed in Table 2, DB potential produces a lower migration energy of SIAs, which results in diffusing further away from the cascade core. Therefore, the mechanism of shock wave punching is dominant for ICs formation relative to the thermal diffusion and association mechanism of SIAs.

Fig. 2 Cascade energy dependence of the fraction of clustered defects (a) ICs and (b) VCs with DB and AJ potentials at 300 K.

Following interstitial clustering behaviors, Fig. 2(b) shows the fraction of clustered vacancies as a function of cascade energy. These two potentials produce close values when the cascade energies are less than 3 keV. While AJ potential produces larger values than DB potential when the cascade energies higher than 3 keV. As listed in Table 2, the vacancy migration energies (E^v_m) for these two potentials are so large that vacancies will be considered immobile in 100 ps time-scale even at 1000 K. Therefore, it is impossible to form CVs by vacancy migration at the displacement cascade stage. Corresponding to the ICs formation mechanism of shock wave punching, when large ICs form, it induces a depletion of atoms in other regions, which potentially facilitates the formation of VCs. This scenario is reflected within the maximum size of defects clusters as a function of cascade energy as shown in Fig. 3, i.e., large VCs are obtained in simulations where large ICs form. Hence the formation of a large VC eventually depends on the interplay between the atomic recrystallization near the core and the motion of displaced atoms. In other words, the controlling factor seems to be the recrystallization and recombination rates of interstitials with vacancies. On one hand, DB potential produces a lower melting temperature, so the cascade melting persists for longer, resulting in adequate recrystallization. On the other hand, DB potential produces a much lower interstitial migration energy (0.013 eV) which increases the chance for those displaced atoms to refill the cascade core before the atoms surrounding the core recrystallize. This analysis is consistent with the observation that large VCs are rarely observed in W cascades at 2050 K.⁸

Fig. 3 The maximum size of (a) ICs and (b) VCs for DB and AJ potentials at 300 K.

Fig. 3 presents the maximum size of defect clusters formed at the primary damage stage as a function of cascade energy. The maximum size of defect clusters increases obviously with increasing cascade energy. It shows a power-law function with cascade energy, i.e., 0.0447 × E_MD^1.6931 for DB potential and 0.0684 × E_MD^1.3778 for AJ potential. Obviously, DB potential produces a larger maximum size of ICs than that of AJ potential when the cascade energies are larger than 20 keV. The maximum size of ICs for DB potential reaches the size of 110 with the cascade energy of 100 keV, whereas AJ potential only reaches the size of 40. The maximum size of VCs varies slightly between these two potentials, as shown in Fig. 3(b), which is much different from that of ICs.

Fig. 4 shows superposition of all cascade configurations for DB (Fig. 4(a)) and AJ potentials (Fig. 4(b)) and radial distributions of defects (Fig. 4(c)) with the center of vacancies. We can see that AJ potential produces more discrete distributions both in size and space of SIAs. In addition, the radial distribution of vacancies is nearly the same for these two potentials, as shown in Fig. 4(c). However, further analysis reveals that the average distance between SIAs and the center of vacancies are 5.128 and 4.304 nm for AJ and DB potentials, respectively. In other words, SIAs are much far away from vacancies for AJ potential compared to that for DB potential.

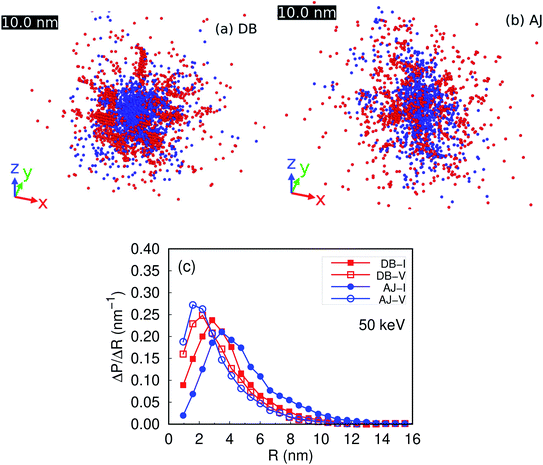Fig. 4 Superposition of 20 cascade configurations with cascade energy of 50 keV at 300 K for (a) DB potential and (b) AJ potential. (c) The comparison of radial distribution of defects. All cascade configurations are put together by superposing the center of vacancies of each cascade configuration. OVITO³⁶ is used to visualize all atomic configurations. Here blue spheres and red spheres represent vacancies and SIAs, respectively. The black scale bars are also shown in (a) and (b).

3.2. Annealing process of individual cascades

From the above analyses of defect production, as well as the size and spatial distributions of defects for these two potentials concerned, we could reveal that a close value of defect production is given in a wide range of cascade energy by these two potentials, while DB potential produces larger ICs and defects distributed closely in space compared to AJ potential when the cascade energies larger than 30 keV. The size and spatial distributions of defect clusters certainly have an impact on the long-term evolution of cascade damage. We will demonstrate the details in the following.

Fig. 5 shows the survival defect fraction of SIAs and vacancies as a function of annealing time with the cascade energy of 50 keV at 300 K for DB and AJ potentials. The initial decrease in the number of survival defects occurs within about 10 ns due to only I–V recombination (recombination phase) characterized by the survival fraction of SIAs being equal to that of vacancies. Beyond the recombination phase, the survival fraction of vacancies remains nearly constant, while SIAs drops continually. SIAs migrate very fast, whereas vacancies are immobile at 300 K. Consequently with SIAs diffusing beyond the simulation box boundary, the total number of SIAs becomes lower than that of vacancies. Comparing survival defects fraction of these two potentials, two characteristics are found. First, the survival fraction of vacancies for AJ potential with the value of 0.878 differs obviously from that of 0.752 for DB potential. Second, the rate at which SIAs escape from the simulation box also differs obviously. Compared to AJ potential, DB potential produces larger-sized ICs which are also distributed closely to the center of collapsed vacancy region, as discussed in the previous section. This facilitates the sufficient recombination of interstitials and vacancies, and suppresses the escape of SIAs from the simulation box.

Fig. 5 Survival fraction of defects as a function of annealing time with cascade energy of 50 keV at 300 K for DB and AJ potentials. The survival fraction of defects (SIAs or vacancies) is the ratio of the number of survival defects (N) and the average number of initial defects (N₀).

Fig. 6 shows the fraction of defects lost to intra-cascade recombination (recombination fraction) as a function of cascade energy at 300 K for DB and AJ potentials. It is obviously noted that the recombination fraction of DB potential is only slightly elevated compared to that of AJ potential for the cascade energies less than 30 keV, whereas the value of DB potential is much higher than that of AJ potential for the cascade energies larger than 30 keV. We also note that the recombination fraction of AJ potential is maintained in the range of 5–20%, in other words 80–95% of SIAs will eventually escape from intra-cascade recombination and contribute to long-range defect migration. However, the recombination fraction of DB potential increases continuously with increasing cascade energy, and reaches 40% at 100 keV. The annealing behavior of individual cascade is determined by the outcome of two key properties, including (1) the size and spatial distributions of defects and (2) the relative mobilities of those defects. Due to the very high SIA mobility and the very low vacancy mobility in W, the recombination fraction is strongly affected by the size and spatial distributions of defects in cascades. On the one hand, according to our position analysis of SIAs and vacancies, SIAs are much far away from vacancies for AJ potential compared to that of DB potential. On the other hand, larger-sized ICs are produced by DB potential, which results in decreasing diffusion of SIAs away from the cascade core. This facilitates the efficient recombination of SIAs and vacancies in the intra-cascade region. The same mechanism occurs for SIA recombination with vacancy by Re addition in W.³⁷ A mixed dumbbell is formed when a SIA meets a substituted Re atom. The mixed dumbbell diffuses slowly via 3D jumps compared to 1D fast migration of SIAs. Therefore, voids growth is suppressed by the improved recombination fraction.

Fig. 6 The recombination fraction of SIAs and vacancies as a function of cascade energy at 300 K for DB and AJ potentials.

SIAs move far enough away from the cascade region such that they can be considered spatially uncorrelated with the original cascade. The probability for these defects returning and contributing to intra-cascade recombination is negligible, thus they are counted as freely migrating defects. The fraction of freely migrating defects is a key parameter in the modeling of microstructure evolution based on the mean-field rate theory. Depending on this parameter, many major microstructural changes occur,³⁸ such as the development of voids, dislocation networks and radiation-induced precipitation. Therefore, the size and spatial distributions of defects for primary radiation damage significantly influence the long-term evolution of defects and macroscopic changes of materials.

4. Conclusion

MD cascade simulations of single crystal tungsten are carried out for two typical EAM potentials with the cascade energies ranging from 0.1 to 100 keV at 300 K. The simulation results show that even though the defect production is very close for all the cascade energies studied, these two potentials concerned produce very different results of the size and spatial distributions of ICs for the cascade energies larger than 30 keV. Furthermore, based on the defects produced by these two potentials, OKMC is used to model individual cascade annealing. It indicates that larger-sized ICs and closely distributed SIAs in the cascade region will induce a much higher recombination fraction. Therefore, it should pay special attention to the size and spatial distributions of defects for primary damage in the multi-scale simulation framework.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant No. 11975018, the National MCF Energy R&D Program (Grant No. 2018YEF0308100), the outstanding member of Youth Innovation Promotion Association CAS (Grant No. Y202087), the GHfund A (20220201, Grant No. 2711) and Director Grants of CASHIPS. Some of the calculations were performed at the Center for Computational Science of CASHIPS, the ScGrid of Supercomputing Center, and the Computer Network Information Center of the Chinese Academy of Sciences. This research work was also supported by the Tianhe-2JK computing time award of the Beijing Computational Science Research Center (CSRC).

References

1. R. E. Stoller, G. R. Odette and B. D. Wirth, Primary damage formation in bcc iron, J. Nucl. Mater., 1997, 251, 49.
2. X. Yi, M. L. Jenkins and M. Briceno, et al., In situ study of self-ion irradiation damage in W and W-5Re at 500 °C, Philos. Mag., 2013, 93, 1715.
3. A. E. Sand, S. L. Dudarev and K. Nordlund, High energy collision cascades in tungsten: dislocation loops structure and clustering scaling laws, Europhys. Lett., 2013, 103, 46003.
4. M. Fukuda, N. K. Kumar and T. Koyanagi, et al., Neutron energy spectrum influence on irradiation hardening and microstructural development of tungsten, J. Nucl. Mater., 2016, 479, 249.
5. X. Hu, T. Koyanagi and M. Fukuda, et al., Irradiation hardening of pure tungsten exposed to neutron irradiation, J. Nucl. Mater., 2016, 480, 235.
6. M. Klimenkov, U. Jäntsch and M. Rieth, et. al., Effect of neutron irradiation on the microstructure of tungsten, Nucl. Mater. Energy, 2016, 1.
7. C. S. Becquart, A. Barbu and J. L. Bocquet, et al., Modeling the long-term evolution of the primary damage in ferritic alloys using coarse-grained methods, J. Nucl. Mater., 2010, 406, 39.
8. W. Setyawan, G. Nandipati and K. J. Roche, et al., Displacement cascades and defects annealing in tungsten, Part I: Defect database from molecular dynamics simulations, J. Nucl. Mater., 2015, 462, 329.
9. C. G. Zhang, W. H. Zhou and Y. G. Li, et al., Primary radiation damage near grain boundary in bcc tungsten by molecular dynamics simulations, J. Nucl. Mater., 2015, 458, 138.
10. A. E. Sand, K. Nordlund and S. L. Dudarev, Radiation damage production in massive cascades initiated by fusion neutrons in tungsten, J. Nucl. Mater., 2014, 455, 207.
11. C. Björkas, K. Nordlund and S. Dudarev, Modelling radiation effects using the ab initio based tungsten and vanadium potentials, Nucl. Instrum. Methods Phys. Res., Sect. B, 2009, 267, 3204.
12. J. Fikar and R. Shäublin, Molecular dynamics simulation of radiation damage in bcc tungsten, J. Nucl. Mater., 2009, 38, 97.
13. G. Nandipati, W. Setyawan and H. L. Heinisch, et al., Displacement cascades and defect annealing in tungsten, Part II: Object kinetic monte carlo simulation of tungsten cascade aging, J. Nucl. Mater., 2015, 462, 338.
14. G. Nandipati, W. Setyawan and H. L. Heinisch, et al., Displacement cascades and defect annealing in tungsten, Part III: The sensitivity of cascade annealing in tungsten to the values of kinetic parameters, J. Nucl. Mater., 2015, 462, 345.
15. A. E. Sand, J. Dequeker and C. S. Becquart, et al., Non-equilibrium properties of interatomic potentials in cascade simulations in tungsten, J. Nucl. Mater., 2016, 470, 119.
16. G. Bonny, D. Terentyev and A. Bakaev, et al., Many-body central force potentials for tungsten, Modell. Simul. Mater. Sci. Eng., 2014, 22, 053001.
17. C. Björkas, K. Nordlund and M. J. Caturla, Influence of the picosecond defect distribution on damage accumulation in irradiated α-Fe, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 024105.
18. C. Björkas, K. Nordlund and S. Dudarev, Erratum to: “Modelling radiation effects using the ab initio based tungsten and vanadium potentials”, Nucl. Instrum. Methods Phys. Res., Sect. B, 2010, 268, 1529.
19. S. Plimpton, Fast parallel algorithms for short-range molecular-dynamics, J. Comput. Phys., 1995, 117, 1.
20. P. M. Derlet, D. Nguyen-Manh and S. L. Dudarev, Multiscale modeling of crowdion and vacancy defects in body-centered-cubic transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 054107.
21. J. F. Ziegler, J. P. Biersack and U. Littmark, The Stopping and Range of Ions in Matter, Pergamon, New York, 1985.
22. G. J. Ackland and R. Thetford, An improved N-body semi-empirical model for body-centred cubic transition metals, Philos. Mag. A, 1987, 56, 15.
23. N. Juslin and B. D. Wirth, Interatomic potentials for simulation of he bubble formation in W, J. Nucl. Mater., 2013, 432, 61.
24. A. Verma, S. M. Rangappa, S. Ogata and S. Siengchin, Forcefields for Atomistic-Scale Simulations: Materials and Applications, Springer Singapore, 2022.
25. V. Singla, A. Verma and A. Parashar, A molecular dynamics based study to estimate the point defects formation energies in graphene containing stw defects, Mater. Sci. Eng., 2018, 6, 015606.
26. S. D. Stoddard, Identifying clusters in computer experiments on systems of particles, J. Comput. Phys., 1978, 27, 291.
27. I. Martin-Bragado, A. Rivera and G. Valles, et al., MMonCa: an Object Kinetic Monte Carlo simulator for damage irradiation evolution and defect diffusion, Comput. Phys. Commun., 2013, 184, 2703.
28. M. H. Kalos and P. A. Whitlock, Monte Carlo Methods, John Wiley & Sons, 1986, vol. I, Basics.
29. C. S. Becquart, C. Domain, U. Sarkar, A. Debacker and M. Hou, Microstructural evolution of irradiated tungsten: ab initio parameterisation of an OKMC model, J. Nucl. Mater., 2010, 403, 75.
30. M. J. Norgett, M. T. Robinson and I. M. Torrens, Proposed method of calculating displacement dose rates, Nucl. Eng. Des., 1975, 33, 50.
31. K. Nordlund, S. J. Zinkle and A. E. Sand, et al., Improving atomic displacement and replacement calculations with physically realistic damage models, Nat. Commun., 2018, 9, 1084.
32. W. H. Zhou, Y. G. Li, L. F. Huang, Z. Zeng and X. Ju, Dymical behaviors of self-interstitial atoms in tungsten, J. Nucl. Mater., 2013, 437, 438.
33. A. F. Calder, D. J. Bacon, A. V. Barashev and Y. N. Osetsky, On the origin of large interstitial clusters in displacement cascades, Philos. Mag., 2010, 90, 863.
34. Q. Peng, F. J. Meng and Y. Z. Yang, et al., Shockwave generates <100> dislocation loops in bcc iron, Nat. Commun., 2018, 9, 4880.
35. R. E. Stoller, A. Tamm and L. K. Bėland, et al., Impact of short-range forces on defect production from high energy collisions, J. Chem. Theory Comput., 2016, 12, 2871.
36. A. Stukowski, Visualization and analysis of atomistic simulation data with ovito-the open visualization tool, Mater. Sci. Eng., 2010, 18, 015012.
37. T. Suzudo, M. Yamaguchi and A. Hasegawa, Migration of rhenium and osmium interstitials in tungsten, J. Nucl. Mater., 2015, 467, 418.
38. S. I. Golubov, A. V. Barashev and R. E. Stoller, Comprehensive Nuclear Materials, Chapter 1.13 Radation Damage Theory, Elsevier, 2012.

---