Open Access Article
Open Access ArticleStructures, and electronic and spectral properties of single-atom transition metal-doped boron clusters MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni)†
Shi-Xiong Li *a,
Yue-Ju Yanga,
De-Liang Chena and
Zheng-Wen Longb
*a,
Yue-Ju Yanga,
De-Liang Chena and
Zheng-Wen Longb
aSchool of Physics and Electronic Science, Guizhou Education University, Guiyang 550018, Guizhou, People's Republic of China. E-mail: leesxoptics@163.com
bCollege of Physics, Guizhou University, Guiyang 550025, Guizhou, People's Republic of China
First published on 6th June 2022
Abstract
A theoretical study of geometrical structures, electronic properties, and spectral properties of single-atom transition metal-doped boron clusters MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) is performed using the CALYPSO approach for the global minimum search, followed by density functional theory calculations. The global minima obtained for the MB24− (M = Sc, Ti, V, and Cr) clusters correspond to cage structures, and the MB24− (M = Mn, Fe, and Co) clusters have similar distorted four-ring tubes with six boron atoms each. Interestingly, the global minima obtained for the NiB24− cluster tend to a quasi-planar structure. Charge population analyses and valence electron density analyses reveal that almost one electron on the transition-metal atoms transfers to the boron atoms. The electron localization function (ELF) of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) indicates that the local delocalization of MB24− (M = Sc, Ti, V, Cr, and Ni) is weaker than that of MB24− (M = Mn, Fe, and Co), and there is no obvious covalent bond between doped metal and B atoms. The spin density and spin population analyses reveal that open-shell MB24− (M = Ti, Cr, Fe, and Ni) has different spin characteristics which are expected to lead to interesting magnetic properties and potential applications in molecular devices. The polarizability of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) shows that MB24− (M = Mn, Fe, and Co) has larger first hyperpolarizability, indicating that MB24− (M = Mn, Fe, and Co) has a strong nonlinear optical response. Hence, MB24− (M = Mn, Fe, and Co) might be considered as a promising nonlinear optical boron-based nanomaterial. The calculated spectra indicate that MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) has different and meaningful characteristic peaks that can be compared with future experimental values and provide a theoretical basis for the identification and confirmation of these single-atom transition metal-doped boron clusters. Our work enriches the database of geometrical structures of doped boron clusters and can provide an insight into new doped boron clusters.
1. Introduction
Clusters are relatively stable microscopic or submicroscopic aggregates composed of several to thousands of atoms, molecules or ions, which have completely different structures and physical properties from bulk, and are also transition states from atoms to solid matter. Clusters are ideal models for correlating macroscopic properties and microscopic structures of substances, and cluster research is of great significance to deeply understand the laws of matter transformation. The physical properties of clusters are dependent on their size and shape, which can be changed to give them different physical properties owing to the quantum effect of electrons. Study of the structure and physical properties of clusters can provide guidance for the design and manufacture of new materials and new devices at the atomic level. The unique properties of clusters and doped clusters make their research a vibrant field of cluster science. For example, the emergence of fullerene C60 is a new breakthrough in nanomaterials and nanotechnology,1 and the discovery of carbon nanotubes and graphene2,3 promoted carbon nanomaterials to become a vibrant scientific field. The boron atom, with only three valence electrons (one less than carbon), can form polycentric chemical bonds and produce several interesting structures and properties.4–9 Experimental studies have found that anionic pure boron clusters, Bn−, with less than 38 atoms have a planar or quasi-planar structure.10,11 Theoretical studies have found that neutral pure boron clusters of different sizes of Bn have planar, tubular, cage-like, or other three-dimensional structures.4,8,12–14 Until 2014, scientists had been exploring whether boron could also form caged fullerene structures, but had been unable to experimentally determine the existence of caged boron clusters. In 2014, the cage-type all-boron cluster borospherene B40− was experimentally found.15 Borospherene B40− exhibits a hollow cage-like structure, but has different electronic structures and properties from C fullerenes. B40− is the second inorganic non-metallic cage-like cluster that has been fully confirmed experimentally and theoretically after C60 and produced a lot of research on boron clusters.16–24 In 2015, graphene's brother borophene was synthesized on the Ag(111) base,25 and the basic unit of borophene happened to be a deformed B7 cluster. In 2021, uniform and large-scale (millimeter-scale) bilayer borophene was synthesized on the surface of Cu(111).26 Compared with borophene, bilayer borophene is more difficult to oxidize. Almost in the same period, a borophene crystal form comparable to graphene was experimentally synthesized,27 and atomic hydrogen was used to hydrogenate borophene to synthesize borophene that can be stable in the external environment for a week. The discovery of borospherene and borophene provides important clues for the development of new boron materials. In view of the difference in electronic structure with fullerenes and carbon nanomaterials, boron clusters and low-dimensional boron nanostructures can offer new ideas and technologies for new nanomaterials and nano devices.Similar to fullerenes, doped (especially for mono-atom) boron clusters can produce new structures or properties.18,20–22,28–41 For example, B20−, B22−, and B24 have a quasi-planar, quasi-planar, and double-ring tubular structure,10,42 respectively. However, after adding alkali metal atoms, both LiB20− and MB22− (M = Na, K) possess a double-ring tubular structure and Li2B24 possesses a three-ring tubular structure.29,43,44 In addition, Li-, Na-, or K-doped B40 is expected to become a nonlinear optical nanomaterial.21 Because of their rich electronic structure characteristics, transition metal atom can combine with boron clusters to produce rich structures and properties. For example, the quasi-planar B12 cluster has a semi-sandwich structure after being doped with a metal atom such as Co and Rh.6,28 Neutral B24 has a double-ring tubular structure, while TiB24 and CrB24 have a cage structure after doping with one Ti or Cr atom.45 The single-atom Sc- or Ti-doped B40 is expected to become a hydrogen storage material,18,20,22 doped boron clusters MB12− (M = Co, and Rh) can enhance chemical activity,31 and the Co-doped B40 is expected to be applied in molecular devices.30 Experimental and theoretical studies have found that transition metal atom doped boron clusters ReBn− (n = 3–4, 6, 8–9), MnBn− (n = 6, 16), BiBn− (n = 6–8), CoB16−, La2Bn− (n = 10–11) and La3B18− have various unique structures.33–41 Metal encapsulation is known as an effective approach to modify the chemical bonding and occupancy of energy levels of clusters. Metal (or metal cluster) encapsulation has also been suggested as a possible synthesis pathway for stabilizing the unstable boron fullerene analogue. Therefore, the study of transition metal-doped boron clusters provides important theoretical guidance for the study of new structures and new properties of boron clusters and the preparation of new boron nanomaterials. Herein, to obtain the structures and properties of transition metal-doped boron clusters MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni), extensive research has been conducted on the geometric structure, spectral properties, and electronic structure using the CALYPSO approach,46 in combination with the density functional theory method PBE0.47 The calculation results will be useful for future experimental data of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni).
2. Computational methods
Geometric structure searches of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) clusters were implemented using particle swarm optimization (CALYPSO) software. CALYPSO is a powerful cluster structure search method, which has been successfully applied to boron and doped boron clusters.14,29 The PBE0/3-21G level was used for the preliminary structural search. In each generation, 70% of the structures were produced by particle swarm optimization (PSO) operations, while the others were randomly generated. There were nearly 2000 isomers initially obtained for each doped boron cluster. In addition, some plane structural constructions were also produced by the artificial bee colony algorithm (ABCluster) software48 at the PBE0/3-21G level.Low-energy structures were then fully optimized at the PBE0/6-311+G* and TPSSH/6-311+G* levels.47,49,50 Moreover, density functional theory with dispersion correction (DFT-D3) was tested in the energy calculation.51 At present, there are many methods of dispersion correction, such as dispersion-corrected atom-centered potentials (DCACPs), functional with van der Waals corrections (vdW-DF), dispersion correction as an add-on to standard Kohn–Sham density functional theory (DFT-D3) etc.51 The DFT-D3 method is more advantageous,52 and can be performed in Gaussian 16 software. We used the PBE0/6-311+G(d) and PBE0-D3/6-311+G(d) methods to calculate the low-energy structures of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni), and the results show that the relative energy trend of isomers (low-energy structures) in each cluster is found to be almost the same by using two methods. Moreover, PBE0/6-311+G(d) and PBE0-D3/6-311+G(d) methods were tested in the calculation of infrared spectra, Raman spectra, and polarizability of lowest energy structure for NiB24−, and the results also show that the infrared spectra, Raman spectra, and polarizability are found to be almost the same by using two methods. Therefore, density functional theory with dispersion correction (PBE0-D3) does not have a significant effect on the results, however, it further verifies the reliability of the PBE0 method. In addition, the PBE0/6-311+G* level is reliable method for boron cluster,15,53–57 specifically, theoretical calculation results with the PBE0/6-311+G* level agrees with the experimental results.15 Therefore, after the geometry optimizations, frequency analyses, electronic structures and spectroscopic properties were studied at the PBE0/6-311+G* level. All computations were performed using Gaussian 16 software.58 The dipole moment, spin density, atomic charge, and electronic structures can be obtained directly from the calculation results of geometry optimizations. The harmonic frequency can be obtained from the calculation results of frequency analyses (add keyword Freq in Gaussian 16). All analyses and various types of isosurface map drawings were realized using the Multiwfn 3.7(dev) code.59 The energy of a system in the weak and uniform external electric field F can be revealed as21,60
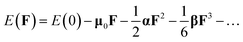 | (1) |
| α = (αxx + αyy + αzz)/3 | (2) |
Anisotropy of polarizability can be defined as61
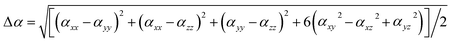 | (3) |
Magnitude of first hyperpolarizability β0 can be defined as21
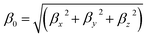 | (4) |
 . These components can be calculated using Gaussian 16 software and analyzed using Multiwfn 3.7(dev) code.
. These components can be calculated using Gaussian 16 software and analyzed using Multiwfn 3.7(dev) code.
3. Results and discussion
3.1 Structures and electronic properties
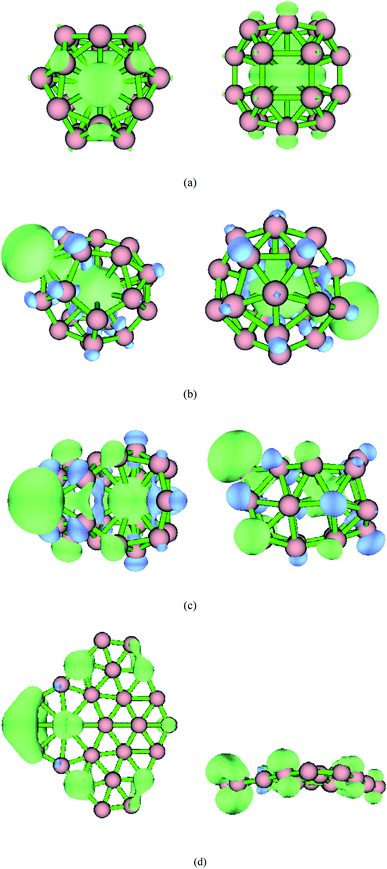
The five low-energy structures of transition metal-doped boron clusters MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) are shown in Fig. S1–S8 (ESI†). As shown in Fig. S1–S8,† the relative energy trend of five low-energy structures in each cluster is found to be almost the same by using PBE0/6-311+G*, TPSSH/6-311+G*, and PBE0-D3/6-311+G* levels. The calculation results show that the low-energy structures of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, and Co) tend to form cage structure or tubular structure, and NiB24− tend to form quasi-planar structure. Early research found that B24 has a double-ring tubular structure, and B24− has a planar structure. It can be seen from Fig. 1 and the calculated results that after adding metal atoms, the lowest energy structures MB24− (M = Sc, Ti, V, and Cr) have endohedral borospherene structures. The lowest energy structure TiB24− has high symmetry (D3h), and the Ti atom is located at the center of the cage. The calculated results and Fig. 1 show that the lowest energy structures of VB24− and CrB24− have similar cage structures comprising 12 five-membered rings and there are four five-membered rings with a boron atom embedded in the center of five-membered rings. Among them, VB24− has higher symmetry (C2v) than CrB24− (C2), and the V atom is almost located at the center of the cage.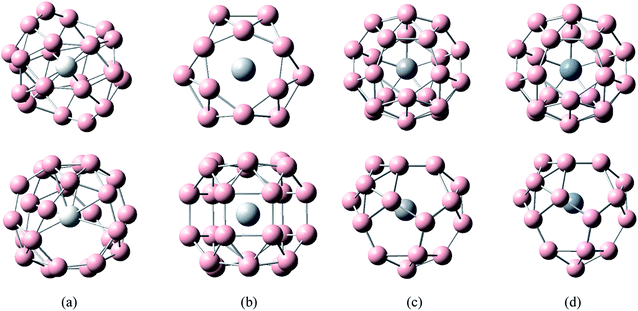 | ||
| Fig. 1 Structures of doped boron clusters MB24− (M = Sc, Ti, V, and Cr). The upper row is top view and the bottom row is side view. (a) ScB24− C2; (b) TiB24− D3h; (c) VB24− C2v; (d) CrB24− Cs. | ||
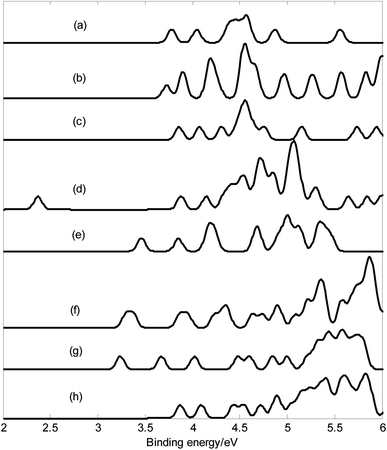
The calculated results and Fig. 2 show that the lowest energy structures of MB24− (M = Mn, Fe, and Co) have similar distorted four-ring tube with six boron atoms each. This structure can also be viewed as a distorted cage. In particular, the ring where the metal atom is located is not closed, further leading to an open seven-membered ring on the wall. MB24− (M = Mn, Fe, and Co) have low symmetry (Cs), and the doped atom is located at the center of a six-membered ring. Similar to tubular B clusters, these doped boron clusters are expected to become the basic unit of boron nanotube materials, which will be further synthesized into boron nanotubes. It can be seen from Fig. 2 that the lowest energy structure of NiB24− has quasi-planar structure similar to a warplane shape. The metal atom is located right at the nose, surrounded by an eight-membered boron ring. Similar to deformed B7 cluster, the quasi-planar NiB24− is expected to become the basic unit of doped borophene, which will be further synthesized into borophene. In the following discussion, the main focus is on the study of the lowest energy structure.
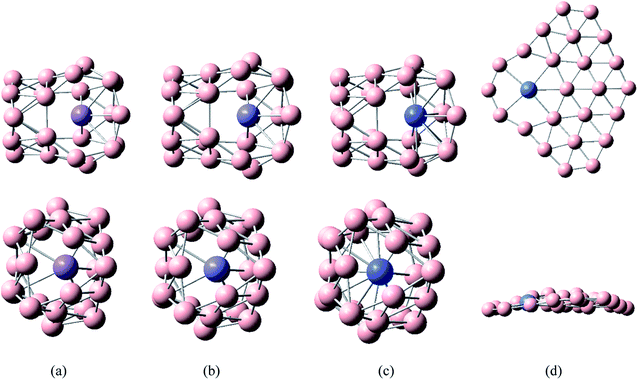 | ||
| Fig. 2 Structures of doped boron clusters MB24− (M = Mn, Fe, Co, and Ni). The upper row is top view and the bottom row is side view. (a) MnB24− Cs; (b) FeB24− Cs; (c) CoB24− Cs; (d) NiB24− Cs. | ||
Some of the ground-state parameters of transition metal-doped boron clusters MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) are listed in Table 1, including the lowest harmonic frequency, dipole moment, atomic charge on doped transition-metal atoms, and Mayer bond level.62 The lowest harmonic frequency analysis (see Table 1 for the lowest harmonic frequencies of each cluster) confirmed that these lowest energy structures are indeed stable (no imaginary frequency). The charge population analysis shows that all the metal atoms show positive charges, indicating that electrons have been transferred to the boron atoms and the metal atoms have transferred almost one electron. Because there is more than one outer valence electron of doped atom, only a small part of the electrons has been transferred. Analysis shows that the Mayer bond level of the metal atom M and B atom of these clusters is between 0.05 and 0.55 and it is less than 1, indicating that no obvious covalent bond is formed between the metal atom and the B atom. Because TiB24− has high symmetry, D3h, the dipole moment is 0. Among these nanoclusters MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni), it is found that the closed-shell MB24− (M = Sc, V, Mn, and Co) clusters have large HOMO–LUMO gap of 3.49, 4.02, 2.22, and 3.14 eV, respectively. For the open-shell MB24− (M = Ti, Cr, Fe, and Ni) clusters, alpha HOMO–LUMO gaps are 3.84, 2.63, 3.17 and 1.91 eV, respectively, and beta HOMO–LUMO gaps are 1.97, 3.87, 2.45, and 2.03 eV, respectively. To show more clearly the influence of the transition metal-doping toward the electronic structure, total density of states (TDOS) of each cluster and partial density of states (PDOS) of the transition metal atom were analyzed using the Multiwfn 3.7(dev) code, as shown in Fig. S9 (ESI†). For the closed-shell MB24− (M = Sc, Mn, and Co), metal atoms contribute a part to HOMO and LUMO. However, for the closed-shell VB24−, V atom contributes nothing to HOMO and LUMO. For the open-shell TiB24−, alpha HOMO is entirely contributed by the orbitals of Ti atom, while Ti atom does not contribute to alpha LUMO, moreover, beta LUMO is mainly contributed by the orbitals of Ti atom, and Ti atom contributes a part to beta HOMO. For open-shell CrB24−, Cr atom contributes a part to alpha HOMO, alpha LUMO and beta LUMO, but Cr atom does not contribute to beta HOMO. For open-shell MB24− (M = Fe, and Ni), metal atoms contribute a part to alpha HOMO, alpha LUMO, beta HOMO, and beta LUMO. It can be seen from the Fig. S9(b, c, e, f, h, i, k and l)† that for open-shell MB24− (M = Ti, Cr, Fe, and Ni) clusters, the spin polarization of the electronic states of these systems is obvious.
| Lowest frequencies/cm−1 | Symmetry | Charges on doped atom | Dipole moments/debye | Mayer bond order between doped atom M and B atom | |
|---|---|---|---|---|---|
| ScB24− | 181 | C2 | 0.56 | 1.43 | 0.16–0.19 |
| TiB24− | 160 | D3h | 0.69 | 0.00 | 0.16–0.20 |
| VB24− | 297 | C2v | 0.70 | 2.22 | 0.21–0.26 |
| CrB24− | 234 | Cs | 0.81 | 2.45 | 0.16–0.26 |
| MnB24− | 212 | Cs | 0.85 | 1.07 | 0.06–0.55 |
| FeB24− | 212 | Cs | 0.89 | 2.65 | 0.05–0.47 |
| CoB24− | 198 | Cs | 0.90 | 3.21 | 0.10–0.38 |
| NiB24− | 40 | Cs | 0.92 | 0.14 | 0.28–0.39 |
Fig. S10–S12† show the electron localization function (ELF)63 of the valence electrons of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni). ELF can well describe the delocalization (or localization) of electrons and chemical bonds. Under the same isosurface value, a wider connected area occupied by an isosurface map means that electron delocalization is easier, and a narrower connected area occupied by an isosurface map means that electron delocalization is relatively difficult. When the isosurface value is 0.60 (Fig. S10†), the isosurface maps of NiB24− are connected on the plane of the molecule and the isosurface maps of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, and Co) are connected on the surface of the cage. Fig. S11† shows the ELF when the isosurface value is 0.70. With this isosurface value, the isosurface diagram of NiB24− is broken on the part of the molecule, and the isosurface diagrams of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, and Co) are broken on the surface of the cage. Fig. S10–S11† also show that there is a wide blank area around the metal atom, showing that the metal atom does not form an obvious covalent bond with the surrounding B atoms, which is consistent with the Mayer bond level analysis. Fig. S12† shows the ELF when the isosurface value is 0.80. Under this isosurface value, all the isosurface maps of MB24− (M = Sc, Ti, V, Cr, and Ni) are disconnected and there are no connected regions. However, the isosurface maps of MB24− (M = Mn, Fe, and Co) show that there is still a connected area on the surface of the cage, indicating that the local delocalization of MB24− (M = Sc, Ti, V, Cr, and Ni) is weaker than the MB24− (M = Mn, Fe, and Co). Quasi-planar structure NiB24−, cage-type MB24− (M = Sc, Ti, V, and Cr) and tubular MB24− (M = Mn, Fe, and Co) are expected to become the basic units of boron nanomaterials and be further synthesized into borophene, boron nanotubes or other three-dimensional materials. Considering the electron delocalization characteristics of these clusters, they are expected to be applied to molecular devices or switches.
Fig. S13–S16† show the isosurface diagrams of valence electron density for MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) with isosurface values of 0.10, 0.14, 0.20 and 0.52, respectively. Electron density describes the characteristics of electron distribution. Under the same isosurface value, a fatter (represents the bigger volume and wider connected area occupied by an isosurface map) isosurface means more electrons and a thinner isosurface means fewer electrons. The isosurface diagram of Sc is the thinnest (disappeared) and that of Ni is the thickest under the same isosurface value of 0.10, indicating that the electron density of Sc is the minimum and the electron density of Ni is the highest. From the previous atomic charge population analysis, we found that the charges on Sc, Ti, V, Cr, Mn, Fe, Co, and Ni were 0.56, 0.69, 0.70, 0.81, 0.85, 0.89, 0.90 and 0.92, respectively. The valence electrons of Sc, Ti, V, Cr, Mn, Fe, Co, and Ni are 3, 4, 5, 6, 7, 8, 9, and 10, respectively, so when the transferred electrons are removed, the remaining valence electrons of Sc, Ti, V, Cr, Mn, Fe, Co, and Ni should be 2.44, 3.31, 4.3, 5.19, 6.15, 7.11, 8.10, and 9.08. From this, it can be inferred that under the same isosurface value, the isosurface map of the Ni atom is the thickest and that of Sc is the thinnest. In addition, because the B atom has three valence electrons in addition to part of the electrons transferred from the metal atom, it has between 3 and 4 valence electrons. Therefore, the electron density of the B atom should be greater than that of Sc but less than that of V, Cr, Mn, Fe, Co, and Ni atoms. The calculation results (isosurface diagrams of valence electron density) show that as the value of the isosurface increases, the isosurface diagram of the Sc atom will disappear first and that of the B atoms in the ScB24− will disappear later (as shown in Fig. S13(a) and S15(a)),† indicating that the electron density of the B atoms is greater than that of Sc. With the increase of the isosurface value, the isosurface diagrams of the B atoms in MB24− (M = V, Cr, Mn, Fe, Co, and Ni) will disappear first, and the electron density isosurfaces of M (V, Cr, Mn, Fe, Co, and Ni) atoms will disappear later (as shown in Fig. S15(c–h)†), indicating that the electron density of the B atoms is less than those of the M (M = V, Cr, Mn, Fe, Co, and Ni) atoms. The electron density isosurface diagrams are qualitatively consistent with the atomic charge analysis results.
Fig. 3 shows the isosurface diagram of the spin density of MB24− (M = Ti, Cr, Fe, and Ni) with open shell structure at the PBE0/6-311G* level. Spin density reveals the distribution of unpaired electrons (single electrons) in three-dimensional space. A positive spin density means that there are more alpha electrons than beta electrons, while a negative spin density means that there are more beta electrons than alpha electrons. Fig. 3 shows a spin density diagram for an isosurface value of 0.002. Green represents a positive value (alpha electrons), while blue represents a negative value (beta electrons). It can be seen from Fig. 3 that the unpaired single electrons of TiB24− are alpha electrons that are distributed on Ti and B atoms. The unpaired single electrons of CrB24−, FeB24−, and NiB24− are both alpha and beta electrons. For CrB24− system, part of the unpaired alpha electrons are distributed on the Cr atom and part of the unpaired alpha electrons are on one B atoms, and the unpaired beta electrons of CrB24− are distributed on the other B atoms. For FeB24− system, part of the unpaired alpha electrons are distributed on the Fe atom and part of the unpaired alpha electrons are on seven B atoms, and the unpaired beta electrons of FeB24− are distributed on the other B atoms. For NiB24− system, only a small part of the unpaired alpha electrons is on the Ni atom and most of the unpaired alpha electrons are on the B atoms, and the unpaired beta electrons of NiB24− are distributed on the two B atoms.
To further quantitatively analyze the distribution of unpaired single electrons on different atoms, the spin population is calculated at the PBE0/6-311G* level. The spin population is defined as the alpha electron population minus the beta electron population. For example, if the spin population of an atom is one, the alpha electron population of this atom is one more than its beta electron population. A positive population corresponds to an alpha single electron, while a negative population corresponds to a beta single electron. The spin population analysis shows that there is one unpaired alpha electron in the TiB24− system, of which 0.54 is on the Ti atom and the remaining 0.46 is on the B atoms. This result is consistent with the spin density diagram (Fig. 3(a)). Although the total number of unpaired electrons in the CrB24−, FeB24−, and NiB24− systems are both 1, 1.64 unpaired alpha electrons and 0.64 unpaired beta electrons, 1.66 unpaired alpha electrons and 0.66 unpaired beta electrons, 1.24 unpaired alpha electrons and 0.24 unpaired beta electrons are distributed in the CrB24−, FeB24−, and NiB24− systems, respectively. For CrB24− system, 1.11 alpha electrons are on the Cr atom and 0.53 alpha electrons are on the one B atom, and the 0.64 beta electrons are distributed on the remaining B atoms. For FeB24− system, 0.75 alpha electrons are on the Fe atom and 0.91 alpha electrons are on the seven B atoms, and the 0.66 beta electrons are distributed on the remaining B atoms. For NiB24− system, 0.20 alpha electrons are on the Ni atom and 1.04 alpha electrons are on the ten B atoms, and the 0.24 beta electrons are distributed on the two B atoms. These results are also consistent with the spin density diagram of MB24− (M = Cr, Fe, and Ni). The spin density reflects chemical reactions or adsorption to a certain extent. The single electrons of TiB24− are all alpha electrons and distributed on the Sc and B atoms that can pair with free radicals or small molecules containing beta single electrons to form new covalent bonds. For the CrB24− system, one B atom with single alpha electrons can adsorb or react with free radicals or small molecules with single beta electron, while other B atoms with single beta electrons can adsorb or react with atoms, free radicals, or small molecules with alpha single electrons. Spin features of these clusters are expected to be applied to catalysis. In addition, these spin features are expected to produce interesting magnetic properties, which will further lead to potential applications in molecular devices.
3.2 Polarization properties
To understand the polarization properties of the clusters, the polarizability of the each cluster was calculated, including average isotropic polarizability α, anisotropic polarizability Δα, and the first hyperpolarization β0. α is also called the linear optical coefficient and Δα describes the response of the system to electric fields from different directions. The larger the value of Δα, the stronger is the anisotropic response to the external electric field. The first hyperpolarizability is also called the second-order nonlinear optical (NLO) coefficient, which evaluates the nonlinear optical properties of molecules. It can be seen from Table 2 that the isotropic polarizability of NiB24− is higher than that of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, and Co), indicating that the bonding interactions between the atoms within NiB24− are stronger than those of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, and Co), and NiB24− is more likely to be polarized by an external electric field. The anisotropic polarizability of VB24− is the smallest and that of NiB24− is the largest, indicating that VB24− has the weakest anisotropic response and NiB24− has the strongest response to an external electric field. It can be seen from Table 2 that the first hyperpolarizability of TiB24− is equal to 0, indicating that there is no nonlinear optical response. The first hyperpolarizability of ScB24− is 2, indicating that the nonlinear optical response is extremely small, and MB24− (M = Mn, Fe, and Co) have larger first hyperpolarizability, indicating that MB24− (M = Mn, Fe, and Co) have strong nonlinear optical response. Hence, the MB24− (M = Mn, Fe, and Co) might be considered as a promising nonlinear optical boron-based nanomaterial.| α/a.u. | Δα/a.u. | β0/a.u. | |
|---|---|---|---|
| ScB24− | 342 | 11 | 2 |
| TiB24− | 320 | 9 | 0 |
| VB24− | 308 | 2 | 57 |
| CrB24− | 318 | 32 | 416 |
| MnB24− | 322 | 76 | 1673 |
| FeB24− | 324 | 75 | 1236 |
| CoB24− | 328 | 75 | 1100 |
| NiB24− | 457 | 416 | 494 |
3.3 Photoelectron spectra
Photoelectron spectroscopy is powerful experimental technique to probe the electronic structure of cluster. Photoelectron spectroscopy in combination with theoretical calculations has been used to understand and identify the structures of size-selected boron clusters.6,15,64 To facilitate future identifications of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni), the adiabatic detachment energies (ADEs) for MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) were calculated at the PBE0 level, then, we calculated the vertical detachment energies (VDEs) and simulated the photoelectron spectra for MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) with the time-dependent DFT (TD-DFT) method.15,64,65 Adiabatic detachment energy of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) represents the electron affinity (EA) of corresponding neutral MB24 (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni). The larger EA can lead to the stronger probability of capturing an electron, i.e., the neutral MB24 with larger EA is easier to capture an electron. MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) give the ground-state ADEs of 3.62 (ScB24−), 3.57 (TiB24−), 3.60 (VB24−), 1.92 (CrB24−), 3.08 (MnB24−), 3.11 (FeB24−), 3.01 (CoB24−) and 3.79 (NiB24−) eV, respectively. Among the MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni), quasi-planar NiB24− has the largest ADE (3.79 eV), which is larger than the ADE (3.55 eV)10 of quasi-planar B24−.Fig. 4 presents the photoelectron spectra of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni). The predicted photoelectron spectra show that CrB24− has the lowest first vertical detachment energy (VDE) and the largest energy gap (about 1.51 eV) between the first and second bands. The first several bands of photoelectron spectra were used to identify boron clusters,6,15 so we will focus on the bands at the low binding energy side. The first peaks of these photoelectron spectra(except for FeB24−) come from the calculated ground-state VDEs of ScB24−, TiB24−, VB24−, CrB24−, MnB24−, CoB24− and NiB24− at 3.78, 3.73, 3.86, 2.37, 3.46, 3.24 and 3.87 eV, respectively. The calculated ground-state VDEs of MB24− (M = Sc, V, Mn, and Co) originate from the detachment of the electron from the molecular orbital (HOMO). However, for open-shell structure MB24− (M = Ti, Cr, and Ni), the calculated ground-state VDE of each cluster originates from the detachment of the electron from the singly occupied molecular orbital (α-SOMO). The first peak of FeB24− comes from the ground-state VDE and second VDE at 3.30 and 3.38 eV, respectively, which originate from detaching the electrons from singly occupied molecular orbital (α-SOMO) and β-HOMO−1, respectively. The second peaks of ScB24−, VB24−, MnB24−, and CoB24− come from the second calculated VDEs at 4.05, 4.07, 3.85, and 3.67 eV, respectively, which originate from detaching the electrons from HOMO−1. The second peak of TiB24− comes from the second and third VDEs at 3.90 and 3.89 eV, respectively, which originate from detaching the electrons from singly occupied molecular orbital β-HOMO−1 and β-HOMO−2, respectively. The second peaks of CrB24− and NiB24− come from the second VDE at 3.87 and 4.09 eV, respectively, which originate from detaching the electrons from β-HOMO−1. The second peak of FeB24− comes from the third VDE and fourth VDE at 3.86 and 3.95 eV, respectively, which originate from detaching the electrons from singly occupied molecular orbital β-HOMO−2 and α-HOMO−1, respectively. In addition, the peaks with higher binding energy originate from detaching the electrons from lower molecular orbitals.
Fig. 4 indicates that MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) have different spectral features, especially they have different spectral bands at the low binding energy side. These features can be used to distinguish the MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) and provide important information for the identification of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni). It is worth to note that the structures of clusters cannot directly be identified by common analytical experimental methods, but they can indirectly be determined by using combined theoretical and experimental studies. As the discovery of other anionic boron clusters, if the photoelectron spectra of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) are obtained in experiments, these calculated characteristic bands may be used as theoretical basis for the identification of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni).
3.4 Infrared and Raman spectra
Fig. 5 and 6 show plots of the calculated infrared and Raman spectra of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) with PBE0/6-311+G* method. The lowest harmonic frequencies of these clusters are listed in Table 1. From Table 1 and Fig. 5, it can be seen that the cluster structure has a strong influence on the harmonic frequency because these vibration modes are derived from the stretching or bending vibrations of the atoms. Differences in the arrangement of atoms will lead to different modes of vibration. From the calculation results, it can be seen that among the 69 vibration modes of MB24− (M = Sc, Cr, Mn, Fe, Co, and Ni), all modes are infrared active and Raman active. The calculation results show that among the 69 vibration modes of TiB24−, 44 modes are infrared-active vibration modes and 25 are inactive modes. Among the 69 vibration modes of TiB24−, there are 62 Raman-active modes and 7 inactive modes. Among the 69 vibration modes of VB24−, 55 vibration modes are infrared active and 14 vibration modes are inactive, and only one mode is Raman-inactive mode and other are Raman-active vibration modes. Under the resonance approximation, the infrared intensity is not zero for only the mode where vibration changes the dipole moment and the Raman activity is not zero for only the mode where vibration changes the polarizability. Therefore, all vibration modes of MB24− (M = Sc, Cr, Mn, Fe, Co, and Ni) can cause changes in polarizability and dipole moment, these vibration characteristics are mainly due to the low symmetry of MB24− (M = Sc, Cr, Mn, Fe, Co, and Ni). However, for TiB24−, the 25 infrared inactive modes did not cause changes in dipole moment and the 7 Raman-inactive modes did not cause changes in polarizability. Similarly, for VB24−, the 14 infrared inactive modes did not cause changes in dipole moment and one Raman-inactive modes did not cause changes in polarizability. These vibration characteristics are mainly due to the high D3h symmetry of TiB24− and lower C2v symmetry of VB24−.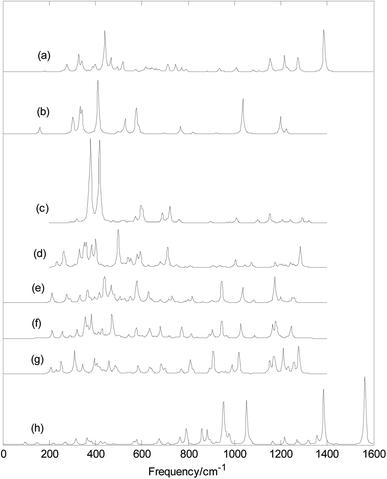 | ||
| Fig. 5 Calculated infrared spectra with PBE0/6-311+G* method. (a) ScB24−; (b) TiB24−; (c) VB24−; (d) CrB24−; (e) MnB24−; (f) FeB24−; (g) CoB24−; (h) NiB24−. | ||
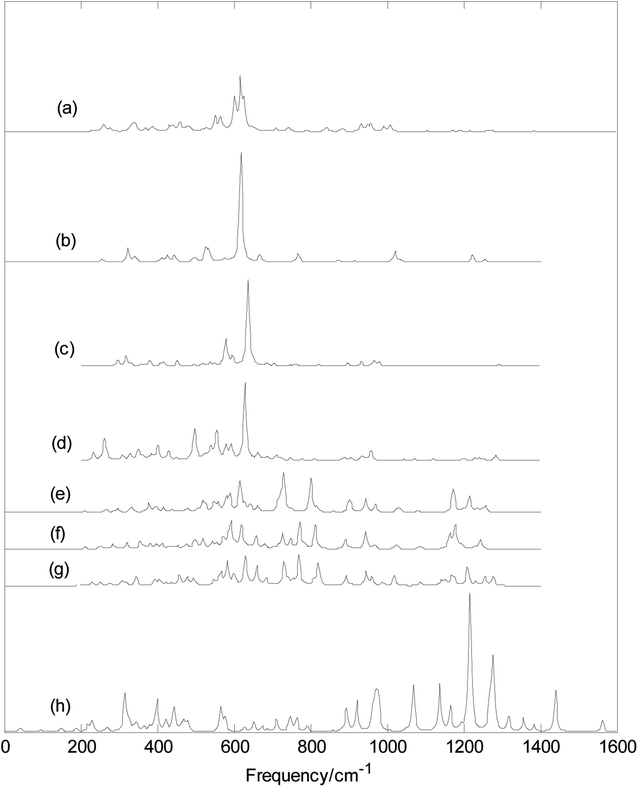 | ||
| Fig. 6 Calculated Raman spectra with PBE0/6-311+G* method. (a) ScB24−; (b) TiB24−; (c) VB24−; (d) CrB24−; (e) MnB24−; (f) FeB24−; (g) CoB24−; (h) NiB24−. | ||
It can be seen from Fig. 5 and 6 that MnB24−, FeB24−, and CoB24 have some similar band characteristics for their similar structure. Although VB24− and CrB24− have similar cage structures, they have different infrared spectra. In particular, infrared spectra of VB24− presents two adjacent strong peaks in the low-frequency region. In addition, from Fig. 6 and the calculation results, the strongest Raman peaks of MB24− (M = Sc, Ti, V, and Cr) are all located at approximately 620 cm−1, and it maybe due to cage structures of MB24− (M = Sc, Ti, V, and Cr). The characteristic peaks and band characteristics of these clusters can be used to identify these structures, which can be compared and analyzed in future experiments.
These different results such as the dipole moment, atomic charge, polarizability, and spectral properties are closely related to the structure of clusters. These clusters possess cage structure, tubular structure, and quasi-planar structure, which lead to different electron structures. In addition, the doping of metal atom also has an effect on the electronic structure, as the previous analysis of density of states. Therefore, these clusters show different properties.
4. Conclusions
Research results include the following points. The global minima obtained for the MB24− (M = Sc, Ti, V, and Cr) clusters correspond to cage structures, and the MB24− (M = Mn, Fe, and Co) clusters have similar distorted four-ring tube with six boron atoms each. Interestingly, the global minima obtained for the NiB24− cluster tend to a quasi-planar structure. The electron localization function of MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) indicates that the local delocalization of MB24− (M = Sc, Ti, V, Cr, and Ni) is weaker than that of MB24− (M = Mn, Fe, and Co), and there is no obvious covalent bond between doped metals and B atoms. Similar to tubular B clusters and deformed B7 cluster, quasi-planar structure NiB24−, cage-type MB24− (M = Sc, Ti, V, and Cr) and tubular MB24− (M = Mn, Fe, and Co) are expected to become the basic units of boron nanomaterials and be further synthesized into borophene, boron nanotubes or other three-dimensional materials. Considering the electron delocalization characteristics of these clusters, they are expected to be applied to molecular devices or switches. The spin density and spin population analyses reveal that MB24− (M = Ti, Cr, Fe, and Ni) have different spin characteristics, for example, single electrons of TiB24− are all alpha electrons and distributed on the Sc and B atoms that can pair with free radicals or small molecules containing beta single electrons to form new covalent bonds. Spin features of these clusters are expected to be applied to catalysis. In addition, these spin features are expected to produce interesting magnetic properties, which will further leads to potential applications in molecular devices. The polarization analysis indicates that MB24− (M = Mn, Fe, and Co) have larger first hyperpolarizability, indicating that they have strong nonlinear optical response and might be considered as a promising nonlinear optical boron-based nanomaterial. The calculated photoelectron spectra indicate that MB24− (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni) has different characteristic peaks that can be compared with future experimental values and provide a theoretical basis for the identification and confirmation of these single-atom transition metal-doped boron clusters. This research has enriched the structure of single-atom transition metal-doped boron clusters and has certain theoretical guiding significance for the preparation of new boron nanomaterials, such as borophene and boron nanotubes.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 11804065), the Growth Foundation for Young Scientists of Education Department of Guizhou Province, China (Grant No. QJH KY[2022]310), and the Central Guiding Local Science and Technology Development Foudation of China (Grant No. QK ZYD[2019]4012).Notes and references
- H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl and R. E. Smalley, Nature, 1985, 318, 162–163 CrossRef CAS.
- S. Iijima, Nature, 1991, 354, 56–58 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- I. Boustani, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 16426–16438 CrossRef CAS.
- H.-J. Zhai, L.-S. Wang, A. N. Alexandrova and A. I. Boldyrev, J. Chem. Phys., 2002, 117, 7917–7924 CrossRef CAS.
- H. J. Zhai, B. Kiran, J. Li and L. S. Wang, Nat. Mater., 2003, 2, 827–833 CrossRef CAS PubMed.
- B. Kiran, S. Bulusu, H. J. Zhai, S. Yoo, X. C. Zeng and L. S. Wang, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 961–964 CrossRef CAS PubMed.
- D. E. Bean and P. W. Fowler, J. Phys. Chem. C, 2009, 113, 15569–15575 CrossRef CAS.
- Q. Chen, G. F. Wei, W. J. Tian, H. Bai, Z. P. Liu, H. J. Zhai and S. D. Li, Phys. Chem. Chem. Phys., 2014, 16, 18282–18287 RSC.
- A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W. L. Li, C. Romanescu, L. S. Wang and A. I. Boldyrev, Acc. Chem. Res., 2014, 47, 1349–1358 CrossRef CAS PubMed.
- T. Jian, X. Chen, S. D. Li, A. I. Boldyrev, J. Li and L. S. Wang, Chem. Soc. Rev., 2019, 48, 3550–3591 RSC.
- R. Casillas, T. Baruah and R. R. Zope, Chem. Phys. Lett., 2013, 557, 15–18 CrossRef CAS.
- H. T. Pham, L. V. Duong, B. Q. Pham and M. T. Nguyen, Chem. Phys. Lett., 2013, 577, 32–37 CrossRef CAS.
- J. Lv, Y. Wang, L. Zhu and Y. Ma, Nanoscale, 2014, 6, 11692–11696 RSC.
- H. J. Zhai, Y. F. Zhao, W. L. Li, Q. Chen, H. Bai, H. S. Hu, Z. A. Piazza, W. J. Tian, H. G. Lu, Y. B. Wu, Y. W. Mu, G. F. Wei, Z. P. Liu, J. Li, S. D. Li and L. S. Wang, Nat. Chem., 2014, 6, 727–731 CrossRef CAS PubMed.
- H. Bai, Q. Chen, H. J. Zhai and S. D. Li, Angew. Chem., Int. Ed., 2015, 54, 941–945 CrossRef CAS.
- S.-X. Li, Z.-P. Zhang, Z.-W. Long and S.-J. Qin, RSC Adv., 2017, 7, 38526–38537 RSC.
- H. Dong, T. Hou, S. T. Lee and Y. Li, Sci. Rep., 2015, 5, 9952 CrossRef CAS.
- Y. An, M. Zhang, D. Wu, Z. Fu, T. Wang and C. Xia, Phys. Chem. Chem. Phys., 2016, 18, 12024–12028 RSC.
- H. Bai, B. Bai, L. Zhang, W. Huang, Y. W. Mu, H. J. Zhai and S. D. Li, Sci. Rep., 2016, 6, 35518 CrossRef CAS PubMed.
- E. Shakerzadeh, Z. Biglari and E. Tahmasebi, Chem. Phys. Lett., 2016, 654, 76–80 CrossRef CAS.
- C. Tang and X. Zhang, Int. J. Hydrogen Energy, 2016, 41, 16992–16999 CrossRef CAS.
- S. Li, Z. Zhang, Z. Long and D. Chen, ACS Omega, 2019, 4, 5705–5713 CrossRef CAS.
- S.-X. Li, Z.-P. Zhang, Z.-W. Long and D.-L. Chen, ACS Omega, 2020, 5, 20525–20534 CrossRef CAS PubMed.
- A. J. Mannix, X. F. Zhou, B. Kiraly, J. D. Wood, D. Alducin, B. D. Myers, X. Liu, B. L. Fisher, U. Santiago, J. R. Guest, M. J. Yacaman, A. Ponce, A. R. Oganov, M. C. Hersam and N. P. Guisinger, Science, 2015, 350, 1513–1516 CrossRef CAS PubMed.
- C. Chen, H. Lv, P. Zhang, Z. Zhuo, Y. Wang, C. Ma, W. Li, X. Wang, B. Feng, P. Cheng, X. Wu, K. Wu and L. Chen, Nat. Chem., 2022, 14, 25–31 CrossRef CAS.
- Q. Li, V. S. C. Kolluru, M. S. Rahn, E. Schwenker, S. Li, R. G. Hennig, P. Darancet, M. K. Y. Chan and M. C. Hersam, Science, 2021, 371, 1143–1148 CrossRef CAS.
- I. A. Popov, W. L. Li, Z. A. Piazza, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2014, 118, 8098–8105 CrossRef CAS PubMed.
- W. Y. Liang, A. Das, X. Dong and Z. H. Cui, Phys. Chem. Chem. Phys., 2018, 20, 16202–16208 RSC.
- W. Wang, Y.-D. Guo and X.-H. Yan, RSC Adv., 2016, 6, 40155–40161 RSC.
- R. Saha, S. Kar, S. Pan, G. Martinez-Guajardo, G. Merino and P. K. Chattaraj, J. Phys. Chem. A, 2017, 121, 2971–2979 CrossRef CAS PubMed.
- S.-X. Li, D.-L. Chen, Z.-P. Zhang and Z.-W. Long, Acta Phys. Sin., 2020, 69, 193101 CrossRef.
- L. F. Cheung, G. S. Kocheril, J. Czekner and L. S. Wang, J. Am. Chem. Soc., 2020, 142, 3356–3360 CrossRef CAS.
- I. A. Popov, T. Jian, G. V. Lopez, A. I. Boldyrev and L. S. Wang, Nat. Commun., 2015, 6, 8654 CrossRef CAS.
- T. Jian, W. L. Li, I. A. Popov, G. V. Lopez, X. Chen, A. I. Boldyrev, J. Li and L. S. Wang, J. Chem. Phys., 2016, 144, 154310 CrossRef PubMed.
- T. T. Chen, W. L. Li, H. Bai, W. J. Chen, X. R. Dong, J. Li and L. S. Wang, J. Phys. Chem. A, 2019, 123, 5317–5324 CrossRef CAS PubMed.
- L. F. Cheung, J. Czekner, G. S. Kocheril and L. S. Wang, J. Am. Chem. Soc., 2019, 141, 17854–17860 CrossRef CAS PubMed.
- T. T. Chen, W. L. Li, W. J. Chen, X. H. Yu, X. R. Dong, J. Li and L. S. Wang, Nat. Commun., 2020, 11, 2766 CrossRef CAS PubMed.
- L. F. Cheung, G. S. Kocheril, J. Czekner and L. S. Wang, J. Phys. Chem. A, 2020, 124, 2820–2825 CrossRef CAS.
- W. J. Chen, M. Kulichenko, H. W. Choi, J. Cavanagh, D. F. Yuan, A. I. Boldyrev and L. S. Wang, J. Phys. Chem. A, 2021, 125, 6751–6760 CrossRef CAS PubMed.
- Z. Y. Jiang, T. T. Chen, W. J. Chen, W. L. Li, J. Li and L. S. Wang, J. Phys. Chem. A, 2021, 125, 2622–2630 CrossRef CAS PubMed.
- S. Chacko, D. G. Kanhere and I. Boustani, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 035414 CrossRef.
- W.-y. Liang, A. Das, X. Dong, M.-h. Wang and Z.-h. Cui, New J. Chem., 2019, 43, 6507–6512 RSC.
- X. Dong, S. Jalife, A. Vasquez-Espinal, J. Barroso, M. Orozco-Ic, E. Ravell, J. L. Cabellos, W. Y. Liang, Z. H. Cui and G. Merino, Nanoscale, 2019, 11, 2143–2147 RSC.
- J. Lv, Y. Wang, L. Zhang, H. Lin, J. Zhao and Y. Ma, Nanoscale, 2015, 7, 10482–10489 RSC.
- J. Lv, Y. Wang, L. Zhu and Y. Ma, J. Chem. Phys., 2012, 137, 084104 CrossRef.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2015, 17, 24173–24181 RSC.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- B. Le Chen, W. G. Sun, X. Y. Kuang, C. Lu, X. X. Xia, H. X. Shi and G. Maroulis, Inorg. Chem., 2018, 57, 343–350 CrossRef PubMed.
- P. Li, X. Du, J. J. Wang, C. Lu and H. Chen, J. Phys. Chem. C, 2018, 122, 20000–20005 CrossRef CAS.
- S. Jin, B. Chen, X. Kuang, C. Lu, W. Sun, X. Xia and G. L. Gutsev, J. Phys. Chem. C, 2019, 123, 6276–6283 CrossRef CAS.
- M. Ren, S. Jin, D. Wei, Y. Jin, Y. Tian, C. Lu and G. L. Gutsev, Phys. Chem. Chem. Phys., 2019, 21, 21746–21752 RSC.
- Y. Tian, D. Wei, Y. Jin, J. Barroso, C. Lu and G. Merino, Phys. Chem. Chem. Phys., 2019, 21, 6935–6941 RSC.
- M. J. Frisch, G. W. Trucks and H. B. Schlegel, et al.Gaussian 16, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- H. Sekino and R. J. Bartlett, J. Chem. Phys., 1993, 98, 3022–3037 CrossRef CAS.
- A. Alparone, Chem. Phys., 2013, 410, 90–98 CrossRef CAS.
- I. C. Mayer, Chem. Phys. Lett., 1983, 97, 270–274 CrossRef CAS.
- A. D. Becke and K. E. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403 CrossRef CAS.
- Q. Chen, W. L. Li, Y. F. Zhao, S. Y. Zhang, H. S. Hu, H. Bai, H. R. Li, W. J. Tian, H. G. Lu, H. J. Zhai, S. D. Li, J. Li and L. S. Wang, ACS Nano, 2015, 9, 754–760 CrossRef CAS.
- R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See https://doi.org/10.1039/d2ra02500k |
| This journal is © The Royal Society of Chemistry 2022 |