Open Access Article
Open Access ArticleEIS analysis of the electrochemical characteristics of the metal–water interface under the effect of temperature
Funan Sun a,
Xiao Peng
a,
Xiao Peng b,
Xiangling Bai
b,
Xiangling Bai a,
Zhiwei Chen
a,
Zhiwei Chen a,
Ruizhen Xie
a,
Ruizhen Xie c,
Bin He
c,
Bin He a and
Pengju Han
a and
Pengju Han *a
*a
aCollege of Civil Engineering, Taiyuan University of Technology, Taiyuan, 030024, China. E-mail: 13834569544@163.com
bSchool of Architecture and Civil Engineering, Jiangsu University of Science and Technology, Zhenjiang, 212003, China
cDepartment of Mechanics, Jinzhong University, Jinzhong, 030619, China
First published on 7th June 2022
Abstract
The corrosion performance of metals is closely related to their durability. Available studies on metal corrosion have seldom focused on the interfacial reaction behaviour influenced by a conductive medium under different temperatures. In this work, a laboratory corrosion simulation environment has been designed for EIS measurements to investigate the electrochemical behaviour of copper immersed in distilled water in different temperature environments. The relationship between the mathematical model of impedance response and the equivalent circuit model is determined based on electrochemical kinetics theory. The complex process of the dielectric properties of distilled water affected by temperature is analysed, and a simple method for calculating the kinetic parameters is presented. The experimental and model results have a good fit, and the analysis results indicate that the semicircle in the high-frequency region of the complex impedance curve represents the charge transfer process of the conductive medium. The decrease in temperature is the major factor that inhibits the rate of dissolution and passivation, resulting in the change rate of surface coverage slowing down, until the attenuation of the mass transfer process of the conductive medium dominates the full range of AC frequencies. This model provides an improved approach for determining physical parameters based on electrochemical impedance spectroscopy to characterize the electrochemical properties of materials.
1. Introduction
Buried pipelines have a wide range of industrial and technical applications in transportation. However, a large amount of buried metal is used in construction and other applications, which forms an electrochemical system with the soil that reacts to cause corrosive damage, which will affect the production and health of the population.1,2 In fact, the corrosion reaction is a complex charge transfer process that occurs at the interface between the metal and the electrolyte. In the entire corrosion process, soil plays a key role in the speed of corrosion as a complex and nonuniform three-phase conductive medium;3 water as an electrolyte in the soil is the most important factor that directly affects the charge transfer between the interior of the soil and the metal interface.4 In the past several decades, extensive studies have been conducted on the electrochemical behaviour of metal in acidic solutions, neutral sodium chloride solutions and alkaline solutions.5–10 The research shows that the corrosion mechanism and charge transfer law of the metal interface in different electrolytic environments exhibit diversity (hydrogen evolution corrosion, oxygen absorption corrosion) and complexity (impedance of the film formation process, ion diffusion pathway). According to various studies, temperature, water content, salt content and so on are the main factors that directly affect the internal electrical and chemical properties of the soil system and the solution dielectric,11–14 and indirectly affect the reaction rate of the metal or alloy surface.15 Although researchers have studied the law of charge transfer in high-resistivity media, factors such as the basic solute that dissolves carrier-distilled water, the electrochemical kinetics, and the electrochemical thermodynamics law of the metal surface before and after the phase transition of the conductive medium are still not fully understood under the effect of temperature. Service durability of metallic facilities is a technical problem faced by the construction engineering sector. In this study, theoretical and applied studies on the electrochemical characteristics and corrosion mechanism of metals in a basic medium were conducted, contributing to the deepening of the electrochemical theory of microscopic corrosion interfaces and guiding metal structure design, material selection, construction and other engineering applications. This is significant in promoting regional economic development and economic transformation.Electrochemical impedance spectroscopy (EIS) is a powerful method for characterizing the dynamics of bound or mobile charges in the bulk or interfacial regions of any kind of solid or liquid material and their interfaces with electronically conducting electrodes.15 However, an accurate mathematical model is usually developed to satisfy the impedance data obtained from the experiment to disentangle the contributions from the electrical response of the various processes to the impedance. The current general approach is to try to fit the impedance data to the equivalent circuit model. The impedance response represented in a different range of frequencies may be related to many complex material variables, from mass transport, rates of chemical reactions, corrosion, and dielectric properties to the microstructure and compositional influences on the conductance of solids. Therefore, the ideal distribution of elements in the equivalent circuit used to fit the corresponding value at the specific frequency to interpret the physical process is somewhat elusive.16
This study aims to provide a research method to study the mechanism of charge transfer in water and the mathematical model in this study has been determined by describing the basic reaction process of the electrode system response from electrochemical kinetic theory to solve the uncertainty of the traditional equivalent circuit method in the interpretation of impedance data, which will provide a research foundation for future research on the law of metal–water interface charge transfer. The model should clearly include the key features of the electrochemical reactions at the electrode surface under the effect of distilled water in different temperature environments. In order to verify this model, an electrochemical impedance spectroscopy test system is used in the laboratory experiments. Copper electrodes are used as the experimental metal. Although the corrosion process of copper is very fast, it is still the material of choice for engineering applications due to its easy availability and economic applicability.17 Distilled water is used as the electrolyte. Then, the impedance spectrogram is obtained, and the least-squares method is used to verify the fit of the model. The parameters obtained from the model fitting are interpreted by this approach according to the kinetics of rate control and the transport process. The present EIS results show that based on the charge balance, the electrochemical reaction on the surface of the copper electrode is effectively suppressed because the distilled water (capacitance medium) is influenced by different temperatures and undergoes physical and chemical changes (phase changes) that cause the attenuation of the mass transfer process. Continuous exploration of the mechanism and law of metal corrosion is a basic requirement for the electrochemical application of materials. Charge transfer and chemical reactions in a solution–electrode system are complex electrochemical processes. By breaking through the basic scientific problems of electrochemical theory, the results can further broaden the traditional electrical testing methods and provide a new method for evaluating the corrosion law and adaptability of metal materials.
2. Experiments
This experiment involved a three-electrode system. The working electrode was a copper bar with ≥99.99% purity, and the working area was sealed to 1 cm2 with polyvinyl chloride insulating tape and epoxy resin. The reference electrode was a saturated calomel electrode (SCE). The counter electrode was a platinum electrode. Before each operation, the electrode surface was treated as follows: the working surface was polished with silicon carbide sandpaper (grade 2000), then washed with alcohol, degreased with acetone, rinsed with deionized water, and finally immersed in the solution. The electrochemical experiment was carried out in a rubber mold (immersed in the refrigerating fluid) with a capacity of 350 mL, and distilled water was the conductive medium; the top of the mold was covered with a waterproof film. The experiment was continuously cooled using thermostatic equipment, and the temperature was controlled at 20, 10, 5, 0, −5, −10, and −20 °C. The experimental apparatus is shown in Fig. 1. Electrochemical impedance spectroscopy was carried out on a CS 350 electrochemical workstation and measurements were collected after the electrode surface reached a steady-state at each temperature. The testing range of frequency was 100 kHz to 0.01 Hz, and linear sinusoidal perturbation was used for a total time of 12 h.3. Modeling for impedance response
3.1 Electrochemical model for the reaction mechanisms
The generalized process of metal corrosion consists of the following steps:(1) Metal-ion formation by anodic corrosion, which may either be a direct electrochemical dissolution or a multistep electrochemical chemical process resulting in precipitation.
(2) Metal-ion migration through the electrolyte under the electric field towards the cathode.
(3) Electrochemical metal deposition at the cathode, forming metallic deposits.
The above reaction scheme was characterized by Wilhelm's cyclic voltammetry continuous scan.18 The cathode reaction represents a series of reduction reactions of oxides and hydroxides of Cu(I) and Cu(II) to Cu.
| Cu → Cusurface2+ + 2e− | (1) |
After reaction (1) occurs, Cu2+ migrates from the anode surface to the bulk solution through the oxide film, and the reactive particles OH− migrate from the bulk solution to the anode surface and react with Cu(I) to form the main passivation product Cu2O; a series of complex oxidation reactions will still occur afterwards.18
| Cusurface2+ → Cubulk2+ | (2) |
| OHbulk− → OHsurface− | (3) |
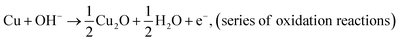 | (4) |
| O2bulk → O2surface | (5) |
| O2surface + 2H2O + 4e− → 4OH− | (6) |
Meanwhile, Cu2+ migrates from the bulk solution to the cathode surface, and Cu2+ associates with OH− to form the oxidation product Cu(OH)2. In fact, the oxidation product still undergoes a series of complex reduction reactions afterwards.
| Cubulk2+ → Cusurface2+ | (7) |
| Cu2+ + 2OH− → Cu(OH)2, (series of reduction reactions) | (8) |
Although there are many complex chemical reactions on the surface of the cathode accompanied by charge transfer, the accumulation of oxidation products on the surface of the cathode does not have a significant impact on the reduction current as time increases. The cathode reaction is mainly controlled by the charge transfer process.
| 2H2O ⇌ H3O+ + OH− | (9) |
Self-dissociated ions (H3O+, OH−) of H2O molecules migrate to the cathode and anode under the action of an electric field. Certainly, when distilled water changes to solid ice as the temperature decreases, the conduction mechanism is completely different. Ice is a crystal structure formed by the arrangement of H2O molecules through hydrogen bonding. The H2O molecules are fixed and immovable. The conduction process of ice is mainly the dissociation of H+ ions from the H2O molecules, resulting in a weak current of transferring protons.19
However, the above conductive process is weak, and the insulation of distilled water is still obvious. The end faces of the two test electrodes in distilled water can be used as alternating current parallel plate capacitors, with distilled water as the capacitor medium.20,21
3.2 Mathematical model of the metal interface
The faradaic current density and the non-faradaic current density of the electrode interface constitute the total current density Itotal through each interface of the electrode system (Fig. 3). Two independent current densities have no influence on each other, and their addition constitutes the total current density.22,23| Itotal = Idl + IF = IS | (10) |
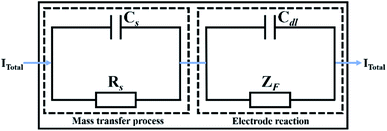 | ||
| Fig. 3 Schematic diagram of the total current density through each interface of the electrode system. | ||
One part of the current density develops from the charging and discharging current caused by the change of the charge density on both sides of the electric double-layer when the potential changes.
 | (11) |
 | (12) |
 The current density of the oxidation reaction is
The current density of the oxidation reaction is
 | (13) |
The passivation product on the electrode surface interdicts the anode dissolution and passivation reaction. θ represents the surface coverage of the passivation product. Reactions (1) and (4) still occur in the areas not covered by the oxide film before the electrode surface is completely covered.
 | (14) |
 | (15) |
In general, the formation of an oxide film proceeds by a series of reactions. Thus, various reactions involved in the formation of the oxide film are simplified as one representative reaction in reaction (4). However, no matter how many electrons are transferred by each kind of passivation reaction, the metal electrode surface can carry out both dissolution and passivation reactions simultaneously. The final faradaic current through the electrode is equal to I1 + I2. Finally, the total current density Itotal (Fig. 3) is expressed as the sum of the anode dissolution current density, the passivation current density and the capacitor charge and discharge current densities.
 | (16) |
Generally, the faradaic current density IF = f(E, X, C) is a function of the electrode potential E, the system variable X on the electrode surface, and the ion concentration C on the electrode surface.24 Two time-constants appear in the range of the middle and low frequencies (Fig. 6) in the experimental results of this study (20 °C, 10 °C, 5 °C). After clarifying the capacitive reactance arc generated by the electric double-layer (Cdl) and the charge transfer resistance Rt at the electrode interface,25 the influence of the passivation process on the electrode control step is first determined. Therefore, under the perturbation of the small amplitude sine wave potential signal ΔE = |ΔE|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(jωt), the function IF produces a variation ΔIF according to the causality condition. The expansion of the multivariate functions IF as a Taylor series simply leads to equal signs on the left and right-hand-side of the equation.
exp(jωt), the function IF produces a variation ΔIF according to the causality condition. The expansion of the multivariate functions IF as a Taylor series simply leads to equal signs on the left and right-hand-side of the equation.
 | (17) |
According to the definition of faradaic admittance YF = ΔI/ΔE,
 | (18) |
![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) in this study is a function of all system variables, including electrode potential. According to the linear condition of electrochemical impedance spectroscopy, this experimental condition was tested after the system reached a steady-state. The change value of the fractional surface coverage Δθ corresponds to the sine wave disturbance response and presents the sine wave disturbance response at the same frequency as Δθ = |Δθ|
in this study is a function of all system variables, including electrode potential. According to the linear condition of electrochemical impedance spectroscopy, this experimental condition was tested after the system reached a steady-state. The change value of the fractional surface coverage Δθ corresponds to the sine wave disturbance response and presents the sine wave disturbance response at the same frequency as Δθ = |Δθ|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(jωt + φ). Thus, dθ/dt = dΔθ/dt = jω|Δθ|
exp(jωt + φ). Thus, dθ/dt = dΔθ/dt = jω|Δθ|![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(jωt + φ) = jωΔθ. In a physical sense, the conversion coefficient K is expressed as the relationship between the electric quantity passed on the electrode and the weight of the reaction product of the electrode, which is based on Faraday's electrolysis law. The necessary condition for the formation of a completely precipitated film on the metal surface is that the dissolution rate of the formed film is very slow; otherwise, it is difficult to form a complete film. Generally, when there is no erosion effect of anions such as Cl− on the oxide film, the dissolution rate of the oxide film is very low and can be effectively ignored. Therefore, the change rate of the fractional surface coverage
exp(jωt + φ) = jωΔθ. In a physical sense, the conversion coefficient K is expressed as the relationship between the electric quantity passed on the electrode and the weight of the reaction product of the electrode, which is based on Faraday's electrolysis law. The necessary condition for the formation of a completely precipitated film on the metal surface is that the dissolution rate of the formed film is very slow; otherwise, it is difficult to form a complete film. Generally, when there is no erosion effect of anions such as Cl− on the oxide film, the dissolution rate of the oxide film is very low and can be effectively ignored. Therefore, the change rate of the fractional surface coverage ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) can be simply expressed as a proportional relationship of the passivation reaction current
can be simply expressed as a proportional relationship of the passivation reaction current ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) = KI2. Expansion of the multivariate function
= KI2. Expansion of the multivariate function ![[small straight theta, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e12d.gif) as a Taylor series affords
as a Taylor series affords
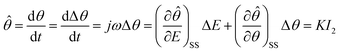 | (19) |
 | (20) |
Unifying eqn (16), (18) and (20), and further transforming the form to obtain the faradaic impedance ZF, we get
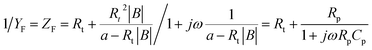 | (21) |
The above faradaic impedance expression is equivalent to the impedance expression of the equivalent circuit R(RC).26
 | (22) |
Thus, the explicit expressions of Rp and Cp are obtained:
 | (23) |
 | (24) |
According to eqn (16) and (19), the expression of each parameter is
 | (25) |
 | (26) |
 | (27) |
Therefore, the relationship between the equivalent circuit model of the impedance spectrum and the mathematical model of copper in a conductive medium at different temperatures is established by integrating the above reaction processes (Fig. 4). Rs and Cs represent the bulk resistance and bulk capacitance of the dielectric medium, respectively, Cdl is the double-layer capacitance, Rt is the charge transfer resistance, and Rp and Cp represent the resistive and capacitive behaviour of the passive film, respectively.27,28
4. Results
4.1 Open circuit potential curves
Thermodynamic stability information of the metal electrode surface at different temperatures can be reflected by the OCP value, as shown in Fig. 5. The OCP monitoring results indicate that each corrosion system is in an aerobic state and the OCP value gradually becomes stable over time. Obviously, the OCP value increases with a drop in temperature. The increase in OCP value indicates the enhancement of the corrosion resistance of the metal to some extent. | ||
| Fig. 5 Open circuit potential–time curves of copper electrodes in the conductive medium at different temperatures. | ||
4.2 Experimental results of electrochemical impedance spectroscopy
Nyquist plots of the copper electrode in the conductive medium at different temperatures are shown in Fig. 6. Obviously, the Nyquist plots of the same experimental system in different temperature environments exhibit two different performances with 0 °C as the boundary. The complex impedance curves at 20, 10, and 5 °C are composed of three capacitive reactance arcs. The semicircle in the high-frequency region is controlled by the mass transfer process of distilled water.29 The dissolution reaction and passivation reaction on the surface of the electrode occupy the control step of the speed response in the range of the middle and low frequencies. The intercept of the high-frequency semicircle and the real axis Z′ gradually shifts to the right as the temperature gradually decreases; the increase in the radius of the high-frequency semicircle also indicates that the impedance of the conductive medium increases with the decline in temperature. The same law is also reflected in the range of the middle and low frequencies,30 where the rate of the dissolution reaction and passivation reaction decays as the temperature decreases, which is the focus of this study to analyse the kinetics parameters of the electrode interface. However, the development of a high-frequency semicircle is remarkable at 0 °C, where the electrochemical impedance spectroscopy in the environment of ≤0 °C is completely composed of the bulk resistance Rs and the bulk capacitance Cs. The capacitive reactance arc occupies the main control process in the whole range of frequencies. This shows that the high-impedance solid ice blocks the charge transfer on the electrode surface, and Cu2+ and OH− can hardly penetrate the crystal structure to complete the charge transfer.The modulus and phase Bode impedance plots of the copper electrodes in a conductive medium at different temperatures are shown in Fig. 7(a) and (b), respectively. Several time-constant characteristics of impedance spectroscopy at different temperatures can be clearly distinguished from the peaks in the phase plot.31 The phase angle curves in the environments of 20, 10 and 5 °C are similar, the phase angle peaks generated by the relaxation of distilled water (capacitive medium) are all located at 104 to 105 Hz, and the relaxivity generated by the dissolution reaction and the passivation reaction at the electrode interface peaks at around 100 to 101 Hz and 10−2 Hz, respectively. The characteristic frequency values corresponding to the above three time constants shift slightly to the left as the temperature drops, and the extension of the relaxation time of each control process can be judged according to τ = 1/ω*,32 where τ is the time constant and ω* is the characteristic frequency. The time constant τ can usually be understood as the time course for the state variable to return to the steady-state after being disturbed, which indirectly indicates that the reaction rate of the state variable slows down as the temperature decreases.33 The relaxivity caused by the phase change to ice (≤0 °C) of distilled water only shows one peak in the phase plot, and the range of their frequencies is 3 orders of magnitude lower than the frequency response of liquid media.
Fig. 7(a) shows that the total impedance moduli of the electrochemical system increase significantly while the temperature and frequency are attenuated. The contribution of impedance is mainly composed of the dissolution and passivation reactions in the environments of 20, 10 and 5 °C. Below 0 °C, the impedance modulus increases linearly with the decrease in the frequency, and the impedance in the medium and low-frequency regions is 3 ∼ 4 orders of magnitude higher than that in the liquid water environment, which is enough to confirm that the solid ice hinders the charge transfer at the metal interface.
4.3 Application of the model to experimental impedance spectra
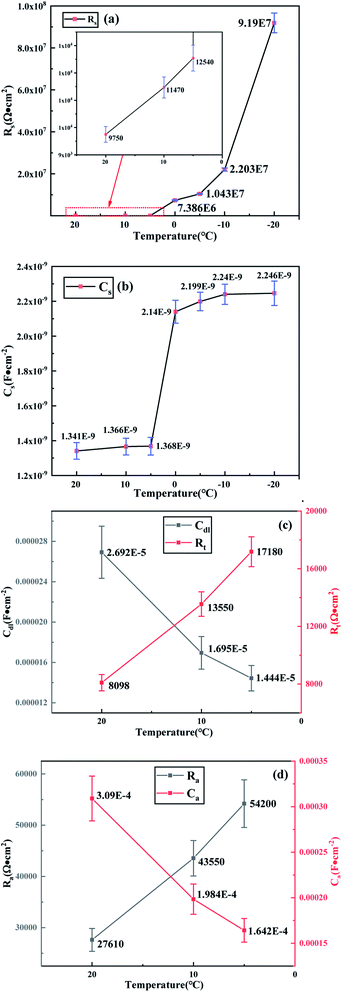
The models (RC)(C(R(RC))) and (RC) were fitted to the experimental impedance spectra (Fig. 6) by a least-squares fitting routine (ZSimdemo software) to obtain each circuit component parameter (Fig. 8) of the copper electrode in a conductive medium at different temperatures, and the fitting errors are all less than 10%.The intercept between the high-frequency semicircle and the real axis Z′ represents the bulk resistance Rs of the capacitive medium; the Rs value increases as the temperature decreases, indicating that the radius of the high-frequency capacitive reactance gradually expands, which confirms the phenomenon observed in Fig. 6. As the water phase changes to ice at 0 °C, the bulk resistance Rs of ≤0 °C is 4 orders of magnitude higher than the Rs at 20 °C, which is enough to confirm that the development of the high-frequency semicircle represents the overall electrical performance of the capacitive medium at different temperatures. The Cs value increased significantly at 0 °C with the decrease in temperature, and as the temperature continues to slightly increase, the ion polarization of the medium may cause a change in the capacitance content at both ends of the electrode plate, which is the focus of this study on the dielectric properties of the capacitive medium.
At the same time, the value of the charge transfer resistance Rt gradually increases with the decrease in temperature, and the value of the electric double-layer capacitance Cdl at the electrode interface continuously decreases. Furthermore, the resistance Rp of the oxide film increases and the capacitance Cp decreases. The above laws confirm a decrease in the dissolution and passivation reaction rates on the electrode surface.
5. Discussion
5.1 Impedance and dielectric properties of distilled water and ice at different temperatures
When the impedance characteristics of electrolytes are analyzed by the equivalent circuit model, as mentioned in Section 4.2, the law expressed from Rs and Cs is followed. Electrochemical impedance spectroscopy has been used to study the conductivity of different dielectric materials such as ceramics, crystals and liquids as a method of electrical relaxation. Impedance Z(ω) is a complex quantity involving macroscopic relaxation data.34–36 Therefore, some other impedance-related quantities can be derived, which usually play an important role in evaluating the dielectric properties of the material. The structure of water in different environmental conditions can be proved by an effective method: calculating the dielectric constant.The impedance spectra can be transformed into the dielectric spectra with the use of the relationship ε(ω) = 1/jωC0Z(ω), which leads to the following equations for the real (ε′) and imaginary (ε′′) parts of the complex permittivity ε(ω) = ε′ − jε′′:
| ε′ = Z′′/ωC0Z2 | (28) |
| ε′′ = Z′/ωC0Z2 | (29) |
Fig. 9 shows the frequency-dependent spectra of the real and imaginary parts of the complex dielectric function ε of distilled water at different temperatures. Obviously, the microscopic mechanism of distilled water before and after the phase transition is different. As shown in Fig. 9(a), the dielectric constant of distilled water is higher in the low-frequency region and decreases rapidly as the frequency increases to 10 Hz until it stabilizes, which also shows that high frequency has little effect on the conductive media. Under the influence of a low-frequency electric field, the self-dissociated ions (hydrogen ions H3O+ and hydroxide ions OH−) inside the distilled water undergo shift polarization and move to the electrode interface, forming an electric double layer capacitance at the interface. Meanwhile, the polar H2O molecules show turning polarization. These two changes show macroscopically that bound charges appear at the metal interface,37 and the rise in temperature promotes the thermal movement of H2O molecules and self-dissociated ions in the direction of the electric field, thus contributing to a high apparent dielectric constant as the temperature rises.
 | ||
| Fig. 9 Real (a) and imaginary (b) parts of the dielectric spectra of the conductive medium at different temperatures. | ||
After the distilled water changes into ice, the dielectric constant of ice also decreases as the frequency increases to 1000 Hz until it stabilizes. Ice is a crystal composed of polar molecules. After solidification, the hydroxyl group (O–H) in the polar molecules of H2O still has a degree of freedom of rotation, the turning polarization mainly contributes to the dielectric constant of the polar crystal, and the decrease in temperature also restricts the turning movement of H2O molecules to a certain extent; therefore, as the temperature decreases, the developed dielectric constant becomes lower than that of liquid water. The dielectric constant of the media in the two physical states decreases as the frequency increases. As the frequency increases, the polarization response time of the self-dissociated ions and H2O molecules in the medium is not enough to cope with the oscillation of the AC electric field, which leads to a decrease in the dielectric constant.
The dielectric loss of liquid water and solid ice decreases with frequency over the entire frequency range and increases with the increase in temperature, as shown in Fig. 10. The reason for this phenomenon is that the self-dissociated ions and H2O molecules in the medium cannot establish a relaxed polarization in the high-frequency environment of the AC electric field, and the polarization of the medium is mainly contributed by the displacement polarization; thus, the resulting relaxation loss is little. Meanwhile, the increase in temperature strengthens the thermal movement of molecules in the medium, which results in increased collisions and friction between molecules, showing an increase in dielectric loss.
From the above analysis, we can try to explain the sharp increase in the capacitance content of the metal electrode plate before and after the phase transition of the conductive medium, as shown in Fig. 8(b). Some studies have shown that the surface properties of any solid differ from its bulk properties. This is the reason for the formation of a liquid-like layer at the interface, at temperatures below the bulk melting point. The formation of this layer is often called premelting.38 This phenomenon also occurs at the interface between the metal and the solid ice, where a tiny amount of unfrozen liquid water exists between the metal and the ice.
Before and after the phase transition, H2O molecules exhibit turning polarization inside the medium to balance the electric field. Obviously, the decrease in temperature will make the turning motion of the H2O molecules more difficult. In order to compensate for the electric field balance, the liquid water at the interface between the metal and the solid ice needs to have more dissociated ions (H3O+, OH−) displaced on the electrode surface. Therefore, as the temperature decreases, the capacitance value Cs rises observably before and after the phase change. In the process of going from distilled water to ice, the self-dissociation of H2O molecules and the recombination of H3O+–OH− ion pairs always occur (reaction (9)). The decrease in temperature slows down the diffusion of the self-dissociated ions H3O+ and OH− to the electrode surface, thereby changing the balance to increase the life of the separated charges, and increasing the ion concentration on the electrode surface. The capacitance Cdl value increases as the temperature decreases, as shown in Fig. 8(c).39
Fig. 10 shows the frequency-dependent spectra of tanδ (=ε′′/ε′) at different temperatures. The tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ spectra have a peak value corresponding to the relaxation frequency ωm, which is used to evaluate the electrode polarization relaxation time τ (=ωm−1). The relaxation peaks of distilled water at 20, 10 and 5 °C appear at 102 to 103 Hz. When distilled water undergoes a phase change to ice, the frequency of the relaxation peak drops to 10−1 to 10−2 Hz.
δ spectra have a peak value corresponding to the relaxation frequency ωm, which is used to evaluate the electrode polarization relaxation time τ (=ωm−1). The relaxation peaks of distilled water at 20, 10 and 5 °C appear at 102 to 103 Hz. When distilled water undergoes a phase change to ice, the frequency of the relaxation peak drops to 10−1 to 10−2 Hz.
Values of the relaxation frequency ωm and relaxation time τ of distilled water at different temperatures are presented in Table 1. The relaxation of the medium occurs in a certain range of frequency and temperature. As the temperature decreases, the molecular thermal motion becomes weak, preventing the orientation of H2O in the direction of the electric field, and the frequency of the system response slows down, so the relaxation time τ (=ωm−1) is too long to orient with the applied alternating electric field. At this time, only electron displacement polarization occurs, and the dielectric loss and tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ are stable with temperature. As the temperature decreases, the relaxation time continues to increase, further verifying that the rate of ion migration and molecular steering movement in a conductive medium slows down, and the charge transfer rate of the electrode system is inhibited.
δ are stable with temperature. As the temperature decreases, the relaxation time continues to increase, further verifying that the rate of ion migration and molecular steering movement in a conductive medium slows down, and the charge transfer rate of the electrode system is inhibited.
| Temperature (°C) | tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ δ |
ωm (Hz) | τ (s) |
|---|---|---|---|
| 20 | 13.54 | 469.57 | 0.0021 |
| 10 | 18.19 | 372.41 | 0.0027 |
| 5 | 20.80 | 232.26 | 0.0043 |
| 0 | 9.34 | 0.08 | 12.5 |
| −5 | 11.12 | 0.05 | 20 |
| −10 | 14.32 | 0.02 | 50 |
| −20 | 31.91 | 0.01 | 100 |
5.2 Passivation reaction and the site fraction occupied by Cu2O
It can be seen from Fig. 8(c) and (d) that the element parameters obtained from the equivalent circuit model fitting macroscopically confirm the increase of the charge transfer resistance in the dissolution and passivation reactions on the metal surface. Previous studies have derived the base current density formula to fit potentiodynamic current–potential curves to obtain various kinetics parameters.31 Aiming to establish the relationship between the equivalent circuit model and electrochemical kinetic theory, this study proposes an easy method to calculate kinetic parameters only by the circuit element parameters obtained by electrochemical impedance spectroscopy fitting.First, eqn (25)–(27) are further simplified to form a system of algebraic equations.
 | (30) |
We then substitute the parameters Rt, Rp, and Cp (Fig. 8) of the fitting results at 20, 10 and 5 °C into eqn (23) and (24) to obtain a and |B| (Table 2). r1 = 2α1F/RT and r2 = α2F/RT. In order to simplify the calculation process, we approximately consider that α1 ≈ α2 ≈ 0.5;40 the parameters required for the calculation for r1 and r2 are shown in Table 3.
| T (°C) | a (s−1) | |B| (Ω−1 cm−2 s−1) | r1 (C J−1) | r2 (C J−1) |
|---|---|---|---|---|
| 20 | 0.5168 | 4.935 × 10−5 | 39.58 | 19.79 |
| 10 | 0.4876 | 2.745 × 10−5 | 40.99 | 20.49 |
| 5 | 0.4669 | 2.063 × 10−5 | 41.72 | 20.86 |
| Parameters | Value |
|---|---|
| α1 | 0.5 |
| α2 | 0.5 |
| F | 96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 485 C mol−1 485 C mol−1 |
| R | 8.314 J (mol K)−1 |
| T | 293.15 K, 283.15 K, 278.15 K |
The constants required at different temperatures in eqn (30) are shown in Table 2. The current density of the dissolution reaction I1 and the passivation reaction I2 are obtained by solving eqn (30).
As previously mentioned, K is the coverage-electricity conversion coefficient.41 According to Faraday's second law of electrolysis.42
| K = M/Fn | (31) |
| Parameters | Value |
|---|---|
| M | 143.08 |
| n | 4 |
| ρ | 6.0 g cm−3 |
| h | 1 Å (10−10 m) |
The physical parameters θ, I1, and I2 of the anode surface of the copper electrode at 20, 10 and 5 °C are shown in Fig. 11. The relationships between the physical parameters θ, I1, and I2 and temperature are studied and summarized in Table 5. A good correlation between temperature and corrosion rate was obtained. The increased viscosity of distilled water causes the ion transfer speed to slow down with the decrease in temperature, that is, the thermal movement of ions in the capacitor medium attenuates, and the current density of the dissolution reaction and the passivation reaction decreases based on the charge balance. However, the gradual slowing down of the reaction rate directly affects the coverage rate of the oxide film on the electrode surface. As shown in Fig. 11, the increasing slope of the passivation film coverage rate slows down, which further confirms that the calculation approach proposed in this study can provide a reference for the kinetics response of the electrode interface to a certain extent. As the temperature decreases, the current density of the dissolution and passivation reactions gradually decreases. The transfer rate of oxygen in the electrolyte is the determining factor that limits the dissolution and passivation reactions because of the viscosity of the electrolyte. The impedance of the metal during the corrosion process is controlled by the response of the metal–electrolyte interface connected by the dissolution reaction and passivation reaction, which is exhibited by two capacity reactance arcs in the middle and low-frequency regions in the Nyquist plot. Meanwhile, after the water phase transformation into ice, oxygen is bound in the ice crystal and moves slowly, which directly influences the rate and the relaxation frequency of the dissolution reaction and passivation reaction. No interface impedance response was detected when the test frequency was lower than 10−2 Hz. Impedance responses at different temperatures also confirm that the anodic reaction is limited by the cathodic process.
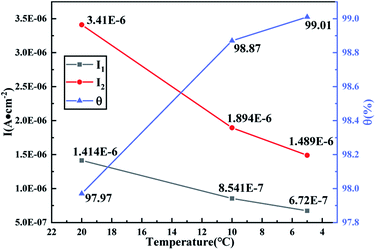 | ||
| Fig. 11 Temperature-dependence of the estimated kinetic parameters I1 and I2 and the physical parameter θ from EIS. | ||
| Relation | Relative equation | Function | Trend | Correlation |
|---|---|---|---|---|
| T–θ | θ = −0.051![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(0.156T) + 99.121 exp(0.156T) + 99.121 |
Exponential | Increasing | R2 = 0.99 |
| T–I1 | I1 = 4.086 × 10−7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(0.057T) + 1.277 × 10−7 exp(0.057T) + 1.277 × 10−7 |
Exponential | Decreasing | R2 = 0.99 |
| T–I2 | I2 = 5.054 × 10−7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(0.084T) + 7.215 × 10−7 exp(0.084T) + 7.215 × 10−7 |
Exponential | Decreasing | R2 = 0.99 |
6. Interpretation of the mechanism
When the metal contacts the electrolyte, the metal interface begins to undergo a complex and special corrosion process, which is shown in Fig. 12. Anodic reactions during corrosion indicate metal dissolution or the formation of metal oxides. When the anode dissolves to form Cu+ and Cu2+, a concentration gradient difference is generated and gradually diffuses into the electrolyte with great internal heterogeneity. As a result, most of the copper ions continue to react to form oxides or hydroxides (CuO, Cu2O) attached to the electrode surface, with a small portion migrating to the cathode with the action of the electric field. It is worth noting that the cathode is controlled by the reduction reaction of oxygen, and the migration process of dissolved oxygen near the cathode affects the formation process and the proportion of the dissolution reaction and corrosion products. In the aerobic condition, the effective reduction substance O2 in the electrolyte plays an important role in controlling the corrosion process. When the temperature decreases, it becomes difficult for O2 to migrate to the cathode, resulting in the decreased efficiency of the dissolution reaction and passivation reaction.When the distilled water phase transitions into ice, the internal electron/ion conduction is blocked, and oxygen is fixed and dispersed in the ice crystal, making it difficult for it to migrate to the cathode. In this case, the conductivity inside the ice mainly originates from the weak ion current of H+. The H+ reduction reaction generates H. However, the combination of atomic H to produce H2 requires high activation energy and the formation of the H adsorption film on the cathode surface hinders the cathode reaction. Thus, the dissolution and passivation reactions are weak and cannot be detected in the low-frequency region in the Nyquist plots. As the temperature decreases and the distance between the molecules shrinks, H3O+ and OH− find it more difficult to migrate to the electrodes on both sides, which inhibits the charge from crossing the electrical barrier at the electrode–liquid film boundary. The capacitance value Cs increases significantly before and after the phase transition.
Before and after the phase transition, H2O molecules shift towards polarization inside the medium to balance the electric field. Obviously, decreasing the temperature makes it more difficult for the H2O molecule to rotate. To compensate for the electric field balance, liquid water at the interface between copper and solid ice needs to displace more ions (H3O+, OH−) onto the electrode surface. In the transition from distilled water to ice, the decreasing temperature slows down the diffusion of H3O+ and OH− to the electrode surface, changing the equilibrium to increase the lifetime of the separated charge and increasing the ion concentration on the electrode surface. Thus, the capacitance Cdl increases significantly.
7. Conclusions
In this work, a mathematical model was established for the impedance response of copper in distilled water at different temperatures. This model can be used to investigate the kinetic parameters, structural parameters, and macro-dielectric properties of an electrochemical system on electrode performance.(1) The mathematical model considers the kinetics response of the electrode interface I1 and I2, and the degree of oxide film coverage θ on the electrode surface. The experimental results and model results in a well-fitting wide frequency range.
(2) Based on the real and imaginary parts of the complex permittivity converted from the test results, it is characterized that decreasing the temperature effectively inhibits the ion transfer rate and molecular polarization redirection. The relaxation process of the conductive medium controls the whole frequency region after the temperature is lower than 0 °C.
(3) A simple method is proposed to calculate the rates of the dissolution reaction and passivation reactions I1 and I2, respectively, and the fractional coverage of the oxide film θ through further derivation. As the temperature decreases, the rate of the dissolution and passivation reactions slows down, which also indicates the attenuation of oxide film growth.
(4) In this work, we aim to study the applicability of the mathematical model under a single condition, and provide a research basis for the subsequent study of the corrosion model in coupled environments. Future research will focus on electrochemical corrosion with the coupling of multiple environments.
Abbreviations
| ri | Charge transfer coefficient of the reaction i, C J−1 |
| COH− | Anion concentration, mol cm−3 |
| COH−bulk | Anion concentration in bulk solution, mol cm−3 |
| F | Faraday's constant, C mol−1 |
| J | Square root of −1 |
| ki | Rate constant of the reaction i |
| αi | Charge transfer coefficient |
| R | Ideal gas constant, J (mol K)−1 |
| T | Absolute temperature, K |
| K | A conversion coefficient, cm2 C−1 |
| E | Electrode potential, V |
| X | System variable |
| Itotal | Total current density, A cm−2 |
| Idl | Non-faradaic current density, A cm−2 |
| IF | Faradaic current density, A cm−2 |
| Ii | Faradaic current density of reaction i, A cm−2 |
| Q | Quantity of electric charge, C |
| Cdl | Electric double-layer capacitance, F |
| t | Time, s |
| θ | Oxide film coverage, % |
| YF | Faradaic admittance, Ω−1 cm−2 |
| ZF | Faradaic impedance, Ω cm2 |
| ω | Angular frequency, Hz |
| ω* | Characteristic frequency, Hz |
| τ | Time constant, s |
Subscripts
| dl | Double-layer |
| F | Faradaic current |
| SS | Steady-state |
| 1 | Dissolution reaction |
| 2 | Passivation reaction |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the National Natural Science Foundation of China (No. 51879180) and the Applied Basic Research Program in Shanxi Province (No. 20210302123139).Notes and references
- P. Han, R. Xie, N. Lin and B. He, Int. J. Electrochem. Sci., 2016, 11, 9491–9507 CrossRef CAS.
- X. Zeng, Z. Wang, J. Fan, L. Zhao, D. Lin and J. Zhao, J. Rock Mech. Geotech. Eng., 2011, 3, 250–259 CrossRef.
- S. P. Friedman, Comput. Electron. Agric., 2005, 46, 45–70 CrossRef.
- G. Kear, B. D. Barker and F. C. Walsh, Corros. Sci., 2004, 46, 109–135 CrossRef CAS.
- F. King, M. J. Quinn and C. D. Litke, J. Electroanal. Chem., 1995, 385, 45–55 CrossRef.
- J. H. Hong, S. H. Lee, J. G. Kim and J. B. Yoon, Corros. Sci., 2012, 54, 174–182 CrossRef CAS.
- D. Q. Zhang, Q. R. Cai, L. X. Gao and K. Y. Lee, Corros. Sci., 2008, 50, 3615–3621 CrossRef CAS.
- G. M. O'Connor, K. Lepkova, J. J. Eksteen and E. A. Oraby, Hydrometallurgy, 2018, 181, 221–229 CrossRef.
- H. H. Strehblow and H. D. Speckmann, Mater. Corros., 1984, 35, 512–519 CrossRef CAS.
- N. Boulay and M. Edwards, Wat. Res., 2001, 35, 683–690 CrossRef CAS PubMed.
- Y. Wan, X. Wang, H. Sun, Y. Li, K. Zhang and Y. Wu, Int. J. Electrochem. Sci., 2012, 7, 7902–7914 CAS.
- P. Szakálos, G. Hultquist and G. Wikmark, Electrochem. Solid-State Lett., 2007, 10, 63–67 CrossRef.
- B. O. Hasan, Coll. Eng. J., 2010, 13, 66–73 CrossRef.
- M. Wu, Z. Gao, S. Wu, Y. Liu and W. Hu, Int. J. Electrochem. Sci., 2021, 16, 1–14 Search PubMed.
- E. Barsoukov and J. R. Macdonald, Impedance Spectroscopy Theory, Experiment, and Applications, John Wiley & Sons, Hoboken, Third., 2018 Search PubMed.
- A. M. Svensson, L. O. Valøen and R. Tunold, Electrochem. Sci., 2005, 50, 2647–2653 CAS.
- K. F. Khaled, Mater. Chem. Phys., 2011, 125, 427–433 CrossRef CAS.
- S. M. Wilhelm, Y. Tanizawa, C. Y. Liu and N. Hackerman, Corros. Sci., 1982, 22, 791–805 CrossRef CAS.
- G. Cassone, P. v. Giaquinta, F. Saija and A. M. Saitta, J. Phys. Chem. B, 2014, 118, 4419–4424 CrossRef CAS.
- P. Han, Y. Zhang, F. Y. Chen and X. Bai, J. Cent. South Univ., 2015, 22, 4318–4328 CrossRef.
- G. Song, Cem. Concr. Res., 2000, 30, 1723–1730 CrossRef CAS.
- D. C. Grahame’, J. Electrochem. Soc., 1952, 89, 370–385 CrossRef.
- J. P. Meyers, M. Doyle, R. M. Darling and J. Newman, J. Electrochem. Soc., 2000, 147, 2930–2940 CrossRef CAS.
- J. Zhang, Electrochemical Measurement Technology, Chemical Industry Press, Beijing, First., 2010, vol. 5 Search PubMed.
- A. Lasia, Electrochemical Impedance Spectroscopy and its Applications, Kluwer Academic/Plenum Publishers, New York, First., 1999, vol. 32 Search PubMed.
- M. Keddam, H. Takenouti, X. R. Nvoa, C. Andrade and C. Alonso, Cem. Concr. Res., 1997, 27, 1191–1201 CrossRef CAS.
- D. Kong, C. Dong, M. Zhao, X. Ni, C. Man and X. Li, Corros. Eng. Sci. Technol., 2018, 53, 122–130 CrossRef CAS.
- C. Wang, W. Li, Y. Wang, X. Yang and S. Xu, Constr. Build. Mater., 2020, 247, 1–15 Search PubMed.
- M. A. Danzer, Batteries, 2019, 5, 1–16 CrossRef.
- C. Wang, W. Li, Y. Wang, X. Yang and S. Xu, Constr. Build. Mater., 2020, 247, 118562 CrossRef CAS.
- P. Mishra, D. Yavas, A. F. Bastawros and K. R. Hebert, Electrochim. Acta, 2020, 346, 1–11 CrossRef.
- D. Clematis, T. Ferrari, A. Bertei, A. M. Asensio, M. P. Carpanese, C. Nicolella and A. Barbucci, Electrochim. Acta, 2021, 391, 138916 CrossRef CAS.
- D. A. Harrington, ECS Trans., 2013, 45, 3–14 CrossRef.
- N. S. Shah, P. S. Shah and V. A. Rana, Ionics, 2015, 21, 3217–3222 CrossRef CAS.
- J. Świergiel and J. Jadźyn, Ind. Eng. Chem. Res., 2011, 50, 11935–11941 CrossRef.
- S. Lanfredi and A. C. M. Rodrigues, J. Appl. Phys., 1999, 86, 2215–2219 CrossRef CAS.
- W. Jin, Dielectric physics, China Machine Press, Beijing, First., 1997 Search PubMed.
- L. Daikhin and V. Tsionsky, J. Phys. Condens. Matter, 2007, 19, 1–16 CrossRef.
- V. G. Artemov and A. A. Volkov, Ferroelectr, 2014, 466, 158–165 CrossRef CAS.
- C. N. Cao and J. Q. Zhang, An Introduction to Electrochemical Impedance Spectroscopy, Science Press, Beijing, First., 2002 Search PubMed.
- C. N. Cao, Electrochim. Acta, 1990, 35, 831–836 CrossRef CAS.
- F. C. Walsh, Trans. Inst. Met. Finish., 1991, 69, 155–157 CrossRef CAS.
- Y. Feng, W. K. Teo, K. S. Siow, K. L. Tag and A. K. Hsieh, Corros. Sci., 1996, 38, 369–385 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |