Open Access Article
Open Access ArticleDeeply-recursive convolutional neural network for Raman spectra identification
Wei Zhou ,
Yujun Tang,
Ziheng Qian,
Junwei Wang and
Hanming Guo
,
Yujun Tang,
Ziheng Qian,
Junwei Wang and
Hanming Guo *
*
College of Optical-Electrical and Computer Engineering, University of Shanghai for Science & Technology, Shanghai, China. E-mail: hmguo@usst.edu.cn
First published on 10th February 2022
Abstract
Raman spectroscopy has been widely used in various fields due to its unique and superior properties. For achieving high spectral identification speeds and high accuracy, machine learning methods have found many applications in this area, with convolutional neural network-based methods showing great advantages. In this study, we propose a Raman spectral identification method using a deeply-recursive convolutional neural network (DRCNN). It has a very deep network structure (up to 16 layers) for improving performance without introducing more parameters for recursive layers, which eases the difficulty of training. We also propose a recursive-supervision extension to ease the difficulty of training. By testing several different open-source spectral databases, DRCNN has achieved higher prediction accuracies and better performance in transfer learning compared with other CNN-based methods. Superior identification performance is demonstrated, especially by identification, for characteristically similar and indistinguishable spectra.
1. Introduction
Raman spectroscopy has been applied extensively in many fields for substance characterization due to its advantages of rich information, convenient and fast detection, small interference from water, and so on.1–7 As the databases continue to expand and become more complex, classical linear methods of processing information are no longer sufficient and thus machine learning methods for extracting chemical information have been implemented due to their strong ability to analyse big data.8 Among the many machine learning methods, convolutional neural network (CNN)-based methods observably outperform other methods because CNNs not only greatly simplify the machine identification system of Raman spectroscopy but also achieve significantly higher accuracy.9 As an end-to-end processing method, CNNs can complete the integration process from input data to output results directly. Pre-processing such as baseline correction and noise filtering are not necessary for CNN-based models; Liu et al. have made comparisons and demonstrated this point.9Since the first CNN-based method was introduced for the identification of Raman spectroscopy by Liu et al. in 2017,9 various applications in different fields have been proposed. Jahoda et al. summarized and synthesized the previous methods and verified them.10 Fan et al. proposed the DeepCID approach to solve component identification problems.11 Zhang et al. described a transfer learning method using both CNNs and DNNs to improve the classification accuracy of organics.12 Huang et al. also used a transfer learning method based on a GoogLeNet model for the field identification and classification of gasoline evidence.13 Ho et al. applied CNN-based deep learning approaches to accurately identify 30 common bacterial pathogens.14 Deng et al. proposed a method that can learn multi-scale features using the automatic combination of multi-receptive fields of convolutional layers.15
There are also other CNN-based methods applied in prostate cancer detection,16 microbial identification,17 diagnosis of hepatitis B,18 blood species identification,19 diagnosis of breast cancer,20 tongue squamous cell carcinoma classification,21 and so on.
However, most of these methods are only for binary classification problems16,18,20,21 or for a few categories of spectra.14,15,17,19 These proposed models have shallow networks and simple structures9–12 while deeper and more complex CNN models have achieved great success in image problems. In theory, with the depth and complexity of the network model, its receptive field will continue to grow and its feature extraction ability will continue to be enhanced.22–24 The identification function is expected to be better fitted as more parameters are introduced and finally, a most appropriate model can be found to make a more accurate classification prediction. However, complex models are very hard to train. Too many parameters will easily lead to gradient disappearance or gradient explosion, that is, the model cannot be effectively fitted or will result in over-fitting. Intuitively speaking, the prediction accuracy of the validation set cannot be improved all the time, or soon reach 100%, while the identification performance of the test set is very poor. Meanwhile, very large models are difficult to save and modify, and each training takes a long time.25,26
In this study, we propose a Raman spectral identification method using a deeply-recursive convolutional neural network (DRCNN). DRCNN can repeatedly apply the same convolutional layer (recursive layer) as many times as wanted without increasing the number of parameters, while the network becomes deeper by more recursions being performed. The recursions have been done 9 times in this study and eventually formed a 16-layer network. DRCNN is easily trained and converges quickly. Problems like gradient disappearance or explosion and over-fitting have been well avoided. We also propose an extension that all recursions are supervised, which makes the model easier to train. Feature maps after each recursion are used to reconstruct the identification results with the same reconstruction method for all recursions but different level weights. We have tested various Raman spectral databases and compared them with other methods. DRCNN has better performance in prediction accuracy and transfer learning.
2. Method
2.1 Database
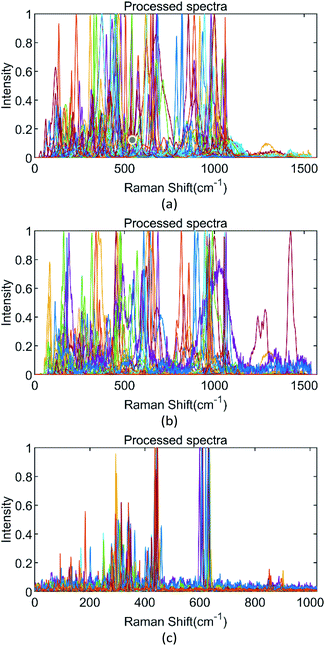
In this study, two different Raman spectral databases have been applied.One suitable database for testing the efficacy of DRCNN is the RRUFF mineral database. It was founded in 2006 at Arizona State University by Prof. Robert Downs.27 The RRUFF database contains a complete set of Raman spectral data from well-characterized minerals. It is the most widely applied database by related researchers because of its abundant data, comprehensive categories and high spectral quality. To make a more exact comparison, we used the same selection method as Sang et al.22 to construct two data subsets. Dataset_1 only retained the spectral data of the same category with no less than ten samples, which can be considered as having sufficient samples. Dataset_2 only retains the spectral data of the same category with no less than two samples. Data augmentation was not performed with these two subsets. Dataset_1 finally contains 192 classes of 5292 spectra and Dataset_2 contains 1332 classes of 8578 spectra. Parts of the spectra in these two subsets are shown in Fig. 1(a), in the wavenumber range from 30 to 1599 cm−1, a total of 1570 data points, with the intensity ranging from 0 to 1 by individual normalization. To verify the possible impact of data augmentation, Dataset_3 was constructed, containing 4794 Raman spectra in total and 1322 classes after removing some classes whose data volumes were only one or greater than 20. The amount of data in each class was increased to around 20 by making simple copies. As a result, Dataset_3 contains 1322 classes of 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 479 spectra in total. Each spectrum in Dataset_3 has been converted to a vector of 1024 intensity values from 0 to 1700 cm−1, and the intensity is from 0 to 1 by normalization. Parts of the spectra are shown in Fig. 1(b).
479 spectra in total. Each spectrum in Dataset_3 has been converted to a vector of 1024 intensity values from 0 to 1700 cm−1, and the intensity is from 0 to 1 by normalization. Parts of the spectra are shown in Fig. 1(b).
Another source of data is from the Bio-Rad Company, which provides high-quality Raman spectral databases with their renowned Sadtler databases. Their KnowItAll Raman spectral library offers access to over 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Raman spectra. Like Zhang et al.,12 we applied the Raman spectra of 377 organics from KnowltAll pre-processed with baseline correction and scaling. We also downloaded a total of 216 Raman spectra containing 72 organics (each class contains 3 Raman spectra) collected by Zhang as the target dataset. For the Raman spectral organics dataset from KnowItAll, data augmentation was applied by shifting wavenumbers and adding Gaussian noises, generating a total of 5278 spectral data. Part of the organics spectra is shown in Fig. 1(c). The wavenumber range is from 200 to 3600 cm−1 in 1024 data points, with intensity from 0 to 1 by normalization. This database was prepared for transfer learning based on DRCNN.
000 Raman spectra. Like Zhang et al.,12 we applied the Raman spectra of 377 organics from KnowltAll pre-processed with baseline correction and scaling. We also downloaded a total of 216 Raman spectra containing 72 organics (each class contains 3 Raman spectra) collected by Zhang as the target dataset. For the Raman spectral organics dataset from KnowItAll, data augmentation was applied by shifting wavenumbers and adding Gaussian noises, generating a total of 5278 spectral data. Part of the organics spectra is shown in Fig. 1(c). The wavenumber range is from 200 to 3600 cm−1 in 1024 data points, with intensity from 0 to 1 by normalization. This database was prepared for transfer learning based on DRCNN.
Re-sampling was applied for all databases above.
2.2 DRCNN model
The network takes an input Raman spectrum as input x and predicts the accurate class y of the spectrum in the Raman spectral identification method. Our goal is to learn a model f that predicts values y′ = f(x), where y′ is the estimate of the ground truth output y. Four subnet functions were introduced and denoted by f1, f2, f3, f4 which express embedding, inference, reconstruction and exportation, respectively. Our model is the composition of four functions: f(x) = f4(f3(f2(f1(x)))).Embedding the subnet takes the input spectral data and represents it as a set of feature maps. The inference subnet is the main component of DRCNN. It was constructed by a single repeat recursive layer with supervision extensions. The receptive field is widened with every recursion applying the same convolution followed by supervision layers. The reconstruction subnet collects every recursive layer and transforms the multi-channel feature maps back into the original one-dimensional data. Finally, the exportation of the subnet makes the identification.
For the sake of subsequent representations, we will define some operations.
 | (1) |
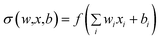 | (2) |
We take the rectified linear unit (ReLU) as our activation function, which is defined as
| ReLU(x) = max(0,xi) | (3) |
Pooling can be regarded as non-linear down-sampling, which can reduce the size of the representation, the number of parameters and the amount of computation.28 We use the MaxPooling method to increase the robustness of Raman spectrum peak displacement. The pooling size and the stride we used were all 2; this was defined as
| MaxPooling(x) = max(xi,j,xi+1,j,xi,j+1,xi+1,j+1) | (4) |
A SoftMax function was needed in the final layer as a classifier to predict the output result. It is defined as
 | (5) |
Embedding net f1(x) takes the input Raman spectrum as the vector x and computes the output matrix L0. The formulas are as follows:
| Linput = x | (6) |
| L−1 = ReLU(conv(W−1,Linput,b−1)) | (7) |
| L0 = ReLU(conv(W0, L−1, b0)) | (8) |
| f1(x) = L0 | (9) |
The weight W−1 has 64 out-channels and W0 has 128 out-channels and their biases have the same features.
The inference net f2(x) takes the input matrix L0 and computes the inference layers from L1 to LD. Each inference layer has been supervised simultaneously and Y layers and Z layers have been acquired by conv calculation as supervision layers.
Let g denote the single recursion function in a recursive layer:
| g(L) = conv(W,L,b) | (10) |
The recurrence relation is
| Li = g(Li−1) = ReLU(conv(W,Li−1,b)), | (11) |
Then, we get supervision layers for each inference layer:
| Yi = MaxPooling(ReLU(conv(WY,Li,bY))) | (12) |
| Zi = MaxPooling(ReLU(conv(WZ,Yi,bZ))) | (13) |
We introduced G to denote the whole inference processing including supervision:
| G(Li) = Z(Y(g(Li−1))) | (14) |
Inference net f2 is equivalent to the composition of the same elementary function G:
| f2(L) = (G°G°⋯G°)G(L) = GD(L), | (15) |
Reconstruction net f3 integrated D inference layers into a reconstruction layer through a level weights matrix WD. The initial weights were averaged for each inference layer and the optimal weights are automatically learned during training. The sum of all the elements in WD is WD−sum. One more conv was applied for better feature extraction. The formulas of this subnet are as follows:
 | (16) |
| LD+2 = MaxPooling(ReLU(conv(Wrec,LD+1,brec))) | (17) |
| Lrec = flatten(LD+2) | (18) |
| f3(L) = Lrec | (19) |
As the convolution layers continue to increase, the channels of weights also increase. This is to obtain more characteristic information and improve the fitting ability of the model.
Flatten is a process of turning the multidimensional nested array into a one-dimensional array. Here, it is used as a transition from the convolution layer to the fully connected layer.
The exportation net f4(L) takes the flattened layer Lrec as the input and gives out the final identification prediction via SoftMax function. DNN-based methods have been applied in this subnet. Normalization and dropout have also been applied to avoid overfitting.
| Ld1 = ReLU(Norm(σ(Wd1,Lrec,bd1))) | (20) |
| Dropout(Ld1,0.5) | (21) |
| Ld2 = ReLU(Norm(σ(Wd2,Ld1,bd2))) | (22) |
| Dropout(Ld2,0.5) | (23) |
| y′ = SoftMax(Ld2,n) | (24) |
| f4(L) = y′ | (25) |
Ld1 has 1024 units and Ld2 has 512 units related by Wd1 and Wd2. n denotes the number of total classes of all spectra in the database. The detailed parameters of each layer in DRCNN are presented in Table 1.
| Subnet | Layers | Type | Output shape | Parameters |
|---|---|---|---|---|
| a The parameters of the Conv1D represent filters, kernel size, strides, the MaxPooling1D represent pool size, strides, the dense represent units, and the dropout represent rate. | ||||
| Input | Input | (Batch, 1024, 1) | — | |
| Embedding | L−1 | Conv1D | (Batch, 1024, 64) | (64, 3, 1) |
| L0 | Conv1D | (Batch, 1024, 128) | (128, 3, 1) | |
| Inference | LD | Conv1D | (Batch, 1024, 128) | (128, 3, 1) |
| Max_pooling1d | (Batch, 512, 128) | (2, 2) | ||
| Y | Conv1D | (Batch, 512, 256) | (256, 3, 1) | |
| Max_pooling1d | (Batch, 256, 256) | (2, 2) | ||
| Z | Conv1D | (Batch, 256, 512) | (512, 3, 1) | |
| Max_pooling1d | (Batch, 128, 512) | (2, 2) | ||
| Reconstruction | LD+1 | tf.math.add_n | (Batch, 128, 512) | — |
| LD+2 | Conv1D | (Batch, 128, 1024) | (1024, 3, 1) | |
| Max_pooling1d | (Batch, 64, 1024) | (2, 2) | ||
| Lrec | Flatten | (Batch, 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 536) 536) |
— | |
| Exportation | Ld1 | Dense | (Batch, 1024) | (1024) |
| Normalization | (Batch, 1024) | — | ||
| Dropout | (Batch, 1024) | (0.5) | ||
| Ld2 | Dense | (Batch, 512) | (512) | |
| Normalization | (Batch, 512) | — | ||
| Dropout | (Batch, 512) | (0.5) | ||
| Output | Dense | (Batch, #classes) | (#Classes) | |
We have all components for our model, and the graphic description of the DRCNN architecture is shown in Fig. 2.
The importance of picking the optimal depth of recursions is reduced as our supervision enables utilizing the reconstruction layer from all intermediate inference layers. If recursions are too deep for the given task, the early inference layers are expected to receive high-level weights while the later layers are low. In our experiment, recursions were performed 9 times and the 6th layer of recursions has the maximal level weight.
2.3 Training
For an input spectrum x, there may be consistency or inconsistency between the model's predicted classification y′ and its real class y. For a Raman spectral database, there will be a comprehensive difference between all the predicted results and the true values. The loss function is introduced to judge the degree of this classification difference. In this study, categorical cross-entropy29 loss function has been applied.
 | (26) |
X and Y represent a collection of all spectra and their categories, respectively; parms denotes all the parameters in DRCNN. The target of training is to minimize the loss function by searching for the most appropriate combination of parameters. In principle, the prediction becomes more accurate as the loss function decreases and gets closer to zero.
The adaptive moment estimation (Adam)30 is used to train DRCNN as an optimizer since it requires little memory and has high computational efficiency. It is invariant to the diagonal rescaling of the gradients and is well suited for non-stationary objective functions that have a large amount of data. The parameters of the Adam optimizer are set to learning_rate = 0.0001, beta_1 = 0.9, beta_2 = 0.999.
The spectra in each dataset are split into the training set and test set in the fixed ratio of 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 randomly according to category labels in order to ensure that each category has samples in the training set and test set around the approximate proportion. Here, 20% of the data in the training set are set as the validation set to evaluate the fit of the model being trained and understand the situation of model training. Based on the size of the data set, the ratio is selected as the training set
3 randomly according to category labels in order to ensure that each category has samples in the training set and test set around the approximate proportion. Here, 20% of the data in the training set are set as the validation set to evaluate the fit of the model being trained and understand the situation of model training. Based on the size of the data set, the ratio is selected as the training set![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) validation set
validation set![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test set = 56
test set = 56![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 in general. As a result, for Dataset_1, after dividing the data set using this ratio, the training set, validation set, and test set contain 2964, 740, and 1588 spectral data, respectively. For Dataset_2, the training set, validation set, and test set contain 4803, 1201, and 2574 spectral data, respectively. For Dataset_3, the training set, validation set, and test set contain 14
30 in general. As a result, for Dataset_1, after dividing the data set using this ratio, the training set, validation set, and test set contain 2964, 740, and 1588 spectral data, respectively. For Dataset_2, the training set, validation set, and test set contain 4803, 1201, and 2574 spectral data, respectively. For Dataset_3, the training set, validation set, and test set contain 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 828, 3707, and 7944 spectral data, respectively. Therefore, it can not only ensure that the training set has sufficient data to train the model, the validation set evaluates the training situation of the model during the training process correctly, but also the reliability of the results of the test set.22 The weights and biases of DRCNN are initialized randomly and the batch size is 32. We set the upper limit epoch as 200 while early stopping is applied to prevent overfitting and save time. The training will be terminated if the prediction accuracy of the validation set does not improve within 30 epochs.
828, 3707, and 7944 spectral data, respectively. Therefore, it can not only ensure that the training set has sufficient data to train the model, the validation set evaluates the training situation of the model during the training process correctly, but also the reliability of the results of the test set.22 The weights and biases of DRCNN are initialized randomly and the batch size is 32. We set the upper limit epoch as 200 while early stopping is applied to prevent overfitting and save time. The training will be terminated if the prediction accuracy of the validation set does not improve within 30 epochs.
The loss, recall, precision and AUC epoch curve are shown in Fig. 3.
As for transfer learning, we first trained the base model with 5278 organic spectra of 377 categories downloaded from KnowltAll. As shown in Fig. 2, DRCNN converged very quickly when various figures of merits reached the maximum or minimum value with 20 epochs, and the training was completed within 40 epochs while most of the other models usually take hundreds of epochs for training like Liu's9 and Fan's.11 The model weights were saved after training. The model was reconstructed and the dimension of the final layer for the prediction result was changed to be the same as the number of target organic spectral categories. The parameter weights of other layers were loaded from the saved base model. After retraining 144 target spectra of 72 organics, the prediction result of the remaining 72 spectra was determined.
DRCNN was implemented in Python programming language and based on NumPy and Keras.31 The training of DRCNN was performed on a single NVidia GTX Titan GPU. The operating system was Ubuntu 16.0 with an Intel Core i9-7900X processor and 256G DDR4 memory.
3. Results and discussion
We firstly trained and tested DRCNN based on the RRUFF database. The prediction confusion matrix of Database_1 is shown in Fig. 4 as an example. It can be seen that little green squares are linearly distributed diagonally in the figure, which means that there is a high degree of consistency between the predicted label and the actual label. It proves the reliability and veracity of DRCNN. | ||
| Fig. 4 The confusion matrix of the prediction results on Database_1. There are 192 classes of 1588 spectra in the test set. | ||
Precision, recall and F1-score were used to evaluate the performance of the models and make comparisons in this study; their definitions are as follows:
 | (27) |
 | (28) |
 | (29) |
In the databases, the number of spectral samples in each class is imbalanced. One class might have more than 100 spectra while another class only has 3 spectra. Because we randomly split the data into the training set and test set according to a fixed ratio, the number of samples in the test set is also imbalanced. Therefore, it is more appropriate to use the weighted average method, which gives different weighted calculated values to different classes. The weighted flag is defined as follows:
 | (30) |
The formulas for weighted-precision, weighted-recall and weighted-F1-score are defined as follows:
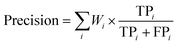 | (31) |
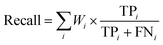 | (32) |
 | (33) |
The top 1, 3 and 5 accuracies have also been applied and accuracy is defined as follows:
 | (34) |
We compared DRCNN with four other CNN models proposed by Liu et al.,9 Fan et al.,11 Zhang et al.,12 and Sang et al.22 on the RRUFF database, which includes three subsets. Due to the random initialization of parameters and random split of the data set, there will be some small differences in the results obtained from each model training and prediction. Therefore, we ran each model 30 times in a circular fashion without repetition. Each run is independent, and its initialization parameters and spectral distribution of training set, validation set and the test set will all change, thus exerting some influence on the results. The results of each run are saved. We take the average results of 30 independent runs as the final result of the model. For each model, the above 30 independent runs were measured and the comparison of averaged results was enumerated in Table 1. We also compared the transfer learning performance with that of Zhang et al.12 on an organics database and the results are shown in Table 2. Because there is only one spectrum in the test set for each category, other figures of merits are not listed.
| Liu et al. | Fan et al. | Zhang et al. | Sang et al. | DRCNN | |
|---|---|---|---|---|---|
| Dataset_1 | |||||
| Precision | 0.9660 | 0.9718 | 0.9653 | 0.9799 | 0.9813 |
| Recall | 0.9601 | 0.9679 | 0.9583 | 0.9772 | 0.9798 |
| F1-score | 0.9587 | 0.9667 | 0.9563 | 0.9763 | 0.9794 |
| Top1 acc. | 0.9601 | 0.9679 | 0.9583 | 0.9772 | 0.9798 |
| Top3 acc. | 0.9927 | 0.9938 | 0.9940 | 0.9976 | 0.9981 |
| Top5 acc. | 0.9944 | 0.9955 | 0.9962 | 0.9984 | 0.9981 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Dataset_2 | |||||
| Precision | 0.8846 | 0.8893 | 0.8990 | 0.9127 | 0.9298 |
| Recall | 0.8309 | 0.8368 | 0.8466 | 0.8791 | 0.8842 |
| F1-score | 0.7950 | 0.8070 | 0.8192 | 0.8511 | 0.8579 |
| Top1 acc. | 0.8309 | 0.8368 | 0.8466 | 0.8791 | 0.8818 |
| Top3 acc. | 0.9096 | 0.8981 | 0.9140 | 0.9279 | 0.9347 |
| Top5 acc. | 0.9199 | 0.9094 | 0.9233 | 0.9339 | 0.9347 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Dataset_3 | |||||
| Precision | — | 0.8549 | 0.9006 | 0.9181 | 0.9271 |
| Recall | — | 0.6581 | 0.7950 | 0.8305 | 0.8419 |
| F1-score | — | 0.5921 | 0.7523 | 0.7925 | 0.8055 |
| Top1 acc. | — | 0.6581 | 0.7950 | 0.8305 | 0.8419 |
| Top3 acc. | — | 0.7746 | 0.8880 | 0.9062 | 0.9115 |
| Top5 acc. | — | 0.8041 | 0.9130 | 0.9221 | 0.9251 |
As can be seen from the data in Table 2, DRCNN showed better performance in all evaluation figures of merits for various datasets. For Database_1, which can be considered as having sufficient samples, DRCNN has a weighted precision of 0.9813, which indicates the ability to have high accuracy in predicting positive samples. The 0.9798 recall rate shows that DRCNN is correctly identified with a high percentage of positive samples. The good balance between accuracy and recall has also been approved by the 0.9794 F1-score. For Database_2, although the figures of merits for each model are very close, DRCNN still shows slight advantages. For Database_3, the Raman spectra of which are seen as general-quality, DRCNN gets the highest prediction accuracy once again. It is worth mentioning that simple network structure models are powerless for general-quality spectral data. The model of Liu et al. cannot make a valid prediction for Dataset_3, while deep and complex network models maintain good performances like those of Sang et al.22 and ours.
In conclusion, those evaluation figures of merits together with the top 1, 3 and 5 accuracies of DRCNN are all higher than that of the models proposed by others towards three different subsets of the RRUFF mineral database, which demonstrates its superiority, stability and robustness.
As shown in Table 3, for transfer learning, DRCNN has great advantages as a CNN-based model that predicts more than 10 percent accuracy as compared to Zhang et al.‘s CNN model and is also higher than Zhang et al.‘s DNN model. The prediction confusion matrix for target organics Raman spectra is shown in Fig. 6. There is only one spectrum that DRCNN has not predicted accurately but is in the third accuracy possibility, which means that the top-3 accuracy of the target Raman spectra is 100%.
| Zhang et al. DNN | Zhang et al. CNN | DRCNN | |
|---|---|---|---|
| Top-1 acc. | 96.4% | 86.0% | 98.1% |
 | ||
| Fig. 6 The confusion matrix of the prediction results on 72 organics target tests set by DRCNN-based transfer learning. | ||
We further analysed the identification of typical spectra that are characteristically similar and indistinguishable.
Because some substances have similar chemical properties, that is, similar molecular structures, their Raman spectral responses will be very close, so the obtained Raman spectra have similar positions and intensities of Raman peaks. In the process of model training and prediction, the feature extraction of similar spectra becomes difficult and the spectra are hard to distinguish. We selected some typical similar spectral contrast images as shown in Fig. 7. DRCNN performed well in identifying and classifying some of them while failing to classify others because they were too similar. However, compared with other models, DRCNN showed better recognition accuracy for these similar spectra. In the comparison tables above, DRCNN's higher accuracy is mainly due to the better prediction results obtained in these similar spectral classifications.
4. Conclusions
In this study, a deeply-recursive convolutional neural network (DRCNN) has been proposed for Raman spectral identification. DRCNN has a very deep network without too many parameters, which makes it easy to train and it converges quickly. Problems like gradient disappearance or explosion and over-fitting have been well avoided. By testing with different RRUFF mineral databases, DRCNN has shown a better performance as compared with other CNN-based models. DRCNN predicted 0.9813 accuracy for Dataset_1, 0.9298 accuracy for Dataset_2 and 0.9258 accuracy for Dataset_3. It is also useful in transfer learning and achieved 98.1% accuracy for the target organics database. After the training, DRCNN responded quickly to the test spectra within milliseconds for a spectrum. Proper parameter initialization will make the model converge faster. Larger spectral data volume and more spectral databases are expected to further improve its performance.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Funded by the National Natural Science Foundation of China (Grant No. 61975125) and Science & Technology Commission of Shanghai Municipality (STCSM) (Grant No. 21010502900).References
- K. Kneipp, H. Kneipp and V. Kartha, et al., Detection and identification of a single DNA base molecule using surface-enhanced Raman scattering (SERS), Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 57(6), 1667–1670 CrossRef.
- K. Kneipp and H. Kneipp, et al., Ultrasensitive Chemical Analysis by Raman Spectroscopy, Chem. Rev., 1999, 99, 2957–2975 CrossRef CAS PubMed.
- N. Stone, C. Kendall and J. Smith, et al., Raman spectroscopy for identification of epithelial cancers, Faraday Discuss., 2004, 126, 141 RSC.
- P. Rösch, M. Harz and M. Schmitt, et al., Raman spectroscopic identification of single yeast cells, J. Raman Spectrosc., 2005, 36(5), 377–379 CrossRef.
- M. B. Fenn, V. Pappu and P. G. Georgeiv, et al., Raman spectroscopy utilizing Fisher-based feature selection combined with Support Vector Machines for the characterization of breast cell lines, J. Raman Spectrosc., 2013, 44(7), 939–948 CrossRef CAS.
- J. J. González-Vidal, R. Perez-Pueyo and M. J. Soneira, et al., Automatic identification system of Raman spectra in binary mixtures of pigments, J. Raman Spectrosc., 2012, 43(11), 1707–1712 CrossRef.
- R. L. Aggarwal, S. Di Cecca and L. W. Farrar, et al., Chemical aerosol detection and identification using Raman scattering, J. Raman Spectrosc., 2015, 45(8), 677–679 CrossRef.
- F. Lussier, V. Thibault and B. Charron, et al., Deep learning and artificial intelligence methods for Raman and surface-enhanced Raman scattering, TrAC, Trends Anal. Chem., 2020, 124, 115–796 CrossRef.
- J. Liu, M. Osadchy and L. Ashton, et al., Deep convolutional neural networks for Raman spectrum recognition: a unified solution, Analyst, 2017, 142(21), 4067–4074 RSC.
- P. Jahoda, I. Drozdovskiy and S. J. Payler, et al., Machine learning for recognizing minerals from multispectral data, Analyst, 2021, 146(1), 184–195 RSC.
- X. Fan, W. Ming and H. Zeng, et al., Deep learning-based component identification for the Raman spectra of mixtures, Analyst, 2019, 144(5), 1789–1798 RSC.
- R. Zhang, H. Xie and S. Cai, et al., Transfer-learning-based Raman spectra identification, J. Raman Spectrosc., 2020, 51(1), 176–186 CrossRef CAS.
- T. Y. Huang and J. C. Yu, Development of Crime Scene Intelligence Using a Hand-Held Raman Spectrometer and Transfer Learning, Anal. Chem., 2021, 93(25), 8889–8896 CrossRef CAS PubMed.
- C. S. Ho, N. Jean and C. A. Hogan, et al., Rapid identification of pathogenic bacteria using Raman spectroscopy and deep learning, Nat. Commun., 2019, 10(1), 1–8 CrossRef PubMed.
- L. Deng, Y. Zhong and M. Wang, et al., Scale-adaptive Deep Model for Bacterial Raman Spectra Identification, IEEE J. Biomed. Health Inform., 2021 Search PubMed.
- W. Lee, A. T. M. Lenferink and C. Otto, et al., Classifying Raman spectra of extracellular vesicles based on convolutional neural networks for prostate cancer detection, J. Raman Spectrosc., 2020, 51(2), 293–300 CrossRef CAS.
- M. K. Maruthamuthu, A. H. Raffiee and D. M. De Oliveira, et al., Raman spectra-based deep learning: A tool to identify microbial contamination, MicrobiologyOpen, 2020, 9(11), e1122 CrossRef CAS PubMed.
- H. Lu, S. Tian and L. Yu, et al., Diagnosis of hepatitis B based on Raman spectroscopy combined with a multiscale convolutional neural network, Vib. Spectrosc., 2020, 107, 103038 CrossRef CAS.
- S. Huang, P. Wang and Y. Tian, et al., Blood species identification based on deep learning analysis of Raman spectra, Biomed. Opt. Express, 2019, 10(12), 6129–6144 CrossRef CAS PubMed.
- L. W. Shang, D. Y. Ma and J. Fu, et al., Fluorescence imaging and Raman spectroscopy applied for the accurate diagnosis of breast cancer with deep learning algorithms, Biomed. Opt. Express, 2020, 11(7), 3673–3683 CrossRef CAS PubMed.
- M. Yu, H. Yan and J. Xia, et al., Deep convolutional neural networks for tongue squamous cell carcinoma classification using Raman spectroscopy, Photodiagn. Photodyn. Ther., 2019, 26, 430–435 CrossRef PubMed.
- X. Sang, R. Zhou and Y. Li, et al., One-Dimensional Deep Convolutional Neural Network for Mineral Classification from Raman Spectroscopy, Neural Process. Lett., 2021, 1–14 Search PubMed.
- A. Krizhevsky, I. Sutskever and G. Hinton, Imagenet classification with deep convolutional networks, Proceedings of the Conference Neural Information Processing Systems (NIPS), 1097 Search PubMed.
- K. Simonyan and A. Zisserman, Very deep convolutional networks for large-scale image recognition, 2014, arXiv preprint arXiv: 1409.1556.
- J. Kim, J. K. Lee and K. M. Lee, Deeply-recursive convolutional network for image super-resolution, Proceedings of the IEEE conference on computer vision and pattern recognition, 2016, pp. 1637–1645 Search PubMed.
- Y. Bengio, P. Simard and P. Frasconi, Learning long-term dependencies with gradient descent is difficult, IEEE Trans. Neural Netw., 1994, 5(2), 157–166 CAS.
- T. Armbruster and R. M. Danisi, The power of databases: the RRUFF project, Highlights in mineralogical crystallography, 2015, pp. 1–30 Search PubMed.
- I. Goodfellow, Y. Bengio and A. Courville, Deep learning, MIT Press, 2016 Search PubMed.
- J. Shore and R. Johnson, Axiomatic derivation of the principle of maximum entropy and the principle of minimum cross-entropy, IEEE Trans. Inf. Theory, 1980, 26(1), 26–37 CrossRef.
- D. P. Kingma and J. Ba, Adam: a method for stochastic optimization, 2014, arXiv preprint arXiv:1412.6980.
- F. Chollet, et al., Keras, 2015, https://github.com/fchollet/keras Search PubMed.
| This journal is © The Royal Society of Chemistry 2022 |