 Open Access Article
Open Access ArticleEffect of ligand groups on photoexcited charge carrier dynamics at the perovskite/TiO2 interface†
Landon Johnsona and
Dmitri Kilin *b
*b
aDepartment of Physics, North Dakota State University, Fargo, ND 58108, USA
bDepartment of Chemistry and Biochemistry, Fargo, ND 58108, USA. E-mail: dmitri.kilin@ndsu.edu
First published on 21st December 2021
Abstract
The work proposed here aims to describe the dynamics of photoexcited charge carriers at the interface between the perovskite and electron transport layer (ETL) in perovskite solar cells (PSCs) and the effect that the interface morphology has on these dynamics. This is done in an effort to further develop the understanding of these materials so that their chemical composition and morphology may be better utilized to improve PSCs by means of increasing the power conversion efficiency (PCE), maximizing the chemical stability of PSCs to lengthen their lifespan, finding the cheapest and easiest materials to synthesize which have beneficial properties in photovoltaics, etc. This is done by using density functional theory to model the interface and open system Redfield theory to describe the charge carrier dynamics. We find that the charge transfer characteristics at the perovskite/ETL interface depend greatly on the choice of ligands adsorbed on the ETL that act as a bridge between the perovskite and ETL. The two ligand choices discussed here go so far as to determine whether the system will undergo a Förster energy transfer or a Dexter energy transfer upon photoexcitation.
Introduction
Lead halide perovskites have been a popular research topic over the last several years for their applications to both photovoltaics1–6 and photoluminescence.7–10 Lead halide perovskites demonstrate promising features that include bandgap tunability,11,12 long range charge transfer,13 extended lifetime of excited-states,14–16 high quantum yield of photoluminescence,17–20 and high defect tolerance.21–24 Noticeable efficiency of perovskite devices25,26 can be attributed to the large values of their dielectric constants, which effectively cancel electron–hole interactions and allow for easy spatial separation of photoinduced electrons and holes.27 Certain materials have shown the ability to accept these separated charges from the perovskite when placed in contact with the perovskite.28–30 This increases the efficiency of charge separation and extraction, thereby improving the power conversion efficiency (PCE) of perovskite-based photovoltaic devices.31 Materials that accept electrons have been dubbed electron transport materials (ETMs) and hole accepting materials are likewise called hole transport materials (HTMs). Polyoxotitanate (POT) clusters and bulk TiO2 are frequently used as ETMs due to their low cost, ease of fabrication, chemical stability, and wide band gap.32 POTs can also be synthesized in a variety of molecular geometries including thin films, nanoclusters, and microporous structures.33–35 Perovskite-based solar cell designs that layer the perovskite between ETM and HTM layers have demonstrated PCEs above 20%,1 which is competitive with traditional p–n doped silicon diode solar cell efficiencies. In addition to this, perovskite-based solar cells are easier to produce than traditional solar cells and the fabrication process is much less demanding.36 TiO2 is often used as an ETM for photovoltaic interfaces, however the atomistic details of the interface between perovskite and titania need deeper exploration from both experimental and computational viewpoint. The formation of the interface between TiO2 and perovskite depends, in particular, on the choice of the precursor used in nucleation on TiO2 nanoparticles. In the work37 one used titanium isopropoxide. Before the TiO2 nanoparticles are deposited on indium tin oxide transparent electrode substrate and calcinated, one can practice ligand exchange chemistry for the control of the groups that will later interface the perovskite layer.Despite the success of perovskite-based solar cells in the laboratory, there are still aspects of their operation that are not fully understood. There is ongoing research into the origin of the hysteretic behavior of their I–V curves1 as well as the ultrafast (<1 ps) charge injection into ETMs/HTMs.28–30 This work focuses on the effects of ligands adsorbed to a POT ETM. More specifically, the ground state properties and photoexcited charge carrier dynamics of two different perovskite/ETM structures are explored. The difference between these two structures comes in the form of two different ligand groups acting as a bridge between the perovskite and ETM.
There are several challenges in computationally modeling the dynamics of these kinds of systems. For instance, there must be a method of achieving electronic transitions between orthogonal electronic states in order to simulate any charge carrier dynamics. In a closed quantum system, this is impossible. Therefore, we must perform our calculations in the framework of a more computationally expensive open quantum system,38,39 where our system of interest can interact with an external thermal bath. This is done by introducing additional nuclear degrees of freedom that act as this thermal bath. In order to treat the electron dynamics accurately with the nuclei in motion, one must go beyond the Born–Oppenheimer approximation and utilize the non-adiabatic coupling between the electronic and nuclear degrees of freedom.40,41 Another complication is that these dynamic processes are irreversible in reality and should be treated as such computationally. This is problematic because even with the inclusion of non-diagonal terms in the Hamiltonian matrix, standard Hamiltonian dynamics will result in reversible transfers back and forth between the electron donor (perovskite) and acceptor (TiO2).42
There are a handful of methods that are commonly utilized to address these challenges, based on time-dependent density functional theory,43 surface hopping,44 and Redfield theory45,46 to name a few. This work makes uses Redfield theory to analyze charge carrier relaxation, as described in the Methods section.
Methods
Static electronic structure
To find the ground state properties, the Vienna Ab initio Simulation Package (VASP) was used to perform Density Functional Theory (DFT) calculations. DFT is based on the Hohenberg–Kohn theorems.47 The first theorem states that the total ground state energy of a system is a functional of the electron density, which means that the electron density is sufficient to describe any ground state properties. The second theorem states that the electron density which minimizes the ground state energy is the exact ground state density. In order to find the ground state density, the self-consistent Kohn–Sham equations48 are solved recursively. This starts by supplying a trial density ρ. This trial density is used to determine the total and kinetic energy of the system, which in turn are used to solve for the potential energy:
 | (1) |
Here v, E, and T are the one-electron potential (potential energy per electron), total energy, and kinetic energies, respectively. The one-electron potential is then used to find the eigenstates of the fictitious one-electron Kohn–Sham equation:
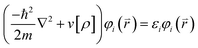 | (2) |
Here  stands for the eigenstates, or Kohn–Sham orbitals, while εi stands for the energy of the Kohn–Sham orbitals. With these orbitals, the electron density can be recalculated as:
stands for the eigenstates, or Kohn–Sham orbitals, while εi stands for the energy of the Kohn–Sham orbitals. With these orbitals, the electron density can be recalculated as:
 | (3) |
Static observables
After the ground state geometry was optimized, the density of states (DOS) was calculated using eqn (4) below:
 | (4) |
The absorption spectrum was also calculated using the optimized ground state. First, the transition dipole moment between orbitals i and j, Dij, is calculated as follows:
 | (5) |
Where  . The transition dipole moment is then used to calculate the oscillator strength, fij, using eqn (6) below:
. The transition dipole moment is then used to calculate the oscillator strength, fij, using eqn (6) below:
 | (6) |
Where me is the mass of an electron and Eij is the energy difference between orbitals i and j. The absorption of light at a given transition energy can then be written as
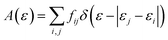 | (7) |
Treatment of dynamics
In order to calculate excited state electron dynamics with maximal accuracy, the nonequilibrium processes beyond the Born–Oppenheimer approximation are computed by accounting for the response of the electronic degrees of freedom to the changes in the nuclear configuration. This is done by using Redfield theory.49 In the ground state, and in the equilibrium geometry, the KS orbitals are orthogonal, meaning that
 | (8) |
However, upon an infinitesimal shift of one of the nuclear positions,  , the orthogonality of the KS orbitals breaks as quantified in the following equation:
, the orthogonality of the KS orbitals breaks as quantified in the following equation:
 | (9) |
This can be interpreted as “the overlap” of orbitals i and j with respect to ionic position I. In a real system, all of the ions will be moving so it is more accurate to assess an overlap when all of the ions are launched into thermal motion defined by the following two equations:
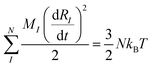 | (10) |
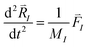 | (11) |
Where MI is the mass of the Ith ion, N is the total number of ions, kB is the Boltzmann constant, T is the temperature, and  is the net force acting on the ion. Now the overlap between two orbitals at any given time becomes
is the net force acting on the ion. Now the overlap between two orbitals at any given time becomes
 | (12) |
These overlaps can then be used to calculate the autocorrelation functions as functions of time interval τ:
 | (13) |
The transition rates can be calculated as Fourier transforms of the autocorrelation functions:
 | (14) |
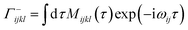 | (15) |
Here  is the angular frequency of a photon with energy equal to the energy gap between orbitals k and l. With the transition rates, the Redfield tensor is calculated as:
is the angular frequency of a photon with energy equal to the energy gap between orbitals k and l. With the transition rates, the Redfield tensor is calculated as:
 | (16) |
Finally, the Redfield tensor is used to compute the time dependent electron density matrix by solving the following equation:
 | (17) |
 is the electronic energy dissipation.
is the electronic energy dissipation.
Observables that characterize non-equilibrium dynamics
There are two main observables computed here with the time dependent electron density matrix. First, the time dependent charge distribution is calculated as:
 | (18) |
Second, the expectation value of the energy of excited charge carriers as a function of time are computed with these charge distributions as:
 | (19a) |
 | (19b) |
Where e and h represent electrons and holes, respectively. From the expectation value of the energy, the relaxation time to the frontier KS orbital (LUMO for electrons and HOMO for holes) is calculated as follows:
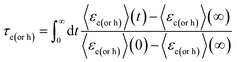 | (19c) |
The dynamics of spatial distribution of charges along z-axes is calculated as:
 | (20) |
Computational details
In order to obtain results that are representative of physical perovskite solar cells, auxiliary effects must be mitigated as much as possible. To this end, a sufficiently large system must be simulated to limit quantum confinement effects. However, as systems become larger, they become vastly more computationally expensive. There are also effects caused by strain on the species due to mismatched crystalline lattice periods of the perovskite and TiO2 which may skew results in an undesirable fashion.50,51 With this in mind, we model the two unit-cell-thick perovskite layer as Cs18Pb18Br54 with two dimensions repeating periodically. This should be sufficiently large to reduce quantum confinement effects without drastically increasing computational expense. The TiO2 is modeled as a Ti6O6 POT nanocluster core with isopropoxide, acetate, and hydroxyl ligands adsorbed to it. Nanoclusters are used instead of periodic POT structures to eliminate stress caused by mismatching periodicity of neighboring species.In order to test the effects of ligands attached to the POT ETM, the two identical periodic thin films of cesium lead bromide perovskite (Cs18Pb18Br54) are interfaced with different ligand groups of the POT nanoclusters adjacent to their respective boundaries. This simplifies the systems so that the effects of the ligands can be more directly observed. One POT cluster, Ti6O6(O2C2H3)6(OC3H7)3(OH)3, has hydroxyl groups that are situated adjacent to the perovskite, so this model is called the hydroxyl model. The other POT cluster, Ti6O6(O2C2H3)6(OC3H7)6, has acetate ligands adjacent to the perovskite, so this model is referred to as the acetate model. Visualizations of these models and the POT clusters are shown in Fig. 1, while binding energies can be found in Table 1.
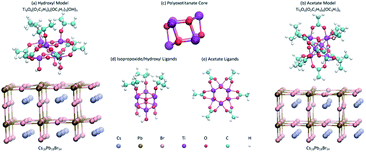 | ||
| Fig. 1 (a) Hydroxyl model and (b) acetate model used for simulations. The names of the models come from the ligands adjacent to the perovskite surface. Both models consist of a periodic cesium lead bromide perovskite film (bottom) and a POT nanocluster (top). The periodic boundary conditions are displayed in Fig. 7. The perovskite acts as an optical absorber while the POT acts as an electron transport material (ETM) to enhance charge separation and improve solar cell efficiency. The difference between these models is the orientation of and ligands attached to the POT. The perovskite films are stoichiometrically equivalent in both models. (c) shows the same POT core present in both models. All ligands except the hydroxyl groups are present in both models. (d) shows the attachment scheme of the isopropoxide ligands and the hydroxyl ligands. (e) shows the attachment scheme of the acetate ligands. | ||
| Observable/model | Hydroxyl | Acetate |
|---|---|---|
| Binding energy, eV | 1.176 | 0.445 |
| Bandgap, eV | 2.62 | 2.99 |
Electronic structure calculations have been done by density functional theory in a plane wave basis, with PAW pseudopotentials representing core electrons and the PBE exchange correlation functional as implemented in VASP software.
Molecular dynamics are computed at 1 fs time intervals for 1000 steps, totaling to 1 ps trajectories. The threshold energies are 10−3 eV between atomic iterations and 10−4 eV between electronic iterations. These trajectories are computed at 300 K.
Results
The band gap of the hydroxyl model was found to be less than that of the acetate model. For the numerical values, see Table 1. The projected density of states (PDOS) shown in Fig. 2 demonstrates different alignments of the band edges for these two systems. In the hydroxyl model, the valence band edge is localized on the perovskite while the conduction band edge is localized on the POT. In the acetate model, both band edges are localized on the POT. To visualize this, the frontier KS orbitals are inset in Fig. 2. The different band alignments result in two distinct processes of photo-excited charge carrier relaxation. In the hydroxyl model, the system will undergo a charge transfer, while the acetate model will see a Dexter energy transfer.A schematic diagram of typical photoexcitation pathways as determined by binding morphology and band alignment is summarized in Fig. 3. The available pathways of photoexcitation are dictated by relative alignment of energies of band edges. Here we compare energies of the band edges associated with each component of the interface: the edge of the conduction band for both perovskite (Eperov,CB) and POT (EPOT,CB) as well as the edge of the valence band for both perovskite (Eperov,VB) and POT (EPOT,VB). Interestingly, the hydroxyl-linked binding morphology results in alternating order of these energies
| Eperov,CB > EPOT,CB > Eperov,VB > EPOT,VB |
While the acetate model results in sequential ordering
| Eperov,CB > EPOT,CB > EPOT,VB > Eperov,VB | (21) |
The different band alignments, upon non-radiative relaxation of photoexcited charge carriers, cause a charge transfer in the hydroxyl model and a Dexter energy transfer in the acetate model.
The absorption spectra of the two models, shown in Fig. 4, are extremely similar qualitatively despite the differences in the POT clusters. This is because the perovskite is the major optical absorber in these systems. Note that there are no bright transitions from the valence band edge to the conduction band edge. This means that the charges must be excited to a state deeper within their respective bands and then relax to the band edges.
 | ||
| Fig. 4 Absorption spectra of (a) hydroxyl and (b) acetate models. Note that the two spectra are almost identical qualitatively. This is because the perovskite is the main absorber of visible light. | ||
As the main effort to assess the nonradiative pathways of the photoexcitation, we compute the nonradiative transitions as a consequence of electron–phonon interaction. The electron–phonon interaction is computed in the form of “on-the-fly” nonadiabatic couplings along thermalized molecular dynamics trajectory, as introduced in the Methods section. Averaged rates of elementary phonon-assisted electronic transitions are referred to as “elements of the Redfield tensor” and are illustrated in Fig. 5. Similar qualitative features are observed for both models. The diagonal elements are zero which is to be expected as electronic transitions between a state and itself are forbidden. The sub diagonal elements take maximal values, meaning that transitions are most likely to happen between energetically neighboring states. The elements which are far from the main diagonal are approximately equal to zero, meaning that transitions between energetically non-neighboring states are very unlikely.
 | ||
| Fig. 5 Sample of the Redfield tensors near the band gap of (a) hydroxyl and (b) acetate models. Riijj represents the transition rate from orbital i to orbital j. This is calculated using eqn (16). Observe the similar qualitative features for both models. The elements far from the main diagonal are approximately zero, the elements along the main diagonal are zero, and the elements along the sub diagonals take maximal values. This can also be approximated as Riijj ≈ δi+1,j + δi−1,j, meaning that transitions between energetically neighboring orbitals will dominate relaxation pathways. The “band gap” labels are placed between HO and LU rather than marking both HO and LU for the sake of visual clarity. | ||
The elements of the Redfield tensor parametrize the equation of motion for electronic degrees of freedom as introduced in the Methods section and allows computation of nonequilibrium dynamics of occupations of KS orbitals for any initial excitations. Fig. 6 shows a representative example of such dynamics. The initial excitations are chosen based on the likelihood of electronic excitation. This is determined with respect to the excitation energy and maximal oscillator strength for a particular pair of orbitals. Specifically, Fig. 6 illustrates dynamics for the (HO−3) → (LU+13) excitation in the hydroxyl model and the (HO−2) → (LU+10) excitation in the acetate model. The dynamics of transient occupation of orbitals are computed in the conduction band, ρii(t), i ≥ LU for electrons, while the dynamics for transient abscence of occupation of orbitals are calculated in the valence band, ρjj(t), j ≤ HO for holes. As expected from the Redfield tensor elements shown in Fig. 5, the nonequilibrium occupation in the conduction band sequentially “visits” orbitals in a descending order of energies
| i → i − 1 →…→ LU+1 → LU | (22) |
 | ||
| Fig. 6 Electron (a and b) and hole (c and d) state occupations, ρij(t), for (a and c) hydroxyl and (b and d) acetate models along excited state trajectory. This is calculated using eqn (17). The initial excitations used for each model are those with the highest oscillator strength. They hydroxyl model features an excitation from HO−3 to LU+13 and the acetate model features an excitation from HO−2 to LU+10. Observe the sequential redistribution of charge carriers between states. This is to be expected from the Redfield tensor elements shown in the Fig. 5. | ||
The nonequilibrium absence of occupation in the valence band sequentially “visits” orbitals in an ascending order of energies
| j → j + 1 →…→ HO−1 → HO | (23) |
Thus, at the end of the computed time interval, the system relaxes to the lowest available excitation (HO) → (LU), independent of the initial excitation. This observation emphasizes the critical importance of the band alignment differences shown in Fig. 2 and 3.
However, the most interesting and illustrative analysis of the photoinduced dynamics as well as perhaps the most appropriate judgement of applicability of a specific interface morphology for photovoltaic application could be deduced from the following analysis of the dynamic charge density distribution as a function of energy and space, shown in Fig. 7. These distributions are based on calculations for the same initial excitations as mentioned above, namely the (HO−3) → (LU+13) excitation in the hydroxyl model and the (HO−2) → (LU+10) excitation in the acetate model, illustrated in Fig. 6.
 | ||
| Fig. 7 Dynamics of charge distribution (a and b) with respect to energy and (c and d) with respect to position in simulation cell for (a and c) hydroxyl and (b and d) acetate models. This is a visualization of n′(ε,t) from eqn (18) and n(z,t) from eqn (20). The green background color represents no change from the ground state charge density distribution, while the brighter yellow represents high electron density and darker blue represents high hole density compared to the ground state. In (c) and (d), the densities are integrated over the “x” and “y” dimensions to yield a single value for each “z” position. The atomistic models are shown adjacent to these plots to help visualize the “z” positions in plots (c) and (d). The blue boxes around the models specify the periodic boundaries of the simulation cells. | ||
The charge distribution as a function of energy is needed to assess the different energy offsets between orbitals, i.e. the same rate of transitions between orbitals may result in drastically different rates of energy dissipation from the electronic system to nuclear degrees of freedom. In Fig. 7, panels (a) and (b) the green background color represents no change from the ground state charge density, while the brighter yellow represents high electron density and darker blue represents high hole density compared to the ground state. As time passes, the center of the electron density distribution moves from higher energy to lower energy, as summarized by the average electron energy (dashed line). Likewise, the center of the hole density distribution migrates from lower energies to higher energies (solid line). Both electron and hole reach quasi-stationary states at the long-living lowest excitation HO → LU. Fitting of the curvatures of the dashed and solid lines allows us to assess the average rate of electron and hole cooling to the lowest available excitation for each system.
Interestingly, information on cooling of a charge carrier is not sufficient for assessing the ability of an interface to efficiently participate in the photovoltaic process. While cooling, a charge carrier may either keep the original localization (perovskite film in this case) or experience a transfer across the interface to another material (POT cluster in this case). The overall features, rates, and directions of charge transfer can change drastically depending on the chosen morphology of the interface.
We also analyze details of interfacial charge transfer based on the distribution of charge as a function of position and time, shown in Fig. 7(c) and (d) for the same interfaces and initial conditions as usual, the (HO−3) → (LU+13) excitation in the hydroxyl model and the (HO−2) → (LU+10) excitation in the acetate model. This analysis shows that in the hydroxyl model, the initial excitation localizes the hole to the Cs–Pb layers of the perovskite, mostly to top layer nearest the POT, and spreads the electron just above and below these layers. The electron is then injected into the core of the POT cluster and settles at the Ti 3d atomic orbitals, see animation in ESI.†
In addition to simulating the “most likely” excitation in each model, i.e. the excitation with the highest oscillator strength, we also simulate the top 20 “most likely” excitations for both models. This allows us to track and compare the charge relaxation times for both electrons and holes in both the hydroxyl and acetate models, as seen in Fig. 8. The abscissa labeled “Dissipation Energy” represents the energy which must be dissipated for the excited charges to relax to the frontier orbital. This is the energy difference between HOMO and the initial excited state for holes, and is the energy difference between the initial excited state and LUMO for electrons. What we see is that the excited charges tend to obey the energy gap law in localized ranges of dissipation energy, with electrons that are excited by more than about 0.75 eV beyond LUMO in the acetate model being the most notable exception. As far as differences between the models go, the excited holes relax more slowly in the hydroxyl model which is preferable for PV applications as highly excited charges can be extracted more readily than less excited charges. The exited electrons appear to have similar relaxation times for both models.
 | ||
| Fig. 8 Relaxation times for electrons (solid dots, τe from eqn (19c)) and holes (hollow dots, τh from eqn (19c)) in hydroxyl (red) and acetate (blue) models as a function of dissipation energy. The dissipation energy is defined as the energy difference between the excited charge carrier and its frontier orbital upon photoexcitation, e.g. the energy difference between LU+10 and LU for an electron photoexcited into the LU+10 orbital. The relaxations times appear to mostly obey the energy gap law in local segments. | ||
Discussion
The first of these is the classical path approximation, i.e. the nuclei are treated as classical point charges, so any nuclear quantum mechanical effects are neglected. This should not have any significant effect on the MD trajectory or electronic structure about the nuclei, since the classical forces externally acting on the nuclei are orders of magnitude larger than quantum mechanical forces. Second, a GGA functional (PBE) is chosen to reduce computational time. This likely leads to quantitative discrepancies in observables like the band gap energy, but should not alter qualitative differences between the two models, e.g. the hydroxyl model having a smaller band gap than the acetate model. Third, neither spin polarization nor non-collinear spin are used in these calculations since the models have a closed shell, i.e. the valence orbitals are fully occupied by electrons. This again saves computational time and will cause quantitative discrepancies from experimental values, but should not alter qualitative trends. Ideally, one would use a hybrid functional, such as HSE06, and include non-collinear spin in the calculations, but this is prohibitively expensive computationally. Fourth, it is implicitly assumed in Redfield theory that the MD trajectory is a Markov chain, meaning that only the present nuclear configuration, and no past configuration, has an impact on future configurations. This is justified by the rapid decay of correlation functions during the MD trajectory. Fifth, it is also implicitly assumed in Redfield theory that there is no excited state nuclear reorganization. That is to say the nuclear configuration does not change upon photo-excitation. Sixth, the initial excited states are approximated as a single electron/hole pair. This neglects the possibility of a superposition of excitons with the same energy. Finally, it is assumed that there is no electron/hole interaction, i.e. no bound excitons are formed.The following represents the main result of the paper. For both hydroxyl and acetate interfaces, the initial excitation consists of electron (yellow in Fig. 7) and hole (blue in Fig. 7) density localized in the spatial region corresponding to the perovskite slab (z < 0 in Fig. 7). The major difference between the interfaces lies in the dynamics of how the excited charges relax. This is outlined below.
Hydroxyl: the excited hole remains in the spatial region of the perovskite film (z < 0) while the electron experiences a transfer to the spatial region corresponding to the POT cluster (z > 0) at a time of around 100 fs. This reaction can be summarized as follows
| (CsPbBr3)*(TiO2) → (CsPbBr3)+(TiO2)− | (24) |
Acetate: contrarily for the acetate interface, the hole first experiences a transfer to the POT cluster at around 50 fs, leaving the electron at the perovskite and creating a charge transfer in the opposite direction
| (CsPbBr3)*(TiO2) → (CsPbBr3)−(TiO2)+ | (25) |
However, shortly afterward, at a time of around 500 fs the electron also transfers to the POT cluster, and thus brings the system back to a neutral, albeit excited, state.
| (CsPbBr3)−(TiO2)+ → (CsPbBr3)(TiO2)* | (26) |
There are two criteria of charge transfer efficiency, namely charge transfer rate and charge transfer yield. Here we assumed the charge transfer rates are defined similarly to the rates of energy dissipation, take similar values, and can substitute each other. Fig. 8 summarizes the similarities and differences of such rates for hydroxyl and acetate linkers. For both models, the rates are of a similar order of magnitude. However, the second criterion, charge transfer yield, is dramatically different for these two linkers: the hydroxyl linker provides near 100% yield since the electron and hole are separated in space. The acetate linker provides near 0% yield since the electron and hole both transfer to TiO2 creating no charge separation at all. This results in the hydroxyl linker being a more favorable morphology for solar cell design.
It is also interesting to comment on the possibility of experimental confirmation of the computed results. A direct monitoring of the excited state dynamics in nanostructures can be performed in terms of the ultrafast time resolved spectroscopy, where charge transfer states will have darker optical response. An indirect and industrially relevant experimental test would be an effort to record the photocurrent conversion efficiency (PCE) created at devices with specific interfaces between layers. A computational prediction of PCE needs several additional factors such as atomistic geometry of contacts and details on bias voltage, which is beyond the scope of this paper, but is planned in future studies.
Conclusions
Finally, one concludes that a minor change in linkage morphology of the interface may alter the band alignment, direction of photoinduced charge transfer, and applicability of an interface to photovoltaic technology. It also effects the charge transfer rates, relaxation rates, and can be used to fine tune the band gap energy. The interface morphology did not, however, have any significant impact on the absorption spectra or the mode of relaxation through energetically adjacent states in this case. In the considered two examples, hydroxyl linking morphology matches the criteria for a photovoltaic interface nicely and acetate linking morphology is not suitable for photovoltaic applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
D. K. acknowledges partially support by NSF CHE 1944921 for excited state dynamics methods development. L. J. acknowledges partial support of NSF CHE 2004197 for exploration of charge transfer in quantum dots and nanostructures. Authors thank the National Energy Research Scientific Computing Center (NERSC) via DOE, BES Chemical Sciences, NERSC Contract No. DE-AC02-05CH11231, allocation award, ‘Computational Modeling of Photocatalysis and Photoinduced Charge Transfer Dynamics on Surfaces’ for computational facilities. Finally, the authors thank Aaron Forde, Yulun Han, Fatima, Svetlana Kilina, Levi Lystrom, Jabed Mohamed, Braden Weight, and Daniel Ramirez for their feedback and inspiring discussions.Notes and references
- X. Zhou, J. Jankowska, H. Dong and O. V. Prezhdo, Recent theoretical progress in the development of perovskite photovoltaic materials, J. Energy Chem., 2018, 27(3), 637–649 CrossRef.
- H. Tsai, W. Nie, J.-C. Blancon, C. C. Stoumpos, R. Asadpour, B. Harutyunyan, A. J. Neukirch, R. Verduzco, J. J. Crochet, S. Tretiak, L. Pedesseau, J. Even, M. A. Alam, G. Gupta, J. Lou, P. M. Ajayan, M. J. Bedzyk, M. G. Kanatzidis and A. D. Mohite, High-Efficiency Two-Dimensional Ruddlesden–Popper Perovskite Solar Cells, Nature, 2016, 536(7616), 312–316 CrossRef CAS PubMed.
- Q. Luo, H. Ma, Q. Hou, Y. Li, J. Ren, X. Dai, Z. Yao, Y. Zhou, L. Xiang, H. Du, H. He, N. Wang, K. Jiang, H. Lin, H. Zhang and Z. Guo, All-Carbon-Electrode-Based Endurable Flexible Perovskite Solar Cells, Adv. Funct. Mater., 2018, 28(11), 1706777 CrossRef.
- B. Cao, H. Liu, L. Yang, X. Li, H. Liu, P. Dong, X. Mai, C. Hou, N. Wang, J. Zhang, J. Fan, Q. Gao and Z. Guo, Interfacial Engineering for High-Efficiency Nanorod Array-Structured Perovskite Solar Cells, ACS Appl. Mater. Interfaces, 2019, 11(37), 33770–33780 CrossRef CAS PubMed.
- E. M. Sanehira, A. R. Marshall, J. A. Christians, S. P. Harvey, P. N. Ciesielski, L. M. Wheeler, P. Schulz, L. Y. Lin, M. C. Beard and J. M. Luther, Enhanced Mobility CsPbI3 Quantum Dot Arrays for Record-Efficiency, High-Voltage Photovoltaic Cells, Sci. Adv., 2017, 3(10), eaao4204 CrossRef PubMed.
- Y. Han and D. S. Kilin, Nonradiative Relaxation Dynamics of a Cesium Lead Halide Perovskite Photovoltaic Architecture: Effect of External Electric Fields, J. Phys. Chem. Lett., 2020, 11(23), 9983–9989 CrossRef CAS PubMed.
- S. Ananthakumar and S. M. Babu, Progress on synthesis and applications of hybrid perovskite semiconductor nanomaterials—a review, Synth. Met., 2018, 246, 64–95 CrossRef CAS.
- F. Yan, J. Xing, G. Xing, L. Quan, S. T. Tan, J. Zhao, R. Su, L. Zhang, S. Chen, Y. Zhao, A. Huan, E. H. Sargent, Q. Xiong and H. V. Demir, Highly Efficient Visible Colloidal Lead-Halide Perovskite Nanocrystal Light-Emitting Diodes, Nano Lett., 2018, 18(5), 3157–3164 CrossRef CAS PubMed.
- Y.-H. Kim, C. Wolf, Y.-T. Kim, H. Cho, W. Kwon, S. Do, A. Sadhanala, C. G. Park, S.-W. Rhee, S. H. Im, R. H. Friend and T.-W. Lee, Highly Efficient Light-Emitting Diodes of Colloidal Metal–Halide Perovskite Nanocrystals beyond Quantum Size, ACS Nano, 2017, 11(7), 6586–6593 CrossRef CAS PubMed.
- K. Lin, J. Xing, L. N. Quan, F. P. G. de Arquer, X. Gong, J. Lu, L. Xie, W. Zhao, D. Zhang, C. Yan, W. Li, X. Liu, Y. Lu, J. Kirman, E. H. Sargent, Q. Xiong and Z. Wei, Perovskite Light-Emitting Diodes with External Quantum Efficiency Exceeding 20 per cent, Nature, 2018, 562(7726), 245–248 CrossRef CAS PubMed.
- M. R. Filip, G. E. Eperon, H. J. Snaith and F. Giustino, Steric Engineering of Metal-Halide Perovskites with Tunable Optical Band Gaps, Nat. Commun., 2014, 5(1), 5757 CrossRef CAS PubMed.
- Y. Hassan, Y. Song, R. D. Pensack, A. I. Abdelrahman, Y. Kobayashi, M. A. Winnik and G. D. Scholes, Structure-Tuned Lead Halide Perovskite Nanocrystals, Adv. Mater., 2016, 28(3), 566–573 CrossRef CAS PubMed.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Grätzel, S. Mhaisalkar and T. C. Sum, Long-Range Balanced Electron- and Hole-Transport Lengths in Organic-Inorganic CH3NH3PbI3, Science, 2013, 342(6156), 344–347 CrossRef CAS PubMed.
- F. Ambrosio, J. Wiktor, F. De Angelis and A. Pasquarello, Origin of Low Electron–Hole Recombination Rate in Metal Halide Perovskites, Energy Environ. Sci., 2018, 11(1), 101–105 RSC.
- J. He, M. Guo and R. Long, Photoinduced Localized Hole Delays Nonradiative Electron–Hole Recombination in Cesium–Lead Halide Perovskites: A Time-Domain Ab Initio Analysis, J. Phys. Chem. Lett., 2018, 9(11), 3021–3028 CrossRef CAS PubMed.
- D. Ghosh, D. Acharya, L. Zhou, W. Nie, O. V. Prezhdo, S. Tretiak and A. J. Neukirch, Lattice Expansion in Hybrid Perovskites: Effect on Optoelectronic Properties and Charge Carrier Dynamics, J. Phys. Chem. Lett., 2019, 10(17), 5000–5007 CrossRef CAS PubMed.
- L. Protesescu, S. Yakunin, M. I. Bodnarchuk, F. Krieg, R. Caputo, C. H. Hendon, R. X. Yang, A. Walsh and M. V. Kovalenko, Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut, Nano Lett., 2015, 15(6), 3692–3696 CrossRef CAS PubMed.
- A. Forde, T. Inerbaev, E. K. Hobbie and D. S. Kilin, Excited-State Dynamics of a CsPbBr3 Nanocrystal Terminated with Binary Ligands: Sparse Density of States with Giant Spin–Orbit Coupling Suppresses Carrier Cooling, J. Am. Chem. Soc., 2019, 141(10), 4388–4397 CrossRef CAS PubMed.
- D. J. Vogel, A. Kryjevski, T. Inerbaev and D. S. Kilin, Photoinduced Single- and Multiple-Electron Dynamics Processes Enhanced by Quantum Confinement in Lead Halide Perovskite Quantum Dots, J. Phys. Chem. Lett., 2017, 8(13), 3032–3039 CrossRef CAS PubMed.
- A. Forde, J. A. Fagan, R. D. Schaller, S. A. Thomas, S. L. Brown, M. B. Kurtti, R. J. Petersen, D. S. Kilin and E. K. Hobbie, Brightly Luminescent CsPbBr3 Nanocrystals through Ultracentrifugation, J. Phys. Chem. Lett., 2020, 11(17), 7133–7140 CrossRef CAS PubMed.
- J. Kang and L.-W. Wang, High Defect Tolerance in Lead Halide Perovskite CsPbBr3, J. Phys. Chem. Lett., 2017, 8(2), 489–493 CrossRef CAS PubMed.
- A. Walsh, D. O. Scanlon, S. Chen, X. G. Gong and S.-H. Wei, Self-Regulation Mechanism for Charged Point Defects in Hybrid Halide Perovskites, Angew. Chem., Int. Ed., 2015, 54(6), 1791–1794 CrossRef CAS PubMed.
- W. Li, R. Long, J. Tang and O. V. Prezhdo, Influence of Defects on Excited-State Dynamics in Lead Halide Perovskites: Time-Domain ab Initio Studies, J. Phys. Chem. Lett., 2019, 10(13), 3788–3804 CrossRef CAS PubMed.
- A. Forde and D. Kilin, Defect Tolerance Mechanism Revealed! Influence of Polaron Occupied Surface Trap States on CsPbBr3 Nanocrystal Photoluminescence: Ab Initio Excited-State Dynamics, J. Chem. Theory Comput., 2021, 17(11), 7224–7236 CrossRef CAS PubMed.
- A. Dey, J. Ye, A. De, E. Debroye, S. K. Ha, E. Bladt, A. S. Kshirsagar, Z. Wang, J. Yin, Y. Wang, L. N. Quan, F. Yan, M. Gao, X. Li, J. Shamsi, T. Debnath, M. Cao, M. A. Scheel, S. Kumar, J. A. Steele, M. Gerhard, L. Chouhan, K. Xu, X.-g. Wu, Y. Li, Y. Zhang, A. Dutta, C. Han, I. Vincon, A. L. Rogach, A. Nag, A. Samanta, B. A. Korgel, C.-J. Shih, D. R. Gamelin, D. H. Son, H. Zeng, H. Zhong, H. Sun, H. V. Demir, I. G. Scheblykin, I. Mora-Seró, J. K. Stolarczyk, J. Z. Zhang, J. Feldmann, J. Hofkens, J. M. Luther, J. Pérez-Prieto, L. Li, L. Manna, M. I. Bodnarchuk, M. V. Kovalenko, M. B. J. Roeffaers, N. Pradhan, O. F. Mohammed, O. M. Bakr, P. Yang, P. Müller-Buschbaum, P. V. Kamat, Q. Bao, Q. Zhang, R. Krahne, R. E. Galian, S. D. Stranks, S. Bals, V. Biju, W. A. Tisdale, Y. Yan, R. L. Z. Hoye and L. Polavarapu, State of the Art and Prospects for Halide Perovskite Nanocrystals, ACS Nano, 2021, 15(7), 10775–10981 CrossRef CAS PubMed.
- W. Li, Y. She, A. S. Vasenko and O. V. Prezhdo, Ab initio nonadiabatic molecular dynamics of charge carriers in metal halide perovskites, Nanoscale, 2021, 13(23), 10239–10265 RSC.
- J. M. Frost, K. T. Butler, F. Brivio, C. H. Hendon, M. van Schilfgaarde and A. Walsh, Atomistic Origins of High-Performance in Hybrid Halide Perovskite Solar Cells, Nano Lett., 2014, 14(5), 2584–2590 CrossRef CAS PubMed.
- C. Liu and E. Jakubikova, Two-step model for ultrafast interfacial electron transfer: limitations of Fermi's golden rule revealed by quantum dynamics simulations, Chem. Sci., 2017, 8(9), 5979–5991 RSC.
- A. Forde and D. Kilin, Hole Transfer in Dye-Sensitized Cesium Lead Halide Perovskite Photovoltaics: Effect of Interfacial Bonding, J. Phys. Chem. C, 2017, 121(37), 20113–20125 CrossRef CAS.
- F. Liu, Y. H. Zhang, C. Ding, T. Toyoda, Y. Ogomi, T. S. Ripolles, S. Hayase, T. Minemoto, K. Yoshino, S. Y. Dai and Q. Shen, Ultrafast Electron Injection from Photoexcited Perovskite CsPbI3 QDs into TiO2 Nanoparticles with Injection Efficiency near 99%, J. Phys. Chem. Lett., 2018, 9(2), 294–297 CrossRef CAS PubMed.
- J. F. Liao, W. Q. Wu, Y. Jiang, D. B. Kuang and L. Z. Wang, Maze-Like Halide Perovskite Films for Efficient Electron Transport Layer-Free Perovskite Solar Cells, Sol. RRL, 2019, 3(3), 1800268 CrossRef.
- J. B. Benedict and P. Coppens, The Crystalline Nanocluster Phase as a Medium for Structural and Spectroscopic Studies of Light Absorption of Photosensitizer Dyes on Semiconductor Surfaces, J. Am. Chem. Soc., 2010, 132(9), 2938–2944 CrossRef CAS PubMed.
- J. B. Benedict, R. Freindorf, E. Trzop, J. Cogswell and P. Coppens, Large Polyoxotitanate Clusters: Well-Defined Models for Pure-Phase TiO2 Structures and Surfaces, J. Am. Chem. Soc., 2010, 132(39), 13669–13671 CrossRef CAS PubMed.
- C. F. A. Negre, K. J. Young, M. B. Oviedo, L. J. Allen, C. G. Sanchez, K. N. Jarzembska, J. B. Benedict, R. H. Crabtree, P. Coppens, G. W. Brudvig and V. S. Batista, Photoelectrochemical Hole Injection Revealed in Polyoxotitanate Nanocrystals Functionalized with Organic Adsorbates, J. Am. Chem. Soc., 2014, 136(46), 16420–16429 CrossRef CAS PubMed.
- J. H. Bao, L. Gundlach, Z. H. Yu, J. B. Benedict, R. C. Snoeberger, V. S. Batista, P. Coppens and P. Piotrowiak, Hot Hole Hopping in a Polyoxotitanate Cluster Terminated with Catechol Electron Donors, J. Phys. Chem. C, 2016, 120(36), 20006–20015 CrossRef CAS.
- M. A. Loi and J. C. Hummelen, Hybrid Solar Cells Perovskites under the Sun, Nat. Mater., 2013, 12(12), 1087–1089 CAS.
- D. Junkman, D. J. Vogel, Y. Han and D. S. Kilin, Ab Initio Analysis of Charge Carrier Dynamics in Organic-Inorganic Lead Halide Perovskite Solar Cells, MRS Online Proc. Libr., 2015, 1776, 19–29 CrossRef.
- D. A. Micha, A self-consistent eikonal treatment of electronic transitions in molecular collisions, J. Chem. Phys., 1983, 78(12), 7138–7145 CrossRef CAS.
- D. A. Micha and K. Runge, Time-dependent many-electron approach to slow ion-atom collisions: the coupling of electronic and nuclear motions, Phys. Rev. A, 1994, 50(1), 322–336 CrossRef CAS PubMed.
- S. Kilina, D. Kilin and S. Tretiak, Light-Driven and Phonon-Assisted Dynamics in Organic and Semiconductor Nanostructures, Chem. Rev., 2015, 115(12), 5929–5978 CrossRef CAS PubMed.
- S. V. Kilina, P. K. Tamukong and D. S. Kilin, Surface Chemistry of Semiconducting Quantum Dots: Theoretical Perspectives, Acc. Chem. Res., 2016, 49(10), 2127–2135 CrossRef CAS PubMed.
- L. G. C. Rego and V. S. Batista, Quantum Dynamics Simulations of Interfacial Electron Transfer in Sensitized TiO2 Semiconductors, J. Am. Chem. Soc., 2003, 125(26), 7989–7997 CrossRef CAS PubMed.
- S. Meng, J. Ren and E. Kaxiras, Natural Dyes Adsorbed on TiO2 Nanowire for Photovoltaic Applications: Enhanced Light Absorption and Ultrafast Electron Injection, Nano Lett., 2008, 8(10), 3266–3272 CrossRef CAS PubMed.
- J. C. Tully, Molecular dynamics with electronic transitions, J. Chem. Phys., 1990, 93(2), 1061–1071 CrossRef CAS.
- A. G. Redfield, On the Theory of Relaxation Processes, IBM J. Res. Dev., 1957, 1(1), 19–31 Search PubMed.
- J. M. Jean, R. A. Friesner and G. R. Fleming, Application of a multilevel Redfield theory to electron transfer in condensed phases, J. Chem. Phys., 1992, 96(8), 5827–5842 CrossRef CAS.
- P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1964, 136(3B), B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev. A, 1965, 140(4A), A1133–A1138 CrossRef.
- A. G. Redfield, The Theory of Relaxation Processes**This work was started while the author was at Harvard University, and was then partially supported by Joint Services Contract N5ori-76, Project Order I, in Advances in Magnetic and Optical Resonance, ed. J. S. Waugh, Academic Press, 1965, vol. 1, pp. 1–32 Search PubMed.
- E. Mosconi, E. Ronca and F. De Angelis, First-Principles Investigation of the TiO2/Organohalide Perovskites Interface: The Role of Interfacial Chlorine, J. Phys. Chem. Lett., 2014, 5(15), 2619–2625 CrossRef CAS PubMed.
- V. Roiati, E. Mosconi, A. Listorti, S. Colella, G. Gigli and F. De Angelis, Stark Effect in Perovskite/TiO2 Solar Cells: Evidence of Local Interfacial Order, Nano Lett., 2014, 14(4), 2168–2174 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1ra05306j |
| This journal is © The Royal Society of Chemistry 2022 |


