Open Access Article
Open Access ArticleControl of near-infrared dye fluorescence lifetime in all-polymer microcavities†
Heba
Megahd
 a,
Mariela
Villarreal Brito
a,
Andrea
Lanfranchi
a,
Mariela
Villarreal Brito
a,
Andrea
Lanfranchi
 a,
Paola
Stagnaro
a,
Paola
Stagnaro
 b,
Paola
Lova
b,
Paola
Lova
 a and
Davide
Comoretto
a and
Davide
Comoretto
 *a
*a
aDipartimento di Chimica e Chimica Industriale, Università di Genova, Via Dodecaneso 31, 16146 Genova, Italy. E-mail: davide.comoretto@unige.it
bIstituto di Scienze e Tecnologie Chimiche “Giulio Natta”, Consiglio Nazionale delle Ricerche, SCITEC-CNR, Via de Marini,6, 16149 Genova, Italy
First published on 20th July 2022
Abstract
The control of radiative decay rate is a crucial issue both for fundamental studies in quantum electrodynamics and for the development of efficient lasers, light emitting devices and photovoltaic cells. In this paper we investigate the integration of a near-infrared molecular fluorophore in an all-polymer planar microcavity. Subsequently, we report the modulation of the fluorescence decay and radiative rate of the dye used and, in addition, of its fluorescence spectral line-shape and intensity. These effects have been possible through engineering the dielectric contrast of the polymers used to grow the flexible dielectric mirrors, thus blazing a trail to innovative opportunities for invisible near-infrared-light communications and wireless technologies.
Introduction
Optical microcavities of different morphologies have long been a popular means of controlling photoluminescence (PL) and electroluminescence of various emitters.1 As they confine electromagnetic fields at their resonant frequencies to a small volume, they strongly influence the light-matter interaction for fluorophores inside the cavity. Spontaneous emission rate is, in fact, not an intrinsic property of emitters, but highly influenced by the surrounding electromagnetic medium in what is known as the Purcell effect, first theorized by its namesake in 1946.2 As such, through quantum electrodynamic effects, it is possible to engineer the radiative rate of an emitter placed in an appropriately engineered medium, which allows for higher efficiency optical devices, such as light emitting devices (LEDs)3,4 or photovoltaics.5,6One of the simplest microcavity architectures to fabricate is the planar variety based on one-dimensional photonic crystals, also known as distributed Bragg reflectors (DBRs) or dielectric mirrors. Due to their facile fabrication and scalability, DBRs have found use in applications ranging from lasers, photovoltaics and sensors, to aesthetic applications in architecture and art.7 These structures consist of a repeating motif of bilayers of dielectric materials with different refractive indices that gives rise to constructive or destructive interference due to refraction and reflection at the layer interfaces at distinct wavelengths. These wavelengths depend on the refractive index of the layers as well as their thickness, which accordingly results in controllable reflectance maxima for wavelengths where light cannot propagate into the structure, known as Photonic Bandgaps (PBGs).8 However, when the periodicity of these structures is interrupted by an anomalous layer, allowed modes are introduced where some wavelengths in the PBG spectral region are permitted to propagate in the structure,9 termed the microcavity modes (MC).10 This is similar to microcavities consisting of metallic mirrors, however, dielectric mirrors provide lower losses than their metallic counterparts.1,11,12
At both the edges of the PBG and at the microcavity mode, the local photonic density of states (LPDOS) is highly increased while at the PBG it is drastically diminished, ideally to zero. The LPDOS describes the number of photonic states available to the system per unit energy,13 which controls the radiative rate and the PL intensity. The radiative rate (Γrad) can be interpreted in terms of the LPDOS as described by the modified Fermi's golden rule (eqn (1)),13 where ω is the angular frequency and r is the position of the emitter in the cavity.
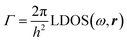 | (1) |
Thus, depending on the tuning of the cavity mode with respect to the PL of the emitter and its geometrical positioning, both radiative rate enhancement and suppression can be achieved.14 As polymers possess unique flexibility and processability, all-polymer microcavities allowing enhancement effects in combination with the recent leaps in polymer-based devices -such as organic LEDs and solar cells- would allow efficiency enhancement of these flexible and solution-processed devices.15–17 The possibility of emission rate control was theorized to be achievable through the use of special polymers or nanocomposites that provide particularly high or low refractive index in dielectric mirrors.18 While radiative rate control has been routinely achieved in planar microcavities based on inorganic dielectrics, the effect has only recently been confirmed in all-polymer microcavities, partly due to the use of low-index perfluorinated polymers.19 Perfluorinated sulfonic acid dispersions are promising solution-processable polymers with unique electrical, optical and thermal properties that have found applications in a myriad of fields.20–23 Thus, we have previously reported on the use of microcavities employing the low refractive index perfluorinated polymer Aquivion (AQ) to achieve not only intensity enhancement of an organic emitter in the visible range, but more importantly its effect on altering the radiative lifetime by virtue of increasing the dielectric contrast between the polymers used in constructing the DBRs forming the dielectric mirrors.19
In this paper, we demonstrate that this effect is also achievable for near infrared (NIR) organic emitters, which is critical due to the importance of the NIR range for communication, sensing, biological imaging and solar cells.24–29 Even though careful molecular design,30 supramolecular assemblies31–33 and dye blends34,35 provide an approach to fluorescence kinetics control, using photonic structures offers an additional tool having broad applicability, high effectiveness and straight-forward experimental method.19,36,37 This offers more flexibility in achieving fluorescence control in solid state devices through simply incorporating the microcavities without changing the dye system, in particular when polymer and flexible materials are used.
While different polymer-based fluorophores were investigated in polymer cavities supporting whispering-gallery modes,38–40 they require more sophisticated nano lithographic or self-assembly fabrication that can be difficult to scale and more prone to disorder. Herein, we report on the modulation of radiative lifetime of 2-[2-[2-(4-methylbenzene oxy)-3-[(1,3-dihydro-1,3,3-trimethyl-2H-indol-2-ylidene)ethylidene]-1-cycloxen-1-yl]-ethenyl]-1,3,3-trimethyl-1H indolium perchlorate, a NIR emitting dye (thereafter referred to simply as “dye”) blended with polyacrylic acid (PAA) and embedded in an all-polymer microcavity. The use of AQ as a low-index polymer and poly(vinyl carbazole) (PVK) as a high-index one in the DBRs results in refractive index contrast of Δn ≈ 0.33 at the spectral range of interest, comparable to that achievable in some inorganic structures.41 The engineering of the PBG and the MC mode to the PL spectral range of the dye provides an opportunity to observe interesting cavity effects.
Experimental section
Microcavity fabrication
All samples were fabricated through sequential spin coating deposition of 100 μL of polymer solutions at 170–190 revolutions per second on glass substrates. Aquivion D79-25BS was provided by Solvay Specialty Polymers and used as a water/ethanol dispersion of different ratios depending on the desired thickness. PVK (Acros Organics) was used as a solution in toluene (Sigma Aldrich, anhydrous 99.8%) at a concentration of 40 mg mL−1. The NIR emitter dye (ADS760MP) was acquired from American Dye Source, Inc. and used as a blend (1 mg mL−1) in PAA (Aldrich)/ethanol solution (188 mg mL−1), referred to as Dye:PAA. Spinning velocity and AQ dispersion concentrations were engineered to tune the position of the bandgap as required. We prepared two sets of microcavities: one tuned on the dye fluorescence (MCtuned) and the other fully detuned form the fluorescence (MCdetuned) to be used as a reference for dye emission without cavity effects.Optical characterization
Normal-incidence reflectance measurements were recorded through a customized optical fiber-based setup consisting of deuterium and tungsten–halogen sources (spectral range 230–2500 nm) using reflectance from a UV-enhanced aluminium mirror or a protected silver mirror as a reference (Thorlabs). The reflected signal was collected using an AvaSpec-ULS4096CL-EVO (CMOS) (spectral range 200–1100 nm, resolution 1.4 nm) spectrometer. Angle-resolved transmittance and PL spectra were recorded using a homemade setup of angular resolution ≤1° employing the same spectrometer. Steady-state PL measurements were performed by exciting the samples with an Oxxius 405 nm CW laser focused on a 1 mm2 spot, and the signal was collected with a parabolic mirror and then detected with the aforementioned spectrometer. The collection setup allowed the measurement of transmittance and PL at the same spot.Time-resolved PL measurements
PL decay was recorded using a PicoQuant Time-Correlated Single-Photon Counting system (Time Harp 260 PICO board with a temporal resolution of 150 ps, a PMA Hybrid 40 detector, and a 405 nm LDH-P-C-405 laser (PicoQuant, Berlin, Germany) with a PDL 800B driver with a 5–80 MHz repetition rate as the excitation source). The PL signal was filtered through a premium long-pass filter, with a cut-on wavelength of 700 nm (Thorlabs, FELH0700) to exclude any possible interference from PL of the polymers used in the DBR at shorter wavelengths.Quantum yield measurements
External PL quantum yield for microcavities and references were determined through the method described by de Mello et al.42 An integrating sphere (Avantes AvaSphere-50) was used, with a 405 nm LDH-P-C-405 laser as an excitation source and the signal was collected with the same spectrometer used for steady-state optical characterization.Results and discussion
Dye properties and microcavity design
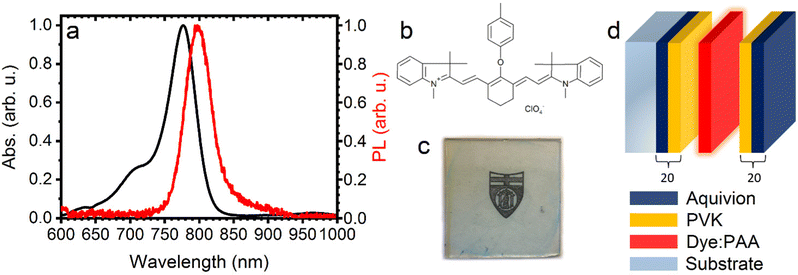
Panel a of Fig. 1 reports the PL and absorption spectra of the Dye:PAA blend cast on a glass substrate. The absorption maximum is observed at 777 nm (12870 cm−1) followed by a broader shoulder at about 710 nm (14084 cm−1), probably masking an additional vibronic replica. On excitation using a 405 nm laser, the fluorescence spectrum shows a maximum at 798 nm and is not symmetrical with respect the absorbance spectrum. Indeed, vibronic features are not detected, indicating a different electron-phonon coupling in the ground and excited electronic states and a small Stokes shift of 21 nm. The chemical structure of the dye is shown in Fig. 1b. This dye consists of a polymethine chain linking two terminal heterocycles, each of which is bonded to a nitrogen atom conjugated to the chain. In the present case, the heterocycles are coplanar to the conjugated bonds thanks to the saturated bridges, which prevent ring torsions thus extending the delocalization of electrons. The central conjugated bond of the molecule is also stabilized by a cyclic saturated bridge carrying in the opposite position a phenyl-oxy electron donor group. All these features induce a strong reduction of the HOMO-LUMO transition energy to the NIR.43,44 A digital photograph in Fig. 1c shows the microcavity containing the Dye:PAA blend cast on a glass substrate, where the PBG and MC mode wavelengths are tuned to the emission of the dye. The sample demonstrates high transparency and remarkable lack of colouring, as its first order PBG lies in the infrared range, with a slight tint due to the low-intensity second-order PBG in the violet range (see Fig. 2a and b). Casting parameters were engineered to produce multiple sample types: one where the PBG overlaps the emission of the dyes (MCtuned), and another where the PBG is instead offset to shorter wavelengths (MCdetuned) to act as a reference emulating the physicochemical environment, yet without the photon localization effect in the NIR range. The microcavities comprise two identical DBRs formed of 20 bilayers of AQ/PVK pairs, sandwiching a layer of the Dye:PAA blend as schematized in Fig. 1d.Steady-state optical characterisation
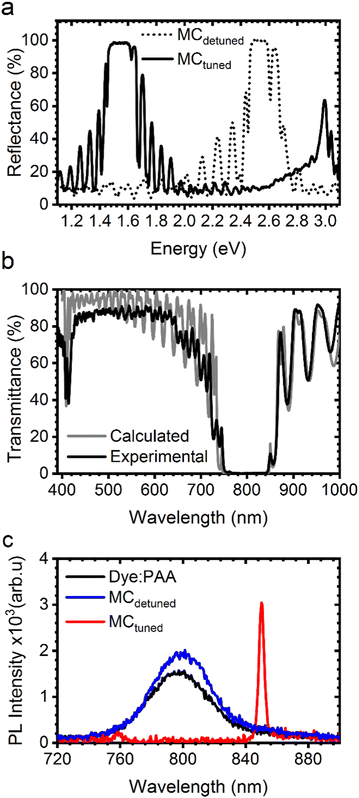
The normalized reflectance spectra of MCtuned and the control MCdetuned are plotted in Fig. 2a, showing the characteristic signatures of 1D planar microcavities.7,9 The two samples have a comparable bandwidth of 0.21 (MCtuned) and 0.19 (MCdetuned) eV, in the range 1.45–1.66 eV or 750–870 nm for MCtuned and 2.47–2.66 eV or 462–513 nm for MCdetuned. The principal microcavity modes are observed at 850 and 475 nm, respectively. Reflectance spectra of the bottom DBR for MCtuned is reported in ESI† Fig. S1, while Fig. S2 shows the reflectance at different spots of MCtuned, confirming the high degree of homogeneity in the sample. The photonic structure of the microcavities is further confirmed through angle-resolved transmittance measurements for both S and P polarizations (Fig. S3, ESI†), that demonstrate the typical shift of the PBG and the microcavity mode to shorter wavelengths on increasing the collection angle.13The complementary absolute transmittance of MCtuned at normal collection is reported in Fig. 2b (solid black line) while the calculated value is shown in grey. Using the refractive index of AQ,20 PVK,45 and the Dye:PAA blend (see ESI,† Fig. S4 and Table S1 for the latter) as an input for the transfer matrix method (TMM) calculations,46 we retrieved the thicknesses of the polymer layers to be approximately 112 and 420 nm for PVK and the Dye:PAA cavity layer, respectively. Due to the affinity of AQ for water, the layers in the lower DBR (which were cast first) have a thickness of around 156, slightly thicker than the 153 nm of the layers in the upper DBR, providing minor asymmetry to the structure. The peak positions and intensities of the cavity modes, both the first and second order PBGs and the interference fringes agree to a great extent. Panel (c) of Fig. 2 shows the fluorescence spectra collected normal to the surface from the Dye:PAA blend thin film (black), MCdetuned (blue) and MCtuned (red) excited by a 405 nm laser.
Clearly, the PL for MCdetuned has a similar emission shape to that of the Dye:PAA blend. Contrarily, the spectral overlap between the PBG and the microcavity mode of MCtuned and the emission of the NIR dye completely alters the fluorescence shape and intensity, giving rise to a dramatic spectral redistribution well known in these systems independently of the emitter used.41,47,48 As expected from the typical LPDOS, the emission from wavelengths that correspond to the PBG are completely suppressed due to the near-zero LPDOS, and the emission is funnelled instead into the wavelengths with higher LPDOS at the cavity mode. Remarkably, due to the relatively wide PBG, approximately all off-resonance PL is suppressed, which was not the case for all-polymer microcavities previously reported.45,47–49 A careful comparison of fluorescence and transmittance of the tuned microcavity is reported in Fig. S5 (ESI†) in order to highlight the overlap of the PL enhanced peak and the cavity mode. Due to the MCtuned mode (∼850 nm), the intensity of CW fluorescence is increased 10-fold compared to MCshifted and 15-fold compared to the Dye:PAA blend film. Interestingly, the full width at half maximum (FWHM) of the cavity mode is ∼4 nm, making its quality factor around 210, comparable to the highest reported so far in all-polymer microcavities (255)49 and to inorganic microcavities of similar dielectric contrast.41 In addition, the angular dispersion of the fluorescence is highly modulated by the photonic structure of the tuned microcavity up to 35° when the cavity mode is no longer overlapping with the dye fluorescence spectrum. In contrast, for the detuned one no angular dependence is observed, as shown in ESI† Fig. S6, further confirming the cavity effects in MCtuned.
Thus far, the efficient leverage of using microcavities for the control of fluorescence spectral characteristics is evident. Most importantly, as mentioned in the introduction, these effects also extend to the exceptional change of the radiative lifetime of the fluorophore embedded in the microcavity.
Radiative lifetime effects
Measurements of fluorescence lifetime show that there exists a significant effect of the microcavities on the dynamics of PL from the dye, indicating a clear effect on the quantum electrodynamics of the system. Integrated time-resolved fluorescence signal in the spectral range 700–870 nm and their best fit are displayed in Fig. 3. The intrinsic response function (IRF) of the setup is also reported in a solid grey line, showing the limit of the instrument temporal resolution. It is immediately apparent that the decay is different for all three samples, with the fastest being that of the standalone Dye:PAA, and the slowest that of the tuned cavity. Detailed fitting parameters are reported in the ESI† Table S2. As the photophysics of the dye itself is unknown and of little interest to this work, we focus on comparing its behaviour in the thin polymer blend film to the microcavities. To make a preliminary comparison of the radiative (ΓR) and non-radiative (ΓNR) processes occurring in the three systems being analysed; we first calculate the intensity-averaged fluorescence decay lifetime in Table 1 (see ESI,† Table S2 and its commentary). We notice an increase in fluorescence lifetime for both MCdetuned, and MCtuned.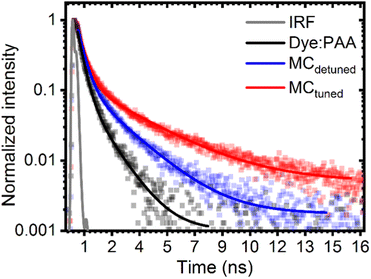 | ||
| Fig. 3 Photoluminescence decay (squares) and fitted data (lines) for the Dye:PAA film (black), the detuned microcavity (blue) and the tuned microcavity (red). | ||
| Sample | τ PL (ns) | η (%) | τ rad (ns) | τ NR (ns) | Γ rad (ns−1) | Γ NR (ns−1) |
|---|---|---|---|---|---|---|
| Dye:PAA | 0.7 ± 0.2 | 19 ± 3 | 3.6 ± 1.7 | 0.9 | 0.27 | 1.2 |
| MCdetuned | 1.2 ± 0.2 | 8 ± 2 | 12.4 ± 4.6 | 1.3 | 0.08 | 0.8 |
| MCtuned | 1.9 ± 0.2 | 5 ± 2 | 39.6 ± 18.2 | 2.0 | 0.03 | 0.5 |
Even though the PL lifetimes inferred from the measurement show the significant effect on the overall fluorescence lifetime from the tuned microcavity with respect to references, it is not possible to confirm any modulation of the radiative rate without the proper measurement of the external quantum yield, which allows to disentangle radiative from non-radiative decays  .50 Therefore, η for each sample is reported in Table 1 as well.
.50 Therefore, η for each sample is reported in Table 1 as well.
The standalone Dye:PAA film shows a moderately high PL quantum efficiency of 19%. However, this is roughly halved for the detuned microcavity, and quartered for the tuned one. As the quantum yield is calculated for all orientations and angles for a range of wavelengths 700–1100 nm, it is not possible to neither spectrally nor angularly resolve its value to evaluate the radiative rate for different decays. However, using average values, it is possible to estimate the average radiative and non-radiative lifetimes  , also reported in Table 1. For both the tuned and detuned microcavities, there exists a significant change in both radiative and nonradiative lifetimes. However, that extent of change is smaller in the reference MCdetuned, indicating that there are some unintended effects that might include, but are not limited to, exciton chemical traps, impurities, local disorder, polarity of the medium and residual solvent diffusion among layers,18 which are not observed in the Dye:PAA film being related to the microcavity structure and its growth process. For this reason, the effect of electric field confinement in the tuned cavity can be clearly estimated only using MCdetuned as a reference. As such, the ratio between the radiative rate of emission
, also reported in Table 1. For both the tuned and detuned microcavities, there exists a significant change in both radiative and nonradiative lifetimes. However, that extent of change is smaller in the reference MCdetuned, indicating that there are some unintended effects that might include, but are not limited to, exciton chemical traps, impurities, local disorder, polarity of the medium and residual solvent diffusion among layers,18 which are not observed in the Dye:PAA film being related to the microcavity structure and its growth process. For this reason, the effect of electric field confinement in the tuned cavity can be clearly estimated only using MCdetuned as a reference. As such, the ratio between the radiative rate of emission  from the tuned and detuned cavities (i.e the Purcell effect) can be quantified as approximately 0.3, indicating a reduction of the radiative rate comparable with values obtained for inorganic planar 1D MC.51,52 On the other hand, the non-radiative decay rate varies to a smaller extent between the two samples.
from the tuned and detuned cavities (i.e the Purcell effect) can be quantified as approximately 0.3, indicating a reduction of the radiative rate comparable with values obtained for inorganic planar 1D MC.51,52 On the other hand, the non-radiative decay rate varies to a smaller extent between the two samples.
Electric field propagation at microcavity mode
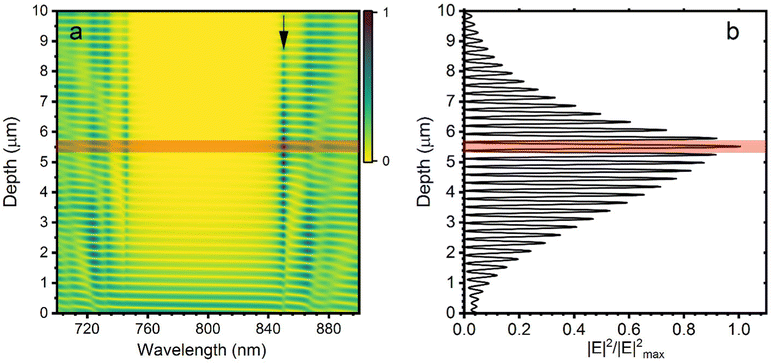
To explain the observation of radiative lifetime increase, and thus radiative rate suppression, in the fabricated all-polymer microcavity, the effect of the cavity on the electric field distribution must be evaluated quantitatively. We calculated the electric field propagation through the structure at all the wavelengths of interest by the Transfer Matrix approach.7,53Fig. 4a shows the results of these calculations of the normalized squared modulus of the field in the range 700–900 nm throughout the depth of the structure. The plot shows the relative intensity of the propagating electric field impinging at normal incidence, starting at the surface (i.e. depth = 0 μm), highlighting the cavity layer in red. The yellow shades of the contour plot indicate a negligible intensity of the electric field, while the dark blue indicates the maximum values. For the wavelengths in the range of the PBG, the field propagation is exponentially damped throughout the structure until it completely disappears. On the other hand, the field for wavelengths around the cavity mode (850 nm) increase in intensity, reaching their highest value at the defect layer (∼5 μm, red). Different behaviour is observed for the interference fringes which oscillate in intensity through the structure of the microcavity. Fig. 4 b reports the electric field intensity at the cavity mode wavelength (850 nm), showing clearly that its maximum value is achieved in the defect layer, highlighted in red. However, it also shows that the defect layer overlaps not only an antinode of the electric field (the peak in Fig. 4b, red area), but also two nodes (the side minima in Fig. 4b, red area). The ratio of radiative lifetime in a microcavity (1/ΓMC) relative to that in a homogeneous medium (1/Γ0), is related to the microcavity wavelength (λMC), the refractive index in the cavity n, the quality factor Q and the effective volume V. In addition, the placement relating to the electric field intensity (E(r) is its amplitude in the cavity and |Em|2 is the maximum of its intensity), the spectral overlap between the cavity mode wavelength and the emitted wavelength (for a monochromatic emitter (λc) as well as a leaky mode factor f, as outlined in a modified form of the Purcell factor (eqn (2))10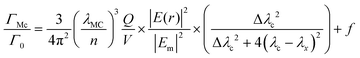 | (2) |
Clearly, there is a significant radiative rate inhibition mechanism occurring as most fluorescence from the dye overlaps the PBG wavelength, causing an inhibition effect. Ideally, the use of a narrow emitter and thinner cavity layer would allow more finer control on the effect and observing only radiative rate enhancement or inhibition, depending on the spectral and positional overlap. In addition, the position of the emitter in the cavity with respect to the resonant electric field can influence the decay kinetics. Preliminary results show that the radiative rate suppression effect is reproducible for cavities having similar primary cavity mode wavelengths and same active layer thickness, even if the cavity length is varied using spacers (see ESI† Fig. S7 and Table S3).
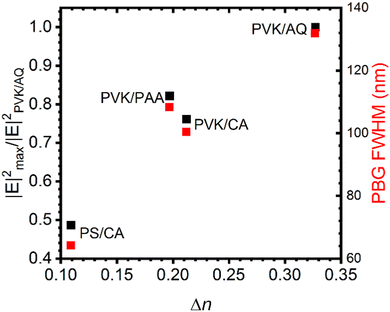
To explain why strong radiative rate variation effects were hardly reported before in literature, we compare the microcavity structure used in this investigation using PVK/AQ as building blocks of the DBRs with previously studied polymer pairs. These are polystyrene (PS)/cellulose acetate (CA) (PS/CA, (Δn = 0.109),54 PVK/CA (Δn = 0.212)48 and PVK/PAA (Δn = 0.197) with PS and PVK being the higher index polymers.47 More information about the optical properties of the polymer pairings is available in the ESI† and in suitable literature where the problem of dielectric contrast has been addressed.18,55,56 Transfer matrix method calculations were performed for microcavities of identical cavity mode wavelengths and overall structures, whose calculated transmittance spectra are reported in Fig. S8 (ESI†).
The ratio between the maximum square modulus of the electric field at the cavity mode in different microcavities and that in the investigated PVK/AQ microcavity (black) are plotted as a function of the dielectric contrast in the DBR in Fig. 5. An almost linear relationship between the extent of electric field enhancement as a function of the dielectric contrast between the polymers used to form the DBR is noted. It thus solidifies the extreme importance between engineering the dielectric contrast between mutually processable polymers and the extent of confinement that the microcavities can achieve. A similar linear trend is noticed for the FWHM of the PBG (red squares), where polymer pairs of higher refractive index contrast reflect a wider PBG at normal incidence. The PVK/AQ pairing shows the highest refractive index contrast and consequently the widest PBG, which ideally has to be broader than the fluorescence spectrum. This is essential for suppressing as much of the off-resonance fluorescence as possible, especially in the case of polychromatic fluorescent dyes like organic emitters to funnel the majority of emitted light within the cavity mode. Correspondingly, it is of high importance to further develop polymers, blends, and hybrid systems56,57 pushing the limits of refractive index of traditional polymers for more advanced photonic applications.
Conclusions
In conclusion, we have shown the possible effects of light confinement in a suitably engineered dielectric microcavity for controlling the radiative rate in the NIR spectral range. Through simply changing the casting parameters we were able to engineer fully solution-processed planar microcavities both tuned to the emission of the embedded dye and a reference to account for any unintended effects. Despite providing only one-dimensional confinement, the properly tuned microcavity enhanced the fluorescence of the near infrared dye by more than 10-fold. More importantly, we demonstrate that the combination between the high-dielectric contrast and defect layer positioning can influence the radiative and non-radiative rates of a fluorophore in an aptly designed microcavity compared to both the stand-alone dye and a reference simulating the chemical and dielectric environment. Additional developments in the field are possible upon increasing the dielectric contrast of the polymer DBRs, using sharper emitters as well as further reducing the cavity width, thus demonstrating polymer chemistry as a tool to develop quantum electrodynamics.Author contributions
H. M. and M. V. B. fabricated the samples and analysed the data along with A. L. H. M. drafted the manuscript. P. L. and D. C. jointly supervised the investigation, reviewed, and edited the manuscript. D. C. organized provision of materials. D. C. and P. S. conceived the project. The final article was written through contributions from all authors. All authors have given approval to the final version of the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the Compagnia di San Paolo (Turin, Italy) Research Project “PIVOT” (IDROL 20583). Authors also acknowledge funding from the University of Genoa (FRA2019 and FRA2020) and PRIN, Research Project “PETALS” (2020TS9LXS). M. V. B. acknowledges financial support from the Erasmus Mundus SERP+ Master program funded by the European Commission. We also acknowledge Solvay Specialty Polymers for providing Aquivion material.References
- K. J. Vahala, Optical microcavities, Nature, 2003, 424, 839–846 CrossRef CAS PubMed.
- E. M. Purcell, H. C. Torrey and R. V. Pound, Resonance Absorption by Nuclear Magnetic Moments in a Solid, Phys. Rev., 1946, 69, 37–38 CrossRef CAS.
- G. Shambat, B. Ellis, A. Majumdar, J. Petykiewicz, M. A. Mayer, T. Sarmiento, J. Harris, E. E. Haller and J. Vučković, Ultrafast direct modulation of a single-mode photonic crystal nanocavity light-emitting diode, Nat. Commun., 2011, 2, 539 CrossRef PubMed.
- H. Cho, J. Chung, J. Song, J. Lee, H. Lee, J. Lee, J. Moon, S. Yoo and N. S. Cho, Importance of Purcell factor for optimizing structure of organic light-emitting diodes, Opt. Express, 2019, 27, 11057–11068 CrossRef CAS PubMed.
- L. T. Vuong, G. Kozyreff, R. Betancur and J. Martorell, Cavity-controlled radiative recombination of excitons in thin-film solar cells, Appl. Phys. Lett., 2009, 95, 233106 CrossRef.
- F. Sgrignuoli, P. Ingenhoven, G. Pucker, V. D. Mihailetchi, E. Froner, Y. Jestin, E. Moser, G. Sànchez and L. Pavesi, Purcell effect and luminescent downshifting in silicon nanocrystals coated back-contact solar cells, Sol. Energy Mater. Sol. Cells, 2015, 132, 267–274 CrossRef CAS.
- P. Lova, G. Manfredi and D. Comoretto, Advances in functional solution processed planar 1d photonic crystals, Adv. Opt. Mater., 2018, 6, 1800730 CrossRef.
- B. E. Saleh and M. C. Teich, Fundamentals of Photonics, John Wiley & Sons, Hoboken, New Jersey, 2019 Search PubMed.
- H. Megahd, D. Comoretto and P. Lova, Planar microcavities: Materials and processing for light control, Opt. Mater.: X, 2022, 13, 100130 Search PubMed.
- A. Kavokin, J. J. Baumberg, G. Malpuech and F. P. Laussy, Microcavities, Oxford University Press, Oxford, 2nd edn, 2017 Search PubMed.
- J. B. Khurgin, How to deal with the loss in plasmonics and metamaterials, Nat. Nanotechnol., 2015, 10, 2–6 CrossRef CAS PubMed.
- A. Lanfranchi, H. Megahd, P. Lova and D. Comoretto, Multilayer Polymer Photonic Aegises Against Near-Infrared Solar Irradiation Heating, ACS Appl. Mater. Interfaces, 2022, 14, 14550–14560 CrossRef CAS PubMed.
- M. Barth, A. Gruber and F. Cichos, Spectral and angular redistribution of photoluminescence near a photonic stop band, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 085129 CrossRef.
- P. Lodahl, A. Floris van Driel, I. S. Nikolaev, A. Irman, K. Overgaag, D. Vanmaekelbergh and W. L. Vos, Controlling the dynamics of spontaneous emission from quantum dots by photonic crystals, Nature, 2004, 430, 654–657 CrossRef CAS PubMed.
- M. Athanasiou, P. Papagiorgis, A. Manoli, C. Bernasconi, M. I. Bodnarchuk, M. V. Kovalenko and G. Itskos, Efficient Amplified Spontaneous Emission from Solution-Processed CsPbBr3 Nanocrystal Microcavities under Continuous Wave Excitation, ACS Photonics, 2021, 8, 2120–2129 CrossRef CAS.
- N. Puthiya Purayil, V. Kakekochi, U. K. Dalimba and C. Keloth, All-Optical Diode Action through Enhanced Nonlinear Response from Polymeric Photonic Crystal Microcavity, ACS Appl. Electron. Mater., 2022, 4, 138–148 CrossRef CAS.
- M. V. Vijisha, J. Ramesh, C. Arunkumar and K. Chandrasekharan, Impressive nonlinear optical responses of a cationic porphyrin derivative in a flexible all-polymer Bragg stack on optical Tamm mode coupling, J. Mater. Chem. C, 2020, 8, 12689–12697 RSC.
- P. Lova, H. Megahd, P. Stagnaro, M. Alloisio, M. Patrini and D. Comoretto, Strategies for dielectric contrast enhancement in 1D planar polymeric photonic crystals, Appl. Sci., 2020, 10, 4122 CrossRef CAS.
- H. Megahd, P. Lova, S. Sardar, C. D'Andrea, A. Lanfranchi, B. Koszarna, M. Patrini, D. Gryko and D. Comoretto, All-Polymer Microcavities for Fluorescence Radiative Rate Modification of a Diketopyrrolopyrrole Derivative, ACS Omega, 2022, 7, 15499–15506 CrossRef CAS PubMed.
- H. Megahd, C. Oldani, S. Radice, A. Lanfranchi, M. Patrini, P. Lova and D. Comoretto, Aquivion–Poly(N-vinylcarbazole) Holistic Flory–Huggins Photonic Vapor Sensors, Adv. Opt. Mater., 2021, 9, 2170017 CrossRef.
- A. Skulimowska, M. Dupont, M. Zaton, S. Sunde, L. Merlo, D. J. Jones and J. Rozière, Proton exchange membrane water electrolysis with short-side-chain Aquivion® membrane and IrO2 anode catalyst, Int. J. Hydrogen Energy, 2014, 39, 6307–6316 CrossRef CAS.
- J. Lin, Y. Liu and Q. M. Zhang, Charge dynamics and bending actuation in Aquivion membrane swelled with ionic liquids, Polymer, 2011, 52, 540–546 CrossRef CAS PubMed.
- C. D'Urso, C. Oldani, V. Baglio, L. Merlo and A. S. Aricò, Towards fuel cell membranes with improved lifetime: Aquivion® Perfluorosulfonic Acid membranes containing immobilized radical scavengers, J. Power Sources, 2014, 272, 753–758 CrossRef.
- L. Dou, Y. Liu, Z. Hong, G. Li and Y. Yang, Low-Bandgap Near-IR Conjugated Polymers/Molecules for Organic Electronics, Chem. Rev., 2015, 115, 12633–12665 CrossRef CAS PubMed.
- S. A. McDonald, G. Konstantatos, S. Zhang, P. W. Cyr, E. J. D. Klem, L. Levina and E. H. Sargent, Solution-processed PbS quantum dot infrared photodetectors and photovoltaics, Nat. Mater., 2005, 4, 138–142 CrossRef CAS PubMed.
- A. Minotto, P. A. Haigh, G. Łukasiewicz, E. Lunedei, D. T. Gryko, I. Darwazeh and F. Cacialli, Visible light communication with efficient far-red/near-infrared polymer light-emitting diodes, Light: Sci. Appl., 2020, 9, 70 CrossRef PubMed.
- G. Hong, A. L. Antaris and H. Dai, Near-infrared fluorophores for biomedical imaging, Nat. Biomed. Eng., 2017, 1, 0010 CrossRef CAS.
- S. Hao, Y. Shang, D. Li, H. Ågren, C. Yang and G. Chen, Enhancing dye-sensitized solar cell efficiency through broadband near-infrared upconverting nanoparticles, Nanoscale, 2017, 9, 6711–6715 RSC.
- L. Tejerina, A. G. Rapidis, M. Rickhaus, P. Murto, Z. Genene, E. Wang, A. Minotto, H. L. Anderson and F. Cacialli, A porphyrin pentamer as a bright emitter for NIR OLEDs, J. Mater. Chem. C, 2022, 10, 5929–5933 RSC.
- S. Shimizu, T. Iino, A. Saeki, S. Seki and N. Kobayashi, Rational Molecular Design towards Vis/NIR Absorption and Fluorescence by using Pyrrolopyrrole aza-BODIPY and its Highly Conjugated Structures for Organic Photovoltaics, Chem. – Eur. J., 2015, 21, 2893–2904 CrossRef CAS PubMed.
- X.-M. Chen, X.-F. Hou, H. K. Bisoyi, W.-J. Feng, Q. Cao, S. Huang, H. Yang, D. Chen and Q. Li, Light-fueled transient supramolecular assemblies in water as fluorescence modulators, Nat. Commun., 2021, 12, 4993 CrossRef CAS PubMed.
- X.-M. Chen, Q. Cao, H. K. Bisoyi, M. Wang, H. Yang and Q. Li, An Efficient Near-Infrared Emissive Artificial Supramolecular Light-Harvesting System for Imaging in the Golgi Apparatus, Angew. Chem., Int. Ed., 2020, 59, 10493–10497 CrossRef CAS PubMed.
- Z. Yu, H. K. Bisoyi, X.-M. Chen, Z.-Z. Nie, M. Wang, H. Yang and Q. Li, An Artificial Light-Harvesting System with Controllable Efficiency Enabled by an Annulene-Based Anisotropic Fluid, Angew. Chem., Int. Ed., 2022, 61, e202200466 CAS.
- A. Minotto, P. Murto, Z. Genene, A. Zampetti, G. Carnicella, W. Mammo, M. R. Andersson, E. Wang and F. Cacialli, Efficient Near-Infrared Electroluminescence at 840 nm with “Metal-Free” Small-Molecule:Polymer Blends, Adv. Mater., 2018, 30, 1706584 CrossRef PubMed.
- A. A. Ishchenko, Photonics and molecular design of dye-doped polymers for modern light-sensitive materials, Pure Appl. Chem., 2008, 80, 1525–1538 CrossRef CAS.
- I. Murataj, M. Channab, E. Cara, C. F. Pirri, L. Boarino, A. Angelini and F. Ferrarese, Lupi, Hyperbolic Metamaterials via Hierarchical Block Copolymer Nanostructures, Adv. Opt. Mater., 2021, 9, 2001933 CrossRef CAS.
- E. F. Schubert, N. E. J. Hunt, M. Micovic, R. J. Malik, D. L. Sivco, A. Y. Cho and G. J. Zydzik, Highly Efficient Light-Emitting Diodes with Microcavities, Science, 1994, 265, 943–945 CrossRef CAS PubMed.
- T. Kobayashi and R. Hogan, Near-infrared polymer semiconductor laser, Appl. Phys. Lett., 2010, 97, 143303 CrossRef.
- X. Wang, Q. Liao, H. Li, S. Bai, Y. Wu, X. Lu, H. Hu, Q. Shi and H. Fu, Near-infrared lasing from small-molecule organic hemispheres, J. Am. Chem. Soc., 2015, 137, 9289–9295 CrossRef CAS PubMed.
- S. Kushida, D. Okada, F. Sasaki, Z.-H. Lin, J.-S. Huang and Y. Yamamoto, Low-Threshold Whispering Gallery Mode Lasing from Self-Assembled Microspheres of Single-Sort Conjugated Polymers, Adv. Opt. Mater., 2017, 5, 1700123 CrossRef.
- D. Goldberg and V. M. Menon, Enhanced amplified spontaneous emission from colloidal quantum dots in all-dielectric monolithic microcavities, Appl. Phys. Lett., 2013, 102, 081119 CrossRef.
- J. C. de Mello, H. F. Wittmann and R. H. Friend, An improved experimental determination of external photoluminescence quantum efficiency, Adv. Mater., 1997, 9, 230–232 CrossRef CAS.
- A. Mishra, R. K. Behera, P. K. Behera, B. K. Mishra and G. B. Behera, Cyanines during the 1990s:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Review, Chem. Rev., 2000, 100, 1973–2012 CrossRef CAS PubMed.
A Review, Chem. Rev., 2000, 100, 1973–2012 CrossRef CAS PubMed. - J. Lee, A. J. Kalin, T. Yuan, M. Al-Hashimi and L. Fang, Fully conjugated ladder polymers, Chem. Sci., 2017, 8, 2503–2521 RSC.
- P. Lova, V. Grande, G. Manfredi, M. Patrini, S. Herbst, F. Würthner and D. Comoretto, All-polymer photonic microcavities doped with perylene bisimide j-aggregates, Adv. Opt. Mater., 2017, 5, 1700523 CrossRef.
- L. Nevou, https://github.com/LaurentNevou/Light_WaveTransmission1D_dispersion, (accessed January 22, 2021).
- P. Lova, M. Olivieri, A. Surace, G. Topcu, M. Emirdag-Eanes, M. M. Demir and D. Comoretto, Polymeric Planar Microcavities Doped with a Europium Complex, Crystals, 2020, 10, 287 CrossRef CAS.
- V. M. Menon, M. Luberto, N. V. Valappil and S. Chatterjee, Lasing from InGaP quantum dots in a spin-coated flexible microcavity, Opt. Express, 2008, 16, 19535–19540 CrossRef CAS PubMed.
- G. Manfredi, P. Lova, F. Di Stasio, R. Krahne and D. Comoretto, Directional Fluorescence Spectral Narrowing in All-Polymer Microcavities Doped with CdSe/CdS Dot-in-rod Nanocrystals, ACS Photonics, 2017, 4, 1761–1769 CrossRef CAS.
- M. Pelton, Modified spontaneous emission in nanophotonic structures, Nat. Photonics, 2015, 9, 427–435 CrossRef CAS.
- K. Tanaka, T. Nakamura, W. Takamatsu, M. Yamanishi, Y. Lee and T. Ishihara, Cavity-Induced Changes of Spontaneous Emission Lifetime in One-Dimensional Semiconductor Microcavities, Phys. Rev. Lett., 1995, 74, 3380–3383 CrossRef CAS PubMed.
- A. M. Vredenberg, N. E. J. Hunt, E. F. Schubert, D. C. Jacobson, J. M. Poate and G. J. Zydzik, Controlled atomic spontaneous emission from Er3+ in a transparent Si/SiO2 microcavity, Phys. Rev. Lett., 1993, 71, 517–520 CrossRef CAS PubMed.
- M. Skorobogatiy and J. Yang, Fundamentals of Photonic Crystal Guiding, Cambridge University Press, Cambridge, 2008 Search PubMed.
- G. Canazza, F. Scotognella, G. Lanzani, S. De Silvestri, M. Zavelani-Rossi and D. Comoretto, Lasing from all-polymer microcavities, Laser Phys. Lett., 2014, 11, 035804 CrossRef CAS.
- S. Gazzo, G. Manfredi, R. Pötzsch, Q. Wei, M. Alloisio, B. Voit and D. Comoretto, High refractive index hyperbranched polyvinylsulfides for planar one-dimensional all-polymer photonic crystals, J. Polym. Sci., Part B: Polym. Phys., 2016, 54, 73–80 CrossRef CAS.
- C. Tavella, G. Luciano, P. Lova, M. Patrini, C. D'Arrigo, D. Comoretto and P. Stagnaro, 2,5-Diisopropenylthiophene by Suzuki–Miyaura cross-coupling reaction and its exploitation in inverse vulcanization: a case study, RSC Adv., 2022, 12, 8924–8935 RSC.
- T. S. Kleine, L. R. Diaz, K. M. Konopka, L. E. Anderson, N. G. Pavlopolous, N. P. Lyons, E. T. Kim, Y. Kim, R. S. Glass, K. Char, R. A. Norwood and J. Pyun, One Dimensional Photonic Crystals Using Ultrahigh Refractive Index Chalcogenide Hybrid Inorganic/Organic Polymers, ACS Macro Lett., 2018, 7, 875–880 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Details of optical characterisation, blend refractive index, lifetime, and calculations. See DOI: https://doi.org/10.1039/d2qm00313a |
| This journal is © the Partner Organisations 2022 |