Large easy-axis magnetic anisotropy in a series of trigonal prismatic mononuclear cobalt(II) complexes with zero-field hidden single-molecule magnet behaviour: the important role of the distortion of the coordination sphere and intermolecular interactions in the slow relaxation

Abstract

The complexes [Co(L)]X·S (X = CoCl₄²⁻, S = CH₃CN (1); X = ZnCl₄²⁻, S = CH₃OH (2)), [Co(L)]X₂·S (X = ClO₄⁻, S = 2CH₃OH (3) and X = BF₄⁻ (4)) and [Co(L)(NCS)₂] (5), where L = the N₆-tripodal ligand tris(pyridylhydrazonyl)phosphorylsulfide, were prepared and studied by X-ray crystallography, ac and dc magnetic data, FIRMS and HFEPR spectra, and theoretical calculations. On passing from 1 to 4, the change of the counteranion decreases slightly the distortion of the CoN₆ coordination polyhedron from trigonal prismatic to octahedral, with a parallel increase of the easy-axis magnetic anisotropy. Compound 1 does not show slow magnetic relaxation, even in the presence of a dc magnetic field, due to fast QTM triggered by dipolar interactions. Although the complexes 2–4 show a weak frequency and temperature dependence of the ac susceptibility below 10 K at zero field, they exhibit slow relaxation and single-molecule magnet (SMM) behaviour under the corresponding optimal field. The relaxation of the magnetization takes place mainly through a Raman relaxation process above 4 K, whereas below this temperature QTM and/or direct processes dominate. The relaxation time increases with the parallel increase of the uniaxial anisotropy on passing from 1 to 4. The width of the hysteresis for the trigonal prismatic complexes at 0.4 K decreases in the order 3 > 2 > 4 > 1, which is due to combined effects of QTM relaxation and axial anisotropy. Magnetic dilution of complexes 3 and 4 with Zn^II triggers the slow relaxation of the magnetization at zero-field, so that these complexes can be considered as “hidden mononuclear SMMs”. Compound 5, with a compressed octahedral geometry, exhibits easy-plane magnetic anisotropy (D = +34.7 cm⁻¹), and it is a field-induced mononuclear SMM with magnetization relaxation faster than compounds 2–4 and a smaller hysteresis loop.

---

Introduction

Open-shell metal complexes showing magnetic bistability at the molecular level, called Single-Molecule Magnets (SMMs),¹ have attracted much attention during the last few decades, because they show rich classical and quantum properties that make them potential candidates as components of high-density information storage,² molecular spintronics³ and quantum computing devices.⁴ In recent years, the synthetic efforts in the field of SMMs have moved from large-spin ground state metal clusters to mononuclear complexes with only one spin carrier, also called mononuclear Single-Molecule Magnets (MSMMs).^5,6 In these relatively simple systems, large axial (easy-axis) anisotropies with marginal rhombicity terms, leading to high effective energy barriers for magnetization reversal (U_eff), can be deliberately achieved by regulating the electronic structure of the metal centres, which depends on the features of the metal and coordination environment.^5,6 The aim of this research is not only to build molecules with a very high magnetic anisotropy barrier, but also to develop strategies for the improvement of the spin lifetime in these molecules. The latter is of crucial importance because it has been demonstrated that phonons occurring in the THz energy range partly supress the benefit of having a large magnetic anisotropy.⁷ It is worth mentioning that even though the best MSMM behaviour was observed for lanthanide mononuclear complexes,⁸ since the discovery of the first 3d-metal based MSMM, a trigonal pyramidal high spin Fe^II complex with a very high effective energy barrier,⁹ the research activity in this area has been boosted. Among 3d-based MSMMs, those containing high-spin Co^II metal ions are by far the most numerous, exhibiting a large variety of geometries and coordination numbers (ranging from two- to eight) and significant magnetic anisotropy, which arises from either first- or second-order spin–orbit coupling (SOC).^6,10 Moreover, as Co^II is a non-integer spin metal ion (Kramers ion), in absence of magnetic field, direct and under-the-barrier quantum tunnelling (QTM) mechanisms should not be operative.¹¹ The absence of fast QTM occurring between degenerate ±Ms levels at zero field facilitates Orbach and Raman thermally dependent relaxation processes. In spite of this, only a limited number of Co-based MSMMs with slow relaxation at zero-field have been reported so far.⁶ Good examples of zero field Co^II MSMMs are the linear two-coordinated carbene complexes reported by Gao et al.^12a and Long et al.,^12b which exhibit effective energy barriers of 413 cm⁻¹ and 450 cm⁻¹, respectively, and the latter represents the record of U_eff for a 3d-MSMM. Despite these breakthroughs, the fabrication of molecule devices based on coordinatively unsaturated air-sensitive Co^II complexes, such as those indicated above, is a very hard task. In view of this, the research in this field has set its sights on simple air-stable Co^II complexes with large axial anisotropy (i.e. where the axial zero-field splitting parameter D is negative). This is because this kind of complexes have diminished transverse anisotropy and, as a result, the QTM relaxation pathway is more efficiently suppressed, which is mandatory to observe MSMM behaviour at zero dc field.⁶ In fact, typical MSMM behaviour either at zero field or in the presence of a small dc field, the latter for suppressing fast QTM, is generally observed for complexes with large axial anisotropy. It is worth noting that, in a few cases, magnetic dilution is able to activate the MSMM behaviour at zero field (“hidden MSMM”) in this kind of easy-axis anisotropic Co^II complexes.¹³ Conversely, for Co^II complexes with large positive D values (easy-plane anisotropy), the application of a magnetic field is imperative to observe MSMM behaviour.¹⁴

Ruiz and co-workers recently predicted the sign and magnitude of D for 3d metal complexes based on their coordination numbers, geometries and electronic structures using theoretical methods.^6b,10 Among the most common and thermodynamically stable geometries observed for Co^II complexes, the proposed method predicted large D < 0 values for trigonal prismatic complexes. Such predictions have been validated for the limited number of trigonal prismatic Co^II-based MSMM complexes reported so far, because most of them exhibit SMM behaviour at zero field.^10,15

Although two theoretical studies dealing with the structure/anisotropy relationship in trigonal prismatic Co^II complexes have been recently reported,^15d,e which point out that the anisotropy decreases with the increase of the distortion of the coordination environment from trigonal prismatic (TPR-6) to octahedral geometry (OC-6), however, as far as we know, no experimental correlations have been reported to date. Moreover, even though there are studies analysing the influence of the anions present in the crystal lattice on the anisotropy parameters in distorted tetrahedral¹⁶ and trigonal antiprismatic Co^II complexes,¹⁷ to the best of our knowledge there exists no such type of study for trigonal prismatic complexes. In view of this, we decided to prepare a series of trigonal prismatic Co^II mononuclear complexes with the N₆-tripodal ligand tris(pyridylhydrazonyl)phosphorylsulfide, (S)P[N(Me)N=C(H)Py]₃ (L), and different counter-anions, which present the molecular formulas [Co(L)]X·S (where X = [CoCl₄]²⁻, S = CH₃CN (1); [ZnCl₄]²⁻, S = CH₃OH (2)), [Co(L)]X₂·S (X = ClO₄⁻, S = 2CH₃OH (3); X = BF₄⁻ (4)) and [Co(L)(SCN)₂] (5). Although complexes 1–4 have the expected distorted trigonal prismatic geometry, complex 5 is an axially compressed octahedral complex. It is worth noting that dc measurements and ab initio theoretical calculations recently reported for the compressed octahedral mononuclear complex [Co(tu)₄Cl₂] (tu = thiourea),¹⁸ bearing sulfur donor atoms in the equatorial positions and chloride ligands in axial positions, have shown that it exhibits easy-axis anisotropy, whereas the elongated octahedral [Co(py)₄Cl₂] complex, with nitrogen donor atoms in equatorial positions, possesses easy-plane anisotropy.^18,19 The type of magnetic anisotropy was unambiguously supported by polarized neutron diffraction method (PND) in the former complex and by high-frequency and -field (HFEPR) measurements in the latter. Moreover, from theoretical ab initio calculations on model compounds (constructed from the above indicated complexes by changing axial or equatorial distances and keeping other structural parameters the same), it was deduced that both easy-axis and easy-plane anisotropies can be attained by fine-tuning the ligand field. Thus, Co^II complexes combining strong axial and weak equatorial bonds (axially compressed octahedral geometry), as it occurs in [Co(tu)₄Cl₂], stabilize a large axial anisotropy, whereas the combination of large axial bonds and short equatorial bonds, like in [Co(py)₄Cl₂], favors large positive D values.^18,19 This qualitative magneto-structural correlation seems not to be of general applicability, because compressed octahedral CoN₆ complexes, such as [Co(py)₄(NCS)₂]¹⁹ and [Co(pto)₄(NCS)₂] (pto = 2-(pyridine-2-yl)-5-thiophen-2-yl)-1,3,4-oxadiazole,²⁰ have a similar ratio between the axial and equatorial bond distances, however, they exhibit D values of opposite sign. Therefore, in order to clarify this apparent contradiction more examples of this type of complexes, like 5, where the sign of D is unambiguously supported by a combination of theoretical and experimental methods, such as HFEPR, PND and single-crystal torque anisotropy, are needed.^18,21

In light of the above considerations, the aim of this work is fourfold: (i) to confirm that complexes 1–4 show large axial magnetic anisotropy. The previous results of Ruiz and co-workers¹⁰ and Costes²² and co-workers for Co^II and Co^IIY^IIICo^II complexes (the latter can be considered as formed by two almost isolated mononuclear complexes) with CoN₆ and CoN₃O₃ trigonal prismatic coordination environments, respectively, bearing similar tripodal ligands to L, showed negative D values of −72 cm⁻¹ and −38.8 cm⁻¹, respectively; (ii) to analyse how the change of the anion alters the Co^II coordination sphere and, consequently, the axial magnetic anisotropy. Likewise, we want to support the above indicated theoretical variation of the anisotropy with the distortion of the TPR-6 coordination sphere; (iii) to study how the change of the anion affects the crystal packing and the relaxation dynamic, focusing specially on the role played by the dipolar interactions, and (iv) to unequivocally determine the sign and magnitude of D for the tetragonally compressed octahedral compound 5 by a combination of experimental and theoretical methods, including HFEPR and FIRMS spectroscopies.

Results and discussion

Synthetic procedures and details of the experimental and theoretical methods used for studying the reported complexes are described in the ESI.†

In order to obtain mononuclear complexes with trigonal prismatic geometry (TPR-6), we chose a tripodal N₆-ligand, L = (S)P[N(Me)N=C(H)Py]₃, which was originally used for preparing Cu^II, Y^III and Fe^II spin-crossover complexes.^23,24 The reaction of L with different cobalt(II) salts in either MeOH or CH₃CN afforded complexes of formulas [Co(L)]X·S (X = CoCl₄²⁻, S = CH₃CN (1); X = ZnCl₄²⁻, S = CH₃OH (2)), [Co(L)]X₂·S (X = ClO₄⁻, S = 2CH₃OH (3) and X = BF₄⁻ (4)) and [Co(L)(NCS)₂] (5).

The reaction of the ligand L with CoCl₂·6H₂O in acetonitrile and 1 : 1 molar ratio did not lead to the expected [Co(L)₂]Cl₂ complex, but to compound 1 with the in situ formation of the CoCl₄²⁻ counteranion. A similar reaction was previously reported for the complex [CoL1][CoCl₄] (L1 = N₆-tripodal ligand obtained by reaction of 1,3,5-triaminocyclohexane and 2-formyl-5-(N-tert-butyl)-nicotinamide).^5d Interestingly, complex 2, which could be considered as a magnetic diluted version of complex 1, was obtained using the same reaction conditions as for 1, but adding an equimolar amount of ZnCl₂ and using methanol as solvent. The reaction of L with cobalt(II) salts containing non-coordinated anions, such as Co(ClO₄)₂·6H₂O or Co(BF₄)₂·6H₂O, and using methanol as solvent, led to compounds 3 and 4, respectively. It is worth noting that complexes 2–4 are orange in colour, whereas complex 1 is green in colour. This fact supports the absence of CoCl₄²⁻ counteranions in complex 2. In this regard, the reflectance spectra for complex 1 shows d–d bands arising from both the cation (shoulder at around 450 nm and a very broad band centred at 1000 nm) and the anion (625–700 nm and 1650–2000 nm),²⁵ whereas the complex 2 spectrum only shows d–d bands belonging to the [Co(L)]²⁺ cations (see Fig. S1†). The HFEPR spectrum of 2 (see below) also supports the absence of CoCl₄²⁻ in this compound. It is worth mentioning that the reflectance diffuse spectra due to the [Co(L)]²⁺ cations for complexes 2–4 are superimposable, with allowed bands centred at 470 nm and 1050 nm. The hypsochromic shift of the bands of compound 1, regarding those of compounds 2–4, can be due to the slightly larger distortion of the CoN₆ coordination sphere from TPR-6 to OC-6 for the former with respect to the latter (see below). The bands for 1 are slightly blue shifted, because the octahedral field is stronger than the prismatic trigonal field.²⁵

The complex 5 was prepared by the reaction of the ligand L with Co(SCN)₂ in methanol solution and in 1 : 1 molar ratio, and further redissolution of the precipitate formed in acetonitrile. The IR spectrum indicates that the SCN⁻ anions are κN-coordinated to the Co^II ions (ν_CN = 2100 cm⁻¹), thus showing that the formation of two Co–NCS bonds is thermodynamically more stable than the formation of two N–Co bonds with the nitrogen atoms of one of the arms of the tripodal ligand (see below). The fact that in 1 the Cl⁻ anions do not replace one of the arms of the ligand in the Co^II coordination sphere is in agreement with the fact that the ligand field stabilization energy promoted by the Cl⁻ ligand is weaker than that created by the κN-coordinated thiocyanate ligand.

Crystal structures

The structures of the complexes 1–4 consist in cationic mononuclear [Co(L)]²⁺ units neutralized with monovalent or divalent anions, in particular, [CoCl₄]²⁻, [ZnCl₄]²⁻, ClO₄⁻ and BF₄⁻, while compound 5 is formed by neutral mononuclear [Co(L)(SCN)₂] molecules. In addition, compounds 1 and 2 crystallize with one acetonitrile and one methanol solvent molecule, respectively, whereas complex 3 crystallizes with two methanol molecules.

The [Co(L)]²⁺ cationic units of complexes 1–4 are very similar and, therefore, we will only describe the structure of 3 as a representative example to illustrate the common characteristics of these compounds. Within the cationic unit [Co(L)]²⁺, the Co^II ion is coordinated by the imine and pyridine nitrogen atoms belonging to the three arms of the ligand, leading to a CoN₆ trigonal prismatic coordination sphere (Fig. 1).

Fig. 1 Perspective view of the molecular structure of 3. Hydrogen atoms, perchlorate anions and solvent molecules are omitted for clarity. Only the Δ enantiomer is given in this figure.

The nitrogen atoms from the pyridine rings occupy one triangular face and the nitrogen atoms belonging to the imine groups are placed in the other triangular face. The Co–N bond distances are very similar with values in the range of 2.1216(18)–2.1600(17) Å. The main bond distances and angles for complexes 1–4 are given in Table S1.† The shortest Co⋯Co distances between the [Co(L)]²⁺ units are 8.2812 (6) Å, 8.1675 (8) Å, 8.9742 (8) Å and 8.2237 (12) Å for 1–4, respectively. The fact that the Co⋯Co distance is shorter for 4 than for 3, could be due to the smaller size of the BF₄⁻ anion compared to the ClO₄⁻ anion. Moreover, for compound 1, the shortest Co⋯Co distance between the [Co(L)]²⁺ and the [CoCl₄]²⁻ ions is 5.962(2) Å. In the case of 2, the shortest Co⋯Zn distance between the [Co(L)]²⁺ units and the [ZnCl₄]²⁻ counteranions is 6.559 Å.

The screw-type coordination of the ligand around the Co^II ions induces chirality [Δ (clockwise) and Λ (anticlockwise)] in the complexes 1–4. The compounds 2, 3 and 4 crystallise as racemic compounds where both Δ and Λ configurations are present in the crystal structure, whereas for compound 1 only the Δ form is found in the crystal analysed. In view of this, compound 1 should be a conglomerate of Δ and Λ crystals.

The cationic mononuclear units in 1–4 are well isolated in the structure as there are no π⋯π staking interactions between the aromatic pyridine rings. However, intermolecular C–H⋯π interactions can be observed between the pyridine rings in compounds 1, 2 and 4, with shortest C–H⋯·π distances of 3.232 Å, 3.317 Å and 2.705 Å, respectively. Additionally, in compound 2 the methanol molecule interacts through a hydrogen bond with the [ZnCl₄]²⁻ ion (O⋯Cl distance of 3.162 Å), whereas in compound 3 one of the methanol molecules is involved in intermolecular hydrogen bond interactions with one perchlorate anion (donor–acceptor O⋯O distance of 2.810 Å), as well as with the sulphur atom of the ligand (donor–acceptor O⋯S distance of 3.280 Å).

In compound 1, the CoCl₄²⁻ ion is slightly distorted from Td symmetry, with Co–Cl distances and Cl–Co–Cl angles falling in the 2.2566(6)–2.2951(6) Å and 107.15(2)–112.10(2)° ranges, respectively. Continuous shape measures theory with SHAPE software²⁶ indicates that the CoCl₄ coordination sphere is very close to an ideal tetrahedral geometry (S = 0.04).

Compound 5 consists of neutral mononuclear [Co(L)(SCN)₂] molecules with the Co^II exhibiting a distorted octahedral CoN₆ coordination sphere, which is formed by the coordination of two nitrogen atoms from two SCN⁻ anions in trans axial positions and two pyridine and two imine nitrogen atoms belonging to two of the three arms of the tripodal ligand in the equatorial positions. As a result, the third arm of the ligand remains uncoordinated (Fig. 2).

Fig. 2 Perspective view of the molecular structure of compound 5. Hydrogen atoms are omitted for clarity.

The main bond distances and angles are listed in Table S2.† The Co–N distances belonging to SCN⁻ groups are slightly shorter (∼2.07 Å) than the Co–N distances involving the nitrogen atoms from the ligand, which are almost coincident (in the 2.15–2.19 Å range), and so the CoN₆ coordination sphere can be described as tetragonally compressed octahedral.

It has to be highlighted that one of the SCN⁻ ligands is practically linear with an N–C–S angle of 178.79 (18)°, whereas the other one is bent with an N–C–S angle of 167.3 (2)°. In connection with this, the Co–N distance in the bent SCN⁻ anion is larger than that found for the almost linear SCN⁻ one, which is due to a weak overlapping in the former between the d orbitals of the Co^II and the σ and π orbitals of the SCN⁻ anion.

Molecules are connected by weak intermolecular π⋯π interactions between the pyridine rings belonging to different complexes with a centroid–centroid distance of 3.877 Å, which gives rise to a shortest intermolecular Co⋯Co distance of 9.121 (3) Å.

The CoN₆ coordination sphere has been calculated for 1–5 by using the continuous shape measures theory and SHAPE software (Table S3†),²⁶ which indicates that in all these complexes the coordination geometry is intermediate between the ideal six-vertex polyhedral octahedron (OC-6) and trigonal prism (TPR-6). A representation of the calculated values in a shape map is given in Fig. 3.

Fig. 3 Octahedron-trigonal prism shape map showing the Bailar pathway (blue line) and the experimental data (circles). Bailar twist angle (θ) is also displayed (inset up right).

As it can be observed, the S values for the coordination complexes 1–4 confirm that their coordination spheres are much closer to the ideal TPR-6 polyhedron than to the octahedron, and that they do not significantly deviate from the Bailar path for the interconversion of the TPR-6 and OC-6 geometries. In good agreement with this, the mean Bailar twist angles, θ, for compounds 1–4 are 29.84°, 26.91°, 25.62° and 24.9°, respectively, whereas the dihedral angles between the triangular faces are found in the 0.35–0.88° range, thus indicating that the triangular faces are almost parallel. This distortion can be due, among other reasons, to the constrained symmetry of the ligand, the molecular packing forces, and the preference of the high spin Co^II ion for the OC-6 ligand field over the TPR-6 counterpart. The mean s h⁻¹ ratios (defined as the mean donor–donor distance across a triangular face divided by the mean donor–donor distances between the triangular faces) are found in the 1.16–1.18 Å range and point out to a small compression of the ideal TPR-6 geometry. The fact that the distances between the coordinated imine nitrogen atoms across the triangular face (∼2.85 Å) are slightly shorter than the same distances across the face defined by the pyridyl donor nitrogen atoms (∼3.09 Å) also indicates a small degree of truncation in the geometry. However, the coordination sphere for complex 5 is very close to an ideal octahedron and, moreover, deviates significantly from the Bailar pathway. In this case, the octahedral preference of the Co^II ion and the ability of the SCN⁻ ligand to form stronger Co–N bonds that the imine and pyridine nitrogen donors lead to the observed compressed octahedral geometry. All these results show that, in some cases, the change of the anion in this type of compounds can significantly affect the geometry of the Co^II ions and the dipolar interactions between them.

Static magnetic properties

The dc magnetic properties of 1–5 were studied in the 2–300 K temperature range with an applied magnetic field of 1000 Oe, and they are given in the form of the temperature dependence of χ_MT (χ_M is the molar magnetic susceptibility) in Fig. 4–6 for complexes 1, 2 and 5, respectively, which are given as examples, and in Fig. S2 and S3† for compounds 3 and 4, respectively.

Fig. 4 Temperature dependence of χ_MT for compound 1 (red circles). Field dependence of magnetization at the indicated temperatures (inset left) and M vs. H/T isotherms (inset right). Solid lines represent the best fit to eqn (1) with the parameters indicated in Table 1. The blue solid line in the χ_MT vs. T plot represents the ab initio calculated curve (sum of the calculated χ_MT values for [CoCl₄]²⁻ and [Co(L)]²⁺).

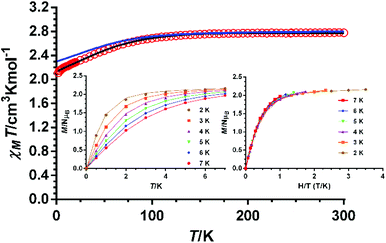Fig. 5 Temperature dependence of χ_MT for compound 2 (red circles). Field dependence of magnetization at the indicated temperatures (inset left) and M vs. H/T isotherms (inset right). Solid lines represent the best fit to eqn (1) with the parameters indicated in Table 1. The blue solid line in the χ_MT vs. T plot represents the ab initio calculated curve scaled by a factor of 0.9.

Fig. 6 Temperature dependence of χ_MT for compound 5 (red circles). Solid lines represent the best fit to eqn (1) (black line) and (2) (blue line). The solid green line corresponds to the ab initio calculated χ_MT vs. T plot. M vs. H/T isotherms (inset left) and qualitative energy splitting of the ⁴T_1g term in Oh symmetry by axial compression and rhombic distortion, SO and Zeeman effect (right). Solid lines in the reduced magnetization plot represent the best fit to eqn (1).

Table 1 SH parameters for 1–5 extracted from dc magnetic measurements

Compound	D (cm^−1)	E (cm^−1)	g perp	g parallel	zJ (cm^−1)
a To fit the data it was necessary to include a TIP term (0.0015(2)).
1	D 1 = −60.6(1)	E 1 = −0.03 (9)	g 1 = 2.548(2)	g 1 = 2.548(2)	0.0045(4)
	D 2 = 5.25 EPR (fixed)	E 2 = 1.75 EPR (fixed)	g 2 = 2.25 EPR (fixed)	g 2 = 2.25 EPR (fixed)
2	−87.2(4)	−0.02(9)	2.186(1)	2.754(1)	—
3	−116.6(6)	−3.1(9)	2.151(1)	2.847(1)	−0.026(3)
4	−127.6(8)	−0.22(6)	2.263(1)	2.782(1)	−0.007(5)
5	+34.7(1)	+11.5(2)	2.478(4)	2.072(2)

---

The χ_MT values at room temperature for complexes 1–5 of 5.78, 2.77, 2.88, 2.89 and 2.75 cm³ mol⁻¹ K, respectively, are significantly larger than the expected values for non-interacting Co^II ions with S = 3/2 and g = 2 (3.75 cm³ mol⁻¹ K for 1 and 1.875 cm³ mol⁻¹ K for the rest of compounds). The above values indicate a considerable unquenched orbital contribution of the Co^II ion as expected for compressed octahedral and trigonal prismatic geometries. Upon cooling, the χ_MT product diminishes first slightly from room temperature to around 100 K and then in a deeper manner to reach values of 3.73, 2.11, 2.08, 2.10 and 1.58 cm³ mol⁻¹ K at 2 K for 1–5, respectively. The decrease of χ_MT until 10 K is mainly due to spin–orbit coupling (SOC) effects, leading to low-lying excited states, whereas the faster diminution of χ_MT at very low temperature is due to ZFS single-ion anisotropy and eventually weak intermolecular antiferromagnetic interactions.

The field dependence of the magnetization at 2 K is almost saturated at 7 T for all the compounds, reaching values of 5μ_B for 1 and in the 2.15–2.20μ_B range for 2–5. These values are significantly lower than the values expected for isolated Co^II ions with S = 3/2 in the ground state and g = 2. These results indicate the presence of significant magnetic anisotropy.

For trigonal prismatic Co^II complexes with C₃ symmetry the ground spin quartet term is ⁴E, L = 2 and first order spin–orbit coupling (SOC) occurs, resulting in a large separation between the low-lying Kramers doublets.²⁷ Moreover, the first order SOC leads to axial anisotropy with an effective g_z factor (g′_z) of around 9 and the anisotropy axis parallel to the C₃ axis.^27,28 A small departure from C₃ symmetry, due, among other factors, to Jahn–Teller (JT) distortion, intermolecular contacts, ligands constrains and so forth, causes the splitting of the ⁴E ground state into two spin quartet states, and small transverse components of the g tensor appear. Nevertheless, the first SOC is still strong (Lz > 3/2), the energy gap between the two lowest Kramers doublets is larger than 200 cm⁻¹ and, moreover, they are very well separated from the other excited KDs.²⁸ In this situation, the lowest Kramers doublets are usually the only ones populated at low temperature, so that a phenomenological approach using ZFS in the S = 3/2 state that considers only these two KDs could be tentatively used. In fact, pseudo-trigonal prismatic complexes, like 1–4, have been generally analyzed with the ZFS spin Hamiltonian given in eqn (1). It is worth noting that this strategy is always valid below 100 K and frequently up to room temperature.

H = D[S_z² – S(S + 1)/3] + E(S_x² – S_y²) + gμ_BHS (1)

where S is the ground state spin, D and E are the axial and transverse (rhombic) magnetic anisotropy parameters, respectively, μ_B is the Bohr magneton, H the applied magnetic field and the third term corresponds to the Zeeman interaction. If E is zero, then 2D represents the energy gap between ±1/2 and ±3/2 Kramers doublets (KDs). If D > 0, the doublet with M_s = ±1/2 is located at lower energy than the doublet with M_s = ±3/2, whereas when D < 0 the reverse order occurs.

In tetragonally distorted octahedral complexes like 5, the axial crystal field splits the ⁴T_1g ground term of the ideal O_h symmetry into the ⁴A_2g (in D_4h notation) and ⁴E_g terms separated by an energy gap, Δ, which increases with tetragonality. For tetragonal compression, the axial crystal field parameter, Δ, is positive and the ⁴A_2g crystal field term is located at lower energy (easy plane anisotropy).²⁹ The second-order spin–orbit coupling (SOC) splits the ground ⁴A_2g term into two Kramers doublets (KDs). When these two Kramers doublets are well separated from those arising from the ⁴E_g term, the splitting of the former term can be described in a simple manner as a zero-field splitting (ZFS) within the spin Hamiltonian formalism (Fig. 6, inset). If the radial distortion is considered, then the CoN₆ coordination sphere of 5 is compressed octahedral and therefore a positive axial crystal field parameter (Δ) would be expected. In order to confirm the sign and magnitude of Δ and then the nature of the ground term for complex 5, its magnetic susceptibility data were analysed with a Figgis–Griffith Hamiltonian, which takes into account: (i) first order SOC effects associated with the ⁴T₁ ground term of the octahedral Co(II) ion, using the T–P isomorphism with an effective orbital moment L = 1; (ii) an axial distortion of the octahedral geometry and (iii) Zeeman interactions. The corresponding Hamiltonian can be written as:³⁰

where u = x, y, z, Δ is the axial splitting parameter, κ is the orbital reduction factor, λ is the spin–orbit coupling parameter, and L and S are the orbital and spin angular momentum operators, respectively. The factor −3/2 appears to consider that the real angular momentum for the ⁴T_1g ground state in an ideal O_h geometry is equal to the angular momentum of the ⁴P free ion term multiplied by −3/2. The best fit of the magnetic data of 5 with the above Hamiltonian using the MagSaki³¹ software led to the following parameters: λ = −112 cm⁻¹, κ = 0.97, Δ = +650 cm⁻¹, TIP = 34 × 10⁻⁶ cm³ mol⁻¹ with an agreement factor R = 1.6 × 10⁻⁵. These results confirm that Δ is large and positive (easy-plane anisotropy) and, therefore, ⁴A_2g is the ground state. In this case, the second order SOC splitting into two Kramer doublets can be described by the ZFS spin Hamiltonian. The energy gap between the two lowest KDs was calculated to be 108.7 cm⁻¹.

In view of the above considerations, the magnetic data for complexes 1–5 were also analyzed with the ZFS spin Hamiltonian. Thus, the temperature dependence of χ_MT and the field dependence of the magnetization in the 2–7 K range were simultaneously fitted with the PHI program (Fig. 4–6 and Fig. S2–S3†).³² In some cases, a mean field term was also introduced to take into account the intermolecular interactions.

It is worth noting that for complexes 1–4 either worse quality fits or physically-meaningless parameters are obtained when D is forced to be positive, whereas for compound 5 similar positive and negative values are possible. Nevertheless, the fit is an order of magnitude better when D is positive. These results support easy-axis magnetic anisotropy for the ground state of [Co(L)]²⁺ units in complexes 1–4, and easy-plane magnetic anisotropy for the ground state of 5. Furthermore, these results are in line with the sign and magnitude of the D values experimentally found for trigonal prismatic Co^II complexes¹⁵ and compressed octahedral Co^IIN₆ complexes with two κN-thiocyanate ligands in trans positions, respectively.^19,33 In the case of 1, where tetrahedral and trigonal prismatic Co^II ions coexist in the structure, the magnetic parameters for the tetrahedral centre were fixed to those extracted from HF-EPR measurements to avoid overparametrization (see below). It should be noted that the energy gap between the two lowest KDs in 5 calculated using the expression 2D* = [2(D² + 3E²)^1/2] = 121.2 cm⁻¹ is similar to that extracted from the Hamiltonian in eqn (2).

It is worth mentioning that the M vs. H/T isotherms for compounds 2–4 depend only slightly on the temperature (the changes of the thermal depopulation of the two Kramers doublets below 7 K are almost negligible) and moreover practically superimpose in a single master curve (see Fig. 5 for compound 2 and Fig. S2 and S3† for compounds 3 and 4), thus corroborating that the ZFS is very large for these compounds. Nevertheless, for compound 1 the superposition degree of the curves is smaller than in the rest of the compounds, which is in accordance with the presence in this compound of a distorted tetrahedral CoCl₄²⁻ anion with a relatively small D value (the small energy gap between the two lowest KDs allows changing the thermal population below 7 K). As expected, complex 5, with a D value larger than that corresponding to the CoCl₄²⁻ anion in 1, but rather slower than 2–4, shows a small, but non negligible, dependence with H/T (Fig. 6).

At this point, it should be mentioned that the low sensitivity of the magnetic measurements for determining E and |E/D| parameters, as well as the limitations of the phenomenological approach based on ZFS Hamiltonian, avoid extracting very reliable ZFS parameters for complexes 1–5, particularly the magnitude of E and the sign of D. Therefore, the D values extracted from the dc magnetic measurements for these complexes, even if they match very well with the calculated ones (see below), should be taken with caution and, in any case, supported by other techniques.

It should be remarked that there exists a linear correlation between the continuous shape measures (or the Bailar θ angle) and the experimentally extracted D values for complexes 1–4 (Fig. 7 and Fig. S4†), so that the negative D values decrease in absolute value with increasing of the distortion from TPR-6 to OC-6. This result is in line with the theoretical calculations performed for homo- and heteroleptic TPR-6 Co^IIN_xO_6−x (x = 6–0) model complexes with a progressive distortion from the trigonal prismatic coordination.^15d,e The calculated S(TPR-6) value for the crossing point between positive and negative D values is 4.74 (or at θ = 34.02°). This value is close to the isosymmetric point with respect to the OC-6 and the TPR-6 geometries, which has S(TPR-6) = S(OC-6) = 4.42 (or θ = 30°). The fact that octahedral Co^II complexes generally exhibit D positive values, whereas the trigonal prismatic counterparts show D negative values, seems to support this correlation. In connection with this, a similar correlation was recently obtained for a series of octahedral Co^IIY^III complexes with easy-plane anisotropy, which points out that the calculated D positive values decrease with increasing the distortion from octahedral to trigonal prismatic geometries.^14b,34

Fig. 7 Plot of the axial anisotropy parameter versus the continuous symmetry measures parameter for the TPR-6 complexes 1–4. The black solid line represents the best linear fitting leading to the equation D = 63 × S(TPR-6) − 300.

HFEPR studies

In order to support the sign and magnitude of the anisotropic parameters extracted from dc magnetic data, we have recorded HFEPR spectra for complexes 1–5 at low temperature (5–10 K) in the frequency range 9.5–402 GHz (Fig. 8–9 and S5–S6†). First we focus on the analysis of the spectra of 2–4. Using spin Hamiltonian parameters extracted from dc magnetic data for these compounds, the calculated energy gap between the two lowest Kramers doublets, 2D* = [2(D² + 3E²)^1/2], is indeed much larger than the quantum energy of the microwave frequency. Moreover, at the low temperature employed, only the ground KD will be populated. In view of this, it is reasonable to assume that the resonances observed in the HFEPR spectra of 2–4 are due to intra-Kramers transitions within the lowest KD and then the EPR spectra of these compounds could be analysed assuming an effective S_eff = 1/2 ground state and effective g′ values.

Fig. 8 EPR spectrum of 1 as a pellet at 10 K and 402 GHz (black trace) and its simulation (red trace) using |D| = 5.25 cm⁻¹, |E| = 1.75 cm⁻¹, g_iso = 2.4 (left). Field vs. frequency dependence of EPR turning points in 1 (squares) along with simulations using |D| = 5.25 cm⁻¹, |E| = 1.75 cm⁻¹, g_iso = 2.25 (right). Blue curves: Turning points with magnetic field parallel to the Z-axis of the ZFS tensor; red curves: B₀ parallel to Y-axis; green curves: off-axis turning points. The color plot of FIRMS data is described in the next section.

Fig. 9 (Left) EPR spectrum of 5 as a pellet at 4.5 K and 237 GHz (black trace) and its simulation (red trace) using D = +36.36 cm⁻¹, E = +8.97 cm⁻¹, g_x = g_y = 2.44 and g_z = 2.16. A group of narrow resonances near 7.95 T (g = 2.12) is due to unidentified impurities. (Right) Experimental 2-D (magnetic field vs. energy) contour maps of FIRMS response of the same complex. HFEPR-observed turning points of the intra-Kramers transition are included as circles. The colour scales the field-induced changes in the transmission spectrum. The most intense change is observed at 80 cm⁻¹ in zero field. Lines are simulation of the EPR turning points. Other FIRMS data are shown in the Fig. S7.†

The HFEPR spectrum of 2 at 261 GHz shows very weak resonances in the 6.1–8.9 g_eff region (Fig. S5†), whereas that of compound 4 at 269 GHz presents a high-amplitude resonance at g′ = 7.2 and two weak resonances close to g′ = 10 (Fig. S6†). Compound 3 is EPR-silent at 10 K and 250–270 GHz, the highest sensitivity frequency region of the spectrometer. The g′ region where the resonances for 2 and 4 appear, suggests that the sample torques in field and orients with the z-axis of the g-tensor near the direction of the B₀ magnetic field. The resonances are thus g′_z transitions, whereas the g′_x and g′_y orientations are not observed. In this regard, it is worth noting that for large negative D values and very small E/D values, the g′_x and g′_y transitions would appear at unaffordable high fields even at the lowest accessible frequency. The fact that values of g′_z > 7 can only be reached by considering D < 0 and very small rhombicity values (λ = E/D) in the equations relating the effective g′ values for S_eff = 1/2 with the g values for the true spin S = 3/2^13d,35 is a good supporting evidence of large easy-axis anisotropy in these compounds. In addition to this, the g′_z values extracted from theoretical calculations for these compounds (see below) are all close to 9, which also underpins their large D < 0. In view of the above considerations, the observed resonances for 2 and 4 must be due to intra-Kramers transitions within the ±3/2 manifold, which is fully in accordance with the dc magnetic results. It is worth noting that similar HFEPR results have been obtained for other Co^II complexes with very large easy-axis anisotropy.^13c,d,36 The presence of multiple resonances in the low-field region of the spectra of complexes 2 and 4 and their shape seem to indicate that the torquing of the sample in the magnetic field (field-induced alignment of the polycrystalline powder with the magnetic field) is not ideal. To probe the torquing effects, HFEPR measurements were also performed on a pellet of 4 to prevent them. The spectrum (Fig. S6†) shows a complete disappearance of the resonances originating from the loose sample and an apparition of a new weak resonance at g′ = 9.1, which can be assigned to the true z turning point of the intra-Kramers transition within the ±3/2 manifold.

It is worth noting at this point that in the absence of rhombicity (E = 0), transitions within ±3/2 manifold are forbidden by the selection rules (ΔM_S = ±1) because ΔM_S = ±3. However, they appear in the presence of rhombicity, because the E component of the ZFS Hamiltonian mixes the M_S = ±1/2 and M_S = ±3/2 states, so that weak resonances with non-zero probability can be observed. It has been recently determined that the limit for observing detectable g′_z signal is E/D > ∼0.03.³⁷Ab initio theoretical calculations (see below) indicate that this would be the case of compounds 2 and 4. In the case of compound 3, the spectrum is silent because the rhombicity is almost zero, leading to unmeasurable transition probabilities of the ΔM_S = ±3 intra-doublet transitions. In fact, theoretical calculations demonstrate that this compound displays the lowest E/D value (0.03) of this family of compounds, just in the above indicated upper limit.

The HFEPR spectra of 1 (Fig. 8) are different from those obtained for 2–4, and they display multiple resonances within the available sub-THz frequency range. It is informative to note that a near-zero field resonance is observed at 384 GHz. The extrapolation of this spectrum to zero field yields the 2D* (energy gap between the two lowest Kramers doublets) of ∼360 GHz (12 cm⁻¹). The spectrum at 402 GHz could be simulated (Fig. 8) using spin Hamiltonian parameters |D| = 5.25 cm⁻¹, |E| = 1.75 cm⁻¹, g_iso = 2.4. To refine the above spin Hamiltonian parameters, a multifrequency dataset was collected, and the results were plotted with simulations, as shown in Fig. 8. The multifrequency experiment did not modify the zfs values, but slightly adjusted the g_iso-value. It is worth noting that one of the perpendicular branches of turning points (blue) coincides with the parallel branch and this is the reason why one cannot differentiate between g_⊥ and g_∥ and, therefore, g was considered to be isotropic. In the case of near-maximum zfs rhombicity, like it occurs for the CoCl₄²⁻ spectrum in 1 (E/D = 0.33), the sign of D is undefined. Recent calculations have shown that this is due to the fact that at E/D = 1/3 an abrupt change from positive to negative values occurs, which is associated with a change of axes.³⁸ This situation describes a perfect triaxial magnetic anisotropy, where g_x < g_y < g_z instead of either g_x = g_y < g_z (easy-axis anisotropy) or g_x = g_y > g_z (easy plane anisotropy). Therefore, when E/D is ∼1/3 the determination of D is not a simple choice between easy-plane or easy-axis magnetic anisotropies, and the sign of D is meaningless.

In case of compound 1 no HFEPR resonances are observed from the Co^II ion inside the TPR [Co(L)]²⁺ unit, because these signals are much less intense than those arising from the pseudo-tetrahedral CoCl₄²⁻ anion.

HFEPR spectra of compound 5 are very different from those observed in 1–4. At 4.5 K and 237 GHz (Fig. 9) it presents multiple resonances corresponding to intra-Kramers turning points, as the D value extracted from dc magnetic data is too large to observe inter-Kramers transitions at sub-THz frequencies. From this spectrum, we were able to obtain through simulations an estimate of the ZFS tensor rhombicity (E/D) under the usual assumption that g_x = g_y (as these values and E are intercorrelated). The extracted parameters were g_x = g_y = 2.44 and g_z = 2.16 with E/D = 0.25. By using the D* value obtained from FIRMS spectroscopy (see below), the HFEPR spectra were successfully simulated using D = +36.36 cm⁻¹, E = +8.97 cm⁻¹. It is worth noting that all attempts to simulate the spectra with negative D values failed as they always led to unphysical g values. This is a good example of the advantages of using different and complementary methods such as HFEPR and FIRMS for extracting ZFS parameters in large-anisotropy transition-metal complexes. A full multi-frequency map of HFEPR turning points in compound 5 is presented together with FIRMS spectra of this compound in Fig. 9.

FIRMS

Far-InfraRed Magnetic Spectroscopy (FIRMS) allows directly evaluating the zero-field (zf) energy gap(s) between the lowest-energy Kramers doublets (KDs) in an S = 3/2 spin system. However, information on the rhombicity of the ZFS tensor cannot be obtained for the Kramers ions. For that purpose, as indicated above, a combination of two spectroscopic techniques FIRMS and HFEPR, whenever applicable, is an appropriate choice. The FIRMS map of compounds 1–4 are shown in Fig. 10 along with transmission spectra for 0 and 17.5 Tesla. Although large field-induced changes in the transmission are observed for these compounds, D* values cannot be accurately extracted, because all the spectra are affected by strong spin-phonon coupling effects.³⁹ Even when several spectral features appear at zero field, none of them can be unambiguously assigned to the energy gap between the KDs. Some of them can be assigned to the phonon absorption peaks. The ground state in these complexes is vibronic (crystal field + phonon), therefore resulting in the hybridization of the crystal field levels leading to a complex pattern for FIRMS map compared to the powder spectrum simulated for S = 3/2 spin-Hamiltonian model (Fig. S8†). For instance, the vibronic state is remarkable for compound 4, where zf energy appears to be in a close vicinity to the phonon peak at 205 cm⁻¹, also observed in other compounds. Due to the spin–phonon coupling, this mode splits into the three peaks at zero field and restores back to the single peak shape at 17.5 T, while the magnetic resonance energy is shifted away. From analysis of peaks parameters in the normalized transmission spectrum (Fig. S8†) as well as the anticipated crossing of simulated turning points with the pronounced phonon peaks, we suggest 2D* (energy gap between the ground and first excited KD in an S = 3/2 system) to be 153.9, 187.7, 195.5 and 201 cm⁻¹ for 1–4 compounds, respectively. It is clear that these magnetic complexes with soft crystal structures sensitive to the magnetic field cannot be treated as “pure” S = 3/2 spin systems.

Fig. 10 (Top) Experimental 2-D (magnetic field vs. energy) contour maps of FIRMS response for complexes 1–4. Regions marked in blue represent resonance absorption that is sensitive to changing magnetic field. Regions in yellow are insensitive to the field. The lines are simulations of turning points for spin Hamiltonian, using a S = 3/2, the extracted 2D* values, g_iso = 2.4 and E = 0 (they are only guidelines to illustrate how the energies of magnetic absorption are spreading in the applied magnetic field). (Bottom) Transmission spectra recorded on powder pellet of the complexes at T = 4.2 K and at the indicated magnetic fields. Arrows indicate the 2D* positions suggested for these compounds.

In the FIRMS spectrum of compound 1 (Fig. 10, left) there appears a zf magnetic transition at 154(4) cm⁻¹, which readily yields the value of 2D*. This value is larger than that extracted from dc magnetic data (121.2 cm⁻¹). This difference is not surprising in view of the crude model used to analyse the magnetic data, with isotropic g values for the cationic and anionic units to avoid overparametrization. It should be noted that the 2D* value extracted from the FIRMS spectrum is significantly lower than that extracted from ab initio calculations (184.3 cm⁻¹ from NEVPT2 calculations, see below). This result is also not unexpected as the theoretical values are usually overestimated, mainly due to inherent limitations of the method and the approach based on the ZFS Hamiltonian. The 2D* values for compounds 2–4 are 187.8 cm⁻¹, 195.5 cm⁻¹ and 201.0 cm⁻¹, respectively (arrows in Fig. 10 bottom panels). It is worth noting that 2 and, particularly, 4 have the largest impact of the spin–phonon coupling (hybridization of the phonon at 205 cm⁻¹ with zf energy).⁴⁰ These FIRMS-obtained 2D* values for compounds 2–4 values are indeed very close to those extracted from dc magnetic data and ab initio calculations (see below), which support the D* values for these compounds.

It is worth mentioning that FIRMS spectrum reveals the substantial magnetic resonance absorption from tetrahedral Co^II centre in compound 1 corresponding to the CoCl₄²⁻ anion (Fig. 8, right panel). The spin-Hamiltonian parameters extracted from HFEPR data were used to simulate the low-frequency part of the FIRMS spectrum (Fig. S9†). As it can be observed, the simulated FIRMS spectrum is in good agreement with the experimental one, supporting the D, E and g values for this counterion. The FIRMS spectrum of compound 5 presents a zf magnetic transition at 79.07 cm⁻¹ (Fig. 9), which is very close to the 2D* value extracted from magnetic data and NEVPT2 ab initio calculations.

Theoretical studies

In order to support the extracted D and E values and to get a deep understanding of the magnetic properties and electronic structure of compounds 1–5, we have performed ab initio multiconfigurational calculations on the experimental X-ray crystal structures using the ORCA program package.⁴¹ This program allows extracting the energy of the spin-free states (ligand field terms) and the energy of the KDs arising from the spin–orbit coupling (SOC), which is introduced by the quasi-degenerated perturbation theory (QDPT). The energy of the mentioned states is given in Tables S4 and S5,† whereas the computed D and E values and first excitation energies before and after including spin–orbit effects are gathered in Table 2. The ORCA software package provides CASSCF and CASSCF + NEVPT2 results, both incorporating SO coupling effects. In order to calculate the electronic structure of [Co(L)]²⁺ in compound 1, the Co^II ion of CoCl₄²⁻ was replaced by Zn^II in its crystal structure. Likewise, to calculate the electronic structure of the pseudo-tetrahedral CoCl₄²⁻ anion, the Co^II ion of the [Co(L)]²⁺ unit was substituted by Zn^II. Both approaches, CASSCF and CASSCF + NEVPT2, produce very similar sets of results for the electronic structure of the [Co(L)]²⁺ units in complexes 1–4, which are in rather good agreement with those extracted from dc magnetic measurements and support their large easy-axis anisotropy. Moreover, the large effective g′_z values (g′_z > 9) confirm the axiality of the ground state, the anisotropy axis being located close to the pseudo-C₃ axis passing through the P–S–Co direction, as expected (Fig. 11, left).

Fig. 11 Orientation of the axial anisotropy axis of compound 2, which almost coincides with the pseudo C₃ axis of the molecule (left). NEVPT2-AILFT computed d-orbital energy diagram for complexes 1–5 (right). Colours code: d_z² (red), d_x²−y² (orange), d_xy (black), d_xz (blue), d_yz (green).

Table 2 Computed ZFS parameters D, E, |E/D| and g values for the ground states of 1–5. ΔE₁ and 2D* are the calculated first excitation energies before and after considering spin–orbit effects, respectively

Compound	Method	D (cm^−1)	E/D	E (cm^−1)	SF states ΔE1 (cm^−1)	SO states 2D* (cm^−1)	g x , gy, gz ^a
							g′x, g′y, g′z ^b
a g-Tensor for the true spin S = 3/2. b Effective g′-tensors assuming a pseudospin S = ½ are included for compounds 1–4.
1	CASSCF	−105.585	0.063898	−6.7466	385.7	212.46	1.93, 2.01, 3.16
							0.41, 0.44, 9.12
	NEVPT2	−91.713	0.055518	−5.0917	560.6	184.27	1.97, 2.04, 3.04
							0.35, 0.37, 8.89
CoCl4^2−	CASSCF	+11.39	0.330441	+3.7637	2350.0	26.25	2.36, 2.45, 2.54
	NEVPT2	+9.05	0.287554	+2.6024	3381.7	20.23	2.27 2.34, 2.40
2	CASSCF	−104.067	0.048481	−5.0453	426.1	208.87	1.97, 2.03, 3.16
							0.32, 0.33, 9.18
	NEVPT2	−91.311	0.040349	−3.6843	599.2	183.07	1.99, 2.05, 3.05
							0.26, 0.27, 8.94
3	CASSCF	−116.747	0.038658	−4.5132	320.6	234.02	1.89, 1.94, 3.26
							0.26, 0.27, 9.36
	NEVPT2	−107.718	0.030206	−3.2537	450.6	215.73	1.94, 1.97, 3.17
							0.20, 0.20, 9.20
4	CASSCF	−118.260	0.038988	−4.6107	303.7	237.06	1.87, 1.93, 3.27
							0.26, 0.27, 9.37
	NEVPT2	−109.502	0.031230	−3.4197	426.8	219.32	1.92, 1.97, 3.18
							0.20, 0.21, 9.23
5	CASSCF	+54.210	0.305857	+16.5805	1021.5	122.69	2.05, 2.38, 2.74
	NEVPT2	−44.435	0.269859	−11.9912	1346.9	98.10	2.05, 2.30, 2.61

---

For the CoCl₄²⁻ in compound 1, both approaches give similar results for D and E (+11.39 cm⁻¹ and +3.76 cm⁻¹ from CASSCF and +9.05 cm⁻¹ and +2.60 cm⁻¹ from NEVPT2, respectively), which are not far from the HFEPR results. The small distortion of this anion provokes the splitting of the e and t₂ orbitals in T_d symmetry, so that the energy gap between the first excited doubly occupied orbital arising from the e set and the lowest single-occupied excited state arising from the splitting of the t₂ orbitals set, remains rather large. As a result, a small to medium D value is found.

For the [Co(L)]²⁺ unit of complexes 1–4, the energy gap between the ground and first excited spin quartet states is in the 300–600 cm⁻¹ range depending on the calculations approach (CASSCF or CASSCF + NEVPT2), whereas the second excited quartet state is around 4500 cm⁻¹ above the ground state (Tables S4 and S5†). These results show that the distortion from C₃ symmetry is not too high and then the first order SO coupling and the anisotropy should be important. The SOC mixes the ground and excited states to afford a set of KDs, with an energy gap between the ground and first excited state of about 200 cm⁻¹. The third KD, which is located at the 750–850 cm⁻¹ range above the ground state, should have a very small population and, therefore, as above mentioned, the use of the effective ZFS Hamiltonian is appropriate to get a reasonable estimation of D from experimental magnetic data and theoretical calculations.

The splitting of the d-orbitals for complexes 1–5 has been obtained by using the ab initio ligand field (AILFT) method³⁷ implemented in ORCA.⁴¹ The extracted energy diagram for these compounds is given in Fig. 11 (right panel), whereas complete energy diagrams for each of them, including drawings of the computed d orbitals, are given in Fig. S10.† Additionally, the composition of the one-electron states is given in Table S6.† The splitting spans the range 8430–9493 cm⁻¹ for compounds 1–4 and 10 492 cm⁻¹ for 5 (energy span of 1 > 2 > 3 ≈ 4). The d-orbital splitting for the former complexes increases with the distortion from TPR-6 to OC-6, which agrees well with the fact that the energy spans of the d orbitals in OC-6 complexes is larger than in the TPR-6 counterparts (10 Dq vs. 20/3 Dq).²⁵ As expected, the energy span for the d orbitals in 5 is larger than in 2–4.

As it can be seen in Table S6† and Fig. 11, the lowest energy orbital is almost a pure doubly occupied d_z² atomic orbital, whereas the next second double and single occupied excited orbitals are mainly linear combinations of d_xy and d_x²−y² atomic orbitals. At higher energy, the half-occupied states are essentially linear combinations of d_xz and d_yz orbitals, thus indirectly revealing the multiconfigurational character of the ground and first excited states. For 1, 3 and 4 the dominant electronic configuration of the ground state is (d_z²)², (d_xy)², (d_x²−y²)¹(d_xz)¹(d_yz)¹, whereas for 2 is (d_z²)², (d_x²−y²)², (d_xy)¹(d_xz)¹(d_yz)¹. For the first excited state, the dominant electronic distribution is (d_z²)², (d_xy)¹, (d_x²−y²)²(d_xz)¹(d_yz)¹ for the former and (d_z²)², (d_x²−y²)¹, (d_xy)²(d_xz)¹(d_yz)¹ for the latter (see Table S7†). In any case, the distortion of the TPR-6 complexes from the C₃ symmetry breaks the degeneration of the e orbitals (d_xy and d_x²−y²), so that the first excitation energy involves these two orbitals with the same m_l value (m_l = ±2). The sign and magnitude of D can be estimated by evaluating the D_ii components (i = x,y,z), which depend on the excitation energies, as well as on the m_l values of the orbitals implicated in the lowest energy transition.¹⁰ Thus, when the first excitation energy involves two orbitals with Δm_l = ±1, the M_s = ±1/2 KD is found at lower energy and the contribution to D is positive (easy-plane anisotropy). However, when the excitation between d orbitals does not involve a change of m_l (Δm_l = 0) the M_s = ±3/2 KD is stabilized and a negative contribution to D is anticipated (easy axis anisotropy). Therefore, for complexes 2–4 with a Δm_l = 0 change in the orbitals involved in the lowest energy transition, a negative D value can be predicted. Moreover, the energy gap between these two orbitals is small (in the 300–600 cm⁻¹ range) and consequently a large D value can be anticipated (D and the energy gap are inversely proportional). These predictions (large and negative D values) are in good agreement with the D values derived from theoretical calculations and magnetic measurements.

The theoretical analysis of the principal contributions to D points out that the largest negative contribution to D comes from the first excited quartet state, ⁴Φ₁ (see Table S8†), which is not unexpected as this state is the closest in energy to the ground quartet state.

In the case of 5, both methods lead to d orbitals splittings, (Fig. S10d and S10e†) that point out to a negative D value. This result agrees with the sign of the D value extracted from NEVPT2 calculations but it is opposite to that extracted from CASSCF calculations and dc magnetic measurements. This discrepancy could be due to a calculation artefact because the E/D parameter calculated for this compound is near to 1/3 (the compound shows triaxial anisotropy rather than easy-axis or easy plane anisotropies, so that the sign of D is meaningless). Therefore, it appears that for E/D values close to 1/3, in some cases, the sign of D cannot be reliably determined from ab initio theoretical calculations based on the ZFS Hamiltonian, and then the use of experimental methods (such as PND, HFEPR and single-crystal torque magnetometry), or specific theoretical calculations^38,42 for assessing magnetic anisotropy are needed. In this regard, the HFEPR spectrum of 5 (Fig. 9) univocally demonstrates that this compound presents D > 0. In good agreement with this, to the best of our knowledge and with one exception, all the compressed octahedral CoN₆ complexes containing two trans-thiocyanate groups exhibit, like 5, D > 0.^19,20,33 All the complexes with analogous structures to 5 exhibit a similar d_ax/d_eq ratio (d_ax and d_eq are the average axial and equatorial bond distances, respectively) within the 0.94–0.96 range, and it appears that to observe negative D values for this type of complexes, a comparative rather smaller d_ax/d_eq ratio is required.¹⁸

Dynamic magnetic properties

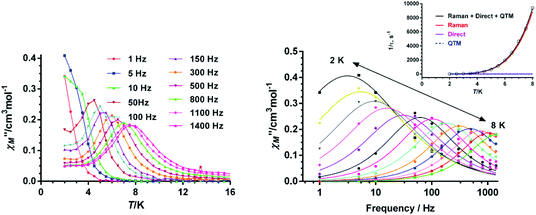
The dynamic of the magnetization for complexes 1–5 was studied by means of temperature- and frequency-dependent alternating current (ac) magnetic susceptibility measurements on polycrystalline samples of the compounds, with the aim of unveiling if they show slow magnetization relaxation and, if so, to accomplish a comparative study of their dynamic magnetic properties.

In compound 1, slow magnetization relaxation could, in principle, arise from the Co^II atoms belonging to both the anionic and cationic units. However, under a zero static magnetic field, compound 1 does not show out-phase magnetic susceptibility signals (χ′′_M). The absence of slow relaxation in this compound could be essentially due to the relatively strong dipolar interactions involving the tetrahedral and trigonal prismatic Co^II ions, with a short Co⋯Co distance (<6 Å), which favour fast QTM relaxation (dipolar interactions create an internal transverse magnetic field that opens channels for QTM relaxation). The same behaviour has been recently shown for an analogous trigonal prismatic complex with a tripodal ligand derived from 1,3,5-triaminocyclohexane and Co⋯Co distances between the cobalt(II) ions belonging to the cationic and anionic units of 5.862 Å.^15d

In order to try to eliminate the QTM, ac measurements in the presence of small dc fields were performed. However, no χ′′_M signals were observed at the tested magnetic fields (0–2000 Oe). This fact seems to indicate the strength of the dipolar interactions, which cannot be overridden by the magnetic field. Afterwards, with the aim of decreasing intermolecular dipolar interactions, we tried to obtain magnetic diluted compounds with different Co/Zn molar ratios and Zn^II ions in both Co^II sites of 1, but all attempts were unsuccessful. However, we were able to prepare the compound [Co(L)]ZnCl₄ (2), which is analogous to 1, but having ZnCl₄²⁻ instead of CoCl₄²⁻ anions. Obviously, this can be considered as a magnetic diluted version of 1, where the strongest Co⋯Co intermolecular interaction should vanish. Compound 2, under zero applied magnetic field, shows temperature and frequency dependent χ′′_M signals below 10 K, thus indicating the presence of slow magnetic relaxation (Fig. S11†). Nevertheless, these signals are wide and do not show clear maxima above 2 K in the studied frequency range. This behaviour is most likely due to the existence of QTM promoted by weak intermolecular interactions, hyperfine interactions with the Co^II nuclear spin (I = 7/2) and transverse anisotropy. In this regard, it is worth noting at this point that even though compound 2 has a very large axial anisotropy, the calculated g′_xy/g′_z ratio, which could be used as a measurement of the strength of the QTM, is small but not negligible (0.03, see Table 2). In view of the above considerations, it is understood why QTM is difficult to be attenuated enough as to observe slow relaxation under zero-field. In order to eliminate fully or partly the QTM, a good strategy is that of applying a small dc magnetic field. For this reason, we have studied the field dependence of the ac magnetic susceptibility at low temperature (2 K) in the 1–1400 Hz frequency range for complex 2, using dc magnetic fields varying between 0.025 T and 0.4 T. The aim of this study is not only to know if this compound with a large negative D value shows field induced slow magnetization relaxation, but also to investigate how the relaxation time changes with the applied magnetic field and to determine the optimal field at which the magnetic relaxation is the slowest. The field and frequency dependence of the out-of-phase signals χ′′_M at 2 K is given in Fig. S12† (left panel). The relaxation times at each magnetic field were extracted from the fitting of the frequency dependence of the χ′′_M signals to the generalized Debye model. The field dependence of the relaxation time in form of τ⁻¹vs. H (in tesla units) is given in Fig. S12† (right panel). As expected, the magnetic relaxation slows down up to 0.2 T (optimal field) due to the progressive quenching of the QTM. For H_dc > 0.2, τ⁻¹ strongly increases as the field increases, pointing out the predominance of a direct relaxation process that is strongly field dependent. The temperature dependence of the magnetization relaxation time in molecules exhibiting slow relaxation of the magnetization is commonly described by the equation:

where the two first terms correspond to the field dependent direct and QTM relaxation processes, respectively, whereas the third and fourth terms represent the field independent relaxation processes (Raman and Orbach). The field dependence of the magnetization at 2 K was fitted to the above equation considering the sum of Raman and Orbach contributions as a constant. The best fit allows extracting the parameters indicated in Fig. S12,† right. Full set of temperature- and frequency-dependent ac susceptibility measurements were then carried out at the optimal field of 0.2 T below 15 K (Fig. 12). The temperature dependence of the χ′′_M signals at different frequencies shows slow relaxation of the magnetization, typical of SMM behaviour, with maxima in the 7.5 K (1488 Hz)–4.5 K (50 Hz) temperature range (Fig. 12). As it can be seen in this figure, the χ′′_M at 50 Hz displays a small increase in intensity at very low temperature, whereas the signals at higher frequencies do not decrease down to zero after the maximum. This behavior can be due to QTM and/or a direct process promoted by the applied magnetic field.

Fig. 12 Temperature dependence of χ′′_M at different frequencies (left) and frequency dependence at different temperatures (right) for 2 under a field of 0.2 T. Contribution of each relaxation process to the slow relaxation of the magnetization (inset).

The high-temperature extracted relaxation times for compound 2 were fitted to an Arrhenius law for a thermally activated process (Orbach process) leading to an effective energy barrier for the magnetization reversal (U_eff) of 34.6(2) K and a τ₀ = 1.6(2) × 10⁻⁶ s. It is interesting to note that the value of the effective energy barrier (U_eff) is much lower than the activation energy of ∼|2D| extracted from ab initio calculations, dc magnetic measurements and FIRMS (150–205 cm⁻¹). Taking into consideration that the Orbach process involves real magnetic energy levels, and that complex 2 does not have energy levels below ∼150 cm⁻¹, the relaxation should not take place through an Orbach process. In fact, all attempts to fit the temperature dependence of τ for 2 with the total sum of the processes indicated in eqn (3) were unsuccessful. However, the relaxation data could be fitted to eqn (3) considering the simultaneous presence of direct, Raman and QTM relaxation processes (Fig. 12 inset). To avoid overparametrization, the parameters corresponding to the direct (A) and QTM (B₁ and B₂) were fixed to the values extracted from field dependence of the relaxation time (see Fig. S12† right). The best fit led to the parameters indicated in Table 3. The Raman process is largely dominant, although the direct and QTM relaxation processes have to be considered to fit the data below 3 K. Although for Kramers ions a n value of 9 is expected,¹¹ however, lower n values can be considered as acceptable depending on the structure of the levels, and if both, acoustic and optical phonons are taken into account.⁴³

Table 3 Magnetic relaxation parameters for complexes 1–5

Compound	U eff ^a (K)	τ 0 (s)	C (s^−1 K^−n)	n	QTM s^−1	A (s^−1 T^4 K^−1)
a Virtual values extracted from the Arrhenius plot using high temperature relaxation times. b The field dependence of the relaxation time could not be extracted at 2 K in the studied frequency range.
2	34.6(5)	1.6(1) × 10^−6	0.10(1), H = 0.2 T	5.48(4)	0.22	490
3	38.6(7)	1.7(1) × 10^−6	0.17(3), H = 0.1 T	4.91(8)	0.32	2993
4	39.2(4)	1.85(5) × 10^−6	0.19(2), H = 0.2 T	4.75(4)	0.13	959
3′	51(2)	4.2(6) × 10^−7	2.1(2), H = 0 T	3.870(5)	0.0045(3)	—
	54.9(9)	3.7(2) × 10^−7	0.52(8), H = 0.12 T	4.37(6)
4′	44(2)	7(1) × 10^−7	4.1(5), H = 0 T	3.64(5)	0.00041(3)	—
	52.1(9)	4.5(3) × 10^−7	0.66(3), H = 0.12 T	4.29(2)
5	10.30(7)	1.2(2) × 10^−5	184(10)	2.50(4)	0.014	11 866

---

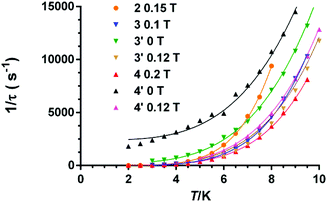
The results of the ac measurements for 3 and 4 are very similar to those of 2 under zero field (Fig. S13 and S17†), as well as at the corresponding optimal fields of 0.1 T and 0.2 T, respectively (Fig. S14–S16 and S18–S20†). After applying the corresponding dc optimal field, 3 and 4 show frequency and temperature dependence of the χ′′_M component of the ac susceptibility in the 5 K (50 Hz)–9 K (1400 Hz) and 2.5 K (1 Hz)–9 K (1400 Hz) temperature ranges (Fig. S15–S16 and S19–S20,† respectively). This behaviour indicates slow relaxation of the magnetization and SMM behaviour, as expected for TPR-6 Co^II complexes with large axial anisotropy and small E/D rhombicity of ∼0.03. As in the case of 2, the virtual U_eff values are much smaller than the energy gap extracted from dc magnetic measurements, FIRMS and theoretical calculations (∼200 cm⁻¹) and, therefore, the thermal activated Orbach process would not contribute to the magnetization relaxation. In view of this, the temperature dependence of the relaxation times were analysed as for 2. The best fit to eqn (3) afforded the Raman parameters indicated in Table 3. It should be noted that the small remaining contribution of QTM to the magnetization relaxation is larger for 4 than for 3. This might be because the shortest Co⋯Co intermolecular distance for 4 is significantly smaller than that for 3, which could be promoted by the smaller size of the tetrafluoroborate anion with respect to the perchlorate one (8.224 Å vs. 8.974 Å). This fact would favour dipolar interactions and QTM for the former. In recent works,^17,44,45 it has been postulated that the packing arrangement also plays a significant role in the magnetization relaxation process. In this regard, when the magnetic anisotropy axes involving neighbouring molecules with the shortest Co⋯Co distances are mutually parallel (or nearly parallel) the QTM is not favoured. This is the case of compound 3 with parallel magnetic axes (Fig. S21†). However, when they form an angle the QTM is favoured (the largest QTM contribution being expected for the perpendicular orientation of the magnetic anisotropy axes). This is the case of compounds 2 and 4 with an angle between the magnetic anisotropy axes of 23.99° and 35.59°, respectively (Fig. S22 and S23†). The fact that the angle in 2 is lower than in 4 could justify why 2, with a shortest Co⋯Co distance similar to that of 4 (8.167 Å vs. 8.224 Å), has a less contribution of the QTM to the relaxation mechanism (see Table 3).

It is worth mentioning that some few mononuclear Co^II complexes present “hidden SMM behaviour” under zero field, that is to say, the SMM behaviour can be activated by quenching intermolecular magnetic interactions by magnetic dilution of the pristine complexes.¹³ Although these systems have easy-axis magnetic anisotropy, intermolecular interactions provoke fast QTM, so that the SMM behaviour cannot be observed at zero applied magnetic field. Considering this, we decided to analyse if the SMM behaviour could emerge after magnetic dilution of complexes 3 and 4. For it, we studied the magnetic diluted compounds 3′ and 4′ containing a Co/Zn = 1/6 ratio. The dc magnetic measurements on 3′ and 4′ confirm this molar ratio, whereas X-ray powder diffraction diagrams (Fig. S24†) support their isostructurality with the corresponding undiluted complexes. Temperature and frequency dependence ac magnetic measurements under zero field indicate that both 3′ and 4′ (Fig. 13 and Fig. S27†) show χ′′_M signals with maxima in the 6.5 K (354 Hz)–12.50 K (10 000 Hz) and 6.75 K (570 Hz)–13.25 K (10 000 Hz) ranges, respectively, which are typical of slow magnetization relaxation and SMM behaviour. Therefore, compounds 3 and 4 are “hidden MSMMs”, their SMM behaviour being triggered by magnetic dilution. As it can be observed in Fig. 13 for 3′ and Fig. S27† for 4′, both complexes show in the low temperature region below the maxima, the typical tail due to QTM, which is not fully eliminated by magnetic dilution. It is worth noting that, as it has been shown to occur for the pristine compounds 3 and 4, the QTM contribution to the magnetic relaxation is smaller for 3′ than for 4′. The temperature dependence of relaxation times was analysed with the eqn (3), but taking into account only Raman and QTM processes (under zero magnetic field the direct product should be negligible). The parameters extracted from this fitting procedure are given in Table 3.

Fig. 13 Temperature dependence of χ′′_M at different frequencies for 3′ at zero field (top left) and at 0.12 T (bottom left) and frequency dependence of the relaxation time τ at different temperatures for complex 3′ at zero field (top right) and at 0.12 T (bottom right). The dotted black line represents the best fit of the experimental data to a combination of Raman and QTM processes, whereas the green and blue lines represent the Raman and QTM contribution to the magnetic relaxation, respectively (inset top right), and to a Raman process (inset bottom right).

In order to estimate the optimal field in compounds 3′ and 4′, field dependent ac measurements were performed at 7 K (at 2 K the maxima in the frequency dependence of the χ′′_M are beyond the accurate low frequency limit of the PPMS instrument) in the 0.0375–0.3 T range. In both cases, the estimated field was determined to be 0.12 T (see Fig. S26–S28†). The ac measurements at the optimal fields clearly indicate, as expected, that the QTM has been practically eliminated in both compounds. It is worth mentioning that the temperature dependence of the relaxation times could only be fitted to a Raman process, leading to the parameters gathered in Table 3.

Complex 5 does not show out-of-phase signals (χ′′_M) above 2 K at zero applied dc field, which is due to the fact that for Kramers ions like Co^II with D > 0, the electronuclear spin states arising from the hyperfine interactions have negligible magnetic moments at zero field.^14a Conversely, when a magnetic dc field is applied the electronuclear spin states acquire magnetic moment and, as a result, slow relaxation of the magnetization could be observed provided that the compound behaves as a SMM.^14a In light of the above considerations, we have analysed the field dependence of the ac magnetic susceptibility at T = 2 K for complex 5 and for dc magnetic fields varying between 0.025 and 0.4 T (Fig. S28†). The application of a dc magnetic field triggers a clear frequency dependency of the in-phase (χ′_M) and out-of-phase signals (Fig. S29†), thus indicating the existence of slow magnetization relaxation. It is worth mentioning that below 0.2 T only one relaxation process can be observed, whereas for H_dc > 0.2 T, a second and slower relaxation process begins to appear. This latter relaxation process is rather common for Co^II MSMMs that are exposed to a magnetic field and it has its origin in either a spin–phonon direct relaxation process stimulated by the split of the Kramers degeneration under the applied magnetic field (as the energy gap between the two M_S ground states increases with the field, the phonon density also increases with an energy equal to this gap)⁴⁶ or intermolecular interactions.⁴⁷

Fig. S26† also represents the field dependence of the inverse of the relaxation times (τ) at 2 K. As it can be observed in this figure, for fields below 0.2 T, τ⁻¹ decreases as the field increases, which indicates the progressive quenching of the QTM. For H_dc > 0.2, τ⁻¹ increases as the field increases, indicating the predominance of a direct relaxation process. Field- and frequency-dependent ac susceptibility measurements were performed at the optimal field of 0.2 T. These ac measurements indicate that 5 exhibits maxima in the χ′′_M signals in the 2 K (150 Hz)–4.5 K (1100 Hz) region (Fig. S29†). The value of the effective energy barrier (U_eff) given in Table 3 is much lower than the 2D* values determined from dc magnetic data, FIRMS and theoretically from ab initio calculations (in the 122–240 cm⁻¹ range). In view of this, the relaxation should not proceed via an Orbach process and then the temperature dependence of τ⁻¹ for 5 was fitted to the eqn (3) following the same procedure as for 2–4 (Fig. S26†). The best fit led to the parameters indicated in Table 3, which are similar to those found for distorted octahedral Co^II complexes with large easy-plane anisotropy.^{19,20,33,34,48}

It should be noted that for complexes 1–5 under the optimal field, the Raman process predominates above approximately 4 K, whereas below this temperature QTM and/or direct processes dominate. In connection with this, the α values extracted from the Cole–Cole plot for compounds 2–4 (Fig. S30†) in the 5–8 K region are very small (∼0.04) and the curves have semicircular shape, thus indicating the existence of an unique relaxation process. Nevertheless, below 5 K, the α values increase until values of 0.29 and 0.12 for 2 and 3, respectively, which points out the existence of a wide distribution of relaxation times, in agreement with the existence of various overlapping relaxation processes (QTM, direct and Raman) at very low temperature. It is worth mentioning that for 4, with a larger contribution of QTM than 2 and 3, α values as high as 0.27 are yet reached at 5 K. Magnetic diluted compounds 3′ and 4′ at 0 Oe exhibits similar behavior to 2–4, with α values in the 0.34 (5 K)–0.08 (11 K) range for the former and 0.42 (5 K)–0.11 (11 K) for the latter, which agree with the existence of a larger QTM below 5 K in these compounds and specifically in the latter. When the optimal field is applied the α values decrease below 5 K as expected for the at least partial quenching of the QTM and they are found in the ranges 0.25 (5 K)–0.04 (12 K) and 0.25 (5 K)–0.04 (12 K), respectively.

As it can be observed in Table 3, on passing from 2 to 4 under the optimal field, the Raman coefficient C increases with the concomitant diminution of n, leading to an increase of the relaxation time above 4 K (see Fig. 14). This would agree with the parallel increase of the uniaxial anisotropy in these compounds. The magnetic diluted compounds under zero-field show an increase of one order of magnitude in C, whereas n slightly decreases, which leads to a significant acceleration of the magnetization relaxation (Fig. 14). This fact is not unexpected because of the QTM observed for both compounds. The application of an optimal field to these magnetic diluted complexes leads to relaxation times very close to those of the pristine compounds under the corresponding optimal field. This result points out that the effect of the applied dc field for quenching QTM is larger than that of magnetic dilution, which has been also previously observed for other MSMMs.^13a,49

Fig. 14 Temperature dependence of the inverse of the relaxation times for the indicated compounds and magnetic fields. Solid lines represent the best fits to the relaxation processes specified in the text.

It is worth noting that a recent first principles investigation of spin–phonon relaxation in a Co^II MSMM with a large energy gap between the ground and the first excited state of 230 cm⁻¹, which is similar to those found in complexes 1–4, indicates that low energy phonons are always able to bring about spin relaxation even at very low temperature through anharmonic Orbach and/or Raman mechanism, thus restricting the spin lifetime.⁸ Moreover, this study points out that to preserve spins from these relaxation processes, in addition to control the crystal field to increase single-ion anisotropy, as well as the coupling between magnetic centres and magnetic dilution to eliminate QTM, molecular vibrations play an important role in coupling the spin states and phonons that contribute to the spin-relaxation pathways. In this regard, theoretical calculations have shown that the energy of the lowest energy vibrational modes of some Co^II MSMMs are close to the experimental extracted thermal energy barriers for the Orbach relaxation mechanisms.^8,50 This result suggested that the thermal energy barrier is connected to the lowest vibrational modes of the MSMM. Thus, when these vibrational modes are thermally populated, a strong spin–phonon coupling for some of them could be able to induce short times spin relaxation. This must be the reason why compounds 2–4, despite having the first excited state around 200 cm⁻¹ above the ground state, show relatively short relaxation times. Compounds 2–4 have the same ligand and very close molecular structures, so that the effect of the molecular vibrations should be similar in all of them. Therefore, the difference in relaxation times should be almost only due to the effect of the anisotropy and QTM, the latter mainly due to packing effects. In fact, as indicated above, the relaxation slows down with the increase of the uniaxial anisotropy on going from 2 to 4 (see Fig. 14).

Pulse magnetization

To deepen in the SIM behavior of the cobalt complexes 1–5, magnetization curves in a full cycle pulsed magnetic field at ³He temperature, 0.4 K, were performed on a polycrystalline sample using different applied maximum fields under adiabatic conditions to minimize the population on thermally activated states. Fig. 15 shows pulse magnetization curves for complexes 1–5 at different sweep rates up to 4.10 T ms⁻¹ for the maximum pulse field studied of 11 T. As we can see, the magnetic field strength is not symmetric for the magnet between the positive and the negative directions during the pulsing and, for the five compounds, magnetization curves show small hysteresis loops that enlarge with the increasing magnetic sweep rate, as expected for Co^II SMMs,^15f,47d,51 and saturation at higher field with values of ≈ 2.5Nμ_B for 2–4, and ≈ 6Nμ_B for 1. In the down sweep from the highest field, we can notice a progressively decrease of the magnetization value for these complexes related to the competition between the thermal relaxation and the fast change of the magnetic field. Finally, the sharp reversal around zero indicates that there is an adiabatic reversal associated to QTM. It is worth noting that the hysteresis loop for 1 is the smallest in agreement with the presence of significant dipolar interactions between the Co^II ions of the cationic unit [CoL]²⁺ and the [CoCl₄]²⁻ anion, which favors the presence of QTM. Hysteresis for 4 is smaller than for 3, which could be due to the larger QTM for the former promoted by stronger dipolar interactions. Hysteresis in 2 is larger than in 4 mainly due to the larger angle between the anisotropy axes in the latter with regard to the former. Thus, the combined action of the axial anisotropy and fast QTM relaxation leads to the following decreasing order of magnetic hysteresis 3 > 2 > 4 > 1 (Fig. S31†). The complex 5, exhibits smaller hysteresis than complexes 2–4 according to its faster relaxation.

Fig. 15 Pulse-field magnetization curves per cobalt atom for 1–5 at 0.4 K and a sweep rate of 4.10 T ms⁻¹.

The diluted complexes 3′ and 4′ show hysteresis loops very similar to that of the pristine complexes (Fig. S32†), but with much lower magnetization saturation, as expected. The hysteresis for 3′ is larger than for 4′, so that they follow the same trend as in the pristine compounds. The observation of sharp reversal around zero indicates that QTM remains in the diluted complexes. Therefore, the QTM preventing the blocking of the magnetization at zero-field is mainly due to hyperfine interactions and transverse anisotropy rather than to dipolar interactions.

Additional information about the origin of the loop can be obtained through the differential magnetization versus field plot (dM/dB vs. B, Fig. S33†). For the five cobalt complexes, a first peak, P1, corresponding to a magnetization step, is observed in the initial up-sweep shifting as a function of the sweep rate. The position of this peak shifts as a function of the sweep rate, probably caused by a nonadiabatic effect. When the maximum magnetic field is reached, in the down-sweep to the zero field, dM/dB is very small and the magnetization curve is nearly flat. After the sharp drop of the magnetization at around zero field, the magnetization curve in the negative-field side shows a second peak, P2, in the initial sweep from the zero field to the negative maximum. The shift of this peak from zero is similar to that in the positive-field side. Besides, in Fig. S34,† the slight sweep rate dependence of the peak field P1–P2 observed in all compounds confirms that the magnetization behavior is symmetric for the magnetic field reversal. This is normally caused by the balance between the thermal relaxation time and the short sweeping time.

Conclusions

A family of Co^IIN₆ trigonal prismatic cationic complexes [Co(L)]²⁺ bearing different counter-anions (CoCl₄²⁻ (1), ZnCl₄²⁻ (2), ClO₄⁻ (3) and BF₄⁻ (4)) have been successfully prepared from the tripodal ligand (S)P[N(Me)N=C(H)Py]₃ and diverse cobalt(II) metal salts. The strong binding ability of the thiocyanate anion does not lead to the formation of the cationic complex, but to a neutral compressed octahedral complex, [Co(L)(NCS)₂] 5, where one of the arms of the tripodal ligand has been replaced by two κN-NCS in trans axial positions. The change of the counter-anion induces slight but non-negligible variations of the distortion of the CoN₆ coordination sphere from TPR-6 to OC-6 following the Bailar pathway, so that this distortion decreases on passing from 1 to 4.

The combination of dc magnetic, FIRMS and HFEPR measurements and theoretical calculations unambiguously support large easy axis magnetic anisotropy for the ground state of complexes 1–4 (with D values extracted from the ZFS Hamiltonian approach between −60.0 cm⁻¹ for 1 and −127.6 cm⁻¹ for 4, and easy-plane magnetic anisotropy in the case of complex 5, with D = +34.7). Supporting previous theoretical calculations, there is a correlation between the experimental axial anisotropy values and the continuous shape measurements parameter S(TPR-6) (or the θ Bailar angle) for complexes 1–4, so that the easy-axis anisotropy increases linearly as the distortion from TPR-6 to OC-6 decreases on going from 1 to 4.

Although compound 1 contains two different types of anisotropic Co^II ions (belonging to the cationic [Co(L)]²⁺ and the anionic [CoCl₄]²⁻ units), it does not show slow magnetic relaxation even in the presence of a dc magnetic field. The absence of slow relaxation in this compound is essentially due to the relatively strong dipolar interactions involving both units, with a short Co⋯Co distance (<6 Å), which favour fast QTM relaxation. Complex 2, which can be considered as a magnetic diluted counterpart of 1, and complexes 3 and 4, exhibit below 10 K slow magnetic relaxation, but the ac susceptibility signals are wide and do not show clear maxima above 2 K in the studied frequency range. However, these complexes exhibit slow relaxation and MSMM behaviour under the corresponding optimal field (that inducing the slowest relaxation), with χ′′_M peaks up to 9 K at 1400 Hz. It is worth mentioning that for these complexes, the Raman relaxation process dominates above approximately 4 K, whereas below this temperature QTM and/or direct processes preponderate. Under the corresponding optimal fields, on passing from 2 to 4, the Raman coefficient C increases and n simultaneously diminishes, leading to an increase of the relaxation time above 4 K, which agrees with the parallel increase of the uniaxial anisotropy in these compounds. The small remaining contribution of QTM to the magnetization relaxation follows the order 4 > 2 > 3. This sequence can be justified by making use of the shortest Co⋯Co distance for each complex (mainly determining the dipolar interactions) and the orientation of the magnetic axes of the Co^II ions involved in this distance in the crystal packing. This is because shortest Co⋯Co distances and largest angles between the magnetic axes favour QTM. The Co/Zn = 1/6 magnetic diluted versions of 3 and 4, namely 3′ and 4′ (for 2 the isostructural magnetic diluted compound could not be obtained) show slow relaxation at zero-field with peaks up to 13.5 K (at 10 000 Hz). Therefore, the MSMM behaviour of compounds 3 and 4 is triggered by magnetic dilution and then these complexes are “hidden MSMMs”.

The hysteresis for the trigonal prismatic complexes decreases in the order 3 > 2 > 4 > 1, which is due to combined effects of the axial anisotropy and QTM relaxation.

In summary, the ongoing results show that, the change of the counter-anion in this type of complexes not only can significantly affect the geometry of the Co^II ions and, therefore, their axial and transverse anisotropies, but also the Co⋯Co intermolecular distances and crystal packing. Considering that hyperfine interactions within the trigonal prismatic cationic unit should be almost of identical magnitude for complexes 1–4, the above-indicated factors would determine the contribution of the QTM to the magnetization relaxation.

The combination of HFEPR and FIRMS experimental techniques unambiguously support the axial anisotropy of the ground state of 5 with a D value of +36.36 cm⁻¹ using the ZFS Hamiltonian. Owing to the fast relaxation observed for this compound, its hysteresis loop is smaller than those of compounds 2–4.

Work is in progress in our lab to prepare similar Co^II trigonal prismatic complexes with other related tripodal ligands for the purpose of decreasing the distortion from the ideal prismatic geometry, thus increasing axial magnetic anisotropy with the simultaneous diminution of the transverse anisotropy and so improving the SMM behaviour. Likewise, using rigid tripodal ligands we will intend to limit the low energy spin–phonons and to increase relaxation times.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Spanish Ministerio de Ciencia e Innovación project (PGC2018 102052-B-C21) MCIN/AEI/10.13039/501100011033/FEDER “Una manera de hacer Europa”, to Junta de Andalucía (FQM-195) and the project I +D+i (P20_00692) and the University of Granada. Part of this work was performed at the NHMFL, which is funded by the National Science Foundation (Cooperative Agreement DMR 1644779) and the State of Florida. HN and IFDO acknowledge GIMRT and ICC-IMR. M. M. Q. M. thanks Junta de Andalucía for a postdoctoral fellowship (DOC_01282) and Ministerio de Ciencia, Innovación y Universidades for a Juan de la Cierva formación contract (grant FJC2018-035709-I supported by MCIN/AEI/10.13039/501100011033). We acknowledge Gloria Pelayo for her help in the synthesis of compound 2 and Silvia Gómez Coca for insightful discussions and help with the quantum-chemical calculations.

References

1. (a) D. Gatteschi and R. Sessoli, Quantum tunneling of magnetization and related phenomena in molecular materials, Angew. Chem., Int. Ed., 2003, 42, 268–297; (b) D. Gatteschi, R. Sessoli and J. Villain, Molecular nanomagnets, Oxford University Press, Oxford, 2006; (c) J. Bartolomé, F. Luis and J. F. Fernández, Molecular magnets: physics and applications, Springer-Verlag, Berlin-Heidelberg, 2014; (d) S. Gao, Molecular nanomagnets and related phenomena, Structure and Bonding, Springer-Verlag, Berlin-Heidelberg, 2015, vol. 164; (e) J. Tang and P. Zhang, Lanthanide single molecule magnets, Springer-Verlag, Berlin Heidelberg, 2015; (f) S. T. Liddle and J. van Slageren, Improving f-element single molecule magnets, Chem. Soc. Rev., 2015, 44, 6655–6669; (g) A. Zabala-Lekuona, M. Seco and E. Colacio, Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 213984.
2. M. Mannini, F. Pineider, P. Sainctavit, C. Danieli, E. Otero, C. Sciancalepore, A. M. Talarico, M. A. Arrio, A. Cornia, D. Gatteschi and R. Sessoli, Magnetic memory of a single-molecule quantum magnet wired to a gold surface, Nat. Mater., 2009, 8, 194–197.
3. (a) A. R. Rocha, V. M. García-Suárez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Towards molecular spintronics, Nat. Mater., 2005, 4, 335–339; (b) L. Bogani and W. Wernsdorfer, Molecular spintronics using single-molecule magnets, Nat. Mater., 2008, 7, 179–186; (c) R. Vincent, S. Klyatskaya, M. Ruben, W. Wernsdorfer and F. Balestro, Electronic read-out of a single nuclear spin using a molecular spin transistor, Nature, 2012, 488, 357–360; (d) M. Ganzhorn, S. Klyatskaya, M. Ruben and W. Wernsdorfer, Strong spin–phonon coupling between a single-molecule magnet and a carbon nanotube nanoelectromechanical system, Nat. Nanotechnol., 2013, 8, 165–169; (e) M. Jenkins, T. Hümmer, M. J. Marínez-Pérez, J. García-Ripoll, D. Zueco and F. Luis, Coupling single-molecule magnets to quantum circuits, New J. Phys., 2013, 15, 095007; (f) E. Coronado and M. Yamashita, Molecular spintronics: the role of coordination chemistry, Dalton Trans., 2016, 45, 16553–16555; (g) E. Coronado, Molecular magnetism: from chemical design to spin control in molecules, materials and devices, Nat. Rev. Mater., 2020, 5, 87–104.
4. (a) M. N. Leuenberger and D. Loss, Quantum computing in molecular magnets, Nature, 2001, 410, 789–793; (b) A. Ardavan, O. Rival, J. L. Morton, S. J. Blundell, A. M. Tyryshkin, G. A. Timco and R. E. P. Winpenny, Will spin-relaxation times in molecular magnets permit quantum information processing?, Phys. Rev. Lett., 2007, 98, 057201; (c) M. J. Martínez-Pérez, S. Cardona-Serra, C. Schlegel, F. Moro, P. J. Alonso, H. Prima-García, J. M. Clemente-Juan, M. Evangelisti, A. Gaita-Ariño, J. Sesé, J. Van Slageren, E. Coronado and F. Luis, Gd-based single-ion magnets with tunable magnetic anisotropy: molecular design of spin qubits, Phys. Rev. Lett., 2012, 108, 247213; (d) M. Atzori, S. Benci, E. Morra, L. Tesi, M. Chiesa, R. Torre, L. Sorace and R. Sessoli, Structural effects on the spin dynamics of potential molecular qubits, Inorg. Chem., 2018, 57, 731–740; (e) L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Quantum coherence in a processable vanadyl complex: new tools for the search of molecular spin qubits, Chem. Sci., 2016, 7, 2074–2083; (f) E. Moreno-Pineda, C. Godfrin, F. Balestro, W. Wernsdorfer and M. Ruben, Molecular spin qudits for quantum algorithm, Chem. Soc. Rev., 2018, 47, 501–513.
5. (a) J. J. Baldovi, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and A. Palii, Rational design of single-ion magnets and spin qubits based on mononuclear lanthanoid complexes, Inorg. Chem., 2012, 51, 12565–12574; (b) R. Layfield and M. Murugesu, Lanthanides and actinides in molecular magnetism, Wiley-VCH, Weinheim, 2015; (c) M. Atanasov, D. Aravena, E. Suturina, E. Bill, D. Manganas and F. Neese, Coord. Chem. Rev., 2015, 289–290, 177–214; (d) M. Feng and M. L. Tong, Single ion magnets from 3d to 5f: developments and strategies, Chem. – Eur. J., 2018, 24, 7574–7594; (e) Z. Zhu and J. Tang, Geometry and Magnetism of Lanthanide Compounds, Top. Organomet. Chem., 2019, 64, 191–226.
6. (a) G. Aromi and E. K. Brechin, Synthesis of 3d metallic single-molecule magnets, in Structure and Bonding, ed. R. Winpenny, Springer-Verlag, Berlin-Heidelberg, 2006, vol. 122, pp. 1–67; (b) S. Gómez-Coca, D. Aravena, R. Morales and E. Ruiz, Large magnetic anisotropy in mononuclear metal complexes, Coord. Chem. Rev., 2015, 289–290, 379–392; (c) J. M. Frost, K. L. M. Harriman and M. Murugesu, The rise of 3-d single-ion magnets in molecular magnetism: towards materials from molecules, Chem. Sci., 2016, 7, 2470–2491; (d) A. K. Bar, C. Pichon and J. P. Sutter, Magnetic anisotropy in two- to eight-coordinated transition–metal complexes: recent developments in molecular magnetism, Coord. Chem. Rev., 2016, 308, 346–380; (e) G. A. Craig and M. Murrie, 3d single-ion magnets, Chem. Soc. Rev., 2015, 44, 2135–2147; (f) S. Tripathi, A. Dey, M. Shanmugam, R. S. Narayanan and V. Chandrsekhar, Cobalt(II) Complexes as Single-Ion Magnets, Top. Organomet. Chem., 2018, 64, 35–76 ( Top. Organomet. Chem. , 2019 , 64 , 191–226 ); (g) A. Sarkar, S. Dey and G. Rajaraman, Role of Coordination Number and Geometry in Controlling the Magnetic Anisotropy in Fe^II, Co^II, and Ni^II Single-Ion Magnets, Chem. – Eur. J., 2020, 26, 14036–14058.
7. A. Lunghi and S. Sanvito, Multiple spin–phonon relaxation pathways in a Kramer single-ion magnet, J. Chem. Phys., 2020, 153, 174113.
8. (a) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442; (b) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, A dysprosium metallocene single-molecule magnet functioning at the axial limit, Angew. Chem., Int. Ed., 2017, 56, 11445–11449; (c) F. S. Guo, B. M. Day, Y. C. Chen, M. L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403.
9. D. E. Fredman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, Slow magnetic relaxation in a high-spin iron(II) complex, J. Am. Chem. Soc., 2010, 132, 1224–1225.
10. S. Gómez-Coca, E. Cremades, N. Aliaga-Alcalde and E. Ruiz, Mononuclear single-molecule magnets: tailoring the magnetic anisotropy of first-row transition-metal complexes, J. Am. Chem. Soc., 2013, 135, 7010–7018.
11. A. Abragam, B. Bleaney and B. Electron, Paramagnetic Resonance of Transition Ions, Dover, 1970.
12. (a) X. N. Yao, J. Z. Du, Y. Q. Zhang, X. B. Leng, M. W. Yang, S. D. Jiang, Z. X. Wang, Z. W. Ouyang, L. Deng, B. W. Wang and S. Gao, Two-coordinate Co(II) imido complexes as outstanding single-molecule magnets, J. Am. Chem. Soc., 2017, 139, 373–380; (b) P. C. Bunting, M. Atanasov, E. Damgaard-MØller, M. Perfetti, I. Crassee, M. Orlita, J. Overgaard, J. van Slageren, F. Neese and J. R. Long, A linear cobalt(II) complex with maximal orbital angular momentum from a non-Aufbau ground state, Science, 2018, 362, 7319.
13. (a) J. Li, Y. Han, F. Cao, R.-M. Wei, Y.-Q. Zhang and Y. Song, Two field-induced slow magnetic relaxation processes in a mononuclear Co(II) complex with a distorted octahedral geometry, Dalton Trans., 2016, 45, 9279; (b) R. Mitsuhashi, S. Hosoya, T. Suzuki, Y. Sunatsuki, H. Sakiyama and M. Mikuriya, Zero-field slow relaxation of magnetization in cobalt(II) single-ion magnets: suppression of quantum tunneling of magnetization by tailoring the intermolecular magnetic coupling, RSC Adv., 2020, 10, 43472; (c) L. Rigamonti, N. Bridonneau, G. Poneti, L. Tesi, L. Sorace, D. Pinkowicz, J. Jover, E. Ruiz, R. Sessoli and A. Cornia, A Pseudo-octahedral cobalt(II) complex with bispyrazolylpyridinel ligands acting as a zero-field single-molecule magnet with easy axis anisotropy, Chem. – Eur. J., 2018, 24, 8857–8868; (d) S. Sottini, G. Poneti, S. Ciattini, N. Levesanos, E. Ferentinos, J. Krzystek, L. Sorace and P. Kyritsis, Magnetic Anisotropy of Tetrahedral Co^II Single-Ion Magnets: Solid-State Effects, Inorg. Chem., 2016, 55, 9537–9548.
14. (a) S. Gómez-Coca, A. Urtizberea, E. Cremades, P. J. Alonso, A. Camón, E. Ruiz and F. Luis, Origin of slow magnetic relaxation in Kramers ions with non-uniaxial anisotropy, Nat. Commun., 2014, 5, 4300; (b) M. A. Palacios, J. Nehrkorn, E. A. Suturina, E. Ruiz, S. Gómez-Coca, K. Holldack, A. Schnegg, J. Krzystek, J. M. Moreno and E. Colacio, Analysis of magnetic anisotropy and the role of magnetic dilution in triggering single–molecule magnet (SMM) behavior in a family of CoIIYIII dinuclear complexes with easy–plane anisotropy, Chem. – Eur. J., 2017, 23, 11649–11661 and references therein.
15. (a) A. A. Pavlov, Y. V. Nelyubina, S. V. Kats, L. V. Penkova, N. N. Efimov, A. O. Dmitrienko, A. V. Vologzhanina, A. S. Belov, Y. Z. Voloshin and V. V. J. Novikov, Polymorphism in a cobalt-based single-ion magnet tuning its barrier to magnetization relaxation, Phys. Chem. Lett., 2016, 7, 4111–4116; (b) Y. Y. Zhu, Y. Q. Zhang, T. T. Yin, C. Gao, B. W. Wang and S. Gao, A family of Co^IICo^III₃ single-ion magnets with zero-field slow magnetic relaxation: fine tuning of energy barrier by remote substituent and counter cation, Inorg. Chem., 2015, 54, 5475–5486; (c) Y. Y. Zhu, C. Cui, Y. Q. Zhang, J. H. Jia, X. Guo, C. Gao, K. Qian, S. D. Jiang, B. W. Wang, Z. M. Wang and S. Gao, Zero-field slow magnetic relaxation from single Co(II) ion: a transition metal single-molecule magnet with high anisotropy barrier, Chem. Sci., 2013, 4, 1802–1806; (d) T. J. Ozumerzifon, I. Bhowmick, W. C. Spaller, A. K. Rappé and M. P. Shores, Toward steric control of guest binding modality: a cationic Co(II) complex exhibiting cation binding and zero-field relaxation, Chem. Commun., 2017, 53, 4211–4214; (e) Y. Peng, T. Bodenstein, K. Fink, V. Mereacre, C. E. Anson and A. K. Powell, Magnetic anisotropy of a Co^II single ion magnet with distorted trigonal prismatic coordination: theory and experiment, Phys. Chem. Chem. Phys., 2016, 18, 30135–30143; (f) B. Yao, Y. F. Deng, T. Li, J. Xiong, B. W. Wang, Z. Zheng and Y. Y. Zhang, Construction and magnetic study of a trigonal-prismatic cobalt(II) single-ion magnet, Inorg. Chem., 2018, 57, 14047–14051; (g) V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M. E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, A trigonal prismatic mononuclear cobalt(II) complex showing single-molecule magnet behaviour, J. Am. Chem. Soc., 2015, 137, 9792–9795; (h) A. A. Pavlov, D. Y. Aleshin, S. A. Savkina, A. S. Belov, N. N. Efimov, J. Nehrkorn, M. Ozerov, Y. Z. Voloshin, Y. V. Nelyubina and V. V. Novikov, A trigonal prismatic cobalt(II) complex as a single molecule magnet with a reduced contribution from quantum tunnelling, ChemPhysChem, 2019, 20, 1001–1005; (i) C. Villa-Pérez, I. Oyarzabal, G. A. Echeverría, G. C. Valencia-Uribe, J. M. Seco and D. B. Soria, Single-ion magnets based on mononuclear cobalt(II) complexes with sulfadiazine, Eur. J. Inorg. Chem., 2016, 4835–4841; (j) C. M. Klug, T. J. Ozumerzifon, I. Bhowmick, B. N. Livesay, A. K. Rappé and M. P. Shores, Anionic guest-dependent slow magnetic relaxation in Co(II) tripodal iminopyridine complexes, Dalton Trans., 2019, 48, 9117–9126; (k) A. A. Pavlov, S. A. Savkina, A. S. Belov, Y. V. Nelyubina, N. N. Efimov, Y. Z. Voloshin and V. V. Novikov, Trigonal Prismatic Tris-pyridineoximate Transition Metal Complexes: A Cobalt(II) Compound with High Magnetic Anisotropy, Inorg. Chem., 2017, 56, 6943–6951; (l) A. S. Belov, Y. Z. Voloshin, A. A. Pavlov, Y. V. Nelyubina, S. A. Belova, Y. V. Zubavichus, V. V. Avdeeva, N. N. Efimov, E. A. Malinina, K. Y. Zhizhin and N. T. Kuznetsov, Solvent-Induced Encapsulation of Cobalt(II) Ion by a Boron-Capped tris-Pyrazoloximate, Inorg. Chem., 2020, 59, 5845–5853; (m) M. R. Saber, M. K. Singh and K. R. Dunbar, Geometrical control of the magnetic anisotropy in six coordinate cobalt complexes, Chem. Commun., 2020, 56, 8492–8495.
16. S. Tripathi, S. Vaidya, K. U. Ansari, N. Ahmed, E. Rivière, L. Spillecke, C. Koo, R. Klingeler, T. Mallah, G. Rajaraman and M. Shanmugam, Influence of a Counteranion on the Zero-Field Splitting of Tetrahedral Cobalt(II) Thiourea Complexes, Inorg. Chem., 2019, 58, 9085–9100.
17. Y.-Z. Zhang, S. Gómez-Coca, A. J. Brown, M. R. Saber, X. Zhang and K. R. Dunbar, Trigonal antiprismatic Co(II) single molecule magnets with large uniaxial anisotropies: importance of Raman and tunneling mechanisms, Chem. Sci., 2016, 7, 6519–6527.
18. S. Tripathi, S. Vaidya, N. Ahmed, E. A. Klahn, H. Cao, L. Spillecke, C. Koo, S. Spachmann, R. Klingeler, G. Rajaraman, J. Overgaard and M. Shanmugam, Structure-property correlation in stabilizing axial magnetic anisotropy in octahedral Co(II) complexes, Cell Rep. Phys. Sci., 2021, 2, 100404.
19. Y.-F. Deng, M. K. Singh, D. Gan, T. Xiao, Y. Wang, S. Liu, Z. Wang, Z. Ouyang, Y.-Z. Zhang and K. R. Dunbar, Probing the Axial Distortion Effect on the Magnetic Anisotropy of Octahedral Co(II) Complexes, Inorg. Chem., 2020, 59, 7622–7630.
20. P. Zoufalý, A. Kliuikov, E. Čižmár, I. Císařová and R. Herchel, Cis and Trans Isomers of Fe(II) and Co(II) Complexes with Oxadiazole Derivatives- Structural and Magnetic Properties, Eur. J. Inorg. Chem., 2021, 1190–1199.
21. D. Luneau and B. Gillon, Polarized Neutron Diffraction: An Excellent Tool to Evidence the Magnetic Anisotropy—Structural Relationships in Molecules, Magnetochemistry, 2021, 7, 158 and references therein.
22. J.-P. Costes, G. Novitchi, V. Vieru, L. F. Chibotaru, C. Duhayon, L. Vendier, J.-P. Majoral and W. Wernsdorfer, Effects of the Exchange Coupling on Dynamic Properties in a Series of CoGdCo Complexes, Inorg. Chem., 2019, 58(1), 756–768.
23. M. W. Löble, M. Casimiro, D. T. Thielemann, P. Oña-Burgos, I. Fernandez, P. W. Roesky and F. Breher, ¹H,⁸⁹Y HMQC and Further NMR Spectroscopic and X-ray Diffraction Investigations on Yttrium-ContainingComplexes Exhibiting Various Nuclearities, Chem. – Eur. J., 2012, 18, 5325–5334.
24. (a) P. Stock, P. T. Pedzinski, N. Spintig, A. Grohmann and G. Hörner, High Intrinsic Barriers against Spin-State Relaxation in Iron(II)-Complex Solutions, Chem. – Eur. J., 2013, 19, 839–842; (b) I. Trapp, M. W. Löble, J. Meyer and F. Breher, Copper complexes of tripodal κ-6N-donor ligands: A structural, EPR spectroscopic and electrochemical study, Inorg. Chim. Acta, 2011, 374, 373–384.
25. J. C. Knight, S. Alvarez, A. J. Amoroso, P. G. Edwards and N. Singha, A novel bipyridine-based hexadentate tripodal framework with a strong preference for trigonal prismatic co-ordination geometries, Dalton Trans., 2010, 39, 3870–3883.
26. M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, SHAPE, v2.1, Universitat de Barcelona, Barcelona, Spain, 2013.
27. M.-H. Whangbo, M.-H. Whangbo, H. Xiang, H.-J. Koo, E. E. Gordon and J.-L. Whitten, Electronic and Structural Factors Controlling the Spin Orientations of Magnetic Ions, Inorg. Chem., 2019, 58, 11854–11874.
28. L. Ungur, M. Thewissen, J.-P. Costes, W. Wernsdorfer and L. F. Chibotaru, Interplay of Strongly Anisotropic Metal Ions in Magnetic Blocking of Complexes, Inorg. Chem., 2013, 52, 6328–6633.
29. (a) R. Boča, Magnetic Parameters and Magnetic Functions in Mononuclear Complexes Beyond the Spin Hamiltonian Formalism, Struct. Bonding, 2006, 117, 1–260; (b) D. V. Korchagin, A. V. Palii, E. A. Yureva, A. V. Akimov, E. Y. Misochko, G. V. Shilov, A. D. Talantsev, R. B. Morgunov, A. A. Shakin, S. M. Aldoshin and B. S. Tsukerblat, Evidence of field induced slow magnetic relaxation in cis-[Co(hfac)₂(H₂O)₂] exhibiting tri-axial anisotropy with a negative axial component, Dalton Trans., 2017, 46, 7540–7548.
30. (a) J. S. Griffith, the Theory of Transition Metal Ions, University Press, Cambridge, UK, 1961; (b) F. Lloret, M. Julve, J. Cano, R. Ruiz-García and E. Pardo, Magnetic properties of six-coordinated high-spin cobalt(II) complexes: Theoretical background and its application, Inorg. Chim. Acta, 2008, 361, 3432–3445.
31. H. Sakiyama, Development of MagSaki(A) software for the magnetic analysis of dinuclear high-spin cobalt(II) complexes considering anisotropy in exchange interaction, J. Comput. Chem., Jpn., 2007, 6, 123–134.
32. N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: a powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175.
33. (a) J. Vallejo, F. R. Fortea-Pérez, E. Pardo, S. Benmansour, I. Castro, J. Krzystek, D. Armentano and J. Cano, Guest-dependent single-ion magnet behaviour in a cobalt(II) metal–organic framework, Chem. Sci., 2016, 7, 2286–2293; (b) Y. Y. Zhu, M. S. Zhu, T. T. Yin, Y. S. Meng, Z. Q. Wu, Y. Q. Zhang and S. Gao, Cobalt(II) coordination polymer exhibiting single-ion-magnet-type field-induced slow relaxation behaviour, Inorg. Chem., 2015, 54, 3716–3718; (c) G. Brunet, D. A. Safin, J. Jover, E. Ruiz and M. Murugesu, Single-molecule magnetism arising from cobalt(II) nodes of a crystalline sponge, J. Mater. Chem. C, 2017, 5, 835–841.
34. (a) A. Masegosa, M. A. Palacios, E. Ruiz, S. Gómez-Coca, J. Krzystek, J. M. Moreno and E. Colacio, Dinuclear vs Tetranuclear Co^IIY^III complexes: The effect of increasing molecular size on the relaxation dynamics, Dalton Trans., 2019, 48, 14873–14884; (b) E. Colacio, Mannich base ligands as versatile paltforms for SMMs, Organometallic Magnets, in Topics in Organimetallic Chemistry, ed. V. Chandrasekhar and F. Pointillart, 2018, vol. 64, pp. 101–161.
35. J. R. Pilbrow, Effective g values for S = 3/2 and S = 5/2, J. Magn. Reson., 1978, 31, 479–490.
36. (a) H.-H. Cui, Y.-Q. Zhang, X.-T. Chen, Z. Wang and Z.-L. Xue, Magnetic anisotropy and slow magnetic relaxation processes of cobalt(II)-pseudohalide complexes, Dalton Trans., 2019, 48, 10743–10752; (b) P. Cucos, F. Tuna, L. Sorace, I. Matei, C. Maxim, S. Shova, R. Gheorghe, A. Caneschi, M. Hillebrand and M. Andruh, Magnetic and Luminescent Binuclear Double-Stranded Helicates, Inorg. Chem., 2014, 53, 7738–7747.
37. E. A. Suturina, J. Nehrkorn, J. M. Zadrozny, J. Liu, M. Atanasov, T. Weyhermüller, D. Maganas, S. Hill, A. Schnegg, E. Bill, J. R. Long and F. Neese, Magneto-Structural Correlations in Pseudotetrahedral Forms of the [Co(SPh)₄]²⁻ Complex Probed by Magnetometry, MCD Spectroscopy, Advanced EPR Techniques, and ab Initio Electronic Structure Calculations, Inorg. Chem., 2017, 56, 3102–3118.
38. E. Damgaard-Møller, L. Krause, H. Lassen, L. A. Malaspina, S. Grabowsky, H. Bamberger, J. McGuire, H. N. Miras, S. Sproules and J. Overgaard, Investigating Complex Magnetic Anisotropy in a Co(II) Molecular Compound: A Charge Density and Correlated Ab Initio Electronic Structure Study, Inorg. Chem., 2020, 59, 13190–13200.
39. D. H. Moseley, S. E. Stavretis, Z. Zhu, M. Guo, C. M. Brown, M. Ozerov, Y. Cheng, L. L. Daemen, R. Richardson, G. Knight, K. Thirunavukkuarasu, A. J. Ramirez-Cuesta, J. Tang and Z. Xue, Inter-Kramers Transitions and Spin-Phonon Couplings in a Lanthanide-Based Single-Molecule Magnet, Inorg. Chem., 2020, 59, 5218–5230.
40. D. H. Moseley, S. E. Stavretis, K. Thirunavukkuarasu, M. Ozerov, Y. Cheng, L. L. Daemen, J. Ludwig, Z. Lu, D. Smirnov, C. M. Brown, A. Pandey, A. J. Ramirez-Cuesta, A. C. Lamb, M. Atanasov, E. Bill, F. Neese and Z.-L. Xue, Spin–phonon couplings in transition metal complexes with slow magnetic relaxation, Nat. Commun., 2018, 9, 2572.
41. F. Neese, Software update: The ORCA program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
42. R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Slow Magnetic Relaxation in Octahedral Cobalt(II) Field-Induced Single-Ion Magnet with Positive Axial and Large Rhombic Anisotropy, Inorg. Chem., 2014, 53, 5896–5898.
43. (a) A. Singh and K. N. Shrivastava, Optical–acoustic two–phonon relaxation in spin systems, Phys. Status Solidi B, 1979, 95, 273–277; (b) K. N. Shirivastava, Theory of Spin–Lattice Relaxation, Phys. Status Solidi B, 1983, 117, 437–458.
44. T. J. Woods, M. F. Ballesteros-Rivas, S. Gómez-Coca, E. Ruiz and K. R. Dunbar, J. Am. Chem. Soc., 2016, 138, 16407–16416.
45. J. Zhang, J. Li, L. Yang, C. Yuan, Y.-Q. Zhang and Y. Son, Magnetic Anisotropy from Trigonal Prismatic to Trigonal Antiprismatic Co(II) Complexes: Experimental Observation and Theoretical Prediction, Inorg. Chem., 2018, 57, 3903–3912.
46. (a) A. Arauzo, A. Lazarescu, S. Shova, E. Bartolomé, R. Cases, J. Luzón, J. Bartolomé and C. Turta, Structural and magnetic properties of some lanthanide (Ln = Eu(III), Gd(III) and Nd(III)) cyanoacetate polymers: field-induced slow magnetic relaxation in the Gd and Nd substitutions, Dalton Trans., 2014, 43, 12342–12356; (b) H. X. Zhang, S. Y. Lin, S. F. Xue, C. Wang and J. K. Tang, Employment of triketones to construct a dysprosium(III) single-molecule magnet, Dalton Trans., 2015, 44, 4648–4654.
47. (a) F. Habib, I. Korobkov and M. Murugesu, Exposing the intermolecular nature of the second relaxation pathway in a mononuclear cobalt(II) single-molecule magnet with positive anisotropy, Dalton Trans., 2015, 44, 6368–6373; (b) Z. B. Hu, Z. Y. Jing, M. M. Li, L. Yin, Y. D. Gao, F. Yu, T. P. Hu, Z. Wang and Y. Song, Important role of intermolecular interaction in cobalt(II) single-ion magnet from single slow relaxation to double slow relaxation, Inorg. Chem., 2018, 57, 10761–10767; (c) J. Li, Y. Han, F. Cao, R. M. Wei, Y. Q. Zhang and Y. Song, Two field-induced slow magnetic relaxation processes in a mononuclear Co(II) complex with a distorted octahedral geometry, Dalton Trans., 2016, 45, 9279–9284; (d) M. A. Palacios, I. F. Díaz-Ortega, H. Nojiri, E. A. Suturina, M. Ozerov, J. Krzystek and E. Colacio, Tuning magnetic anisotropy by the π−bonding features of the axial ligands and the electronic effects of gold(I) atoms in 2D {Co(L)2[Au(CN)2]2}n metal-organic frameworks with field-induced single-ion magnet behaviour, Inorg. Chem. Front., 2020, 7, 4611–4630.
48. E. Colacio, J. Ruiz, E. Ruiz, E. Cremades, J. Krzystek, S. Carretta, J. Cano, T. Guidi, W. Wernsdorfer and E. K. Brechin, Angew. Chem., Int. Ed., 2013, 52, 9130–9134.
49. S. Titos-Padilla, J. Ruiz, J. M. Herrera, E. K. Brechin, W. Wersndorfer, F. Lloret and E. Colacio, Dilution-Triggered SMM Behavior under Zero Field in a Luminescent Zn2Dy2 Tetranuclear Complex Incorporating Carbonato-Bridging Ligands Derived from Atmospheric CO2 Fixation, Inorg. Chem., 2013, 52(16), 9620–9626.
50. J. Vallejo, M. Viciano-Chumillas, F. Lloret, M. Julve, I. Castro, J. Krzystek, M. Ozerov, D. Armentano, G. De Munno and J. Cano, Coligand effects on the field-induced double slow magnetic relaxation in six-coordinate cobalt(II) single-ion magnets (SIMs) with positive magnetic anisotropy, Inorg. Chem., 2019, 58, 15726–15740.
51. K. Saito and S. Miyashita, Magnetic Foehn effect in adiabatic transition, Phys. Soc. Jpn., 2001, 70, 3385–3390.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2144913–2144917. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d2qi00275b

‡ These authors contributed equally to this work.

---