Synthesis and structures of fluoride-bridged dysprosium clusters: influence of fluoride ions on magnetic relaxation behaviors†
Qiong
Yuan
a,
Yin-Shan
Meng
 b,
Yi-Quan
Zhang
b,
Yi-Quan
Zhang
 c,
Chen
Gao
a,
Shan-Shan
Liu
c,
Chen
Gao
a,
Shan-Shan
Liu
 d,
Bing-Wu
Wang
d,
Bing-Wu
Wang
 *a and
Song
Gao
*a and
Song
Gao
 *ae
*ae
aBeijing National Laboratory of Molecular Science, State Key Laboratory of Rare Earth Materials Chemistry and Applications, Beijing Key Laboratory for Magnetoelectric Materials and Devices, Peking University, College of Chemistry and Molecular Engineering, Peking University, Beijing 100871, P. R. China
bState Key Laboratory of Fine Chemicals, Dalian University of Technology, 2 Linggong Rd., Dalian 116024, P. R. China
cJiangsu Key Laboratory for NSLSCS, School of Physical Science and Technology, Nanjing Normal University, Nanjing 210023, P. R. China
dBeijing Key Laboratory of Fuels Cleaning and Advanced Catalytic Emission Reduction Technology, College of Chemical Engineering, Beijing Institute of Petrochemical Technology, Beijing 102617, PR China
eSchool of Chemistry and Chemical Engineering, South China University of Technology, Guangzhou 510640, P. R. China
First published on 18th March 2022
Abstract
The synthesis of fluoride-bridged tri-([{Cp′2Dy}{μ-F}]3·tol, 1Dy, Cp′ = C5H4Si(CH3)3; tol = toluene), tetra-([{Cp′2Dy(μ-F)2}2{(Cp′)(THF)Dy(μ-F)}2]·hex, 2Dy, THF = tetrahydrofuran; hex = n-hexane), and hepta-nuclear (3Dy) dysprosium complexes is reported here and a hydroxy-bridged dinuclear dysprosium complex [Cp′2Dy(μ-OH)]2(4Dy) is synthesized for comparison. The nucleation number of the fluoride-bridged complexes highly depends on the reaction solvents and the molar ratio of the dysprosium and fluoride precursors. The three Dy ions in 1Dy are arranged in a triangular fashion and the tetranuclear 2Dy displays a butterfly shape geometry. 3Dy shows a much more complicated structure with three types of fluoride bridges. 1Dy and 2Dy exhibit slow relaxation of magnetization with the energy barriers of 95 K and 98 K, respectively, while the dinuclear and heptanuclear dysprosium complexes barely show any behaviors of molecular nanomagnets. Ab initio calculations demonstrated that the thermo-assisted relaxation of magnetization of 1Dy and 2Dy originated from the {Cp′2Dy} fragment. Analysis of magneto-structural correlation revealed that the fluoride ions had a great influence on the orientation of the easy axis of magnetization and the exchange interactions.
Introduction
Recently, polynuclear lanthanide clusters possessing diverse structures and topologies have attracted increasing interest in coordination chemistry, owing to not only the fundamental pursuit of complicated and novel structures but also the challenging synthesis, interesting physical properties and potential applications.1–4 Compared with transition metal ions, the orbital angular momentum of 4f metal ions is largely conserved due to the localization of 4f electrons near the nucleus and hence there is no significant perturbation from the ligand field.5 Thus, the 4f metal ions exhibit much stronger spin–orbit coupling. The large magnetic anisotropy of lanthanide ions makes them ideal candidates for synthesizing single-molecule magnets (SMMs).6–10 With respect to the molecular nanomagnets, great efforts have been made in understanding and fine-tuning the uniaxial magnetic anisotropy and exchange interactions in order to generate high barriers for spin-reversal. So far, the highest barriers and blocking temperatures have been realized in dysprosium single-ion magnets (Dy-SIMs).11–15 In light of the lack of progress in multinuclear Dy-SMMs, we explore the effect of the nucleation number and exchange interactions on the magnetic relaxation of Dy-SMMs in this work.A panoply of lanthanide clusters with a variety of core motifs and nucleation numbers have been successfully synthesized with widely used bridging ligands such as carboxylates,16–18 phosphates,19 sulfonates,20 nitronylnitroxide radicals,21–24 halides,25–29etc.30 It is known that the fluoride ion possesses a smaller ionic radius and larger electronegativity than the N and O atoms. Therefore, the F ion in the terminal Dy–F bond is believed to provide stronger crystal field splitting and stabilize the |MJ| = 15/2 ground state of Dy, as predicted by Liviu Ungur and co-workers.31 The recent work by Norel and co-workers28 rationalized this theoretical prediction by showing that the terminal fluoride complex [Dy(Tppy)F(dioxane)](PF6) (Tppy = tris(3-(2-pyridyl)pyrazolyl)hydroborate) exhibits a high spin-reversal barrier of 432 cm−1. We are also curious about the effects of fluoride ions on the magnetic properties of multifluorido lanthanide complexes where small F bridges can also shorten the distance between two Dy ions and may reinforce the magnetic interactions between them. However, pure fluoride-bridged lanthanide complexes are very limited because the highly insoluble LnF3 can be easily formed. Most of the reported fluoride-bridged complexes are transition metals and 3d–4f species. The synthesis of fluoride-bridged lanthanide clusters needs careful control of multifluorido lanthanide cores to avoid the formation of LnF3. Besides, the introduction of fluoride ions using suitable fluoride precursors is also challenging as most of the fluoride salts are insoluble in organic solvents. The fluoride precursor Et3N·HF caught our attention as it can dissolve in THF easily. It also provides good reactivity with lanthanide metallocenes. In this work, we chose [Cp′3Dy] to react with Et3N·HF and obtained several clusters with varied numbers of Dy ions through changing different solvents or different molar ratios of reactants. The hydroxide-bridged complex 4Dy was also prepared using a similar method to compare the effects of hydroxide and fluoride bridges on their magnetic properties.
Results and discussion
Synthesis and structural characterization
The synthesis of fluoride-bridged dysprosium clusters was performed by adding an equivalent of Et3N·HF into a cold THF solution of [Cp′3Dy] very slowly. After filtering and removing the solvent, the raw products crystallizing in toluene and hexane could result in two different complexes 1Dy [Cp′2Dy(μ-F)]3·tol and 2Dy[{Cp′2Dy(μ-F)2}2{(Cp′)(THF)Dy(μ-F)}2]·hex. The reaction is promoted by the protonation of the Cp′ anion. The protonation degree depends highly on the crystallizing solvent and molar ratio of Et3N·HF and [Cp′3Dy] (see the ESI† Experimental section). An X-ray diffraction experiment indicated that 1Dy and 2Dy crystallize in the space group of P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) and P21/c, respectively. Their molecular structures are shown in Fig. 1 and 2, respectively.
and P21/c, respectively. Their molecular structures are shown in Fig. 1 and 2, respectively.
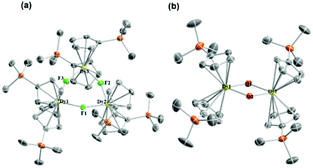 | ||
| Fig. 1 Molecular structures of 1Dy (a) and 4Dy (b). Co-crystallized THF and toluene and hydrogens are omitted for clarity. Color code: C, grey; Dy, yellow; Si, light orange; O, red; and F, green. | ||
 | ||
| Fig. 2 Molecular structures of 2Dy. Co-crystallized THF and toluene and hydrogens are omitted for clarity. Color code: C, grey; Dy, yellow; Si, light orange; O, red; and F, green. | ||
Complex 1Dy possesses a typical cyclic trimer structure. The three [Cp′2Dy]+ motifs are connected by μ-F bridges in a triangular manner. Each motif possesses very similar structural parameters, as listed in Table S2.† Each DyIII ion is coordinated by two Cp′ anions and bridged by two fluoride ions with the other two DyIII ions. The Dy–F bond lengths fall in a narrow range of 2.194(2)–2.204(2) Å. The Dy–C bond lengths are in a relatively broader range of 2.630(5)–2.721(5) Å. The DyIII ions and F− ions are almost within a plane. The structurally related 4Dy is a dinuclear complex, wherein the [Cp′2Dy]+ motifs are connected by two hydroxide bridges (Dy–O: 2.232(2)–2.261(2) Å). The specific bond length and bond angle information is listed in Table S5.†
Complex 2Dy is obtained in the hexane solution and crystallizes with a highly disordered hexane molecule in the unit cell. The tetranuclear complex adopts a chair-like structure, in which the DyIII ions can be divided into two kinds. In 2Dy, there are four DyIII ions and four fluoride ions composed of an eight-membered ring. Dy3 and Dy4 ions are coordinated by two Cp′ anions (Dy–C: 2.64(1)–2.69 Å) and two bridging fluoride ions (Dy–F: 2.172(5)–2.199(6) Å). The angles for F3–Dy3–F4 and F5–Dy4–F6 are 90.6° and 88.4°, respectively, which are slightly larger than those in 1Dy (85.9°–87.5°). Within the Dy3 and Dy4 metallocenes, one of the Dy–F bonds shows a smaller distance. Both Dy1 and Dy2 ions coordinate with only one Cp′ ring, one THF (Dy–C: 2.68(1)–2.72(1) Å), Dy–O: 2.396(7)–2.409(6) Å) and four bridged fluoride ions (Dy–F: 2.204(5)–2.267(5) Å). Dy1 and Dy2 are further bridged by two fluoride ions.
When the molar ratio of [Cp′3Dy] and Et3N·HF was changed to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
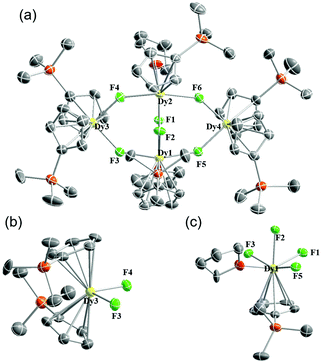
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.5, a structurally more complicated heptanuclear dysprosium core 3Dy (C64H110Dy7F15O4Si6·hex) was obtained. Five DyIII ions and five fluoride ions form a ten-membered ring with two DyIII ions locating on the two sides of the plane. The DyIII ions in the heptanuclear core can be divided into four kinds (Fig. 3). The Dy1 motif (Fig. 3c) is composed of two Cp′ anions (Dy–C: 2.671(5)–2.690(5) Å) and three fluoride ions (Dy–F: 2.268(3)–2.340(2) Å). Dy2 and Dy5 ions are coordinated only by fluoride ions (Dy–F: 2.182(2)–2.308(3) Å) and THF molecules (Dy–O: 2.370(5)–2.402(4) Å) without Cp′ rings. Dy3, Dy4, Dy6 and Dy7 ions are all capped by mono-Cp′ anions (Dy–C: 2.629(6)–2.696(6) Å). The difference lies in the central F15 ion being closer to Dy3 and Dy4 (2.515(3) and 2.550(3) Å for Dy3–F15 and Dy4–F15; 2.813(2) and 2.695(2) Å for Dy6–F15 and Dy7–F15). As can be seen, through fine-tuning the reaction and crystallizing conditions in the {Cp′3Dy + Et3N·HF} system, we can obtain well-defined Cp′–Dy–F clusters with various numbers of Dy ions. The diverse structures also highlight the versatility of fluoride ions as bridging ions to offer rich coordination chemistry.
1.5, a structurally more complicated heptanuclear dysprosium core 3Dy (C64H110Dy7F15O4Si6·hex) was obtained. Five DyIII ions and five fluoride ions form a ten-membered ring with two DyIII ions locating on the two sides of the plane. The DyIII ions in the heptanuclear core can be divided into four kinds (Fig. 3). The Dy1 motif (Fig. 3c) is composed of two Cp′ anions (Dy–C: 2.671(5)–2.690(5) Å) and three fluoride ions (Dy–F: 2.268(3)–2.340(2) Å). Dy2 and Dy5 ions are coordinated only by fluoride ions (Dy–F: 2.182(2)–2.308(3) Å) and THF molecules (Dy–O: 2.370(5)–2.402(4) Å) without Cp′ rings. Dy3, Dy4, Dy6 and Dy7 ions are all capped by mono-Cp′ anions (Dy–C: 2.629(6)–2.696(6) Å). The difference lies in the central F15 ion being closer to Dy3 and Dy4 (2.515(3) and 2.550(3) Å for Dy3–F15 and Dy4–F15; 2.813(2) and 2.695(2) Å for Dy6–F15 and Dy7–F15). As can be seen, through fine-tuning the reaction and crystallizing conditions in the {Cp′3Dy + Et3N·HF} system, we can obtain well-defined Cp′–Dy–F clusters with various numbers of Dy ions. The diverse structures also highlight the versatility of fluoride ions as bridging ions to offer rich coordination chemistry.
Magnetic properties
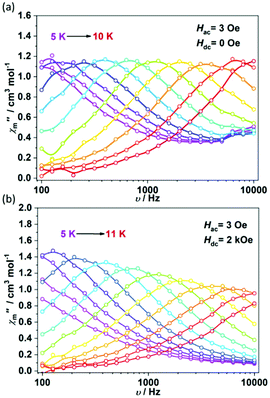
The variety of dysprosium cores provides a good platform to investigate the impact of fluoride ions on their magnetic properties. The direct current (dc) magnetic susceptibility measurements were performed between 2 K and 300 K under a 1 kOe applied dc field. At room temperature, the χmT values for the four complexes are 28.93, 42.34, 57.19 and 101.29 cm3 mol−1 K, as shown in Fig. 4, which are in good agreement with the calculated values for the uncoupled Dy3+ ions (for one free Dy the value is 14.17 cm3 mol−1 K). Upon cooling, the χmT values of the four complexes decrease slowly and begin to decrease rapidly below 25 K. At 2 K, the χmT values are 13.07, 15.28, 20.19 and 47.31 cm3 mol−1 K, respectively, which are all less than half of their initial values at room temperature. Such a decrease is probably caused by the thermal depopulation of the Stark levels. The intramolecular antiferromagnetic interaction could also lead to a decrease of χmT values and would be more predominant below 25 K. Field-dependent magnetization data were collected from 0 to 50 kOe at selected temperatures (see ESI Fig. S1–S4†). At 2 K, the magnetization values for the four complexes increase steeply at low fields and finally reach 10.51, 15.76, 20.34 and 37.96 Nβ at 50 kOe, respectively, which are comparable to the magnetization value per DyIII ion (4.7–5.3 Nβ). The non-superposition of the M versus HT−1 plots suggests the presence of magnetic anisotropy.To further investigate the effects of fluoride ions on the slow magnetic relaxation, alternating current (ac) susceptibility measurements were performed in the frequency range of 100–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Hz. For 1Dy, measurements of ac susceptibilities conducted in the absence of a dc field showed frequency-dependent signals between 2 K and 10 K (Fig. 5a). This result clearly indicates the slow relaxation of magnetization, a behavior of the SMMs. It is worth noting that below 4 K (Fig. S5†), χ′′m surges up to significantly high values, suggesting a very fast relaxation rate above 104 Hz. This fast relaxation behavior was also previously observed in a cyclic dysprosium tetramer32 and was possibly caused by thermally assisted quantum tunneling of magnetization (QTM) via the low-lying exchange-coupled excited states. Above 4 K, Cole–Cole plots confirmed a single thermo-related relaxation in the experimental temperature range, with a relatively narrow distribution of relaxation time (α: 0.29–0.08) (see ESI Fig. S8†). The plots of extracted relaxation times τ versus T−1 show the nonlinearity in the measured temperature range (Fig. 6). Such curvature is probably caused by the low-temperature QTM and other processes. Therefore, Arrhenius fitting cannot be applied to obtain the effective energy barrier. Therefore, the Orbach, Raman and QTM process fitting is introduced to the experimental data points, that is, the fitting formula (1), τ−1 = 1/τ0 × e−Ueff/T + CTn + 1/τtunneling, yielded an effective energy barrier of Ueff = 87 K, a pre-exponential factor τ0 = 3.22 × 10−9 s, n = 7.49, C = 0.0017 s−1 K−n and τtunneling = 4.23 × 10−5 s. To suppress the quantum tunneling, a 1.5 kOe dc field was applied. As shown in Fig. 6 and Fig. S6,† the relaxation rates decreased to some extent. Fitting the data set with eqn (2), τ−1 = 1/τ0 × e−Ueff/T + CTn, yielded an effective energy barrier of Ueff = 95 K, a pre-exponential factor τ0 = 2.27 × 10−9 s, n = 4.27 and C = 0.186 s−1 K−n. The obtained τ0 is in the typical range expected for molecular nanomagnets. The relatively small value of n is more likely due to the second-order Raman process for Kramers dysprosium ions. The theoretically calculated magnetization blocking barrier is 80 K (55.8 cm−1) (see ESI Table S6 and Fig. S12†), which is close to the experimental results.
000 Hz. For 1Dy, measurements of ac susceptibilities conducted in the absence of a dc field showed frequency-dependent signals between 2 K and 10 K (Fig. 5a). This result clearly indicates the slow relaxation of magnetization, a behavior of the SMMs. It is worth noting that below 4 K (Fig. S5†), χ′′m surges up to significantly high values, suggesting a very fast relaxation rate above 104 Hz. This fast relaxation behavior was also previously observed in a cyclic dysprosium tetramer32 and was possibly caused by thermally assisted quantum tunneling of magnetization (QTM) via the low-lying exchange-coupled excited states. Above 4 K, Cole–Cole plots confirmed a single thermo-related relaxation in the experimental temperature range, with a relatively narrow distribution of relaxation time (α: 0.29–0.08) (see ESI Fig. S8†). The plots of extracted relaxation times τ versus T−1 show the nonlinearity in the measured temperature range (Fig. 6). Such curvature is probably caused by the low-temperature QTM and other processes. Therefore, Arrhenius fitting cannot be applied to obtain the effective energy barrier. Therefore, the Orbach, Raman and QTM process fitting is introduced to the experimental data points, that is, the fitting formula (1), τ−1 = 1/τ0 × e−Ueff/T + CTn + 1/τtunneling, yielded an effective energy barrier of Ueff = 87 K, a pre-exponential factor τ0 = 3.22 × 10−9 s, n = 7.49, C = 0.0017 s−1 K−n and τtunneling = 4.23 × 10−5 s. To suppress the quantum tunneling, a 1.5 kOe dc field was applied. As shown in Fig. 6 and Fig. S6,† the relaxation rates decreased to some extent. Fitting the data set with eqn (2), τ−1 = 1/τ0 × e−Ueff/T + CTn, yielded an effective energy barrier of Ueff = 95 K, a pre-exponential factor τ0 = 2.27 × 10−9 s, n = 4.27 and C = 0.186 s−1 K−n. The obtained τ0 is in the typical range expected for molecular nanomagnets. The relatively small value of n is more likely due to the second-order Raman process for Kramers dysprosium ions. The theoretically calculated magnetization blocking barrier is 80 K (55.8 cm−1) (see ESI Table S6 and Fig. S12†), which is close to the experimental results.
 | ||
| Fig. 5 Plots of out-of-phase susceptibilities (χ′′m) versus frequency (ν) for 1Dy, under a zero applied dc field (a), and under a 1.5 kOe dc field, with an ac field of 3 Oe (b). | ||
Ac susceptibility measurements on 2Dy indicate the characteristic SMM behavior below 10 K under zero dc field (Fig. 7 and Fig. S7†). The relaxation of magnetization for 2Dy occurs in a similar temperature range to that for 1Dy (Fig. S9†). The magnitudes of χ′′m are also comparable with those of 1Dy. The plot ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) τ versus T−1 still deviates from linearity even in a higher temperature region (Fig. 8). Similarly, using the Orbach, Raman and QTM processes for fitting, we obtained Ueff = 89 K, τ0 = 4.47 × 10−9 s, n = 8.61, C = 0.00015 s−1 K−n and τtunneling = 2.21 × 10−5 s. A 2 kOe applied dc field can suppress the fast relaxation process effectively and reduce the relaxation rate. The fitting with eqn (1) gives Ueff = 97 K, τ0 = 1.38 × 10−9 s, n = 3.87 and C = 0.268 s−1 K−n, similar to the results for 1Dy. The results of the theoretical calculations of the magnetization blocking barriers for the four Dy(III) ions in compound 2Dy are shown in ESI Fig. S13.† The theoretically calculated magnetization blocking barriers for Dy3 and Dy4 (ESI Fig. S13c, d and Table S6†) are 162 K (112.9 cm−1) and 166 K (115.7 cm−1), which are quite different from the experimental results of 97 K. This may be due to the influence of weaker magnetic coupling in the system.
τ versus T−1 still deviates from linearity even in a higher temperature region (Fig. 8). Similarly, using the Orbach, Raman and QTM processes for fitting, we obtained Ueff = 89 K, τ0 = 4.47 × 10−9 s, n = 8.61, C = 0.00015 s−1 K−n and τtunneling = 2.21 × 10−5 s. A 2 kOe applied dc field can suppress the fast relaxation process effectively and reduce the relaxation rate. The fitting with eqn (1) gives Ueff = 97 K, τ0 = 1.38 × 10−9 s, n = 3.87 and C = 0.268 s−1 K−n, similar to the results for 1Dy. The results of the theoretical calculations of the magnetization blocking barriers for the four Dy(III) ions in compound 2Dy are shown in ESI Fig. S13.† The theoretically calculated magnetization blocking barriers for Dy3 and Dy4 (ESI Fig. S13c, d and Table S6†) are 162 K (112.9 cm−1) and 166 K (115.7 cm−1), which are quite different from the experimental results of 97 K. This may be due to the influence of weaker magnetic coupling in the system.
 | ||
| Fig. 7 Out-of-phase signals (χ′′m) versus frequency (ν) plots for 2Dy, under a zero applied dc field (a), and under a 2 kOe dc field, with an ac field of 3 Oe (b). | ||
For the heptanuclear 3Dy, no frequency-dependent resonant χ′′m peaks were observed in any applied fields (see ESI Fig. S10†). As mentioned earlier, the magnetic properties of these compounds mainly depend on the structure of [Cp2Dy]+ motifs. This is rational as the introduction of additional fluoride ions using Et3N·HF in the coordination spheres of Dy would undermine [Cp2Dy]+ motifs, which are the origin of the observed magnetic relaxation in 1Dy and 2Dy (vide infra). For the hydroxide-bridged complex 4Dy, no frequency-dependent in-phase (χ′m) and out-of-phase susceptibilities (χ′′m) were observed in the measured temperature range under zero dc field. When a 2.5 kOe dc field was applied, the out-of-phase components showed broad resonant peaks below 3 K (see ESI Fig. S11†). Thus, extracted relaxation times are not restricted due to the lack of well-defined resonant peaks. It can be seen from Fig. S14† that there is an obvious QTM process between the ground double states. The relatively high possibility of QTM between the ground state doublets will quench (accelerate) the relaxation at the initial stage. As a result, compound 4Dy does not exhibit obvious slow magnetic relaxation behavior under zero field.
Theoretical analysis
Previous study has demonstrated that ancillary ligands within the equatorial plane can greatly affect the slow magnetic relaxation behavior of dysprosium metallocenes.33 A weak ancillary ligand field would help stabilize the Ising type ground doublet of dysprosium metallocenes. Because of the larger electronegativity and the smaller radii of F than those of O, the interaction between DyIII ions and F− ions would induce more significant transverse components. However, an ac susceptibility study reveals that 1Dy and 2Dy are SMMs while the hydroxide-bridged 4Dy does not show slow magnetic relaxation behavior within the frequency measurement range of the instrument. To further elucidate the influence of fluoride and hydroxide bridges on their energy levels and magnetic properties, complete-active-space self-consistent field (CASSCF) calculations on individual DyIII fragments for the three complexes on the basis of X-ray determined geometries have been performed with MOLCAS 8.0 and SINGLE_ANISO programs.The eight lowest spin–orbit energies and the corresponding g tensors of complexes 4Dy, 1Dy and 2Dy are shown in Table S6.† The calculated ground gz values of the individual DyIII fragments of 4Dy are close to 20, and the gx,y values are not negligible. The orientations of easy axes for the cyclic trimer are nearly perpendicular to the plane consisting of the Dy3F3 core (Fig. 9b and Fig. S15†), in agreement with the previously reported dysprosium metallocene SMMs. For 2Dy, the orientations of the two types of DyIII fragments are very different. The Dy3 and Dy4 fragments supported by two Cp′ anions exhibit similar orientations of the easy axis to that in 1Dy, while the easy axes for Dy1 and Dy2 fragments supported by mono-Cp′ are almost perpendicular to the Cp ring, orienting towards the bridging F2 ion (Fig. 9c and Fig. S16†).
Despite the DyIII fragments except Dy1 and Dy2 in 2Dy having some deviations from 20, the Lines model was applied to estimate the exchange interactions in 4Dy, 1Dy and 2Dy using the POLY_ANISO5,13,34–39 program. All parameters in Table 1 were calculated with respect to the pseudospin  of the DyIII ions corresponding to the Hamiltonian representation in eqn (1)–(3). For complexes 4Dy, 1Dy and 2Dy, the total coupling parameters J (dipolar and exchange) were included to fit the magnetic susceptibilities. The calculated and experimental χmT versus T plots of complexes 4Dy, 1Dy and 2Dy are shown in Fig. 4, where the fit for both 4Dy and 1Dy is close to the experimental data. For 2Dy, however, the fit appeared a little deviated from the experimental data since the individual DyIII fragments of Dy1 and Dy2 cannot be treated as an ideal Ising type considering their ground gz being relatively far from 20 (see in ESI Table S6†). As seen in Table 1, the Dy⋯Dy interaction in complex 4Dy within the Lines model40–42 is antiferromagnetic. For 1Dy, the Dy1⋯Dy2 and Dy1⋯Dy3 interactions are both antiferromagnetic, while the Dy2–Dy3 interaction is ferromagnetic. For 2Dy, the Dy1–Dy3, Dy1–Dy4, Dy2–Dy4 and Dy2–Dy3 interactions are all antiferromagnetic, while the Dy2–Dy1 interaction is ferromagnetic. The exchange energies and the main values of gz for the lowest two exchange doublets for all complexes are given in Table S7.† The gz values of the ground exchange state for 4Dy, 1Dy and 2Dy are 38.04, 18.48 and 29.75, respectively. Both the experimental and theoretical results demonstrate that introducing more fluoride ions would impair the uniaxial anisotropy of the dysprosium metallocene SMMs. It is more obvious when we refer to the Dy1 fragment in 3Dy wherein three fluoride ions coordinated to a DyIII ion within the equatorial plane result in the fast relaxation of magnetization.
of the DyIII ions corresponding to the Hamiltonian representation in eqn (1)–(3). For complexes 4Dy, 1Dy and 2Dy, the total coupling parameters J (dipolar and exchange) were included to fit the magnetic susceptibilities. The calculated and experimental χmT versus T plots of complexes 4Dy, 1Dy and 2Dy are shown in Fig. 4, where the fit for both 4Dy and 1Dy is close to the experimental data. For 2Dy, however, the fit appeared a little deviated from the experimental data since the individual DyIII fragments of Dy1 and Dy2 cannot be treated as an ideal Ising type considering their ground gz being relatively far from 20 (see in ESI Table S6†). As seen in Table 1, the Dy⋯Dy interaction in complex 4Dy within the Lines model40–42 is antiferromagnetic. For 1Dy, the Dy1⋯Dy2 and Dy1⋯Dy3 interactions are both antiferromagnetic, while the Dy2–Dy3 interaction is ferromagnetic. For 2Dy, the Dy1–Dy3, Dy1–Dy4, Dy2–Dy4 and Dy2–Dy3 interactions are all antiferromagnetic, while the Dy2–Dy1 interaction is ferromagnetic. The exchange energies and the main values of gz for the lowest two exchange doublets for all complexes are given in Table S7.† The gz values of the ground exchange state for 4Dy, 1Dy and 2Dy are 38.04, 18.48 and 29.75, respectively. Both the experimental and theoretical results demonstrate that introducing more fluoride ions would impair the uniaxial anisotropy of the dysprosium metallocene SMMs. It is more obvious when we refer to the Dy1 fragment in 3Dy wherein three fluoride ions coordinated to a DyIII ion within the equatorial plane result in the fast relaxation of magnetization.
 | (1) |
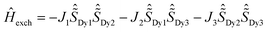 | (2) |
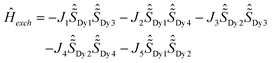 | (3) |
| 4Dy | 1Dy | 2Dy | |||||||
|---|---|---|---|---|---|---|---|---|---|
| J dip | J exch | J | J dip | J exch | J | J dip | J exch | J | |
| J 1 | −2.95 | −0.25 | −3.18 | −1.90 | −0.10 | −2.00 | −1.13 | −1.50 | −2.63 |
| J 2 | −1.86 | −0.14 | −2.00 | −1.10 | −1.50 | −2.60 | |||
| J 3 | −1.89 | 3.89 | 2.00 | −0.86 | −1.50 | −2.36 | |||
| J 4 | 0.99 | −1.50 | −0.51 | ||||||
| J 5 | 5.45 | −1.25 | 4.20 | ||||||
Conclusions
In summary, through systematically tuning the crystallizing solvents and molar ratios of reactants we can obtain three fluoride-bridged tri-, tetra-, and hepta-nuclear Cp-based Dy–F clusters along with a related hydroxy-bridged dinuclear dysprosium complex. The tri- and tetra-nuclear compounds can exhibit slow magnetic relaxation with almost identical energy barriers of 95 and 97 K, while the hydroxide-bridged dinuclear and F-bridged heptanuclear clusters barely display any SMM behavior. Ab initio calculations demonstrated that the thermo-assisted relaxation of magnetization arises from the [Cp′2Dy(μ-F)2] motifs. Through this work on Dy–F clusters, it is rationalized that the fluoride ions mainly affect the orientation of the easy axis and the exchange interactions. In short, for a high-performance single-molecule magnet, the suppression of quantum tunneling through the magnetic interaction of the metal center is an important means to improve the magnetic properties. However, for lanthanide ions, it is also crucial to improve local symmetry.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (21971006, 21621061, 21571008, 22173015 and 21801037), the National Key Basic Research Program of China (2018YFA0306003, 2017YFA0206301 and 2017YFA0204903) and the Natural Science Foundation of Jiangsu Province of China (BK20151542).Notes and references
- R. Sessoli, H. L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, High-spin molecules: [Mn12O12(O2CR)16(H2O)4], J. Am. Chem. Soc., 1993, 115, 1804 CrossRef CAS.
- W. Wernsdorfer and R. Sessoli, Quantum Phase Interference and Parity Effects in Magnetic Molecular Clusters, Science, 1999, 284, 133 CrossRef CAS PubMed.
- D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford express, 2006 Search PubMed.
- M. Shiddiq, D. Komijani, Y. Duan, A. Gaita-Ariño, E. Coronado and S. Hill, Enhancing coherence in molecular spin qubits via atomic clock transitions, Nature, 2016, 531, 348 CrossRef CAS PubMed.
- J. D. Rinehart and J. R. Long, Exploiting single-ion anisotropy in the design of f-element single-molecule magnets, Chem. Sci., 2011, 2, 2078 RSC.
- P. Zhang, Y.-N. Guo and J.-K. Tang, Recent advances in dysprosium-based single molecule magnets: Structural overview and synthetic strategies, Coord. Chem. Rev., 2013, 257, 1728 CrossRef CAS.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide Single-Molecule Magnets, Chem. Rev., 2013, 113, 5110 CrossRef CAS PubMed.
- Z.-H. Zhu, M. Guo, X.-L. Li and J.-K. Tang, Molecular magnetism of lanthanide: Advances and perspectives, Coord. Chem. Rev., 2019, 378, 350 CrossRef CAS.
- R. A. Layfield, Organometallic Single-Molecule Magnets, Organometallics, 2014, 33, 1084 CrossRef CAS.
- D. Shao and X.-Y. Wang, Development of Single-Molecule Magnets, Chin. J. Chem., 2020, 38, 1005 CrossRef CAS.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit, Angew. Chem., Int. Ed., 2017, 56, 11445 CrossRef CAS PubMed.
- C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439 CrossRef CAS PubMed.
- J. Liu, Y.-C. Chen, J.-L. Liu, V. Vieru, L. Ungur, J.-H. Jia, L. F. Chibotaru, Y. Lan, W. Wernsdorfer and S. Gao, A Stable Pentagonal Bipyramidal Dy(III) Single-Ion Magnet with a Record Magnetization Reversal Barrier over 1000 K, J. Am. Chem. Soc., 2016, 138, 5441 CrossRef CAS PubMed.
- S. K. Gupta, T. Rajeshkumar, G. Rajaraman and R. Murugavel, An air-stable Dy(iii) single-ion magnet with high anisotropy barrier and blocking temperature, Chem. Sci., 2016, 7, 5181 RSC.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400 CrossRef CAS PubMed.
- I. A. Gass, B. Moubaraki, S. K. Langley, S. R. Batten and K. S. Murray, A π–π 3D network of tetranuclear μ2/μ3-carbonato Dy(iii) bis-pyrazolylpyridine clusters showing single molecule magnetism features, Chem. Commun., 2012, 48, 2089 RSC.
- G. Brunet, E. Sebastiao, T. G. Witkowski, L. Korobkov, B. Gabidullin and M. Murugesu, A nitrogen-rich ligand as a scaffold for slow magnetic relaxation in dysprosium-based 0D and 1D architectures, Dalton Trans., 2018, 47, 11782 RSC.
- A. Raya-Barón, I. Oyarzabal, F. M. Arrabal-Campos, J. M. Seco, A. Rodríguez-Diéguez and I. Fernández, Dinuclear Coordination Compounds Based on a 5-Nitropicolinic Carboxylate Ligand with Single-Molecule Magnet Behavior, Inorg. Chem., 2017, 56, 8768 CrossRef PubMed.
- T. Pugh, F. Tuna, L. Ungur, D. Collison, E. J. L. McInnes, L. F. Chibotaru and R. A. Layfield, Influencing the properties of dysprosium single-molecule magnets with phosphorus donor ligands, Nat. Commun., 2015, 6, 7492 CrossRef PubMed.
- F. Tuna, C. A. Smith, M. Bodensteiner, L. Ungur, L. F. Chibotaru, E. J. L. McInnes, R. E. P. Winpenny, D. Collison and R. A. Layfiled, A High Anisotropy Barrier in a Sulfur-Bridged Organodysprosium Single-Molecule Magnet, Angew. Chem., Int. Ed., 2012, 51, 6976 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Strong exchange and magnetic blocking in N23−-radical-bridged lanthanide complexes, Nat. Chem., 2011, 3, 538 CrossRef CAS PubMed.
- J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, A N23− Radical-Bridged Terbium Complex Exhibiting Magnetic Hysteresis at 14 K, J. Am. Chem. Soc., 2011, 133, 14236 CrossRef CAS PubMed.
- S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Giant coercivity and high magnetic blocking temperatures for N23− radical-bridged dilanthanide complexes upon ligand dissociation, Nat. Commun., 2017, 8, 2144 CrossRef PubMed.
- F.-S. Guo and R. A. Layfield, Strong direct exchange coupling and single-molecule magnetism in indigo-bridged lanthanide dimers, Chem. Commun., 2017, 53, 3130 RSC.
- Y.-S. Meng, J. Xiong, M.-W. Yang, Y.-S. Qiao, Z.-Q. Zhong, H.-L. Sun, J.-B. Han, T. Liu, B.-W. Wang and S. Gao, Experimental Determination of Magnetic Anisotropy in Exchange-Bias Dysprosium Metallocene Single-Molecule Magnets, Angew. Chem., Int. Ed., 2020, 59, 13037 CrossRef CAS PubMed.
- B. M. Day, N. F. Chilton and R. A. Layfield, Molecular and electronic structures of donor-functionalized dysprosium pentadienyl complexes, Dalton Trans., 2015, 44, 7109 RSC.
- T. Han, Y.-S. Ding, Z.-H. Li, K.-X. Yu, Y.-Q. Zhai, N. F. Chilton and Y.-Z. Zheng, A dichlorido-bridged dinuclear Dy(iii) single-molecule magnet with an effective energy barrier larger than 600 K, Chem. Commun., 2019, 55, 7930 RSC.
- L. Norel, L. E. Darago, B. L. Guennic, K. Chakarawet, M. I. Gonzalez, J. H. Olshansky, S. Rigaut and J. R. Long, A Terminal Fluoride Ligand Generates Axial Magnetic Anisotropy in Dysprosium Complexes, Angew. Chem., Int. Ed., 2018, 57, 1933 CrossRef CAS PubMed.
- Y. Huo, Y.-C. Chen, S.-G. Wu, J.-L. Liu, J.-H. Jia, W.-B. Chen, B.-L. Wang, Y.-Q. Zhang and M.-L. Tong, Effect of Bridging Ligands on Magnetic Behavior in Dinuclear Dysprosium Cores Supported by Polyoxometalates, Inorg. Chem., 2019, 58, 1301 CrossRef CAS PubMed.
- F.-S. Guo, A. K. Bar and R. A. Layfield, Main Group Chemistry at the Interface with Molecular Magnetism, Chem. Rev., 2019, 119, 8479 CrossRef CAS PubMed.
- L. Ungur and L. F. Chibotaru, Ab Initio Crystal Field for Lanthanides, Chem. – Eur. J., 2017, 23, 3708 CrossRef CAS PubMed.
- S. K. Langley, C. M. Forsyth, B. Moubaraki and K. S. Murray, A fluoride bridged {CrIII4DyIII4} single molecule magnet, Dalton Trans., 2015, 44, 912 RSC.
- Y.-S. Meng, Y.-Q. Zhang, Z.-M. Wang, B.-W. Wang and S. Gao, Weak Ligand-Field Effect from Ancillary Ligands on Enhancing Single-Ion Magnet Performance, Chem. – Eur. J., 2016, 22, 12724 CrossRef CAS PubMed.
- J. J. Baldoví, J. J. Borrás-Almenar, J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Modeling the properties of lanthanoid single-ion magnets using an effective point-charge approach, Dalton Trans., 2012, 41, 13705 RSC.
- D. Aravena and E. Ruiz, Shedding Light on the Single-Molecule Magnet Behavior of Mononuclear DyIII Complexes, Inorg. Chem., 2013, 52, 13770 CrossRef CAS PubMed.
- N. F. Chilton, D. Collison, E. J. L. McInnes, R. E. P. Winpenny and A. Soncini, An electrostatic model for the determination of magnetic anisotropy in dysprosium complexes, Nat. Commun., 2013, 4, 2551 CrossRef PubMed.
- S.-D. Jiang and S.-X. Qin, Prediction of the quantized axis of rare-earth ions: the electrostatic model with displaced point charges, Inorg. Chem. Front., 2015, 2, 613 RSC.
- Y.-C. Chen, J.-L. Liu, L. Ungur, J. Liu, Q.-W. Li, L.-F. Wang, Z.-P. Ni, L. F. Chibotaru, X.-M. Chen and M.-L. Tong, Symmetry-Supported Magnetic Blocking at 20 K in Pentagonal Bipyramidal Dy(III) Single-Ion Magnets, J. Am. Chem. Soc., 2016, 138, 2829 CrossRef CAS PubMed.
- Y.-S. Meng, S.-D. Jiang, B.-W. Wang and S. Gao, Understanding the Magnetic Anisotropy toward Single-Ion Magnets, Acc. Chem. Res., 2016, 49, 2381 CrossRef CAS PubMed.
- E. M. Pineda, N. F. Chilton, R. Marx, M. Dörfel, D. O. Sells, P. Neugebauer, S.-D. Jiang, D. Collison, J. van Slageren, E. J. L. McInnes and R. E. P. Winpenny, Direct measurement of dysprosium(III)˙˙˙dysprosium(III) interactions in a single-molecule magnet, Nat. Commun., 2014, 5, 5243 CrossRef PubMed.
- R. Marx, F. Moro, M. Dorfel, L. Ungur, M. Waters, S. D. Jiang, M. Orlita, J. Taylor, W. Frey, L. F. Chibotaru and J. van Slageren, Spectroscopic determination of crystal field splittings in lanthanide double deckers, Chem. Sci., 2014, 5, 3287 RSC.
- M. Gysler, F. El Hallak, L. Ungur, R. Marx, M. Hakl, P. Neugebauer, Y. Rechkemmer, Y. Lan, I. Sheikin, M. Orlita, C. E. Anson, A. K. Powell, R. Sessoli, L. F. Chibotaru and J. van Slageren, Multitechnique investigation of Dy3 – implications for coupled lanthanide clusters, Chem. Sci., 2016, 7, 4347 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Additional computational details and magnetic and crystallographic data are provided in the ESI. CCDC 2121103, 2121109, 2121120 and 2121121 for compounds 1Dy–4Dy. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d1qi01422f |
| This journal is © the Partner Organisations 2022 |





