Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Frictionless nanohighways on crystalline surfaces†
Emanuele
Panizon‡
 ae,
Andrea
Silva‡
ae,
Andrea
Silva‡
 bc,
Xin
Cao
bc,
Xin
Cao
 a,
Jin
Wang
a,
Jin
Wang
 c,
Clemens
Bechinger
c,
Clemens
Bechinger
 a,
Andrea
Vanossi
a,
Andrea
Vanossi
 bc,
Erio
Tosatti
bc,
Erio
Tosatti
 bce and
Nicola
Manini
bce and
Nicola
Manini
 *d
*d
aFachbereich Physik, University Konstanz, 78464 Konstanz, Germany
bCNR-IOM, Consiglio Nazionale delle Ricerche – Istituto Officina dei Materiali, c/o SISSA, 34136 Trieste, Italy
cInternational School for Advanced Studies (SISSA), Via Bonomea 265, 34136 Trieste, Italy
dDipartimento di Fisica, Università degli Studi di Milano, Via Celoria 16, 20133 Milano, Italy. E-mail: nicola.manini@unimi.it
eInternational Centre for Theoretical Physics (ICTP), Strada Costiera 11, 34151 Trieste, Italy
First published on 1st December 2022
Abstract
The understanding of friction at nano-scales, ruled by the regular arrangement of atoms, is surprisingly incomplete. Here we provide a unified understanding by studying the interlocking potential energy of two infinite contacting surfaces with arbitrary lattice symmetries, and extending it to finite contacts. We categorize, based purely on geometrical features, all possible contacts into three different types: a structurally lubric contact where the monolayer can move isotropically without friction, a corrugated and strongly interlocked contact, and a newly discovered directionally structurally lubric contact where the layer can move frictionlessly along one specific direction and retains finite friction along all other directions. This novel category is energetically stable against rotational perturbations and provides extreme friction anisotropy. The finite-size analysis shows that our categorization applies to a wide range of technologically relevant materials in contact, from adsorbates on crystal surfaces to layered two-dimensional materials and colloidal monolayers.
I. Introduction
When two macroscopically rough surfaces are brought close to each other, they interact only locally at the touching asperities. The progressive increase of touching asperities with load at constant nominal area leads to a contact friction that is proportional to load while independent of area. Contact friction at the atomic scale, on the other hand, follows remarkably different rules.1–5 At small length scales, static friction is largely dependent on the atomic arrangement, and, specifically for crystalline materials, on the mutual relation between the lattice periodicities of the two contacting surfaces. When two atomically flat surfaces come close to each other, the atoms or molecules on one surface can fall into the interatomic gaps of another, leading to an interlocking potential that is strongly dependent on the atomic arrangement at the two contacting surfaces. Such atomic interlocking potentials have strong influences on many nanoscopic frictional processes such as scanning tunneling microscopy experiments,6,7 nanomanipulations8–10 and fabrications of layered two dimensional (2D) materials.11 However, our knowledge of such interlocking effects is incomplete and often obtained in a case-by-case manner, largely due to the material-dependent properties and the complexities of the contacting interfaces such as the contact incommensurabilities and strong finite-size effects.In an exemplary commensurate contact where the atoms on one surface can perfectly match the inter-atom gaps of the other, interlocking effects are strong as the forces required to unlock individual atoms add up, thus producing a total friction that grows linearly with contact size. On the other hand, when the contacting periodicities are incommensurate, or not perfectly aligned, interlocking forces cancel out, tendentially leading to superlubric sliding or structural superlubricity.12–15 The relative orientation and directions of motion of a rigid crystalline cluster interacting with an underlying periodic surface were recently shown to be dominated by the possible emergence of common lattice vectors (CLVs) in real and in reciprocal space.16,17 Despite results for specific geometries and potentials,18–20 a precise and general quantitative classification of the degree and type of commensurability of contacting lattices and its connection to friction is still currently called for. The present paper aims at filling this gap.
In concrete, we answer the following question: given a crystal–crystal interface that involves two 2D lattices, what kind of ideal frictional behavior can we predict? For a 1D interface, idealized in the Frenkel-Kontorova model,21 the answer to this question depends on whether the lattice-spacing ratio a/b is rational (high friction) or irrational (superlubric sliding for sufficiently rigid crystals). For the 2D geometry at hand, we classify three very different friction regimes that can arise depending on the (in)commensuration detail in the relation between the two lattices. In between the standard fully commensurate and fully incommensurate conditions, we identify and characterize an intermediate situation, involving an effective 1D-commensuration that produces a finite friction in one direction, but leaves incommensurate superlubric sliding in the perpendicular direction. This condition leads to the “locked” free-sliding direction which in the title we refer to as a frictionless nanohighway, a case of directional structural lubricity. This phenomenon arises when two surfaces lock into a specific orientation, such that static friction vanishes in one specific direction, while remaining finite in all other directions.
Relaxing the condition of infinite size, we obtain theoretical bounds – plus numerical and experimental evidence – of finite-size contacts where approximate versions of each of the infinite-size regimes are realized. In these quasi-commensurate contacts the friction forces along different directions grow as a function of the contact size following very different scaling laws: sublinear and linear in low- and high-friction directions respectively. The emerging anisotropy of friction effectively reproduces the main features of the infinite-size limit also for real-life finite-size contacts.
The results obtained in this paper are derived for rigid lattices. The geometric conditions to differentiate the different friction regimes represents necessary – but possibly not sufficient – conditions for real (i.e. elastic) systems.22,23
II. The geometric context
We start by recalling a few useful results in the framework of the algebra of reciprocal (dual) lattices, which will allow us to provide a full classification of the contacts between rigid periodic solids.Consider the problem of moving a monolayer adsorbate crystal across another crystalline surface. Each adsorbate atom interacts with the lateral corrugation potential generated by the underlying crystal surface  , characterized by the following periodicity:
, characterized by the following periodicity:  , where S1 and S2 are primitive vectors of the underlying crystal lattice. For example, we construct
, where S1 and S2 are primitive vectors of the underlying crystal lattice. For example, we construct  as
as
 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−r2/σ2), with σ = 0.1|S1|. Fig. 1a, e and i illustrates the crystal overlayered on a square-symmetry substrate potential.
exp(−r2/σ2), with σ = 0.1|S1|. Fig. 1a, e and i illustrates the crystal overlayered on a square-symmetry substrate potential.
 | ||
Fig. 1 The three types of contacts between two 2D lattices. (a–d) Fully commensurate, type A; (e–h) 1D-commensurate, type B; (i–m) fully incommensurate, type C. Panels (a, e and i) display the two contacting lattices in real space: grayscale map of the potential  with unit-side square-lattice periodicity (black to white = low to high energy); blue dots = adsorbate crystal; orange-edge blue dots = CLVs in real space; light blue arrows = the primitive vectors of the adsorbate lattice. (b, f and j) The corresponding two dual lattices: red dots = adsorbate reciprocal lattice with unit-side square-lattice periodicity (black to white = low to high energy); blue dots = adsorbate crystal; orange-edge blue dots = CLVs in real space; light blue arrows = the primitive vectors of the adsorbate lattice. (b, f and j) The corresponding two dual lattices: red dots = adsorbate reciprocal lattice  ; gray dots = substrate reciprocal lattice ; gray dots = substrate reciprocal lattice 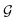 ; arrows = coincidence vectors (elements of the set Ω). (c, g and k) the linear sum ; arrows = coincidence vectors (elements of the set Ω). (c, g and k) the linear sum  of the of the  and and  lattices in the Wigner–Seitz cell of the substrate. (d, h and m) the resulting interlocking potential energy (eqn (2), colorbar at the right) as a function of the adsorbate translation within the substrate Wigner–Seitz cell; for the adopted corrugation potential of eqn (1), lattices in the Wigner–Seitz cell of the substrate. (d, h and m) the resulting interlocking potential energy (eqn (2), colorbar at the right) as a function of the adsorbate translation within the substrate Wigner–Seitz cell; for the adopted corrugation potential of eqn (1),  . The adsorbate lattices are: (a–d) a square lattice with . The adsorbate lattices are: (a–d) a square lattice with  , and orientation θo = tan−1(1/2); (e–h) a triangular lattice with , and orientation θo = tan−1(1/2); (e–h) a triangular lattice with  , and orientation θo = 15°; (i–m) a rhombic lattice with primitive vectors of length , and orientation θo = 15°; (i–m) a rhombic lattice with primitive vectors of length  separated by an angle ψ = 1 rad, with orientation θo = tan−1(1/2). separated by an angle ψ = 1 rad, with orientation θo = tan−1(1/2). | ||
The surface forces that contrast the motion of a rigid overlayer result from the gradient of the total (interlocking) potential energy. Its value normalized per monolayer particle is
 | (2) |
As derived previously,16,17 in the N → ∞ limit of a macroscopically large perfect crystalline monolayer, the interlocking potential is
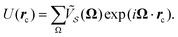 | (3) |
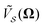 are the relevant Fourier components of
are the relevant Fourier components of  , defined as:
, defined as: | (4) |
 is the area of the primitive cell of
is the area of the primitive cell of  , i is the imaginary unit. Expression (3) is a 2D generalization of the well-known “Poisson summation formula”,
, i is the imaginary unit. Expression (3) is a 2D generalization of the well-known “Poisson summation formula”,  where
where ![[s with combining tilde]](https://www.rsc.org/images/entities/i_char_0073_0303.gif) is the Fourier transform of s, and the summations run from −∞ to ∞. The dependence of the potential U(rc) upon the relative orientation of the two contacting lattices enters the expression in eqn (3) implicitly via the CLVs Ω.
is the Fourier transform of s, and the summations run from −∞ to ∞. The dependence of the potential U(rc) upon the relative orientation of the two contacting lattices enters the expression in eqn (3) implicitly via the CLVs Ω.
Notice that the Ω's included in the summation have unlimited size. A hypothetical purely sinusoidal potential 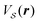 , as commonly used in friction modeling,18,24–27 involves few nonzero Fourier components, resulting in few (or even no) non-zero terms in the sum of eqn (3). In contrast however, our example potential constructed as a sum of Gaussian wells, eqn (1), involves infinitely many nonzero Fourier components, so that all terms in eqn (3) are potentially relevant.
, as commonly used in friction modeling,18,24–27 involves few nonzero Fourier components, resulting in few (or even no) non-zero terms in the sum of eqn (3). In contrast however, our example potential constructed as a sum of Gaussian wells, eqn (1), involves infinitely many nonzero Fourier components, so that all terms in eqn (3) are potentially relevant.
The focus of the present paper is how the shape of U(rc) and the consequent friction phenomenology change (often dramatically), depending on the specifics of the intersection of the reciprocal lattices of the two contacting crystals.
III. Algebraic basics
A lattice in d dimension is the set of all vectors obtained as linear combinations with integer coefficients of a set of primitive vectors {R1, R2,…, Rd}. For the lattice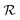 generated by this set of primitive vectors we use the following notation:
generated by this set of primitive vectors we use the following notation: | (5) |
The dual of an arbitrary set of vectors  (not necessarily a lattice), indicated by
(not necessarily a lattice), indicated by  , is defined as the set of all elements
, is defined as the set of all elements  , such that the scalar product 〈Q,ρ〉 is an integer multiple of 2π for all
, such that the scalar product 〈Q,ρ〉 is an integer multiple of 2π for all  , i.e.
, i.e.
 | (6) |
Note that we include a factor 2π, usually omitted from the standard mathematical definition of a dual. With such convention, the dual of the lattice is its reciprocal lattice.
Let  be the lattice generated by a second set of primitive vectors {S1, S2,…, Sd}. The linear sum
be the lattice generated by a second set of primitive vectors {S1, S2,…, Sd}. The linear sum 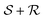 (defined as the set of all sums of one element in
(defined as the set of all sums of one element in  plus another element in
plus another element in  ) of the two lattices is generally not a lattice, but it is a set of vectors, of which we wish to evaluate the dual.
) of the two lattices is generally not a lattice, but it is a set of vectors, of which we wish to evaluate the dual.
It is a known properties of duals28,29 that 
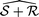 +, where
+, where  is the intersection of the individual duals
is the intersection of the individual duals  and
and  .
.
We adopt the following notation for the d = 2 problem at hand: the lattice  and its reciprocal
and its reciprocal  refer to the overlayer crystal;
refer to the overlayer crystal;  and its reciprocal
and its reciprocal 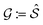 refer to the periodic substrate potential.
refer to the periodic substrate potential.
We also indicate the linear sum as  and its dual
and its dual  . By construction, Ω is then the set of CLVs in reciprocal space, namely those belonging to both reciprocal lattices
. By construction, Ω is then the set of CLVs in reciprocal space, namely those belonging to both reciprocal lattices  and
and 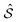 . For this reason, we will occasionally refer to Ω as the coincidence set.
. For this reason, we will occasionally refer to Ω as the coincidence set.
Note that any two arbitrary lattices  and
and 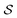 can be mapped to a linearly-transformed lattice
can be mapped to a linearly-transformed lattice  and a unit square lattice
and a unit square lattice  . The explicit isomorphism is S−1 where S is the matrix whose columns are the vectors {S1, S2} generating
. The explicit isomorphism is S−1 where S is the matrix whose columns are the vectors {S1, S2} generating  . With this transformation,
. With this transformation, 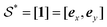
 =
=  , namely the square lattice of unit lattice spacing, and
, namely the square lattice of unit lattice spacing, and 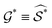 consists of all reciprocal vectors whose Cartesian components are 2π× integers. In practice then, to classify the structure of
consists of all reciprocal vectors whose Cartesian components are 2π× integers. In practice then, to classify the structure of  , one can equivalently focus on
, one can equivalently focus on  , i.e. the linear sum of the unit square lattice with a properly transformed lattice
, i.e. the linear sum of the unit square lattice with a properly transformed lattice  .
.
In the following we stick to the S−1-transformed lattices 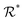 and
and  . For compactness’ sake we omit all stars. Fig. 1 already adheres to this convention.
. For compactness’ sake we omit all stars. Fig. 1 already adheres to this convention.
In the next section, we show that three different categories of  (or its dual Ω) can arise, depending on the mutual (in)commensuration of
(or its dual Ω) can arise, depending on the mutual (in)commensuration of  and
and  . We further show that the specific type of
. We further show that the specific type of  pertinent to a given interface between two flat crystalline surfaces bears important implications for the friction exhibited by this interface when the surfaces are set in relative motion.
pertinent to a given interface between two flat crystalline surfaces bears important implications for the friction exhibited by this interface when the surfaces are set in relative motion.
IV. Three categories of commensurability
For a 1D interface, the degree of commensuration is dictated by the ratio a/b between the lattice spacing of the adsorbate and that of the substrate:30–32 if this ratio is a rational number, then the two lattices are commensurate; if this ratio is irrational, the lattices are incommensurate. In the rational case the coincidence set Ω is a 1D lattice where the periodicity is given by the denominator of the ratio. Then the linear-sum space is also a discrete set of points repeating along the 1D line, i.e. a 1D lattice. In the irrational case there are no CLVs and Ω contains the null element only. Hence the sum space
is also a discrete set of points repeating along the 1D line, i.e. a 1D lattice. In the irrational case there are no CLVs and Ω contains the null element only. Hence the sum space  covers densely the 1D line. For a rigid contact, the rational case has finite friction, while the irrational case is frictionless.
covers densely the 1D line. For a rigid contact, the rational case has finite friction, while the irrational case is frictionless.
In 2D the linear sum  is a set of vectors in
is a set of vectors in 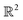 . The friction experienced by the overlayer when it is translated relative to the substrate potential is determined by the geometric mutual commensuration relations of the vectors in
. The friction experienced by the overlayer when it is translated relative to the substrate potential is determined by the geometric mutual commensuration relations of the vectors in  and
and  , and their implications for
, and their implications for  . These relations characterize how the real plane
. These relations characterize how the real plane  is covered by the vectors in the sum space
is covered by the vectors in the sum space  . This coverage occurs in one of three qualitatively different types:
. This coverage occurs in one of three qualitatively different types:
• a sparse coverage by a discrete set of points forming a 2D lattice – Fig. 1c,
• a “comb” coverage by an array of parallel lines – Fig. 1g, and
• a dense33 area coverage – Fig. 1k.
These geometric alternatives result in three dramatically different patterns of interlocking potential, illustrated in the rightmost column of Fig. 1, and therefore different friction properties. In the following subsections we detail the conditions determining these coverage categories in terms of the reciprocal lattice 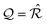 and of the coincidence set Ω.
and of the coincidence set Ω.
A. Discrete coverage
Discrete coverage occurs when there exist two linearly independent vectors {Q1, Q2} in the dual of the adsorbate crystal lattice
of the adsorbate crystal lattice  such that all components of these vectors are 2π× integer numbers, i.e.
such that all components of these vectors are 2π× integer numbers, i.e.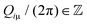 with i = 1, 2 and μ = x, y.
with i = 1, 2 and μ = x, y.
The above condition means that Q1, Q2 exist in  as well, i.e.
as well, i.e.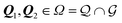 . In this case, summarised in the first row of Table 1, Ω is a 2D lattice. As a corollary of the above condition, all reciprocal vectors
. In this case, summarised in the first row of Table 1, Ω is a 2D lattice. As a corollary of the above condition, all reciprocal vectors  are such that their components Qiμ/(2π) are rational numbers; see Methods section IX for a proof.
are such that their components Qiμ/(2π) are rational numbers; see Methods section IX for a proof.
 of the overlayer crystal match the reciprocal
of the overlayer crystal match the reciprocal  of the substrate unit square lattice
of the substrate unit square lattice
We pick two primitive vectors Ω1 and Ω2 of this coincidence reciprocal lattice Ω = [Ω1, Ω2], as illustrated in Fig. 1b. The resulting interlocking potential, as expressed in eqn (3), exhibits a non-vanishing corrugation along both independent directions of Ω1 and Ω2. The interlocking potential energy landscape for the center-of-mass translation takes on a nontrivial shape, such as e.g. the one depicted in Fig. 1d. It can be expressed as
 | (7) |
 . Fig. 1d reports this function as resulting from the Fourier components of the potential of eqn (1). The potential energy landscape reveals a new lattice periodicity, precisely the one emerging in the sum space
. Fig. 1d reports this function as resulting from the Fourier components of the potential of eqn (1). The potential energy landscape reveals a new lattice periodicity, precisely the one emerging in the sum space  , Fig. 1c. In general, this new periodicity is either equal to or shorter than that of the original substrate.
, Fig. 1c. In general, this new periodicity is either equal to or shorter than that of the original substrate.
When the monolayer is forced across the periodic surface, it will move more easily along certain directions than along others, due to potential-barrier directional anisotropies. In the example of Fig. 1d, the easy directions are the substrate lattice symmetry directions which avoid the maxima of the energy landscape.
Motion along these preferential directions is usually named directional locking. This phenomenon was observed experimentally in several systems, e.g., for a triangular colloidal crystalline 2D cluster sliding across a triangular substrate,16,17,34,35 for AFM-pushed gold islands on MoS2,36 for magnetic vortex lattice under a Lorentz force,37 and for Wigner crystals on a periodic substrate.38 Directional locking has also been observed by numerical simulations in several different contexts,39–44e.g. the motion of magnetic skyrmions45,46 and dusty plasma47 on a periodic potential.
B. Line coverage
A second nontrivial condition occurs when the coverage is neither discrete nor dense in the whole space. This condition is realized when the dual set
is neither discrete nor dense in the whole space. This condition is realized when the dual set  is a 1-dimensional lattice, as in Fig. 1f. In practice, one can identify a nonzero reciprocal lattice vector
is a 1-dimensional lattice, as in Fig. 1f. In practice, one can identify a nonzero reciprocal lattice vector  with the property of having both integer components
with the property of having both integer components  . All other vectors in
. All other vectors in  either are multiples of Q1 or have at least a component divided by 2π that is an irrational number. Pick one of the two shortest nonzero inversion-symmetric CLV, namely the vectors with the properties of Q1, and call it Ω. As a result the coincidence set Ω contains a unique linearly-independent direction, that of Ω. In other words, Ω is a 1-dimensional lattice Ω = [Ω], simply the set of all integer multiples of Ω. When this condition is met, the linear sum space
either are multiples of Q1 or have at least a component divided by 2π that is an irrational number. Pick one of the two shortest nonzero inversion-symmetric CLV, namely the vectors with the properties of Q1, and call it Ω. As a result the coincidence set Ω contains a unique linearly-independent direction, that of Ω. In other words, Ω is a 1-dimensional lattice Ω = [Ω], simply the set of all integer multiples of Ω. When this condition is met, the linear sum space  is a set of discretely-spaced parallel lines aligned perpendicularly to Ω, and covered densely in a 1-dimensional sense, see Fig. 1g. This condition is summarised in the second row of Table 1.
is a set of discretely-spaced parallel lines aligned perpendicularly to Ω, and covered densely in a 1-dimensional sense, see Fig. 1g. This condition is summarised in the second row of Table 1.
In terms of the shortest CLV Ω, the interlocking potential energy of eqn (3) becomes:
 | (8) |
A natural name for this condition is directional structural lubricity.
We are not aware of any previous work where this regime of frictionless nanohighways is hypothesized, nor any existing experiment where this condition was pointed out. In section V.D below we report its realization in a colloidal experiment, and propose possible heterogeneous contacts between 2D nanomaterials where it should also be accessible.
We realize that in general, if two lattices share the same rotational symmetry of order n > 2, then there arise either two or no linearly independent CLVs in Ω. Therefore the resulting contact cannot belong to this type B. In Methods section X we report an argument to illustrate this point.
C. Dense coverage
The final possibility occurs when no nonzero reciprocal lattice vector in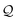 exists such that both its components divided by 2π are integer. This statements amount to say that the coincidence set is Ω = {0}, as summarised in the final row of Table 1. The corresponding sum set
exists such that both its components divided by 2π are integer. This statements amount to say that the coincidence set is Ω = {0}, as summarised in the final row of Table 1. The corresponding sum set  is dense, as shown in Fig. 1k.
is dense, as shown in Fig. 1k.
The Fourier expansion (3) only includes the null vector: as a result, the interlocking potential energy is perfectly flat
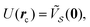 | (9) |
Interestingly, two lattices can even share CLVs in real space, but still have a dense sum space 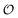 . This occurs in the example of Fig. 1i–m: these two lattices happen to have infinitely many coincidence points along the substrate direction S′ = (2, 1), i.e. the intersection
. This occurs in the example of Fig. 1i–m: these two lattices happen to have infinitely many coincidence points along the substrate direction S′ = (2, 1), i.e. the intersection  (orange-edged blue circles in Fig. 1i). However this real-space intersection is irrelevant to the lubricity of this contact. Instead, the relevant coincidence set Ω contains only the null vector (Fig. 1j), and, as a result, the 2D linear space is covered densely (Fig. 1k), the average potential energy is flat (eqn (9) and Fig. 1m), and the static friction vanishes equally in all directions.
(orange-edged blue circles in Fig. 1i). However this real-space intersection is irrelevant to the lubricity of this contact. Instead, the relevant coincidence set Ω contains only the null vector (Fig. 1j), and, as a result, the 2D linear space is covered densely (Fig. 1k), the average potential energy is flat (eqn (9) and Fig. 1m), and the static friction vanishes equally in all directions.
V. Finite size
The formulas (7)–(9) for the interlocking potential U(rc) are valid for an infinite 2D crystalline overlayer interacting with an infinite periodic surface. In practice, however, no contact is infinitely extended. In real-life conditions the overlayer region in contact with the substrate forms a crystalline cluster of finite size N. Its finite size and shape do affect the details of the interlocking potential energy U(rc): in the following, we derive analytical expressions for finite-size contacts and their implications on the frictional behaviour.As in eqn (2), we express the position of each particle as a function of the cluster center of mass displacement rc and lattice vectors: rj = rc + Rj, where precisely the list of the N translations 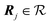 defines the cluster shape and size.
defines the cluster shape and size.
Starting from eqn (2), we write the explicit expression for the interlocking potential energy U(rc) in terms of the substrate-potential Fourier decomposition.
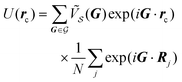 | (10) |
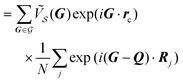 | (11) |
 is an arbitrary vector of the reciprocal lattice of the adsorbate.
is an arbitrary vector of the reciprocal lattice of the adsorbate.
In going from eqn (10) to eqn (11) we use the property of the reciprocal vectors Q that  . We take advantage of the freedom in the choice of
. We take advantage of the freedom in the choice of  to pick Q =
to pick Q = ![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) such that |G −
such that |G − ![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) | is minimum, and we define
| is minimum, and we define
δΩ(G) = G − ![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) | (12) |
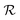 . Note how this notation relates with the infinite-size classification of section IV: if G is a common vector between the substrate and adsorbate reciprocal lattices, i.e.G ∈ Ω, then δΩ(G) = 0 for that G.
. Note how this notation relates with the infinite-size classification of section IV: if G is a common vector between the substrate and adsorbate reciprocal lattices, i.e.G ∈ Ω, then δΩ(G) = 0 for that G.
The interlocking potential energy in eqn (11) now reads
 | (13) |
 | (14) |
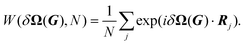 | (15) |
In the following, we omit the explicit dependence of δΩ(G) on the substrate lattice vector G, δΩ = δΩ(G).
Eqn (14) expresses the interlocking potential energy U(rc) as a Fourier summation over all the components  of the substrate potential.16 The novelty of finite size compared to eqn (3) is that the summation of eqn (14) is not limited to CLVs and it involves the extra size-dependent weight factor defined in eqn (15).
of the substrate potential.16 The novelty of finite size compared to eqn (3) is that the summation of eqn (14) is not limited to CLVs and it involves the extra size-dependent weight factor defined in eqn (15).
In the N → ∞ limit, this weight W(δΩ, N) vanishes for those Fourier components with δΩ ≠ 0. Therefore, only the δΩ = 0 components determine the overall corrugation of the infinite-size crystal, in agreement with the classification discussed in the previous section.
At finite size, W(δΩ, N) needs not vanish for any G, regardless of whether δΩ vanishes or not. As a consequence, a priori any Fourier component  of the substrate potential can contribute to the interlocking potential energy U(rc).
of the substrate potential can contribute to the interlocking potential energy U(rc).
In general, the weight W(δΩ, N) is a nontrivial function of δΩ, which depends on the cluster shape. However, for special shapes, analytic expressions for W(δΩ, N) can be derived.
A. Special shapes
As a concrete example, consider a parallelogram-shaped cluster of N particles whose particle positions can be expressed as Rj = j1R1 + j2R2, with integer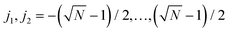 , where
, where 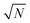 is assumed to be an odd integer, and
is assumed to be an odd integer, and  . By construction, the cluster center of mass coincides with the particle indexed by j1 = j2 = 0. For this cluster shape, the weight function of eqn (15) can be written as
. By construction, the cluster center of mass coincides with the particle indexed by j1 = j2 = 0. For this cluster shape, the weight function of eqn (15) can be written as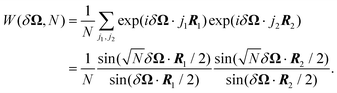 | (16) |
Each factor  in eqn (16) relates to the Fraunhofer diffraction from a narrow-slit grating.49 As a function of x = δΩ·Ri, each oscillating factor f(x) peaks at x = 2nπ (for
in eqn (16) relates to the Fraunhofer diffraction from a narrow-slit grating.49 As a function of x = δΩ·Ri, each oscillating factor f(x) peaks at x = 2nπ (for  ), where it reaches its extreme values
), where it reaches its extreme values 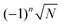 , i.e.
, i.e.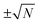 . As a special consequence, whenever δΩ vanishes, both fractions becomes equal to
. As a special consequence, whenever δΩ vanishes, both fractions becomes equal to 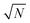 , leading to W(δΩ, N) = 1: the weight of the corresponding Fourier components in eqn (14) is independent of size.
, leading to W(δΩ, N) = 1: the weight of the corresponding Fourier components in eqn (14) is independent of size.
The peak width of f(x) is inversely proportional to  , and away from the peaks, say in the intervals 2π(n + N−1/2) < x < 2π(n + 1 − N−1/2) f(x), oscillates around 0, with values of order 1. As a result, for large cluster size, weights associated to both nonzero δΩ·R1 and δΩ·R2 decay as N−1. Instead, when just one of these factors vanishes, we expect a nontrivial leading large-size behavior of the associated weight factor, typically as N−1/2. These observations account for the leading importance of the Fourier component in the interlocking potential U(rc) as detailed in the following subsections.
, and away from the peaks, say in the intervals 2π(n + N−1/2) < x < 2π(n + 1 − N−1/2) f(x), oscillates around 0, with values of order 1. As a result, for large cluster size, weights associated to both nonzero δΩ·R1 and δΩ·R2 decay as N−1. Instead, when just one of these factors vanishes, we expect a nontrivial leading large-size behavior of the associated weight factor, typically as N−1/2. These observations account for the leading importance of the Fourier component in the interlocking potential U(rc) as detailed in the following subsections.
B. Coincidence lattice vectors (CLVs)
When there are CLVs in the dual space, an infinite subset of vectors (those belonging to Ω) is associated to vanishing δΩ. For all these terms the weights W(δΩ, N) equal unity, and as a result, the corresponding Fourier components in eqn (14) contribute as much as for the infinite-size layer, independently of size. All other Fourier components, characterized by nonzero δΩ, can contribute with size-dependent weights. This distinction between size-independent and size-dependent Fourier weights applies to systems with discrete-
vectors (those belonging to Ω) is associated to vanishing δΩ. For all these terms the weights W(δΩ, N) equal unity, and as a result, the corresponding Fourier components in eqn (14) contribute as much as for the infinite-size layer, independently of size. All other Fourier components, characterized by nonzero δΩ, can contribute with size-dependent weights. This distinction between size-independent and size-dependent Fourier weights applies to systems with discrete- (type-A) and line coverage (type-B) geometries, as discussed for the infinite size-limit in section IV.
(type-A) and line coverage (type-B) geometries, as discussed for the infinite size-limit in section IV.
Let us focus first on type-A contacts, where two linearly independent CLVs Ω1, Ω2, with δΩ = 0, exist. Consider also two non-CLV vectors G1, G2, with δΩ ≠ 0, as exemplified in Fig. 2a. It is possible to obtain instructive results for the special parallelogram-shaped clusters introduced in previous section. For Ω1,2 and G1,2, Fig. 2b reports the Fourier amplitudes  , modulated by the weights W, computed according to eqn (16). The weight factor W is identically unity at any size for the CLVs (orange dashed line), while it oscillates and decreases as a function of size for non CLVs (blue solid line).
, modulated by the weights W, computed according to eqn (16). The weight factor W is identically unity at any size for the CLVs (orange dashed line), while it oscillates and decreases as a function of size for non CLVs (blue solid line).
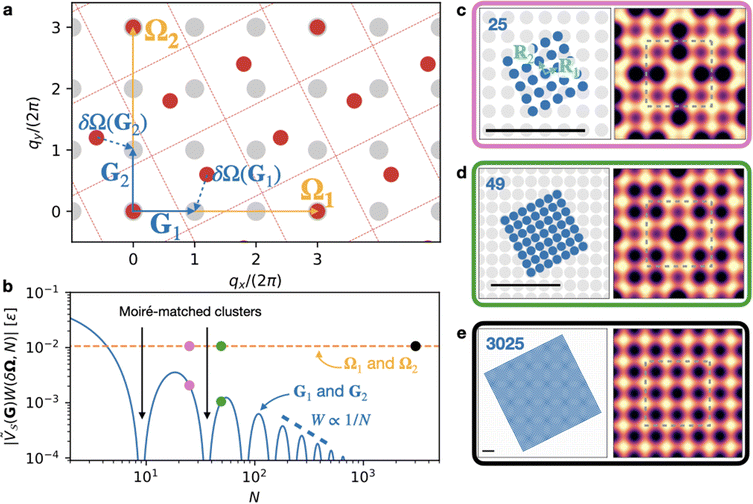 | ||
Fig. 2 Finite size effects in a contact with discrete coverage. Finite-size analysis for the discrete-coverage (type A) condition in Fig. 1a–d, i.e. a square-lattice adsorbate with 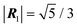 , and orientation θo = tan−1(1/2). (a) Reciprocal lattices of the adsorbate (Q points, red dots) and of the substrate (G points, gray dots); orange arrows highlight two CLVs Ωi = 1,2; blue arrows indicate the substrate primitive vectors Gi. Red dashed squares show the first Brillouin zone of the , and orientation θo = tan−1(1/2). (a) Reciprocal lattices of the adsorbate (Q points, red dots) and of the substrate (G points, gray dots); orange arrows highlight two CLVs Ωi = 1,2; blue arrows indicate the substrate primitive vectors Gi. Red dashed squares show the first Brillouin zone of the 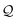 lattice at each lattice point Q. The dashed blue arrows indicate δΩ(Gi), defined in eqn (12), i.e. the Q-translated vectors Gi = 1,2. Note that δΩ(Ωi) = 0. (b) The size dependence of the Fourier components lattice at each lattice point Q. The dashed blue arrows indicate δΩ(Gi), defined in eqn (12), i.e. the Q-translated vectors Gi = 1,2. Note that δΩ(Ωi) = 0. (b) The size dependence of the Fourier components  (eqn (14)) associated with the CLVs Ωi (dashed orange line) and for the primitive vectors Gi (solid blue line). The pink, green and black circles mark the cluster sizes N = 25, 49, 3025 of panels (c), (d), and (e), respectively. (c–e) Interlocking potential energy as a function of the cluster center-of-mass position rc across the square [−1, 1] × [−1, 1] for the displayed clusters. Solid black scalebars in panels (c–e) stand for five lattice spacings. The color scale is the same as in Fig. 1. The gray dashed line highlights the Wigner–Seitz cell of the (eqn (14)) associated with the CLVs Ωi (dashed orange line) and for the primitive vectors Gi (solid blue line). The pink, green and black circles mark the cluster sizes N = 25, 49, 3025 of panels (c), (d), and (e), respectively. (c–e) Interlocking potential energy as a function of the cluster center-of-mass position rc across the square [−1, 1] × [−1, 1] for the displayed clusters. Solid black scalebars in panels (c–e) stand for five lattice spacings. The color scale is the same as in Fig. 1. The gray dashed line highlights the Wigner–Seitz cell of the  lattice, namely the area shown in Fig. 1d. lattice, namely the area shown in Fig. 1d. | ||
To elucidate the origin of the G1,2-weight oscillations it is convenient to focus on a subset of cluster sizes. Consider the clusters constructed as  repetitions of a parallelogram supercell constructed on a pair of independent real-space CLVs R1CLV and R2CLV, namely vectors with all integer components (e.g. the blue orange-edge dots in Fig. 1a). The existence of these real-space CLVs is demonstrated in Methods section IX. The supercell defined by these (usually non-primitive) vectors contains K vectors and thus the number of particles is N = KN′. By construction, these special clusters consist of an integer number of identical moiré tiles of K particles in which the relative position of adsorbate and substrate is the same in all repeated units, since R1CLV and R2CLV belong to the substrate
repetitions of a parallelogram supercell constructed on a pair of independent real-space CLVs R1CLV and R2CLV, namely vectors with all integer components (e.g. the blue orange-edge dots in Fig. 1a). The existence of these real-space CLVs is demonstrated in Methods section IX. The supercell defined by these (usually non-primitive) vectors contains K vectors and thus the number of particles is N = KN′. By construction, these special clusters consist of an integer number of identical moiré tiles of K particles in which the relative position of adsorbate and substrate is the same in all repeated units, since R1CLV and R2CLV belong to the substrate  lattice too. As a consequence, the average corrugation U(rc) for this class of “moiré-matched clusters” is independent of the number N′ of moiré patterns in the cluster and coincides with that of the infinite layer. Thus, the only surviving components in eqn (16) are the CLV with δΩ = 0 that contribute to the corrugation at infinite size: the weight W of any non-CLV vanishes exactly for these “moiré-matched clusters”, as indicated by black arrows in Fig. 2b. The vanishing of W is equivalent to the suppression of the artefact Bragg peaks arising when a non-primitive (e.g., conventional) unit cell is adopted, a well-known feature of the structure factor in crystallography,50 as elaborated in Methods section XI. This effect was previously noted in realistic crystalline interfaces:51,52 these “moiré-matched clusters” exhibit no size effects, as long as they remain perfectly rigid.
lattice too. As a consequence, the average corrugation U(rc) for this class of “moiré-matched clusters” is independent of the number N′ of moiré patterns in the cluster and coincides with that of the infinite layer. Thus, the only surviving components in eqn (16) are the CLV with δΩ = 0 that contribute to the corrugation at infinite size: the weight W of any non-CLV vanishes exactly for these “moiré-matched clusters”, as indicated by black arrows in Fig. 2b. The vanishing of W is equivalent to the suppression of the artefact Bragg peaks arising when a non-primitive (e.g., conventional) unit cell is adopted, a well-known feature of the structure factor in crystallography,50 as elaborated in Methods section XI. This effect was previously noted in realistic crystalline interfaces:51,52 these “moiré-matched clusters” exhibit no size effects, as long as they remain perfectly rigid.
For all other parallelepiped clusters of sizes in between these “moiré-matched clusters”, this cancellation does not occur, leading to W(δΩ, N) ≠ 0 for non CLVs: the weight function W oscillates as a function of size. |W| reaches a sequence of maxima, whose peak height decays ∝ N−1 (blue curve in Fig. 2b). Hence the incomplete moiré tiles at the edges result in a size-dependent corrugation, as illustrated in Fig. 2c–e.
C. Development of directional structural lubricity
Let us now focus on type-B systems, where Ω is a 1D lattice. The novelty is that a more restricted class of δΩ's vanishes, and, as a result, the vast majority of the G vectors in the summation of eqn (14) lead to size-dependent Fourier contributions.In the (not guaranteed) circumstance that, beside reciprocal CLVs, we also identify a real-space CLV R1CLV, we can adopt it as one of the primitive vectors for a supercell. The second supercell primitive vector R2 can be chosen freely among the lattice vectors linearly independent of R1CLV, e.g.R2 in Fig. 1e. Compared to the discrete-  condition, here R2 is certainly not a CLV. As in the previous section, such a supercell contains K vectors Rk, yielding a cluster of size N = N′K. See Fig. 3a, c and e for examples of clusters built with this protocol.
condition, here R2 is certainly not a CLV. As in the previous section, such a supercell contains K vectors Rk, yielding a cluster of size N = N′K. See Fig. 3a, c and e for examples of clusters built with this protocol.
 | ||
Fig. 3 The development of directional structural lubricity with increasing contact size. (a), (c) and (e) Adsorbate clusters of different sizes with the same contact incommensurability (type B) as of Fig. 1(e), namely a triangular-lattice adsorbate with spacing 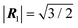 and orientation θo = 15° sliding across a square-lattice substrate with unit lattice spacing. These special-shaped clusters here are constructed by repeating a K = 4-particle unit (shaded area in panel a) based on a real-space CLV R1CLV (red arrow in panel a) and a primitive vector R2 (light-blue arrow in panel a). The corners of the repeated cell are highlighted in blue. The black bar in each panel spans 10 substrate lattice spacings. The insets report the corresponding coverage and orientation θo = 15° sliding across a square-lattice substrate with unit lattice spacing. These special-shaped clusters here are constructed by repeating a K = 4-particle unit (shaded area in panel a) based on a real-space CLV R1CLV (red arrow in panel a) and a primitive vector R2 (light-blue arrow in panel a). The corners of the repeated cell are highlighted in blue. The black bar in each panel spans 10 substrate lattice spacings. The insets report the corresponding coverage  for that given size. (b), (d) and (f) The interlocking potential energy of the clusters in (a), (c) and (e) respectively as a function of rc ∈ [−1, 1] × [−1, 1]. The color code is the same as in Fig. 1. The gray dashed line highlights the Wigner–Seitz cell. (g) The cluster-size dependence of static friction for the directionally superlubric interface. Filled (empty) symbols refer to the unpinning force parallel (perpendicular) to the low-energy corridors, or perpendicular/parallel to the CLV Ω, respectively. These directions are sketched in panel (f). The investigated shapes of the clusters (circles, hexagons, parallelograms) are reflected in the data-point shapes and colors (red, blue, and orange/green). Parallelograms are generated by replicating two kinds of supercells: either based on a real-space CLV (orange) or not (green); the adopted supercell lattice vectors are respectively 4R1 + 2R2 and 2R2 (orange), or 2R1 and 2R1 + 2R2 (green), where R1R2 are identified in Fig. 1e. The dotted, solid, and dashed lines report the Fs ∝ N0, Fs ∝ N−1/2, and Fs ∝ N−1 scalings as guides to the eye. for that given size. (b), (d) and (f) The interlocking potential energy of the clusters in (a), (c) and (e) respectively as a function of rc ∈ [−1, 1] × [−1, 1]. The color code is the same as in Fig. 1. The gray dashed line highlights the Wigner–Seitz cell. (g) The cluster-size dependence of static friction for the directionally superlubric interface. Filled (empty) symbols refer to the unpinning force parallel (perpendicular) to the low-energy corridors, or perpendicular/parallel to the CLV Ω, respectively. These directions are sketched in panel (f). The investigated shapes of the clusters (circles, hexagons, parallelograms) are reflected in the data-point shapes and colors (red, blue, and orange/green). Parallelograms are generated by replicating two kinds of supercells: either based on a real-space CLV (orange) or not (green); the adopted supercell lattice vectors are respectively 4R1 + 2R2 and 2R2 (orange), or 2R1 and 2R1 + 2R2 (green), where R1R2 are identified in Fig. 1e. The dotted, solid, and dashed lines report the Fs ∝ N0, Fs ∝ N−1/2, and Fs ∝ N−1 scalings as guides to the eye. | ||
For this class of clusters, the first factor in eqn (16) has δΩ·R1CLV = 0, and thus  , because R1CLV belongs to both the adsorbate and substrate lattice, i.e.
, because R1CLV belongs to both the adsorbate and substrate lattice, i.e. . As a result, the second factor leads to a scaling N−1/2 for any δΩ ≠ 0: the weight is constant for the CLV Ω while the envelope of non-CLV weights decays as N−1/2.
. As a result, the second factor leads to a scaling N−1/2 for any δΩ ≠ 0: the weight is constant for the CLV Ω while the envelope of non-CLV weights decays as N−1/2.
The corrugation of this system can be expressed as the sum of the size-independent term, namely the Ω-sum of eqn (8) (resulting in the corrugation of Fig. 1h), plus the remaining contributions, which decay as a function of size:
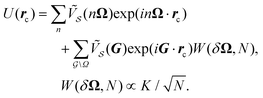 | (17) |
An example of size evolution of the energy landscape resulting from eqn (17) is reported in Fig. 3b, d and f. For large size, U(rc) approaches the straight and flat energy corridors of Fig. 1h.
The Fourier amplitude of each term in eqn (17) is the product of the weight W(δΩ(G), N) times the substrate Fourier component  evaluated at the same vector G. Assuming, as is usually the case, that the surface corrugation potential
evaluated at the same vector G. Assuming, as is usually the case, that the surface corrugation potential 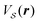 is a smooth function, then its Fourier amplitudes
is a smooth function, then its Fourier amplitudes  tend to decay with |G|. As a consequence, long G vectors even if leading to nearly perfect matching (i.e. small δΩ(G)), usually yield quite small, practically negligible contributions to the energy landscape. As a result, the size-dependent term in eqn (17) is usually dominated by a few small-|G| Fourier components.
tend to decay with |G|. As a consequence, long G vectors even if leading to nearly perfect matching (i.e. small δΩ(G)), usually yield quite small, practically negligible contributions to the energy landscape. As a result, the size-dependent term in eqn (17) is usually dominated by a few small-|G| Fourier components.
This size-dependent energy corrugation has important implication for friction. In an overdamped context where inertia is negligible, the minimum per-particle force Fs needed to sustain the motion of the adsorbate crystal in a given direction  , namely the static friction force Fs in that direction, can be estimated by
, namely the static friction force Fs in that direction, can be estimated by  , where
, where  is the straight line connecting two successive energy minima in the
is the straight line connecting two successive energy minima in the  direction. In the present type-B condition, if
direction. In the present type-B condition, if  is aligned along the energy corridors, then only the δΩ(G) ≠ 0 components contribute, leading to Fs ∝ N−1/2, whereas if
is aligned along the energy corridors, then only the δΩ(G) ≠ 0 components contribute, leading to Fs ∝ N−1/2, whereas if  has a nonzero component perpendicular to the corridors, then Fs contains a leading component ∝ N0 from the G ∈ Ω Fourier components.
has a nonzero component perpendicular to the corridors, then Fs contains a leading component ∝ N0 from the G ∈ Ω Fourier components.
We have verified numerically that the same power laws-scaling of Fs holds not just for special-shaped parallelogram clusters, but also for different shapes, as reported in Fig. 3g: similar decays of Fs parallel to the energy corridor are found for each shape. However, it is apparent that, for a given size, different cluster shapes can change the value of this parallel friction component by an order of magnitude. In contrast, the size-independent perpendicular friction component is nearly independent of the cluster shape, too.
These direction-dependent scaling laws justify the name directional structural lubricity for the type-B interface condition: along the energy corridor the total friction NFs scales sublinearly with the cluster size, as in standard structural lubricity, while parallel to these corridors the total friction NFs grows linearly with size, like for a ordinary structurally-matched interface.
D. Close-matching vectors
We come now to extend the exact classification of section IV to interfaces which – strictly speaking – belong to type C, but come with a set of relatively short G vectors characterized by a very small mismatch |δΩ(G)|, see eqn (12): close-matching vectors (CMVs). This approximate classification holds for finite, and not-too-large clusters.When the two crystals are incommensurate (type-C), the “standard” properties of structural lubricity should apply. However we argue here that in the presence of CMVs the categories and size scaling introduced above survive, up to a maximum cluster size related inversely to |δΩ(G)|. In this section we focus on directional locking and directional structural lubricity, showing that, in specific size ranges, they are to be expected for type-C interfaces with CMVs. This analysis is especially relevant for heterocontacts, where perfect matches (whether of type A or B) are unlikely.
We recall that, for each substrate Fourier component identified by G, the N-dependence of both factors f(x) in eqn (16) implies a critical size below which W(δΩ(G), N) ≃ 1 because both f(x) factors in W are of order N1/2. For a special-shape cluster (see section V.A) based on the vectors R1 and R2, the critical size associated with a substrate vector G is
 | (18) |
| W(δΩ(G), N) ≃ 1. | (19) |
Let us assume that there exists a single independent CMV G′ ≃ Q′ such that, at its critical size N+ = Nc(G′), G′ gives the dominant contribution to the corrugation energy U(rc) of the contact in eqn (14). The G′ Fourier component becomes the dominating one only beyond some minimum size N−, defined as the largest N < N+ such that  which satisfies
which satisfies  .
.
If the contact conditions are such that N− is significantly smaller than N+ then this contact exhibits approximate directional superlubricity for all sizes in the range N− < N < N+. In this size range, the direction perpendicular to G′ exhibits a very small corrugation associated to minor Fourier components, negligible compared to the  term, which is responsible for a sizeable corrugation in the direction parallel to G′. As the size N exceeds N+, also this sizeable corrugation perpendicular to the superlubric “corridor” begins to fade away due to the decay of W(δΩ(G′), N), until “standard” direction-independent structural lubricity of an extended type-C contact is recovered.
term, which is responsible for a sizeable corrugation in the direction parallel to G′. As the size N exceeds N+, also this sizeable corrugation perpendicular to the superlubric “corridor” begins to fade away due to the decay of W(δΩ(G′), N), until “standard” direction-independent structural lubricity of an extended type-C contact is recovered.
We report an experimental test of these predictions, executed letting a triangularly-packed colloidal cluster slide over a surface patterned with a square lattice, as shown in Fig. 4a and b. This setup consists of the fully tunable microscale system mimicking an atomistic interface reported previously in ref. 16,17 and 53, see Methods XII for details. The geometry of the system generates a CMV G′ ≈ Q1 − 2Q2 which leads to a nearly-type-B contact across a broad range of sizes, with clear energy corridors shown in Fig. 4c. We can estimate the critical sizes of this system to be N− ≃ 15 and N+ ≃ 1620, adopting a Gaussian model for the corrugation profile of each substrate well, as in eqn (1), with parameters taken from ref. 53. Fig. 4d reports the measured static-friction forces in the direction of the energy corridors (filled purple circles in Fig. 4d), and perpendicular to it (empty gray circles in Fig. 4d), as a function of the cluster size N. The results are in good agreement with the predicted scalings. Indeed the static friction perpendicular to the energy corridor is approximately constant from 2N− (dash-dotted line in Fig. 4d) up to the largest experimental size, with a fitted power-law exponent γ = 0.01 ± 0.02 (dotted gray purple line in Fig. 4d). On the contrary, the static friction along the energy corridors, exhibits a power law of exponent γ in between −1 and −1/2 (dashed purple line in Fig. 4d), in remarkable agreement with the theory given the random shapes of experimental clusters.
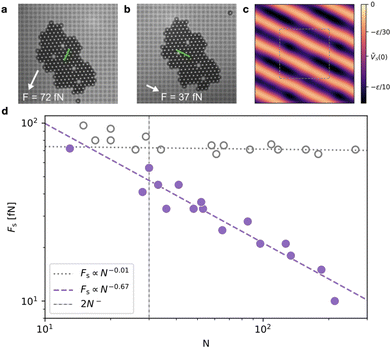 | ||
| Fig. 4 Experimental realisation of directional structural lubricity. (a and b) A triangularly packed colloidal cluster of size N = 185 with spacing a = 4.45 μm sliding across a square-lattice surface with spacing b = 5.0 μm. The green lines in both panels indicate the cluster's center of mass trajectory (see also movie 1†) over a period of 85 seconds under the indicated applied forces perpendicular (a) and parallel (b) to the energy corridor. If the same force strength of 37 fN was applied in the direction of panel (a), the cluster would not move at all: a strong friction anisotropy is revealed. (c) The calculated potential energy landscape of the cluster in panels (a and b) at orientation θo = 3.4°, revealing corridors along the −25.6° direction. (d) The experimentally measured static friction force for many different-sized experimental clusters perpendicular (empty gray circles) and parallel (filled purple circles) to the energy corridor. Lines are power-law fits Fs = F0Nγ to the corresponding data for clusters of N > 2N− ≃ 30 particles (dot-dash black line). The fitted parameters are F0 = 467.4 fN, γ = −0.67 ± 0.07 and F0 = 76.3 fN, γ = −0.01 ± 0.02 for the parallel and perpendicular directions, respectively. A detailed description of the experiment is provided in Methods section XII. | ||
VI. Stability against rotation
So far, the relative orientation of the two crystals, has been implicitly fixed by the angle θo between the first primitive vectors of the two lattices, R1 and S1. Clearly, upon rotation the same system may realize a type-A contact (2D array of CLVs), or a type-B contact (1D CLV array), or a type-C contact (fully incommensurate, no CLVs). In practice it is unlikely that one can artificially keep the contact at an arbitrarily fixed mutual angle: in most concrete setups the contact will eventually relax to an energetically stable condition. It is therefore essential to examine the angular energetics of such contacts and their stability upon rotation.For example, it is well known that structural lubricity in homocontacts arises from the misalignment of the two lattices. However, this misalignment comes with an energy cost, that makes the superlubric contact unstable.48,54,55 In homocontacts therefore energetics acts to stabilize the type-A geometry.
We argue that for heterocontacts the same stabilization occurs. Depending on the geometric details, this stabilization may lead to either a type-A or a type-B contact. Under such conditions, the important outcome is that directional locking and directional structural lubricity are energetically stable. If the crystals mutually rotate from a fully incommensurate kind-C geometry where the interlocking energy is given by eqn (9), to such an angle that CLVs in the reciprocal space arise, additional terms appear in the interlocking potential of eqn (3), leading to potentials of the form (7) or (8). Consequently, for these orientations, these Fourier components in the interlocking potential provide an energy lowering at the equilibrium position, not available in type-C configurations. This means that when a contact allows for type-A or type-B conditions, the corresponding orientations are indeed the most stable ones.
It is straightforward to check this energetics numerically, not only for the infinite contacts of eqn (3), but also for finite-N cluster of eqn (14). As an illustration, we select a system quite close to the type-B one of Fig. 1e–h (triangular-lattice adsorbate over a square substrate), but with a small mismatch δ = 0.1% introduced in the adsorbate lattice spacing 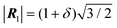 . Due to the small δ, at relative orientation θo = 15° the CLV Ω of Fig. 1f turns into a CMV G′ = 2π(2, 2), with a corresponding critical size
. Due to the small δ, at relative orientation θo = 15° the CLV Ω of Fig. 1f turns into a CMV G′ = 2π(2, 2), with a corresponding critical size 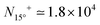 . To study the relative stability of the consequent nearly-type-B contact, this orientation has to be compared with all others. Fig. 5a reports the potential energy U(rc = 0) of eqn (2) as a function of the misalignment angle θo. The energy profiles of Fig. 5a indicate an evident local energy minimum at θo = 15° for N = 91, which becomes the global minimum for
. To study the relative stability of the consequent nearly-type-B contact, this orientation has to be compared with all others. Fig. 5a reports the potential energy U(rc = 0) of eqn (2) as a function of the misalignment angle θo. The energy profiles of Fig. 5a indicate an evident local energy minimum at θo = 15° for N = 91, which becomes the global minimum for  .
.
 | ||
Fig. 5 Stability of structural directional lubricity against rotation at finite sizes. (a) The interlocking potential eqn (2) evaluated at fixed rc = 0 for varying misalignment angle θo for three clusters with size N = 91, N = 1141, and N = 119![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401, respectively. The contact consists of a triangular-lattice adsorbate spaced by 401, respectively. The contact consists of a triangular-lattice adsorbate spaced by  , with δ = 0.1% on a unit square-lattice substrate. (b–g) Particle-resolved interlocking energy (blue-to-white scale) for the three clusters at two different θo, at fixed rc = 0. (h) The minimum value of U(rc) (minimized by allowing all possible center-mass translations rc) for fixed alignments θo = 0° (blue dashed) and θo = 15° (orange solid), as a function of size N. The blue dash-dotted line marks , with δ = 0.1% on a unit square-lattice substrate. (b–g) Particle-resolved interlocking energy (blue-to-white scale) for the three clusters at two different θo, at fixed rc = 0. (h) The minimum value of U(rc) (minimized by allowing all possible center-mass translations rc) for fixed alignments θo = 0° (blue dashed) and θo = 15° (orange solid), as a function of size N. The blue dash-dotted line marks  and the orange dotted line marks and the orange dotted line marks  . . | ||
For sizes N ≲ 100 the global minimum is found for a different orientation, θo = 0°. This second minimum corresponds to a different (shorter, but worse matched) CMV G′′ = 2π(0, 1), with critical size  . The moiré patterns associated with these two CMVs at θo = 0° and θo = 15° are shown for different sizes in Fig. 5b–g, respectively. To illustrate the relative stability between these two orientation, Fig. 5h reports the equilibrium interlocking energy as a function of size. This alternative θo = 0° orientation is also a nearly-type-B contact. The direct comparison between the CMV at the two orientations of
. The moiré patterns associated with these two CMVs at θo = 0° and θo = 15° are shown for different sizes in Fig. 5b–g, respectively. To illustrate the relative stability between these two orientation, Fig. 5h reports the equilibrium interlocking energy as a function of size. This alternative θo = 0° orientation is also a nearly-type-B contact. The direct comparison between the CMV at the two orientations of  and
and  as a function of size gives a crossover point at N ≃ 100, which coincides to the crossing point in Fig. 5h, above which θo = 15° becomes the equilibrium orientation.
as a function of size gives a crossover point at N ≃ 100, which coincides to the crossing point in Fig. 5h, above which θo = 15° becomes the equilibrium orientation.
At larger sizes,  , no CMVs retains a significantly large Fourier component in eqn (3) and, as expected for a type-C contact, the energy profile as a function of orientation becomes nearly flat, as in the N = 119
, no CMVs retains a significantly large Fourier component in eqn (3) and, as expected for a type-C contact, the energy profile as a function of orientation becomes nearly flat, as in the N = 119![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 401 example of Fig. 5a.
401 example of Fig. 5a.
These observations indicate that directional locking and directional structural lubricity are not just a hypothetical eventuality. On the contrary, they prove that with the condition that at some orientation θo the contact geometry generates a CLV, or even just a CMV, sufficiently short to be associated to a sizeable corrugation Fourier component, then precisely this Fourier component is responsible for the energy stabilization of this orientation, which the contact will reach spontaneously if allowed to realign.
Indeed, in the colloidal experimental realizations reported here in section IV.D and in ref. 16 and 17 where the clusters are free to reorient, directional locking phenomena and reorientation emerge spontaneously as the result of self-alignment and not of external manipulation.
VII. Directional structural lubricity in real-life contacts
By taking advantage of CMVs, we can identify interfaces of real materials that should exhibit approximate directional structural lubricity across significant size ranges.Consider the system depicted in Fig. 6a: for the adsorbate we take a flake of hexagonal boron nitride (hBN), a layered material with hexagonal symmetry and spacing a = 0.2512 nm;56 for the substrate we adopt the (001) surface of VO.57 This surface has square symmetry and spacing b = 0.310 nm.56
When the hBN flake is rotated at θo = 15° as in Fig. 6a, the interface exhibits a CMV G′ = 2π/b(1, 1) (orange arrow in Fig. 6b), that fosters an energetically stable configuration. The two next most significant Fourier components are associated to G′′ = 2π/b(−1, 1) (perpendicular to G′) and G′′′ = 2π/b(0, 1).
To illustrate the effect at hand, here we adopt a radically simplified energy landscape, obtained by summing the attraction of each N and B atom in the adsorbate with every substrate atom (regardless of it begin V or O), represented by a negative Gaussian function V(r), with a straightforward extension of eqn (1). The resulting interlocking potential depends on two parameters only: the width σ = 0.1b of the Gaussian function, and its peak attraction ε, which we keep undefined, and adopt as the energy scale of this example, thus expressing all energies in Fig. 6 in terms of ε. Of course, a realistic force field would imply quantitatively different Fourier components 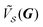 , but we do not expect the results to change radically, because the size-dependent weights W(δΩ(G′), N) would be identical. Note that N indicates the number of lattice cells, consistently with the rest of the paper. In the hBN flake the total number of atoms is 2N.
, but we do not expect the results to change radically, because the size-dependent weights W(δΩ(G′), N) would be identical. Note that N indicates the number of lattice cells, consistently with the rest of the paper. In the hBN flake the total number of atoms is 2N.
Fig. 6c reports the size dependence of the Fourier amplitude  (solid orange line), plus the analogous quantity for G′′ (dotted green) and G′′′ (dahsed blue). The G′ component dominates across the size range from N− ≃ 1 up to a critical size N+ = 779. As a result, at small size, multiple substrate G vectors contribute significantly to the interlocking potential, resulting in a relatively irregular landscape dominated by pronounced energy corridors modulated by a secondary weaker corrugation, as exemplified in Fig. 6d for N = 9. This secondary corrugation associated mainly to G′′ and G′′′ decays rapidly with increasing size, see Fig. 6c. Across the size range N− ≪ N < N+ spanning over two orders of magnitude in area, the ±G′ Fourier components remain effectively the dominant contribution to the interlocking potential, with the result that this interface exhibits approximate directional structural lubricity as exemplified in Fig. 6e for N = 729. For sizes larger than N+, the energy landscape flattens out and the infinite-size limit of ordinary (kind-C) structural lubricity is approached, as exemplified in Fig. 6f for N = 14
(solid orange line), plus the analogous quantity for G′′ (dotted green) and G′′′ (dahsed blue). The G′ component dominates across the size range from N− ≃ 1 up to a critical size N+ = 779. As a result, at small size, multiple substrate G vectors contribute significantly to the interlocking potential, resulting in a relatively irregular landscape dominated by pronounced energy corridors modulated by a secondary weaker corrugation, as exemplified in Fig. 6d for N = 9. This secondary corrugation associated mainly to G′′ and G′′′ decays rapidly with increasing size, see Fig. 6c. Across the size range N− ≪ N < N+ spanning over two orders of magnitude in area, the ±G′ Fourier components remain effectively the dominant contribution to the interlocking potential, with the result that this interface exhibits approximate directional structural lubricity as exemplified in Fig. 6e for N = 729. For sizes larger than N+, the energy landscape flattens out and the infinite-size limit of ordinary (kind-C) structural lubricity is approached, as exemplified in Fig. 6f for N = 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 641.
641.
The hBN/VO(001) interface is just an example where we predict directional structural lubricity to arise. Another interface where it could be observed is WSe2 on CuF(001), as discussed in ESI section 1,† and others can be discovered by going through existing materials databases.56,58–60
In addition, the geometric conditions for directional structural lubricity can be achieved by means of strain engineering, a method that has been recently used to tailor frictional properties.61–63 For example, the well-studied structurally lubric hBN/graphite contact can be modified by a uni-axial strain applied to the graphite substrate in the armchair direction, as shown in Fig. 7a. This deformation, at εarmchair ≃ 1.8%, i.e. within experimental feasibility,64 would generate the geometrical conditions for a type-B directional structural lubricity along the zig-zag direction as discussed in Methods section XIII. On such a strained graphene surface, we evaluate the static-friction unpinning threshold for aligned hBN flakes of different sizes, based on a realistic force field.65–67
 | ||
Fig. 7 Directional structural lubricity via strain engineering. (a) An aligned hBN flake on a graphene substrate strained by εarmchair ≃ 1.8% in the armchair =  direction. The aspect x direction. The aspect x![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) y ratio of the hBN flake is approximately 1 y ratio of the hBN flake is approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The wavelength of the linear moiré pattern is highlighted with a black arrow. (b–e) Corrugation potential U(rc) for hBN flakes of size (b) 6.5 nm × 12.7 nm (N = 170), (c) 13 nm × 25.5 nm (N = 2760), (d) 39 nm × 76.5 nm (N = 11 2. The wavelength of the linear moiré pattern is highlighted with a black arrow. (b–e) Corrugation potential U(rc) for hBN flakes of size (b) 6.5 nm × 12.7 nm (N = 170), (c) 13 nm × 25.5 nm (N = 2760), (d) 39 nm × 76.5 nm (N = 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 120), (e) PBC in the region [0, 0.45 nm] × [0, 0.25 nm]. Like in Fig. 6, N is the number of lattice cells, so that the flake consists of 2N atoms in total. (f) Static friction in the armchair lattice-matched direction (red empty symbols) and zig-zag (blue filled symbols), respectively parallel and perpendicular to the CLV Ω. The dashed (dotted) line indicates the scaling in the direction parallel (perpendicular) to the energy corridors, as indicated in panel (e). The vertical dash-dotted black line marks the critical size Nc of the largest non-matching component G′. 120), (e) PBC in the region [0, 0.45 nm] × [0, 0.25 nm]. Like in Fig. 6, N is the number of lattice cells, so that the flake consists of 2N atoms in total. (f) Static friction in the armchair lattice-matched direction (red empty symbols) and zig-zag (blue filled symbols), respectively parallel and perpendicular to the CLV Ω. The dashed (dotted) line indicates the scaling in the direction parallel (perpendicular) to the energy corridors, as indicated in panel (e). The vertical dash-dotted black line marks the critical size Nc of the largest non-matching component G′. | ||
Fig. 7f reports our prediction for this static-friction force in two orthogonal directions: perpendicular to the valleys of the interlocking potential, i.e. in the strained armchair direction, and parallel to them, i.e. in the unstrained zig-zag direction, as depicted in Fig. 7e. Like in the colloid experiment of Fig. 4, the numerical results agree with the expectation for a type-B contact: in the directions perpendicular to the valleys Fs ∝ N0, while parallel to the valleys Fs ∝ N−1/2.
To probe the effect of elasticity, we allow for relaxation of the atomic positions, both of the hBN cluster and of the graphite substrate, while controlling the respective center-of-mass positions. We adopt periodic boundary conditions (PBC), which unavoidably introduce a secondary, much weaker strain on the zig-zag edges. This small strain leads to a commensurate (type-A) configuration, that fits in a periodic cell. This forced commensuration is responsible for the tiny, but nonzero friction in the zig-zag direction reported in the rightmost point in Fig. 7f.
As detailed in the Methods section XIII, at each center-mass position rc, we perform a systematic evaluation of the total interlocking energy and lateral force after a full atomic relaxation. The friction force parallel to the valleys after relaxation is nearly a factor three larger than when they are evaluated for rigid layers as reported in Table 2. Despite this reduction, these results indicate that elastic deformations preserve the substantial friction anisotropy.
| Force component | Rigid [nN] | Flexible [nN] |
|---|---|---|
| F armchairs | 1.90 × 10–2 | 2.20 × 10–2 |
| F zig-zags | 5.46 × 10–5 | 1.58 × 10–4 |
| F armchairs/Fzig-zags | 347 | 140 |
The adopted value of strain leads to an exact type-B contact. Small deviations from that value would lead to a type-C contact that, for not-too-large hBN clusters, would lead to an approximate type-B behavior, as discussed in section V.D.
VIII. Discussion
In this work we formulate a precise classification of the matching/mismatching conditions of 2D crystalline contacts. In addition to the well-known lattice-matching condition and to the structurally lubric fully mismatched condition, we discover an intriguing intermediate condition, characterized by vanishing static friction in just one special direction. We extend this rigorous theory from the rather abstract domain of infinite lattices to the approximate but experimentally more relevant situation of finite-size contacts, where we provide estimations of the range of validity of the resulting frictional regimes.This theory, summarized in eqn (7) and (8), shows how both directional locking and structural lubricity can occur in non-trivial preferential directions, i.e. directions that generally do not coincide with those of highest symmetry for either the substrate or the adsorbate. This is possible only when the dominant contributions to the interlocking potential originates from higher Fourier components Ω of the corrugation potential. Non-trivial directions are consequently absent for purely sinusoidal potentials, as was noted in ref. 18. Furthermore, the existence of directional structural lubricity is possible only when adsorbate and substrate have either low symmetries or different symmetries (see Methods X). This excludes the commonly studied cases of homocontacts, and even heterocontacts of triangular-on-triangular and square-on-square lattices, which perhaps explains why directional structural lubricity has gone unnoticed so far. Regarding this novel frictional regime, we provide concrete examples of its realization, including an experiment based on colloidal particles driven across a patterned surface.
Most importantly, we investigate the angular energetics of the problem, and show that the same contact orientations that support directional locking and directional structural lubricity are the most energetically stable. Hence the well-known spontaneous decay of superlubricity in homocontacts54 does not apply to directional structural lubricity.
Precisely this intrinsic stability could suggest applications of directional structural lubricity in contexts where a dramatic friction anisotropy is required. The natural field of application involves nanoparticles/nanocontacts, whose small size can accommodate the not-quite-perfect CMVs that one is likely to encounter in real life. By tuning temperature and taking advantage of the different thermal expansion of the contacting materials, or by applying strain to one of the crystals, as discussed in section VII, precise CLVs can be achieved: this condition allows one to realize perfect directional structural lubricity even for a macroscopically large contact, as long as elastic effects are negligible.
The present investigation does not include elasticity. For rigid materials, the effect of the elastic response should remain small and even negligible as long as the contact size remains below a critical value. Such critical sizes range from N ≃ 105 for the colloidal clusters of Fig. 4, to N ≃ 1012 corresponding to linear dimensions in the millimeter region for hBN/strained graphene (see Methods, section XIII) and MoS2/graphene heterostructures.53,68 For softer materials, which could include colloids27,34,69 and dusty plasma,47 or real material interfaces with larger sizes, elasticity will acquire an increasingly important role, usually leading to higher friction.24,70 For type-C contacts, the Aubry-transition paradigm21,27,32 leads us to predict that structural lubricity gives way to a high-friction regime as soon as the strength of the adsorbate–substrate interaction starts to prevail over the adsorbate and substrate rigidity. For soft type-B and near-type-B contacts, we expect a regular 1D Aubry-type physics, although other effects related to Novaco-McTague distortions71 might play a role too.27,72,73 These questions however go beyond the scope of this paper, and as such their investigation is left to future work.
IX. Materials and methods
A. Properties of the discrete-coverage dual and real-space lattices
In the discrete-coverage condition, summarized in row A of Table 1, the following two statements hold: (i) for all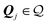 , their components
, their components  (μ = x, y), i.e. they are rational numbers; (ii) likewise, for all
(μ = x, y), i.e. they are rational numbers; (ii) likewise, for all  , their components
, their components 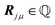 , rational numbers too.
, rational numbers too.
The demonstration of (i) goes as follows: we can express any lattice vector in 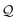 as a linear combination of the primitive lattice vector Qa, Qb, with integer coefficients. In particular, for the lattice vectors Q1, Q2 whose components Qiα/(2π) are integers (line A of Table 1),
as a linear combination of the primitive lattice vector Qa, Qb, with integer coefficients. In particular, for the lattice vectors Q1, Q2 whose components Qiα/(2π) are integers (line A of Table 1),
| Q1 = n1Qa + n2Qb | (20) |
| Q2 = m1Qa + m2Qb, | (21) |
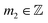 The relations in eqn (20) and (21) can be inverted to express the primitive vectors in term of Q1, Q2:
The relations in eqn (20) and (21) can be inverted to express the primitive vectors in term of Q1, Q2: | (22) |
 | (23) |
Similar relations hold for these vectors divided by 2π:
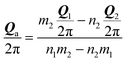 | (24) |
 | (25) |
Since at the right hand side of eqn (24) and (25) all vectors have integer components, the primitive vectors Qa/(2π), Qb/(2π) have rational components. As an arbitrary lattice vector  can be written as an integer-coefficient combination of these primitive vectors, Qj = l1Qa + l2Qb (with
can be written as an integer-coefficient combination of these primitive vectors, Qj = l1Qa + l2Qb (with  ), we conclude that all lattice points in
), we conclude that all lattice points in  divided by 2π have rational components.
divided by 2π have rational components.
The demonstration of the real-lattice statement (ii) goes as follows: given the primitive vectors Qa, Qb of  , then the primitive vectors of
, then the primitive vectors of  can be obtained through the following formulas:50
can be obtained through the following formulas:50
 | (26) |
 | (27) |
 have rational components.
have rational components.
Finally, by multiplying Ra and Rb by the least common denominator of their respective (rational) components, one readily obtains two independent vectors in  characterized by all integer components.
characterized by all integer components.
X. Necessary condition for line coverage
To allow for the possibility of line coverage (type B), the two lattices must not share a rotational symmetry of order n > 2: in practice they cannot be both square or triangular lattices. To prove this, consider two such lattices sharing a rotational symmetry by an angle α of order n > 2. First of all, if they do not have any nonzero CLV in reciprocal space then they are in the dense coverage case (type C). Let us then assume that they do have a nonzero CLV Ω*. As a consequence of the common symmetry, also the rotated vector Rα(Ω*) is a CLV (where Rα represents a rotation by α). Moreover, if the symmetry order is larger than 2, then Ω* and Rα(Ω*) are both CLVs and independent, which leads by definition to the case of discrete coverage, type A. We conclude that to have line coverage (type B) either the two lattices must have different symmetries, or share the same low-order symmetry.XI. Weight function structure factor
When, as is usually the case, R1CLV and R2CLV are not primitive vectors of , they define a supercell, namely the unit cell of the moiré pattern formed by
, they define a supercell, namely the unit cell of the moiré pattern formed by  and
and  . This supercell contains K vectors Rk, such that any lattice-translation vector Rj defining the cluster can now be identified as Rj = j1R1CLV + j2R2CLV + Rk, with
. This supercell contains K vectors Rk, such that any lattice-translation vector Rj defining the cluster can now be identified as Rj = j1R1CLV + j2R2CLV + Rk, with 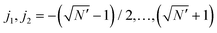 , k = 1, …, K, and we assume that
, k = 1, …, K, and we assume that  is an odd integer such that N = N′K.
is an odd integer such that N = N′K.
We then express the weight function as
 | (28) |
 | (29) |
The main observation here is that since RiCLV are CLV belonging to both  and
and  , this structure factor vanishes exactly for all nonzero δΩ's. By definition δΩ·RiCLV = G·RiCLV −
, this structure factor vanishes exactly for all nonzero δΩ's. By definition δΩ·RiCLV = G·RiCLV − ![[Q with combining macron]](https://www.rsc.org/images/entities/b_i_char_0051_0304.gif) ·RiCLV = 2πq with
·RiCLV = 2πq with  . Hence, the sinc terms in eqn (28) are equal to 1 and the weights W associated with any substrate vector G are size-independent. But only CLV contributions can be size independent and survive for infinite monolayer. Thus the non-CLV contribution must vanish, hence S(δΩ) = 0.
. Hence, the sinc terms in eqn (28) are equal to 1 and the weights W associated with any substrate vector G are size-independent. But only CLV contributions can be size independent and survive for infinite monolayer. Thus the non-CLV contribution must vanish, hence S(δΩ) = 0.
XII. Experimental details
The data shown in section V.D are obtained using the experimental apparatus described in ref. 16 and 17, where monolayers of triangularly packed colloidal crystalline clusters of up to hundreds of particles in size are firstly created and then driven across a periodic (square lattice) potential under an applied force. To form the colloidal clusters, we inject a colloidal suspension into a sample cell of 20 × 30 × 0.3 mm3 in size, where the 0.3 mm is the sample thickness and the 20 × 30 mm2 is the sample area. The colloidal suspension contains a dilute amount (∼107 mL−1) of colloidal particles (Dynabeads M450 with a diameter of a = 4.45 μm) in a water-based solution that contains a small amount of polyacrylamide (0.02% by weight) and sodium dodecyl sulfate (50% critical micelle concentration). The polyacrylamide induces a bridging flocculation effect which causes the colloidal particles to attract strongly when they get close to each other. Due to gravity, the colloidal particles (buoyant weight mg = 286 fN) sediment on the bottom surface of the sample cell. Under Brownian motion, the colloidal particles on the sample surface meet one another and aggregate to form random-shaped small clusters up to several tens of particles in size. To facilitate the formation of larger clusters, we tilt the sample so that the small clusters can move quickly on the sample surface and grow larger via accretion. This process also clears the sample surface so that during future sliding the clusters will hardly bump into each other.The sample surface contains portions of periodically corrugated regions created by photolithography. To create the periodic structures, a thin layer (thickness 100 nm) of photoresist (SU8 2000) was firstly coated to the sample surface and then exposed by UV light (wavelength 365 nm) under a photomask that contains the predefined periodic patterns. The surface is then washed in SU8 developers, after which the unexposed part of the thin film dissolve away, forming a periodically corrugated structure on the surface. This creates a periodic potential for the colloidal particles with a lattice spacing b = 5 μm and potential barrier 25.8 kBTroom.
Due to the orientational locking effect, during sliding the clusters will become orientationally locked to an angle θo = −3.4° relative to the periodic surface's lattice direction. At this angle a CMV appears at G′ ≈ Q1 − 2Q2 which leads to a nearly-type-B contact. This creates a low-energy corridor along the 25.6° direction on the interlocking potential energy landscape of the clusters.
To apply a driving force F, we tilt the sample in such a way that the in-plane component of the gravitational force is either parallel to the low energy corridor or perpendicular to it. To determine the static friction force component Fs reported in Fig. 4, we firstly increase F in the 80–100 fN region to ensure that the cluster can move along or perpendicular to the low-energy corridor. We then gradually lower F until the cluster is no longer moving: this is the measured Fs.
XIII. Simulating directional structural lubricity of hBN on strained graphite
We simulate a realistic model for the hBN/strained graphene interaction, consisting of a finite-size rectangular hBN slider in contact with a graphene substrate to which PBC are applied along the armchair (x) and zig-zag (y) directions, see Fig. 7a. To obtain a contact with a CLV Ω = (4.625, 0) nm−1 compatible with directional structural lubricity along the zigzag direction, we strain the graphene substrate (with original bond length bgraphene = 1.42039 Å) along the armchair direction by εarmchair = (ahBN/bgraphene − 1) = 1.81799% to match the hBN lattice (bond length ahBN = 1.44621 Å), while along the zig-zag direction the graphene substrate is shrunk by εzig-zag = −0.34542% to account for the Poisson ratio ν = 0.19.56 The strained graphene has armchair-directed bonds of length 1.44621 Å, zig-zag bonds of length 1.42323 Å, and the angle between them amounts to 120.5357°. The negative stress required for this elongation is estimated to be 8 GPa, assuming a Young modulus of graphene of 1 TPa. This is within the experimentally achievable strain of graphene.64 For all simulations of finite-size hBN clusters, both hBN and graphene are kept rigid. The hBN-graphene interaction is described by the accurate registry-dependent inter-layer potential (ILP).74 In this system the reciprocal vector yielding the next most significant Fourier component of the interlocking potential is G′ = (2.312, 4.076) nm−1.We also simulate the infinite-size layer, by applying PBC to both hBN and graphene in a common supercell of size 5.64 nm × 11.5 nm (N = 1196), that imposes a minimal residual strain of 0.00294% to hBN in the zig-zag direction.
The ratio of friction between the pinned armchair direction and the directionally structurally lubric direction is rather large, as expected. Beside simulating rigid layers, in order to probe the effect of elastic deformation, in this PBC model we perform additional flexible simulations, with z-direction springs tethered to each slider and substrate atom to mimic the elasticity of the bulk materials.75 The average external load is kept to zero during the sliding. When modeling the elastic infinite-size contact, both the slider (hBN) and the substrate (graphene) are fully flexible and periodically repeated. The intralayer interaction of hBN and graphene are described by shifted-Tersoff76–78 and REBO65 force fields, respectively. A standard (quasi-static) simulation protocol79,80 is adopted to compute the interlocking potential energy U(rc) while changing the position rc of the slider relative to the graphene substrate, whose center-of-mass (COM) is kept fixed throughout the simulation. The COM rc of the slider is scanned on a 0.1 Å grid over x and y. At fixed COM, the structure is relaxed until the force experienced by each atom decreases below 10–5 eV Å−1. All calculations of the interface potential energy for the rigid layers, and its relaxation in the elastic case are conducted by means of the open-source LAMMPS code.81
After obtaining the energy field U(rc), we estimate the static friction Fs along the expanded armchair  and weakly shrunk zig-zag
and weakly shrunk zig-zag  direction by taking the maximum value of
direction by taking the maximum value of  and
and  between two successive minima, as in section V.C and Fig. 3g. Table 2 compares the static friction obtained taking elastic displacement into account with that obtained for the rigid layer.
between two successive minima, as in section V.C and Fig. 3g. Table 2 compares the static friction obtained taking elastic displacement into account with that obtained for the rigid layer.
The overall anisotropy and thus the armchair/zigzag friction ratio, while still very large, is reduced by elasticity. Note that the finite size of the supercell of PBC calculations effectively implements a small-wavevector cutoff, that forbids all long-wavelength deformation. The size at which long-wavelength elastic deformations become important can be estimated by the critical length defined by Sharp et al.:23
| λ = Gd/τ, | (30) |
Author contributions
E. P., A. S., and N. M. derived the mathematical formulation. X. C. carried out the experiments. A. S. and E. P. wrote the computer code for the rigid simulations. A. S. and J. W. performed the numerical simulations. All authors contributed to the theoretical understanding, discussed the results and wrote the paper.Data and code availability statements
Data used in this work is available from the corresponding author on reasonable request.Conflicts of interest
The authors declare no competing interests.Acknowledgements
A. S. thanks D. Kramer and A. de Wijn for the useful discussions. X. C. acknowledges funding from Alexander von Humboldt Foundation. E. T. acknowledges support by ERC ULTRADISS Contract No. 834402. N. M., A. V., and A. S. acknowledge support by the Italian Ministry of University and Research through PRIN UTFROM N. 20178PZCB5. Open Access is provided through the collective agreement by the Italian CRUI.References
- aY. Mo, K. T. Turner and I. Szlufarska, Nature, 2009, 457, 1116–1119 CrossRef PubMed
.
- R. Guerra, U. Tartaglino, A. Vanossi and E. Tosatti, Nat. Mater., 2010, 9, 634–637 CrossRef CAS PubMed
.
- S. Kawai, A. Benassi, E. Gnecco, H. Söde, R. Pawlak, X. Feng, K. Müllen, D. Passerone, C. A. Pignedoli, P. Ruffieux, R. Fasel and E. Meyer, Science, 2016, 351, 957–961 CrossRef CAS PubMed
.
- B. Liu, J. Wang, S. Zhao, C. Qu, Y. Liu, L. Ma, Z. Zhang, K. Liu, Q. Zheng and M. Ma, Sci. Adv., 2020, 6, eaaz6787 CrossRef CAS PubMed
.
- G. He, M. H. Muser and M. O. Robbins, Science, 1999, 284, 1650–1652 CrossRef CAS PubMed
.
- M. Hirano, K. Shinjo, R. Kaneko and Y. Murata, Phys. Rev. Lett., 1997, 78, 1448 CrossRef CAS
.
- X. Feng, S. Kwon, J. Y. Park and M. Salmeron, ACS Nano, 2013, 7, 1718–1724 CrossRef CAS PubMed
.
- D. Dietzel, C. Ritter, T. Mönninghoff, H. Fuchs, A. Schirmeisen and U. D. Schwarz, Phys. Rev. Lett., 2008, 101, 125505 CrossRef PubMed
.
- L. Gigli, N. Manini, E. Tosatti, R. Guerra and A. Vanossi, Nanoscale, 2018, 10, 2073–2080 RSC
.
- A. Silva, E. Tosatti and A. Vanossi, Nanoscale, 2022, 14, 6384–6391 RSC
.
- K. Novoselov, o. A. Mishchenko, o. A. Carvalho and A. Castro Neto, Science, 2016, 353, aac9439 CrossRef CAS PubMed
.
- O. Hod, E. Meyer, Q. Zheng and M. Urbakh, Nature, 2018, 563, 485–492 CrossRef CAS PubMed
.
- A. Vanossi, C. Bechinger and M. Urbakh, Nat. Commun., 2020, 11, 4657 CrossRef CAS PubMed
.
- Y. Song, D. Mandelli, O. Hod, M. Urbakh, M. Ma and Q. Zheng, Nat. Mater., 2018, 17, 894–899 CrossRef CAS PubMed
.
- M. Z. Baykara, M. R. Vazirisereshk and A. Martini, Appl. Phys. Rev., 2018, 5, 041102 Search PubMed
.
- X. Cao, E. Panizon, A. Vanossi, N. Manini and C. Bechinger, Nat. Phys., 2019, 15, 776–780 Search PubMed
.
- X. Cao, E. Panizon, A. Vanossi, N. Manini, E. Tosatti and C. Bechinger, Phys. Rev. E, 2021, 103, 1–12 Search PubMed
.
- A. S. de Wijn, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 85429 CrossRef
.
- D. Dietzel, M. Feldmann, U. D. Schwarz, H. Fuchs and A. Schirmeisen, Phys. Rev. Lett., 2013, 111, 235502 CrossRef PubMed
.
- O. Hod, ChemPhysChem, 2013, 14, 2376–2391 CrossRef CAS PubMed
.
- O. M. Braun and Y. S. Kivshar, Phys. Rep., 1998, 306, 1–108 CrossRef
.
- A. Benassi, M. Ma, M. Urbakh and A. Vanossi, Sci. Rep., 2015, 5, 1–13 Search PubMed
.
- T. A. Sharp, L. Pastewka and M. O. Robbins, Phys. Rev. B, 2016, 93, 121402 CrossRef
.
- E. Gnecco, R. Bennewitz, T. Gyalog and E. Meyer, J. Phys.: Condens. Matter, 2001, 13, R619 CrossRef CAS
.
- C. Fusco and A. Fasolino, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 45413 CrossRef
.
- T. Brazda, A. Silva, N. Manini, A. Vanossi, R. Guerra, E. Tosatti and C. Bechinger, Phys. Rev. X, 2018, 8, 011050 CAS
.
- J. Norell, A. Fasolino and A. S. de Wijn, Phys. Rev. E, 2016, 94, 023001 CrossRef PubMed
.
-
D. Micciancio and S. Goldwasser, Complexity of lattice problems: a cryptographic perspective, Springer Science & Business Media, 2002, vol. 671 Search PubMed
.
-
D. Micciancio, CSE 206A Lattice Algorithms and Applications, Lecture at University of California, San Diego, 2010. Online material visited on 2022-07-17 Search PubMed
.
- Y. I. Frenkel and T. Kontorova, Phys. Z. Sowjetunion, 1938, 13, 1 CAS
.
- S. Aubry and P.-Y. Le Daeron, Phys. D, 1983, 8, 381–422 CrossRef
.
-
O. M. Braun and Y. S. Kivshar, The Frenkel-Kontorova model: concepts, methods, and applications, Springer, 2004 Search PubMed
.
- A set
 is dense if it has the following property: for any
is dense if it has the following property: for any  and for any point P in the vector space, there exists a
and for any point P in the vector space, there exists a  such that |P − O1| < ε.
such that |P − O1| < ε. - T. Bohlein and C. Bechinger, Phys. Rev. Lett., 2012, 109, 058301 CrossRef PubMed
.
- P. T. Korda, M. B. Taylor and D. G. Grier, Phys. Rev. Lett., 2002, 89, 128301 CrossRef PubMed
.
- F. Trillitzsch, R. Guerra, A. Janas, N. Manini, F. Krok and E. Gnecco, Phys. Rev. B, 2018, 98, 1–6 CrossRef
.
- J. Villegas, E. Gonzalez, M. Montero, I. K. Schuller and J. Vicent, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 224504 CrossRef
.
- Y. Xu, S. Liu, D. A. Rhodes, K. Watanabe, T. Taniguchi, J. Hone, V. Elser, K. F. Mak and J. Shan, Nature, 2020, 587, 214–218 CrossRef CAS PubMed
.
- C. Reichhardt and F. Nori, Phys. Rev. Lett., 1999, 82, 414 CrossRef CAS
.
- A. Gopinathan and D. G. Grier, Phys. Rev. Lett., 2004, 92, 130602 CrossRef PubMed
.
- J. Frechette and G. Drazer, J. Fluid Mech., 2009, 627, 379–401 CrossRef
.
- D. Speer, R. Eichhorn and P. Reimann, Phys. Rev. Lett., 2010, 105, 090602 CrossRef PubMed
.
- C. Reichhardt and C. O. Reichhardt, Phys. Rev. Lett., 2011, 106, 060603 CrossRef CAS PubMed
.
- M. Pelton, K. Ladavac and D. G. Grier, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 031108 CrossRef PubMed
.
- J. Feilhauer, S. Saha, J. Tobik, M. Zelent, L. J. Heyderman and M. Mruczkiewicz, Phys. Rev. B, 2020, 102, 184425 CrossRef CAS
.
- C. Reichhardt, D. Ray and C. J. O. Reichhardt, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 104426 CrossRef
.
- W. Zhu, C. Reichhardt, C. J. O. Reichhardt and Y. Feng, Phys. Rev. E, 2022, 106, 015202 CrossRef CAS PubMed
.
- M. Dienwiebel, G. S. Verhoeven, N. Pradeep, J. W. M. Frenken, J. A. Heimberg and H. W. Zandbergen, Phys. Rev. Lett., 2004, 92, 126101 CrossRef PubMed
.
-
M. Born and E. Wolf, Principles of optics: electromagnetic theory of propagation, interference and diffraction of light, Elsevier, 2013 Search PubMed
.
-
N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt, Rinehart and Winston, 1976 Search PubMed
.
- E. Koren and U. Duerig, Phys. Rev. B, 2016, 94, 1–11 Search PubMed
.
- J. Wang, W. Cao, Y. Song, C. Qu, Q. Zheng and M. Ma, Nano Lett., 2019, 19, 7735–7741 CrossRef CAS PubMed
.
- X. Cao, A. Silva, E. Panizon, A. Vanossi, N. Manini, E. Tosatti and C. Bechinger, Phys. Rev. X, 2022, 12, 021059 CAS
.
- A. E. Filippov, M. Dienwiebel, J. W. M. Frenken, J. Klafter and M. Urbakh, Phys. Rev. Lett., 2008, 100, 046102 CrossRef PubMed
.
- A. S. de Wijn, C. Fusco and A. Fasolino, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 046105 CrossRef PubMed
.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder,
et al.
, APL Mater., 2013, 1, 011002 CrossRef
.
- M. Della Negra, M. Sambi and G. Granozzi, Surf. Sci., 2000, 461, 118–128 CrossRef CAS
.
- N. Mounet, M. Gibertini, P. Schwaller, D. Campi, A. Merkys, A. Marrazzo, T. Sohier, I. E. Castelli, A. Cepellotti, G. Pizzi and N. Marzari, Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS PubMed
.
-
I. D. B. G. Bergerhoff and F. Allen, International Union of Crystallography, Chester, 1987, 360, 77–95 Search PubMed
.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, npj Comput. Mater., 2015, 1, 1–15 Search PubMed
.
- C. Androulidakis, E. N. Koukaras, G. Paterakis, G. Trakakis and C. Galiotis, Nat. Commun., 2020, 11, 1595 CrossRef CAS PubMed
.
- S. Zhang, Y. Hou, S. Li, L. Liu, Z. Zhang, X.-Q. Feng and Q. Li, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 24452–24456 CrossRef CAS PubMed
.
- K. Wang, W. Ouyang, W. Cao, M. Ma and Q. Zheng, Nanoscale, 2019, 11, 2186–2193 RSC
.
- K. Cao, S. Feng, Y. Han, L. Gao, T. Hue Ly, Z. Xu and Y. Lu, Nat. Commun., 2020, 11, 284 CrossRef CAS PubMed
.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783–802 CrossRef CAS
.
- I. Leven, T. Maaravi, I. Azuri, L. Kronik and O. Hod, J. Chem. Theory Comput., 2016, 12, 2896–2905 CrossRef CAS PubMed
.
- A. Kınacı, J. B. Haskins, C. Sevik and T. Çağın, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 115410 CrossRef
.
- M. Liao, P. Nicolini, L. Du, J. Yuan, S. Wang, H. Yu, J. Tang, P. Cheng, K. Watanabe and T. Taniguchi,
et al.
, Nat. Mater., 2022, 21, 47–53 CrossRef CAS PubMed
.
- J. Hasnain, S. Jungblut and C. Dellago, Soft Matter, 2013, 9, 5867 RSC
.
- N. Varini, A. Vanossi, R. Guerra, D. Mandelli, R. Capozza and E. Tosatti, Nanoscale, 2015, 7, 2093–2101 RSC
.
- A. D. Novaco and J. P. McTague, Phys. Rev. Lett., 1977, 38, 1286–1289 CrossRef CAS
.
- D. Mandelli, A. Vanossi, N. Manini and E. Tosatti, Phys. Rev. Lett., 2015, 114, 108302 CrossRef PubMed
.
- D. Mandelli, A. Vanossi, N. Manini and E. Tosatti, Phys. Rev. B, 2017, 95, 245403 CrossRef
.
- I. Leven, I. Azuri, L. Kronik and O. Hod, J. Chem. Phys., 2014, 140, 104106 CrossRef PubMed
.
- Z. Guo, T. Chang, X. Guo and H. Gao, J. Mech. Phys. Solids, 2012, 60, 1676–1687 CrossRef CAS
.
- C. Sevik, A. Kinaci, J. B. Haskins and T. Çağın, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 085409 CrossRef
.
- W. Ouyang, I. Azuri, D. Mandelli, A. Tkatchenko, L. Kronik, M. Urbakh and O. Hod, J. Chem. Theory Comput., 2019, 16, 666–676 CrossRef PubMed
.
- D. Mandelli, W. Ouyang, M. Urbakh and O. Hod, ACS Nano, 2019, 13, 7603–7609 CrossRef CAS PubMed
.
- F. Bonelli, N. Manini, E. Cadelano and L. Colombo, Eur. Phys. J. B, 2009, 70, 449–459 CrossRef CAS
.
- D. Mandelli, I. Leven, O. Hod and M. Urbakh, Sci. Rep., 2017, 7, 1–10 CrossRef CAS PubMed
.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ‘t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS
.
-
K. L. Johnson and K. L. Johnson, Contact mechanics, Cambridge University Press, 1987 Search PubMed
.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr04532j |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2023 |