Open Access Article
Open Access ArticleRationalization of the sub-surface segregation in nanoalloys of weakly miscible metals
Christine
Goyhenex

Institut de Physique et Chimie des Matériaux de Strasbourg, Université de Strasbourg, CNRS UMR 7504, 23 rue du Lœss, BP 43, F-67034 Strasbourg, Cedex 2, France. E-mail: christine.goyhenex@ipcms.unistra.fr
First published on 17th October 2022
Abstract
The origin of the stability of sub-surface precipitates in core–shell bimetallic nanoparticles is investigated from the perspective of atomic-size effects for systems where the core atoms have a size equal to, or lower than, the shell atoms. With the aim of providing more general assessments, a systematic study is proposed by considering three model systems combining weakly miscible metals: IrPd (negligible lattice mismatch, Δr/rPd = −1%), AuRh (moderate lattice mismatch, Δr/rAu = −7%) and AuCo (large lattice mismatch, Δr/rAu = −13%). The main driving forces for sub-surface segregation and the characteristic core morphologies are quantified from the combination of Monte Carlo and quenched molecular dynamics simulations. The preferential occupation of the sub-surface shell by an impurity of Ir or (Co or Rh) in a Pd or Au nanoparticle, respectively, in particular at the sub-vertex sites, is found to be a common feature in these dilute nanosystems. With the help of a model of the decomposition of the segregation enthalpies, it is shown that the dominant driving forces leading to the preferential sub-surface segregation at the vertex sites can be very different from one system to another: atomic size (AuCo, large lattice mismatch), coupled alloy-size-cohesion (AuRh, moderate lattice mismatch) or coupled alloy-cohesion (IrPd, negligible lattice mismatch) effects. As a consequence, in the core–shell nanoalloys, in the first stage of enrichment of an Au nanoparticle with Co or Rh core atoms, or a Pd nanoparticle with Ir core atoms, all the equilibrium structures consist of similar off-center solute clusters anchored at sub-vertex sites, and this is regardless of the lattice mismatch.
1. Introduction
During the past two decades, nanoalloys have been widely investigated, both experimentally and theoretically, in regard to many technological applications,1–4 among which nanomedicine and catalysis have given rise to an abundance of literature because of current issues facing society.5–10 The mixing of at least two metallic species in one nanoparticle offers the possibility of tuning properties and improving the known properties of the pure constituents.A major concern with nanoalloys is their stability after synthesis related to their thermodynamically stable structure towards which the system could evolve over time while possibly losing the targeted properties. It is therefore essential to be able to rationalize this structure in terms of the driving forces towards thermodynamic equilibrium: atomic size or lattice mismatch between components, chemical ordering/demixing tendency, difference in surface or cohesion energies, particle size and shape, etc. The possible relative importance between these characteristics and their intricate correlation makes it difficult to predict atomic arrangements in a nanoalloy through a simple model and explains the long-standing efforts of research in this area. This complexity is finally illustrated by the occurrence of a great variety of nanoalloy structures in terms of their chemical arrangement, going from random or fully ordered to phase-separated (Janus nanoparticles).11 In the latter class, one finds the so-called core–shell nanoparticles, which are obtained by associating weakly miscible elements in the bulk phase. In core–shell nanoalloys, a shell of the surface-segregating element covers a core of the other element. The core can take various morphologies: centered, off-centered, or multi-shell.11 Although a considerable number of studies have been carried out on core–shell nanoalloys, a rationalization of the link between segregation and precipitate morphology in a nanoparticle has been only partially achieved. The greatest amount of theoretical studies in this regard have been made in the case of systems where the atomic-size mismatch between the two metallic species is very large, like in AgCu, AgCo, AuCo and AgNi.12–19 In this case, the largest element is also the one corresponding to the greatest surface energy and more attention has been paid to its surface segregation, particularly in dilute systems where it is the impurity. On the other hand, sub-surface segregation has been much less studied in these systems. Even scarcer studies aimed at building nanoalloy phase diagrams can be found for systems with a much lower size mismatch, like AuPt, IrPt or PdRh.16,20–22 However, the knowledge and understanding of the segregation behavior in a nanoalloy are of considerable importance for predicting the evolution of the core morphology and its stability, which could have a strong implication on its properties, such as gas sorption and catalysis, which are very sensitive to composition changes.23,24 One missing aspect, finally, is the rationalization in terms of atomic size or lattice mismatch of the segregation behaviour in the core–shell systems, which should involve the comparison, in a single systematic study, between systems having similar surface segregation behavior and mixing tendency, but differing in the atomic-size mismatch between the constituent elements.
In this context, three model systems have been investigated for the present theoretical work, IrPd (negligible lattice mismatch), AuRh (moderate lattice mismatch) and AuCo (large lattice mismatch). Atomistic simulations were used to first explore the segregation behavior in the most dilute configuration where one atom of a monometallic nanoparticle is substituted by one foreign metallic impurity atom. In particular, the segregation enthalpy is calculated using quenched molecular dynamics simulations by considering the variation of energy for an impurity located in the center of the nanoparticle and at all the other different possible sites under the surface shell. The results have been interpreted thanks to a model of segregation driving forces involving three distinct terms of atomic size, alloying and cohesion effects (and possibly their coupling), and which was until now mostly applied to AgCu nanoalloys.15,25,26 In the following sections, it will be shown that this accurate study enables a better description of the first stages of enrichment of a nanoparticle in another metal, in the case where phase separation occurs in the bulk corresponding alloy, and where the core atoms have a size equal to or lower than the shell atoms. The characteristic configurations of small precipitates were derived from off-site equilibrium Monte Carlo simulations at low temperature (200 K), while the associated local atomic stress was obtained from the quenched molecular dynamics algorithm in the same way as for the impurity.
2. Materials and methods
2.1 IrPd, AuRh and AuCo nanoalloys
The following notations will be used depending on the addressed configuration of the studied AB alloy system constituted by A and B metallic species:• AB: general formula for an AB (nano)alloy system,
• A(B): dilute (nano)alloy constituted by an A matrix containing one impurity of B,
• B@A: core–shell nanoalloy made of an A shell coating a B core.
The initial pure Pd and Au nanoparticles and the further modelled nanoalloys have an ideal Wulff shape corresponding to a face-centered cubic (fcc) truncated octahedron (denoted as TOh). The fcc TOh is an archetypal shape for metallic nanoparticles and nanoalloys.3,27 It relates to the Wulff equilibrium shape of transition metal fcc crystals driven by the relative surface energy associated with the exposed facets, mainly (100) and (111). It is worth noting that many other geometrical shapes can be developed, especially at very small size (≈20–200 atoms or diameter <1 nm), and lead to many homotops for nanoalloys.28,29 The fcc truncated octahedral shape has been observed experimentally in the size (or diameter) range of 1.5–4 nm in IrPd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 and AuRh
30 and AuRh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31 samples of nanoparticle catalysts. For AuCo, experimental works report more rounded shapes for nanoalloys (but still with an fcc structure) than geometrically well-defined ones.32–35 In this case, the TOh shape can be considered as the geometrical one closest to a sphere. From the point of view of the theoretical approach, the most important thing is to have in the model different sites with characteristic coordination numbers in order to rationalize the phenomena of segregation at the atomic scale. The used particle contains 405 atoms distributed on the fcc lattice. The corresponding diameter is ≈2 nm, a usual size in experiments.7,30,36Fig. 1 shows this typical TOh nanoparticle. It can be viewed as a structure of concentric shells, each having the same geometry as shown in the cross-sectional view of Fig. 1 (right-hand side). The concentric shells are denoted by Si, where i = 0, 1, or 2, and indicate the level of the concerned shell starting from the surface. The index i = 3 relates to the remaining central atoms. Starting from pure Au and Pd nanoparticles, Au or Pd atoms are then replaced by Ir, Rh and Co atoms to form, respectively, IrPd, AuRh and AuCo nanoalloys with different concentrations. The phase diagrams of the corresponding bulk alloys present a large miscibility gap, and the pure Pd and Au materials both have a much lower surface energy than Ir, Rh and Co, leading to a strong surface segregation of Au and Pd in the considered nanoalloys. These systems differ mostly by their atomic size or lattice mismatch. This mismatch is usually quantified by relating the lattice parameter mismatch between the fcc structures of the pure materials. The bulk lattice mismatch relative to the matrix element (here Au or Pd), Δr/rAu,Pd, is the highest for AuCo (−13%), the lowest for IrPd (−1%) and intermediate for AuRh (−7%). The minus sign relates to the smaller atomic size of Co, Ir and Rh relative to that of the matrix element.
31 samples of nanoparticle catalysts. For AuCo, experimental works report more rounded shapes for nanoalloys (but still with an fcc structure) than geometrically well-defined ones.32–35 In this case, the TOh shape can be considered as the geometrical one closest to a sphere. From the point of view of the theoretical approach, the most important thing is to have in the model different sites with characteristic coordination numbers in order to rationalize the phenomena of segregation at the atomic scale. The used particle contains 405 atoms distributed on the fcc lattice. The corresponding diameter is ≈2 nm, a usual size in experiments.7,30,36Fig. 1 shows this typical TOh nanoparticle. It can be viewed as a structure of concentric shells, each having the same geometry as shown in the cross-sectional view of Fig. 1 (right-hand side). The concentric shells are denoted by Si, where i = 0, 1, or 2, and indicate the level of the concerned shell starting from the surface. The index i = 3 relates to the remaining central atoms. Starting from pure Au and Pd nanoparticles, Au or Pd atoms are then replaced by Ir, Rh and Co atoms to form, respectively, IrPd, AuRh and AuCo nanoalloys with different concentrations. The phase diagrams of the corresponding bulk alloys present a large miscibility gap, and the pure Pd and Au materials both have a much lower surface energy than Ir, Rh and Co, leading to a strong surface segregation of Au and Pd in the considered nanoalloys. These systems differ mostly by their atomic size or lattice mismatch. This mismatch is usually quantified by relating the lattice parameter mismatch between the fcc structures of the pure materials. The bulk lattice mismatch relative to the matrix element (here Au or Pd), Δr/rAu,Pd, is the highest for AuCo (−13%), the lowest for IrPd (−1%) and intermediate for AuRh (−7%). The minus sign relates to the smaller atomic size of Co, Ir and Rh relative to that of the matrix element.
2.2 Atomistic simulations
The A(B) dilute systems, implying the introduction by substitution of one impurity B in a nanoparticle of species A, were studied with a classical molecular dynamics algorithm. More specifically, in the present work, a quenched molecular dynamics (QMD) method has been used as a relaxation procedure to optimize the crystal structure at T = 0 K. It means that the equations of motion are solved for atoms i while cancelling their velocity vi, when its product with the force Fi becomes negative. Such atomistic simulations enable us to obtain the total energy of a configuration while including realistic atomic relaxations. They also enable some site specific analysis, in particular through local pressures, which should be useful to explore local stress effects due to the atomic size difference between the impurity and its matrix. The local pressure is given by the variation of the interaction energy Eij as a function of the local deformations of the interatomic distances rij:
becomes negative. Such atomistic simulations enable us to obtain the total energy of a configuration while including realistic atomic relaxations. They also enable some site specific analysis, in particular through local pressures, which should be useful to explore local stress effects due to the atomic size difference between the impurity and its matrix. The local pressure is given by the variation of the interaction energy Eij as a function of the local deformations of the interatomic distances rij: | (1) |
According to this definition, a positive value of the local pressure corresponds to an atomic compressive stress, while a negative one corresponds to an atomic tensile stress. The local pressure is calculated on each site of the system after the relaxation within the QMD algorithm.
Following the goal of this work to rationalize the sub-surface impurity segregation behaviour and its link with the subsequent core-morphology evolution when increasing the concentration of species B in a nanoparticle of A, it was required to have systems with an optimal atomic/chemical arrangement as a function of the concentration. For this, Monte Carlo (MC) simulations were implemented in the canonical ensemble. With this method, one starts from a binary nanoalloy with an arbitrary distribution (random, for instance) of the two species on the fcc lattice of the initial TOh structure. Random atomic exchanges are then successively proposed, as well as small random atomic displacements (≈0.1 Å). In a canonical simulation, the concentration remains constant so that several configurations with different concentrations are considered in order to have a representative set of systems. Using the Metropolis sampling, one reaches a Boltzmann distribution of the atomic/chemical configuration of a system at equilibrium, provided that a sufficiently large number of Monte Carlo iterations are performed. Around 300 000 so-called macrosteps were performed. Each macrostep includes N microsteps where Nat (number of atoms) exchanges and Nat × Ndisp atomic displacements are proposed, so that N = Nat + Nat × Ndisp (Ndisp = 1 to 3 displacements). At each microstep, a trial (exchange or displacement) is accepted if it leads to a lowering of the total energy of the system. Otherwise, the new tested configuration can still be accepted according to an acceptance probability  . ΔE is the energy difference between the new proposed configuration and the previous one, k is the Boltzmann constant and T the temperature.
. ΔE is the energy difference between the new proposed configuration and the previous one, k is the Boltzmann constant and T the temperature.
In this work, the study of the equilibrium structures was performed at a low temperature, T = 200 K, for specific concentrations. This simulation temperature has been chosen in order to characterize the low-temperature part of the phase diagram, which should correspond to the ground state. This choice could be questionable for nanoalloys where chemical or structural transitions can occur at much lower temperatures than in the bulk because of size effects.37 For nanoalloys containing between 400 and 1000 atoms, it has been shown, however, that the ordering or the distribution of the different chemical species in the particles is only affected at temperatures higher than 400 K.37–39 In this work, some benchmark simulations have been performed between 100 K and 300 K in order to verify that, apart from small local fluctuations of atomic positions, there are no significant changes in the obtained equilibrium configurations. The structures obtained in the MC simulations can then be used further in the MD procedure to again evaluate the local pressures, for instance, or other energy quantities. One serious advantage of combining both methods, MC and MD, is that they can be implemented using the same energy model, ensuring good consistency between the results. This energy model is based on a semi-empirical many-body interatomic potential derived from the electronic structure in the tight-binding second moment approximation. It was initially proposed by Gupta40 and by Rosato et al.41 and was widely and successfully used for studying the structure of alloys and alloy surfaces. As a matter of fact, nowadays, it remains extensively used for nanoalloys (see, for instance, in a non-exhaustive list of examples, ref. 16–18, 42 and 43). Within the tight-binding second moment approximation (TB-SMA), the total energy at a site i having j neighbors of a system of atoms is written as the sum of an attractive band term Ebi, derived from the electronic structure, and a repulsive Born–Mayer one (Eri):
| Ei = Ebi + Eri, | (2) |
 | (3) |
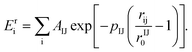 | (4) |
| α | β | A αβ | ξ αβ | p αβ | q αβ |
|---|---|---|---|---|---|
| Au | Au | 0.189 | 1.743 | 10.400 | 3.867 |
| Co | Co | 0.106 | 1.597 | 10.867 | 2.36 |
| Au | Co | 0.141 | 1.614 | 10.634 | 3.11 |
| Au | Au | 0.208 | 1.812 | 10.140 | 4.008 |
| Rh | Rh | 0.241 | 2.465 | 10.346 | 3.444 |
| Au | Rh | 0.257 | 2.207 | 10.243 | 3.726 |
| Pd | Pd | 0.114 | 1.494 | 12.070 | 3.120 |
| Ir | Ir | 0.139 | 2.431 | 15.000 | 2.864 |
| Pd | Ir | 0.127 | 1.904 | 13.535 | 2.992 |
| α | β | Δrα–β/rβ | ΔEα–βcoh/Eβcoh | Δα–β(100)/γβ | Δγα–β(111)/γβ | E sol (α in β) | E sol (β in α) |
|---|---|---|---|---|---|---|---|
| Ir | Pd | −1% | 0.250 | 0.50 | 0.40 | 0.250 | 0.250 |
| Rh | Au | −7% | 0.311 | 0.30 | 0.23 | 0.280 | 0.311 |
| Co | Au | −13% | 0.342 | 0.28 | 0.25 | 0.259 | 0.342 |
3. Results and discussion
3.1 Sub-surface impurity segregation: energetics and local pressures
In the dilute systems, both total energies and local pressures can easily be mapped by substituting one atom of the pure Pd or Au TOh405 by one impurity atom of Ir or (Rh or Co), respectively, and repeating the procedure for all the inequivalent sites of the nanoparticle. This was achieved by using the QMD procedure. MC simulations have been used only in a preliminary stage to verify that the occupation rate of the impurity at the surface (shell S0) of the nanoparticle is always 0 for any system at T = 100–300 K. In addition, these simulations show that the occupation of the least-coordinated sub-vertex sites prevails for all systems at 100 ≤ T ≤ 300 K. The analyses can therefore be related only to the inner sites, from sub-surface to the center. These sites can themselves be classified in five main categories: sub-vertex, sub-edge1, sub-edge2, sub-(100) facet and sub-(111) facet. The names sub-edge1 and sub-edge2 correspond, respectively, to the position below the edge joining a (100) and a (111) facet, and the edge joining two (111) facets. The characteristic sites are marked with numbers (Z-coordination with upper-shell atoms) in the graphical representation of Fig. 2a for S1 (the surface shell S0 is also represented in this figure). Taking as the reference state the substitution by one impurity of the central atom of the nanoparticle, the variation of total energies after substitution and relaxation at the characteristic sites of sub-shells S1 and S2 have been calculated and reported in the graph of Fig. 2b (energy variations in the S3 region are negligible). These variations are similar to segregation energies. The sub-surface S1 sites are usually the most favorable ones, whatever the considered materials, particularly under edges and vertices. An interesting fact is that going from the center of the nanoparticle to sub-vertex sites (at S1), the variations are much more important for the Pd(Ir) and Au(Rh) systems, which have a moderate or low lattice mismatch, the strongest variation being obtained for the least mismatched Pd(Ir) one. So, whatever the size mismatch, the sub-surface positions are the most favorable, with increasing energy variations going from the central position to a sub-vertex one, the latter site being definitely the most favorable for the substitution. Let us, however, note that segregation to the S2 shell has significant energy values for some sites of the highly size-mismatched Au(Co) dilute system, although they are close to zero for Pd(Ir) and Au(Rh). These results will be discussed in more detail in section 3.2. | ||
| Fig. 2 (a) Atomic representation of the surface shell (S0) and the sub-surface shell (S1) of a TOh405 nanoparticle. The numbers on the S1 structure relate to the Z-coordination (first neighbors) with atoms of the upper-surface shell S0. (b) Variation of the total energy as a function of the location of one impurity of Ir, Rh or Co in the Pd or Au nanoparticle, at the first (S1) and second (S2) shells under the surface (see Fig. 1). The variation is relative to the energy of one impurity placed in the center of the nanoparticle. The x-axis label corresponds to the number of bonds Z with the next upper-shell atoms above the site where the impurity is located. | ||
At this stage, it is hardly possible to establish a clear and general rule about the driving forces for sub-surface segregation towards the single preferential S1 sub-vertex site, in particular regarding the lattice mismatch effect. For other systems like AgCu, AgNi, AgCo or AuCo nanoalloys, which are all weakly miscible and exhibit very large absolute values of lattice mismatch (>10%), studies have focused on the atomic-size effect for explaining sub-surface segregation and/or off-center core formation.14,16,18,39 For these systems, a good correlation is found between the energetics and the local pressure acting on a substituted impurity.14 When the size of the atom impurity is much lower than the atomic size of the matrix element, the local pressure is always negative and reaches its lowest absolute values in the initially most-compressed sites of the matrix nanoparticle, located under the surface due to the inward relaxation of surface atoms. In this description, the site under the vertex is obviously the most favorable for the substitution by an impurity of lower atomic radius than the matrix atoms. Fewer systems with a smaller lattice mismatch have been investigated so far. One example is the weakly miscible AuPt (lattice mismatch Δr/rAu = −4%). In the form of a nanoparticle, at low Pt concentration (<1%), Monte Carlo simulations have clearly shown the favored sub-surface segregation, which was also interpreted as a local minimization of the stress.20 Going to systems with no or almost no lattice mismatch, off-centered Ir core configurations in IrPt nanoalloys (lattice mismatch Δr/rPt = −2%) have been studied at the DFT (density functional theory) level and it was concluded, in this case, that the preferential strengthening of surface–sub-surface Ir–Pt bonds was due to specific electronic features.21 In the present work, it is shown that the energy balances are very similar whatever the lattice mismatch, in particular for sub-surface segregation. The sub-surface segregation can be even stronger for systems with a negligible lattice mismatch, like IrPd.
3.2 Impurity at the sub-surface: quantification of the driving forces for segregation
From the previous observations, it is fundamental to question the relative importance of the atomic-size effect for the sub-surface segregation in order to estimate its relevance and to possibly evaluate the actual driving forces leading to the same favorable sites whatever the lattice mismatch in core–shell metallic nanoparticles. As mentioned before, the local pressure should be a relevant quantity for exploring the atomic-size effect. The local pressure at one impurity atom of Ir or (Rh or Co) in a Pd or Au nanoparticle (TOh405), respectively, has been calculated after relaxation within QMD using eqn (1). The results are presented in the bottom graph of Fig. 3; the top graph presents the reference values in pure Au and Pd nanoparticles.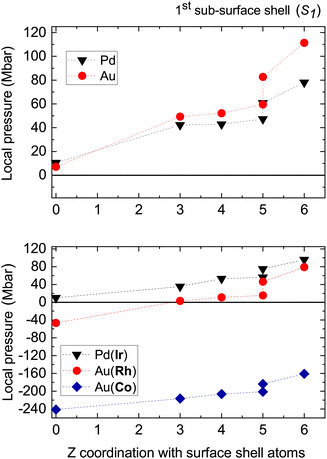 | ||
| Fig. 3 Top graph: local pressure at the characteristic sites of S1 for pure Au and Pd nanoparticles, before substitution by one impurity. The points at Z = 0 correspond to the inner central site. Bottom graph: local pressure at one impurity atom of Ir or (Rh or Co) substituted into a Pd or Au nanoparticle (TOh405), respectively. The points at Z = 0 correspond to the substitution at the inner central site. The dashed lines are just guidelines for the eye. As with Fig. 2, the x-axis label corresponds to the number of bonds, Z, with the next upper-shell atoms above the site where the impurity is located. | ||
Clearly the energetics and the local pressure are very well correlated only for the Au(Co) system. The numerical values for this system are also in very good agreement with the ones obtained in the work of Bochicchio et al.14 In this case, the local pressure is always negative because of the tensile strain related to the hosting of an impurity atom of much smaller size than the matrix atoms so that the strain-lowering seems to be the main driving force for favoring the most compressed site under the surface vertex (see the top graph of Fig. 3), in good agreement with the previous works on systems with a large lattice mismatch.14 When the absolute value of the lattice mismatch decreases from AuCo (Δr/r = −13%) to AuRh (Δr/r = −7%) and IrPd (Δr/r = −1%), the correlation with the local pressure is completely lost, although the energetics always favor the site under the surface vertices. For AuRh, the lowest absolute values of local pressure correspond to the substitution sites under (100) and (111) facets and under the surface edge joining two (111) facets. Then the largest local pressure (compressive) is obtained at the site under the surface vertex. For Ir@Pd, the local pressure remains positive whatever the substitution site and reaches its largest value under the surface vertex site. These observations led to a more detailed consideration of the driving forces for sub-surface segregation and their relative contributions as a function of the lattice mismatch, which is important to predict the subsequent core morphology when a metal nanoparticle is progressively enriched with another metal, in the case of weakly miscible metals. Segregation in bimetallic systems, at bulk defects as well as at surfaces, is, of course, not a new subject, but remains less rationalized in nanoalloys. One efficient approach initially proposed for interpreting the segregation enthalpy in dilute systems (bulk and surfaces) is based on the tight-binding formalism.25 In this approach, it is proposed to reconstruct the segregation enthalpy within three independent (or quasi-independent) contributions: the cohesion, the alloy and the size effects. The main quantity involved in this reconstruction is the permutation enthalpy, which is written as the sum of three terms:25
| ΔHpperm = ΔHpperm,coh + ΔHpperm,alloy + ΔHpperm,size, | (5) |
| ΔHpperm,coh = HpA − HpB, | (6) |
 | (7) |
| ΔHpperm,size = Hptot[B(B*)] − Htot(B). | (8) |
In eqn (6), Hp(A,B) is the energy of the site p in the pure metal A or B. In eqn (7), Zpk is the coordination number of the kth neighbors. Vpk corresponds to the effective pair interactions calculated up to the kth neighbors using the SMA-QMD procedure25,47 (typically, interactions are taken up to the 2nd next-nearest-neighbors). In brief, this is done by determining the energy difference between a system containing two isolated impurities in the initial state and two impurities in the 1st and the 2nd next-nearest-neighboring positions in the final state. Finally, in eqn (8), Hptot[B(B*)] is the total energy of the dilute B(B*) system, where B* designates an impurity differing from the B atoms’ matrix only by its atomic size, the latter being taken as the atomic size of the A element of the considered A(B) system for which Hpperm,size is evaluated.47 Using this so-called three-effects rule, it has been possible to successfully describe the segregation in various AgCu-based systems including nanoalloys.12,15 The possibility of decomposing the sub-surface segregation energy into these three components should help to better interpret the results on the sub-surface segregation in the Pd(Ir), Au(Rh) and Au(Co) diluted nanoalloys. It has been shown, however, that one limitation of this model decomposition of the permutation energy is that the alloy contribution is more or less strongly coupled to the cohesion and/or size contribution, which comes from the N-body character of the SMA interatomic potential and the atomic relaxations.26 It was then proposed to explicitly reintroduce this coupling in order to reconstruct more accurately the segregation energy.26 In the first step of the present work, the three separate contributions to the segregation energy and their sum have been calculated at the three inner shells S1, S2 and S3 using eqn (6)–(8) and taking as reference the permutation energies at the central core site.
The corresponding results for the segregation at sub-shells 1 and 2 (energy variations in the S3 region are still negligible) are reported in Fig. 4 for the A(B) dilute systems, where B is the impurity. Let us note that a negative or positive sign of the segregation energy indicates a preferential segregation for B over A, or A over B, respectively, at the p site.
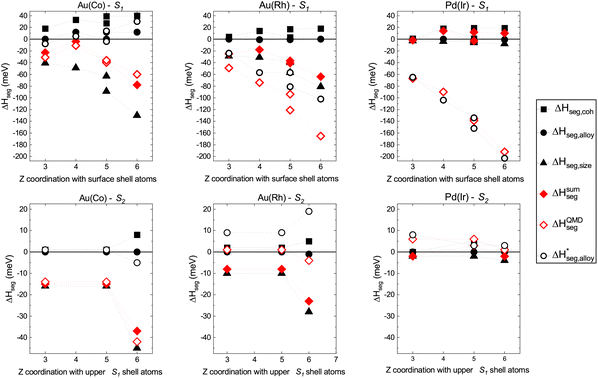 | ||
| Fig. 4 Top graphs: S1, first sub-surface shell: decomposition of site-segregation energies, ΔHseg on sub-surface sites for one impurity of (left to right) Co in Au, Rh in Au, and Ir in Pd. Values are given in meV. Bottom graphs: same as the top graphs but for S2. As with Fig. 2 and 3, the x-axis label corresponds to the number of bonds Z with the next upper-shell atoms above the site where the impurity is located. | ||
Looking first at the curves for S1 in the top graphs of Fig. 4, one clearly sees that the reconstruction of the sub-surface segregation energy with the initial version of the three-effects rule is really efficient for the system Au(Co), which has a large lattice mismatch, a result that was already obtained in earlier studies of Ag(Cu), another system with a similar large lattice mismatch. For Au(Rh), the reconstruction still predicts the right segregation tendency even though there is a significant difference between the curves of ΔHsumseg and ΔHQMDseg. Finally, the different effects are weak for Pd(Ir) (negligible lattice mismatch) and the simple reconstruction fails for this system. As can also be seen in the graphs, the two sets of red data points representing ΔHsumseg and ΔHQMDseg increasingly move further apart when going from the center (coordination, Z = 12) of the nanoparticle to the sub-vertex site (coordination with the surface shell atoms, Z = 6). Therefore, the coupling of the alloy term with the cohesion and/or size effects cannot be neglected and has to be reintroduced by some means. In the present work, instead of an explicit calculation like the one performed in the work of Creuze et al.,26 a pragmatic approach has been applied, based on the assessment that ΔHpperm,coh and ΔHpperm,size are unambiguously determined since they do not involve mixed A–B interactions in their formulation. The total segregation energies at the sub-surface sites, presented in Fig. 2b, are given by the total energy calculations within the SMA-QMD procedure. The effective alloy term  , including the coupling with size and cohesion, can be estimated by calculating the difference:
, including the coupling with size and cohesion, can be estimated by calculating the difference:
 | (9) |
The results for ΔH*seg,alloy are plotted in Fig. 4 with the other results of segregation contributions. While the coupling is weak for Au(Co) with values of ΔHseg,alloy* of the same order of magnitude as the values determined from eqn (7), it becomes stronger for the other two systems for which the values of ΔHseg,alloy* are the largest ones out of the contributions from all of the effects.
Looking next at the curves for the S2 sub-shell in the bottom graphs of Fig. 4, the reconstruction of the segregation energy with the initial version of the three-effects rule is still efficient for Au(Co). For Au(Rh), the coupling is no longer negligible and a positive value of ΔHseg,alloy* is obtained to recover the correct segregation energy on this shell. The segregation effects at S2 in Ir(Pd) are very small and the reconstruction using the corrected alloy term is mainly useful to recover the correct sign (positive) of the segregation energy at the sites of this shell. It is worth noting that the definition used for the effective alloy enthalpy (eqn (9)) may seem somewhat artificial, but it has the merit here of revealing the complexity of the alloy contribution to the segregation energies. The further analysis of the results in terms of the corrected three-effects model26 is indeed very informative and enables the elucidation of the relative contributions of the possible driving forces for sub-surface segregation. One common feature for all systems is the positive sign for the cohesion segregation term at any site of the matrix nanoparticle, implying that the cohesion effect always favors the segregation of the element matrix relative to the center of the nanoparticle (i.e., ≈bulk). It is easily understandable since the matrix elements Au and Pd have much lower cohesion and surface energies than the element taken as the impurity, Co, Rh or Ir, or, in other words, the considered bimetallic systems have a rather large positive cohesion factor (see Table 2). Then, for a given nanoparticle, the contribution of ΔHseg,size to the segregation energy increases when going from the center to the sub-surface shell, the maximal contribution being always at the site under the surface vertex, which is the most compressed in the nanoparticle, as already discussed in the previous section. However, as already suggested by the local pressure calculations, the size effect alone cannot explain the preferential segregation at the sub-surface vertex apart from the systems with a very large lattice mismatch like Au(Co). In Ir(Pd), the size-effect term is very small and the major contribution to the preferential segregation at S1, in particular at the sub-vertex site, is clearly coming from the effective alloy term ΔHseg,alloy*.
The results, including this effective alloy effect (looking only at ΔHseg,alloy*), can be examined closer following an increasing order of lattice mismatch starting, therefore, with Au(Co). In this case, it is clear that the size effect characterized by a large negative value is the dominant one. It largely outweighs the alloy and cohesion effects, the latter giving rise to positive segregation energies favoring the segregation of A on all sites of sub-shells 1 and 2 when taking the center of the nanoparticle as the reference. The alloy effect has the weakest importance in the case of this system, even taking into account its coupling with the cohesion and size effects. It is worth noting that there is a great similarity between these results and the one obtained for Ag(Cu) dilute systems (including nanoparticles).12,15,25,26 More generally, other known nanoalloys of weakly miscible metals and with a large lattice mismatch (|Δr/r| > 10%), like AgNi and AgCo (where Ag is the matrix element), have shown a similar sub-surface segregation behavior, which could be unambiguously attributed to a dominant size (strain) effect.14,16
Au(Rh), the second system to examine, corresponds to a so-called moderate lattice mismatch (Δr/r = −7%). The size effect is still important but less so than the alloying one. Both effects contribute to strongly favor sub-surface segregation at S1 and the preferential segregation at the sub-vertex site. It can then be concluded that the driving force for segregation is a coupled alloy-size-cohesion effect.
Finally, Pd(Ir) can be considered as an archetype for a system with no atomic-size effect or a negligible lattice mismatch. The atomic-size contribution to the total sub-surface segregation energy is very small. However, the main contribution to the segregation comes from the effective alloying effect characterized by a very large negative value of ΔHseg,alloy*. Owing to the fact that the size effect is negligible, the segregation is clearly driven by the alloying effect and its coupling with the cohesion effect.
The last interesting feature that should have an impact on the morphology of the core, when increasing the concentration, is that values of ΔHQMDseg at the S2 sites can be significant and of the same order of magnitude as at the S1sites, which occurs only for Au(Co), as previously mentioned (section 3.1). For Au(Rh), some values are still negative at S2 sites, but close to 0 eV despite an important atomic-size effect. For Pd(Ir), the values at S2 sites are positive. This suggests that when growing a precipitate of Ir in the Pd nanoparticle, it could tend to be more confined in the first sub-surface shell than the two other systems, AuRh and AuCo. Further simulations with MC of such precipitates are presented in the next section.
3.3 Evolution of the core solute morphology in equilibrium precipitates
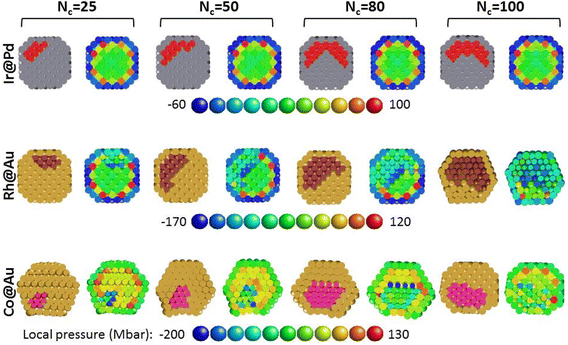
Different stages of the core enrichment in the TOh405 are addressed within equilibrium MC simulations in the canonical ensemble at a fixed temperature (T = 200 K) for four different compositions: A405−NBN where N = 25, 50, 80 or 100, which corresponds to concentrations cB = N × 100/405 ranging between 6% and 25% (A = Au or Pd; B = Co, Rh or Ir). Some snapshots of the obtained structures are represented in Fig. 5. Let us recall here that the considered core–shell nanoalloys are referred to as Co@Au, Rh@Au and Ir@Pd, where the surface shell S0 is always occupied by Au or Pd segregated species as confirmed by MC simulations. In the chosen range of composition, a biphasic structure is always obtained where the precipitate of the B element is anchored at the sub-surface leading to an off-center solute core inside the matrix nanoparticle of element A. Some observations can be made for the Au or Pd matrix phase. In the case of Ir@Pd and Rh@Au, where the lattice mismatch is negligible or moderate, the nanoparticle keeps a regular TOh shape. In the case of Co@Au, the Au matrix nanoparticle undergoes distortions around the Co core, which can be attributed to the large mismatch between the Co lattice and the Au one leading to incoherent interfaces between the two materials. This can be easily seen in the snapshots of Fig. 5 where the Co@Au nanoparticles are represented with the actual atomic-size ratio between Co and Au. In addition, also visible in Fig. 5, a structural transition is observed at the Au surface where square facets (100) reconstruct into diamond ones as they become more and more in contact with Co atoms. This phenomenon was already observed and investigated in detail for Cu@Ag nanoparticles13,48 and various bimetallic systems with a large lattice mismatch.49 In these studies, it was shown that an initial B@A TOh structure with a monolayer of A at the surface often transforms, through relaxations in atomistic simulations, from the TOh into a structure where the square (100) facets distort into a rhombus or diamond shape, with a close-packed arrangement of the surface atoms. This transformation has been shown to reduce the compression on the A atoms at the surface in contact with the B core atoms.49 It can be seen in the images of Fig. 5 that this transformation also occurs in Co@Au nanoalloys already at a lower Co concentration (biphasic regime here) as soon as some Co is in contact with a square (100) facet. This phenomenon is also very similar to the (111) reconstruction experimentally observed with scanning tunneling microscopy on some (100) metallic surfaces, like Au(100)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 or highly compressed Cu(100).51
50 or highly compressed Cu(100).51
Coming to the core description, it was observed that the Rh and Co precipitates extend from the S1 to S3 shells over the entire investigated concentration range. In comparison, the Ir core extends preferentially over the internal Pd surface shell in a bilayer morphology and the S3 shell starts to be occupied only from Nc = 100. The shape of the Ir precipitate remains close to a hollow shell, contrary to the Co and Rh ones, which are more compact. This description has been correlated to a more quantified approach performed by calculating in the MC simulations the average site occupation rate by Ir, Rh and Co in their matrix nanoparticle. The Ir, Rh and Co occupation probabilities per site are represented in the cross-sectional views of Fig. 6 using a color code going from 0 (blue) to 1 (red). It can be seen that the first description is indeed well corroborated by the site occupation rate representation. It can also be seen that there are different filling profiles of the S1 to S3 shells depending on the competition between the preferential sub-surface (S1) occupation and the demixing tendency of the investigated bimetallic systems.
 | ||
| Fig. 6 Cross-sectional views of the nanoparticles of Fig. 5. The color code is related to the Co, Rh or Ir occupation rate or probability on each site of the Au or Pd nanoparticle ranging from 0 (blue) to 1 (red). The orientations of the shown nanoparticles have been selected in order to best visualize the core solute structure. | ||
Therefore, the results have also been gathered in the curves of Fig. 7, this time by reporting the rate of shell occupation by Ir, Rh and Co atoms from S0 (surface) to S3 (central part of the nanoparticle). The obtained evolution of the shell-occupation rate as a function of the number of solute atoms is similar for Rh@Au and Co@Au, with an equal probability of filling for S1, S2 and S3 at low concentration (at Nc = 25 for Co@Au, and until Nc = 50 for Rh@Au), followed by a gradual splitting of the curves with a greater increase of the occupation probabilities going from S1 to S3. The latter effect is more pronounced in the case of Co@Au and this translates into the structures by a more important extension of the core solute towards the inner part of the nanoparticle (see Fig. 5). The strengthening of the mixed bonds under the surface is clearly most important in the Ir@Pd system, for which the curve of the S1 shell occupation rate (red curve in Fig. 7) is always above the others, in agreement with the found strong alloy-cohesion coupling for the impurity located under the surface shell (section 3.2). A clear difference between Ir@Pd and the two other systems is visible for the filling of the S3 shell, which occurs only from a certain concentration of Ir (here for Nc = 80), again showing the strong preference for Ir to decorate the sub-surface shell, leading to a bilayer hollow-shell shape in the biphasic systems, where small off-center precipitates are formed. Otherwise the Co and Rh solute cores have a three-layer shape from the beginning and more compact shapes. One can try to return to what could be inferred from the study of dilute systems, although it is not trivial to extrapolate results from a dilute system to a concentrated one. The increasing extension of the core solute towards the inner shells going from Ir@Pd to Co@Au can be qualitatively related to the fact that the segregation energies of the impurity still have rather large negative values on the shells below S1 for Co@Au, some small negative values for Rh@Au, while all values are positive below S1 for Ir@Pd. The occupation of S2 in the bilayer Ir core and of S3 in the trilayer Rh and Co cores can then be related to the demixing effect favoring homoatomic bonds.
Finally, following the approach adopted for dilute systems in section 3.2, a general view of the local strain in the nanoalloys is given in Fig. 8, where cross-sectional views of the final MC snapshots are represented. For each composition, the right-hand side image shows the mapping of the local pressure at each site of the left-hand side bimetallic nanoparticle. For similar core morphologies, the strain landscapes are different depending on the lattice mismatch. Comparing Ir@Pd and Rh@Au, the highest absolute value of pressure remains under the vertices with a major difference in the values since it is in the Ir solute for the first and in the Au matrix nanoparticle for the second. In the Co@Au system, the strain landscape in the core is rather homogeneous, with the highest local pressure at sites under the vertices of the Au matrix nanoparticle not occupied by Co atoms, similar to AuRh.
4. Conclusion
The preferential occupation of the sub-surface shell by an impurity in a nanoparticle, in particular at the sub-vertex sites, was found to be a common feature for weakly miscible bimetallic nanosystems in which the impurity has an atomic size equal to, or smaller than, the matrix atoms. Remarkably, the origin of this unique phenomenon at the sub-vertex site can be very different from one system to another. Three main effects have been highlighted in the present work from the study of three systems with very different lattice mismatches: strong alloy-cohesion coupling (Ir@Pd, no lattice mismatch), mixed size-alloy-cohesion coupling (Rh@Au, moderate lattice mismatch) and a strong atomic-size effect (Co@Au, large lattice mismatch). If, in this latter case, local pressure maps are well correlated with the segregation energies, it is no longer the case for smaller lattice mismatches. Already for Δr/r = −7% (the case of Rh@Au in this work), the correlation is lost, which is visible in the local pressure curves, where the lowest absolute value of the local pressure (≈0) is obtained under the facets and the edges joining two (111) facets, while the largest local pressure (compressive) is obtained at the site under the surface vertex, although this latter site corresponds to the most favorable for the substitution by a Rh impurity. For a lattice mismatch Δr/r ≈ 0 (the case of Ir@Pd), the same segregation energy hierarchy is obtained as for nanoalloys with a large lattice mismatch, while this time the variation of the local pressures shows an increasing positive absolute value from the center to the sub-surface of the Pd matrix nanoparticle.Equilibrium Monte Carlo simulations at different compositions, in the low concentration range of the solute element, revealed similar precipitate morphologies for the three studied model systems, which can be described by a biphasic structure showing an extension of an off-center core solute anchored under the surface at sub-vertex sites. This structure originates again from the different driving forces, which could be roughly guessed from the study of the impurity solute. Some differences between the three studied systems were nevertheless noted in the core morphology evolution in this low concentration range. Indeed, the strengthening of the mixed bonds under the surface is clearly the most important in the Ir@Pd system for which the S1 shell occupation rate is dominant due to a strong alloy-cohesion coupling without any size effects at play. The main difference between Ir@Pd and the two other systems can be summarized as follows. In Ir@Pd, one obtains an extended bilayered structure with the filling of the next inner shell (fourth shell from the surface, S3, in the TOh shape), occurring only from a certain concentration threshold of Ir (here for Nc > 80 in a TOh containing 405 atoms). On the other hand, the systems with a non-negligible lattice mismatch develop a three-layered core solute from the first stages of enrichment and keep more compact shapes in their nanoparticle matrix. To conclude more generally, through atomistic simulations, it was possible to show that all equilibrium structures consist of similar off-center solute clusters anchored at sub-vertex sites, regardless of the lattice mismatch. Assessing the dominant driving forces leading to these similar morphologies appeared to be non-trivial. They can indeed be very different from one system to another: atomic size (in the case of a large lattice mismatch), alloy-size-cohesion coupling (in the case of a moderate lattice mismatch) or alloy-cohesion coupling (in the case of a negligible lattice mismatch).
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Dr Guy Tréglia (CINaM, Marseille, France) is gratefully thanked for very fruitful discussions and his thorough reading of the manuscript.References
- Nanoalloys: From Theory to Applications, ed. R. L. Johnston and R. Ferrando, The Royal Society of Chemistry, 2008 Search PubMed.
- P. Entel and M. Gruner, J. Phys.: Condens. Matter, 2009, 21, 064228 CrossRef CAS PubMed.
- F. Calvo, Phys. Chem. Chem. Phys., 2015, 17, 27922–27939 RSC.
- R. Ferrando, R. L. Johnston and C. Louis, Phys. Chem. Chem. Phys., 2015, 17, 27920–27921 RSC.
- K. McNamara, S. A. Tofail, N. D. Thorat, J. Bauer and J. J. Mulvihill, Nanoalloys, Elsevier, Oxford, 2nd edn, 2020, pp. 381–432 Search PubMed.
- M. Kamp, A. Tymoczko, R. Popescu, U. Schurmann, R. Nadarajah, B. Gokce, C. Rehbock, D. Gerthsen, S. Barcikowski and L. Kienle, Nanoscale Adv., 2020, 2, 3912–3920 RSC.
- M. Cardona-Farreny, P. Lecante, J. Esvan, C. Dinoi, I. del Rosal, R. Poteau, K. Philippot and M. R. Axet, Green Chem., 2021, 23, 8480–8500 RSC.
- S. Gao, L. Wang, H. Li, Z. Liu, G. Shi, J. Peng, B. Wang, W. Wang and K. Cho, Phys. Chem. Chem. Phys., 2021, 23, 15010–15019 RSC.
- E. Gioria, P. Ingale, F. Pohl, R. Naumann d'Alnoncourt, A. Thomas and F. Rosowski, Catal. Sci. Technol., 2022, 12, 474–487 RSC.
- Q. Liu, M. Ranocchiari and J. A. van Bokhoven, Chem. Soc. Rev., 2022, 51, 188–236 RSC.
- R. Ferrando, J. Nanopart. Res., 2018, 20, 179 CrossRef.
- V. Moreno, J. Creuze, F. Berthier, C. Mottet, G. Tréglia and B. Legrand, Surf. Sci., 2006, 600, 5011–5020 CrossRef CAS.
- M. Briki, J. Creuze, F. Berthier and B. Legrand, Solid State Phenom., 2011, 172–174, 658–663 CAS.
- D. Bochicchio and R. Ferrando, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165435 CrossRef.
- M. Briki, Ph.D. thesis, Université Paris-Sud, 2013.
- R. Ferrando, J. Phys.: Condens. Matter, 2015, 27, 013003 CrossRef CAS PubMed.
- D. Nelli and R. Ferrando, Nanoscale, 2019, 11, 13040–13050 RSC.
- M. Settem, A. K. Srivastav and A. K. Kanjarla, Phys. Chem. Chem. Phys., 2021, 23, 26165–26177 RSC.
- P. Andreazza, A. Lemoine, A. Coati, D. Nelli, R. Ferrando, Y. Garreau, J. Creuze and C. Andreazza-Vignolle, Nanoscale, 2021, 13, 6096–6104 RSC.
- Y. Wang and M. Hou, J. Phys. Chem. C, 2012, 116, 10814–10818 CrossRef CAS.
- M. Polak and L. Rubinovich, Phys. Chem. Chem. Phys., 2014, 16, 1569–1575 RSC.
- M. Fèvre, Y. Le Bouar and A. Finel, Phys. Rev. B, 2018, 97, 195404 CrossRef.
- C. Goyhenex and L. Piccolo, Phys. Chem. Chem. Phys., 2017, 19, 32451–32458 RSC.
- H. Fang, J. Yang, M. Wen and Q. Wu, Adv. Mater., 2018, 30, 1705698 CrossRef PubMed.
- F. Berthier, B. Legrand and G. Tréglia, Acta Mater., 1999, 47, 2705–2715 CrossRef CAS.
- J. Creuze, I. Braems, F. Berthier, C. Mottet, G. Tréglia and B. Legrand, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 075413 CrossRef.
- R. Ferrando, J. Jellinek and R. L. Johnston, Chem. Rev., 2008, 108, 845–910 CrossRef CAS PubMed.
- R. L. Johnston, Metal Nanoparticles and Nanoalloys, Elsevier, 2012, vol. 3, pp. 1–42 Search PubMed.
- J. Montejano-Carrizales, F. Aguilera-Granja, C. Goyhenex, V. Pierron-Bohnes and J. Morán-López, J. Magn. Magn. Mater., 2014, 355, 215–224 CrossRef CAS.
- L. Piccolo, S. Nassreddine, M. Aouine, C. Ulhaq and C. Geantet, J. Catal., 2012, 292, 173–180 CrossRef CAS.
- L. Piccolo, Z. Li, I. Demiroglu, F. Moyon, Z. Konuspayeva, G. Berhault, P. Afanasiev, W. Lefebvre, J. Yuan and R. L. Johnston, Sci. Rep., 2016, 6, 35226 CrossRef CAS PubMed.
- D. Llamosa Pérez, A. Espinosa, L. Martínez, E. Roman, C. Ballesteros, A. Mayoral, M. Garcia-Hernandez and Y. Huttel, J. Phys. Chem. C, 2013, 117, 3101–3108 CrossRef.
- D. Llamosa, M. Ruano, L. Martínez, A. Mayoral, E. Roman, M. García-Hernández and Y. Huttel, Nanoscale, 2014, 6, 13483–13486 RSC.
- L. Li, S.-H. Chai, A. Binder, S. Brown, S.-Z. Yang and S. Dai, RSC Adv., 2015, 5, 100212–100222 RSC.
- D. A. Garfinkel, N. Tang, G. Pakeltis, R. Emery, I. N. Ivanov, D. A. Gilbert and P. D. Rack, ACS Appl. Mater. Interfaces, 2022, 14, 15047–15058 CrossRef CAS PubMed.
- C. Zlotea, F. Morfin, T. Nguyen, N. Nguyen, J. Nelayah, C. Ricolleau, M. Latroche and L. Piccolo, Nanoscale, 2014, 6, 9955–9959 RSC.
- D. Alloyeau, C. Ricolleau, C. Mottet, T. Oikawa, C. Langlois, Y. Le Bouar, N. Braidy and A. Loiseau, Nat. Mater., 2009, 8, 940–946 CrossRef CAS PubMed.
- G. Rossi, R. Ferrando and C. Mottet, Faraday Discuss., 2008, 138, 193–210 RSC.
- I. Atanasov, R. Ferrando and R. L. Johnston, J. Phys.: Condens. Matter, 2014, 26, 275301 CrossRef CAS PubMed.
- R. P. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 6265–6270 CrossRef CAS.
- V. Rosato, M. Guillopé and B. Legrand, Philos. Mag. A, 1989, 59, 321–336 CrossRef.
- I. Parsina, C. DiPaola and F. Baletto, Nanoscale, 2012, 4, 1160–1166 RSC.
- Z. Zhao, H. Xu, Y. Gao and D. Cheng, Nanoscale, 2019, 11, 1386–1395 RSC.
- T. H. Andriamiharintsoa, A. Rakotomahevitra, L. Piccolo and C. Goyhenex, J. Nanopart. Res., 2015, 17, 217 CrossRef.
- I. Chado, C. Goyhenex, H. Bulou and J. Bucher, Appl. Surf. Sci., 2004, 226, 178–184 CrossRef CAS.
- C. Goyhenex, Surf. Sci., 2012, 606(3–4), 325–328 CrossRef CAS.
- G. Tréglia, B. Legrand, F. Ducastelle, A. Saúl, C. Gallis, I. Meunier, C. Mottet and A. Senhaji, Comput. Mater. Sci., 1999, 15, 196–235 CrossRef.
- L. Delfour, J. Creuze and B. Legrand, Phys. Rev. Lett., 2009, 103, 205701 CrossRef CAS PubMed.
- E. Panizon and R. Ferrando, Nanoscale, 2016, 8, 15911–15919 RSC.
- R. Hammer, A. Sander, S. Förster, M. Kiel, K. Meinel and W. Widdra, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035446 CrossRef CAS.
- M. Yamada, K. Yagyu, S. Ohno, T. Iimori, K. Nakatsuji and F. Komori, Surf. Sci., 2022, 721, 122063 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2022 |