Interfacial layering of hydrocarbons on pristine graphite surfaces immersed in water

Abstract

Interfacial water participates in a wide range of phenomena involving graphite, graphite-like and 2D material interfaces. Recently, several high-spatial resolution experiments have questioned the existence of hydration layers on graphite, graphite-like and 2D material surfaces. Here, 3D AFM was applied to follow in real-time and with atomic-scale depth resolution the evolution of graphite–water interfaces. Pristine graphite surfaces upon immersion in water showed the presence of several hydration layers separated by a distance of 0.3 nm. Those layers were short-lived. After several minutes, the interlayer distance increased to 0.45 nm. At longer immersion times (∼50 min) we observed the formation of a third layer. An interlayer distance of 0.45 nm characterizes the layering of predominantly alkane-like hydrocarbons. Molecular dynamics calculations supported the experimental observations. The replacement of water molecules by hydrocarbons on graphite is spontaneous. It happens whenever the graphite–water volume is exposed to air.

---

Introduction

Aqueous interfaces with graphite, graphite-like materials and other 2D materials are relevant in a wide range of phenomena and applications from lubrication, water purification or energy-storage.^1–4 Despite their relevance, the structure and composition of graphite–liquid water interfaces are controversial. In the past few years, the interfacial liquid water structure on graphite-like surfaces was described in terms of three different molecular species: water,^5–9 dissolved gases^10–15 and hydrocarbons.^16–19

Recently some experimental¹⁷ and theoretical²⁰ results have ruled out the existence of layers made from dissolved gas (N₂) molecules. High-spatial resolution images of graphite and 2D materials surfaces immersed in water revealed the presence of 1–3 alkane layers.^16,17 The alkanes appeared to originate from the adsorption of airborne hydrocarbons^21–23 during the time the surface was exposed to indoor air. Those surfaces were exposed to ambient air for several minutes before being immersed in pure water.¹⁷ Atomic-scale depth images of a graphite–water interface inside a nanoscale capillary²⁴ revealed the presence of solvation layers separated by 0.3 nm (average). That value agreed with molecular dynamics (MD) simulations describing the interfacial structure of pure water on graphite.^6,7,17 Nanocapillary experiments²⁴ and the simulations^6,7,17 demonstrated that liquid water molecules formed 1–2 hydration layers at pristine graphite surfaces. However, those findings did not address their time stability. How long would a pristine graphite surface immersed in pure water remain free from hydrocarbon adsorbates?

Here, real-time and atomic-scale depth three-dimensional AFM (3D AFM) measurements were performed on a pristine graphite surface immersed in ultra-pure water. Initially, the interface was characterized by the presence of 1–2 layers separated by a distance of 0.3 nm (average value). At about 40 minutes an increase of the interlayer distance from 0.3 to 0.45 nm (average value) was observed. Another layer was observed at longer immersion times (90 min). The interlayer distance between the new and the previous layer was about 0.55 nm. From then on, the interfacial layer structure remained largely unchanged until the end of the experiment (3 hours).

Interlayer distances of 0.3 nm are characteristic of hydration layers while interlayer distances of 0.45 nm characterize layers of straight-chain alkanes. Molecular dynamics simulations backed the experimental findings by showing that the cumulative free energy of the process associated with transfer of an alkane molecule from air to water and from water to its adsorption on the graphite surface was negative. The atomic-scale resolution images in combination with MD simulations demonstrated the replacement of water molecules by hydrocarbon layers in the vicinity of a graphite surface.

The interaction of water with a graphite surface might be involved in some chemical reactions.²⁵ Those reactions were triggered by an external force. In contrast, the process discussed here was spontaneous and did not involve chemical reactions.

The invention and development of three-dimensional AFM enabled the generation of atomic-scale resolution images of solid–water interfaces in the three spatial coordinates.^26–28 This method is becoming the tool of choice for imaging with high-spatial resolution a large variety solid–liquid interfaces.^28–35

Results and discussion

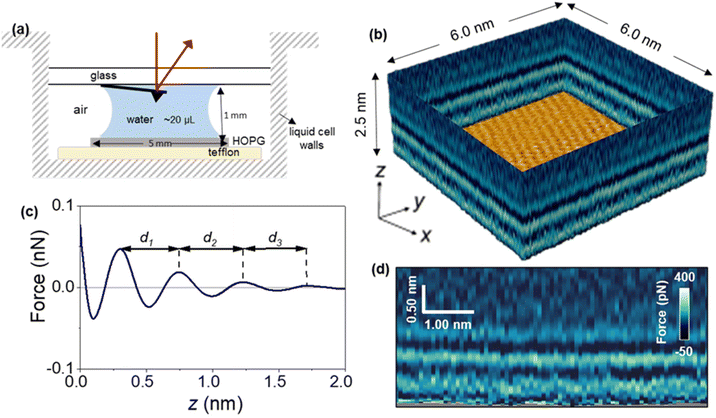
Fig. 1 shows a 3D AFM volume image, a 2D force map and the force–distance curves included in the 2D force map. The force–distance curves (FDC) showed an oscillatory behaviour that alternates between attractive and repulsive regions until the tip contacts with the graphite surface. The peak-to-peak distances observed in the FDC were associated with peaks of the liquid density.^36–38 The MD simulations suggest that the solvent component of the force on the AFM tip at a given distance from the surface is monotonically related to the gradient of the solvent density at that distance; therefore, the zero-crossings of the FDC correspond to distances of minimum or maximum solvent density and the peaks of the FDC correspond to distances about halfway between a maximum and minimum of solvent density. However, the interlayer distances measured as the separation between maxima are identical.

Fig. 1 (a) Scheme of liquid cell and its size. (b) 3D AFM image of a graphite–water interface. The 3D image might be split into different 2D maps. An image of the graphite lattice is shown at the bottom. (c) Definition of the interlayer distances in force–distance curves; d₁ is the distance between the closest layer to the solid surface and second solvation layer; d₂: is the distance between second and third solvation layers. (d) 2D force (x, z) map extracted from the 3D AFM image.

Fig. 2 shows a sequence of 2D force (x, z) maps and their corresponding force–distance curves as a function of the time the surface of graphite was immersed in water. The experiment was performed by using pristine graphite surfaces. Here, a graphite surface qualified as pristine by meeting simultaneously two requirements. First, it was freshly cleaved from a bulk piece of graphite. Upon cleavage, the surface was immediately immersed (1–2 s) in ultra-pure water. Second, 3D AFM images obtained within the first 10 minutes showed an interfacial liquid structure characterized by a periodicity of 0.3 nm (average value). This value is characteristic of hydration layers.^6,7,17 Freshly cleaved graphite surfaces that within the first 10 minutes of immersion in water showed interlayer distances above 0.4 nm did not qualify as pristine.

Fig. 2 2D force (x, z) maps and force–distance curves of graphite–water interfaces. The maps were extracted from 3D AFM volume images. (a) 2D force (x, z) map (top) and corresponding force–distance curves (bottom) for an immersion time of t = 5 minutes. (b) 2D force (x, z) map (top) and force–distance curves (bottom) for an immersion time of t = 50 minutes. (c) 2D force (x, z) map (top) and force–distance curves (bottom) for an immersion time of t = 180 minutes. The average force–distance curve is highlighted by a thick continuous line. Additional experimental parameters: f₁ = 798.7 kHz, k₁ = 9.8 N m⁻¹, Q₁ = 8.1, A₀ = 140 pm, A_sp = 100 pm.

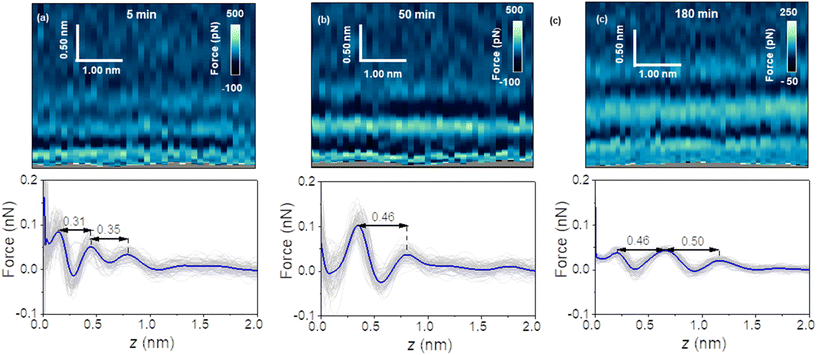
Fig. 2a shows the first images of the interfacial liquid structure on a pristine graphite surface. The data was obtained 5 minutes after the cleavage. That time was the minimum time required to set the sample in the liquid cell and to optimize the 3D AFM parameters. The interlayer spacings d₁ and d₂ were, respectively, 0.3 and 0.35 nm. Those values agreed with the values obtained by MD simulations performed with pure water and pristine graphite surfaces.^6,7,17 After 50 minutes, a significant increase in the interlayer distance d₁ was observed (Fig. 2b). The average value of d₁ was 0.46 nm. At longer immersion times (90 min), we observed another layer (3 in total).

From then on, the interfacial solvation structured remained practically unchanged (Fig. 2c). MD simulations showed that interlayer distances of d₁ = 0.45 nm agreed with the distances predicted for the solvation layers of organic liquids (hexane, pentadecane) on graphite. The simulation confirmed also that the distance between the first overlayer and the graphite surface was larger for alkanes than for water molecules.

Fig. 3 shows the evolution of the interlayer distances d₁ and d₂ as a function of the immersion time for several experiments. Initially, the interlayer distances matched the values predicted by MD simulations for hydration layers. After 50 min, the value of d₁ was similar to the ones measured on graphite surfaces immersed in organic solvents such as hexane or pentadecane (0.45 nm).¹⁷ We observed the presence of an additional layer at 90 min. From then on, the average interfacial water structure remained unchanged. The interlayer distances d₁ and d₂ were, respectively, 0.45 and 0.52 nm (average values). While MD simulations have indicated that distances of 0.45 nm are characteristic of well-ordered straight-chain alkane layers, small amounts of branching, heteroatom substitution, or cyclic moieties led to slightly larger interlayer distances of 0.47–0.52 nm.^17,20 Furthermore, the simulations revealed that the tails of straight-chain alkanes sometimes extend out-of-plane, forming defects in the layer that disrupt the structure of layers above and slightly increase the interlayer distance. Hence, defects in the lower layers cumulatively make the third layer more disordered and d₂ slightly larger than d₁. Sometimes, large interlayer distances (≈0.7 nm) were also observed in the experiments. It remains unclear what molecules or mixtures of molecules might form layers with such structure. However, the dominant interlayer distance in the experiments was about ∼0.5 nm, which agrees with MD simulations including molecules with predominantly straight-chain alkane moieties. These distances are not consistent with other possible constituents such as polyaromatic compounds, which exhibit smaller interlayer distances.^17,20

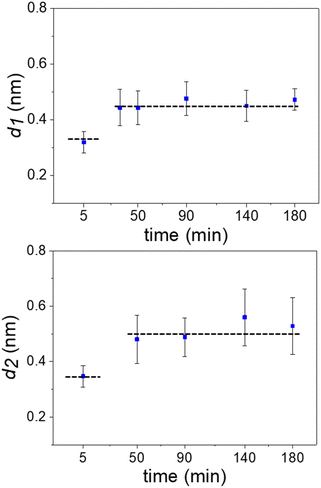Fig. 3 Time evolution of the interlayer distances. Average values extracted from several 2D maps like the ones shown in Fig. 2. The average involved maps from three different experimental rounds. The dash lines indicate the distances (MD simulations) for hydration (bottom line) and alkane (top) layers. The interlayer distance d₂ ≥ d₁ because the layering effect decreases with the distance to the solid surface.

The results indicated that hydration layers were initially formed on a pristine graphite surface. However, those layers were replaced over time by 2–3 layers of alkane-like hydrocarbons likely originating from the air. The transition between hydration to hydrocarbon layers is discontinuous. It is characterized by an increase of the noise in the 2D zx panels to the point that measuring interlayer distances became impossible. Eventually, the noise disappears. The new interlayer distances were in the 0.45 to 0.55 nm range.

A possible pathway is schematized in Fig. 4a. First, trace amounts of volatile hydrocarbon species commonly present in indoor air adsorb to the air–water interface. Adsorption to this interface is favorable for straight-chain alkanes (Fig. 4b), as well as other volatile organic compounds.²⁰ These molecules can then dissolve into the water of the liquid cell, from where they are finally adsorbed to the graphite–water interface. However, the free energy barrier for dissolution into the aqueous phase (Fig. 4b) is quite high for hydrocarbons and increases with chain length, making the kinetics rather slow. Less direct pathways such as transfer from the surface of air bubbles or migration across solid surfaces might occur at a faster rate. In any case, our thermodynamic analysis remains valid regardless of the pathway. Upon reaching the graphite–water interface, the molecules become strongly bound. However, they are able to diffuse freely across the 2D surface and nucleate to form an aligned monolayer.²⁰ Once a complete monolayer is formed, simulations suggest layer-by-layer (Frank-van der Merwe) growth.

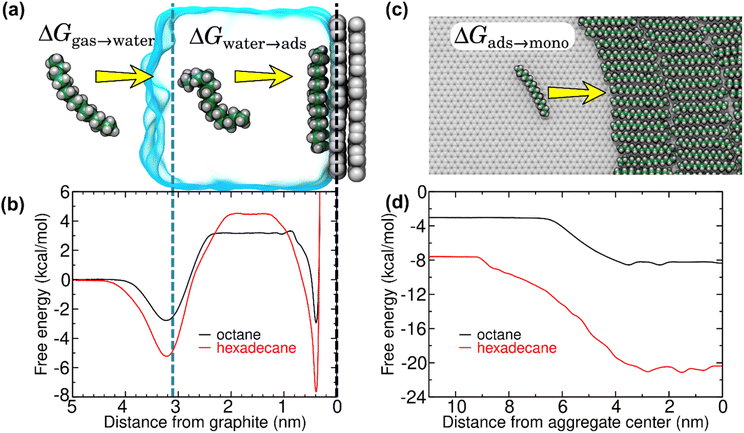Fig. 4 Free energy for transfer of alkanes from air to overlayers at the graphite–water interface, as calculated from MD simulations. (a) Snapshots from an MD simulation used to calculate the hydration (ΔG_gas→water) and isolated adsorption (ΔG_water→ads) free energies. (b) Gibbs free energy as function of distance from the center of mass of the graphene sheet for octane and hexadecane. The dashed black and blue lines indicate the center of mass of the graphene sheet and the distance at which the density of water falls to half of its bulk value, respectively. (c) Atomistic representation of the (coarse-grain) MD simulations used to calculate the free energy for transfer of isolated alkanes at the graphite–water interface to a monolayer phase (ΔG_ads→mono). (d) Free energy as a function of distance between the center of mass of an isolated alkane molecule and an alkane monolayer at the graphite–water interface. For efficiency, this quantity was calculated using our previously developed²⁰ coarse–grain model. By convention, the free energy of the gas phase is considered zero.

To fully understand the thermodynamics of this process, we applied efficient free-energy calculation techniques in the context of MD simulations. The Gibbs free energy of the process ΔG_{air→monolayer} was separated into three components: the free energy associated with the hydration of the hydrocarbon molecule (ΔG_air→water), the free energy for adsorption of the hydrocarbon molecule to the graphite–water interface, and, finally, the free energy associated with transfer of the adsorbed, but isolated, hydrocarbon molecule into a hydrocarbon monolayer (ΔG_ads→mono). Fig. 4b shows the free energy curves for the adsorption of two straight-chain alkanes (octane and hexadecane) on graphite, which are routinely detected in indoor air.²¹ Theoretical work²⁰ has shown that heavy hydrocarbons such as hexadecane form complete monolayers at the graphite–water interface even at trace ambient concentrations in air (∼1–100 μg m⁻³). The free energy profiles showed two local minima, one at the gas–water interface and the other at the graphite surface. The minimum at the gas–water interface indicates that the equilibrium concentration of an alkane molecule is larger at this interface than in bulk air or water. These minima were separated by an energy barrier associated with hydration of such hydrophobic molecules. The free energy at the graphite surface is associated with the lowest free energy, implying that the equilibrium concentration at the graphite–water interface is much higher than the ambient concentration. Moreover, adsorption of alkanes to the graphite–water interface is cooperative.²⁰ Isolated adsorbed alkane molecules nucleate to form aggregates (Fig. 4c), further reducing the free energy (Fig. 4d) until a complete monolayer is formed. Overall, the calculations show that adsorption of alkanes from the gas phase to a graphite surface immersed in water is highly thermodynamically favorable, and therefore spontaneous:

ΔG_{air→monolayer} = ΔG_air→water + ΔG_water→ads + ΔG_ads→mono < 0.

It should be noted that Fig. 4c depicts only a single configuration of the hexadecane aggregate. The shape of the hexadecane aggregate fluctuates considerably during the simulation (see Fig. S1 of the ESI†). Hence, the transition between the isolated adsorbed phase and the monolayer phase in Fig. 4d is not abrupt, but smeared out due to fluctuations of the position of the edge of the aggregate. However, the distances greater than 7 nm always represent a fully isolated molecule and distances less than 2 nm always represent a molecule fully surrounded by other hexadecane, so the overall free energy change between these two states should not depend on the geometry of the aggregate.

The Brownian dynamics calculations suggest that pure diffusion from air through bulk water to the graphite–water interface is unable to explain accumulation of contaminants on time scales of minutes to hours. Therefore, we suggest that other processes might be at play. First, it is possible that advection and turbulent mixing of the water accelerate accumulation at the interface. Second, Fig. 4b shows a strong local minimum of free energy at the air–water interface, which means that small air bubbles might carry a significant number of alkane-like molecules at their surfaces. If these bubbles make contact with the graphite–water interface, any such molecules they carry would be transferred to the graphite without these molecules having to cross the large free energy barrier associated with entering the bulk aqueous phase. Similarly, surfaces of the apparatus that have been exposed to air for long periods are expected to have already accumulated contaminants and these contaminants might migrate from one solid surface to another without ever entering the bulk water phase. Modelling the kinetics of any of these alternative pathways, such as turbulent mixing or migration across solid–solid interfaces, would be difficult given the many uncertainties in their details.

Conclusion

The interactions of liquid water with graphite, graphene and, in general, hydrophobic 2D materials have many features in common,^16,17 therefore, these findings should be also applied to nanopore devices that involve 2D material-aqueous interfaces.³⁹

In summary, real-time and atomic-scale depth resolution images demonstrated that the interfacial water structure on pristine graphite surfaces transitioned from hydration to hydrocarbon layers. Free energy minimization drives the transfer of hydrocarbons, in particular, alkane-like molecules from the gas phase through water to adsorption on graphite surfaces. These findings underline the difficulties in keeping water-immersed graphite surfaces, and more generally, crystalline hydrophobic surfaces free from airborne hydrocarbons.

Experimental

Crystalline surfaces

Highly oriented pyrolytic graphite (HOPG, grade ZYB) was purchased from Bruker (USA) and cleaved with adhesive tape before the experiment.

Solvents

Ultrapure water was freshly obtained before the experiments (ELGA Maxima, 18.2 MΩ cm⁻¹). The water's pH value reached a value of 5.6 a few minutes after obtaining it from the machine (Hanna Instruments HI 9024).

AFM setup

A home-made three-dimensional AFM implemented in a Cypher VRS (Asylum Research Inc., USA) platform was used. The AFM was operated in the amplitude modulation mode.⁴⁰ The cantilever oscillates with respect to its equilibrium position by exciting it at its first resonance. At the same time, a sinusoidal signal (f_m = 100 Hz) was applied to the z-piezo to modulate the relative z-distance between the sample and the tip. The z-piezo signal was synchronized with the x-displacement. For each x-position on the surface of the material, the tip performed a single and complete z-cycle. The z-data was read out every 20 μs and stored in 512 pixels (256 pixels half cycle). Each x-plane of the 2D map contained 80 points. Hence, the total time to acquire a 2D force map is 0.82 s.

The oscillation of the cantilever was driven by photothermal excitation. The free amplitude values A₀ are in the range of 50–100 pm (in water). The feedback monitored the instantaneous amplitude and acts on the z-piezo to keep the lowest amplitude reached during the approach close to a fixed value (A_sp ≈ 0.75–0.35A₀). We used a feedback bandwidth of 2 kHz. This bandwidth did not compensate for the small changes in the amplitude during the z-piezo displacement but it is fast enough to track the surface topography.

Silicon cantilevers with silicon tips were used (ArrowUHF, NanoAndMore, Germany). Cantilevers were cleaned first in a mixture (50 : 50 in volume) of isopropanol (99.6%, Acros Organics) and ultrapure water, rinsed with ultrapure water and then placed in a UV-Ozone cleaner (PSD-UV3, Novascan Technologies, USA) for ≈1 h. A contactless method was used to calibrate the microcantilevers.⁴¹ The values are summarized in the figure captions.

Force–distance curves were computed^16,42,43 from the amplitude modulation AFM observables A and ϕ. The z-range of the reconstructed force–distance curves was slightly reduced with respect to the amplitude and phase shift-distance curves (reduced by the zero-to-peak amplitude, i.e., A₀) because the force reconstruction process required an integration over the oscillation cycle. To increase the signal-to-noise ratio in the force-distance curves we have calculated the value of the force by averaging the values of the observables for the different x positions at the same z.

MD simulations

Simulations were performed using NAMD 2.14⁴⁴ and the CHARMM General Force Field⁴⁵ using protocols and atomic models described in previous work.²⁰ Free energies were calculated using the adaptive biasing force method^46,47 as implemented in the Colvars module.⁴⁸ The calculations depicted in Fig. 4a and b were performed in the isobaric isothermal ensemble (NpT)⁴⁹ with a pressure of 200 kPa, rather than the isochoric isothermal ensemble (NVT) as in our previous work, by adding 8 nitrogen molecules to form a gas region. However, the results were statistically indistinguishable from our previous NVT ensemble results that used a vacuum region instead. The calculation of the free energy for transfer of the alkanes from the isolated adsorbed phase to the monolayer phase (Fig. 4c and d) was calculated using the coarse-grain model (two CH₂ or CH₃ groups per coarse-grain particle) of alkanes at the graphene–water interface developed in our previous work.²⁰ The two coarse-grained systems consisted of 800 beads, representing 100 hexadecane or 200 octane molecules. The free energy was computed along a transition coordinate defined as the x-projected distance between a tagged hexadecane or octane molecule and the center of mass of the remaining molecules. The remaining molecules were also subjected to a flat bottom harmonic restraint (turning on for x < −6.2 nm or x > 6.2 nm) to keep them near the center of simulation box. The adaptive biasing force calculations lasted over 30 μs of simulated time. The image in Fig. 4c was created by converting an equilibrated coarse–grain structure to an all-atom representation including explicit water and graphene and further equilibrating under the all-atom CHARMM General Force Field.

Author contributions

D. M. A. performed the experiments. M. R. U. wrote the code to operate the 3D AFM. J. C. designed and performed the simulations. R. G. conceived the project and designed the experiments. R. G. wrote the manuscript with contributions from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Simone Benaglia for useful discussions. R. G. acknowledges financial support from the Ministerio de Ciencia e Innovación (PID2019-106801GB-I00) and the CSIC (202050E013). J. C. acknowledges financial support by US National Science Foundation under grant no. DMR-1945589.

References

1. D. Zhang, Z. Li, L. K. Hyldgaard, Q. Li and M. D. Dong, Mater. Today Phys., 2022, 27, 100771.
2. L. Chen and L. Qian, Friction, 2021, 9, 1–28.
3. H. Wang, X. Mi, Y. Li and S. Zhan, Adv. Mater., 2020, 32, 1806843.
4. Y. Wang, L. Zhang, H. Hou, W. Xu, G. Duan, S. He, K. Liu and S. Jiang, J. Mater. Sci., 2021, 56, 173–200.
5. L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Science, 2018, 360, 1339–1342.
6. J. G. Vilhena, C. Pimentel, P. Pedraz, F. Luo, P. A. Serena, C. M. Pina, E. Gnecco and R. Pérez, ACS Nano, 2016, 10, 4288–4293.
7. H. Söngen, Y. M. Jaques, L. Zivanovic, S. Seibert, R. Bechstein, P. Spijker, H. Onishi, A. S. Foster and A. Kühnle, Phys. Rev. B, 2019, 100, 205410.
8. J.-Y. Lu, C.-Y. Lai, I. Almansoori and M. Chiesa, Phys. Chem. Chem. Phys., 2018, 20, 22636–22644.
9. Q. Yang, P. Z. Sun, L. Fumagalli, Y. V. Stebunov, S. J. Haigh, Z. W. Zhou, I. V. Grigorieva, F. C. Wang and A. K. Geim, Nature, 2020, 588, 250–253.
10. Y. H. Lu, C. W. Yang and I. S. Hwang, Langmuir, 2012, 28, 12691–12695.
11. Y. H. Lu, C. W. Yang, C. K. Fang, H. C. Ko and I. S. Hwang, Sci. Rep., 2014, 4, 7189.
12. I. Schlesinger and U. Sivan, J. Am. Chem. Soc., 2018, 140, 10473–10481.
13. H. Teshima, Q. Li, Y. Takata and K. Takahashi, Phys. Chem. Chem. Phys., 2020, 22, 13629–13636.
14. H. Peng, G. R. Birkett and A. V. Nguyen, Langmuir, 2013, 29, 15266–15274.
15. I. Schleisinger and U. Sivan, Langmuir, 2017, 33, 2485–2496.
16. M. R. Uhlig, D. Martin-Jimenez and R. Garcia, Nat. Commun., 2019, 10, 2606.
17. M. R. Uhlig, S. Benaglia, R. Thakkar, J. Comer and R. Garcia, Nanoscale, 2021, 13, 5275–5283.
18. T. T. Duignan and X. S. Zhao, J. Phys. Chem. C, 2019, 123, 4085.
19. S. Seibert, S. Klassen, A. Latus, R. Bechstein and A. Kühnle, Langmuir, 2020, 36, 7789–7794.
20. R. Thakkar and J. Comer, Nanoscale Adv., 2022, 4, 1741–1757.
21. S. K. Brown, M. R. Sim, M. J. Abramson and C. N. Gray, Indoor Air, 1994, 4, 123–134.
22. Z. Li, A. Kozbial, N. Nioradze, D. Parobek, G. J. Shenoy, M. Salim, S. Amemiya, L. Li and H. Liu, ACS Nano, 2016, 10, 349–359.
23. J. M. Hurst, L. Li and H. Liu, Carbon, 2018, 134, 464–469.
24. M. R. Uhlig and R. Garcia, Nano Lett., 2021, 21, 5593–5598.
25. W. Foster, J. A. Aguilar, H. Kusumaatmajah and K. Voϊtchovskyk, ACS Appl. Mater. Interfaces, 2018, 10, 34265–34271.
26. T. Fukuma and R. Garcia, ACS Nano, 2018, 12, 11785–11797.
27. T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 016101.
28. K. Kimura, S. Ido, N. Oyabu, K. Kobayashi, Y. Hirata, T. Imai and H. Yamada, J. Chem. Phys., 2010, 132, 194705.
29. E. T. Herruzo, H. Asakawa, T. Fukuma and R. Garcia, Nanoscale, 2013, 5, 2678–2685.
30. K. Umeda, L. Zivanovic, K. Kobayashi, J. Ritala, H. Kominami, P. Spijker, A. S. Foster and H. Yamada, Nat. Commun., 2017, 8, 2111.
31. K. Kuchuk and U. Sivan, Nano Lett., 2018, 18, 2733–2737.
32. S. Zhou, K. S. Panse, M. H. Motevaselian, N. R. Aluru and J. Zhang, ACS Nano, 2020, 14, 17515.
33. S. Su, I. Siretanu, D. van den Ende, B. Mei, G. Mul and F. Mugele, Adv. Mater., 2021, 33, 2106229.
34. P. Z. Li, Q. Liu, D. Zhang, Y. Wang, Y. Zhang, Q. Li and M. Dong, Nanoscale Horiz., 2022, 7, 368–375.
35. S. Benaglia, M. R. Uhlig, J. Hernández-Muñoz, E. Chacón, P. Tarazona and R. Garcia, Phys. Rev. Lett., 2021, 127, 196101.
36. T. Fukuma, B. Reischl, N. Kobayashi, K. Miyazawa and A. S. Foster, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155412.
37. K. Miyazawa, N. Kobayashi, M. Watkins, A. L. Shluger, K. I. Amano and T. Fukuma, Nanoscale, 2016, 8, 7334–7342.
38. J. Hernández-Muñoz, E. Chacón and P. Tarazona, J. Chem. Phys., 2019, 151, 034701.
39. R. Saija, Y. You, R. Qi, S. Goutham, A. Bhardwaj, A. Rakowski, S. Haigh, A. Keerthi and B. Radha, Nanoscale, 2021, 13, 9553–9560.
40. R. Garcia, Amplitude Modulation Atomic Force Microscopy, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010.
41. J. E. Sader, R. Borgani, C. T. Gibson, D. B. Haviland, M. J. Higgins, J. I. Kilpatrick, J. Lu, P. Mulvaney, C. J. Shearer, A. D. Slattery, P.-A. Thorén, J. Tran, H. Zhang and T. A. Zheng, Rev. Sci. Instrum., 2016, 87, 093711.
42. A. F. Payam, D. Martin-Jimenez and R. Garcia, Nanotechnology, 2015, 26, 185706.
43. H. Holscher, Appl. Phys. Lett., 2006, 89, 123109.
44. J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802.
45. K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell Jr., J. Comput. Chem., 2010, 31, 671–690.
46. E. Darve and A. Pohorille, J. Chem. Phys., 2001, 115, 9169.
47. J. Comer, J. C. Gumbart, J. Hénin, T. Lelièvre, A. Pohorille and C. Chipot, J. Phys. Chem. B, 2015, 119, 1129–1151.
48. G. Fiorin, M. L. Klein and J. Hénin, Mol. Phys., 2013, 111, 3345–3362.
49. S. E. Feller, Y. Zhang and R. W. Pastor, J. Chem. Phys., 1995, 103, 4613.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr04161h

---