Open Access Article
Open Access ArticleNon-equilibrium heating path for the laser-induced nucleation of metastable skyrmion lattices†
Pablo
Olleros-Rodríguez
 *a,
Mara
Strungaru
b,
Sergiu
Ruta
b,
Paul-Iulian
Gavriloaea
*a,
Mara
Strungaru
b,
Sergiu
Ruta
b,
Paul-Iulian
Gavriloaea
 *bc,
Adrián
Gudín
a,
Paolo
Perna
*bc,
Adrián
Gudín
a,
Paolo
Perna
 a,
Roy
Chantrell
a,
Roy
Chantrell
 b and
Oksana
Chubykalo-Fesenko
b and
Oksana
Chubykalo-Fesenko
 c
c
aIMDEA Nanoscience Institute, Campus de Cantoblanco, 28049, Madrid, Spain. E-mail: pablo.olleros@imdea.org
bDepartment of Physics, University of York, YO10 5DD, York, UK
cMaterials Science Institute ICMM-CSIC, Campus de Cantoblanco, 28049, Madrid, Spain. E-mail: paul.gavriloaea@csic.es
First published on 14th September 2022
Abstract
Understanding formation of metastable phases by rapid energy pumping and quenching has been intriguing scientists for a long time. This issue is crucial for technologically relevant systems such as magnetic skyrmions which are frequently metastable at zero field. Using Atomistic Spin Dynamics simulations, we show the possibility of creating metastable skyrmion lattices in cobalt-based trilayers by femtosecond laser heating. Similar to the formation of supercooled ice droplets in the gas phase, high temperature ultrafast excitation creates magnon drops and their fast relaxation leads to acquisition and quenching of the skyrmion topological protection. The interplay between different processes corresponds to a specific excitation window which can be additionally controlled by external fields. The results are contrasted with longer-scale heating leading to a phase transition to the stable states. Our results provide insight into the dynamics of the highly non-equilibrium pathway for spin excitations and pave additional routes for skyrmion-based information technologies.
1 Introduction
In many physical systems metastable phases can be formed by means of rapid energy pumping (e.g. by heat, light or electricity), leading to a highly non-equilibrium state, and employing subsequent fast quenching. Multiple examples include rapid thermal and thermo-mechanical processes used in metallurgy with the aim to obtain non-equilibrium phases,1 formation of metastable phases upon a quench in colloidal crystals,2 ionization of the liquid without cracking and void formation by ultrafast high electric fields,3 liquid–liquid transitions in specific molecular and atomic systems from a supercooled phase,4 formation of Bose–Einstein condensate in magnetic systems by heating and rapid cooling etc.5 Many of the above systems share similarities based on a general theory for non-adiabatic phase transitions. At the same time, microscopic understanding of non-equilibrium kinetics of metastable phase formation involving nucleation theory and energy transfer physics is far from being complete. The prominent important example of nucleation kinetics is the formation of supercooled ice droplets in clouds directly from the gas state (vapor). The droplet formation occurs in highly non-equilibrium conditions when a warm air mass passes into a relatively cold air and the nucleation of ice is thermodynamically preferred. Importantly, the stage of freezing is very rapid because the heat is efficiently removed.6 Many physical systems in close situations are governed by similar kinetics, although of course each case is governed by its own internal energies. Understanding similarities and differences in terms of the nature of non-equilibrium fluctuations and correlations is the key point for the control of the conditions for the generation of metastable states.Magnetic Skyrmions (Sk) are nanometer sized topologically protected spin textures appearing in magnetic systems that exhibit Dzyalonshinskii–Moriya interaction (DMI).7,8 The nucleation of these structures in the metastable state is an interesting problem to address, since skyrmions have a non-trivial topology which should be constructed upon nucleation. Hence, in the present article, we investigate the kinetics of forming metastable skyrmions by following a non-adiabatic path produced by the application of a femtosecond laser pulse onto a ferromagnetic sample, i.e. by taking the spin system to a “superheated” far-from-equilibrium state with an excess of exchange energy. Finding conditions to get a metastable long-lived topologically-protected skyrmion phase and understanding its formation is especially important because of its technological relevance. Due to their reduced sizes, and transport properties (via spin-polarized currents), magnetic skyrmions are considered promising candidates as information carriers in the next-generation of spintronic devices9–12 or novel reservoir and neuromorphic computing.13,14 Among several possibilities, skyrmions in thin multilayer transition metals/high spin–orbit coupling materials9,12,15 are especially interesting due to their potential usage at room temperature (RT) and long-time thermal stability. The use of skyrmions in technological applications is constrained by the necessity to nucleate them. Since in thin film multilayers small Néel skyrmions in the absence of an external field are typically metastable structures,12 these skyrmions are usually nucleated in the presence of an external field, i.e. when they become the system ground state. Alternatively, special protocols such as bipolar current pulse trains,16 current injection through nanocontacts12 or specially designed patterned constrictions and injectors17,18 are employed.
Recently, research on optically induced ultrafast magnetization dynamics triggered by femtosecond laser pulses in ferro- and ferrimagnetic materials is gaining considerable interest given its localized and ultrafast character.19 In this scenario, non-equilibrium magnetization dynamics can be induced due to purely thermal magnetic excitations by ultrafast heat produced by a linearly polarized laser pulse.20 Particularly, it has been experimentally shown that skyrmionic bubbles (large ground state magnetic configurations) can be nucleated by applying ultra-fast laser pulses in ferrimagnetic21 or fully compensated synthetic antiferromagnetic structures respectively,22 in the absence of external fields. In recent works by Je et al.23 and Büttner et al.24 the nucleation of skyrmion lattices was obtained with laser pulses in ferromagnetic multilayers under constant magnetic field, i.e. in the conditions when skyrmions were the ground state. The fact that skyrmions were nucleated independently of the polarization of the laser source revealed that the nucleation of such topological structures was due to thermal fluctuations, i.e. either by overcoming the energy barrier from the saturated to the skyrmion state or by an adiabatic phase transition from the paramagnetic to the ferromagnetic skyrmion ground state. In the above situation the slow heating would also lead to the same results, but importantly the heating with pulse duration above 1 picosecond24 was sufficient to produce the phase transition. Numerical modeling of skyrmion nucleation under ultrafast laser-induced heating24–26 was also performed in the situation when skyrmions were the ground states. The question arises: is it possible to nucleate the skyrmion phase when it is metastable, i.e. in the absence of any external field by rapid energy pumping and cooling, as is reported in other physical systems?
In the present article we demonstrate, using atomistic spin dynamics (ASD) modelling, the efficient generation of small skyrmions (with diameters below 20 nm) in realistically parametrized Pt/Co(3ML)/Heavy-metal (HM) ferromagnetic trilayers27,28 in the absence of external fields and under the effect of a femtosecond laser excitation. It has been shown that Co layers sandwiched between different heavy metals exhibit a strong DMI that leads to stabilization of small skyrmions.15,28,29 Moreover, the large and tunable perpendicular magnetic anisotropy (PMA) of Co-based systems and the topological protection of these nanostructures can benefit their long-time thermal stability. Using this prototype system, we show that a zero-field slow cooling process from an initial paramagnetic state creates a stripe-domain configuration in accordance with previous work23,24 and the well-known behavior of systems with PMA. At the same time for a set of specific laser-pulse parameters with femtosecond duration, it is possible to nucleate skyrmions in the absence of magnetic fields due to the rapid energy pumping leading to creation and freezing of localized unstable spin excitations, called magnon droplets.30 We demonstrate that their topological protection arises on the hundreds of fs timescale although within this timeframe the topological charge fluctuates and stabilizes around 10 ps. We present a phase diagram of the skyrmion nucleation in terms of the laser pulse duration and intensity at zero and non-zero applied field. Application of an external field leads to the situation when skyrmions become the ground state and the ultrafast heating timescale is not necessary. Interestingly, we show that for certain applied fields, skyrmions with both polarizations (i.e. metastable and stable) can be obtained by varying the laser parameters. Finally, we present micromagnetic simulations resembling a laser pulse actuation on the central part of the sample, demonstrating that a pattern consisting of skyrmions surrounded by stripe domains is stable for longer timescale. We discuss that the ultrafast nucleation scenario resembles many other physical systems where metastable states are created by rapid energy pumping and cooling.1–6
2 Results
2.1 Laser-induced nucleation of skyrmions in zero-field
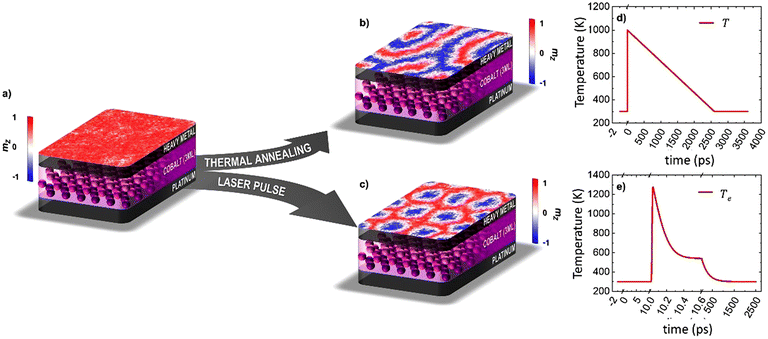
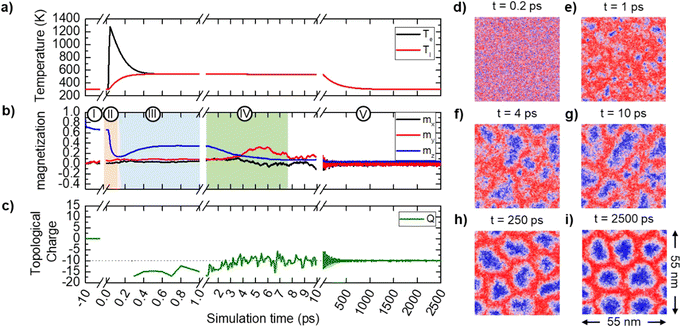
Our modelling is based on a thermodynamical approach where we explore non-equilibrium spin dynamics under the rapid action of high temperatures produced by the laser pulse. ASD models have demonstrated to be a powerful technique in studying laser-induced magnetization dynamics,20,24,31,32 concerning especially the rapid heating to temperatures close or above the Curie temperature Tc. The effect of the laser pulse is introduced in the ASD via the Two-Temperature Model (2TM),33 that couples the electronic temperature (Te) to the lattice temperature (Tl) and the laser power density P(t) (see Methods). The spin coupling to the electron temperature is defined by the coupling-to-the bath (atomistic damping) parameter. In a microscopic picture this parameter is proportional to the spin–flip probability34 which in turn is defined by the underlying mechanism and the spin–orbit coupling. Fig. 1 illustrates the nucleation protocols used in this work for skyrmion generation in zero external field. In our simulations we start from an initial saturated state with the magnetization pointing along the out-of-plane (OOP) direction (as indicated in Panel a) and equilibrate the system at room temperature (RT) (T = 300 K). Fig. 1a shows schematically the modelled Co trilayer. Following a quasi-equilibrium dynamical path via simulated thermal annealing, i.e., firstrapidly increasing temperature up to T = 1000 K > TC (TC = 754 K); see section 1 in (ESI†) and obtaining a paramagnetic state and then following a slow cooling process from this temperature to the RT as indicated in Fig. 1d. The final magnetic configuration (the most thermodynamically favorable one) consists in this case of labyrinth-like domains (Fig. 1b) as typically obtained in systems with PMA. In the following, we will refer as ground states of the systems at different temperatures to the most stable configurations that are reached following a slow field-cooling process from the paramagnetic state. On the contrary, starting from a saturated state (Fig. 1a) the application of a non-polarized laser pulse of fluence F0 = 5.6 mJ cm−2 and temporal width tp = 10 fs shown in Fig. 1e, excites highly non-equilibrium electronic states (leading to a non-equilibrium spin dynamics) which is responsible for the nucleation of a skyrmion lattice shown in Fig. 1c. As corresponds to these materials, the nucleated skyrmions are of the Néel type with the clock-wise chirality (see section 2 in ESI† for more details). Although in both cases the final temperature of the systems is RT, the nucleation of skyrmions is only achieved with ultrafast temperature dynamics resulting from the application of the femtosecond laser pulse, proving that the skyrmion lattice is a metastable configuration and that a non-equilibrium dynamical path is responsible for its generation. This is different from modelling results of ref. 25 and 26 where skyrmions were a ground state created due to a phase transition from ferromagnetic to the paramagnetic state and consequent cooling in which case there is no necessity for specific ultrafast non-equilibrium excitation. Note that at zero temperatures the difference between the skyrmion and the stripedomain energies in the simulated system of 55 nm is 0.33 × 10–18 J, the skyrmionic configuration being more energetic.Fig. 2 shows the temperature profile (Panel a) and the magnetization dynamics (Panel b) following the application of a laser pulse of tp = 50 fs and F0 = 6 mJ cm−2. After equilibrating the system for 10 ps (Region I, left white area in Fig. 2b) the laser pulse is applied, leading to an increased electronic temperature close or in this case even higher than the Curie temperature. The highly excited electrons change the spin thermal reservoir driving the system to a quasi-demagnetized state (Region II, yellow area in Fig. 2b). Eventually, a mutual thermalization between the electronic, lattice and spin subsystems takes place on the timescale of hundreds of femtoseconds (Region III, grey area in Fig. 2b). Finally, in Region IV (green area) and V (extreme right white region), the heat diffusion dissipates the deposited energy outside the system leading to its thermalization at RT.
Similar to the multi-scale domain nucleation processes in ferrimagnetic alloys,32 we can separate the ultrafast dynamics and the subsequent skyrmion lattice formation in several stages. First, the laser pulse rapidly quenches the magnetization (see Fig. 2d). The fast energy pumping into the spin system excites thermal high-frequency magnons with a non-equilibrium population.31 Due to the intrinsic delay in the transfer of energy between the electronic and the spin subsystems, although the electronic temperature is higher than TC, the magnetization is small but not zero, i.e. the spin system is still ferromagnetic and is characterized by the presence of correlations and strong excitations, as was reported in ultrafast magnetization switching modelling in amorphous ferrimagnets.31,35 As the temperature goes down, thermal magnons decay into magnons of lower frequency on longer timescale. The high-frequency magnons are also responsible for thermally activated nucleation processes. During the so-called magnon localization process (Region III, grey in Fig. 2b and e) the recovery of the ferromagnetic order takes place in localized areas of the system. The rapid energy input creates a state with an excess of the exchange energy, leading to the nucleation of unstable and localized spin textures, namely magnon droplets (MDs),30,32,36 following a non-equilibrium path in the spin configuration space. After a time-scale of hundreds of femtoseconds, following rapid cooling, the so-called magnon coalescence process starts (Region IV, green in Fig. 2b and f–g). MDs can scatter, split or merge until some quasi-equilibrium configuration is achieved (Fig. 2h). Relaxing the spin system to RT by a heat-sink coupling (Region Vin Fig. 2b), which occurs on the nanosecond timescale, little change in the spin dynamics is observed and the skyrmion structures remain stable versus thermal fluctuations at RT (Fig. 2i). To quantify the topology of the structures created by the laser pulse, we evaluate the total topological charge Q of the simulated system. For a discrete lattice, the topological charge is calculated as in Rózsa,37 based on the sum of spherical areas given by sets of 3 neighboring spins placed in a triangle. For a skyrmion lattice with a well-defined chirality of the domain walls and a unique skyrmion polarization PCore = ±1, the total topological charge of the system characterizes the number of nucleated skyrmions NSk, i.e. Q = NSkPCore. For the numerical characterization of the nucleated skyrmion lattices, independent of the simulated system size, we compute the topological charge surface density q = Q/S, S being the surface of the simulated sample (i.e. nm2).
The dynamics of the topological charge during the skyrmion nucleation is presented in Fig. 2c. The topological charge is zero during the pre-equilibration time (t < 0) as the system is saturated along the positive axis of the OOP direction. When the laser is introduced and the electronic temperature is drastically increased above TC, the topological charge strongly fluctuates and it can even show spurious large positive and negative values. Once the magnon localization has taken place starting at ca. 300 fs, the topological charge acquires meaningful values demonstrating that the magnon drops start to gain a topological character. However, topological charge fluctuates due to the fact that those magnon drops that have not earned topological stability, or those with an unstable topological protection, rearrange and merge until a certain number of them survive. Up to 17 topologically protected MDs were observed in this simulation, although finally only 10 survived. Thus, the complete topological phase transition associated to the nucleation of topological spin texture does not occur until the magnon localization takes place at a time t ≈ 0.3–0.5 ps. For the presented simulation, at t = 4 ps the topological charge stabilizes around the constant value Q = −10. Note that, although thermal fluctuations are quite large (T = 450 K), no new skyrmions are arising neither they disappear after this time. Following the observations made during the present study with many thermal realizations, we deduce that in all cases the complete topological protection is acquired in timescales of several picoseconds.
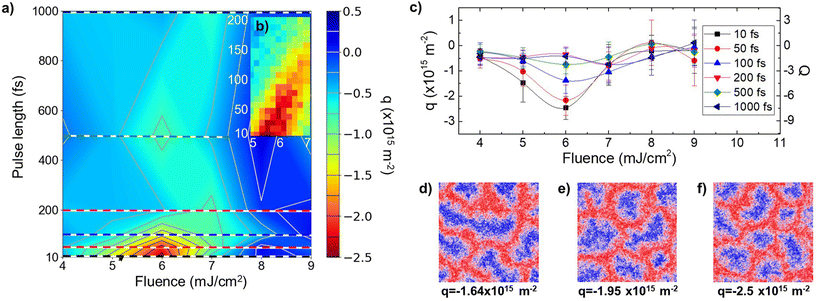
To find the optimum conditions for the nucleation of skyrmion lattices, we have computed the phase diagram of the topological charge density q as function of laser-pulse width tp and fluence F0 in the absence (Fig. 3) and in the presence (Fig. 4) of a magnetic external field. This is computed at a short time (250 ps) after the laser pulse is applied, but when all three subsystems (electrons, phonons and spins) are in mutual equilibrium, i.e. have the same temperature. After this time, skyrmions remain stable in our simulations. To neglect the effect of a subsequent slow thermal relaxation, a vanishing heat-sink coupling (i.e. κe = 0, see Methods) is considered. Due to the stochastic nature of the dynamics in the presence of temperature, the computed phase diagrams were averaged over 10 random realizations. It is important to note that the skyrmions can nucleate either with their core pointing parallel (P-Sk), i.e. q > 0, or antiparallel (AP-Sk) i.e. q < 0, to the initial magnetization direction.
Fig. 3a shows the nucleation results in zero external field. The diagram indicates that the skyrmion nucleation takes place for short pulse durations (below tp < 200 fs) and in a window of fluences around F0 = 6 mJ cm−2 (see region in Panel b). Fig. 3c presents the topological charge density dependence on the laser fluence for selected laser pulse lengths (corresponding to the horizontal lines in Fig. 3a). It can be observed that |q| increases initially with the fluence, showing a maximum at a fluence of about 6 mJ cm−2, which corresponds to 8 skyrmions generated in the simulated area (see Fig. 3f). By analyzing the spin configurations, a well-defined skyrmion lattice can be obtained with a minimum topological density of |q| ≈ 1.9 × 1015 m−2. This value is considered here as a criterion for the nucleation of a skyrmion lattice. For smaller values of |q|, labyrinth-like domains coexisting with skyrmions are obtained.
A closer inspection of the magnetization dynamics reveals that the successful nucleation of skyrmion lattices depends on two aspects: (i) it is necessary to populate the sample with a sufficiently large number of MDs during the magnon localization; (ii) once the MDs are nucleated, they must gain topological protection so their merging is impeded. Thus, for short pulses and below F0 ≤ 5 mJ cm−2 the system is not demagnetized sufficiently to nucleate a large number of MDs. At the same time, the topological protection is achieved with fast cooling. For fluences larger than F0 > 7 mJ cm−2 the energy deposited in the system is too high and the temperature fluctuations are too strong to allow for stable MDs that merge into larger labyrinth-like domains (ground state). For pulses longer than 200 fs, the system stays longer at high temperature and thermal activation is therefore more likely to lead the system towards the ground state. The detailed analysis (see discussion in section 3 of ESI†) shows that the MD creation requires a large demagnetization below 0.25 (in reduced units) and the quasi-equilibrium laser-induced temperatures below 580 K. Thus, the competition of different factors defines a unique window for laser parameters where the skyrmion lattice is obtained.
2.2 Laser-induced nucleation of skyrmions in applied field
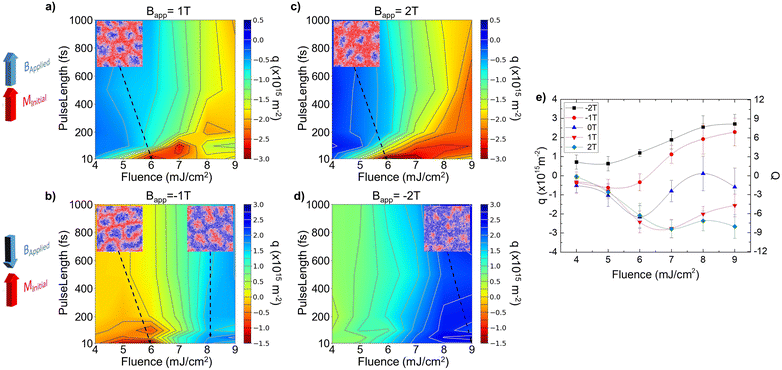
Fig. 4 shows the nucleation phase diagrams under different magnetic fields that are applied parallel (Bapp > 0) or anti-parallel (Bapp < 0) to the initial magnetization direction. Note that the above situations are not equivalent since the anti-parallel field is expected to stabilize skyrmions while the parallel one – to destabilize them and to promote the saturated state. Another important difference is related to the dependence of the skyrmion size on the applied field (see section 6 in ESI†). Particularly, under positive applied field skyrmion sizes are reduced. Focusing on short pulses (below tp < 200 fs) for applied fields parallel to the initial magnetization direction (Fig. 4a and c) we observe that the region where skyrmion lattices are obtained is substantially increased for fluences F0 > FC = 6 mJ cm−2 with respect to what is observed at zero field. This behavior can be ascribed to the hindering of the growth of domains oriented antiparallel to the field.Fig. 4b and d show the nucleation phase diagrams for anti-parallel fields. Very interestingly, as can be observed in Fig. 4b and e (red line), both positive and negative polarizations of skyrmion core (i.e. stable and metastable skyrmions) can be obtained with field Bapp = −1T for short pulse durations. This happens because under an applied negative field, a ferromagnetic system can undergo ultrafast switching. In this case, the MDs are nucleated with their core pointing parallel to the initial magnetization. Thus, P-Sk lattices arise and the topological charge density carries a positive sign. The negative q values correspond to metastable states in this case, showing again the possibility to nucleate them with ultrafast laser pulses. In this case, once the skyrmion is created, an external field parallel to its core increases the energy barrier separating it from the other states,38,39 and the structure is more stable against fluctuations. For Bapp = −2T, the Co trilayer magnetization always switches its orientation. The effect of external fields is summarized in Fig. 4e for a fixed ultrashort pulse width of tp = 50 fs.
It is worth noting that in the presence of external fields of these magnitudes, the skyrmion lattices are stable ground states of the system (see Fig. S5 in section 4 of ESI† where we present the states obtained via slow cooling process from an initial paramagnetic state and under applied field). Consequently, under sufficiently long heating and subsequent cooling (for pulses longer than tp ≥ 200 fs and high fluences), the system reaches the skyrmion state. This effect, which agrees with the results presented in ref. 24, suggests that for such pulse durations, the nucleation of skyrmion lattices is due to a phase transition from the paramagnetic state towards the skyrmion ground state. The latter results go along with the fact that for pulses larger than tp ≥ 200 fs in Fig. 4 the trends observed barely depend on the laser pulse duration. Importantly, there is a substantial influence of the non-equilibrium excitation. For example, in Fig. 4a the region with fluences larger than F0 > 8 mJ cm−2 and for tp < 200 fs does not show the formation of the stable skyrmion lattice, while for less intense pulses the skyrmion lattice is nucleated. This effect reveals once again that for pulses below tp < 200 fs the system follows a non-equilibrium excitation in such a way that it is possible to access metastable states different to the ground states obtained for longer pulses (tp ≥ 200 fs).
2.3 Comparison between nucleation with ultrafast, fast and adiabatic protocols
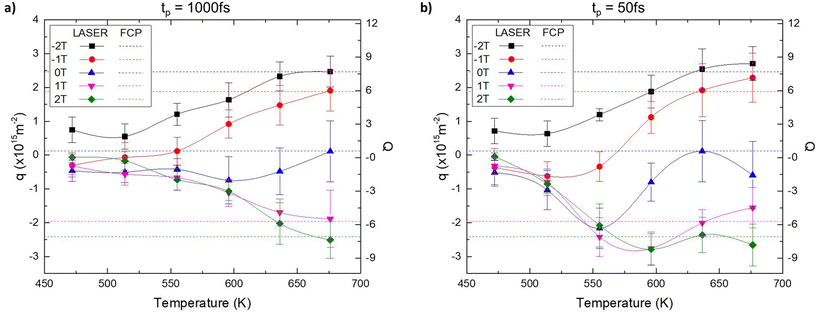
The role of the non-equilibrium character of the laser-induced nucleation of skyrmion lattices is emphasized by contrasting them with the ground states of the system (see Fig. S5 in section 4 of ESI†) obtained when following a slow field cooling process (FCP) from an initial paramagnetic state. In Fig. 5 we present the comparison of the topological charge density computed when following a FCP (dashed lines) and an ultrafast laser heating with 1 ps (Fig. 5a) and 50 fs (Fig. 5b) laser pulses (symbols and solid lines). The final temperatures for the FCP were selected to be comparable to the final quasi-equilibrium temperatures after a laser pulse. Note that the topological charge is strongly fluctuating and its values were averaged for time series during the last simulated picosecond time interval.During the FCP, the computed topological charge depends on the applied field as expected given the reduced skyrmion sizes due to increased applied fields (see section 6 in ESI†). Although the skyrmion size increases with temperature, the number of nucleated skyrmions is almost constant and consequently, the topological density is independent of final temperature. It is also important to note that the behavior of the absolute value of |q| is in this case symmetric with respect to the applied field direction (due to the fact that the skyrmions were nucleated from the paramagnetic state). For applied fields |Bapp| = 2T and |Bapp| = 1T we obtain values of the topological charge density around |q| ≈ 2.5 × 1015 m−2 and |q| ≈ 2 × 1015 m−2 respectively.
Next we focus on the long pulses cases (Panel a) in which the system reaches its final state by following a 1 ps laser pulse (solid lines and symbols). For low fluences (i.e. low temperatures) the system does not reach a skyrmion lattice, but rather some small number of skyrmions and labyrinth-like domains coexist. It is important to note that now the situation is not symmetric with respect to the field sign change. Indeed, for a positive applied field Bapp = 1T with a fluence below F0 < 6 mJ cm−2 (purple solid triangles for temperatures T < 550 K) AP-Sk (i.e. q < 0) are nucleated, similarly to the field Bapp = −1T. For larger fluences the situation gradually approached the FCP case. It is interesting to mention that at these pulse durations, the level of demagnetization after the laser is applied starts to be independent of the laser fluence. The latter shows that these timescale and thermal excitations lead to the phase transition to a stable (ground) skyrmion state.
Now, we consider the results for short laser-pulses (solid symbols at Panel b). The asymmetry with respect to the change of the field sign is now larger and the values of the topological charge higher. In the absence of an applied field (blue solid triangle), the skyrmion densities are similar to the ones obtained by FCP under an external field of Bapp = 2T, indicating a metastable skyrmion lattice. The largest number of nucleated skyrmions (|q| ≈ 3 × 10–15 m−2) is obtained at T ≈ 580 K. Thus, the strong asymmetry with respect to the opposite fields |q(Bapp = +2)| ≫ |q(Bapp = −2)| reinforces the picture in which the skyrmion survival is defined by MD nucleation and quenching due to non-equilibrium dynamics (see further discussions in section 5 of ESI†). When the final temperatures are larger than T > 580 K (i.e. F0 > 6 mJ cm−2) the skyrmion densities converge to the equilibrium case. In these cases, the final temperature is so large that the transition to the ground state through thermal activation is more likely to occur and the evolution of the system is similar to the adiabatic FCP.
2.4 Longer-time simulations of an extended system
Due to the limitation of the atomistic approach the simulated system corresponds roughly to 55 nm × 55 nm and most of images are taken at a quasi-equilibrium temperature around T ≈ 450 K. Larger simulations are possible with micromagnetics, however those should use temperature-dependent macroscopic parameters. We also point out that in the ASD model the magnetostatic interaction is not considered due to computational limitations. It is known that on the ultrafast timescale and at high temperatures (leading to very non-collinear spins) magnetostatic interaction plays a very minor role. Consequently, we do not expect this interaction to play a significant role in the nucleation of magnon droplets, as it is fully screened by the strong inter-site exchange interaction due to the system disordering and even it would help to prevent the merging of topologically protected skyrmions during the magnon coalescence phase. However, it will play a role on much longer timescales when the temperature cools down. It will be also responsible for the increase of the skyrmion sizes as the average magnetization is recovered.Furthermore, the ASD simulations are performed under the assumption that the energy of the laser pulse is homogeneously deposited in the whole system, even though in laboratory experiments, the laser spot has a finite micron size and is characterized by a temperature gradient. In this case, the nucleation of skyrmions will take place most probably in the central part of the spot but their long-time relaxation dynamics will be affected by the temperature gradient and magnetostatic interactions. Additionally, our modelled skyrmions are constrained due to the finite size of the simulated system and their mutual interaction. In the absence of periodic boundary conditions and with more realistic laser pulse temperature distribution, a slow expansion of the magnetic skyrmions lattice is expected with time (as observed experimentally in ref. 23), along with a convergence of the radii towards a single value that depends solely on the magnetic parameters.
In our attempt to reproduce this effect on a longer timescale with a finite spot size we perform micromagnetic simulations on a larger system (with lateral dimension of 512 nm) and for longer timescale. The micromagnetic parameters were evaluated at 300 K following the scaling relations with magnetisation: (see section 7 in ESI†) which ensure a similar skyrmion size as obtained in the ASD at this temperature. The initial state (see Fig. 6a) corresponded to 37 skyrmions placed on a hexagon lattice in the sample centre with the sizes and distances from that of the atomistic simulations. The magnetostatic energy is now present. The system was then integrated at 300 K during 5 ns. The resulting pattern is presented in Fig. 6b. We observe the survival of skyrmions in the centre of the simulated area while those at the edge merge with the stripe domains. The distances between skyrmions and their sizes slightly increase, however skyrmions remain confined inside the stripe domain pattern which do not allow further expansion of the skyrmion lattice. This structure is similar to the one experimentally observed by Je et al.23
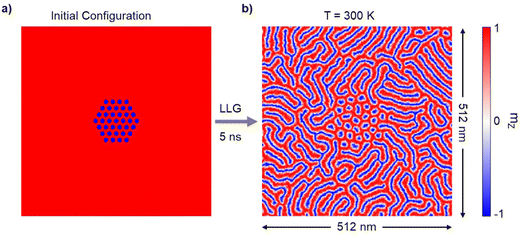 | ||
| Fig. 6 Extended micromagnetic simulations emulating skyrmion nucleation in the sample center by laser pulse. (a) An initial configuration consisting of the skyrmion lattice with sizes and distances as nucleated by the atomistic simulations was placed in the sample center. Temperature-dependent micromagnetic parameters (see section 7 in ESI†) were used. (b) The resulting configuration obtained by micromagnetic simulations after integrating the system during 5 ns in the presence of thermal fluctuations at 300 K. | ||
3 Conclusions
In the present work we have modelled the linearly-polarized laser (heat-induced) nucleation of skyrmion lattices in epitaxial cobalt-based asymmetric trilayers with perpendicular magnetic anisotropy and Dzyaloshinkii–Moriya interactions. For zero applied field, the system presents a ground state with labyrinth-like domains. The computed phase diagram for topological charge shows a nucleation window for skyrmions in terms of laser pulse intensity and duration, corresponding to ultra-fast laser pulses shorter than tp < 200 fs. This shows the importance of a highly thermodynamically non-equilibrium path for skyrmion generation. This path involves magnon droplets nucleation after the sample demagnetization, and stable creation of their topological protection (created in the hundreds of fs timescale) during the magnon coalescence following the ultrafast cooling. Importantly, the results show that it is possible to nucleate metastable skyrmion lattices in the absence of external fields by following non-equilibrium magnetization dynamics. Additionally, external fields enlarge the nucleation window and change the nucleation probability. Interestingly, even under applied fields, both stable and metastable skyrmion lattices can be created with ultrafast lasers. These results are important for the control of skyrmion nucleation for novel applications.It is worth emphasizing that the magnetization dynamics leading to the generation of metastable skyrmion lattices can only be excited by femtosecond lasers following a rapid temperature change in the timescale below 1 ps, i.e. in a highly thermodynamically non-equilibrium situation. Instead, slow zero-field cooling from a temperature above TC in a time scale of a few nanoseconds always leads to a complex labyrinth-like configuration. By applying external fields, skyrmions become the system ground state and the heating/cooling processes with sufficient duration always lead to a skyrmion lattices so the use of an ultrafast source is not necessary. We observed that all heating/cooling scenarios share the same fundamental mechanisms of magnon droplets nucleation via the action of short-range exchange interactions. This is understandable since the heterogeneous nucleation of the stable phase inside the metastable one would also involve the formation of magnonic drops that serve as aggregation centers for the stable phase. However, it also indicates that there must exist essential differences of the ultrafast laser-induced dynamics which leads to nucleation of the long-time living metastable phase.
Our understanding of the process is based on physics of ultrafast magnetization dynamics on femtosecond timescale which is characterized by strong non-equilibrium between electrons, phonons and spin energies. During the laser excitation on this timescale, the spin system is brought to a “superheated” state with an excess of the exchange energy. Indeed, the laser energy is rapidly pumped into the system and the electronic temperature rises close to or even higher than the Curie temperature. However, the spin system on this timescale is slower20,31,35 and not able to follow the electronic temperature, remaining in the ferromagnetic low magnetization correlated state characterized by very strong fluctuations. Importantly, on the femtosecond timescale the spin system practically does not exchange energy with the external environment and the dynamics is mainly governed by exchange interactions. Our analysis shows that this state is characterized by a large amount of magnon droplets and much larger dispersion in the number of nucleated skyrmions as compared to the FCP nucleation. This indicates that the skyrmion nucleation is defined by the survival of magnetic droplets rather than by their temperature-dependent equilibrium properties. Importantly, magnon droplets already have the shape of skyrmions and show topological protection on the fs timescale. A stabilized state is achieved on timescales of around ≈10 ps. Note that for long pulses (i.e. tp = 1000 fs) the trends of the topological charge are symmetric with respect to the sign of external fields, whereas for short pulses, the computed topological charges show an asymmetric behavior. We relate the former with the possibility of manipulating the magnon growth using external fields. Thus, for short pulses we can impede the merging of two magnons by reducing their growth enough to gain topological protection before they meet.
It is known from literature that when the system is relaxed from a disordered state, topologically non-trivial structures can be quenched.40 One would expect the above process to be stochastic in nature and that the topological charge would be a strongly fluctuating property. Herewith, in contrast, we nucleate skyrmions from an ordered saturated state without going to a real paramagnetic state since the magnetization never reaches the zero value. Also, although fluctuating, the topological charge acquires (on average) a non-zero large value. Our results indicate an important interplay of intensities and timescales for energy pumping and heat transfer which defines the laser parameter window accessed by femtosecond lasers only. A relatively small parameter window probably explains why zero-field nucleation of metastable skyrmions has not been observed in experiments up to now.23,24 In contrast, nucleation of skyrmions in the situation when they are stable involves a phase transition from paramagnetic to ferromagnetic (skyrmion ground state) phases. This transition is very robust in terms of laser parameters. In fact, the ultrafast heating is not really necessary and as it is shown in ref. 24 any heating with the timescale above 1 ps is sufficient.
Our final remark is about the importance of the spin–orbit coupling in the ultrafast magnetization dynamics.41 From a basic physics viewpoint, all microscopic processes leading to energy uptake and its subsequent relaxation involve spin–flip phenomena and are defined by the spin–orbit coupling. In our model, its value is phenomenologically included in the coupling-to-the bath (damping) parameter.34 Note that the reversal window and laser fluency necessary for skyrmion creation has been calculated for one value of this parameter. A smaller value could be compensated by larger pulse intensities but ultimately very small damping impedes the system to take sufficient thermal energy and skyrmion nucleation will not be possible. Note that typical multilayers systems hosting skyrmions have large damping values due to the influence of interfaces.
Our results underline the similarity of most physical situations in which the nucleation of metastable states is achieved by rapid energy pumping and subsequent transfer to the environment. The overall nucleation process resembles the nucleation of supercooled droplets freezing on surfaces.6 Similar to our case, the freezing stage in this case is very rapid and is accelerated by the efficient removal of the generated heat by the unsaturated gas flow.6 This also underlines the hydrodynamic analogy of spin systems noticed by Iacocca et al.32 In brief, as the skyrmions at zero field, the supercooled ice droplets, which exist in a vapor clouds below the transition temperature, are metastable state too. The ice droplets can be nucleated directly from the gas by rapidly remove heat. This is exactly the same way the ultra fast laser excitation temporarily drives the ferromagnetic system above the Curie temperature in a metastable state, which is not a paramagnetic since since it conserves all correlations. Indeed, slow cooling in the water dropletcase would make them water and in our case – would nucleate stripe domains instead of the skyrmions. Many other similarities can be noticed as for example, that the metastable skyrmions are created in the conditions when they acquire the topological creation of metastable phases in colloidal crystals which take place because the nucleation kinetics of the stable phase is slower than that of an intermediate metastable phase.1 Similarly, in light-induced melting of charge density waves40 metastable topological defects are created and play an important role in the dynamics of slow recovery.
4 Methods
4.1 Atomistic simulations
The ASD simulations were carried out using the software package VAMPIRE.42 The spin Hamiltonian, consisting of the Heisenberg exchange, anisotropy, Zeeman and DMI energies, is written as: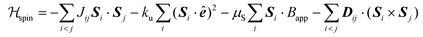 | (1) |
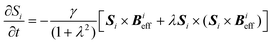 | (2) |
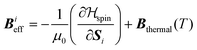 contains contributions from
contains contributions from
| Atomistic | Micromagnetic (0 K) | Micromagnetic (300 K) |
|---|---|---|
| μ S = 1.61μB | M S = 1.35 MA m−1 | M S = 1.11 MA m−1 |
| J ij = 4.8 × 10−21 J per atom | A ex = 14.8 pJ m−1 | A ex = 10.4 pJ m−1 |
| D ij = 4.8 × 10−22 J per atom | D ind = 9 mJ m−2 | D ind = 6.3 mJ m−2 |
| k u = 5.85 × 10−24 J per atom | K u = 0.53 MJ m−3 | K u = 0.29 MJ m−3 |
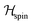 and it is augmented by the stochastic thermal field Bthermal(T) coupled to the electronic temperature Tevia the scattering mechanisms. The thermal stochastic field is introduced following the usual Langevin dynamics as
and it is augmented by the stochastic thermal field Bthermal(T) coupled to the electronic temperature Tevia the scattering mechanisms. The thermal stochastic field is introduced following the usual Langevin dynamics as 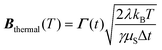 where Γ(t) is a 3D Gaussian distribution with a mean of zero and standard deviation equal to one and T = Te.42 The electron temperature is governed by the Two-Temperature Model (2TM).33 This model couples the electronic Te and lattice Tl temperatures of the system with the laser power density P(t):
where Γ(t) is a 3D Gaussian distribution with a mean of zero and standard deviation equal to one and T = Te.42 The electron temperature is governed by the Two-Temperature Model (2TM).33 This model couples the electronic Te and lattice Tl temperatures of the system with the laser power density P(t):
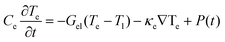 | (3) |
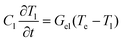 | (4) |
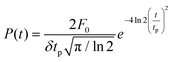 | (5) |
For micromagnetic modelling the standard micromagnetic software MuMax3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 49 with thermal fluctuations was employed. The micromagnetic parameters were considered temperature-dependent and scaled with magnetization as indicated in Table 1 and further discussed in the section 7 of ESI.†
49 with thermal fluctuations was employed. The micromagnetic parameters were considered temperature-dependent and scaled with magnetization as indicated in Table 1 and further discussed in the section 7 of ESI.†
4.2 The field-cooling protocol
In these simulations the system is initially placed at a temperature T = 1000 K and is cooled down at a constant rate of dT/dt = 175 K ns−1 until different final temperatures are reached. In all cases the LLG equation is integrated during a total simulated time of 4.5 ns. In order to minimize the thermal noise, the final states have been averaged during the last 100 ps of simulation when the skyrmions were stable.Data availability statement
Data for this paper, included in both the manuscript and the ESI† figures are available online (at https://zenodo.org/record/7032453).Author contributions
P. O.-R., M. S., P. P., R. C. and O. C.-F. conceived and designed the project. P. O.-R. and M. S. designed and conducted the simulations. P. O.-R and P. G. wrote the scripts for data analysis. P. O.-R., M. S., S. R., A. G., P. P., R. C. and O. C.-F. analyzed the results. All authors contributed to the writing and revision of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the networking opportunities provided by the European COST Action CA17123 “Magnetofon” and in particular the short-time scientific missions awarded to P. O.-R. and M. S. The work in Spain was supported by the Regional Government of Madrid through project P2018/NMT-4321 (NANOMAGCOST-CM) and by the Ministry of Science and Innovation MCIN/AEI through projects RTI2018-097895-B-C42 (FUN-SOC) and PID2021-122980OB-C52 (ECLIPSE-ECoSOx) respectively. This project has received funding from the European Union's Horizon 2020 research and innovation programme under grant agreement no. 737093 FEMTOTERABYTE and under the Marie Skłodowska-Curie grant agreement no. 861300 COMRAD as well as the FLAG-ERA JTC2019 Project SOgraphMEM (MINECO PCI2019-111867-2). IMDEA Nanoscience Institute is supported by the “Severo Ochoa” Programme for Centres of Excellence in R&D, (MINECO grant SEV-2016-0686). We acknowledge Dr Rubén Guerrero for fruitful discussions. We acknowledge NVIDIA corporation for the donation of the GPU Quadro P6000 used in the micromagnetic simulations.References
- A. Inoue, T. Minemura, A. Kitamura and T. Masumoto, Metall. Mater. Trans. A, 1981, 12, 1041–1046 CrossRef CAS.
- R. Alert, P. Tierno and J. Casademunt, Nat. Commun., 2016, 7, 1–7 CrossRef PubMed.
- A. Starikovskiy, Y. Yang, Y. I. Cho and A. Fridman, Plasma Sources Sci. Technol., 2011, 20, 024003 CrossRef.
- M. Kobayashi and H. Tanaka, Nat. Commun., 2016, 7, 1–8 Search PubMed.
- M. Schneider, T. Brächer, D. Breitbach, V. Lauer, P. Pirro, D. A. Bozhko, H. Y. Musiienko-Shmarova, B. Heinz, Q. Wang, T. Meyer, F. Heussner, S. Keller, E. T. Papaioannou, B. Lägel, T. Löber, C. Dubs, A. N. Slavin, V. S. Tiberkevich, A. A. Serga, B. Hillebrands and A. V. Chumak, Nat. Nanotechnol., 2020, 15, 457–461 CrossRef CAS PubMed.
- S. Jung, M. K. Tiwari, N. V. Doan and D. Poulikakos, Nat. Commun., 2012, 3, 1–8 Search PubMed.
- I. Dzyaloshinsky, J. Phys. Chem. Solids, 1958, 4, 241–255 CrossRef CAS.
- T. Moriya, Phys. Rev., 1960, 120, 91 CrossRef CAS.
- A. Fert, N. Reyren and V. Cros, Nat. Rev. Mater., 2017, 2, 17031 CrossRef CAS.
- R. Wiesendanger, Nat. Rev. Mater., 2016, 1, 1–11 Search PubMed.
- S. Krause and R. Wiesendanger, Nat. Mater., 2016, 15, 493–494 CrossRef CAS PubMed.
- J. Sampaio, V. Cros, S. Rohart, A. Thiaville and A. Fert, Nat. Nanotechnol., 2013, 8, 839–844 CrossRef CAS PubMed.
- Y. Huang, W. Kang, X. Zhang, Y. Zhou and W. Zhao, Nanotechnology, 2017, 28, 08LT02 CrossRef PubMed.
- G. Bourianoff, D. Pinna, M. Sitte and K. Everschor-Sitte, AIP Adv., 2018, 8, 055602 CrossRef.
- C. Moreau-Luchaire, C. Moutafis, N. Reyren, J. Sampaio, C. A. Vaz, N. Van Horne, K. Bouzehouane, K. Garcia, C. Deranlot, P. Warnicke, P. Wohlhüter, J. M. George, M. Weigand, J. Raabe, V. Cros and A. Fert, Nat. Nanotechnol., 2016, 11, 444–448 CrossRef CAS.
- S. Woo, K. Litzius, B. Krüger, M. Y. Im, L. Caretta, K. Richter, M. Mann, A. Krone, R. M. Reeve, M. Weigand, P. Agrawal, I. Lemesh, M. A. Mawass, P. Fischer, M. Kläui and G. S. Beach, Nat. Mater., 2016, 15, 501–506 CrossRef CAS.
- W. Jiang, P. Upadhyaya, W. Zhang, G. Yu, M. B. Jungfleisch, F. Y. Fradin, J. E. Pearson, Y. Tserkovnyak, K. L. Wang, O. Heinonen, S. G. Te Velthuis and A. Hoffmann, Science, 2015, 349, 283–286 CrossRef CAS PubMed.
- S. Finizio, K. Zeissler, S. Wintz, S. Mayr, T. Weßels, A. J. Huxtable, G. Burnell, C. H. Marrows and J. Raabe, Nano Lett., 2019, 19, 7246–7255 CrossRef CAS PubMed.
- A. Kirilyuk, A. V. Kimel and T. Rasing, Rev. Mod. Phys., 2010, 82, 2731–2784 CrossRef.
- T. A. Ostler, J. Barker, R. F. Evans, R. W. Chantrell, U. Atxitia, O. Chubykalo-Fesenko, S. El Moussaoui, L. Le Guyader, E. Mengotti, L. J. Heyderman, F. Nolting, A. Tsukamoto, A. Itoh, D. Afanasiev, B. A. Ivanov, A. M. Kalashnikova, K. Vahaplar, J. Mentink, A. Kirilyuk, T. Rasing and A. V. Kimel, Nat. Commun., 2012, 3, 1–6 Search PubMed.
- M. Finazzi, M. Savoini, A. R. Khorsand, A. Tsukamoto, A. Itoh, L. Duò, A. Kirilyuk, T. Rasing and M. Ezawa, Phys. Rev. Lett., 2013, 110, 177205 CrossRef CAS PubMed.
- R. Juge, N. Sisodia, J. U. Larrañaga, Q. Zhang, V. T. Pham, K. G. Rana, B. Sarpi, N. Mille, S. Stanescu, R. Belkhou, M.-A. Mawass, N. Novakovic-Marinkovic, F. Kronast, M. Weigand, J. Gräfe, S. Wintz, S. Finizio, J. Raabe, L. Aballe, M. Foerster, M. Belmeguenai, L. D. Buda-Prejbeanu, J. Pelloux-Prayer, J. M. Shaw, H. T. Nembach, L. Ranno, G. Gaudin and O. Boulle, Nat. Commun., 2022, 13, 4807 CrossRef CAS PubMed.
- S. G. Je, P. Vallobra, T. Srivastava, J. C. Rojas-Sánchez, T. H. Pham, M. Hehn, G. Malinowski, C. Baraduc, S. Auffret, G. Gaudin, S. Mangin, H. Béa and O. Boulle, Nano Lett., 2018, 18, 7362–7371 CrossRef CAS.
- F. Büttner, B. Pfau, M. Böttcher, M. Schneider, G. Mercurio, C. M. Günther, P. Hessing, C. Klose, A. Wittmann, K. Gerlinger, L. M. Kern, C. Strüber, C. von Korff Schmising, J. Fuchs, D. Engel, A. Churikova, S. Huang, D. Suzuki, I. Lemesh, M. Huang, L. Caretta, D. Weder, J. H. Gaida, M. Möller, T. R. Harvey, S. Zayko, K. Bagschik, R. Carley, L. Mercadier, J. Schlappa, A. Yaroslavtsev, L. Le Guyarder, N. Gerasimova, A. Scherz, C. Deiter, R. Gort, D. Hickin, J. Zhu, M. Turcato, D. Lomidze, F. Erdinger, A. Castoldi, S. Maffessanti, M. Porro, A. Samartsev, J. Sinova, C. Ropers, J. H. Mentink, B. Dupé, G. S. Beach and S. Eisebitt, Nat. Mater., 2021, 20, 30–37 CrossRef PubMed.
- W. Koshibae and N. Nagaosa, Nat. Commun., 2014, 5, 1–11 Search PubMed.
- S. Lepadatu, Phys. Rev. B, 2020, 102, 094402 CrossRef CAS.
- R. Moreno, R. F. Evans, S. Khmelevskyi, M. C. Muñoz, R. W. Chantrell and O. Chubykalo-Fesenko, Phys. Rev. B, 2016, 94, 104433 CrossRef.
- H. Yang, A. Thiaville, S. Rohart, A. Fert and M. Chshiev, Phys. Rev. Lett., 2015, 115, 267210 CrossRef PubMed.
- O. Boulle, J. Vogel, H. Yang, S. Pizzini, D. De Souza Chaves, A. Locatelli, T. O. Menteş, A. Sala, L. D. Buda-Prejbeanu, O. Klein, M. Belmeguenai, Y. Roussigné, A. Stashkevich, S. M. Chérif, L. Aballe, M. Foerster, M. Chshiev, S. Auffret, I. M. Miron and G. Gaudin, Nat. Nanotechnol., 2016, 11, 449–454 CrossRef CAS.
- F. Macià and A. D. Kent, J. Appl. Phys., 2020, 128, 100901 CrossRef.
- J. Barker, U. Atxitia, T. A. Ostler, O. Hovorka, O. Chubykalo-Fesenko and R. W. Chantrell, Sci. Rep., 2013, 3, 1–6 Search PubMed.
- E. Iacocca, T. M. Liu, A. H. Reid, Z. Fu, S. Ruta, P. W. Granitzka, E. Jal, S. Bonetti, A. X. Gray, C. E. Graves, R. Kukreja, Z. Chen, D. J. Higley, T. Chase, L. Le Guyader, K. Hirsch, H. Ohldag, W. F. Schlotter, G. L. Dakovski, G. Coslovich, M. C. Hoffmann, S. Carron, A. Tsukamoto, A. Kirilyuk, A. V. Kimel, T. Rasing, J. Stöhr, R. F. Evans, T. Ostler, R. W. Chantrell, M. A. Hoefer, T. J. Silva and H. A. Dürr, Nat. Commun., 2019, 10, 1–11 CrossRef CAS PubMed.
- L. Jiang and H. L. Tsai, J. Heat Transfer, 2005, 127, 1167–1173 CrossRef CAS.
- P. Nieves, D. Serantes, U. Atxitia and O. Chubykalo-Fesenko, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 104428 CrossRef.
- N. Kazantseva, U. Nowak, R. W. Chantrell, J. Hohlfeld and A. Rebei, Europhys. Lett., 2007, 81, 27004 CrossRef.
- M. D. Maiden, L. D. Bookman and M. A. Hoefer, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 180409 CrossRef.
- L. Rózsa, E. Simon, K. Palotás, L. Udvardi and L. Szunyogh, Phys. Rev. B, 2016, 93, 024417 CrossRef.
- F. Tejo, A. Riveros, J. Escrig, K. Y. Guslienko and O. Chubykalo-Fesenko, Sci. Rep., 2018, 8, 1–10 CAS.
- R. Tomasello, K. Y. Guslienko, M. Ricci, A. Giordano, J. Barker, M. Carpentieri, O. Chubykalo-Fesenko and G. Finocchio, Phys. Rev. B, 2018, 97, 060402 CrossRef CAS.
- A. Zong, A. Kogar, Y. Q. Bie, T. Rohwer, C. Lee, E. Baldini, E. Ergeçen, M. B. Yilmaz, B. Freelon, E. J. Sie, H. Zhou, J. Straquadine, P. Walmsley, P. E. Dolgirev, A. V. Rozhkov, I. R. Fisher, P. Jarillo-Herrero, B. V. Fine and N. Gedik, Nat. Phys., 2018, 15, 27–31 Search PubMed.
- C. Boeglin, E. Beaurepaire, V. Halté, V. López-Flores, C. Stamm, N. Pontius, H. A. Dürr and J. Y. Bigot, Nature, 2010, 465, 458–461 CrossRef CAS PubMed.
- R. F. Evans, W. J. Fan, P. Chureemart, T. A. Ostler, M. O. Ellis and R. W. Chantrell, World J. Condens. Matter Phys., 2014, 26, 103202 CrossRef CAS PubMed.
- F. Ajejas, V. Křižáková, D. De Souza Chaves, J. Vogel, P. Perna, R. Guerrero, A. Gudin, J. Camarero and S. Pizzini, Appl. Phys. Lett., 2017, 111, 202402 CrossRef.
- F. Ajejas, A. Gudín, R. Guerrero, A. Anadón Barcelona, J. M. Diez, L. De Melo Costa, P. Olleros, M. A. Niño, S. Pizzini, J. Vogel, M. Valvidares, P. Gargiani, M. Cabero, M. Varela, J. Camarero, R. Miranda and P. Perna, Nano Lett., 2018, 18, 5364–5372 CrossRef CAS PubMed.
- P. Olleros-Rodríguez, R. Guerrero, J. Camarero, O. Chubykalo-Fesenko and P. Perna, ACS Appl. Mater. Interfaces, 2020, 12, 25419–25427 CrossRef PubMed.
- P. J. Metaxas, J. P. Jamet, A. Mougin, M. Cormier, J. Ferré, V. Baltz, B. Rodmacq, B. Dieny and R. L. Stamps, Phys. Rev. Lett., 2007, 99, 217208 CrossRef CAS PubMed.
- R. Chimata, A. Bergman, L. Bergqvist, B. Sanyal and O. Eriksson, Phys. Rev. Lett., 2012, 109, 157201 CrossRef PubMed.
- J. Y. Bigot, M. Vomir, L. H. Andrade and E. Beaurepaire, Chem. Phys., 2005, 318, 137–146 CrossRef CAS.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, AIP Adv., 2014, 4, 107133 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr03903f |
| This journal is © The Royal Society of Chemistry 2022 |