Large piezoelectric response in ferroelectric/multiferroelectric metal oxyhalide MOX₂ (M = Ti, V and X = F, Cl and Br) monolayers

Abstract

Flexible two-dimensional (2D) piezoelectric materials are promising for applications in wearable electromechanical nano-devices such as sensors, energy harvesters, and actuators. A large piezo-response is required for any practical applications. Based on first-principles calculations, we report that ferroelectric TiOX₂ and multiferroelectric VOX₂ (X = F, Cl, and Br) monolayers exhibit large in-plane stress (e₁₁) and strain (d₁₁) piezoelectric coefficients. For example, the in-plane piezo-response of TiOBr₂ (both e₁₁ = 28.793 × 10⁻¹⁰ C m⁻¹ and d₁₁ = 37.758 pm V⁻¹) is about an order of magnitude larger than that of the widely studied 1H-MoS₂ monolayer, and also quite comparable to the giant piezoelectricity of group-IV monochalcogenide monolayers, e.g., SnS. Moreover, the d₁₁ of MOX₂ monolayers – ranging from 29.028 pm V⁻¹ to 37.758 pm V⁻¹ – are significantly higher than the d₁₁ or d₃₃ of commonly used 3D piezoelectrics such as w-AlN (d₃₃ = 5.1 pm V⁻¹) and α-quartz (d₁₁ = 2.3 pm V⁻¹). Such a large d₁₁ of MOX₂ monolayers originates from low in-plane elastic constants with large e₁₁ due to large Born effective charges (Z_ij) and atomic sensitivity to an applied strain. Moreover, we show the possibility of opening a new way of controlling piezoelectricity by applying a magnetic field.

---

1 Introduction

Insulators or semiconductors that lack inversion symmetry exhibit a piezoelectric effect, which is an electromechanical coupling that allows energy conversion from mechanical to electrical, and vice versa. This effect is used in many important applications such actuators, sensors, and transducers.^1,2 Current trends in the miniaturization of devices require piezoelectricity at the nanoscale. Being at most a few atomic-layers thick, 2D piezoelectrics have potential for miniaturizing these electromechanical devices down to nanoscale. Moreover, compared with 3D piezoelectrics (e.g., bulk crystals or thin-films), few layered (typically 1–3 layers) piezoelectric materials can generally exhibit larger deformation.^1,2 Importantly, nowadays these 2D materials can be grown with good crystalline quality. Hence, 2D piezoelectrics become promising for self-powered, flexible, and wearable nano-devices. These 2D piezoelectrics can also find interesting applications in new types of electronics such as piezotronics¹ – where the electronic band gap is controlled by the electric potential stemming from piezoelectricity – and in piezo-photonics,² where light is coupled with the piezoelectrically induced charges. For example, it has been predicted that the performance of MoS₂-based solar cells can be enhanced by the coupling of semiconducting and piezoelectric properties.³

Quite often, reduction in materials dimension promotes unique properties. For example, bulk 2H-MoS₂ is a non-piezoelectric due to its centrosymmetry, whereas the monolayer (also odd numbered layers e.g., trilayer) has no inversion symmetry – and exhibits piezoelectric properties.⁴ In agreement with the theory,⁴ in-plane piezoelectricity in a 1H-MoS₂ monolayer, which is comparable to the piezo-response of commercially used wurtzite nitrides, e.g., the d₃₃ of w-AlN (5.1 pm V⁻¹), has been confirmed by recent experiments.⁵ However, generally speaking, a high piezo-response in these 2D materials is desired for any device-level applications. Therefore, enhancement of piezoelectricity and discovery of new 2D piezoelectrics have drawn significant research interest. Typically, 1H-type (D_3h symmetry)^6–9 (e.g., d₁₁ = 13.45 pm V⁻¹ for 1H-CrTe₂)⁶ and Janus 1T-type^10–12 (e.g., d₂₂ = 4.12 pm V⁻¹ for 1T-MoSSe)¹⁰ 2D materials have been investigated for a large piezoelectric response. So far, piezoelectricity has been predicted in several families of non-ferroelectric 2D materials, like doped or chemically modified graphene,^13–15 metal dichalcogenides or oxides, and Janus monolayers.^{6–9,11,16–18} Encouragingly, although 2D ferroelectrics are relatively rare to date, giant in-plane piezoelectric response is present in the ferroelectric monolayers of group-IV monochalcogenides¹⁹ and MXenes (e.g., Sc₂CS₂).²⁰ A huge out-of-plane piezo-response (d₃₃ = 172.61 pm V⁻¹) is observed in buckled monolayers.²¹ Ferroelectric In₃Se₃ nanoflakes²² also show a moderate out-of-plane piezo-response. Furthermore, the co-existence of piezoelectricity and magnetism and their coupling in 2D materials – namely vanadium dichalcogenide monolayers,²³ Janus ferromagnetic NiClI monolayers,¹¹ and 1H-LaBr₂ monolayers²⁴– have been investigated. Any strong coupling between piezoelectricity and magnetism can be utilized for making piezoelectric-based multifunctional nano-devices. In this regard, multiferroelectric materials are interesting because they usually exhibit good coupling between electric polarization and magnetic order. Piezoelectricity is linked with electric polarization – for instance, the piezoelectric stress co-efficient (e_ij) is defined as where strain ∂η_j along the j-direction induces polarization along the i-direction (∂P_i). However, how changes in the magnetic order will change the piezo-response in 2D multiferroelectrics – where polarization couples with the magnetic order – remains unanswered to the best of our knowledge.

Based on first-principles calculations, several approaches such as defect engineering,²⁵ doping/charging,²⁶ and chemical functionalization^27,28 have been proposed for combining ferroelectricity and magnetism in 2D materials. There are also a limited number of intrinsically multiferroelectric 2D materials discovered recently – including the metal phosphorus chalcogenides family,^29,30 buckled CrN and CrB₂ monolayers,³¹ and MXene Hf₂VC₂F₂ monolayers.³² Multiferroelectricity in the monolayers of the metal oxyhalide VOX₂ family^33–37 has been predicted with interesting violation of the d⁰ rule.³⁸ In VOX₂ monolayers, the ferroelectric polarization direction is perpendicular to the partially occupied d_xy orbital that is the origin of magnetism. As a result, the partially occupied d orbital does not suppress the ferroelectric atomic displacement. Moreover, compared to ferroelectric TiOX₂ monolayers with the empty d orbital, the presence of an electron in the d_xy of VOX₂ monolayers rather positively contributes to the total electric polarization.³⁴ Initially, the ground state of the VOI₂ monolayer was predicted as ferromagnetic and ferroelectric.³⁴ However, later it has been predicted that the ferroelectric VOI₂ monolayer can exhibit spiral magnetism for a short period due to iodine's strong (compared to other halogens) spin–orbit coupling (SOC).^36,37 Alternatively, ferroelectricity in the VOI₂ monolayer can also be suppressed by on-site strong Coulomb interaction making it a ferromagnetic metal.³⁷ The coexistence of ferroelectricity and ferromagnetism is predicted in the VOF₂ monolayer,³⁵ whereas VOCl₂ and VOBr₂ monolayers have a ferroelectric ground state with antiferromagnetic (AFM) spin order.^33,34 Note that the VOCl₂ monolayer can be exfoliated experimentally from its bulk layered van der Waals structure (space group: Immm).³³ Generally, ferroelectric materials exhibit good piezoelectricity. Although ferroelectricity and multiferroelectricity of MOX₂ monolayers have been investigated,^33–37 their piezoelectric properties remain unknown to date. In this paper, we investigate the piezoelectric properties of both TiOX₂ and VOX₂ monolayers and how the piezo-response changes with magnetic order, which remain unexplored to date. We find that these monolayers exhibit a remarkably large piezo-response compared to most of the known 2D piezoelectrics, and they are promising materials for nanoscale electromechanical applications.

2 Computational details

Our first-principles calculations are performed in the framework of spin-polarized density functional theory as implemented in the Vienna Ab initio Simulation Package (VASP) based on a plane-wave basis set.³⁹ The projector augmented wave (PAW) potentials⁴⁰ are used for describing the core electrons. The generalized gradient approximation (GGA) of Perdew, Burke, and Ernzernhof (PBE)⁴¹ is employed for treating the exchange and correlation. The valence electron configurations considered for Ti, V, O, F, Cl, and Br are 3d³ 4s¹ (4 electrons), 3d⁴ 4s¹ (5 electrons), 2s² 2p⁴ (6 electrons), 2s² 2p⁵ (7 electrons), 3s² 3p⁵ (7 electrons), and 4s² 4p⁵ (7 electrons), respectively. A cutoff energy of 500 eV is used for the plane-wave expansion in all calculations. All structures are fully relaxed until the Hellmann–Feynman forces on all the atoms are less than 10⁻³ eV Å⁻¹. The lattice parameters a and b are relaxed, keeping c fixed as required for 2D materials, and the internal coordinates of the 2D structures are fully relaxed to achieve the lowest energy configuration using the conjugate gradient algorithm. To prevent the interaction between the periodic images in the calculations, a vacuum layer with a thickness of approximately 25 Å is added along the z-direction (perpendicular to the monolayer) in the supercell. Note that previous reports^33–35 employed about 15–20 Å vacuum layers, and also considered the van der Waals interaction between the layers.^33,35 However, we have not considered the van der Waals interaction as we simulate an isolated monolayer. The convergence for the total energy is set as 10⁻⁷ eV. For a 1 × 1 × 1 unit cell, the Brillouin zone integration is sampled using a regular 12 × 12 × 1 Monkhorst–Pack k-point grid for geometry optimizations, while a denser grid of 18 × 18 × 1 is used for density functional perturbation theory (DFPT) calculations. To study magnetic ordering, 1 × 2 × 1, 2 × 1 × 1, and 2 × 2 × 1 VOX₂ supercells (shown in Fig. 1(c)) with 12 × 6 × 1, 6 × 12 × 1, and 6 × 6 × 1 Monkhorst–Pack k-point grids, respectively are used. The elastic stiffness coefficients (C_ij) are obtained using a finite difference method as implemented in the VASP code. DFPT is used to calculate the Born effective charges (Z_ij) and ionic and electronic parts of piezoelectric (e_ij) tensors. A 4 × 4 × 1 supercell is used for the phonon dispersion calculations of the monolayers, which is obtained with PHONOPY code⁴² using the DFPT method. Recently it has been found that the Hubbard effective U (U_eff) correction does not alter the magnetic and ferroelectric properties of VOF₂.³⁵ However, to confirm the lack of impact of the Hubbard + U correction on the piezoelectric response of VOBr₂, we apply the GGA + U_eff (U_eff ranging from 1 eV to 3 eV) approach⁴³ for the 3d orbitals of V. We find that the Hubbard U_eff correction increases both e₁₁ and d₁₁ (see the ESI†). This further supports our conclusion that VOBr₂ has a large piezoelectric response.

Fig. 1 As a representative of MOX₂ monolayers, top and side views of the TiOBr₂ monolayer in (a) the paraelectric and (b) ferroelectric phases are shown. Beside the structure, the phonon band structure is also shown. We see an imaginary phonon (soft) mode at the Γ-point for paraelectric TiOBr₂; the vibration mode is indicated by the black arrow, whereas yellow arrows represent the direction of atomic displacement associated with the imaginary mode. In the phonon band structure, Γ(0,0,0), X(1/2,0,0), S(1/2,1/2,0), and Y(0,1/2,0) are the high symmetric points in the Brillouin zone. Blue, red, and green balls represent Ti/V, O, and F/Cl/Br, respectively. (c) The four magnetic configurations for VOX₂ monolayers are shown; yellow arrows represent the collinear spin direction (up or down). The dashed lines represent the rectangle simulation cells.

3 Results and discussion

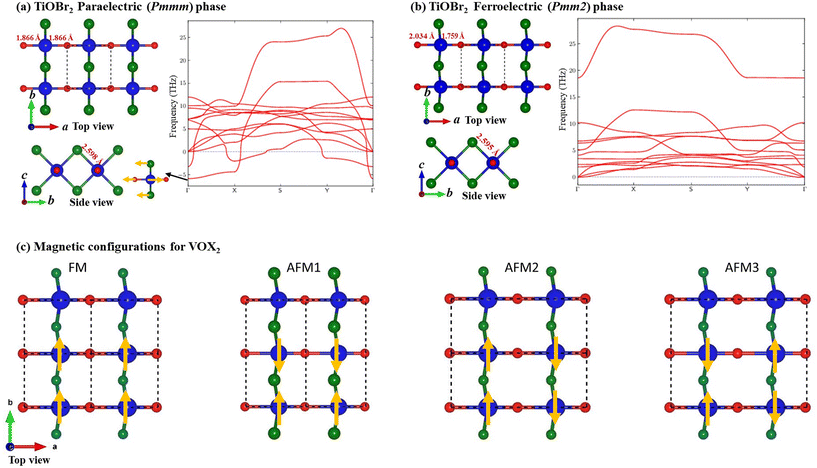
We start with the fully optimized centrosymmetric paraelectric (and also ferromagnetic for VOX₂) phase (space group: Pmmm) of MOX₂ monolayers and calculated their phonon dispersion. We find that there is an imaginary (soft) optical vibration mode at the center of the Brillouin zone (Γ-point) for the PE phase (see Fig. 1(a) for TiOBr₂ and also the ESI† for other MOX₂ monolayers). The frequency (iω_Γ) associated with the polar soft mode is given in Table 1. This suggests that there is a spontaneous atomic displacement of Ti(V) along the Ti–O (V–O) chain, breaking the inversion symmetry, thus producing a spontaneous in-plane (along the a-direction) electric polarization. This can also be understood in terms of long and short Ti–O (V–O) bonds along the a-direction in the FE phase (space group: Pmm2), whereas all M–O bonds are the same in the PE phase. Therefore, the a lattice parameter of the FE phase becomes slightly larger than that of the PE phase, although the b lattice parameter remains almost unchanged (see Table 1). As Ti⁴⁺ and V⁴⁺ have almost the same ionic radii, their lattice parameters are close. We see an increase in b as the radius of X increases from F to Br, which is expected because X atoms are only along the b-direction. With the exception of TiOF₂ (FE), the phonon dispersion of FE MOX₂ monolayers shows no appreciable soft mode, indicating their stability. Interestingly, we find that the ground state of the TiOF₂ monolayer is not the FE (Pmm2) phase – rather the non-polar (Pmma) phase (see the ESI†), which is 26.620 meV per atom lower in energy than the FE phase – therefore, we will not discuss its properties in the main paper.

Table 1 Structural information of the monolayers: optimized lattice parameters (a and b; see the rectangular cells in Fig. 1). M–O (M–X) represents the bond length between metal (M) and oxygen (halogen; X) atoms. Z₁₁ is the Born effective charge in |e| unit. The values in the parentheses are for paraelectric phases. P₁ and ΔE are the in-plane electric polarization in 2D unit (C m⁻¹) and the energy difference between the ferroelectric and paraelectric phases (the positive ΔE value suggests that the FE phase is lower in energy compared to the PE phase). iω_Γ stands for the lowest imaginary frequency of the PE phase at the Γ-point

	a (Å)	b (Å)	M–O (Å)	M–X (Å)	Z 11 (M)	Z 11 (O)	Z 11 (X)	P 1 (10^−12 C m^−1)	ΔE (meV per fu)	iω Γ (cm^−1)
VOF2(FM)	3.765(3.600)	3.025(3.055)	1.649(1.800)	1.969(1.971)	5.458(13.235)	−4.142 (−10.188)	−0.659 (−1.415)	309.192	124.809	385.919
VOCl2(FM)	3.773(3.610)	3.454(3.480)	1.653(1.805)	2.388(2.397)	4.893(14.703)	−4.255 (−12.174)	−0.319 (−1.197)	288.284	119.122	351.430
VOCl2(AFM1)	3.784(3.609)	3.367(3.408)	1.650(1.804)	2.383(2.395)	4.825(15.171)	−4.186 (−12.926)	−0.319 (−1.122)	311.609	129.095	396.542
VOBr2(FM)	3.764(3.620)	3.649(3.620)	1.664(1.810)	2.545(2.557)	5.018(15.076)	−4.579 (−12.965)	−0.219 (−1.029)	254.575	82.916	285.802
VOBr2(AFM1)	3.769(3.619)	3.577(3.615)	1.661(1.810)	2.542(2.555)	5.025(14.931)	−4.580 (−13.065)	−0.222 (−0.933)	271.205	85.646	301.611
TiOCl2	3.793(3.719)	3.504(3.518)	1.745(1.859)	2.438(2.441)	7.506(12.291)	−6.723 (−11.011)	−0.391 (−0.391)	185.430	26.519	227.851
TiOBr2	3.792(3.732)	3.677(3.689)	1.759(1.866)	2.595(2.598)	7.931(11.973)	−7.347 (−11.012)	−0.289 (−0.480)	160.291	16.254	170.826

---

As electric polarization (P₁) arises due to the polar distortion from the PE phase, we calculated P₁ in the 2D unit (C m⁻¹) using Z₁₁ and the atomic displacement (Δu_k,1) of the k-th atom along the a-direction as . The sum runs over all the atoms in the simulation cell; A is the area of the cell and e is charge of an electron. We use mean BECs (Z̄_k,11) – i.e., 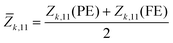because Z₁₁ changes during the PE-to-FE phase transition. For the PE phase, we find anomalously large Z₁₁, which decreases after the PE-to-FE transition (see Table 1). Similar anomalous BECs have been observed for other well-known ferroelectric materials.⁴⁴ In agreement with previous reports,³⁵ we find that MOX₂ monolayers have quite large P₁, which is comparable with that of group-IV monochalcogenide orthorhombic monolayers, e.g., SnS (P₁ = 2.47 × 10⁻¹⁰ C m⁻¹).^45,46 We also estimated the energy barrier for FE polarization switching. We take the difference in energy (ΔE) between FE and PE phases; lattice parameters a and b are fully relaxed in both phases. Our ΔE values are in good agreement with the reported values. We see a general trend that P₁, ΔE, and iω_Γ decrease as the ionic radius of X increases from F to Br. Interestingly, we also observed that magnetic VOX₂ monolayers have significantly larger P₁ than non-magnetic TiOCl₂ or TiOBr₂. This is in line with the previous report that the presence of an electron in the d_xy orbital of V does not suppress but rather enhances ferroelectric polarization.³⁴ This is also confirmed by the larger iω_Γ of VOX₂ (see Table 1).

To examine the impact of magnetic configuration on VOX₂ monolayers, we consider four (1 FM and 3 AFM) collinear magnetic spin configurations (see Fig. 1(c) and Table 2). Each V⁴⁺ contributes 1μ_B, which comes from an unpaired electron in the d_xy orbital.³⁴ Comparing the energy difference of an AFM configuration with respect to the FM order, in agreement with previous reports, we find that the FE VOF₂ monolayer has an FM ground state.³⁵ However, we find that the AFM3-type AFM order (see Fig. 1(c)) is more stable than other configurations in VOCl₂ and VOBr₂ monolayers.^33,34 The alternating up and down collinear spin configuration of V atoms along the b-direction (see Fig. 1(c)) shortens the b lattice parameter, compared with that of the FM state (shown in Table 1). By applying an external magnetic field in an experiment, the AFM order can be changed to FM. This will also lead a change in P₁ with a reduction of 7.49% and 6.13% for AFM1-to-FM transition in VOCl₂ and VOBr₂ monolayers, respectively. The AFM1-to-FM transition slightly hardens the soft mode (iω_Γ; see Table 1; also see the ESI† for AFM3), and consequently reduces the ferroelectric switching barrier (ΔE) slightly. This indicates that there is a weak coupling between the magnetic and ferroelectric orders in VOX₂.

Table 2 Energy difference (ΔE_AFM = E_AFM − E_FM; E_AFM and E_FM are the energy per unit-formula of fully-relaxed structures in AFM and FM magnetic orders, respectively) in meV per unit formula of 3 magnetic configurations with respect to the FM order; negative means the AFM configuration is more stable than the FM order

	ΔEAFM1	ΔEAFM2	ΔEAFM3
VOF2	9.183	2.170	9.789
VOCl2	−20.331	3.652	−22.019
VOBr2	−9.437	4.774	−11.257

---

All ferroelectrics exhibit piezoelectricity. It is interesting to know the piezo-response of our FE MOX₂ monolayers as strong in-plane piezoelectricity has already been predicted in 2D FE group-IV monochalcogenides.¹⁹ Our calculated piezoelectric stress coefficients (e_ij) are shown in Table 3. e_ij are important coefficients for estimating the figure-of-merit of a piezoelectric thin-film (TFFOM); usually the larger the e_ij, the higher the figure-of-merit. Because strain along the z-direction (vacuum) is ill-defined in 2D materials, we have only three independent piezoelectric coefficients: e₁₁, e₁₂, and e₁₆. There is a mirror symmetry along the b-direction, which does not allow any polarization in that direction, thus e₂₂ = 0. However, strain along the b-direction can induce polarization along the a-direction, which results in a non-zero e₁₂ coefficient. The FE MOX₂ monolayer (space group: Pmm2) due to the mm2 point group has a symmetry of reflection with reference to the M–O atomic plane. This prohibits an out-of-plane electric polarization, thus e₃₁ = 0. We mainly focus on the piezo-response related to uniaxial strain along the a-direction (η₁) and the b-direction (η₂), which are e₁₁(d₁₁) and e₁₂(d₁₂), respectively. e₁₆ is associated with shear strain (η₁₂),¹⁹ and we exclude it for simplicity.

Table 3 The electronic (e^elc₁₁ and e^elc₁₂) and ionic (e^ion₁₁ and e^ion₁₂) parts of the total piezoelectric stress constants e₁₁ and e₁₂ in the 2D piezoelectric unit of 10⁻¹⁰ C m⁻¹ of the MOX₂ monolayers, and the Born effective charges (Z₁₁) of metals (Ti and V), O, and halogens (X = F, Cl, and Br) in the charge of an electron (|e|) unit. or represents the change of the atomic coordinates along the a-direction in response to a strain along the a-direction (η₁) or the b-direction (η₂), respectively

	e ^elc11	e ^ion11	e 11				e ^elc12	e ^ion12	e 12
VOF2(FM)	5.776	13.850	19.625	0.271	−0.242	−0.015	4.513	−0.867	3.646	−0.073	−0.060	0.066
VOCl2(FM)	4.524	11.397	15.921	0.315	−0.213	−0.051	3.354	−0.639	2.716	−0.044	−0.037	0.041
VOCl2(AFM1)	4.693	11.407	16.100	0.314	−0.209	−0.052	3.309	−0.693	2.616	−0.029	−0.021	0.025
VOBr2(FM)	4.217	11.937	16.153	0.371	−0.195	−0.088	2.974	−0.824	2.150	−0.039	−0.031	0.035
VOBr2(AFM1)	4.331	12.384	16.715	0.371	−0.191	−0.090	2.962	−0.437	2.526	−0.029	−0.022	0.025
TiOCl2	3.764	22.345	26.109	0.494	−0.177	−0.159	1.819	−1.103	0.716	−0.038	−0.028	0.033
TiOBr2	3.250	25.543	28.793	0.599	−0.162	−0.218	1.531	−0.737	0.794	−0.034	−0.024	0.029

---

Table 3 shows that the TiOCl₂ or TiOBr₂ monolayer has quite large e₁₁ but small e₁₂, compared to those of VOX₂ monolayers. We also notice that unlike 1H-type monolayers, e.g., 1H-MoS₂ where e₁₁ = −e₁₂ due to the 6̄m2 point group symmetry, MOX₂ monolayers exhibit a highly anisotropic piezo-response, where e₁₁ is significantly larger than e₁₂. This is also expected as the monolayers have a strong in-plane electric polarization P₁, hence atomic displacement in response to strain along the a-direction can change P₁ directly. Interestingly, we observe a general trend that the in-plane piezo-response (e₁₁) decreases as the in-plane polarization increases (see Tables 1 and 3). To understand the origin of the large/small piezoelectric constant, we split e₁₁ and e₁₂ into two terms – (i) the clamped-ion term (e^elc₁₁ or e^elc₁₂), which is the electronic contribution where the atoms are fixed at their equilibrium internal coordinates (u) and (ii) the ionic contribution term (e^ion₁₁ or e^ion₁₂), due to the atomic displacements in response to a macroscopic strain η₁ (η₂) along the a-direction (b-direction). The e^ion₁₁ of TiOCl₂ and TiOBr₂ monolayers is almost twice larger than that of VOX₂. Interestingly, we notice that both ionic and electronic parts of e₁₁ are positive (see Table 3), thus they contribute positively to the total e₁₁ – similar to 1H-MoS₂.²⁴ That is why the TiOCl₂ or TiOBr₂ monolayer has significantly large e₁₁, compared to that of VOX₂, although the e^elc₁₁ of TiOCl₂ and TiOBr₂ monolayers is slightly smaller than that of VOX₂. On the other hand, the ionic and electronic parts of e₁₂ are opposite in sign, hence they reduce the total e₁₂. We see that because of their small positive e^elc₁₂ but large negative e^ion₁₂, TiOCl₂ and TiOBr₂ monolayers have quite small e₁₂ (see Table 3). We further split the ionic part:^24,47,48

e^ion₁₁ or e^ion₁₂ involves summation running over all the atoms (k) in a cell, e is the charge of an electron, and A is the area of the cell of the 2D unit. The response of the k-th atom's internal coordinate along the a-direction (u₁(k)) in response to a macroscopic strain (η₁) in the same direction is measured by . Similarly, represents the change in the k-th atom's internal coordinate along the a-direction (u₁(k)) in response to a macroscopic strain (η₂) along the b-direction. Relaxing the atomic positions in response to the strains η₁ and η₂, we obtain the slopes and , respectively. We notice that the large e^ion₁₁ of TiOCl₂ and TiOBr₂ monolayers comes from their large Z₁₁ (see Table 1) and (see Table 3). Also, we see that the of Ti/V/O is an order of magnitude larger than 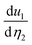– i.e., the uniaxial strain η₁ can displace atoms along the a-direction more than η₂. This also gives the large difference between e^ion₁₁ and e^ion₁₂. Moreover, we observe that the AFM1 order of VOCl₂ and VOBr₂ marginally enhances e₁₁ because of a slight increase in both e^elc₁₁ and e^ion₁₁ (see Table 3). Note that a change in the magnetic order also changes the e_ij of other magnetic 2D piezoelectrics.²⁴ Piezoelectric constants for AFM3 of VOCl₂ and VOBr₂ are presented in the ESI†.

Note that the e₁₁ of MOX₂ monolayers is significantly (about 6–10 times) larger than that of the well-known 1H-type piezoelectric monolayers e.g., 1H-MoS₂ (e₁₁ = 3.64 × 10⁻¹⁰ C m⁻¹).^4,6,8 We notice that the e^ion₁₁ of MOX₂ monolayers is an order of magnitude larger than that of 1H-MoS₂ or 1H-VS₂,²⁴ although their electronic parts are quite comparable.²⁴ Both the Z₁₁ and of MOX₂ monolayers are remarkably higher than those of 1H-MoS₂ or 1H-VS₂.²⁴ Our e₁₁ is quite comparable with that of group-IV monochalcogenide monolayers such as SnS,¹⁹ although the difference between e₁₁ and e₁₂ in group-IV monochalcogenides is not as pronounced as in MOX₂ monolayers. Note that the large piezo-response of our MOX₂ is very similar to that of ferroelectric niobium oxyhalide monolayers.⁴⁹

For piezoelectric thin-film-based applications, , where ε₀ and ε₁₁ are the vacuum permittivity and static dielectric constant, respectively, is a key figure-of-merit (TFFOM).⁴⁹ A recent high-throughput calculation has found that niobium oxyhalide monolayers have a significantly large TFFOM (in the range of 59.60 nN–71.70 nN) compared to other 2D piezoelectrics (e.g., the TFFOM of CuInP₂Se₆ is 3.10 nN).⁴⁹ We find that the TFFOM of MOX₂ monolayers is remarkably higher than that of niobium oxyhalide monolayers,⁴⁹ in the range of 105.43 nN for VOBr₂–203.43 nN for TiOBr₂, indicating their potential for flexible piezoelectric nano-devices. The TFFOMs of TiOCl₂, VOF₂, and VOCl₂ are 201.57 nN, 187.57 nN, and 118.47 nN, respectively, which are huge compared to the TFFOM of 1H-MoS₂ (3.45 nN; note that our calculated ε₁₁ of 1H-MoS₂ is 4.51, which is consistent with the previous report of 4.20⁵⁰). Such high TFFOMs of MOX₂ monolayers are the result of their low dielectric constants (ε₁₁) and large e₁₁ values. The ε₁₁ values of TiOCl₂, TiOBr₂, VOF₂, VOCl₂, and VOBr₂ are 3.82, 4.60, 2.32, 2.42, and 2.80, respectively, whereas the ε₁₁ values of niobium oxyhalide monolayers are in the range of 12–15.⁴⁹

Our piezoelectric strain constants (d_ij) – another important figure of merit for many piezoelectric applications – are obtained using e_ij and elastic constants (C_ij) (see Table 4): and . The nonzero and independent C_ij in the Voigt notation of FE MOX₂ monolayers are given in Table 4, and they also are positive (i.e., C₁₁, C₂₂, C₁₂, and C₆₆ > 0), indicating their mechanical stability; our orthorhombic monolayers clearly satisfy the Born elastic stability criterion:⁵¹C₁₁C₂₂ − C₁₂² > 0. Unlike 1H-type monolayers, MOX₂ are anisotropic elastically (i.e., C₁₁ ≠ C₂₂ – Young's modulus (Y) and Poisson's ratio (ν) along the a-direction are also different from those along the b-direction; these are presented in the ESI.† Note that Y quantifies how easily a material can be stretched and deformed, whereas ν quantifies the deformation in the material in a direction perpendicular to the applied force's direction). We find large d₁₁ for MOX₂ monolayers – and small d₁₂. However, the d₁₂ of TiOCl₂ or TiOBr₂ is quite comparable with that of 1H-MoS₂ (3.73 pm V⁻¹)⁴ or 1H-VS₂ (4.104 pm V⁻¹).²⁴ TiOBr₂ has the largest d₁₁ (37.758 pm V⁻¹), which is 2–10 times larger than those of 1H-type monolayers^4,6,8 (e.g., d₁₁ of 1H-MoS₂ and 1H-CrTe₂ is 3.65 pm V⁻¹ and 13.45 pm V⁻¹, respectively⁶). This is because compared to 1H-type piezoelectrics, MOX₂ have significantly larger e₁₁ and relatively smaller elastic constants (e.g., the C₁₁ of 1H-MoS₂ is 130 N m⁻¹⁴). Note that the d₁₁ of MOX₂ is very similar to that of niobium oxyhalide monolayers (27.4 pm V⁻¹ to 42.20 pm V⁻¹).⁴⁹ Interestingly, in comparison to bulk piezoelectric materials, we find that the piezo-response of MOX₂ monolayers is remarkably strong. For example, the d₁₁ (37.758 pm V⁻¹) of TiOBr₂ is an order of magnitude larger than that of α-quartz (d₁₁ = 2.3 pmV⁻¹)⁵² or the d₃₃ of w-GaN (3.1 pm V⁻¹);⁵³ and also about 7 times higher than the d₃₃ of w-AlN (5.1 pm V⁻¹).⁵³ Note that group-IV monochalcogenide monolayers¹⁹ have relatively smaller – indicating their softness – C₁₁ and C₂₂ (e.g., C₁₁ = 20.87 N m⁻¹ and C₂₂ = 53.40 N m⁻¹ for GeS monolayer¹⁹) than MOX₂ monolayers. That is why group-IV monochalcogenide monolayers have larger d₁₁ (e.g., d₁₁ = 75.43 pm V⁻¹ of the GeS monolayer)¹⁹ than that of MOX₂.

Table 4 Elastic constants (C₁₁, C₂₂, C₁₂, and C₆₆) in the 2D unit of N m⁻¹ and the piezoelectric strain coefficient in d₁₁ and d₁₂ in pm V⁻¹. *VOCl₂(FM) and *VOBr₂ (FM) represent the structures with the FM order but their lattice parameters and atomic positions are fixed at those of their AFM1 configurations

	C 11	C 22	C 12	C 66	d 11	d 12
VOF2(FM)	67.999	96.795	15.073	22.404	29.028	−0.753
VOCl2(FM)	53.761	58.255	8.711	18.808	29.575	0.239
VOCl2(AFM1)	50.810	42.460	6.887	18.640	31.545	1.045
*VOCl2(FM)	49.929	58.242	6.381	18.557	31.288	0.874
VOBr2(FM)	54.694	50.240	7.528	17.176	29.555	−0.149
VOBr2(AFM1)	52.998	40.485	6.196	17.132	31.372	1.437
*VOBr2(FM)	53.134	51.124	5.935	17.021	30.779	2.054
TiOCl2	78.264	56.536	8.318	16.971	33.753	−3.700
TiOBr2	76.942	47.862	6.879	15.029	37.758	−3.768

---

As VOCl₂ and VOBr₂ monolayers have an AFM ground state, we also study how their piezo-response will change in response to the AFM-to-FM phase transition, which can be experimentally possible under an external magnetic field.⁵⁴ Note that the FM-to-AFM transition can be a challenge in experiments. We find that the AFM1-to-FM transition somewhat increases the elastic constants – especially C₂₂ – thus slightly decreases d₁₁. Interestingly, such hardening of C₂₂ is intrinsic to the AFM1-to-FM transition as we see that it comes from the mere magnetic order change even if the lattice parameters and atomic positions are fixed at AFM1 (see Table 4). There is a significant decrease in d₁₂ (see Table 4). Interestingly, d₁₂ changes its sign during the AFM1-to-FM transition for the VOBr₂ monolayer, indicating that subject to an external electric field the monolayer can shrink or expand depending on the presence of a magnetic field. This can allow us to control piezoelectricity by magnetism, which may find applications in realizing multifunctional nano-devices. We believe that other magnetic piezoelectrics, especially 2D multiferroelectric, can also exhibit such coupling between piezo-response and magnetic order.

4 Conclusion

Our first principles calculations demonstrate that FE MOX₂ monolayers have a strong in-plane piezoelectric response, which is not only significantly larger than that of the well-known 1H-type 2D piezoelectrics – e.g., both the e₁₁ and d₁₁ of MOX₂ are about an order of magnitude larger than those of 1H-MoS₂ – but also remarkably stronger than some of bulk piezoelectrics such as w-AlN or w-GaN. These monolayers also exhibit a remarkably large anisotropy in their piezo-response – i.e., piezo-response due to strain along the a-direction is about an order of magnitude larger than that of along the b-direction. We also show that a change in the magnetic order can change the piezo-response in multiferroelectric VOX₂ monolayers, which can potentially couple piezoelectricity and magnetism. We believe that this work will inspire more research in searching for new piezoelectric materials that can couple strongly with magnetism. Also, such a large in-plane piezo-response can particularly be beneficial for 2D nanoscale flexible piezo-devices – e.g., actuators purely based on in-plane displacement.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This publication has emanated from research conducted with the financial support of Science Foundation Ireland (SFI) under Grant Number 20/EPSRC/3710. The calculations were performed using the high-performance computing facilities of the Tyndall National Institute. The authors also acknowledge access to computing resources at the Irish Centre for High-End Computing (ICHEC).

References

1. Q. Zhang, S. Zuo, P. Chen and C. Pan, InfoMat, 2021, 3, 987–1007.
2. Y. Liu, E. T. N. Wahyudin, J.-H. He and J. Zhai, MRS Bull., 2018, 43, 959–964.
3. G. Michael, Y. Zhang, J. Nie, D. Zheng, G. Hu, R. Liu, M. Dan, L. Li and Y. Zhang, Nano Energy, 2020, 76, 105091.
4. K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876.
5. H. Zhu, Y. Wang, J. Xiao, M. Liu, S. Xiong, Z. J. Wong, Z. Ye, Y. Ye, X. Yin and X. Zhang, Nat. Nanotechnol., 2015, 10, 151–155.
6. M. N. Blonsky, H. L. Zhuang, A. K. Singh and R. G. Hennig, ACS Nano, 2015, 9, 9885–9891.
7. K. H. Michel, D. Çakir, C. Sevik and F. M. Peeters, Phys. Rev. B, 2017, 95, 125415.
8. M. M. Alyoruk, Y. Aierken, D. Çakır, F. M. Peeters and C. Sevik, J. Phys. Chem. C, 2015, 119, 23231–23237.
9. Y. Lu and S. B. Sinnott, ACS Appl. Nano Mater., 2020, 3, 384–390.
10. P. Nandi, A. Rawat, R. Ahammed, N. Jena and A. De Sarkar, Nanoscale, 2021, 13, 5460–5478.
11. S.-D. Guo, Y.-T. Zhu, K. Qin and Y.-S. Ang, Appl. Phys. Lett., 2022, 120, 232403.
12. Z. Kahraman, A. Kandemir, M. Yagmurcukardes and H. Sahin, J. Phys. Chem. C, 2019, 123, 4549–4557.
13. M. T. Ong and E. J. Reed, ACS Nano, 2012, 6, 1387–1394.
14. M. T. Ong, K.-A. N. Duerloo and E. J. Reed, J. Phys. Chem. C, 2013, 117, 3615–3620.
15. H. J. Kim, M. Noor-A-Alam and Y.-H. Shin, J. Appl. Phys., 2015, 117, 145304.
16. M. Noor-A-Alam, H. J. Kim and Y.-H. Shin, J. Appl. Phys., 2015, 117, 224304.
17. M. Noor-A-Alam, H. J. Kim and Y.-H. Shin, Phys. Chem. Chem. Phys., 2014, 16, 6575–6582.
18. R. Ahammed, N. Jena, A. Rawat, M. K. Mohanta, Dimple and A. De Sarkar, J. Phys. Chem. C, 2020, 124, 21250–21260.
19. R. Fei, W. Li, J. Li and L. Yang, Appl. Phys. Lett., 2015, 107, 173104.
20. L. Zhang, C. Tang, C. Zhang and A. Du, Nanoscale, 2020, 12, 21291–21298.
21. M. K. Mohanta, F. IS, A. Kishore and A. De Sarkar, ACS Appl. Mater. Interfaces, 2021, 13, 40872–40879.
22. Y. Zhou, D. Wu, Y. Zhu, Y. Cho, Q. He, X. Yang, K. Herrera, Z. Chu, Y. Han, M. C. Downer, H. Peng and K. Lai, Nano Lett., 2017, 17, 5508–5513.
23. J. Yang, A. Wang, S. Zhang, J. Liu, Z. Zhong and L. Chen, Phys. Chem. Chem. Phys., 2019, 21, 132–136.
24. M. Noor-A-Alam and M. Nolan, ACS Appl. Electron. Mater., 2022, 4, 850–855.
25. Y. Zhao, L. Lin, Q. Zhou, Y. Li, S. Yuan, Q. Chen, S. Dong and J. Wang, Nano Lett., 2018, 18, 2943–2949.
26. C. Huang, Y. Du, H. Wu, H. Xiang, K. Deng and E. Kan, Phys. Rev. Lett., 2018, 120, 147601.
27. Q. Yang, W. Xiong, L. Zhu, G. Gao and M. Wu, J. Am. Chem. Soc., 2017, 139, 11506–11512.
28. Z. Tu, M. Wu and X. C. Zeng, J. Phys. Chem. Lett., 2017, 8, 1973–1978.
29. J. Qi, H. Wang, X. Chen and X. Qian, Appl. Phys. Lett., 2018, 113, 043102.
30. X. Feng, J. Liu, X. Ma and M. Zhao, Phys. Chem. Chem. Phys., 2020, 22, 7489–7496.
31. W. Luo, K. Xu and H. Xiang, Phys. Rev. B, 2017, 96, 235415.
32. J.-J. Zhang, L. Lin, Y. Zhang, M. Wu, B. I. Yakobson and S. Dong, J. Am. Chem. Soc., 2018, 140, 9768–9773.
33. H. Ai, X. Song, S. Qi, W. Li and M. Zhao, Nanoscale, 2019, 11, 1103–1110.
34. H. Tan, M. Li, H. Liu, Z. Liu, Y. Li and W. Duan, Phys. Rev. B, 2019, 99, 195434.
35. H.-P. You, N. Ding, J. Chen and S. Dong, Phys. Chem. Chem. Phys., 2020, 22, 24109–24115.
36. C. Xu, P. Chen, H. Tan, Y. Yang, H. Xiang and L. Bellaiche, Phys. Rev. Lett., 2020, 125, 037203.
37. N. Ding, J. Chen, S. Dong and A. Stroppa, Phys. Rev. B, 2020, 102, 165129.
38. N. A. Hill, J. Phys. Chem. B, 2000, 104, 6694–6709.
39. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
40. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
42. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
43. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
44. P. Ghosez, J.-P. Michenaud and X. Gonze, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 6224–6240.
45. M. Wu and X. C. Zeng, Nano Lett., 2016, 16, 3236–3241.
46. H. Wang and X. Qian, 2D Mater., 2017, 4, 015042.
47. M. Noor-A-Alam, O. Z. Olszewski and M. Nolan, ACS Appl. Mater. Interfaces, 2019, 11, 20482–20490.
48. F. Bernardini, V. Fiorentini and D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, R10024–R10027.
49. Y. Wu, I. Abdelwahab, K. C. Kwon, I. Verzhbitskiy, L. Wang, W. H. Liew, K. Yao, G. Eda, K. P. Loh, L. Shen and S. Y. Quek, Nat. Commun., 2022, 13, 1884.
50. T. Cheiwchanchamnangij and W. R. L. Lambrecht, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 205302.
51. F. Mouhat and F.-X. Coudert, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 224104.
52. R. Bechmann, Phys. Rev., 1958, 110, 1060–1061.
53. C. M. Lueng, H. L. W. Chan, C. Surya and C. L. Choy, J. Appl. Phys., 2000, 88, 5360–5363.
54. L. V. B. Diop, T. Faske, O. Isnard and W. Donner, Phys. Rev. Mater., 2021, 5, 104401.

---

Footnote

† Electronic supplementary information (ESI) available: Phonon band structures of MOX₂ monolayers in paraelectric and ferroelectric phases, phonon band structures of the TiOF₂ monolayer, Young's modulus and Poisson's ratio, GGA+U_eff calculations for e_ij, C_ij, and d_ij, structural and piezoelectric properties of VOCl₂(AFM3) and VOBr₂(AFM3). See DOI: https://doi.org/10.1039/d2nr02761e

---