Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hansen parameter evaluation for the characterization of titania photocatalysts using particle size distributions and combinatorics†
Osama
Anwar
 a,
Shalmali
Bapat
a,
Shalmali
Bapat
 a,
Jalil
Ahmed
b,
Xiaofeng
Xie
a,
Jalil
Ahmed
b,
Xiaofeng
Xie
 c,
Jing
Sun
c,
Jing
Sun
 c and
Doris
Segets
c and
Doris
Segets
 *ad
*ad
aParticle Science and Technology, Institute of Combustion and Gas Dynamics – (IVG-PST), Carl-Benz-Straße 199, 47057 Duisburg, Germany. E-mail: doris.segets@uni-due.de
bClinic of Neuroradiologie, Universitätsklinikum Bonn, Venusberg-Campus 1, 53127 Bonn, Germany
cShanghai Institute of Ceramics, Chinese Academy of Sciences, 1295 Dingxi Road, Shanghai 200050, China
dCentre for Nanointegration Duisburg-Essen (CENIDE), University of Duisburg-Essen (UDE), Carl-Benz-Straße 199, 47057 Duisburg, Germany
First published on 30th August 2022
Abstract
Titania photocatalysts have great potential as remediators of air pollution. Although various aspects of photocatalyst synthesis, adsorption and photoactivity have been investigated, a thorough understanding of the particle surface behavior has not yet been fully realized. In order to learn more about the principles behind the surface behavior, we investigate the Hansen solubility/similarity parameters (HSPs) for analyzing and evaluating three photocatalysts synthesized by the gas phase method, solvothermal reaction and sol–gel method, respectively. A particle size distribution-based categorization scheme is introduced for characterizing each material's Hansen parameters based on its interaction with a list of selected probe liquids. The latter was deduced from particle size distributions assessed by analytical centrifugation. Subsequent comparison of the Hansen parameters of the investigated materials shows how HSPs can potentially be used as a model for predicting the pollutant adsorption behavior on the photocatalyst surface. This serves as a first step in heading towards an improved understanding of the particle behavior and translating it into a knowledge-based design, i.e., synthesis and hybridization of novel photocatalysts.
Introduction
Air pollution is a critical issue all over the world due to the increasing use of fossil fuels, urbanization and increasing population demands. According to the World Health Organization (WHO), about 7 million people die yearly due to air pollution related diseases while 91% of the world's population lives in areas with a higher pollutant content than WHO guideline limits.1 This comes with an added cost of several trillion dollars for medical treatments and environmental damage. Air pollution remediation, thus, remains an important topic in research. Volatile organic compounds (VOCs) have been identified to have a severe impact on air quality and a number of techniques have been employed to degrade them such as liquid adsorption, thermal catalysis and photocatalysis.2–4 Titania has been actively investigated due to its versatility in the degradation of a variety of VOCs, ease of processing, improved charge carrier separation, non-toxicity, and possibility of composite formation.5–7Several synthesis methods are used for the preparation of titania-based photocatalysts such as gas phase, sol–gel, and solvothermal methods.8–12 Such diverse synthesis procedures very often lead to differences in the particle surface crystallinity, reactivity, size, dispersity, shape, and morphology.13–15 The synthesis method can be chosen based on the desired product properties for a particular application such as liquid phase photocatalysis,16 manufacture of thin films,17 or pigments for paints to coat surfaces.18 Ignoring economic and ecological boundary conditions that make the selection of the best approach more complicated, the synthesis step has the largest effect on the particle crystallinity and surface properties.9 Hence, when to choose what synthesis protocol and how to judge on the quality of the generated particles remain a huge and ongoing challenge.
Although each synthesis procedure results in a particular surface, products of the same base material are similar such as titanium dioxide in the case of photocatalysts. Titanium dioxide can exist in three crystallographic phases, namely anatase, rutile and brookite.5 The investigation of the synthesis of a wide range of titania-based materials, adsorption studies and studies on their photocatalytic efficiency have been widely performed.5,7,8 However, to explicitly analyze particle properties individually in dependence of synthesis conditions and adsorption features is of critical importance. From our viewpoint, as shown in Fig. 1, knowledge about the particle surface behavior, together with the input on surface adsorption and efficiency, is the missing link (black box) that can potentially allow us to reverse the design approach to a more directed one (green arrow).19,20
To analyze the surface adsorption of VOCs on titania nanoparticles, it is important to know more about their interfacial behavior. Many analytical techniques such as electron microscopy, X-ray diffraction, ultraviolet spectroscopy, photoluminescence, and others are available and dutifully used to characterize the particle core and surface and their reactivity in detail. However, information obtained from these techniques cannot be linked directly to the state of the dispersibility or polarity of the particles in question. In this context, a generalized model is needed that enables linking the chemistry of a particle surface to its behavior under actual in situ conditions. In principle, such a model would allow for a comparison of the same materials, however produced through different synthesis methods, and eventually laboratories around the globe independent of size characteristics and structures. This design strategy should not be limited to titania photocatalysts alone and potentially lead to better design choices for a vast variety of materials.20
A number of such models have been investigated in the literature in the context of understanding disperse particle system production and processing.20 One such model that relates surface behavior to its interfacial interactions is the concept of Hansen parameters that has held up over time quite well21 and will be explained in the next section.
Hansen solubility parameters
In 1967, Hansen came up with the concept of Hansen solubility parameters (HSPs). Originally developed for polymer–solvent systems, the theory improved upon the solubility model developed by Hildebrand.22 For more details on the origin of the solubility parameters and the theoretical background, the reader is referred to textbooks and other works.23–25Hildebrand used the solubility parameter δ, expressed as energy per molar volume (MPa0.5), to describe the interaction of solutes and solvents. Hansen further divided the solubility parameter into hydrogen bonding (δH), polar (δP) and dispersive interactions (δD) to describe the interaction of molecules with solvents (eqn (1)).23 Each of the three interactions are represented by an axis in the three-dimensional Hansen space where each material has a particular location defined by its HSP coordinates. By dividing the solubility parameter (δ) into three individual components, surface behavior could be related directly to final product properties. Solutes having similar HSPs seemed to be more compatible with each other and vice versa:
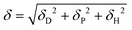 | (1) |
Each material or solvent is represented by its HSPs in this space and its volume of interaction can be represented by a sphere. The center of this sphere represents the solubility parameter of the solute under consideration. In eqn (2), the sphere's boundaries are defined by the ratio of Ra and Ro (radius of sphere) where Ra is defined as:
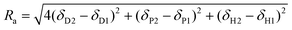 | (2) |
Here, the differences between the HSPs of the solute (δD1δP1δH1) and solvent (δD2δP2δH2) are used for the calculations:
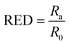 | (3) |
Eqn (3) shows the ratio of radii Ra and Ro known as the relative energy difference (RED) with the boundary of the sphere with RED < 1 showing good solvents and RED > 1 showing poor solvents. The constant 4 was experimentally derived to represent the data from solubility experiments in the form of a sphere.
The HSP derivation method involves dissolution of a particular solute into a number of solvents with distinct HSPs, followed by the binary categorization of solvents into good or poor based on their compatibility with the solute. From this division of solvents, an empirically defined sphere of interaction volume is generated in such a way that all the good solvents are inside, and the poor solvents are outside the sphere boundary (Fig. 2). The basic condition for making the sphere is to have two good interacting solvents and one poorly interacting solvent.
The boundary regions of the so-defined sphere are where deviations are possible. This is attributed to the differences in the molar volumes of the solvents where smaller molar volumes lead to a lower ΔGM and improve the solubility. Once calculated properly, the HSP coordinates of a particular solute are characteristic and can be used to relate to its interaction with different solvents.23
In principle, any difference in the degree of compatibility of a solute with solvents can be used to classify the solute via HSPs. HSPs have found considerable success in the region of solvent selection for a variety of purposes such as green extraction solvents for separation processes.26 In the case of molecule–solvent systems, the interaction of drug molecules with DNA was predicted.24 Interestingly, the HSP concept has found profound use in the cosmetics and pharma industries in relation to skin permeation to various chemicals,25 and in selecting appropriate coformers for the intelligent design of active pharmaceutical ingredient-cocrystals.27 In the case of polymers, HSPs can be calculated based on the uptake of the solvent into the polymer, i.e., swelling, or a difference in the permeation rate.23,28
HSPs for particulate systems
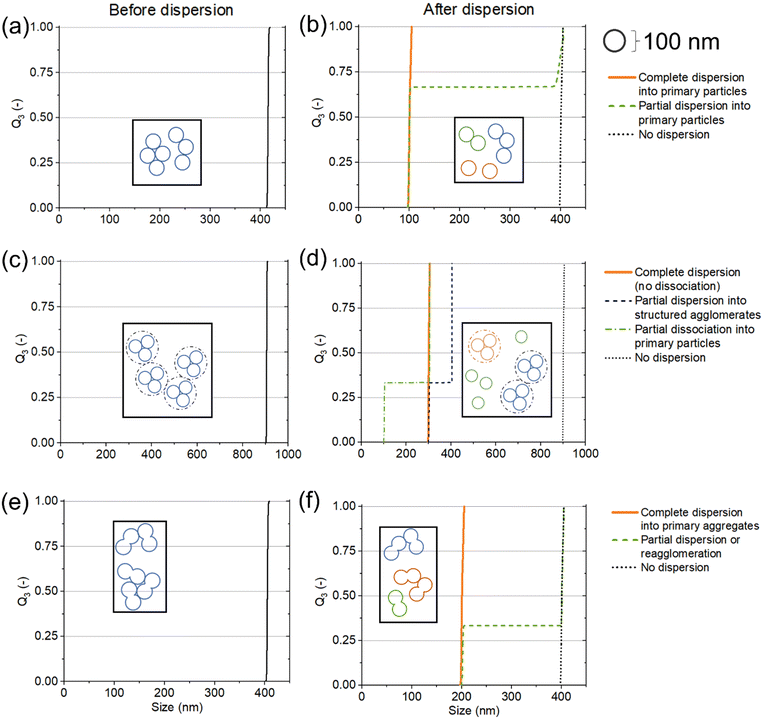
Although originally developed for polymer–solvent interactions, HSPs can provide valuable information in particle–solvent systems as well. In relation to particle systems, solvents will be henceforth referred to as probe liquids (PLs).The state of dispersions is of prime importance. When making dispersions from powders, the state of particles inside the dispersions can vary based on the concentration, dispersion procedure and type of material. Fig. 3 shows four typical types of structures that particles can exist in, namely individual primary particles (Fig. 3a – blue), agglomerates that can be unstructured (Fig. 3b – orange) or structured (as in the case of spray drying, Fig. 3c – orange), or aggregates (Fig. 3d – green). Agglomerates consist of primary particles joined together by physical forces that can be broken by sonication or mechanical stirring. Aggregates in contrast are formed at high temperatures and consist of necks of solid bridges of primary particles joined together. They cannot be broken down by sonication or stirring and require high intensity techniques for comminution such as ball milling or high pressure dispersion.29 Subsequently, numerous combinations are possible, i.e., aggregates can further interact with each other or primary particles and form larger agglomerates (Fig. 3e – green). Notably, a good strategy for the determination of HSPs for particulates would be able to consider all of these different showcases.
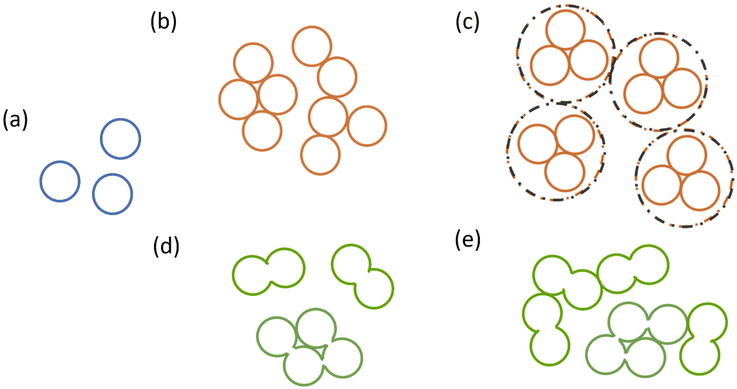 | ||
| Fig. 3 Different states of particles inside dispersions, namely (a) primary particles, (b) unstructured agglomerates, (c) structured agglomerates, (d) aggregates, and (e) agglomerates of aggregates. | ||
Hansen calculated the HSPs of particulate materials such as titania and carbon black by visual inspection of the particle sedimentation behavior.23 Wieneke et al. used both visual observation and particle sizes (measured by DLS) of the settling dispersions of titania and hydroxyapatite nanoparticles to determine their HSPs.30 Recently, nuclear magnetic resonance (NMR) relaxation times of different zinc oxide and alumina nanoparticles in 16 PLs have been used as a categorization method for HSP determination.31
For HSP calculation, the role of a well-defined categorization procedure is paramount. In the pursuit of coming up with new methods that reduce subjectivity and provide ways of clear-cut characterization, work was done to move towards more straightforward ways of PL categorization. Süβ et al. developed a characterization method using accelerated sedimentation in an analytical centrifuge.32 There, integral extinctions (IEs) of carbon black (Printex-L, Evonik Industries) dispersed in various PLs across a region of interest in an analytical centrifugation (AC) measurement cell were determined followed by a ranking based on the varying relative sedimentation times (RST). This approach laid the groundwork for further advancements and worked well for the chosen material. However, difficulties in the allocation of good/poor PLs arise when working with materials where overlapping IE profiles were observed.32,33
In the methods mentioned above, each technique is used to make a PL ranking based on differences between the interactions of the material and the PL. However, when it comes to designation of PLs as either good or poor, a large degree of subjectivity is involved in HSP calculation. All methods involve a cutoff for designation of good or poor, and this can vary between repeats as well as operators or labs.
To account for this issue, Süβ et al. also proposed a non-subjective method for good/poor scoring which comprised of a stepwise addition of PLs until a minimum in the distance between iteratively generated Hansen spheres was reached – upon switching on one PL after the other as “good” sorted by RST values.32 However, the stepwise addition of good PLs does not always lead to the same minima of HSP values over repetitions of the same experiment which make HSP derivation difficult.33
Recently, in the pursuit of moving towards standard practices, a technology-agnostic framework of reporting HSPs was proposed by Bapat et al.33 The framework allows any method to be used for categorizing PLs and reporting HSPs, given that care is taken of using the data to designate the PLs as good or poor only until it is supported by sufficient evidence. For all PLs, where the evidence is not strong enough for designation into good or poor, the combinatorics method is used and the HSPs calculated and reported as a range. This way of reporting allows for the uncertainty in data to be part of the results and can help the experimenter in making more informed decisions about their material and method. The reporting of HSPs according to the framework consists of the following three aspects:
• The number of PLs used for the investigation.
• All outliers (good liquids with RED > 1 outside the Hansen sphere/poor liquids with RED < 1 inside the Hansen sphere) should be reported.
• The total number of tried permutations for reaching the HSP range should be reported.
Once performed in a well-defined way, HSPs can guide the choice of the synthesis process based on the proximity of the HSPs of the photocatalyst tested and the HSPs of the target VOC. It could first let one know that they may need to change the synthesis and work with different precursors/synthesis processes to obtain to a material with HSPs that are closer to the target VOC. In addition, during the synthesis process, the TiO2/C ratio could be adjusted in the case of hybrids as well as the dopants in the case of doped photocatalysts. Titania surfaces covered with different types of carbon materials will have different HSPs and can be activated using post-treatment methods such as ultrasound. This will result in a change in HSPs which can then be documented and form a database of the behavior indicators of photocatalysts with different surfaces. In addition, one can see where the HSPs of the synthesized photocatalyst are and which VOCs already lie in its vicinity or perhaps inside its Hansen sphere. These may be well suited for adsorption onto the photocatalyst surface.
Furthermore, the HSPs with a chosen set of PLs can be used as a quality control check for batches of the same material and synthesis. Repeated checks can ensure that only photocatalysts having similar dispersibility profiles in the same PLs and, by extension, similar HSP ranges can be chosen for further VOC adsorption and degradation. Similarly, one can check the shelf life, i.e., changes over time, of the hybridized photocatalyst since overtime the carbon coating will be degraded by the photocatalyst itself. This will change the HSPs, and such surface changes can be documented easily.
In this context, we present a PL categorization methodology based on particle size distributions (PSDs) calculated from sedimentation velocities that were measured via AC for HSP evaluation. We report HSPs of three photocatalysts prepared via different synthesis routes according to the technology-agnostic framework.33 In this way, the predictive capacity of HSPs is highlighted and their use can be further improved upon by systematic studies to learn more about VOC surface adsorption as an important forerunner towards directed photocatalyst design.
Experimental
Materials and methods
PLs used are shown in Table 1 along with their abbreviations. Further liquid properties such as density, viscosity and Hansen parameters, CAS numbers and qualities are listed in Table S1.†
| Probe liquid | Abbreviation |
|---|---|
| 1,4-Dioxane | Diox |
| Ethyl acetate | EA |
| Acetone | Ace |
| Ethanol | EtOH |
| N-Methyl-2-pyrrolidone | NMP |
| Diacetone alcohol | DAA |
| Dimethyl formamide | DMF |
| Acetonitrile | ACN |
| Dimethyl sulfoxide | DMSO |
| Propylene carbonate | PC |
Aeroxide P25 titania: sample P25
Titania aeroxide P25 powder was purchased from Evonik Industries AG. The materials' properties are shown in Table S2.† P25 was chosen as a commonly used gas-phase synthesized photocatalyst to show the effect of high temperature gas pyrolysis on titania surface properties.Solvothermal titania synthesis: sample T1
5 g of tetrabutyl orthotitanate was added to a round bottom flask containing 400 ml of ethanol absolute. 4 mL of deionized water was added dropwise into the solution while stirring at ambient temperature. The flask was placed in an oil bath at 78 °C and refluxed for six hours. The collected powder was isolated by centrifugation, washed by repeatedly dispersing in ethanol and distilled water three times each and centrifuging while throwing away the supernatant. The titania collected from this procedure was in the amorphous form and it was then crystallized by a subsequent hydrothermal step. Therefore, it was dispersed in a mixture of water and ethanol in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. The pH of the suspension was adjusted to 4 by adding dilute sulfuric acid. A homogeneous suspension was obtained by ultrasonication for an hour followed by stirring for a further two hours. The suspension was then placed in a Teflon-lined stainless-steel autoclave and maintained at 160 °C for six hours. The final titania product was obtained after washing as explained before with distilled water and subsequent drying at 50 °C for three days. The complete characterization of the material is already published by Lin et al.34 For the purpose of this investigation, pure titania was chosen to show the effect of the solvothermal synthesis process. The titania was experimentally reproduced and designated T1.
1 ratio. The pH of the suspension was adjusted to 4 by adding dilute sulfuric acid. A homogeneous suspension was obtained by ultrasonication for an hour followed by stirring for a further two hours. The suspension was then placed in a Teflon-lined stainless-steel autoclave and maintained at 160 °C for six hours. The final titania product was obtained after washing as explained before with distilled water and subsequent drying at 50 °C for three days. The complete characterization of the material is already published by Lin et al.34 For the purpose of this investigation, pure titania was chosen to show the effect of the solvothermal synthesis process. The titania was experimentally reproduced and designated T1.
Erbium-doped titania synthesis: sample T2
The sol–gel method was used to synthesize Er-doped TiO2 nanoparticles. 9.8 mL of titanium(IV) isopropoxide was dissolved in a mixture solution containing 42 mL of ethanol and 8 mL of acetic acid under vigorous stirring for 15 minutes. Next, 4 mL of distilled water was slowly dropped into the above solution. Furthermore, a predetermined amount of erbium nitrate hexahydrate was added into the final mixture, which was further stirred for 80 minutes in a closed beaker to achieve a clear sol. The sol was aged for an hour and placed in a vacuum oven at 80 °C for 15 hours to obtain a dried gel. Finally, the gel was calcined in a muffle furnace at 500 °C for 2.5 hours in air and subsequently grounded with an agate mortar to collect the final products. The complete characterization of the material is published by Rao et al.35 For the current investigation, the 1.5 wt% erbium-doped titania was chosen to show the effect of synthesis by the sol–gel method. The 1.5 wt% erbium-doped titania was experimentally reproduced and designated T2.Dispersion
For AC analysis, low concentrations of the powder dispersions were prepared (Table S2†). This was done to counter effects such as zone sedimentation,36 and multiple scattering of light and to maintain the linear concentration–absorbance relationship according to the Lambert–Beer law.37,38Three dispersions of each powder in the respective PLs were prepared to assure reproducibility between the measurements. An ultrasonic homogenizer with a sonotrode (Bandelin Sonopuls HD 2200.2) was used with a TT-13 tip at 50% amplitude for 1 minute in pulsation mode. The heating dynamics of the sonotrode are shown in section S2.† For all sample preparations, the tip was dipped 5 mm into the dispersion as recommended by the device manufacturer. To counteract the heat produced during sonication, the vials were placed in an ice water bath. After sonication, aliquots of 440 μl were pipetted into 2 mm polyamide cuvettes. After a vortex of ∼5 seconds (IKA Vortex 2), the measurement cells were placed inside the analytical centrifuge.
Analytical centrifugation
AC was performed using a Lumisizer 6514-44 (LUM GmbH, Berlin, Germany). The analytical centrifuge measures the space and time resolved extinction profiles (STEP ® technology) over the length of the dispersion laden measurement cells using infrared or blue light. It uses charge coupled device detectors to capture the light passing through the measurement cells and resolves it to transmission fingerprints which have spatial and temporal data of settlement behavior of the suspension. Following the dispersion by probe sonication, visual inspection was performed to check if immediate settling occurred in any of the samples. The time between sonication and loading of the measurement cells into the AC device was maintained less than a minute to avoid immediate settling. Measurements were carried out at 10 °C or 20 °C depending on the dispersion settling behavior of each PL. A wavelength of 410 nm was used.Two requirements for a suitable transmission fingerprint for PSD derivation exist. First, an appropriate initial turbidity is needed. Second, an appropriate centrifugal speed was chosen to accurately monitor the movement of the sedimentation front with time such that enough transmission profiles are available for PSD derivation. From the AC data, the initial profiles were scrutinized to see if immediate settling occurred and whether the chosen centrifugal speed was appropriate. If immediate settling was observed, a lower centrifugal speed was selected. At the end of the measurement, in order to check whether complete sedimentation was observed for all dispersions, the settling behavior was played back from the beginning of the experiment (feature available in SEPView version 6.4.678.6069 software) to check for anomalies such as fluctuating transmission profiles or artifacts that could negatively impact PSD derivation. In such case, the cause was diagnosed, and the experiment was repeated if the results were impaired. Rotational speeds and measurement durations for each particle system are presented in Table S2.†
Finally, PSDs were calculated from transmission profiles. The choice of number, intensity or volume weighted PSDs is remained open for the experimenter. In this work, volume densities were utilized to achieve a high sensitivity against agglomerates. Particle/PL densities, refractive indices, and PL viscosity which are needed for the derivation of PSDs from sedimentation velocity distributions are presented in Table S1.† The constant position method and five nodal positions (122, 123.5, 125, 126.5, and 128 mm) with a nodal width of 1.0 mm to give an average PSD value were selected. For more details on PSD derivation by the SEPView software, the reader is referred to the work of Detloff et al.39
Electron microscopy
High resolution transmission electron microscopy (HRTEM, JEM-2100F) and scanning electron microscopy (SEM, Magellan 400) were used to characterize the morphology and microstructure of the three photocatalysts. An acceleration voltage of 200 kV was used for TEM while in the case of SEM, 5.0 kV was applied with a magnification of 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
Hansen parameter calculation
HSPiP software 5th edition (version 5.3.06) was used for HSP calculation (license kindly provided by LUM GmbH). For HSP calculation, the Hansen parameters of each PL were taken from the available master list provided by the software. As mentioned, the program requires designation of at least two PLs as good and one PL as poor for sphere generation. After scoring all chosen PLs as good (1) or poor (0), the HSP values for each material-PL combination were noted down as described in Bapat et al.33 Combinations which resulted in Hansen spheres where the condition of all good PLs in and all poor PLs out was fulfilled were chosen for providing the range of HSPs for each material.Results and discussion
Powder characterization
P25 was chosen as a mainstream gas phase synthesized photocatalyst with the other two photocatalysts being made from liquid phase crystallization. P25 has found widespread use in photocatalysis applications. It is well characterized in the literature with several works showing successful doping,40–42 composite formation with graphene oxide,43 and coatings.44 It is the benchmark material against which most photocatalytic studies compare VOC adsorption and degradation.34,45 Similarly, solvothermal and sol–gel syntheses are commonly used for preparing titania photocatalysts. As representative materials, T1 and T2 were chosen to reflect the differences arising from these methods, for instance, in the specific surface area and crystallinity.The primary particle sizes of P25 and T2 were analyzed via SEM and for T1 via TEM. As shown in Fig. 4, all materials exhibit primary particle sizes in the size range of 10–30 nm that are agglomerated/aggregated into larger structures. According to the manufacturer, P25 has an average primary particle size of 21 nm, and size measurements of T1 and T2 reveal average primary particle sizes of ∼10 nm and ∼15 nm, respectively. It is imperative to explain at this point that powders can contain primary particles, primary aggregates as the smallest dispersible units,29 and agglomerates. As discussed, aggregates consist of primary particles arranged together with solid bridges which cannot be broken during dispersion. In contrast, agglomerates are weakly bound by physical forces and can thus be broken down during dispersion in a good liquid where re-agglomeration is sufficiently suppressed during the time scale of observation. Depending on the interaction of the material with each PL along with the set energy input via an ultrasonic homogenizer, the breakage of agglomerates will vary. This will thus lead to a difference in the PSDs assessed via AC. In the following section, this will be discussed based on experimental results as well as theoretical considerations based on the generalized scenarios that were already introduced in Fig. 3.
 | ||
Fig. 4 SEM image of P25 (a) at ×100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 5.0 kV, TEM image of T1 (b) at 200 kV and SEM image of T2 (c) at ×200 000 and 5.0 kV, TEM image of T1 (b) at 200 kV and SEM image of T2 (c) at ×200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 5.0 kV. 000 and 5.0 kV. | ||
Evolution of particle size distributions
We can see exemplary cumulative volume distributions of the investigated photocatalysts in PC and EtOH (Fig. 5). It becomes clear from the comparison of these two liquids already that P25 forms a better dispersion with smaller sized particulates in PC (x50,3 = 0.08 μm) than in EtOH which contained larger agglomerates (x50,3 = 1.4 μm). The PSD for P25 in PC (relative standard deviation (RSD = 0.58) was also slightly narrower than in EtOH (RSD = 0.40).46 In contrast, both T1 and T2 exhibit the opposite behavior. Already visual inspection revealed less optically opaque dispersions in EtOH than in PC (Fig. S1†). This was confirmed by the median sizes where T1 showed a size of 1.7 μm in EtOH vs. 3.2 μm in PC and in the case of T2 2.68 μm in EtOH vs. 5.5 μm in PC. T1 had an RSD of 0.85 in PC and 0.89 in EtOH while T2 had an RSD of 0.62 in PC and 0.60 in EtOH, so both nearly remained unchanged regarding the width of the distribution. | ||
| Fig. 5 Volume PSDs of P25 (solid line), T1 (dashed line) and T2 (triangles) in PC (black) and EtOH (red). | ||
Several conclusions can be made when comparing the PSDs. First, only in the case of P25 in PC the probe sonication is able to break down agglomerates into smaller structures (∼80 nm) close to the primary particle size (∼20 nm). For T1 and T2 in both PC and ethanol, such break-up of agglomerates was not achieved to the same extent as structures clearly remain around 1 μm and beyond. Thus, the energy input by sonication is either not enough to break down the agglomerates, the primary particles combine into larger aggregates during the solvothermal treatment or the ones broken down reagglomerate quickly due to insufficient stabilization.47–49 This comparison of PSDs for the three materials in just two PLs already shows how complex dispersibility studies can be performed when aggregates/agglomerates are present. Therefore, before any HSP can be derived from PSDs, a brief survey on model scenarios using artificially generated size distributions will be introduced to gain more clarity on the data interpretation.
Model scenarios during powder dispersion
In real-world, ideal particulate systems, i.e., perfectly spherical powders with a defined PSD width, that can be dispersed down to the primary particle size in the absence of swelling or any other specific interaction with the chosen PLs are hardly found. Thus, artificial distributions were generated via a python script to simulate monodisperse and polydisperse PSDs. Volume distributions were generated. In the following section, we explain three typical cases and encourage others to add showcase scenarios in the future we might have forgotten that can occur during dispersion. These scenarios are commonly observed during particle processing and thus carry significant importance for dispersion studies.PSD-scheme exemplified by P25
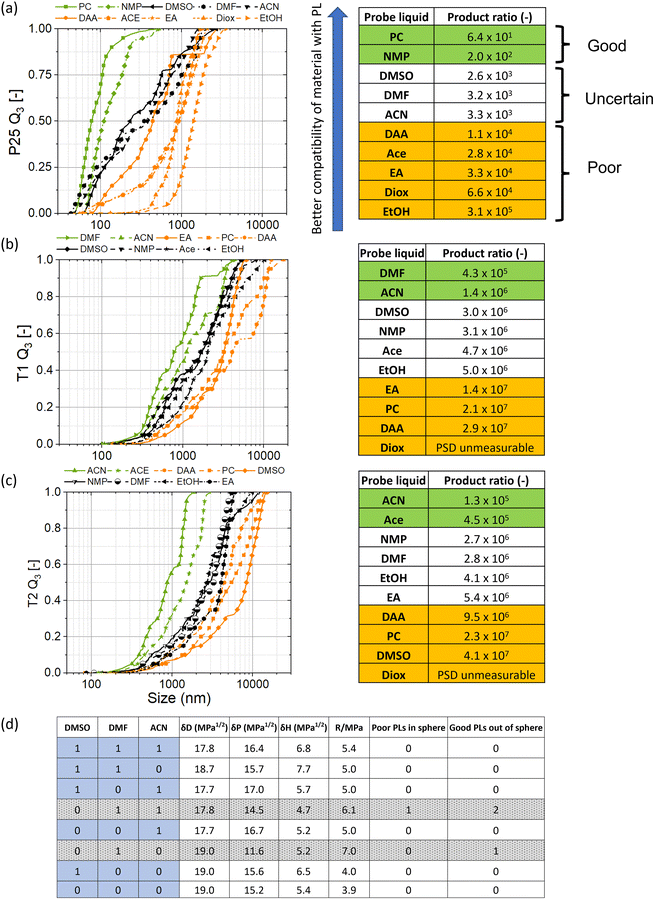
It can be seen from the previous section that PSDs are rich in information about their material behavior. However, in particular when the size range between samples varies by orders of magnitude, it is difficult to compare several PSDs directly. The aim of the scheme developed and presented here is to extract information from the PSD data in a way that most of the details of its behavior are retained while providing a numerical value that can be compared across various PLs and materials.As already shown in Fig. 5 and analyzed in more detail via cases 1–3, PSDs of a given material in different PLs can vary in both the width of the PSD and the range of median particle sizes. Exemplified by titania (P25, T1, and T2), we will show how a PSD-based categorization of PLs can be used as a widely applicable method for determining HSPs. The developed scheme was executed with the list of ten PLs summarized in Table 1.
In the following section, the developed scheme (Fig. 7) will be explained stepwise with exemplary application to P25. The PSDs, ranking and categorization for all three materials and detailed HSP results for P25 are summarized in Fig. 8. Details of the equations for the calculation of permutations are presented in section S3.†
 | ||
| Fig. 7 PSD-based PL categorization scheme with the incorporation of reporting of HSPs according to the HSP reporting framework. | ||
1. The materials were dispersed in the ten chosen PLs (N) (Fig. 7, yellow panel). According to the Hansen reporting framework, this gives us total permutations of 1012 (Q10 = 210 − 100C − 1010C − 101C) eqn (S2).†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33
33
2. Visual inspection of dispersions was carried out after sonication or a relevant dispersion method. In case immediate sedimentation is observed, such PLs are directly designated as poor PLs.
3. PSD measurements were performed (here by AC) on the dispersions that remain stable, and no immediate settling is observed.
4. The products of the three percentiles of the cumulative PSD, x10, x50 and x90, were calculated. The choice of these three percentiles ensures on the one hand that most of the information of the PSD is preserved. On the other hand, this procedure enables to extract information of a complex PSD and numerically express it with one characteristic value without losing too much information. In the case of P25, the PSDs are shown in Fig. 8a, left.
5. The herewith introduced product ratio (PR) of the percentile product to the volume of the primary particle size D was calculated, estimated, for instance, by scanning or transmission electron microscopy:
Division by the primary particle size cubed makes the ratio dimensionless which can ease comparison across different materials. It is important to note that the PR is inversely proportional to good particle-PL compatibility. Notably, if no clear information on the primary particle size is available, the scheme can work with just the product of the absolute sizes as well. In the case of P25, the primary particle size of D = 20 nm is used.
6. Using the calculated PRs, the PLs are ranked in the ascending order. The PLs are clustered together that are close based on their numerical values and designated into good, uncertain and poor categories. The PRs are used to cluster the PLs together based on their numerical value. The first two PLs and the last one is designated as good and poor respectively to fulfill the criterion for the formation of an HSP sphere. The PLs are broadly clustered together based on their exponents to the powers of 10. Thus, the PLs with similar exponents are clustered together and a move to the next exponent can generally be considered a difference enough to designate them as being part of the next cluster. The criterion to move from good to uncertain and poor PLs is therefore similar. Furthermore, a numerical difference of double between two subsequent PLs can also be taken as a difference enough to designate the next PL as belonging to the next cluster. It should be however clearly noted that this still brings in some subjectivity on behalf of the researcher. Nevertheless, in combination with proper reporting explained in point 9, the decision is made transparent. In the case of P25, the PRs are shown in Fig. 8a, right alongside the three categories.
7. Check if at least two PLs were ranked good and at least one PL was ranked poor. This is the minimum requirement for calculation of a Hansen sphere and parameters. If it is not fulfilled, more PLs should be added starting from step 1 (yellow panel). The PR is highly dependent on the individual numerical value of each percentile. Thus, each increase or decrease in any percentile value will significantly influence the PR. It can be deduced that a change in the order of magnitude may be a sign of the change of type of PL (good/uncertain/poor).
In the case of P25, PC and NMP (green) can be seen as two good PLs and EtOH as the poor PL (orange), respectively. Hence, the requirement of two good PLs and one poor PL is fulfilled and no more PLs need to be added. Based on the clustering, we can additionally see poor PLs with PRs in orders of 104 such as DAA, Ace, EA, and Diox (orange). With regards to the reporting framework, we therefore have 2 good (M) and 5 poor (L) PLs.33 The number of permutations remaining now are 8 (QML = 210-2-5 eqn (S5)†).
8. Check to see whether there are any uncertain PLs. In case there are none and only two categories of PLs results – namely good and poor –HSP was calculated using the HSPiP software and moved forward with step 10.
9. In the case of the appearance of uncertain PLs, the combinatorics method developed by Bapat et al. was applied for dealing with them.33 Each of the possible permutations resulting from an uncertain PL when it is designated good or poor is explored and calculated. This provides a range of HSP values of the investigated material. All permutations where a PL designated as good lies out of the generated sphere, or one designated poor PL lies in the generated sphere are not chosen for the HSP range but are designated as outliers. The remaining HSP combinations are considered valid and represent – in addition to the results from step 7 – the range of HSPs for the material investigated with the chosen PLs. In case no valid combinations are found at all, continue with the reporting in step 10. Thus, though also with our approach subjectivity is not fully erased from the HSP determination, we hope that the transparence obtained by its application in combination with an appropriate reporting will suffice to make the decision-making transparent and comparable across experimenters, materials and laboratories.
For P25, we can see a cluster of uncertain PLs in an order of 103, namely DMSO, DMF and ACN. Fig. 8d shows the combinatorics analysis for the three uncertain PLs resulting in two outliers (gray) and six possible permutations left (blue).
10. The calculated HSP values are reported along with the number of PLs evaluated. In the case of uncertain PLs, the HSP range for the material are additionally reported alongside the number of permutations investigated, the number of outliers and the total permutations possible based on the number of PLs evaluated.33 For P25, the HSPs are reported in Table 2 and discussed in the next section.
| Materials | P25 | T1 | T2 |
|---|---|---|---|
| Disperse interactions δD (MPa1/2) | 17.7–19.0 | 13.1–16.8 | 13.0–16.5 |
| Polar interactions δP (MPa1/2) | 15.6–17.0 | 14.4–18.8 | 11.4–17.6 |
| Hydrogen bonding δH (MPa1/2) | 5.2–7.7 | 7.8–14.7 | 5.0–14.5 |
| Sphere radius (MPa1/2) | 3.9–5.4 | 4.0–11.5 | 3.9–11.6 |
| Total combinations possible | 1012 | ||
| Combinations chosen for HSP | 6 out of 8 | 14 out of 16 | 7 out of 16 |
| Outliers | 2 | 2 | 9 |
The application of the scheme to the other two titania T1 and T2 is shown in section S4† for simplicity. The most important findings and finally obtained results are summarized in Table 2 and will be discussed in the following section.
It is worth mentioning the type of materials the scheme can – in principle – be applied to. Here, we applied it to three powders of similar sized titania without any specific surface modifications. However, the scheme can be applied to nanoparticles which have clear measurable differences in the settling behavior of their dispersions of various PLs – even when the true density is unknown as results are compared qualitatively on a relative scale. This can include non-porous and porous nano- and microparticles, as long as particles are small enough that surface interactions play a role in their macroscopic behavior. For polymer coated nanoparticles, the method will work fine as it was performed in a similar way to the dispersion and centrifugation of polymer coated nanoparticles before visual inspection by Mathioudaki et al.50
However, for particles in the micrometer range, it is expected that they will be less susceptible to aggregation by surface interactions and HSPs will in general, therefore, not be applicable. Moreover, particles that are too small for sedimentation at 2300 RCA, like sub-10 nm quantum dots, need to be analyzed with another technique than AC. For gel-like particles, the sedimentation behavior will be complex and HSP determination by the proposed method may not work. In those cases, especially to account for the effect of polymer swelling or uptake of PLs, HSP determination via contact angles and/or the capillary penetration method by Tsutsumi et al. may suffice.51 Finally, a defined powder is needed as a starting point and safety issues need to be kept in mind. That means highly reactive powders like technical catalysts might be difficult as they might start burning upon contact with pure organic solvents like 2-propanol.
PSD scheme application to the photocatalysts T1 and T2
Applying the derived PSD scheme to T1 and T2 (Fig. 8b and c) shows that for T1, DMF and ACN are designated as good PLs while for T2, ACN and Ace are designated as good PLs. In both cases, Diox is designated poor as its PSDs are underivable due to immediate sedimentation during AC. Both T1 and T2 exhibit two clusters of PRs in the orders of 106 and 107. The former is designated uncertain and the latter poor. For T1, NMP, DMSO, Ace and EtOH were assigned uncertain. For T2, NMP, DMF, EtOH and EA are the uncertain PLs. For T1 and T2, the HSP reporting summary is presented in section S4.† Furthermore, to establish the importance of a well-chosen PL list in combination with appropriate reporting, the effect of removal of particular PLs on the HSP range is shown in section S5† using T1 as a model case.With regards to combinatorics as explained before, for the ten PLs, a total of 1012 permutations are possible. For P25, with three uncertain PLs in our experiment, eight permutations were analyzed resulting in two outliers and six remaining combinations setting up the finally derived HSP range. For T1 and T2, with four uncertain PLs remaining, 16 permutations were checked (QML = 210-2-4, eqn (S3)†). In the case of T1, two outliers and 14 combinations setting up the HSP range were finally derived. In the case of T2, it was nine outliers and seven combinations. As will become clear in the next section where HSPs are compared with each other, this additional information is highly beneficial to judge on the quality of the finally reported HSP ranges. We believe that it significantly eases the comparison of different materials and results obtained by various characterization methods, laboratories and operators.
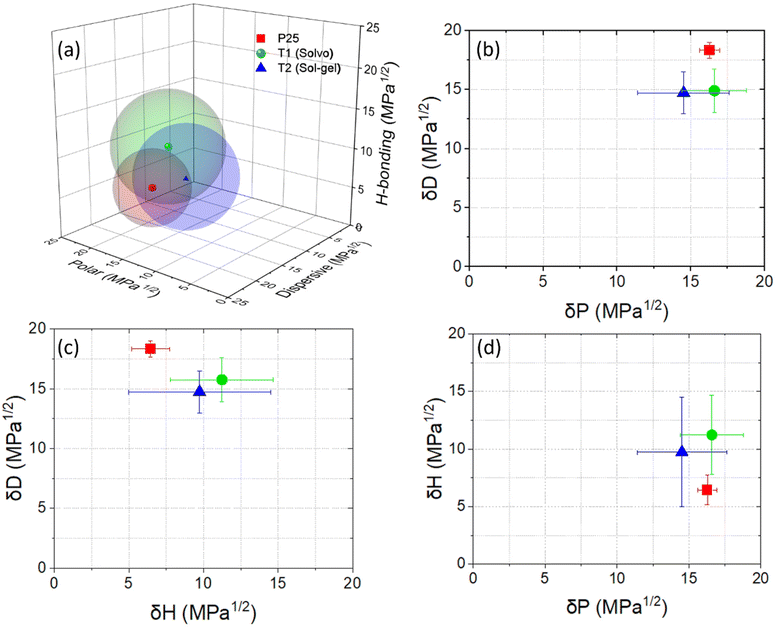
Hansen parameters of the photocatalysts
The HSPs and the resulting Hansen spheres are shown in Fig. 9 and Table 2 respectively. For visual simplicity, the averages of the ranges of HSPs are plotted and compared. The results show that P25 has a higher dispersive component than both T1 and T2 while the hydrogen bonding contribution is significantly lower. All three photocatalysts have similar polar contributions while T2 has a slightly reduced value, however with a still pronounced overlap with T1. The average radius of the Hansen sphere for gas phase P25 is smaller than that of the materials prepared by liquid phase synthesis. Both T1 and T2 have the same average radius. Interestingly, the range of P25 is smaller for all its parameters in comparison to T1 and T2. This is a direct consequence of the uncertain PLs in combination with the use of combinatorics.This highlights the benefit of using a significant number of PLs in combination with a strict methodology for the analysis. It should be noted that the PL list chosen was the result of several preliminary experiments for shortlisting those used in this study. To speed up the result collection for the HSP study, it is recommended to always use a pre-screening of PLs to see which would work best for the chosen material system and where additional PLs should be added to back up the gained results. The proximity of the HSPs for T1 and T2 can be attributed to their similar synthesis approach. Based on the HSP results of the three photocatalysts, we attributed the main difference in Hansen radii to the presence of surface ligands that are either physi- or chemisorbed on the catalyst surface and originate from the liquid phase synthesis of T1 and T2. A much broader distribution of these ligands and precursor molecules is expected here than on the surface of P25 as a much “cleaner” gas phase product. The presence of residual precursors can be carefully ascribed to be responsible for the high hydrogen bonding components. In line with our expectations, the surface of these titania materials has a higher number of hydroxyl groups in comparison to P25 which has mostly Ti–O bonds on its surface. The larger spheres of T1 and T2 show that they – in comparison to P25 – better interact with PLs with higher hydrogen bonding and polar components. For instance, ethanol and acetone both formed more stable dispersions as shown with higher PRs in the case of T1 and T2 than in the case of P25. In the case of ethanol, with its large hydrogen bonding component, it drastically increases the overall HSPs and radii of T1 and T2. Similarly, PC was the best PL for P25 while for both T1 and T2 it was a poor dispersing PL. PC has a very low hydrogen bonding component and may therefore not interact so well with liquid phase photocatalysts. Overall, PLs with high polar components such as DMF and ACN interact better with T1 and T2.
One exception to be noted is that while NMP and acetone have similar HSPs, acetone is a poor PL for P25 which can be attributed to the different surface groups (carbonyl) in comparison to NMP which has both carbonyl and amine groups. Except this case, PLs with high hydrogen bonding and polar contributions generally form better dispersions with the investigated liquid phase photocatalysts.
The difference of the HSPs of gas and liquid phase photocatalysts is also in part since dispersive forces are quite different for the hydrogen and polar components due to their origins. Dispersive interactions are attributed to the temporary induced dipoles due to the electron cloud movement at the atomic level while the other two HSPs are more molecular orientation dependent and – at least partly – permanent. Additionally, both T1 and T2 have a similar anatase crystal structure while P25 is a mixture of anatase and rutile with varying ratios usually comprising of about 70–80% anatase.52 The difference in crystallography means that specific crystallographic planes are exposed and have different reactivities. This is also observed in the case of the HSPs of the three photocatalysts which are closer together for T1 and T2 than for P25. Thus, it becomes clear that HSPs derived from the presented PSD-based scheme, combined with combinatorics, provide a powerful tool to analyze the surface properties of particulate materials.33 The gained results are in line with expectations and previously acquired knowledge on TiO2. In our future work, we will apply the developed methodology to new materials with unknown properties and relate our findings with VOC adsorption in both gas and liquid phases.
Conclusions and outlook
In the quest towards intelligent design of photocatalysts, a few points need to be explored. Primary among them is the understanding of surface interactions, and its relationship with VOC adsorption on the photocatalyst surface. This work aims to show the viability of using Hansen parameters as a model for gaining insights into the surface properties of titania photocatalysts prepared via different synthesis procedures. A new PSD-based categorization scheme including the recently established combinatorics method was developed. The HSPs of three representative TiO2-based photocatalysts were determined and reported according to the Hansen reporting framework developed previously.33 The calculated HSPs from the developed scheme could differentiate between different synthesis methods and show that materials prepared via similar methods have closer HSPs than those prepared otherwise. We believe that our combinatorics based HSP scheme can be applied to a wide range of particulate materials regardless of the way the PSDs are obtained. Further work will focus on understanding the effect of addition of dopants, formation of composites and hybrids on HSP values and how they can be related to VOC adsorption and desorption at the surface of TiO2-based photocatalysts.Author contributions
OA implemented the method, performed the experiments, analysed the data, and wrote the manuscript. SB contributed to the implementation of the method and manuscript writing. JA wrote the Python program for artificial distributions. XX synthesized the titania particles under supervision of JS who also reviewed the manuscript. DS supervised the study, conceptualized the idea, interpreted the results, and contributed to manuscript writing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
OA and DS gratefully thank the Deutsche Forschungs gemeinschaft (grant number SE 2526/3) while XX and JS thank the National Natural Science Foundation of China (project number 51761135107) for funding of the project. SB thanks BMWK for the financial support (WIPANO funding scheme, project number 03TN0013A). OA gratefully acknowledges LUM GmbH for providing the license for the HSPiP software. OA thanks Dr. Ulrich Hagemann and Thai bin Nguyen from ICAN for SEM imaging.References
- WHO, Air Pollution, https://www.who.int/health-topics/air-pollution, (accessed 11 May 2022).
- C. Pirola and M. Mattia, Int. J. Thermofluids, 2021, 9, 100060 CrossRef.
- A. Vega-González, X. Duten and S. Sauce, Catalysts, 2020, 10, 1–16 CrossRef.
- R. Ameta and S. C. Ameta, Photocatalysis: Principles and Applications, CRC Press, 2016 Search PubMed.
- A. Fujishima, X. Zhang and D. A. Tryk, Surf. Sci. Rep., 2008, 63, 515–582 CrossRef CAS.
- Z. Rao, G. Lu, A. Mahmood, G. Shi, X. Xie and J. Sun, Appl. Catal., B, 2021, 284, 119813 CrossRef CAS.
- S. G. Kumar and L. G. Devi, J. Phys. Chem. A, 2011, 115, 13211–13241 CrossRef CAS PubMed.
- X. Chen and S. S. Mao, Chem. Rev., 2007, 107, 2891–2959 CrossRef CAS PubMed.
- D. Dastan, Appl. Phys. A: Mater. Sci. Process., 2017, 123 DOI:10.1007/s00339-017-1309-3.
- S. Yin, Y. Fujishiro, J. Wu, M. Aki and T. Sato, J. Mater. Process. Technol., 2003, 137, 45–48 CrossRef CAS.
- J. Liu, W. Qin, S. Zuo, Y. Yu and Z. Hao, J. Hazard. Mater., 2009, 163, 273–278 CrossRef CAS PubMed.
- M. P. Seabra, I. M. M. Salvado and J. A. Labrincha, Ceram. Int., 2011, 37, 3317–3322 CrossRef CAS.
- A. Sanchez-Martinez, C. Koop-Santa, O. Ceballos-Sanchez, E. R. López-Mena, M. A. González, V. Rangel-Cobián, E. Orozco-Guareño and M. García-Guaderrama, Mater. Res. Express, 2019, 6, 8 Search PubMed.
- J. Yu, J. Lei, L. Wang, J. Zhang and Y. Liu, J. Alloys Compd., 2018, 769, 740–757 CrossRef CAS.
- V. Syzrantsev, E. Paukshtis, T. Larina, Y. Chesalov, S. Bardakhanov and A. Nomoev, J. Nanomater., 2018, 2018, 2065687 Search PubMed.
- V. Guzsvány, L. Rajić, B. Jović, D. Orčić, J. Csanádi, S. Lazić and B. Abramović, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2012, 47, 1919–1929 CrossRef.
- R. S. Sonawane and M. K. Dongare, J. Mol. Catal. A: Chem., 2006, 243, 68–76 CrossRef CAS.
- U. I. Gaya and A. H. Abdullah, J. Photochem. Photobiol., C, 2008, 9, 1–12 CrossRef CAS.
- H. Rumpf, Particle Technology, Springer Netherlands, 2012 Search PubMed.
- W. Peukert, D. Segets, L. Pflug and G. Leugering, in Advances in Chemical Engineering, Academic Press Inc., 2015, vol. 46, pp. 1–81 Search PubMed.
- S. Abbott, Curr. Opin. Colloid Interface Sci., 2020, 48, 65–76 CrossRef CAS.
- M. L. Huggins, J. Phys. Chem., 1951, 55, 619–620 CrossRef.
- C. M. Hansen, Hansen Solubility Parameters: A User's Handbook, CRC Press, 2nd edn, 2007 Search PubMed.
- C. M. Hansen, Eur. Polym. J., 2008, 44, 2741–2748 CrossRef CAS.
- S. Abbott, Int. J. Cosmet. Sci., 2012, 34, 217–222 CrossRef CAS.
- A. del P. Sánchez-Camargo, M. Bueno, F. Parada-Alfonso, A. Cifuentes and E. Ibáñez, TrAC, Trends Anal. Chem., 2019, 118, 227–237 CrossRef.
- A. Kumar and A. Nanda, J. Drug Delivery Sci. Technol., 2021, 63, 102527 CrossRef CAS.
- A. Zhou, M. M. A. Almijbilee, J. Zheng and L. Wang, Sep. Purif. Technol., 2021, 263, 118394 CrossRef CAS.
- A. Teleki, R. Wengeler, L. Wengeler, H. Nirschl and S. E. Pratsinis, Powder Technol., 2008, 181, 292–300 CrossRef CAS.
- J. U. Wieneke, B. Kommob, O. Gaer, I. Prykhodko and M. Ulbricht, Ind. Eng. Chem. Res., 2012, 51, 327–334 CrossRef CAS.
- D. Fairhurst, R. Sharma, S.-I Takeda, T. Cosgrove and S. W. Prescott, Powder Technol., 2021, 377, 545–552 CrossRef CAS.
- S. Süβ, T. Sobisch, W. Peukert, D. Lerche and D. Segets, Adv. Powder Technol., 2018, 29, 1550–1561 CrossRef.
- S. Bapat, S. O. Kilian, H. Wiggers and D. Segets, Nanoscale Adv., 2021, 3, 4400–4410 RSC.
- W. Lin, X. Xie, X. Wang, Y. Wang, D. Segets and J. Sun, Chem. Eng. J., 2018, 349, 708–718 CrossRef CAS.
- Z. Rao, X. Xie, X. Wang, A. Mahmood, S. Tong, M. Ge and J. Sun, J. Phys. Chem. C, 2019, 123, 12321–12334 CrossRef CAS.
- S. E. Jørgensen, Industrial Waste Water Management, Elsevier Scientific Publishing Company, 1979 Search PubMed.
- T. G. Mayerhöfer, H. Mutschke and J. Popp, ChemPhysChem, 2016, 17, 1948–1955 CrossRef PubMed.
- W. Mäntele and E. Deniz, Spectrochim. Acta, Part A, 2017, 173, 965–968 CrossRef PubMed.
- T. Detloff, T. Sobisch and D. Lerche, Powder Technol., 2007, 174, 50–55 CrossRef CAS.
- H. Znad and Y. Kawase, J. Mol. Catal. A: Chem., 2009, 314, 55–62 CrossRef CAS.
- S. Wadhai, Y. Jadhav and P. Thakur, Sol. Energy Mater. Sol. Cells, 2021, 223, 110958 CrossRef CAS.
- J. Talat-Mehrabad, M. Khosravi, N. Modirshahla and M. A. Behnajady, Desalin. Water Treat., 2016, 57, 10451–10461 CrossRef CAS.
- H. Zhang, X. Lv, Y. Li, Y. Wang and J. Li, ACS Nano, 2010, 4, 380–386 CrossRef CAS.
- R. E. Kalan, S. Yaparatne, A. Amirbahman and C. P. Tripp, Appl. Catal., B, 2016, 187, 249–258 CrossRef CAS.
- L. W. Zhang, H. B. Fu and Y. F. Zhu, Adv. Funct. Mater., 2008, 18, 2180–2189 CrossRef CAS.
- D. Segets, C. Lutz, K. Yamamoto, S. Komada, S. Süβ, Y. Mori and W. Peukert, J. Phys. Chem. C, 2015, 119, 4009–4022 CrossRef CAS.
- N. Mandzy, E. Grulke and T. Druffel, Powder Technol., 2005, 160, 121–126 CrossRef CAS.
- V. S. Nguyen, D. Rouxel, R. Hadji, B. Vincent and Y. Fort, Ultrason. Sonochem., 2011, 18, 382–388 CrossRef CAS.
- A. M. Horst, Z. Ji and P. A. Holden, J. Nanopart. Res., 2012, 14, 1014 CrossRef.
- S. Mathioudaki, B. Barthélémy, S. Detriche, C. Vandenabeele, J. Delhalle, Z. Mekhalif and S. Lucas, ACS Appl. Nano Mater., 2018, 1, 3464–3473 CrossRef CAS.
- S. Tsutsumi, K. Kondo, Y. Kato, N. Fujiwara and H. Yamamoto, Chem. Phys., 2019, 521, 115–122 CrossRef CAS.
- M. J. Uddin, F. Cesano, A. R. Chowdhury, T. Trad, S. Cravanzola, G. Martra, L. Mino, A. Zecchina and D. Scarano, Front. Mater., 2020, 7, 192 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr02711a |
| This journal is © The Royal Society of Chemistry 2022 |