Plasmonic photocatalysis in aqueous solution: assessing the contribution of thermal effects and evaluating the role of photogenerated ROS

Abstract

Plasmon-induced photocatalysis can drive photochemical processes with an unprecedented control of reactivity, using light as sole energy source. Nevertheless, disentangling the relative importance of thermal and non-thermal features upon plasmonic excitation remains a difficult task. In this work we intend to separate the role played by the photogenerated charge carriers from thermal mechanisms in the plasmonic photo-oxidation of a model organic substrate in aqueous solution and using a metal–semiconductor hybrid as model photocatalyst. Accordingly, we present a simple set of experimental procedures and simulations that allow us to discard the thermal dissipation upon plasmonic excitation as the main driving force behind these chemical reactions. Moreover, we also study the photogeneration of reactive oxygen species (ROS), discussing their fundamental role in photo-oxidation reactions and the information they provide regarding the reactivity of the photogenerated electrons and holes.

---

Introduction

Plasmonic photocatalysis and plasmon-induced photosensitization of semiconductors have the potential to drive chemical reactions in a greener and more efficient manner by using solar light as only fuel thanks to the ability of noble metal nanoparticles (NPs) to support collective electronic oscillations.^1–3 When used as photocatalysts and photosensitizers, plasmonic NPs can modulate chemical reactivity through the generation of excited charge carriers,^4,5 the local enhancement of the electromagnetic field at their surfaces^6,7 or by the photothermal generation of heat.⁸ The hot charge carriers (electrons and holes) produced upon plasmonic excitation are particularly relevant since they can modulate chemical selectivity,⁹ opening a new landscape of reactivity that cannot be achieved with classical thermally-induced catalysis.¹⁰ Along these lines, redox reactions involving the generation of electron–hole pairs or chemical processes that do not have appreciable reaction rates in the dark (even at high temperatures) are perfect candidates for hot charge carrier-driven photocatalysis.¹¹ Nevertheless, the elucidation of the mechanisms behind plasmon-induced photocatalysis remains elusive given that multiple photoactivation processes can coexist in the same system.^12–14 Recent examples demonstrate that the photoactivation mechanism driving a given plasmon-induced photochemical reaction depends on several parameters such as the reaction under study, the shape, size and composition of the plasmonic resonator, its surface functionalization and the irradiation conditions used.^15,16

In the last years, a passionate debate has risen amongst the scientific community with respect to the physical processes behind plasmonic photocatalysis. Even though a general consensus exists with respect to the important role played by hot charge carriers as main driving force in many photocatalytic transformations, several authors claim that the importance of thermal dissipation upon plasmonic excitation has been underestimated for certain bond-dissociation reactions.^17–19 Under this premise, the potential interest of non-thermal plasmonic photocatalysis for the promotion of novel reaction pathways would be secondary. Such exciting debate, together with the lack of a complete mechanistic understanding behind hot electron/hot hole generation processes exemplify the need for a better fundamental insight in plasmonic photocatalysis if this field is to be developed further.²⁰ Accordingly, the implementation of simple experimental techniques that discriminate between thermal contributions and non-thermal plasmonic effects (generation of hot charge carriers and plasmon-induced energy transfer processes) is a necessary step in this direction.^13,16,19,21

In our group, we have investigated the synergistic combination of plasmonic metals and wide bandgap semiconductors leading to the formation of broadband photocatalysts with enhanced activities and efficiencies.^22,23 The population of hot electrons created at the metal component upon electromagnetic excitation can be subsequently transferred to a nearby n-type semiconductor, leaving a population of hot holes at the Fermi level of the former. In this manner, an efficient separation of charges with prolonged lifetimes that can be used to drive chemical reactions is created. In addition to this phenomenon, the plasmonic NPs are constantly heating their environment as the plasmonic excitation dephases.²⁴ Here we present an explicit exploration of this effect, presenting an upper limit for its contribution in a typical laboratory photocatalytic setup.

In parallel to this, we have recently postulated the important role played by exciton-driven reactive oxygen species (ROS) generated under irradiation in the plasmonic photosensitization of semiconductor photocatalysts in aqueous solutions.²⁵ ROS are a family of highly reactive, oxygen bearing molecules (mostly radicals) that form through the interaction between H₂O and O₂ with the photoexcited electrons and holes provided by a heterogeneous photocatalyst.^26,27 These species play an important role in many biological processes such as oxidative stress or cellular signaling.^28,29 Four molecules are usually considered as the most relevant: hydroxyl radical (OH˙), hydrogen peroxide (H₂O₂), superoxide radical (˙O₂⁻) and singlet oxygen (¹O₂). Since ROS are transient intermediates formed under photocatalytic conditions, their identification can provide information about the relative importance of the photogenerated hot electrons and holes and, ultimately, shade light on the physical processes behind plasmon-induced photocatalysis. In the particular case of TiO₂, the most widely-used semiconductor for heterogeneous photocatalysis in aqueous solutions, the most important photoactivation reactions are the reduction of O₂ by electrons situated at the conduction band to form ˙O₂⁻ and the oxidation of H₂O to generate OH˙ by the holes formed in the valence band.³⁰ The latter species is also generated by the multistep reduction of O₂ at the conduction band of the semiconductor. Nevertheless, we cannot exclude the concomitant generation of other transient species, and the important repercussions that their presence may entail to the photosensitization process.

In the present work we discuss two fundamental aspects involved in the plasmonic photosensitization of large bandgap semiconductors: the role played by thermal contributions and the nature of the photogenerated ROS, using a colloidal hybrid as model photocatalyst. These objects are formed by the assembly of TiO₂ NPs and Au nanorods (NRs). In this manner, simple experiments are performed in order to discern the role of temperature in the photodegradation of rhodamine B (RhB) as a model reaction.²⁵ In parallel, theoretical modelling allows us to predict the temperature increase expected under the photocatalytic conditions presented herein. In a second set of experiments, we identify the ROS formed through the interaction between photogenerated charge carriers and water/oxygen molecules, discussing their relevance in the framework of the photocatalytic transformations under study. Accordingly, these studies allow us to discern the relative importance of the hot electrons transferred to the conduction band of the semiconductor and the hot holes produced at the Fermi level of the metal in the photocatalytic organic transformation under study.

Results and discussion

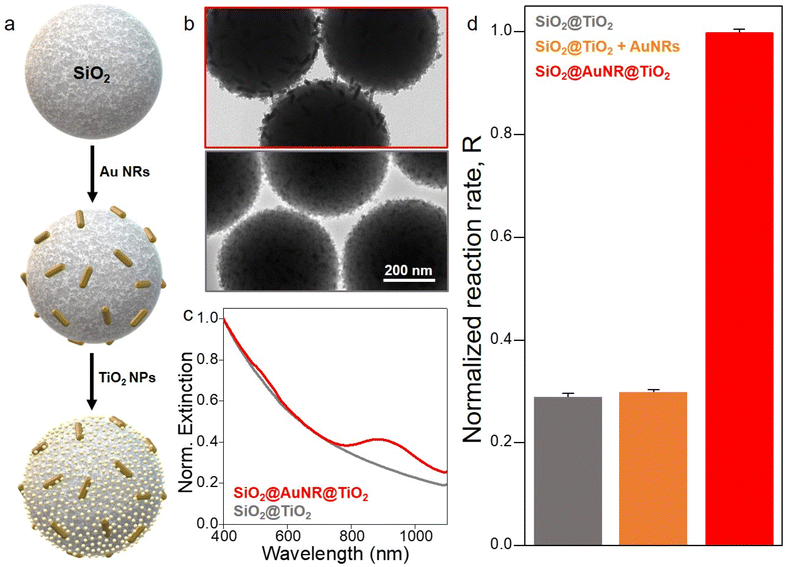
The model photocatalyst is formed by the electrostatic assembly of Au NRs and 5 nm TiO₂ NPs (anatase phase) onto 500 nm silica spheres (Fig. 1a, S1 and experimental details in the ESI† ), which has proven to be a reliable material for the study of the photophysical interaction between a plasmonic and a semiconductor component.^22,23 The hybrid formed with such geometry, named SiO₂@AuNR@TiO₂ ensures a homogeneous distribution of both active components onto the inorganic substrate (Fig. 1b) and the formation of a physical interface between them (Fig. S2†). This characteristic is of paramount importance for an efficient hot electron transfer process through which electrons with sufficient kinetic energy can traverse from the metal to the semiconductor. Moreover, the use of the colloidal substrate ensures the easy recovery of the photocatalyst after the photochemical reaction. The longitudinal plasmon band of the Au NRs is red shifted from 818 nm when they are isolated in aqueous solution to 884 nm when adsorbed onto the silica substrates, also in water (red line in Fig. 1c), which is below the energy barrier between the Fermi energy of Au and the conduction band of TiO₂ (∼1 eV = 1240 nm). This absorption signature is accompanied by a strong scattering contribution of the silica spheres and the excitation band of TiO₂ at lower wavelengths. As a reference sample, we have synthesized a photocatalyst without the plasmonic component (SiO₂@TiO₂) that is active only in the UV segment of the solar spectrum (Fig. 1b and c).

Fig. 1 (a) Schematic representation of the assembly process leading to the formation of the photocatalytic hybrids. (b) TEM images and (c) extinction spectra of SiO₂@AuNR@TiO₂ (red) and SiO₂@TiO₂ (gray), respectively. (d) Normalized reaction rates obtained from the photodegradation profiles of RhB at 20 °C in the presence of SiO₂@TiO₂ (dark gray), SiO₂@TiO₂ mixed in solution with Au NRs (orange) and SiO₂@AuNR@TiO₂ (red). The photodegradation reactions have been performed with a 150 W SLS401 xenon short-arc light source and a range of 360–2400 nm. The normalized reaction rate is obtained from ΔAbs = Abs(t = 180) − Abs(t = 0); R = ΔAbs/ΔAbs_ref.

When working with colloidal systems, as opposed to gas-phase photocatalysis, individual resonators do not lead to the formation of strong thermal gradients when illuminated at low light fluencies, as the thermal conductivity of water is one order of magnitude higher than that of air, thus allowing an efficient heat removal by conduction. Moreover, stirring the colloidal solution can enhance heat and mass transport, thus smoothing the macroscopic thermal distribution.^11,31 Such scenario is particularly interesting for us since the total temperature increase of the system can be monitored by introducing a thermocouple in the solution during irradiation. In our experimental setup we have minimized any possible thermal effects by performing all our photocatalytic tests with a thermostatic reactor (under magnetic agitation) that allows to keep a stable reaction temperature (in our case at 20 °C) (Fig. S3†). Under these specific experimental conditions, we can assume that the photocatalytic activity can only be the result of the generation of hot charges and/or plasmon-induced energy transfer since there is no variation of temperature at the macroscopic level.

We performed a number of control catalytic and photocatalytic experiments in order to elucidate the role played by plasmonic thermal dissipation in our system. Among them, the photodegradation of RhB has proven to be a reliable means to quantify the photocatalytic activity of Au–TiO₂ hybrids, allowing straightforward monitoring with simple spectroscopic techniques.^23,25 Firstly, we tested the degradation profile of RhB when exposed to high temperatures in the dark (in the absence of photocatalyst). As can be seen in Fig. S4a,† the organic dye remains stable when exposed to 60 °C over a prolonged period of time (8 hours), proving that the chosen model reaction cannot proceed in the dark even at macroscopic temperatures well above those expected from plasmon-induced heating (vide infra). Moreover, when the same dye is irradiated in the presence of SiO₂@TiO₂ at two different temperatures (20 and 40 °C), no apparent difference in the photodegradation profile can be observed (Fig. S4b†). The partial degradation of the dye is the result of the direct activation of the semiconductor with λ: 360–385 nm. As we will see, 40 °C is well in excess of the photo-temperature achieved by plasmonic photoheating in our setup. Consequently, this second experiment shows that the thermal activation of the photocatalyst under irradiation is not responsible for the increase in efficiency of the chemical transformation. Finally, we have monitored the photocatalytic reaction with the same catalyst (SiO₂@TiO₂) alone or accompanied by a plasmonic resonator in two different configurations: either functionalized with a layer of Au NRs forming a Schottky barrier with the semiconductor (SiO₂@AuNR@TiO₂) or by adding the same amount of Au NRs to the solution (SiO₂@TiO₂ + Au NRs). In Fig. 1d we present the normalized reaction rates (R) obtained from the photodegradation profiles of RhB under irradiation, assuming a linear fit with R = ΔAbs/ΔAbs_ref, where ΔAbs = Abs(t = 180) − Abs(t = 0) (for more details, please refer to Fig. S4c†). As we have seen in previous studies, the formation of a hybrid photocatalyst with a physical interface between the photosensitizer and the semiconductor leads to an improved activity (red column in Fig. 1d).³² In the absence of a physical connection between the materials the photosensitization mechanism does not function and the activity of the catalyst (orange column in Fig. 1d) is the same previously observed for the SiO₂@TiO₂ hybrid alone (gray column in Fig. 1d). This, of course, highlights the importance of using materials, such as TiO₂, with reaction-appropriate redox potentials. Moreover, this last result further demonstrates that the temperature increase associated to the thermal dissipation of the plasmonic resonators cannot be the main parameter behind the photo-oxidation of RhB.

The experimental data are complemented with theoretical simulations of the thermal contributions of the system under the irradiation conditions presented above. Our simulations analyze both the macroscopic and microscopic response of our photocatalytic system. For the latter, we have first simulated the optical response of an individual Au NR with the same dimensions of the ones obtained experimentally, as measured by TEM (Fig. S5†). These data, alongside additional theoretical characterization of the hot electron excitation properties of Au NRs, are presented in the ESI.† We have also simulated the microscopic response of a SiO₂@Au nanohybrid, modelled with a random distribution of 36 Au NRs onto a 500 nm SiO₂ sphere (the Au/SiO₂ ratio has been calculated with respect to the concentrations used in our experiments). Subsequently, we have used the simulation results for the hybrid, together with experimental information, to calculate the total photoheating due to the plasmonic NRs in the macroscopic system. This ensemble calculation was conducted by simulating the thermal response of the solution in a model of the cuvette that included relevant experimental factors influencing its thermal evolution (Fig. 2a). Two factors are particularly relevant: (i) as mentioned above the cuvette was surrounded by a thermal bath at T_room = 20 °C, so that the computational model has fixed the temperature of the external lateral walls of the cuvette at that value; and (ii) the experiment was conducted under continuous magnetic stirring, justifying the approximation of taking the heat input as being homogeneously distributed across the volume of the solution. The total heat input has been calculated as the fraction of the power irradiated from the lamp absorbed by the solution, taken as the complementary of its transmittance, T(λ), computed through the Beer–Lambert law:^33,34

Fig. 2 Thermal simulations. (a) Model of the cuvette holding the photocatalytic solution. Inset: model of a SiO₂@AuNRs hybrid. (b) Transient data of the temperature increase in the middle of the solution's volume (marked in inset), as the system progresses to the steady-state temperature. (c) Temperature increase map on a cross-section of the system, in the steady state. One should note that the outer lateral walls of the cuvette are fixed at T_room to model the experimental thermal bath. (d) Temperature increases along a vertical line crossing the center of the cuvette (see diagram on the right). (e) Microscopic temperature increase, with respect to the macroscopic temperature of the sample, in a single SiO₂@AuNRs hybrid under linearly polarized light.

Here, Q_input is the total heat absorbed by the solution and P_lamp(λ) is the emission spectrum of the lamp, as provided by the manufacturer, and which has a total output power of 1.3 W. The light traverses the solution in a cuvette with a depth of l_cuvette, and the total absorbance of the sample accounts for the absorbance of water, μ_water(λ), and that of the hybrids, computed as the product of the absorption cross section of the SiO₂@AuNRs hybrid (σ_abs,hybrid), and the total number of such hybrids in solution, n_hybrid, obtained from the experimental Au concentration in the sample.

Au has a complex permittivity ε_Au, ω is the frequency of the incoming radiation, I₀ is the incoming light's intensity, E is the electric field, and the volume integral is computed into all the AuNRs covering the SiO₂ sphere.

Having defined the heat input in the solution, we can compute the thermal evolution of the system, of which we present a summary of results in Fig. 2. Panel b showcases the progressive heating up of the solution, as measured at a point in the middle of its volume, in which we can see the system reaching a steady state excess temperature, ΔT = T_macro − T_room, of approximately ΔT = 2.3 K after ∼3 minutes. The remaining panels (Fig. 2c–e) show the temperature distribution in the steady state. As expected, the highest values of this magnitude are found in the middle of the solution's volume, given the temperature conditions imposed at the outer walls of the glass cuvette by the thermal bath in our setup. As mentioned above, this increase in temperature is much smaller than the increments taken exploring the thermal response of RhB in water (Fig. S4a†) and in a solution with the SiO₂@TiO₂ catalyst (Fig. S4b†).

The possibility remains, however, that the photoheating of Au NRs generate steep thermal gradients in their immediate environment. If that were the case, one could expect that molecules adsorbed to the metal surface would be excited to modes commensurate with a higher temperature. Besides arguing that the relatively high thermal conductivity of water does not facilitate such steep gradients and noting that this possibility was ruled out experimentally (see above), we can also lean on a computational approach to show the local gradients in temperature. We return then to the microscopic model of our system and in Fig. 2e we show the steady-state increase in temperature, over that of the solution in the background, at the surface of a SiO₂@AuNRs hybrid under linearly polarized light. The simulation was performed with a background temperature equal to the macroscopic steady-state temperature found above, T_macro = T_room + ΔT = 22.3 °C. As we can see, the maximum temperature reached at these Au NRs is in the order of 10⁻⁴ K over that of the rest of the sample, a clearly insufficient difference to drive the chemical reaction. When irradiating a large group of mostly non-interacting NPs, the most important parameter directing the variation of temperature is not the absorption of the NP but rather the absorbance of the sample as a whole. Thus, by virtue of the large number of NPs involved, the collective effect is several orders of magnitude higher than the single NP contribution.

As postulated previously, the plasmonic activation of a large bandgap semiconductor in aqueous solution leads to the formation of ROS (Fig. 3a). The identification of their nature will give us information about the relative importance of the hot electrons transferred to the conduction band of TiO₂ and the hot holes generated below the Fermi level of Au on the chemical reaction under study. Herein, we investigate the presence of the four most important ROS in the reaction medium by using molecular scavengers that interact selectively with each one of them. Firstly, we assessed the formation of OH˙ by using the transformation of terephthalic acid (TPA) into the fluorescent product 2-hydroxyterephthalic acid (2-HTPA) (Fig. 3b). Secondly, ¹O₂ was detected using 9,10-anthracenediyl-bis(methylene) dimalonic acid (ABDA) (Fig. 3c), while H₂O₂ was detected by the photo-assisted decomposition of pentafluorobenzenesulfonyl fluorescein (PBSF), leading to the formation of the fluorescent dye fluorescein (Fig. 3d). Finally, the transformation of Nitro Blue tetrazolium (NBT) into its formazan form was used for the detection of ˙O₂⁻ (Fig. 3e). All these reactions are presented in the ESI (eqn (S1)–(S4)†). Our results demonstrate that the four species are found under the photocatalytic conditions reported previously. In all cases, the concentration of ROS is enhanced in the presence of SiO₂@AuNR@TiO₂ hybrids with respect to SiO₂@TiO₂ due to the prolonged excitonic lifetimes within a broader electromagnetic spectrum.

Fig. 3 Schematic representation of the photocatalytic experiments for the elucidation of the radical species present in the reaction medium and in the presence of the chosen photocatalyst: SiO₂@AuNR@TiO₂ (red) and SiO₂@TiO₂ (gray). (b) Formation profile of 2-HTPA by the reaction of TPA with OH˙ by fluorescence spectroscopy. (c) Detection profile of ¹O₂ by the reaction with ABDA by absorption spectroscopy. (d) Detection of H₂O₂ by the phototransformation of PBSF by fluorescence spectroscopy. (e) Detection of ˙O₂⁻ by its reaction with NBT by absorption spectroscopy. The blue dots represent the phototransformation of the scavenger in the absence of photocatalyst. The dashed lines are a guide to the eye.

In order to ascertain the relative importance of the hot charge carriers in the photo-oxidation of RhB, we have repeated the photocatalytic reaction in the presence of two short-chain alcohols: tert-butanol (tBuOH) and isopropanol (iPrOH). While the former is broadly used as OH˙ scavenger, the latter can also act as an electron donor, reacting with the photogenerated holes.^35–37Fig. 4a shows that the degradation of RhB is quenched when any of these two scavengers is introduced in the reaction medium. In the same way, when we repeated the photocatalytic transformation of TPA into 2-HTPA in the presence of tBuOH, using SiO₂@AuNR@TiO₂ as photocatalyst, we observe that the reaction is deactivated (Fig. 4b). These results lead us to assume that the photogenerated holes created at the Fermi level of the plasmonic resonator upon excitation are responsible for the photo-oxidation of the organic substrate. At this point, one could argue that OH˙ radicals can also be generated at the conduction band of the semiconductor through the multistep reduction of O₂ (equation in Fig. 3a). In this manner, the hot electrons could also participate in the phototransformation of the organic substrate. To clarify this, we repeated the photodegradation of RhB under argon atmosphere in order to eliminate any presence of O₂ and therefore of OH˙ formed by the hot electrons at the conduction band of TiO₂. In this case, the dye degradation rate is very similar to that obtained under air (Fig. 4c). This last result excludes the generation of OH˙ from the transformation of ˙O₂⁻ as a major driving force behind the photocatalytic transformation of RhB. As a consequence, we can conclude that TiO₂ plays here the role of an electron sink that prolongs the lifetime of the electron–hole pair, rather than being the active photocatalyst in the photo-oxidation of the organic substrate.

Fig. 4 Photocatalytic experiments for the elucidation of the relative importance of the photogenerated hot electrons and holes. (a) Normalized reaction rates for the photo-oxidation of RhB in the presence of SiO₂@AuNR@TiO₂ hybrids with and without different hole and OH˙ scavengers (iPrOH and tBuOH). (b) Normalized reaction rates for the formation of 2-HTPA by the reaction of TPA with OH˙ with and without tBuOH as a radical scavenger. (c) Normalized reaction rates for the photo-oxidation of RhB under air (red) and under argon (pink). The normalized reaction rate is obtained from ΔAbs = Abs(t = 180) − Abs(t = 0); R = ΔAbs/ΔAbs_ref in the case of RhB and from ΔEm = Em(t = 180) − Em(t = 0); R = ΔEm/ΔEm_ref in the case of 2-HTPA.

Conclusions

In this work we address two important issues related with plasmonic photocatalysis in aqueous solutions: the role played by thermal effects and the importance of photogenerated ROS in the activation of an hybrid Au–TiO₂ catalyst. The first issue is investigated following simple experimental procedures, using a theoretical model to corroborate our assumptions. Our results show that dissipation of temperature at the macroscopic level is sufficient to remove any possible thermal contribution induced by plasmonic excitation from the photocatalytic reaction. In parallel to this, we investigated the nature of the ROS generated upon plasmonic photosensitization of TiO₂. In this vein, the presence of OH˙, H₂O₂, ˙O₂⁻ and ¹O₂ has been confirmed by selective reactivity with scavengers under photocatalytic conditions. Experimental evidence demonstrates that the OH˙ radicals generated by the hot holes formed at the Fermi level of Au NRs are the main driving force for the photo-oxidation of RhB.

The present study does not intend to justify the role played by hot charge carriers on a broad spectrum of photocatalytic plasmonic systems nor it is translatable to a vast number of chemical processes. Rather, it is proposed to demonstrate the importance of plasmonic charge carriers as the main driving force behind the photo-oxidation of organic substrates in aqueous solutions when the plasmonic-semiconductor hybrid presents a Schottky junction. Other chemical processes in which thermal effects are relevant may allow their rational combination with the photogeneration of hot charges and/or plasmon-induced energy transfer, leading to interesting synergies and improved activities.^12,38 We believe that the elucidation of the physical and chemical processes behind any plasmon-induced photocatalytic reaction should be performed on a case-by-case basis. Similarly, a better understanding of ROS reactivity must be considered a major step towards the implementation of these transient species in other photocatalytic applications.

Author contributions

Y. N.-M. and C. B. performed experimental work under the supervision of J.-Y. P., M. A. C.-D. and M. C.-H.; A. O. G. and L. V. B. contributed to the theoretical aspects of the work; M. C.-H. and L. V. B. wrote the manuscript, with all authors viewing and contributing to its content.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. C.-H. thanks CNRS for support. L. V. B. acknowledges support from the Spanish Ministerio de Ciencia e Innovación under Project PID2020-118282RA-I00. Authors at Universidade de Vigo thank Spanish Ministerio de Economía y Competitividad (CTM2017-84050-R), Xunta de Galicia (Centro Singular de Investigación de Galicia – Accreditation 2019–2022 ED431G 2019/06 and IN607A 2018/5), and European Union-ERDF (Interreg V-A – Spain-Portugal 0245_IBEROS_1_E, 0712_ACUINANO_1_E, and 0624_2IQBIONEURO_6_E, and Interreg Atlantic Area NANOCULTURE 1.102.531). A. O. G. thanks the Nanoscale & Quantum Phenomena Institute at Ohio University for its support.

Notes and references

1. S. Linic, P. Christopher and D. B. Ingram, Nat. Mater., 2011, 10, 911–921.
2. M. J. Kale, T. Avanesian and P. Christopher, ACS Catal., 2014, 4, 116–128.
3. T. Tatsuma, H. Nishi and T. Ishida, Chem. Sci., 2017, 8, 3325–3337.
4. M. L. Brongersma, N. J. Halas and P. Nordlander, Nat. Nanotechnol., 2015, 10, 25–34.
5. J. S. Duchene, G. Tagliabue, A. J. Welch, X. Li, W. H. Cheng and H. A. Atwater, Nano Lett., 2020, 20, 2348–2358.
6. J. Li, S. K. Cushing, F. Meng, T. R. Senty, A. D. Bristow and N. Wu, Nat. Photonics, 2015, 9, 601–607.
7. R. Asapu, N. Claes, R. G. Ciocarlan, M. Minjauw, C. Detavernier, P. Cool, S. Bals and S. W. Verbruggen, ACS Appl. Nano Mater., 2019, 2, 4067–4074.
8. G. Baffou, F. Cichos and R. Quidant, Nat. Mater., 2020, 19, 946–958.
9. S. Linic, S. Chavez and R. Elias, Nat. Mater., 2021, 20, 916–924.
10. S. Yu, A. J. Wilson, J. Heo and P. K. Jain, Nano Lett., 2018, 18, 2189–2194.
11. P. K. Jain, J. Phys. Chem. C, 2019, 123, 24347–24351.
12. S. Rej, L. Mascaretti, E. Y. Santiago, O. Tomanec, S. Kment, Z. Wang, R. Zboril, P. Fornasiero, A. O. Govorov and A. Naldoni, ACS Catal., 2020, 10, 5261–5271.
13. R. Kamarudheen, G. W. Castellanos, L. P. J. Kamp, H. J. H. Clercx and A. Baldi, ACS Nano, 2018, 12, 8447–8455.
14. Y. Yu, V. Sundaresan and K. A. Willets, J. Phys. Chem. C, 2018, 122, 5040–5048.
15. C. Zhan, X. J. Chen, Y. F. Huang, D. Y. Wu and Z. Q. Tian, Acc. Chem. Res., 2019, 52, 2784–2792.
16. R. Kamarudheen, G. J. W. Aalbers, R. F. Hamans, L. P. J. Kamp and A. Baldi, ACS Energy Lett., 2020, 5, 2605–2613.
17. Y. Dubi, I. W. Un and Y. Sivan, Chem. Sci., 2020, 11, 5017–5027.
18. Y. Dubi and Y. Sivan, Light: Sci. Appl., 2019, 8, 89.
19. G. Baffou, I. Bordacchini, A. Baldi and R. Quidant, Light: Sci. Appl., 2020, 9, 108.
20. E. Cortés, L. V. Besteiro, A. Alabastri, A. Baldi, G. Tagliabue, A. Demetriadou and P. Narang, ACS Nano, 2020, 14, 16202–16219.
21. E. Cortés, R. Grzeschik, S. A. Maier and S. Schlücker, Nat. Rev. Chem., 2022, 6, 259–274.
22. A. Sousa-Castillo, M. Comesaña-Hermo, B. Rodríguez-González, M. Pérez-Lorenzo, Z. Wang, X.-T. Kong, A. O. Govorov and M. A. Correa-Duarte, J. Phys. Chem. C, 2016, 120, 11690–11699.
23. Y. Negrín-Montecelo, M. Comesaña-Hermo, L. K. Khorashad, A. Sousa-Castillo, Z. Wang, M. Pérez-Lorenzo, T. Liedl, A. O. Govorov and M. A. Correa-Duarte, ACS Energy Lett., 2020, 5, 395–402.
24. G. Baffou and R. Quidant, Laser Photonics Rev., 2013, 7, 171–187.
25. A. Sousa-Castillo, J. R. Couceiro, M. Tomás-Gamasa, A. Mariño-López, F. López, W. Baaziz, O. Ersen, M. Comesaña-Hermo, J. L. Mascareñas and M. A. Correa-Duarte, Nano Lett., 2020, 20, 7068–7076.
26. W. He, J. Cai, X. Jiang, J. J. Yin and Q. Meng, Phys. Chem. Chem. Phys., 2018, 20, 16117–16125.
27. Z. Cui, L. Zhang, Y. Wang and W. He, Appl. Surf. Sci., 2022, 584, 152655.
28. M. Schieber and N. S. Chandel, Curr. Biol., 2014, 24, R453–R462.
29. M. Wrzaczek, M. Brosché and J. Kangasjärvi, Curr. Opin. Plant Biol., 2013, 16, 575–582.
30. M. Buchalska, M. Kobielusz, A. Matuszek, M. Pacia, S. Wojtyła and W. Macyk, ACS Catal., 2015, 5, 7424–7431.
31. I. W. Un and Y. Sivan, ACS Photonics, 2021, 8, 1183–1190.
32. Y. Negrín-Montecelo, A. Movsesyan, J. Gao, S. Burger, Z. M. Wang, S. Nlate, E. Pouget, R. Oda, M. Comesaña-Hermo, A. O. Govorov and M. A. Correa-Duarte, J. Am. Chem. Soc., 2022, 144, 1663–1671.
33. J. Yang, N. J. Kramer, K. S. Schramke, L. M. Wheeler, L. V. Besteiro, C. J. Hogan, A. O. Govorov and U. R. Kortshagen, Nano Lett., 2016, 16, 1472–1477.
34. L. V. Besteiro, K. Gungor, H. V. Demir and A. O. Govorov, J. Phys. Chem. C, 2017, 121, 2987–2997.
35. J. T. Schneider, D. S. Firak, R. R. Ribeiro and P. Peralta-Zamora, Phys. Chem. Chem. Phys., 2020, 22, 15723–15733.
36. I. Carrizosa and G. Munuera, J. Catal., 1977, 49, 189–200.
37. E. M. Rodríguez, G. Márquez, M. Tena, P. M. Álvarez and F. J. Beltrán, Appl. Catal., B, 2015, 178, 44–53.
38. W. Koopman, R. M. Sarhan, F. Stete, C. N. Z. Schmitt and M. Bargheer, Nanoscale, 2020, 12, 24411–24418.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental methods; irradiation set-up; photochemical tests; control experiments and simulations. See DOI: https://doi.org/10.1039/d2nr02431d

---