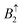Rhombohedral trilayer graphene is more stable than its Bernal counterpart

Abstract

Stackings in graphene have a pivotal role in properties that could be useful in the future, as seen in the recently found superconductivity of twisted bilayer graphene. Beyond bilayer graphene, the stacking order of multilayer graphene can be rhombohedral, which shows flat bands near the Fermi level that are associated with interesting phenomena, such as tunable conducting surface states that can be expected to exhibit spontaneous quantum Hall effect, surface superconductivity, and even topological order. However, the difficulty in exploring rhombohedral graphenes is that in experiments, the alternating, hexagonal stacking is the most commonly found geometry and has been considered to be the most stable configuration for many years. Here we reexamine this stability issue in line with current ongoing studies in various laboratories. We conducted a detailed investigation of the relative stability of trilayer graphene stackings and showed how delicate this aspect is. These few-layer graphenes appear to have two basic stackings with similar energies. The rhombohedral and Bernal stackings are selected using not only compressions but anisotropic in-plane distortions. Furthermore, switching between stable stackings is more clearly induced by deformations such as shear and breaking of the symmetries between graphene sublattices, which can be accessed during selective synthesis approaches. We seek a guide on how to better control – by preserving and changing – the stackings in multilayer graphene samples.

---

1 Introduction

Graphene remains a key two-dimensional material that continues to reveal intriguing properties when stacked into just a few layers. As an example, bilayer graphene in the twisted form has been found to exhibit superconductivity properties.¹ Large graphene samples are obtained experimentally by mechanical exfoliation of graphite, so they are supposed to favor Bernal stacking, which for graphite has been considered to be more stable than rhombohedral stacking.² However, this stability is far from being fully settled. Firstly, recent calculations have shown that graphite is energetically more stable in rhombohedral stacking, so it is suggested that crystal growing conditions under high temperatures and pressures in a geological scale are responsible for Bernal stacking in graphite.³ Secondly, experimental and synthesizing techniques in 2D materials have been so improved over the years that graphene is being investigated nowadays with a defined number of layers.^4,5 Research works that have focused on the same exfoliated sample of trilayer graphene (TLG) simultaneously found regions with Bernal and rhombohedral stacking.^6–10 Rhombohedral trilayer graphene is today being synthesized with a renewed interest to show its unique properties primarily due to flat band regions near the K, K′ points, that are low-energy van Hove singularities related to magnetism, superconductivity and other strongly correlated phenomena.^11–14 The stability between the Bernal and rhombohedral stacking in few layer graphenes therefore stands as a crucial question to be discussed.

Techniques are currently being developed on how to obtain, preserve or change stacking in trilayer graphene. The phase change between rhombohedral (ABC) and Bernal (ABA) stacking can be induced by external driving forces. The ABC stacking was experimentally found when graphene layers were grown on SiC substrates, and it was stable up to a temperature of around 1200 °C when it reverts to the ABA stacking.^15,16 The transition from ABA to ABC stacking can be caused by a scanning tunneling microscope (STM) tip on highly ordered pyrolytic graphite (HOPG) samples due to the small barriers involved (∼1.0 meV per atom), as recently reported.^7,17 The transition between ABC and ABA stacking was also achieved using triazine decoration, which causes a large energy difference to induce the stacking transition.¹⁸ Recent experiments in twisted trilayer graphene heterostructures show multiple ABC and ABA stacking domains that can be reversibly changed by electric field orientation and doping.¹⁹ The stacking in few-layer graphene heterostructures was stabilized mechanically by strain, using electric fields and even doping.^19–21

In order to fabricate high-quality encapsulated ABC trilayer–hBN devices used for quantum transport investigations, it has been shown that often the ABC trilayer converts to ABA during van der Waals transfer, even though ABA regions had been carefully removed prior to stamping.²² The rhombohedral to Bernal transition has been theoretically studied by modeling the continuous sliding deformation of a side layer and by parameterizing the results for two layers, calculations that were performed within density functional theory (DFT) using local density approximation (LDA).^23,24 Although the van der Waals energies per atom are small, the total bonding energies are sizeable when the sample areas are considered, total energies that are large but needed to keep a certain phase were locked in a metastable stacking after being synthesized. These findings suggest that not only should the relative stability between these TLG stackings be studied, but that their dependence on the lattice deformations deserves further study.

In this work, we address the stability between rhombohedral and Bernal stacking in trilayer graphene by calculations performed using density functional theory (DFT) using explicitly van der Waals functionals. We study different deformations that induced the energetic exchange between these stackings by looking at their relative stability. We first show that as the TLG ground state, the rhombohedral stacking is slightly more stable than the Bernal one. Then we perform several deformations in the quest to induce the transition from rhombohedral stacking to the Bernal one. In our simulations we find that Bernal stacking is energetically more stable than the rhombohedral one under some distortions based on the planar expansion of the lattice parameters and their perpendicular compression. Furthermore, we show that under distortions such as shear and the atomic shifts in graphene sublattices, structural anisotropy helps to stabilize the ABA stackings in certain directions. These mechanisms point out that the stacking transition is achieved by breaking the sublattice symmetries of layer–layer interactions involved in each stacking. These findings indicate that different practical applications are possible, such as depositing samples in sandwiches, substrates, and molecule decoration, where stacking transitions may take place.

2 Computational method

We performed our study using density functional theory (DFT) in the ab initio simulation package VASP.^25–27 This method based on plane waves is applied using a well converged kinetic energy cut-off of 700 eV. For the energy range that we are interested in, the mesh grid on the reciprocal space is key to get consistent results (see the ESI†), a 288 × 288 × 1 centered at the Γ point is used. For the dispersive interactions between layers, we perform our calculations using the van der Waals functional vdW-DF2 that seems to improve overbinding in the DF functional found when comparing with non-routine Monte-Carlo calculations for bilayer graphene.^28–30 The electronic convergence was performed with 10⁻⁷ eV. We test the parameter convergence separately on each of the two stackings in absolute values. Thus, we guaranteed that when the energy differences between stackings are calculated both with the same parameters, we can eliminate systematic errors. We relax the cell shape and keep the volume constant, and we fix the ions in the xy plane while allowing them to move in the z direction. Tests performed with other functionals, as well as a detailed convergence test in k-points, and electronic and ionic relaxations are included in the ESI.† Note that a fine k-mesh is required to be applied with the number of sampling k points in the x and y directions being a multiple of 3 to explicitly include the points K, K′ and a region around them, regions in the reciprocal space where the low energy physics of multilayer graphene occurs.

3 TLG stability and electronic structures

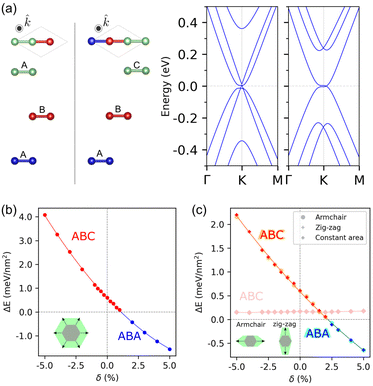
Fig. 1(a) shows the relaxed unit cells of trilayer graphene with the Bernal stacking on the left and the rhombohedral stacking on the right. Each stacking has a relaxed intralayer atomic distance of a_c–c = 1.43 Å, and the interlayer distance of d = 3.55 Å in agreement with experiments and quantum Monte-Carlo calculations, where the distances in few-layer graphenes have clearly expanded from bulk graphite.^30–35 The relative stability between Bernal and rhombohedral stackings is next analyzed by looking at the difference between their total energies. We present the relative energy per area as it is common in papers about bilayer graphene, where the considered area refers to the unit cell calculated after deformations.

Fig. 1 (a) (Left) Side views of the units cells and (right) band structures for the Bernal and rhombohedral stacking of trilayer graphene (TLG). (b) Energy differences between Bernal and rhombohedral TLG versus in-plane homogeneous strains δ with compression (δ < 0) and stretching (δ > 0) in lattice parameters. (c) Energy differences for uniaxial deformations along zigzag and armchair directions. Blue-cyan and red-orange colors refer to the strain values when the Bernal and rhombohedral stackings are more stable, respectively. Energy differences are also given with strains assuming a constant area per nm² area, shown in light red. The insets in panels (b) and (c) indicate the homogeneous and uniaxial deformations in-plane, respectively. The TLG rhombohedral stacking is more stable without surface strain, and a transition to Bernal stacking is shown under expansions with δ ≥ 1%.

After geometry relaxations, the energy differences per unit of area are calculated as ΔE = (E_B − E_r)/S, where E_B and E_r are the total energies of Bernal and rhombohedral stacking respectively, and S is the area of each deformation. In addition, we use a constant volume to avoid non-systematic errors. For pristine TLG, our earlier results show a total energy difference of 0.60 meV nm⁻² between both stackings.

We have performed a detailed analysis of converging parameters to the accuracy required here, as shown in the ESI.† The required accuracy is about 0.01 meV nm⁻², which is enough to discuss the energy differences covered in this work. It seems theoretically established that Bernal stacking is more stable than rhombohedral stacking in the literature, but this statement is based on inconsistent results.³ In fact, we find that in TLG the rhombohedral stacking is slightly more favorable than the Bernal one.

The energy differences although small are in agreement with enthalpy experiments between hexagonal and rhombohedral graphene.^19,36 Kinetic conditions such as temperatures and pressures seem to be the key in obtaining Bernal stacking. All atoms have to shift the entire layer in order to pass from ABA to ABC stacking, and the other way around. We propose that these processes have to be considered in order to compare with the room temperature energy taking into account the total contact area. This means that there is a minimum area in the flakes so as to obtain a stacking stable at room temperature. Depending on the value of stacking energy times the area, there is a blocking temperature above which the separate layers can slide. In other words there is also a minimum area at a given temperature so that the flake stacking remains stable to be observed in experiments. An implication is that stackings can be different depending on the synthesis methods used, namely exfoliation and CVD growth.

We compare the electronic band structures of the Bernal and rhombohedral stackings along the ΓKM path near the Fermi energy, as shown in Fig. 1(a). At the K point, the Bernal stacking bands display superposed massive and massless electronic behaviors, and the rhombohedral electronic structure shows massive electrons only; these two types of dispersion bands for each stacking are in agreement with ref. 37. The Bernal stacking can be seen as a superposition of single layer graphene bands and Bernal bilayer graphene bands; however, the graphene-like bands are slightly shifted up indicating the source of some intrinsic electric field between the layers to be added to the external fields.³⁸ For the rhombohedral stacking, there is a non-linear dispersion with a flat region around the K K′ points, a source of many interesting properties, such as tunable conducting surface states¹¹ expected to exhibit spontaneous quantum Hall effect,³⁹ surface superconductivity,⁴⁰ and even topological order.⁴¹ The massless band in Bernal stacking now has acquired mass in the rhombohedral geometry. The conduction and valence bands are degenerate and are slightly displaced from the K point in the KM direction, a source of spectroscopic signatures of electronic excitations in Raman scattering.⁴² At lower energies, the rhombohedral stacking presents split bands that justify its stability found in the calculations. A simple image can allow us to explain this stability. Bernal stacking has directly connected three atoms between layers so that there are states at zero energy. However, the rhombohedral case has two pairs of atoms between layers so the corresponding electronic states are split from the zero energy, a fact that could be somehow linked to its higher stability. In more detail, rhombohedral stacking presents coupling in “dimers” between the sublattices of the middle layer to the other layers due to interlayer hopping. The sublattice A₂ in the middle layer overlaps with the B₁ one in the upper layer, while the B₂ sublattice overlaps with the A₃ one in the bottom layer. Thus, these coupling in dimers made that zero energy states split from the Fermi energy suggesting a larger stability for the rhombohedral stacking.^11,43,44

4 In-plane deformations

Because the nature of covalent intralayer and vdW interlayer bonds is very different, we decided first to understand each deformation separately correlated with the different interlayer and intralayer distances. We now study different in-plane deformations of the lattice vectors. First, we consider a homogeneous (or isotropic) deformation of lattice vectors described by . In this sense, having λ = 1 (or strain δ = 0%) shows the previous relaxed lattice vectors, while a value of λ = 1.05 indicates an expansion strain of 5% (λ = 0.95 is a compression of 5%). This causes a proportional deformation of the lattice vectors keeping the interlayer distance constant. Fig. 1(b) shows the total energy differences per unit of area between Bernal and rhombohedral stacking for the in-plane deformations explained above. Positive values of the energy differences (colored in red) indicate that the rhombohedral stacking is more stable than the Bernal one. In contrast, negative values for the energy differences (colored in blue) refer to the case of Bernal stacking being more stable. We show that although under homogeneous deformation Bernal stacking becomes more favorable on expansion, the energy difference decreases for positive strains until it changes sign for ∼1%. At this point, Bernal stacking becomes more favourable.

Next, we consider anisotropic deformations with uniaxial strain without and with constant area, described by the lattice vectors () and 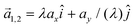along the x̂ (ŷ) direction, respectively. The energy difference induced by the anisotropic deformation considering a constant area is slightly decreasing and remains almost constant in the whole range of the considered positive or negative strains in the order of 5%, as shown in Fig. 1(c). Furthermore, this figure includes the energy differences with the anisotropic uniaxial deformations, and we find that Bernal stacking becomes more stable during stretching. The values of energy in the strain range ±5% show smaller response compared with those of homogeneous deformation, 2- versus 5-tenths of meV. Rhombohedral stacking with anisotropic strains is more stable for strain values until δ ∼ 2.2%, to be compared with Bernal stacking with isotropic strains that becomes more stable under small strains δ ∼ 1.1%.

Fig. 2 summarizes the trends found between the Bernal and rhombohedral energy differences versus the in-plane deformations in TLG. There is an asymmetry in strains that induces the most stable rhombohedral stacking switches into Bernal stacking. The strain values when this transition is taking place are within the experimental range of reversible strains attained for samples in substrates, already found for a single layer of graphene.⁴⁵ In fact, strain values of beyond 1% could be artificially applied to graphene heterostructures⁴⁶ and strain up to 0.3% has been seen in graphene encapsulated in hBN.⁴⁷ Thus detailed care must then be taken in experiments when depositing exfoliated graphenes on substrates, and when using patterned contacts,^10,48 so that the strain is induced by top contacts while edge contacts can help in reducing the strain.⁴⁹

Fig. 2 Summary of energy differences with respect to in-plane deformations δ_x and δ_y. Note the anisotropy of the rhombohedral–Bernal stability versus in-plane deformations.

5 Out of plane deformations

We further study the relative stability order induced by the strain ε in the interlayer distance by stretching and compression between layers, as shown in Fig. 3. Although the energies of both stackings are almost degenerate at zero strain, ΔE under stretching shows that the rhombohedral stacking continues being more stable even for an interlayer distance up to d = 4.26 Å (ε ≤ 20%). For a compression at d = 3.11 Å (ε = −2.5%), the ΔE values show that Bernal stacking becomes more favorable, in agreement with another current calculation using the empirically fitted vdW Grimme functional.⁵⁰ Small compressions induced by processes during transfer and protective layers will be enough to end into the ABA stacking. While we are not aware of direct measurements of compressions during h-BN encapsulation or subsequent cleaning by squeezing out residues,⁵¹ one can anticipate that compression of a trilayer can take place during these processing steps.

Fig. 3 Out-of-plane deformations: total energy differences versus out-of-plane strain ε related to the interlayer distance.

The next question is to determine how under a perpendicular pressure also the atomic in-plane layers are modified. It is noteworthy that under a constant volume a perpendicular pressure implies that the layers are expanding on the plane. For instance assuming a constant volume, a value of ε = −3.5% corresponds to a homogeneous expansion of δ = 1.88%. Looking for applied stresses implies performing derivatives and higher accuracy calculations beyond the actual scope of the paper. The critical δ value reinforces that the transition to Bernal stacking comes coupled to the in-plane deformations, as shown in Fig. 1(b) and (c) above. These results indicate that the TLG stackings have to be analyzed in the sample once they are covered and isolated in the operating device whenever is possible to be certain that rhombohedral stacking has not changed into Bernal. Furthermore, the role of temperature is linked with the temperature expansion on a and c lattice constants. Even at room temperature, the thermal expansion is very low, below the few percent limit we get for the transition between rhombohedral and Bernal stacking in our calculations. Of course, when increasing the temperature much higher, the thermal expansion a(T) and c(T) would be large enough to change stability between stackings, but this would happen at temperatures much above room temperature, in agreement with the reference.⁵⁰

6 Shear strain deformations

To assess the role of symmetry breaking we analyze the shear strain deformations. We consider the shear deformations along the perpendicular layer direction using the azimuthal ϕ and polar θ angles, as shown in the inset of Fig. 4 and the movie included in the ESI.† The question is what θ values must be chosen before entering into different stackings from the rhombohedral and Bernal ones, i.e. how close the structures with shear can be seen as deformations of the original ABA and ABC stackings. The shear structures remain close to the pristine ABC and ABA stackings for the values with θ < 15°, as shown in the ESI,† where shears beyond this critical angle show layers that can hardly be seen anymore as small deformations of the Bernal and rhombohedral stackings.

Fig. 4 Stability energy difference between Bernal and rhombohedral stackings versus shear deformation, which is indicated by angles θ and ϕ shown in the upper panel. The inset shows the shear ϕ angles for which the ABA and ABC stacking are more stable.

Fig. 4 shows energy differences between Bernal and rhombohedral stackings for the shears with θ = 10°, 5° changing ϕ angles. The shear for θ = 10° also shows that the interlayer distance d decreases from the value in pristine lattices so that ε = −1.5%; however, this ε value is still well below the critical distance to get the ABA stacking with perpendicular pressure. Therefore, obtaining Bernal stackings is not just correlated with the distance but more related with the shear angle. Note that for θ ≠ 0° the shear is displacing the layers in the in-plane with respect to the perfect stacking as cones, shown in the upper panel, so that the overlap of the carbon p_z orbitals between layers change related not only to distances but also to angles. In fact, the ε value for θ = 5° (ε ∼ 0.3%) just decreases slightly the interlayer distance, being larger than the critical distance to obtain ABA stacking under pressure. On the one hand, the energies of Bernal stacking exhibit a 60° periodicity in ϕ, while increasing θ makes the energy profile just wider. That means that these deformations destabilize Bernal stacking minimally up to ϕ = 30°. On the other hand, the energies for rhombohedral stacking does not show the same periodicity along the ϕ angle, because their periodicity (120° in ϕ) is twice that of the one found for Bernal stacking. Thus we find a region where rhombohedral stacking is more destabilized than the Bernal one.

In Fig. 4 we show the energy difference per unit of area between the two stackings under shear deformations. The curve for θ = 5° shows the ΔE in the range of ∼±10.17 meV nm⁻² decreasing as ϕ values increase. For the case of θ = 10°, the ΔE values are in the range of ∼±75 of meV nm⁻², values which are larger than the meV nm⁻² found for previous studied deformations. In fact the energy differences become an order of magnitude larger. For values of ϕ less than 30°, rhombohedral stacking still remains as more favorable, and for the values of ϕ > 30°, we find that Bernal stacking is more stable than the rhombohedral one. Taking into account the symmetry, we find that Bernal stacking becomes favorable for three fold directions of ϕ = 60° as shown in the inset included in Fig. 4. Interestingly, the ABA stackings for θ = 5° are observed even for a very small interlayer distance, values with very small ε. Even for a test case with ε = 0, i.e. with no change in interlayer distance, the energies remain in the order of tenths of meV. In general, considering that those ΔE values are larger than previous considered deformation cases, the shear deformation of the stackings promotes Bernal stacking in certain directions, so that the area of the stacking regions can even be reduced by a factor ten to be stable using shear deformations. These findings are in line with previous experimental results in which shear is induced by contacts,¹⁰ by other encapsulating layered graphenes within BN,‡ ²⁰ and by explicitly putting shear to the samples.⁵²

7 Perpendicular sublattice distortions

Up to now all the investigated deformations affected both graphene sublattices within the same layer in the same way. We have then shown that shear introduced mostly anisotropy in plane. For the sake of completeness, we now assess the role of deformations out of plane by looking at the anisotropy induced by the sublattices sites. We study the displacement up and down for each of the sublattices in both stackings. We characterize how much the same perpendicular shift affects the relative stability of each stacking. Here, we apply a perpendicular displacement to A or B sublattice type nodes, shifts that are breaking the sublattice layer symmetry. We shift an atom of a particular sublattice in the direction perpendicular to the layer plane by less than the layer compression to get ABA stacking, and compare how much the total energy of each stacking is changed.

First we note that in each stacking, atoms of both side layers have the same number of interlayer neighbors. The energy response for atom shifts in side layers is very small; it does not exceed 0.01 meV. Thus we focus on the middle layer analyzing the coordination numbers of its atoms. Fig. 5(a) shows the Bernal and rhombohedral stacking schemes indicating the nearest neighbours in next layers. The vertical lines are linking the middle layer atoms to the first neighbors belonging to the side layers and shaded prisms with numbers mark the second interlayer neighbors. In both stackings, the A and B type nodes have in total 2 first neighbors and 18 seconds neighbors belonging to the side layers. However, the number of neighbors for each sublattice calculated separately is different. We can expect different responses when breaking the symmetry by shifting A or B atoms. In the case of Bernal stacking, the number of interlayer neighbors for a sublattice site is the same with the top and bottom layer. Thus the up or down shifts will be symmetric. In rhombohedral stacking, the number of neighbors for each sublattice site is “antisymmetric” i.e. shifting the A atom up is equivalent to shifting the B type atom down and vice versa. For the rhombohedral geometry, the number of cases to be discussed is reduced to two: (i) 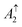equivalent to and (ii) equivalent to , where subscripts refer to the layer number, and arrows indicate the perpendicular displacement.

Fig. 5 (a) Models for the Bernal and rhombohedral stacking including the number of interlayer next nearest neighbors of the middle layer atoms, to be discussed in text. (b) Comparison of relative energies with respect the ground state of the perpendicular displacements of the and graphene sublattices in the middle layer. The subscript denotes layer number, and the superscript arrow indicates the corresponding up and down shift of the sublattice atom.

Fig. 5(b) shows the comparison of energy response difference defined as E_shift − E₀, where for each stacking in the two types of displacements E₀ is the ground state energy, and E_shift is the total energy when the atoms are shifted. We shift the atoms by 1% of interlayer distance, i.e. 0.0335 Å. In all the considered cases, the total energy in each stacking increases by ≈0.5 meV. The energy response due to each sublattice shift remains nearly the same for the ABA stacking, and for the ABC stacking it changes further depending on the shift direction. For ABC stacking, moving the A atom up – equivalent to shift the B atom down – causes different energy responses in the two directions. In the case of rhombohedral stacking, the energy increase is higher by 8.12 meV nm⁻². As a result, Bernal stacking becomes more stable. The situation is just the opposite when moving the A atom down (equivalent to shifting the B atom up) – in this case Bernal stacking is more destabilized, and the rhombohedral geometry remains favourable. The perpendicular sublattice shift studied here is a lattice deformation that causes an energy difference between stackings about 8.14 meV nm⁻². This finding points out that breaking the sublattice symmetry is another way to stabilize the Bernal and rhombohedral stackings.

These energy differences due to the breaking of sublattice symmetry can be explained by having the TLG stackings interpreted again in terms of trimers and dimers between layers. The total energy can be written in two parts as a sum of eigenvalues and a sum of interatomic potentials with other atoms. Looking at the total contribution of interatomic potentials, the second neighbour atoms in the nearest layers are held responsible for these energy differences. This energy contribution adds to the difference in the sum of eigenvalues, already commented, in which the levels for the case of Bernal stacking split from zero energy when the atoms are shifted up or down. These calculations raise further intringuing experiments regarding how the sublattice symmetry of stackings could be considerably broken by substrates and adatoms, or even better by having molecules and nanoparticles conforming these graphene heterostructures.^53,54

8 Conclusions

The aim of the present paper was to determine when the graphene stacking changes from rhombohedral to Bernal due to small lattice deformations. Under compression, rhombohedral stacking suffers a phase transformation to Bernal with strains ε < 2.5%. For even smaller compressions, shear deformations and shifts breaking graphene sublattice symmetries induce an anisotropy that stabilizes the Bernal stacking. These findings provide insights into the role of substrate-associated strains when graphene layers are integrated into devices, so that the stacking order and consequently their ultimate electronic properties are modified. Nowadays, the experimental community can obtain rhombohedral stacking as they apply twisting angles and move solitons between stackings. Furthermore, because graphene layers have well-defined directions such as armchair and zig-zag, we claim that anisotropic deformations can provoke a stacking change, specifically, the stretching ones. This work would be of interest in relevant technological areas such as patterning contacts, and encapsulating graphene flakes between other materials. Our results then ask for further experiments looking at the role of directional shears along and the adsorption of adatoms and molecules on graphene stackings.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Spanish Ministry of Science and Innovation (grants no. PID2019-105488GB-I00), the Gobierno Vasco UPV/EHU (project no. IT-1569-22), and the European Commission NRG-STORAGE project (project no. GA 870114) and H2020-FET OPEN Project MIRACLE (No. GA 964450). This research was conducted in the scope of the Transnational Common Laboratory (LTC) “Aquitaine-Euskadi Network in Green Concrete and Cement-based Materials”.

References

1. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50.
2. D. Tománek and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 8327–8336.
3. R. Xiao, F. Tasnadi, K. Koepernik, J. W. F. Venderbos, M. Richter and M. Taut, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 165404–165418.
4. K. Sugawara, N. Yamamura, K. Matsuda, W. Norimatsu, M. Kusunoki, T. Sato and T. Takahashi, NPG Asia Mater., 2018, 10, e466.
5. J. Park, H. An, D.-C. Choi, S. Hussain, W. Song, K.-S. An, W.-J. Lee, N. Lee, W.-G. Lee and J. Jung, Nanoscale, 2016, 8, 14633–14642.
6. C. H. Lui, Z. Li, Z. Chen, P. V. Klimov, L. E. Brus and T. F. Heinz, Nano Lett., 2011, 11, 164–169.
7. P. Xu, Y. Yang, D. Qi, S. D. Barber, M. L. Ackerman, J. K. Schoelz, T. B. Bothwell, S. Barraza-Lopez, L. Bellaiche and P. M. Thibado, Appl. Phys. Lett., 2012, 100, 201601–201604.
8. C. Cong, T. Yu, K. Sato, J. Shang, R. Saito, G. F. Dresselhaus and M. S. Dresselhaus, ACS Nano, 2011, 5, 8760–8768.
9. J. H. Warner, M. Mukai and A. I. Kirkland, ACS Nano, 2012, 6, 5680–5686.
10. F. Geisenhof, F. Winterer, S. Wakolbinger, T. Gokus, Y. Durmaz, D. Priesack, J. Lenz, F. Keilmann, K. Watanabe, T. Taniguchi, R. Guerrero-Avilés, M. Pelc, A. Ayuela and R. Weitz, ACS Appl. Nano Mater., 2019, 2(9), 6067–6075.
11. Y. Shi, S. Xu, Y. Yang, S. Slizovskiy, S. V. Morozov, S.-K. Son, S. Ozdemir, C. Mullan, J. Barrier, J. Yin, A. I. Berdyugin, B. A. Piot, T. Taniguchi, K. Watanabe, V. I. Fal'ko, K. S. Novoselov, A. K. Geim and A. Mishchenko, Nature, 2020, 584, 210–214.
12. H. Zhou, T. Xie, A. Ghazaryan, T. Holder, J. R. Ehrets, E. M. Spanton, T. Taniguchi, K. Watanabe, E. Berg, M. Serbyn and A. F. Young, Nature, 2021, 598, 429–433.
13. H. Zhou, T. Xie, T. Taniguchi, K. Watanabe and A. F. Young, Nature, 2021, 598, 434–438.
14. G. Chen, L. Jiang, S. Wu, B. Lyu, H. Li, B. L. Chittari, K. Watanabe, T. Taniguchi, Z. Shi, J. Jung, Y. Zhang and F. Wang, Nature, 2019, 15, 237–241.
15. A. C. Ferrari, J. C. Meyer, V. Scardaci, C. Casiraghi, M. Lazzeri, F. Mauri, S. Piscanec, D. Jiang, K. S. Novoselov, S. Roth and A. K. Geim, Phys. Rev. Lett., 2006, 97, 187401–187406.
16. D. Graf, F. Molitor, K. Ensslin, C. Stampfer, A. Jungen, C. Hierold and L. Wirtz, Nano Lett., 2007, 7, 238–242.
17. M. Yankowitz, J. I.-J. Wang, A. G. Birdwell, Y.-A. Chen, K. Watanabe, T. Taniguchi, P. Jacquod, P. San-Jose, P. Jarillo-Herrero and B. J. LeRoy, Nat. Mater., 2014, 13, 786–789.
18. W. Zhang, J. Yan, C.-H. Chen, L. Lei, J.-L. Kuo, Z. Shen and L.-J. Li, Nat. Commun., 2013, 4, 2074–2081.
19. H. Li, M. I. B. Utama, S. Wang, W. Zhao, S. Zhao, X. Xiao, Y. Jiang, L. Jiang, T. Taniguchi, K. Watanabe, A. Weber-Bargioni, A. Zettl and F. Wang, Nano Lett., 2020, 20, 3106–3112.
20. Y. Yang, Y.-C. Zou, C. R. Woods, Y. Shi, J. Yin, S. Xu, S. Ozdemir, T. Taniguchi, K. Watanabe, A. K. Geim, K. S. Novoselov, S. J. Haigh and A. Mishchenko, Nano Lett., 2019, 19, 8526–8532.
21. Z. Gao, S. Wang, J. Berry, Q. Zhang, J. Gebhardt, W. M. Parkin, J. Avila, H. Yi, C. Chen, S. Hurtado-Parra, M. Drndić, A. M. Rappe, D. J. Srolovitz, J. M. Kikkawa, Z. Luo, M. C. Asensio, F. Wang and A. T. C. Johnson, Nat. Commun., 2020, 11, 1–10.
22. G. Chen, A. L. Sharpe, P. Gallagher, I. T. Rosen, E. J. Fox, L. Jiang, B. Lyu, H. Li, K. Watanabe, T. Taniguchi, J. Jung, Z. Shi, D. Goldhaber-Gordon, Y. Zhang and F. Wang, Nature, 2019, 572, 215–219.
23. M. Aoki and H. Amawashi, Solid State Commun., 2007, 142, 123–127.
24. J. P. Nery, M. Calandra and F. Mauri, Nano Lett., 2020, 20, 5017–5023.
25. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
26. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
27. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
28. K. Lee, a. D. Murray, L. Kong, B. I. Lundqvist and D. C. Langreth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081101.
29. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
30. E. Mostaani, N. Drummond and V. Fal'ko, Phys. Rev. Lett., 2015, 115, 115501.
31. C. Kittel, P. McEuen and P. McEuen, Introduction to solid state physics, Wiley New York, New York, 1996, vol. 8.
32. J. Hass, R. Feng, J. E. Millán-Otoya, X. Li, M. Sprinkle, P. N. First, W. A. de Heer, E. H. Conrad and C. Berger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 214109.
33. F. Varchon, R. Feng, J. Hass, X. Li, B. N. Nguyen, C. Naud, P. Mallet, J.-Y. Veuillen, C. Berger, E. H. Conrad and L. Magaud, Phys. Rev. Lett., 2007, 99, 126805.
34. D. Zhu, H. Gao, X. Zhang, T. Yang, L. Li, G. Yin, X. Li, C. Nicklin, X. Gao, Z. Li, L. Yi and X. Li, Carbon, 2015, 94, 775–780.
35. Y. K. Koh, M.-H. Bae, D. G. Cahill and E. Pop, ACS Nano, 2011, 5, 269–274.
36. H. P. Boehm and R. W. Coughlin, Carbon, 1964, 2, 1–6.
37. M. G. Menezes, R. B. Capaz and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 35431–35435.
38. C. H. Lui, Z. Li, K. F. Mak, E. Cappelluti and T. F. Heinz, Nat. Phys., 2011, 7, 944–947.
39. F. Zhang, J. Jung, G. A. Fiete, Q. Niu and A. H. MacDonald, Phys. Rev. Lett., 2011, 106, 1568011–1568014.
40. N. B. Kopnin, M. Ijäs, A. Harju and T. T. Heikkilä, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 140503–140506.
41. S. Slizovskiy, E. McCann, M. Koshino and V. I. Fal'ko, Commun. Phys., 2019, 2, 1–10.
42. A. García-Ruiz, S. Slizovskiy, M. Mucha-Kruczyński and V. I. Fal'ko, Nano Lett., 2019, 19, 6152–6156.
43. J. W. McClure, Carbon, 1969, 7, 425–432.
44. R. R. Haering, Can. J. Phys., 2011, 36, 352–362.
45. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710.
46. L. Wang, S. Zihlmann, A. Baumgartner, J. Overbeck, K. Watanabe, T. Taniguchi, P. Makk and C. Schönenberger, Nano Lett., 2019, 19, 4097–4102.
47. T. Vincent, V. Panchal, T. Booth, S. R. Power, A.-P. Jauho, V. Antonov and O. Kazakova, 2D Mater., 2018, 6, 15021–15022.
48. C. Bouhafs, S. Pezzini, F. R. Geisenhof, N. Mishra, V. Mišeikis, Y. Niu, C. Struzzi, R. T. Weitz, A. A. Zakharov, S. Forti and C. Coletti, Carbon, 2021, 177, 282–290.
49. A. D. Sanctis, J. D. Mehew, S. Alkhalifa, F. Withers, M. F. Craciun and S. Russo, Nano Lett., 2018, 18, 7919–7926.
50. J. P. Nery, M. Calandra and F. Mauri, 2D Mater., 2021, 8, 35006–35015.
51. D. G. Purdie, N. M. Pugno, T. Taniguchi, K. Watanabe, A. C. Ferrari and A. Lombardo, Nat. Commun., 2018, 9, 5387–5398.
52. L. Jiang, S. Wang, Z. Shi, C. Jin, M. I. B. Utama, S. Zhao, Y.-R. Shen, H.-J. Gao, G. Zhang and F. Wang, Nat. Nanotechnol., 2018, 13, 204–208.
53. H. Zhao, Y.-C. Lin, C.-H. Yeh, H. Tian, Y.-C. Chen, D. Xie, Y. Yang, K. Suenaga, T.-L. Ren and P.-W. Chiu, ACS Nano, 2014, 8, 10766–10773.
54. M. Huang, P. V. Bakharev, Z.-J. Wang, M. Biswal, Z. Yang, S. Jin, B. Wang, H. J. Park, Y. Li, D. Qu, Y. Kwon, X. Chen, S. H. Lee, M.-G. Willinger, W. J. Yoo, Z. Lee and R. S. Ruoff, Nat. Nanotechnol., 2020, 15, 289–295.

---

Footnotes

† Electronic supplementary information (ESI) available: Movie to visually follow the shear deformations of trilayer graphene stackings. See DOI: https://doi.org/10.1039/d2nr01985j

‡ Along zigzag and armchair direction the ABC and ABA stackings were favored, respectively.

---