Vibrational anatomy of C₉₀, C₉₆, and C₁₀₀ fullertubes: probing Frankenstein's skeletal structures of fullerene head endcaps and nanotube belt midsection

Abstract

Fullertubes are tubular fullerenes with nanotube-like middle section and fullerene-like endcaps. To understand how this intermediate form between spherical fullerenes and nanotubes is reflected in the vibrational modes, we performed comprehensive studies of IR and Raman spectra of fullertubes C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d. An excellent agreement between experimental and DFT-computed spectra enabled a detailed vibrational assignment and allowed an analysis of the localization degree of the vibrational modes in different parts of fullertubes. Projection analysis was performed to establish an exact numerical correspondence between vibrations of the belt midsection and fullerene headcaps to the modes of nanotubes and fullerene C₆₀-I_h. As a result, we could not only identify fullerene-like and CNT-like vibrations of fullertubes, but also trace their origin in specific vibrational modes of CNT and C₆₀-I_h. IR spectra were found to be dominated by vibrations of fullerene-like caps resembling IR-active modes of C₆₀-I_h, whereas in Raman spectra both caps and belt vibrations are found to be equally active. Unlike the resonance Raman spectra of CNTs, in which only two single-phonon bands are detected, the Raman spectra of fullertubes exhibit several CNT-like vibrations and thus provide additional information on nanotube phonons.

---

Introduction

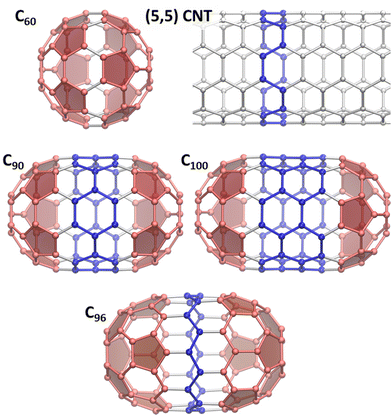
The discovery of arc-discharge synthesis of fullerenes¹ brought new attention to carbonaceous materials leading soon to re-focusing on carbon nanotubes (CNTs) and later on graphene. Fullerene and CNT research went hand-in-hand from the start, as both feature curved C-sp² network, and it was natural to think about CNTs as of strongly elongated, tubular fullerenes. Although ideal CNT is infinitely long, real nanotubes must have an end, and a seamless termination of the tubes can be achieved with fullerene-like caps. This imaginary is also supported from the fullerene side. By the Euler's theorem, all classical fullerenes have 12 pentagons, and the growth of fullerenes size inevitably means increase of the number of hexagons. The latter can be arranged in many ways, from quasi-spherical structures with uniform distribution of pentagons to tubular fullerenes with curved caps and CNT-like belts. Spherical fullerenes tend to be more thermodynamically stable, and high-resolution trapped ion mobility spectrometry suggested spherical shapes of large fullerenes, such as C₁₁₀–C₁₅₀.² Nevertheless, tubular fullerenes are also well documented. C₇₀-D_5h can be considered as the first tubular fullerene, and its structure can be obtained from that of C₆₀-I_h by insertion of a belt of 10 carbon atoms between two C₃₀ hemispheres and rotation of one of the hemispheres by 36°. Consequent addition of C₁₀ fragments into the belt and 36° rotation of one cap creates a family of C_60+10n tubular fullerenes with alternating D_5h and D_5d symmetry and a growing (5, 5) CNT fragment. The next after C₇₀-D_5h is C₈₀-D_5d(1) isolated in 2000,³ the minor isomer of C₈₀ seconds to the main C₈₀-D₂(2).⁴ Then follows C₉₀-D_5h(1), first characterized in 2010 in a pristine form⁵ as well as chlorofullerenes C₉₀Cl_10,12.⁶ These works proved formation of C₉₀-D_5h(1) in the arc-discharge process despite the low relative stability of this isomer. Likewise, computational studies of C₁₀₀ isomers showed that the tubular structure C₁₀₀-D_5d(1) is not among the most stable ones.^7,8 However, this isomer was captured as a chloride C₁₀₀Cl₁₂,⁹ and a molecular structure of the non-derivatized C₁₀₀-D_5d(1) was recently proved by single-crystal X-ray diffraction of its co-crystal with decapyrrylcorannulene.¹⁰ Another structurally characterized tubular fullerene is C₉₆-D_3d(1).¹¹ In this molecule, the caps are not resembling C₆₀ hemispheres and have hexagon in the base, while the belt is a fragment of a zigzag (9,0) CNT.

The number of possible fullerene isomers grows dramatically with the fullerene size, and the separation of multiple similar isomeric structures turns into a complex and tedious procedure. Fortuitously, the studies of tubular fullerenes, aka fullertubes, gained the new boost with the discovery of the isolation route based on their reduced chemical reactivity.^10,12 While fullerenes usually readily react with amino-alcohols, tubular fullerenes appeared to be significantly less reactive, which allowed their facile separation from other fullerenes. The main fullertubes obtained this way are C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d (Fig. 1), but a possibility to isolate even larger tubular fullerenes was demonstrated in ref. 10, opening the way to their systematic exploration. C₉₆-D_3d was found to be an efficient O₂-reduction electrocatalyst in the recent study.¹³

Fig. 1 Molecular structures of fullertubes C₉₀-D_5h, C₁₀₀-D_5d, and C₉₆-D_3d as well as the fullerene C₆₀-I_h and (5, 5) CNT. In each fullertube, fullerene-like caps are highlighted in pink with shaded pentagons, whereas CNT-like belts are colored blue. In the (5, 5) CNT fragment, a unit cell of 20 carbon atoms is also highlighted in blue.

The increasing availability of such tubular structures, which can be seen as intermediates between spherical fullerenes and 1D nanotubes, raises a question of whether fullertubes exhibit the properties of fullerenes, CNTs, or should be treated as a unique phenomenon. On the other hand, the systematic study of fullertubes may help to pinpoint a transition between discrete molecular properties to periodic 1D behavior. There is hardly a universal answer to this question because different properties have different degree of locality. For instance, the low chemical reactivity of fullertubes with amino-alcohols and selective chlorination of cap regions^6,9 seems to indicate that belt regions may be similar in their reactivity to CNTs. On the hand, the study of the electronic properties of fullertubes with (5, 5) and (9, 0) CNTs fragments concluded that the convergence is far from reach in realistic fullerene sizes and requires much longer tubes.^14,15 In this work, we will address this problem from the point of view of vibrational spectroscopy as the latter played a fundamental role in the studies of nanocarbon materials, from the very first indication of C₆₀ presence in the carbon soot confirmed by IR spectroscopy¹⁶ to resonance Raman techniques which became indispensable for CNTs and graphene.^17–19 Force constants usually vanish over several bonds and therefore vibrations can be considered as more local than electronic excitations. Thus, the transition between confined and periodic properties may happen on a smaller length scale. Here we combine IR and Raman spectroscopy with DFT computations to obtain comprehensive information on vibrational modes of fullertubes C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d, and then use projection technique to establish genetic relationships between vibrations of C₁₀₀-D_5d, (5, 5) CNT and C₆₀-I_h.

Experimental and computational details

The synthesis and characterization of fullertubes C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d were described in ref. 10. In brief, the fullerene-containing soot produced by arc-discharge synthesis was extracted with xylene. The fullerene mixture was then reacted with 3-amino-1-propanol. While most fullerenes react readily with 3-amino-1-propanol and form products soluble in water, fullertubes are much less reactive in these conditions and remain in the organic phase. Individual compounds were then isolated by HPLC.

For vibrational spectroscopic studies, the samples were drop-casted from toluene solution onto KBr single-crystalline substrates and dried under vacuum. IR measurements were performed at room temperature in transmission mode using a Hyperion FTIR microscope attached to Vertex 80 spectrometer (Bruker). Raman measurements were performed with T64000 spectrometer (Horiba). The samples on KBr substrates were cooled down to 78 K, and the spectra were measured with laser excitation at 532 nm (Nd:YAG laser Torus by Laser Quantum), 620 nm and 656 nm (Matisse dye laser by Sirah Lasertechnik). The spectra were also excited with 785 nm laser (BrixX diode laser by Omicron Laserage). For the latter, the samples were drop-casted on gold SERS substrates (Metrohm DropSens DRP-C220BT) and immersed in water to improve the heat transfer, and the measurements were performed at room temperature using immersion objective.

DFT calculations of fullerenes molecules were performed with PBE density functional²⁰ using two DFT codes. Vibrational frequencies, IR and off-resonance Raman intensities were calculated with molecular code Priroda^21,22 using Λ2 basis set²³ with {4,3,2,1}/{12s,8p,4d,2f} contraction scheme. Vibrational calculations were also performed with periodic code VASP 5.4.4,^24–26 using recommended pseudopotentials and energy cut-offs for projector-augmented wave (PAW) scheme and 6 Å of vacuum layer to prevent interaction between periodic images. Importantly, calculations with molecular and periodic codes gave very similar vibrational frequencies, ensuring the use of balanced wavefunction description in both codes. In calculations of (5, 5) CNT, the Γ-centered sampling of the Brillouin zone along the periodic axis used 4 Monkhorst–Pack grid points per unit cell. With an accurate grid option, the tube was optimized to a mean gradient of 10⁻⁵ eV Å⁻¹. The Hessian matrix was calculated using density-functional-perturbation theory for a supercell of four primitive unit cells. Phonopy libraries²⁷ and in-house python scripts were used to analyze phonon spectra and dynamic matrix operation/analysis at different q-points. Vibrational symmetry analysis was performed using DISP/SYMM package.²⁸

Results and discussion

Fig. 2 shows UV-vis absorption spectra of C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d measured in toluene solution. Although (5, 5) and (9, 0) CNTs are metallic, the CNT fragments in fullertubes are obviously not long enough to develop CNT-like electronic properties and close the band gap.¹⁴ Thus, all studied fullertubes have considerable gaps exceeding at least 1.5–2 eV. The spectra closely resemble those reported in the literature^5,10,11,15 thus confirming the structural identity of studied molecules.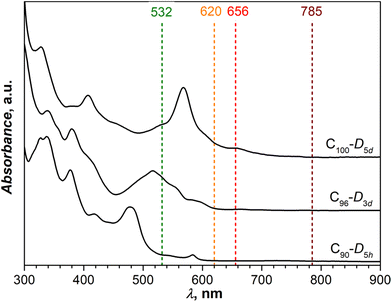

Fig. 2 UV-vis absorption spectra of C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d in toluene solution. Vertical dashed lines mark laser wavelengths used in Raman measurements.

Experimental vibrational spectra

Vibrational modes of fullertubes span the following irreducible representations of their point-symmetry groups:where R and IR in parentheses denote Raman and IR activity, respectively. Despite rather high molecular symmetries, a large number of optically active modes are expected for all three compounds. Vibrational density of states of these molecules is thus quasi-continuous, and reliable vibrational assignment based only on computed frequencies and symmetry analysis is impossible. Therefore, we have to consider not only frequencies, but also computed IR and Raman intensities.

Experimental IR spectra of fullertubes are compared to the computed ones in Fig. 3. To benchmark the computational method, Fig. 3 also shows the spectra of well-known fullerene C₇₀-D_5h. Based on the latter, we can conclude that the computational method gives a very good match of experimental vibrational frequencies. The difference between experiment and theory is usually less than 5 cm⁻¹ and increases up to 10 cm⁻¹ only at the highest frequencies. At the same time, computed IR intensities are less satisfactory. Relative intensities of the bands deviate significantly from experimental counterparts even for vibrations of the same type. Besides, theory tends to strongly overestimate the relative intensity of tangential modes at frequencies above 1300 cm⁻¹. These caveats notwithstanding, computations provide a reasonable guide for the interpretation of the IR spectra of fullertubes. The full list of experimental and computed frequencies for C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d can be found in ESI (Tables S1–S3†). Table 1 lists the assignment of the IR spectrum of C₁₀₀-D_5d. The spectrum of C₉₀-D_5h obtained this work closely resembles the data reported in a recent study of vibrational spectra of C_90-D_5h under high pressure.²⁹

Fig. 3 Experimental (dark blue) and calculated (pink, PBE/Λ2 level) IR spectra of C₇₀-D_5h, C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d. The peak of the most intense band in the calculated spectrum of C₇₀ at 1430 cm⁻¹ is cut for a better presentation of other parts of the spectrum.

Table 1 Selected IR-active vibrational modes of C₁₀₀-D_5d with their computed frequencies, intensities, experimental assignment, and description in terms of (5, 5) CNT and C₆₀ modes

Mode	PAW	Λ2	Int, %	Exp	d CNT	% CNT modes	d C60	% C60 modes
d frag and mode compositions are given in %, contributions of less than 8–9% are omitted. Experimental intensity scale: vw < w < w + < m < s < vs, where w – weak, m – medium, s – strong, v – very.
A2u(3)	475	477	15.1	480 m	34	30 A1g(1)	66	60 F1u(1)
E1u(5)	480	480	20.3	480 m	46	36 E1u(2)	54	35 F1u(2), 14 Hu(1)
A2u(4)	518	518	23.7	511 vw	22	18 A2u(1)	79	56 F1u(2)
E1u(8)	545	546	27.0	548 vs	24	18 E4g(1)	75	65 F1u(1)
E1u(9)	626	627	0.9	628 w	66	36 E4g(2), 12 E4u(1)	35	17 Hu(3)
E1u(10)	643	643	5.2	648 w	58	37 E4u(1), 13 E4g(2)	43	20 Hu(3)
E1u(11)	711	711	5.6	716 vw	22	—	78	30 Gu(2), 22 Hu(3), 20 Hu(4)
E1u(13)	760	760	4.5	761 w	16	—	83	69 Gu(3), 10 Hu(4)
E1u(14)	772	772	11.4	771 vw	28	18 E1g(1)	72	31 Gu(4), 28 F1u(2)
E1u(15)	822	821	0.8	818 vw	88	88 E1u(3)	11	10 Gu(3)
A2u(8)	1013	1011	2.7	1023 vw	32	28 B1g(1)	69	66 F2u(3)
E1u(18)	1101	1099	2.0	1099 vw	48	30 E4g(3)	51	19 Gu(2), 10 F1u(3)
A2u(9)	1155	1153	20.4	1156 w	42	24 B1g(1), 12 A1g(2)	58	41 F2u(4)
A2u(10)	1218	1212	8.8	1196 vw	24	16 A1g(2)	76	72 F2u(4)
E1u(20)	1238	1235	4.4	1237 w	12	—	88	66 F1u(3)
E1u(26)	1429	1428	100.0	1430 vs	4	—	96	51 F1u(4), 42 Gu(6)
A2u(14)	1462	1461	47.4	1459 w	10	8 A1g(2)	89	74 F1u(4)

---

Raman spectra of C₉₀-D_5h, C₉₆-D_3d, and C₁₀₀-D_5d are shown in Fig. 4, 5, and 6, respectively. To obtain the most detailed information, the spectra were excited with several laser lines. From Fig. 2, comparing laser wavelengths in relation to the absorption spectra of fullerenes, we find that the 785 nm laser should produce a non-resonant Raman scattering, whereas other laser lines appear close to or overlap with the fullerene absorptions and may therefore induce resonant effects. Indeed, the computed spectra agree well with the experimental spectra recorded with 785 nm excitation. At the same time, the spectra measured with shorter laser wavelengths demonstrate considerable redistribution of intensity pointing to their pre-resonance character. A particular strong difference from the non-resonance scattering is found for the green laser (532 nm), which strongly enhances the intensity of the high-frequency tangential modes. Overall, the spectral information obtained with a combined set of spectra is very rich with 60–70 peaks detected for each compound. The assignment of the spectra is facilitated by a good agreement between experiment and theory. Using computed intensities as a guide, we could first identify the peaks in the off-resonance spectra with a high degree of certainty and then continue with the remaining peaks detected only in resonant conditions. The procedure allowed determination of almost all fully symmetric modes (A₁′ or A_1g types), which as a rule are more prominent in the spectra, as well as a large part of E-type modes (E₁′′/E₂′, E_g, or E_1g/E_2g types, see eqn (1)). Besides, a certain number of weak lines did not match the Raman active modes and could be tentatively assigned to silent modes, as was observed earlier in Raman spectra of C₆₀-I_h and C₇₀-D_5h.^30–34 A complete list of experimental Raman features and computed frequencies are given in ESI,† whereas Table 2 lists all A_1g and selected E_1g and E_2g modes of C₁₀₀-D_5d.

Fig. 4 Experimental Raman spectra of C₉₀-D_5h compared to the calculations for off-resonance conditions (dark blue curve, PBE/Λ2 level).

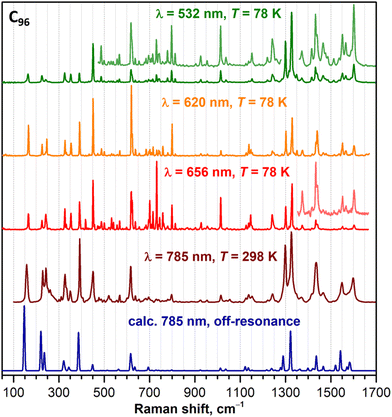Fig. 5 Experimental Raman spectra of C₉₆-D_3d compared to the calculations for off-resonance conditions (dark blue curve, PBE/Λ2 level).

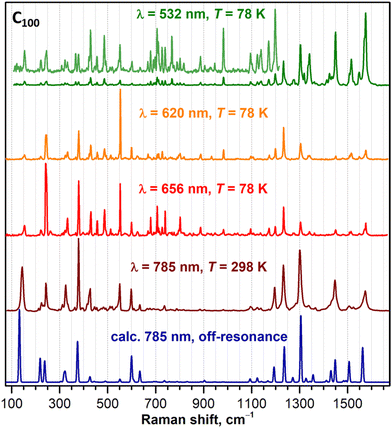Fig. 6 Experimental Raman spectra of C₁₀₀-D_5d compared to the calculations for off-resonance scattering (dark blue curve, PBE/Λ2 level).

Table 2 All A_1g and selected E_1g and E_2g Raman-active vibrational modes of C₁₀₀-D_5d with their computed frequencies, intensities, experimental assignment, and description in terms of (5, 5) CNT and C₆₀-I_h modes

Mode	PAW	Λ2	Int, %	Exp. 785	Exp. 532	d CNT	% CNT modes	d C60	% C60 modes
Computed Raman intensity is for off-resonance conditions. dfrag and mode compositions are given in %, contributions of less than 8–9% are omitted. Experimental intensity scale: vw < w < w + < m < s < vs, where w – weak, m – medium, s – strong, v – very, sh – shoulder.
A1g(1)	238	238	28.7	243 ms	243/245 w	12	8 A1g(1)	87	68 Hg(1), 9 Ag(1)
A1g(2)	323	323	12.6	325 m	325 w	76	64 A1g(1), 12 B2u(1)	23	14 Hg(1)
A1g(3)	375	375	57.4	379 vs	379 w	26	18 A1g(1)	74	43 Ag(1)
A1g(4)	425	426	8.4	427 m	429 w	32	30 B2u(1)	69	65 Hg(2)
A1g(5)	550	551	4.2	551 m	551 w	64	56 B2u(1)	36	20 Hg(2)
A1g(6)	560	599	38.1	599 m	602 w	16	12 A2u(1)	79	34 Hg(4), 32 Ag(1)
A1g(7)	708	707	0.1	—	706 w+	2	—	99	97 Hg(3)
A1g(8)	890	889	0.5	887 vw	887 w	44	38 A2u(1)	56	40 Hg(4)
A1g(9)	1094	1093	2.6	1095 w	1096 w	32	18 A2u(1), 12 B2u(2)	69	67 Hg(5)
A1g(10)	1197	1193	22.3	1195 m	1198 w+	64	52 B2u(2)	35	14 Hg(5)
A1g(11)	1241	1236	44.1	1232 s	1233 m	12	—	88	80 Hg(6)
A1g(12)	1312	1305	94.0	1301 vs	1303 s	82	32 B1g(1), 28 B2u(2), 14 A2u(1)	17	10 Hg(7)
A1g(13)	1361	1356	10.3	1366 w	—	66	48 B1g(1), 14 A1g(2)	34	20 Hg(7), 9 Hg(6)
A1g(14)	1450	1448	32.2	1447 m	1450 vs	14	14 A1g(2)	85	46 Hg(7), 37 Ag(2)
A1g(15)	1496	1493	2.6	—	—	50	48 A1g(2)	50	42 Ag(2)
A1g(16)	1562	1564	27.7	1574 m	1575 vs	8	—	92	83 Hg(8)
E2g(1)	132	132	100.0	144 s	154 w	80	78 E2g(1)	20	18 Hg(1)
E1g(9)	6345	634	16.6	634 w	636 vw	34	14 E1u(2)	61	32 Hg(4)
E2g(9)	678	677	0.2	—	679 w	48	36 E3u(2)	52	40 Hg(3)
E1g(26)	1432	1430	16.6	1434 sh	1434 vw	14	—	86	67 Hg(7)
E1g(28)	1509	1506	28.0	1506 w	1508 w+	64	64 E1g(2)	36	35 Gg(6)
E2g(30)	1552	1552	0.0	—	1548 w+	9	—	93	85 Hg(8)
E1g(29)	1554	1562	24.1	—	1571 s, sh	18	—	82	47 Hg(8), 22 Gg(6)

---

Projection analysis and symmetry considerations

Having established the correspondence between experimental spectral features and computed normal modes, we can proceed to the main goal of this work, the analysis of the fullertube vibrations in terms of their fullerene and CNT fragments. For the sake of convenience, the analysis will be performed for C₁₀₀-D_5d as its belt region comprises two CNT periods, while two caps build up fullerene C₆₀-I_h if the belt is removed (Fig. 1). Establishing a resemblance of vibrations of different molecules is straightforward with projection analysis used earlier by some of us for fullerene derivatives^35–37 and endohedral fullerenes.³⁸ The method is based on the fact that normal modes in mass-weighed Cartesian coordinates form an orthonormal basis, and vibrations of one molecule (C₁₀₀-D_5d in this work) can be projected onto the space of vibrational eigenvectors of another molecule (C₆₀-I_h or CNT) using scalar products:

a_frag,ij = (Q_C100,i,Q_frag,i),

where Q_C100,i is ith vibrational mode of the fullertube C₁₀₀-D_5d, Q_frag,i is the jth mode of the fragment of interest (C₆₀-I_h or CNT), and Q_C100,i vector includes only a subset of atomic displacements corresponding to this fragment. Consequently, the square a_frag,ij² gives the contributions of the jth fragment mode to the ith mode of C₁₀₀-D_5d, and the sum of a_frag,ij² over all fragment modes amounts to the contribution of a given fragment to the ith vibrational mode of the whole C₁₀₀-D_5d molecule:

In fact, d_frag,i can be also obtained from vibrational eigenvectors in cartesian coordinates without the projection, and we will use that for C₉₀-D_5h and C₉₆-D_3d. It is also important to note that in case of a uniform distribution of a given vibration over the whole fullertube molecule, the CNT-like belt will contribute 33.3% in C₉₀-D_5h, 18.8% in C₉₆-D_3d, and 40% in C₁₀₀-D_5d. A predominant localization of the vibration on the belt region can be concluded when d_CNT considerably exceeds these values.

To summarize, using DFT-computed vibrational eigenvectors, we can establish exact correspondence between the vibrations of C₁₀₀-D_5d caps and the modes of C₆₀-I_h, as well as between vibrations of the C₁₀₀-D_5d belt and the modes of (5, 5) CNT. When one particular fragment mode has dominant contribution (a_frag,ij² is close to 1 or at least to d_frag,i), there is a close resemblance of the corresponding vibrations of C₁₀₀-D_5d and C₆₀-I_h or CNT. When two or more fragment modes have comparable contributions, it is said that these modes are mixing. The full list of DFT-computed vibrational frequencies of C₆₀-I_h and (5, 5) CNT can be found in ESI, Tables S4 and S5.† For C₆₀-I_h, Table S4† also compares the frequencies with complete set of fundamentals, including silent modes, determined in ref. 39.

It is also useful to establish a relation between symmetry types of the vibrations as the symmetry restricts the optical activity and a possibility of the mode mixing. Since D_5d is a subgroup of I_h, the connection between C₆₀-I_h modes and vibrations of C₁₀₀-D_5d caps is straightforward (Table 3). All gerade (g-type) modes of C₆₀-I_h become Raman active in the D_5d group as they include either A_1g, E_1g, or E_2g representations. However, only Raman-active A_g and H_g modes of C₆₀-I_h have A_1g component in the D_5d group, and as mentioned above, the vast majority of strong Raman modes of C₁₀₀-D_5d are of A_1g symmetry. As for ungerade modes, C₆₀-I_h has only 4 IR-active vibration of F_1u type, but all its degenerate u-type modes become IR active in the D_5d symmetry as they have either A_2u or E_1u representations. Only A_u mode of C₆₀-I_h remains silent.

Table 3 Correlation between symmetry types of vibrational modes in C₆₀-I_h and C₁₀₀-D_5d^a

C60-Ih	→	C 100-D5d, caps
a R and IR in parentheses denote Raman and IR-active modes.
2 Ag(R)	→	2 A1g(R)
3 F1g	→	3 (E1g(R) + A2g)
4 F2g	→	4 (E2g(R) + A2g)
6 Gg	→	6 (E1g(R) + E2g(R))
8 Hg(R)	→	8 (E1g(R) + E2g(R) + A1g(R))
1 Au	→	1 A1u
4 F1u(IR)	→	4 (E1u(IR) + A2u(IR))
5 F2u	→	5 (E2u + A2u(IR))
6 Gu	→	6 (E1u(IR) + E2u)
7 Hu	→	7 (E1u(IR) + E2u + A1u)

---

The situation with the CNT is more complex and requires a deeper discussion. (5, 5) CNT is described by the T¹₁₀D_5h linear group, which is isogonal to the D_10h point symmetry group.⁴⁰ In the following, we will mainly use the irreducible representations of the D_10h group to label vibrational modes of the (5, 5) CNT. As with any other armchair CNT, it has 8 Raman active modes (2A_1g + 2E_1g + 4E_2g) and 5 IR-active modes (A_2u + 4E_1u, of which A_2u and one E_1u are acoustic modes with zero frequency in Γ-point).⁴¹ In C₁₀₀, the symmetry is reduced to D_5d. Irreducible representations for the CNT in T¹₁₀D_5h, D_10h, and D_5d groups are compared in Table 4. Furthermore, the CNT-like belt of C₁₀₀-D_5d has 40 atoms, in which 20-atomic unit cell of the (5, 5) CNT is repeated twice. For this reason, it is insufficient to consider only Γ-point modes of the CNT when comparing its vibrations to those of C₁₀₀-D_5d. Vibrations of the double-cell fragment can be formally described by two sets of the unit cell modes, one with both unit cells vibrating in phase and corresponding to Γ-point, and one with unit cells vibrating in anti-phase to each other and thus corresponding to X-point on the edge of the Brillouin zone. Fig. 7a and b shows DFT-computed dispersions of CNT phonons and variation of the composition of selected modes with k obtained by projecting k-point eigenvectors on Γ-point eigenvectors. Fig. 7 shows that both frequencies and composition of the modes can change considerably in k-space along going from Γ to X. For instance, whereas B_2u(1) and A_1g(2) modes tend to retain their shape at k ≠ 0, A_2u(1) mode is mixing with A_1g(1), and B_2u(1) is mixing with B_1g(1). When k ≠ 0, the point symmetry is effectively lowered to C_5v, in which A_1g and A_2u irreducible representations of the D_5d group reduce to the same A₁ type and can mix. Similarly, mixing occurs in A_2g/A_1u, E_1g/E_1u, and E_2g/E_2u pairs as they reduce to A₂, E₁, and E₂ symmetry types of the C_5v group, respectively. Furthermore, in the X-point, the modes become degenerate and therefore exhibit an additional mixing. The X-to-Γ projection matrix plotted in Fig. 7c has substantially non-diagonal pattern.

Fig. 7 (a) Phonon dispersion of (5, 5) CNT; the branches originating in Γ-point from A_1g, B_1g, A_2u, and B_2u modes (corresponding to A_1g and A_2u in D_5d group) are shown in thick color. (b) Changes in the composition of these modes on going from Γ to X point in k-space; colored circles visualize contributions of the Γ-point modes, with their radius scaling as the contribution of a given Γ-point mode to the mode at a given k-value. (c) Projection matrix of X-point modes onto Γ-point modes (a_ij² coefficients). The modes are numbered in the order of increasing frequency and include acoustic modes. Dashed lines show an example of mixing of A_1g(1)/B_2u(1) and B_2u(2)/A_1g(2) pairs of Γ-point modes in X-point.

Table 4 Correlation between symmetry types of vibrational modes in (5, 5) CNT and C₁₀₀-D_5d ^a

(5, 5) CNT, T^110D5h	(5, 5) CNT, D10h ^b	→	(5, 5) CNT, D5d	→	C100-D5d, belt
a R and IR in parentheses denote Raman and IR-active modes b Note that E1u and A2u are acoustic modes with zero frequency in Γ-point, leaving 3E1u optical IR-active mode in armchair CNTs; one of the A2g modes corresponds to the rotation of CNT around its axis and also has zero frequency in Γ-point.
2 0A0^+ + 0A5^−	2 A1g(R) + B1g	→	3 A1g	→	3 (A1g(R) + A2u(IR))
2 0B0^+ + 0B5^−	2 A2g + B2g	→	3 A2g	→	3 (A2g + A1u)
2 0E1^− + 4 0E4^+	2 E1g(R) + 4 E4g	→	6 E1g	→	6 (E1g(R) + E1u(IR))
4 0E2^+ + 2 0E3^−	4 E2g(R) + 2 E3g	→	6 E2g	→	6 (E2g(R) + E2u)
2 0B5^+ + 0B0^−	2 B1u + A1u	→	3 A1u	→	3 (A1u + A2g)
2 0A5^+ + 0A0^−	2 B2u + A2u(IR)	→	3 A2u	→	3 (A2u(IR) + A1g(R))
4 0E1^+ + 2 0E4^−	4 E1u(IR) + 2 E4u	→	6 E1u	→	6 (E1u(IR) + E1g(R))
2 0E2^− + 4 0E3^+	2 E2u + 4 E3u	→	6 E2u	→	6 (E2u + E2g(R))

---

From this analysis we can infer that each CNT vibrational mode will contribute to vibrations of two symmetry types in C₁₀₀-D_5d, one of the same type (in D_5d symmetry) and one of its conjugate of the opposite parity reducing to the same irreducible representation in the C_5v subgroup. This leads to the situation when, for instance, A_1g mode of C₁₀₀-D_5d may have contributions from A_1g and A_2u CNT modes considered in D_5d symmetry, or more precisely from A_1g, B_1g, A_2u, and B_2u modes of the CNT in its rigorous D_10h symmetry (Table 4).

Normal mode analysis for C₁₀₀-D_5d

For a hypothetical situation in which all fullertube vibrations are exclusively localized either on the caps or the belt with each fullertube mode exhibiting one-to-one resemblance to a certain vibrational mode of C₆₀ or CNT, the projection matrices {a_frag,ij²} would be quasi-diagonal with a handful of a_frag,ij² elements equal 1 and most of others being 0. Visualization of {a_C60,ij²} and {a_CNT,ij²} projection matrices for C₁₀₀ in Fig. 8 shows that it is not the case (numerical values of d_frag,i and leading a_frag,ij² terms can be found in Tables 1, 2 and Table S3†). First, C₁₀₀-D_5d modes rarely localize on either the belt or the caps, and more often are distributed over the whole fullertube. This obviously results in a_frag,ij² values being considerably smaller than 1. Second, C₁₀₀-D_5d modes often have several contributing fragment modes, which in other words means that fragment modes mix in C₁₀₀. Nevertheless, {a_frag,ij²} matrices are still rather sparse, and there is a clear tendency of the largest a_frag,ij² values to cluster near diagonal, showing that a certain similarity of vibrations is indeed present. This resemblance is more evident for vibrations of C₆₀-like caps (Fig. 8a), whereas the belt vibrations have a more pronounced mixed character (Fig. 8b). The latter can be explained by the symmetry factor (there are more symmetry types of CNT modes which can mix in C₁₀₀-D_5d) as well as the contribution of the CNT modes outside of the Γ-point. We also tried to perform projection analysis using CNT modes computed at X-point, but this resulted in a much more pronounced mixing, so we will stay with Γ-point modes of the (5, 5) CNT in the following discussion.

Fig. 8 Visualization of projection matrices (a_frag,ij² coefficients) for C₁₀₀-D_5d modes onto the spaces of (a) modes of C₆₀-I_h, and (b) modes of (5, 5) CNT in Γ-point. In (b), horizontal lines denote A_1g modes of CNT. The modes are numbered in the order of increasing frequency, CNT modes also include acoustic modes. Degenerate modes are counted once, giving 176 modes for C₁₀₀-D_5d, 46 modes for C₆₀-I_h, and 36 modes for (5, 5) CNT.

With all these caveats, the analysis of C₁₀₀-D_5d mode composition in terms of C₆₀ and CNT fragments is still quite instructive. In the IR spectrum, all strong bands have predominant contributions from C₁₀₀ caps and can be traced back to IR-active F_1u modes of C₆₀. For instance, the strong peak at 1430 cm⁻¹ is assigned to the E_1u(26) mode of C₁₀₀ with 51% contribution from F_1u(4) (1429 cm⁻¹ in C₆₀). Another very strong IR peak of C₁₀₀ at 548 cm⁻¹ corresponds to the E_1u(8) mode with 65% of F_1u(2) (576 cm⁻¹ in C₆₀). Finally, the peak at 480 cm⁻¹ can be assigned to two C₁₀₀ modes with close frequencies and large weights of F_1u(1) (526 cm⁻¹) and F_1u(2) C₆₀ modes. Vibrations of the CNT-like belt have lower IR intensities. The only range where they have some prominence is around 600–850 cm⁻¹, where several weak absorptions can be seen. Particularly, a weak band at 818 cm⁻¹ is caused by the C₁₀₀ vibration resembling the E_1u(3) CNT mode, which in due turn originates from the IR-active phonon of graphene detectable in graphite at 868 cm⁻¹. Further details of IR spectral assignment can be found in Table 1.

In Raman spectra, C₆₀-like and CNT-like vibrations are represented more uniformly as can be deduced from the data in Table 2 and Fig. 9. The majority of prominent Raman features in the spectra of C₁₀₀ are assigned to vibrations of A_1g symmetry type (see Table 2), and according to the symmetry analysis (Table 3), the A_1g modes with predominant localization on caps can be traced to A_g or H_g modes of C₆₀. For instance, the Raman feature of C₁₀₀ at 243 cm⁻¹ is related to the H_g(1) mode of C₆₀ at 272 cm⁻¹, the peak at 427 cm⁻¹ corresponds to the H_g(2) mode (432 cm⁻¹), the strong peak at 1232 cm⁻¹ is related to the H_g(6) mode (1248 cm⁻¹), whereas the peak at 1575 cm⁻¹ corresponds to the H_g(8) mode (1574 cm⁻¹ in C₆₀).

Fig. 9 Comparison of the Raman spectra of C₁₀₀-D_5d (λ_ex = 785 nm) and C₆₀-I_h (λ_ex = 1064 nm) and the correspondence of the most intense C₁₀₀ Raman lines to the vibrational modes of C₆₀ and (5, 5) CNT. Large contributions of A_g and H_g modes of C₆₀-I_h to C₁₀₀-D_5d vibrations are denoted with gray dashed lines, C₁₀₀-D_5d vibrations with large contribution of CNT modes are marked with cyan arrows and labels of leading CNT vibrations.

Considerable components of two A_g modes of C₆₀ are found in 4 modes of C₁₀₀. The strongest peak in the non-resonant spectrum of C₁₀₀ at 379 cm⁻¹ is assigned to A_1g(3), which has 26% belt and 74% cap contributions, including 43% A_g(1) mode of C₆₀ (495 cm⁻¹). The latter is known as the fullerene breathing mode. Interestingly, the CNT part in this vibration is mainly represented by the radial breathing mode (RBM), A_1g(1), detected in the experimental spectrum of (5, 5) CNT at 338 cm⁻¹ (ref. 42; our DFT-computed frequency for RBM is 332 cm⁻¹). Note that the study of fullerene vibrations based on the isotropic spherical shell model demonstrated that the breathing mode frequency scales as M^−1/2, where M is the fullerene mass, and this scaling works very well even for tubular fullerenes.⁴³ The shift of the breathing mode frequency from 495 cm⁻¹ in C₆₀ to 379 cm⁻¹ in C₁₀₀-D_5d agrees well with this scaling. The breathing mode of C₆₀ also contributes to the A_1g(6) mode of C₁₀₀ at 599 cm⁻¹, in which it is mixed with H_g(4) (772 cm⁻¹).

The second totally symmetric vibration of C₆₀, A_g(2) (1468 cm⁻¹) known as the pentagonal pinch mode, mixes with H_g(7) (1422 cm⁻¹) in the A_1g(14) mode of C₁₀₀. In the experimental Raman spectrum it is detected as the medium-intensity feature at 1447 cm⁻¹. Another C₁₀₀ vibration with the large weight of the pentagonal pinch mode is A_1g(15) predicted at 1493 cm⁻¹. Here the cap and the belt parts contribute equally, each represented by a totally symmetric mode, A_g(2) for C₆₀ and A_1g(2) for CNT. However, this vibration has low predicted Raman intensity, and we cannot assign it with an acceptable degree of certainty – the only plausible experimental signal in the corresponding frequency range is a very weak and broad feature at 1482 cm⁻¹.

On the CNT side, several totally symmetric modes of C₁₀₀-D_5d with considerable Raman activity can be pointed out. The vibration resembling the CNT RBM mode is found at 325 cm⁻¹, not far from the actual RBM mode frequency in the (5, 5) CNT at 338 cm⁻¹ (ref. 42). The relative intensity of this vibration in C₁₀₀ is rather low in pre-resonant conditions, when the spectra are excited with 620 nm or 532 nm lasers. Quite interesting is the A_1g(5) mode of C₁₀₀ at 551 cm⁻¹, which resembles the radial B_2u(1) CNT mode predicted at 625 cm⁻¹. Its intensity is strongly enhanced under 620 nm excitation so that it becomes the strongest feature in the spectrum. A_1g(10) at 1195 cm⁻¹ is another medium-intensity Raman feature of C₁₀₀ largely originating from ungerade CNT vibration, this time B_2u(2) predicted at 1319 cm⁻¹. This CNT mode, mixed with B_1g(1) (predicted at 1377 cm⁻¹), also contributes to the second strongest non-resonant Raman feature of C₁₀₀, A_1g(12) at 1301 cm⁻¹. In fact, the latter can be described as the Kekule vibration of the belt hexagons. Note that Kekule vibrations are usually rather strong in Raman spectra of aromatic compounds.

Only a handful of E_1g and E_2g modes of C₁₀₀ have considerable Raman intensity. Those of them with enhanced cap contribution can be traced back to H_g modes of C₆₀, similar to A_1g vibrations discussed above (Table 2). A specific example of the belt-localized mode worth highlighting here is the lowest-frequency E_2g(1) vibration at 144 cm⁻¹ with the strong non-resonance Raman intensity. It shows considerable temperature dependence and is shifted to 154 cm⁻¹ at 78 K. This mode is traced back to the squashing CNT vibration, also of E_2g(1) type, predicted at 69 cm⁻¹ in the (5, 5) CNT. Note that in the aforementioned treatment of fullerene vibrations as that of an elastic sphere,^43,44 this vibration can be identified as the component of the 5-fold degenerate quadrupolar mode. Other components are cap-based vibrations at 220–245 cm⁻¹ with a large weight of the H_g(1) C₆₀ mode. Ref. 44 showed that the average frequency of the quadrupolar mode also scales with the fullerene mass roughly as M^−1/2, whereas the splitting degree in non-spherical fullerenes was found to be a function of the cage form, being the largest for elongated molecular shapes.

Another CNT-like vibration of C₁₀₀ of E-type, E_1g(28) at 1508 cm⁻¹, corresponds to the E_1g(2) mode of the CNT with longitudinal oscillations of carbon atoms along the tube axis. This is one of the CNT modes, whose origin comes from the Raman-active phonon of graphene at 1582 cm⁻¹ known as the G-band, but it is not active in the Raman spectrum of the (5, 5) CNT.⁴²

It is quite remarkable that the Raman spectra of C₁₀₀ have several pronounced features of CNT-like vibrations. Vibrational studies of CNTs usually rely on strong resonance enhancement in Raman spectra when the laser matches transition between van-Hove singularities. In such resonance spectra, only two single-phonon bands are observed, the lower-frequency RBM mode and the high-energy G-band, which in CNTs includes several modes originated from the graphene optical phonon at 1582 cm⁻¹. In armchair (n, n) CNTs, three modes of this type are Raman active, E_2g(4) + A_1g(2) + E_1g(2).⁴¹ However, unlike chiral CNTs, demonstrating the G-band splitting into G⁺ and G⁻ components with longitudinal and circumferential motions of carbon atoms, armchair CNTs exhibit only one narrow G⁺-band in resonance Raman spectra, presumably due to the A_1g(2) mode with circumferential atomic dsplacements.^42,45–49 In the (5, 5) CNT, such G⁺ feature was detected at 1573 cm⁻¹, whereas the RBM mode is found at 338 cm⁻¹ (ref. 42). While the resonance enhancement is extremely useful for CNTs as it enables the measurement of tiny sample amounts, down to a single nanotube, it also imposes a limitation on the information obtained from such spectra as it only attests to enhanced modes. Other IR and Raman active vibration usually remain obscure, and even though some studies focusing on such vibration were reported,^17,50–53 their assignment is rather unspecific because bulk samples of individual CNTs were not available.

The situation is quite different for fullertubes. As they have no van-Hove singularities and therefore specific resonance conditions typical for CNTs are absent, there is no physical reason for the belt vibrations resembling A_1g modes of CNT to show enhanced Raman intensity. Indeed, the RBM-like vibration of C₁₀₀ has considerable relative intensity only in non-resonance conditions and becomes weaker when the spectra are excited at 656, 620, or 532 nm (Fig. 6), while the fullertube vibration derived from the G⁺-A_1g(2) CNT mode is so weak that we cannot reliably identify it in our spectra. It may certainly be that these vibrations show higher intensity at shorter excitation wavelengths, as the (5, 5) CNT has its E₁₁^M transition at 412 nm,⁴⁸ but such a short wavelength laser is not available to us at this moment. On the other hand, we have found several other belt-localized vibrations of C₁₀₀, which can be traced to CNT vibrations that cannot be observed in the spectra of CNT itself.

Vibrational spectra of C₉₀-D_5h and C₉₆-D_3d

As C₉₀-D_5h also has the belt derived from the (5, 5) CNT and two C₆₀-like caps, albeit rotated at a different angle than in C₁₀₀-D_5d, vibrational features of C₉₀-D_5h and C₁₀₀-D_5d are rather similar. The strongest IR bands in C₉₀-D_5h are found near 500–600 cm⁻¹, as in many other fullerenes. Among the CNT-like vibrations, the most prominent is the band at 815 cm⁻¹ with rather high IR intensity. It has 72% belt contribution and can be assigned to the IR-active phonon of graphene (868 cm⁻¹ in graphite). Similar vibration in C₁₀₀-D_5d is found at 818 cm⁻¹, but with a much lower intensity. In Raman spectra, the prominent peaks with strong CNT contribution are found at 165 cm⁻¹ (CNT squashing mode), 338 cm⁻¹ (RBM), 1216 cm⁻¹ and 1329 cm⁻¹ (Kekule vibration). Compared to C₁₀₀-D_5d, CNT squashing and RBM modes in C₉₀-D_5h are upshifted by 21 and 13 cm⁻¹, respectively. High-intensity fullerene-like vibrations in C₉₀-D_5h occur at 234/257 cm⁻¹ (fullerene squashing mode, H_g(1)), 397 cm⁻¹ (breathing mode), and 1446/1484 cm⁻¹ (both with a significant contribution of pentagonal pinch mode).

In C₉₆-D_3d, the belt has only one unit cell of the (9, 0) CNT with 18 carbon atoms, and thus the contribution of the belt to vibrations is on average rather low. Yet, several Raman modes with enhanced contribution still can be pointed out. The squashing mode with 43% of the belt involvement is found at 158 cm⁻¹. Vibration with a pronounced RBM character occurs at 353 cm⁻¹. We are not aware of vibrational spectroscopic studies of isolated (9, 0) CNTs, but when identified as internal tubes in double-walled and triple-walled CNTs, their RBM mode was found at 324–325 cm⁻¹ (ref. 54 and 55). The strongest non-resonance Raman line at 1327 cm⁻¹ also has noteworthy belt contribution of 40%. Finally, the highest-frequency vibration at 1599 cm⁻¹ may have a considerable belt contribution resembling A_1g(2) mode with longitudinal displacement of carbon atoms. The assignment is however rather ambiguous since another vibration of C₉₆-D_3d with only 2% of the belt has a similar DFT-predicted frequency. In the IR spectrum, the strong belt participation is found for the mode at 829 cm⁻¹. The rest of IR bands are caused by fullerene-like vibrations. In Raman spectra, the prominent fullerenes modes are the squashing modes at 229 and 243 cm⁻¹ as well as the radial breathing mode at 392 cm⁻¹. Assignment of other lines is less straightforward since the caps are not resembling of C₆₀ shape, and we cannot use projection analysis here.

Variation of the low-frequency Raman modes in the C₉₀–C₉₆–C₁₀₀ series can be also rationalized with the elastic shell model^43,44 already discussed above in application to C₁₀₀. The radial breathing mode frequency in the series decreases systematically from 397 cm⁻¹ (C₉₀-D_5h) to 392 cm⁻¹ (C₉₆-D_3d) to 379 cm⁻¹ (C₁₀₀-D_5d) following the mass increase. The quadrupolar mode in these fullerenes is split into 3 components, two two-fold degenerate and one totally symmetric with the highest frequency: 165/234/257 cm⁻¹ (C₉₀-D_5h), 158/229/243 cm⁻¹ (C₉₆-D_3d), and 144/223/243 cm⁻¹ (C₁₀₀-D_5d). The averaged frequency again decreases gradually with fullerene mass from 211 cm⁻¹ in C₉₀-D_5h to 203 cm⁻¹ in C₉₆-D_3d to 195 cm⁻¹ in C₁₀₀-D_5d, but the degree of splitting has a different order: the largest one of 99 cm⁻¹ is found in C₁₀₀-D_5d, followed by 92 cm⁻¹ in C₉₀-D_5h and 85 cm⁻¹ in C₉₆-D_3d. This sequence is in line with the shape variation among the three, and goes from the most elongated C₁₀₀-D_5d to the least tubular C₉₆-D_3d.

Conclusions

Detailed IR and Raman study of tubular fullerenes augmented with computational analysis allowed to address the problem of the resemblance between vibrational modes of fullertubes, nanotubes, and fullerenes. Using C₁₀₀-D_5d(1) for a case study, we employed projection analysis to establish precise numerical correspondence between vibrations of fullertube belt and caps and normal modes of (5, 5) CNT and fullerene C₆₀. This analysis showed that IR spectra are dominated by vibrations of the caps, which can be traced back to IR-active F_1u modes of C₆₀. The only belt vibrations with some, although still rather low IR intensity are found near 820 cm⁻¹ and can be traced back to CNT modes related to the IR-active phonon of graphene. In the Raman spectra, C₆₀-like and CNT-like vibrations are presented more uniformly. For caps-localized modes, we again observed a high degree of transferability from C₆₀ as the most intense Raman features could be associated with Raman-active A_g and H_g modes of C₆₀. Vibrations with significant belt contributions showed more unusual pattern. Raman spectra of CNTs have strong resonance character and are dominated by two single-phonon bands, radial breathing mode and components of the G-mode. But in the Raman spectra of fullertubes, these vibrations have modest intensity. We could identify RBM-derived vibrations close to their position in CNTs, but the modes originating from the G-type CNT modes are hard to identify in fullertubes. On the other hand, we found several intense Raman features corresponding to CNT vibrations, which are not observed in the spectra of CNTs. This finding shows that fullertubes may provide additional information on CNTs, which is hard to obtain otherwise.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

The authors acknowledge funding from the Deutsche Forschungsgemeinschaft (grant PO 1602/6-1 to A. A. P.) and the National Science Foundation (grant 1856461 to S. S.). Computational facilities were partially provided by the Center for High Performance Computing at the TU Dresden. We appreciate the technical support with local computational resources in IFW Dresden by Ulrike Nitzsche.

Notes and references

1. W. Kratschmer, L. D. Lamb, K. Fostiropoulos and D. R. Huffman, Solid C₆₀ - a New Form of Carbon, Nature, 1990, 347(6291), 354–358.
2. P. Weis, F. Hennrich, R. Fischer, E. K. Schneider, M. Neumaier and M. M. Kappes, Probing the structure of giant fullerenes by high resolution trapped ion mobility spectrometry, Phys. Chem. Chem. Phys., 2019, 21(35), 18877–18892.
3. C. R. Wang, T. Sugai, T. Kai, T. Tomiyama and H. Shinohara, Production and isolation of an ellipsoidal C₈₀ fullerene, Chem. Commun., 2000,(7), 557–558.
4. F. H. Hennrich, R. H. Michel, A. Fischer, S. Richard-Schneider, S. Gilb, M. M. Kappes, D. Fuchs, M. Burk, K. Kobayashi and S. Nagase, Isolation and characterization of C₈₀, Angew. Chem., Int. Ed. Engl., 1996, 35(15), 1732–1734.
5. H. Yang, C. M. Beavers, Z. Wang, A. Jiang, Z. Liu, H. Jin, B. Q. Mercado, M. M. Olmstead and A. L. Balch, Isolation of a Small Carbon Nanotube: The Surprising Appearance of D_5h(1)-C₉₀, Angew. Chem., Int. Ed., 2010, 49(5), 886–890.
6. N. S. Chilingarov and S. I. Troyanov, Unstable Isomer of C₉₀ Fullerene Isolated as Chloro Derivatives, C₉₀(1)Cl_10/12, Chem. – Asian J., 2016, 11(13), 1896–1899.
7. X. Zhao, H. Goto and Z. Slanina, C₁₀₀ IPR fullerenes: temperature-dependent relative stabilities based on the Gibbs function, Chem. Phys., 2004, 306(1–3), 93–104.
8. N. Shao, Y. Gao, S. Yoo, W. An and X. C. Zeng, Search for lowest-energy fullerenes: C₉₈ to C₁₁₀, J. Phys. Chem. A, 2006, 110(24), 7672–7676.
9. M. A. Fritz, E. Kemnitz and S. I. Troyanov, Capturing an unstable C₁₀₀ fullerene as chloride, C₁₀₀(1)Cl₁₂, with a nanotubular carbon cage, Chem. Commun., 2014, 50(93), 14577–14580.
10. R. M. Koenig, H.-R. Tian, T. L. Seeler, K. R. Tepper, H. M. Franklin, Z.-C. Chen, S.-Y. Xie and S. Stevenson, Fullertubes: Cylindrical Carbon with Half-Fullerene End-Caps and Tubular Graphene Belts, Their Chemical Enrichment, Crystallography of Pristine C₉₀-D_5h(1) and C₁₀₀-D_5d(1) Fullertubes, and Isolation of C₁₀₈, C₁₂₀, C₁₃₂, and C₁₅₆ Cages of Unknown Structures, J. Am. Chem. Soc., 2020, 142(36), 15614–15623.
11. H. Yang, H. Jin, Y. Che, B. Hong, Z. Liu, J. A. Gharamaleki, M. M. Olmstead and A. L. Balch, Isolation of Four Isomers of C₉₆ and Crystallographic Characterization of Nanotubular D_3d(3)-C₉₆ and the Somewhat Flat-Sided Sphere C₂(181)-C₉₆, Chem. – Eur. J., 2012, 18(10), 2792–2796.
12. S. Stevenson, X. Liu, D. M. Sublett, R. M. Koenig, T. L. Seeler, K. R. Tepper, H. M. Franklin, X. Wang, R. Huang, X. Feng, K. Cover, D. Troya, N. Shanaiah, R. J. Bodnar and H. C. Dorn, Semiconducting and Metallic [5,5] Fullertube Nanowires: Characterization of Pristine D_5h(1)-C₉₀ and D_5d(1)-C₁₀₀, J. Am. Chem. Soc., 2021, 143(12), 4593–4599.
13. M. F. Sanad, H. M. Franklin, B. A. Ali, A. R. Puente Santiago, A. N. Nair, V. S. N. Chava, O. Fernandez-Delgado, N. K. Allam, S. Stevenson, S. T. Sreenivasan and L. Echegoyen, Cylindrical C₉₆ Fullertubes: A Highly Active Metal-Free O₂-Reduction Electrocatalyst, Angew. Chem., Int. Ed., 2022, 61(21), e202116727.
14. J. Cioslowski, N. Rao and D. Moncrieff, Electronic structures and energetics of [5,5] and [9,0] single-walled carbon nanotubes, J. Am. Chem. Soc., 2002, 124(28), 8485–8489.
15. C. M. Schüßlbauer, M. Krug, T. Ullrich, H. M. Franklin, S. Stevenson, T. Clark and D. M. Guldi, Exploring the Threshold between Fullerenes and Nanotubes: Characterizing Isomerically Pure, Empty-Caged, and Tubular Fullerenes D_5h-C₉₀ and D_5d-C₁₀₀, J. Am. Chem. Soc., 2022, 144(24), 10825–10829.
16. W. Kratschmer, K. Fostiropoulos and D. R. Huffman, The Infrared and Ultraviolet-Absorption Spectra of Laboratory-Produced Carbon Dust - Evidence for the Presence of the C₆₀ Molecule, Chem. Phys. Lett., 1990, 170(2–3), 167–170.
17. A. M. Rao, E. Richter, S. Bandow, B. Chase, P. C. Eklund, K. A. Williams, S. Fang, K. R. Subbaswamy, M. Menon, A. Thess, R. E. Smalley, G. Dresselhaus and M. S. Dresselhaus, Diameter-Selective Raman Scattering from Vibrational Modes in Carbon Nanotubes, Science, 1997, 275(5297), 187–191.
18. A. Jorio, M. A. Pimenta, A. G. S. Filho, R. Saito, G. Dresselhaus and M. S. Dresselhaus, Characterizing carbon nanotube samples with resonance Raman scattering, New J. Phys., 2003, 5, 139–139.
19. R. Saito, M. Hofmann, G. Dresselhaus, A. Jorio and M. S. Dresselhaus, Raman spectroscopy of graphene and carbon nanotubes, Adv. Phys., 2011, 60(3), 413–550.
20. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
21. D. N. Laikov and Y. A. Ustynuk, PRIRODA-04: a quantum-chemical program suite. New possibilities in the study of molecular systems with the application of parallel computing, Russ. Chem. Bull., 2005, 54(3), 820–826.
22. D. N. Laikov, Fast evaluation of density functional exchange-correlation terms using the expansion of the electron density in auxiliary basis sets, Chem. Phys. Lett., 1997, 281, 151–156.
23. D. N. Laikov, A new class of atomic basis functions for accurate electronic structure calculations of molecules, Chem. Phys. Lett., 2005, 416(1–3), 116–120.
24. J. Hafner, Ab initio simulations of materials using VASP: Density-functional theory and beyond, J. Comput. Chem., 2008, 29(13), 2044–2078.
25. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561.
26. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775.
27. A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5.
28. A. G. Yagola, I. V. Kochikov, G. M. Kuramshina and Y. A. Pentin, Inverse Problems of Vibrational Spectroscopy, VSP, Utrecht, 1999.
29. Y. Wang, M. Yao, X. Hua, F. Jin, Z. Yao, H. Yang, Z. Liu, Q. Li, R. Liu, B. Liu, L. Jiang and B. Liu, Structural Evolution of D_5h-C₉₀ under High Pressure: A Mediate Allotrope of Nanocarbon from Zero-Dimensional Fullerene to One-Dimensional Nanotube, Chin. Phys. Lett., 2022, 39(5), 056101.
30. K. Lynch, C. Tanke, F. Menzel, W. Brockner, P. Scharff and E. Stumpp, FT-Raman Spectroscopic Studies of C₆₀ and C₇₀ Subsequent to Chromatographic-Separation Including Solvent Effects, J. Phys. Chem., 1995, 99(20), 7985–7992.
31. Z.-H. Dong, P. Zhou, J. M. Holden, P. C. Eklund, M. S. Dresselhaus and G. Dresselhaus, Observation of higher-order Raman modes in C₆₀ films, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48(4), 2862–2865.
32. P. H. M. Van Loosdrecht, P. J. M. Vanbentum, M. A. Verheijen and G. Meijer, Raman-Scattering in Single-Crystal C₆₀, Chem. Phys. Lett., 1992, 198(6), 587–595.
33. P. Bowmar, W. Hayes, M. Kurmoo, P. A. Pattenden, M. A. Green, P. Day and K. Kikuchi, Raman and Infrared Determination of Vibrational Fundamentals of Single-Crystal C₆₀ and Derivatives and of C₇₀, J. Phys.: Condens. Matter, 1994, 6(17), 3161–3170.
34. V. Schettino, M. Pagliai and G. Cardini, The infrared and Raman spectra of fullerene C₇₀. DFT calculations and correlation with C₆₀, J. Phys. Chem. A, 2002, 106(9), 1815–1823.
35. A. A. Popov, V. M. Senyavin and A. A. Granovsky, Vibrations of bromofullerene C₆₀Br₂₄: C₆₀ cage confined into static bromine sphere, Chem. Phys. Lett., 2004, 383(1–2), 149–155.
36. A. A. Popov, A. A. Goryunkov, I. V. Goldt, I. E. Kareev, I. V. Kuvychko, W. D. Hunnius, K. Seppelt, S. H. Strauss and O. V. Boltalina, Raman, infrared, and theoretical studies of fluorofullerene C₆₀F₂₀, J. Phys. Chem. A, 2004, 108(51), 11449–11456.
37. I. V. Kuvychko, A. V. Streletskii, A. A. Popov, S. G. Kotsiris, T. Drewello, S. H. Strauss and O. V. Boltalina, Seven-minute synthesis of pure C_s-C₆₀Cl₆ from [60]fullerene and iodine monochloride: First IR, Raman, and mass spectra of 99 mol% C₆₀Cl₆, Chem. – Eur. J., 2005, 11(18), 5426–5436.
38. A. A. Popov, C. Kästner, M. Krause and L. Dunsch, Carbon Cage Vibrations of M@C₈₂ and M₂@C_2n (M = La, Ce; 2n = 72, 78, 80): The Role of the Metal Atoms, Fullerenes, Nanotubes, Carbon Nanostruct., 2014, 22(1–3), 202–214.
39. S. F. Parker, S. M. Bennington, J. W. Taylor, H. Herman, I. Silverwood, P. Albers and K. Refson, Complete assignment of the vibrational modes of C₆₀ by inelastic neutron scattering spectroscopy and periodic-DFT, Phys. Chem. Chem. Phys., 2011, 13, 7789–7804.
40. M. Damnjanović, I. Milošević, T. Vuković and R. Sredanović, Full symmetry, optical activity, and potentials of single-wall and multiwall nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60(4), 2728–2739.
41. C. Thomsen and S. Reich, Raman Scattering in Carbon Nanotubes, in Light Scattering in Solid IX, ed. M. Cardona and R. Merlin, Springer Berlin Heidelberg, Berlin, Heidelberg, 2007, pp 115–234,  DOI:10.1007/978-3-540-34436-0_3.
42. H. Telg, E. H. Hároz, J. G. Duque, X. Tu, C. Y. Khripin, J. A. Fagan, M. Zheng, J. Kono and S. K. Doorn, Diameter dependence of TO phonon frequencies and the Kohn anomaly in armchair single-wall carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90(24), 245422.
43. H. J. Eisler, S. Gilb, F. H. Hennrich and M. M. Kappes, Low frequency Raman active vibrations in fullerenes. 1. Monopolar modes, J. Phys. Chem. A, 2000, 104(8), 1762–1768.
44. H. J. Eisler, F. H. Hennrich, S. Gilb and M. M. Kappes, Low frequency Raman active vibrations in fullerenes. 2. Quadrupolar modes, J. Phys. Chem. A, 2000, 104(8), 1769–1773.
45. E. H. Hároz, J. G. Duque, W. D. Rice, C. G. Densmore, J. Kono and S. K. Doorn, Resonant Raman spectroscopy of armchair carbon nanotubes: Absence of broad G⁻ feature, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(12), 121403.
46. Y. Wu, J. Maultzsch, E. Knoesel, B. Chandra, M. Huang, M. Y. Sfeir, L. E. Brus, J. Hone and T. F. Heinz, Variable Electron-Phonon Coupling in Isolated Metallic Carbon Nanotubes Observed by Raman Scattering, Phys. Rev. Lett., 2007, 99(2), 027402.
47. X. Tu, A. R. Hight Walker, C. Y. Khripin and M. Zheng, Evolution of DNA Sequences Toward Recognition of Metallic Armchair Carbon Nanotubes, J. Am. Chem. Soc., 2011, 133(33), 12998–13001.
48. E. H. Hároz, J. G. Duque, B. Y. Lu, P. Nikolaev, S. Arepalli, R. H. Hauge, S. K. Doorn and J. Kono, Unique Origin of Colors of Armchair Carbon Nanotubes, J. Am. Chem. Soc., 2012, 134(10), 4461–4464.
49. E. H. Hároz, J. G. Duque, E. B. Barros, H. Telg, J. R. Simpson, A. R. Hight Walker, C. Y. Khripin, J. A. Fagan, X. Tu, M. Zheng, J. Kono and S. K. Doorn, Asymmetric excitation profiles in the resonance Raman response of armchair carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(20), 205446.
50. Á. Pekker, Á. Botos, Á. Rusznyák, J. Koltai, J. Kürti and K. Kamarás, Vibrational Signatures in the Infrared Spectra of Single- and Double-Walled Carbon Nanotubes and Their Diameter Dependence, J. Phys. Chem. Lett., 2011, 2(16), 2079–2082.
51. J. L. Bantignies, J. L. Sauvajol, A. Rahmani and E. Flahaut, Infrared-active phonons in carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(19), 195425.
52. C. Branca, F. Frusteri, V. Magazù and A. Mangione, Characterization of Carbon Nanotubes by TEM and Infrared Spectroscopy, J. Phys. Chem. B, 2004, 108(11), 3469–3473.
53. U. Kuhlmann, H. Jantoljak, N. Pfänder, P. Bernier, C. Journet and C. Thomsen, Infrared active phonons in single-walled carbon nanotubes, Chem. Phys. Lett., 1998, 294(1), 237–240.
54. F. Villalpando-Paez, L. G. Moura, C. Fantini, H. Muramatsu, T. Hayashi, Y. A. Kim, M. Endo, M. Terrones, M. A. Pimenta and M. S. Dresselhaus, Tunable Raman spectroscopy study of CVD and peapod-derived bundled and individual double-wall carbon nanotubes, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(15), 155416.
55. T. C. Hirschmann, P. T. Araujo, H. Muramatsu, X. Zhang, K. Nielsch, Y. A. Kim and M. S. Dresselhaus, Characterization of Bundled and Individual Triple-Walled Carbon Nanotubes by Resonant Raman Spectroscopy, ACS Nano, 2013, 7(3), 2381–2387.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr01870e

---