Diameter-dependent single- and double-file stacking of squaraine dye molecules inside chirality-sorted single-wall carbon nanotubes

Abstract

The filling of single-wall carbon nanotubes (SWCNTs) with dye molecules has become a novel path to add new functionalities through the mutual interaction of confined dyes and host SWCNTs. In particular cases, the encapsulated dye molecules form strongly interacting molecular arrays and these result in severely altered optical properties of the dye molecules. Here, we present the encapsulation of a squaraine dye inside semiconducting chirality-sorted SWCNTs with diameters ranging from ∼1.15 nm, in which the dye molecules can only be encapsulated in a single-file molecular arrangement, up to ∼1.5 nm, in which two or three molecular files can fit side-by-side. Through the chirality-selective observation of energy transfer from the dye molecules to the surrounding SWCNTs, we find that the absorption wavelength of the dye follows a peculiar SWCNT diameter dependence, originating from the specific stacking of the dye inside the host SWCNTs. Corroborated by a theoretical model, we find that for each SWCNT diameter, the dye molecules adopt a close packing geometry, resulting in tunable optical properties of the hybrid when selecting a specific SWCNT chirality.

---

Introduction

Single-wall carbon nanotubes (SWCNTs) are well-known for their remarkable and unique electronic and optical properties, and these depend strongly on their exact diameter and chiral structure.^1–4 Thanks to the extensive variability of chiral structures, a large variety of electronic and optical properties can be accessed, making them extremely promising for diverse applications such as solar energy harvesting and high-performance (opto-)electronic devices.^5,6 Besides these very peculiar intrinsic properties, SWCNTs also exhibit a hollow core, which can be exploited as a template for aligning molecules into one-dimensional molecular arrays, resulting in new hybrid structures with different functionalities. In the past decade, the confinement of molecules inside SWCNTs has shown great potential for the templated synthesis of unique materials,^7–12 observation of new phase transitions of water,^13,14 and for the modulation of the electronic properties of the host SWCNTs.^15–20 For example, the encapsulation of solvents can be used to tune the optical properties of the SWCNTs as electronic transitions shift with the dielectric constant of the encapsulated material.^21,22 Most interestingly, the encapsulation of dyes inside SWCNTs has not only been shown to enhance the photochemical stability of the dye molecules,³ but has also resulted in the photosensitization of the SWCNTs through efficient energy transfer from the encapsulated dye molecules to the surrounding host SWCNTs.^23–25 This photosensitization is essential for the future use of SWCNTs in solar harvesting devices. Indeed, while the SWCNTs themselves show very narrow-band absorption in a few discrete parts of the solar spectrum, encapsulation of dye molecules that absorb light in complementary ranges followed by the transfer of energy to the SWCNTs is anticipated to improve the sensitivity of such devices dramatically.⁵

The properties of these novel nanohybrids not only depend on the SWCNT chiral structure but also on the specific alignment and molecular arrangement of the encapsulated molecules inside the host SWCNTs. For example, Cambré et al. showed that the encapsulation of dipolar dye molecules inside sufficiently narrow diameter SWCNTs results in a head-to-tail alignment with all dipoles pointing in the same sense, resulting in a nanohybrid structure with enhanced nonlinear optical properties.²⁴ Moreover, the aggregation of planar dye molecules inside SWCNTs resulted in a J-aggregate formation with multiple stacked aggregates inside the SWCNTs which gave rise to giant Raman scattering cross-sections.²⁶ The stacking of dye molecules inside SWCNTs was found to be driven by the combined effect of the mutual interactions of the dyes with each other and the interaction of the dyes with the SWCNT walls. Moreover, the dye stacking configuration not only depends on the SWCNT diameter,^25,27,28 but can also depend on the electronic properties of the surrounding SWCNTs²⁹ and the exact synthesis conditions used,³⁰ providing an enormous variety of possible dye@SWCNT combinations. Importantly, for each of these hybrid dye@SWCNT structures, different properties of the encapsulated dye molecules, the SWCNTs, and the combined nanohybrids can be observed.^25,29,30

Li et al. recently demonstrated the single-chirality sorting of SWCNTs with sufficiently large diameters to encapsulate a dye.³¹ This breakthrough now enables the sorting of dye@SWCNT hybrids down to the single-SWCNT-chirality level in macroscopic quantities, and this allows for a more in-depth characterization of the specific stacking and molecular arrangement of dye molecules inside SWCNTs with different diameters. In this work, we analyze these different molecular arrangements through the changing absorption spectra of the differently interacting dye molecules, which can be observed through the consecutive energy transfer to the surrounding host SWCNTs resulting in distinctive peaks in photoluminescence-excitation spectra (PLE). Indeed, as previously demonstrated, encapsulation of a squaraine dye leads to the formation of J-aggregates inside the nanotubes, whose interaction and orientation depend strongly on the specific SWCNT diameter.²⁵ However, a detailed chirality-dependent analysis over a sufficiently broad range of SWCNT diameters remained elusive, due to the overlapping emission of various SWCNT chiralities.²⁵ In this work, thanks to the chiral sorting combined with the detailed wavelength-dependent spectral fitting of the PLE spectra, we were able to unambiguously identify the diameter-dependent stacking of squaraine molecules in more than twenty different SWCNT chiralities, with diameters ranging from a single-file molecular arrangement up to a potential double- or triple-file filling, essential to understand the chromophore organization at the nanoscale. In particular, we also highlight a general trend of the shift of the dye emission with diameter. We corroborate the observed diameter trend with a theoretical model for the closest packing geometry of such dye molecules inside different diameters. Using that model, we calculated the dipole–dipole interaction between the dye molecules, allowing for the prediction of the encapsulated dye absorption spectra as a function of the diameter of the surrounding SWCNT.

Experimental

Filling of SWCNTs: SQ@SWCNTs

Filling of SWCNTs with the squaraine dye 1,3-bis[4-(dimethylamino)phenyl]-2,4 dihydroxycyclobutenediylium dihydroxide, bis(inner salt) (SQ) was carried out using a similar strategy as published in ref. 25. Electric arc discharge SWCNTs (EA-P2, lot no. 02-A011, from Carbon Solutions) (20 mg) were mixed with 20 mg of the SQ dye (lot# MKBG1223 V, Sigma-Aldrich) in 5 mL dichloromethane (DCM, Sigma-Aldrich) bath sonicated for 5 min and incubated for 1 h by refluxing. The filled SWCNT powders (denoted SQ@SWCNT) were filtered (PTFE membrane, 0.45 μm pore size, Phenex) and washed with copious amounts of DCM to remove the non-encapsulated SQ. The filter cake was then placed in an oven at 100 °C to evaporate all the DCM, before further dispersion.

Aqueous suspension and rate-zonal centrifugation of SQ@EA

The preparation of aqueous SWCNT suspensions and rate-zonal centrifugation have been described in prior work.^31,32 Briefly, SWCNT suspensions were prepared by dispersing the filtered SQ@EA powders in 20 mL of 2% sodium deoxycholate (DOC) in H₂O (20 g L⁻¹, BioXtra 98+%) by sonication for 45 min (tip, 0.9 W mL⁻¹) in an ice bath followed by centrifugation (45 560g, Beckman Optima L-80 XP, SW 40 Ti rotor) for 1 h. 80% of the supernatant was collected and used for the next rate-zonal centrifugation. Approximately 8 mL aliquots of the supernatant were then layered on top of 28 mL of 11% (volume/volume) iodixanol (Opti-Prep solution with a density of 1.32 g mL⁻¹ in H₂O) with 1 wt/v% DOC (10 g L⁻¹) in H₂O and centrifuged for 2 h and 45 min in a VTi-50 rotor (Beckman-Coulter) at 5240 rad s⁻¹ (50 000 rpm) at 20 °C. The bands containing well-individualized nanotubes were collected and concentrated with 1 wt/v% DOC (10 g L⁻¹) in a pressurized ultrafiltration stirred cell (Millipore) with a 300 kDa molecular weight cut-off membrane for further ATPE sorting.

Aqueous two-phase extraction

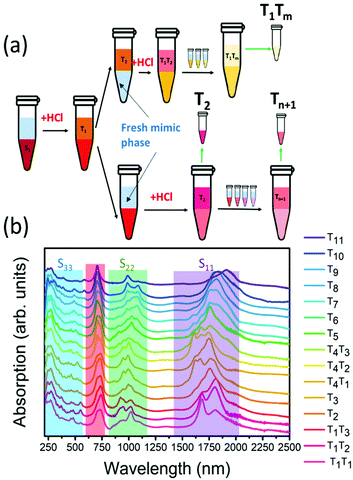
The chirality sorting of SQ@EA tubes was performed as previously reported³¹ and also extensively described by Fagan et al.³³ First, the semiconducting parent populations were prepared with a desired global surfactant concentration of 0.9 wt/v% sodium cholate (SC) (Sigma-Aldrich), 0.7 wt/v% sodium dodecyl sulfate (SDS) (Sigma-Aldrich) along with 10 μL mL⁻¹ sodium hypochlorite (NaClO) (Honeywell) as the oxidant. Dextran (MW 70 kDa, TCI) and poly(ethylene glycol) (PEG, MW 6 kDa, Alfa Aesar) were used to form the two-phase system with global concentrations of 6% and 8% in H₂O (m/m), respectively. The semiconducting fractions were taken for further diameter sorting after concentration and adjustment to a DOC concentration of 1 wt/v% using a pressurized ultrafiltration cell (Millipore) with a 300 kDa MW cut-off membrane. For diameter sorting, the global concentrations of surfactants were adjusted to 0.225 wt/v% SDS, 0.9 wt/v% SC and 0.15 wt/v% DOC, with similar PEG and dextran concentrations as mentioned above. Then 0.5 M hydrochloric acid (HCl) (12.5–33 μL mL⁻¹) was added to the ATPE system step by step for pushing the nanotubes with different diameters to the top phases, as such obtaining fractions from T₁, T₂⋯to T_n (see Fig. 1a for a scheme illustrating the ATP sorting and Fig. 1b for the absorption spectra of the different fractions).

Fig. 1 (a) Scheme to illustrate the ATPE of the samples and their nomenclature (b) Absorption spectra of the different chirality-sorted SQ@SWCNT samples. The different ranges of the optical transitions of the SWCNTs (S₁₁, S₂₂ and S₃₃) are highlighted by purple, green and blue boxes, respectively. The wavelength-range of the SQ dye absorption is highlighted by the red background.

Afterward, all samples were dialyzed to a 1 wt/v% DOC/D₂O solution for optical characterization. Deuterated water (D₂O) was chosen for its optical transparency in the NIR, allowing the measurement of fluorescence-excitation (PLE) spectra of SWCNTs with diameters up to 1.5 nm, and optical absorption spectra for the full diameter range (wavelength range: 200–2500 nm).

Optical spectroscopy of SQ@SWCNTs

Absorption spectra were recorded using a Cary 5000 UV-vis-IR spectrophotometer in the wavelength range of 200–2500 nm using a 60 μL quartz microcell with an optical path length of 3 mm (for subsequent PLE experiments) or a quartz cell with an optical path length of 1 mm (absorption spectroscopy only). Spectra were corrected for the absorption of the surfactant and D₂O.

PLE spectra were recorded using an in-house developed setup consisting of a pulsed Xenon lamp (Edinburgh Instruments, custom adapted XE900-XP920) equipped with a 300 mm focal length grating monochromator (Acton SpectraPro 2355, 1200 gr mm⁻¹ grating) for selecting the excitation wavelengths (typical slit-selected instrumental resolution of 8 nm). The emission was analyzed through a 150 mm focal length grating spectrometer (Acton SpectraPro 2156, 150 gr mm⁻¹ grating, slit-selected instrumental resolution of 10 nm) and detected with a liquid-nitrogen-cooled extended InGaAs photodiode array detector (Princeton Instruments OMA V:1024/LN-2.2) with sensitivity up to 2.2 μm. Spectra were recorded in 90° geometry in a 3 mm microcell (60 μL volume) with 5 nm steps in the excitation wavelength. All PLE maps were corrected for detector and spectrograph efficiency, filter transmission, and spectral and temporal variations of the excitation intensity. Moreover, PLE maps were also corrected for (re)absorption of the excitation light and emitted light, using the absorption spectrum of the samples measured just after the PLE experiment.

Fitting of the PLE maps

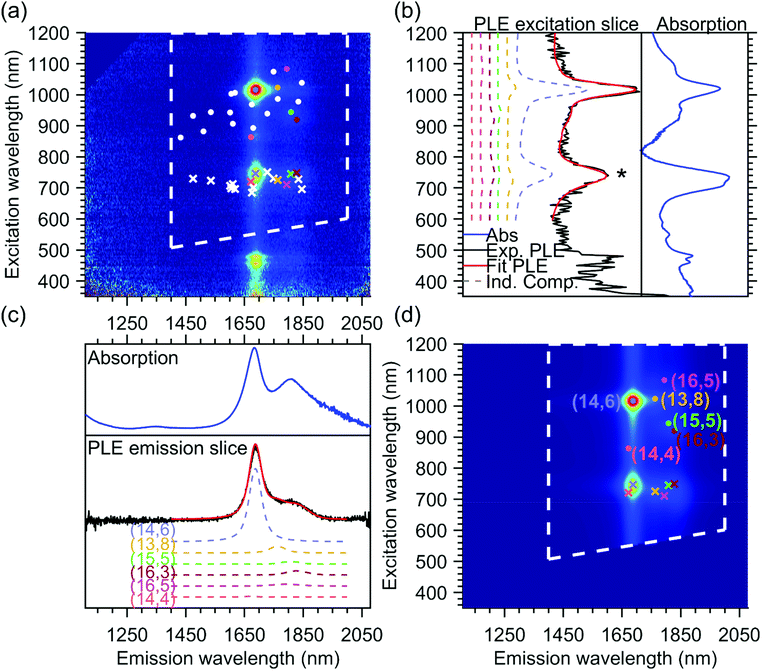
The PLE maps of all the samples were fitted simultaneously using a two-dimensional fit model, previously discussed in detail in ref. 24, 25, 31 and 34, where the PLE spectrum of each chiral structure is modeled by the product of an emission line shape and an excitation line shape, and the full PLE map is fitted by taking a linear combination of these individual contributions. In Fig. 2, we provide an example of the final fit for one of the PLE maps, namely the T₁T₁ sample, which will help to explain the fit model used since this particular sample contains only one dominant chiral species, the (14,6) chirality (more details on the different parts of the PLE maps can be found further in the Results and discussion section).

Fig. 2 Example PLE map and fit for the T₁T₁ sample: (a) experimental PLE map with indicated fit range (dashed white lines) to exclude the PLE range of the S₃₃/S₄₄ excitation which is not included in the fit model (b) right: absorption spectrum zoomed in on the excitation range (blue) left: PLE excitation slice obtained by summing the experimental PLE map (black) and fit (red) between emission wavelengths of 1200 and 1900 nm. In addition, a selection of individual chirality contributions with their relative amplitudes are also presented in dashed colored lines, and the respective positions of these peaks are presented by dots on the PLE maps (panels (a) and (d)), with the same color coding as the dashed lines. The * indicates the position of the energy transfer peak. (c) Top: Absorption spectrum zoomed in on the emission range (blue) bottom: PLE emission slice obtained by summing the PLE maps between excitation wavelengths of 850 of 1200 nm, the same colour coding as in panel (b). Individual contributions to the emission slice are also presented with the same colour coding as in panel (b). (d) Fitted PLE map, with superimposed the positions of the selected chiralities for which the individual components are given in panels (b) and (c).

In brief, the emission line shape of the 2D fit model consists of a Voigt function, with its central position S₁₁, full width at half maximum FWHM₁₁ and a shape parameter that quantifies the contribution of Lorentzian and Gaussian components to the Voigt function. In principle, the model also allows adding the phonon side bands (PSB) in the emission line shape, but for these large-diameter SWCNTs, the amplitudes of these PSBs were found to be negligible, hence we did not need to include them in the current fit. Fig. 2c shows the summed emission spectrum of the T₁T₁ sample (in black, obtained from the PLE map by summing the PL intensities between excitation wavelengths 850–1200 nm) together with the summed emission fit (in red), which is composed of multiple contributions from all the chiralities that are fitted. The fitted chiralities are visualized by white dots superimposed on the PLE map in Fig. 2a, and for some of those chiralities (highlighted by coloured dots), their contribution to the total fit is plotted (dashed colored lines) with their fitted relative amplitude shown in Fig. 2c. For comparison, we also show the absorption spectrum in the same range as the emission spectrum in Fig. 2c.

The excitation line shape in our model includes a Voigt line shape centered at S₂₂ (with S₂₂, FWHM₂₂, and shape parameter as fit parameters) plus a band-to-band transition, modeled as the regularized version of the density of states of the SWCNTs, convoluted with a Gaussian (with position and line width S₂₂ and FWHM₂₂) to avoid the band-to-band transitions from becoming infinite at S₂₂. The band-to-band contribution of the first optical transition is also added, but without the convolution, as the S₁₁ singularity is far outside the measured range. The relative amplitudes of the band-to-band contributions with respect to the main excitonic emission peak are two additional fit parameters and are taken the same for all chiralities to reduce the number of fit parameters in the model. In the excitation profile, a PSB originating from the K-momentum dark exciton is also fitted, adding three additional parameters to the total model, namely the position of the PSB relative to S₁₁, which is taken the same for all chiralities to again reduce the number of fit parameters, and two additional fit parameters that model the amplitude of this PSB with respect to S₁₁A_PSB and β that account for the diameter-dependent (d) relative amplitude of this PSB with the excitonic transition in the following manner: A_PSBd^β.^24,25,31,34

In addition to the expected intrinsic PLE spectrum of a single SWCNT, the excitation energy transfer peak is modeled as an additional band in the excitation profile, with a shape defined by the absorption spectrum of the unencapsulated dye in toluene solution and with the peak position, the line width and the relative amplitude with respect to the excitonic peak as chirality-dependent fit parameters. Similarly, as shown in Fig. 2c, Fig. 2b shows the excitation spectrum of the T₁T₁ PLE map (in black, obtained by summing the PL intensities between emission wavelengths of 1200 and 1900 nm), the total fit (in red) and the contributions of a few concrete chiralities (in dashed colored lines).

The position of the energy transfer peak can be found between 680 nm and 800 nm and is indicated by the asterisk in Fig. 2b and by crosses in Fig. 2a and d. One can observe that it changes for each different chiral structure. Note that the emission of the energy transfer peak is taken to be the same as the emission spectrum of the SWCNTs, since the same SWCNT is emitting the light, but after the optical excitation of the encapsulated dye molecules instead of the excitation through the S₂₂ optical transition. While in the previous work, the line width was modeled to be the same for all SWCNT chiralities for simplicity,²⁵ in this work, thanks to the very broad set of chirality-sorted samples, the line width could be fitted for each chirality separately, and was found to vary significantly with SWCNT chirality (see further).

Overall, the above fit model comprises 3N fit parameters for the emission spectrum, with N as the total number of chiralities, 3N + 3 fit parameters for the excitation spectra and 3M parameters for the position, line width and amplitude of the energy transfer peak for the M chiralities that present such an energy transfer peak. Note that for the fit, we zoom in the PLE maps, to exclude the region where emission is observed due to excitation in S₃₃ and S₄₄ (which are not included in our fit model), as indicated by the white dashed lines superimposed on the PLE map and fit shown in Fig. 2.

In the end, the excitation and emission profiles are combined in a 2D model function for each chiral structure (see Fig. 2d). While the mentioned fit parameters are optimized using a nonlinear least-squares algorithm, the amplitudes of these 2D model functions (intensities of each chirality) are determined by a simple analytical linear regression. Moreover, we performed a simultaneous fit of all our experimental data, with shared fit parameters for each chirality (all of which originate from the same parent suspension), but varying amplitudes (due to different abundances of each of these chiralities in different samples). This simultaneous fit improves the accuracy of the fit parameters significantly. In particular, it allows to unambiguously assign the various energy-transfer peaks of overlapping chiralities to specific chiralities, as their relative abundances (and thus amplitudes) change in different PLE maps and helps to fit the amplitudes of very small PLE peaks of chiralities that are less abundant in a specific map. For instance, the T₁T₁ PLE map shown in Fig. 2 has been fitted with all chiralities represented by white and colored dots in Fig. 2a. Without the simultaneous fit, only the contribution of the majority chiralities (like the (14,6) shown in light blue in Fig. 2) could have been fitted properly.

Results and discussion

Absorption and PLE spectroscopy

The absorption spectra of the chirality-sorted SQ@SWCNT samples are presented in Fig. 1b. First of all, the absorption spectra show the SWCNTs’ excitonic transitions (highlighted in purple for S₁₁, green for S₂₂ and blue for the higher order transitions (S₃₃, S₄₄, etc.) in Fig. 1b), with both spectra of highly-pure samples consisting of mainly one single chirality (e.g. samples T₁T₁, T₅, and T₁₀) as well as spectra of samples in which still multiple semiconducting chiral species are present. Superimposed on the SWCNTs’ intrinsic absorption peaks, the absorption of the encapsulated dye molecules is observed in the range of 680–800 nm (highlighted in red in Fig. 1b). For comparison, in Fig. S1 of the ESI,† the absorption spectra of the parent sample before and after dye-filling are also added, clearly showing the absorption of this dye only in the latter. Moreover, when comparing the SQ-filled and non-filled samples’ intrinsic SWCNT transitions, a clear shift of the SWCNT transitions is observed (see Fig. S1†). This shift was also compared to water- and alkane-filled SWCNTs for the (14,6) sorted SWCNT samples and those are clearly distinct from the filling of the SWCNTs with the dye (see Fig. S2†), as also previously observed by van Bezouw et al.²⁵ Strikingly, as shown in Fig. 1b, the location and shape of the absorption band of the dye is different for the different SWCNT samples and is composed of a superposition of various narrow bands absorbing at different wavelengths (see also Fig. S3† which zooms-in on this dye absorption).

More detailed information can be obtained by measuring the PLE maps of these chirality-sorted SQ@SWCNT samples. Fig. 3 presents an overview of 9 representative PLE maps (the complete set of 15 PLE maps is shown in the ESI, Fig. S5†). For each of the 2D PLE maps, three different families of peaks can be observed. In the excitation range of 800–1200 nm, the typical excitation–emission peaks of the semiconducting SWCNTs (s-SWCNTs) can be found, corresponding to the S₁₁ emission of s-SWCNT (on the X-axis), after the excitation of the second optical transitions S₂₂ (on the Y-axis). Likewise, in the excitation range of 400–600 nm, the same S₁₁ emission can be observed after optical excitation in the higher optical transitions of the s-SWCNTs, S₃₃ and S₄₄.

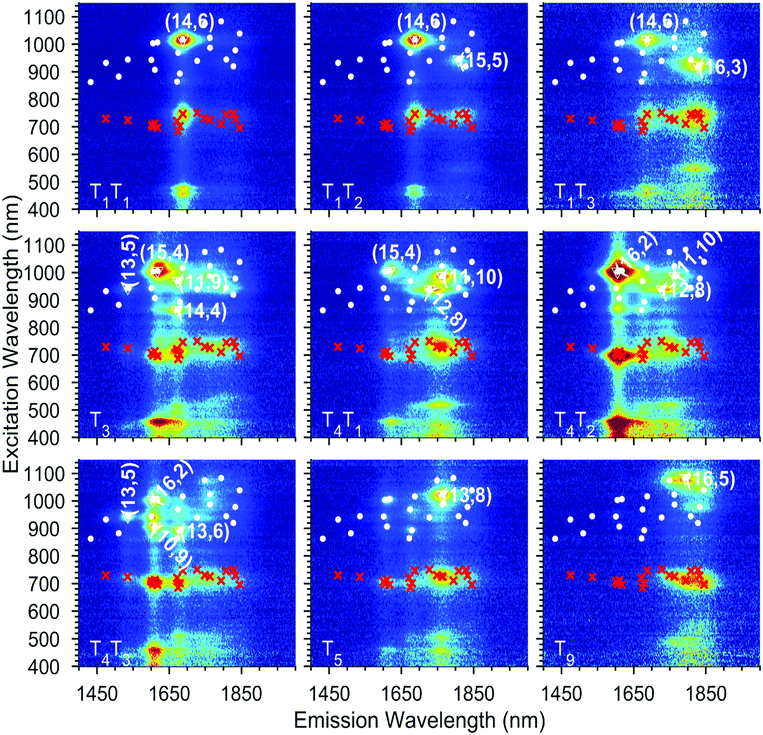Fig. 3 Exemplary experimental PLE maps of nine of the chirality-sorted samples. A complete overview is provided in the ESI Fig. S5.† The white dots represent all the chiralities that have been fitted and the red crosses the fitted EET. The most abundant chiralities in each map are labelled with their chiral indices and surrounded by a white triangle.

In addition to these intrinsic SWCNT emission peaks, in the excitation range of 680–800 nm, additional peaks can be observed corresponding to emission from the SWCNTs at the same emission energy (S₁₁) but for an excitation matching the previously described encapsulated dye absorption range (680–800 nm). This feature indicates an excitation energy transfer (EET) from the dye to the surrounding nanotubes, as previously observed in the literature for SQ and other dyes.^23–25 As shown in Fig. 3 and S5,† thanks to the sorting, each sample contains only a select set of SWCNT chiralities, which allows for an almost direct assignment of the EET peaks to a particular structure of the surrounding SWCNT after fitting.

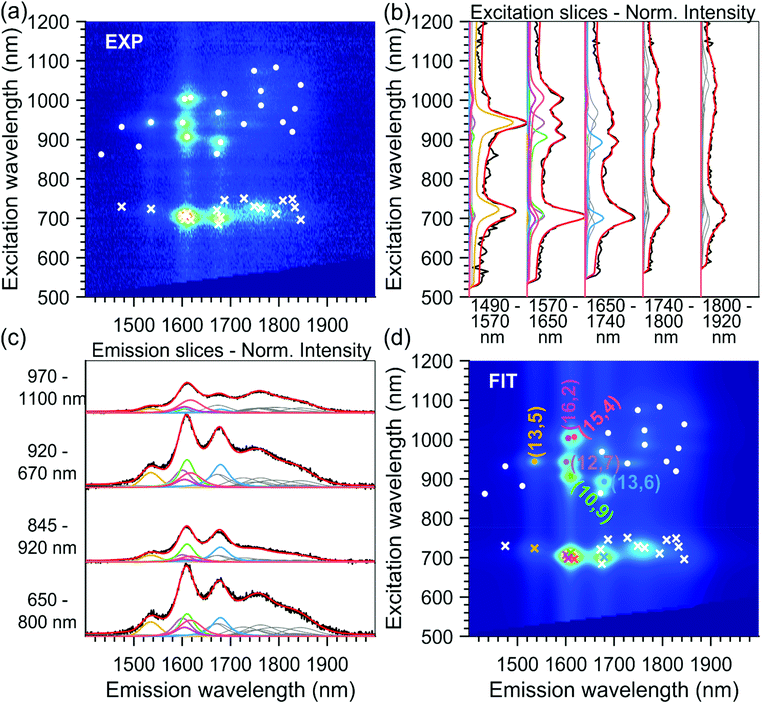
As discussed before, to obtain precisely the EET excitation energy and correlate it to a specific SWCNT chirality, these 15 PLE maps, from sorted samples originating from the same parent sample, were fitted simultaneously, with shared fit parameters for the SWCNT transitions and EET absorption bands, but varying absolute amplitudes to account for the varying abundances of the different chiralities in the different samples (also see the Experimental section). Due to the different abundances, this simultaneous fit allows to accurately correlate each EET peak to a specific SWCNT chirality, as the ratio between the EET peak intensity and the SWCNT chirality does not change in the simultaneous fit, while the absolute intensity can vary. Moreover, SWCNT chiralities that are weakly present in one particular PLE map (low absolute PL intensity) can be much more accurately fitted from their much larger intensity in another PLE map, and thus also the peak positions of the SWCNT emission can be much more accurately determined. The results of two representative fits are given in Fig. 2 and 4 (all others can be found in the ESI Fig. S6†).

Fig. 4 Example PLE map and fit for the T₄T₃ sample: (a) experimental PLE map cut to the desired fitting range (b) normalized excitation and (c) emission slices obtained by integrating the PLE maps over certain emission and excitation ranges, respectively, as indicated on the bottom (panel b) or left (panel c) of each slice. Experimental data are plotted in black and fitted data in red. Moreover, we also show the contributions of the different chiral structures in the PLE fit. The contribution of the chiralities labelled in panel (d) are highlighted with the same colour, the contribution of the other chiralities are plotted in grey. (d) Fitted PLE map with overlaid fitted SWCNT peak positions (white and coloured dots) and fitted EET peak positions (white and coloured crosses).

In Fig. 2b, the fitted excitation profiles of a discrete set of individual chiralities are extracted from the PLE fit. In the range of 680–800 nm, the observed peaks correspond to the excitation of the dye inside the SWCNT. In this range, comparing the dashed colored lines (individual contributions) and the red line (total fit), it can be seen that the excitation wavelength of the dye depends on the structure of the SWCNT in which they are encapsulated, and that the complete excitation profile (in red) is composed of a combination of the different individual components. This excitation profile can also be directly compared with the absorption spectrum of the same sample, as shown in Fig. 2b. Indeed, the main absorption peak of the dye (in this sample dominated by the (14,6) chirality occurring at around 740 nm) matches the excitation profile obtained from the PLE map. However, the absorption spectrum also shows a shoulder at about 712 nm, which is not observed in the excitation slices of the PLE map. This discrepancy finds its origin in two aspects of the PLE collection. First, in PLE, the dye absorption is observed through the emission of the surrounding SWCNTs, thus the difference in PL quantum efficiency of different SWCNTs plays a crucial role and can, in particular in this large diameter range, be very different from chirality to chirality. Secondly, all the samples are measured in a solution of 1 wt/v% DOC in D₂O. Although D₂O was chosen for its higher optical transparency in the infrared region compared to H₂O, it has a strong absorption starting from about 1870 nm, thus limiting the PL detection of SWCNTs with diameters larger than approximately 1.5–1.6 nm. Then, in the PLE maps, the dye absorption cannot be extracted for SWCNTs with a diameter above 1.5 nm. The combined effect of these two limiting factors results in a discrepancy between the absorption spectrum of the encapsulated dye molecules and the excitation spectrum of the dye molecules from the PLE maps. This difference in PL detection efficiency can also be clearly seen from the comparison of the absorption spectrum with the emission spectra (in Fig. 2c). One can note that the ratio between the main peak of the absorption (around 1688 nm) and the lower energy peaks (around 1806 nm) is very different in PLE compared to absorption, and that above 1870 nm no PL intensity is detected, due to the differences in PL quantum efficiency and the non-transparency of D₂O above 1870 nm.

Finally, similar to what was observed previously,²⁵ we also confirm that the absorption of the encapsulated dye molecules is strongly red-shifted with respect to that of a solution of the free dye in dichloromethane, where it peaks at around 625 nm, as shown for comparison in Fig. S3.†

Note that to ensure that the dye is encapsulated inside the SWCNTs and not adsorbed on the SWCNTs’ outer walls, we previously repeated the same filling procedure with closed SWCNTs²⁵ and in this work with open CoMoCat SWCNTs that have a diameter too small to encapsulate the SQ dye molecules (see Fig. S4†). In these two cases, no dye absorption was observed in the absorption spectra of both the closed, larger diameter SWCNTs²⁵ and opened, but small-diameter CoMoCat SWCNTs, proving that the used washing procedure efficiently removes any residual dye molecules on the outside of the SWCNTs.

Comparison of different samples

A good simultaneous fit was achieved, implying that the SWCNT peak positions and EET parameters are the same for the different samples, which is a logical assumption since the chirality-sorted SWCNTs arise from the same parent dye-filled semiconducting sample, and all samples are dialyzed after sorting to the same external environment (surfactant and heavy water). Nevertheless, we checked that this was the case, by carefully analysing the peak positions and EETs in all 15 PLE maps, and by checking the quality of the obtained fits, e.g. by comparing emission and excitation slices from the experimental data with the obtained fit, overall providing an excellent agreement between model and experimental data (see e.g.Fig. 2, 4 and Fig. S5–S6 in the ESI†).

It was previously shown that the exact parameters used during the solvent-based filling of SWCNTs, e.g. the reflux temperature and dye concentration, can influence the specific stacking of molecules inside the SWCNTs.³⁰ Moreover, it was demonstrated for SQ-filling that when starting from a different SWCNT batch which is not fully opened, the ratio of the dye EET peak intensity with respect to the SWCNT emission can change from sample to sample (i.e. different filling efficiency) which also leads to slight shifts of the SWCNT transitions.²⁵ Therefore, we decided to compare the PLE maps obtained in this work, with the experimental data reported earlier²⁵ for mixed-chirality SQ-filled SWCNT samples originating from a different SWCNT starting batch and slightly different filling procedure (that is, refluxing overnight (previous work) versus 1 h (this work)).

Fig. 5a compares the SWCNT peak positions obtained in this work with those of the previous work by van Bezouw et al.²⁵ Different filling fractions due to the different filling procedures and starting SWCNT batch can explain the small shifts observed. Indeed, it is well-known that SWCNT filling induces a PLE shift, which depends strongly on the encapsulated molecules’ nature and properties.²² Thus, one can expect that in the case of a slightly different filling efficiency, the obtained SWCNT emission peaks, representing the average SWCNT emission in the bulk sample, will result in a slightly different peak position, as observed here. In order to better illustrate the effect of the filling on the shift of the SWCNT transition, the peak positions of the corresponding empty SWCNTs^22,25 are also presented in Fig. 5a. Most importantly, the comparison of the fitted EET peak positions in both batches is presented in Fig. 5b. Overall, the results are in good agreement, except for a few chiralities. Due to the broad diameter distribution of the sample in the previous work, the assignment of EET peak positions to a specific SWCNT chirality was obviously more complicated, and thus errors in attributing EET peaks to the correct chiralities could easily occur, in particular for different chiralities having similar emission energies (as also discussed in the previous work of van Bezouw et al.²⁵). For example, the (14,6), (14,4), (11,9), and (13,6) filled chiralities present overlapping emission energies, so that, in a sample comprising each of these chiralities (i.e. to which the chiral sorting is not applied), it is impossible to assign a particular EET peak to a specific chiral structure. Moreover, the experimental data at that time did not allow for fitting the line width of the EET peaks for each chirality separately in the fit, while the current data with multiple close to single-chirality or few-chirality samples allows to accurately determine this changing linewidth, thereby resulting in much more accurate fits as compared to those in the previous work (see Fig. 2 and 4 for the contribution of discrete chiralities to the fit). Importantly, the use of sorted samples significantly simplifies the EET peak assignments, allowing us to now unambiguously assign each observed EET peak to a specific chirality. Indeed, a PLE map of the unsorted sample investigated previously is presented in Fig. S8,† showing strongly overlapping EET peaks in comparison to the individual PLE maps of the sorted samples studied in this work and presented in Fig. 3 and Fig. S5.† In particular, the position of the EET peak related to the SQ encapsulation in (14,6) SWCNTs could be incontestably assigned using the PLE map of sample T₁T₁ (see Fig. 2), revealing that the EET of (14,4) and (14,6) was swapped in the previous work. Similarly, the (14,7)/(12,10) and the (12,7)/(10,9) chiralities (see yellow arrows in Fig. 5b) were previously swapped, while the EET positions of (10,9), (11,10), (15,5), (13,6) and (13,5) have now been confirmed (see Fig. 5b). Finally, for larger SWCNT diameters, the observation of the EET peaks was very difficult in the previous work, due to the low abundances of those chiralities in the samples. Therefore we had to rely on their characterization in polymer-wrapped/toluene samples, in which the dye was found to exit the SWCNTs. This resulted in much lower filling efficiencies, which can also drastically change the dye configuration inside the SWCNTs. Assignment of those larger diameters was now possible due to chiral sorting. Finally, we refitted the previous experimental data, starting from the optimized parameters found from the chirality-sorted samples and using the optimized version of the fitting model, which now includes the possibility of fitting the line width of the EET peak for each separate SWCNT chirality. While fixing the values of the EET linewidth for the largest diameters, which are much less abundant in the PLE maps of the previous samples, to the values fitted from the chirality-sorted samples, i.e. diameters larger than the (14,3) chirality, the previous sample also allows extracting the EET positions for smaller diameter SWCNTs down to the (9,8) chirality that was previously found to be the smallest diameter in which SQ could be encapsulated.²⁵ The results of these combined fits (see also Fig. S8 and S9†) are presented in Fig. 5c and d.

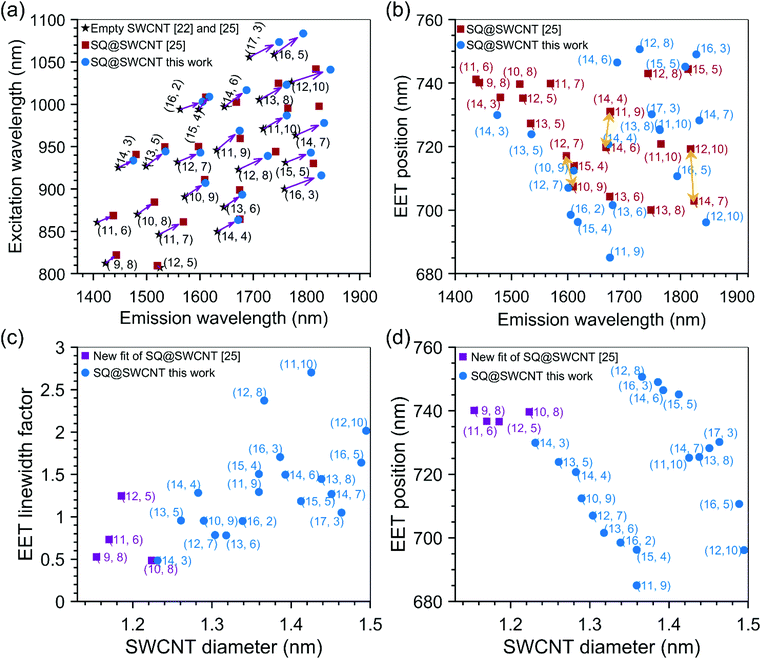Fig. 5 (a) Fitted SWCNT peak positions of squaraine filled SWCNTs compared to those of previous work, and empty SWCNTs as presented in the legend of this panel. (b) Comparison of fitted EET peak positions of squaraine encapsulated inside SWCNTs, as a function of the SWCNT emission wavelength, between our work and ref. 25. (c) Linewidth broadening factor for the EET peak positions as a function of the SWCNT diameter. The spectrum of the dye absorption was shifted to the EET position and afterwards contracted or expanded with this factor. A value larger than one thus means broadening, a value smaller than one corresponds to a narrower line as compared to the ‘free’ dye molecules in solution. (d) Fitted EET peak positions as a function of the SWCNT diameter showing a peculiar dependence on the SWCNT diameter.

Overall, a good agreement of the EET peak positions for both samples is obtained, even for larger diameter SWCNTs where a stack of two or three SQ molecules can fit inside the SWCNT cross-section. This excellent agreement of the EET positions in both batches shows that for each given chirality, a particular dye arrangement seems to be favoured.

As described in the Methods section, for each chirality, a peak position, line width, and amplitude of the EET peak are fitted. The line width is modelled by contracting or expanding the absorption spectrum of the free dye in toluene solution. In practice, this is achieved by starting from the absorption spectrum of the dye in toluene solution in energy, then shifting the energy axis of this absorption spectrum to the EET peak position, and afterwards expanding or contracting this energy axis with the specific ‘EET line width factor’ (presented in Fig. 5c), such that the absorption spectrum gets narrower or broader, respectively. An example is given in Fig. S7 in the ESI.†

Fig. 5c presents this EET line width factor, and Fig. 5d presents the EET absorption wavelength as a function of SWCNT diameter and chiral structure. For the smallest diameters, e.g. the (9,8) SWCNT, the line width factor is smaller than 1, meaning that the line width is narrower than for free dye molecules in solution. In these small diameters, in which the dye can just fit inside the internal SWCNT cross-section, only a single file of aligned dye molecules can be obtained (see the next section). This reduces inhomogeneous broadening (i.e. each dye molecule experiencing the same environment) and combined with the particular one-dimensional J-aggregate-like arrangement, a narrower linewidth than the dye in solution is observed. For SWCNT having a larger diameter, a broadening of the line width compared to the free dye in solution, is observed up to a factor of 2.7 for the largest diameters. This broadening contradicts the typically observed line narrowing in J-aggregates of SQ molecules, however, it could originate from the more significant variability of different structures confined inside the SWCNTs, resulting in different stacked combinations.³⁵ When going to slightly larger diameters (but still below 1.27 nm which was previously calculated to be the smallest diameter for which two files of molecules can fit side-by-side inside the SWCNTs cross-section²⁵), the dye molecules could adopt a configuration with optimized van der Waals interactions between the dye molecules and the SWCNTs, and therefore adopt a tilted configuration, similar to that previously observed for copper acetylacetonate molecules³⁶ encapsulated inside SWCNTs (see also Fig. 6a for a schematic model and the next section). In such a configuration, the J-aggregate (dipole–dipole) coupling between the adjacent dye molecules will initially decrease with increasing tilt angle of the molecules with the SWCNT axis (labeled α in Fig. 6a) in good agreement with our experimental data showing decreasing red-shift of the encapsulated dye EET position (see Fig. 5d) over a range from ∼1.15 to 1.35 nm. Starting from diameters of 1.27 nm and larger, a double-file arrangement can be formed, where the dye molecules couple within one file as J-aggregates, but can get coupled additionally as J- or H-aggregates between the adjacent files (depending on the offset between both files), thereby resulting in higher or lower EET peak positions shifts, respectively, as those within the (9,8) chirality. In this configuration, the band broadening is expected due to a combination of H-aggregate formation and different absorptions of different aggregate types.³⁵

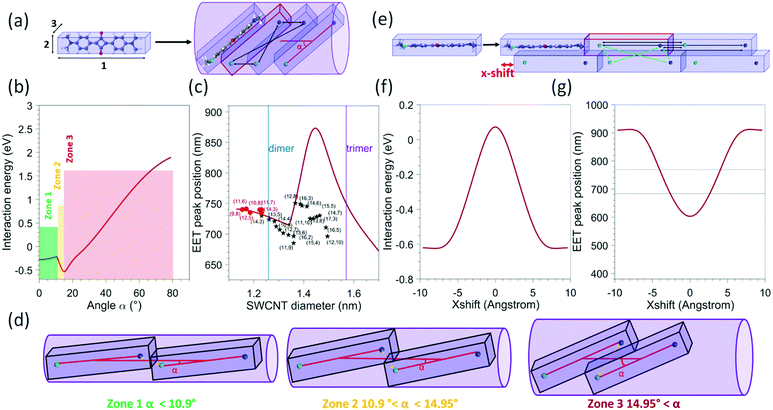Fig. 6 (a) Schematic view of the model used for a single file of molecules 1: lattice parameter of a SQ 1D chain (1.925 nm) 2: H_(phenyl) − H_(phenyl) (0.672 nm), 3: interplanar distance in the optimized dimer configuration (0.358 nm) and an example of a tilted configuration of the dye molecules inside the SWCNTs, with the tilt angle (α) with respect to the SWCNT axis. The black arrows represent the four point-charge–point-charge interactions that are calculated between two adjacent molecules, with the partial charges assumed to be located on the N-atoms, and the lighter and darker blue colours representing N-atoms with opposite partial charges. In the array of N = 200 molecules, each time four additional interactions are taken into account for each next neighbouring molecule. (b) Calculated interaction energy as a function of the angle between the SWCNT axis and the molecule (represented by α in panel (a)), presented for a molecular array of N = 200 molecules. (c) Calculated EET peak positions as a function of the nanotube diameter for an array of N = 200 molecules (red solid line). The black stars and red dots represent the experimental data points of this work and ref. 25 respectively. The blue and purple lines represent the diameters above which a double- or triple-file arrangement could exist in the SWCNT diameter. (d) Schematic view of the molecular arrangement for different angles corresponding to the different zones indicated in figure b (e) schematic view of the model used for a double array of molecules. The green arrows represent the four interactions that need to be added to account for interactions between the two arrays. (f) Calculated interaction energy as a function of the x-shift for a double file of N = 200 molecules in each array (g) calculated EET peak positions as a function of the x-shift. The two horizontal lines represent the range in which experimental EET peak positions are observed.

Model for dye interaction in a 1D array inside SWCNTs

In order to model the interaction of the dye molecules in a 1D array inside the SWCNTs, we calculated the largest tilt angles of such molecules and the accompanying distance between the dye molecules for each of these tilt angles, when adopting the most compact filling arrangement inside SWCNTs with diameters ranging from 1.1 to 1.5 nm (see Fig. 6a for a schematic view). Practically, we first approximate the molecule using a rectangular box, with dimensions obtained by a quantum-chemically optimized structure of the dye. For that, our previous quantum-chemical calculations at the Hartree–Fock level with the semiempirical Hamiltonian PM7 (MOPAC) were used²⁵ and this structure was surrounded by standard van der Waals radii for all the atoms (the obtained values are detailed in the caption of Fig. 6). Then, the boxes were tilted with an angle in the range from 0° to 80°. Subsequently, for each tilt angle, the minimal distance between two molecules was calculated analytically as the distance for which the boxes are in contact. Note that the molecules cannot slip over each other for small tilt angles and distances are relatively large. Starting from an angle of about 10.9°, the boxes start to slip over each other, drastically reducing the distance between the molecules (see Fig. 6d). It should be noted that the angle at which this slip-over can occur is not well defined in the ‘box-type’ model as the molecule itself is more flexible and rounded at the edge (with the methyl groups) so that this slip-over can occur for a smaller angle. Nevertheless, it provides a sufficiently good model to explain the experimental observations (see below). Then, for each tilt angle and the resulting intermolecular distance, we calculate the minimum diameter of a cylinder that can fit around the tilted boxes. Finally, we add the van der Waals radii of the carbon atoms in the SWCNT structure to this calculated diameter (taken at half of the graphite layer spacing, i.e. 0.1677 nm) and we additionally increase this diameter with a small constant value of 0.0313 nm, that we previously reported being required to match the calculated diameters with the experimentally determined minimal encapsulation diameters.^22,24,25 In this way (inverting this relation), for each SWCNT diameter, we obtain the maximum angle the molecules can adopt, as well as the corresponding minimal distance between the molecules, or in other words, the most compact filling arrangement possible in a particular SWCNT chirality, see Fig. 6a and d.

To model the interaction energy in such a tilted molecular array, we assume that the transition dipole in the molecule's excited state corresponds to a delocalization of the charge over the two nitrogen atoms of the dye.^37,38 Then, we calculate the coulombic interactions between the point charges on the nitrogen atoms (together constituting the transition dipole moment of the molecule) of two molecules, as shown with the black arrows in Fig. 6a.

Finally, to approximate the interaction energy per molecule in an infinite array, we sum all the interaction energy terms of a molecule with the other molecules in a finite array, at a distance of up to N = 200 molecules to obtain the interaction energy for each angle (Fig. 6b). An array of N = 200 was chosen to approximate the limit of an infinite chain (see ESI Fig. S10†) and since it corresponds to the typical arrays that could be expected for completely filled SWCNTs with lengths of the order of a few hundred nanometers. We also calculated the interaction energy for arrays with a smaller number of molecules (see Fig. S9†), showing that for N = 200 the infinite limit is approached (hardly a difference between N = 20 and N = 200). This interaction energy, depending on the choice of partial charge q, then shifts the absorption peak position from that of the free dye in solution, i.e determined to be 625 nm (see Fig. S3 and S7 in the ESI†), to the value of the encapsulated EET peak positions.

The partial charge was then determined using the experimental shift observed for the dye encapsulated in the (9,8) SWNT, being the smallest experimentally observed SWCNT diameter in which the SQ molecules can be encapsulated and thus assuming the angle with the SWCNT axis to be negligibly small, resulting in a value of q = 0.4308 e when an array of N = 200 dye molecules is considered. With this partial charge, the total interaction energy was calculated for each angle as shown in Fig. 6b, while in Fig. 6c, the expected calculated EET peak positions for such tilted dye configurations are compared to the observed experimental EET positions. A remarkably good agreement is observed between the model and the experimental data for the smallest diameters (up to 1.35 nm), in particular when considering the simplicity of the applied model. Indeed, the same trend is observed, first a decrease of the shift (with respect to the free dye) with the increase in the diameter of the SWCNT, corresponding to an increase of the tilt angle without slip-over of the boxes (see Fig. 6a and d), followed by a strong increase at about 1.3 nm, which corresponds to the slip-over of the boxes such that the N-atoms with opposite charge of adjacent molecules come very close to each other, after which the boxes slide more over each other such that the distance between those N-atoms increases again, which is represented by the decrease observed for diameters larger than 1.45 nm. We find that the transition point of this slip-over (start of increase at about 1.35 nm) appears at the point where experimentally also we find the second branch of the experimental data to occur. However, the size of the shift is very different in that range, but very sensitive to the exact distance between those N-atoms with opposite charges in the two adjacent molecules, and therefore very sensitive to the exact choice of the box size and more importantly the flexibility of the end groups of the molecules. Even though the magnitude of the shift that is found for diameters above 1.35 nm does not agree with the experimental data, the position at which it occurs and the direction in which the EET peak position shifts is in good agreement with the experimental data. Importantly, it should be noted that for SWCNTs with a diameter larger than 1.27 nm (see blue line in Fig. 6c) in principle, it is also possible to fit a double file of molecules inside the SWCNT (Fig. 6e). For SWCNTs with a diameter larger than 1.27 nm (i.e. larger than the (13,5) SWCNT in our data set) a more complicated arrangement can thus occur, making it difficult to predict the exact stacking configurations in those larger diameters. Nevertheless, the good agreement in the overall trend of the EET peak position shift between our simple model and the experimental data for diameters below 1.35 nm might hint that the tilted configurations occur more likely. However, a configuration with a double file of molecules could also, in principle, lead to similar shifts. Using the simple model described previously, we also calculated the Coulomb interaction obtained for a double file of molecules, taking the distance between the two molecular files as the distance between two molecules in a SQ dimer, similarly optimized as the monomer, at the PM7 level in MOPAC.

For simplification, in that case, we consider that the molecules in the same file are in a head-to-tail configuration, as shown in the scheme of Fig. 6e. The interaction energy previously described within one row of molecules was modelled in the same manner (black arrows on Fig. 6e), and additionally, an H-aggregate type interaction was added to consider the interaction between molecules on different files, as shown with green arrows in Fig. 6e. The partial charge is kept the same, and we add the possibility to shift the two files of molecules with respect to each other along the SWCNT axis, referred to as the x-shift in Fig. 6e. We then calculated the interaction energy for different values of x-shift which is presented in Fig. 6f. The expected absorption shift in comparison to the free dye molecules in solution was also calculated (Fig. 6g). As shown in Fig. 6g, we can see that for an x-shift from 3–4 Å, reasonable values compared to our experimental data are obtained, indicating that it is difficult for SWCNTs with a diameter above 1.27 nm to discriminate with this simple model from the experimentally obtained shift, if the dye molecules are arranged in a single file with an optimum tilt angle, or in an arrangement with two files and a specific x-shift between the two files. Nevertheless, even though the model is a very simplified representation of the experimental work, the good agreement in the diameter range below 1.27 nm provides direct evidence of the molecules adopting a tilted, optimized closest packing geometry in diameters below 1.27 nm.

Conclusions

In this work, we report squaraine dye encapsulation in large diameter single-wall carbon nanotubes. For the first time, we obtained near-to single-chirality sorted and dye-filled large-diameter SWCNTs. Thanks to the new sorting procedure, we were able to characterize the energy transfer between twenty different SWCNT chiralities and their encapsulated dye molecules precisely, using a robust fitting process that can be extended to the filling of SWCNTs with other dyes. We also confirm the influence of the SWCNT diameter on the encapsulated dye absorption with the highlight of some typical patterns showing that the stacking of the dye leads to different signatures. We also proposed a simple model to explain the obtained shift. Besides the fundamental study of new stacking configurations of dye molecules that cannot be accessed in a bulk arrangement, obtaining close to single-chirality filled SWCNTs and identifying these patterns gives insight into how the hybrid molecules@nanotubes should be chosen as a function of the targeted absorption range and paves the way for future applications in photodetection and photovoltaic applications.

Author contributions

S. F. and S. C. wrote the paper with contributions from all the authors. S. F. measured the absorption and PLE maps of different samples and performed the fit of the data using an updated version of the fitting procedure developed by S. C. and W. W. S. F., W. W., and S. C. developed the model for the stacking of the molecules. W. W. developed the PLE setup. H. L., L. W., and B. S. F. prepared the chirality-sorted SWCNT samples for analysis. S. v. B. and J. C. prepared multi-chirality filled SWCNT samples.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. F. and S. C. acknowledge funding from the European Research Council, ERC Starting Grant No 679841 (ORDERin1D). The work in Antwerp was partially funded by the Fund for Scientific Research Flanders (FWO) through projects G040011N, G02112N, G035918N and G036618N and the EOS CHARMING project G0G6218N [EOS-ID 30467715]. H. L. and B. S. F. acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG) under grants FL 834/2-2, FL 834/5-1, FL 834/7-1 and FL 834/9-1.

Notes and references

1. J. C. Charlier, X. Blase and S. Roche, Rev. Mod. Phys., 2007, 79, 677–732.
2. G. J. Brady, A. J. Way, N. S. Safron, H. T. Evensen, P. Gopalan and M. S. Arnold, Sci. Adv., 2016, 2, e1601240.
3. K. Yanagi, Y. Miyata and H. Kataura, Adv. Mater., 2006, 18, 437–441.
4. R. B. Weisman and J. Kono, Handbook of Carbon Nanomaterials, World Scientific, 2019, vol. 10.
5. L. Wieland, H. Li, C. Rust, J. Chen and B. S. Flavel, Adv. Energy Mater., 2021, 11, 2170014.
6. P. Avouris, M. Freitag and V. Perebeinos, Nat. Photonics, 2008, 2, 341–350.
7. A. V. Talyzin, I. V. Anoshkin, A. V. Krasheninnikov, R. M. Nieminen, A. G. Nasibulin, H. Jiang and E. I. Kauppinen, Nano Lett., 2011, 11, 4352–4356.
8. J. Zhang, Y. Feng, H. Ishiwata, Y. Miyata, R. Kitaura, J. E. P. Dahl, R. M. K. Carlson, H. Shinohara and D. Tománek, ACS Nano, 2012, 6, 8674–8683.
9. J. K. Qin, P. Y. Liao, M. Si, S. Gao, G. Qiu, J. Jian, Q. Wang, S. Q. Zhang, S. Huang, A. Charnas, Y. Wang, M. J. Kim, W. Wu, X. Xu, H. Y. Wang, L. Yang, Y. Khin Yap and P. D. Ye, Nat. Electron., 2020, 3(3), 141–147.
10. H. Kuzmany, L. Shi, M. Martinati, S. Cambré, W. Wenseleers, J. Kürti, J. Koltai, G. Kukucska, K. Cao, U. Kaiser, T. Saito and T. Pichler, Carbon, 2021, 171, 221–229.
11. L. Shi, P. Rohringer, K. Suenaga, Y. Niimi, J. Kotakoski, J. C. Meyer, H. Peterlik, M. Wanko, S. Cahangirov, A. Rubio, Z. J. Lapin, L. Novotny, P. Ayala and T. Pichler, Nat. Mater., 2016, 15, 634–639.
12. M. Nagata, S. Shukla, Y. Nakanishi, Z. Liu, Y.-C. Lin, T. Shiga, Y. Nakamura, T. Koyama, H. Kishida, T. Inoue, N. Kanda, S. Ohno, Y. Sakagawa, K. Suenaga and H. Shinohara, Nano Lett., 2019, 19, 4845–4851.
13. X. Ma, S. Cambré, W. Wenseleers, S. K. Doorn and H. Htoon, Phys. Rev. Lett., 2017, 118, 027402.
14. S. Chiashi, Y. Saito, T. Kato, S. Konabe, S. Okada, T. Yamamoto and Y. Homma, ACS Nano, 2019, 13(2), 1177–1182.
15. T. Takenobu, T. Takano, M. Shiraishi, Y. Murakami, M. Ata, H. Kataura, Y. Achiba and Y. Iwasa, Nat. Mater., 2003, 2, 683–688.
16. A. A. Tonkikh, D. V. Rybkovskiy, A. S. Orekhov, A. I. Chernov, A. A. Khomich, C. P. Ewels, E. I. Kauppinen, S. B. Rochal, A. L. Chuvilin and E. D. Obraztsova, Carbon, 2016, 109, 87–97.
17. B. Nieto-Ortega, J. Villalva, M. Vera-Hidalgo, L. Ruiz-González, E. Burzurí and E. M. Pérez, Angew. Chem., Int. Ed., 2017, 56, 12240–12244.
18. M. V. Kharlamova, M. Sauer, T. Saito, Y. Sato, K. Suenaga, T. Pichler and H. Shiozawa, Nanoscale, 2015, 7, 1383–1391.
19. T. Kato, E. C. Neyts, Y. Abiko, T. Akama, R. Hatakeyama and T. Kaneko, J. Phys. Chem. C, 2015, 119, 11903–11908.
20. Y. Almadori, L. Alvarez, R. Arenal, R. Babaa, T. Michel, R. Le Parc, J.-L. Bantignies, B. Jouselme, S. Palacin, P. Hermet and J. Sauvajol, Phys. Status Solidi, 2011, 248, 2560–2563.
21. J. Campo, Y. Piao, S. Lam, C. M. Stafford, J. K. Streit, J. R. Simpson, A. R. Hight Walker and J. A. Fagan, Nanoscale Horiz., 2016, 1(4), 317–324.
22. J. Campo, S. Cambré, B. Botka, J. Obrzut, W. Wenseleers and J. A. Fagan, ACS Nano, 2021, 15, 2301–2317.
23. K. Yanagi, K. Iakoubovskii, H. Matsui, H. Matsuzaki, H. Okamoto, Y. Miyata, Y. Maniwa, S. Kazaoui, N. Minami and H. Kataura, J. Am. Chem. Soc., 2007, 129, 4992–4997.
24. S. Cambré, J. Campo, C. Beirnaert, C. Verlackt, P. Cool and W. Wenseleers, Nat. Nanotechnol., 2015, 10, 248–252.
25. S. van Bezouw, D. H. Arias, R. Ihly, S. Cambré, A. J. Ferguson, J. Campo, J. C. Johnson, J. Defillet, W. Wenseleers and J. L. Blackburn, ACS Nano, 2018, 12, 6881–6894.
26. E. Gaufrès, N. Y. W. Tang, F. Lapointe, J. Cabana, M. A. Nadon, N. Cottenye, F. Raymond, T. Szkopek and R. Martel, Nat. Photonics, 2014, 8(1), 72–78.
27. M. Chorro, G. Kané, L. Alvarez, J. Cambedouzou, E. Paineau, A. Rossberg, M. Kociak, R. Aznar, S. Pascarelli, P. Launois and J. L. Bantignies, Carbon, 2013, 52, 100–108.
28. Y. Almadori, G. Delport, R. Chambard, L. Orcin-Chaix, A. C. Selvati, N. Izard, A. Belhboub, R. Aznar, B. Jousselme, S. Campidelli, P. Hermet, R. Le Parc, T. Saito, Y. Sato, K. Suenaga, P. Puech, J. S. Lauret, G. Cassabois, J. L. Bantignies and L. Alvarez, Carbon, 2019, 149, 772–780.
29. T. Koyama, K. Fujiki, Y. Nagasawa, S. Okada, K. Asaka, Y. Saito and H. Kishida, J. Phys. Chem. C, 2018, 122, 5805–5812.
30. E. Gaufrès, N. Y. W. Tang, A. Favron, C. Allard, F. Lapointe, V. Jourdain, S. Tahir, C.-N. Brosseau, R. Leonelli and R. Martel, ACS Nano, 2016, 10, 10220–10226.
31. H. Li, G. Gordeev, O. Garrity, N. A. Peyyety, P. B. Selvasundaram, S. Dehm, R. Krupke, S. Cambré, W. Wenseleers, S. Reich, M. Zheng, J. A. Fagan and B. S. Flavel, ACS Nano, 2020, 14, 948–963.
32. H. Li, G. Gordeev, D. Toroz, D. Di Tommaso, S. Reich and B. S. Flavel, J. Phys. Chem. C, 2021, 125, 7476–7487.
33. J. A. Fagan, Nanoscale Adv., 2019, 1, 3307–3324.
34. A. Castan, S. Forel, F. Fossard, J. Defillet, A. Ghedjatti, D. Levshov, W. Wenseleers, S. Cambré and A. Loiseau, Carbon, 2021, 171, 968–979.
35. F. Würthner, T. E. Kaiser and C. R. Saha-Möller, Angew. Chem., Int. Ed., 2011, 50, 3376–3410.
36. S. Cambré, W. Wenseleers and E. Goovaerts, J. Phys. Chem. C, 2009, 113, 13505–13514.
37. D. Peceli, H. Hu, D. A. Fishman, S. Webster, O. V. Przhonska, V. V. Kurdyukov, Y. L. Slominsky, A. I. Tolmachev, A. D. Kachkovski, A. O. Gerasov, A. E. Masunov, D. J. Hagan and E. W. Van Stryland, J. Phys. Chem. A, 2013, 117, 2333–2346.
38. S. Webster, D. Peceli, H. Hu, L. A. Padilha, O. V. Przhonska, A. E. Masunov, A. O. Gerasov, A. D. Kachkovski, Y. L. Slominsky, A. I. Tolmachev, V. V. Kurdyukov, O. O. Viniychuk, E. Barrasso, R. Lepkowicz, D. J. Hagan and E. W. Van Stryland, J. Phys. Chem. Lett., 2010, 1, 2354–2360.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr01630c

---