Tailoring magnetic anisotropy by graphene-induced selective skyhook effect on 4f-metals

Abstract

From macroscopic heavy-duty permanent magnets to nanodevices, the precise control of the magnetic properties in rare-earth metals is crucial for many applications used in our daily life. Therefore, a detailed understanding and manipulation of the 4f-metals’ magnetic properties are key to further boosting the functionalization and efficiency of future applications. We present a proof-of-concept approach consisting of a dysprosium-iridium surface alloy in which graphene adsorption allows us to tailor its magnetic properties. By adsorbing graphene onto a long-range ordered two-dimensional dysprosium-iridium surface alloy, the magnetic 4f-metal atoms are selectively lifted from the surface alloy. This selective skyhook effect introduces a giant magnetic anisotropy in dysprosium atoms as a result of manipulating its geometrical structure within the surface alloy. Introducing and proving this concept by our combined theoretical and experimental approach provides an easy and unambiguous understanding of its underlying mechanism. Our study sets the ground for an alternative path on how to modify the crystal field around 4f-atoms and therefore their magnetic anisotropies.

---

Introduction

Nowadays a large variety of devices exploit magnetic anisotropy as their fundamental operating principle. Due to their strong spin–orbit coupling, which can lead to high magnetic anisotropies within a specific environment, 4f-metals are indispensable in hard ferromagnets for heavy-duty applications (e.g. permanent magnets for generators and electric motors), where their anisotropy assures a high remanence.^1,2 4f-metals are also the most promising candidates to be used in future nanosized and therefore energy-efficient magnetic-based devices e.g. in spintronic applications^3–6 and as data storage.^7–11 Giant magnetic anisotropies have been realized by introducing single-molecule magnets and single-atom magnets containing 4f-electrons.^6–11

In single-molecule magnets, the local environment defines the magnetic anisotropy of a central atom, which can lead to a magnetic bistability of the metal atom. While constantly optimizing these systems, hysteresis at temperatures up to 80 K have been reported for dysprosium-based single-molecule magnets.^7,8 Going one step further to increase the possible bit density of data storage devices, single-atom magnet arrays use the symmetry of the substrate and the resulting magnetic anisotropy of the single 4f-atoms.⁹ Another approach to manipulate magnetic anisotropy is incorporating atoms in a surface-molecular network,^12,13e.g. manipulating the properties of dysprosium atoms by oxygen coordination.¹³

Dysprosium in general is hereby an interesting candidate^6,10 which is also used in example systems when it comes to the exploration of the limits of current ab initio models.¹¹

It is obvious that the ability to tailor the magnetic anisotropy relies on understanding its origin that further helps in developing and controlling specific mechanisms used to manipulate the crystal fields around the 4f-electrons.

In this study, we demonstrate that graphene (Gr) induces a selective skyhook effect on the 4f-metal dysprosium (Dy) that in turn leads to a giant increase of its magnetic anisotropy. In general, the skyhook effect describes the weakening of the binding of a surface atom to the surface and therefore changing its physical properties by the absorption of an atom or a molecule.¹⁴

On magnetic surfaces, the skyhook effect has yet only been theoretically predicted when molecular systems containing π-electrons adsorb onto 3d-metal surfaces.¹⁵ It exploits the interaction between π-electrons and d-metal states which provides a unique engine to change and manipulate the magnetic properties at the hybrid interface formed between the π-conjugated systems and 3d-metals.^16,17

We propose a new type of magnetic skyhook mechanism, which enables us to tailor the magnetic anisotropy of Dy atoms by bringing them in contact with a Gr layer: the selective skyhook effect, i.e. lifting exclusively Dy atoms of a 4f-metal iridium (Ir) surface alloy. The surface alloy formation of Dy on Ir provides a stable in-plane superstructure that allows us to directly investigate the effect of Gr adsorption on magnetic properties. By combining our experimental and theoretical approaches, we can reveal the exact role of Gr: the C–Dy chemical interaction induces a selective skyhook effect that strongly modifies the magnetic properties of this specific system, a result that can be certainly generalized to a wide range of 4f-Gr based materials.

Results and discussion

Synthesis and structure determination

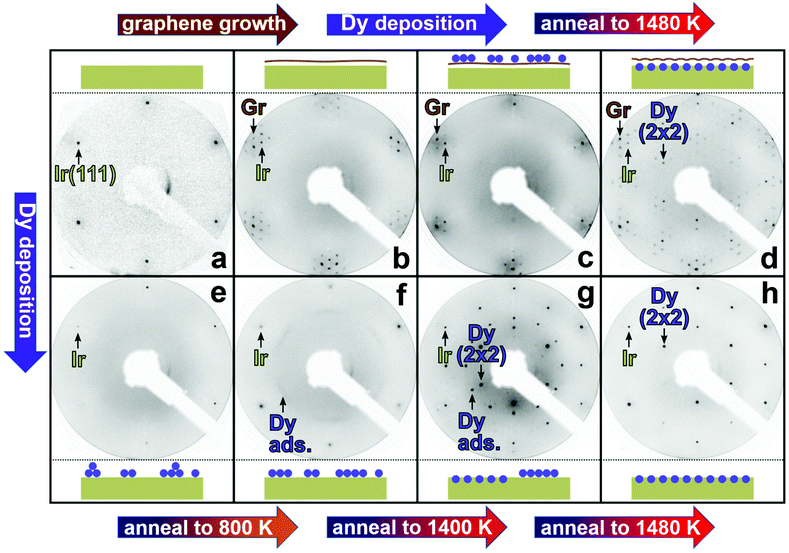
Fig. 1 depicts two different synthesis paths for a Dy(2 × 2)/Ir(111) surface alloy: the Gr-covered surface alloy path follows Fig. 1a–d, whereas the one without Gr starts from Fig. 1a, followed by the steps presented in Fig. 1e–h.

Fig. 1 LEED series of the synthesis of the (2 × 2) Dy surface alloy and graphene-covered (2 × 2) Dy surface alloy. (a–h) Inverted contrast LEED patterns at 100 eV primary electron energy after the synthesis steps of the (2 × 2) Dy surface alloy with (a–d) and without Gr (a and e–h). The arrows indicate the associated LEED spots. Schematic illustrations of the samples are presented next to the LEED patterns. The Ir(111) crystal is depicted in olive, Gr in brown, and Dy atoms in purple. (a) LEED pattern of clean Ir(111); (b) after Gr growth; (c) after the Dy deposition of 0.25 ML_Ir at 300 K; (d) after sample annealing to 1480 K. (e) LEED pattern after the Dy deposition of 0.25 ML_Ir at 300 K on the clean Ir(111); (f) after annealing to 800 K, the arrow highlights ring-segment shaped diffraction intensity of Dy adsorption layer; (g) after annealing to 1400 K; (h) after annealing to 1480 K.

The starting point for both synthesis paths is a clean Ir(111). In Fig. 1a, the low-energy electron diffraction (LEED) pattern of the sample at 100 eV is shown. The first-order reflexes of the Ir(111) are clearly visible.

To synthesize the Dy surface alloy on Ir(111), 0.25 monolayers Dy with respect to the Ir(111) surface density (ML_Ir) are deposited on clean Ir(111). Disordered adsorption causes an enhanced diffuse background and a reduced intensity of the Ir first order spots, as shown in Fig. 1e. By annealing to 800 K ordering of the adsorbed Dy is initiated, indicated by the weak diffraction ring with enhanced intensity along the directions of the first order Ir spots shown in Fig. 1f. Upon further annealing to 1400 K, a complex structure and well-ordered LEED pattern arise, as shown in Fig. 1g. Two phases coexist: an intermediate adsorbate phase giving rise to 12 spots with an angular separation of 30° and in a distance from the (0,0) spot, together with diffraction spots of a (2 × 2) pattern that we attribute to the Dy surface alloy formation. Upon annealing to 1480 K, the Dy adsorbate phase disappears and only sharp (2 × 2) surface alloy spots are left as depicted in Fig. 1h. Direct annealing to 1480 K results in a LEED pattern indistinguishable from Fig. 1h, i.e. the intermediate annealing steps do not affect the final result.

To obtain a Gr-covered surface alloy of high quality, it is necessary to grow a closed Gr layer as a first step. As depicted in Fig. 1b, the sharp Gr, Ir, and moiré spots indicate the order and exceptional quality of Gr/Ir(111). After Dy deposition of 0.25 ML_Ir onto the Gr layer at room temperature, most moiré spots vanish indicating its less regular corrugation, as visible in Fig. 1c. Upon annealing to 1480 K, the Dy penetrates through the Gr layer – we speculate via nanoscale cracks at wrinkles as proposed for Eu penetration through Gr on Ir(111)¹⁸ – and readily forms the (2 × 2) surface alloy underneath the Gr sheet and the moiré recovers. In turn sharp (2 × 2) spots of the Dy–Ir surface alloy, Gr, and Ir first order spots are visible in Fig. 1d. In addition, moiré satellites surround all main reflections. For annealing temperatures below 1480 K disordered and two phase structures form, of which the structural investigation is beyond the scope of the present manuscript. We also note that in principle one could form the Dy/Ir(111) alloy first and due to its high thermal stability, overgrow it subsequently with Gr. However, because of strong interaction of Dy with C the quality of the resulting Gr layer is inferior.

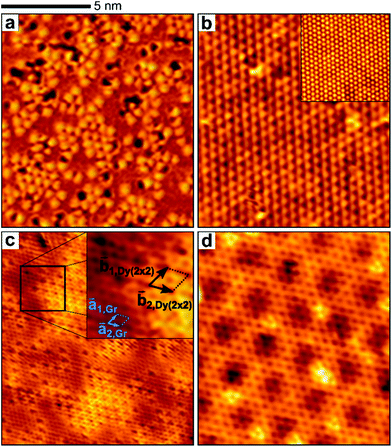
Fig. 2 provides for each system scanning-tunnelling microscopy (STM) topographs for small (Fig. 2a and c) and saturation Dy coverage of 0.25 ML_Ir (Fig. 2b and d).

Fig. 2 Focus on Synthesis – STM topographs of the Dy (2 × 2) surface alloy and the graphene-covered Dy (2 × 2) surface. (a) STM topograph of (2 × 2) Dy surface alloy patches. (b) STM topograph of a complete (2 × 2) Dy surface alloy. Inset: atomic resolution STM topograph of clean Ir(111). (c) Atomic resolution STM topograph of (2 × 2) Dy surface alloy patches under Gr. Primitive cells of Gr and the surface alloy are indicated in the zoom-in. (d) STM topograph of a complete (2 × 2) Dy surface alloy under the Gr cover. (Topograph sizes are 10.8 nm × 12 nm, inset is 5 nm × 5 nm, zoom-in is 2.5 nm × 2.5 nm).

The deposited Dy on bare Ir(111) forms islands of (2 × 2) superstructure wherein the Dy atoms are imaged as bright protrusions (Fig. 2a), separated by flat areas corresponding to bare Ir(111).

The corrugation in the (2 × 2) alloy patches is around 0.5 Å, whereas adsorbed Dy has an apparent height of 2.8 Å (compare ESI. Fig. 1†). Also, dark defects are visible, possibly due to missing surface atoms or imperfections in the alloy, which may be stabilized by stress due to alloy formation.

When the deposited Dy coverage matches the saturation value needed for a (2 × 2) formation as in Fig. 2b, the surface alloy is rather perfect. The STM topograph shows the superstructure, whereas the inset presents the atomic resolution of a clean Ir(111) surface, which cannot be resolved in the presence of the surface alloy.

Fig. 2c displays islands of the surface alloy under the Gr cover. The Gr lattice is visible throughout, while the pronounced dark spots, incommensurate with the Gr periodicity, indicate the position of Dy atoms in the (2 × 2) surface alloy islands. Note that Dy forms a (2 × 2) structure with respect to Ir(111), not with respect to Gr. The clear visibility of the Dy atoms in the Ir surface layer through the Gr cover indicates a strong interaction between Gr and Dy. The areas of the larger alloy islands display an increased overall brightness, which may indicate a reduced work function that could result from Gr doping. For a full (2 × 2) pattern, as depicted in Fig. 2d, additionally to the dark spots at the Dy atom locations, the moiré of Gr with its substrate is visible.

Ab initio calculations

In order to understand better the details of alloy formation, we performed density functional theory (DFT) simulations. For Ir(111), embedding a (2 × 2) structure of Dy atoms within the first surface layer is energetically preferred by −2.702 eV per atom as compared to the case when Dy atoms adsorb on Ir(111). The same energetic preference of the alloy holds with Gr cover. Then the alloy is still preferred by −1.889 eV/atom. Therefore, we conclude that the formation of the surface Ir alloy with a Dy atom within a (2 × 2) surface layer unit cell is energetically favourable with and without Gr cover.

Fig. 3 displays the relaxed geometries of Dy embedded within the Ir(111) surface layer without (Fig. 3a and b) and with lattice-matched Gr (Fig. 3d and e). To cover the different relative positions of the Gr due to the incommensurate lattices, we performed calculations for several configurations (comp. ESI Fig. 4†), which all show qualitatively the same results. A significant effect of the Gr cover is to lift the Dy atoms away from the surface.

Fig. 3 DFT calculation – Structure and charge density difference. (a, b, d and e) Top and side views of the ground state geometries for Dy atoms embedded within a (2 × 2) in-plane unit cell of the first surface layer of the Ir substrate (a and b) and Gr adsorbed onto the surface alloy (d and e). The calculated in-plane (2 × 2) unit cell is indicated by the black lines. With respect to the first Ir layer, the Dy atom sits 0.667 Å above the clean surface alloy, by adsorbing Gr onto the substrate the Dy atom is lifted 0.826 Å above the surface. The arrow indicates the lifting. Gr is 3.448 Å away from the Ir substrate and 2.622 Å above Dy embedded into the Ir(111) surface. (c and f) Charge density difference cuts plotted through the [1−10] direction in the absence (c) and presence of Gr (f). The colour scale bar indicates a charge depletion from −0.008 e Å⁻¹ in blue to a charge accumulation of 0.008 e Å⁻¹ in red.

The increased distance between Dy atoms and Ir substrate is similar to the skyhook effect induced by molecules.¹⁵ For our specific Gr/Dy/Ir(111) system, the Gr–Dy distance indicates an attractive chemical interaction while as discussed in¹⁹ the Gr–Ir(111) one is repulsive. As a consequence, the physisorbed Gr is located high above the Ir substrate and the Dy atoms are lifted by 0.16 Å due to C-Dy chemical interaction.

This effect is also shown in the charge density difference cuts plotted through the [1−10] direction in Fig. 3c and f. These are calculated as the difference between the total charge density of the combined system and the sum of the isolated parts and help us to visualize in which regions of the space the charge density is accumulated or depleted after the binding takes place. As seen in Fig. 3c and f upon binding for both clean and graphene-covered Dy/Ir(111) systems, the charge density is depleted at the interface between Dy and the Ir substrate and accumulated above the Dy atom. The presence of Gr above the Dy/Ir(111) substrates leads to a charge accumulation at the interface between Dy and C atoms that extends further away from the Ir substrate as compared to the system without Gr.

The in-plane or out-of-plane charge density gradients created at the interfaces can have a drastic effect on the direction of the magnetization in systems with large spin–orbit coupling. More precisely, as demonstrated in ref. 20 the spin–orbit splitting and the spin direction of the surface Rashba spin-split states can be manipulated by creating in-plane or out-of-plane charge density gradients. In our specific case, the enhanced out-of-plane charge density gradient created by Gr at the interface could induce a larger in-plane component of the magnetic anisotropy. Therefore, the charge redistributions around the Dy atoms also suggest that their magnetic properties could be altered through a Gr cover as we will demonstrate below.

For the embedded Dy/Ir(111) system we find that at the Dy site new hybrid electronic states are formed below and above the Fermi level in both spin-channels. Some of these states have a large 4f- and small 5d-character, while other electronic states contain significant 5d- and minor 4f-contributions. Interestingly, by adsorbing Gr onto the Dy/Ir(111) substrate, these hybrid electronic states are combinations not only of the Dy 5d- and 4f-states but also of carbon π-like orbitals originating from p_z-atomic like orbitals of carbon atoms, i.e. some hybrid states have a large 4f- and small 5d- and π-contribution while other hybrid states have a larger π- and smaller 5d- and 4f-character (comp. ESI Fig. 5†). It is important to note that Gr becomes n-doped since upon binding with the Dy the charge density is accumulated into the π-like orbitals at the Gr site.

Furthermore, the projection of the total charge density onto a sphere around the Dy atom onto the s, p, d, and f atomic-like orbitals leads to the following number of electrons: 0.26 in s, 1.03 in d, and 9.26 in f for embedded Dy/Ir(111) system and 0.24 in s, 1.01 in d, and 9.24 in f for Gr covered Dy/Ir(111) substrate, respectively.

The metallic electronic states of Ir substrate and the π-orbitals of Gr modify the chemical environment around the Dy atom so that the atomic 5d and 4f states are allowed to mix while this is forbidden for an isolated atom. These atomic-like df-hybrid states have a strong 4f atomic character close to the nucleus and long tails that extend further away from the nucleus since they originate from the Dy 5d atomic-like orbitals. As a consequence of the long spatial extend, these hybrid atomic-like df-orbitals of Dy overlap and hybridize with the electronic states of Ir substrate and Gr π-orbitals.

The graphene-induced selective skyhook effect has a significant impact on the magnetic properties. Our calculations show that for the Gr/Dy/Ir(111) system the magnetic exchange interaction is 9.93 meV per μ_B. This is significantly increased as compared to the one of the clean Dy/Ir(111) systems where magnetic exchange interaction is very small, i.e. it amounts to 0.36 meV per μ_B. Interestingly, the magnetic exchange interaction between the Dy atoms embedded at the interface formed by Gr and the Ir surface has the same order of magnitude as the magnetic anisotropy energy (MAE) present in compounds containing 4f-metals.^2,9 This observation implies that a complex magnetic structure could be formed at the interface between Gr and Dy/Ir(111).

It is important to note here, that the stretching of the Gr to get a matched 1 × 1 unit cell with the substrate may induce errors in the meV range. While this has negligible implications on the structural relaxations and the magnetic exchange interactions, the changes of the MAE are in this range. Performing simulations taking the incommensurability of the two lattices – the (2 × 2) Dy/Ir(111) surface alloy lattice and the Gr lattice – into account would require a much larger commensurate approximation as DFT supercell. At least (20 × 20) Gr unit cells would need to match (9 × 9) unit cells of the (2 × 2) Dy/Ir(111) surface alloy, which would make the problem computationally unfeasible and would require demanding investigations which are the subject of further studies.

Magnetic and structural investigations of the surface alloy

To reveal the magnetic and structural properties of the surface alloy without and with a Gr cover, we performed synchrotron-based X-ray absorption investigations, accompanied by multiplet simulations based on the structural results from the DFT calculations.

X-ray absorption near-edge spectroscopy (XANES) and especially X-ray magnetic circular dichroism (XMCD) allow one to probe the element-specific electronic and magnetic properties of a sample. Investigating the electronic properties by XANES and X-ray linear dichroism (XLD) provides additional information on structural changes. By using the total electron yield method, the measurement is surface sensitive and therefore especially suits our samples. Fig. 4a presents the XANES and XMCD of the Dy M_5,4-edge of the (2 × 2) surface alloy without Gr cover. The XANES provides information about the oxidation state and the local environment, whereas the XMCD indicates the magnetic properties of the Dy atoms. The electronic properties can be extracted by comparing the spectra to calculations, whereas the magnetic information can be directly received by using the sum rules introduced by Carra et al.²¹ It is important to note that XMCD only measures the projected moments along the beam direction. A deeper insight into the sum rules, deviation of Hund's rule by projected moments, and the handling of the T_z-term in this work is provided in the supplement.

Fig. 4 Magnetization and electronic structure – simulation and experimental data. (a and d) Experimental XANES and XMCD of the Dy surface alloy (a) and graphene-covered Dy surface alloy (d) for normal (0°) and grazing (60°) incidence at a temperature of 3 K and a magnetic field of 6.8T. (b and e) Respective calculated multiplet spectra. (c and f) Experimental and calculated magnetization curves of the two samples, normalised to the maximal magnetisation of the graphene-covered Dy surface alloy for grazing incidence.

The spectral shape of the XANES of the surface alloy indicates a 4f occupancy of 4f.^9,22 In addition, the spectra do not deviate for normal and grazing incidence, indicating no electronic anisotropy of the 4f shell. Also, our theoretical multiplet calculation presented in Fig. 4b strongly agrees with the experiment, supporting a Dy 4f occupancy of 4f⁹. This is in strong contrast to the 4f¹⁰ occupancy reported for single Dy atoms on Gr/Ir(111).¹⁰ By using the sum-rules, the effective magnetic moments are measurevad as μ_s = −2.15 ± 0.32μ_B and μ_l = −2.53 ± 0.38μ_B for normal incidence and μ_s = −2.22 ± 0.33μ_B and μ_l = −2.51 ± 0.38μ_B for grazing incidence (μ_s = −2.49μ_B and μ_l = −2.63μ_B, respectively μ_s = −2.37μ_B and μ_l = −2.48μ_B for the multiplet calculation). Deviating from Hund's rule, the effective moments are significantly smaller, which is also described by the multiplet structure of this system, illustrated in more detail below.

Comparing the magnetisation curves of the surface alloy shown in Fig. 4c, a paramagnetic behaviour is seen, as a Brillouin function would perfectly fit the experimental data. The theoretical curves show, besides their slightly higher maximum, a similar behaviour. Also, there is no deviation between the different incidence angles in the error range indicating isotropic behaviour.

The XANES of the graphene-covered surface alloy in Fig. 4d shows also a 4f occupancy of 9 4f-electrons but differs from the one of the surface alloy. The intensity change of the feature at ∼1292.8 eV indicates a strong anisotropy present in the system. The changes of the XANES and XLD will be discussed in detail below, as they are the experimental fingerprint of the lifting of the Dy atoms. The calculated spectra in Fig. 4e describe the experimental one very well. Concerning magnetism, the XMCD spectra reveal a giant magnetic anisotropy which is in line with the anisotropic XANES.²³ While the projected magnetic moment is rather small for normal incidence, the XMCD signal for grazing incidence is even larger than the one for the surface alloy. In numbers, the effective magnetic moments resulting from the sum-rules are μ_s = −0.75 ± 0.11μ_B and μ_l = −0.82 ± 0.12μ_B for normal incidence and μ_s = −2.84 ± 0.43μ_B and μ_l = −3.32 ± 0.50μ_B for grazing incidence (μ_s = −0.93μ_B and μ_l = −0.94μ_B, respectively μ_s = −2.70μ_B and μ_l = −2.84μ_B for the multiplet calculation).

This giant measured anisotropy is also represented in the magnetisation curves displayed in Fig. 4f. Again, paramagnetic-like curves are depicted. Although the DFT shows a drastic increase in the magnetic exchange interaction, an opening of the hysteresis curve is not expected due to the limited resolution of the magnetic field in our experimental spectra. One would expect coercive field in the range of a few mT, as reported for comparable systems²⁴ due to the negligible in-plane anisotropy of this system (compare ESI Fig. 9a and b†). The ferromagnetic coupling could explain the deviation between theory and experiment in the low-field region. The drift to higher values for grazing incidence at higher fields is attributed to the offset of the quantisation axis from the magnetically favoured surface plane caused by experimental limitations. Remarkably, these features are nicely reproduced in our multiplet calculation. A more detailed analysis of this issue is also presented in the supplement.

To understand the origin of how Gr induced a change of the magnetic anisotropy, we use our combined DFT-multiplet approach. Hereby, we use the atomic positions of the DFT calculation to create a crystal field, which is the basis for our multiplet calculations besides the electron–electron interaction and the spin–orbit coupling. Other than the interatomic interactions, the crystal field (CF) is sensitive to different local environments. In Fig. 5a the CF scheme of the surface alloy is presented. The arrows sketch the synchrotron radiation colinear with the magnetic field that defines the quantisation axis. The charges of this point charge modelled CF are taken from our DFT simulations. Similarly, Fig. 5b displays the employed CF scheme for the graphene-covered surface alloy, which takes the graphene-induced skyhook effect into account by the elevated Dy as well as the additional carbon atoms. The manipulation of this elevation also allows us to quantitatively investigate the strength of the selective skyhook as presented below in Fig. 6. Similar to the DFT, different Gr configurations have been tested, leading to qualitative same results.

Fig. 5 Employed crystal field schemes and multiplet level. (a) Representation of point charge crystal field scheme employed in multiplet calculation for the Dy/Ir(111) 2 × 2 surface alloy and (b) the graphene-covered Dy surface alloy. The red spheres represent the Ir atom, the blue sphere the Dy atoms, and the grey spheres the C atoms. The size of the spheres represents the charge assigned to its lattice position. The quantisation axis according to the incoming synchrotron radiation is indicated by the grey (0°) and red (60°) lines. Distances are given in Å. (c) Multiplet level of the surface alloy and (d) graphene-covered surface alloy dependent on the expectation value M_J for normal (grey) and grazing (red) incidence at a magnetic field of 6.8 T.

Fig. 6 Detailed look at the influence of Dy lifting on XANES and XLD spectra. (a) Experimental XANES and XLD spectra of the Dy M₅-edge of graphene-covered (2 × 2) Dy surface alloy at 50 mT for grazing x-ray incidence. Multiplet calculations for elevated and non-elevated Dy atoms, in comparison to the (2 × 2) Dy surface alloy, are displayed next to it. (b) Theoretical XANES and XLD spectra of the structure presented in Fig. 5b and for a variation of the Dy z-component by −0.05 Å, +0.05 Å, and +0.1 Å.

The results of our multiplet calculations shown in Fig. 4 are in very good agreement with the experimental data. The calculated multiplet levels are presented in Fig. 5c and d. The in the comparison with Hund's rule reduced effective (projected) moments can be directly explained by the lowest-lying multiplets. Fig. 5c displays the expectation value of the projected angular momentum along the quantisation axis perpendicular to the surface (0°) and with grazing incidence (60°). Focusing on the lowest-lying multiplet, we see that there is no significant magnetic anisotropy, as also visible in the experiment. Comparing this to the level with the lowest energy in Fig. 5d for the graphene-covered surface alloy, we see a strong deviation between 0° and 60°, which explains the strong in-plane component of the magnetic anisotropy measured in our experiments.

As mentioned above, comparing XANES and XLD measurements with multiplet calculation provides information about electronic properties as well as the local structure surrounding the probed atom. In our case, the change of the local structure, more exact the lifting of the Dy atoms due to the selective skyhook effect is of special interest. To allow a detailed view of the changes, we will focus on the Dy M₅-edge in the following.

While there is a negligible XLD signal for the (2 × 2) Dy surface alloy as well as for normal incidence measurements of the (2 × 2) Dy surface alloy (comp. ESI Fig. 8†), the grazing incidence measurement presented in Fig. 6a displays a clear linear dichroic signal at 50 mT. As we are especially interested in the elevation of the Dy by the Gr–Dy interaction we compare the experimental spectra to two multiplet spectra. The blue and green curves show the multiplet results based on the DFT structural information, which allowed us to reproduce the experimental XANES, XMCD, and magnetisation curves very well (comp. Fig. 4d–f and 5b). For the purple and olive curves, the structure is manipulated by lowering the Dy atom to the position it has in the surface alloy, e.g. it is not lifted by the skyhook effect.

Comparing the XANES, we see a quantitatively better fit with the calculation for elevated Dy, specifically the height of the peak at ∼1292.8 eV is better reproduced. Comparing the XLD, we see a significantly better fit with the calculation for elevated Dy. Without lifting the charge anisotropy of the Dy 4f-shell is negligible at variance with the experiment, while the lifted spectra represent a really good fit with the experimental data.

In order to have a quantitative view on this experimental evidence of the proposed skyhook effect, a number of calculations have been conducted, presented in Fig. 6b. The spectra range from −0.05 Å below to 0.1 Å above the position extracted from the DFT data. While lowering the atom leads to a negligible XLD signal, slightly increasing the elevation leads to an increased XLD signal as well as an increased weight on the feature at ∼1294.6 eV. Lifting the atom even further changes the XANES drastically. Within our model, an elevation of the Dy by ∼ 0.16–0.23 Å compared to the surface alloy is plausible, which is in line with our DFT results.

At last, we would like to emphasize that our manuscript throws a spotlight on how the chemical interaction between Gr and Dy/Ir(111) surface increases (i) on one side the magnetic anisotropy of embedded Dy atoms and (ii) on the other side the magnetic exchange interactions that occur between the 4f-metals embedded within the surface. Qualitatively, this behaviour is similar to one of the hybrid systems formed between a π-conjugated system and a ferromagnetic surface layer that becomes a stronger ferromagnet as compared to the clean metallic substrate.^{15–17,25,26} Our results point out the strong influence of the graphene-induced selective skyhook effect on the magnetic properties of the 4f-metals and to the best of our knowledge, this effect has not been reported yet for materials containing rare-earth atoms.

Methods

Synthesis and structure determination

The synthesis, STM, and LEED measurements were performed in a UHV variable-temperature STM system in Cologne. The samples have been synthesized on Ir(111) single crystals prepared by cycles of sputtering and annealing to 1480 K. The Dy has been deposited on either a well-oriented and perfectly closed Gr monolayer for the graphene-covered surface alloy, which was prepared by the combined temperature-programmed growth and chemical vapour deposition (TPG+CVD) method,²⁷ or directly on the clean Ir surface for the surface alloy. This was followed by annealing to 1480 K. The LEED measurements were performed using a multichannel plate (MCP) LEED. STM measurements have been performed at room temperature using an Ir tip and were digitally post-processed with WSxM.²⁸ The tunnelling parameters of the STM images in Fig. 2 are (a) I = 1.1 nA, U = −1.05 V; (b) I = 0.5 nA, U = −1.68 V, inset I = 50 nA, U = −0.005 V; (c) I = 30 nA, U = −0.09 V; (d) I = 5 nA, U = −0.50 V.

Ab initio calculation

We performed first-principles spin-polarized calculations using the density functional theory (DFT)²⁹ and the projector augmented plane wave method³⁰ as implemented in the VASP code.^31,32 A cut-off energy of 500 eV was used for the plane wave expansion of the Kohn–Sham wave function.³³

The geometry optimization was performed using the vdW-DF2³⁴ with a revised Becke (B86b) exchange^35–37 functional to account for the nonlocal correlation effects like van der Waals interactions. For the structural relaxation, we considered a (2 × 2) Ir(111) in-plane unit cell (Ir lattice constant of 3.873 Å) with one Dy atom, while the Brillouin zone was sampled with a (12 × 12 × 1) k-point mesh. However, the analysis of the electronic structures was done using the PBE exchange–correlation energy functional.³⁸ We used the GGA+U approach³⁹ to correctly account for the orbital dependence of the Coulomb and exchange interactions of the Dy 4f states. We performed several simulations in which we varied systematically the Hubbard parameter (U_eff) from 4 to 9 eV. A Hubbard parameter of U_eff = 7 eV was used. For Gr on the 2 × 2 Dy/Ir(111) surface alloy, we matched the Gr lattice constant to the one of the Ir(111) surface. We also note that the evaluation of the magnetic exchange interactions was done using a large (4 × 4) Ir(111) in-plane unit cell containing four Dy atoms.

X-ray absorption spectroscopy

The X-ray absorption measurements were performed at the X-Treme beamline at the Swiss Light Source (SLS), PSI.⁴⁰ The samples were prepared in situ as described before. The absorption measurements were carried out in total electron yield mode at 2.5–3.0 K. The spectra were acquired with the magnetic field (B = 6.8 T) collinear with the photon beam at normal (θ = 0°) and grazing (θ = 60°) incidence. The XANES corresponds to the average of left- and right-circularly polarized light (σ⁺ + σ⁻)/2, whereas the XMCD corresponds to the difference (σ⁺ − σ⁻). A linear background is subtracted and the spectra are normalized to its integral. The magnetization curves were obtained by measuring the maximum of the XMCD response at given photon energy as a function of the magnetic field normalized to the pre-edge intensity.

Multiplet calculation

The calculated spectra presented in this work are based on the multiX code.⁴¹ multiX includes electron–electron interaction, spin–orbit coupling, magnetic field, and crystal field in a non-perturbative manner. A detailed description of each term is provided in the supplement. The expectation values presented are based on the 16 lowest-lying multiplets. The spectra have been normalised the same way as the experimental spectra and no additional scaling has been applied.

Conclusions

By introducing the Dy–Ir surface alloy and investigating the influence of graphene adsorption we could show theoretically and experimentally that the attractive chemical interaction between carbon atoms of Gr and the Dy atoms of the surface alloy leads to a selective lifting of the 4f-metal within the surface alloy. This specific manipulation of the geometrical structure reshapes the crystal field around the Dy atoms that in turn enhances its spin–orbit coupling and results in an increase of the 4f-metal magnetic anisotropy. Furthermore, our DFT calculations demonstrate that, as compared to the clean Dy/Ir(111) substrate, the Gr–Dy interaction induces a substantial increase in the magnetic exchange interaction between the 4f-metal atoms.

Therefore, the selective skyhook effect mechanism induced by Gr – 4f-metal – substrate chemical interaction enables us to directly address the magnetic properties of 4f-electrons that potentially lead us to take another step towards nano-scaled and energy-efficient spintronic devices.

Author contributions

A. H., S. K., and T. M. contributed the synthesis part; S. T., V. C., and N. A. the ab initio calculations; A. H., S. K., L. K., T. L., J. D., K. O., and H. W. the synchrotron-based measurements; and A. H., D. G., J. D., and B. D. the multiplet calculations. A. H. and N. A. wrote the manuscript and all authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank F. de Groot for the fruitful discussions and T. Hartl for experimental support. We acknowledge financial support by DFG trough the projects WE 2623/17-1, MI 581/23-1, AT 109/5-1, CRC 1238 (project no. 277146847, subprojects C01 and B06) and the Paul Scherrer Institut, Villigen, Switzerland for provision of synchrotron radiation beamtime at beamline X-Treme of the SLS and would like to thank S. Zeugin for assistance. L. K. and T. L. acknowledge partial funding by the DFG through the CRC 1242 (project no. 278162697, subprojects A05 and A07). The authors gratefully acknowledge the computing time granted by the JARA Vergabegremium and provided on the JARA Partition part of the supercomputer JURECA at Forschungszentrum Jülich.

Notes and references

1. K. Skokov and O. Gutfleisch, Heavy rare earth free, free rare earth and rare earth free magnets - Vision and reality, Scr. Mater., 2018, 154, 289–294.
2. J. Coey, Perspective and Prospects for Rare Earth Permanent Magnets, Engineering, 2020, 6, 2.
3. M. Urdampilleta, et al., Supramolecular spin valves, Nat. Mater., 2011, 10, 7.
4. P. Nemec, et al., Antiferromagnetic opto-spintronics, Nat. Phys., 2018, 14, 3.
5. S. Manipatruni, et al., Scalable energy-efficient magnetoelectric spin–orbit logic, Nature, 2019, 565, 7737.
6. A. Singha, Engineering atomic-scale magnetic fields by dysprosium single atom magnets, Nat. Commun., 2021, 12, 1.
7. C. Goodwin, et al., Molecular magnetic hysteresis at 60 kelvin in dysposocenium, Nature, 2017, 548, 7668.
8. F. Guo, et al., Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 6421.
9. F. Donati, et al., Magnetic remanence in single atoms, Science, 2016, 352, 6283.
10. R. Baltic, et al., Superlattice of Single Atom Magnets on Graphene, Nano Lett., 2016, 16, 12.
11. C. Gao, et al., Observation of the asphericity of 4f-electron density and its relation to the magnetic anisotropy axis in single-molecule magnets, Nat. Chem., 2020, 12, 2.
12. C. Hirjibehedin, et al., Large Magnetic Anisotropy of a Surface Molecular Network, Science, 2007, 317, 5842.
13. S. Parreiras, et al., Tuning the Magnetic Anisotropy of Lanthanides on a Metal Substrate by Metal–Organic Coordination, Small, 2021, 17, 35.
14. R. Stumpf, H-enhanced mobility and defect formation at surfaces: H on Be(0001), Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 8.
15. R. Friedrich, et al., Molecular induced skyhook effect for magnetic interlayer softening, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 19.
16. K. Raman, et al., Interface-engineered templates for molecular spin memory devices, Nature, 2013, 493, 7433.
17. J. Brede, et al., Long-range magnetic coupling between nanoscale organic-metal hybrids mediated by a nanoskyrmion lattice, Nat. Nanotechnol., 2014, 9, 12.
18. S. Schumacher, et al., Europium underneath graphene on Ir(111): Intercalation mechanism, magnetism, and band structure, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 23.
19. C. Busse, et al., Graphene on Ir(111): Physisorption with Chemical Modulation, Phys. Rev. Lett., 2011, 107, 3.
20. R. Friedrich, et al., Creating anisotropic spin-split surface states in momentum space by molecular adsorption, Phys. Rev. B, 2017, 96, 8.
21. P. Carra, et al., X-ray circular dichroism and local magnetic fields, Phys. Rev. Lett., 1993, 70, 5.
22. J. Goedkoop, et al., Calculations of magnetic X-ray dichroism in the 3 d absorption spectra of rare-earth compounds, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 4.
23. R. Kappert, et al., Linear-dichroism studies of thin Dy overlayers on Ni(110) and Cu(110) substrates, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4.
24. M. Ormaza, et al., High Temperature Ferromagnetism in a GdAg 2 Monolayer, Nano Lett., 2016, 16, 7.
25. R. Friedrich, et al., Exchange interactions of magnetic surfaces below two-dimensional materials, Phys. Rev. B, 2016, 93, 22.
26. M. Callsen, et al., Magnetic hardening induced by nonmagnetic organic molecules, Phys. Rev. Lett., 2013, 111, 10.
27. R. Van Gastel,  et al., Selecting a single orientation for millimeter sized graphene sheets, Appl. Phys. Lett., 2009, 95, 12.
28. I. Horcas, et al., WSXM: a software for scanning probe microscopy and a tool for nanotechnology, Rev. Sci. Instrum., 2007, 78, 1.
29. P. Hohenberg and W. Kohn, Inhomogeneous Electron Gas, Phys. Rev., 1964, 136, 3B.
30. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 24.
31. G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 1.
32. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16.
33. W. Kohn and L. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, 4A.
34. K. Lee, et al., Higher-accuracy van der Waals density functional, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 8.
35. A. Becke, On the large–gradient behavior of the density functional exchange energy, J. Chem. Phys., 1986, 85, 12.
36. I. Hamada, van der Waals density functional made accurate, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 12.
37. F. Huttmann, et al., Tuning the van der Waals Interaction of Graphene with Molecules via Doping, Phys. Rev. Lett., 2015, 115, 23.
38. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 18.
39. V. Anisimov, F. Aryasetiawan and A. Lichtenstein, First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA + U method, J. Phys.: Condens. Matter, 1997, 9, 4.
40. C. Piamonteze, et al., X-Treme beamline at SLS: X-ray magnetic circular and linear dichroism at high field and low temperature, J. Synchrotron Radiat., 2005, 19, 5.
41. A. Uldry, et al., Systematic computation of crystal-field multiplets for X-ray core spectroscopies, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 12.

---

Footnotes

† Electronic supplementary information (ESI) available: More details on the synthesis, the applied sum rules, and the DFT calculation. In addition, XPS measurements, magnetisation dependence of the XLD measurements, and a short introduction to the multiX code with the exact crystal field parametrisation used. See DOI: https://doi.org/10.1039/d2nr01458k

‡ Corresponding author for DFT calculations.

---