Open Access Article
Open Access ArticleProtein-coated nanoparticles exhibit Lévy flights on a suspended lipid bilayer†
Jean-Baptiste
Fleury
 *a,
Vladimir A.
Baulin
b and
Xavier
Le Guével
*a,
Vladimir A.
Baulin
b and
Xavier
Le Guével
 c
c
aUniversitat des Saarlandes, Experimental Physics and Center for Biophysics, 66123 Saarbruecken, Germany. E-mail: jean-baptiste.fleury@physik.uni-saarland.de
bDepartament Química Física i Inorgànica, Universitat Rovira i Virgili, Marcel.lí Domingo s/n, 43007 Tarragona, Spain
cCancer Targets & Experimental Therapeutics, Institute for Advanced Biosciences (IAB), University of Grenoble Alpes - INSERM U1209 - CNRS UMR 5309-38000 Grenoble, France
First published on 25th August 2022
Abstract
Lateral diffusion of nano-objects on lipid membranes is a crucial process in cell biology. Recent studies indicate that nanoparticle lateral diffusion is affected by the presence of membrane proteins and deviates from Brownian motion. Gold nanoparticles (Au NPs) stabilized by short thiol ligands were dispersed near a free-standing bilayer formed in a 3D microfluidic chip. Using dark-field microscopy, the position of single NPs at the bilayer surface was tracked over time. Numerical analysis of the NP trajectories shows that NP diffusion on the bilayer surface corresponds to Brownian motion. The addition of bovine serum albumin (BSA) protein to the solution led to the formation of a protein corona on the NP surface. We found that protein-coated NPs show anomalous superdiffusion and that the distribution of their relative displacement obeys Lévy flight statistics. This superdiffusive motion is attributed to a drastic reduction in adhesive energies between the NPs and the bilayer in the presence of the protein corona. This hypothesis was confirmed by numerical simulations mimicking the random walk of a single particle near a weakly adhesive surface. These results may be generalized to other classes of nano-objects that experience adsorption–desorption behaviour with a weakly adhesive surface.
1. Introduction
In the context of the development of the next generation of therapeutic nanomaterials, the prediction of nanoparticle (NP) trajectories and their behaviour on the cell surface is considered the Holy Grail.1,2 Determining how engineered NPs would escape or enter cells in a complex cellular environment that can interact on the NP surface is of great importance and would impact their efficacy for drug delivery, antibacterial action, or the ability to hide from the immune system.1,3,4 For instance, gold nanoparticles (Au NPs) are relevant carriers for delivering biomolecules of interest into living cells, as antibacterial agents or as a diagnostic platform5–8 due to their inertness and the ability to tailor their size, shape, surface chemistry and to exploit their unique interaction with light for imaging, sensing and phototherapy purposes.5–9 When NPs approach the surface of a living cell, they can attach to it and move along the cell surface in a complex manner.1 This phenomenon may determine their fate within the cellular environment. Depending on NP motion, they can cluster on the cell surface, be internalized, or return to the host phase.10With recent developments in microscopy techniques, it is now possible to visualize individual NPs and track the diffusion of these NPs at the surface of bilayers.11 The resulting trajectories can occasionally be characterized by a classical two-dimensional random walk,12 but are often reported as anomalous diffusion, where their diffusive behaviour evolves over time.13–18 The physical origins of such anomalous diffusion is still under debate.13–20 The presence of obstacles,21,22 heterogeneous diffusion,23 non permanent binding,24 diffusing diffusivity,25 hopping,26 excluded area fractions20 and compartmentalization19 are commonly considered to be possible origins. All these effects highlight the pivotal role of biomolecules present in the cell membrane (such as transmembrane proteins), as sources of anomalous diffusion. However, in these studies, the possible role of biomolecules present outside the cell is not considered a possible source for such anomalous behaviour. One example of biologically relevant biomolecule that can affect the interaction of NPs with lipid membranes, is the class of water-soluble proteins.27–29 A protein corona is a protein layer that is adsorbed on the NP surface.27 The presence of the protein corona modifies the surface properties of the NPs, which influence the interactions between NPs and cells, such as cellular recognition.30–32
In this work, we investigated the influence of the protein corona on the diffusion of 75 nm and 100 nm Au NPs stabilized by ligands in contact with a large, horizontal free-standing lipid bilayer formed on a 3D microfluidic chip.33 To this end, we observed the motion of individual water-soluble Au NPs near a lipid bilayer using dark-field microscopy.34,35 We, also, studied the motion of NPs coated with a protein corona that is only composed of bovine serum albumin (BSA)36 (see Methods section). We demonstrated that, in the absence of a protein corona, NPs exhibit Brownian motion, while in the presence of a protein corona, NPs exhibit Lévy flight.37 We suppose that these results may be generalized to many other classes of nano-objects that experience adsorption–desorption around a weakly adhesive surface.
2. Results and discussion
2.1. Au NP characterization
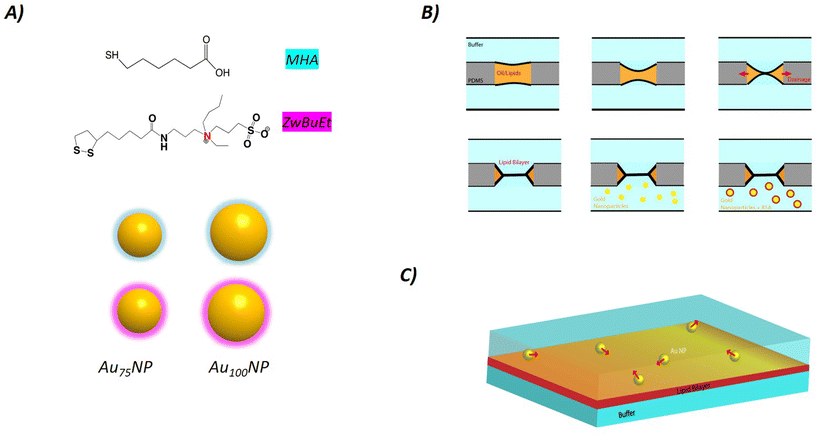
We prepared batches of Au NPs with narrow size distributions (CV < 5%) of 75 nm and 100 nm as confirmed by Transmission Electron Microscopy (TEM) (Fig. S1†). We used a previously described protocol9 to functionalize the Au NP surface with either a short thiolated ligand containing a terminal acid group (MHA) or with a slightly hydrophobic modified-bidentate sulfobetaine zwitterionic (ZwBuEt).38 We determined the hydrodynamic diameter and the surface charge of these four samples: Au75NP-MHA, Au75NP-ZwBuEt, Au100NP-MHA, and Au100NP-ZwBuEt before and after incubation with BSA (Table S1†). We measured a negatively charged surface for Au NPs coated with MHA (ζ ≈ 20 mV) and with ZwBuEt (ζ ≈ 7 mV) which were not strongly influenced by the NP size or after BSA incubation. The hydrodynamic diameter of the 75 nm and 100 nm Au NPs, determined by DLS, increased in the same range between 10 and 30 nm in the presence of BSA independent of the NP core size and the nature of the ligands. This finding is consistent with a previous study that examined a series of Au NPs-citrate of different sizes where a protein corona thickness in the same order for the 80 nm and 100 nm particle size.39 The thickness of the protein corona can be estimated to be a maximum of three layers of protein considering the globular shape of BSA (3 nm × 4 nm × 7 nm). We did not notice any aggregation of the different NPs after BSA incubation over time indicating the good stability of these coated Au NPs.2.2. Adsorption of Au NPs on a free-standing lipid bilayer
To measure the adsorption energy between Au NPs and a free-standing lipid bilayer, Au NPs coated with ligands of different hydrophobicity were used because of their different interactions and adhesion on the lipid bilayer; the MHA ligand is more hydrophobic than the ZwBuEt ligand considering their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P value.9 While both types of NPs present good colloidal stability in aqueous solution, their ligands affect the global surface properties of NPs, thereby affecting NP adsorption, as previously demonstrated.38
P value.9 While both types of NPs present good colloidal stability in aqueous solution, their ligands affect the global surface properties of NPs, thereby affecting NP adsorption, as previously demonstrated.38
A free-standing bilayer was formed as described in the Methods section. Au100NPs, at a low concentration (c ≈ 20 μg ml−1), were dispersed around the bilayer by means of microfluidic pumps according to the schematic (Fig. 1). These Au NPs can be easily detected over time on the bilayer surface by dark-field microscopy.9,34,35 Brownian analysis of the NPs confirmed that the NPs were individual (see Table 1). Thus, the NPs did not aggregate into clusters and moved freely around the bilayer. Surprisingly, a small fraction of these Au NPs also adhered to the bilayer and were stacked permanently at the surface. They could be easily distinguished from other free NPs, as they were drastically slower than unbound NPs, and could be automatically sorted out using image analysis. Over time, adsorption from the bulk material resulted in an increasing number of surfaces covered by adsorbed NPs. Due to the larger size of the NPs compared to the lipid bilayer thickness (≈5 nm), we can safely assume that these immobile NPs were not inserted into the bilayer core and stayed on the bilayer surface.9,38,40 This analysis provides the NP adsorption rate at the surface of the bilayer.
| Size (nm) | 100 | 100 + BSA | 75 | 75 + BSA |
|---|---|---|---|---|
| D ZwBuEt (μm2 s−1) | 5.6 | 4.8 | 5.5 | 4.4 |
| D MHA (μm2 s−1) | 4.8 | 4.1 | 4.7 | 3.9 |
| ζ ZwBuEt (nm) | — | 16 | — | 25 |
| ζ MHA (nm) | — | 17 | — | 25 |
| ΔG′ZwBuEt (kBT) | — | 0.2–3 | — | 0.2–3 |
| ΔG′MHA (kBT) | — | 0.2–3 | — | 0.2–3 |
This lipid bilayer corresponds to a potential well that holds the particles, and that they have to cross otherwise they are irreversibly trapped. Indeed, we did not observe any spontaneous desorption of these NPs after they were irreversibly adsorbed. Thus, this process corresponds to irreversible adsorption with only a one way adsorption constant taken into account. The energy barrier of this irreversible adsorption can be estimated through the Arrhenius expression:41,42
 | (1) |
When the NPs are coated with BSA, there is no irreversible NP adsorption on the bilayer surface (Fig. 2B). This is a regime of reversible adhesion, where the NPs are touching and leaving the bilayer reversibly. In this regime, the NPs are also in the presence of an energy barrier that is provided by the adsorption–desorption rates. The adsorption rate kads and desorption rate kdes are connected as follows  with ΔG′ is the adsorption–desorption energy barrier.41 Thus, using experimental movies, it is possible to evaluate the range of the adsorption–desorption barrier of 0.2–3 kBT for 100 nm coated with BSA (for both ligands). This value of adsorption–desorption energy barrier is used later in our Langevin simulations.
with ΔG′ is the adsorption–desorption energy barrier.41 Thus, using experimental movies, it is possible to evaluate the range of the adsorption–desorption barrier of 0.2–3 kBT for 100 nm coated with BSA (for both ligands). This value of adsorption–desorption energy barrier is used later in our Langevin simulations.
2.3. Diffusion of Au NPs at the bilayer surface with and without BSA
First, we dispersed Au NPs around a formed free-standing lipid bilayer. The motion of these Au NPs at the surface of the bilayer was recorded for two Au NP sizes (100 nm, 75 nm) and with the two coatings (MHA, ZwBuEt). Notably, Au NP trajectories cannot be recorded for times longer than few minutes. It is very likely that at longer times Au NPs either detach from the bilayer and return to the bulk, or simply stick to the bilayer. As described in the previous section, if some NPs may become quasi-immobile. If so they were not more considered and were sorted out numerically by their speed. Thus, the corresponding Au NP trajectories and mean square displacements (Fig. 2A), were automatically extracted43 using numerical methods (see Methods section).44We can approximate the studied Au NP motion on a bilayer surface, as a two-dimensional motion. In 2D, the mean square displacement is represented by:  , where r(0) = r0 is the reference position of particle i as a function of time t. It provides an estimate for the corresponding diffusion constant D of diffusing Au NPs,
, where r(0) = r0 is the reference position of particle i as a function of time t. It provides an estimate for the corresponding diffusion constant D of diffusing Au NPs,
| 〈r2〉 = 4Dt | (2) |
The measured diffusion constants D are summarized in Table 1 for all different types of NP sizes and ligands, used in this study. The extracted random motion presents Brownian diffusion, as the mean square displacement 〈r2〉 is linear with time t (see eqn (2)). However, the diffusion constants were ≈ 1–3 times smaller than the expected values predicted from the Stokes–Einstein equation.45 It is important to note that this discrepancy has not come from cluster formation, since dynamic light scattering (DLS) measurements show that the Au NPs in the bulk are stable individual particles (Table S1†). However, this difference may come from the difficulty of quantifying friction between the bilayer surface and the NPs.46–48 Considering friction for the case of NPs moving at the bilayer surface, the corrected Stokes–Einstein equation can be expressed as:46–48
 | (3) |
We repeated these experiments with the same NPs, but incubated them with BSA to generate a protein corona (see Methods). The statistical analysis of the recorded particle trajectories revealed that the diffusion of the BSA-NPs was anomalous over time. These results were presented in Fig. 3. The mean square displacement 〈r2〉 presented a linear behaviour as a function of t, at a short time (before a few seconds). However at longer times, the mean square displacement 〈r2〉 varied and presented a linear behaviour as a function of t1.2, which is a superdiffusive behaviour (see Fig. 3).45,51 This behaviour was particularly visible for the 75 nm NPs and independent of the nature of the ligands. The difference in the behaviour of BSA-NPs could be explained by the weak adhesive interaction between the BSA-NPs and the lipid bilayer in the presence of the protein corona. In contrast, the stronger adsorption energy between pure NPs and the bilayer may hinder pure NP escape. Thus, this superdiffusion may originate from the corona that shields the attractive bilayer interactions and thus escapes the bilayer surface more easily.51
This particle-hopping hypothesis is similar to a Lévy-flight diffusion model and thus can be tested.52 For this purpose, we extracted the NP relative displacement r(t) (with r0 = 0) frequency for thousand of single NP trajectories (see Fig. 4A). It appeared that this distribution respected a Lévy-stable probability density function defined as
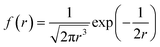 | (4) |
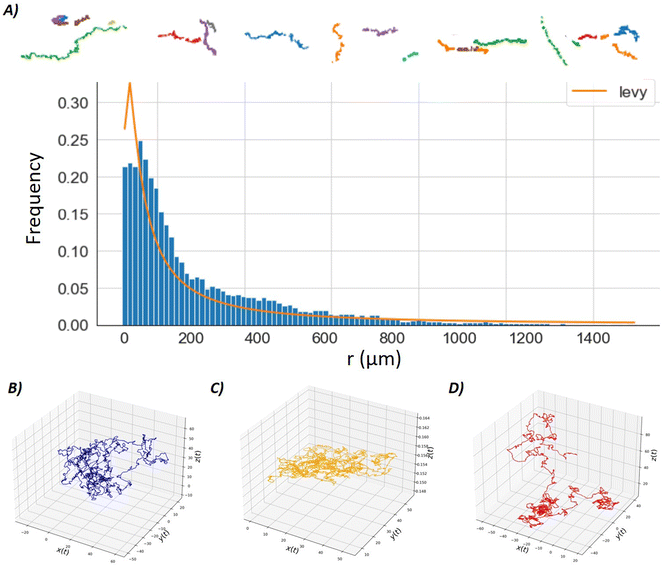 | ||
| Fig. 4 (A) Frequency of several thousand NP relative displacements r(t), centred on their initial position (r(t = 0) = 0) for BSA-coated NP (75 nm, ZwBuEt ligand). This histogram is fitted by a Lévy-stable distribution (see eqn (4)). Above row: A few Levy-flight trajectories are plotted and could be directly compared with Brownian trajectories plotted in Fig. 3B. Lower panel, 3D-trajectories of as single particle calculated from the Langevin equation by numerical simulations (see Methods). (B) A blue particle moves around a solid surface with no adhesive attraction between the surface and the particle (see Methods). The corresponding motion is a standard Brownian motion. (C) An orange particle moves around a solid surface with a strong adhesive attraction between the surface and the particle (see Methods). The corresponding motion is quasi 2D only. (D) A red particle moves around a solid surface with a weak adhesive attraction between the surface and the particle (see Methods). In that case, the particle is hopping along the surface. | ||
Interestingly, the ratio between the diffusion constant of pure NPs and BSA coated NPs is:
 | (5) |
3. Conclusion
In this study, we explored the effects of a BSA coating on the diffusive properties of Au-NPs moving on the surface of a free-standing bilayer by tracking single NPs by dark field microscopy. The diffusive motion of ≈100 nm Au NPs with two different surface chemistry was recorded with and without protein coating. In the absence of proteins, individual Au NPs showed a typical Brownian motion. The extracted diffusion constant of Au NPs near the bilayer surface was slightly lower than the diffusion constant for the particles in the bulk, which might be due to the complex interaction and friction between the bilayer and the NPs. A slight change in the diffusion constant accompanied by a superdiffusive motion for BSA coated Au NPs was observed after a few seconds (Fig. 3), indenpendent of the size and nature of the ligands tested in this study. The origin of this superdiffusive behaviour is attributed to the weak adhesive interaction between BSA-coated Au NP and the bilayer. The trajectory analysis reveals that the BSA-coated NPs follow Lévy-flight distribution, which confirms the nature of a particle-hopping motion (as expected for Lévy flights). This conclusion was also confirmed by performing simulations based on a 3D-Langevin equation in the presence of an adhesive surface.Protein corona strongly affects the adsorption energies between a model cell membrane and Au NPs, which are related to the rates of adsorption and desorption. Lévy flight diffusion can be a manifestation of a vicinity to the critical point of the adsorption–desorption transition for the NPs at the bilayer. Finally, our method provides a new experimental tool to estimate protein layer thickness. The thickness of the protein layer can strongly affect the NP motion on a surface and even induce superdiffusion. However, a limitation of this new experimental method is the limited precision for small NPs. Certain universality of the mechanism behind Lévy-flight diffusion of nanoparticles and modulation of this behaviour with protein corona suggests generalizations to other types of nanoparticles and highlights the role of protein corona in interaction with lipid bilayers near adsorption–desorption transition.
4. Materials and methods
4.1. Molecules and proteins
The buffer is composed of phosphate buffered saline (PBS) at PH 7.4 (Sigma-Aldrich). 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC) and 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine (DOPE) were purchased from Avanti Polar Lipids. Squalene oil is from Sigma Aldrich. The Bovin Serum Albumine (BSA) protein was purchased from Sigma Aldrich. The NPs are incubated ≈30 minutes with BSA, at the concentration indicated in the manuscript, before being injected into the μchip.4.2. Gold nanoparticle fabrication
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 20 min) to remove excess free thiol molecules. Sols were stored in DI H2O at 1 mg Au mL−1. Sulfobetaine presents a crucial advantage over cysteine coatings, as it does not contain any primary amines or carboxylic acids, is chemically inert, highly stable in high salinity or over a wide pH range, can be easily functionalised and displays reduced opsonization in the presence of high serum content.9,38
000 rpm for 20 min) to remove excess free thiol molecules. Sols were stored in DI H2O at 1 mg Au mL−1. Sulfobetaine presents a crucial advantage over cysteine coatings, as it does not contain any primary amines or carboxylic acids, is chemically inert, highly stable in high salinity or over a wide pH range, can be easily functionalised and displays reduced opsonization in the presence of high serum content.9,38
4.3. Gold nanoparticles incubated with bovine serum albumine (BSA)
Au NPs of different sizes (75 nm, 100 nm) and coated with MHA or ZwBuEt ligands were dispersed in an aqueous solution of BSA (50 mg.mL−1) during 1 hour at 37 degrees. Au NPs were then centrifuged twice at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 rpm for 5 min to remove the free BSA and the NPs were resuspended in water before use.
000 rpm for 5 min to remove the free BSA and the NPs were resuspended in water before use.
4.4. Gold nanoparticle characterization
High-resolution transmission electron microscopy (HRTEM) images were measured on a JEOL 2010 LaB6 microscope operating at 200 kV with a 0.19 nm point-to-point resolution after the deposition of the Au NPs on a Formvar carbon grid. The images of at least 100 NPs collected were analyzed with ImageJ software. DLS and zeta potential measurements of the different Au NP samples were performed on a Zetasizer (Malvern). Measurements were performed in triplicate at 25 °C. For water, 1.33 and 0.89 mPa s were taken as the refractive index and viscosity values, respectively.4.5. Horizontal lipid bilayer formation with microfluidics
A 3D microfluidic chip was obtained from the fabrication technique detailed in ref. 9, 33, 35 and 60. Then the chip was obtained by curing PDMS (polydimethylsiloxane) at 60 °C for 3 h in an oven, Sylgard 184, purchased from Dow Corning. The solidified PDMS chip is then bonded to a glass substrate after plasma treatment (plasma cleaner from Diener). After connecting the 3D-chip with tubings to homemade computer-controlled microfluidic pumps, the chip was filled with an oil–lipid mixture (with a 2 mg ml−1 lipids concentration). After carefully injecting buffers into the bottom and top microchannels, two liquid fingers were separated by an thin oil film, which was spontaneously drained by the PDMS porous material. As the two water/oil interfaces are covered by a lipid monolayer, they red spontaneously form a free standing lipid bilayer at a contact. Finally, bilayer formation was demonstrated by electrophysiological and optical investigations.9,33,35,43,60 The motion over time of the dispersed Au NPs near the bilayer was monitored by dark-field microscopy (Leica DM2700 microscope). In this article, the lipid composition of the bilayer is DOPC/DOPE (70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 in molar ratio). The measured relative lateral pressure for this bilayer is ≈ 3 mN m−1, the measurement method is detailed in ref. 61. The chip is maintained at constant temperature, under a Teflon chamber, to avoid temperature drift.
30 in molar ratio). The measured relative lateral pressure for this bilayer is ≈ 3 mN m−1, the measurement method is detailed in ref. 61. The chip is maintained at constant temperature, under a Teflon chamber, to avoid temperature drift.
4.6. Image analysis and statistical Analysis
Movies are analysed using Python and Python libraries: the NPs trajectories and MSD are extracted using TrackPy.44 NP relative displacements are extracted using Pandas and automatically fitted with a Lévy-stable distribution using Seaborn and SciPy libraries. To avoid statistical artefacts when measuring the NP relative displacement, we consider only particles that stay inside the region of interest. The distribution for a Lévy stable distribution is the following characteristic function:ϕ(t,α,β,c,μ) = eitμ−|ct|α(1−iβ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sign(t)Φ(α,t)) sign(t)Φ(α,t)) | (6) |
 | (7) |
The corresponding Lévy probability density function is
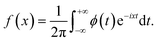 | (8) |
In the case, r ≥ 0, α = 1/2 and β = 1, we obtained the Lévy probability density function employed in this manuscript53
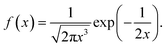 | (9) |
4.7. Simulation of a Brownian particle based on a 3D Langevin equation
The Langevin equation was used to describe the motion of a Brownian particle due to its stochastic nature. The equation is derived directly from Newton's second law (F = ma = mdv(t)/dt), taking into account friction through a random force due to the ambient molecule collisions mdv(t)/dt = −γv(t) + η(t), where m is the mass of a nanoparticle, γ is the friction, v(t) is the nanoparticle velocity, x(t) is the nanoparticle position and η(t) is the noise/stochastic force. These parameters are fixed to m = 1, γ = 1, kB = 1, T = 300. The noise term satisfies the conditions 〈η(t)〉 = 0 and 〈ηi(t)ηi(t)(t′)〉 = Aγδijδ(t – t′), where A is a positive constant, δij is the Kronecker symbol and δ the Dirac Delta function. The attractive adhesion energy of the nanoparticle to the surface is introduced according to ref. 62. Depending on the adhesion strength, the particle motion could be completely free (when this term is zero), totally confined in 2D (strong adhesion, energy barrier above a few kBT) or hopping motion on the surface (weak adhesion, in the range of 0.2–0.5kBT). Example of trajectories are displayed in Fig. 4B–D, other trajectories with velocities are available in ESI.† It shows that the Brownian motion can also be anomalous as in ref. 26. This simulation is performed using MATLAB code described in ESI† of ref. 63 and converted into Python. More details are provide in the ESI.†Author contributions
J.-B. F. designed and performed the experiments and the numerical simulations. V. A. B and J. B.-F. performed the image analysis. X. L. synthesized and characterized the nanoparticles. All the authors discussed the results and wrote the article.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
J.-B. F. acknowledges funding from the SFB1027 (sub project B4) and the Young Investigator Grant 2021 (University of Saarland). VAB acknowledges financial assistance from the Ministerio de Ciencia, Innovación y Universidades of the Spanish Government through research project PID2020-114347RB-C33, financed by MCIN/AEI 10.13039/501100011033. XLG would like to thank Ligue contre le cancer (R21004CC), plan cancer (C18038CS), and ANR SIREN (ANR-20-CE92-0039-01) for their financial support.References
- M. J. Mitchell, M. M. Billingsley, R. M. Haley, M. E. Wechsler, N. A. Peppas and R. Langer, Nat. Rev. Drug Discovery, 2021, 20, 101–124 CrossRef CAS PubMed.
- N. G. Lamson, A. Berger, K. C. Fein and K. A. Whitehead, Nat. Biomed. Eng., 2020, 4, 84–96 CrossRef CAS PubMed.
- Y. Liu, J. Hardie, X. Zhang and V. M. Rotello, Semin. Immunol., 2017, 34, 25–32 CrossRef CAS PubMed.
- T.-O. Peulen and K. J. Wilkinson, Environ. Sci. Technol., 2011, 45, 3367–3373 CrossRef CAS PubMed.
- E. C. Cho, Q. Zhang and Y. Xia, Nat. Nanotechnol., 2011, 6, 385–391 CrossRef CAS PubMed.
- S. E. Skrabalak, J. Chen, Y. Sun, X. Lu, L. Au, C. M. Cobley and Y. Xia, Acc. Chem. Res., 2008, 41, 1587–1595 CrossRef CAS PubMed.
- C. Sun, J. S. H. Lee and M. Zhang, Adv. Drug Delivery Rev., 2008, 60, 1252–1265 CrossRef CAS PubMed.
- Y.-C. Yeh, B. Creran and V. M. Rotello, Nanoscale, 2012, 4, 1871–1880 RSC.
- D. P. Linklater, V. A. Baulin, X. L. Guével, J.-B. Fleury, E. Hanssen, T. H. P. Nguyen, S. Juodkazis, G. Bryant, R. J. Crawford, P. Stoodley and E. P. Ivanova, Adv. Mater., 2020, 32, 2005679 CrossRef PubMed.
- Y. Cao, J. Wang, Q.-Y. Jiang, L. Hu, Y.-J. Yu, Y.-F. Yu and F. Chen, Nanotheranostics, 2020, 4, 201–209 CrossRef PubMed.
- S. Sloan-Dennison and Z. D. Schultz, Chem. Sci., 2018, 10, 1807–1815 RSC.
- G. H. Weiss and R. J. Rubin, Advances in Chemical Physics, John Wiley & Sons, Ltd, 1982, pp. 363–505 Search PubMed.
- V. E. Debets, L. M. C. Janssen and A. Šarić, Soft Matter, 2020, 16, 10628–10639 RSC.
- K. M. Spillane, J. Ortega-Arroyo, G. de Wit, C. Eggeling, H. Ewers, M. I. Wallace and P. Kukura, Nano Lett., 2014, 14, 5390–5397 CrossRef CAS PubMed.
- Y. Yu, Y. Gao and Y. Yu, ACS Nano, 2018, 12, 11871–11880 CrossRef CAS PubMed.
- Y.-H. Liao, C.-H. Lin, C.-Y. Cheng, W. C. Wong, J.-Y. Juo and C.-L. Hsieh, ACS Nano, 2019, 13, 10918–10928 CrossRef CAS PubMed.
- S. Block, V. P. Zhdanov and F. Höök, Nano Lett., 2016, 16, 4382–4390 CrossRef CAS PubMed.
- P. Kukura, H. Ewers, C. Müller, A. Renn, A. Helenius and V. Sandoghdar, Nat. Methods, 2009, 6, 923–927 CrossRef CAS PubMed.
- M. J. Saxton, Biophys. J., 2012, 103, 2411–2422 CrossRef CAS PubMed.
- H. L. E. Coker, M. R. Cheetham, D. R. Kattnig, Y. J. Wang, S. Garcia-Manyes and M. I. Wallace, Biophys. J., 2019, 116, 1085–1094 CrossRef CAS PubMed.
- M. J. Saxton, Biophys. J., 1987, 52, 989–997 CrossRef CAS PubMed.
- H. Berry and H. Chaté, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 022708 CrossRef PubMed.
- C. Manzo, J. A. Torreno-Pina, P. Massignan, G. J. Lapeyre, M. Lewenstein and M. F. Garcia Parajo, Phys. Rev. X, 2015, 5, 011021 Search PubMed.
- A. V. Weigel, B. Simon, M. M. Tamkun and D. Krapf, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6438–6443 CrossRef CAS PubMed.
- M. V. Chubynsky and G. W. Slater, Phys. Rev. Lett., 2014, 113, 098302 CrossRef PubMed.
- B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15160–15164 CrossRef CAS PubMed.
- M. Mahmoudi, I. Lynch, M. R. Ejtehadi, M. P. Monopoli, F. B. Bombelli and S. Laurent, Chem. Rev., 2011, 111, 5610–5637 CrossRef CAS PubMed.
- P. d. Pino, B. Pelaz, Q. Zhang, P. Maffre, G. U. Nienhaus and W. J. Parak, Mater. Horiz., 2014, 1, 301–313 RSC.
- C. Gunawan, M. Lim, C. P. Marquis and R. Amal, J. Mater. Chem. B, 2014, 2, 2060–2083 RSC.
- F. Giulimondi, L. Digiacomo, D. Pozzi, S. Palchetti, E. Vulpis, A. L. Capriotti, R. Z. Chiozzi, A. Laganà, H. Amenitsch, L. Masuelli, G. Peruzzi, M. Mahmoudi, I. Screpanti, A. Zingoni and G. Caracciolo, Nat. Commun., 2019, 10, 3686 CrossRef CAS PubMed.
- P. C. Ke, S. Lin, W. J. Parak, T. P. Davis and F. Caruso, ACS Nano, 2017, 11, 11773–11776 CrossRef CAS PubMed.
- X. l. Guével, F. Palomares, M. J. Torres, M. Blanca, T. D. Fernandez and C. Mayorga, RSC Adv., 2015, 5, 85305–85309 RSC.
- P. Heo, S. Ramakrishnan, J. Coleman, J. E. Rothman, J.-B. Fleury and F. Pincet, Small, 2019, 15, 1900725 CrossRef PubMed.
- M. Hu, C. Novo, A. Funston, H. Wang, H. Staleva, S. Zou, P. Mulvaney, Y. Xia and G. V. Hartland, J. Mater. Chem., 2008, 18, 1949–1960 RSC.
- J.-B. Fleury, M. Werner, X. L. Guével and V. A. Baulin, J. Colloid Interface Sci., 2021, 603, 550–558 CrossRef CAS PubMed.
- R. Wu, H. Peng, J.-J. Zhu, L.-P. Jiang and J. Liu, Front. Chem., 2020, 8, 121 CrossRef CAS PubMed.
- V. Vallaeys, R. C. Tyson, W. D. Lane, E. Deleersnijder and E. Hanert, J. R. Soc., Interface, 2017, 14, 20160889 CrossRef PubMed.
- E. Porret, L. Sancey, A. Martín-Serrano, M. I. Montañez, R. Seeman, A. Yahia-Ammar, H. Okuno, F. Gomez, A. Ariza, N. Hildebrandt, J.-B. Fleury, J.-L. Coll and X. Le Guével, Chem. Mater., 2017, 29, 7497–7506 CrossRef CAS.
- J. Piella, N. G. Bastús and V. Puntes, Bioconjugate Chem., 2017, 28, 88–97 CrossRef CAS PubMed.
- Y. Guo, E. Terazzi, R. Seemann, J. B. Fleury and V. A. Baulin, Sci. Adv., 2016, 2, e1600261 CrossRef PubMed.
- F. Fang, J. Satulovsky and I. Szleifer, Biophys. J., 2005, 89, 1516–1533 CrossRef CAS PubMed.
- P. Hänggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef.
- J.-B. Fleury and V. A. Baulin, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(31), e2104610118 CrossRef CAS PubMed.
- D. Allan, C. van der Wel, N. Keim, T. A. Caswell, D. Wieker, R. Verweij, C. Reid, T. L. Grueter, K. Ramos, A. Zoeith, R. W. Perry, F. Boulogne, P. Sinha, P. N. Bruot, L. Uieda, J. Katins, H. Mary and A. Ahmadia, soft-matter/trackpy: Trackpy v0.4.2, 2019, https://zenodo.org/record/3492186#.YD-bSWhKiUk Search PubMed.
- J. T. Hynes, Annu. Rev. Phys. Chem., 1977, 28, 301–321 CrossRef CAS.
- P. E. Jahl and R. Parthasarathy, Assessing the use of ellipsoidal microparticles for determining lipid membrane viscosity, 2021 Search PubMed.
- S. V. Koniakhin, I. E. Eliseev, I. N. Terterov, A. V. Shvidchenko, E. D. Eidelman and M. V. Dubina, Microfluid. Nanofluid., 2015, 18, 1189–1194 CrossRef CAS.
- G. J. Amador, D. van Dijk, R. Kieffer, M.-E. Aubin-Tam and D. Tam, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2100156118 CrossRef CAS PubMed.
- T. T. Hormel, S. Q. Kurihara, M. K. Brennan, M. C. Wozniak and R. Parthasarathy, Phys. Rev. Lett., 2014, 112, 188101 CrossRef PubMed.
- H. A. Faizi, R. Dimova and P. M. Vlahovska, Viscosity of fluid membranes measured from vesicle deformation, 2021 Search PubMed.
- G. Campagnola, K. Nepal, B. W. Schroder, O. B. Peersen and D. Krapf, Sci. Rep., 2015, 5, 17721 CrossRef CAS PubMed.
- V. V. Palyulin, G. Blackburn, M. A. Lomholt, N. W. Watkins, R. Metzler, R. Klages and A. V. Chechkin, New J. Phys., 2019, 21, 103028 CrossRef CAS.
- Lévy Processes and Stochastic Calculus, ed. D. Applebaum, Cambridge University Press, Cambridge, 2nd edn, 2009, pp. 1–81 Search PubMed.
- E. Bouchaud and M. Daoud, J. Phys. A: Math. Gen., 1987, 20, 1463–1470 CrossRef CAS.
- M. S. Abe, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 24336–24344 CrossRef CAS PubMed.
- M. Nygaard, B. B. Kragelund, E. Papaleo and K. Lindorff-Larsen, Biophys. J., 2017, 113, 550–557 CrossRef CAS PubMed.
- H. Larsericsdotter, S. Oscarsson and J. Buijs, J. Colloid Interface Sci., 2005, 289, 26–35 CrossRef CAS PubMed.
- W. Wang, Z. Huang, Y. Li, W. Wang, J. Shi, F. Fu, Y. Huang, X. Pan and C. Wu, Acta Pharm. Sin. B, 2021, 11, 1030–1046 CrossRef CAS PubMed.
- S. D. Perrault and W. C. W. Chan, J. Am. Chem. Soc., 2009, 131, 17042–17043 CrossRef CAS PubMed.
- S. Puza, S. Caesar, C. Poojari, M. Jung, R. Seemann, J. S. Hub, B. Schrul and J.-B. Fleury, Small, 2022, 2106524 CrossRef CAS PubMed.
- J.-B. Fleury, RSC Adv., 2020, 10, 19686–19692 RSC.
- K. L. Johnson, K. Kendall, A. D. Roberts and D. Tabor, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CAS.
- G. Volpe and G. Volpe, Am. J. Phys., 2013, 81, 224–230 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr01339h |
| This journal is © The Royal Society of Chemistry 2022 |