A theory of skyrmion crystal formation

Abstract

A generic theory about skyrmion crystal (SkX) formation in chiral magnetic thin films and its fascinating thermodynamic behaviours is presented. A chiral magnetic film can have many metastable states with an arbitrary skyrmion density up to a maximal value when the parameter κ, which measures the relative Dzyaloshinskii–Moriya interaction (DMI) strength, is large enough. The lowest energy state of an infinite film is a long zig-zag ramified stripe skyrmion occupying the whole film in the absence of a magnetic field. Under an intermediate field perpendicular to the film, the lowest energy state has a finite skyrmion density. This is why a chiral magnetic film is often in a stripy state at a low field and a SkX only around an optimal field when κ is above a critical value. The lowest energy state is still a stripy helical state no matter with or without a field when κ is below the critical value. The multi-metastable states explain the thermodynamic path dependences of the various metastable states of a film. The decrease of the κ value with the temperature explains why SkXs become metastable at low temperatures in many skyrmion systems. These findings open a new avenue for SkX manipulation and skyrmion-based applications.

---

1. Introduction

Skyrmion crystals (SkXs) have attracted great attention in the past decade because of their academic interest and potential applications^1,2 since they were first unambiguously observed in chiral magnets.^3–6 Skyrmions and SkXs are good platforms for studying various physics^1,7–12 such as the emergent electromagnetic fields and topological Hall effect.^1,8–10 Three types of circular skyrmions in chiral magnets^1,4,13–16 have been identified, namely, Bloch skyrmions, hedgehog skyrmions, and anti-skyrmions. SkXs have been observed in many magnetic materials with the Dzyaloshinskii–Moriya interaction (DMI)^3–6,15,16 or with geometric frustration.^17–19

Although many theories^20–24 predicted SkXs at low or even zero temperatures and in the absence of a magnetic field, it is an experimental fact^25,26 that SkXs form thermodynamically under the assistance of an optimal magnetic field and near the Curie temperature to date. Once formed, however, SkXs can be metastable in very large temperature-field regions. For example, a SkX can exist at zero magnetic field and a field much higher than the optimal value by cooling a SkX first at the optimal field to a low temperature followed by the removal or increase of the magnetic field. SkXs disappear during the zero field warming and high field warming.^1,26,27 SkXs exhibit a thermal equilibrium state only in a narrow magnetic-field range and near the Curie temperature. The phase region for stable SkXs is normally larger in a thinner film^25,28,29 than in a thicker film or a bulk material.^3,26 Outside of the range, SkXs can only be metastable states.^20,21 At zero field and a temperature much lower than the Curie temperature, the thermal equilibrium phase becomes a collection of stripe spin textures known as the helical state.^30,31 Existing theories^20–24 have not provided a satisfactory answer to the field effects and the thermodynamic path dependences of various experimentally observed phases.

The thermal equilibrium state of a system results from the competition between the internal energy and entropy. Entropy dominates the higher temperature phases while the internal energy determines the lower-temperature ones. If one views a long flexible stripe as a long flexible polymer, then stripe entropy, according to the de Gennes theory,³² is proportional to the logarithm of the stripe length: the end–end distribution function of a flexible polymer of N monomers is , where a is the monomer size. In information theory, it is well known that the Gaussian probability distribution with a fixed mean and variance gives the maximal entropy. The polymer entropy is . A previous study,³ under the assumption of infinite long rigid stripes, argued that the translational entropy of helical states is much smaller than SkX entropy which is proportional to the logarithm of the number of sites in one unit cell of the SkX. Obviously, real stripes are flexible as shown in both micromagnetic simulations and experiments and the rigid assumption is incorrect. In reality, translational entropy cannot compete with the entropy of very long stripes in the helical states mentioned. This view is consistent with experimental facts that numerous stripe structures, including ramified stripes and mazes, were observed while few variations of SkX structures are possible.^6,25,33,34 One interesting mystery about low entropy SkXs is their metastability at lower temperatures even when SkXs are in thermal equilibrium states at higher temperatures.¹ This seemingly contradicts the general principle that a higher temperature prefers a higher entropy state. Thus, a proper understanding is needed.

In this paper, the roles of magnetic fields in SkX formation are revealed. We show that a chiral magnetic thin film of a given size with an arbitrary number of skyrmions up to a critical value is metastable when the skyrmion formation energy is negative and skyrmions are stripes that are usually called helical states. The energy and morphology of these metastable states depend on the skyrmion density and the magnetic field perpendicular to the film. At zero field, the energy increases with skyrmion number or skyrmion density. Thus, a film at thermal equilibrium below the Curie temperature and at zero field should be in a helical state consisting of a few stripe skyrmions. At non-zero field, the film with Q_m skyrmions has the lowest energy. Q_m first increases with the field up to an optimal value and then decreases with the field. A parameter called κ that measures the relative DMI strength to the exchange stiffness and magnetic anisotropy plays a crucial role. For κ above a critical value, Q_m near the optimal field is large enough such that the average distance between two neighbouring skyrmions is comparable with the skyrmion stripe width, and skyrmions form a SkX. For κ below the critical value, the system prefers a stripy phase or a mixing phase consisting of stripes and circular skyrmions even at the optimal fields.

2. Model and methodology

We consider a chiral magnetic thin film of thickness d in the xy-plane. The magnetic energy of a spin structure m̂ with an interfacial (itf.) DMI isand the energy with a bulk DMI is,, A, D, K_u, H, M_s, and μ₀ are the unit vector of magnetization, the exchange stiffness constant, the DMI coefficient, the magneto-crystalline anisotropy, the perpendicular magnetic field, the saturation magnetization, the demagnetizing field and the vacuum permeability, respectively. The ferromagnetic state of m_z = 1 is set as zero energy E = 0. For an ultrathin film, the demagnetization effect can be included in the effective anisotropy K = K_u − μ₀M_s²/2. This is a good approximation when the film thickness d is much smaller than the exchange length.³⁵ It is known that isolated circular skyrmions are in a metastable state of energy when κ = π²D²/(16AK) < 1.³⁵

Spin dynamics in a magnetic field is governed by the Landau–Lifshitz–Gilbert (LLG) equation,

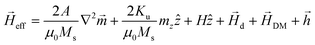where γ and α are, respectively, the gyromagnetic ratio and the Gilbert damping constant. is the effective field including the exchange field, the anisotropy field, the external magnetic field along ẑ, the demagnetizing field, the DMI field , and a temperature-induced random magnetic field of magnitude 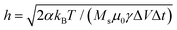, where ΔV, Δt, and T are the cell volume, the time step, and the temperature, respectively.^36,37

In the absence of energy sources such as an electric current or a heat bath, the LLG equation describes a dissipative system whose energy can only decrease.^38,39 Thus, solving the LLG equation is an efficient way to find the stable spin textures of eqn (1) and (2). The typical required time for a sample of 200 nm is about 1 ns that can be estimated as follows. The spin wave speed is over 1000 m s⁻¹, thus two spins 200 nm apart can communicate with each other within a time of 0.2 ns. If two spins can relax after 5 cycles of information-exchange, it gives a relaxation time of 1 ns that is much longer than the individual dynamic time h/(k_BT_c) ≃ 1.6 ps if we use T_c ≃ 30 K.

Solving LLG equation is much faster and more reliable than Monte Carlo simulations and direct optimizations of predefined spin textures.^20–24 Researchers²⁴ have used predefined spin structures to determine whether helical states or SkXs are more stable than the other. Such an approach requires the superb ability of guessing solutions of a complicated nonlinear differential equation in order to obtain correct physics, a formidable task. Very often, this approach ends with an inaccurate trial solution. The inaccuracy can easily be demonstrated by using the trial solution as the input of a simulator such as MuMax3 and seeing how far it ends at a steady state. We do not know of any work that used a reasonably good profile for stripe skyrmions in this approach. This may be why researchers using this approach did not carry out a self-consistent check because it is doomed to fail.

Interestingly and unexpectedly, for a magnetic film described by energy (1) or (2) with 5 parameters, stable/metastable structures are determined by only 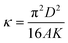and . Let us use the bulk DMI as an example to prove this assertion,

Upon replacing with the dimensionless variable and then relabelling as , the steady spin structures satisfy the equation

A/D is the natural length of the system. Similarly, for the case of interfacial DMI, the equation is

Both equations depend only on and 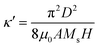. To shed some light on the meaning of these two parameters, we note that the exchange interaction (A), anisotropy (K) and external magnetic field (H) prefer spins aligning along the same direction while DMI (D) prefers spin curling. K and H are two different anisotropy parameters. We can further see the similarity of κ and κ′ by examining the equations for static stripe skyrmions whose profile is m̂ = (cos γ sin Θ, sin γ sin Θ, cos Θ) and γ = 0 for interfacial DMI and γ = π/2 for bulk DMI.^44–46 From eqn (5) and (6), the equation for Θ is with boundary conditions of Θ(x = 0) = 0 and Θ(x = 2L) = 2π, here 2L being the stripe width.⁴⁴ In the absence of a magnetic field, it is known that κ = 1 separates an isolated circular skyrmion from condensed stripe skyrmions.^44,45 We expect then that, in the absence of the anisotropic constant K = 0, κ′ = 4 separates an isolated circular skyrmion from condensed stripe skyrmions. Thus both parameters describe the competition between collinear order and curling (spiral) order. With that being said, the two anisotropies are also fundamentally different. H is obviously unidirectional, i.e. spins parallel and anti-parallel to the field are not the same, in contrast to the bidirectional nature of K. We will also see below how H can make a SkX the lowest energy state while K does not have such an effect.

3. Results and discussion

Several sets of very different model parameters relevant to various bulk chiral magnets are used to illustrate our main findings. These sets are listed in Table 1 as samples A, B, and C. Since DMI in films is mostly interfacial, we replace the bulk DMI by the interfacial DMI in most of our studies. However, the results are essentially the same no matter which DMI is used. The verification of this assertion is given in section 3.7.

Table 1 Three sets of parameters

Sample	A (pJ m^−1)	D (mJ m^−2)	K u (mJ m^−3)	M s (MA m^−1)	H (T)	DMI type	Materials
A	0.4	0.33	0.036	0.15	Variable	Itf. & Bulk	MnSi^40,41
B	0.39	0.0544	0.00103	0.03	0.014	Bulk	Fe0.5Co0.5Si^42
C	5	2	0.063	0.15	0.3	Bulk	Co8Mn8Zn4 ^43

---

Stripe skyrmions exist in all three samples with κ > 1.^44,45 The typical spin precession time is in the order of THz, and the spin relaxation time across the sample is in the order of nano-seconds as demonstrated in both E(t) and Q(t). It should be pointed out that all results reported here are similar although very different sets of parameters are used. These parameters mimic very different materials whose Curie temperature differs by more than 10 times. Periodic boundary conditions are used to eliminate boundary effects and the MuMax3 package³⁷ is employed to numerically solve the LLG equation for films of 200 nm × 200 nm × 8 nm. The static magnetic interactions are fully included in all of our simulations. The mesh size is 1 nm × 1 nm × 1 nm unless otherwise stated. The number of stable states and their structures should not depend on the Gilbert damping constant. We use a large α = 0.25 to speed up our simulations.

3.1. Metastable spin structures and density dependence of the skyrmion morphology

Fig. 1 shows typical stable structures of 10, 50, and 150 skyrmions in a 200 nm × 200 nm × 8 nm film at various perpendicular magnetic fields of μ₀H = 0, 0.1, and 0.4 T for sample A with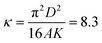 . They are steady-state solutions of the LLG equation at zero temperature with initial configurations of 10, 50, and 150 nucleation domains of m_z = −1 in the background of m_z = 1. Each domain is 5 nm in diameter, and domains are initially arranged in a square lattice. Fig. 1(a1–a3) show zero field structures of 10 (a1), 50 (a2), and 150 (a3) skyrmions characterized by skyrmion number Q defined as , here is the skyrmion charge density. The colour encodes the skyrmion charge distribution. Each small domain of the initial zero skyrmion number becomes a skyrmion of Q = 1 after a few picoseconds. Interestingly, both positive and negative charges appear in a stripe skyrmion while only positive charges exist in a circular skyrmion. Fig. 1(d1–d3) show how total Q (the left y-axis and the red curves) and energy E (the right y-axis and the blue curves) change with time. Q reaches its final stable values within picoseconds while E decreases to its minimal values in nanoseconds. The negative skyrmion formation energy explains well the stripe skyrmion morphology that tries to fill up the whole film in order to lower its energy, in contrast to circular skyrmions for positive formation energy.³⁵ Unexpectedly, the film can host an arbitrary number of skyrmions up to a large value (see Fig. 4 below). At a low skyrmion number of Q = 10, the film is in a helical state consisting of ramified stripe skyrmions of well-defined width of 8.1 nm. The spin profile of stripes is well characterized by width L and wall thickness w. The stripe width depends on material parameters: L = a(κ)A/D, where a = 2π for κ ≫ 1.⁴⁵ The film with Q = 50 is in a helical state consisting of rectangular stripe skyrmions while it is a SkX of triangular lattice with Q = 150 skyrmions. The skyrmion density for Q = 150 is so high that the distance between two neighbouring skyrmions is comparable to the stripe width, and skyrmion–skyrmion repulsion compresses each skyrmion into a circular object. Skyrmions at a high skyrmion density prefer a triangular lattice as shown in Fig. 1(a3) instead of the initial square lattice.

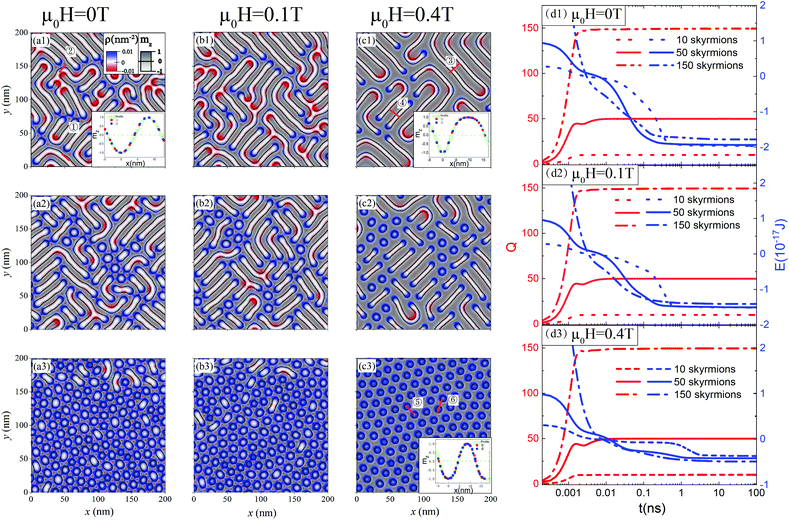Fig. 1 Metastable structures of 10 (a1–c1), 50 (a2–c2) and 150 (a3–c3) skyrmions in a 200 nm × 200 nm × 8 nm film at zero temperature for μ₀H = 0 T (a1–a3), 0.1 T (b1–b3) and 0.4 T (c1–c3), respectively, from MuMax3.³⁷ The insets of (a1), (c1), and (c3) are the spin profiles along the red lines. The enlarged figures and descriptions are shown in Fig. 2. (d1–d3) Q (the left y-axis and the red curves) and E (the right y-axis and the blue curves) of 10 (the dash lines), 50 (the solid lines), and 150 (the dot-dash lines) skyrmions as functions of the time (in the logarithmic scale) for μ₀H = 0 T (d1), 0.1 T (d2) and 0.4 T (d3). The initial configurations are 10, 50 and 150 nucleation domains of zero skyrmion number and of 5 nm in diameter each arranged in a square lattice.

Fig. 1(b1–b3 and c1–c3) show plots of the metastable structures under fields μ₀H = 0.1 T (b1–b3) and μ₀H = 0.4 T (c1–c3) with the same initial states as those in (a1–a3). Stripes of m_z > 0 (the grey regions) parallel to H expand while the white regions of m_z < 0, anti-parallel to H, shrink. This is shown in Fig. 1(b1, b2, c1, and c2). Moreover, the increase and decrease of the amount of white and grey stripes are not symmetric such that the skyrmion–skyrmion repulsion is enhanced by the field, and SkXs tend to occur at lower skyrmion densities. This trend can be clearly seen in Fig. 1(c2) and (c3). Fig. 1(d2) and (d3) show similar behaviour for μ₀H = 0.1 T (d2) and 0.4 T (d3) to their counterparts (d1) at zero field: skyrmion number Q grows to its final values rapidly in picoseconds and E monotonically decreases to its minimum in nanoseconds. Fig. 1 shows unexpectedly that the natural shape of skyrmions is various types of stripes when κ > 1 and at low skyrmion densities, in contrast to the current belief that all skyrmions are circular.

Spin profiles of stripe skyrmions in the presence of a magnetic field are described by^44,45 (m_z < 0) and (m_z > 0), respectively, with |x| ≤ L_i/2. Θ is the polar angle of the magnetization at position x and x = 0 is the center of a stripe where m_z = −1, 1 respectively. L_i and w_i (i = 1, 2) are the width and wall thickness of stripes. The spin profile of skyrmions in a SkX can be well described by along a line connecting the centers of two neighbouring skyrmions, where r labels the points on the line with r = 0 being the center of a chosen skyrmion. R and L are respectively the skyrmion size (the radius of m_z = 0 contour) and the lattice constant. L relates to skyrmion density n of a SkX in a triangular lattice as L ≈ 1.07/√n.⁴⁴Fig. 2(a) shows the excellence of this approximate spin profile for those stripe skyrmions labelled by circled n in Fig. 1(a3–c3) (with model parameters of sample A in Table 1). The y-axis is m_z and x = 0 is the stripe center where m_z = −1. Symbols are numerical data and the solid curve is the fit of for −L₁/2 < x < L₁/2 and for L₁/2 < x < L₁/2 + L₂ with L₁ = L₂ = 8.1 nm and w₁ = w₂ = 2.7 nm. All data from different stripes fall on the same curve and demonstrate that stripes, building blocks of the structures, are identical. Fig. 2(b) shows the nice fit of numerical data of all stripes under a magnetic field of 0.4 T to the approximate spin profile with L₁ = 6.05 nm, L₂ = 12.10 nm, and w₁ = w₂ = 2.63 nm. Fig. 1(c) shows that spins along a line connecting the centers of two neighbouring skyrmions fall on our proposed profile with L = 16.88 nm, and R = 4.35 nm. The spin profile has been used to find the stripe width formula L = f(κ)A/D.⁴⁵ The value of f(κ) is 2π when κ ≫ 1.

Fig. 2 The red and blue points in (a), (b) and (c) are the z-component of magnetization along the red lines in Fig. 1(a1), (c1) and (c3). The green lines are the fit to our approximate profile. The cyan arrows indicate the widths of stripes of m_z < 0 or m_z > 0 and skyrmion diameter.

3.2. Stable/metastable spin structures defined by κ and

We have analytically proved in the previous section that stable/metastable structures are fully determined by κ and κ′ out of five model parameters, and A/D defines the length scale. In other words, the spin structures of the same κ and κ′ are scale invariant. To verify the results, we use samples B and C listed in Table 1 to simulate metastable structures of 10 skyrmions in a film of 600 nm × 600 nm × 1 nm as was done in Fig. 1. Both sample B and sample C have the same κ = 10 and κ′ = 22 although their A and D differ by more than ten times. The stable structures are similar as shown in Fig. 3(a) for sample B and 3(b) for sample C. To further verify that the two structures are scaled by A/D, the spin profiles along the red and blue lines in Fig. 3(a) and (b) are presented in Fig. 3(c). When we scale the x-axis coordinate by A/D for sample B (the red curve and bottom x-axis) and sample C (the blue curve and top x-axis), the two curves are overlapped which verifies our theoretical predictions.

Fig. 3 Metastable structures of 10 skyrmions in a 600 nm × 600 nm × 1 nm film of κ = 10 and κ′ = 22 for samples B (a) and C (b) in Table 1. (c) Spin profiles along the red and blue lines in (a) and (b). The x-axis is scaled by A/D. The red curve and the bottom x-axis are for sample B while the blue curve and the top x-axis are for sample C.

3.3. The role of magnetic field in SkX formation

We compute below the skyrmion-number-dependence of energy at various magnetic fields in order to understand the role of a field in SkX formation. We limit this study to the Q's far below its maximal value of more than 500. The physics around the maximal Q is very interesting by itself, but not our concern here, and it will be investigated in the future. Q nucleation domains of 5 nm in diameter each arranged in a square lattice are used as the initial configuration to generate a stable structure of Q skyrmions with energy E. The left panel of Fig. 4 is the Q-dependence of E from MuMax3 simulations for μ₀H = 0, 0.1, 0.2, 0.3, 0.39, 0.5, 0.6 and 0.7 T denoted by circled 1–7. At zero field, E increases monotonically with skyrmion number Q. States with few skyrmions or low skyrmion densities are preferred. Since long stripe skyrmions have more ways to deform than circular skyrmions, the entropy of a helical phase is larger than that of a SkX (see numerical evidence according to the approach in ref. 47 below). Thus, helical states should always be the thermal equilibrium phase below the Curie temperature, and a SkX can be a metastable state at most. E of helical states at zero field is not very sensitive to Q. Thus the thermal equilibrium helical states can have a different number of irregular skyrmions with many different forms or morphologies. This understanding agrees with experimental facts of rich stripe morphologies.¹ Things are different when a magnetic field is applied. Firstly, E of fixed Q increases with H. Secondly, E is minimal at Q_m for a fixed field below a critical value. Q_m first increases with H up to an optimal field of around μ₀H = 0.3 T in our case and then decreases with H. Above μ₀H = 0.7 T (the brown stars), positive E means that the ferromagnetic state of m_z = 1 has a lower energy of E = 0. Thus, m_z = 1 is the thermal equilibrium state below the Curie temperature when μ₀H > 0.7 T. Q_m, at the optimal field of μ₀H = 0.3 T, can be as large as more than 141 or a skyrmion density more than 3500 μm⁻² at which two nearby skyrmions are in contact. All skyrmions are compressed into circular objects and form a SkX. Strictly speaking, they are not circular, as evident from our simulations. Our results agree qualitatively with experiments.^1,6,25,33,34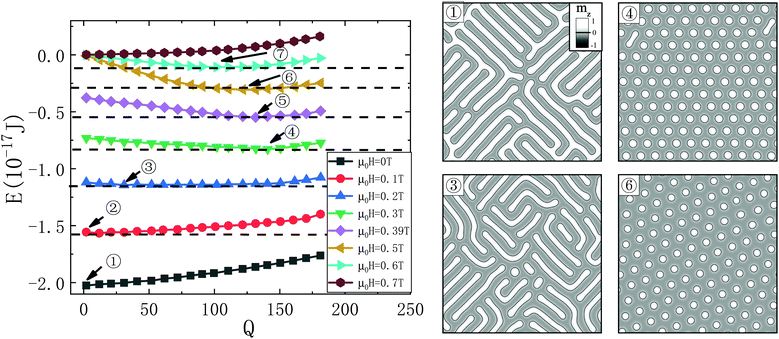

Fig. 4 Skyrmion-number dependence of energy at various magnetic fields of μ₀H = 0 T (the squares and the black curve), 0.1 T (the circles and the red curve), 0.2 T (the up-triangles and the blue curve), 0.3 T (the down-triangles and the green curve), 0.39 T (the diamonds and the violet curve), 0.5 T (left-triangles and the yellow curve), 0.6 T (right-triangles and the cyan curve), and 0.7 T (the stars and the brown curve) (the left panel). The film size is the same as that shown in Fig. 1. Arrows denote the Q_m for μ₀H = 0, 0.1, 0.2, 0.3, 0.39, 0.5 and 0.6 T, respectively. The corresponding structures are shown in the right panel. The structures vary from a highly ramified stripe of Q_m = 1 for μ₀H = 0 T, to the mixture of helical order and SkX of Q_m = 31 for μ₀H = 0.2 T, and to beautiful SkX of Q_m = 141 for μ₀H = 0.3 T. Equally nice SkXs for μ₀H = 0.5, 0.6 T with a smaller Q_m demonstrate the importance of a field in SkX formation.

To substantiate our claim that there is a maximal skyrmion density for a given film, we consider a 200 nm × 200 nm × 8 nm film for sample A. To find the approximate maximal number of skyrmions that can maintain its metastability, we simply add more 2 nm-domains in square lattices in the initial configurations. The system always settles to a metastable state in which the number of skyrmions is the same as the number of initial nucleation domains as long as the number is less than 500. If the number is bigger than 700, the final number of skyrmions in stable states would be less than the initial number of nucleation domains. Occasionally, we obtain metastable states containing about 700 skyrmions in a triangular lattice, corresponding to a skyrmion density of 17 500 μm⁻². Fig. 5 shows a SkX of 567 skyrmions when the initial configuration contains 625 nucleation domains of 2 nm radius each arranged in a square lattice. The details of how the final metastable states depend on the initial number of nucleation domains and their arrangement, as well as the boundary conditions, deserves further studies.

Fig. 5 A SkX of 567 skyrmions when 625 nucleation domains of radius 2 nm each are initially arranged in a square lattice.

3.4. Condensed skyrmion states in various thermodynamic processes

To substantiate our assertion that topology prevents a metastable helical state from transforming into a thermal equilibrium SkX state at μ₀H = 0.3 T and far below the Curie temperature, we study stochastic LLG equation at a finite temperature starting from the structure of Fig. 1(c1) with 10 skyrmions. We run MuMax3³⁷ at 20 K and 29 K, respectively below and near the Curie temperature of T_c = 33 K. Fig. 6(a) and (b) show the structures after 30 ns evolution. Thermal fluctuations at 20 K are not strong enough to either create enough nucleation centers or cut a short stripe into two which are the processes of destroying the conservation of skyrmion number, at least within tens of nanoseconds. The system is still in a helical state with Q = 11 skyrmions after 30 nanoseconds, one more than the initial value (see Movie a in the ESI†). However, at 29 K, a helical state transforms to the thermal equilibrium SkX state with Q = 132 skyrmions through cutting stripes into smaller pieces and creating nucleation centers to generate more skyrmions thermodynamically (see Movie b in the ESI†). For a comparison, we have also started from the SkX shown in Fig. 1(c3) with 150 skyrmions at μ₀H = 0.3 T. The SkX under 29 K becomes another SkX with Q = 136 skyrmions as shown in Fig. 6(c) after 10 ns evolution (see Movie c in the ESI†), 14 less than the starting value. This is expected because the average skyrmion number at the thermal equilibrium state should be smaller than Q_m = 141 according to the energy curve of μ₀H = 0.3 T in Fig. 4.

Fig. 6 (a and b) Structures after 30 ns evolution at μ₀H = 0.3 T, and T = 20 K (a) and 29 K (b), starting from the initial configuration of Fig. 1(c1). (c) Structures after 10 ns evolution at μ₀H = 0.3 T and T = 29 K, starting from the initial configuration of Fig. 1(c3). (d and e) Structures after 30 ns zero field cooing (d) and warming (e), starting from the SkX in Fig. 1(c3). (f) A SkX of 133 skyrmions at μ₀H = 0.3 T and 29 K comes from the thermally generated nucleation centers.

We demonstrate below that a SkX at zero field is not a thermal equilibrium state by showing the disappearance of a SkX in both zero field cooling and warming. Starting from the SkX in Fig. 1(c3) and gradually increasing (decreasing) the temperature from 0 K (30 K) to 30 K (0 K) at a sweep rate of 1 K ns⁻¹ at μ₀H = 0 T (see Movies d and e in the ESI†), the final structures shown in Fig. 6(d) (zero field cooling) and (e) (zero field warming) are helical states consisting of stripe skyrmions. In contrast, field cooling at the optimal field of μ₀H = 0.3 T from 30 K to 0 K at the same sweep rate does not change the nature of the SkX. This is consistent with our assertion that SkXs are the thermal equilibrium states at μ₀H = 0.3 T below the Curie temperature.

The nucleation centers can also be thermally generated near the Curie temperature such that skyrmions can develop from these thermally generated nucleation centers, rather than from artificially created nucleation domains. To substantiate this claim, we carried out a MuMax3 simulation at 29 K under the perpendicular field of μ₀H = 0.3 T, Fig. 6(f) is a snapshot of the spin structure of the thermal equilibrium state for the film with same size and the same model parameters as those shown in Fig. 6(a–e). A SkX with 133 skyrmions is observed. The birth of these skyrmions and how the SkX is formed can be seen from Movie f in the ESI.†

A small energy gain or loss from the transition between two states of different Q's makes such a transformation difficult because of the conservation of skyrmion number under continuous spin structure deformation and entanglements among stripes. This study shows that, similar to liquid drop formation, new skyrmions can be generated only from nucleation centers or by splitting a stripe skyrmion into two. These processes require external energy sources such as a thermal bath and result in topological protection and energy barrier between states of different Q’s. Although the energy of Q = 141 SkX has the lowest energy at μ₀H = 0.3 T at zero temperature (Fig. 4), an initial state with a few stripe skyrmions would not resume its lowest energy state at a low temperature (Fig. 6(a)) within the simulation time. This demonstrates the multi-metastable states of various Q and topological protection to prevent SkXs and helical states from relaxing to the thermal equilibrium phases. People have studied the thermal effects on stripes and SkXs,⁴⁸ but early studies did not reveal the role of κ and magnetic field and cannot come up with a unified picture. The present new understanding can perfectly explain the fascinating appearance and disappearance of SkX and helical states along different thermodynamic paths.^26,27 For example, the disappearance of a SkX in zero field warming and high field warming is because the helical state is the thermal equilibrium phase. At a high enough temperature below the Curie temperature, thermal fluctuations can spontaneously generate enough nucleation centers such that the system can change its skyrmion number and reach its thermal equilibrium phase of either the helical state of low skyrmion density or the SkX state of high skyrmion density.

3.5. κ and SkX formation

All results presented so far are for relatively large κ > 8. It is not clear how the results change with other κ's. It should be emphasized that the results above are based on the assumptions that all model parameters do not change with the temperature. Obviously, this assumption does not apply to real materials. Exchange stiffness A and magnetic anisotropy K depend on the temperature, and behave as a power law of .⁴⁹ For example, it is known that magnetic anisotropy in many materials can change appreciably with the temperature. The magnetic anisotropy of a 1.2 nm CoFeB film could reduce by 50% as the temperature increases from 300 K to 400 K.⁵⁰ More importantly, it is known experimentally^51–54 that SkXs are not stable at low temperatures in almost all systems so far. Thus, a proper explanation of metastability of SkXs at low temperatures and at the optimal magnetic field is required. κ = 1 separates condensed skyrmion states from isolated skyrmions.⁴⁴κ, in general, decreases as the temperature is lowered since both A and K increase as the temperature decreases. Thus, it is interesting to find out how the results in Fig. 7 are modified when κ = 8.3 for sample A becomes not too far from κ = 1 in order to mimic the effect of lowering the temperature far from the Curie temperature. We repeat the same calculations as those in Fig. 4 by changing crystalline magnetic anisotropy in our model from 0.036 MJ m⁻³ to 0.165 MJ m⁻³, 0.131 MJ m⁻³, 0.098 MJ m⁻³, 0.064 MJ m⁻³, and 0.030 MJ m⁻³ without changing other parameters. This corresponds to the change of κ from 8.3 for Fig. 4 to 1.11, 1.42, 2.0, 3.3, and 10. The results are shown in Fig. 7. It is interesting to notice Q_m ≈ 0 when κ = 1.11, 1.42 such that the stripy phase is the thermal equilibrium state (E > 0 means ferromagnetic state more stable). Q_m ≈ 132, 142 and the optimal field is μ₀H = 0.3 T for κ = 3.3, 10, respectively. Q_m ≈ 92 at the optimal field of μ₀H = 0.15 T for κ = 2, and the corresponding spin texture is a mixture of stripe skyrmions and circular skyrmions as shown in the insets of the figure. Our numerical simulations on two very different sets of model parameters suggest that Q_m will not be large enough to support a thermal equilibrium SkX state whenever κ < 1.6.

Fig. 7 Skyrmion-number dependence of energy at various magnetic fields for κ = 1.11 (a), 1.42 (b), 2. (c), 3.33 (d) and 10 (e). Corresponding spin textures at Q_m are shown in the insets. All other model parameters are the same as those for Fig. 2.

We see that Q_m is not large enough to form a SkX even at the optimal field when κ < 1.6. To see that this is in general true, we vary κ by increasing the magneto-crystalline anisotropy for both samples B and C in Table 1 such that κ changes from 10 to 3.33, 2.0, 1.42 and 1.11. The film size of samples B and C is 600 nm × 600 nm × 1 nm. Fig. 8 shows E(Q) for various μ₀H and for κ = 10 (a), 3.33 (b), 2.0 (c), 1.42 (d), 1.11 (e). The red curves are for sample B while the blue ones are for sample C. Clearly, Q_m is small and the helical state has the lowest energy for both sets of parameters differing by more than ten times whenever κ < 1.6.

Fig. 8 E(Q) for sample B (red curves and axes) and sample C (blue curves and axes) for various μ₀H (given by ) and for κ = 10 (a), 3.33 (b), 2. 0 (c), 1.45 (d), and 1.11 (e). A, D and M_s are fixed as given in Table 1. Corresponding spin textures at Q_m are shown in the insets.

In summary, general decreases of κ may explain why SkXs in most systems become metastable at low temperatures. Material parameters vary also with film thickness. This may also explain why the SkX formation and SkX stability are very sensitive to the film thickness. This conjecture needs more detailed studies.

3.6. Entropy difference of SkXs and stripy states at a given temperature

In an isothermal process, the Maxwell relation (∂S/∂H)_T = (∂M/∂T)_H provides a way of calculating the entropy difference at two different fields for a given temperature from the temperature dependence of magnetization,⁴⁷ΔS(T,H_m) measures the entropy change from a stripy state at zero field to a SkX at optimum field H_m when T ≃ T_c. Differing from experiments where the noise is bigger than the signals,⁴⁷ simulations do not suffer from this problem such that one can reliably compute the difference between a SkX entropy and a stripy-state entropy at a fixed temperature. We carried out MuMax3 simulations for M(T,H) of sample A around T = 28 K for various μ₀H ranging from 0 T to 0.3 T. The sample size is 200 nm × 200 nm × 8 nm as before. Fig. 9(a and b) are M(T,H) (a) and (∂M/∂T)_H < 0 (b) for various H. M(T < T_c, 0) ≃ 0 as shown in Fig. 9(a) because of our helimagnet model. This is why (∂M/∂T)_H=0 fluctuates around zero as shown by the red dots in Fig. 9(b) and the one-σ region is bound by two red dash lines. One can confidently conclude that (∂M/∂T)_H < 0 for T > 0.1 T (the yellow dots and curves) at which a stripy state has the lowest energy [see Fig. 4(a)] while one may not be so sure of the sign of (∂M/∂T)_H in experiments. The simulation results clearly support the claim that SkX entropy is smaller than a stripy-phase entropy.

Fig. 9 (a) Temperature dependence of the time-averaged z-component of magnetization M_z at fixed magnetic fields, ranging from 0 mT to 300 mT with a field interval of 25 mT. Every data point is the 2 ns-averaged z-component of magnetization in the thermal equilibrium state at a fixed temperature and a fixed magnetic field. Error bars are the standard deviations of magnetization over the time periods. (b) Solid curves are temperature derivatives of magnetization ∂M_z/∂T at μ₀H = 0, 100, 200, and 300 mT. Dashed curves bound 1-Sigma regions. Inset shows ∂M_z/∂T for all field strengths in (a). (c) Density plot of entropy change ΔS from a stripy state at zero field to a state at a finite field at fixed temperatures in the T–H plane. Clearly, a SkX at T = 28 K and μ₀H = 300 mT has lower entropy than that of a stripy state at T = 28 K and μ₀H = 0 mT.

3.7. Insensitivity of spin structures to DMI-types

There are two types of Dzyaloshinskii–Moriya interaction (DMI), namely interfacial DMI and bulk DMI. We have mainly presented results for the interfacial DMI so far. Although the spin orientations in skyrmion walls depend on the type of DMI, the location of the energy minimum in energy–Q curves for a fixed μ₀H, as well as the thermodynamic properties of the system, is not sensitive to DMI type. When the interfacial DMI is replaced by the bulk DMI for those sets of parameters used above, the results are essentially the same except that the Néel-type stripes (skyrmions) for the interfacial DMI change to Bloch-type stripes (skyrmions).

To substantiate this claim, we used bulk DMI and repeated those simulations shown in Fig. 1, 4, and 6. Fig. 10 shows the metastable structures with 10 (a1–c1), 50 (a2–c2) and 150 (a3–c3) skyrmions under magnetic fields of 0 T (a1–a3), 0.1 T (b1–b3) and 0.4 T (c1–c3). Similar to Fig. 1, the film is in a helical state consisting of ramified stripe skyrmions with a small skyrmion number, and a SkX in a triangular lattice with a large skyrmion number. Q_m is also the same as those in Fig. 4 at various magnetic fields, although the energy curves are slightly different as shown in Fig. 11. To further prove that states with Q_m skyrmions are thermal equilibrium states, Fig. 12(a) and (b) show the spin structures with 11 and 134 skyrmions after 30 ns evolution starting from Fig. 10(c1) at 20 K and 33 K under a magnetic field of 0.3 T. Fig. 12(c) shows the structure with 132 skyrmions after 10 ns evolution starting from Fig. 12(c3) at 33 K under a magnetic field of 0.3 T. Fig. 12(d) and (e) show the spin structures with 12 and 2 skyrmions after 33 ns zero-field warming and zero-field cooling, respectively, starting from 10(c3). The temperature change rates are the same as those in the section 3.4. Fig. 12(f) shows the spin structure with 133 skyrmions after 30 ns evolution starting from the ferromagnetic state at 33 K. Clearly, the formation and disappearance of SkXs are the same as in Fig. 6, the only difference is the skyrmion walls change from a Néel type to a Bloch type.

Fig. 10 Metastable structures of 10 (a1–c1), 50 (a2–c2) and 150 (a3–c3) skyrmions in a 200 nm × 200 nm × 8 nm film with the bulk DMI at zero temperature for μ₀H = 0 T (a1–a3), 0.1 T (b1–b3) and 0.4 T (c1–c3), respectively. (d1–d3) show how Q (the left y-axis and the red curves) and E (the right y-axis and the blue curves) of 10 (the dash lines), 50 (the solid lines), and 150 (the dot-dash lines) skyrmions vary with time (in the logarithmic scale) for μ₀H = 0 T (d1), 0.1 T (d2) and 0.4 T (d3). The insets of (a1), (c1), (c3) show the spin profiles of stripe and circular skyrmions. The initial configurations are 10, 50 and 150 nucleation domains arranged in a square lattice. Initially, each domain is 5 nm in diameter and has zero skyrmion number.

Fig. 11 Skyrmion-number dependence of energy for various magnetic fields of μ₀H = 0 T (the squares and the black curve), 0.1 T (the circles and the red curve), 0.2 T (the up-triangles and the blue curve), 0.3 T (the down-triangles and the green curve), 0.39 T (the diamonds and the violet curve), 0.5 T (the left-triangles and the yellow curve), 0.6 T (the right-triangles and the cyan curve), and 0.7 T (the stars and the brown curve) (the left panel). The film size is the same as that in Fig. 10. Arrows denote the Q_m for μ₀H = 0, 0.1, 0.2, 0.3, 0.39, 0.5 and 0.6 T, respectively. The corresponding structures are shown in the right panel. The structures vary from highly ramified stripes of Q_m = 1 for μ₀H = 0 T, to the mixture of helical order and SkX of Q_m = 31 for μ₀H = 0.2 T, and to a beautiful SkX of Q_m = 141 for μ₀H = 0.3 T. Equally nice SkXs for μ₀H = 0.5, 0.6 T with a smaller Q_m demonstrate the importance of a field in SkX formation.

Fig. 12 (a and b) Structures after 30 ns evolution at μ₀H = 0.3 T, and T = 20 K (a) and 33 K (b), starting from the initial configuration shown in Fig. 10(c1). (c) Structures after 10 ns evolution at μ₀H = 0.3 T and T = 33 K, starting from the initial configuration of Fig. 10(c3). (d and e) Structures after 33 ns zero field warming (d) and cooing (e), starting from the SkX in Fig. 10(c3). (f) A SkX of 133 skyrmions at μ₀H = 0.3 T and 33 K comes from the thermally generated nucleation centers.

4. Conclusion and perspectives

In conclusion, both helical states and SkXs are collections of skyrmions. Stripes, not disks, are the natural shape of skyrmions when their formation energy is negative. The distinct morphologies of helical and SkX states come from the skyrmion density. Skyrmions become circular objects in a triangle lattice due to the compression and strong repulsion among highly packed skyrmions. Unexpectedly, there are an enormous number of metastable states with an arbitrary skyrmion density. These metastable states result in the thermodynamic path dependence of an actual state that a film is in. The energy of these states depends on the skyrmion number and the magnetic field. The role of a magnetic field in SkX formation is to create the lowest energy state being a skyrmion condensate with a high skyrmion density for κ above a critical value. Below the critical value, the lowest energy state is still a collection of condensed stripe skyrmions even at the optimal field. The possible reason for the metastability of SkXs in most chiral magnetic films at low temperatures is due to the increase of the exchange stiffness constant and magnetic anisotropy such that κ is below the critical value at low temperatures. It is shown that our findings are robust to parameter variations as long as κ is given. Whether the chiral magnets have the interfacial DMI or bulk DMI does not change the physics. Of course, the stripes and skyrmions will change from the Néel type to the Bloch type. We have also numerically shown that the SkX entropy is lower than that of a collection of stripes. In order to realize truly stable SkXs at extremely low temperatures, one may use those chiral magnets whose κ is larger than the critical value in the required energy range. Our findings have profound implications in skyrmion-based applications.

Looking forward, several issues require further studies. According to the current findings, the criteria for SkX formation in a chiral magnetic film are κ > 2 and a suitable perpendicular magnetic field. Although all known materials support stable SkXs only in a small pocket in the field-temperature plane near the Curie temperature to date while SkXs are metastable at low temperatures, it should be interesting to search for materials that support stable SkXs at low temperatures and metastable ones near the Curie temperature. In fact, there is no reason why one cannot have a film that supports stable SkXs at all temperatures below the Curie temperature under a suitable field. The physics around the maximal skyrmion density has not been revealed yet in this study. The critical κ is a purely numerical fact based on three sets of very different material parameters. No clear understanding of its value and related physics has been obtained here. In fact, even why a chiral magnetic film prefers a state with a finite skyrmion density in a magnetic field is not clear. It again is a purely numerical observation at the moment. Thus, we are still in the infant stage of the true understanding of SkX formation.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work is supported by the National Key Research and Development Program of China (grant no. 2020YFA0309600), the NSFC (grant no. 11974296), and Hong Kong RGC Grants (no. 16301518, 16301619 and 16302321).

References

1. C. Back, V. Cros, H. Ebert, K. Everschor-Sitte, A. Fert, M. Garst, T. P. Ma, S. Mankovsky, T. L. Monchesky, M. Mostovoy, N. Nagaosa, S. P. ParkinS, C. Pfleiderer, N. Reyren, A. Rosch, Y. Taguchi, Y. Tokura, K. von Bergmann and J. D. Zang, J. Phys. D, 2020, 53(36), 363001.
2. K. Litzius and M. Kläui, Magnetic Skyrmions and Their Applications, ed. G. Finocchio and C. Panagopoulos, Woodhead Publishing, Sawston, 2021, vol. 2, pp. 31–54.
3. S. Mühlbauer, B. Binz, F. Jonietz, C. Pfleiderer, A. Rosch, A. Neubauer, R. Georgii and P. Böni, Science, 2009, 323(5916), 915–919.
4. X. Z. Yu, Y. Onose, N. Kanazawa, J. H. Park, J. H. Han, Y. Matsui, N. Nagaosa and Y. Tokura, Nature, 2010, 465(7300), 901–904.
5. S. Heinze, K. V. Bergmann, M. Menzel, J. Brede, A. Kubetzka, R. Wiesendanger, G. Bihlmayer and S. Blügel, Nat. Phys., 2011, 7(9), 713–718.
6. N. Romming, C. Hanneken, M. Menzel, J. E. Bickel, B. Wolter, K. V. Bergmann, A. Kubetzka and R. Wiesendanger, Science, 2013, 341(6146), 636–639.
7. W. Munzer, A. Neubauer, T. Adams, S. Mühlbauer, C. Franz, F. Jonietz, R. Georgii, P. Böni, B. Pedersen, M. Schmidt, A. Rosch and C. Pfleiderer, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(4), 041203.
8. B. Binz, A. Vishwanath and V. Aji, Phys. Rev. Lett., 2006, 96(20), 207202.
9. M. Lee, W. Kang, Y. Onose and Y. Tokura, Phys. Rev. Lett., 2009, 102(18), 186601.
10. A. Neubauer, C. Pfleiderer, B. Binz, A. Rosch, R. Ritz, P. G. Niklowitz and P. Böni, Phys. Rev. Lett., 2009, 102(18), 186602.
11. H. Y. Yuan, X. S. Wang, M.-H. Yung and X. R. Wang, Phys. Rev. B, 2019, 99(1), 014428.
12. X. Gong, H. Y. Yuan and X. R. Wang, Phys. Rev. B, 2020, 101(6), 064421.
13. A. N. Bogdanov and U. K. Rößler, Phys. Rev. Lett., 2001, 87(3), 037203.
14. U. K. Rößler, A. N. Bogdanov and C. Pfleiderer, Nature, 2006, 442(7104), 797–801.
15. I. Kézsmárki, S. Bordács, P. Milde, E. Neuber, L. M. Eng, J. S. White, H. M. Rønnow, C. D. Dewhurst, M. Mochizuki, K. Yanai, H. Nakamura, D. Ehlers, V. Tsurkan and A. Loidl, Nat. Mater., 2015, 14(11), 1116–1122.
16. A. K. Nayak, V. Kumar, T. Ma, P. Werner, E. Pippel, R. Sahoo, F. Damay, U. K. Rößler, C. Felser and S. S. P. Parkin, Nature, 2017, 548(7669), 561–566.
17. T. Okubo, S. Chung and H. Kawamura, Phys. Rev. Lett., 2012, 108(1), 017206.
18. A. O. Leonov and M. Mostovoy, Nat. Commun., 2015, 6(1), 8275.
19. T. Kurumaji, T. Nakajima, M. Hischberger, A. Kikkawa, Y. Yamasaki, H. Sagayama, H. Nakao, Y. Taguchi, T. Arima and Y. Tokura, Science, 2019, 365(6456), 914–918.
20. A. O. Leonov, Y. Togawa, T. L. Monchesky, A. N. Bogdanov, J. Kishine, Y. Kousaka, M. Miyagawa, T. Koyama, J. Akimitsu, Ts. Koyama, K. Harada, S. Mori, D. McGrouther, R. Lamb, M. Krajnak, S. McVitie, R. L. Stamps and K. Inoue, Phys. Rev. Lett., 2016, 117(8), 087202.
21. F. N. Rybakov, A. B. Borisov, S. Blügel and N. S. Kiselev, New J. Phys., 2016, 18(4), 045002.
22. S. Buhrandt and L. Fritz, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(19), 195137.
23. S. D. Yi, S. Onoda, N. Nagaosa and J. H. Han, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(5), 054416.
24. J. H. Han, J. Zang, Z. Yang, J.-H. Park and N. Nagaosa, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82(9), 094429.
25. X. Z. Yu, N. Kanazawa, Y. Onose, K. Kimoto, W. Z. Zhang, S. Ishiwata, Y. Matsui and Y. Tokura, Nat. Mater., 2011, 10(2), 106–109.
26. K. Karube, J. S. White, D. Morikawa, M. Bartkowiak, A. Kikkawa, Y. Tokunaga, T. Arima, H. M. Rønnow, Y. Tokura and Y. Taguchi, Phys. Rev. Mater., 2017, 1(7), 074405.
27. K. Karube, J. S. White, N. Reynolds, J. L. Gavilano, H. Oike, A. Kikkawa, F. Kagawa, Y. Tokunaga, H. M. Rønnow, Y. Tokura and Y. Taguchi, Nat. Mater., 2016, 15(12), 1237.
28. X. Z. Yu, A. Kikkawa, D. Morikawa, K. Shibata, Y. Tokunaga, Y. Taguchi and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91(5), 054411.
29. M.-G. Han, J. A. Garlow, Y. Kharkov, L. Camacho, R. Rov, J. Sauceda, G. Vats, K. Kisslinger, T. Kato, O. Sushkov, Y. Zhu, C. Ulrich, T. Söhnel and J. Seidel, Sci. Adv., 2020, 6(13), aax2138.
30. S. Rohart and A. Thiaville, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(18), 184422.
31. M. Uchida, Y. Onose, Y. Matsui and Y. Tokura, Science, 2006, 311(5759), 359–361.
32. P.-G. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1st edn, 1979.
33. Z. Wang, M. Guo, H. Zhou, L. Zhao, T. Xu, R. Tomasello, H. Bai, Y. Dong, S. Je, W. Chao, H. Han, S. Lee, K. Lee, Y. Yao, W. Han, C. Song, H. Wu, M. Carpentieri, G. Finocchio, M. Im, S. Lin and W. Jiang, Nat. Electron., 2020, 3(11), 672–679.
34. W. Legrand, D. Maccariello, N. Reyren, K. Garcia, C. Moutafis, C. Moreau-Luchaire, S. Collin, K. Bouzehouane, V. Cros and A. Fert, Nano Lett., 2017, 17(4), 2703–2712.
35. X. S. Wang, H. Y. Yuan and X. R. Wang, Commun. Phys., 2018, 1(1), 31.
36. W. F. Brown, Phys. Rev., 1963, 130(5), 1677.
37. A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. V. Waeyenberge, AIP Adv., 2014, 4(10), 107133.
38. X. R. Wang, P. Yan, J. Lu and C. He, Ann. Phys., 2009, 324(8), 1815.
39. X. R. Wang, P. Yan and J. Lu, Europhys. Lett., 2009, 86(6), 67001.
40. J. Sampaio, V. Cros, S. Rohart, A. Thiaville and A. Fert, Nat. Nanotechnol., 2013, 8(11), 839–844.
41. E. A. Karhu, U. K. Rößler, A. N. Bogdanov, S. Kahwaji, B. J. Kirby, H. Fritzsche, M. D. Robertson, C. F. Majkrzak and T. L. Monchesky, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85(9), 094429.
42. P. Sinha, N. A. Porter and C. H. Marrows, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89(13), 134426.
43. V. Ukleev, Y. Yamasaki, D. Morikawa, K. Karube, K. Shibata, Y. Tokunaga, Y. Okamura, K. Amemiya, M. Valvidares, H. Nakao, Y. Taguchi, Y. Tokura and T. Arima, Phys. Rev. B, 2019, 99(14), 144408.
44. H. T. Wu, X. C. Hu, K. Y. Jing and X. R. Wang, Commun. Phys., 2021, 4(1), 210.
45. X. R. Wang, X. C. Hu and H. T. Wu, Commun. Phys., 2021, 4(1), 142.
46. H. T. Wu, X. C. Hu and X. R. Wang, Sci. China, 2022, 65(4), 247512.
47. J. D. Bocarsly, R. F. Need, R. Seshadri and S. D. Wilson, Phys. Rev. B, 2018, 97(10), 100404(R).
48. H. Y. Kwon, K. M. Bu, Y. Z. Wu and C. Won, J. Magn. Magn. Mater., 2012, 324(13), 2171.
49. F. Schlickeiser, U. Ritzmann, D. Hinzke and U. Nowak, Phys. Rev. Lett., 2014, 113(9), 097201.
50. K.-M. Lee, J. W. Choi, J. Sok and B.-C. Min, AIP Adv., 2017, 7(6), 065107.
51. H. Oike, A. Kikkawa, N. Kanazawa, Y. Taguchi, M. Kawasaki, Y. Tokura and F. Kagawa, Nat. Phys., 2016, 12(1), 62–66.
52. K. Karube, J. S. White, V. Ukleev, C. D. Dewhurst, R. Cubitt, A. Kikkawa, Y. Tokunaga, H. M. Rønnow, Y. Tokura and Y. Taguchi, Phys. Rev. B, 2020, 102(6), 064408.
53. M. T. Birch, R. Takagi, S. Seki, M. N. Wilson, F. Kagawa, A. Štefančič, G. Balakrishnan, R. Fan, P. Steadman, C. J. Ottley, M. Crisanti, R. Cubitt, T. Lancaster, Y. Tokura and P. D. Hatton, Phys. Rev. B, 2019, 100(1), 014425.
54. M. Crisanti, M. T. Birch, M. N. Wilson, S. H. Moody, A. Štefančič, B. M. Huddart, S. Cabeza, G. Balakrishnan, P. D. Hatton and R. Cubitt, Phys. Rev. B, 2020, 102(22), 224407.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr01300b

---