 Open Access Article
Open Access ArticleComputational predictions of quantum thermal transport across nanoscale interfaces
Hangbo
Zhou†
 ,
Zhun-Yong
Ong†
,
Zhun-Yong
Ong†
 ,
Gang
Zhang
,
Gang
Zhang
 * and
Yong-Wei
Zhang
* and
Yong-Wei
Zhang
 *
*
Institute of High Performance Computing, A*STAR, 138632, Singapore. E-mail: zhangg@ihpc.a-star.edu.sg; zhangyw@ihpc.a-star.edu.sg
First published on 14th June 2022
Abstract
Interfaces are essential elements in nanoscale devices and their properties can differ significantly from their bulk counterparts. Because interfaces often act as bottlenecks in heat dissipation, the prediction and control of the interfacial thermal conductance is critical to the design of nanoscale devices. In this review, we examine the recent advances in quantum interfacial thermal transport from a theoretical and computational perspective. We discuss in detail recent advances in the Atomistic Green's Function method which is an important tool for predicting interfacial thermal transport. We also discuss recent progress in the understanding of interfacial transport mechanisms, including the role of interfacial modes, the role of anharmonic phonon–phonon coupling, the role of electron–phonon interaction, and the ways to tune the interfacial thermal conductance. Finally, we give an overview of the challenges and opportunities in this research field.
I. Introduction
With the progressive reduction of electronic device size, the concentration of generated waste heat has sharply increased and this could significantly affect the performance and lifespan of the device. Therefore, heat dissipation becomes a critical issue in the design of nanoscale devices. As the device size decreases, the density of interfaces usually increases. As a result, interfacial thermal conduction becomes important and sometimes even dominates the thermal transport, especially when the length scale of a device is comparable to the phonon mean free path.1Traditionally, phonon-mediated interfacial thermal transport is described by the phonon gas model.2 It is commonly assumed that interfacial thermal conduction occurs when an incident phonon, propagating in one medium from the bulk towards the interface, is transmitted across the boundary with the probability of transmission given by the phonon transmission coefficient. This physical picture is the basis for the two major acoustics-based theoretical models,2,3 namely the acoustic mismatch model (AMM) and the diffuse mismatch model (DMM), which are widely used to interpret experimental and simulation studies of interfacial thermal transport. Nevertheless, they suffer from a couple of shortcomings. Firstly, they assume an idealized model of the phonon dispersion and ignore the contribution from optical phonons. Secondly, they cannot determine the dependence of phonon transmission on the atomistic structure of the interface.
Two other conventional methods to handle interfacial thermal transport are the semi-classical Boltzmann Transport Equation (BTE) and molecular dynamics (MD). In these two methods, the effects of anharmonicity are incorporated with ease.4 Nonetheless, the BTE and MD approaches have their drawbacks. For example, the BTE approach assumes a particle-like behavior for the phonons and cannot be applied to regimes or length scales where the coherent behavior of phonons cannot be neglected. The MD approach is inherently classical and unsuitable at low temperatures where the quantum statistics are important.5 To overcome these issues, a fully quantum-mechanical approach, such as the non-equilibrium Green's function (NEGF), is therefore needed to capture the coherent and incoherent aspects of thermal transport.
In this review, we will first introduce the recent advances in the Atomistic Green's Function (AGF) method in section II, as a fully quantum-mechanical approach to treat interfacial thermal transport. We will discuss mode-resolved phonon transmission and reflection, a recent extension to the AGF method. In section III, we will review the recent advances in and new insights into interfacial thermal transport, which include the role of interfacial modes, the role of anharmonic phonon–phonon coupling and the effects of electron–phonon coupling at a conductor-insulator interface. We will also review the recent progress in the methods to tune the interfacial thermal conductance.
II. Atomistic green's function method
A. Phonon transmission
The Atomistic Green's Function method was first introduced by Mingo and Yang6 to study coherent phonon transport and low-temperature thermal conductance through ultrathin nanowires coated with an amorphous material. By exploiting the analogy between the equation of motion for phonons and the Schrodinger equation, they developed the AGF method that, unlike the AMM and DMM, automatically takes into consideration the atomistic structure of the system. In the AGF method, which has become the workhorse for simulating the low-temperature thermal conductance in nanostructures and interfaces,7–10 the system is partitioned into three parts: the left lead, the center, and the right lead as shown in Fig. 1. The center consists of a finite region corresponding to the interface while the semi-infinite left and right leads represent the bulk crystal lattices on each side of the interface. The AGF method uses the interatomic force constants (IFCs), which describe the lattice dynamics of the leads and the center and can be extracted from either empirical interatomic potentials or first-principles calculations, as its inputs for the calculation of the interfacial heat flux. As in other microscopic theories of interfacial thermal transport (e.g. the acoustic and diffuse mismatch models3), the interfacial heat flux in the AGF method is modeled as the transmission of phonons across the center between the left and right leads and given by the Landauer–Buttiker expression8
in the AGF method is modeled as the transmission of phonons across the center between the left and right leads and given by the Landauer–Buttiker expression8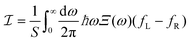 | (1) |
B. Mode-resolved phonon transmission and reflection
In spite of its atomistic fidelity, one of the principal drawbacks of the original AGF method is its inability to describe individual phonon transmission explicitly in terms of the bulk phonon dispersion. Physically, the transmission function is equal to the sum of the individual modal transmission coefficient, i.e., , where NL(ω) denotes the number of left-lead modes at frequency ω and ΞL,n(ω) denotes the probability that the n-th left-lead mode is transmitted across the interface. We may interpret NL(ω) as the frequency-dependent bandwidth of the left lead since it limits the maximum left-lead phonon flux at frequency ω. Similarly, we also have
, where NL(ω) denotes the number of left-lead modes at frequency ω and ΞL,n(ω) denotes the probability that the n-th left-lead mode is transmitted across the interface. We may interpret NL(ω) as the frequency-dependent bandwidth of the left lead since it limits the maximum left-lead phonon flux at frequency ω. Similarly, we also have  , where NR(ω) denotes the number of right-lead modes at frequency ω and ΞR,m(ω) denotes the transmission probability of the m-th right-lead mode. However, the individual transmission probabilities ΞL,n(ω) and ΞR,m(ω) cannot be computed efficiently with the original AGF method.
, where NR(ω) denotes the number of right-lead modes at frequency ω and ΞR,m(ω) denotes the transmission probability of the m-th right-lead mode. However, the individual transmission probabilities ΞL,n(ω) and ΞR,m(ω) cannot be computed efficiently with the original AGF method.
To address this challenge, Ong and Zhang13 introduced an extension of the AGF method for computing the mode-resolved transmission coefficient. The mathematical details of the method are described in ref. 14. The key idea of the extended AGF method is that the surface Green's functions, which are used to represent the decoupled leads in the original AGF method, can be linearly transformed into the Bloch matrices,15,16 which describe the incoming and outgoing phonon eigenmodes of the leads as well as their crystal momentum in the transmission direction. We illustrate the use of the extended AGF method with the example of the phonon transmission between a (16,0) carbon nanotube (CNT) and an (8,0) CNT across an intramolecular junction with 4 heptagon–pentagon defect pairs, as shown in Fig. 2(a). Fig. 2(b) shows the left-lead phonon transmission coefficient sum  together with NL(ω) from the left lead and NR(ω) from the right lead. The mode-resolved transmission coefficients for the (16,0) CNT phonons are superimposed on its phonon dispersion curves in Fig. 2(c), which shows how the contributions to the phonon flux vary with frequency and polarization. We likewise plot the right-lead phonon transmission coefficient sum
together with NL(ω) from the left lead and NR(ω) from the right lead. The mode-resolved transmission coefficients for the (16,0) CNT phonons are superimposed on its phonon dispersion curves in Fig. 2(c), which shows how the contributions to the phonon flux vary with frequency and polarization. We likewise plot the right-lead phonon transmission coefficient sum  in Fig. 2(d) as well as the mode-resolved transmission coefficients for the (8,0) CNT phonons superimposed on its phonon dispersion curves in Fig. 2(e). Comparing Fig. 2(b) and (d), we find that the left and right-lead transmission coefficient sums are equal for every frequency as expected since
in Fig. 2(d) as well as the mode-resolved transmission coefficients for the (8,0) CNT phonons superimposed on its phonon dispersion curves in Fig. 2(e). Comparing Fig. 2(b) and (d), we find that the left and right-lead transmission coefficient sums are equal for every frequency as expected since 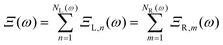 .
.
 | ||
Fig. 2 (a) Set up of the (16,0)/(8,0) CNT intramolecular junction (IMJ) with 4 heptagon-pentagon defect pairs. The left and right leads are the (16,0) and (8,0) CNTs, respectively while the center corresponds to the IMJ. (b) Plot of the left-lead phonontransmission coefficient sum  (green solid line), together with NL(ω), the number of incident channels in the (16,0) CNT (pink), and NR(ω), the number of channels in the (8,0) CNT (gray), at different frequencies. (c) The distribution of the transmission coefficients ΞL,n(ω), represented in color, is superimposed on the phonon dispersion curves of the (16,0) CNT. (d) Plot of the right-lead phonon transmission coefficient sum (green solid line), together with NL(ω), the number of incident channels in the (16,0) CNT (pink), and NR(ω), the number of channels in the (8,0) CNT (gray), at different frequencies. (c) The distribution of the transmission coefficients ΞL,n(ω), represented in color, is superimposed on the phonon dispersion curves of the (16,0) CNT. (d) Plot of the right-lead phonon transmission coefficient sum  (green solid line), together with NR(ω), the number of incident channels in the (8,0) CNT (pink), and NL(ω), the number of channels in the (16,0) CNT (gray). (e) The distribution of the right-lead transmission coefficients ΞR,m(ω) is superimposed on the phonon dispersion curves of the (8,0) CNT. The figure is reproduced with permission from ref. 14, ©2018 American Institute of Physics. (green solid line), together with NR(ω), the number of incident channels in the (8,0) CNT (pink), and NL(ω), the number of channels in the (16,0) CNT (gray). (e) The distribution of the right-lead transmission coefficients ΞR,m(ω) is superimposed on the phonon dispersion curves of the (8,0) CNT. The figure is reproduced with permission from ref. 14, ©2018 American Institute of Physics. | ||
Given the fidelity of the extended AGF method for characterizing mode-resolved transmission, it has been used in a variety of ways to model phonon transmission in recent years. An obvious advantage of this technique is that its modal resolution allows one to categorize the contributions of different phonon polarizations. As an example, Lawson and co-workers used the method to quantify the relative contributions of the longitudinal and transverse acoustic phonons to the thermal boundary conductance (TBC) of the MoS2-WS2 lateral interface17 and found that the non-acoustic phonons account for only 16 percent of the total TBC at room temperature. In addition to its high modal resolution, the extended AGF method can also be used as a tool to model how the interface affects the transmission of individual phonon modes. This idea was employed by Hu and Tian to provide direct evidence of Anderson localization18 in disordered Si/Ge superlattices sandwiched between regular Si/Ge superlattice leads.19 By modeling how the transmission coefficients of the lead modes vary exponentially with the length of the disordered superlattice, they were able to observe signatures of localized modes and demonstrate their co-existence with delocalized modes as well as quantify their relative contributions to thermal transport in disordered Si/Ge superlattices. Another example is in the modeling of phonon transmission and reflection in nanocrystalline solids, which are of fundamental interest and importance to understanding thermal conduction in nanocrystalline solids, where phonon transport is typically impeded by the high density of interfaces. Yang, Latour and Minnich20 used this method to characterize the modal transmission and reflection of THz phonons across an amorphous Si region connected to two crystalline Si leads, an archetypical model for interfaces in nanocrystalline solids. They found that the disordered interface acts as a low-pass filter by limiting the transmission of phonons to those with sub-3 THz frequencies, with minimal momentum relaxation for these sub-3 THz phonons.
Apart from its utility for understanding the role of phonon transmission in interfacial thermal transport, the extended AGF method has also been used by Chen and co-workers to explore valley phononics and valley-selective transport in graphene.21 They were able to show that in a graphene sheet with a “zero-angle” grain boundary (GB), the GB can selectively scatter different phonon modes. In a small frequency window around the K and K′ valleys of the Brillouin zone, the flexural acoustic (ZA) and optical (ZO) phonon modes become valley-polarized as the GB acts as a filter that selectively allows the transmission of phonons from either the K or K′ valleys.
The extended AGF method was further developed22 into an atomistic S-matrix method that treats bulk phonon modes as the scattering channels and can determine the numerically exact scattering amplitudes for individual two-phonon processes. This method was also exploited by Ong, Schusteritsch and Pickard to characterize the specularity of the acoustic phonons scattered by the grain boundary between armchair and zigzag-edge graphene.23 They used the scattering amplitudes to estimate the mode-resolved phonon coherence and specularity, and to predict their dependence on phonon momentum, frequency, and polarization. As expected, the specularity of the in-plane longitudinal (LA) and transverse acoustic (TA) phonons decreases monotonically as the frequency increases. However, the long-wavelength ZA phonons, which play a key role in the high thermal conductivity of suspended pristine graphene, are highly susceptible to diffuse scattering by the GB and this is attributed to the quadratic ZA phonon dispersion in which the group velocity converges to zero at low frequency. Using the same GB models, Ong also characterized the specularity of the forward and backward scattered phonons by graphene GBs24 and showed that separate specularity parameters are needed to describe the behavior of transmitted and reflected phonons because backscattered phonons are more diffusely scattered than forward-scattered phonons. Song and Chen also used mode-resolved AGF simulations to investigate diffuse phonon scattering by a disordered interface.25 They examined the limitations of the commonly used diffuse mismatch model and demonstrated that the assumption of memory loss by the phonon from scattering with the disordered interface is not valid. Their results also revealed that distinct specularity parameters are needed to characterize the transmitted and reflected phonons.
C. AGF theory and interface conductance modal analysis
The AGF method can be contrasted with the Interface Conductance Modal Analysis (ICMA) method of Gordiz and Henry.26–28 At its heart, the AGF method is a scattering-based description of the so-called phonon gas model for interfacial thermal transport, conceptually analogous to the acoustic and diffuse mismatch models.3 The phonons in the AGF method refer to the bulk phonon modes of the leads, which can be characterized by their phonon dispersion (frequency and wave vector) because of the long-range order in the lattice, and correspond to the stationary states of the decoupled leads. When the leads are coupled to the center (as shown in Fig. 1), these bulk phonon modes are no longer in the stationary states of the overall system (leads and center) and instead undergo scattering, i.e., transmission and reflection that contribute to interfacial thermal transport. Hence, the leftward (rightward) interfacial heat flux comprises the left-lead (right-lead) bulk phonons propagating and transmitting partially across the interface. In the process, the energy of the incoming left-lead (right-lead) bulk phonon is redistributed to the outgoing right-lead (left-lead) bulk phonon modes of the same frequency. In the absence of anharmonicity, the modes of the decoupled center, which contains the interface, play no role in interfacial thermal transport, unlike the bulk phonon modes of the leads, because the former are localized to the center and can be regarded as vibrational ‘bound states’ that cannot be scattered after the leads are coupled to the center.On the other hand, in the ICMA method, the modes are those stationary states of the harmonic part of the Hamiltonian of the overall system, which lacks long-range order, and cannot be characterized by phonon dispersion. Hence, a scattering treatment for them is not applicable, unlike the case of the AGF modes. The two pictures, AGF and ICMA, can be reconciled as follows: when the leads are coupled to the center to form the overall system, the physical coupling introduces a perturbation to the isolated bulk phonon modes of the leads and results in the bulk phonon modes evolving into the stationary states of the overall system. The modes of the decoupled center similarly evolve into interface-localized modes of the overall system. These modes can be classified by their spatial distribution of their atomic displacements in the overall system27 and the extent they are localized at the interface. Gordiz and Henry report that the interface-localized modes constitute a small minority of the overall eigenmode spectrum but have a finite contribution to the interfacial heat flux that is facilitated by lattice anharmonicity.27
III. Recent advances in understanding interfacial thermal transport
A. The role of interfacial modes
Phonon transmission depends on details of interfacial coupling and the bulk phonon properties of each side of the interface. Therefore, a simple way to estimate interfacial thermal resistance is to evaluate the overlap of the phonon density of states (PDOS) or spectral density of the two bulk materials, which can be calculated from first-principles. This technique is still widely used today, especially for interfaces formed by materials with similar lattice structures and bond strengths. For example, Sun and co-workers reported that the overlap of the PDOS plays a decisive role in interfacial thermal transport between the cubic compounds of boron with selected group V elements (BP, BN, BAs and BSb) and different substrates (Si, 6H-SiC and 3C-SiC).29Although the overlap of the PDOS provides reasonable predictions for certain interfaces, this treatment over-simplifies the phonon transmission phenomenon as it ignores the coupling details at the interface. More importantly, it neglects the role of interfacial modes and the phonon scattering at the interface. As a result of lattice mismatch, lattice re-construction and roughness at the interface, the phonon modes at the interface may differ significantly from those of the bulk. Recently, different groups have used high-resolution electron energy-loss spectroscopy to measure the interface phonon vibrational spectra and dispersion relation,30,31 and they observed localized phonon modes at the interface, which significantly affect the interfacial thermal conductance.
Many theoretical works also predict that these interfacial modes contribute significantly to the interfacial thermal conductance in different ways. For example, Feng and co-workers reported that at the Si/Ge interface, the thermal conductance is dominated by interfacial modes,32 which are strong in non-equilibrium state and act as a bridge connecting the bulk phonons modes that effectively enhances multiple phonon scattering processes and boosts the thermal conductance. Li and co-workers also reported the localized phonons and bridge effect at the AlN/Si interface, which improves phonon transport.33 Han and co-workers reported the discovery of local phonon modes at the antiphase boundary of SrTiO3.34 However, in this study, the thermal conductivity is reduced as a result of the enhanced energy mismatch between the interfacial phonons and the bulk phonons. Recently, a theoretical work by Zhou and co-workers found that the phonon–phonon scattering between extended phonons and localized phonons can significantly enhance or suppress the transmission of extended phonons across the interface.35 Xu and co-workers showed that these bridge effects can sometimes exhibit anomalous behaviours in which a weak van der Waals interface can have a higher thermal boundary conductance than a strong covalently bonded one when the interface has a high degree of lattice mismatch.36 These interfacial modes become even more important when the interface has defects or disorders.37,38 A recent study by Lu and co-workers showed that with 6.3% of atomic vacancies at the Cu/Si interface, the thermal conductance increases by 76%, arising from the inelastic phonon scattering enhanced by the defects.38
B. The role of anharmonic phonon–phonon scattering
Strong phonon–phonon scattering often takes place at an interface as a result of the presence of interfacial phonon modes, non-equilibrium conditions and nonlinear interatomic interactions. Unlike elastic phonon scattering in harmonic models where the exact solution is known,39 inelastic phonon–phonon scattering with anharmonic coupling remains unsolvable in general. Nevertheless, several physical models with different approximation schemes have been proposed to explore the effects of inelastic phonon–phonon scattering.Although the NEGF formalism for treating anharmonic phonon interactions quantum mechanically is known,39,40,48,49 difficulties in its computational implementation remain and its applications have largely been limited to simple one-dimensional systems.40,48 Nonetheless, some promising progresses have been made in applying this approach to more complex structures. Recently, Dai and Tian extended the formalism to higher dimensions50 using a Fourier decomposition method for third-order tensors to simplify the calculation of the many-body self-energy terms. They applied their extended formalism to study the Si/Ge interface and showed that the anharmonicity can enhance the thermal boundary conductance, especially at high temperatures, by enabling heat current contributions from high-frequency phonons. Guo and co-workers also developed a similar and more extensive NEGF-based framework to model the effects of phonon anharmonicity for thermal conduction in one and three-dimensional nanostructures.45 Their improved treatment was used to investigate the role of inelastic scattering in the thermal boundary conductance of the Si/Ge interface.46 They found that the anharmonic decay of interfacial phonon modes is critical for bridging the bulk modes across the interface even when the overall contribution of anharmonicity is moderate.
Beyond treating anharmonicity in the system, researchers have also extended the NEGF models to treat anharmonicity in the baths and system-bath coupling. Ming and co-workers investigated the nonlinear system-bath coupling in a harmonic system51 and found that the nonlinear system-bath coupling introduces multi-phonon scattering processes. When the linear component of the system-bath coupling is weak, the nonlinearity enhances interfacial thermal conductance. When the linear componenent is strong, however, it suppresses the interfacial thermal conductance. Recently, Fang and co-workers also introduced anharmonicity to baths by simulating phonon propagation across a nonlinear lattice and interface.52 They found that the cut-off frequency for phonon transmission across the nonlinear lattice increases due to phonon renormalization. The anharmonicity also enhances interfacial thermal conductance by redistributing the spectral flux.
 | ||
| Fig. 3 Schematic of the bath-lead–lead-bath model. The interface comprises a left lead and a right lead, which weakly interact with each other. Each lead is coupled to its respective thermal bath. | ||
Anharmonicity can be introduced to the leads or to the lead-lead coupling. For example, He and co-workers developed a quantum self-consistent phonon theory to study the anharmonic leads connected through harmonic lead-lead coupling.53,54In this theory, an effective harmonic Hamiltonian is used to obtain analytically canonical averages based on the equilibrium condition of the bath. Their study showed that anharmonicity creates phonon localization and delocalization, which affect the thermal transport. In another work, Cao and He showed that in the regime of weak lead-lead coupling, the thermal conductance is proportional to the square of the coupling strength.54
Recently, the effects of anharmonicity on the lead–lead coupling have been studied by using the bath-lead–lead-bath model. For example, Zhou and co-workers investigated the three-phonon and four-phonon scattering processes35,55 and found that the contribution from the three-phonon scattering processes increases linearly with temperature.55 In the four-phonon processes, the localized phonons contribute to phonon transmission through the scattering of upcoming travelling phonons.35
C. The role of electron–phonon interaction
Another pathway involves the direct exchange of energy between electrons and phonons across the interface. Fig. 4(a) shows an example of a physical process in which a quanta of energy is transmitted from an insulator (left side of the interface) to a conductor (right side of the interface) through the interfacial EPI. In titanium silicide (metal)-silicon (semiconductor) interface, Sadasivam and co-workers reported that the coupling strength of electrons with interfacial phonon modes is of the same order of magnitude as that of electrons to the phonon modes in the bulk metal, and its contribution to the electron–phonon interfacial conductance is comparable to the harmonic phonon–phonon conductance across the interface.58 Recently, a similar observation was also made for the Ni/Al2O3 and W/Al2O3 interfaces.59 In this scenario, the electron temperature differs from that of phonons in metal. Hence, two temperature models60,61 and even multi-temperature models62 have been proposed to characterize the non-equilibrium states between the phonons and other heat carriers near the interface. This temperature difference between the electrons and phonons can explain the measured thermal rectification.59 Nevertheless, the understanding of the significance and role of interfacial electron–phonon coupling remains largely unclear. The contribution to the thermal conductance from the interactions between electrons and interfacial phonons is estimated as  , where G is the electron–phonon coupling constant and kp is the phonon thermal conductivity in metal.63 This relation suggests that interfacial EPI becomes more important at higher temperatures.
, where G is the electron–phonon coupling constant and kp is the phonon thermal conductivity in metal.63 This relation suggests that interfacial EPI becomes more important at higher temperatures.
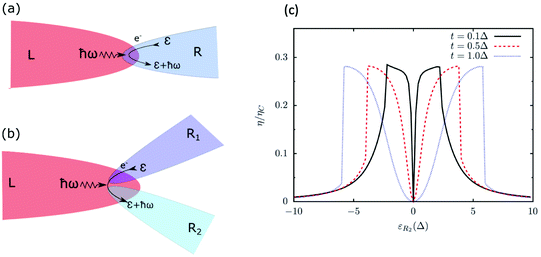 | ||
Fig. 4 (a) Schematic of the electron–phonon interaction at an interface comprising an insulator (L) and a conductor (R). Thermal transport is mediated via a process in which an electron in the insulator absorbs a phonon of energy ħω from the insulator through the interfacial electron–phonon coupling. (b) Schematic of the three-terminal thermoelectric setup comprising an insulator (L) and two conductors (R1 and R2). A phonon from the insulator can mediate the electron transporting from R1 to R2 through the electron–phonon interaction at an three-terminal interface. (c) The thermoelectric efficiency (normalized by Carnot efficiency ηC) predicted by using the model in panel (b). The insulator is modelled by a Rubin chain with spring constant k and mass m. 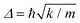 is used as a reference unit of energy. The conductors are modelled by electron hopping model with same hopping energy t and different onsite energies of εR1 and εR2, respectively. The parameters are set to be εR1 = 0, the temperature T = Δ/kB. The figure is reproduced with permission from ref. 71, ©2020 American Physical Society. is used as a reference unit of energy. The conductors are modelled by electron hopping model with same hopping energy t and different onsite energies of εR1 and εR2, respectively. The parameters are set to be εR1 = 0, the temperature T = Δ/kB. The figure is reproduced with permission from ref. 71, ©2020 American Physical Society. | ||
D. Other methods and discoveries
Recently, machine learning has emerged as a new method to solve the problem of interfacial thermal conductance due to advances in computational technology and the availability of more data. For example, machine learning has been used to predict the interatomic potentials at the interface,74 which then serve as the basis for molecular dynamics or AGF simulations. Machine learning has also been used to directly predict the interfacial thermal conductance, based on the parameters of the materials that make up the interface.75,76With improved algorithms, the non-equilibrium molecular dynamics (NEMD) simulations and Boltzmann transport equation have become important tools for predicting the interfacial thermal conductance and many new discoveries are found continuously.77–80 Molecular dynamics (MD) simulations are particularly useful for structures with irregular atomic configurations. For example, Wang and co-workers used MD simulations to show that interfacial thermal resistance at the VO2/Si interface markedly depends on its roughness.77 In another example, Ren and co-workers found that the surface fluctuations are responsible for the transmission of low-frequency phonons across the graphene/boron nitride van der Waals heterostructures and are the cause of the rotational dependence of the interfacial thermal conductance.78
E. Interface engineering
With the in-depth understanding of the phonon transmission at interfaces, the interfacial thermal conductance can be tuned via interface engineering. Recently, Zhang and Liu demonstrated that hierarchically arranged hydrogen bonds can significantly enhance the interfacial thermal conductance between graphene and polymer. Thus, the interfacial thermal resistance can be modulated via the density of hydrogen bonds.81 Another commonly used way to tune the interfacial thermal conductance is by adding interlayers to engineer the transmission of phonons. Rastgarkafshgarkolaei and co-workers reported a simulation study by NEGF which suggests that the interfacial thermal conductance can be enhanced by mass-graded interlayers.82 Other than thermal conductance, Wang and co-workers reported that the phonon chirality and phonon polarization can also be manipulated through interface transmission due to the difference in phase change across the interface.83Same as phonon–phonon scattering, the interfacial thermal resistance arising from EPI can also be tuned by inserting interlayers. Several studies have shown that an enhancement of the interfacial thermal conductance can be achieved by inserting a metal interlayer.84,85 A recent work by Tao and co-workers demonstrated the enhancement of heat conduction across the metal/graphite interface treated with a focused ion beam due to the formation of enormous dipoles on the milled metal/graphite interface leads.86
IV. Summary and outlook
Although certain progress has been made in the recent years, thermal management across interfaces remains a critical issue in nanoscale devices, and much effort is still being devoted to improving existing or developing new theoretical and computational methods to more accurately predict interfacial thermal transport. On one hand, existing theories and methods have been further refined and extended. For example, the Atomistic Green's Function has been extended to address the issue of mode-resolved phonon transmission, which enables the categorization of contributions from different phonon modes. Despite the computational difficulties in implementing anharmonicity within the non-equilibrium Green's function framework, considerable progress has been made in extending this method beyond simple one-dimensional models to more realistic materials models. On the other hand, new models and theories have been developed to obtain new physical insights. For example, a quantum self-consistent phonon theory has been developed to study anharmonic leads. Another example is the use of perturbative methods to investigate the contribution of quantum three-phonon and four-phonon scattering processes near a weakly-interacting interface.It should be noted that interfacial transport is a non-equilibrium and dynamically nonlinear problem that is often challenging to solve. Despite the progress that has been made recently, the issue of nonlinear scattering at the interfaces, which includes both anharmonic phonon–phonon scattering and electron–phonon scattering, has not been fully understood and will continue to attract significant research attention in the future. Due to the good progress made in computational and simulation methods in recent years, a promising trend is the application of many existing theoretical tools in combination with these newly developed computational and simulation tools to treat real materials. This trend will lead to quantitative prediction of interfacial thermal properties that can be directly compared with experiments. An effective interplay between simulations and experiments will greatly accelerate the advances in understanding interfacial thermal transport.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge the National Research Foundation (NRF-CRP24-2020-0002), the A*STAR SERC CRF Award, and the use of computing resources at the A*STAR Computational Centre and National Supercomputer Centre.References
- Y. Hong, L. Li, X. C. Zeng and J. Zhang, Nanoscale, 2015, 7, 6286 RSC.
- G. Chen, Nanoscale energy transport and conversion: a parallel treatment of electrons, molecules, phonons, and photons, publisher Oxford University Press, New York, 2005 Search PubMed.
- E. T. Swartz and R. O. Pohl, Rev. Mod. Phys., 1989, 61, 605 CrossRef.
- P. E. Hopkins, J. L. Kassebaum and P. M. Norris, J. Appl. Phys., 2009, 105, 023710 CrossRef.
- M. Käso and U. Wulf, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 134309 CrossRef.
- N. Mingo and L. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 245406 CrossRef.
- W. Zhang, T. S. Fisher and N. Mingo, J. Heat Transfer, 2007, 129, 483 CrossRef CAS.
- W. Zhang, T. S. Fisher and N. Mingo, Numer. Heat Transfer, Part B, 2007, 51, 333 CrossRef CAS.
- I. Savić, N. Mingo and D. A. Stewart, Phys. Rev. Lett., 2008, 101, 165502 CrossRef PubMed.
- G. Stoltz, N. Mingo and F. Mauri, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 113408 CrossRef.
- P. K. Schelling, S. R. Phillpot and P. Keblinski, Appl. Phys. Lett., 2002, 80, 2484 CrossRef CAS.
- P. K. Schelling, S. R. Phillpot and P. Keblinski, J. Appl. Phys., 2004, 95, 6082 CrossRef CAS.
- Z.-Y. Ong and G. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 174302 CrossRef.
- Z.-Y. Ong, J. Appl. Phys., 2018, 124, 151101 CrossRef.
- T. Ando, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 8017 CrossRef PubMed.
- P. A. Khomyakov, G. Brocks, V. Karpan, M. Zwierzycki and P. J. Kelly, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 35450 CrossRef.
- M. Lawson, I. Williamson, Z. Y. Ong and L. Li, Comput. Condens. Matter., 2019, 19, e00389 CrossRef.
- Y. Ni and S. Volz, J. Appl. Phys., 2021, 130, 190901 CrossRef CAS.
- R. Hu and Z. Tian, Phys. Rev. B, 2021, 103, 045304 CrossRef CAS.
- L. Yang, B. Latour and A. J. Minnich, Phys. Rev. B, 2018, 97, 205306 CrossRef CAS.
- X. Chen, Y. Xu, J. Wang and H. Guo, Phys. Rev. B, 2019, 99, 064302 CrossRef.
- Z.-Y. Ong, Phys. Rev. B, 2018, 98, 195301 CrossRef CAS.
- Z. Y. Ong, G. Schusteritsch and C. J. Pickard, Phys. Rev. B, 2020, 101, 195410 CrossRef CAS , 2004.07424.
- Z. Y. Ong, EPL, 2021, 133, 66002 CrossRef CAS , 2103.06444.
- Q. Song and G. Chen, Phys. Rev. B, 2021, 104, 085310 CrossRef CAS , 2106.04745.
- K. Gordiz and A. Henry, New J. Phys., 2015, 17, 103002 CrossRef.
- K. Gordiz and A. Henry, J. Appl. Phys., 2016, 5, 015101 CrossRef.
- K. Gordiz and A. Henry, Sci. Rep., 2016, 6, 23139 CrossRef CAS PubMed.
- Z. Sun, K. Yuan, X. Zhang and D. Tang, Phys. Chem. Chem. Phys., 2019, 21, 6011 RSC.
- R. Qi, R. Shi, Y. Li, Y. Sun, M. Wu, N. Li, J. Du, K. Liu, C. Chen, J. Chen, F. Wang, D. Yu, E.-G. Wang and P. Gao, Nature, 2021, 599, 399 CrossRef CAS PubMed.
- Z. Cheng, R. Li, X. Yan, G. Jernigan, J. Shi, M. E. Liao, N. J. Hines, C. A. Gadre, J. C. Idrobo, E. Lee, K. D. Hobart, M. S. Goorsky, X. Pan, T. Luo and S. Graham, Nat. Commun., 2021, 12, 6901 CrossRef CAS PubMed.
- T. Feng, Y. Zhong, J. Shi and X. Ruan, Phys. Rev. B, 2019, 99, 045301 CrossRef CAS.
- Y.-H. Li, R.-S. Qi, R.-C. Shi, J.-N. Hu, Z.-T. Liu, Y.-W. Sun, M.-Q. Li, N. Li, C.-L. Song, L. Wang, Z.-B. Hao, Y. Luo, Q.-K. Xue, X.-C. Ma and P. Gao, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2117027119, DOI:10.1073/pnas.2117027119.
- B. Han, R. Shi, H. Peng, Y. Lv, R. Qi, Y. Li, J. Zhang, J. Du, P. Yu and P. Gao, arXiv:2203.01772, 2022.
- H. Zhou, G. Zhang and Y.-W. Zhang, arXiv:2202.11037, 2022.
- B. Xu, S. Hu, S. W. Hung, C. Shao, H. Chandra, F. R. Chen, T. Kodama and J. Shiomi, Sci. Adv., 2021, 7, 1 Search PubMed.
- T. Beechem, S. Graham, P. Hopkins and P. Norris, Appl. Phys. Lett., 2007, 90, 054104 CrossRef.
- Z. Lu, A. M. Chaka and P. V. Sushko, Phys. Rev. B, 2020, 102, 075449 CrossRef CAS.
- J. S. Wang, J. Wang and J. T. Lü, Eur. Phys. J. B, 2008, 62, 381 CrossRef CAS.
- J.-S. Wang, J. Wang and N. Zeng, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 033408 CrossRef.
- J. S. Wang, N. Zeng, J. Wang and C. K. Gan, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 1 Search PubMed.
- L. Zhang, P. Keblinski, J. S. Wang and B. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 064303 CrossRef.
- H. Yang, Y. Tang and P. Yang, Nanoscale, 2019, 11, 14155 RSC.
- P. Z. Jia, Y. J. Zeng, D. Wu, H. Pan, X. H. Cao, W. X. Zhou, Z. X. Xie, J. X. Zhang and K. Q. Chen, J. Phys.: Condens. Matter, 2020, 32, 055302 CrossRef CAS PubMed.
- Y. Guo, M. Bescond, Z. Zhang, M. Luisier, M. Nomura and S. Volz, Phys. Rev. B, 2020, 102, 195412 CrossRef CAS.
- Y. Guo, Z. Zhang, M. Bescond, S. Xiong, M. Nomura and S. Volz, Phys. Rev. B, 2021, 103, 174306 CrossRef CAS.
- J. Thingna, J. L. García-Palacios and J. S. Wang, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 195452 CrossRef.
- N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 125402 CrossRef.
- J. S. Wang, B. K. Agarwalla, H. Li and J. Thingna, Front. Phys., 2014, 9, 673 CrossRef , 1303.7317.
- J. Dai and Z. Tian, Phys. Rev. B, 2020, 101, 041301(R) CrossRef.
- Y. Ming, H. M. Li and Z. J. Ding, Phys. Rev. E, 2016, 93, 032127 CrossRef PubMed.
- J. Fang, X. Qian, C. Y. Zhao, B. Li and X. Gu, Phys. Rev. E, 2020, 101, 022133 CrossRef CAS PubMed.
- D. He, J. Thingna and J. Cao, Phys. Rev. B, 2018, 97, 195437 CrossRef CAS.
- X. Cao and D. He, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 92, 032135 CrossRef PubMed.
- H. Zhou, G. Zhang, J.-S. Wang and Y.-W. Zhang, arXiv:2202.11026, 2022.
- J. Lee, E. Bozorg-Grayeli, S. Kim, M. Asheghi, H.-S. Philip Wong and K. E. Goodson, Appl. Phys. Lett., 2013, 102, 191911 CrossRef.
- Y. R. Koh, J. Shi, B. Wang, R. Hu, H. Ahmad, S. Kerdsongpanya, E. Milosevic, W. A. Doolittle, D. Gall, Z. Tian, S. Graham and P. E. Hopkins, Phys. Rev. B, 2020, 102, 205304 CrossRef CAS.
- S. Sadasivam, U. V. Waghmare and T. S. Fisher, J. Appl. Phys., 2015, 117, 134502 CrossRef.
- Y. J. Wu, T. Yagi and Y. Xu, Int. J. Heat Mass Transfer, 2021, 180, 121766 CrossRef CAS.
- M. An, Q. Song, X. Yu, H. Meng, D. Ma, R. Li, Z. Jin, B. Huang and N. Yang, Nano Lett., 2017, 17, 5805 CrossRef CAS PubMed.
- C. Deng, Y. Huang, M. An and N. Yang, Mater. Today Phys., 2021, 16, 100305 CrossRef.
- Z. Lu, J. Shi and X. Ruan, J. Appl. Phys., 2019, 125, 085107 CrossRef.
- A. Majumdar and P. Reddy, Appl. Phys. Lett., 2004, 84, 4768 CrossRef CAS.
- L. Zhang, J. T. Lü, J. S. Wang and B. Li, J. Phys.: Condens. Matter, 2013, 25, 445801 CrossRef PubMed.
- J. Zhou, H. D. Shin, K. Chen, B. Song, R. A. Duncan, Q. Xu, A. A. Maznev, K. A. Nelson and G. Chen, Nat. Commun., 2020, 11, 1 CrossRef PubMed.
- H. Liu, C. Yang, B. Wei, L. Jin, A. Alatas, A. Said, S. Tongay, F. Yang, A. Javey, J. Hong and J. Wu, Adv. Sci., 2020, 7, 1902071 CrossRef CAS PubMed.
- Z. Tong, S. Li, X. Ruan and H. Bao, Phys. Rev. B, 2019, 100, 144306 CrossRef CAS.
- C. Liu, M. Yao, J. Yang, J. Xi and X. Ke, Mater. Today Phys., 2020, 15, 100277 CrossRef.
- Y. Huang, J. Zhou, G. Wang and Z. Sun, J. Am. Chem. Soc., 2019, 141, 8503 CrossRef CAS PubMed.
- Y. Sun, Z. Shuai and D. Wang, J. Phys. Chem. C, 2019, 123, 12001 CrossRef CAS.
- H. Zhou, G. Zhang, J. S. Wang and Y. W. Zhang, Phys. Rev. B, 2020, 101, 235305 CrossRef CAS.
- H. Zhou, J. Thingna, J. S. Wang and B. Li, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 045410 CrossRef.
- J. Ren and J. X. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 241412(R) CrossRef.
- S. Wyant, A. Rohskopf and A. Henry, Comput. Mater. Sci., 2021, 200, 110836 CrossRef CAS.
- Y. J. Wu, L. Fang and Y. Xu, npj Comput. Mater., 2019, 5, 56 CrossRef.
- H. Zhou, G. Zhang and Y.-W. Zhang, Phys. Chem. Chem. Phys., 2020, 22, 16165 RSC.
- J. Wang, Z. Zhang, R. Shi, B. N. Chandrashekar, N. Shen, H. Song, N. Wang, J. Chen and C. Cheng, Adv. Mater. Interfaces, 2020, 7, 1901582 CrossRef CAS.
- W. Ren, Y. Ouyang, P. Jiang, C. Yu, J. He and J. Chen, Nano Lett., 2021, 21, 2634 CrossRef CAS PubMed.
- X. Peng, P. Jiang, Y. Ouyang, S. Lu, W. Ren and J. Chen, Nanotechnology, 2021, 33, 035707 CrossRef PubMed.
- J. He, Y. Hu, D. Li and J. Chen, Nano Res., 2022, 15, 3804 CrossRef CAS.
- L. Zhang and L. Liu, Nanoscale, 2019, 11, 3656 RSC.
- R. Rastgarkafshgarkolaei, J. Zhang, C. A. Polanco, N. Q. Le, A. W. Ghosh and P. M. Norris, Nanoscale, 2019, 11, 6254 RSC.
- J. Wang, H. Chen, G. Xiong, X. Xu and L. Zhang, New J. Phys., 2018, 20, 073006 CrossRef.
- X. Li, W. Park, Y. Wang, Y. P. Chen and X. Ruan, J. Appl. Phys., 2019, 125, 045302 CrossRef.
- D. Ma and L. Zhang, J. Phys.: Condens. Matter, 2020, 32, 425001 CrossRef CAS PubMed.
- Y. Tao, C. Wu, H. Qi, C. Liu, X. Wu, M. Hao, Z. Wei, J. Yang and Y. Chen, Nanoscale, 2020, 12, 14838 RSC.
Footnote |
| † The two authors contributed equally to this paper. |
| This journal is © The Royal Society of Chemistry 2022 |

