An ab initio investigation of the temperature-dependent energetic barriers towards CrAlB and (Mo,Cr)AlB formation in a metastable synthesis scenario

Abstract

The orthorhombic CrAlB MAB phase has not been synthesized so far and was shown to be energetically unstable vs. the competing Cr₂AlB₂ phase in previous theoretical reports, which, however, did not explicitly investigate the magnitude of the energetic barrier towards CrAlB formation as a function of temperature. Temperature-dependent Gibbs energies of formation, obtained from density-functional-theory-based lattice dynamics simulations performed in this study, reveal that this barrier is very small (around 10 kJ mol⁻¹ ≈ 0.008 eV per atom, on average) and may readily be overcome during high-energy synthesis scenarios, likely resulting in metastable phase formation. Furthermore, the electronic structures of MoAlB, a phase synthesized experimentally both in bulk and thin film form, and CrAlB are shown to be similar in direct comparison, with MoAlB exhibiting a higher electronic stability due to a local DOS minimum in proximity to the Fermi level, and quaternary compositions lying between the ternaries. Likewise, bonding characteristics are qualitatively very similar between both phases, with the transition metal–boron bonds being the dominant interaction in the entire unit cell, even though individual B–B bonds are stronger; quantitatively, all interactions are again stronger in MoAlB compared to CrAlB. It is reasonable to assume that, considering the successful synthesis of phase-pure MoAlB and known formation of metastable phases during physical vapor deposition, direct synthesis of metastable CrAlB thin films is possible due to the aforementioned small energy barrier. Furthermore, stability is enhanced upon alloying with Mo as this lowers the energy of formation, with a Mo/Cr ratio of approx. 0.33 sufficient to stabilize the Cr-rich (Mo,Cr)AlB solid solution vs. the primary competing phases, allowing for deposition of Mo-concentration-dependent stable and metastable (Mo,Cr)AlB solid solution phases.

---

Introduction

In recent years, layered ternary transition metal borides, commonly labelled MAB phases in analogy to the structurally similar MAX phases, have become a topic of intense interest, previously having been largely unexplored. In various investigations, properties such as low electrical resistivity (and corresponding good conductivity), especially for the best-studied MAB phase, MoAlB,^1,2 acceptable electrocatalytic performance with simultaneous low toxicity for MoAlB and Cr₂AlB₂ ³ and high strength and fracture toughness values for several compositions^1,2 have been reported. Another potentially highly application-relevant trait is the oxidation resistance of MoAlB in particular, which remains stable at temperatures up to 1600 °C due to formation of protective Al₂O₃ scales.^2,4–6 However, only a few MAB phases are well-characterized, or even reported, so far, with data on other compositions frequently incomplete or entirely lacking.

A convenient structural description of this class of materials is that of boron atoms coordinated by six transition metal (M) atoms, thus forming face-sharing M₆B trigonal prisms extending along two crystallographic directions (typically a and c), and separated by dual layers of A atoms along the third direction (typically b).⁷ MAB phases are furthermore of high technological interest as precursors towards quasi-two-dimensional MBene materials in which the described A element layers are removed, obtained by chemical etching^8,9 or directly as a thin film via physical vapor deposition.¹⁰

While MoAlB, as a prominent member of the MAB phases, has been synthesized and characterized already in the 1960s,^11,12 with subsequent successful syntheses in both bulk^2,4,5,13 and thin film^6,14 form, the isostructural CrAlB phase has not been found so far. This is in stark contrast to other phases in the ternary Cr–Al–B system of non-equistoichiometric composition such as Cr₂AlB₂, Cr₃AlB₄ and Cr₄AlB₆ ^7,15 as well as Cr₄AlB₄,¹⁶ all of which have been obtained experimentally. This discrepancy has been partially explained by theoretical studies such as those by Bai et al.¹⁷ and Khazaei et al.,¹⁸ which have shown the hypothetical CrAlB phase to be unstable vs. the competing phase Cr₂AlB₂ and Al in the ground state at 0 K, while being stable upon formation from the elements, with the latter finding also reported by Rastogi et al.¹⁹ and Wei et al.²⁰ It was also observed, via electronic structure analysis and force constant calculations, that the B–B bonds are strongest in CrAlB, followed by the Cr–B bonds, with Cr–Al and Al–B bonds being significantly weaker,^17,18 allowing for extrapolations of the mechanical properties.¹⁷

However, while reporting both enthalpies of formation (ΔH) and Gibbs reaction energies (ΔG) in the ground state, none of the hitherto published theoretical studies, to our knowledge, examined the temperature dependence ΔG(T) of the Gibbs energy, either vs. the elements or competing phases. ΔG(T) is crucial to estimate the magnitude of the energetic barrier towards CrAlB formation at different temperatures, as in certain synthesis scenarios, such as physical vapor deposition (PVD), comparatively small energetic barriers may be readily overcome, leading to the formation of off-equilibrium, metastable phases as thin films, as previously found for, e.g., fcc-TiAlN²¹ as well as for defects formed in MoAlB.¹⁰ Estimating the likelihood of metastable CrAlB phase formation by evaluation of the temperature-dependent energy barrier may be helpful for identifying possible synthesis pathways and is one of the rationales for the present study.

Looking beyond the ternary Cr–Al–B to the quaternary Mo–Cr–Al–B system, single crystals of various Mo-rich compositions, ranging from Mo_0.93Cr_0.07AlB ²² to Mo_0.61Cr_0.39AlB ²³ have been synthesized and characterized, establishing that Cr occupies the same lattice site as Mo²² and thus indicating that phase-pure CrAlB would indeed be isostructural to MoAlB. However, no Cr-rich quaternary phase has hitherto been found and, unlike for the ternary Cr–Al–B system, theoretical predictions are entirely absent here. Yet, given that phase-pure MoAlB has been shown to form upon PVD synthesis and its structural similarity to CrAlB, and stressing the aforementioned possibility of metastable phase formation in PVD, it should in principle be possible to obtain a Cr-rich (Mo,Cr)AlB phase (in other terms, Mo-stabilized CrAlB) upon addition of Mo.

In this contribution, we have investigated both the energies of formation in the ground state of MoAlB, CrAlB and several quaternary Mo_1−xCr_xAlB phases of varying composition, and their temperature-dependent Gibbs energies, both vs. the elements and vs. stable competing phases (as detailed further below) via density-functional theory (DFT) approaches. We have identified a minimum Mo concentration to stabilize the Cr-rich (Mo,Cr)AlB phase, serving as a prediction for guiding PVD-based synthesis attempts. Furthermore, we performed electronic structure and bonding analysis for CrAlB and MoAlB, as well as for select (Mo,Cr)AlB compositions, in order to elucidate electronic arguments for improved (Mo,Cr)AlB stability compared to the ternary CrAlB phase.

Methodology/computational details

All ab initio calculations for this study were performed using density-functional theory^24,25 as implemented in the Vienna ab initio Simulation Package (VASP, version 5.4.4., University of Vienna).^26–28 Basis set generation was handled via the projector-augmented wave method (PAW),^29,30 with a cut-off energy of 500 eV. Electronic exchange and correlation effects were accounted for using the well-established generalized gradient approximation functional as parametrized by Perdew, Burke and Ernzerhof (PBE).³¹ In addition to the valence electrons of each system, electrons in lower-lying levels were explicitly considered in the construction of the basis set (“semi-core state” approach) for the transition metals, resulting in electron configurations of 5s²4d⁴4s²4p⁶ for Mo, 4s²3d⁴3p⁶ for Cr, 3s²3p¹ for Al and 2s²2p¹ for B according to the VASP potential library. Brillouin zone integration was handled with the method of Methfessel–Paxton³² for a k-mesh generated with the Monkhorst–Pack approach.³³ The k-mesh sizes varied with the structures of the individual systems, which varied significantly depending on composition (as the use of supercells was necessitated in some cases), ranging from 17 × 5 × 17 for the formation energy calculations on the ternary systems to 1 × 1 × 1 Γ-point calculations for the lattice dynamics runs. A full list of k-mesh dimensions will not be given here; the k-mesh was in all cases set to be sufficiently dense to ensure energetic convergence, verified via trial runs. Unless otherwise specified, all systems were non-spin-polarized.

The initial structural model for MoAlB was obtained from literature,⁷ and subsequently fully optimized with respect to lattice parameters and atomic positions. The thus far experimentally unknown CrAlB phase as well as the quaternary compositions were generated by successively replacing Mo with Cr, using 2 × 1 × 1 supercells (with Z = 8) to model the compositions where, in Mo_1−xCr_xAlB, x = 0.125, 0.375, 0.625, 0.875, and using the MoAlB unit cell (with Z = 4) if x = 0, 0.25, 0.5, 0.75, 1. This resulted in the existence of several distinct ordered configurations for a given composition, which were subsequently fully optimized and compared in terms of their total energy. While the energetic difference between the individual configurations proved to be negligible, typically below 10 meV per system, the configurations with the lowest energy for each composition were chosen for further investigations. Modelling of disordered structures using larger supercells was not performed due to the significantly higher computational cost. An exemplary structural model for the Mo_0.5Cr_0.5AlB quaternary system is shown in Fig. 1.

Fig. 1 Structure of an exemplary 1 × 1 × 2 Mo_0.5Cr_0.5AlB supercell. Mo and Cr occupy the same lattice site, allowing for generation of different compositions by stepwise replacement of Mo in MoAlB. The characteristic MAB phase structural motif of trigonal prisms composed of transition metal and B atoms is highlighted. Mo blue, Cr red, Al turquoise, B black.

After optimization, the energies of formation at 0 K, ΔE_f, were then calculated vs. the elements and the most stable competing phases according to:

ΔE_f (0 K) = E_DFT (product) − ∑χ_iE_DFT (educts) (1)

with E_DFT as the total ground-state energy of the products, i.e. MoAlB, CrAlB and Mo_1−xCr_xAlB with varying x, and the educts, which are either the elements in their ground states (body-centered cubic (bcc) Mo, bcc-Cr, face-centered cubic (fcc) Al and rhombohedral α-B, chosen for reasons of computational feasibility) or the most stable competing phases Cr₂AlB₂, Mo₂AlB₂ and MoB.¹⁸ The correct stoichiometric coefficients, symbolized by χ_i, were considered in each case.

Analysis of the density of states and the crystal orbital Hamilton population (COHP)³⁴ to estimate electronic stability and bonding characteristics were performed via the LOBSTER package (version 4.0.0, Institute of Inorganic Chemistry, RWTH Aachen University),^35–38 post-processing wavefunctions obtained from VASP in single-point simulations of the optimized systems.

Lattice dynamics simulations based on finite displacement of atoms and phonon frequency sampling were performed to obtain ΔG(T) data using the phonopy package (version 2.11.0, University of Kyoto).³⁹ This allows for automated generation of supercells of varying size (depending on stoichiometry), but always near-cubic structure with a, b, c >10 Å, in which symmetry-inequivalent atoms are displaced from their equilibrium positions along a given vector with a length of 0.01 Å. The exact number of displacements strongly depends on the space group of the system for which they are generated, with high-symmetry structures requiring lower amounts of displacements; as such, the quaternary compositions, being lower in symmetry, require more. For each such displacement, a single-point VASP calculation yielded interatomic force constants for the given configuration, which were then extracted and post-processed by phonopy across all displacements for a given system. From the changes in the force constant matrices resulting from the displacements of individual atoms, the dynamical matrix D was calculated via a Fourier transformation, and from this the phonon frequencies were obtained. These in turn yield the lattice vibration contribution to the Helmholtz energy, A_ph, which is a dominant term, together with the electronic ground-state energy E₀, in the calculation of A(T,V):

A(T, V) = E₀(V) + A_ph(T, V) + ΔA_el(T, V) + A_conf(T) + A_{vib, ah}(T, V)

The electronic excitation energy ΔA_el can be summed with E₀, while the configurational term A_conf can be omitted for strictly ordered systems and the anharmonic part of the vibrational energy A_vib,ah is typically neglected due to computational cost. The volume dependence of the dominant terms E₀ and A_ph is accounted for by performing each set of simulations, containing all symmetry-inequivalent displacements for a given system, at several different volumes. Finally, fitting of the resulting data to the Birch–Murnaghan equation of state^40,41 yields the temperature dependence, allowing the calculation of ΔG(T) functions for a given reaction, analogous to eqn (1), but for G (following from A) instead of E_DFT. Further details for this approach are given elsewhere.⁴²

Results and discussion

Formation energies of the Mo–Cr–Al–B system in the ground state

As a first step in this investigation, the formation energies ΔE_f at T = 0 K were calculated for the ternary CrAlB and MoAlB phases as well as several quaternary compositions, corresponding to x = 0, 0.125, 0.25, 0.375, 0.5, 0.625, 0.75, 0.875 and 1 in Mo_1−xCr_xAlB. Formation from the constituting elements and from the most stable competing phases Mo₂AlB₂/MoB and Cr₂AlB₂ (as described in the methodology) were considered as scenarios, shown in Fig. 2a and b, respectively.

Fig. 2 DFT-derived energies of formation in the ground state (0 K) in the Mo_1−xCr_xAlB system vs. the elements Mo, Cr, Al, B (blue graph) and the corresponding equilibrium molar volumes (red graph) of each (Mo,Cr)AlB composition (a); vs. the most stable competing phases Mo₂AlB₂/Cr₂AlB₂/Al (blue graph) and MoB/Cr₂AlB₂/Al (pink graph) (b). Elemental Al is required to fulfil the stoichiometric ratio.

Considering formation from the elements, it is evident that the ternary and quaternary (Mo,Cr)AlB product phases are stable across the entire probed compositional range, with the formation energy for MoAlB (known to exist both in bulk^2,4,7 and as a phase-pure thin film^6,14) being approx. −131 kJ mol⁻¹ ≈ −0.113 eV per atom (as Z = 4). This is in excellent agreement with prior literature data by Khazaei et al. who reported a value of −0.114 eV per atom¹⁸ and Kota et al. with −132 kJ mol⁻¹.⁴³ While still negative, ΔE_f increases with higher Cr content, indicating a less energetically favored reaction, in a quasi-linear manner up to x = 0.5, broadly following an energetics version of Vegard's law. At higher x, the slope changes and ΔE_f reaches an energetic plateau at x ≈ 0.75, with further changes in the Mo/Cr ratio having no impact on the trend. This may serve as a first indicator that potential stabilization of the Cr-rich phase with Mo will likely begin to occur at Cr concentrations below that plateau, as the concentration of Mo at higher x is likely too dilute to significantly affect the potential energy surface of the system, with no discernible energetic gain. A linear decrease in equilibrium molar volume is also observed with increasing Cr content, which is to be expected due to the smaller radius -both atomic⁴⁴ and ionic⁴⁵- of Cr. The lattice parameters of MoAlB, CrAlB and the quaternary compositions (normalized to one constituting unit cell in the case of supercells to enable meaningful comparisons) are given in Table 1, likewise following Vegard's law.

Table 1 Lattice parameters from DFT of MoAlB, CrAlB and the quaternary compositions after full optimization at 0 K

Composition	a (Å)	b (Å)	c (Å)	α (°)	β (°)	γ (°)
MoAlB	3.22	14.04	3.11	90	90	90
Mo0.875Cr0.125AlB	3.20	14.02	3.10	90	90	90
Mo0.75Cr0.25AlB	3.18	13.97	3.08	90	90	90
Mo0.625Cr0.375AlB	3.14	14.00	3.06	90	90	90
Mo0.5Cr0.5AlB	3.13	13.92	3.05	90	90	90
Mo0.375Cr0.625AlB	3.09	13.95	3.03	90	90	90
Mo0.25Cr0.75AlB	3.07	13.91	3.01	90	90	90
Mo0.125Cr0.875AlB	3.03	13.90	2.99	90	90	90
CrAlB	3.00	13.89	2.97	90	90	90

---

When, however, formation from the competing phases (Fig. 2b) is considered, it is immediately evident that several Cr-rich (Mo,Cr)AlB phases are unstable (ΔE_f > 0), both for the ternary composition CrAlB (x = 1) and for quaternary compositions with low Mo content, such as Mo_0.125Cr_0.875AlB. This corresponds to prior findings for CrAlB^17–20 and may partially explain the lack of successful experiments synthesizing that phase in equilibrium, as alluded to in the introduction. Conversely, it is also evident that addition of Mo does indeed stabilize the quaternary system, with x ≈ 0.8 (corresponding to a Mo/Cr ratio of 1/5) sufficient for phase formation if MoB and Cr₂AlB₂ are the competing phases. If Mo₂AlB₂ (along with Cr₂AlB₂) is considered as the competing phase on the Mo side instead, the Mo/Cr ratio required for stabilization shifts to ca. 1/3, at x ≈ 0.67. In this case, the energetic plateau observed for the Cr-rich phases in Fig. 2a is also present (blue curve), while disappearing for the former scenario (pink curve): the reason for this divergent behaviour is unclear at present. To our knowledge, this is the first study expressly identifying these concentration thresholds and yielding a stability window for the Cr-rich quaternary (Mo,Cr)AlB system. However, we reiterate that these findings pertain to the T = 0 K scenario only, and thus, dependence of the Gibbs formation energies on temperature must be considered to obtain the full thermodynamic picture, as seen in the next section.

Temperature-dependent Gibbs energies for CrAlB and MoAlB vs. competing phases

To extend the described observations made in the ground state towards application-relevant temperatures, ΔG(T) curves from lattice dynamics simulations, followed by fitting to the Birch–Murnaghan equation of state, were performed, as detailed in the methodological section. Both the formation of the ternary systems CrAlB and MoAlB from the elements and the most stable competing phases (from literature¹⁸) as well as the formation of different quaternary Mo_1−xCr_xAlB compositions from either Mo₂AlB₂ and Cr₂AlB₂ or MoB and Cr₂AlB₂ were considered. The results are depicted in Fig. 3.

Fig. 3 Free Gibbs energies of formation ΔG(T) of the investigated systems for the temperature range 0 K–1500 K, obtained from lattice dynamics calculations and Birch–Murnaghan equation of state fits. (a and b) Formation of ternary CrAlB and MoAlB, respectively, from the elements and some of the primary competing phases (per literature 18). (c and d) Formation of quaternary (Mo,Cr)AlB for various Mo/Cr compositional ratios, as indicated in the key, from Mo₂AlB₂ and Cr₂AlB₂ and MoB and Cr₂AlB₂, respectively.

It is evident that the formation of CrAlB from Cr₂AlB₂ and Al is endergonic throughout the entire examined range (Fig. 3a), with ΔG ≈ 8 kJ mol⁻¹ at 0 K, in very good agreement with the calculation of the energy of formation (roughly equivalent to the enthalpy) in the preceding section (see Fig. 2b), and ΔG slightly increasing with higher T. Formation from the next-stable competing phase, CrB, and Al is exergonic in the ground state and at temperatures up to approx. 725 K, after which CrB and Al are thermodynamically more stable. The steeper slope of the ΔG(T) curve for the latter reaction in comparison to formation from Cr₂AlB₂ also suggests that at higher T, the ternary diboride is less stable vs. CrB and Al; however, as these phases were not the focus of the present study, this was not investigated further. Formation from all other phases (as indicated in the figure) and the elements is exergonic throughout the temperature range. Thus, the observation that Cr₂AlB₂ has been experimentally synthesized,⁷ while CrAlB could not be obtained is reflected in the course of the Gibbs energies. However, the energetic barrier towards formation is very small, with the highest difference in the observed temperature range being approx. 12 kJ mol⁻¹ ≈ 10 meV per atom at 1500 K. In a kinetically limited growth scenario such as during PVD synthesis, where the incident flux frequently exhibits high kinetic energies depending on the deposition parameters, this high-energy flux is rapidly quenched due to the difference in thermodynamic temperature between the substrate/growing film (in effect serving as a heat sink) and the incident particles. This may significantly kinetically limit atomic mobility and enable formation of CrAlB as a metastable phase (likely in coexistence with Cr₂AlB₂). Similar formation of metastable phases which were only slightly energetically disfavored has been previously observed for fcc-(Ti,Al)N with varying Ti/Al ratios, agreeing with theoretical predictions,²¹ as well as, recently, in orthorhombic MoAlB thin films, in which a two-dimensional MoB phase (MBene) and several metastable defects, which are energetically disfavored, coexist in the main phase.^10,46

In the case of MoAlB (Fig. 3b), all examined competing phases are thermodynamically disfavored, explaining the stability of said compound and its experimentally observed phase-pure formation;^6,7,14 however, the competing MoB phase is energetically very close at higher temperatures, and, if the curve is extrapolated, eventually likely forms instead of MoAlB, or as a main phase in a MoB/MoAlB/Al (or Al oxide) phase mixture. This agrees well with the prior finding that MoB formation in a two-dimensional MBene structure is possible not only through chemical etching and annealing,^8,9 but, crucially, also in a direct PVD synthesis route.¹⁰ Nonetheless, for the examined temperature range, the stability of MoAlB is unequivocal and, coupled with the observations from the ground-state energies of formation detailed above, suggests that a temperature-dependent investigation of select quaternary systems is worthwhile to find a potential Mo-induced stabilization effect, as depicted in Fig. 3c and d.

Analogous to the ground-state formation energy calculations, two scenarios were considered: formation of the quaternary Mo_1−xCr_xAlB phases with varying compositions from Cr₂AlB₂, Mo₂AlB₂ and Al (Fig. 3c) or from Cr₂AlB₂, MoB and Al (Fig. 3d). The selection of Mo₂AlB₂ and MoB as competing phases on the Mo side is reinforced by their status of being the least energetically disfavored compared to MoAlB, as outlined in the preceding paragraph. As lattice dynamics calculations are computationally highly expensive, particularly for systems whose stoichiometric ratios necessitate low-symmetry supercells, only the Cr-rich side of the compositional space was sampled, i.e., the area around the cross-over point identified in Fig. 2b. Thus, x in Mo_1−xCr_xAlB was chosen as 0.5, 0.625, 0.75 and 0.875. The ΔG(T) curves for the formation of CrAlB and MoAlB (x = 1 and 0, respectively) are also shown again as boundaries.

Once again, the (Mo,Cr)AlB system exhibits a Vegard-like behavior in terms of its energetics, as the progressive addition of Mo continually lowers the Gibbs energy of formation: while the formation of the composition Mo_0.125Cr_0.875AlB is thermodynamically disfavored in both scenarios across the entire temperature range, Mo_0.25Cr_0.75AlB forms from MoB, Cr₂AlB₂ and Al at 0 K (Fig. 3d), agreeing well with the cross-over point identified for this scenario in Fig. 2b, while formation from Mo₂AlB₂, Cr₂AlB₂ and Al is still disfavored; however, the exergonic energy is very small for this composition. For Mo_0.375Cr_0.625AlB, formation occurs vs. both MoB and Mo₂AlB₂ (Fig. 3c), yet again in good agreement with the data in Fig. 2b, where the cross-over point, if formation from Mo₂AlB₂ is considered, lies around x ≈ 0.67. Furthermore, it is immediately evident that addition of Mo extends the stability of the system towards higher temperatures, regardless of choice of competing phases.

To summarize, our postulate is two-fold: first, due to the low energetic barrier for formation of ternary CrAlB, it is likely that this phase forms in high-energy synthesis routes, at least as a metastable side phase, and may be isolated there. Second, energetic stabilization occurs upon substitution of Cr with Mo, so that a quaternary (Mo,Cr)AlB phase ought to form spontaneously, allowing phase-pure isolation for a given composition if the metal–metal ratio is tightly controlled. However, we must stress that we are considering thermodynamic arguments only – potential kinetic barriers (or pathways) that may influence the actual stability of (Mo,Cr)AlB are not examined here, lying outside the scope of this study.

Electronic structure comparison and bonding analysis of MoAlB, CrAlB and (Mo,Cr)AlB

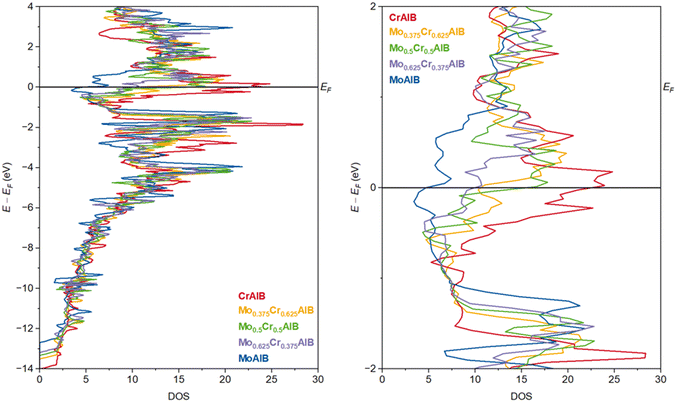
Having investigated the energetic trends in the ground state and at non-zero temperatures, we will briefly discuss the electronic structure of MoAlB, CrAlB and select quaternary systems as well as characteristic interatomic interactions to reinforce the outlined hypotheses from an electronic point of view. The total density of states (DOS) curves for MoAlB, CrAlB and the quaternary compositions Mo_0.375Cr_0.625AlB, Mo_0.5Cr_0.5AlB and Mo_0.625Cr_0.375AlB are depicted in Fig. 4, with the right-hand side figure magnifying the energetic area close to the Fermi level (E_F). It can be clearly seen that the DOS for all systems qualitatively strongly resemble each other, as expected from the structural and electronic similarity: in particular, the DOS of the quaternary compositions lie roughly between those of CrAlB and MoAlB (red and blue curves, respectively), fulfilling yet again the expectation from Vegard's law, generalized to the electronic structure.

Fig. 4 Comparison of the total density of states of MoAlB (blue curve), Mo_0.625Cr_0.375AlB (lilac curve), Mo_0.5Cr_0.5AlB (green curve), Mo_0.375Cr_0.625AlB (yellow curve) and CrAlB (red curve), with the region in proximity to the Fermi level (E_F) magnified in the right-hand excerpt.

However, particularly in proximity to E_F (between −0.5 and 0.5 eV relative to it), the Mo_0.5Cr_0.5AlB DOS (green curve) is closer to that of CrAlB, with both exhibiting local near-maxima at E_F, indicating localized states and, for metallic systems at E_F, serving as a marker for electronic instability due to reduced orbital mixing between adjacent atoms.⁴⁷ In contrast, the MoAlB DOS does not exhibit such a peak, with the electronic stability of the material in the ground state likely being higher. While this by no means precludes the formation of the other two phases per the arguments given above, it contributes to an explanation of why MoAlB is the more stable phase and the only one found experimentally so far despite the broad structural similarity of the phases. In the same vein, the Mo-rich quaternary phase Mo_0.625Cr_0.375AlB (lilac curve) lies closer to the MoAlB DOS at E_F, in good agreement with the expectation of Mo stabilizing the quaternary system. However, the behaviour of the Cr-rich quaternary Mo_0.375Cr_0.625AlB composition is an outlier here, as its DOS value at E_F, while lying above that of the Mo-rich phase, is markedly below that of Mo_0.5Cr_0.5AlB, and exhibits a local minimum. Nonetheless, generally speaking, the trend qualitatively follows the expectations.

While DOS plots are instructive to compare the electronic structures of different systems, they are less suited to a clear description of interatomic interactions, as antibonding and bonding character cannot readily be distinguished from the DOS alone. Thus, crystal orbital Hamilton population (COHP) analyses have been performed for MoAlB and CrAlB as the two ternary endpoints of the Mo–Cr–Al–B system, as well as for the equistoichiometric Mo_0.5Cr_0.5AlB, with the results shown in Fig. 5.

Fig. 5 Interatomic interaction analysis for MoAlB (blue squares), CrAlB (red squares) and Mo_0.5Cr_0.5AlB (red/blue half-filled circles signifying Cr and Mo species, respectively) via the crystal orbital Hamilton population (COHP) technique. (a) Comparison of the interatomic distances for each interaction type. (b) Average integrated COHP (ICOHP) values for a single bond of a given type, in eV, with the 1^st coordination shell of each atom in question considered. (c) Sum of the ICOHP values for a given interaction type for the entire unit cell, in eV.

From the visualization of the interatomic distances in Fig. 5a, it is immediately evident that they are quite similar in all phases, with the highest deviation occurring for the homoatomic transition metal bonds (Mo–Mo/Cr–Cr, respectively) at approx. 10%. It should be noted here that, when spin polarization is taken into account for the CrAlB system, the interatomic distances increase and are nearly identical to those in the MoAlB system, yet the interaction strengths are broadly similar to those in the non-spin-polarized case depicted here. Thus, the difference in interaction (bond) strengths is, as a rule, strongly dependent on interatomic distance, and this case is observed here, yet it can be counteracted by magnetic effects. However, the CrAlB system is the only system exhibiting antiferromagnetic behaviour, with all other systems being nonmagnetic, and the difference in total energy is marginal (approx. 5 meV) to the non-spin-polarized case. Thus, for consistency of comparison, and due to the fact that magnetism was not considered for the G(T) calculations due to computational cost, we further discuss only the non-spin-polarized case for CrAlB here.

Visualization of the averaged integrated COHP (ICOHP) values of a single interaction of a given type in the 1^st coordination sphere of an atom (Fig. 5b) and the summation of the ICOHP values per interaction type over the entire unit cell (Fig. 5c) reveals that all interactions are slightly stronger in MoAlB than in CrAlB, with the dominant interaction on a single, individual bond level (Fig. 5b) being the B–B bond, followed by the second-strongest individual interaction, Al–B. The other interactions, such as Al–Al, (Mo,Cr)–B etc., as given in the figure, are all significantly weaker, in good agreement with prior studies,¹⁸ with the homoatomic (Mo,Cr)–(Mo,Cr) interaction being weakest. This general trend is also well reflected in the case of the quaternary system Mo_0.5Cr_0.5AlB, in which the interatomic distances and averaged interactions typically lie between the values of the ternary endpoints, or are very close to the respective interaction in the ternary system with the corresponding metal. All interactions are of bonding character, as indicated by their negative ICOHP values. All interactions beyond the first coordination sphere are weaker by orders of magnitude and thus are not shown here. The individual ICOHP values for interactions in MoAlB and CrAlB, as well as the relative increase of the former vs. the latter, are shown in Table 2 in more detail, with the interactions in Mo_0.5Cr_0.5AlB not shown to improve readability.

Table 2 Average ICOHP value per single bond for the 1^st coordination sphere and the sum of all ICOHP values of a given interaction in the unit cell, in eV, for each type of interaction in MoAlB and CrAlB. The relative difference between both systems is also given. The very high relative difference in case of the homoatomic transition metal interaction is largely due to low strength, and resulting small ICOHP values

Interaction	Avg. ICOHP per bond (eV per bond)			Sum ICOHP per cell (eV)
	MoAlB	CrAlB	Δ rel (%)	MoAlB	CrAlB	Δ rel (%)
B–B	−6.03	−5.14	17.4	−27.62	−20.55	34.4
Al–B	−3.29	−2.73	20.3	−15.48	−13.29	16.5
Al–Al	−2.12	−1.87	13.2	−29.20	−27.43	6.5
(Mo,Cr)–B	−1.88	−1.37	37.1	−46.04	−33.24	38.5
(Mo,Cr)–Al	−1.54	−1.04	47.7	−29.20	−20.69	41.2
(Mo,Cr)–(Mo,Cr)	−0.78	−0.32	144	−11.12	−5.40	106

---

However, when the sum over all bonds of a given type is considered, as shown in Fig. 5c, the number of individual contacts plays a large role, which changes the picture dramatically. Besides the trivial observation that all interactions are bonding, as already shown, the bonding situation in the cell is dominated by the (Mo,Cr)–B interaction for both ternary systems, but dramatically stronger in MoAlB, as seen in Table 2. The (Mo,Cr)–Al interaction is second-strongest in MoAlB, tied with Al–Al, yet only in third place (clearly weaker than the Al–Al interaction) in CrAlB. The B–B interaction is much weaker in CrAlB compared to the MoAlB case, whereas the Al–Al interaction strength is largely unchanged between both systems. The dominant strength of the (Mo,Cr)–B interaction is in agreement with the findings of Bai et al.,¹⁷ who examined bond stiffness, typically well correlated with electronic bond strength; however, the Al–Al and (Mo,Cr)–Al interactions, when categorized by bond strength in this study, are stronger than suggested by the bond stiffness data. For the quaternary system, the ICOHP values split into contributions from Mo–X and Cr–X bonds, with X signifying all other species; when these values are summed, the resulting transition metal-heteroatom interactions again lie between the values in CrAlB and MoAlB.

Thus, summarizing, it can be said that the bonding contribution to MoAlB stability comes from the increased strength of all interatomic bond types, despite largely unchanged distances, with the main drivers being the interactions of Mo with Al and B. However, while these quantitative differences are significant, particularly in terms of increase when comparing CrAlB and MoAlB, the qualitative trends when identifying interactions from weakest to strongest are identical in both cases, yet again reflecting both systems’ similarity. Finally, we should add as a cautionary note that, strictly speaking, the COHP technique only yields the covalent portion of the interaction and is only an indirect (but strongly correlated) descriptor of the actual bond strength;⁴⁷ nonetheless, the technique is regularly used to study metallic systems in literature and typically, trends are reproduced fairly well.^48–50

Conclusions

We have carried out density functional theory-based theoretical studies of MoAlB, the hypothetical isostructural CrAlB and select quaternary Mo_1−xCr_xAlB compositions, with particular focus on their energies of formation and their temperature dependence. CrAlB is shown to be stable vs. the elements both in the ground-state at 0 K and across the investigated temperature range between 0 and 1500 K, but is unstable vs. the main competing phase Cr₂AlB₂. However, the energetic difference is very small, on the order of approx. 10 kJ mol⁻¹ or 0.008 eV per atom, which can readily be overcome in a kinetically limited synthesis scenario, such as physical vapor deposition, where the presence of energetically disfavored defect phases has been experimentally observed for MoAlB before. Furthermore, already in the ground state at 0 K, alloying with small amounts of Mo lowers the formation energy of the quaternary phase vs. that of the most stable competing phases Cr₂AlB₂ and Mo₂AlB₂ or Cr₂AlB₂ and MoB, resulting in critical Mo/Cr ratios of 0.33 and 0.2, respectively, at which the quaternary phase is expected to form based on energetic arguments alone. This is also reflected in the temperature-dependent Gibbs energies of formation, with the composition Mo_0.375Cr_0.625AlB remaining stable at up to 600 K (vs. Mo₂AlB₂) or 1100 K (vs. MoB), and higher Mo concentrations enabling stability at yet higher temperatures. Thus, a predicted compositional threshold for stabilization via alloying is provided for future synthesis attempts. Finally, the experimentally known stability of MoAlB is rationalized via the electronic structure and bonding characteristics, which hints at stronger bonds of all types in MoAlB when compared to CrAlB and identifies the Mo–B interaction as the main stabilizing influence in that respect, even though the B–B interaction is stronger on an individual bond basis.

Author contributions

D. B. and J. M. S.: Conceptualization, methodology. D. B: Investigation (lead), formal analysis, writing of original draft and editing. P. J. P: Visualization, investigation (supporting), writing (review/editing), data curation. J. M. S: Supervision, funding acquisition, resources, writing (review/editing).

All authors have contributed and given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

D. B. and J. M. S. thank the IT Center of RWTH Aachen University for the provision of computational resources and IT support via the Jülich-Aachen Research Alliance's (JARA) JARA0221 grant. J. M. S. acknowledges financial support from the MPG fellow program.

Notes and references

1. S. Kota, M. Sokol and M. W. Barsoum, Int. Mater. Rev., 2020, 65, 226–255.
2. L. Xu, O. Shi, C. Liu, D. Zhu, S. Grasso and C. Hu, Ceram. Int., 2018, 44, 13396–13401.
3. N. F. Rosli, M. Z. M. Nasir, N. Antonatos, Z. Sofer, A. Dash, J. Gonzalez-Julian, A. C. Fisher, R. D. Webster and M. Pumera, ACS Appl. Nano Mater., 2019, 2, 6010–6021.
4. S. Kota, E. Zapata-Solvas, A. Ly, J. Lu, O. Elkassabany, A. Huon, W. E. Lee, L. Hultman, S. J. May and M. W. Barsoum, Sci. Rep., 2016, 6, 26475.
5. O. Shi, L. Xu, A. Jiang, Q. Xu, Y. Xiao, D. Zhu, S. Grasso and C. Hu, Ceram. Int., 2019, 45, 2446–2450.
6. J.-O. Achenbach, R. Sahu, B. Völker, M. Hans, D. Primetzhofer, D. J. Miljanovic, C. Scheu and J. M. Schneider, Coatings, 2019, 9, 510.
7. M. Ade and H. Hillebrecht, Inorg. Chem., 2015, 54, 6122–6135.
8. L. T. Alameda, C. F. Holder, J. L. Fenton and R. E. Schaak, Chem. Mater., 2017, 29, 8953–8957.
9. L. T. Alameda, P. Moradifar, Z. P. Metzger, N. Alem and R. E. Schaak, J. Am. Chem. Soc., 2018, 140, 8833–8840.
10. R. Sahu, D. Bogdanovski, J. O. Achenbach, S. Y. Zhang, M. Hans, D. Primetzhofer, J. M. Schneider and C. Scheu, Nanoscale, 2021, 13, 18077–18083.
11. W. Rieger, H. Nowotny and F. Benesovsky, Monatsh. Chem. Verw. Teile Anderer Wiss., 1965, 96, 844–851.
12. W. Jeitschko, Monatsh. Chem. Verw. Teile Anderer Wiss., 1966, 97, 1472–1476.
13. S. Wang, Y. Xu, Z. Yu, H. Tan, S. Du, Y. Zhang, J. Yang and W. Liu, Ceram. Int., 2019, 45, 23515–23521.
14. S. Evertz, P. Pöllmann, D. M. Holzapfel, E. Mayer and J. M. Schneider, J. Eur. Ceram. Soc., 2021, 41, 6302–6308.
15. S. Kota, W. Wang, J. Lu, V. Natu, C. Opagiste, G. Ying, L. Hultman, S. J. May and M. W. Barsoum, J. Alloys Compd., 2018, 767, 474–482.
16. H. Zhang, F.-z. Dai, H. Xiang, Z. Zhang and Y. Zhou, J. Mater. Sci. Technol., 2019, 35, 530–534.
17. Y. Bai, X. Qi, X. He, D. Sun, F. Kong, Y. Zheng, R. Wang and A. I. Duff, J. Am. Ceram. Soc., 2019, 102, 3715–3727.
18. M. Khazaei, J. Wang, M. Estili, A. Ranjbar, S. Suehara, M. Arai, K. Esfarjani and S. Yunoki, Nanoscale, 2019, 11, 11305–11314.
19. A. Rastogi, P. Rajpoot and U. P. Verma, Mater. Chem. Phys., 2018, 211, 242–248.
20. J. Wei, L. Zhang and Y. Liu, Solid State Commun., 2021, 326, 114182.
21. P. H. Mayrhofer, D. Music and J. M. Schneider, J. Appl. Phys., 2006, 100, 094906.
22. S. Okada, K. Iizumi, K. Kudaka, K. Kudou, M. Miyamoto, Y. Yu and T. Lundström, J. Solid State Chem., 1997, 133, 36–43.
23. Y. Yu and T. Lundström, J. Alloys Compd., 1995, 226, 5–9.
24. P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871.
25. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138.
26. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
27. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
28. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
29. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
30. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
32. M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
33. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
34. R. Dronskowski and P. E. Bloechl, J. Phys. Chem., 1993, 97, 8617–8624.
35. V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461–5466.
36. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2013, 34, 2557–2567.
37. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030–1035.
38. R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940.
39. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
40. F. D. Murnaghan, Proc. Natl. Acad. Sci. U. S. A., 1944, 30, 244–247.
41. F. Birch, Phys. Rev., 1947, 71, 809–824.
42. R. P. Stoffel, C. Wessel, M.-W. Lumey and R. Dronskowski, Angew. Chem., Int. Ed., 2010, 49, 5242–5266.
43. S. Kota, M. Agne, E. Zapata-Solvas, O. Dezellus, D. Lopez, B. Gardiola, M. Radovic and M. W. Barsoum, Phys. Rev. B, 2017, 95, 144108.
44. J. C. Slater, J. Chem. Phys., 1964, 41, 3199–3204.
45. R. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
46. R. Sahu, D. Bogdanovski, J.-O. Achenbach, J. M. Schneider and C. Scheu, Nanoscale, 2022, 14, 2578–2585.
47. R. Dronskowski, Computational chemistry of solid state materials a guide for materials scientists, chemists, physicists and others, Wiley-Blackwell, Weinheim, 2005.
48. G. A. Landrum and R. Dronskowski, Angew. Chem., Int. Ed., 2000, 39, 1560–1585.
49. A. Saksena, D. Bogdanovski, H. Sahasrabuddhe, D. Music and J. M. Schneider, Materials, 2020, 13, 2298.
50. S. Amano, D. Bogdanovski, H. Yamane, M. Terauchi and R. Dronskowski, Angew. Chem., Int. Ed., 2016, 55, 1652–1657.

---