Photothermal motion: effect of low-intensity irradiation on the thermal motion of organic nanoparticles

Abstract

The effect of local photo-triggered heat release on the motion of organic nanopartcles (NP), a process that is itself thermal, is largely unexplored under low-intensity irradiation. Here, we develop organic NP specifically tailored for this study and demonstrate, comparing three different irradiation intensity regimes, that indeed the NP undergo “acceleration” upon light absorption (Photothermal Motion). These NP have a well-defined chemical composition and extremely high molar absorbance coefficient, and upon excitation, they deactivate mostly non radiatively with localized heat dissipation. The residual fluorescence efficiency is high enough to allow the detection of their trajectory in a simple wide field fluorescence microscope under low-intensity irradiation, a typical condition for NP bio-applications. The NP were characterized in detail from the photophysical point of view using UV-VIS absorption, steady-state and time-resolved fluorescence spectroscopy and ultra-fast transient absorption (UF-TA). A detailed analysis of the trajectories of the NP reveals a strong dependency of the diffusion coefficient on the irradiation intensity even in a low power regime. This behavior demonstrates the inhomogeneity of the environment surrounding the NP as a result of local heat generation. Upon irradiation, the effective temperature increase, that emerges from the analysis, is much larger than that expected for plasmonic NP. Anomalous diffusion object-motion analysis (ADOMA) revealed that, in the more intense irradiation regime, the motion of the NP is a fractional Brownian motion, which is a simple generalization of Brownian motion where the steps are not independent of each other.

---

Introduction

The photothermal effect finds applications in fields of high social and economic impact related to energy conversion,^1,2 water purification,^3,4 organic synthesis (e.g., photothermal catalysis)^5,6 and nanomedicine (e.g., tumor photothermal therapy).^7–10 It can be described as the increase of the temperature of both a light absorber, typically nanosized and often termed as a photothermal agent (PA), and of the surrounding environment upon light absorption. The main feature that distinguishes the photothermal effect with respect to conventional heating is that it produces a high spatially localized temperature increase without a global macroscopic enhancement. Plasmonic nanoparticles (NP) (mostly gold) have demonstrated to be very efficient PAs and therefore, photothermal heating of plasmonic NP found outstanding applications.¹¹ Despite the unique properties of plasmonic NP, the possibility of replacing them with organic NP, which are less expensive, more versatile and available on a large scale, is intriguing.^12,13 Nevertheless, since organic NP, in particular those based on organic fluorophores, undergo photodegradation (which becomes a serious issue at high irradiation intensities), understanding if any photothermal effect can be observed at low to moderate light power is a major point in view of their use in photothermal based processes.

Additionally, organic NP are found to have important and widely spread light-based applications for which photothermal effect is not required but may be involved and the light irradiation intensity is typically moderate.^14–17 Hence understanding the effect of photothermal heating on the behavior of organic NP is in general important for all their light-based applications.

Despite this, the investigation of this phenomenon is still incomplete. What is still only partially developed is indeed the comprehension of the most characteristic features of photothermal effect, i.e. how it affects the local microscopic environment in the close proximity of organic NP.^18–20

In particular, it is quite surprising that, although it is well-known that the motion of these NP dispersed in a “solvent” is a thermal process, the effect of light irradiation on this process is almost completely unexplored.

In this work, we investigate the effect of light irradiation on the thermal motion of a family of organic NP that were designed specifically to maximize the photothermal heat generation, while still maintaining a fluorescence signal strong enough to allow their detection by fluorescence microscopy. Our approach is original since PAs are typically plasmonic metal NP which exploit hot-electron generation upon light absorption, and that are typically non-fluorescent, a feature that makes them not easily trackable.²¹ As a further advantage, the NP presented in this work were obtained directly by the self-assembly of a molecular fluorophore in pure water, without the addition of any stabilizer. Therefore, the resulting NP have not only a monodisperse size distribution but also a very well-defined chemical composition.

In order to understand how light intensity affects the average displacement rates of the NP and whether the effect of irradiation changes in time, revealing some “memory” of the irradiation time, we acquired and analyzed the trajectories of the NP under different irradiation intensity regimes. In particular we focused on three different irradiation intensities that we classified as I₁, I₂ and I₃, demonstrating a clear increase of the linear thermal displacements (Δr) of the NP with the irradiation intensity. We would like to stress that in all the three irradiation regimes the irradiance is low when compared to focalized laser excitation typically used in photothermal experiments. This allowed us to explore the effect of illumination on the NP thermal motion under very important and common conditions typical for most applications of organic NP. Additionally, we investigated the change of the displacement, Δr, of the NP as a function of time in the three irradiation regimes. Although the overall behavior of the system could be described assuming a conventional Brownian motion, the most significant trajectories (ten for each irradiation regime) were processed specifically to identify possible deviations from this behavior by exploiting anomalous diffusion object-motion analysis (ADOMA). This latter study revealed that, in the presence of strong irradiation, the motion of the NP is a fractional Brownian motion, which is a simple generalization of Brownian motion where the steps are not independent of each other. Moreover, the diffusion process can be described as due to local inhomogeneities that are caused by the energy dissipation of the absorbed light. The important implications of these results will be discussed in the Conclusions section.

Results and discussion

The main objective of the present study was to demonstrate, using techniques as simple as time-lapse fluorescence microscopy, whether and to what extent the absorption of photons by freely diffusing, self-standing NP could enhance their thermal motion as a result of the local dissipation of the absorbed energy in the form of heat, as schematized in Fig. 1.

Fig. 1 (a) Schematic illustration of the experimental set up indicating the wide field irradiation area (375 μm diameter), and the detected area used in the present work compared to the focused system used in previously reported experiments (b). (c) Schematic structure of the organic NP and representation of the sub nanoparticle level heat dissipation process. (d–f) Schematic illustration of the displacement of the NP upon increasing the irradiation intensity: I₁ < I₂ < I₃.

We would like to stress that our experimental approach (schematized in Fig. 1a) is substantially different from the ones proposed to investigate the photothermal effect^22–24 of plasmonic NP (schematized in Fig. 1b) in the cases of photothermal microscopy and photothermal correlation spectroscopy.^25–27 In these techniques, in fact, the excitation light is focused on a small volume of the sample and a change in the medium properties is detected with a second analysis beam. This means that the irradiation is very localized and intense. In contrast, we irradiate homogenously a wide area of the NP sample and we analyze the trajectories of the NP that, under these conditions, undergo low-intensity excitation. Additionally, instead of measuring changes in the local properties of the medium (those at low irradiation intensities are hardly detectable) we exploit the analysis of the trajectory to visualize the local effect of irradiation. Information achievable with the experiment we propose implies an operating condition which is very different from the one used e.g. in photothermal microscopy. Our experimental conditions, importantly, represent a typical irradiation situation in most light-based applications of organic NP. Excitation of fluorophore based organic NP at low continuous intensity is, in fact, a very general situation for light-based biomedical applications, solar energy conversion, photocatalysis and light-based environmental remediation. Understanding how weak irradiation affects the thermal behavior of the organic NP has hence high impact both from the fundamental and applicative point of views. For this, our experiment and results are totally unique and essential in complementing the information given by photothermal microscopy.

We would like to stress that for this kind of approach the design of NP was of key importance, since in order to enhance this potential “photothermal acceleration” and make it detectable, it is required that: (i) the NP absorb light very efficiently (i.e. they should have a very high molar absorption coefficient, ε); (ii) the NP dissipate the absorbed radiative energy mostly as heat (non-radiative deactivation pathways should be much more efficient than the radiative ones, resulting in a fluorescence quantum yield (QY) close to zero) but at the same time: (iii) the NP brightness, defined as the product of ε by the QY, needs to be high enough to make them detectable.²⁸ Additionally, the NP: (iv) should have an optimal size for the tracking experiment (∼100 nm), since much smaller NP would diffuse very fast and would be difficult to track, while for much larger particles diffusion would be very slow and other phenomena may affect the motion; (v) the NP should have good photostability in order to withstand intense irradiation for enough time and (vi) they should present a large Stokes shift, important to increase the signal to noise ratio in fluorescence microscopy. As we will show, perylene-diimide (PDI) based NP share all these features.

It is important to underline that the photophysics of organic NP and plasmonic NP are very different and in the case of NP made of organic fluorophores, like the one we discussed here, excitation is quite localized and, although excited states or excitons can migrate and evolve fast, deactivation, and hence heat release, occur in a very small volume including few molecules and hence a volume which is much smaller than the size of the NP (as schematized in Fig. 1c).

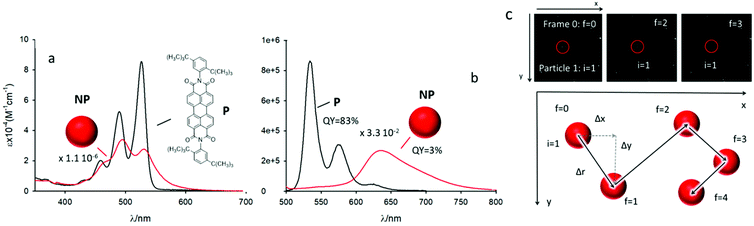
In order to meet all these requirements, we used organic fluorescent NP obtained using the precursor P (N,N′-bis(2,5-di-tert-butylphenyl)-3,4,9,10-perylenedicarboximide), shown in Fig. 2. This molecule belongs to the family of PDI, a well-known class of photostable dyes with high ε that, upon π–π stacking, undergo a large decrease of the high fluorescence QY and a huge red-shift of the fluorescence band.^29–34 Owing to these properties, PDI aggregates (and NP) present large Stokes shifts, as well as fast and efficient non-radiative deactivation while still maintaining a QY high enough to allow their detection. In particular, we succeeded in preparing fluorescent NP by nanoprecipitation of P in water in the absence of any stabilizing agent.³⁵ These NP had a hydrodynamic diameter, d ∼130 nm, corresponding to ∼9.0 × 10⁵ molecules per NP (see the ESI†). For simplicity, the PDI NP described before will be referred in the rest of the article as NP. The strong π–π stacking interaction between the molecules and their substantial insolubility in water made the NP stable for several days even at a very low concentration (1 pM). Dynamic light scattering (DLS) measurements demonstrated that their size is temperature independent in the 20–50 °C range (ESI†). From the hydrodynamic diameter, the diffusion coefficient of the NP in water at 20 °C can be calculated using the Stokes–Einstein equation to be D = 3.3 × 10⁻¹² m² s⁻¹. The NP were characterized in detail from the photophysical point of view in order to demonstrate that they satisfy the requirements listed above for the tracking experiments.

Fig. 2 (a) Molar absorption coefficient, ε, spectra of P (black line, c = 1.2 × 10⁻⁶ M) in dichloromethane and the NP (c_NP = 2.9 × 10⁻¹² M) in H₂O (red line). (b) Fluorescence spectra and fluorescence QYs of P (black line, c = 1.2 × 10⁻⁶ M) in dichloromethane and the NP in H₂O (red line). (c) Representative images of the fluorescent NP acquired during the time-lapsed sequence used for the NP tracking and schematic trajectory of a NP, the coordinates x and y represent the position of the particles in the different frames f.

The photophysics

The UV-Vis absorption and fluorescence spectra of the NP in water at c = 2.9 × 10⁻¹² M are shown in Fig. 2a–b, in which they are compared with the spectra of the P molecule in dichloromethane (DCM, 1.2 × 10⁻⁶ M). The monomer presented the typical vibrational structure of the PDI chromophore both in the absorption and fluorescence bands, its fluorescence QY was as high as 83% and the excited state lifetime, measured by time correlated single photon counting (TCSPC), was τ = 4.3 ns. The formation of NP from the self-assembly of P in water was confirmed by the absorption spectrum shown in Fig. 2a, where the perturbation of the monomeric vibronic progression along with the oscillator strength enhancement of the 0–1 transition, over the 0–0 transition,³⁶ indicating the presence of strongly coupled H-aggregates in the NP. It must be underlined that at 460 nm the molar absorption coefficient was as high as ε₄₆₀ = 1.55 × 10¹⁰ M⁻¹ cm⁻¹.

The fluorescence spectrum of the NP, upon excitation at 460 nm (the same wavelength that will be used for the tracking experiment using a microscope), is shown in Fig. 2b and it presented the typical broad band at ∼635 nm of the PDI excimer with a fluorescence QY 3%.³⁷ A photothermal conversion efficiency of 97% can hence be calculated for the system. This value was substantially confirmed by the direct measurement with a conventional method³⁸ that gave a photothermal conversion efficiency of 95% (see ESI†).

TCSPC allowed the investigation of the kinetics of the fluorescent excited state formation and deactivation: the kinetic traces at 20 °C demonstrated that the formation of the emitting state was fast (less than 100 ps), while the deactivation was multi-exponential and could be fitted with a tri-exponential decay according to the model reported in the ESI giving τ₁ = 1.2 ns (B₁ = 35%), τ₂ = 4.4 ns (B₂ = 46%), and τ₃ = 13.7 ns (B₃ = 19%), corresponding to an average excited state lifetime <τ> = 5.0 ns (Fig. 3d). As shown in the ESI†, only a minor decrease in the fluorescence QY and excited state lifetime of the NP was observed upon increasing the temperature from 20 to 50 °C.

Fig. 3 (a) Ultrafast transient absorption (UF-TA) spectra of the NP in water after 520 nm photoexcitation at 0.5 ps, 5 ps, 100 ps, 500 ps and 950 ps pump–probe delay times. The inset shows the UF-TA temporal traces at 590 nm (red) and 690 nm (blue), until 10 ps. (b) Evolution associated spectra (EAS) obtained from the global analysis of NP, after 520 nm excitation, using a three-level sequential scheme (c) A predicted de-activation model of the NP, after excitation of the upper allowed energy level, summarizing the excited state dynamics measured by UF-TA and time-resolved fluorescence (d) Time resolved emission spectra (TRES) of the NP.

In order to understand better the dynamics of the NP in the excited state, and in particular the heat dissipation process, we performed ultra-fast transient absorption (UF-TA) measurements. The sample was pumped at 520 nm with sub-100 fs pulses, under low fluence conditions (1.5 μJ cm⁻²) in order to minimize multiphoton absorption and exciton–exciton annihilation processes, and probed with a broadband white-light continuum in the visible region.

As a reference the P monomer in DCM was initially evaluated. The UF-TA spectra of the reference P monomer (see the ESI) revealed the mirror-image structures of the ground state bleaching (GSB) and stimulated emission (SE) bands below 650 nm and a sharp excited state absorption (ESA) peak at 700 nm. These spectral features are characteristic of isolated molecules. For the NP, the UF-TA signals (Fig. 3a) showed a GSB band below 530 nm and no SE band, but rather a broad ESA band from 530 nm to 700 nm, which is strong evidence of the S1 → Sn transition resulting from the excimer formation in the excited state.^39,40 At early pump–probe delays (150 fs), one can observe the signatures of the PDI cation at 570 nm⁴¹ and the PDI anion at 615 nm,⁴² as well as the presence of Frenkel exciton at 700 nm, denoting the mixing of charge transfer (CT) and excitonic states.⁴⁰

Moreover, the rise components of the ESA bands in the 540–610 nm region, accompanied by the decay of the excitonic peak at 700 nm, can be attributed to a quenching process of the SE from the Frenkel exciton trapping prior to excimer formation.³⁹ In particular, the highly polar environment of the water solvent enhances the CT contribution to the excimer electronic structure,⁴³ making the ESA signal of the CT band of the excimer state prominent over the whole range of pump–probe delays (1 ns).

We performed a global analysis⁴⁴ of the UF-TA experiments on the NP, where the temporal evolution of the TA spectra was reproduced with a sequence of three exponential decays through the evolution associated spectra (EAS), as shown in Fig. 3b. The mixed CT and excitonic states relax to a CT-resonance excimer state within 1.4 ps via an incomplete symmetry-breaking charge separation (SB-CS) process. Subsequently, further stabilization of the CT-resonance excimer state, following structural re-arrangement towards the optimal emissive geometry, takes place over 140 ps. Finally, the energetically lowest CT-resonance excimer state energy decays back to the ground state within 5 ns (Fig. 3c). According to the energy-level scheme of the system, after the 460 nm (2.69 eV) excitation used for the tracking experiment conditions, the allowed upper energy state of the coherently coupled H-aggregates is populated. Within 1.4 ps, around 11% of the excitation energy is dissipated as heat due to internal conversion, while the lowest energy CT-resonance excimer state is populated. After 140 ps, an additional 29% of the excitation energy is dissipated as heat through the structural stabilization to the optimal excimer geometry. Finally, from the 60% of the excitation energy that survives to the excimer state after 140 ps, only 3% is following a radiative pathway with the remaining 57% undergoing non-radiative recovery to the ground state within 5 ns.

These details about the excited state dynamics confirm that the NP dissipate the absorbed radiative energy fast and efficiently into heat. Nevertheless, in order to understand better the photothermal activity of the NP, it is also important to consider the already mentioned high value of ε₄₆₀ of the NP since it is related to their ability to absorb light or, more properly, to the efficiency of excitation, which can be defined as the rate of excitation under given irradiation conditions. In particular, we can calculate (see the ESI†) that each NP, even under I₁ irradiation intensity conditions (irradiance 71.2 mW mm⁻²), absorbs up to 1 × 10⁹ photons per second with an average of one absorption event every 1 ns. From a different point of view, at a 460 nm excitation wavelength, in this I₁ intensity irradiation regime a single NP absorbs 4.3 × 10⁻¹⁰ J s⁻¹ that can be converted into heat with 95% efficiency giving 4.1 × 10⁻¹⁰ J s⁻¹. In contrast, a single non-aggregated P molecule (ε₄₆₀ = 2.0 × 10⁴ M⁻¹cm⁻¹) is excited only 1290 times per second and hence it absorbs only 5.6 × 10⁻¹⁶ J s⁻¹ that are converted into heat with a low efficiency of 17%, dissipating only 9.5 × 10⁻¹⁷ J s⁻¹. In short, a single NP dissipates as heat 4.3 × 10⁶ times more power than an individual P molecule. For the I₂ irradiation intensity (127.2 mW mm⁻²), the same considerations can be made and a single NP absorbs 1.8 × 10⁹ photons per second, corresponding to the release of 7.5 × 10⁻¹⁰J s⁻¹ as heat. Finally, for the I₃ irradiation regime (168.0 mW mm⁻²), a single NP absorbs 2.4 × 10⁹ photons per second dissipating as heat of 9.8 × 10⁻¹⁰ J s⁻¹.

The motion

For the tracking experiments, the NP were diluted at a concentration of 9.7 pM in pure water and analyzed with a wide field fluorescence microscope. A blue light emitting diode (λ_exc = 460 ± 10 nm) was focused through a lens on the back focal plane of the objective through a fluorescence cube to create a homogeneous light spot of 375 μm diameter on a thin film of NP solution (0.1 mm). The time-lapsed fluorescence image sequences were acquired with an ultrasensitive EMCCD camera at a rate of one image every Δt = 15 ms for a total time of 55.9 s, opening the irradiation beam with a shutter at the beginning of the acquisition. A typical image of the NP is shown in Fig. 2c. In order to measure the local temperature during the irradiation, a thermal camera positioned on the top of the sample was used. The transversal size of the solution was about 10 mm and hence in any case it was much larger than the size of the irradiation spot. As mentioned above, here we will describe and analyze the results obtained with three different irradiation regimes that, for simplicity, are named I₁ < I₂ < I₃ (corresponding to 71.2 mW mm⁻², 127.2 mW mm⁻² and 168.0 mW mm⁻² irradiances).

For the analysis of the trajectories, the time-lapsed image sequences were processed with Image J using the dedicated plug-in called Mosaic (see the ESI†).^45,46 As schematized in Fig. 2c, the trajectories were obtained as a series of pairs of coordinates of the particles x(i,f) and y(i,f), where i is an integer that identifies an individual particle (starting from i = 1) and f corresponds to the number of the frame (f = 0 for the first frame) where particle i was found at the x, y position. Therefore, as schematized in Fig. 2c, going from frame f to frame f + 1 the displacements along the x and y positions of particle i will be Δx = x(f + 1) − x(f), Δy = y(f + 1)−y(f) and the 2D displacement is simply . It should be stressed that: (i) for each particle, i, a set of displacements Δx, Δy and Δr are found and they correspond to a time interval Δt (which is 15 ms in all the cases) and (ii) each displacement is obtained by comparing the position of particle i in two sequential frames, f and f + 1, but conventionally is identified with the number of f that is acquired at time t = fΔt after the beginning of the experiment. As it will be discussed below these data can be analyzed also in a different way.

The diffusion process

First, all the displacements, Δx and Δy, were analyzed for all the NP independently of the frame in which they were observed, representing them in a histogram. The resulting distribution could be fitted with a Gaussian function (see the ESI†) allowing to calculate the diffusion coefficient D = 3.16 × 10⁻¹² m²s⁻¹. This analysis was extended to both the I₂ and I₃ intensity experiments giving, after the fitting, the values of D plotted in Fig. 4, which clearly demonstrate that the average diffusion coefficient D increases considerably with the increase of irradiance, consequently going from I₁ to I₂ to I₃ irradiance. This result demonstrates that the NP motion is augmented by increasing the light source intensity. Additionally, we demonstrated that the effect of irradiation was localized and did not lead to an overall heating of the solution. In fact, the thermal images showed that in all cases the increase of the temperature of the solution in the irradiated area was negligible, independently of the irradiation intensity (see the ESI†) and in all cases the measured temperature was between 21.2 and 21.8 °C with a standard deviation for each experiment lower than 0.2 °C.

Fig. 4 Diffusion coefficient, D, of the NP at different excitation intensity I₁ (71.2 mW mm⁻²), I₂ (127.2 mW mm⁻²) and I₃ (168.0 mW mm⁻²).

Change of the average NP displacement during irradiation

As mentioned above, Δx, Δy and Δr for each experiment correspond to different frames, f, and hence to different irradiation times, fΔt. In order to investigate the effect of irradiation time on the thermal movement of the NP we plotted the average square displacement 〈Δr²〉 as a function of irradiation time fΔt (Fig. 5). This latter calculation was done considering that, in general, a Brownian motion, that is the result of uncorrelated random events, yields a mean square displacement (MSD) 〈Δr²〉 that grows linearly in time according to:

〈Δr²〉 = 4DΔt(1) (1)

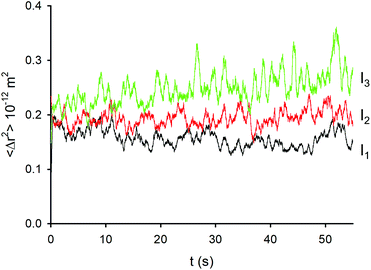Fig. 5 Average square displacements (over 500 data points) of the NP at different excitation intensities, I₁ (71.2 mW mm⁻²), I₂ (127.2 mW mm⁻²) and I₃ (168.0 mW mm⁻²).

Consequently, in the case of a defined time interval Δt, the corresponding expected displacement 〈Δr²〉 is proportional to the diffusion coefficient D. As shown in Fig. 5, a different dependence of 〈Δr²〉 on the irradiation time for the three different irradiation regimes was found. In particular, in the I₁ intensity regime 〈Δr²〉 fluctuates around an average value that does not change significantly during the experiment (and hence during the irradiation). In contrast, at I₃ intensity irradiation, 〈Δr²〉 increases gradually with the irradiation time, revealing a progressive increase of the displacement rate of the NP.

Extraction of the most significant trajectories

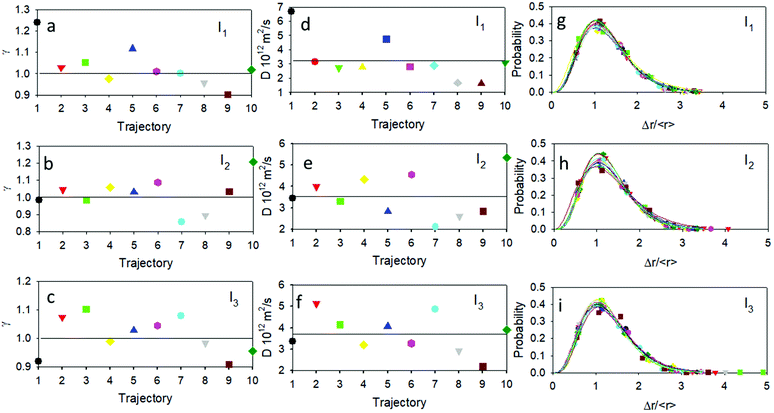
In order to investigate more in detail the nature of the diffusion process, we focused on the trajectory of individual NP selecting, since more statistically significant, the longest trajectories for which it was possible to measure a higher number of displacements. In particular, we extracted for each of the three experiments (I₁, I₂ and I₃ intensities), the ten longest trajectories. These ten trajectories do not in general correspond to the same ten NP at the three irradiation regimes.

The diffusion process in more detail

Brownian motion is the result of uncorrelated random events and yields a mean square displacement (MSD) 〈Δr²〉 that grows linearly in time according to eqn (1). Deviations from linearity have been reported in numerous fields including diffusion processes on surfaces and various models have been developed describing a departure from normal behavior, i.e. anomalous diffusion.⁴⁷ In these cases, the main manifestation of anomalous behavior is the dependence of the MSD on the scaling exponent, γ, can be modelled to eventually give:

〈Δr²〉 = 4DΔt^γ(2) (2)

A sound example concerns a newly observed class of stochastic processes where the motion is Brownian but not Gaussian.^48,49 ADOMA is a method that delivers detailed information on the motion,^50–52 and in particular is used to find the value of the scaling exponent, γ. The trajectories were analyzed by means of ADOMA revealing that the underlying stochastic process is monofractal. Importantly, the scaling exponent of the MSD is spread around a value of 1 as shown in Fig. 6. In more detail, for the lower irradiation intensity, I₁, 7 out of 10 trajectories had a scaling exponent equal to 1 (or very close to 1) pointing to Brownian motion, 2 trajectories had higher scaling exponents γ ≅ 1.1, a manifestation of slightly super-diffusive motion, and one experiment gave a scaling value of 0.9, indicating a slightly sub-diffusive motion. For the medium intensity I₂, 7 out of 10 trajectories had a scaling value equal or very close to one, one trajectory showed a scaling value 1.2, corresponding to super-diffusive motion, and two trajectories had scaling values lower than 0.9, with sub-diffusive motion. For the higher intensity I₃, 7 out of 10 trajectories had scaling values equal or very close to one, two trajectories showed scaling values of ∼0.9 (sub-diffusive behavior) and one showed a scaling value of 1.1 (super-diffusive behavior). The ensemble average, over all trajectories and for each intensity condition, returns scaling equal to one. The presence of a super-diffusive motion has been reported, in the case of plasmonic NP in the case of Janus structures for which photoinduced heat dissipation is non-homogeneous.²⁴ It is hence interesting to note that because of their photo-physics, as schematized in Fig. 1c, heat dissipation is expected to be non-homogeneous as in the case of Janus structures. Moreover, the estimated diffusion coefficient for the ensemble average was D = 3.22/3.53/3.70 (×10⁻¹² m² s⁻¹) for the I₁/I₂/I₃ intensities, values which are in good agreement with the literature for NP of this size⁵³ and can be well compared with the average diffusion coefficients D shown in Fig. 4.

Fig. 6 Plot of the scaling exponent of the scaling exponents (γ) per trajectory at (a) I₁ intensity, (b) I₂ intensity and (c) I₃ intensity. Plot of the effective diffusion coefficients (D) per trajectory at (d) I₁ intensity, (e) I₂ intensity and (f) I₃ intensity. The black solid lines represent the ensemble average values and the mean average value of the scaling exponent for each intensity is 1. Probability distributions of the random variable Δr/( < r > ) at (g) I₁ intensity, (h) I₂ intensity and (i) I₃ intensity.

The scaling exponent for the ensemble average points to Brownian motion and thus the diffusion coefficient, D, can be used for the estimation of the effective temperature of the system through the first dissipation fluctuation theorem. The estimation of the effective temperatures experienced by the NP were found to be 299/328/344 K for the I₁/I₂/I₂ intensity conditions, respectively. We would like to stress that the change in the temperature of the NP would be expected to be, in all the three cases, less than 2 K adopting the model proposed for plasmonic NP,⁵⁴ these results confirm the substantial difference between the photothermal behavior of plasmonic and organic NP. The strong effect of low-intensity irradiation on the thermal motion of the organic NP suggests that they present a strong asymmetry in photogenerated heat dissipation similar to what reported for Janus NP and in contrast to the symmetric temperature distribution expected in the case of spherical plasmonic NP. On the other hand, this asymmetry is consistent with sub-NP level head dissipation as schematized in Fig. 1c.

Importantly, the increase of the temperature followed the increase of illumination intensity and, as shown in the ESI†, the effective temperature is proportional to the irradiation intensity in the investigated range. The deviations of the effective temperature of the individual trajectories with respect to the ensemble average temperature imply that the systems are not in local equilibrium with the environment and, likely, point out a non-Gaussian behavior of molecule displacements.

In fact, the individual trajectories show the presence of local changes in diffusivity. The displacement, Δr, is a random variable whose distribution can express a departure from the normal distribution. We define the variable , where 〈r〉 is the mean value over the entire trajectory. The reason for the choice of parameter 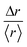is twofold; on one hand, if the probability of distributions was Gaussian, then it would be easily identified since it would be centered around one with symmetric tails; on the other hand, the use of allows the comparison of trajectories of different lengths. The probability distributions of 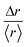are presented in Fig. 6. All particle trajectories showed right-skewed distributions with the maximum close to one. These probability distributions, with a maximum around the value of 1 and long tails, are typical of a fractional Brownian motion, which is a generalization of the Brownian motion where the sequential displacements do not need to be independent from each other.⁴⁷ Intermittency between the steps typical of continuous time random walk motion is not supported by these distributions, since for such a case, the maximum of distribution would be located close to zero.^47,48 As a final issue, we investigated concerns related to the possible accumulation of energy. When a system accumulates energy, reversing of the time series (from right to left) provides significant differences with respect to the original one. Indeed, when ADOMA was run for each trajectory from left to right and from right to left, the results did not change, clearly showing that energy is not accumulated.

Conclusions

In the present work, we demonstrated that the thermal motion of organic NP, which possess a very high molar absorption coefficient (1.55 × 10¹⁰ M⁻¹ cm⁻¹) and a high photothermal efficiency (∼95%), is affected by light irradiation in a way which strongly depends on the irradiation intensity. Heat dissipation upon irradiation produces in fact a local increase of the temperature in close proximity of the NP giving rise to an irradiation intensity-dependent diffusion (Photothermal Motion). The enhancement of the diffusion can be clearly determined by measuring the displacement of the NP using their residual fluorescence (QY < 3%) for their tracking. By comparing three different irradiation intensity regimes (I₁ < I₂ < I₃), we also demonstrated that although the overall motion, during the irradiation, can be described as Brownian motion with a Gaussian distribution of NP displacements: (i) the diffusion coefficient increases considerably going from the lower to the medium and finally to the higher intensity regime and (ii) at the higher intensity regime the diffusion coefficient increases with the irradiation time. This general behavior was confirmed by analyzing a set of ten trajectories for each irradiation regime. Interestingly, this analysis demonstrated that upon irradiation, the NP experience an increased inhomogeneity of the surrounding environment compatible with a local and irradiation intensity-dependent decrease of the viscosity in the presence of local turbulence. Although this latter mechanistic point is still under investigation, our results clearly demonstrate that the thermal diffusion of NP can be enhanced by the photothermal effect, opening new horizons for the local control of the motion of nano-objects.

Author contributions

All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Italian Ministry of Education, University and Research (MIUR), (PRIN project: PRIN 2017) 2017E44A9P (BacHound). VP and GC thank financial support from the Marie Sklodowska-Curie project 812992 – MUSIQ.

Notes and references

1. K.-T. Lin, H. Lin, T. Yang and B. Jia, Nat. Commun., 2020, 11, 1389.
2. Y. Zhang, J. Wang, J. Qiu, X. Jin, M. M. Umair, R. Lu, S. Zhang and B. Tang, Appl. Energy, 2019, 237, 83–90.
3. Z. Xie, Y. Duo, Z. Lin, T. Fan, C. Xing, L. Yu, R. Wang, M. Qiu, Y. Zhang, Y. Zhao, X. Yan and H. Zhang, Adv. Sci., 2020, 7, 1902236.
4. F. Zhao, Y. Guo, X. Zhou, W. Shi and G. Yu, Nat. Rev. Mater., 2020, 5, 388–401.
5. M. Ghoussoub, M. Xia, P. N. Duchesne, D. Segal and G. Ozin, Energy Environ. Sci., 2019, 12, 1122–1142.
6. J.-D. Xiao and H.-L. Jiang, Acc. Chem. Res., 2019, 52, 356–366.
7. S. Liu, X. Pan and H. Liu, Angew. Chem., Int. Ed., 2020, 59, 5890–5900.
8. B.-D. Zheng, Q.-X. He, X. Li, J. Yoon and J.-D. Huang, Coord. Chem. Rev., 2021, 426, 213548.
9. D. Xi, M. Xiao, J. Cao, L. Zhao, N. Xu, S. Long, J. Fan, K. Shao, W. Sun, X. Yan and X. Peng, Adv. Mater., 2020, 32, 1907855.
10. Y. Yang, X. Fan, L. Li, Y. Yang, A. Nuernisha, D. Xue, C. He, J. Qian, Q. Hu, H. Chen, J. Liu and W. Huang, ACS Nano, 2020, 14, 2509–2521.
11. G. Baffou, F. Cichos and R. Quidant, Nat. Mater., 2020, 19, 946–958.
12. F. Wu, L. Chen, L. Yue, K. Wang, K. Cheng, J. Chen, X. Luo and T. Zhang, ACS Appl. Mater. Interfaces, 2019, 11, 21408–21416.
13. T. Sun, H. Liu, N. Jiang, Q. Wu, C. Li, R. Xia, B. Gao and Z. Xie, Adv. Funct. Mater., 2021, 31, 2103714.
14. J. Chen, S. M. A. Fateminia, L. Kacenauskaite, N. Bærentsen, S. Grønfeldt Stenspil, J. Bredehoeft, K. L. Martinez, A. H. Flood and B. W. Laursen, Angew. Chem., Int. Ed., 2021, 60, 9450–9458.
15. K. K. Ng and G. Zheng, Chem. Rev., 2015, 115, 11012–11042.
16. A. Reisch, P. Didier, L. Richert, S. Oncul, Y. Arntz, Y. Mely and A. S. Klymchenko, Nat. Commun., 2014, 5.
17. K. Trofymchuk, A. Reisch, P. Didier, F. Fras, P. Gilliot, Y. Mely and A. S. Klymchenko, Nat. Photonics, 2017, 11, 657–663.
18. B. Davaji, J. E. Richie and C. H. Lee, Sci. Rep., 2019, 9, 6546.
19. R. Kamarudheen, G. W. Castellanos, L. P. J. Kamp, H. J. H. Clercx and A. Baldi, ACS Nano, 2018, 12, 8447–8455.
20. H. Moustaoui, J. Saber, I. Djeddi, Q. Liu, A. T. Diallo, J. Spadavecchia, M. Lamy de la Chapelle and N. Djaker, J. Phys. Chem. C, 2019, 123, 17548–17554.
21. M. Kim, J.-H. Lee and J.-M. Nam, Adv. Sci., 2019, 6, 1900471.
22. D. Rings, R. Schachoff, M. Selmke, F. Cichos and K. Kroy, Phys. Rev. Lett., 2010, 105, 090604.
23. D. Rings, M. Selmke, F. Cichos and K. Kroy, Soft Matter, 2011, 7, 3441–3452.
24. K. Kroy, D. Chakraborty and F. Cichos, Eur. Phys. J.: Spec. Top., 2016, 225, 2207–2225.
25. R. Radünz, D. Rings, K. Kroy and F. Cichos, J. Phys. Chem. A, 2009, 113, 1674–1677.
26. M. Selmke, R. Schachoff, M. Braun and F. Cichos, RSC Adv., 2013, 3, 394–400.
27. P. M. R. Paulo, A. Gaiduk, F. Kulzer, S. F. G. Krens, H. P. Spaink, T. Schmidt and M. Orrit, J. Phys. Chem. C, 2009, 113, 11451–11457.
28. I. Khalin, D. Heimburger, N. Melnychuk, M. Collot, B. Groschup, F. Hellal, A. Reisch, N. Plesnila and A. S. Klymchenko, ACS Nano, 2020, 14, 9755–9770.
29. F. Würthner, C. R. Saha-Möller, B. Fimmel, S. Ogi, P. Leowanawat and D. Schmidt, Chem. Rev., 2016, 116, 962–1052.
30. M. Sun, K. Müllen and M. Yin, Chem. Soc. Rev., 2016, 45, 1513–1528.
31. M. Montalti, G. Battistelli, A. Cantelli and D. Genovese, Chem. Commun., 2014, 50, 5326–5329.
32. V. Caponetti, A. Mavridi-Printezi, M. Cingolani, E. Rampazzo, D. Genovese, L. Prodi, D. Fabbri and M. Montalti, Polymers, 2021, 13.
33. K. Trofymchuk, A. Reisch, I. Shulov, Y. Mély and A. S. Klymchenko, Nanoscale, 2014, 6, 12934–12942.
34. D. Bialas, E. Kirchner, M. I. S. Röhr and F. Würthner, J. Am. Chem. Soc., 2021, 143, 4500–4518.
35. A. J. Gesquiere, T. Uwada, T. Asahi, H. Masuhara and P. F. Barbara, Nano Lett., 2005, 5, 1321–1325.
36. N. J. Hestand and F. C. Spano, Chem. Rev., 2018, 118, 7069–7163.
37. M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, CRC Press, 3rd edn, 2006.
38. Q. Tian, F. Jiang, R. Zou, Q. Liu, Z. Chen, M. Zhu, S. Yang, J. Wang, J. Wang and J. Hu, ACS Nano, 2011, 5, 9761–9771.
39. S. Kang, C. Kaufmann, Y. Hong, W. Kim, A. Nowak-Król, F. Würthner and D. Kim, Struct. Dyn., 2019, 6, 064501.
40. M. S. Myong, J. Zhou, R. M. Young and M. R. Wasielewski, J. Phys. Chem. C, 2020, 124, 4369–4377.
41. T. Kircher and H. G. Löhmannsröben, Phys. Chem. Chem. Phys., 1999, 1, 3987–3992.
42. D. Gosztola, M. P. Niemczyk, W. Svec, A. S. Lukas and M. R. Wasielewski, J. Phys. Chem. A, 2000, 104, 6545–6551.
43. W. Kim, A. Nowak-Król, Y. Hong, F. Schlosser, F. Würthner and D. Kim, J. Phys. Chem. Lett., 2019, 10, 1919–1927.
44. J. Snellenburg, S. Laptenok, R. Seger, K. Mullen and I. Van Stokkum, J. Stat. Softw., 2012, 49, 1–22.
45. I. F. Sbalzarini and P. Koumoutsakos, J. Struct. Biol., 2005, 151, 182–195.
46. N. Chenouard, I. Smal, F. de Chaumont, M. Maška, I. F. Sbalzarini, Y. Gong, J. Cardinale, C. Carthel, S. Coraluppi, M. Winter, A. R. Cohen, W. J. Godinez, K. Rohr, Y. Kalaidzidis, L. Liang, J. Duncan, H. Shen, Y. Xu, K. E. G. Magnusson, J. Jaldén, H. M. Blau, P. Paul-Gilloteaux, P. Roudot, C. Kervrann, F. Waharte, J.-Y. Tinevez, S. L. Shorte, J. Willemse, K. Celler, G. P. van Wezel, H.-W. Dan, Y.-S. Tsai, C. O. de Solórzano, J.-C. Olivo-Marin and E. Meijering, Nat. Methods, 2014, 11, 281–289.
47. R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164.
48. B. Wang, S. M. Anthony, S. C. Bae and S. Granick, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15160.
49. B. Wang, J. Kuo, S. C. Bae and S. Granick, Nat. Mater., 2012, 11, 481–485.
50. L. R. Parent, E. Bakalis, A. Ramírez-Hernández, J. K. Kammeyer, C. Park, J. de Pablo, F. Zerbetto, J. P. Patterson and N. C. Gianneschi, J. Am. Chem. Soc., 2017, 139, 17140–17151.
51. L. R. Parent, E. Bakalis, M. Proetto, Y. Li, C. Park, F. Zerbetto and N. C. Gianneschi, Acc. Chem. Res., 2018, 51, 3–11.
52. E. Bakalis, L. R. Parent, M. Vratsanos, C. Park, N. C. Gianneschi and F. Zerbetto, J. Phys. Chem. C, 2020, 124, 14881–14890.
53. C. B. Müller, K. Weiß, W. Richtering, A. Loman and J. Enderlein, Opt. Express, 2008, 16, 4322–4329.
54. G. Baffou, I. Bordacchini, A. Baldi and R. Quidant, Light: Sci. Appl., 2020, 9, 108.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr01041k

---