Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Ab initio, artificial neural network predictions and experimental synthesis of mischmetal alloying in Sm–Co permanent magnets†
Stefanos
Giaremis
 a,
Georgios
Katsikas
a,
Georgios
Sempros
a,
Georgios
Katsikas
a,
Georgios
Sempros
 a,
Margarit
Gjoka
b,
Charalambos
Sarafidis
a,
Margarit
Gjoka
b,
Charalambos
Sarafidis
 a and
Joseph
Kioseoglou
a and
Joseph
Kioseoglou
 *a
*a
aSchool of Physics, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece. E-mail: sifisl@auth.gr
bInstitute of Nanoscience and Nanotechnology, NCSR “Demokritos”, Athens, Greece
First published on 26th March 2022
Abstract
The use of the mischmetal alloy, comprised of La and Ce in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio, as a partial substitute for Sm in the CaCu5-type structure is explored, as a means for the search of viable alternatives for permanent magnets that require fewer steps in the rare earth separation processing. The structural and magnetic properties of the introduced stoichiometry, containing 50% less Sm, are compared to the ones of the SmCo5, LaCo5 and CeCo5 binary compounds by means of ab initio simulations. The capability of artificial neural networks to accurately predict the relationship between structure and total magnetization from DFT calculations in the supercell approach that was employed, is also demonstrated. Experimental fabrication and structural and magnetic characterization of the proposed stoichiometry verifies the structural configuration and provides insight for the macroscopic hard magnetic properties of the material. The reduction of magnetic properties was found to be favorable compared to the respective reduction of the raw materials cost, while measurements of the Cure temperature verify that the proposed compound is still suitable for high temperature applications.
3 ratio, as a partial substitute for Sm in the CaCu5-type structure is explored, as a means for the search of viable alternatives for permanent magnets that require fewer steps in the rare earth separation processing. The structural and magnetic properties of the introduced stoichiometry, containing 50% less Sm, are compared to the ones of the SmCo5, LaCo5 and CeCo5 binary compounds by means of ab initio simulations. The capability of artificial neural networks to accurately predict the relationship between structure and total magnetization from DFT calculations in the supercell approach that was employed, is also demonstrated. Experimental fabrication and structural and magnetic characterization of the proposed stoichiometry verifies the structural configuration and provides insight for the macroscopic hard magnetic properties of the material. The reduction of magnetic properties was found to be favorable compared to the respective reduction of the raw materials cost, while measurements of the Cure temperature verify that the proposed compound is still suitable for high temperature applications.
1. Introduction
SmCo5 permanent magnets (PM) were originally developed over 4 decades ago and were found to present strong uniaxial magnetocrystalline anisotropy (MCA), high saturation magnetization and Curie temperature, Tc (∼1000 K).1 In fact, to date, they present one of the largest values of magnetocrystalline anisotropy energy (MAE) (∼17.2 MJ m−3). This value is larger than that of Nd2Fe14B (∼4.9 MJ m−3), while also the value of the Tc is almost double (∼588 K for Nd2Fe14B). Recent advances in chemical synthesis2,3 has also led to the fabrication of SmCo5 nanoparticles with equally interesting magnetic properties.4,5 However, Nd2Fe14B based magnets dominate the market with over two thirds of the overall share, due to their record high energy product (theoretical maximum (BH)max = 512 kJ m−3), which is double than the corresponding value for SmCo5 ((BH)max = 231 kJ m−3).6,7Regarding the industrial trends though, there is a growing demand for PMs that are capable to operate at high temperatures for applications such as electric vehicles and turbines. The performance of Nd2Fe14B PMs in such applications is maintained by substitution of Nd by Dy or Tb.6 However, the price of Dy and Tb is several times higher than that of Nd, with Dy and Tb being scarcer than Nd and all the three elements reaching a price peak at the time this paper is written, due to recent geopolitical circumstances.8 SmCo5 magnets, although currently representing a substantially smaller portion of the total market share and having a smaller energy product, are also suitable for high temperature applications due to their thermal stability.6 The remaining one third of the PM market, besides Nd2Fe14B, SmCo5 and the old AlNiCo PMs, is represented by ferrites, which are based on abundant and cheap materials but have a low energy product (<100 kJ m−3). Thus, there is room for development of PMs that are less dependent on commercially critical and expensive elements, with an energy product (BH)max, that lies on the gap between and 100 and 200 kJ m−3, which is the gap between ferrites and Nd2Fe14B based PMs.6,9
Among the family of rare-earth (RE) – transition metal (TM) intermetallic phases, RE-TM5 is of particular interest for the development of new permanent magnets due to their magnetic properties arising from the strongly correlated electrons of the partially filled 3d states in the TM atom network and the anisotropy induced from the 4f electrons of the RE atoms.10 Bonding is dominated by the interaction of the itinerant TM 3d orbitals with the localized 4f ones of the RE atoms.10 They crystallize preferably in the hexagonal, (P6/mmm, No. 191), CaCu5 structure,11 made of alternating hexagonal layers of the TM atoms (2c positions) and ones with the RE atoms in the center of the plane and TM surrounding them (3g positions) arranged in a Kagome network.12 This arrangement of the TM atoms is responsible for the large values of MAE reported for this family of materials, as its associated crystal electric field arising from the itinerant 3d electrons pins the aspherical 4f orbitals at the RE atoms sites.13 The 3d sublattice of the TM atoms is dominant from a structural point of view for the magnetic properties and especially magnetization. This fact implies that, theoretically, the RE atoms are not indispensable for the anisotropy,6 while the use of Co as TM is preferred due to its excellent magnetic properties, arising from its 3d states.14–17
As mentioned above, SmCo5 is currently considered as the most prominent compound of the RE-TM5 family for PMs due to its excellent hard magnetic properties. Regarding the use of other RE atoms in recent studies, CeCo5 is an interesting compound, as it presents high values of uniaxial anisotropy and Ce is the most abundant RE element.18–20 Ce also has one 4f electron which is found to have an itinerant character, leading to a fractional occupation of the 4f states.12 However, these itinerant electrons are found to interact with the 3d electrons of Co, thus reducing their spectral weight at the Fermi level and leading to a drop in the overall magnetization.21 On the other hand, LaCo5 is an interesting compound from a theoretical point of view, as a reference material for the isostructural RE-TM5 compounds, due to its lack of 4f electrons, which, due to their localized nature, are problematic to be treated with traditional one-electron approaches.12 Experimental advances in manufacturing of anisotropic LaCo5 powders,22 along with further substitution of La with Y and Co with Fe and C in La0.5Y0.5Co4.7−yFeyC0.3 ribbons for y = 0.3–0.4, are reported to present improved hard magnetic properties compared to LaCo5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 23 but are still inferior compared to the ones of SmCo5. Regarding other RE elements, Gd as a substituent is found to lead to a high coercivity and remenance, however it is substantially more expensive than Sm.24 NdCo5 presents large magnetization, but also in-plane anisotropy, which is detrimental for the magnetic properties.25 YCo5 also lacks 4f electrons, as LaCo5, but presents interesting properties under pressure due to electron–electron interactions.26 Moreover, advances in mechanochemical synthesis have enabled the fabrication of YCo5 and PrCo5 single crystals with higher coercivity than SmCo5 (although their (BH)max is still smaller than SmCo5).27,28 Guo et al. have recently successfully fabricated the high entropy Sm1/4Nd1/4Y1/4Tb1/4Co5 alloy and investigated the impact of stoichiometry, however they also reported inferior magnetic properties compared to SmCo5.29 The replacement of RE atoms with heavy 4d and 5d TM ones, namely in ZrCo5 and HfCo5, was demonstrated to be thermodynamically viable but without any promising magnetic properties.30
23 but are still inferior compared to the ones of SmCo5. Regarding other RE elements, Gd as a substituent is found to lead to a high coercivity and remenance, however it is substantially more expensive than Sm.24 NdCo5 presents large magnetization, but also in-plane anisotropy, which is detrimental for the magnetic properties.25 YCo5 also lacks 4f electrons, as LaCo5, but presents interesting properties under pressure due to electron–electron interactions.26 Moreover, advances in mechanochemical synthesis have enabled the fabrication of YCo5 and PrCo5 single crystals with higher coercivity than SmCo5 (although their (BH)max is still smaller than SmCo5).27,28 Guo et al. have recently successfully fabricated the high entropy Sm1/4Nd1/4Y1/4Tb1/4Co5 alloy and investigated the impact of stoichiometry, however they also reported inferior magnetic properties compared to SmCo5.29 The replacement of RE atoms with heavy 4d and 5d TM ones, namely in ZrCo5 and HfCo5, was demonstrated to be thermodynamically viable but without any promising magnetic properties.30
In general, the substitution of RE elements in permanent magnets is the subject of numerous academic, public, and private sector initiatives due economic and political issues.31 However, as the role of RE atoms in atomistic level hard magnetic properties appears to be crucial, the optimization of the performance-cost interplay seems to be a more viable approach. It has also been demonstrated via ab initio high throughput screening methods that there is a trend for better magnetic performance in light RE based magnetic compounds,32 which is fortunate as, besides supply, the processing for the separation of the RE elements and especially of the heavy ones present a heavily monopolistic profile.33 Even for light RE elements though, the process of their separation from raw ores is also complex and related with geopolitical issues and monopolistic practices.8,33 Taking all these into account, the use of less critically endangered RE-based materials could be a viable alternative. In this direction, mischmetal (MM), a light RE alloy initially extracted from the monazite ore, presents an interesting candidate. MM is the least expensive RE based metal as it is mainly produced via fused salt electrolysis of RE chlorides, which is a relatively simple and inexpensive process.34 Typically, Ce-rich MM contains La and Ce in a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, which are among the most abundant RE elements, along with smaller compositions of other RE elements such as Pr or Nd and often traces of Mg or Fe, depending on the production processing. However, due to the recent high demand for Pr and Nd, along with advances in commercial processing, a common stoichiometry for modern, commercially available MM is LaCe3.35,36 Therefore, in order to find new compounds of the CaCu5 structure with reduced content of critical and expensive elements that could potentially “plug the gap” regarding magnetic performance,6 one promising route is to explore using cheaper, more abundant and easier to be produced RE substitutes, such as MM with the LaCe3 stoichiometry.
3, which are among the most abundant RE elements, along with smaller compositions of other RE elements such as Pr or Nd and often traces of Mg or Fe, depending on the production processing. However, due to the recent high demand for Pr and Nd, along with advances in commercial processing, a common stoichiometry for modern, commercially available MM is LaCe3.35,36 Therefore, in order to find new compounds of the CaCu5 structure with reduced content of critical and expensive elements that could potentially “plug the gap” regarding magnetic performance,6 one promising route is to explore using cheaper, more abundant and easier to be produced RE substitutes, such as MM with the LaCe3 stoichiometry.
The use of MM as a Nd substituent in the Nd2Fe14B has already been explored very recently by numerous experimental studies and have yielded very promising results, due to advances in sintering techniques and grain refinement.37–40 In the RE-TM5 family, early attempts for the substitution of Sm with MM (50 wt% Ce, 27 wt% La, 16 wt% Nd, 5 wt% Pr, 2 wt% other REs) yielded PMs with high energy product but low coercivity.41 However, in a recent work, Zuo et al. report the fabrication of CeCo5 and La0.35Ce0.65Co5 granular ribbons with improved MR/MS ratio due to strong exchange interactions between the nanograins and coercivity comparable to the Dy-substituted Nd2Fe14B PMs.35 Towards this direction, in this work, we explore the partial substitution of Sm with MM with the LaCe3 stoichiometry as a means of the improvement of performance – cost interplay in the family of RE-Co5 permanent magnets, by a combinatorial approach comprising ab initio calculations, machine learning techniques and experimental synthesis and characterization. The hard magnetic properties and groundstate structural stability of the new candidate compound, MM0.5Sm0.5Co5, with respect to the SmCo5, LaCo5 and CeCo5 stoichiometries were assessed both theoretically and experimentally. The impact of the various ways of distribution of the MM atoms in the Sm sites to the total magnetization was explored with a combination of ab initio and machine learning techniques. We demonstrate that an artificial neural network (ANN) algorithm was found, in principle, to be able to make successful predictions, based on the underlying structure–property relationship that dictates magnetization in the MM0.5Sm0.5Co5 crystal system. Moreover, experimental samples of the proposed stoichiometry were fabricated using the arc-melting technique under Ar atmosphere and treated at high temperatures for homogenization. Structural and magnetic characterization took place to confirm the hexagonal structure and evaluate the main magnetic properties of the system.
2. Computational method
Ab initio calculations were performed within the spin polarized, rotationally invariant DFT+ U approach of Dudarev et al.42 and the Perdew–Burke–Ernzerhof derivation of the generalized gradient approximation pseudopotential43 within the projector augmented-wave method,44 as implemented in the VASP 5.4 code.45 The +U potential was set to 4.7 eV for the 4f electrons of Sm and Ce and to 2.22 eV for the d electrons of Co and La, a value that was found to reproduce experimental data for the structural and electronic properties and is also compatible with previous studies in the literature.46 To investigate the impact of the partial substitution of Sm with MM of the LaCe3 stoichiometry in the proposed MM0.5Sm0.5Co5 compound, two datasets of hexagonal (P6/mmm) CaCu5 type, 2 × 2 × 2 and 2 × 2 × 4 supercell structures, with the La and Ce atoms substituting half of the Sm ones in their lattice sites at a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 ratio in a pseudorandom manner, was generated with the SUPERCELL program.47 These two datasets will henceforth be referred to as the 2 × 2 × 2 and 2 × 2 × 4 dataset, respectively. The 2 × 2 × 2 dataset contains all the 35 possible 48-atom symmetrically inequivalent configurations with the MM0.5Sm0.5Co5 stoichiometry. On the other hand, the 2 × 2 × 4 dataset contains 400 96-atom, also symmetrically inequivalent configurations with the same MM0.5Sm0.5Co5 stoichiometry, out of the 11
3 ratio in a pseudorandom manner, was generated with the SUPERCELL program.47 These two datasets will henceforth be referred to as the 2 × 2 × 2 and 2 × 2 × 4 dataset, respectively. The 2 × 2 × 2 dataset contains all the 35 possible 48-atom symmetrically inequivalent configurations with the MM0.5Sm0.5Co5 stoichiometry. On the other hand, the 2 × 2 × 4 dataset contains 400 96-atom, also symmetrically inequivalent configurations with the same MM0.5Sm0.5Co5 stoichiometry, out of the 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 797 possible configurations (assuming only symmetrically inequivalent structures, with a tolerance to the nearest distance between two atoms set at 0.75 for detecting differences in symmetry). The supercell dimensions in the second case were chosen to be large enough to allow for the generation of a wide landscape of symmetrically inequivalent structures but not lead to infeasible computational demands for a dataset size appropriate for the description of the underlying physical phenomena. For the SmCo5, LaCo5 and CeCo5 reference systems, a Monkhorst–Pack generated, 15 × 15 × 18, Γ-centered, k-point mesh was used for the sampling of the Brillouin zone of the 6-atom hexagonal unit cell structures. 2 × 2 × 3 k point mesh and single-point calculations were performed for the aforementioned 2 × 2 × 2 and 2 × 2 × 4 datasets of the MM0.5Sm0.5Co5 structures, respectively. Magnetic moments were initialized with a ferromagnetic alignment in all cases, with a magnitude of 4 μB. Tests performed with antiferromagnetic initialization yielded virtually the same results in all cases. In all calculations, a value of 10−5 eV for the energy difference between two consecutive steps was set as termination condition for the electronic self-consistent loop, along with an energy cut-off of 520 eV for the plane-wave set basis and a first order Methfessel–Paxton smearing scheme with a 0.05 eV width. The aspherical contributions to the gradient corrections inside the PAW spheres and to the Kohn–Sham potential were also into account in the total energy calculations. The impact of spin orbit coupling (SOC) was also examined by non collinear calculations for selected cases. VESTA48 and sumo49 packages were used for the visualization of the structural and electronic properties of the examined cases, respectively.
797 possible configurations (assuming only symmetrically inequivalent structures, with a tolerance to the nearest distance between two atoms set at 0.75 for detecting differences in symmetry). The supercell dimensions in the second case were chosen to be large enough to allow for the generation of a wide landscape of symmetrically inequivalent structures but not lead to infeasible computational demands for a dataset size appropriate for the description of the underlying physical phenomena. For the SmCo5, LaCo5 and CeCo5 reference systems, a Monkhorst–Pack generated, 15 × 15 × 18, Γ-centered, k-point mesh was used for the sampling of the Brillouin zone of the 6-atom hexagonal unit cell structures. 2 × 2 × 3 k point mesh and single-point calculations were performed for the aforementioned 2 × 2 × 2 and 2 × 2 × 4 datasets of the MM0.5Sm0.5Co5 structures, respectively. Magnetic moments were initialized with a ferromagnetic alignment in all cases, with a magnitude of 4 μB. Tests performed with antiferromagnetic initialization yielded virtually the same results in all cases. In all calculations, a value of 10−5 eV for the energy difference between two consecutive steps was set as termination condition for the electronic self-consistent loop, along with an energy cut-off of 520 eV for the plane-wave set basis and a first order Methfessel–Paxton smearing scheme with a 0.05 eV width. The aspherical contributions to the gradient corrections inside the PAW spheres and to the Kohn–Sham potential were also into account in the total energy calculations. The impact of spin orbit coupling (SOC) was also examined by non collinear calculations for selected cases. VESTA48 and sumo49 packages were used for the visualization of the structural and electronic properties of the examined cases, respectively.
The enthalpies of formation, ΔH, for the configurations with the MM0.5Sm0.5Co5 stoichiometry were calculated in two ways. The first one corresponds to the enthalpy of formation per formula unit with respect to the metallic phases of Sm, Co, Ce and La:
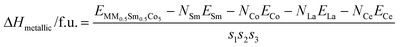 | (1) |
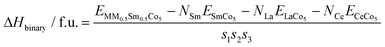 | (2) |
The implementation of the ANN algorithm on the MM0.5Sm0.5Co5 dataset was performed via the TensorFlow package,50 with further use of tools from the scikit-learn python package.51 The Python Materials Genomics (pymatgen) package52 was also used for the extraction of quantities from the relaxed structures of the dataset. For the ANN regression model, the test set comprised 30% of the total dataset, with the rest being split between training and validation. The interatomic distances between all the different atom types, as calculated with the pymatgen package, and their statistical quantities (mean, mode, standard deviation) where used as input variables (features). The feature vector that was used comprised of the total volume, lattice constants and statistical quantities (mean, mode, standard deviation). The output variable was the total magnetization. Cross-validation was performed via 5 k-folds, stratified based on the magnetization classes that will be described in the “Results and discussion” section. Input and output values were transformed with the standard scaler, ensuring a mean of 0 and a standard deviation of 1. A simple sequential model with 16, 3 and 1 neurons in each layer with “ReLU” activation on all except the last one was used, with the last layer utilizing a linear activation function and a dropout layer of 0.25 rate inserted between the layers with 16 and 3 neurons. The dropout layer was found to prevent overfitting while encouraging every neuron to train and contribute to the final prediction. The network was optimized using the mean squared error (MSE) metric, but the root mean squared error (RMSE) metric is displayed in all graphs as it is more physically meaningful. A grid search was executed in order to perform hyperparameter tuning, where the number of epochs ranged from 25 to 100 with a step of 25, and batch sizes ranged from 2 to 64 incrementing as powers of two. The final model was trained for 50 epochs using a batch size of 4, after achieving best results in the corresponding metrics. For the ANN classification model, the test set comprised 40% of the total dataset and the rest was oversampled using the synthetic minority oversampling technique algorithm (SMOTE) with three neighbors for the balanced representation of the minority classes. For evaluating the performance of the model, 3-fold validation, stratified based on the magnetization classes, was performed. A simple sequential model was also used here, with 16, 8 and 3 neurons in each layer and “ReLU” activation in all except the last one, in which the “softmax” activation function was used. The model was also trained for 50 epochs using a batch size of 4.
3. Experimental details
The MM0.5Sm0.5Co5 samples were prepared by arc-melting constituting elements of high purity under Ar atmosphere. All samples were remelted four times to ensure homogeneity and they were subsequently treated at temperatures 1150–1250 K for three days in vacuum for homogenization. Annealed alloys were manually crashed and ground down to less than 50 μm using a sieve of 50 mesh. X-ray diffraction patterns recorded with a SIEMENS D500 diffractometer (Cu-Kα radiation) were used for structural characterization. Magnetically oriented powders in epoxy resin were used to confirm the nature of the magnetocrystalline anisotropy. Magnetic measurements were carried out using a PAR 155 vibrating sample magnetometer (VSM) at room temperature in applied fields up to 2 T while thermomagnetic analysis in low magnetic field (0.02 T) in the temperature range of 300–1100 K was used to determine the Curie temperature.4. Results and discussion
4.1. Magnetic properties of SmCo5
We begin our analysis with the results of the DFT calculations for SmCo5, which will act as a baseline for the next section. In VASP, there are two available configurations for the valence electrons for Sm in the PAW pseudopotentials. Including 11 (5s2 5p6 5d1 6s2) and 16 (5s2 5p6 4f5 5d1 6s2) electrons as valence. The 4f electrons in the first configuration are treated as core and are not hybridizing with valence electrons. This model is referred to as the standard model of lanthanides or standard rare earth model (SRM). In SmCo5, the valency of Sm is 0, fact which has been recently confirmed experimentally.53 However, the second pseudopotential configuration, which corresponds to the correct valency and the explicit treatment of the 4f orbitals, is reported to be associated with issues due to self-interaction errors and the incorrect pinning of the f states to the Fermi level and is not recommended by the VASP documentation.54,55 The 11-valence e− pseudopotential (SRM) assumes a valency of +3 for Sm and for that reason has been used in cases such as SmCoO3, where Sm has a valency of +3.56 In general, the performance of the SRM approach has been extensively studied for the lanthanide series.57,58 For SmCo5, in particular, Söderlind et al.59 demonstrated that the simple SRM description is in good agreement with the methodology proposed by Grånäs et al., based on dynamical mean field calculations with the Hubbard I solver (DMFT–H1A), using the full-potential linear muffin-tin orbital method (FP-LMTO), which is considered to provide the most accurate description of the SmCo5 system up to date.60The simplification of the SRM is sensible for SmCo5, considering that there is evidence that bonding and energetic properties in RE-TM systems are governed by the interaction between the 3d electrons of the TM and the 5d electrons of the RE.61 Moreover, X-ray photoelectron spectroscopy studies have shown that the 4f orbitals of Sm and the 3d orbitals of Co do not overlap and their respective peaks fall almost 6 eV apart from each other.62 Both photoelectron spectroscopy measurements62 and DMFT – H1A calculations59 demonstrated that 4f orbitals lie almost 6 eV below the Fermi level. The DMFT-H1A approach was found to be in better agreement to the experimental photoemission spectrum at deeper energy levels, while the SRM curve falls closer to the experimental photoemission spectrum near the Fermi level.59
In Table S1,† the results for the total average magnetization values per atom type and the total magnetization per formula unit are presented for the two tested pseudopotential configurations. The respective orbital contributions are presented in Table S2.† The values of Ueff = U − J for Sm and Co were set to 4.7 and 2.22 eV, respectively, as explained in the “Computational method” section. The total magnetization of 8.56 μB per f.u. as predicted by the 11-valence e− pseudopotential configuration (SRM) is in good agreement with the experimental value 8.97 μB per f.u.63 and slightly higher than the experimental value of 7.8 μB per f.u.64 In contrast, the 16-valence e− model predicts a total magnetization value of 3.38 μB per f.u., which is less than the half compared to the experimental values. This decrease of the total magnetization is caused by the elevated magnitude of the antiparallel magnetic moment of Sm. The SRM also predicts an antiferromagnetic interaction between Sm and Co atoms, but with a smaller magnitude of the magnetic moments of Sm, which yields a total magnetization closer to the experimental values. Both models yield similar results with previous computational studies using a similar approach.59,65
Regarding the antiferromagnetic interaction between RE and TM atoms, according to the model proposed by Campbell, the 4f electrons of the RE lead to a positive 5d moment, thus the 4f–3d coupling with the TM is indirect and occurs via the direct interaction between the 5d orbitals of the RE and the 3d orbitals of the TM.61 This effective treatment of RE as elements at the beginning of the TM series predicts that interactions between d and f orbitals at the RE sites will be ferromagnetic, while interactions between RE and TM atoms at the opposite end of the TM series (such as Co) will be antiferromagnetic.61 Besides the d–d interaction model of Campbell,61 the antiferromagnetic interaction between RE and TM was also proposed by Wallace via the polarization of the s conduction orbitals.66 According to this study, the s–3d interaction is considered ferromagnetic and the s–4f interaction at the RE-TM distance is considered antiferromagnetic, so the 4f–3d coupling is antiferromagnetic.66 The resulting antiferromagnetic behavior, shown in Tables S1 and S2,† is in accordance with the two aforementioned theoretical descriptions and also with experimental results.67 The parallel alignment of spins between Sm and Co was found to be a metastable state which lies 4 to 7 mRy per atom above the groundstate, by using full-potential linearized augmented plane wave (FPLAPW) and FPLAPW LDA + U simulations.65
Regarding the orbital magnetic moment of the f electrons, for the light RE, it is expected to align parallel to the magnetic moments of the TM elements and almost cancel out with the spin moment (as shown in Fig. 4, Brooks et al.68). The results of the 16-valence e− model agree with this description. In the SRM, the almost negligible orbital moment predicted for Sm is due to the 5d valence electrons. Moreover, the orbital moments of Co atoms in the 2c sites are found to be greater than in the 3g sites for the SRM calculations, reproducing the experimental findings of Streever, according to which, the magnetic anisotropy of SmCo5 is mostly due to the orbital moment of Co atoms in 2c positions.69
To further investigate how the introduction of the Hubbard parameter, Ueff, affects the description provided by the 16-valence e− model, in Tables S3 and S4,† we present the results of simulations without the Hubbard model (USm = UCo = 0 eV) and with a slightly enhanced value of Ueff but only in the 4f orbitals of Sm (USm = 6 eV, UCo = 0 eV). It is evident that without using the Hubbard model, the resulting value of total magnetization (7.14 μB per f.u.) is quantitively closer to the experimental values of 7.864 and 8.97 μB per f.u.63 but the orbital magnetic moment of Sm lies antiparallel to the ones of Co, in contrast to.68 By using a value of U only for the 4f orbitals of Sm, the total magnetic moment of Sm lies parallel to the ones of Co, leading to a value of total magnetization per formula unit that exceeds the experimental values. Moreover, the orbital magnetic moment of Sm also lies antiparallel to the ones of Co, as in the previous case.
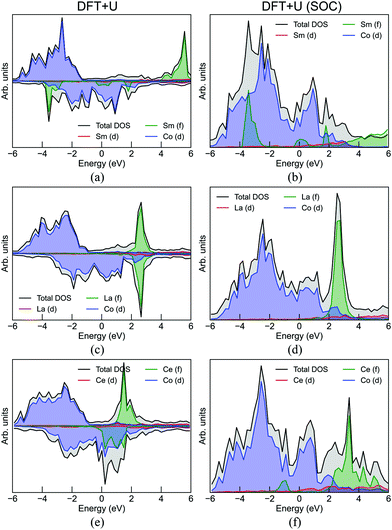
The resulting electronic Density of States (DOS) corresponding to the 16-valence e− configuration with the three aforementioned set of U parameters, and the 11-valence e− configuration (SRM) with USm = 4.7 eV and UCo = 2.22 eV, are presented in Fig. S1.† The spurious pinning of states corresponding to f orbitals of Sm to the Fermi level is evident for all the cases using the 16-valence e− configuration. These orbitals interact with the respective 3d states of Co at the Fermi level. The location of the rest of the peaks associated with the 4f orbitals of Sm are in good agreement with,70 in which the LDA + U method was employed with U = 6.8 eV and J = 0.8 eV. The value of U parameter for Sm seems to affect the spread of the f orbitals around the Fermi level, but the pinned f orbitals are observed in all cases. The introduction of U parameter is also necessary for Co, as in the case where UCo = 0 eV, the 3d orbitals of Co are also observed to be pinned to the Fermi level and strongly interacting with the also pinned 4f orbitals of Sm. The SRM with USm = 4.7 eV and UCo = 2.22 eV successfully predicts an almost similar total DOS with the 16-valence e-model, with the only exception being the sharp peaks corresponding to the strongly localized 4f states of Sm close to −4 eV.
4.2. Structural, electronic and magnetic properties of SmCo5, LaCo5 and CeCo5 binary compounds
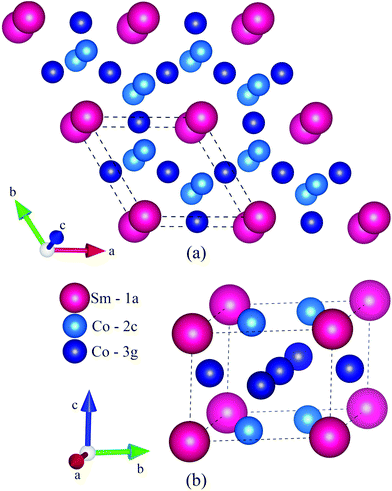
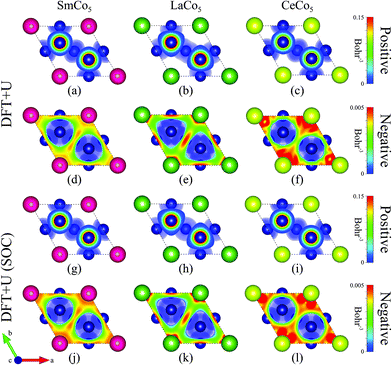
To examine the impact of La and Ce to the RE-Co5 system, as compared to Sm, we present the results of DFT simulations of the respective binary compounds. The same hexagonal (P6/mmm) structure was used for all of the three cases, with the RE atom replacing Sm in the 1a position (Fig. 1). The results for SmCo5 presented in this section were produced by using the SRM, unless stated otherwise. The calculated lattice parameters for the three compounds are presented in Table 1. The inclusion of SOC is found to lead to a small overestimation of a and a small underestimation of c/a for CeCo5, while having a negligible impact in SmCo5 and LaCo5. Both approaches (with and without SOC) are found to slightly overestimate a and underestimate the c/a ratio for SmCo5 and LaCo5. For CeCo5, Results with DFT + U without SOC are in better agreement with the experimental ones than with DFT + U with SOC.The antiferromagnetic behavior of the RE-Co5 compounds, resulting from the corresponding atomic magnetic moments and total magnetization per formula unit for each compound, are demonstrated in Table 2. Their respective orbital moments per atom and per formula unit are shown in Table 3. CeCo5 appears to have a lower value of total magnetization by almost 1 μB per f.u. compared to SmCo5, due to the very pronounced antiferromagnetic contribution of Ce in its structure. This effect is attributed to the itinerant character of the one 4f electron of cerium, which leads to a fractional occupation of the 4f states. These itinerant 4f electrons of Ce create additional bonds with the 3d orbitals of Co, leading to a mixed valency of Ce (between Ce3+ and Ce4+) and reducing magnetization.74–76 By examining the results of the magnetization charge density distributions in Fig. 2, it is evident that the antiferromagnetic contribution of Ce is more spatially pronounced than the respective one for La and Sm. The inclusion of SOC in these cases did not show any different results, both quantitatively and qualitatively for SmCo5 and LaCo5. However, DFT + U with SOC predicted more pronounced values for the magnetic moments of Ce and small differences in the shape of its magnetization density distribution in CeCo5. The total magnetic moments of Co atoms at 2c sites for the binaries which include 4f orbitals (SmCo5, LaCo5) are found to be smaller than the ones in 3g sites.
| m/atom (μB per atom) | DFT + U | DFT + U (SOC) | Ref. |
|---|---|---|---|
| SmCo 5 (SRM) | |||
| 1a (1 × RE) | −0.316 | −0.301 | −0.2165 |
| 2c average (2 × Co) | 1.748 | 1.736 | 1.86,77 1.7665 |
| 3g average (3 × Co) | 1.792 | 1.783 | 1.75,77 1.765 |
| Total (μB per f.u.) | 8.557 | 8.520 | 8.97,63 8.0265 |
| LaCo 5 | |||
| 1a (1 × RE) | −0.279 | −0.295 | −0.3078 |
| 2c average (2 × Co) | 1.736 | 1.712 | 1.673 |
| 3g average (3 × Co) | 1.764 | 1.761 | 1.7673 |
| Total (μB per f.u.) | 8.391 | 8.412 | 8.4679 |
| CeCo 5 | |||
| 1a (1 × RE) | −1.527 | −0.952 | −0.45721 |
| 2c average (2 × Co) | 1.691 | 1.666 | 1.260,80 1.42921 |
| 3g average (3 × Co) | 1.769 | 1.728 | 1.260,80 1.37021 |
| Total (μB per f.u.) | 7.163 | 7.563 | 7.179 |
| SmCo5 | LaCo5 | CeCo5 | |||||
|---|---|---|---|---|---|---|---|
| m L/atom (μB per atom) | DFT + U (SOC) (16-valence e−) | DFT + U (SOC) (SRM) | Ref. | DFT + U (SOC) | Ref. | DFT + U (SOC) | Ref. |
| 1a (1 × RE) | 2.115 | 0.087 | 3.2665 | 0.084 | 0.02421 | 0.693 | 0.23221 |
| 2c average (2 × Co) | 0.315 | 0.437 | 0.2265 | 0.410 | 0.28681 | 0.440 | 0.15021 |
| 3g average (3 × Co) | 0.424 | 0.352 | 0.1865 | 0.400 | 0.25281 | 0.335 | 0.10921 |
From the projected density of states (DOS) plot in Fig. 3, we observe that in the case of CeCo5, the electronic states attributed to Ce are either pinned (no SOC) or very close (SOC) to the Fermi level. These results, along with Table 2 demonstrate that the impact of Ce to the RE-Co5 compound is detrimental for the total magnetization, with this effect being depicted as less pronounced with the inclusion of SOC to the DFT + U calculations. The 4f orbitals of La are empty.
4.3. MM0.5Sm0.5Co5: 2 × 2 × 2 and 2 × 2 × 4 supercell datasets
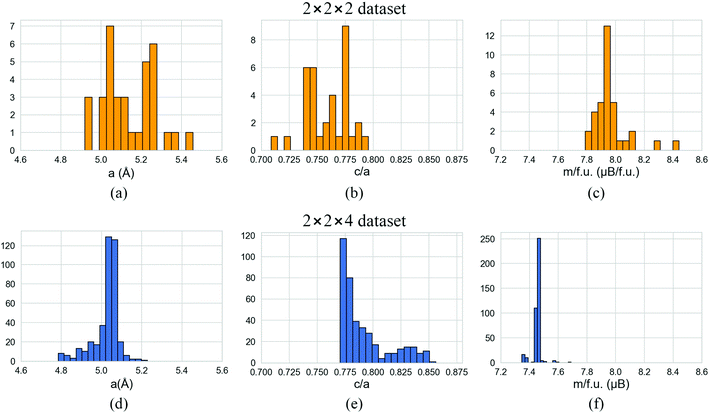
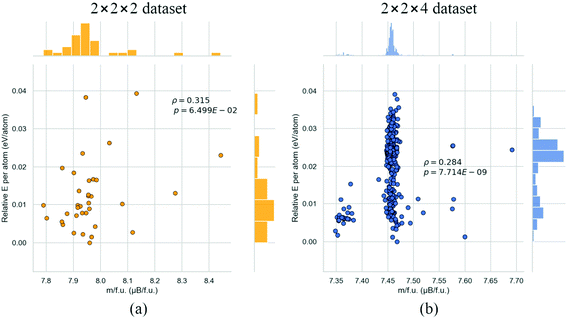
Considering the properties of the of SmCo5, LaCo5 and CeCo5 binary compounds as presented in the previous section as a baseline, we proceed with the investigation for the properties of the proposed MM0.5Sm0.5Co5 stoichiometry with respect to them. The distribution of the lattice parameters a and c/a ratio, along with the total magnetization per formula unit, for the first dataset which contains 45 48 atom 2 × 2 × 2 supercell configurations and the second dataset which contains 400 96 atom 2 × 2 × 4 supercell configurations, is presented in Fig. 4. For the description of Sm, the SRM was used, due its better agreement with previous findings, as discussed in 4.1. The values of the lattice constant, a, are concentrated close to 5.1 Å for the configurations in both datasets, which is also the value of a for SmCo5. Regarding the c/a ratio, the majority of configurations in both datasets is concentrated around the value of 0.775, which is also close to the calculated value of 0.762 for SmCo5. However, we observe that in the smaller supercell configurations, the c/a ratio tends to be smaller, with the opposite effect being observed in the larger ones.The most pronounced impact of the size effect though is observed in the values of the total magnetization per formula unit. In the 2 × 2 × 2 dataset, there is a peak close to 7.9 μB per f.u., which corresponds to an almost 7% reduction of the total magnetization. There are also two outlier cases at approximately 8.30 and 8.45 μB per f.u., which are close to the values of total magnetization per formula unit for LaCo5. On the other hand, the magnetization per formula unit of the vast majority of the 2 × 2 × 4 supercell configurations was found close to 7.46 μB per f.u., which corresponds to a 12.8% reduction compared to the respective value for SmCo5. There are also two other groups of cases with respect to their value of total magnetization with distinct values of total magnetization but fewer members. The first one is centered close to 7.37 μB per f.u. and the second one close to 7.6 μB per f.u., which correspond to a 13.8% and 11.1% reduction, respectively, compared to the calculated total magnetization for SmCo5.
The relationship between the relative energy per atom, defined as the energy difference per atom of each configuration with respect to the energetically preferable configuration of each dataset, with the total magnetization per formula unit for the two datasets, is shown in Fig. 5. The Pearson's correlation coefficient, ρ, is a measurement of correlation between two variables and ranges between −1 and 1. Values close to 1 (−1) indicate a positive (negative) correlation between the two variables, while values close to 0 indicate a weak dependence of one variable to the other. In both datasets, these two variables are found to be very weakly correlated, meaning that there is no obvious trend between the total energy of each configuration with its total magnetization. In the 2 × 2 × 2 dataset, most values appear in the lowest left corner of the plot, with the most preferable cases close to 7.95 μB per f.u. However, in the 2 × 2 × 4 dataset, we observe a slightly more complex situation, with three clusters of values close to 7.37, 7.46 and 7.6 μB per f.u., respectively, as also presented in the corresponding histogram for the values of total magnetization in Fig. 4.
The full scatter matrix plots for a, c/a ratio, total magnetization per formula unit and relative energy per atom for the two datasets, along with their respective correlation matrices can be found in Fig. S2, S3 and Tables S5, S6.† The lattice constant, a, and c/a ratio are also found to be very weakly correlated with the total magnetization per formula unit in both datasets, with their relationship between them and the relative energy per atom and the total magnetization for both datasets being shown in Fig. S3.†
Regarding the enthalpies of formation, as defined by eqn (1) and (2), all configurations in both datasets were found stable compared to the metallic phases of Sm, Co, La and Ce. However, two configurations of the 2 × 2 × 2 dataset and twelve configurations of the 2 × 2 × 4 dataset were found unstable with respect to the SmCo5, LaCo5 and CeCo5 binary phases. The total magnetization per formula unit, lattice constant, a and c/a ratio for these configurations can be found in Tables S7 and S8.† It is also worth mentioning that all of the twelve configurations of the 2 × 2 × 4 dataset also belong to the middle magnetization cluster that was mentioned above.
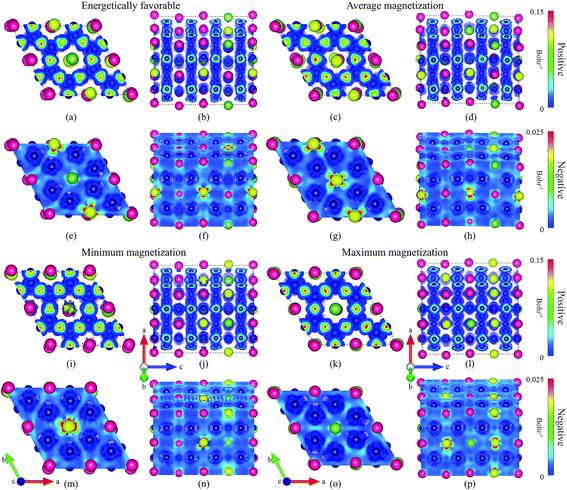
To provide a more critical insight about the 2 × 2 × 4 dataset, we examine the following four particular cases: the energetically preferable configuration, the configuration with a total magnetization value closest to the middle of the average magnetization cluster and the configurations with the minimum and maximum magnetization of the entire dataset. These configurations will be referred to as “energetically preferable”, “average magnetization”, “minimum magnetization” and “maximum magnetization”, respectively. The lattice constant, a, c/a ratio, enthalpy of formation with respect to the Sm, Co, La and Ce metallic phases and to the SmCo5, LaCo5 and CeCo5 binary phases and total magnetization per formula unit for the cases mentioned above are presented in Table 4. The lattice constant, a, for the energetically preferable case is found to be larger than the value for the other three cases, with its total magnetization belonging in the middle magnetization cluster. The c/a ratio of the energetically preferable case, though, is closer to the respective value of the case with the smallest magnetization. All of the four cases are found to be stable both against the metallic phase of Sm, Co, La and Ce and the SmCo5, LaCo5 and CeCo5 binary phases, as indicated by the negative values for the respective enthalpies of formation in Table 4.
| Energetically preferable | Average magnetization | Minimum magnetization | Maximum magnetization | |
|---|---|---|---|---|
| a (Å) | 5.096 | 4.896 | 4.787 | 5.012 |
| c/a | 0.802 | 0.841 | 0.850 | 0.788 |
| ΔHmetallic/f.u. (eV) | −0.698 | −0.657 | −0.682 | −0.553 |
| ΔHbinary/f.u. (eV) | −0.196 | −0.155 | −0.179 | −0.050 |
| m (μB per f.u.) | 7.47 | 7.46 | 7.35 | 7.69 |
Regarding the magnetization of each atom in these four cases in Table 5, the strong impact of Ce is also observed in a similar manner as in our previous results for the binary RE-Co5 compounds. The large value of the total magnetization in the last case can be attributed to the low value of atomic magnetization for the Ce atoms. The magnetic moment of La atoms is also similar to the one of Sm, again as in the cases of the binary compounds. The different topological distributions of the magnetization densities for these four cases are presented in Fig. 6.
| m/atom (μB per atom) | Energetically preferable | Average magnetization | Minimum magnetization | Maximum magnetization |
|---|---|---|---|---|
| 1a (8 × Sm average) | −0.325 | −0.322 | −0.330 | −0.305 |
| 1a (2 × La average) | −0.317 | −0.310 | −0.323 | −0.301 |
| 1a (6 × Ce average) | −1.285 | −1.278 | −1.291 | −0.617 |
| 2c average (2 × Co) | 1.637 | 1.600 | 1.612 | 1.652 |
| 3g average (3 × Co) | 1.626 | 1.645 | 1.604 | 1.603 |
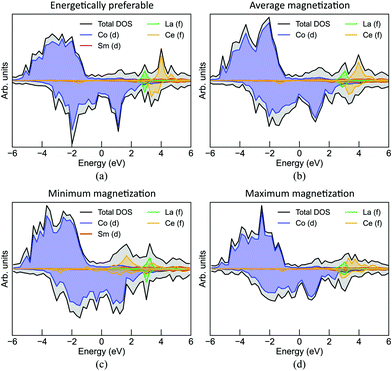
The projected DOS plot for the above four cases of the 2 × 2 × 4 dataset is shown in Fig. 7. We observe that in the case with the minimum magnetization, electronic states that are associated with Ce are more delocalized and are extended over the vicinity close to the Fermi level. The localized states of La close to 3 eV correspond to the empty 4f orbitals.
4.4. Performance of an artificial neural network algorithm in the 2 × 2 × 4 dataset
In this last part of our computational approach, we examine the capability of an ANN algorithm to capture the complicated underlying structure-to-property relationship that dictates magnetization in the 2 × 2 × 4 dataset. From the full scatter plot matrices of Fig. S1 and S2,† there is no obvious relationship between structural properties and the total magnetization. This fact, combined with the sufficient size of data we have collected for the analysis of the properties of the supercell approach, makes this problem suitable as a machine learning task.From the correlations heatmap of the interatomic distances with the total magnetization in Fig. S4,† it is evident that the Co–Co distance is correlated with total magnetization, with this value of correlation being more pronounced compared to the interatomic distances between the other atom types. This result indicates the importance of the Co sublattice in the Kagome network arrangement for the total magnetization of the RE-Co5 compound.
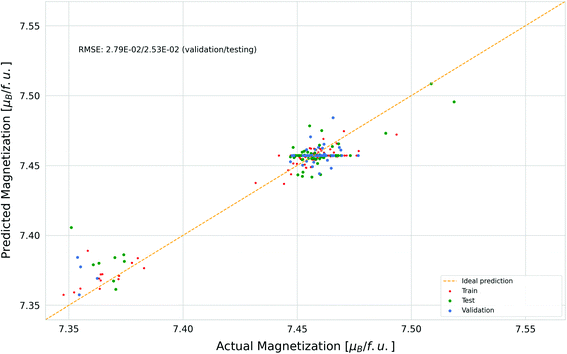
The result of the implementation of an ANN for the prediction of total magnetization of each compound as a regression task are presented in Fig. 8, with the values of the coefficient of determination, R2, for this model shown in Table 6. The choice of parameters of our final model are presented in the “Computational method” section. Despite the satisfactory performance of our model in the training set, R2 was found to drop to 0.501 in the test set.
| Dataset | R 2 |
|---|---|
| Training | 0.822 |
| Validation | 0.665 |
| Testing | 0.501 |
The results of the ANN model were improved by transforming the problem to a classification task. The classification ANN uses a slightly larger hidden layer when compared to the regression ANN. This choice was made so as to alleviate the information bottleneck when transitioning from the 16 neurons to the 3 output neurons. This increase in the number of trainable parameters is further justified because the dataset has been artificially augmented for the purpose of balancing the underrepresented classes. A similar increase in the regression model led to increased overfitting of the model, which rendered it less accurate.
For the ANN classification model, we tried to predict the magnetization cluster of each data point, based on the three discrete magnetization clusters of Fig. 5, instead of directly predicting the value of total magnetization. The details of the parameters of our final model for the classification task are also presented in the “Computational details” section. We evaluated our classifier based on its accuracy, precision and recall, as defined by:
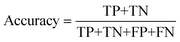 | (3) |
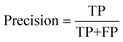 | (4) |
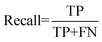 | (5) |
The results of accuracy, precision and recall of the model are presented in Table 7. The confusion matrices for each of fold of the cross-validation can be found in Fig. S6.† The results presented in the confusion matrix make it abundantly clear that the network can correctly predict whether a given arrangement of molecules would result in a typical magnetization. Despite the fact that, because of the uneven distribution of classes, the prediction for these classes suffers, the network may still be used as a supplementary tool to gauge how likely the given configuration is to result in less typical value for the magnetization. With respect to that test, the number of false positive results is much smaller than that of the false negative results, resulting in a partial anomaly detector that may save researchers valuable time.
| accuracy | precision | recall | |
|---|---|---|---|
| Training | 1.000 | 1.000 | 1.000 |
| Validation | 0.982 | 0.982 | 0.982 |
| Test | 0.735 | 0.927 | 0.927 |
Overall, we observe a significantly better performance compared to our regression model, with an accuracy value of 0.735 and a precision and recall value of 0.972. Therefore, we demonstrate that an ANN algorithm can become capable of predicting the trends in the values of magnetization based on the values of the interatomic distances.
4.5. Experimental synthesis and characterization
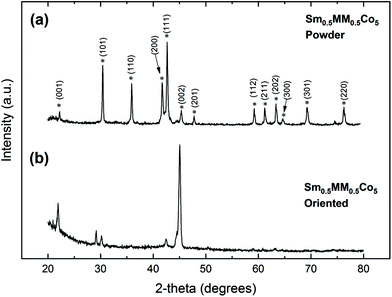
In Fig. 9, X-ray diffraction plots of the material under study are presented (a) for the random and (b) oriented sample, respectively. The samples seem to be single-phased having the typical hexagonal CaCu5-type signature pattern of the SmCo5 system (S.G. No. 191, P6/mmm). Rietveld analysis revealed that the samples are indeed single phase with unit cell parameters a = b = 4.988(2) Å, c = 3.991(1) Å, c/a = 0.800 i.e., very close to the energetically favorable theoretical solution already discussed. In the case of the oriented samples, the (00l) peaks become very strong while the rest of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 phase peaks fade out indicating that the material retains the uniaxial magnetocrystalline anisotropy of the basic SmCo5 compound; a small percentage of misalignment is responsible for the minor intensities present.
5 phase peaks fade out indicating that the material retains the uniaxial magnetocrystalline anisotropy of the basic SmCo5 compound; a small percentage of misalignment is responsible for the minor intensities present.
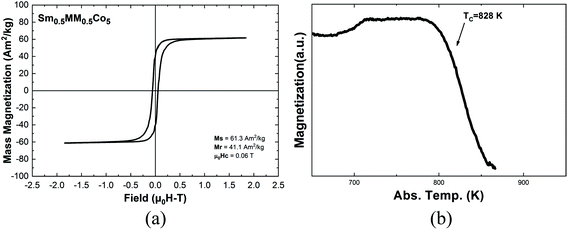
In Fig. 10a, a typical magnetic hysteresis loop of Sm0.5MM0.5Co5 sample at room temperature is presented. Saturation magnetization was determined by extrapolating the data of the high field region and its value was 61.3 Am2 kg−1; which corresponds to 4.9 μB per f.u.. This value is lower than the theoretical calculations presented before and pure SmCo5 phase being closer to Ce and La isostructurals.64,82,83 Curie temperature (TC) of the sample under study, as seen in Fig. 10b, was determined at 828 K, lower than pure SmCo5 compound64 but larger than CeCo5.84Table 8 summarizes the aforementioned magnetic properties, MS and TC.
In Fig. 10a, reference values for remanence and coercivity are also presented. These values correspond to the measurement of the powdered alloy, which consists of grains in the range of 10–50 μm. A permanent magnet based on our material could be prepared by the traditional processing paths. Assuming a square loop, from the formula BHmax = (μ0Ms/2)2, the theoretical maximum energy product would be 85.14 kJ m−3, which is close to other proposed materials for permanent magnet applications and sufficient for “plugging the gap”, as discussed in.6
5. Conclusions
In this work, we explore the partial substitution of Sm in the 1a site of the Kagome network structure of the SmCo5 compound, with mischmetal of the LaCe3 stoichiometry, by using both computational and experimental methods. The structural and magnetic properties of the SmCo5, LaCo5 and CeCo5 binary compounds were also assessed with the same ab initio methodology that we used for the proposed MM0.5Sm0.5Co5 stoichiometry, in order to provide with insight about the impact of each of these RE atoms to the total magnetization of the compound. For SmCo5, the treatment of 4f orbitals as core according to the SRM yielded results closer to previous experimental and theoretical studies. For the binary compounds, CeCo5 was found to yield the lowest value of total magnetization among these three candidates, due to the stronger antiferromagnetic alignment of Ce. From the projected DOS plot, we also observe that the electronic states attributed to Ce are closer to the Fermi level, compared to the ones of the other RE atoms in the rest of the examined binary alloys.To examine the various phenomena associated with the supercell approach, we constructed and analyzed two datasets with DFT + U calculations in 2 × 2 × 2 and 2 × 2 × 4 supercell structures. The breakdown of symmetry by the random substitution was found to introduce a variance to the calculated quantities, as presented by the respective histograms. The distribution of the structural parameters in the two datasets was found to be similar. However, the total magnetization in the configurations of the 2 × 2 × 2 dataset is centered around 7.9 μB per f.u., which corresponds to a 7% reduction compared to SmCo5, but in the case of the 2 × 2 × 4 dataset, there are three distinct clusters observed in the values for the total magnetization, centered at 7.37, 7.46 and 7.6 μB per f.u., which is a 11.1, 12.8 and 13.8% reduction, respectively, compared to SmCo5. Most configurations were found to belong in the second cluster. Also, the energetically preferable case for each dataset is not the one with either the smallest or the largest magnetization of its corresponding dataset. The same was found to hold also for a and c/a. The energetically preferable case of the 2 × 2 × 4 dataset was found to lie in the majority magnetization cluster. Moreover, for the case with the largest value of magnetization, the antiferromagnetic impact of Ce to the total magnetization was less pronounced than in the other cases, while in the case with the smallest magnetization, the electronic states of Ce were found closer to the Fermi level in the projected DOS plot.
Finally, we investigated the possibility of training an ANN machine learning algorithm in the cases of the 2 × 2 × 4 dataset in order to predict the total magnetization of a given compound, by using the interatomic distance between each atom type as features. By looking the correlation of these features with the total magnetization, we observed a degree of correlation between the Co–Co interatomic distance and the total magnetization, result that indicates the pronounced impact of the Co network to the total magnetization of the structure. Regarding the ANN model, by using an ANN algorithm for regression, in order to predict the values of magnetization in a continue manner, our best model achieved an R2 score of 0.822 in the training set, which was decreased to 0.501, however, for the test set. The problem was subsequently treated as a classification task, in which we trained an ANN algorithm to predict the magnetization cluster of each case, based on the three magnetization clusters that were mentioned above. Our best model achieved a value of 0.735 for accuracy and 0.927 for recall and precision, improving by far the predicting capability of the model. We therefore conclude that these results can act as a proof of concept that an ANN algorithm can in fact be capable of making predictions about the trends of total magnetization, trained on features based on the structural properties of the compounds, as also previously demonstrated.85 This underlying structure-to-property relationship is proven to be complex, thus the implementation of predictive statistics algorithms such as machine learning and ANNs in particular, can possibly circumvent theoretical obstacles and yield practical results.
Experimentally prepared Sm0.5MM0.5Co5 samples confirm the theoretical approach as far as it concerns the stability and the structural parameters. The compound retains the typical hexagonal CaCu5-type structure of the SmCo5 system. Magnetic measurements showed a relatively high Curie temperature of 828K and saturation magnetization of about 61 Am2 kg−1 (4.9 μB per f.u.), the latter being lower than theoretical prediction. Possible microstructural effects or undetected minor phases with very low concentration in grain boundaries may account for the difference.
Overall, by exploring the possibility of using MM, an ore that has not yet been fully separated to its constituents, we aim to the production of permanent magnets that may require simpler processing by avoiding the separation of RE elements. Our ab initio simulations show that the replacement of half of Sm with MM leads to a 7 to 13.8% drop in total magnetization. Experimental characterization of single-phase samples with this stoichiometry also revealed a drop in overall magnetic strength of the material. However, as MM is almost 100 times less expensive than Sm at the time that this work is written, we achieve an almost 50% reduction in expenses, at least regarding raw materials. The extensive knowledge of the system may also draw a path to other possible modifications. These results will hopefully act as a baseline for a process which in step will possibly aid to the design of more affordable and commercially accessible devices.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. Giaremis acknowledges support for the research work by the Hellenic Foundation for Research and Innovation (HFRI) under the HFRI PhD Fellowship grant (Fellowship Number: 962). Furthermore, this work was supported by computational time granted from the Greek Research & Technology Network (GRNET) in the “ARIS” National HPC infrastructure under the project NOUS (pr010034) and the Aristotle University of Thessaloniki (AUTh) HPC Infrastructure and Resources.References
- K. Strnat, G. Hoffer, J. Olson and W. Ostertag, A Family of New Cobalt–Base Permanent Magnet Materials, J. Appl. Phys., 1967, 38, 1001, DOI:10.1063/1.1709459.
- B. Shen, C. Yu, D. Su, Z. Yin, J. Li, Z. Xi and S. Sun, A new strategy to synthesize anisotropic SmCo5 nanomagnets, Nanoscale, 2018, 10, 8735–8740, 10.1039/C8NR01690A.
- Z. Ma, M. Yue, Q. Wu, C. Li and Y. Yu, Designing shape anisotropic SmCo5 particles by chemical synthesis to reveal the morphological evolution mechanism, Nanoscale, 2018, 10, 10377–10382, 10.1039/C8NR02893A.
- Z. Ma, J. Liang, W. Ma, L. Cong, Q. Wu and M. Yue, Chemically synthesized anisotropic SmCo5 nanomagnets with a large energy product, Nanoscale, 2019, 11, 12484–12488, 10.1039/C9NR03412A.
- Y. Dong, T. Zhang, Z. Xia, H. Wang, Z. Ma, X. Liu, W. Xia, J. M. D. Coey and C. Jiang, Dispersible SmCo5 nanoparticles with huge coercivity, Nanoscale, 2019, 11, 16962–16967, 10.1039/C9NR06653E.
- J. M. D. Coey, Permanent magnets: Plugging the gap, Scr. Mater., 2012, 67(6), 524–529, DOI:10.1016/j.scriptamat.2012.04.036.
- O. Gutfleisch, M. A. Willard, E. Brück, C. H. Chen, S. G. Sankar and J. P. Liu, Magnetic Materials and Devices for the 21st Century: Stronger, Lighter, and More Energy Efficient, Adv. Mater., 2011, 23, 821–842, DOI:10.1002/adma.201002180.
- N. Dushyantha, N. Batapola, I. M. S. K. Ilankoon, S. Rohitha, R. Premasiri, B. Abeysinghe, N. Ratnayake and K. Dissanayake, The story of rare earth elements (REEs): Occurrences, global distribution, genesis, geology, mineralogy and global production, Ore Geol. Rev., 2020, 122, 103521, DOI:10.1016/j.oregeorev.2020.103521.
- J. Cui, M. Kramer, L. Zhou, F. Liu, A. Gabay, G. Hadjipanayis, B. Balasubramanian and D. Sellmyer, Current progress and future challenges in rare-earth-free permanent magnets, Acta Mater., 2018, 158, 118–137, DOI:10.1016/j.actamat.2018.07.049.
- K. H. J. Buschow, Intermetallic compounds of rare-earth and 3d transition metals, Rep. Prog. Phys., 1977, 40(10), 1179, DOI:10.1088/0034-4885/40/10/002.
- J. H. Wernick and S. Geller, Transition element-rare earth compounds with Cu5Ca structure, Acta Crystallogr., 1959, 12, 662–665, DOI:10.1107/S0365110X59001955.
- H. Ucar, R. Choudhary and D. Paudyal, An overview of the first principles studies of doped RE-TM5 systems for the development of hard magnetic properties, J. Magn. Magn. Mater., 2020, 496, 165902, DOI:10.1016/j.jmmm.2019.165902.
- S. Buck and M. Fahnle, Rare-earth magnetic anisotropy: is the crystal field theory valid?, J. Magn. Magn. Mater., 1997, 166(3), 297–302, DOI:10.1016/S0304-8853(96)00588-4.
- C. S. Cutrano and C. E. Lekka, Fe–Co magnetic nanoclusters by density functional theory calculations, J. Mater. Sci. Technol., 2018, 34(13), 1575–1581, DOI:10.1080/02670836.2018.1506728.
- S. Dhaka, S. Kumar, K. Poonia, V. Singh, K. Dhaka and H. S. Mund, Effect of annealing temperature on structural and magnetic properties of nano-cobalt ferrite, J. Mater. Sci.: Mater. Electron., 2021, 32, 16392–16399, DOI:10.1007/s10854-021-06192-y.
- M. Bohra, V. Singh, M. Sowwan, J.-F. Bobo, C.-J. Chung and B. Clemens, Influence of packaging on the surface oxidation and magnetic properties of cobalt nanocrystals, J. Phys. D: Appl. Phys., 2014, 47(30), 305002, DOI:10.1088/0022-3727/47/30/305002.
- S. Lisenkov, A. N. Andriotis and M. Menon, Magnetic anisotropy and engineering of magnetic behavior of the edges in Co embedded graphene nanoribbons, Phys. Rev. Lett., 2012, 108(18), 187208, DOI:10.1103/PhysRevLett.108.187208.
- R. Choudhary, A. Palasyuk, I. C. Nlebedim, R. T. Ott and D. Paudyal, Atomic cooperation in enhancing magnetism: (Fe, Cu)-doped CeCo5, J. Alloys Compd., 2020, 839, 155549, DOI:10.1016/j.jallcom.2020.155549.
- S. Y. Jekal, J. F. Loeffler and M. Charilaou, Pushing the limits of magnetic anisotropy in the Sm-Co system, arXiv:1807.09257, 2018. https://arxiv.org/abs/1807.09257.
- P. Kim, A. Anderko, A. Navrotsky and R. E. Riman, Trends in structure and thermodynamic properties of normal rare earth carbonates and rare earth hydroxycarbonates, Minerals, 2018, 8(3), 106, DOI:10.3390/min8030106.
- L. Nordström, O. Eriksson, M. S. S. Brooks and B. Johansson, Theory of ferromagnetism in CeCo5, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(13), 9111, DOI:10.1103/PhysRevB.41.9111.
- A. M. Gabay and G. C. Hadjipanayis, Mechanochemical synthesis of LaCo5 magnetically hard anisotropic powder, J. Phys. D: Appl. Phys., 2014, 47(18), 182001, DOI:10.1088/0022-3727/47/18/182001.
- H. W. Chang, Y. M. Guo, S. H. Liao, W. C. Chang and C. C. Shaw, Magnetic property improvement of melt spun LaCo5-based nanocomposites with Y, Fe and C substitutions, J. Alloys Compd., 2020, 821, 153271, DOI:10.1016/j.jallcom.2019.153271.
- W.-Y. Zhang, B.-G. Shen and Z.-H. Cheng, Beneficial effect of Gd substitution on magnetic properties of magnetically anisotropic SmCo5 ribbons, Appl. Phys. Lett., 2001, 79(12), 1843, DOI:10.1063/1.1401789.
- H. Pang, L. Qiao and F. S. Li, Calculation of magnetocrystalline anisotropy energy in NdCo5, Phys. Status Solidi B, 2009, 246(6), 1345–1350, DOI:10.1002/pssb.200844215.
- E. Burzo, P. Vlaic, D. P. Kozlenko, N. O. Golosova, S. E. Kichanov, B. N. Savenko, A. Ostlin and L. Chioncel, Structure and magnetic properties of YCo5 compound at high pressures, J. Mater. Sci. Technol., 2020, 42, 106–112, DOI:10.1016/j.jmst.2019.12.001.
- A. M. Gabay, X. C. Hu and G. C. Hadjipanayis, Preparation of YCo5, PrCo5 and SmCo5 anisotropic high-coercivity powders via mechanochemistry, J. Magn. Magn. Mater., 2014, 368, 75–81, DOI:10.1016/j.jmmm.2014.05.014.
- W. B. Ali, Q. Wu, Z. Ma, L. Cong and M. Yue, Chemically synthesizing PrCo5 single-crystal particles to fabricate high-performance anisotropic nanomagnets, J. Magn. Magn. Mater., 2020, 499, 166205, DOI:10.1016/j.jmmm.2019.166205.
- X. Guo and Y. Guo, Effects on structure and magnetic properties of SmCo5 based intermetallic compounds by increasing configuration entropy from binary to quaternary equiatomic rare earths at Sm site, J. Alloys Compd., 2020, 813, 152230, DOI:10.1016/j.jallcom.2019.152230.
- P. Kumar, A. Kashyap, B. Balamurugan, J. E. Shield, D. J. Sellmyer and R. Skomski, Permanent magnetism of intermetallic compounds between light and heavy transition-metal elements, J. Condens. Matter Phys., 2014, 26(6), 064209, DOI:10.1088/0953-8984/26/6/064209.
- R. Bielawski, Rare earth elements – a novelty in energy security, J. Ecol. Eng., 2020, 21(4), 134–149, DOI:10.12911/22998993/119810.
- N. Drebov, A. Martinez-Limia, L. Kunz, A. Gola, T. Shigematsu, T. Eckl, P. Gumbsch and C. Elsässer, Ab initio screening methodology applied to the search for new permanent magnetic materials, New J. Phys., 2013, 15, 125023, DOI:10.1088/1367-2630/15/12/125023.
- A. Golev, M. Scott, P. D. Erskine, S. H. Ali and G. R. Ballantyne, Rare earths supply chains: Current status, constraints and opportunities, Resour. Policy, 2014, 41, 52–59, DOI:10.1016/j.resourpol.2014.03.004.
- K. Reinhardt and H. Winkler, Cerium Mischmetal, Cerium Alloys, and Cerium Compounds, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag, 2011. DOI:10.1002/14356007.a06_139.
- W.-L. Zuo, J. Mohapatra, J. P. Liu, T.-Y. Zhao, F.-X. Hu, J.-R. Sun, Y.-F. Li, X.-F. Zhang and B.-G. Shen, Cerium-based RCo5 (R = Ce, La0.35Ce0.65, and misch-metal) type nanocrystalline hard magnetic materials with high coercivity, APL Mater., 2019, 091108, DOI:10.1063/1.5104295.
- M. Zhang, Z. Li, B. Shen, F. Hu and J. Sun, Permanent magnetic properties of rapidly quenched (La,Ce)2Fe14B nanomaterials based on La–Ce mischmetal, J. Alloys Compd., 2015, 651, 144–148, DOI:10.1016/j.jallcom.2015.08.044.
- H. Chen, W. Liu, Z. Li, Y. Li, Y. Yin, H. Cui and M. Yue, Optimizing microstructure and magnetic properties of mischmetal-based sintered magnets by grain refinement, Mater. Lett., 2020, 267, 127509, DOI:10.1016/j.matlet.2020.127509.
- K. Chen, S. Guo, H. Zhao, X. Fan, F. Fan, G. Ding, R. Chen, X. Zheng and A. Yan, Microstructural design in LaCe misch-metal substituted 2
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1-type sintered magnets by dual-alloy method, J. Rare Earths, 2021, 39(3), 305–311, DOI:10.1016/j.jre.2020.05.005.
1-type sintered magnets by dual-alloy method, J. Rare Earths, 2021, 39(3), 305–311, DOI:10.1016/j.jre.2020.05.005. - Z.-B. Li, Y. Li, Z.-X. Zhang, Y.-L. Liu, Y.-F. Li and X.-F. Zhang, Improving magnetic properties in mischmetal-based sintered composite magnets by regulating element distribution, AIP Adv., 2019, 9, 075109, DOI:10.1063/1.5097271.
- W. Liu, Z. Zhang, M. Yue, Z. Li, D. Zhang and H. Zhang, Effects of La substitution on the crystal structure and magnetization of MM-Fe-B alloy (MM = La, Ce, Pr, Nd), J. Magn. Magn. Mater., 2018, 464, 61–64, DOI:10.1016/j.jmmm.2018.05.043.
- M. G. Benz and D. L. Martin, Cobalt–Mischmetal–Samarium Permanent Magnet Alloys: Process and Properties, J. Appl. Phys., 1971, 42, 2786, DOI:10.1063/1.1660626.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA + U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505, DOI:10.1103/PhysRevB.57.1505.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865, DOI:10.1103/PhysRevLett.77.3865; J. P. Perdew, K. Burke and M. Ernzerhof, Erratum: Generalized gradient approximation made simple, Phys. Rev. Lett., 1997, 78, 1396, DOI:10.1103/PhysRevLett.78.1396.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758, DOI:10.1103/PhysRevB.59.1758.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169, DOI:10.1103/PhysRevB.54.11169.
- D. van der Marel and G. A. Sawatzky, Electron-electron interaction and localization in d and f transition metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 10674, DOI:10.1103/PhysRevB.37.10674.
- K. Okhotnikov, T. Charpentier and S. Cadars, Supercell program: a combinatorial structure-generation approach for the local-level modeling of atomic substitutions and partial occupancies in crystals, J. Cheminf., 2016, 8, 17, DOI:10.1186/s13321-016-0129-3.
- K. Momma and F. Izumi, VESTA3 for three–dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44(6), 1272–1276, DOI:10.1107/S0021889811038970.
- A. M. Ganose, A. J. Jackson and D. O. Scanlon, Sumo: Command-line tools for plotting and analysis of periodic ab initio calculations, J. Open Source Software, 2018, 3(28), 717, DOI:10.21105/joss.00717.
- M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, R. Jozefowicz, Y. Jia, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, M. Schuster, R. Monga, S. Moore, D. Murray, C. Olah, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, TensorFlow: Large-scale machine learning on heterogeneous systems, 2015. Software available from tensorflow.org Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 2(85), 2825–2830 Search PubMed , https://dl.acm.org/doi/10.5555/1953048.2078195.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319, DOI:10.1016/j.commatsci.2012.10.028.
- D. Liu, F. Niu, X. Zhang, Y. Meng and Y. Yang, Fabrication of SmCo5 alloy via cobalt-induced calciothermic reduction and magnetic properties of its ribbon, J. Rare Earths, 2021, 39(5), 572–578, DOI:10.1016/j.jre.2020.06.009.
- M. S. S. Brooks, O. Eriksson, J. M. Wills and B. Johansson, Density Functional Theory of Crystal Field Quasiparticle Excitations and the Ab Initio Calculation of Spin Hamiltonian Parameters, Phys. Rev. Lett., 1997, 79(13), 2546, DOI:10.1103/PhysRevLett.79.2546.
- The VASP Manual, Available PAW potentials, https://www.vasp.at/wiki/index.php/Available_PAW_potentials (Accessed: 29/12/2021).
- E. Olsson, X. Aparicio-Anglès and N. H. de Leeuw, A DFT + U study of the structural, electronic, magnetic, and mechanical properties of cubic and orthorhombic SmCoO3, J. Chem. Phys., 2016, 145(22), 224704, DOI:10.1063/1.4971186.
- I. L. M. Locht, Y. O. Kvashnin, D. C. M. Rodrigues, M. Pereiro, A. Bergman, L. Bergqvist, A. I. Lichtenstein, M. I. Katsnelson, A. Delin, A. B. Klautau, B. Johansson, I. Di Marco and O. Eriksson, Standard model of the rare earths analyzed from the Hubbard I approximation, Phys. Rev. B, 2016, 94(8), 085137, DOI:10.1103/PhysRevB.94.085137.
- P. Söderlind, P. E. A. Turchi, A. Landa and V. Lordi, Ground-state properties of rare-earth metals: an evaluation of density-functional theory, J. Phys.: Condens. Matter, 2014, 26, 416001, DOI:10.1088/0953-8984/26/41/416001.
- P. Söderlind, A. Landa, I. L. M. Locht, D. Åberg, Y. Kvashnin, M. Pereiro, M. Däne, P. E. A. Turchi, V. P. Antropov and O. Eriksson, Prediction of the new efficient permanent magnet SmCoNiFe3, Phys. Rev. B, 2017, 96(10), 100404(R), DOI:10.1103/PhysRevB.96.100404.
- O. Grånäs, I. Di Marco, P. Thunström, L. Nordström, O. Eriksson, T. Björkman and J. M. Wills, Charge self-consistent dynamical mean-field theory based on the full-potential linear muffin-tin orbital method: Methodology and applications, Comput. Mater. Sci., 2012, 55, 295–302, DOI:10.1016/j.commatsci.2011.11.032.
- I. A. Campbell, Indirect exchange for rare earths in metals, J. Phys. F: Met. Phys., 1972, 2, L47–L50, DOI:10.1088/0305-4608/2/3/004.
- J. R. Cuthill, A. J. McAlister and N. E. Erickson, X-Ray photoemission studies of rare earth hard magnets, AIP Conf. Proc., 1974, 18, 1039, DOI:10.1063/1.2947195.
- Z. Tie-song, J. Han-min, G. Guang-hua, H. Xiu-feng and C. Hong, Magnetic properties of R ions in RCo5 compounds (R=Pr, Nd, Sm, Gd, Tb, Dy, Ho, and Er), Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 8593, DOI:10.1103/PhysRevB.43.8593.
- M. D. Coey, Magnetism and magnetic materials, Cambridge University Press, 2010 Search PubMed.
- A. Landa, P. Söderlind, D. Parker, D. Åberg, V. Lordi, A. Perron, P. E. A. Turchi, R. K. Chouhan, D. Paudyal and T. A. Lograsso, Thermodynamics of SmCo5 compound doped with Fe and Ni: An ab initio study, J. Alloys Compd., 2018, 765, 659–663, DOI:10.1016/j.jallcom.2018.06.264.
- W. E. Wallace, Electronic structure of alloys and intermetallic compounds, Progress in the Science and Technology of the Rare Earths, 1968, vol. 3, pp. 1–37 Search PubMed.
- J. J. Becker, Rare–Earth–Compound Permanent Magnets, J. Appl. Phys., 1970, 41(3), 1055, DOI:10.1063/1.1658811.
- M. S. S. Brooks, O. Eriksson and B. Johansson, 3d–5d band magnetism in rare earth transition metal intermetallics: LuFe2, J. Phys.: Condens. Matter, 1989, 1, 5861, DOI:10.1088/0953-8984/1/34/004.
- R. L. Streever, Individual Co site contributions to the magnetic anisotropy of RCo5 compounds and related structures, Phys. Rev. B: Condens. Matter Mater. Phys., 1979, 19(5), 2704, DOI:10.1103/PhysRevB.19.2704.
- W. Cheng, S. Zhao, X. Cheng and X. Miao, Magnetic moments in SmCo5 and SmCo5−xCux films, J. Supercond. Novel Magn., 2012, 25, 1947–1950, DOI:10.1007/s10948-012-1530-4.
- J. C. Téllez-Blanco, R. Grössinger and R. Sato-Turtelli, Structure and magnetic properties of SmCo5−xCux alloys, J. Alloys Compd., 1988, 281(1), 1–5, DOI:10.1016/S0925-8388(98)00760-9.
- P. Villars and L. D. Calvert, Pearson's handbook of crystallographic data for intermetallic phases, American Society for Metals, Metals Park, Ohio, 1986, vol. 1–3, p. 3258. DOI:10.1002/crat.2170221117.
- O. Moze, L. Pareti, A. Paoluzi and K. H. J. Buschow, Magnetic structure and anisotropy of Ga- and Al-substituted LaCo5 and YCo5 intermetallics, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(17), 11550, DOI:10.1103/PhysRevB.53.11550.
- D. Gignoux, F. Givord, R. Lemaire, H. Launois and F. Sayetat, Valence state of cerium in the hexagonal CeM5 compounds with the transition metals, J. Phys., 1982, 43(1), 173–180, DOI:10.1051/jphys:01982004301017300.
- D. Givord, J. Laforest, R. Lemaire and Q. Lu, Cobalt magnetism in RCo5-intermetallics: Onset of 3d magnetism and magnetocrystalline anisotropy (r=rare earth or Th), J. Magn. Magn. Mater., 1983, 31–34, 1191–1196, DOI:10.1016/0304-8853(83)90212-3.
- R. C. O'Handley, Modern Magnetic Materials: Principles and Applications, Wiley, New York, 1st edn, 1999 Search PubMed.
- D. Givord, Temperature dependence of the samarium magnetic form factor in SmCo5, J. Appl. Phys., 1979, 50, 2008, DOI:10.1063/1.327141.
- T. Ito and H. Ido, Electronic structures and magnetic properties of LaCo5, LaNi5, and LaCo3Ni2, J. Appl. Phys., 2005, 97(10), 10A313, DOI:10.1063/1.1854280.
- M. I. Bartashevich, T. Goto, M. Yamaguchi and I. Yamamoto, Effect of hydrogen on the magnetocrystalline anisotropy of RCo5, J. Magn. Magn. Mater., 1995, 140–144(2), 855–856, DOI:10.1016/0304-8853(94)00790-X.
- H. Yoshie, K. Ogino, H. Nagai, A. Tsujimura and Y. Nakamura, Nuclear Magnetic Resonance of RCo5. III. R=Ce and Sm, J. Phys. Soc. Jpn., 1988, 57(7), 2525–2528, DOI:10.1143/JPSJ.57.2525.
- A. Heidemann, D. Richter and K. H. J. Buschow, Investigation of the hyperfine fields in the compounds LaCo13, LaCo5, YCo5 and ThCo5 by means of inelastic neutron scattering, Z. Phys. B: Condens. Matter, 1975, 22(4), 367–372, DOI:10.1007/BF01312807.
- W.-L. Zuo, J. Mohapatra, J. P. Liu, T.-Y. Zhao, F.-X. Hu, J.-R. Sun, Y.-F. Li, X.-F. Zhang and B.-G. Shen, Cerium-based RCo5 (R = Ce, La0.35Ce0.65, and misch-metal) type nanocrystalline hard magnetic materials with high coercivity, APL Mater., 2019, 7(9), 091108, DOI:10.1063/1.5104295.
- P. Tozman, M. Venkatesan and J. M. D. Coey, Development of hysteresis in ball-milled LaCo5−xFex and La2Co7−xFex, IEEE Trans. Magn., 2014, 50, 11, DOI:10.1109/TMAG.2014.2316914.
- K. J. Strnat and R. M. W. Strnat, Rare earth-cobalt permanent magnets, J. Magn. Magn. Mater., 1991, 100(1–3), 38–56, DOI:10.1016/0304-8853(91)90811-N.
- J. J. Möller, W. Körner, G. Krugel, D. F. Urban and C. Elsässer, Compositional optimization of hard-magnetic phases with machine-learning models, Acta Mater., 2018, 153, 53–61, DOI:10.1016/j.actamat.2018.03.051.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2nr00364c |
| This journal is © The Royal Society of Chemistry 2022 |